
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
EDITORIAL article
Front. Psychiatry , 14 September 2023
Sec. Neuroimaging
Volume 14 - 2023 | https://doi.org/10.3389/fpsyt.2023.1284670
This article is part of the Research Topic Advances in Brain Dynamics in the Healthy and Psychiatric Disorders View all 6 articles
 David Papo1,2*
David Papo1,2* Maide Bucolo3
Maide Bucolo3 Stavros I. Dimitriadis4
Stavros I. Dimitriadis4 Julie A. Onton5
Julie A. Onton5 Athineos Philippu6
Athineos Philippu6 David Shannahoff-Khalsa7,8,9
David Shannahoff-Khalsa7,8,9Editorial on the Research Topic
Advances in brain dynamics in the healthy and psychiatric disorders
Psychiatry aims at diagnosing and treating psychological disorders and other mental health conditions affecting how subjects behave, think, or feel. Psychiatrists resort to a variety of diagnostic techniques, ranging from standard semiotics to physiological testing, and imaging or stimulation techniques, and treatment strategies may be behavioral, pharmacological, or instrumental. However, knowledge of how neural activity translates into behavior is often insufficient to define precise nosological categories and to interact with the brain in a language it can understand. Improvements in both modeling and treatment require a better understanding of the underlying neural processes and finding new meaningful variables to characterize both healthy brain activity and its pathology.
The brain is, in general, thought of as a spatially-extended dynamical system subject to some control parameter. This framework allows not only describing and to some extent predicting healthy (1) and pathological (2–4) brain activity and treatment outcomes (5), but also maintaining activity within or steering it toward desirable dynamical regimes (6). The challenge is specifying the dynamics and identifying its control parameters and the appropriate strategies allowing to effectively act on the system (6).
Dynamical systems can be studied in three main ways: perturbing the system, observing its unperturbed dynamics, and characterizing its symmetries. Prima facie, the most sensible strategy to quantify the neural correlates of psychiatric disorders would seem to require observing task-related brain activity and behavior. However, finding appropriate tasks, capable of testing individuals with tasks they can perform (7) is not always easy, particularly when testing dynamically complex brain functions (8). Moreover, this strategy is necessarily associated with lengthy (possibly anxiogenic) testing sessions, whose neural correlates may be hard to gauge, and whose time and economic costs can also be sizeable.
An alternative strategy involves extracting meaningful properties from spontaneous brain activity. Spontaneous activity can be thought of as a data bank of cortical fluctuation patterns (9) with complex spatio-temporal structure (10), displaying similar non-trivial properties across a wide range of scales (11, 12). These properties are replicated in behavioral fluctuations (13), suggesting that behavior is in essence a coarse-grained version of neural fluctuations. Importantly, these properties are altered in various brain pathologies (14, 15) and can be modulated by pharmacological manipulations (16). These fluctuations are intrinsically multiscale with complex relations among scales (17, 18), so that characterizing the temporal scales of cognitive processes is in general non-trivial (19, 20).
These fluctuations can be thought of as the statistical and dynamical signatures of underlying non-linear dynamical processes in terms of which the system can be described, and the behavioral or neural variables capable of modulating them as control parameters for the dynamics (10).
Dynamics and thermodynamics and, more specifically, non-linearity and non-equilibrium properties constitute two sides of the same coin. This can be appreciated by considering symmetries and their break down. For instance, the breakdown of time-reversal symmetry, a measure of the extent to which it is possible to discern a preferred time direction of a stationary stochastic process (21), which is associated with the presence of strong non-linearities (22), constitutes the hallmark of systems operating away from equilibrium (23). These systems use part of their free energy budget to perform work or store energy in alternative forms, dissipating the rest as heat in the environment. The second law of thermodynamics prescribes that this transformation should be associated with an irreversible increase in entropy of the environment. The higher the price in entropy lost to dissipation, the more conspicuous the irreversibility. Thus, time-reversal symmetry can be used not only as an indicator of whether a system is at equilibrium or not (24, 25), but also as a quantifier of its distance from such a condition (26). Importantly, irreversibility can be quantified from experimental data (27). Not surprisingly, the marked irreversibility of healthy spontaneous brain activity (22, 28, 29) shows specific alterations in various conditions (28–31), including Alzheimer's disease (28), ADHD (29), bipolar disorder (29), and schizophrenia (28, 29).
Dissipation is also proportional to the violation of fluctuation-dissipation relations (FDRs) (32), expressing fundamental symmetries of equilibrium systems (33). In such systems, the autocorrelation of some observable's fluctuations in the unperturbed system is related through temperature to the response to small external perturbations. Brain fluctuations are profoundly different from the Gaussian ones with exponentially vanishing memory of equilibrium systems (34–37), and this relationship must be expressed differently, e.g., close to equilibrium, in terms of an effective temperature (38).
Mirroring dynamics' multiscaleness, irreversibility and FDRs' violations may manifest differently at different spatial and temporal scales (39–41). Accordingly, brain activity and its pathology can be described in terms of the characteristic scales of such properties (10, 28, 42).
Insofar as the brain ultimately manipulates information, one may want to quantify brain activity in terms of information processing, erasure, and transfer. A deep relation exists between information and thermodynamics of a physical system (43, 44). In particular, the Landauer principle states that information erasure is a dissipative process (45), Likewise, effective information use is related to thermodynamic efficiency. This is because neural systems compute implicit models of the environment through their dynamics. However, a fraction of retained information does not improve the system's predictive power and is equivalent to thermodynamic inefficiency (46) (see Figure 1).
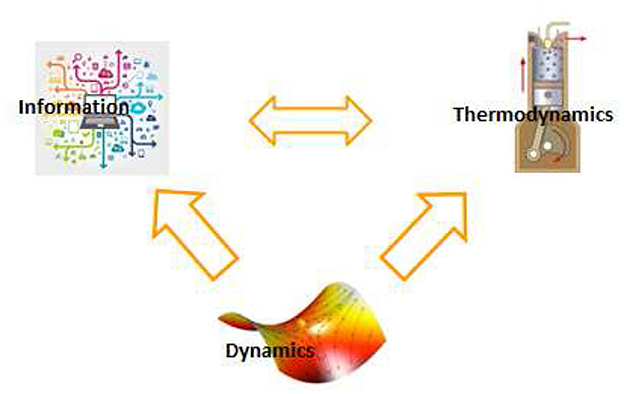
Figure 1. Brain activity in healthy and pathological states are traditionally described by extracting functionally relevant features of its dynamics. Complementary descriptions can be found by using the relationships between dynamics, thermodynamics, and information. Ultimately, brain activity and its pathologies can be characterized in terms of physically meaningful dynamical, thermodynamical and information theoretic variables (10).
This Research Topic presents five contributions dealing with various aspects of psychiatric pathology, particularly of obsessive-compulsive disorder (OCD), but also unipolar depression, ranging from general characterization to symptom provocation, to treatment evaluation, and using various techniques (NIRS, MEG, TMS, but also behavioral techniques). Liu et al. found an association between OCD and brain aging acceleration. Bernardi et al. highlighted differences in the temporal scales of MEG activity's irreversibility in OCD with respect to healthy controls. Maia et al. propose a tutorial for TMS-guided symptom provocation in OCD. Stephenson et al. show the feasibility of an electronically delivered cognitive behavioral therapy program associated with functional neuroimaging evaluation. Finally, Yang et al. used NIRS to highlight topographically specific activations in first-episode vs. recurrent depression patients.
DP: Conceptualization, Writing—original draft. MB: Writing—review and editing. SD: Writing—review and editing. JO: Writing—review and editing. AP: Writing—review and editing. DS-K: Writing—review and editing.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Kelso JAS. Dynamic Patterns: The Self-Organization of Brain and Behavior. New York, NY: MIT press. (1995).
2. Mackey MC, Glass L. Oscillation and chaos in physiological control systems. Science. (1977) 197:287–9. doi: 10.1126/science.267326
3. Glass L, Mackey MC. Pathological conditions resulting from instabilities in physiological control systems. Ann N Y Acad Sci. (1979) 316:214–35. doi: 10.1111/j.1749-6632.1979.tb29471.x
4. Glass L. Dynamical disease: challenges for nonlinear dynamics and medicine. Chaos. (2015) 25:097603. doi: 10.1063/1.4915529
5. Pezard L, Martinerie J, Varela FJ, Bouchet F, Guez D, Derouesné C, et al. Entropy maps characterize drug effects on brain dynamics in Alzheimer's disease. Neurosci Lett. (1998) 253:5–8. doi: 10.1016/S0304-3940(98)00603-X
6. Papo, D. Neurofeedback: principles, appraisal and outstanding issues. Eur. J. Neurosci. (2019) 49:1454–1469. doi: 10.1111/ejn.14312
7. Price C, Friston KJ. Scanning patients with tasks they can perform. Hum Brain Mapp. (1999) 8:102–8. doi: 10.1002/(SICI)1097-0193(1999)8:2/3<102::AID-HBM6>3.0.CO;2-J
8. Papo D. Attaining the recesses of the functional space. Cogn Neurodyn. (2022) 16:767–78. doi: 10.1007/s11571-021-09755-1
9. Arieli A, Sterkin A, Grinvald A, Aertsen A. Dynamics of ongoing activity: explanation of the large variability in evoked cortical responses. Science. (1996) 273:1868–71. doi: 10.1126/science.273.5283.1868
10. Papo D. Functional significance of complex fluctuations in brain activity: From resting state to cognitive neuroscience. Fron Syst Neurosci. (2014) 8:112. doi: 10.3389/fnsys.2014.00112
11. Novikov E, Novikov A, Shannahoff-Khalsa D, Schwartz B, Wright J. Scale-similar activity in the brain. Phys Rev E. (1997) 56:R2387–9. doi: 10.1103/PhysRevE.56.R2387
12. Linkenkaer-Hansen K, Nikouline VV, Palva JM, Ilmoniemi RJ. Long-range temporal correlations and scaling behavior in human brain oscillations. J Neurosci. (2001) 21:1370–7. doi: 10.1523/JNEUROSCI.21-04-01370.2001
13. Palva JM, Zhigalov A, Hirvonen J, Korhonen O, Linkenkaer-Hansen K, Palva S, et al. Neuronal long-range temporal correlations and avalanche dynamics are correlated with behavioral scaling laws. Proc Natl Acad Sci USA. (2013) 110:3585–90. doi: 10.1073/pnas.1216855110
14. Linkenkaer-Hansen K, Monto S, Rytsälä H, Suominen K, Isometsä E, Kähkönen S, et al. Breakdown of long-range temporal correlations in theta oscillations in patients with major depressive disorder. J Neurosci. (2005) 25:10131–7. doi: 10.1523/JNEUROSCI.3244-05.2005
15. Montez T, Poil SS, Jones BF, Manshanden I, Verbunt JP, van Dijk BW, et al. Altered temporal correlations in parietal alpha and prefrontal theta oscillations in early-stage Alzheimer disease. Proc Natl Acad Sci USA. (2009) 106:1614–9. doi: 10.1073/pnas.0811699106
16. Suckling J, Wink AM, Bernard FA, Barnes A, Bullmore E. Endogenous multifractal brain dynamics are modulated by age, cholinergic blockade and cognitive performance. J Neurosci Methods. (2009) 174:292–300. doi: 10.1016/j.jneumeth.2008.06.037
17. Hasson U, Yang E, Vallines I, Heeger DJ, Rubin NA. hierarchy of temporal receptive windows in human cortex. J Neurosci. (2008) 28:2539–50. doi: 10.1523/JNEUROSCI.5487-07.2008
18. Chaudhuri R, Bernacchia A, Wang XJA. diversity of localized timescales in network activity. Elife. (2014) 3:e01239. doi: 10.7554/eLife.01239
19. Papo D. Time scales in cognitive neuroscience. Front Physiol. (2013) 4:86. doi: 10.3389/fphys.2013.00086
20. Papo D. How can we study reasoning in the brain? Front. Hum Neurosci. (2015) 9:222. doi: 10.3389/fnhum.2015.00222
21. Pomeau Y. Symétrie des fluctuations dans le renversement du temps. J Phys. (1982) 43:859–67. doi: 10.1051/jphys:01982004306085900
22. Paluš M. Nonlinearity in normal human EEG: cycles, temporal asymmetry, nonstationarity and randomness, not chaos. Biol Cybern. (1996) 75:389–96. doi: 10.1007/s004220050304
23. Gnesotto FS, Mura F, Gladrow J, Broedersz CP. Broken detailed balance and non-equilibrium dynamics in living systems: a review. Rep Prog Phys. (2018) 81:066601. doi: 10.1088/1361-6633/aab3ed
24. Andrieux D, Gaspard P, Ciliberto S, Garnier N, Joubaud S, Petrosyan A, et al. Entropy production and time asymmetry in nonequilibrium fluctuations. Phys Rev Lett. (2007) 98:150601. doi: 10.1103/PhysRevLett.98.150601
25. Parrondo JM, Van den Broeck C, Kawai R. Entropy production and the arrow of time. New J Phys. (2009) 11:073008. doi: 10.1088/1367-2630/11/7/073008
26. Fodor É, Nardini C, Cates ME, Tailleur J, Visco P, van Wijland F, et al. How far from equilibrium is active matter? Phys. Rev Lett. (2016) 117:038103. doi: 10.1103/PhysRevLett.117.038103
27. Zanin M, Papo D. Algorithmic approaches for assessing irreversibility in time series: review and comparison. Entropy. (2021) 23:1474. doi: 10.3390/e23111474
28. Zanin M, Güntekin B, Aktürk T, Hanoglu L, Papo D. Time irreversibility of resting-state activity in the healthy brain and pathology. Front Physiol. (2020) 10:1619. doi: 10.3389/fphys.2019.01619
29. Deco G, Perl YS, Sitt JD, Tagliazucchi E, Kringelbach ML. Deep learning the arrow of time in brain activity: characterising brain-environment behavioural interactions in health and disease. bioRxiv. (2021) 5:899. doi: 10.1101/2021.07.02.450899
30. Schindler K, Rummel C, Andrzejak RG, Goodfellow M, Zubler F, Abela E, et al. Ictal time-irreversible intracranial EEG signals as markers of the epileptogenic zone. Clin Neurophysiol. (2016) 127:3051–8. doi: 10.1016/j.clinph.2016.07.001
31. Martínez H, Herrera-Diestra, JL, Chavez M Detection of time reversibility in time series by ordinal patterns analysis. Chaos. (2018) 28:123111. doi: 10.1063/1.5055855
32. Harada T, Sasa SI. Equality connecting energy dissipation with a violation of the fluctuation-response relation. Phys Rev Lett. (2005) 95:130602. doi: 10.1103/PhysRevLett.95.130602
33. Kubo R. The fluctuation-dissipation theorem. Rep Progr Phys. (1966) 29:255–84. doi: 10.1088/0034-4885/29/1/306
34. Papo D. Why should cognitive neuroscientists study the brain's resting state? Front. Hum Neurosci. (2013) 7:45. doi: 10.3389/fnhum.2013.00045
35. Sarracino A, Arviv O, Shriki O, Arcangelis L. Predicting brain evoked response to external stimuli from temporal correlations of spontaneous activity. Phys Rev Res. (2020) 2:033355. doi: 10.1103/PhysRevResearch.2.033355
36. Lindner, B. Fluctuation-dissipation relations for spiking neurons. Phys Rev Lett. (2022) 549:101. doi: 10.1103/PhysRevLett.129.198101
37. Nandi MK, Candia D, Sarracino A, Herrmann AJ, de Arcangelis, L Fluctuation-dissipation relations in the imbalanced Wilson-Cowan model. Phys Review E. (2023) 107:064307. doi: 10.1103/PhysRevE.107.064307
38. Puglisi A, Sarracino A, Vulpiani A. Temperature in and out of equilibrium: a review of concepts tools and attempts. Phys Rep. (2017) 710:1–60. doi: 10.1016/j.physrep.2017.09.001
39. Egolf DA. Equilibrium regained: from nonequilibrium chaos to statistical mechanics. Science. (2000) 287:101–4. doi: 10.1126/science.287.5450.101
40. Battle C, Broedersz CP, Fakhri N, Geyer VF, Howard J, Schmidt CF, et al. Broken detailed balance at mesoscopic scales in active biological systems. Science. (2016) 352:604–7. doi: 10.1126/science.aac8167
41. Tan TH, Watson GA, Chao YC, Li J, Gingrich TR, Horowitz JM, et al. Scale-dependent irreversibility in living matter. arXiv [Preprint]. (2021). arXiv:2107.05701. doi: 10.48550/arXiv.2107.05701
42. Papo D. Measuring brain temperature without a thermometer. Fron Physiol. (2014) 5:124. doi: 10.3389/fphys.2014.00124
43. Sekimoto K. Langevin equation and thermodynamics. Prog Theor Phys Supplement. (1998) 130:17–27. doi: 10.1143/PTPS.130.17
44. Parrondo JM, Horowitz JM, Sagawa T. Thermodynamics of information. Nat Phys. (2015) 11:131–9. doi: 10.1038/nphys3230
45. Landauer R. Irreversibility and heat generation in the computing process. IBM J Res Dev. (1961) 5:183–91. doi: 10.1147/rd.53.0183
Keywords: brain dynamics, brain thermodynamics, time-reversal symmetry, fluctuation-dissippation relations, brain fluctuations, dynamical disease
Citation: Papo D, Bucolo M, Dimitriadis SI, Onton JA, Philippu A and Shannahoff-Khalsa D (2023) Editorial: Advances in brain dynamics in the healthy and psychiatric disorders. Front. Psychiatry 14:1284670. doi: 10.3389/fpsyt.2023.1284670
Received: 28 August 2023; Accepted: 31 August 2023;
Published: 14 September 2023.
Edited and reviewed by: Stefan Borgwardt, University of Lübeck, Germany
Copyright © 2023 Papo, Bucolo, Dimitriadis, Onton, Philippu and Shannahoff-Khalsa. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David Papo, cGFwb2RhdkBnbWFpbC5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.