Key role played by mesophyll conductance in limiting carbon assimilation and transpiration of potato under soil water stress

Introduction: The identification of the physiological processes limiting carbon assimilation under water stress is crucial for improving model predictions and selecting drought-tolerant varieties. However, the influence of soil water availability on photosynthesis-limiting processes is still not fully understood. This study aimed to investigate the origins of photosynthesis limitations on potato (Solanum tuberosum) during a field drought experiment.

Methods: Gas exchange and chlorophyll fluorescence measurements were performed at the leaf level to determine the response of photosynthesis-limiting factors to the decrease in the relative extractable water (REW) in the soil.

Results: Drought induced a two-stage response with first a restriction of CO₂ diffusion to chloroplasts induced by stomatal closure and a decrease in mesophyll conductance, followed by a decrease in photosynthetic capacities under severe soil water restrictions. Limitation analysis equations were revisited and showed that mesophyll conductance was the most important constraint on carbon and water exchanges regardless of soil water conditions.

Discussion: We provide a calibration of the response of stomatal and non-stomatal factors to REW to improve the representation of drought effects in models. These results emphasize the need to revisit the partitioning methods to unravel the physiological controls on photosynthesis and stomatal conductance under water stress.

1 Introduction

European ecosystems are facing more intense and frequent water stress events due to altered rainfall patterns and rising temperatures induced by anthropogenic climate change (Samaniego et al., 2018). Precipitation shortage episodes perturbate plant water status and induce disruptions of the water and carbon cycles through the inhibition of carbon assimilation and transpiration (Bertolino et al., 2019; Fahad et al., 2017; Trenberth et al., 2014). As a result, ecosystem services such as food production and carbon storage are strongly impacted by the lack of soil water (Chang and Bonnette, 2016; Hendrawan et al., 2022; Kang et al., 2021). Land–atmosphere feedbacks originating from the perturbation of such processes may exacerbate climate change through water stress intensification (Anderegg et al., 2019; Hartick et al., 2022). An in-depth understanding of the effects of drought on plant physiology is required to predict future ecosystem service capacities and to improve climate model predictions (Ryu et al., 2019).

Photosynthesis is the process by which plants convert CO₂ into carbohydrates. Carbon assimilation is mediated by the physiological barriers on the CO₂ diffusion pathway (i.e., stomatal opening and diffusion within the mesophyll; Gago et al., 2020; Nadal and Flexas, 2018) and by the Rubisco efficiency for fixing CO₂ in the Calvin cycle (Farquhar et al., 1980). Uncertainties remain on the importance of each limiting factor under soil water-limiting conditions (Rogers et al., 2017).

Quantifying the importance of photosynthesis-limiting factors under drought is also pivotal for assessing phenotype plasticity and selecting drought-tolerant plant species (Lupo and Moshelion, 2024; Nguyen et al., 2023). To that end, mechanistic modeling can be used to disentangle the complexity of the mechanisms regulating plant response to water stress (Stirbet et al., 2020). In the Farquhar–von Caemmerer–Berry (FvCB) model (Farquhar et al., 1980), carbon assimilation under high irradiance ($A_{sat}$) is constrained by stomatal conductance (${ɡ}_s$), mesophyll conductance (${ɡ}_m$), and the maximum carboxylation rate of Rubisco ($V_{cmax}$). The quantitative contribution of each of these factors in limiting photosynthesis under water stress can be estimated by, first, writing the total derivative of $A_{sat}$ as a sum of the total derivative of these factors and, second, by estimating the response of these factors to soil water availability. This method, also known as limitation analysis (Grassi and Magnani, 2005; Jones, 1985), can be used to partition photosynthesis limitations between stomatal (i.e., a decrease in $A_{sat}$ originating from ${ɡ}_s$) and non-stomatal factors (i.e., a decrease in $A_{sat}$ originating from ${ɡ}_m$ and/or $V_{cmax}$).

Stomata are the gates of CO₂ diffusion and water transpiration at the leaf surface. Stomatal opening is regulated by a complex interplay of abiotic and biotic factors. For instance, it is well known that an increase in vapor pressure deficit (VPD) drives the closure of stomata through the evaporation of water in the guard cells (McAdam and Brodribb, 2016). In addition, carbon assimilation regulates stomatal opening to balance the CO₂ diffusion with the efficiency of the Calvin cycle (Wong et al., 1979). A mechanistic formulation of these relationships was proposed by Cowan and Farquhar (1977), who hypothesized that stomatal opening is regulated to maximize carbon gains and minimize water losses over a constant time interval. This optimization theory is at the basis of the unified stomatal optimality (USO) model where ${ɡ}_s$ is expressed as a function of VPD, CO₂ concentration at the leaf surface, carbon assimilation, and the stomatal sensitivity to photosynthesis (${ɡ}_1$) (Medlyn et al., 2011). This last, which is the slope of the USO model (${ɡ}_1$), is linked to the water use strategy of the plant by being inversely proportional to the marginal carbon cost of water (Medlyn et al., 2011). During drying-up episodes, short timescale variations of ${ɡ}_1$ can be used as an indicator of plants’ adaptation strategy. In the framework of the optimality theory, plants can maximize carbon gains (increase in ${ɡ}_1$), minimize water losses (decrease in ${ɡ}_1$), or keep the same balance between carbon gains and water losses (constant ${ɡ}_1$). The response of ${ɡ}_1$ to soil water availability is likely species or plant functional type (PFT)-specific (Beauclaire et al., 2023; Gourlez de la Motte et al., 2020; Héroult et al., 2013; Zhou et al., 2013). Although the formulation of the relationship between ${ɡ}_s$ and $A_{sat}$, and the water cost associated with the opening of stomata are still active research topics in the scientific community (Lamour et al., 2022; Mrad et al., 2019), the USO model has become a reference for representing stomatal behavior in land surface models (LSMs) (Kala et al., 2015; Lawrence et al., 2019; Sabot et al., 2022).

As ${ɡ}_s$ is mediated by carbon assimilation, a decrease in ${ɡ}_s$ can also be induced by biochemical or mesophyll limitations, which regulate stomatal opening with the mesophyll demand for CO₂ (Lemonnier and Lawson, 2023; Medlyn et al., 2011; Zhou et al., 2013). As a result, ${ɡ}_s$ and $A_{sat}$ are strongly coupled, and stomatal closure can originate either from an optimal stomatal adaptation or from a disguised effect of mesophyll conductance and/or carboxylation rate of Rubisco (Medlyn et al., 2011; Zhou et al., 2013). This feedback effect complicates the identification of the origins of stomatal closure and photosynthesis limitations under water stress. Using ${ɡ}_1$ as evidence of optimal stomatal control on photosynthesis theoretically allows to identify the feedback effect of non-stomatal factors on stomatal closure by linking photosynthesis limitations to the stomatal optimality theory (Zhou et al., 2013). As a result, coupling the USO and FvCB models in the limitation analysis would enable a quantitative assessment of the effects of ${ɡ}_1$, VPD, ${ɡ}_m$, and $V_{cmax}$ on ${ɡ}_s$ and $A_{sat}$. To our knowledge, this study is the first to develop this approach. The limitations of photosynthesis originating from stomatal closure induced by a decrease in ${ɡ}_1$ or ${ɡ}_s$ are further referred to as a stomatal origin limitation (SOL), while an effect of ${ɡ}_m$ and/or $V_{cmax}$ is referred to as a non-stomatal origin limitation (NSOL) (Beauclaire et al., 2023; Gourlez de la Motte et al., 2020).

Soil water content (SWC) is a key eco-hydrological variable impacting plant metabolism and more globally carbon and water fluxes (Zhou et al., 2021). In particular, lack of soil water triggers complex mechanisms which regulate the water flow in the plant to avoid hydraulic failure (Martínez-Vilalta et al., 2014). When soil edaphic proprieties are known, SWC can be used to determine the relative extractable water (REW) for plant uptake (Granier et al., 2007), which is often used in LSMs as a drought index to implement water stress effects on photosynthesis originating from either SOL or NSOL (Vidale et al., 2021). The response of FvCB and USO model parameters to decreasing soil water availability strongly differs across PFTs, which makes REW a critical variable for modeling the response of terrestrial ecosystems to drought (Peters et al., 2018; Rogers et al., 2017; Vidale et al., 2021; Zhou et al., 2013).

Potato is one of the most important crops, providing food for more than one billion people around the world (Lutaladio and Castaldi, 2009). In Europe, more than 400,000 hectares of arable land are used for potato cultivation (Goffart et al., 2022). This crop are highly sensitive to water stress because of its shallow root system and its inability to extract water from deeper soil layers (Obidiegwu, 2015). In particular, tuber bulking is a critical stage of potato growth, as it determines the yield and quality of the harvest (Gervais et al., 2021). Partitioning photosynthesis limitations is crucial for selecting drought-tolerant varieties and ensuring food security. We have implemented this approach during a drought experiment on field-grown potatoes. The goals of this study were i) to describe the response of $A_{sat}$, ${ɡ}_s$, ${ɡ}_m$, ${ɡ}_1$, and $V_{cmax}$ to the decrease in REW; ii) to perform a limitation analysis on $A_{sat}$ using ${ɡ}_s$ or ${ɡ}_1$, ${ɡ}_m$, $V_{cmax}$, and VPD as explanatory variables; and finally iii) to define REW thresholds from which each of these limitations occurred.

2 Material and methods

2.1 Plant materials and experimental setup

Potato plants were grown on a 4-ha experimental land located in Belgium, approximately 50 km southeast of Brussels (50°33′47.772″N, 4°42′46.403″E). This cropland is usually used for cultivating chicory, sugar beet, and winter wheat. In total, 88 tubers of potato (Solanum tuberosum, cv Agria) were planted under a plastic polytunnel greenhouse 12m long and 5m wide.

SWC and soil temperature were measured using time domain reflectometers (ML3 ThetaProbe, Delta-T Devices Ltd., Cambridge, UK) placed at depths of 10 cm and 30 cm. Air humidity and air temperature were measured using a resistive platinum thermometer and electrical capacitive hygrometer (HMP155, Vaisala Oyj, Helsinki, Finland) placed under the plastic tunnel at 1.5-m height. The tubers were planted on May 15, 2020, and the first leaves appeared on June 4, 2020, which were considered the emergence [i.e., day after emergence (DAE) of 0].

Soil water availability was quantified by calculating the REW of the first soil horizon, where most of the root water uptake of potato is expected to occur (Beauclaire et al., 2023):

$\begin{array}{ll}\begin{array}{c}REW=\{\frac{{\theta }_{H1} -{\theta }_{wp,H1} }{{\theta }_{fc,H1}-{\theta }_{wp,H1}}\end{array}& (1)\end{array}$

where ${\theta }_{wp,H1}$ = 15.6 and ${\theta }_{fc,H1}$ = 35.01 (cm³ cm⁻³) are respectively the wilting point and the field capacity of the first horizon (H₁: 0–30 cm) and ${\theta }_{H1}$ is the SWC measured in H₁, which was calculated as the weighted mean of SWC measurements at depths of 10 cm and 30 cm (with a weight of 2/3 and 1/3, respectively). ${\theta }_{wp,H1}$ and ${\theta }_{fc,H1}$ were estimated from soil water retention curves using the van Genuchten (VG) model (van Genuchten, 1980). Soil samples were collected before the experiment at a 15cm depth (three replicates) and were saturated for at least 24 h in distilled water. The pressure plate method (Richards, 1948—following the ISO 11274 standard) was applied, and the measurements of the suction head and SWC were recorded. ${\theta }_{wp,H1}$ and ${\theta }_{fc,H1}$ were estimated as the SWC at a pF (log of the suction head) of 4.2 and 2.0, respectively. VG model parameters and retention curves of the three soil samples are given in the Supplementary Material (Supplementary Figure S1).

Over a first period of 35 days, all the plants were hand-watered to ensure that ${\theta }_{H1}$ remained near field capacity. The drought treatment consisted in withholding irrigation to simulate a long-term precipitation deficit on half of the plants. The other half was hand-watered during the experiment. The drought treatment started on DAE 40 (corresponding to the beginning of the tuber bulking stage) and stopped on DAE 74 (corresponding to the appearance of the first signs of senescence on the irrigated plants). All plants experienced the same photosynthetic photon flux density (PPFD) in the photosynthetic active radiation (PAR), temperature, and VPD conditions under the plastic tunnel.

2.2 Leaf-level measurements

Gas exchange and chlorophyll fluorescence measurements were conducted during the tuber bulking stage at 14 different dates (between DAE 35 and DAE 74; Figure 1) from 10 a.m. to 4 p.m. Only the youngest leaves in the upper part of the plant were selected by randomly sampling irrigated and non-irrigated plants. Measurements were performed using a LI-COR LI-6400 equipped with a LI-6400-40 fluorescence chamber (LI-COR Inc., Lincoln, NE, USA). The following procedure was applied to each leaf sample. The CO₂ concentration in the chamber ($C_s$) was set to 400 μmol mol⁻¹, the PPFD in the PAR was set to 1,200 µmol m⁻² s⁻¹, and the air humidity and temperature were maintained at ambient levels. After stabilization of the steady-state fluorescence signal ($F_s$), a multiphase flash with a saturation light of 9,000 µmol m⁻² s⁻¹ was applied, and the maximum fluorescence intensity under the light ($F_m^{\text{'}})$ was measured. In addition, $A_{sat}$, leaf temperature, stomatal conductance to water vapor (${ɡ}_{sw}$), CO₂ concentration in sub-stomatal cavities ($C_i$), and the vapor pressure deficit at the leaf surface ($VP{D}_{leaf}$) were recorded. Stomatal conductance to CO₂ (${ɡ}_s$) was calculated by dividing ${ɡ}_{sw}$ by 1.6.

Figure 1

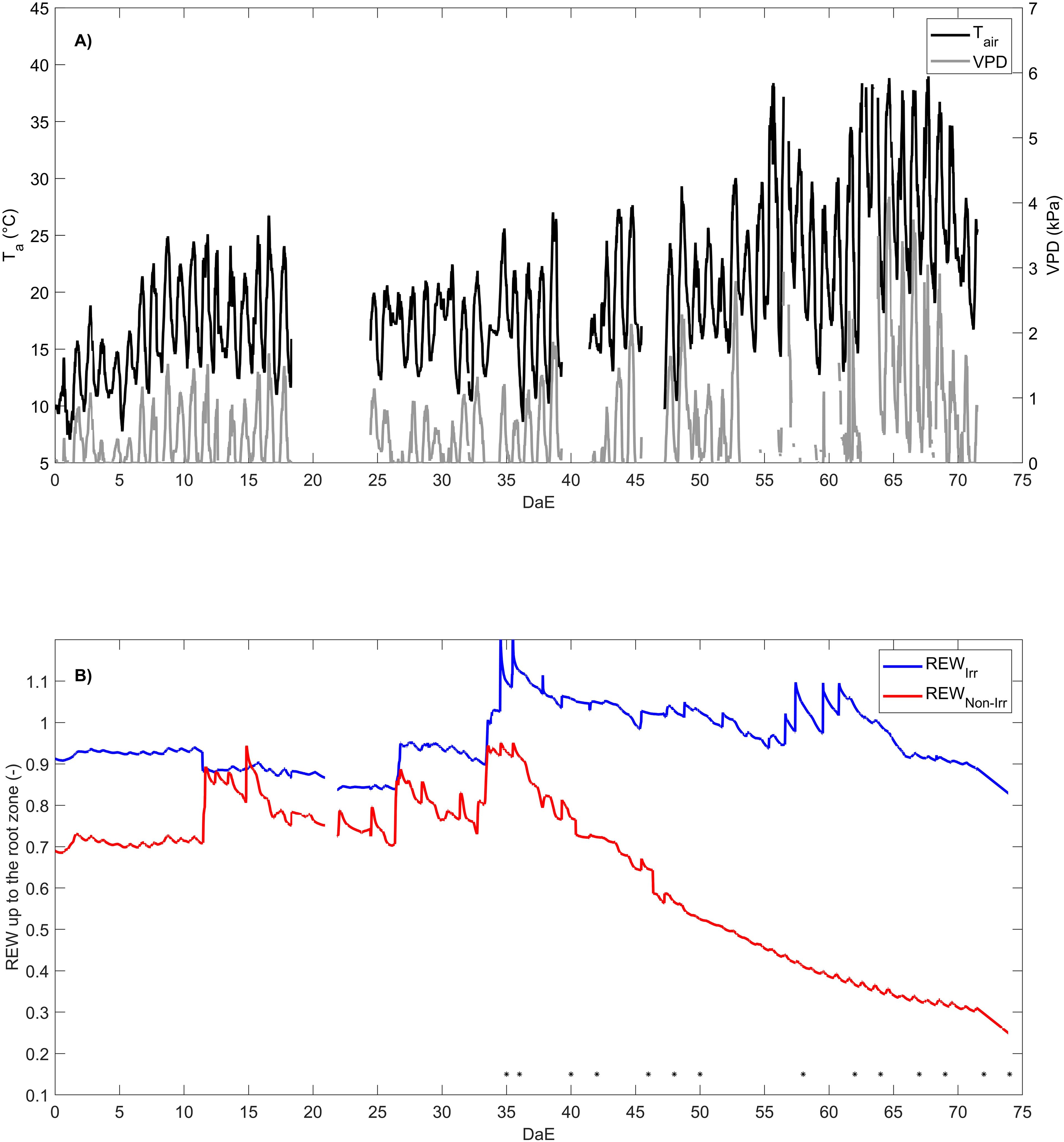
Figure 1. Temporal evolution of air temperature ($T_{\mathrm{air}}$) and air vapor pressure deficit (VPD) under the plastic polytunnel greenhouse (A) and relative extractable water (REW) of the irrigated plot ($RE{W}_{irr}$) and non-irrigated plot ($RE{W}_{non-irr}$) (B). The asterisk indicates the days when leaf-level measurements were conducted. DaE is day after emergence.

2.2.1 NSOL: $V_{cmax}$ and ${ɡ}_m$

$V_{cmax}$was determined using a single measurement of gas exchanges at light saturation (De Kauwe et al., 2016; Wilson et al., 2000):

$\begin{array}{ll}\begin{array}{c}{V}_{cmax}=A_{sat}\frac{C_c+K_m}{C_c-{\Gamma }^{*}}\end{array}& (2)\end{array}$

where $K_m$ is the Michaelis–Menten coefficient, ${\Gamma }^{*}$ the CO₂ compensation point, and $C_c$ the CO₂ concentration in the chloroplast. Equation 2 is based on a single measurement of CO₂ assimilation at light saturation instead of using CO₂-response curves, where $V_{cmax}$ retrieval is impacted by the sensitivity of the fitting method (Miao et al., 2009). Moreover, leaf respiration ($R_d$) was neglected, as it is much smaller than $A_{sat}$ (Knauer et al., 2018; Von Caemmerer, 2013). $K_m$ and ${\Gamma }^{*}$ were estimated using C3 plant-based temperature response curves (Bernacchi et al., 2001). $C_c$ was calculated using the Fick law (Farquhar and Sharkey, 1982):

$\begin{array}{ll}\begin{array}{c}{C}_c=C_i-\frac{A_{sat}}{{ɡ}_m}\end{array}& (3)\end{array}$

where ${ɡ}_m$ is determined using the “variable electron transport” method (Harley et al., 1992):

$\begin{array}{ll}\begin{array}{c}{ɡ}_m=\frac{A_{sat}}{C_i-\frac{{\Gamma }^{*}(J_F+8A_{sat})}{J_F-4A_{sat}}}\end{array}& (4)\end{array}$

where $J_F$ is the electron transport rate estimated from PPFD, $\alpha$ the leaf absorptance in the PAR, ${\phi }_{PSII}$ the photochemical efficiency of PSII open centers, and ${\beta }_{PSII}$ the fraction of the absorbed PAR allocated to PSII (Genty et al., 1989; Valentini et al., 1995):

$\begin{array}{ll}\begin{array}{c}{J}_F=\alpha ·{\beta }_{PSII}·{\phi }_{PSII}·PPFD\end{array}& (5)\end{array}$

In Equation 5, ${\phi }_{PSII}$ was determined from $F_m^{\prime }$ and $F_s$ (Kramer et al., 2004):

$\begin{array}{ll}\begin{array}{c}{\phi }_{PSII}=\frac{F_m^{\prime }-F_s}{F_m^{\prime }}\end{array}& (6)\end{array}$

and $\alpha ·{\beta }_{PSII}$ was determined from the linear relationship between ${\phi }_{PSII}$ and the apparent quantum efficiency of the linear electron transport ${\phi }_{e-}$ (Valentini et al., 1995):

$\begin{array}{ll}\begin{array}{c}\alpha ·{\beta }_{PSII}=\frac{4}{k}\end{array}& (7)\end{array}$

where 4 is the number of electrons needed per CO₂ molecule fixed and $k$ the slope of the linear relationship between ${\phi }_{e-}$ and ${\phi }_{PSII}$. Under non-photorespiratory conditions, ${\phi }_{e-}$ can be estimated by the apparent quantum efficiency of CO₂ uptake ${\phi }_{CO2}$, which is obtained by dividing the net CO₂ assimilation by the incident PAR (Genty et al., 1989). Non-photorespiratory conditions were set by adding pure N₂ (1% O₂) into the LI-COR LI-6400 chamber. The meteorological conditions were maintained at ambient levels, and the incoming PPFD was set to the following values: 2,000, 1,500, 1,200, 1,000, 800, 600, 400, 200, 100, and 0 µmol m⁻² s⁻¹. Gas exchanges and fluorescence intensities were measured for each PPFD value. ${\phi }_{CO2}$ was calculated as the ratio of net carbon assimilation to PAR. The slope of fitted linear relationship between ${\phi }_{CO2}$ and ${\phi }_{e-}$ ($k$) was used to determine $\alpha ·{\beta }_{PSII}$ using Equation 7. These measurements were conducted on three leaf samples for irrigated and non-irrigated plants and were repeated three times during the drought treatment (i.e., DAEs 42, 64, and 73).

2.2.2 SOL: g_s and g₁

In the USO model, ${ɡ}_s$ is a function of $VP{D}_{leaf}$, $C_s$, and $A_{sat}$ (Medlyn et al., 2011):

$\begin{array}{ll}\begin{array}{c}{ɡ}_s=\left(1+\frac{{ɡ}_1}{\sqrt{VP{D}_{leaf}}}\right)\frac{A_{sat}}{C_s}\end{array}& (8)\end{array}$

where the minimum stomatal conductance is neglected under high irradiance (Medlyn et al., 2017), and ${ɡ}_1$ is the stomatal sensitivity to photosynthesis, which is inversely related to the marginal water use efficiency (WUE) (Medlyn et al., 2011). ${ɡ}_1$ can be determined by combining the Fick law describing the CO₂ diffusion through stomata with Equation 8, which gives (Medlyn et al., 2017)

$\begin{array}{ll}\begin{array}{c}{ɡ}_1=\frac{\frac{C_i}{C_s}\sqrt{VP{D}_{leaf}}}{1-\frac{C_i}{C_s}}\end{array}& (9)\end{array}$

2.3 Statistical analysis

${ɡ}_m$ values were discarded when $C_i$ was outside of the range 150–350 μmol mol⁻¹, which minimizes errors in $R_d$ and Γ* and by extension in ${ɡ}_m$ (Harley et al., 1992; Niinemets et al., 2006; Veromann-Jürgenson et al., 2017). Moreover, $V_{cmax}$ and ${ɡ}_m$ were normalized at 25°C ($V_{cmax,25}$, ${ɡ}_{m,25}$) using the Arrhenius temperature response function parameterized on tobacco (Bernacchi et al., 2002, 2001). Gas exchange and chlorophyll fluorescence-related variables (i.e., $A_{sat}$, ${ɡ}_s$, ${ɡ}_{m,25}$, ${ɡ}_1$, and $V_{cmax,25}$) were averaged for each day of measurement and drought treatment (irrigated and non-irrigated), thus regrouping measurements performed under similar meteorological and edaphic conditions.

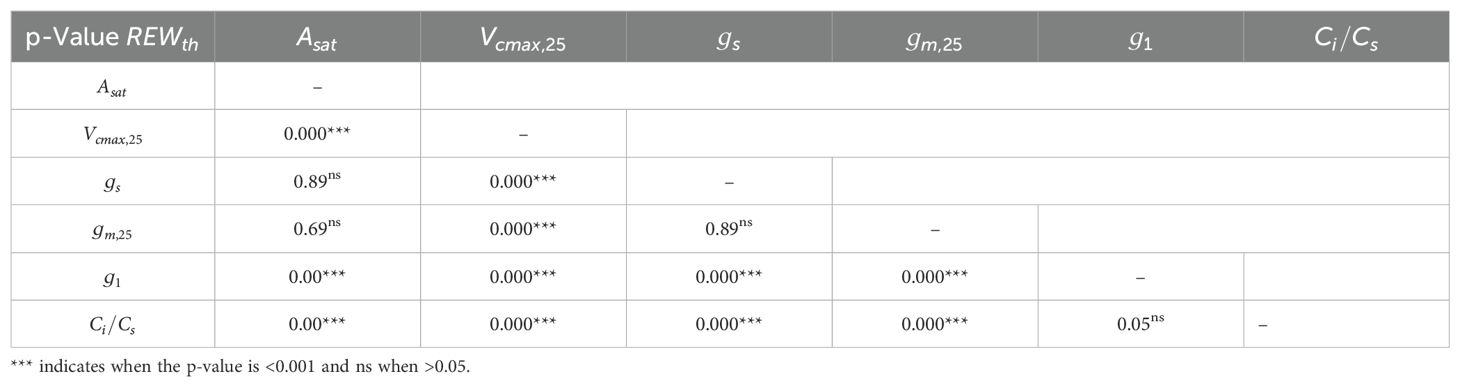
The response of $A_{sat}$, ${ɡ}_s$, ${ɡ}_{m,25}$, ${ɡ}_1$, and $V_{cmax,25}$ to the decrease in REW was assessed using a linear-plateau model, which consists in a constant value ($y_{max}$) and a linear segment (with slope $a$ and intercept $b$) on either side of a threshold ($RE{W}_{th}$). Such model has already been used to describe the response of SOL and NSOL to soil water availability of potato crops at the ecosystem scale (Beauclaire et al., 2023) and is used to implement the response of LSM parameters to drought (Vidale et al., 2021). The statistical significance of the linear-plateau model was assessed by comparing its Akaike information criterion corrected for low sample size (AICc; Burnham et al., 2002) to the one of a higher parsimonious model (i.e., a linear model with one slope and intercept). The model with the lowest AICc explains the greatest amount of variation while being the more parsimonious (Burnham et al., 2011; Scoffoni et al., 2012). Differences between models were considered meaningful when their AICcs differed by at least 7 (Burnham et al., 2011). If the difference was less than 7, the segmented model was selected, as such a relationship has already been observed for potato (Beauclaire et al., 2023). Model performance was assessed using the coefficient of determination (R²) and the standard deviation (SD) of fitted parameters. The segmented regression was fitted using the “nlsm” function from the “nlraa” package in R Studio (Archontoulis and Miguez, 2015; Miguez, 2023). Statistical difference between $RE{W}_{th}$ parameters was tested by calculating the p-value of a t-test using the fitted values and their corresponding standard deviation (Clogg et al., 1995; Paternoster et al., 1998).

2.4 Limitation analysis

The first limitation scheme used in this study was proposed by Jones (1985), where SOL was associated to a decrease in ${ɡ}_s$ caused by a decrease in either $V_{cmax}$ or ${ɡ}_m$. The relative variation of $A_{sat}$ compared to its maximum value $\frac{d{A}_{sat}}{A_{sat}}$ is written as the sum of the relative variations of ${ɡ}_s$, ${ɡ}_m$, and $V_{cmax}$, as follows (Grassi and Magnani, 2005; Jones, 1985):

$\begin{array}{ll}\begin{array}{c}\frac{d{A}_{sat}}{A_{sat}}=\frac{d{ɡ}_s}{{ɡ}_s}{l}_{ɡs}+\frac{d{ɡ}_m}{{ɡ}_m}{l}_{ɡm}+\frac{d{V}_{cmax}}{V_{cmax}}{l}_{Vcmax}=L_{ɡs}+L_{ɡm}+L_{Vcmax}\end{array}& (10)\end{array}$

$\begin{array}{ll}\begin{array}{c}{l}_{ɡs}=\frac{\frac{{ɡ}_t}{{ɡ}_s}\frac{\delta A_{sat}}{\delta C_c}}{{ɡ}_t+\frac{\delta A_{sat}}{\delta C_c}}\end{array}& (11)\end{array}$

$\begin{array}{ll}\begin{array}{c}{l}_{ɡm}=\frac{\frac{{ɡ}_t}{{ɡ}_m}\frac{\delta A_{sat}}{\delta C_c}}{{ɡ}_t+\frac{\delta A_{sat}}{\delta C_c}}\end{array}& (12)\end{array}$

$\begin{array}{ll}\begin{array}{c}{l}_{Vcmax}=\frac{{ɡ}_t}{{ɡ}_t+\frac{\delta A_{sat}}{\delta C_c}}\end{array}& (13)\end{array}$

where $l_{ɡs}$, $l_{ɡm}$, and $l_{Vcmax}$ are respectively the relative stomatal, mesophyll, and biochemical limitations (corresponding to dimensionless quantity between 0 and 1 that gives the proportion of the total limitation), and $L_{ɡs},L_{ɡm}$, and $L_{Vcmax}$ are the contributions of respectively the stomatal, mesophyll, and biochemical limitations to the relative variation of $A_{sat}$. ${ɡ}_t$ is the total conductance to CO₂ diffusion (${ɡ}_t{}^{-1}={ɡ}_s{}^{-1}+{ɡ}_m{}^{-1}$), and $\delta A_{sat}/\delta C_c$ is the partial derivative of $A_{sat}$ with respect to $C_c$ calculated using Equation 2. In this study, Equation 10 was normalized by $d{A}_{sat}/A_{sat}$ to improve the interpretation of the data. The temporal dynamics of these relative variations can be explained solely by REW and VPD, as the relationship to temperature was already considered by normalizing $V_{cmax}$ and ${ɡ}_m$ at 25°C, as well as the one to solar radiation by collecting the data at light saturation.

This approach has two drawbacks. First, the decrease in $A_{sat}$ originating from stomatal closure through a decrease in ${ɡ}_s$ can be induced by ${ɡ}_m$ and $V_{cmax}$, which may result in the underestimation of the contribution of non-stomatal factors in limiting photosynthesis. Second, identifying the contribution of REW to the variation in $L_{ɡs}$ is complex, as VPD has varied during the experiment. To tackle this issue, we used ${ɡ}_1$ instead of ${ɡ}_s$ as SOL. This allows first, to separate the feedback effect of NSOL on stomatal conductance and, second, to consider the effect of VPD on stomatal closure (Zhou et al., 2013). As a result, Equation 10 was modified by calculating the total derivative of ${ɡ}_s$ using the USO model, which gives (derived in Supplementary Method S1):

$\begin{array}{ll}\begin{array}{c}\frac{d{A}_{sat}}{A_{sat}}=\frac{d{ɡ}_1}{{ɡ}_1}(\frac{l_{ɡs}}{1-l_{ɡs}}\frac{C_i}{C_s})+\frac{d{ɡ}_m}{{ɡ}_m}(\frac{l_{ɡm}}{1-l_{ɡs}})+\frac{d{V}_{cmax}}{V_{cmax}}(\frac{l_{Vcmax}}{1-l_{ɡs}})-(\frac{1}{2}\frac{l_{ɡs}}{1-l_{ɡs}}\frac{C_i}{C_s})\frac{dVPD}{VPD}\end{array}& (14)\end{array}$

$\begin{array}{ll}\begin{array}{c}\frac{d{A}_{sat}}{A_{sat}}=\frac{d{ɡ}_1}{{ɡ}_1}{l}_{ɡ1,USO}+\frac{d{ɡ}_m}{{ɡ}_m}{l}_{ɡm,USO}+\frac{d{V}_{cmax}}{V_{cmax}}{l}_{Vcmax,USO}+l_{VPD,USO}\frac{dVPD}{VPD}\end{array}& (15)\end{array}$

$\begin{array}{ll}\begin{array}{c}\frac{d{A}_{sat}}{A_{sat}}=L_{ɡ1,USO}+L_{ɡm,USO}+L_{Vcmax,USO}+L_{VPD,USO}\end{array}& (16)\end{array}$

where $L_{ɡ1,USO}$, $L_{ɡm,USO}$, $L_{Vcmax,USO}$, and $L_{VPD,USO}$ are the contributions of respectively the optimal stomatal, mesophyll, biochemical, and VPD limitations to the relative variation of $A_{sat}$ using the USO model of stomatal conductance. Equations 15, 16 show that $d{A}_{sat}/A_{sat}$ can be written as the sum of the relative variations of ${ɡ}_1$, ${ɡ}_m$, $V_{cmax}$, and VPD. Combining Equations 16, 10 allows to identify the effect of ${ɡ}_m$, $V_{cmax}$, ${ɡ}_1$, and VPD on the contribution of stomatal closure to photosynthesis, as follows:

$\begin{array}{ll}\begin{array}{c}{L}_{ɡs}=L_{ɡm,USO}-L_{ɡm}+L_{Vcmax,USO}-L_{Vcmax}+L_{VPD,USO}+ L_{ɡ1,USO}\end{array}& (17)\end{array}$

$L_{ɡm,USO}-L_{ɡm}+L_{Vcmax,USO}-L_{Vcmax}$ is the effect of NSOL on stomatal closure, while $L_{VPD,USO}+ L_{ɡ1,USO}$ is the effect of VPD and ${ɡ}_1$ on stomatal closure according to the USO model. The relative variations in Equations 10, 15 are calculated from the difference between the value of the variable at a specific REW and the asymptote of the linear-plateau using $dy/y=(y_{max}-y)/(y_{max}-min(y))$, with $y$ being the ordinate at a specific REW value and $y_{max}$ the plateau of the segmented regression. In a similar fashion, $dVPD/VPD$ is determined from the VPD–REW relationship. During precipitation shortage episodes, this relationship is decreasing (i.e., increase in VPD when REW decrease), which was observed during the experiment (Supplementary Figure S2). This relationship was confirmed by the data of the nearby eddy covariance station of Lonzée for similar edaphic proprieties (data not shown). Therefore, this linear relationship was used to determine $dVPD/VPD$ at each REW value.

In Equation 14, the ratio $C_i/C_s$ also plays an important role in the limitation analysis, as it directly influences $L_{ɡ1,USO}$ and $L_{VPD,USO}$. Using ${ɡ}_1$ as SOL implies that any stomatal constraint on $A_{sat}$ should be associated with an increase of the ratio $A_{sat}/{ɡ}_s$. Indeed, following the USO model framework, this constraint corresponds to a maximization of photosynthesis while minimizing water losses. As ${ɡ}_s$ and $A_{sat}$ both regulate CO₂ diffusion through stomatal apertures and CO₂ fixation in the chloroplasts, the increase in $A_{sat}/{ɡ}_s$ is linked to a decrease in $C_i/C_s$, illustrating an optimal stomatal control ($C_i/C_s\sim 1-A_{sat}/{ɡ}_s$). The relationship between $C_i/C_s$ and REW was also evaluated by fitting a linear-plateau model as described in section 2.4. Note that $L_{VPD, USO}$ is per essence negative because of the partial derivative of VPD with respect to $A_{sat}$, as they are inversely related (i.e., VPD at the denominator in the USO model; Equation 8). As a result, any increase in VPD induces a closure of stomata and a decrease in $A_{sat}$. A decrease in $V_{cmax}$, ${ɡ}_m$, or ${ɡ}_1$ induces a decrease in $A_{sat}$ for all the other terms of Equation 16.

3 Results

3.1 Meteorological and edaphic conditions

The decline in soil water availability was synchronized with a period of progressive increase in VPD and air temperature under the plastic polytunnel greenhouse (Figure 1A) up to a maximum value of 4.10 kPa and 39.02°C, respectively (Figure 1A). Both irrigated and non-irrigated plants faced an increase in atmospheric dryness and air temperature. The REW of the non-irrigated plants decreased after stopping the irrigation and reached 0.24 at the end of the experiment, while the REW of the irrigated plants remained higher than 0.83 due to continuous hand watering (Figure 1B).

3.2 Response of gas exchanges and chlorophyll fluorescence to drought

$\alpha ·{\beta }_{PSII}$ was not significantly different between irrigated and non-irrigated leaf samples at each DAE and during the experiment (Supplementary Figure S3). Therefore, the mean of all $\alpha ·{\beta }_{PSII}$ measurements was used in Equation 5 (i.e., $\text{α}·{\beta }_{PSII}$ = 0.73 ± 0.08). The linear-plateau model had the lowest AICc compared to the linear model for representing the dependence of $V_{cmax,25}$, ${ɡ}_1$, and $C_i/C_s$ on REW. For ${ɡ}_s$, ${ɡ}_{m,25}$, and $A_{sat}$, the difference between the AICc of the segmented and the linear model was less than 7 (Supplementary Table S1). Therefore, these differences were not considered significant, and the segmented model was chosen for reproducing the response of $A_{sat}$, $C_i/C_s$, ${ɡ}_s$, ${ɡ}_{m,25}$, and ${ɡ}_1$ to REW (Figure 2, Table 1). The REW thresholds at which $A_{sat}$, ${ɡ}_s$, and ${ɡ}_{m,25}$ started to decrease were higher than those of $V_{cmax,25 }$, ${ɡ}_1$, and $C_i/C_s$ (Figure 2, Table 1), which is confirmed by the p-values of the tests comparing these parameters (Table 2). Overall, CO₂ diffusion factors (i.e., ${ɡ}_{m,25}$ and ${ɡ}_s$) were the first variables to decrease with REW, while biochemical factors (i.e., $V_{cmax,25}$) were only impacted by severe REW restrictions. Because of a non-significant difference, the REW thresholds for ${ɡ}_{m,25}$ and ${ɡ}_s$ were averaged, corresponding to $RE{W}_{th,ɡs,ɡm}=$ 0.72 ± 0.12. Biochemical limitation ($V_{cmax,25 }$) was only negatively impacted by severe soil water restrictions ($RE{W}_{th,Vcmax}=$ 0.43 ± 0.04). ${ɡ}_1$ and $C_i/C_s$ increased from a smaller REW threshold compared to $V_{cmax,25 }$ ($RE{W}_{th, ɡ1,CiCs}=$ 0.37 ± 0.02; Figure 2, Tables 1, 2).

Figure 2

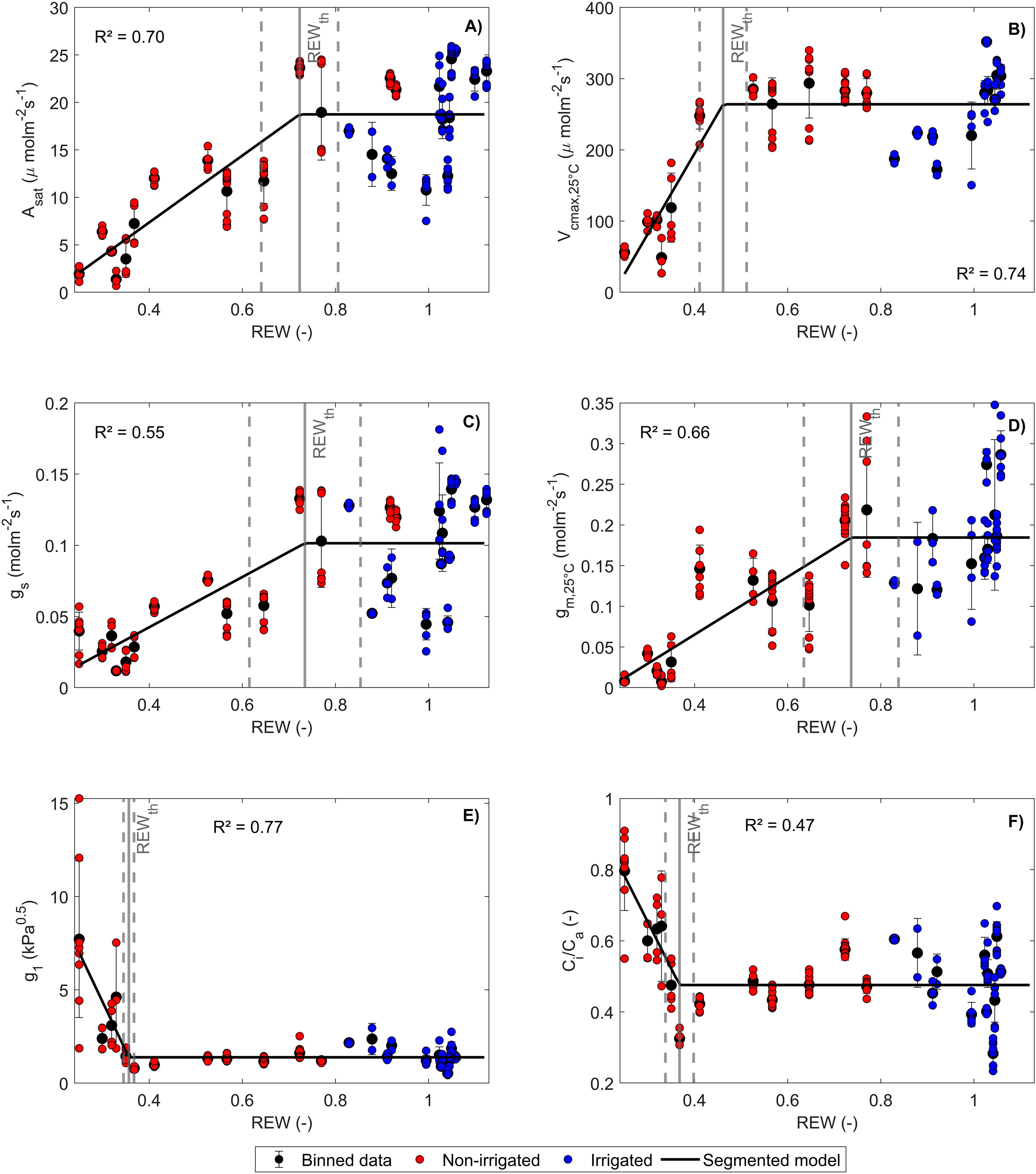
Figure 2. Response of $A_{sat}$ (A), $V_{cmax,25}$ (B), ${ɡ}_s$ (C), ${ɡ}_{m,25}$ (D), ${ɡ}_1$ (E), and $C_i/C_s$ (F) to relative extractable water (REW). Red and blue dots indicate respectively non-irrigated and irrigated potato plants. The fitted curve represents the linear-plateau regression $y=\{\begin{array}{c}{y}_{max}, REW>RE{W}_{th}\\ aREW+b, REW\le RE{W}_{th}\end{array}$. Binned data are shown with the corresponding standard deviation (SD). The gray vertical lines indicate $RE{W}_{th}$ ± SD.

Table 1

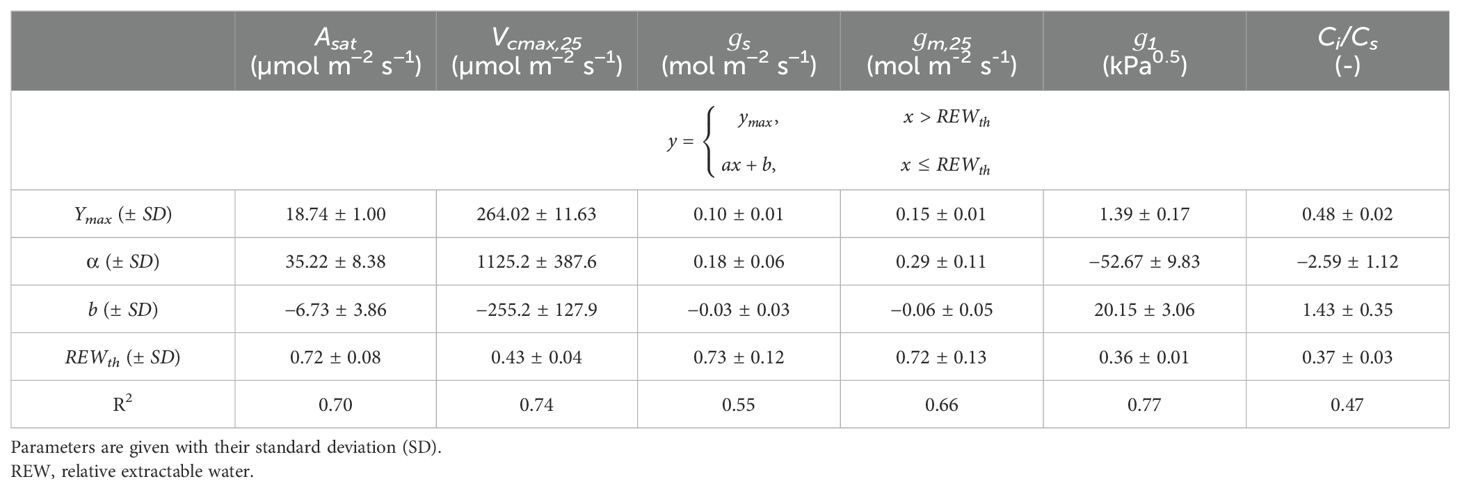
Table 1. Statistics of the segmented linear regression for the response of A_sat, V_cmax,25, g_s, g_m,25, g₁, C_i/C_s and to REW.

Table 2

Table 2. p-Value of the t-test comparing $RE{W}_{th}$ between $A_{sat}$, $V_{cmax,25}$, ${ɡ}_s$, ${ɡ}_{m,25}$, ${ɡ}_1$, and $C_i/C_s$.

3.3 Limitation analysis

The first limitation analysis scheme used in this study consists in partitioning photosynthesis limitations under high irradiance between $L_{ɡm}$, $L_{Vcmax}$, and $L_{ɡs}$ (Jones, 1985). $L_{ɡs}$ was always higher than $L_{ɡm}$ above REW ~ 0.28 (Figure 3A), where $L_{ɡm}$ became predominant over $L_{ɡs}$ (i.e., intersection of $L_{ɡs}$ and $L_{ɡm}$; Figure 3B). When REW was minimum, 34% of the decrease in $A_{sat}$ was explained by $L_{ɡs}$, 20% by $L_{Vcmax}$, and 56% by $L_{ɡm}$ (Figures 3A, B).

Figure 3

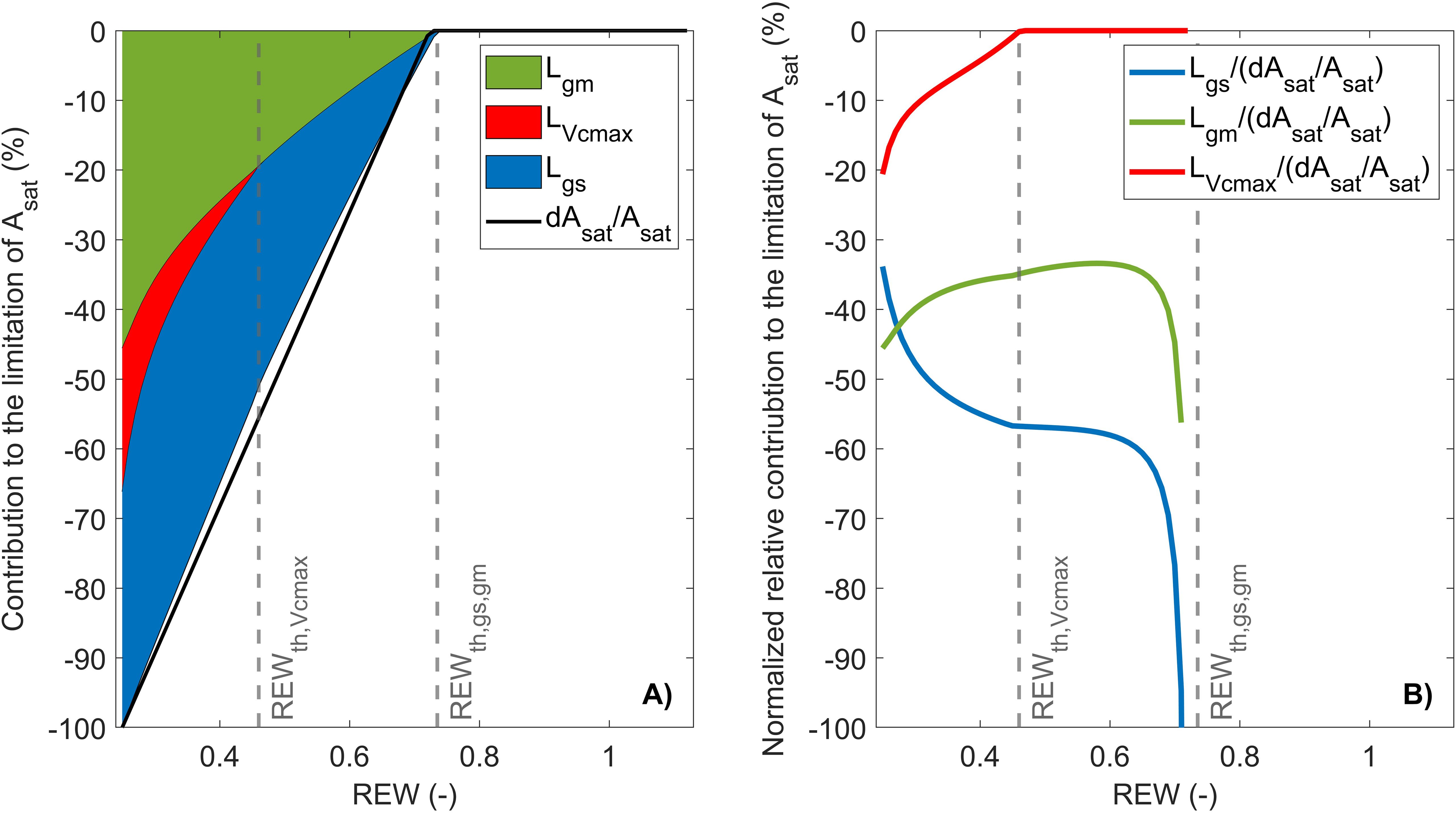
Figure 3. Partitioning of $A_{sat}$ limitations between $L_{ɡs}$, $L_{ɡm}$, and $L_{Vcmax}$ in response to relative extractable water (REW) with stacked limitation curves (A) and normalized relative contribution curves (B). The black line is the relative variation of $A_{sat}$ compared to its maximum value (i.e., $y_{max}$ of the linear-plateau regression), and the gray vertical lines indicate $RE{W}_{th}$ ± SD.

This limitation scheme indicated that CO₂ diffusion factors (i.e., $L_{ɡm}$ and $L_{ɡs}$) explained most of the decrease in $A_{sat}$ with a similar contribution. However, using ${ɡ}_s$ in the partitioning analysis does not allow to fully identify the origin of the early stomatal closure, as ${ɡ}_s$ itself can be influenced by $V_{cmax}$ and ${ɡ}_m$ through $A_{sat}$ (Equation 8). This hypothesis is supported by the similar REW threshold for ${ɡ}_s$ and ${ɡ}_{m,25}$, which suggests that the two variables are closely related. Combining Equations 16, 10 showed that the increase in $L_{ɡs}$ is mostly caused by ${ɡ}_m$ and VPD notably under mild soil water conditions ($REW>RE{W}_{th,CiCs},$; Figure 4). In particular, $L_{ɡm,USO}$ was always higher than $L_{VPD,USO}$ and $L_{Vcmax,USO}$ (Figure 4). Moreover, ${ɡ}_1$ had a positive contribution to $L_{ɡs}$ (Figure 4), which indicates that the increase in ${ɡ}_1$ (Figure 2E) promoted the opening of stomata to sustain CO₂ diffusion to the fixation sites. Once the USO model has been integrated in the limitation analysis on $A_{sat}$, it can be shown that $L_{ɡm,USO}$ was predominant over $L_{VPD,USO}$ regardless of soil water conditions (Figure 5A). When REW was minimum, 69% of the decrease in $A_{sat}$ was explained by $L_{ɡm,USO}$, 31% by $L_{Vcmax,USO}$, and 20% by $L_{VPD,USO}$ (Figure 5A). In these conditions, $L_{ɡ1,USO}$ was positive and reached 40%. The positive contribution of ${ɡ}_1$ can be explained by the increase in $d{ɡ}_1/{ɡ}_1$ (Figure 2E), which resulted in an increase in $L_{ɡ1,USO}$ (Equation 15). Such increase in $L_{ɡ1,USO}$ was observed from $RE{W}_{th, ɡ1,CiCs}$ (Tables 1, 2), which corresponded to low $A_{sat}$ (6.8 μmol m⁻² s⁻¹) and ${ɡ}_s$ (0.04 mol m⁻² s⁻¹). Note that the sum of all curves in Figure 5B may not necessarily equal 1, as the sum of limiting components when using the USO partitioning scheme did not exactly correspond to $d{A}_{sat}/A_{sat}$ because of the uncertainties associated with the fitting of the linear-plateau segmented model on measurements (Figures 2, 5A).

Figure 4

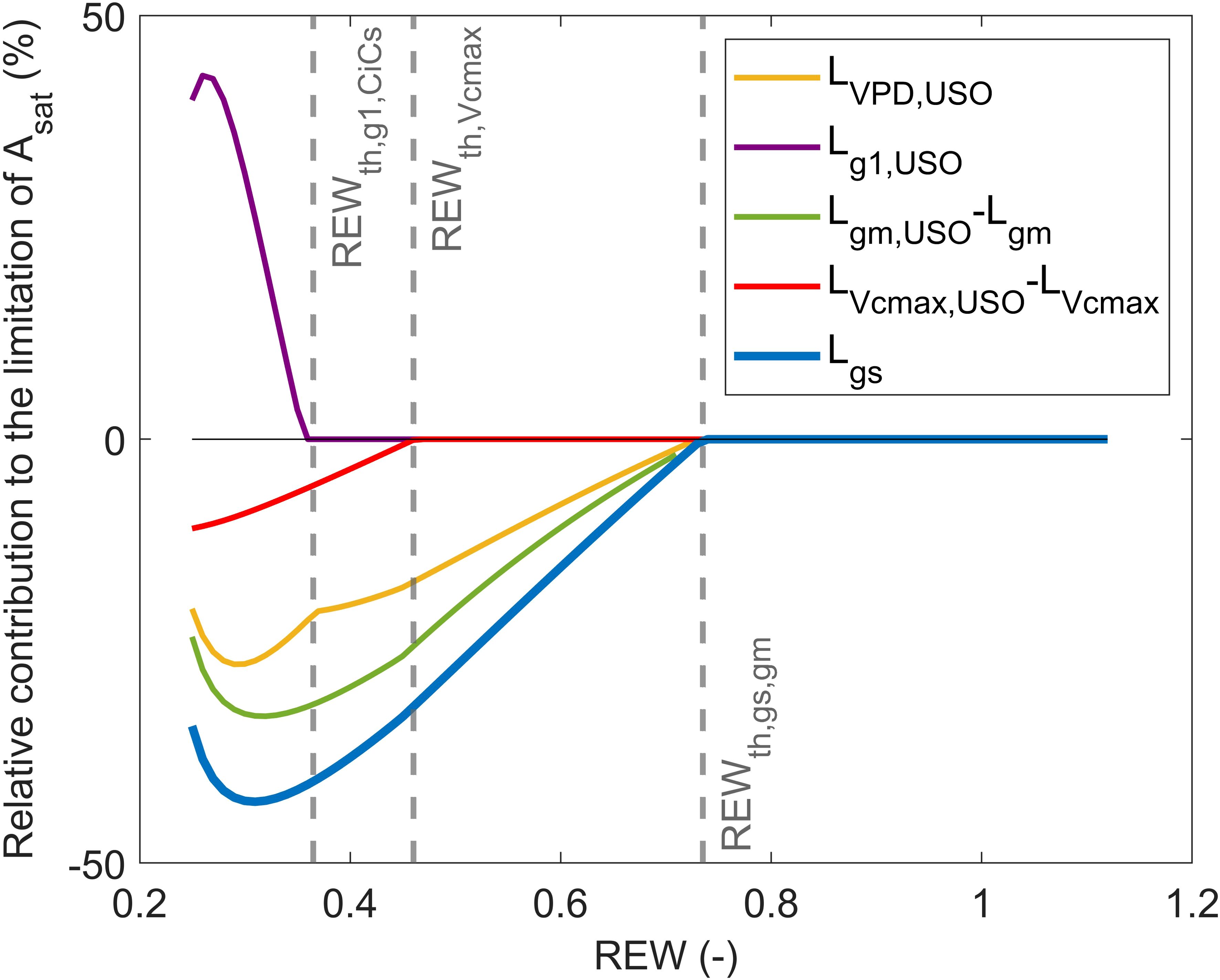
Figure 4. Partitioning of the limiting component induced by stomatal closure ($L_{ɡs}$) into $L_{ɡ1,USO}$, $L_{ɡm,USO}-L_{ɡm}$, $L_{Vcmax,USO}-L_{Vcmax}$, and $L_{VPD,USO}$ in response to relative extractable water (REW). The gray vertical lines indicate $RE{W}_{th}$ ± SD.

Figure 5

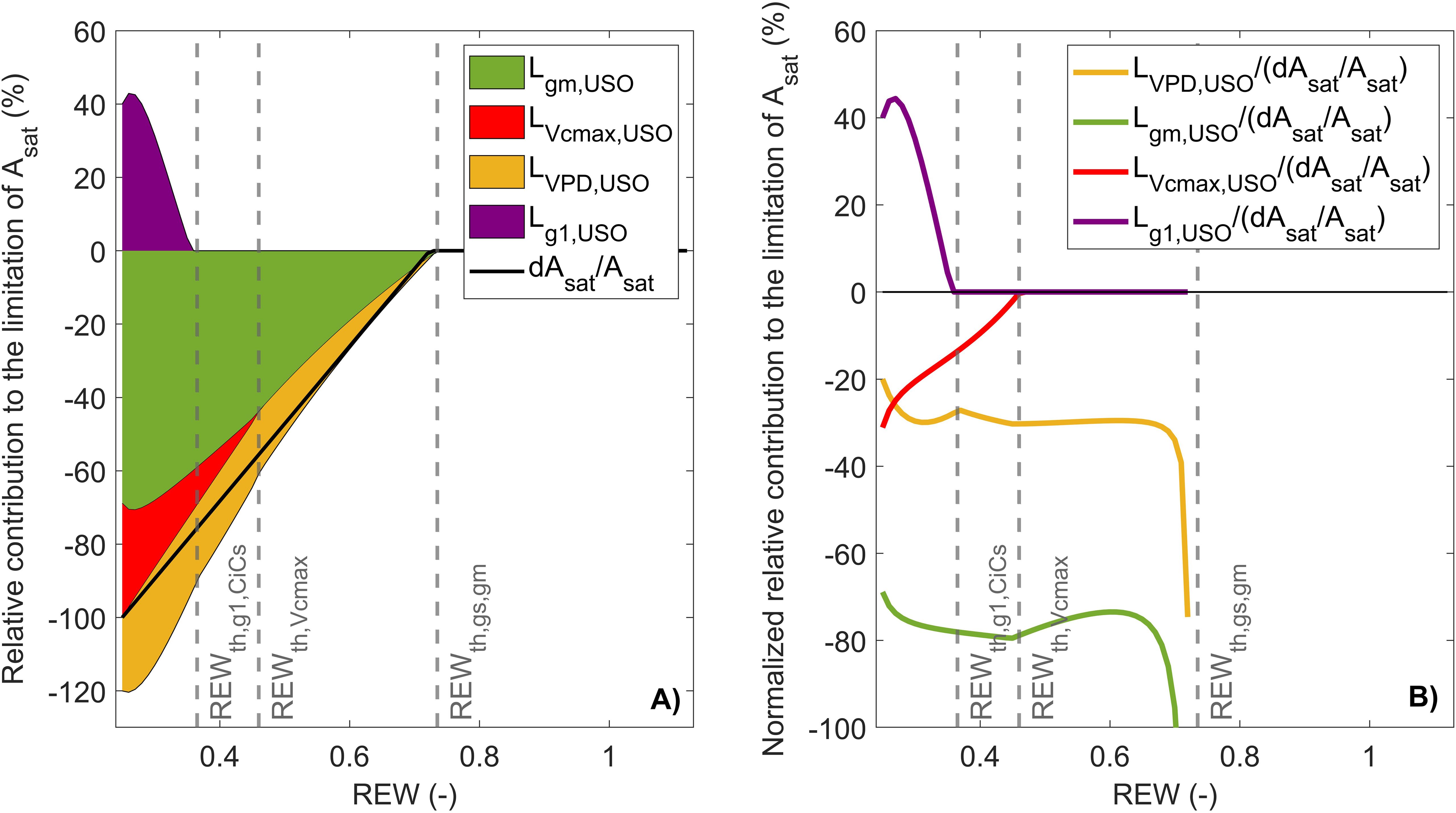
Figure 5. Partitioning of $A_{sat}$ limitations between $L_{ɡ1,USO}$, $L_{ɡm,USO}$, $L_{Vcmax,USO}$, and $L_{VPD,USO}$ in response to relative extractable water (REW) with stacked limitation curves (A) and shows normalized relative contribution curves (B). The black line is the relative variation of $A_{sat}$ compared to its maximum value (i.e., $y_{max}$ of the linear-plateau regression), and the gray vertical lines indicate $RE{W}_{th}$ ± SD.

4 Discussion

The determination of thresholds of soil water availability impacting CO₂ assimilation is pivotal for calibrating the response of photosynthesis model parameters during drying-up episodes (Vidale et al., 2021). The results of this study showed that soil water-limiting conditions induced a two-stage response of potato to water stress, with ${ɡ}_s$ and ${ɡ}_m$ being the first variables impacted by the decrease in REW followed by biochemical limitations through the decrease in $V_{cmax}$. In addition, we used a new partitioning scheme where the total derivative of ${ɡ}_s$ was written as a function of its explanatory variables in the USO model (i.e., ${ɡ}_1$, $V_{cmax}$, $VPD$, and $A_{sat}$). This method allowed to quantify the origins of the decrease in $A_{sat}$ in response to changes in ${ɡ}_m$, $V_{cmax}$, ${ɡ}_1$, and VPD. This partitioning was compared to the original formulation of photosynthesis limitations of Jones (1985), which attributed the origins of the reduction of $A_{sat}$ to the relative variations of ${ɡ}_m$, $V_{cmax}$, and ${ɡ}_s$. The comparison between the two schemes provides an estimation of the importance of the factors influencing ${ɡ}_s$ and $A_{sat}$.

4.1 Predominance of CO₂ diffusion constraints on photosynthesis

Stomatal closure is a well-known mechanism of potato to reduce transpiration under water stress (Gerhards et al., 2016; Gordon et al., 1997; Obidiegwu, 2015; Romero et al., 2017; Vos and Oyarzún, 1987). Stomatal closure dynamics are complex and can be directly caused by the evaporation of the water held by guard cells or by the loss of turgor pressure induced by sensing of signaling molecules (Bharath et al., 2021; Ding and Chaumont, 2020; Obidiegwu, 2015; Pirasteh-Anosheh et al., 2016; Zhang et al., 2022). These mechanisms are likely to be synchronized with those influencing mesophyll conductance as evidenced by a similar REW threshold for ${ɡ}_s$ and ${ɡ}_m$ (Figure 2). In particular, mesophyll and stomatal conductance share similar responses to abscisic acid (Flexas et al., 2012; Li et al., 2021; Sorrentino et al., 2016), internal CO₂ concentration (Engineer et al., 2016; Tan et al., 2017), or starch-derived molecules (Lawson et al., 2014), which leads to similar responses under water stress (Flexas et al., 2004; Wang et al., 2018; Xiong et al., 2018). $L_{ɡm}$ became predominant over $L_{ɡs}$ under severe water stress, which was associated with a very low ${ɡ}_m$ and a strong restriction of CO₂ diffusion to chloroplasts (Figures 2, 3). While this partitioning scheme indicated that photosynthesis limitations mostly originated from ${ɡ}_s$, it did not highlight the influence of non-stomatal factors on stomatal conductance. The origins of the decrease in ${ɡ}_s$ and $A_{sat}$ can be identified using the USO model equation in the limitation analysis. In particular, the USO partitioning scheme showed that most stomatal closure dynamics can be attributed to a combined effect of ${ɡ}_m$ and VPD (Figure 4). More specifically, $L_{ɡm,USO}$ was always higher than the other limiting components (Figures 5A, B), which highlights the strong control of mesophyll conductance on stomatal closure through its influence on $A_{sat}$ regardless of REW values. These results confirm the importance of the mesophyll constraint for potato, as also highlighted in numerous species across PFTs (Cano et al., 2013; Flexas et al., 2009; Galmés et al., 2007; Grassi and Magnani, 2005; Limousin et al., 2010; Perez-Martin et al., 2014; Wang et al., 2018; Wang et al., 2018; Zait and Schwartz, 2018; Zhu et al., 2021) and emphasize the importance of including the effect of REW on ${ɡ}_m$ in LSMs (Knauer et al., 2020). This study also provides a calibration of the water stress factor for potato and contributes to reducing the uncertainties when estimating carbon assimilation and transpiration under water stress (Vidale et al., 2021). Additional information on the description of the physiological effects of mesophyll on stomatal closure can be found in Lemonnier and Lawson (2023). Since disentangling the primary metabolisms that synchronously control photosynthesis, stomatal, and mesophyll conductance remains challenging, future studies would benefit from additional molecular or anatomical measurements to unravel the interplays between stomatal and non-stomatal factors (Gago et al., 2020).

4.2 Relationship between photosynthesis and stomatal conductance under severe drought

Severe restrictions in soil water availability induced a decrease in $V_{cmax}$ as well as an increase in ${ɡ}_1$ and $C_i/C_s$ (Figure 2). An increase in $C_i/C_s$ can be observed under strong limitations in CO₂ diffusion and decreasing photosynthetic activity (Bermúdez-Cardona et al., 2015; Brodribb, 1996; Huang, 2020; Tan et al., 2017). In particular, $C_i/C_s$ increased when ${ɡ}_s$ was lower than 0.04 mol m⁻² s⁻¹, which was already reported as a stomatal conductance threshold for such $C_i$-inflexion point in various species (Blankenagel et al., 2018; Brodribb, 1996; Flexas, 2002; Martin and Ruiz-Torres, 1992; Rouhi et al., 2007) including potato (Ramírez et al., 2016). In these conditions of photosynthesis inhibition, the excess energy carried by sun irradiance must be metabolized by alternative processes such as xanthophyll (Demmig-Adams et al., 2012), lutein (García-Plazaola et al., 2003), and photorespiratory cycles (Osmond et al., 1980). This last may contribute to the increase in $C_i/C_s$ by emitting CO₂ through the glycine decarboxylase enzyme (Busch et al., 2017; Shi and Bloom, 2021).

The increase in ${ɡ}_1$ induced an increase in $d{ɡ}_1/{ɡ}_1$ and $L_{ɡ1}$ when $REW<RE{W}_{th,ɡ1,CiCs}$ (Figures 2, 4A, B). ${ɡ}_1$ is inversely related to the marginal carbon cost of water, which corresponds to the change in carbon gained per unit of water transpired, also known as marginal WUE (Medlyn et al., 2011). The increase in ${ɡ}_1$ can be explained by either i) an increase in transpiration per unit of carbon gained by photosynthesis or ii) a decrease in photosynthesis per unit of water transpired (Medlyn et al., 2011). For example, increasing stomatal conductance to promote transpiration may help in cooling down leaf surfaces during heatwaves at the expense of increasing mortality risks through hydraulic vulnerability and cavitation (Marchin et al., 2022; Urban et al., 2017). Numerous studies have highlighted such cooling effect on potato (Sprenger et al., 2016; Zhang et al., 2022), which can ultimately lead to an increase in ${ɡ}_1$ (Marchin et al., 2023). A decoupling between stomatal conductance and photosynthesis may be the consequence of an adaptive strategy (i.e., sacrificing water for leaf survival and future carbon gains) or the increasing viscosity of water at high temperatures, which facilitates the transport of water in the vascular system (Marchin et al., 2023). In our experiment, the lowest measurement of ${ɡ}_s$ was 0.011 mol m⁻² s⁻¹, which is higher than the reported value of minimum stomatal conductance for CO₂ transfer across plant species (i.e., ${ɡ}_s$ = 0.008 mol m⁻² s⁻¹; Duursma et al., 2019) and suggests that stomata may not be fully closed. It is, however, unlikely that potato plants had access to water to sustain transpiration through stomata or cuticles because of the low REW values that were observed in these conditions (Figure 2). Alternatively, the increase in ${ɡ}_1$ may be caused by a decrease in photosynthesis through the additional effect of NSOL on $A_{sat}$ (Beauclaire et al., 2023; Gourlez de la Motte et al., 2020), which intensifies the decoupling between carbon assimilation and stomatal conductance by decreasing WUE (Manzoni et al., 2011). This hypothesis is supported by previous studies, which have shown that irrigation enhances WUE for potato (Akkamis and Caliskan, 2023; Ati et al., 2012).

The increase in ${ɡ}_1$ induced a positive contribution to $d{A}_{sat}/A_{sat}$ (Figure 5), suggesting that potato plants promoted the loss of water to the benefit of CO₂ diffusion despite the risks for the hydraulic and photosynthetic systems when carbon assimilation reached critical levels under drought (Deva et al., 2020; Reynolds-Henne et al., 2010). It indicates a shift in the optimal balance point between carbon gain and water loss where potato plants are willing to lose more water per unit of carbon gained (Zhou et al., 2013). This prioritization is not likely to be driven by optimizing survival under severe drought conditions where soil water is hardly accessible and hydraulic limitations presumably important. Instead, the increase in ${ɡ}_1$ could be interpreted as a deviation from optimal stomatal behavior. The stomatal optimality theory states that any increase in the plant’s carbon gain should equal the evaporative water loss proportionally to the carbon cost of water (Cowan and Farquhar, 1977). The optimality theory holds under the assumption that the curvature of photosynthesis versus transpiration is negative; that is, increments of $A$ tend to become smaller with increments of ${ɡ}_s$, as stomata reduce the gradient for CO₂ uptake more than that for H₂O loss (Buckley et al., 2017). Any conditions shifting the curve to a positive curvature will cause a deviation from the optimality theory, challenging the interpretation of ${ɡ}_1$ short-term dynamics. Two of these conditions were likely observed in this study: first, an additional restriction of CO₂ diffusion to chloroplasts by mesophyll conductance and, second, a possible hydraulic impairment at very low REW, which ultimately changes the photosynthesis–transpiration relationship (Buckley et al., 2017; Cowan and Farquhar, 1977). This unrealistic stomatal opening response is consistent with previous studies that have shown a similar increase in ${ɡ}_1$ under severe drought (Beauclaire et al., 2023; Gourlez de la Motte et al., 2020; Zhou et al., 2013), arguing for a refinement of stomatal optimality. Novel modeling approaches consider the cost of stomatal opening as a function of an increase in NSOL (Dewar et al., 2018), or hydraulic impairment using profit maximization optimization (Sperry et al., 2017) may be preferred to interpret stomatal dynamics under drought conditions.

4.3 Methodological considerations

${ɡ}_m$ was determined by the “variable J” method at light saturation (Harley et al., 1992), which is sensitive to variation in $R_d$ and ${\Gamma }^{*}$ (Pons et al., 2009; Théroux-Rancourt et al., 2014). These two variables can be impacted by drought and heat stress, which was not considered in the method part. First, it has been shown that $R_d$ can increase under water stress due to the additional release of CO₂ from mitochondria by the photorespiratory cycle (Busch et al., 2017; Pinheiro and Chaves, 2011). Second, the sensitivity of ${\Gamma }^{*}$ to temperature can change under critical levels (usually above 30°C), which may invalidate the parameterization on leaf temperature (Bernacchi et al., 2001). Measuring the CO₂ compensation point (Walker and Ort, 2015) and leaf respiration (Yin and Amthor, 2024) under drought could help resolve these uncertainties.

The diffusion of water vapor through the cuticle and epidermis may become significant compared to stomatal diffusion under water stress (Boyer, 2015a; Boyer, 2015b; Boyer et al., 1997). As the transpiration flux measured by gas exchange measurement systems corresponds to the sum of the diffusion through stomatal and cuticle conductance, $C_i$ overestimations can occur as the Fick law considers an identical gas phase path for CO₂ and H₂O. Direct measurements of $C_i$ by a modified gas exchange device (Boyer and Kawamitsu, 2011) or a modification of the Fick law by quantifying the cuticle conductance (Wang et al., 2018) could increase the accuracy of $C_i$ under water stress.

Lastly, none of the current methods for estimating ${ɡ}_m$ actually measure diffusion plant conductance. This paper interprets ${ɡ}_m$ as an internal diffusion plant conductance limiting CO₂ diffusion from substomatal cavities to carboxylation sites in the chloroplasts. This two-dimensional view of CO₂ diffusion is a simplification of the actual pathway where sink and sources are distributed along the way. The widely adopted definition of mesophyll conductance (i.e., $A/(C_i-C_c)$) simplifies the leaf as a single sink and ignores the complexity of the mesophyll structure, as well as the heterogeneity in photosynthetic capacities and cellular structure of the leaf vertical light absorption profile (Evans et al., 2009). A more realistic view of mesophyll conductance should include i) a decomposition of resistive components on the CO₂ pathway such as cell wall and membrane, cytosol, chloroplast envelope, and stroma resistances (Cousins et al., 2020); ii) three-dimensional modeling across the leaf vertical profile (Théroux-Rancourt and Gilbert, 2017; Xiao and Zhu, 2017); and iii) a quantification of chloroplast movement, which is a key driver of ${ɡ}_m$ (Carriquí et al., 2019) and is sensitive to changes in light absorption peaks (Tholen et al., 2008). However, most of the complexity can be, neglected when measurements are conducted at light saturation (Théroux-Rancourt and Gilbert, 2017). Improvements in the techniques for estimating the contribution of the different resistive components would help in understanding the response of ${ɡ}_m$ to anatomical and biochemical drivers under drought (Evans, 2021).

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

QB: Writing – original draft, Visualization, Resources, Methodology, Investigation, Formal analysis, Conceptualization. FV: Writing – review & editing, Resources, Investigation. BL: Writing – review & editing, Supervision, Project administration, Methodology, Formal analysis, Conceptualization.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The researchers were funded by the Fédération Wallonie-Bruxelles.

Acknowledgments

This study was conducted with the support of the research and teaching support units “Environment Is Life” and “Agriculture Is Life” of Gembloux Agro-Bio Tech, University of Liege, Belgium.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpls.2024.1500624/full#supplementary-material

References

Akkamis, M., Caliskan, S. (2023). Responses of yield, quality and water use efficiency of potato grown under different drip irrigation and nitrogen levels. Sci. Rep. 13, 9911. doi: 10.1038/s41598-023-36934-3

PubMed Abstract | Crossref Full Text | Google Scholar

Anderegg, W. R. L., Trugman, A. T., Bowling, D. R., Salvucci, G., Tuttle, S. E. (2019). Plant functional traits and climate influence drought intensification and land–atmosphere feedbacks. Proc. Natl. Acad. Sci. U.S.A. 116, 14071–14076. doi: 10.1073/pnas.1904747116

PubMed Abstract | Crossref Full Text | Google Scholar

Archontoulis, S. V., Miguez, F. E. (2015). Nonlinear regression models and applications in agricultural research. Agron. J. 107, 786–798. doi: 10.2134/agronj2012.0506

Crossref Full Text | Google Scholar

Ati, A. S., Iyada, A. D., Najim, S. M. (2012). Water use efficiency of potato (Solanum tuberosum L.) under different irrigation methods and potassium fertilizer rates. Ann. Agric. Sci. 57, 99–103. doi: 10.1016/j.aoas.2012.08.002

Crossref Full Text | Google Scholar

Beauclaire, Q., Heinesch, B., Longdoz, B. (2023). Non-stomatal processes are responsible for the decrease in gross primary production of a potato crop during edaphic drought. Agric. For. Meteorology 343, 109782. doi: 10.1016/j.agrformet.2023.109782

Crossref Full Text | Google Scholar

Bermúdez-Cardona, M. B., Filho, J. A. W., Rodrigues, F.Á. (2015). Leaf gas exchange and chlorophyll a fluorescence in maize leaves infected with Stenocarpella macrospora. Phytopathology® 105, 26–34. doi: 10.1094/PHYTO-04-14-0096-R

PubMed Abstract | Crossref Full Text | Google Scholar

Bernacchi, C. J., Portis, A. R., Nakano, H., von Caemmerer, S., Long, S. P. (2002). Temperature response of mesophyll conductance. Implications for the determination of Rubisco enzyme kinetics and for limitations to photosynthesis in vivo. Plant Physiol. 130, 1992–1998. doi: 10.1104/pp.008250

PubMed Abstract | Crossref Full Text | Google Scholar

Bernacchi, C. J., Singsaas, E. L., Pimentel, C., Portis, J. A. R., Long, S. P. (2001). Improved temperature response functions for models of Rubisco-limited photosynthesis: In vivo Rubisco enzyme kinetics. Plant Cell Environ. 24, 253–259. doi: 10.1111/j.1365-3040.2001.00668.x

Crossref Full Text | Google Scholar

Bertolino, L. T., Caine, R. S., Gray, J. E. (2019). Impact of stomatal density and morphology on water-use efficiency in a changing world. Front. Plant Sci. 10. doi: 10.3389/fpls.2019.00225

PubMed Abstract | Crossref Full Text | Google Scholar

Bharath, P., Gahir, S., Raghavendra, A. S. (2021). Abscisic acid-induced stomatal closure: an important component of plant defense against abiotic and biotic stress. Front. Plant Sci. 12. doi: 10.3389/fpls.2021.615114

PubMed Abstract | Crossref Full Text | Google Scholar

Blankenagel, S., Yang, Z., Avramova, V., Schön, C.-C., Grill, E. (2018). Generating plants with improved water use efficiency. Agronomy 8, 194. doi: 10.3390/agronomy8090194

Crossref Full Text | Google Scholar

Boyer, J. S. (2015a). Turgor and the transport of CO2 and water across the cuticle (epidermis) of leaves. J. Exp. Bot. 66, 2625–2633. doi: 10.1093/jxb/erv065

PubMed Abstract | Crossref Full Text | Google Scholar

Boyer, J. S. (2015b). Impact of cuticle on calculations of the CO2 concentration inside leaves. Planta 242, 1405–1412. doi: 10.1007/s00425-015-2378-1

PubMed Abstract | Crossref Full Text | Google Scholar

Boyer, J. S., Kawamitsu, Y. (2011). Photosynthesis gas exchange system with internal CO2 directly measured. Environ. Control Biol. 49, 193–207. doi: 10.2525/ecb.49.193

Crossref Full Text | Google Scholar

Boyer, J. S., Wong, S. C., Farquhar, G. D. (1997). CO2 and Water Vapor Exchange across Leaf Cuticle (Epidermis) at Various Water Potentials. Plant Physiol. 114, 185–191. doi: 10.1104/pp.114.1.185

PubMed Abstract | Crossref Full Text | Google Scholar

Brodribb, T. (1996). Dynamics of Changing Intercellular CO2 Concentration (ci) during Drought and Determination of Minimum Functional ci. Plant Physiol. 111, 179–185. doi: 10.1104/pp.111.1.179

PubMed Abstract | Crossref Full Text | Google Scholar

Buckley, T. N., Sack, L., Farquhar, G. D. (2017). Optimal plant water economy. Plant Cell Environ. 40, 881–896. doi: 10.1111/pce.12823

PubMed Abstract | Crossref Full Text | Google Scholar

Burnham, K. P., Anderson, D. R., Burnham, K. P. (2002). Model selection and multimodel inference: a practical information-theoretic approach, 2nd ed. ed (New York: Springer).

Google Scholar

Burnham, K. P., Anderson, D. R., Huyvaert, K. P. (2011). AIC model selection and multimodel inference in behavioral ecology: some background, observations, and comparisons. Behav. Ecol. Sociobiol 65, 23–35. doi: 10.1007/s00265-010-1029-6

Crossref Full Text | Google Scholar

Busch, F. A., Deans, R. M., Holloway-Phillips, M.-M. (2017). “Estimation of photorespiratory fluxes by gas exchange,” in Photorespiration, Methods in Molecular Biology. Eds. Fernie, A. R., Bauwe, H., Weber, A. P. M. (Springer New York, New York, NY), 1–15. doi: 10.1007/978-1-4939-7225-8_1

PubMed Abstract | Crossref Full Text | Google Scholar

Cano, F. J., Sánchez-Gómez, D., Rodríguez-Calcerrada, J., Warren, C. R., Gil, L., Aranda, I. (2013). Effects of drought on mesophyll conductance and photosynthetic limitations at different tree canopy layers: Limitations to carbon uptake into the canopy. Plant Cell Environ. doi: 10.1111/pce.12103

PubMed Abstract | Crossref Full Text | Google Scholar

Carriquí, M., Roig-Oliver, M., Brodribb, T. J., Coopman, R., Gill, W., Mark, K., et al. (2019). Anatomical constraints to nonstomatal diffusion conductance and photosynthesis in lycophytes and bryophytes. New Phytol. 222, 1256–1270. doi: 10.1111/nph.15675

PubMed Abstract | Crossref Full Text | Google Scholar

Chang, H., Bonnette, M. R. (2016). Climate change and water-related ecosystem services: impacts of drought in California, USA. Ecosyst. Health Sustain 2, e01254. doi: 10.1002/ehs2.1254

Crossref Full Text | Google Scholar

Clogg, C. C., Petkova, E., Haritou, A. (1995). Statistical methods for comparing regression coefficients between models. Am. J. Sociology 100, 1261–1293. doi: 10.1086/230638

Crossref Full Text | Google Scholar

Cousins, A. B., Mullendore, D. L., Sonawane, B. V. (2020). Recent developments in mesophyll conductance in C3, C4, and crassulacean acid metabolism plants. Plant J. 101, 816–830. doi: 10.1111/tpj.14664

PubMed Abstract | Crossref Full Text | Google Scholar

Cowan, I., Farquhar, G. (1977). Stomatal function in relation to leaf metabolism and environment. Symp. Soc. Exp. Biol. 31, 471—505.

Google Scholar

De Kauwe, M. G., Lin, Y.-S., Wright, I. J., Medlyn, B. E., Crous, K. Y., Ellsworth, D. S., et al. (2016). A test of the ‘one-point method’ for estimating maximum carboxylation capacity from field-measured, light-saturated photosynthesis. New Phytol. 210, 1130–1144. doi: 10.1111/nph.13815

PubMed Abstract | Crossref Full Text | Google Scholar

Demmig-Adams, B., Cohu, C. M., Muller, O., Adams, W. W. (2012). Modulation of photosynthetic energy conversion efficiency in nature: from seconds to seasons. Photosynth Res. 113, 75–88. doi: 10.1007/s11120-012-9761-6

PubMed Abstract | Crossref Full Text | Google Scholar

Deva, C. R., Urban, M. O., Challinor, A. J., Falloon, P., Svitákova, L. (2020). Enhanced leaf cooling is a pathway to heat tolerance in common bean. Front. Plant Sci. 11. doi: 10.3389/fpls.2020.00019

PubMed Abstract | Crossref Full Text | Google Scholar

Dewar, R., Mauranen, A., Mäkelä, A., Hölttä, T., Medlyn, B., Vesala, T. (2018). New insights into the covariation of stomatal, mesophyll and hydraulic conductances from optimization models incorporating nonstomatal limitations to photosynthesis. New Phytol. 217, 571–585. doi: 10.1111/nph.14848

PubMed Abstract | Crossref Full Text | Google Scholar

Ding, L., Chaumont, F. (2020). Are aquaporins expressed in stomatal complexes promising targets to enhance stomatal dynamics? Front. Plant Sci. 11. doi: 10.3389/fpls.2020.00458

PubMed Abstract | Crossref Full Text | Google Scholar

Duursma, R. A., Blackman, C. J., Lopéz, R., Martin-StPaul, N. K., Cochard, H., Medlyn, B. E. (2019). On the minimum leaf conductance: its role in models of plant water use, and ecological and environmental controls. New Phytol. 221, 693–705. doi: 10.1111/nph.15395

PubMed Abstract | Crossref Full Text | Google Scholar

Engineer, C. B., Hashimoto-Sugimoto, M., Negi, J., Israelsson-Nordström, M., Azoulay-Shemer, T., Rappel, W.-J., et al. (2016). CO2 sensing and CO2 regulation of stomatal conductance: advances and open questions. Trends Plant Sci. 21, 16–30. doi: 10.1016/j.tplants.2015.08.014

PubMed Abstract | Crossref Full Text | Google Scholar

Evans, J. R. (2021). Mesophyll conductance: walls, membranes and spatial complexity. New Phytol. 229, 1864–1876. doi: 10.1111/nph.16968

PubMed Abstract | Crossref Full Text | Google Scholar

Evans, J. R., Kaldenhoff, R., Genty, B., Terashima, I. (2009). Resistances along the CO2 diffusion pathway inside leaves. J. Exp. Bot. 60, 2235–2248. doi: 10.1093/jxb/erp117

PubMed Abstract | Crossref Full Text | Google Scholar

Fahad, S., Bajwa, A. A., Nazir, U., Anjum, S. A., Farooq, A., Zohaib, A., et al. (2017). Crop production under drought and heat stress: plant responses and management options. Front. Plant Sci. 8. doi: 10.3389/fpls.2017.01147

PubMed Abstract | Crossref Full Text | Google Scholar

Farquhar, G. D., Sharkey, T. D. (1982). Stomatal conductance and photosynthesis. Annu. Rev. Plant Physiol. 33, 317–345. doi: 10.1146/annurev.pp.33.060182.001533

Crossref Full Text | Google Scholar

Farquhar, G. D., von Caemmerer, S., Berry, J. A. (1980). A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149, 78–90. doi: 10.1007/BF00386231

PubMed Abstract | Crossref Full Text | Google Scholar

Flexas, J. (2002). Drought-inhibition of photosynthesis in C3 plants: stomatal and non-stomatal limitations revisited. Ann. Bot. 89, 183–189. doi: 10.1093/aob/mcf027

PubMed Abstract | Crossref Full Text | Google Scholar

Flexas, J., Barbour, M. M., Brendel, O., Cabrera, H. M., Carriquí, M., Díaz-Espejo, A., et al. (2012). Mesophyll diffusion conductance to CO2: An unappreciated central player in photosynthesis. Plant Sci. 193–194, 70–84. doi: 10.1016/j.plantsci.2012.05.009

PubMed Abstract | Crossref Full Text | Google Scholar

Flexas, J., Barón, M., Bota, J., Ducruet, J.-M., Gallé, A., Galmés, J., et al. (2009). Photosynthesis limitations during water stress acclimation and recovery in the drought-adapted Vitis hybrid Richter-110 (V. berlandieri×V. rupestris). J. Exp. Bot. 60, 2361–2377. doi: 10.1093/jxb/erp069

PubMed Abstract | Crossref Full Text | Google Scholar

Flexas, J., Bota, J., Loreto, F., Cornic, G., Sharkey, T. D. (2004). Diffusive and metabolic limitations to photosynthesis under drought and salinity in C ₃ plants. Plant Biol. 6, 269–279. doi: 10.1055/s-2004-820867

PubMed Abstract | Crossref Full Text | Google Scholar

Gago, J., Daloso, D. M., Carriquí, M., Nadal, M., Morales, M., Araújo, W. L., et al. (2020). Mesophyll conductance: the leaf corridors for photosynthesis. Biochem. Soc. Trans. 48, 429–439. doi: 10.1042/BST20190312

PubMed Abstract | Crossref Full Text | Google Scholar

Galmés, J., Medrano, H., Flexas, J. (2007). Photosynthetic limitations in response to water stress and recovery in Mediterranean plants with different growth forms. New Phytol. 175, 81–93. doi: 10.1111/j.1469-8137.2007.02087.x

PubMed Abstract | Crossref Full Text | Google Scholar

García-Plazaola, J. I., Hernández, A., Olano, J. M., Becerril, J. M. (2003). The operation of the lutein epoxide cycle correlates with energy dissipation. Funct. Plant Biol. 30, 319. doi: 10.1071/FP02224

PubMed Abstract | Crossref Full Text | Google Scholar

Genty, B., Briantais, J.-M., Baker, N. R. (1989). The relationship between the quantum yield of photosynthetic electron transport and quenching of chlorophyll fluorescence. Biochim. Biophys. Acta (BBA) - Gen. Subj. 990, 87–92. doi: 10.1016/S0304-4165(89)80016-9

Crossref Full Text | Google Scholar

Gerhards, M., Rock, G., Schlerf, M., Udelhoven, T. (2016). Water stress detection in potato plants using leaf temperature, emissivity, and reflectance. Int. J. Appl. Earth Observation Geoinformation 53, 27–39. doi: 10.1016/j.jag.2016.08.004

Crossref Full Text | Google Scholar

Gervais, T., Creelman, A., Li, X.-Q., Bizimungu, B., De Koeyer, D., Dahal, K. (2021). Potato response to drought stress: physiological and growth basis. Front. Plant Sci. 12. doi: 10.3389/fpls.2021.698060

PubMed Abstract | Crossref Full Text | Google Scholar

Goffart, J.-P., Haverkort, A., Storey, M., Haase, N., Martin, M., Lebrun, P., et al. (2022). Potato production in northwestern europe (Germany, France, the Netherlands, United Kingdom, Belgium): characteristics, issues, challenges and opportunities. Potato Res. doi: 10.1007/s11540-021-09535-8

PubMed Abstract | Crossref Full Text | Google Scholar

Gordon, R., Brown, D. M., Dixon, M. A. (1997). Estimating potato leaf area index for specific cultivars. Potato Res. 40, 251–266. doi: 10.1007/BF02358007

Crossref Full Text | Google Scholar

Gourlez de la Motte, L., Beauclaire, Q., Heinesch, B., Cuntz, M., Foltýnová, L., Sigut, L., et al. (2020). Non-stomatal processes reduce gross primary productivity in temperate forest ecosystems during severe edaphic drought. Philos. Trans. R. Soc. B Biol. Sci. In Press. doi: 10.1098/RSTB-2019-0527

PubMed Abstract | Crossref Full Text | Google Scholar

Granier, A., Reichstein, M., Bréda, N., Janssens, I. A., Falge, E., Ciais, P., et al. (2007). Evidence for soil water control on carbon and water dynamics in European forests during the extremely dry year: 2003. Agric. For. Meteorology 143, 123–145. doi: 10.1016/j.agrformet.2006.12.004

Crossref Full Text | Google Scholar

Grassi, G., Magnani, F. (2005). Stomatal, mesophyll conductance and biochemical limitations to photosynthesis as affected by drought and leaf ontogeny in ash and oak trees. Plant Cell Environ. 28, 834–849. doi: 10.1111/j.1365-3040.2005.01333.x

Crossref Full Text | Google Scholar

Harley, P. C., Loreto, F., Di Marco, G., Sharkey, T. D. (1992). Theoretical considerations when estimating the mesophyll conductance to CO ₂ flux by analysis of the response of photosynthesis to CO ₂. Plant Physiol. 98, 1429–1436. doi: 10.1104/pp.98.4.1429

PubMed Abstract | Crossref Full Text | Google Scholar

Hartick, C., Furusho-Percot, C., Clark, M. P., Kollet, S. (2022). An interannual drought feedback loop affects the surface energy balance and cloud properties. Geophysical Res. Lett. 49, e2022GL100924. doi: 10.1029/2022GL100924

Crossref Full Text | Google Scholar

Hendrawan, V. S. A., Kim, W., Touge, Y., Ke, S., Komori, D. (2022). A global-scale relationship between crop yield anomaly and multiscalar drought index based on multiple precipitation data. Environ. Res. Lett. 17, 014037. doi: 10.1088/1748-9326/ac45b4

Crossref Full Text | Google Scholar

Héroult, A., Lin, Y.-S., Bourne, A., Medlyn, B. E., Ellsworth, D. S. (2013). Optimal stomatal conductance in relation to photosynthesis in climatically contrasting Eucalyptus species under drought: Stomatal responses of eucalyptus under drought. Plant Cell Environ. 36, 262–274. doi: 10.1111/j.1365-3040.2012.02570.x

PubMed Abstract | Crossref Full Text | Google Scholar

Huang, Z. (2020). Soil water availability threshold indicator was determined by using plant physiological responses under drought conditions. Ecol. Indic. 10. doi: 10.1016/j.ecolind.2020.106740

Crossref Full Text | Google Scholar

Jones, H. G. (1985). Partitioning stomatal and non-stomatal limitations to photosynthesis. Plant Cell Environ. 8, 95–104. doi: 10.1111/j.1365-3040.1985.tb01227.x

Crossref Full Text | Google Scholar

Kala, J., De Kauwe, M. G., Pitman, A. J., Lorenz, R., Medlyn, B. E., Wang, Y.-P., et al. (2015). Implementation of an optimal stomatal conductance scheme in the Australian Community Climate Earth Systems Simulator (ACCESS1.3b). Geosci. Model. Dev. 8, 3877–3889. doi: 10.5194/gmd-8-3877-2015

Crossref Full Text | Google Scholar

Kang, H., Sridhar, V., Mainuddin, M., Trung, L. D. (2021). Future rice farming threatened by drought in the Lower Mekong Basin. Sci. Rep. 11, 9383. doi: 10.1038/s41598-021-88405-2

PubMed Abstract | Crossref Full Text | Google Scholar

Knauer, J., El-Madany, T. S., Zaehle, S., Migliavacca, M. (2018). Bigleaf—An R package for the calculation of physical and physiological ecosystem properties from eddy covariance data. PloS One 13, e0201114. doi: 10.1371/journal.pone.0201114

PubMed Abstract | Crossref Full Text | Google Scholar

Knauer, J., Zaehle, S., De Kauwe, M. G., Haverd, V., Reichstein, M., Sun, Y. (2020). Mesophyll conductance in land surface models: effects on photosynthesis and transpiration. Plant J. 101, 858–873. doi: 10.1111/tpj.14587

PubMed Abstract | Crossref Full Text | Google Scholar

Kramer, D. M., Johnson, G., Kiirats, O., Edwards, G. E. (2004). New fluorescence parameters for the determination of Q _A redox state and excitation energy fluxes. Photosynthesis Res. 79, 209–218. doi: 10.1023/B:PRES.0000015391.99477.0d

PubMed Abstract | Crossref Full Text | Google Scholar

Lamour, J., Davidson, K. J., Ely, K. S., Le Moguédec, G., Leakey, A. D. B., Li, Q., et al. (2022). An improved representation of the relationship between photosynthesis and stomatal conductance leads to more stable estimation of conductance parameters and improves the goodness-of-fit across diverse data sets. Global Change Biol. 28, 3537–3556. doi: 10.1111/gcb.16103

PubMed Abstract | Crossref Full Text | Google Scholar

Lawrence, D. M., Fisher, R. A., Koven, C. D., Oleson, K. W., Swenson, S. C., Bonan, G., et al. (2019). The community land model version 5: description of new features, benchmarking, and impact of forcing uncertainty. J. Adv. Model. Earth Syst. 11, 4245–4287. doi: 10.1029/2018MS001583

Crossref Full Text | Google Scholar

Lawson, T., Simkin, A. J., Kelly, G., Granot, D. (2014). Mesophyll photosynthesis and guard cell metabolism impacts on stomatal behaviour. New Phytol. 203, 1064–1081. doi: 10.1111/nph.12945

PubMed Abstract | Crossref Full Text | Google Scholar

Lemonnier, P., Lawson, T. (2023). Calvin cycle and guard cell metabolism impact stomatal function. Semin. Cell Dev. Biol., S1084952123000502. doi: 10.1016/j.semcdb.2023.03.001

PubMed Abstract | Crossref Full Text | Google Scholar

Li, S., Liu, J., Liu, H., Qiu, R., Gao, Y., Duan, A. (2021). Role of hydraulic signal and ABA in decrease of leaf stomatal and mesophyll conductance in soil drought-stressed tomato. Front. Plant Sci. 12. doi: 10.3389/fpls.2021.653186

PubMed Abstract | Crossref Full Text | Google Scholar

Limousin, J.-M., Misson, L., Lavoir, A.-V., Martin, N. K., Rambal, S. (2010). Do photosynthetic limitations of evergreen Quercus ilex leaves change with long-term increased drought severity? Plant Cell Environ. doi: 10.1111/j.1365-3040.2009.02112.x

PubMed Abstract | Crossref Full Text | Google Scholar

Lupo, Y., Moshelion, M. (2024). The balance of survival: Comparative drought response in wild and domesticated tomatoes. Plant Sci. 339, 111928. doi: 10.1016/j.plantsci.2023.111928

PubMed Abstract | Crossref Full Text | Google Scholar

Lutaladio, N., Castaldi, L. (2009). Potato: The hidden treasure. J. Food Composition Anal. 22, 491–493. doi: 10.1016/j.jfca.2009.05.002

Crossref Full Text | Google Scholar

Manzoni, S., Vico, G., Katul, G., Fay, P. A., Polley, W., Palmroth, S., et al. (2011). Optimizing stomatal conductance for maximum carbon gain under water stress: a meta-analysis across plant functional types and climates: Optimal leaf gas exchange under water stress. Funct. Ecol. 25, 456–467. doi: 10.1111/j.1365-2435.2010.01822.x

Crossref Full Text | Google Scholar

Marchin, R. M., Backes, D., Ossola, A., Leishman, M. R., Tjoelker, M. G., Ellsworth, D. S. (2022). Extreme heat increases stomatal conductance and drought-induced mortality risk in vulnerable plant species. Global Change Biol. 28, 1133–1146. doi: 10.1111/gcb.15976

PubMed Abstract | Crossref Full Text | Google Scholar

Marchin, R. M., Medlyn, B. E., Tjoelker, M. G., Ellsworth, D. S. (2023). Decoupling between stomatal conductance and photosynthesis occurs under extreme heat in broadleaf tree species regardless of water access. Global Change Biol. 29, 6319–6335. doi: 10.1111/gcb.16929

PubMed Abstract | Crossref Full Text | Google Scholar

Martin, B., Ruiz-Torres, N. A. (1992). Effects of water-deficit stress on photosynthesis, its components and component limitations, and on water use efficiency in wheat ( Triticum aestivum L.). Plant Physiol. 100, 733–739. doi: 10.1104/pp.100.2.733

PubMed Abstract | Crossref Full Text | Google Scholar

Martínez-Vilalta, J., Poyatos, R., Aguadé, D., Retana, J., Mencuccini, M. (2014). A new look at water transport regulation in plants. New Phytol. 204, 105–115. doi: 10.1111/nph.12912

PubMed Abstract | Crossref Full Text | Google Scholar

McAdam, S. A. M., Brodribb, T. J. (2016). Linking turgor with ABA biosynthesis: implications for stomatal responses to vapor pressure deficit across land plants. Plant Physiol. 171, 2008–2016. doi: 10.1104/pp.16.00380

PubMed Abstract | Crossref Full Text | Google Scholar

Medlyn, B. E., De Kauwe, M. G., Lin, Y.-S., Knauer, J., Duursma, R. A., Williams, C. A., et al. (2017). How do leaf and ecosystem measures of water-use efficiency compare? New Phytol. 216, 758–770. doi: 10.1111/nph.14626

PubMed Abstract | Crossref Full Text | Google Scholar

Medlyn, B. E., Duursma, R. A., Eamus, D., Ellsworth, D. S., Prentice, I. C., Barton, C. V. M., et al. (2011). Reconciling the optimal and empirical approaches to modelling stomatal conductance: RECONCILING OPTIMAL AND EMPIRICAL STOMATAL MODELS. Global Change Biol. 17, 2134–2144. doi: 10.1111/j.1365-2486.2010.02375.x

Crossref Full Text | Google Scholar

Miao, Z., Xu, M., Lathrop, R. G., Wang, Y. (2009). Comparison of the A-C_c curve fitting methods in determining maximum ribulose 1·5-bisphosphate carboxylase/oxygenase carboxylation rate, potential light saturated electron transport rate and leaf dark respiration. Plant Cell Environ. 32, 109–122. doi: 10.1111/j.1365-3040.2008.01900.x

PubMed Abstract | Crossref Full Text | Google Scholar

Miguez, F. (2023). nlraa: Nonlinear regression for agricultural applications. (R PackageVersion 1.9.7). Available at: https://CRAN.R-project.org/package=nlraa.

Google Scholar

Mrad, A., Sevanto, S., Domec, J.-C., Liu, Y., Nakad, M., Katul, G. (2019). A dynamic optimality principle for water use strategies explains isohydric to anisohydric plant responses to drought. Front. For. Glob. Change 2. doi: 10.3389/ffgc.2019.00049

Crossref Full Text | Google Scholar

Nadal, M., Flexas, J. (2018). “M esophyll C onductance to CO 2 D iffusion : E ffects of D rought and O pportunities for I mprovement,” in Water Scarcity and Sustainable Agriculture in Semiarid Environment (Elsevier), 403–438. doi: 10.1016/B978-0-12-813164-0.00017-X

Crossref Full Text | Google Scholar

Nguyen, T. B.-A., Lefoulon, C., Nguyen, T.-H., Blatt, M. R., Carroll, W. (2023). Engineering stomata for enhanced carbon capture and water-use efficiency. Trends Plant Sci. 28, 1290–1309. doi: 10.1016/j.tplants.2023.06.002

PubMed Abstract | Crossref Full Text | Google Scholar

Niinemets, Ü., Cescatti, A., Rodeghiero, M., Tosens, T. (2006). Complex adjustments of photosynthetic potentials and internal diffusion conductance to current and previous light availabilities and leaf age in Mediterranean evergreen species Quercus ilex. Plant Cell Environ. 29, 1159–1178. doi: 10.1111/j.1365-3040.2006.01499.x

PubMed Abstract | Crossref Full Text | Google Scholar

Obidiegwu, J. E. (2015). Coping with drought: stress and adaptive responses in potato and perspectives for improvement. Front. Plant Sci. 6. doi: 10.3389/fpls.2015.00542

PubMed Abstract | Crossref Full Text | Google Scholar

Osmond, C. B., Björkman, O., Anderson, D. J. (1980). “Physiological processes in plant ecology: the structure for a synthesis,” in Physiological Processes in Plant Ecology: Toward a Synthesis with Atriplex. Eds. Osmond, C. B., Björkman, O., Anderson, D. J. (Springer Berlin Heidelberg, Berlin, Heidelberg), 1–11. doi: 10.1007/978-3-642-67637-6_1

Crossref Full Text | Google Scholar

Paternoster, R., Brame, R., Mazerolle, P., Piquero, A. (1998). USING THE CORRECT STATISTICAL TEST FOR THE EQUALITY OF REGRESSION COEFFICIENTS. Criminology 36, 859–866. doi: 10.1111/j.1745-9125.1998.tb01268.x

Crossref Full Text | Google Scholar

Perez-Martin, A., Michelazzo, C., Torres-Ruiz, J. M., Flexas, J., Fernández, J. E., Sebastiani, L., et al. (2014). Regulation of photosynthesis and stomatal and mesophyll conductance under water stress and recovery in olive trees: correlation with gene expression of carbonic anhydrase and aquaporins. J. Exp. Bot. 65, 3143–3156. doi: 10.1093/jxb/eru160

PubMed Abstract | Crossref Full Text | Google Scholar

Peters, W., van der Velde, I. R., van Schaik, E., Miller, J. B., Ciais, P., Duarte, H. F., et al. (2018). Increased water-use efficiency and reduced CO2 uptake by plants during droughts at a continental scale. Nat. Geosci 11, 744–748. doi: 10.1038/s41561-018-0212-7

PubMed Abstract | Crossref Full Text | Google Scholar

Pinheiro, C., Chaves, M. M. (2011). Photosynthesis and drought: can we make metabolic connections from available data? J. Exp. Bot. 62, 869–882. doi: 10.1093/jxb/erq340

PubMed Abstract | Crossref Full Text | Google Scholar

Pirasteh-Anosheh, H., Saed-Moucheshi, A., Pakniyat, H., Pessarakli, M. (2016). “Stomatal responses to drought stress,” in Water Stress and Crop Plants. Ed. Ahmad, P. (John Wiley & Sons, Ltd, Chichester, UK), 24–40. doi: 10.1002/9781119054450.ch3

Crossref Full Text | Google Scholar

Pons, T. L., Flexas, J., von Caemmerer, S., Evans, J. R., Genty, B., Ribas-Carbo, M., et al. (2009). Estimating mesophyll conductance to CO2: methodology, potential errors, and recommendations. J. Exp. Bot. 60, 2217–2234. doi: 10.1093/jxb/erp081

PubMed Abstract | Crossref Full Text | Google Scholar

Ramírez, D. A., Yactayo, W., Rens, L. R., Rolando, J. L., Palacios, S., De Mendiburu, F., et al. (2016). Defining biological thresholds associated to plant water status for monitoring water restriction effects: Stomatal conductance and photosynthesis recovery as key indicators in potato. Agric. Water Manage. 177, 369–378. doi: 10.1016/j.agwat.2016.08.028

Crossref Full Text | Google Scholar

Reynolds-Henne, C. E., Langenegger, A., Mani, J., Schenk, N., Zumsteg, A., Feller, U. (2010). Interactions between temperature, drought and stomatal opening in legumes. Environ. Exp. Bot. 68, 37–43. doi: 10.1016/j.envexpbot.2009.11.002

Crossref Full Text | Google Scholar

Richards, L. A. (1948). Porous plate apparatus for measuring moisture retention and transmission by soil. Soil Sci. 66. doi: 10.1097/00010694-194808000-00003

Crossref Full Text | Google Scholar

Rogers, A., Medlyn, B. E., Dukes, J. S., Bonan, G., von Caemmerer, S., Dietze, M. C., et al. (2017). A roadmap for improving the representation of photosynthesis in Earth system models. New Phytol. 213, 22–42. doi: 10.1111/nph.14283

PubMed Abstract | Crossref Full Text | Google Scholar

Romero, A. P., Alarcón, A., Valbuena, R. I., Galeano, C. H. (2017). Physiological assessment of water stress in potato using spectral information. Front. Plant Sci. 8. doi: 10.3389/fpls.2017.01608

PubMed Abstract | Crossref Full Text | Google Scholar

Rouhi, V., Samson, R., Lemeur, R., Damme, P. V. (2007). Photosynthetic gas exchange characteristics in three different almond species during drought stress and subsequent recovery. Environ. Exp. Bot. 13. doi: 10.1016/j.envexpbot.2005.10.001

Crossref Full Text | Google Scholar

Ryu, Y., Berry, J. A., Baldocchi, D. D. (2019). What is global photosynthesis? History, uncertainties and opportunities. Remote Sens. Environ. 223, 95–114. doi: 10.1016/j.rse.2019.01.016

Crossref Full Text | Google Scholar

Sabot, M. E. B., De Kauwe, M. G., Pitman, A. J., Medlyn, B. E., Ellsworth, D. S., Martin-StPaul, N. K., et al. (2022). One stomatal model to rule them all? Toward improved representation of carbon and water exchange in global models. J. Adv. Model. Earth Syst. 14. doi: 10.1029/2021MS002761

Crossref Full Text | Google Scholar

Samaniego, L., Thober, S., Kumar, R., Wanders, N., Rakovec, O., Pan, M., et al. (2018). Anthropogenic warming exacerbates European soil moisture droughts. Nat. Clim Change 8, 421–426. doi: 10.1038/s41558-018-0138-5

Crossref Full Text | Google Scholar

Scoffoni, C., McKown, A. D., Rawls, M., Sack, L. (2012). Dynamics of leaf hydraulic conductance with water status: quantification and analysis of species differences under steady state. J. Exp. Bot. 63, 643–658. doi: 10.1093/jxb/err270

PubMed Abstract | Crossref Full Text | Google Scholar

Shi, X., Bloom, A. (2021). Photorespiration: the futile cycle? Plants 10, 908. doi: 10.3390/plants10050908

PubMed Abstract | Crossref Full Text | Google Scholar

Sorrentino, G., Haworth, M., Wahbi, S., Mahmood, T., Zuomin, S., Centritto, M. (2016). Abscisic acid induces rapid reductions in mesophyll conductance to carbon dioxide. PloS One 11, e0148554. doi: 10.1371/journal.pone.0148554

PubMed Abstract | Crossref Full Text | Google Scholar

Sperry, J. S., Venturas, M. D., Anderegg, W. R. L., Mencuccini, M., Mackay, D. S., Wang, Y., et al. (2017). Predicting stomatal responses to the environment from the optimization of photosynthetic gain and hydraulic cost: A stomatal optimization model. Plant Cell Environ. 40, 816–830. doi: 10.1111/pce.12852

PubMed Abstract | Crossref Full Text | Google Scholar

Sprenger, H., Kurowsky, C., Horn, R., Erban, A., Seddig, S., Rudack, K., et al. (2016). The drought response of potato reference cultivars with contrasting tolerance. Plant Cell Environ. 39, 2370–2389. doi: 10.1111/pce.12780

PubMed Abstract | Crossref Full Text | Google Scholar

Stirbet, A., Lazár, D., Guo, Y., Govindjee, G. (2020). Photosynthesis: basics, history and modelling. Ann. Bot. 126, 511–537. doi: 10.1093/aob/mcz171

PubMed Abstract | Crossref Full Text | Google Scholar

Tan, Z.-H., Wu, Z.-X., Hughes, A. C., Schaefer, D., Zeng, J., Lan, G.-Y., et al. (2017). On the ratio of intercellular to ambient CO2 (c i/c a) derived from ecosystem flux. Int. J. Biometeorol 61, 2059–2071. doi: 10.1007/s00484-017-1403-4

PubMed Abstract | Crossref Full Text | Google Scholar

Théroux-Rancourt, G., Éthier, G., Pepin, S. (2014). Threshold response of mesophyll CO2 conductance to leaf hydraulics in highly transpiring hybrid poplar clones exposed to soil drying. J. Exp. Bot. 65, 741–753. doi: 10.1093/jxb/ert436

PubMed Abstract | Crossref Full Text | Google Scholar

Théroux-Rancourt, G., Gilbert, M. E. (2017). The light response of mesophyll conductance is controlled by structure across leaf profiles. Plant Cell Environ. 40, 726–740. doi: 10.1111/pce.12890

PubMed Abstract | Crossref Full Text | Google Scholar

Tholen, D., Boom, C., Noguchi, K., Ueda, S., Katase, T., Terashima, I. (2008). The chloroplast avoidance response decreases internal conductance to CO ₂ diffusion in Arabidopsis thaliana leaves. Plant Cell Environ. 31, 1688–1700. doi: 10.1111/j.1365-3040.2008.01875.x

PubMed Abstract | Crossref Full Text | Google Scholar

Trenberth, K. E., Dai, A., van der Schrier, G., Jones, P. D., Barichivich, J., Briffa, K. R., et al. (2014). Global warming and changes in drought. Nat. Clim Change 4, 17–22. doi: 10.1038/nclimate2067

Crossref Full Text | Google Scholar

Urban, L., Aarrouf, J., Bidel, L. P. R. (2017). Assessing the effects of water deficit on photosynthesis using parameters derived from measurements of leaf gas exchange and of chlorophyll a fluorescence. Front. Plant Sci. 8. doi: 10.3389/fpls.2017.02068

PubMed Abstract | Crossref Full Text | Google Scholar

Valentini, R., Epron, D., Angelis, P., Matteucci, G., Dreyer, E. (1995). In situ estimation of net CO2 assimilation, photosynthetic electron flow and photorespiration in Turkey oak (Q. cerris L.) leaves: diurnal cycles under different levels of water supply. Plant Cell Environ. 18, 631–640. doi: 10.1111/j.1365-3040.1995.tb00564.x

Crossref Full Text | Google Scholar

van Genuchten, M. (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. America J. 44, 892–898. doi: 10.2136/sssaj1980.03615995004400050002x

Crossref Full Text | Google Scholar

Veromann-Jürgenson, L.-L., Tosens, T., Laanisto, L., Niinemets, Ü. (2017). Extremely thick cell walls and low mesophyll conductance: welcome to the world of ancient living! J. Exp. Bot. 68, 1639–1653. doi: 10.1093/jxb/erx045

PubMed Abstract | Crossref Full Text | Google Scholar

Vidale, P. L., Egea, G., McGuire, P. C., Todt, M., Peters, W., Müller, O., et al. (2021). On the treatment of soil water stress in GCM simulations of vegetation physiology. Front. Environ. Sci. 9. doi: 10.3389/fenvs.2021.689301

Crossref Full Text | Google Scholar

Von Caemmerer, S. (2013). Steady-state models of photosynthesis: Steady-state models of photosynthesis. Plant Cell Environ. 36, 1617–1630. doi: 10.1111/pce.12098

PubMed Abstract | Crossref Full Text | Google Scholar

Vos, J., Oyarzún, P. J. (1987). Photosynthesis and stomatal conductance of potato leaves?effects of leaf age, irradiance, and leaf water potential. Photosynth Res. 11, 253–264. doi: 10.1007/BF00055065

PubMed Abstract | Crossref Full Text | Google Scholar

Walker, B. J., Ort, D. R. (2015). Improved method for measuring the apparent CO ₂ photocompensation point resolves the impact of multiple internal conductances to CO ₂ to net gas exchange: Photocompensation point measurements. Plant Cell Environ. 38, 2462–2474. doi: 10.1111/pce.12562

PubMed Abstract | Crossref Full Text | Google Scholar

Wang, X., Du, T., Huang, J., Peng, S., Xiong, D. (2018). Leaf hydraulic vulnerability triggers the decline in stomatal and mesophyll conductance during drought in rice. J. Exp. Bot. 69, 4033–4045. doi: 10.1093/jxb/ery188

PubMed Abstract | Crossref Full Text | Google Scholar

Wang, Z., Li, G., Sun, H., Ma, L., Guo, Y., Zhao, Z., et al. (2018). Effects of drought stress on photosynthesis and photosynthetic electron transport chain in young apple tree leaves. Biol. Open bio., 035279. doi: 10.1242/bio.035279

PubMed Abstract | Crossref Full Text | Google Scholar

Wilson, K. B., Baldocchi, D. D., Hanson, P. J. (2000). Quantifying stomatal and non-stomatal limitations to carbon assimilation resulting from leaf aging and drought in mature deciduous tree species. Tree Physiol. 20, 787–797. doi: 10.1093/treephys/20.12.787

PubMed Abstract | Crossref Full Text | Google Scholar

Wong, S. C., Cowan, I. R., Farquhar, G. D. (1979). Stomatal conductance correlates with photosynthetic capacity. Nature 282, 424–426. doi: 10.1038/282424a0

Crossref Full Text | Google Scholar

Xiao, Y., Zhu, X. (2017). Components of mesophyll resistance and their environmental responses: A theoretical modelling analysis. Plant Cell Environ. 40, 2729–2742. doi: 10.1111/pce.13040

PubMed Abstract | Crossref Full Text | Google Scholar

Xiong, D., Douthe, C., Flexas, J. (2018). Differential coordination of stomatal conductance, mesophyll conductance, and leaf hydraulic conductance in response to changing light across species: Coordination of CO ₂ diffusion and H ₂ O transport inside leaves. Plant Cell Environ. 41, 436–450. doi: 10.1111/pce.13111

PubMed Abstract | Crossref Full Text | Google Scholar

Yin, X., Amthor, J. S. (2024). Estimating leaf day respiration from conventional gas exchange measurements. New Phytol. 241, 52–58. doi: 10.1111/nph.19330

PubMed Abstract | Crossref Full Text | Google Scholar

Zait, Y., Schwartz, A. (2018). Climate-related limitations on photosynthesis and drought-resistance strategies of Ziziphus spina-christi. Front. Forests Global Change 1. doi: 10.3389/ffgc.2018.00003

Crossref Full Text | Google Scholar

Zhang, P., Yang, X., Manevski, K., Li, S., Wei, Z., Andersen, M. N., et al. (2022). Physiological and growth responses of potato (Solanum tuberosum L.) to air temperature and relative humidity under soil water deficits. Plants 11, 1126. doi: 10.3390/plants11091126

PubMed Abstract | Crossref Full Text | Google Scholar

Zhou, S., Duursma, R. A., Medlyn, B. E., Kelly, J. W. G., Prentice, I. C. (2013). How should we model plant responses to drought? An analysis of stomatal and non-stomatal responses to water stress. Agric. For. Meteorology 182–183, 204–214. doi: 10.1016/j.agrformet.2013.05.009

Crossref Full Text | Google Scholar

Zhou, H., Zhou, G., He, Q., Zhou, L., Ji, Y., Lv, X. (2021). Capability of leaf water content and its threshold values in reflection of soil–plant water status in maize during prolonged drought. Ecol. Indic. 124, 107395. doi: 10.1016/j.ecolind.2021.107395

Crossref Full Text | Google Scholar

Zhu, K., Yuan, F. H., Wang, A. Z., Wu, J. B., Guan, D. X., Jin, C. J., et al. (2021). Stomatal, mesophyll and biochemical limitations to soil drought and rewatering in relation to intrinsic water-use efficiency in Manchurian ash and Mongolian oak. Photosynt. 59, 49–60. doi: 10.32615/ps.2020.084

Crossref Full Text | Google Scholar