Research on emergency scheduling based on improved genetic algorithm in harvester failure scenarios

In response to the issue of harvesting machine failures affecting crop harvesting timing, this study develops an emergency scheduling model and proposes a hybrid optimization algorithm that combines a genetic algorithm and an ant colony algorithm. By enhancing the genetic algorithm’s crossover and mutation methods and incorporating the ant colony algorithm, the proposed algorithm can prevent local optima, thus minimizing disruptions to the overall scheduling plan. Field data from Deyang, Sichuan Province, were utilized, and simulations on various harvesting machines experiencing random faults were conducted. Results indicated that the improved genetic algorithm reduced the optimal comprehensive scheduling cost during random fault occurrences by 47.49%, 19.60%, and 32.45% compared to the basic genetic algorithm and by 34.70%, 14.80%, and 24.40% compared to the ant colony algorithm. The improved algorithm showcases robust global optimization capabilities, high stability, and rapid convergence, offering effective emergency scheduling solutions in case of harvesting machine failures. Furthermore, a visual management system for agricultural machinery scheduling was developed to provide software support for optimizing agricultural machinery scheduling.

1 Introduction

Wheat harvesting is highly time-sensitive, with the optimal period for harvesting being very short. As the saying goes, “Harvest at ninety percent ripeness for full yield; at full ripeness, ten percent is lost.” Therefore, the scheduling of agricultural machinery is a crucial component of modern agriculture and is closely related to the productivity of agricultural operations (Bochtis et al., 2014). Proper scheduling can strategically organize the operational time and areas for machinery, preventing aimless movement, reducing operational conflicts, and minimizing repeated operations. This optimization substantially enhances agricultural production efficiency, fostering the modernization and sustainable development of agricultural operations. It is evident that the advancement of modernized agriculture relies heavily on effective machinery scheduling processes (Chen et al., 2021; Li, 2022). However, the implementation of scheduling plans is inherently dynamic. During peak seasons, the high demand for harvesters and prolonged continuous operation can lead to inevitable machinery failures. Solely relying on manual emergency scheduling methods based on experience proves insufficient for addressing the complexities of real-life situations. The absence of a proficient emergency scheduling strategy can result in extensive delays in harvests, with crops missing their optimal harvesting periods and consequently delaying the progress of harvesting operations. Adverse effects ripple throughout the entire production chain (Liu D. et al., 2022; Brewer et al., 2022). Therefore, it is urgent to explore advanced emergency scheduling methodologies for harvesters in the event of failures to enhance the overall level of scheduling efficiency (Sun et al., 2022).

Currently, the agricultural machinery scheduling has received much attention and achieved fruitful results. Scholars have tackled the scheduling problem with intelligent algorithms (Zhang W. et al., 2022; Hou et al., 2022), such as genetic algorithms (Ma et al., 2022; Liu et al., 2024), ant colony algorithms (Wang et al., 2023), particle swarm algorithms (Worasan et al., 2020; Huang et al., 2023), and hybrid optimization algorithms (He et al., 2019; He and Li, 2021; Feng et al., 2024). Similar intelligent algorithms have improved computational efficiency and the ability to make fast and accurate decisions in scheduling agricultural machines, providing a powerful tool for realizing rational agricultural machinery scheduling (Zhang W. P. et al., 2022; Zhang F. et al., 2022). In static scheduling research, various scholars have explored different perspectives, presenting a layered progression of logical relationships. Plessen (2019) developed a harvest planning method based on the coupling of crop assignment and vehicle routing, addressing the optimal sequence for servicing fields of the same crop during harvest. He et al. (2018) proposed a wheat harvest scheduling model for agricultural machinery cooperatives in China, aiming to minimize the harvesting period on fragmental farmlands while considering the constraint of minimizing differences in harvesting times among different combine harvesters. Building on this, Wang and Huang (2022) extended the research by proposing a mixed-integer linear programming model that integrates operator assignment, aiming to minimize total working time and costs. Yang et al. (2022) introduced an improved whale optimization algorithm to optimize the scheduling of multiple types of combined harvesters, aiming to comprehensively minimize total costs. Li (2022) presented an intelligent scheduling method based on non-dominated sorting genetic algorithm III (NSGA-III) and an improved ant colony algorithm for multi-machine collaborative operations, aiming to reduce operation time and enhance efficiency. Tian et al. (2023) developed and validated a multi-objective waypoint planning algorithm for drones in orchard spraying, using an improved ant colony algorithm that optimizes nodes through an improved heuristic function and introduces a ranking optimization mechanism to accelerate algorithm iterations. Overall, these studies demonstrate the progressive evolution from basic scheduling models to intelligent optimization algorithms that improve the scheduling efficiency and operational effectiveness of agricultural machinery by comprehensively considering machines, operators, and operational environments.

The aforementioned study has made significant advances in static scheduling; however, it faces challenges in ensuring reasonable scheduling when encountering disruptive events. Agricultural machinery scheduling is a dynamic and complex process, and the emergence of agricultural machinery failures hinders the original scheduling plan, which needs to be changed for the first time. Some scholars have included dynamic factors in the study of agriculture machinery scheduling. For example, Okulewicz and Mańdziuk (2017) simplified dynamic vehicle scheduling by introducing a swift, event-responsive tactic. Cao et al. (2021) optimized task assignments by balancing the workload among agricultural machinery. Seyyedhasani and Dvorak (2018) applied enhanced heuristic algorithms for agricultural machinery scheduling, accommodating field-level dynamics. Hu et al. (2020) proposed a two-stage method for agricultural scheduling planning, validated through case studies. Liu et al. (2021) introduced an improved immune algorithm, enhancing cross-regional machinery scheduling efficiency. Furthermore, Fernandez et al. (2020) employed particle swarm optimization and shuffled frog-leaping algorithms to develop a dynamic charging scheduling scheme, optimizing charging costs and improving the economic efficiency of charging stations. Liu Y. X. et al. (2022) implemented a novel hyper-heuristic algorithm for multi-line bus dynamic scheduling, significantly reducing waiting times. In the realm of agricultural drone scheduling, Chen et al. (2023) introduced a Levy annealing algorithm, demonstrating exceptional performance in schedule optimization. Moreover, Fatemi-Anaraki et al. (2023) explored the impacts of rescheduling within robotic manufacturing, providing insights into dynamic scheduling strategies. Taken together, these investigations signal an evolution toward advanced algorithmic optimization, which is critical for enhancing the dynamic scheduling of agricultural machinery and operational efficiency in farming practices.

However, the aforementioned literature has not yet conducted an in-depth study on harvester malfunctions, and the solutions for other disruptive events mostly involve complete rescheduling for optimization. These methods can cause significant disruption to the entire system, especially in the highly time-sensitive field of agriculture. This paper conducts an in-depth study on harvester malfunctions, aiming to address the disruptions caused by such failures and minimize the resulting losses. This study utilizes genetic algorithms (GA) as its primary framework, enhancing crossover and mutation techniques while incorporating ant colony algorithms to boost the overall algorithm’s local search capabilities. The objective is to enable prompt and precise decision-making in the face of harvester failures, ultimately minimizing the impact of breakdowns on scheduling plans. The key contributions of this study include the following:

(1) Developed an emergency scheduling model focused on minimizing the overall scheduling cost, taking interference management as the central concept and utilizing the theory of multi-agricultural machinery scheduling operations as the foundation. The objective is to mitigate the disruption to the scheduling plan in case of a harvester breakdown.

(2) Designed the solution algorithm of the model. The genetic algorithm was used as the framework, and the crossover and mutation methods were improved. The ant colony algorithm was introduced to improve the local search ability of the overall algorithm to reduce the impact of the scheduling plan due to harvester failure.

(3) In the case study, the improved genetic algorithm proved to be superior in emergency scheduling in case of harvester failure by constructing a visualized management system for scheduling agricultural machinery and selecting actual data for simulation tests.

2 Agricultural emergency scheduling models

2.1 Problem description

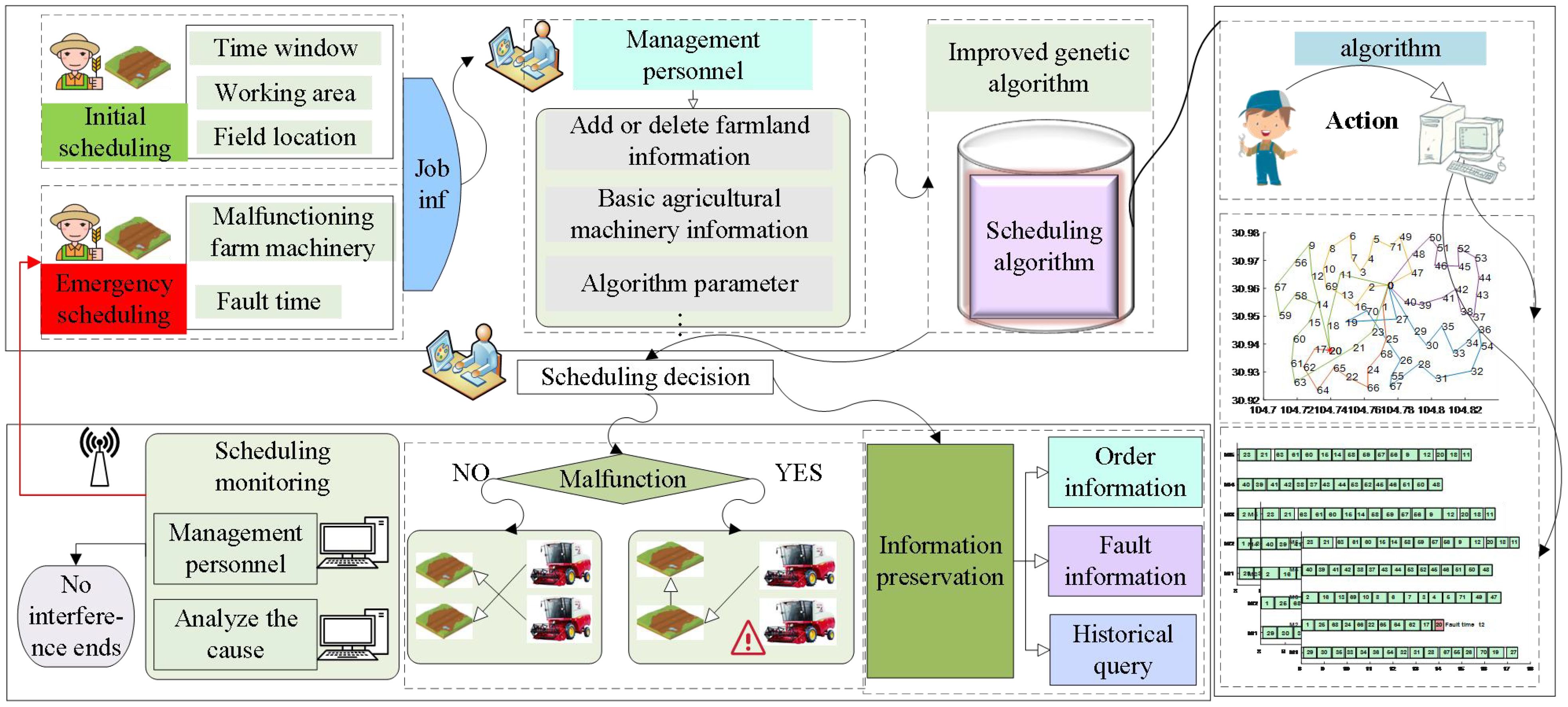
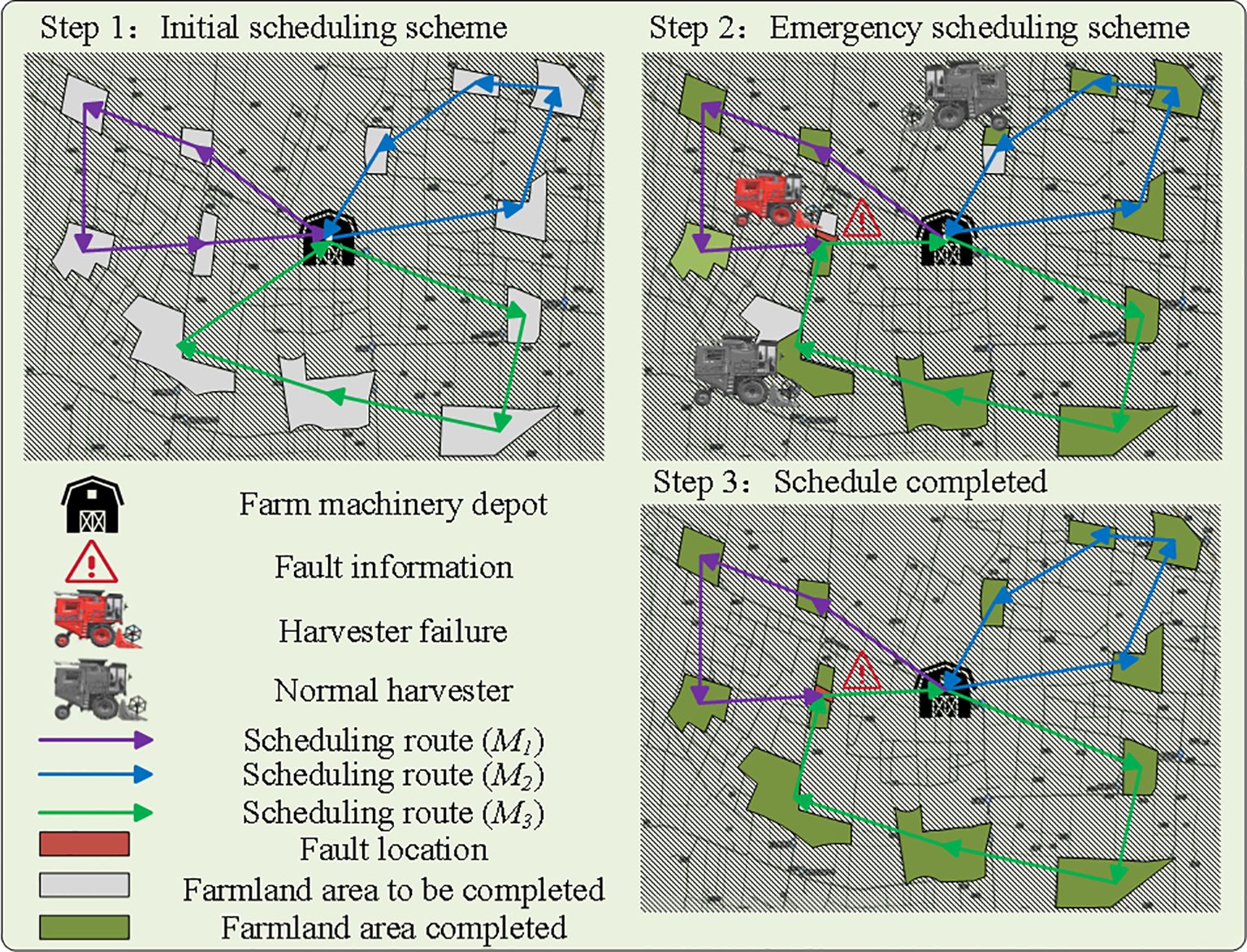
The emergency scheduling problem in case of a harvester breakdown can be described as follows: an agricultural cooperative schedules M = {M₁, M₂,…, M_M} harvesters to F = {F₁, F₂,…, F_N} farmland for operation, and when k harvesters break down and are unable to continue their operational tasks, the remaining M = {M₁, M₂,…, M_{M − k}} harvesters operate on the remaining farmland according to the scheduling goal and return to the agricultural cooperative after completing the operation. The whole scheduling process is shown in Figure 1.

Figure 1

Figure 1 Schematic diagram of the scheduling process for agricultural machinery.

Prior to the study, hypothetical preconditions for this emergency scheduling problem are first presented:

(1) Each farmland requires only one harvester to operate.

(2) All harvesters are traveling at a uniform speed during the transfer process.

(3) Broken-down harvesters return to the farm cooperative for repair by default.

(4) All functioning machinery returns to the machinery depot after completing their tasks.

(5) Only faulty harvesters break down into disturbing events during the scheduling process.

(6) All harvester operations progress according to the scheduling plan.

(7) It is assumed that all harvesters in the farm cooperative have been tasked and that no additional assignments will be considered.

(8) The location information of the farmland and harvesters is known, and the time window of the farmland is known and does not change.

(9) In this research study, a soft time window constraint is used, which will incur waiting costs if the harvester is earlier than the operating time and penalty costs if the operating time is exceeded.

2.2 Mathematical model

Based on the problem description of emergency scheduling, the various influencing factors were measured, and the emergency scheduling model with a soft time window and the optimization objective of minimizing the integrated scheduling cost was developed. The set of farmland F = {F₁, F₂,…, F_N}, with F_i representing the ith farmland, and its attributes are described as F_i = {Loc_F_i, S_F_i}, where Loc_F_i and S_F_i denote the location and area of the farmland F_i, respectively, and i ∈ [1, N]. The set of harvesters M = {M₁, M₂, …, M_M}, with M_k representing the kth harvester, is described by its attributes as M_k = {Loc_M_k, V_M_k, E_M_k}, where Loc_M_k denotes the current position of harvester M_k, V_M_k denotes the average traveling speed of harvester M_k during the plot transfer process, and E_M_k denotes the average operating speed of harvester machinery M_k, k ∈ [1, M]. For the convenience of the study, the following mathematical symbols are defined, as shown in Table 1.

Table 1

Table 1 Symbols and meaning.

Objective function:

$\begin{array}{ll}\min y=C_1{\displaystyle \sum _{k=1}^M{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=1}^N{x}_{ijk}{d}_{ij}+C_2{\displaystyle \sum _{k=1}^M{\displaystyle \sum _{i=1}^N{x}_{ik}{s}_i+}{\displaystyle \sum _{k=1}^M{P}_k+C_5{\displaystyle \sum _{k=1}^M{\displaystyle \sum _{i=1}^N{x}_{ik}\left|{t^{\prime }}_{ki}-t_{ki}\right|}}}}}}}& (1)\end{array}$

Constraints:

$\begin{array}{ll}{\displaystyle \sum _{i=1}^N{x}_{ik}=1; (k\ne k^{\prime })} & (2)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{i=1}^N{x}_{i{k}^{\prime }}=0} ;& (3)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=1}^N{x}_{ijk}{S}_i\le Q_k;(k\in M)}}& (4)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{k=1}^M{\displaystyle \sum _{i=1}^N{x}_{ijk}=1;(j\in N)}}& (5)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=1}^N{x}_{ijk}{d}_{ij}\le D_k;(k\in M)}}& (6)\end{array}$

$\begin{array}{ll}{P}_k=\{\begin{array}{l}{x}_{ik}(E_i-t_{ki})C_3 t_{ki}<E_i\\ 0 E_i\le t_{ki}\le L_i\\ x_{ik}(t_{ki}-L_i)C_4 t_{ki}>L_i\end{array} ;(i\in N)& (7)\end{array}$

$\begin{array}{ll}{w}_{ki}=max(0,Ei-t_{ki});(i\in N,k\in M)& (8)\end{array}$

$\begin{array}{ll}{t}_{ij}=\frac{d_{ij}}{V};(i,j\in N)& (9)\end{array}$

$\begin{array}{ll}{t}_{ki}=t_{kj}+w_{kj}+c_j+t_{ij}& (10)\end{array}$

$\begin{array}{ll}{x}_{ijk}=\{\begin{array}{l}1, \text{Harvester }k\text{ travelling from }i\text{ to }j\\ 0, \text{other}\end{array}& (11)\end{array}$

$\begin{array}{ll}{x}_{ik}=\{\begin{array}{l}1, \text{Harvester }k\text{ operating on farmland} i\\ 0, \text{other}\end{array}& (12)\end{array}$

The objective function Equation 1 represents the comprehensive scheduling cost minimization as the objective function, where the first part is the objective function for the initial scheduling, which is the sum of the three of the scheduling total traveling cost, job cost, and penalty time cost, and the second part is the offset cost after the breakdown occurs; the final objective is to minimize the comprehensive scheduling cost as the goal. Equation 2 ensures that, in the event of a failure, operational harvesters are scheduled from their current locations. Equation 3 ensures that faulty harvesters are not scheduled. Equation 4 indicates that the operating capacity of each piece of agriculture machinery cannot exceed its maximum operating capacity limit. Equation 5 indicates that each piece of agriculture machinery operates only once in each field. Equation 6 indicates that each piece of agriculture machinery does not operate beyond its maximum distribution distance. Equation 7 represents the penalty cost constraint, where the agriculture machinery arrives at the field earlier than the earliest operation time, incurring a waiting cost, and later than the latest operation time, incurring a penalty cost. Equation 8 represents the waiting time constraint. Equation 9 represents the traveling time constraint. Equation 10 represents the time constraint that the current time to reach the farm field = time to reach the previous field + waiting time + previous farm operation time + travelling time. Equation 11 represents the decision variable: the decision variable of whether or not agriculture machinery k travels from farm field i to farm field j. Equation 12 represents another decision variable: the decision variable of whether agriculture machinery k serves in farm field i or not.

3 Design of the improved genetic algorithm

3.1 Analysis of model-solving algorithms

By analyzing the agricultural machinery scheduling problem, it can be approached and solved similarly to the emergency vehicle scheduling problem. The solution process for emergency scheduling is illustrated in Figure 2.

Figure 2

Figure 2 Schematic diagram of the emergency scheduling process.

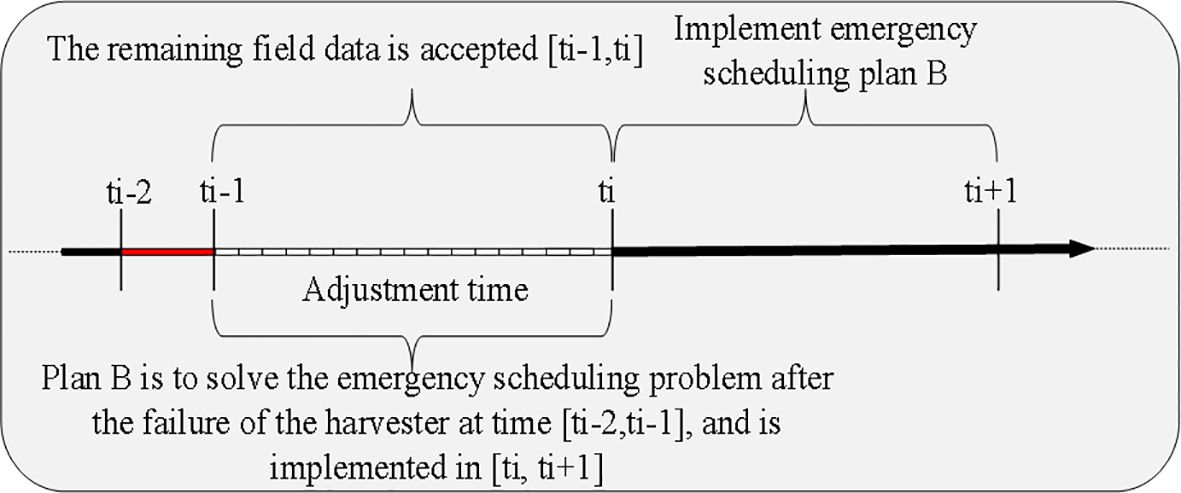
Upon receiving a breakdown scheduling request at the information center of the agricultural cooperative, the breakdown request needs to be processed immediately. The optimization objective is to minimize the comprehensive scheduling cost while ensuring that the remaining operating capacity of the agricultural machine in the farmland, the distance, and the offset time are within feasible limits. An emergency scheduling plan should be quickly incorporated into the operation task rather than completely re-scheduled. The process of receiving and scheduling the remaining farmland after the breakdown of a piece of agriculture machinery is illustrated in Figure 3.

Figure 3

Figure 3 Emergency scheduling process schematic.

3.2 Selection and design of model-solving algorithms

3.2.1 Choice of model-solving algorithms

To solve the emergency scheduling problem in harvester breakdown scenarios, a heuristic algorithm is considered the optimal choice for addressing dynamic problems owing to its capacity to effectively solve challenges through an evolutionary process. Therefore, a genetic algorithm combined with an ant colony algorithm (GA-ACO) was proposed, which is based on the GA framework and introduces ACO to further add a local optimal approach. First, GA, as a typical genetic optimal framework, achieves global optimality in solving various scheduling problems. Second, ACO preserves the pheromone information in the environment in advance, which is very useful when there is a small change in the environment, and constructs the whole scheduling scheme directly by adding the non-working farmland to the current partial scheduling scheme. The combination of the two algorithms not only complements their respective drawbacks but also takes into account the difficulties of scheduling complexity to obtain a better contingency scheduling solution.

3.2.2 Design of model-solving algorithms

The flowchart of the algorithm is shown in Figure 4. The specific design steps of the improved genetic algorithm are as follows:

Figure 4

Figure 4 Improved genetic algorithm flowchart.

(1) Input the number of the faulty harvester, the moment of breakdown, and the parameters of the agriculture machinery; get the farmland to be operated with the normal harvester; and finally, add it to the emergency scheduling sequence. The specific steps are as follows Algorithm 1.

Algorithm 1

Algorithm 1 Emergency scheduling information extraction.

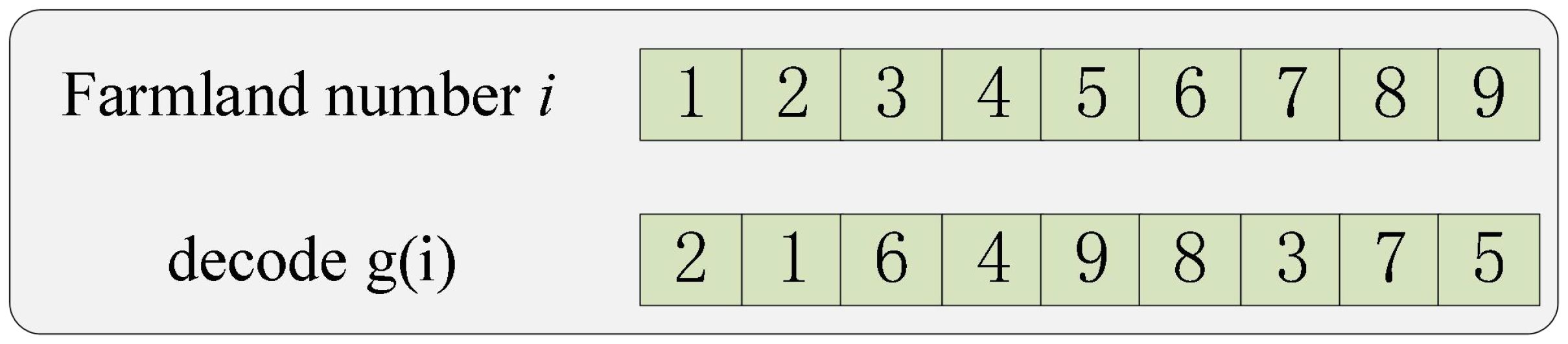
(2) The algorithm uses integer coding for encoding and decoding. The chromosome length corresponds to the number of operating farmlands (1 to n). The initial population is generated randomly. The algorithm prioritizes operations based on the distance between farmlands and agricultural machinery, as well as operation time. It then assigns operation points to each piece of agricultural machinery based on these priorities. As shown in Figure 5, where the number of farmlands is 9, g(i) denotes the priority of operation point i, where the smaller number of g(i) means the higher priority of the operation point. The order of operation of agriculture machinery obtained after decoding is 2–1-7–4-9–3-8–6-5.

Figure 5

Figure 5 Decoding process.

(3) Improvement of the ant colony algorithm operation. The ACO is derived from the behavior of ants in searching for food, where ants mark paths by releasing pheromones and other ants choose paths with more pheromone concentration. In this study, the transfer probability in the ACO algorithm’s optimization strategy is shown in Equation 13, and the pheromone concentration is updated in Equations 14, 15. The solved populations are then merged into the genetic algorithm population for iteration.

$\begin{array}{ll}{p}_{ij}^k(t)=\{\begin{array}{l}\frac{{[{\tau }_{ij}(t)]}^{\alpha }{[{\eta }_{ij}(t)]}^{\beta }}{{\displaystyle \sum _{j\in allowed}{[{\tau }_{ij}(t)]}^{\alpha }{[{\eta }_{ij}(t)]}^{\beta }}} , j\in allowed \\ 0 , otherwise \end{array}& (13)\end{array}$

$\begin{array}{ll}{\tau }_{ij}=(1-p)·{\tau }_{ij}+{\displaystyle \sum _{k=1}^m\Delta {\tau }_{ij}^k}& (14)\end{array}$

$\begin{array}{ll}\Delta {\tau }_{ij}^k=\{\begin{array}{l}\frac{1}{d_{ij}},(i,j)\in T^k\\ 0 ,otherwise\end{array}& (15)\end{array}$

where P^kij(t) is the probability that the kth ant chooses path i to j. α and β are parameters that adjust for the effects of pheromone concentration and heuristic information on path selection. η_ij(t) is the heuristic information on path i → j, τ_ij is the pheromone concentration of i → j, ρ ∈ (0, 1) is the volatility coefficient of the pheromone, m is the number of ants, Δτ^kij is the pheromone left by the kth ant on path i → j, and d_ij is the distance from node i to node j.

To prevent the algorithm from prematurely converging to a local optimum solution, we limit the pheromone concentration of each path to a predefined range (Equation 16), avoiding the “infinite loop” phenomenon.

$\begin{array}{ll}{\tau }_{ij}\{\begin{array}{l}{\tau }_{ij} , {\tau }_{min}<{\tau }_{ij}<{\tau }_{max}\\ {\tau }_{min}, {\tau }_{ij}\le {\tau }_{min}\\ {\tau }_{max}, {\tau }_{max}\le {\tau }_{ij}\end{array}& (16)\end{array}$

where τ_max and τ_min are the maximum and minimum pheromone settings, respectively.

We introduced a methodology (Liu Y. Y. et al., 2022) to enhance the efficiency of the update rule and then utilized a binary approach for optimization. Ants were ranked based on their traversal times across all regions after each iteration, with only the pheromones released by the top 50% fastest ants being retained, as described in Equations 17, 18.

$\begin{array}{ll}{\tau }_{ij}(t+1)=(1-p){\tau }_{ij}(t)+{\displaystyle \sum _{k=1}^{k\frac{m}{2}}[{\displaystyle \sum _{k=1}^{w-1}(w-k)\Delta {\tau }_{ij}^k(t)]+e\Delta {\tau }_{ij}^{bs}(t)}}& (17)\end{array}$

$\begin{array}{ll}\Delta {\tau }_{ij}^{bs}(t)=\{\begin{array}{l}\frac{1}{L^{bs}},f(i,j)\in T^{bs}\\ 0, otherwise\end{array}& (18)\end{array}$

where e is the weight size of the path T^bs, Δτ^bsij(t) is the pheromone added at moment t of the shortest route, T^bs is the shortest route, and L^bs is the length of T^bs.

(4) Fitness. The fitness of the lowest comprehensive scheduling cost as the optimization objective, from the objective function of Equation 1 can be obtained from fitness, as shown in Equation 19:

$\begin{array}{ll}f=1/\min y& (19)\end{array}$

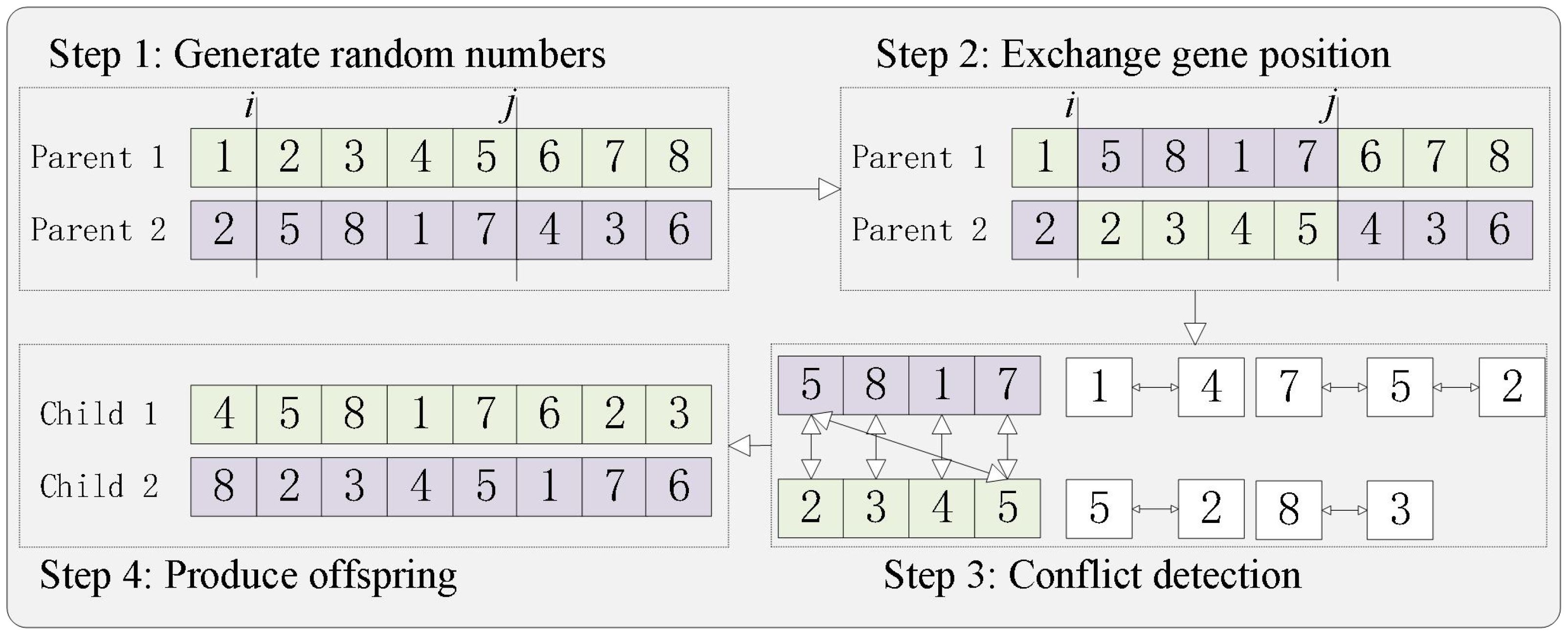
(5) Selection, crossover. A roulette selection operator was used in the operator operation to randomly select and retain the optimal individuals based on the fitness ratio. The crossover method is PMX crossover, as shown in Figure 6. The detailed steps are as follows. Step 1: Randomly select the start and end positions of genes within the parent chromosomes (the selected positions on the two chromosomes are identical). Step 2: Exchange the positions of the two gene groups. Step 3: Perform conflict detection. Based on the swapped gene groups, establish a mapping relationship; taking the 7–5–2 mapping as an example, it is evident that in the results of Step 2, parent 1 has two instances of gene 7. These are then converted into gene 2 through the mapping relationship, and so forth until all conflicts are resolved. Step 4: Ultimately, the offspring are generated.

Figure 6

Figure 6 Schematic diagram of the crossover approach.

The specific steps for PMX are as follows Algorithm 2.

Algorithm 2

Algorithm 2 Crossover steps.

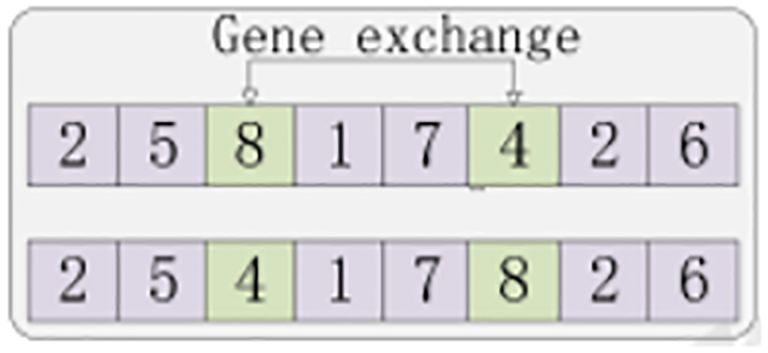
(6) Mutation. Mutation improves the diversity of the population, and it is important to note that the choice of the mutation rate is a critical parameter. An inadequate mutation rate can lead the algorithm to get stuck in local optimal solutions, whereas an excessively high mutation rate may result in the algorithm losing its search direction. Therefore, the selection of the mutation rate should be fine-tuned based on the specific circumstances. The mutation steps are illustrated in Figure 7.

Figure 7

Figure 7 Schematic diagram of the variation.

The specific steps of the mutation are as follows Algorithm 3.

Algorithm 3

Algorithm 3 Steps of mutation.

(7) Elite retention. Elitism is implemented to prevent population degradation. In this process, the best individual from each generation is duplicated. One of these top individuals is directly passed on to the next generation without any genetic alterations, while the other continues to participate in the evolutionary process as usual. The specific steps of Elite retention are as follows Algorithm 4.

Algorithm 4

Algorithm 4 Steps of Elite retention.

4 Example validation

4.1 Experimental data

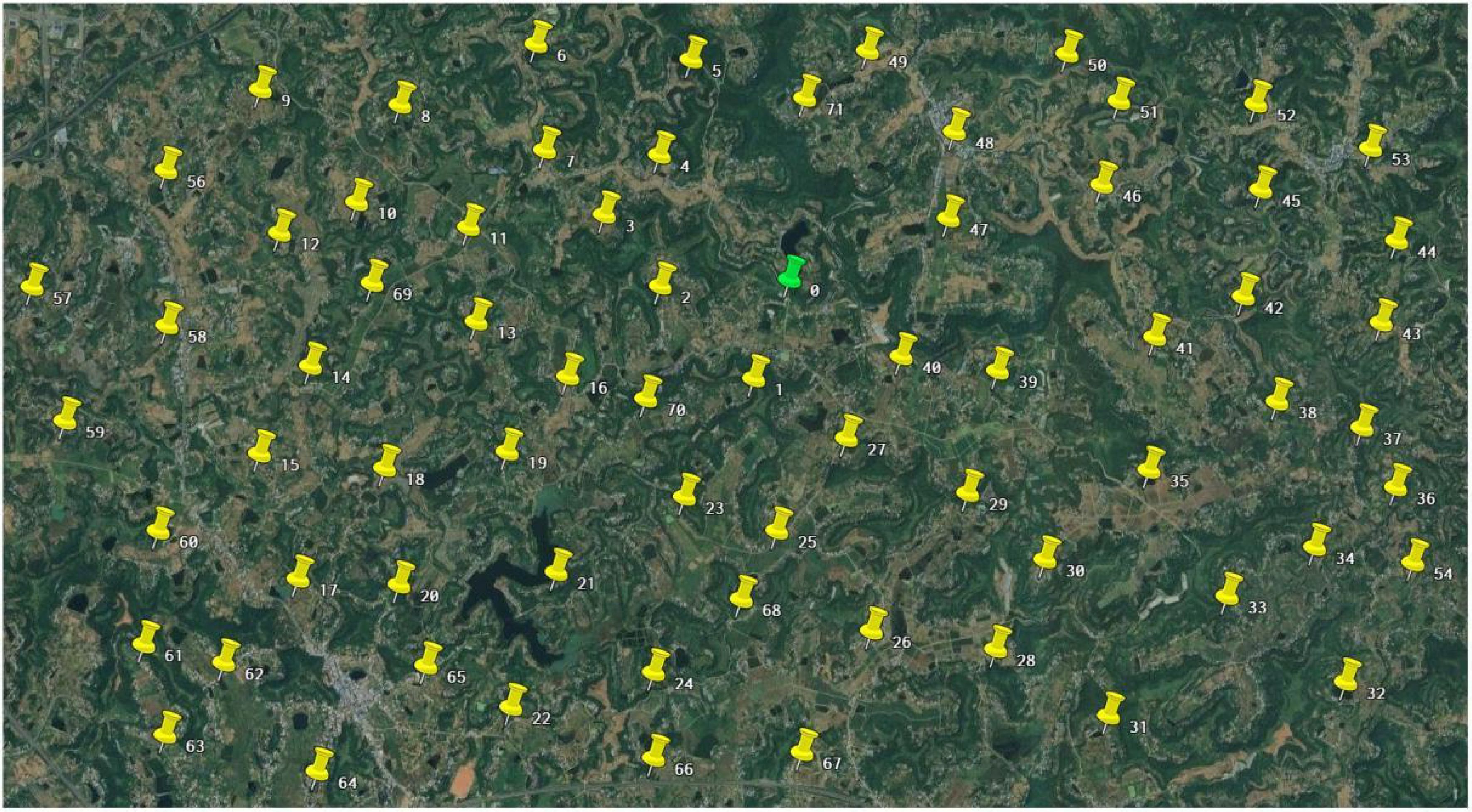
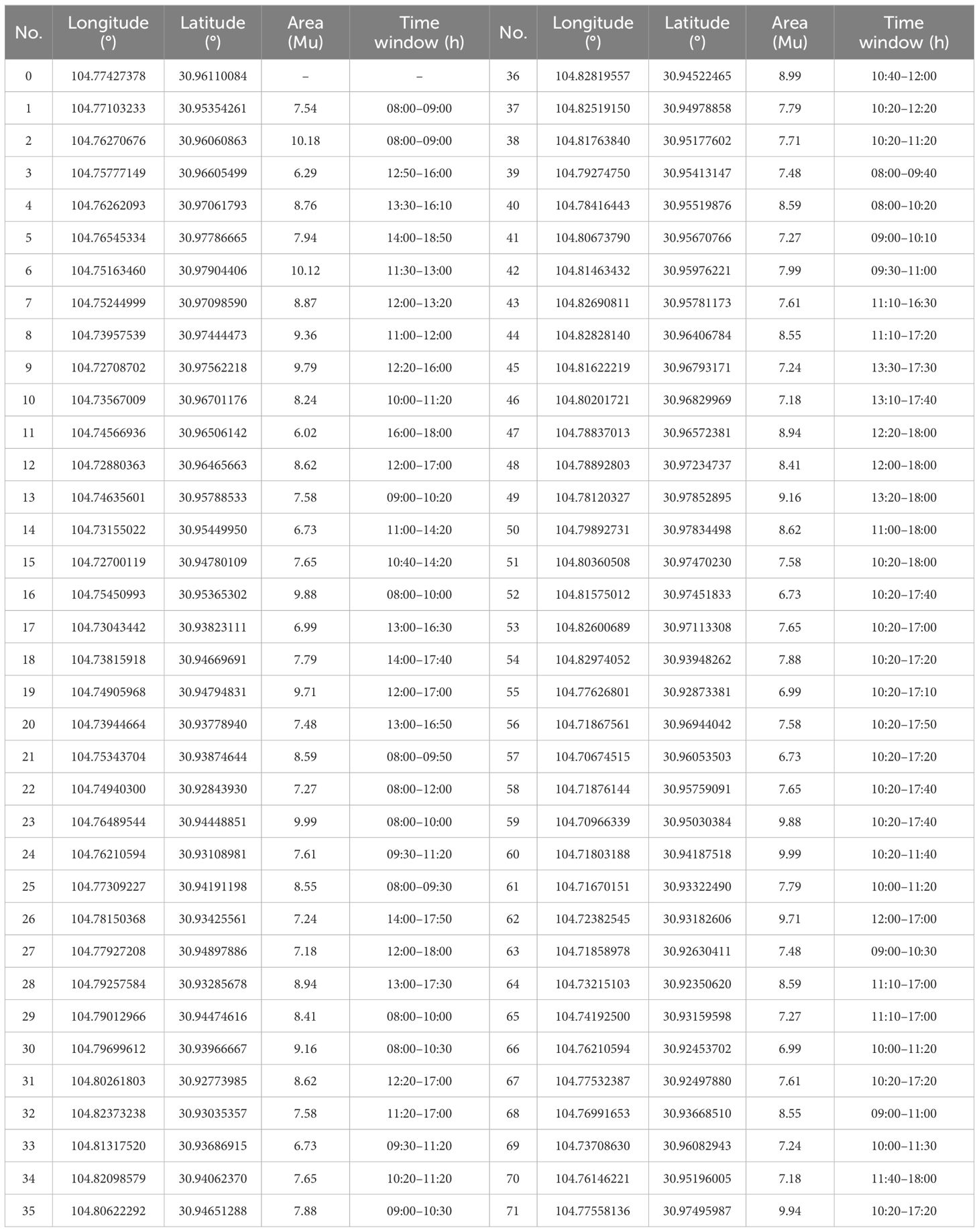
To verify the effectiveness and advantages of the improved genetic algorithm proposed in this study for the emergency scheduling problem in case of harvester breakdown scenarios, the farmland data of this study were taken from Chuanwan District, Deyang City, Sichuan Province, as shown in Figure 8. Simulated operational tasks were set up based on the actual operational environment to verify the performance and stability of the algorithm. The algorithm was run on AMD Ryzen 7 5800H with Radeon Graphics 3.20 GHz, 16 GB of RAM, Windows 11, and MATLAB. The basic information about the management center of the agricultural machinery cooperative and the farmland is shown in Table 2, which mainly includes geographic location information, farmland area, and operation time window, where O denotes the management center of the agricultural machinery cooperative. The harvester was selected as the Lovol Gushen GE80S(4LZ-8E2), and its working efficiency in farmland is 1 hm²/h, and the traveling speed during the transfer of harvester is 24 km/h.

Figure 8

Figure 8 Map of the experiment.

Table 2

Table 2 Experimental data information.

4.2 Initial scheduling program

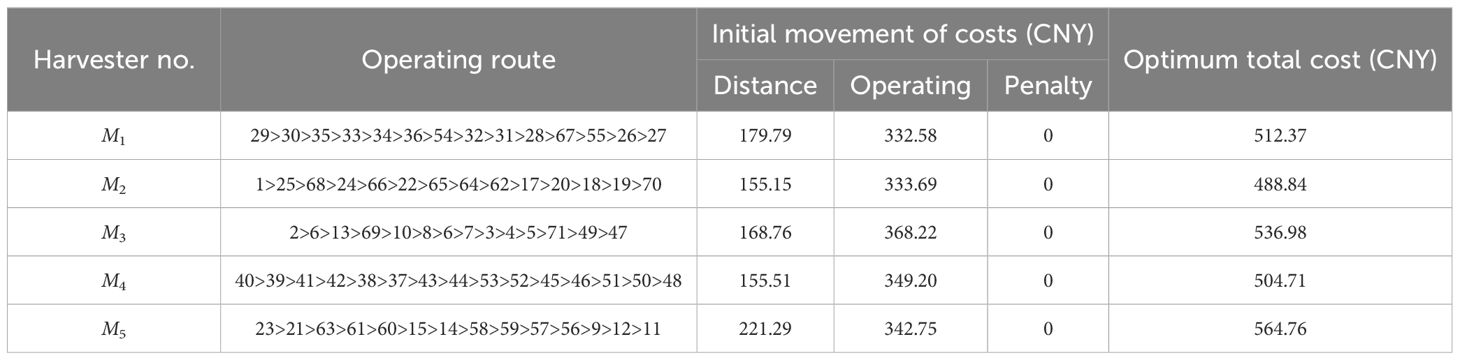
In the initial scheduling stage, the initial values are set for the algorithm parameters: The population size is 500, the maximum number of iterations is 1,000, the crossover probability is 0.9, and the variance probability is 0.05. The number of ants is 50, the pheromone importance factor α = 1, the heuristic factor β = 2, and the pheromone evaporation coefficient is 0.75. The harvester transfer cost is 10, the operation cost is 3, and the penalty cost is 0.5. The experimental data and algorithm parameters are incorporated into the objective function of the initial scheduling, the simulation solution of the algorithm is completed using MATLAB programming, and the results of the initial scheduling are shown in Table 3.

Table 3

Table 3 Initial scheduling results.

The scheduling results of the initial scheme are shown in Figure 9. Figure 9A shows the convergence of the improved genetic algorithm in the operation process; by combining the advantages of the genetic algorithm and the ant colony algorithm, it can be concluded that the objective function tends to be stable in the generation of 470, which plays a positive role in improving the convergence speed and the solution accuracy. Figure 9B shows the route map of the initial scheduling scheme, from which it can be concluded that the farmland where each harvester works maintains the optimal distance. Figure 9C shows the Gantt chart of the initial scheduling scheme, which shows the sequence of the farmland worked by each harvester. The completion time of each harvester’s operation task is approximately the same, where the white part is the harvester’s transfer phase and the green part is the harvester’s operation phase.

Figure 9

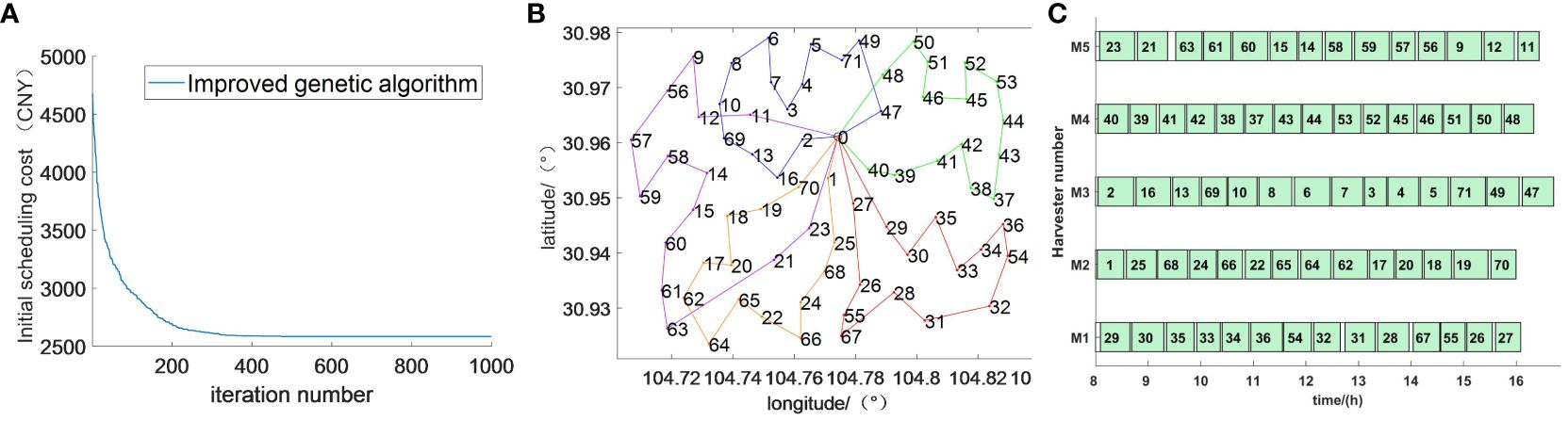
Figure 9 Initial scheduling scheme result graph. (A) Initial scheduling convergence graph. (B) Initial scheduling route map. (C) Initial scheduling Gantt chart.

4.3 Emergency scheduling program

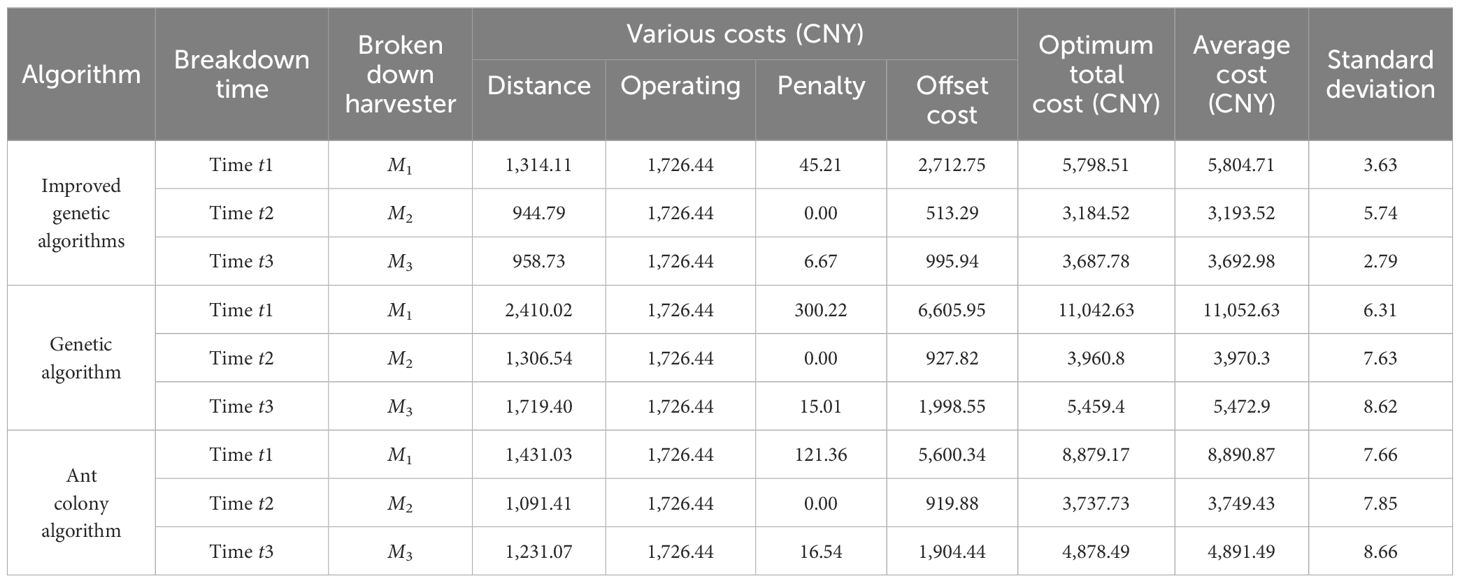
In the contingency scheduling scheme, the improved genetic algorithm, the genetic algorithm, and the ant colony algorithm were used to compare different harvesters and different time periods when they break down. The contingency scheduling results were obtained by the three algorithms by performing operations 10 times at randomly set breakdown moments, and the optimal cost, average cost, standard deviation, and each scheduling cost obtained are shown in Table 4. As can be seen from Table 4, the optimal scheduling integrated costs using the improved genetic algorithm are 47.49% and 34.70% lower than the genetic algorithm and the ACO algorithm, respectively, after the first agriculture machinery breaks down at moment t1. After the second agriculture machinery breaks down at moment t2, the optimal scheduling integrated costs are reduced by 19.60% and 14.80%, respectively. After the third agriculture machinery breaks down at moment t3, the optimal scheduling integrated costs are reduced by 32.45% and 24.40%, respectively. In addition, the standard deviations of the improved genetic algorithm are smaller than those of the other two algorithms, which indicates that the improved genetic algorithm has a greater advantage in the accuracy of the optimal solution and can find the optimal solution in different harvesters and different time periods. Therefore, the improved genetic algorithm can meet the task requirements of emergency scheduling in case of a harvester breakdown.

Table 4

Table 4 Emergency scheduling results.

The emergency scheduling route map and Gantt chart for each fault stage are shown in Figures 10–12, where the red markers in the route map and Gantt chart are the locations where the harvester breaks down. From the route map, it can be intuitively seen that although all three algorithms are capable of completing the operation tasks in all farmlands, the operation route of the genetic algorithm is more complicated, and such an operation route increases the transfer time and prolongs the operation progress. The ant colony algorithm has a better operation route relative to the genetic algorithm, but the second half of the operation route of the farmland is beyond the scope of the time window relative to the improved genetic algorithm, which increases the penalty cost, whereas the improved genetic algorithm maintains the optimal distance and optimal cost in all three randomly set breakdown cases. From the operation progress Gantt chart, it can be concluded that the emergency scheduling scheme of the genetic algorithm and ant colony algorithm has the largest change from the initial scheduling scheme, while the emergency scheduling scheme of the improved genetic algorithm has less perturbation, and the maximum completion time is shorter than that of both the genetic algorithm and ant colony algorithm, so the improved genetic algorithm improves the efficiency of operation, has the optimal operation route and the shortest maximum completion time among all the algorithms, and is able to satisfy the harvester’s scheduling timeliness.

Figure 10

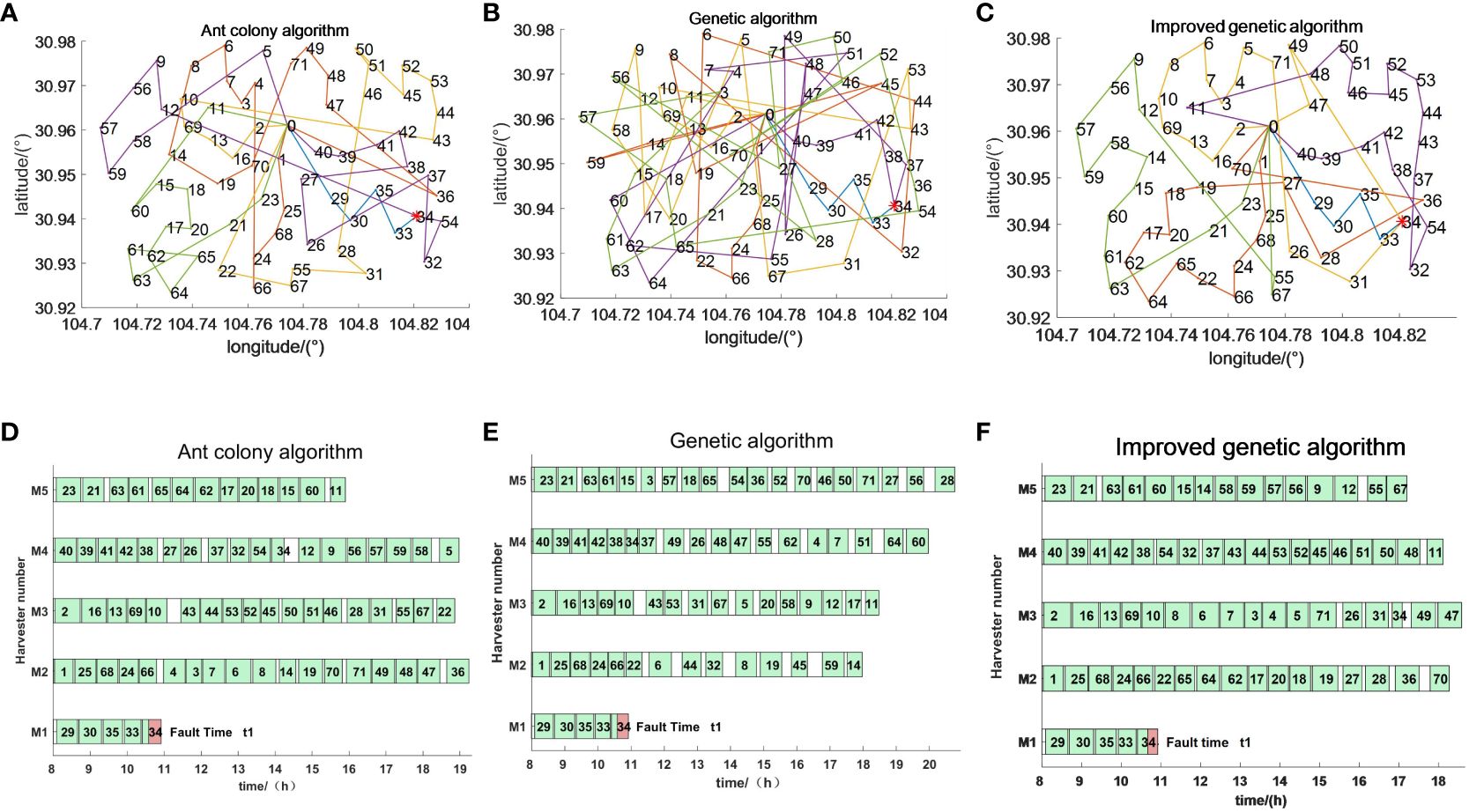
Figure 10 Emergency scheduling results at moment t1. (A–C) Emergency scheduling route map. (D–F) Emergency scheduling Gantt chart.

Figure 11

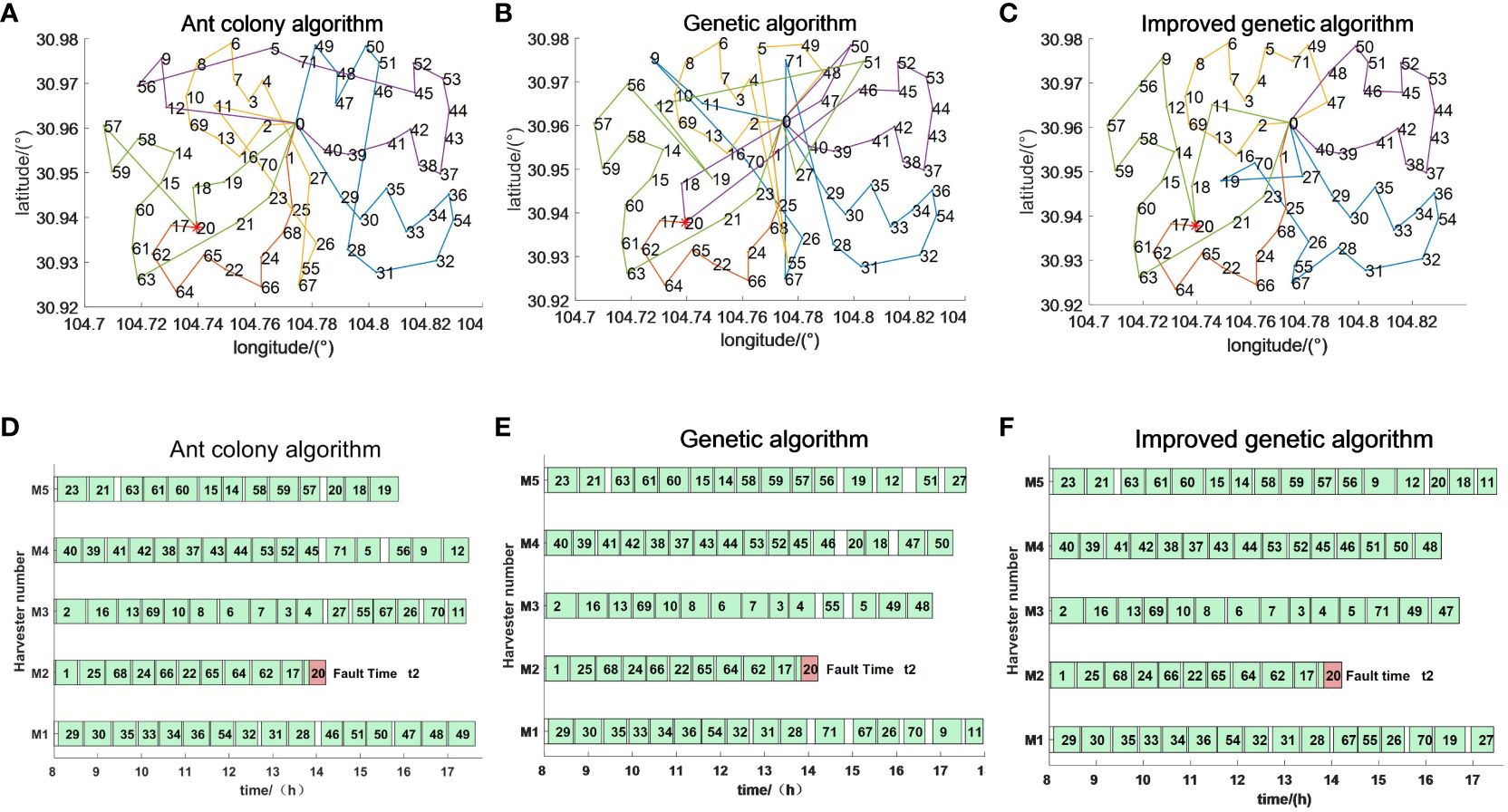
Figure 11 Emergency scheduling results at moment t2. (A–C) Emergency scheduling route map. (D–F) Emergency scheduling Gantt chart.

Figure 12

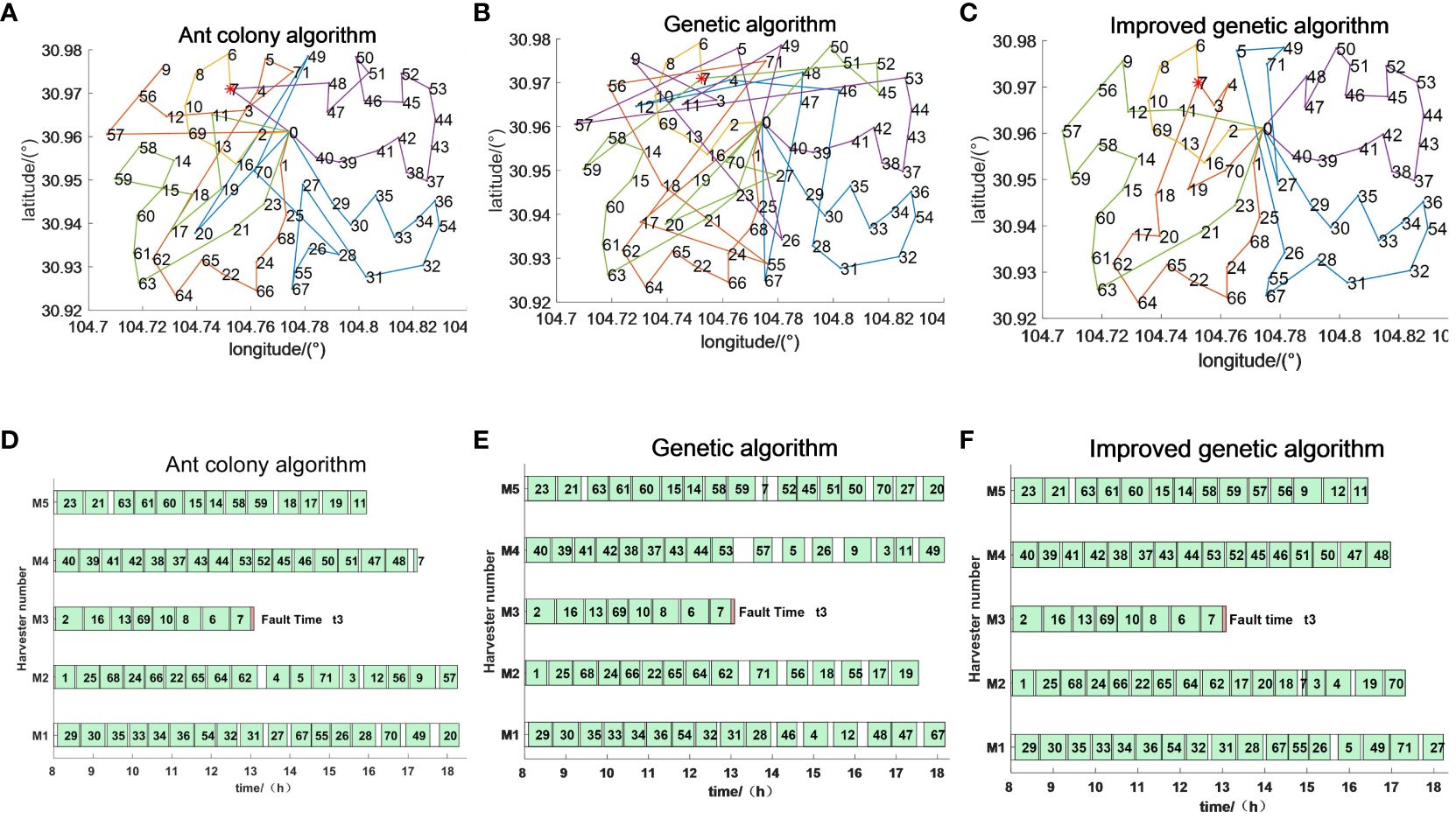
Figure 12 Emergency scheduling results at moment t3. (A–C) Emergency scheduling route map. (D–F) Emergency scheduling Gantt chart.

In addition to comparing the integrated scheduling costs at different time stages and under different harvester breakdown scenarios, the trends of the three algorithms during the iterative process were further analyzed. As shown in Figure 13, the genetic algorithm has a strong global search ability, but it is easy to fall into local optimal with the ant colony algorithm, while the improved genetic algorithm has the advantage of high convergence efficiency in three randomly set breakdown scenarios, which is due to the initial optimization search through the genetic algorithm to obtain the optimal solution quickly, and then the ant colony algorithm is used to carry out a secondary search for the sub-optimal solution and finally merge the populations to obtain the optimal solution. The improved genetic algorithm combines the advantages of the two algorithms; the first step of the algorithm, to a certain extent, determines the size of the optimal solution, and it can be seen from the figure that the improved genetic algorithm can greatly improve the efficiency of the algorithm’s initial search. More specifically, it can improve the evolutionary efficiency of the algorithm, optimize the overall size of the solution in fewer iterations, and reduce the search time. The improved optimization performance of the algorithm is evidenced not only by the high optimization accuracy but also by the highly stable results.

Figure 13

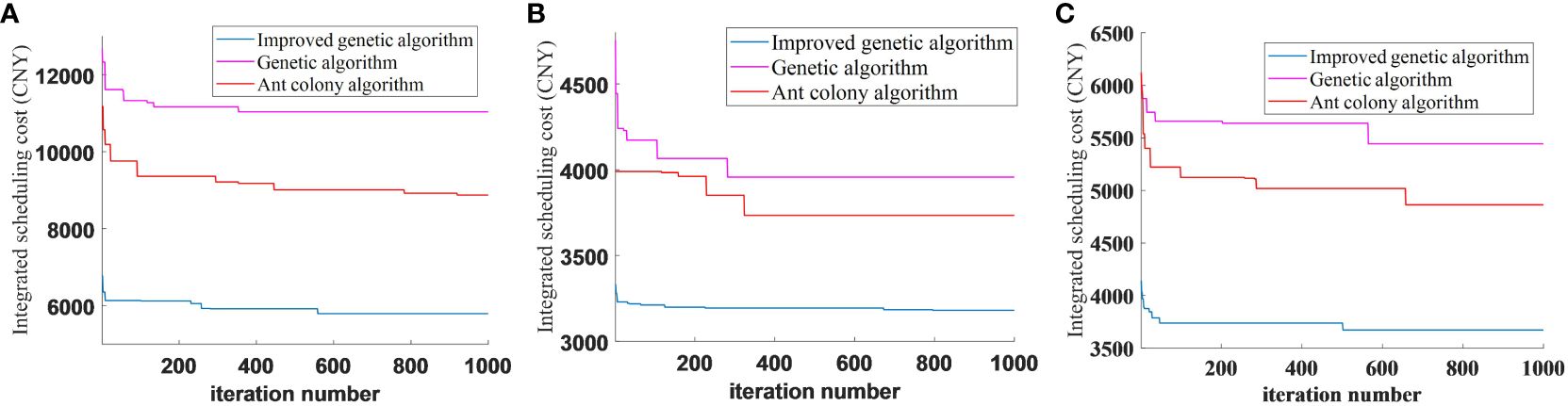
Figure 13 Convergence graph of contingency scheduling results. (A) Convergence graph at moment t1. (B) Convergence graph at moment t2. (C) Convergence graph at moment t3.

4.4 System design

The study presents a scheduling model and algorithm for agricultural machinery, leading to the development of a visual management system. This system utilizes modern information technology and intelligent tools to create an information interaction platform for agricultural management departments, machinery cooperatives, farmers, and households. It enables precise analysis of agricultural machinery operations scheduling, real-time supervision, and handling of massive operational data. The system is structured into five layers: user, application, service, data, and equipment. The framework is illustrated in Figure 14.

Figure 14

Figure 14 System framework diagram.

The system collects fault information and then uploads agriculture machinery data to the back-end of the system to form information interaction and achieve intelligent decision-making, and the visualization of scheduling is shown in Figure 15. The implementation of the system design can effectively achieve human–computer interaction and improve the overall management service level.

Figure 15

Figure 15 Breakdown scheduling visualization interface.

4.5 Discussion

Table 5 compares recent studies on the scheduling of agricultural machinery, including scheduling objectives and research methods, and lists the characteristics of each method to better explain the experimental results obtained in this study.

Table 5

Table 5 Comparison of agriculture machinery scheduling studies for various scheduling objectives.

In this study, the proposed mathematical model and improved algorithm for the problem of the phenomenon of agricultural machines breaking down during the execution of scheduling tasks have the following benefits in terms of results. First, the initial scheduling problem is solved, and the managers of agricultural cooperatives can make quick decisions to allocate the agriculture machinery in the agriculture machinery pool to the operating farmland with high quality. Second, in the event that agricultural machinery breaks down during the scheduling task and is unable to regain operational capability in a short period of time, they are able to respond quickly to the remaining farmland and make timely emergency strategies. Finally, this research study can also be extended to the emergence of new operating farmland situations during the execution of scheduling tasks to develop better emergency scheduling strategies.

Issues related to this study should not be ignored. First, for scheduling agricultural machinery with loading capacity, its own capacity should also be considered when a breakdown occurs. Second, as the system contains many data, including job retrospective data, the data security and system maintenance of the management center should be strengthened to prevent data privacy leakage or even system crash.

5 Conclusion

We addressed an emergency scheduling problem where a harvester breaks down during the execution of a scheduled task and is unable to restore its operating capability in a short time. The objectives were to achieve the lowest comprehensive scheduling cost and resume and complete the remaining farm operations as soon as possible. Upon analysis of influencing factors in agricultural machinery operations, we established an emergency agricultural machinery scheduling model with the lowest comprehensive scheduling cost using an improved genetic algorithm that combined genetic and ant colony algorithms. Finally, compared with the scheduling solutions of the genetic algorithm and the ant colony algorithm, the scheme obtained in this study optimizes the sequence of agricultural machine operation and can meet the emergency scheduling task demands of the harvester in the event of a breakdown. The main conclusions of this study are as follows:

(1) Combined with the current situation of agricultural machine scheduling under a disturbance event, the emergency scheduling problem is proposed when an agricultural machine breaks down and can no longer restore its operating ability in a short time. Combining the influencing factors and characteristics of the scheduling process of agricultural machines, an objective function with the goal of minimizing the operating time offset is added to the initial scheduling. After that, the problem is solved by the improved genetic algorithm, and the results show that the optimal integrated scheduling cost of the improved genetic algorithm in the three breakdown stages is reduced by 47.49%, 19.60%, and 32.45% compared with the genetic algorithm’s 34.70%, 14.80%, and 24.40% compared with the ACO algorithm, which verifies the effectiveness of the improved genetic algorithm.

(2) To avoid getting trapped in local optima during the search for the global optimum, an improved algorithm combining GA and ACO was designed. The algorithm combines the advantages of the two algorithms; convergence speed is fast, and at the same time, it has a good global optimization ability; through three different time periods and different breakdowns of agricultural machinery samples, the three algorithms are compared, and the results show that the improved genetic algorithm enhanced convergence efficiency, resulting from the combination of a genetic algorithm and an ant colony algorithm.

(3) This study designed and developed a set of agricultural machinery scheduling visualization management systems that provide intelligent information references for agricultural machinery scheduling operation scenarios. It can effectively provide all-around service information interaction, realize multi-position integration and complete functions, meet the needs of agricultural machinery operation service scheduling operations, and provide support for the reasonable planning of the whole scheduling scene.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

HL: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. LZ: Conceptualization, Data curation, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. BZ: Conceptualization, Data curation, Investigation, Methodology, Software, Writing – review & editing. JT: Conceptualization, Data curation, Methodology, Software, Writing – review & editing. JL: Data curation, Investigation, Methodology, Software, Validation, Writing – review & editing. SW: Writing – review & editing, Formal analysis, Funding acquisition, Project administration, Resources, Supervision.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was funded by the Research on autonomous precision operation and path planning of unmanned agricultural machinery (no. Z222057), Research on Agricultural Machinery Scheduling Methods and System Design under Complex Land Conditions in Hilly and Mountainous Areas (no. XDNY2023–001), and Remote control electric potato planter development (no. 232206–1).

Acknowledgments

We thank Yuling Tan, Xin Zhao, Zeyu Tan, Lei Peng, and Hao Sun for their help with this research and gratefully acknowledge the editors and reviewers for their constructive comments on our manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bochtis, D. D., Sørensen, C. G., Busato, P. (2014). Advances in agricultural machinery management: A review. Biosyst. Eng. 126, 69–81. doi: 10.1016/j.biosystemseng.2014.07.012

CrossRef Full Text | Google Scholar

Brewer, K., Clulow, A., Sibanda, M., Gokool, S., Odindi, J., Mutanga, O., et al. (2022). Estimation of maize foliar temperature and stomatal conductance as indicators of water stress based on optical and thermal imagery acquired using an unmanned aerial vehicle (UAV) platform. Drones 6, 169. doi: 10.3390/drones6070169

CrossRef Full Text | Google Scholar

Cao, R. Y., Li, S. C., Ji, Y. H., Zhang, Z. Q., Xu, H. Z., Zhang, M., et al. (2021). Task assignment of multiple agricultural machinery cooperation based on improved ant colony algorithm. Comput. Electron. Agric. 182, 105993. doi: 10.1016/j.compag.2021.105993

CrossRef Full Text | Google Scholar

Chen, C., Hu, J. P., Zhang, Q. K., Zhang, M., Li, Y. B., Nan, F., et al. (2021). Research on the scheduling of tractors in the major epidemic to ensure spring ploughing. Math. Probl. Eng. 2021, 3534210. doi: 10.1155/2021/3534210

CrossRef Full Text | Google Scholar

Chen, C., Li, Y. B., Cao, G. Q., Zhang, J. L. (2023). Research on dynamic scheduling model of plant protection UAV based on levy simulated annealing algorithm. Sustainability 15, 1772. doi: 10.3390/su15031772

CrossRef Full Text | Google Scholar

Fatemi-Anaraki, S., Tavakkoli-Moghaddam, R., Foumani, M., Vahedi-Nouri, B. (2023). Scheduling of multi-robot job shop systems in dynamic environments: mixed-integer linear programming and constraint programming approaches. Omega 115, 102770. doi: 10.1016/j.omega.2022.102770

CrossRef Full Text | Google Scholar

Feng, T. P., Li, J. M., Jiang, H., Wang, P. X., Teng, Y. X., Chen, S. Y., et al. (2024). The optimal global path planning of mobile robot based on improved hybrid adaptive genetic algorithm in different tasks and complex road environments. IEEE Access. 12, 18400–18415. doi: 10.1109/ACCESS.2024.3357990

CrossRef Full Text | Google Scholar

Fernandez, G. S., Krishnasamy, V., Kuppusamy, S., Ali, J. S., Ali, Z. M., El-Shahat, A., et al. (2020). Optimal dynamic scheduling of electric vehicles in a parking lot using particle swarm optimization and shuffled frog leaping algorithm. Energies 13, 6384. doi: 10.3390/en13236384

CrossRef Full Text | Google Scholar

He, P., Li, J. (2021). A joint optimization framework for wheat harvesting and transportation considering fragmental farmlands. Inf. Process. Agricult. 8, 1–14. doi: 10.1016/j.inpa.2020.04.006

CrossRef Full Text | Google Scholar

He, P. F., Li, J., Qin, H. L., He, Y. P., Cao, G. Q. (2019). Using hybrid algorithm to reduce non-working distance in intra- and inter-field logistics simultaneously for heterogeneous harvesters. Comput. Electron. Agric. 167, 105065. doi: 10.1016/j.compag.2019.105065

CrossRef Full Text | Google Scholar

He, P. F., Li, J., Wang, X. (2018). Wheat harvest schedule model for agricultural machinery cooperatives considering fragmental farmlands. Comput. Electron. Agric. 145, 226–234. doi: 10.1016/j.compag.2017.12.042

CrossRef Full Text | Google Scholar

Hou, J. L., Zhang, J. T., Wu, W. Y., Jin, T. G., Zhou, K. (2022). Research on agricultural machinery rental optimization based on the dynamic artificial bee-ant colony algorithm. Algorithms 15, 88. doi: 10.3390/a15030088

CrossRef Full Text | Google Scholar

Hu, Y., Liu, Y., Wang, Z., Wen, J., Li, J., Lu, J. (2020). A two-stage dynamic capacity planning approach for agricultural machinery maintenance service with demand uncertainty. Biosyst. Eng. 190, 201–217. doi: 10.1016/j.biosystemseng.2019.12.005

CrossRef Full Text | Google Scholar

Huang, H., Cuan, X. W., Chen, Z., Zhang, L. N., Chen, H. (2023). A multiregional agricultural machinery scheduling method based on hybrid particle swarm optimization algorithm. Agriculture 13, 1042. doi: 10.3390/agriculture13051042

CrossRef Full Text | Google Scholar

Li, W. (2022). Research on scheduling algorithm of agricultural machinery cooperative operation based on particle swarm neural network. Adv. Multimed. 2022, 1231642. doi: 10.1155/2022/1231642

CrossRef Full Text | Google Scholar

Li, S. C., Zhang, M., Wang, N., Cao, R. Y., Zhang, Z. Q., Ji, Y. H., et al. (2023). Intelligent scheduling method for multi-machine cooperative operation based on NSGA-III and improved ant colony algorithm. Comput. Electron. Agric. 204, 107532. doi: 10.1016/j.compag.2022.107532

CrossRef Full Text | Google Scholar

Liu, Y. X., Luo, X. G., Cheng, S. P., Yu, Y., Tang, J. F., Shang, X. Z. (2022). Comparison of two algorithms for multiline bus dynamic dispatching. Discrete Dyn. Nat. Soc. 2022, 2086717. doi: 10.1155/2022/2086717

CrossRef Full Text | Google Scholar

Liu, D., You, J., Wang, R., Deng, H. (2022). Agricultural production optimization and marginal product response to climate change. Agriculture 12, 1403. doi: 10.3390/agriculture12091403

CrossRef Full Text | Google Scholar

Liu, Y. Y., Zhang, P. Y., Ru, Y., Wu, D. L., Wang, S. L., Yin, N. N., et al. (2022). A scheduling route planning algorithm based on the dynamic genetic algorithm with ant colony binary iterative optimization for unmanned aerial vehicle spraying in multiple tea fields. Front. Plant Sci. 13. doi: 10.3389/fpls.2022.998962

CrossRef Full Text | Google Scholar

Liu, H. Y., Zhang, L. H., Zhao, B. D., Tang, J. C., Wang, F. L., Wang, S. (2024). Research on agricultural machine scheduling in hilly areas based on improved non-dominated sorting genetic algorithm-III. IEEE Access. 12, 32584–32596. doi: 10.1109/ACCESS.2024.3371176

CrossRef Full Text | Google Scholar

Liu, X. Y., Zhu, X. M., Hao, K. R. (2021). Dynamic immune cooperative scheduling of agricultural machineries. Complex Intell. Syst. 7, 2871–2884. doi: 10.1007/s40747-021-00454-2

CrossRef Full Text | Google Scholar

Ma, L., Xin, M., Wang, Y. J., Zhang, Y. (2022). Dynamic scheduling strategy for shared agricultural machinery for on-demand farming services. Mathematics 10, 3933. doi: 10.3390/math10213933

CrossRef Full Text | Google Scholar

Okulewicz, M., Mańdziuk, J. (2017). The impact of particular components of the PSO-based algorithm solving the Dynamic Vehicle Routing Problem. Appl. Soft. Comput. 58, 586–604. doi: 10.1016/j.asoc.2017.04.070

CrossRef Full Text | Google Scholar

Plessen, M. G. (2019). Coupling of crop assignment and vehicle routing for harvest planning in agriculture. Artif. Intell. Agric. 2, 99–109. doi: 10.1016/j.aiia.2019.07.001

CrossRef Full Text | Google Scholar

Seyyedhasani, H., Dvorak, J. S. (2018). Dynamic rerouting of a fleet of vehicles in agricultural operations through a Dynamic Multiple Depot Vehicle Routing Problem representation. Biosyst. Eng. 171, 63–77. doi: 10.1016/j.biosystemseng.2018.04.003

CrossRef Full Text | Google Scholar

Sun, Y., Zhao, Z., Li, M. (2022). Coordination of agricultural informatization and agricultural economy development: A panel data analysis from Shandong province, China. PloS One 17, e0273110. doi: 10.1371/journal.pone.0273110

CrossRef Full Text | Google Scholar

Tian, H., Mo, Z., Ma, C., Xiao, J., Jia, R., Lan, Y., et al. (2023). Design and validation of a multi-objective waypoint planning algorithm for UAV spraying in orchards based on improved ant colony algorithm. Front. Plant Sci. 14. doi: 10.3389/fpls.2023.1101828

CrossRef Full Text | Google Scholar

Wang, Y. J., Huang, G. Q. (2022). Harvester scheduling joint with operator assignment. Comput. Electron. Agric. 202, 107354. doi: 10.1016/j.compag.2022.107354

CrossRef Full Text | Google Scholar

Wang, N., Yang, X., Wang, T. H., Xiao, J. X., Zhang, M., Wang, H., et al. (2023). Collaborative path planning and task allocation for multiple agricultural machines. Comput. Electron. Agric. 213, 108218. doi: 10.1016/j.compag.2023.108218

CrossRef Full Text | Google Scholar

Worasan, K., Sethanan, K., Pitakaso, R., Moonsri, K., Nitisiri, K. (2020). Hybrid particle swarm optimization and neighborhood strategy search for scheduling machines and equipment and routing of tractors in sugarcane field preparation. Comput. Electron. Agric. 178, 105733. doi: 10.1016/j.compag.2020.105733

CrossRef Full Text | Google Scholar

Yang, W. Q., Yang, Z. L., Chen, Y. G., Peng, Z. (2022). Modified whale optimization algorithm for multi-type combine harvesters scheduling. Machines 10, 64. doi: 10.3390/machines10010064

CrossRef Full Text | Google Scholar

Zhang, F., Zhang, W. Y., Luo, X. W., Zhang, Z. G., Lu, Y. T., Wang, B. (2022). Developing an ioT-enabled cloud management platform for agricultural machinery equipped with automatic navigation systems 310. doi: 10.3390/agriculture12020310

CrossRef Full Text | Google Scholar

Zhang, W., Zhao, B., Zhou, L., Qiu, C., Wang, J., Niu, K., et al. (2022). Development of a resource optimization platform for cross-regional operation and maintenance service for combine harvesters. Appl. Sci. 12, 9873. doi: 10.3390/app12199873

CrossRef Full Text | Google Scholar

Zhang, W. P., Zhao, B., Zhou, L. M., Wang, J. Z., Qiu, C. H., Niu, K., et al. (2022). Harvester maintenance resource scheduling optimization, based on the combine harvester operation and maintenance platform. Agriculture 12, 1433. doi: 10.3390/agriculture12091433

CrossRef Full Text | Google Scholar