Development and Validation of a Mechanistic, Weather-Based Model for Predicting Puccinia graminis f. sp. tritici Infections and Stem Rust Progress in Wheat

Stem rust (or black rust) of wheat, caused by Puccinia graminis f. sp. tritici (Pgt), is a re-emerging, major threat to wheat production worldwide. Here, we retrieved, analyzed, and synthetized the available information about Pgt to develop a mechanistic, weather-driven model for predicting stem rust epidemics caused by uredospores. The ability of the model to predict the first infections in a season was evaluated using field data collected in three wheat-growing areas of Italy (Emilia-Romagna, Apulia, and Sardinia) from 2016 to 2021. The model showed good accuracy, with a posterior probability to correctly predict infections of 0.78 and a probability that there was no infection when not predicted of 0.96. The model’s ability to predict disease progress during the growing season was also evaluated by using published data obtained from trials in Minnesota, United States, in 1968, 1978, and 1979, and in Pennsylvania, United States, in 1986. Comparison of observed versus predicted data generated a concordance correlation coefficient of 0.96 and an average distance between real data and the fitted line of 0.09. The model could therefore be considered accurate and reliable for predicting epidemics of wheat stem rust and could be tested for its ability to support risk-based control of the disease.

Introduction

Stem rust, also known as black rust, is caused by Puccinia graminis Pers. f. sp. tritici Erik. and E. Henn. (Pgt), and is a major threat to wheat production worldwide (Leonard and Szabo, 2005; Newcomb et al., 2016; Steffenson et al., 2017). Stem rust is potentially the most damaging of the wheat rusts, because it attacks leaf blades as well as leaf sheaths, stems, and heads (Eversmeyer and Kramer, 2000), and it can destroy an entire crop in a few weeks (Roelfs, 1985; Singh et al., 2006; Steffenson et al., 2017) by causing different kinds of damage (Durbin, 1984; Roelfs, 1985; Willocquet et al., 2021). Known since Roman times, the cyclic occurrence of stem rust was recorded in the first half of the 20th century in Europe, United States, India, and Australia (Zadoks, 1963; Rees, 1972; Nagarajan and Joshi, 1975; Roelfs, 1978, 1977). The importance of the disease decreased between the 1960s and 1990s thanks to the introduction of resistance genes in cultivated wheat and to the eradication of the alternate hosts (Berberis spp.; Singh et al., 2015; Saunders et al., 2019). Attention to stem rust has increased since the emergence of the Pgt race Ug99 in 1998 in Uganda; Ug99 was not controlled by Sr31 or other major resistance genes (Pretorius et al., 2000; Singh et al., 2006). Since 2013, outbreaks of wheat stem rust in Europe have been recorded in several countries, and new races have been detected (Shamanin et al., 2016; Bhattacharya, 2017; Saunders et al., 2019; Hovmøller et al., 2021). According to recent studies (Lewis et al., 2018), in addition to the evolution of virulent populations, climate change over the past 25 years may help explain the re-emergence of the disease, because Pgt is favored by high temperatures (Leonard and Szabo, 2005).

Losses due to stem rust have typically ranged between 10 and 50% but can exceed 90% when epidemics occur early in the season and are not controlled (Beard et al., 2006). Severe epidemics have recently occurred worldwide. In 2015, more than one million ha of spring wheat in Western Siberia and Kazakhstan were affected by stem rust, causing average yield losses of 20–30% on a regional scale (Shamanin et al., 2016). In 2016, widespread attacks of stem rust were also observed in Sicily (Italy) and Morocco (Bhattacharya, 2017; Randazzo et al., 2019).

Control of stem rust is based on genetic resistance, eradication of alternate hosts, and application of fungicides. Several breeding programs and international efforts are focused on the development and exploitation of new sources of resistance to wheat stem rust (Schumann and Leonard, 2011). Although more than 50 stem rust resistance genes have been cataloged, effectiveness is limited to some Pgt races or is low under field conditions (Singh et al., 2006). The eradication of alternate hosts, which support the Pgt sexual cycle, has significantly reduced the number of new races and has helped to stabilize Pgt populations (Roelfs, 1982; Jin, 2011). Timely application of fungicides can also control stem rust (Beard et al., 2006; Wanyera et al., 2009; Tadesse et al., 2010; Mengesha, 2020). As documented by Tadesse et al. (2010), fungicides applied at 14- or 21-day intervals reduced disease progress, but only weekly sprays ensured complete control. Repeated calendar sprays, however, are uneconomical (Roelfs, 1985). In Australia, for example, one or two sprays are typically applied to control the disease (Beard et al., 2006). In Sicily (Italy), only one fungicide application is economically sustainable, and many growers do not apply any fungicides to protect their crops against rusts (Randazzo et al., 2019). Time of application must also be considered. Fungicide sprays are more effective when applied early in the disease development, and no control or poor control occurs when fungicides are applied later in the season to severely affected plants (Loughman et al., 2005; Beard et al., 2006).

Simulation and predictive models have been developed for improving stem rust management. Simulation models can support strategic decisions, research priorities, and breeding strategies (Savary et al., 2018). A simulation model developed by Meyer et al. (2017) describes airborne dispersal routes of Pgt uredospores on regional and continental scales and also considers environmental suitability for infection after spore deposition. Willocquet et al. (2021) recently developed a simulation model for estimating the yield losses caused by stem rust. Predictive models mainly support tactical disease management. Because of the importance of preventing the first infections in a season, empirical models have been developed to predict stem rust outbreaks (Rees, 1972; Nagarajan et al., 1977, 1976; Mulatu et al., 2020). For instance, Nagarajan et al. (1977, 1976) used counts of uredospores in rain samples to predict infections of wheat stem rust 20 days in advance of the time when uredia can be first seen on the crop. The use of spore-trapping data, which would require a wide network of spore sampling sites, was also suggested to predict stem rust epidemics in northeastern Australia (Rees, 1972); the presence of uredospores, however, does not necessarily result in infection (Rees, 1972; Nagarajan et al., 1977, 1976). Mulatu et al. (2020) developed an empirical model for stem rust prediction based on temperature and relative humidity in Ethiopia between 2010 and 2019. This model, however, refers to two bread wheat varieties and has not been validated by comparison with independent field data.

Process-based, weather-driven models have been shown to be more accurate and robust than empirical ones because process-based, weather-driven models are mechanistic, i.e., they consider key biological events that determine the development of epidemics and they consider the related driving variables, i.e., weather conditions (Caffi et al., 2007; Narouei-Khandan et al., 2020). Mechanistic models can be developed both conceptually and mathematically by means of a systematic literature review and meta-analysis of published data (Rossi et al., 2015).

The current study had three objectives: (i) to collect and analyze the available information on stem rust of wheat; (ii) to develop a mechanistic, dynamic, weather-driven model; and (iii) to test the model’s ability to predict the first seasonal infections of Pgt and the progress of stem rust epidemics.

Materials and Methods

Literature Search

According to the criteria presented by Okoli and Schabram (2010), a systematic literature review was performed to collect data on the life cycle of Pgt and on the relationships between Pgt and its hosts. Our last literature search was carried out in 2021 in three bibliographical databases: the CAB Abstract database (¹accessed on February 12), the Scopus database (²accessed on February 18), and the Google Scholar database (³accessed on February 19). Papers were searched by combining the following keywords: (i) Puccinia graminis f. sp. tritici; (ii) stem rust of wheat OR black rust of wheat OR other common names; (iii) life cycle OR uredospores OR germination OR penetration OR infection OR incubation OR latency OR survival OR deposition. All of the papers identified through the search were initially screened by title to remove any that were clearly not relevant for the development of the model (e.g., papers regarding other rust species). The papers were then evaluated for relevance. To be considered relevant, the papers had to satisfy the following criteria: (i) the name of the pathogen or the disease appeared in the title, abstract, or the authors’ keywords; (ii) as indicated by the abstract, the paper concerned the biology, ecology, or epidemiology of Pgt; and (iii) the paper was published in a journal, proceeding, or other forms (including reports or web-sites) from competent authorities/organizations. Papers not excluded at these levels were screened at the full-text level to ensure relevance. Reference lists in the reviewed papers were screened, and additional papers (in addition to those retrieved in the mentioned databases) fulfilling the inclusion criteria were also retrieved and reviewed.

Disease Cycle

Puccinia graminis f. sp. tritici is a heteroecious and macrocyclic rust fungus with five spore stages: basidiospores, pycniospores (spermatia), aeciospores, urediniospores (or uredospores), and teliospores. Each spore stage has a role in the fungus life cycle (Littlefield and Heath, 1979; Littlefield, 1981; Roelfs, 2010). Because the fungus develops without the sexual cycle in major wheat-growing areas (Roelfs, 1985), our model focuses on uredospores, which are the main spores responsible for disease development on wheat. In mild and tropical climates, the pathogen survives on volunteer cereals or other gramineous hosts, producing local inoculum that can lead to severe epidemics during the wheat growing season (Roelfs, 1985). In temperate climates, the pathogen generally does not overwinter locally (Roelfs, 1985), and epidemics are caused by airborne uredospores that originate from warmer areas (Zadoks and Bouwman, 1985; Eversmeyer and Kramer, 2000). Capable of long-distance transport, airborne uredospores (Stakman and Christensen, 1946; Hirst et al., 1967; Zadoks and Bouwman, 1985; Eversmeyer and Kramer, 2000) are scrubbed from the atmosphere and deposited onto plant surfaces by rain (Rowell and Romig, 1966; Nagarajan et al., 1976). Given favorable temperatures and the presence of free water, uredospores on host tissues germinate and form appressoria with penetration pegs in 3 to 6 h (Roelfs, 1985). Symptoms usually become visible on stems and leaves a few days after infection as light-colored spots (Roelfs, 1985) from which uredia gradually erupt as masses of reddish-brown uredospores (Zillinsky, 1983). Sporulation continues over several weeks, until plants approach maturity and tissues senesce (Zillinsky, 1983; Roelfs, 1985; Newton et al., 1999). Uredospores detach from uredia and disperse in a diurnal pattern, with spore dispersal peaking at noon (Hirst, 1953). Most of the uredospores produced are deposited within the local wheat canopy (Roelfs and Martell, 1984; Eversmeyer and Kramer, 1992) and survive for several weeks (Roelfs, 1985; Singh et al., 2002).

Model Description

Model Structure

Information retrieved from selected papers was organized based on systems analysis (Leffelaar and Ferrari, 1989) and was used for model development. The model structure is shown in Figure 1. The diagram was drawn following the system representation of Forrester (1997) as used in STELLA^® (abbreviation of Systems Thinking, Experimental Learning Laboratory with Animation), a visual programming language for modeling system dynamics. The diagram combines state variables (rectangles), flows (solid arrows), rates (valves), parameters, and coefficients (circles).

FIGURE 1

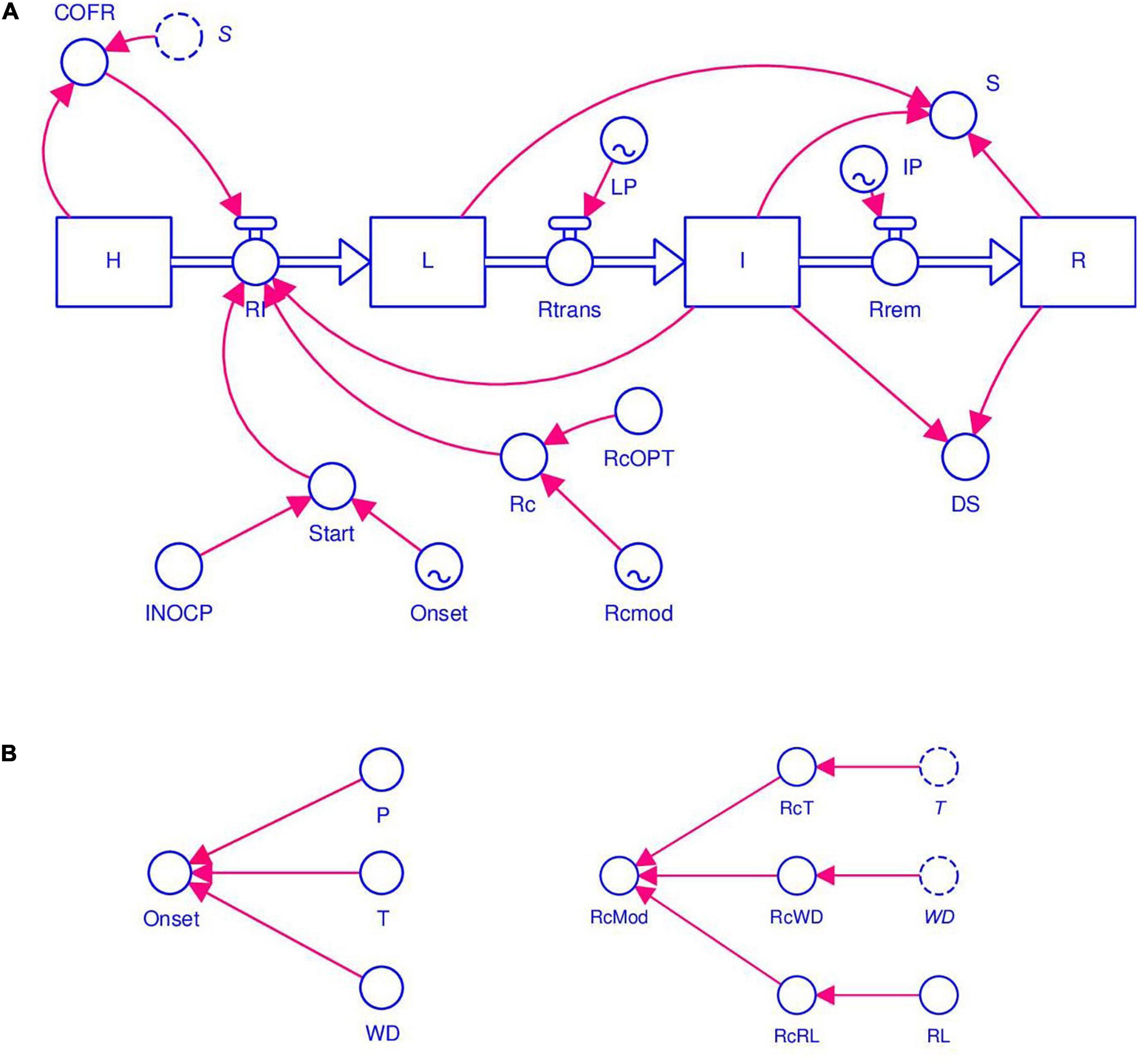
Figure 1. Flow chart of stem rust of wheat. The diagram uses the symbols developed by Forrester (1961). Symbols for state variables, rates, and parameters are listed in Table 1. (A) Core structure of the model based on Zadoks (1971), with sites evolving from healthy (HS), to latent (L), to infectious (I), and finally to removed (R). The initiation of an epidemic depends on primary infections (INOCP, Onset). The progress of the epidemic depends on secondary infections (RI, Rc, and I). The model’s core works with a daily time step. (B) Conditions for primary infections and modifiers of secondary infections (RcWD, RcT, and RcLR), which are calculated with an hourly time step.

TABLE 1

Table 1. List of variables, rates, and parameters used in the model.

The core of the model’s structure is based on the epidemiological model developed by Zadoks (1971), in which the crop is thought to consist of a large but finite number of infection sites that have equal dimensions and equal probability of becoming infected. A site is defined as a fraction of the host tissues where an infection may occur and where a lesion may develop (Zadoks, 1971; Savary et al., 2015). A site occurs under one of the following mutually exclusive conditions: (i) heathy (H); (ii) latent (L), i.e., without symptoms of stem rust; (iii) infectious (I), i.e., with visible lesions producing spores; and (iv) removed (R), i.e., lesions are older and non-sporulating (Figure 1 and Table 1). The structure used here represents the host in a very simple manner and does not incorporate host growth or senescence; it also does not account for lesion expansion from infected sites. Sites becoming infected at an infection rate (RI), i.e., they change from healthy sites into latent sites. Latent sites become infectious at the end of a latency period (LP) at a transfer rate (Rtrans), and infectious sites become removed at the end of an infectious period (IP) with a rate of removal (Rrem) (Figure 1 and Table 1).

At the beginning of model calculations, H = 1 (i.e., the whole crop is healthy), and the model represents the flow from one state to the following one as a proportion of the H, i.e., on a 0 to 1 scale. The model works with a daily time step, with the following exceptions: the onset of primary infection (see Section “Model Structure”) and the modifiers of RI (see Section “Modifiers of RcOPT”) are calculated hourly and are reported on the daily scale.

Development and Parameterization of Model Equations

The effects of temperature and wetness duration on epidemics are incorporated into the model as mathematical equations. The effects of temperature on germination, penetration, the length of the latency period, and the length of the infectious period are described by the following equations: f(T)_GER, f(T)_PEN, f(T)_LP, and f(T)_IP (see Sections “Modifiers of RcOPT,” “Latency Period,” and “Infectious Period”). The effects of wetness duration on germination and penetration are described by the equations f(WD)_GER and f(WD)_PEN, respectively (see Section “Modifiers of RcOPT”).

Equations were developed and parameterized based on the papers that were collected through the systematic literature review. Useful data were retrieved from tables, figures, and texts of the selected papers. The shape of the data and the Akaike information criterion (Burnham and Anderson, 2002) were used to choose the best-fitting mathematical functions. Equation parameters were estimated using the function nls of the “stats” package of R software (Team, R Core. R: A Language and Environment for Statistical Computing. 2019, which is available at⁴). The parameterized equations were evaluated for goodness-of-fit based on the adjusted R², the concordance correlation coefficient (CCC), the root mean square error (RMSE), and the coefficient of residual mass (CRM) (Nash and Sutcliffe, 1970; Lin, 1989). The adjusted R² was estimated by conducting a linear regression between the observed values and the model predicted values; the linear regression was conducted with the lm function of the R “stats” package (Wickham, 2019). The CCC is a measure of model accuracy (Madden, 2006), and is calculated as the product of the Pearson correlation coefficient and the Cb coefficient; the CCC indicates the difference between the best fitting line and the perfect agreement line (Lin, 1989). The CCC was obtained using the CCC function of the R “DescTools” package (Signorell, 2020). The RMSE, which represents the average distance of real data from the fitted line (Nash and Sutcliffe, 1970), was obtained using the rmse function of the R “modelr” package (Wickham, 2019). The CRM is a measure of the tendency of the equation to overestimate or underestimate the observed values (a negative CRM indicates a tendency of the model toward overestimation) (Nash and Sutcliffe, 1970).

First Seasonal Infection

The date of the establishment of the epidemic (Start) depends on Onset, which represents the occurrence of weather conditions favorable for the first infection of the season. Onset is calculated hourly and reported at a daily time step as either Onset = 0, i.e., conditions are not favorable for infection, or Onset = 1, i.e., conditions are favorable for primary infection. Information retrieved from Singh et al. (2006, 2002), Roelfs (1985); Burrage (1970), Rowell and Romig (1966), and Sharp et al. (1958) were used to set Onset = 1 as follows: (i) rain event (P) ≥ 1 mm h^–1; (ii) the wetness period (WD) following rain is ≥3 h; and (iii) mean temperature during WD (Tw) is between 15 and 32°C. At Onset, the proportion of sites entering L depends on the parameter INOCP, which is an estimate of RI for the first seasonal infection.

Secondary Infections

Once the first seasonal infection has established, secondary infections are responsible for the development of epidemics through the transfer of sites from healthy to latent through a rate of infection (RI; i.e., the proportion of newly infected sites per unit of time). RI is modeled as a function of the number of infectious sites (I), a basic infection rate corrected for the removal (Rc; Vanderplank, 1963), and a correction factor for diseased sites (COFR) as follows:

$\mathrm{RI}=\mathrm{Rc}\times \mathrm{I}\times \mathrm{COFR}(1)$

COFR is calculated as follows:

$\mathrm{COFR}=\mathrm{\hspace{0.33em}1}-(\mathrm{S}/(\mathrm{S}+\mathrm{H}))(2)$

where S is the sum of disease sites (S = L + I + R).

In equation (1), Rc represents the proportion of daughter lesions generated per mother lesion. In the model, Rc depends on the optimum corrected basic infection rate (RcOPT), which is the basic infection rate under optimum environmental conditions on a susceptible wheat variety, and on modifiers (RcMod). RcMod is the daily reported value of modifiers for the effect of temperature (RcT), wetness duration (RcWD), and light regime (RcLR) calculated hourly. Rc is calculated as follows:

$\mathrm{Rc}=\mathrm{RcOPT}\times \mathrm{RcMod}(3)$

RcOPT was estimated following Sun and Zeng (1994) from disease progress curves as follows:

$\mathrm{RcOPT}=\frac{r}{\text{exp}(-r\times p)-\exp (-r\times (i+p))}(4)$

where p is the latency period, which was set as 9 days under favorable conditions for epidemics (Mortensen and Green, 1978); i is the infectious period, which was set as 32 days under favorable conditions for epidemics (Mortensen and Green, 1978); and r is the apparent infection rate (Vanderplank, 1963, 1975), calculated as follows:

$r=\frac{\ln ({\mathrm{x}}^2/{\mathrm{x}}^1)}{({\mathrm{t}}^2-{\mathrm{t}}^1)}(5)$

where x₁ and x₂ are disease fractions on two successive dates (t₁ and t₂) at the early stage of the epidemic under conditions conducive to the disease. Equation (5) was used to calculate r from published disease progress curves in susceptible and unprotected crops (Romig and Calpouzos, 1970; Nazareno and Roelfs, 1981; McGrath and Pennypacker, 1991). The first two non-zero severity values (expressed on a 0 to 1 scale) were retrieved from these curves and used for the calculation, resulting in an RcOPT value of 4.5.

Modifiers of RcOPT are used in the model to account for major environmental conditions influencing the infection process (Loomis and Adams, 1983). As mentioned before, modifier contributions are calculated by the model on an hourly basis and are subsequently reported as RcMod on a daily basis; this enabled the model to accurately account for the effects of environmental conditions on infection. RcMod is calculated as follows:

$\mathrm{RcMod}=\mathrm{RcT}\times \mathrm{RcWD}\times \mathrm{RcLR}(6)$

Modifiers of RcOPT

Development and parameterization of modifiers of RcOPT were based on the available literature on urediospore germination and germ tube penetration via stomata.

The modifier RcT accounts for the effect of air temperature (T, in°C) on both germination (f(T)_GER) and penetration (f(T)_PEN), as follows:

$\mathrm{RcT}=\mathrm{f}{(\mathrm{T})}_{\mathrm{GER}}\times \mathrm{f}{(\mathrm{T})}_{\mathrm{PEN}}(7)$

The effect of T on germination is calculated by a Bete equation (Analytis, 1977) in the following form:

$\mathrm{f}{(\mathrm{T})}_{\mathrm{GER}}={(\mathrm{\alpha }\times {\mathrm{Teq}}^{\mathrm{\beta }}\times (1-\mathrm{Teq}))}^{\mathrm{\gamma }}(8)$

where Teq is the equivalent of temperature, calculated as Teq = (Tw – Tmin)/(Tmax – Tmin); Tw is the mean temperature recorded during the wet period; Tmin is the minimum temperature for uredospore germination, i.e., 4°C (Burrage, 1970); and Tmax is the maximum temperature for uredospore germination, i.e., 35°C (Katsuya and Green, 1967). Germination does not occur when Tw < Tmin or Tw > Tmax. Equation (8) was developed and parameterized using the data of Burrage (1970) and Katsuya and Green (1967); estimates and standard errors of equation parameters were α = 4.375 ± 1.016, β = 1.391 ± 0.419, and γ = 0.396 ± 0.201, with adjusted R² = 0.916, CCC = 0.962, MRSE = 0.1, and CRM = 0.004.

The effect of T on penetration is described by the Duthie equation (Duthie, 1997) in the following form:

$\mathrm{f}{(\mathrm{T})}_{\mathrm{PEN}}=\mathrm{\zeta }\times \frac{\exp ((\mathrm{Tw}-\mathrm{\delta })\times \mathrm{\eta }/(\mathrm{\epsilon }+\mathrm{\hspace{0.33em}1}))}{1+\exp ((\mathrm{Tw}-\mathrm{\delta })\times \mathrm{\eta }))}(9)$

with ζ = ((ε + 1)/ε) × ε^{(1/(ε + 1))}; equation (9) was developed and parameterized using the data of Burrage (1970) and Sharp et al. (1958). Estimates and standard errors of equation parameters were ε = 2.699 ± 1.83, δ = 27.02 ± 1.37, and η = 0.683 ± 0.155, with adjusted R² = 0.824, CCC = 0.914, MRSE = 0.139, and CRM = 0.028.

The modifier RcWD accounts for the effect of wetness duration (WD, in h; i.e., cumulative number of h with leaf wetness) on both germination (f ‘(WD)_GER) and penetration (f ’(WD)_PEN), as follows:

$\mathrm{RcWD}=\mathrm{f}{}^{\prime }(\mathrm{WD})_{\mathrm{GER}}\times \mathrm{f}{}^{\prime }(\mathrm{WD})_{\mathrm{PEN}}(10)$

The effect of WD on germination is calculated as the first derivative (f ’(WD)_GER) of the following equation:

$\mathrm{f}{(\mathrm{WD})}_{\mathrm{GER}}=\frac{1}{1+\mathrm{\iota }\times \exp (-\mathrm{\kappa }\times \mathrm{WD})}(11)$

which was developed and parameterized by fitting the data from Burrage (1969, 1970), and Eversmeyer and Kramer (1989). Estimates and standard errors of equation parameters were ι = 35.224 ± 3.663 and κ = 2.27 ± 0.618, with adjusted R² = 0.971, CCC = 0.982, MRSE = 0.073, and CRM = –0.066.

The effect of WD on penetration is calculated as the first derivative (f ’(WD)_PEN) of the following equation:

$\mathrm{f}{(\mathrm{WD})}_{\mathrm{PEN}}=\mathrm{\hspace{0.33em}\hspace{0.33em}1}-\mathrm{\lambda }\times \exp (-\mathrm{\mu }\times \mathrm{WD})(12)$

which was developed and parameterized by fitting the data from Burrage (1970). Because germinated uredospores form germ tubes on stomata about 3 h after the beginning of a wetness period (Roelfs, 1985; Singh et al., 2002), there is no penetration and f(WD)pen = 0 when WD < 3 h. Estimates and standard errors of equation parameter were λ = 1.207 ± 0.124 and μ = 0.068 ± 0.017, with adjusted R² = 0.951, CCC = 0.978, MRSE = 0.084, and CMR = 0.032.

The RcLR modifier accounts for the light/dark regime during infection. Germination of uredospores is slightly higher in the dark than in daylight (Givan and Bromfield, 1963), but penetration of germ tubes is substantially inhibited in the dark. Therefore, RcLR = 1 in daylight hours and =0.452 in dark hours (Sharp et al., 1958).

Latency Period

Latent sites gradually flow from L to I, with a rate of transfer (Rtrans) governed by a temperature-dependent equation accounting for the latency period (LP). The rate of transfer is calculated daily as the first-order derivative of the following Gompertz equation:

$\mathrm{f}{(\mathrm{T})}_{\mathrm{LP}}=\exp (-\mathrm{\nu }\times \exp (-\mathrm{\rho }\times \mathrm{DD}))(13)$

where DD is the degree-days accumulated from the day in which the infection occurred, with 5°C as the minimum temperature (Singh et al., 2002); therefore, when T ≤ 5°C, T = 0; when T > 5°C, T = (T – 5). Equation (13) was developed and parameterized by fitting the data of Katsuya and Green (1967); estimates and standard errors of equation parameters were ν = 2632 ± 255.8 and ρ = 0.07 ± 0.008, with adjusted R² = 0.823, CCC = 0.904, MRSE = 0.084, and CMR = 0.032.

Infectious Period

Sites I remain infectious for a period (IP), the length of which is determined by temperature. The flow from I to R is therefore governed by a temperature-dependent rate of removal (Rrem). The length of the infectious period is determined by the following logistic equation:

$\mathrm{f}{(\mathrm{T})}_{\mathrm{IP}}=\frac{1}{1+\varsigma \times \exp (-\mathrm{\sigma }\times \mathrm{DD})}(14)$

where DD is the degree-days accumulated from the day of transfer of sites from L to I, with 5°C as the minimum temperature. As a consequence, when T ≤ 5°C, T = 0; when T > 5°C, T = (T – 5). The f(T)_IP ranges from 0 to 1, and sites are removed from I when f(T)_IP = 1. Equation (14) was developed and parameterized by fitting the data of Mortensen and Green (1978); estimates and standard errors of equation parameters were ς = 23.97 ± 4.15 and σ = 0.012 ± 0.0006, with adjusted R² = 0.965, CCC = 0.982, MRSE = 0.063, and CMR = –0.005.

Predicted Disease Severity

The model calculates disease severity (DS) during the progress of the epidemic as the sum of the proportion of sites that are carrying visible lesions, i.e., infectious and removed sites, as follows:

$\mathrm{DS}=\mathrm{I}+\mathrm{R}(15)$

Model Evaluation

The model was evaluated for its ability to describe real stem rust epidemics. Model evaluation was conducted separately for the first seasonal infection and for disease progress, using independent data (i.e., data not used in model development).

First Seasonal Infection

To evaluate the ability of the model to predict the first seasonal infection of stem rust, model outputs were validated against real data obtained from nine experimental wheat fields in Italy, which were established for a range of both durum (Triticum durum L., cv. Fuego, Farah, Telemaco, Antalis, Brancaleone, Salgado, Acropolis, RGT Aventadur, Ramirez, Gibraltar, Puro, Platone, Tirex, Teodorico, Don Matteo, and Pigreco) and bread (T. aestivum L., cv. Drusilla, Lucilla, Tocayo, Caronte, Nabucco, Bologna, and Nogal) varieties of wheat between 2016 and 2021 (Table 2). All the tested varieties were susceptible to stem rust. All plots (10 m²) in each experimental field were inspected at 5- to 10-day intervals for the onset of stem rust symptoms in any variety. Weather data were recorded by meteorological stations (PESSL iMetos 3.3) located <2 km from the experimental fields, except for USS16 and USS17, where the weather station was about 15 km away.

TABLE 2

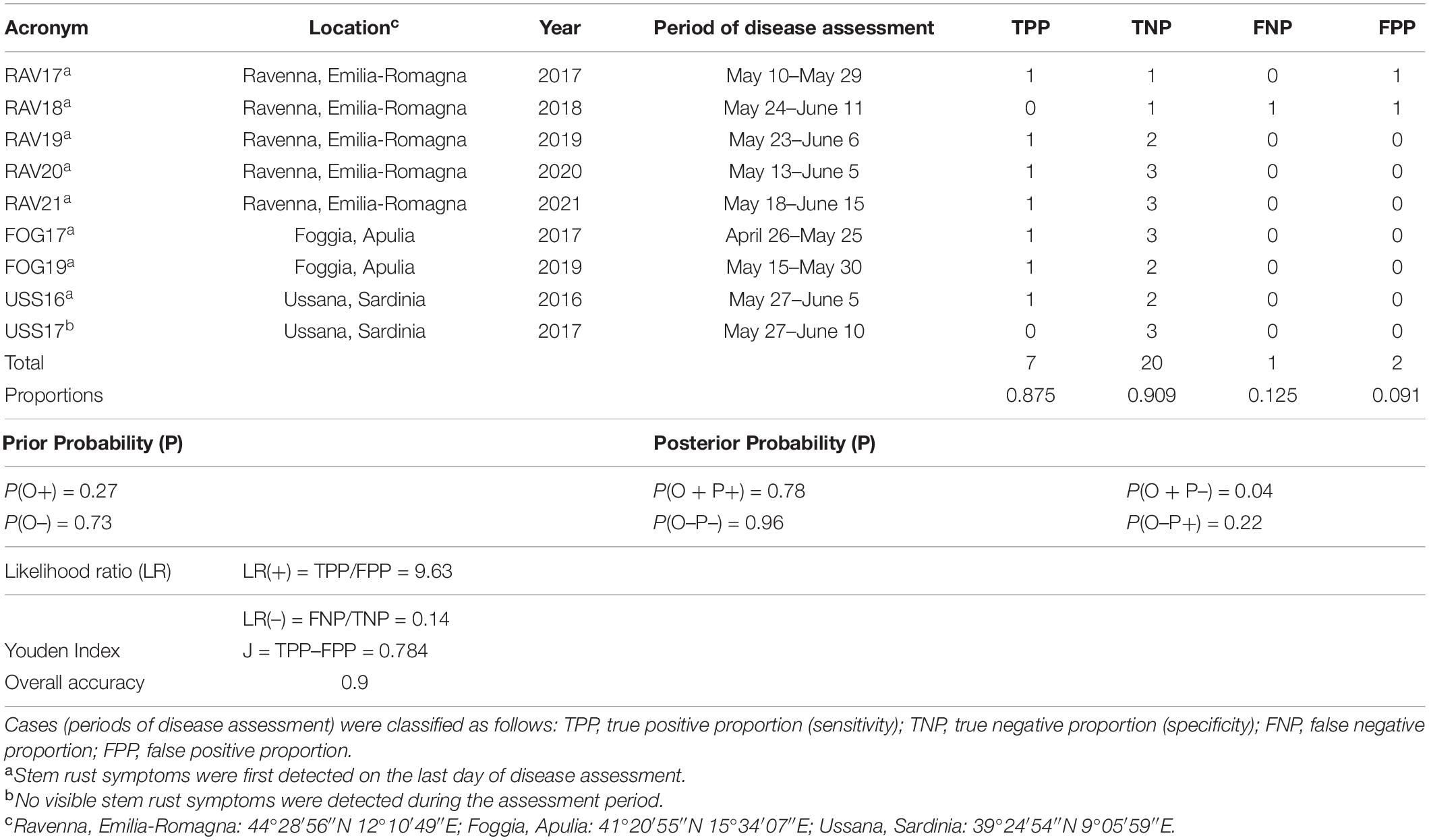
Table 2. Comparison between predicted and observed first seasonal infection in the experimental sites in Italy (acronyms for locations and years), periods of disease assessment, and corresponding properties of the model.

The model was operated by using weather data in each year and location starting from 9 days before the beginning of the disease assessment period (Table 2). Disease assessments (cases) were categorized as either 0 (disease symptoms were not observed on wheat plants, O–) or 1 (disease symptoms were observed on wheat plants, O+). Similarly, cases were categorized as either 0 or 1 based on whether the onset of the disease was predicted (P+) or not (P–) by the model. Because first seasonal infections are seldom severe (Prescott et al., 1986), predicted lesions were considered to be visible for a field assessor when 50% of the uredia generated by the first seasonal infection were predicted to erupt.

According to Madden (2006), a Bayesian analysis was used to evaluate the correspondence between model predictions and stem rust symptoms observed in the field. We tested the hypothesis that new stem rust symptoms were observed in the field (O+) on those days when the model predicted lesion appearance (P+), and that no disease symptoms were observed (O–) on those days when the model did not predict lesion appearance (P–). A contingency table (2 × 2) was prepared containing (i) the true positive proportion (TPP or sensitivity), (ii) the true negative proportion (TNP or specificity), (iii) the false positive proportion (FPP), and (iv) the false negative proportion (FNP).

Prior and posterior probabilities of predicting the first seasonal stem rust occurrence based on model output were calculated (Madden, 2006). The prior probabilities of disease to occur P(O+) or not to occur P(O–) were compared with the following posterior probabilities: (i) the probability of disease occurrence when predicted by the model, P(P + O+); (ii) the probability of disease occurrence when not predicted by the model (i.e., missed real infections), P(P–O+); (iii) the probability of no disease occurrence when not predicted by the model, P(P–O–); and (iv) the probability of no disease occurrence when predicted by the model (i.e., unjustified alarms), P(P + O–). Positive and negative likelihood ratios were calculated as LR(+) = TPP/FPP and LR(–) = FNP/TNP, respectively. The diagnostic ability of the model was evaluated by means of the Youden index, calculated as J = TPP – FPP. Overall model accuracy was estimated as the ratio between correct and total predictions.

Disease Progress

To validate the ability of the model to predict disease development throughout the season, six disease progress curves were retrieved from the literature. Details of experimental sites used for disease progress validation are summarized in Table 3. Initial infections resulted from naturally occurring airborne inoculum in two epidemics and from inoculum originating from artificially and heavily infected “spreader wheat rows” located near the experimental plots in four epidemics (Table 3).

TABLE 3

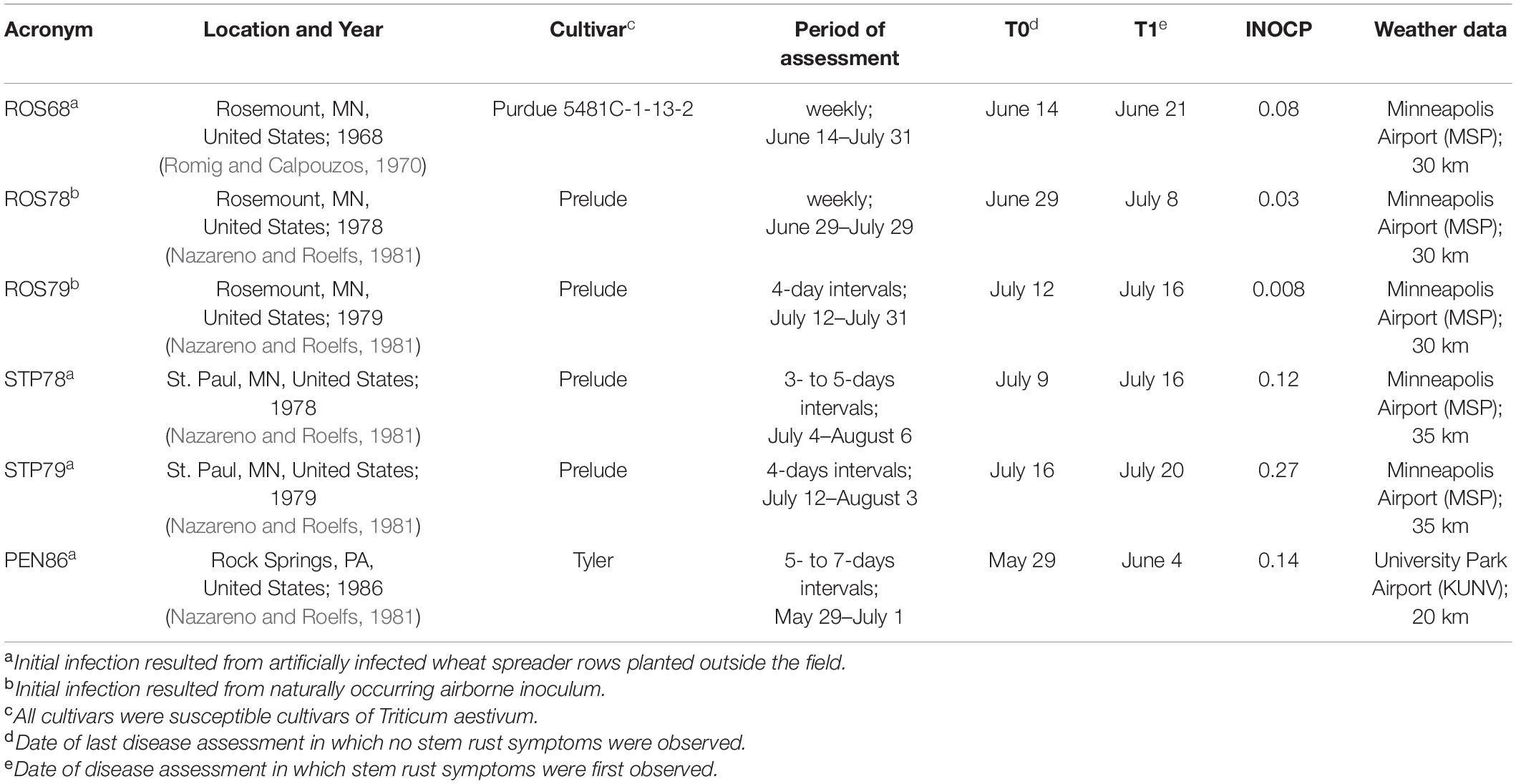
Table 3. Experimental sites (acronyms for locations and years), wheat cultivar, period of disease assessment, INOCP (value of primary inoculum used to initialize model calculations), and weather data used to validate model predictions of epidemic development.

The model was operated beginning at 9 days before the day of the last assessment in which no disease was observed. For epidemics caused by artificially inoculated spreader rows, rain was not considered in the calculation of the variable Onset. Values of INOCP used to initialize model runs are reported in Table 3; because of the use of heavily infected spreader rows, the value of INOCP used for epidemics caused by artificial inoculum was about 10 times greater than the value used for epidemics caused by natural inoculum (Table 3). Because there was no information in the literature for calculating INOCP, values were estimated empirically. For each epidemic, the value of INOCP was determined based on a comparison of predicted and observed final disease severity. The value of INOP that resulted in the closest agreement between the final predicted disease severity and the final observed disease severity was used for model runs.

Predicted disease severities (i.e., sum of infectious and removed sites) and observed disease severities were compared. For the evaluation of model performance, RMSE, CRM, and CCC were calculated (Nash and Sutcliffe, 1970; Lin, 1989).

Results

Evaluation of First Seasonal Infection

Stem rust symptoms were observed in 8 of the 9 experimental fields; no visible symptoms of the disease were detected at USS17. Model predictions concerning the occurrence of infection (P+) or no infection (P-) and observation of stem rust appearance (O+) or no appearance (O-) in wheat experimental fields for each year and location are summarized in Table 2. Among the total of 30 cases (i.e., disease assessments) that were considered, 8 showed infection and 22 did not. Real infections were correctly predicted in 7 of the 8 cases, meaning that only 1 real infection was missed (Table 2). Unjustified alarms were recorded in 2 of 22 cases (Table 2). Results of the Bayesian analysis (Table 2) showed sensitivity TPP = 0.875 and specificity TNP = 0.909; the one missed infection and the two unjustified alarms led to FNP = 0.125 and FPP = 0.091, respectively.

The model had an overall accuracy of 0.9 and a Youden index J = 0.784 (Table 2). An increase from the prior to posterior probabilities of correctly predicting an infection was observed, with P(O+) = 0.27 and P(P + O+) = 0.78. At the same time, the probability of not predicting an infection when there was no infection increased from a prior probability P(O–) = 0.73 to a posterior probability P(P–O–) = 0.96 (Table 2). The effectiveness of the model as a predictor was ensured by the likelihood of a positive prediction LR(+) = 9.63 (larger than 1) and the likelihood of a negative prediction LR(–) = 0.14 (close to 0) (Table 2). These results indicate that the model was able to effectively predict both infection periods and periods in which the disease did not occur.

An example of model output and correct model predictions is shown in Figure 2 for RAV20. Stem rust symptoms were first observed on June 6; no visible lesions were recorded by disease assessments on May 13, 20, or 27. The model predicted the occurrence of the first seasonal infection on May 20 after a rain event of 4.8 mm h^–1; uredia eruption was predicted to occur between May 28 and June 3, with 50% of uredia eruption predicted to occur on May 29.

FIGURE 2

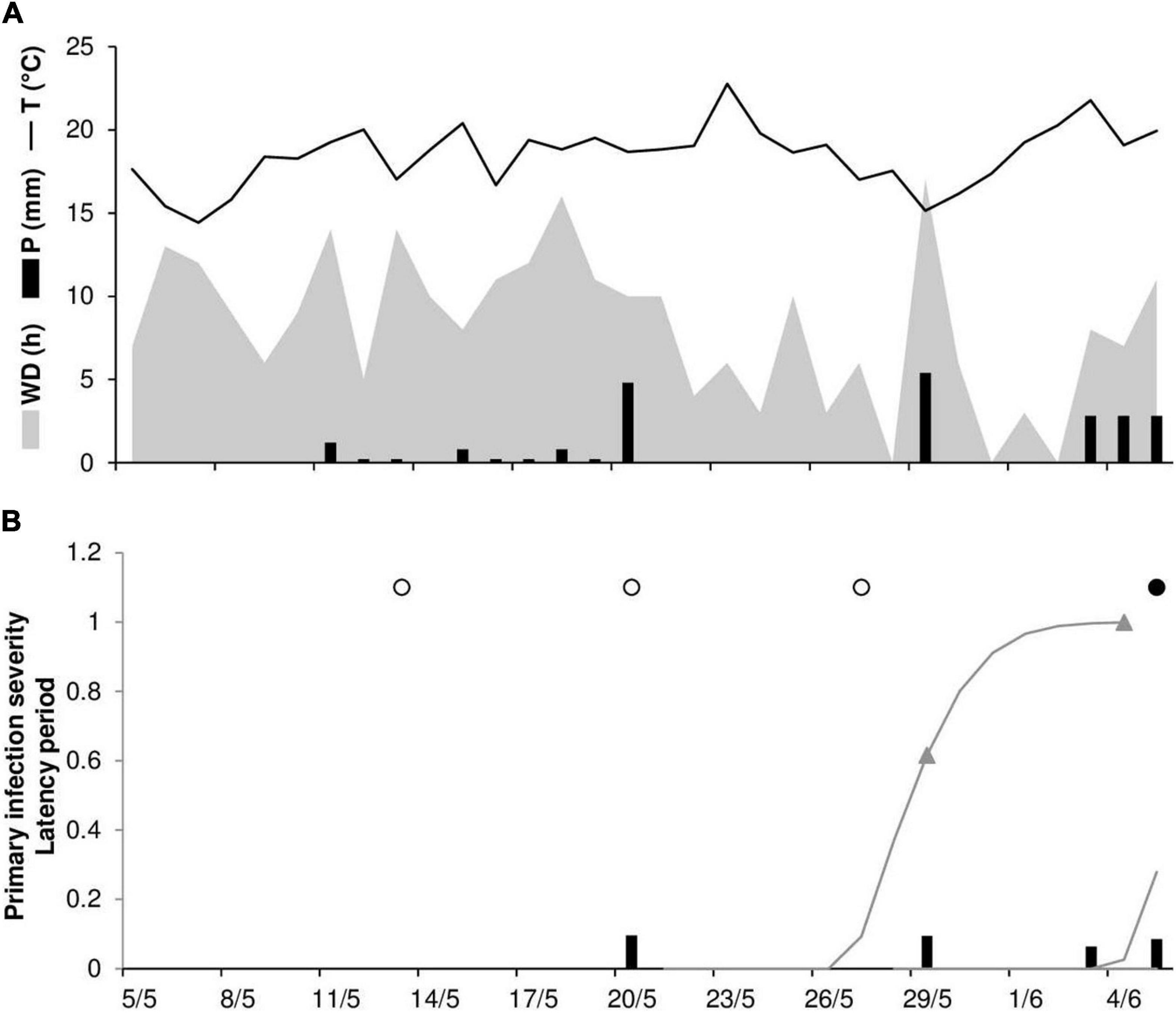
Figure 2. Predicted and observed primary infection onset in the experimental wheat field in Ravenna, Italy, in 2020 (RAV20). (A) Weather variables: air temperature (T, °C, solid line), rainfall (R, mm, black bars), and wetness duration (WD, in h, gray area). (B) Predicted primary infection (black bars); progress of latency (gray line); period of uredia eruption, from 50 to 100% of erupted uredia (line between triangles); days on which stem rust symptoms were not observed (empty dots); days on which uredia were observed in field plots (full dots).

As noted previously, there was one case (RAV18) in which the model did not predict a real infection and two cases in which the model provided a false positive prognosis (RAV17 and RAV18). At RAV18, the last day in which no stem rust symptoms were detected was June 1, and disease onset was recorded in the field on June 11. The false positive prediction was due to rain on May 22 and 23 that triggered model calculations for the infections, which reached 50% of uredia eruption on May 29 and 30 (Figure 3). Because the model assumes that Pgt uredospores are deposited on wheat tissues by rain ≥1 mm h^–1, this single missed real infection may be attributable to rain events ≤1 mm h^–1 that occurred at the end of May (Figure 3). As was the case for the false positive prediction at RAV18, the false positive prediction at RAV17 was due to a rain event that triggered model calculations. The predicted onset of disease occurred only 3 days before the last assessment in which no stem rust symptoms were detected (not shown).

FIGURE 3

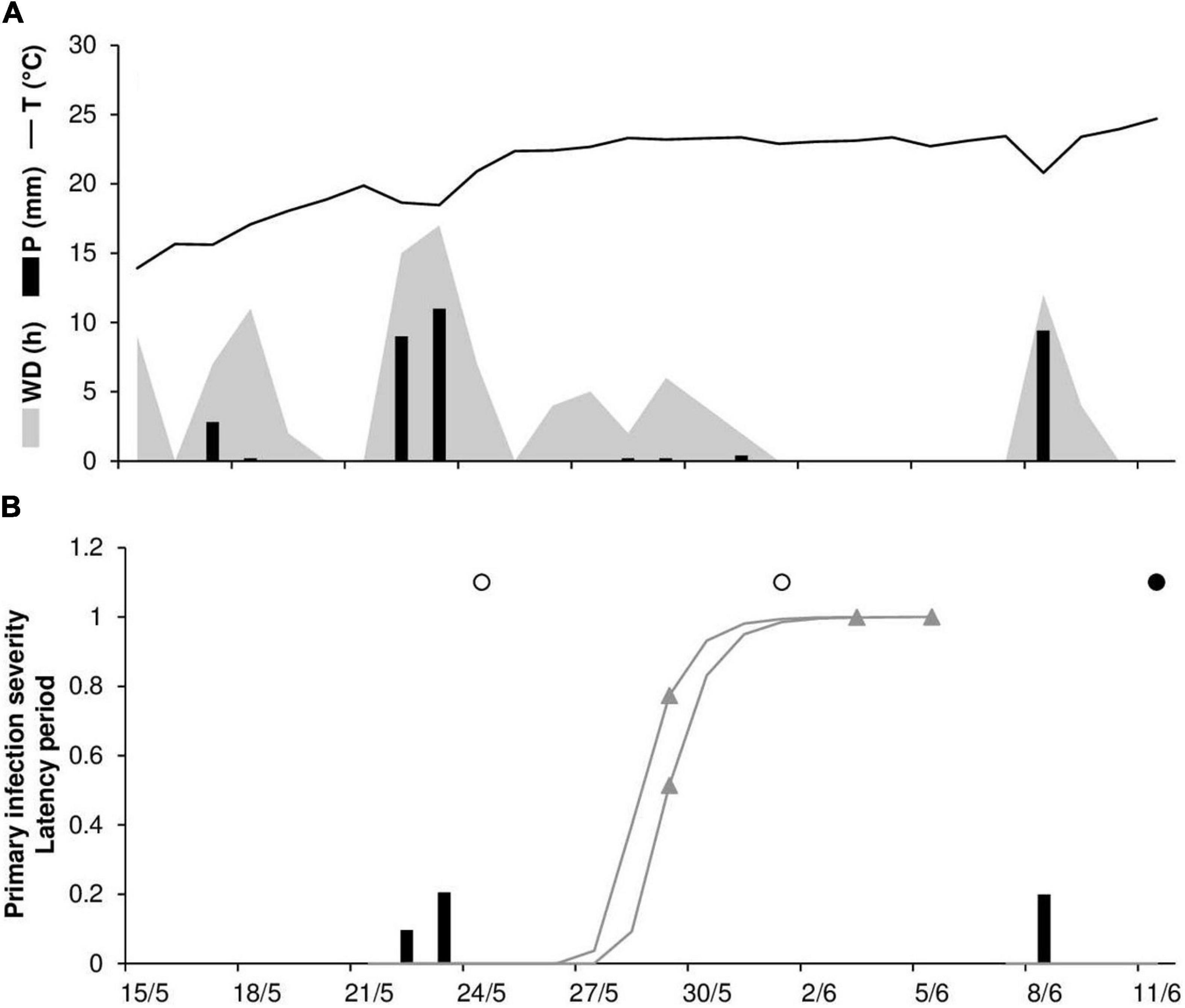
Figure 3. Predicted and observed primary infection onset in the experimental wheat field in Ravenna, Italy, in 2018 (RAV18). (A) Weather variables: air temperature (T, °C, solid line), rainfall (R, mm, black bars), and wetness duration (WD, in h, gray area). (B) Predicted primary infection (black bars); progress of latency (gray line); period of uredia eruption, from 50 to 100% of erupted uredia (line between triangles); days on which stem rust symptoms were not observed (empty dots); days on which uredia were observed in field plots (full dots).

Evaluation of Disease Progress

STELLA^® produced a dynamic representation of healthy (H), latent (L), infectious (I), and removed (R) sites. An example of model output for ROS68 is shown in Figure 4. The first seasonal infection occurred at day of simulation (DOS) 5. Repeated secondary infections triggered the increase of latent and infectious sites so that a rapid increase in disease severity (DS) was observed, especially after DOS 44. The exhaustion of infectious sites occurred only at the end of the epidemic, with a reduction of I and an increase of R.

FIGURE 4

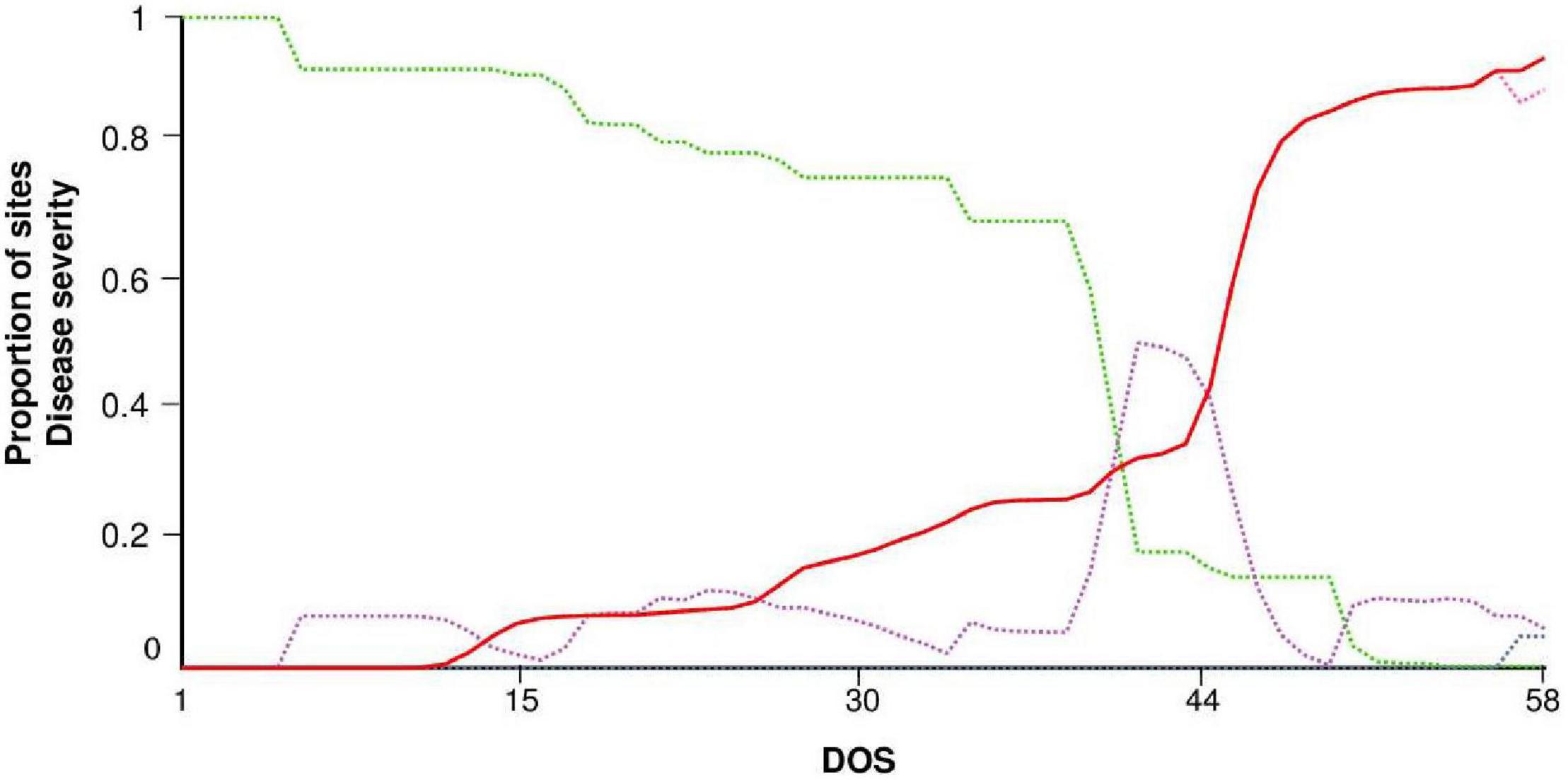
Figure 4. Model output for the experimental field in Rosemount, MN, United States, in 1968 (ROS68). Dynamics of sites: healthy (H, green dotted line), latent (L, purple dotted line), infectious (I, pink dotted line), removed (R, gray dotted line), and disease severity (DS, red solid line). Vertical axis: proportion of sites on a 0 to 1 scale. Horizontal axis: days of simulation (DOS); the model was run from June 5 (i.e., 9 days before the last disease assessment in which no stem rust symptoms were observed, see Table 3).

To evaluate the model’s ability to predict disease progress, predicted disease severity (DS) values were compared to observed disease severity values for six epidemics. At ROS68, the daily temperature ranged from 11°C to 28°C (mean = 21°C), with a total of 215 mm of rain on 20 rainy days and a total of 168 h of leaf wetness (Figure 5A). The disease was first recorded on June 21 and then increased quickly over time (especially between July 10 and 18), resulting in 100% disease severity on July 31 (Figure 5B). Regularly distributed infection periods ensured the progress of the disease, with a final predicted disease severity of 98% (Figure 5B). Goodness-of-fit of predicted versus observed data had a CCC = 0.959 and an RMSE = 0.11. A CRM = –0.043 indicated slight overestimation by the model.

FIGURE 5

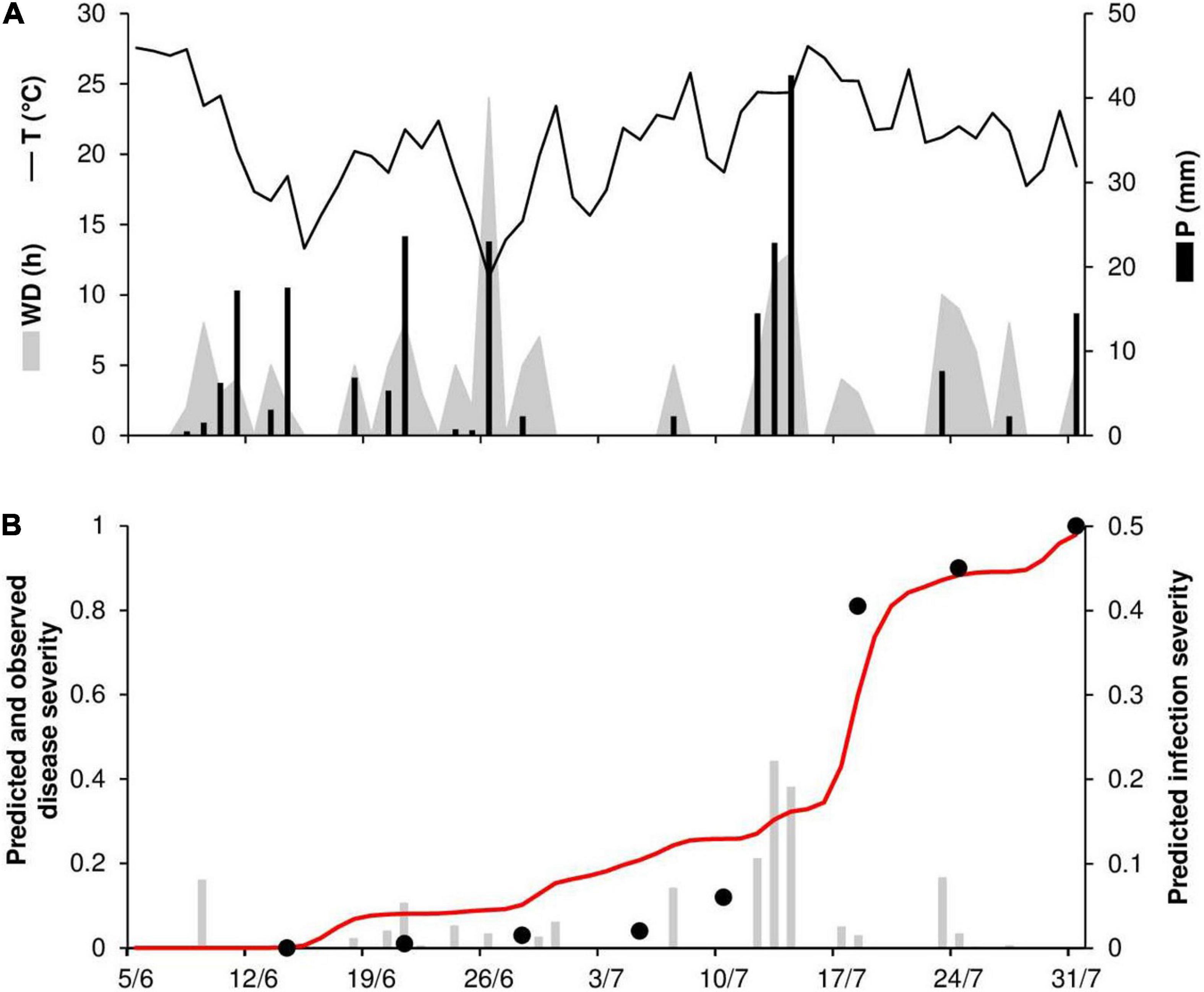
Figure 5. Predicted and observed stem rust progress in the experimental wheat field (susceptible cv. Purdue 5481C-1-13-2) in Rosemount, MN, United States, in 1968 (ROS68). (A) Weather variables: air temperature (T, °C, solid line), rainfall (R, mm, black bars), and wetness duration (WD, in h, gray area). (B) Infection severity predicted by the model (gray bars), disease severity predicted by the model (red line), and observed disease severity (full dots).

At ROS78, the daily temperature ranged from 18°C to 28°C (mean = 22°C), with a total 209 mm of rain on 15 rainy days and a total of 176 h of wetness (Figure 6A). Rains were frequent and intense at the end of June and in the first half of July, with prolonged wetness periods that led to the prediction of numerous infection periods (Figures 6A,B). Disease outbreak was recorded on July 8, and a rapid rise in the disease progress curve was observed, with a final disease severity of 61% (Figure 6B). Contrary to observations, the predicted disease progress was halted by a lack of wetness in mid-July that impeded the prediction of new infections, and it increased again only at the end of July, reaching 64% (Figure 6B). A CCC = 0.914 and an MRSE = 0.088 indicated good agreement between observed and predicted data; despite the failure of the model to predict the increase in disease in the second half of July, a CMR = –0.129 indicated a slight tendency toward overestimation.

FIGURE 6

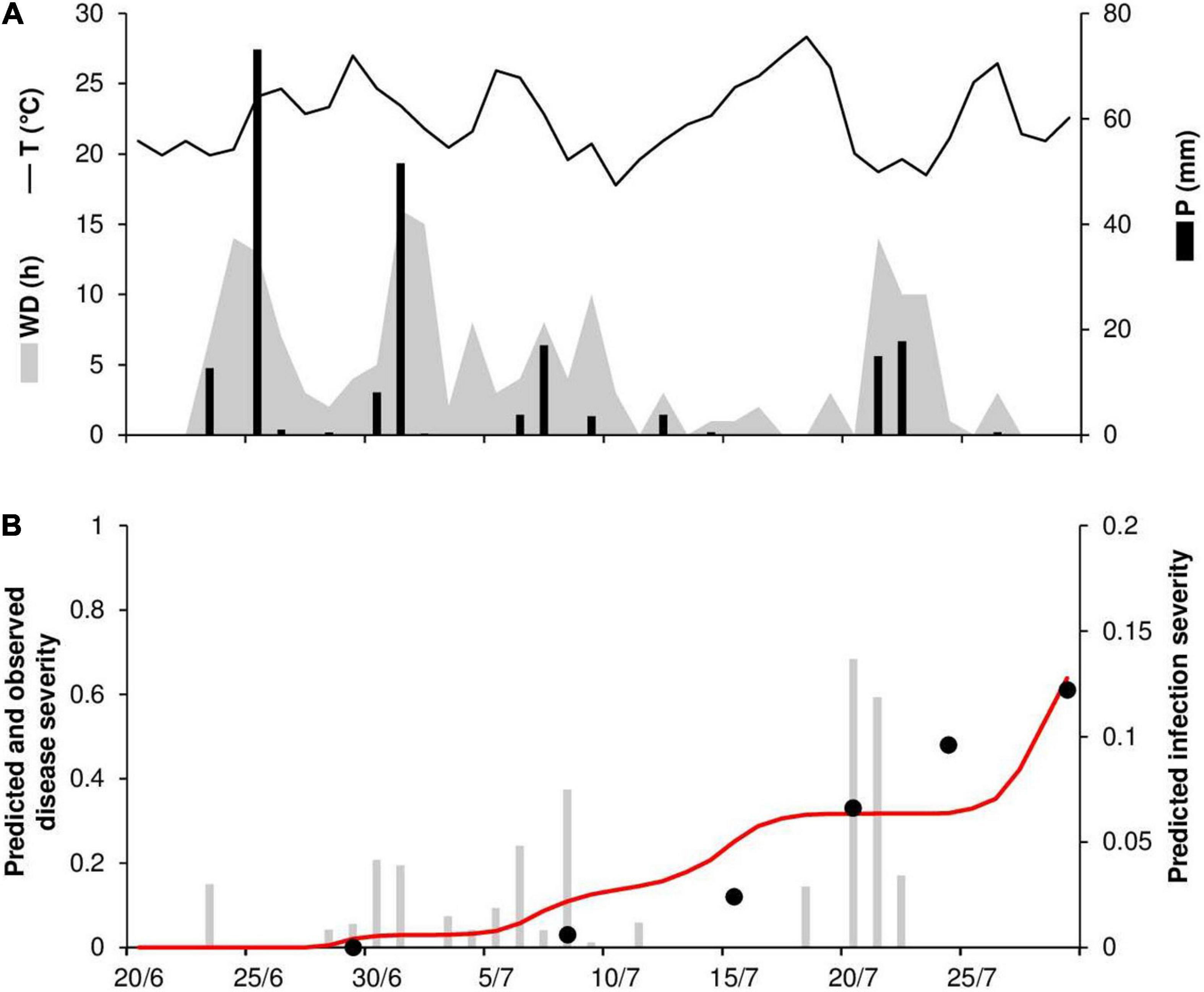
Figure 6. Predicted and observed stem rust progress in the experimental wheat field (susceptible cv. Prelude) in Rosemount, MN, United States, in 1978 (ROS78). (A) Weather variables: air temperature (T, °C, solid line), rainfall (R, mm, black bars), and wetness duration (WD, in h, gray area). (B) Infection severity predicted by the model (gray bars), disease severity predicted by the model (red line), and observed disease severity (full dots).

At ROS79, the daily temperature ranged from 20 to 26°C (mean = 23°C), with 59 mm of rain on 7 rainy days and 92 h of wetness (Figure 7A). Symptoms of stem rust were first observed on July 16; the disease progressed slowly until July 24 (disease severity 2%) but then rapidly increased until July 31, reaching 19% (Figure 7B). The model correctly predicted this dynamic, with a final severity of 19% (Figure 7B). High concordance of observed and predicted disease progress curves was obtained, with CCC = 0.988 and RMSE = 0.01. A CRM = –0.161 indicated a tendency of the model toward overestimation.

FIGURE 7

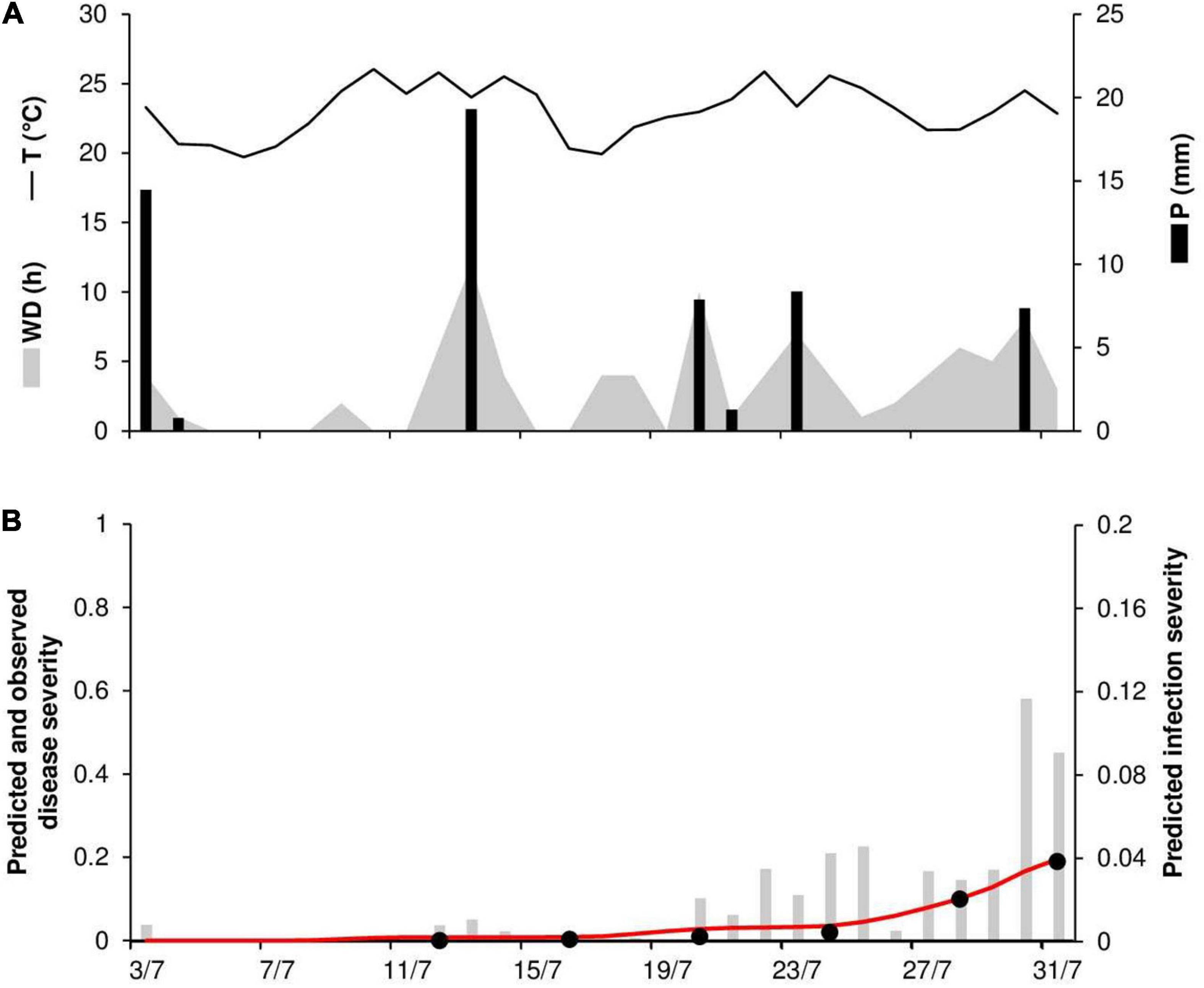
Figure 7. Predicted and observed stem rust progress in the experimental wheat field (susceptible cv. Prelude) in Rosemount, MN, United States, in 1979 (ROS79). (A) Weather variables: air temperature (T, °C, solid line), rainfall (R, mm, black bars), and wetness duration (WD, in h, gray area). (B) Infection severity predicted by the model (gray bars), disease severity predicted by the model (red line), and observed disease severity (full dots).

At STP78, the daily temperature ranged from 16 to 28°C (mean = 22°C), with 71 mm of rain on 9 rainy days and 118 h of wetness (Figure 8A). Long wetness periods occurred between the second half of July and the beginning of August, resulting in several infections predicted by the model (Figure 8B). Disease onset was observed on July 7, and the epidemic was characterized by a substantial increase in disease, with a final severity of 80% (Figure 8B). The model predicted repeated secondary infections causing a substantial increase in disease, with a predicted final disease severity of 81%. For the goodness-of-fit of predicted versus observed data, the CCC = 0.953 and the RMSE = 0.091. The model showed a tendency toward underestimation (CRM = 0.112).

FIGURE 8

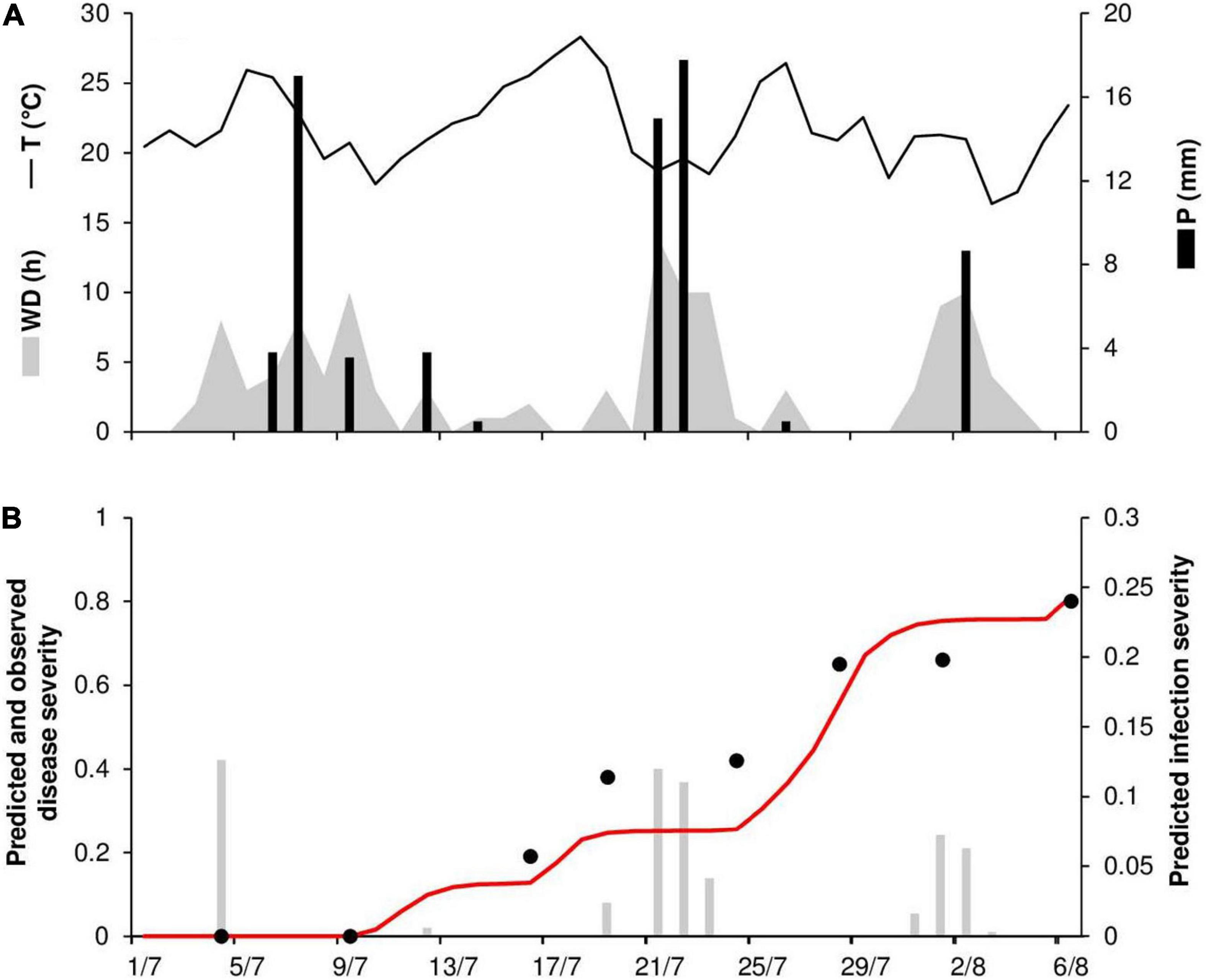
Figure 8. Predicted and observed stem rust progress in the experimental wheat field (susceptible cv. Prelude) in St. Paul, MN, United States, in 1978 (STP78). (A) Weather variables: air temperature (T, °C, solid line), rainfall (R, mm, black bars), and wetness duration (WD, in h, gray area). (B) Infection severity predicted by the model (gray bars), disease severity predicted by the model (red line), and observed disease severity (full dots).

At STP79, the daily temperature ranged from 20 to 26°C (mean = 23°C), with 55 mm of rain on 7 rainy days and 157 h of wetness (Figure 9A). Stem rust symptoms were first recorded on July 20. Long wetness periods occurred at the end of July, leading to a rapid increase of the epidemic and the prediction of repeated secondary infections by the model. Observed and predicted final disease severity was 93% (Figure 9B). Results showed good agreement between observed and predicted data, with CCC = 0.982 and RMSE = 0.071. A CRM = –0.03 indicated a slight tendency toward overestimation.

FIGURE 9

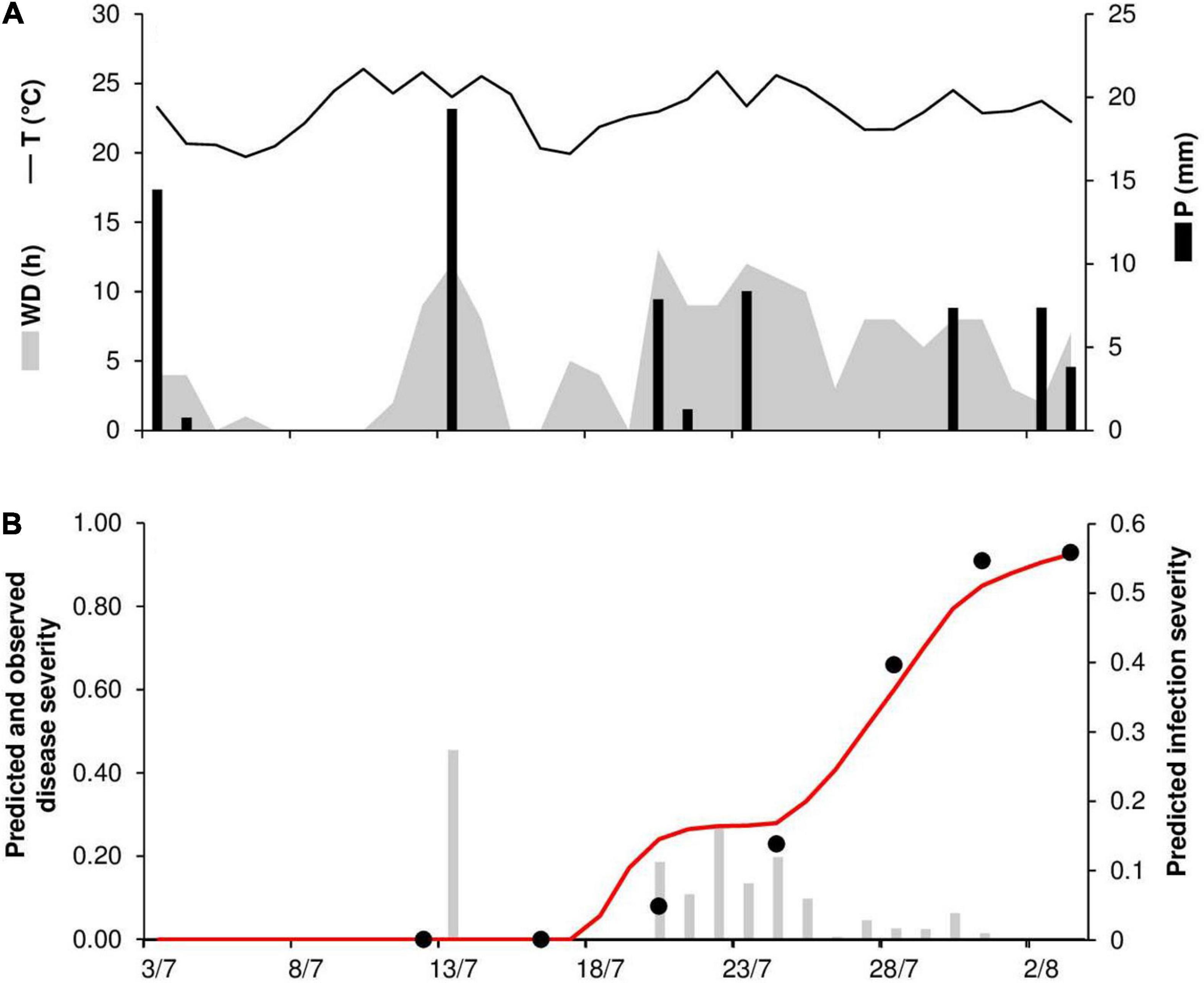
Figure 9. Predicted and observed stem rust progress in the experimental wheat field (susceptible cv. Prelude) in St. Paul, MN, United States, in 1979 (STP79). (A) Weather variables: air temperature (T, °C, solid line), rainfall (R, mm, black bars), and wetness duration (WD, in h, gray area). (B) Infection severity predicted by the model (gray bars), disease severity predicted by the model (red line), and observed disease severity (full dots).

At PEN86, the daily temperature ranged from 12 to 23°C (mean = 18°C), with 81 mm of rain on 14 rainy days and 147 h of wetness (Figure 10A). Disease outbreak occurred on June 4 and was followed by a rapid increase of the epidemic that resulted in a final disease severity of 77%, which was correctly predicted by the model (Figure 10B). Many secondary infections occurred in the first half of June, which was characterized by frequent rains and long wetness periods (Figure 10B). Goodness-of-fit of predicted versus observed data had CCC = 0.96, RMSE = 0.086, and CRM = –0.125.

FIGURE 10

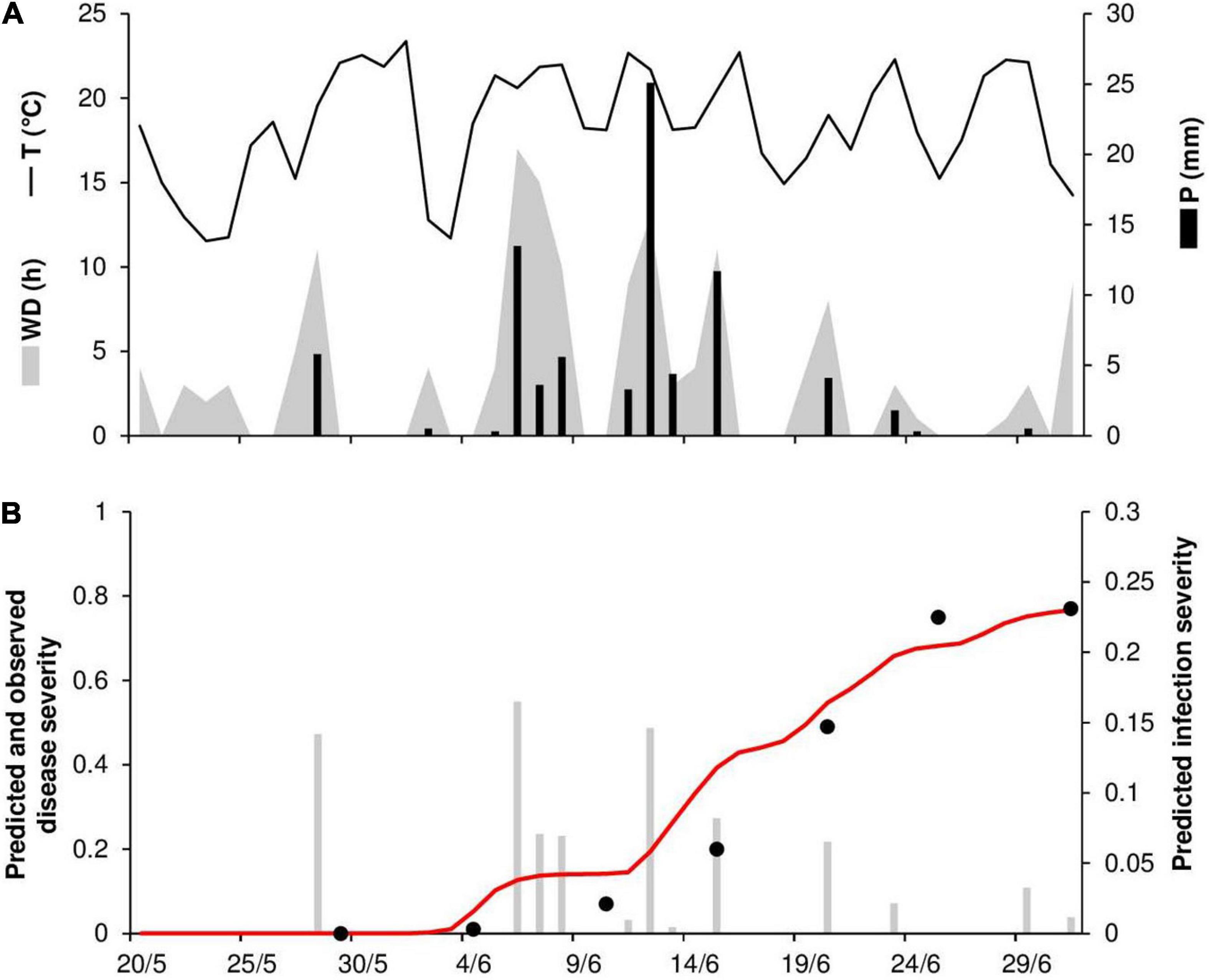
Figure 10. Predicted and observed stem rust progress in the experimental wheat field (susceptible cv. Tyler) in Rock Springs, PA, United States, in 1986 (PEN86). (A) Weather variables: air temperature (T, °C, solid line), rainfall (R, mm, black bars), and wetness duration (WD, in h, gray area). (B) Infection severity predicted by the model (gray bars), disease severity predicted by the model (red line), and observed disease severity (full dots).

An overall comparison of predicted versus observed data (Figure 11) indicated a good agreement between the fitted line and the perfect agreement line (CCC = 0.96), with little average distance between real data and the fitted line (RMSE = 0.09). The model showed a slight tendency toward overestimation (CRM = –0.017).

FIGURE 11

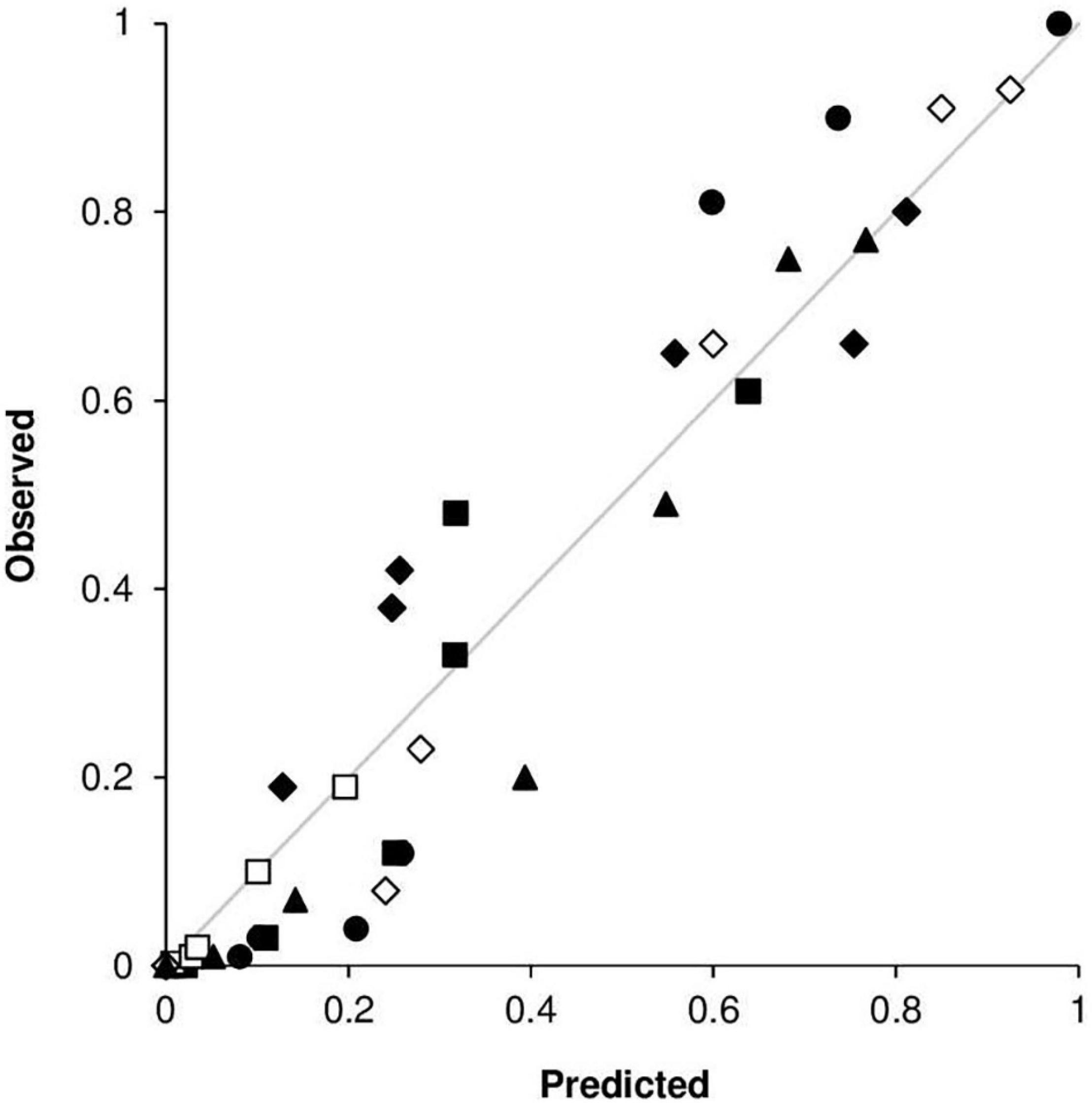
Figure 11. Predicted versus observed values of stem rust severity in the following locations and years: (•) Rosemount, MN, United States, in 1968; (■) Rosemount, MN, United States, in 1978; (□) Rosemount, MN, United States, in 1979; (◆) St. Paul, MN, United States, in 1978; (◆) St. Paul, MN, United States, in 1979; and (▲) Rock Springs, PA, United States, in 1986.

Discussion

The objective of this study was to develop a mechanistic model for stem rust of wheat by exploiting the available information on the pathogen and disease and by mobilizing that information via systems analysis (Leffelaar and Ferrari, 1989; Rossi et al., 2015). Unlike previous models of stem rust (Meyer et al., 2017; Mulatu et al., 2020; Willocquet et al., 2021), our model is predictive and mechanistic in that it considers the biological processes involved in the development of epidemics and the weather factors (i.e., rain, temperature, wetness duration, and light regime) affecting those processes.

The model focuses on uredospores, which are responsible for stem rust epidemics in temperate climates where the inoculum for the first infections in a season consists of air-transported uredospores that travel long distances from warmer areas (Hirst et al., 1967; Roelfs, 1985; Zadoks and Bouwman, 1985; Eversmeyer and Kramer, 2000). Eversmeyer and Kramer (2000) reported that airborne uredospores infecting winter and spring wheat on the Great Plains of the United States were likely produced in Mexico and southern Texas, and that the dissemination northward occurred in short hops of about 100 km. West and East European tracts of uredospore movement from North Africa to Grain Britain and Scandinavia, respectively, were described by Zadoks and Bouwman (1985) and Hirst et al. (1967). Although it was developed and tested in the temperate zone of Europe and North America, the current model should enable predictions in any area where wheat is grown.

The model’s core structure was adapted from the design of Zadoks (1971), which had been developed based on Vanderplank’s (1963) integro-differential equation for epidemics; in that equation, host sites go from healthy, to infected, to infectious, and finally to “removed” during the epidemic. This approach is a well-established modeling framework that has been used in several pathosystems and climates and for diseases of cereals and dicots (Savary et al., 1990, 2015; Djurle and Yuen, 1991; Rossi et al., 1997; Bove et al., 2020). The model’s structure was simple, leading to the assumptions that all sites have equal size that healthy sites have the same vulnerability and that diseased sites have a random distribution. Another simplification was that host growth, host senescence, lesion expansion, and disease management actions (e.g., plant resistance, crop management operations, or timing of crop establishment) were not considered. Because the model was validated against independent data, the model’s accurate predictions of stem rust epidemics indicate that these simplifications did not greatly reduce the model’s ability to make correct predictions. Moreover, the model validation was performed using data collected in a field planted with cultivars that were susceptible to stem rust, showing that the model can predict infection periods. The use of model predictions in crops planted with cultivars exhibiting lower levels of susceptibility to stem rust has to be evaluated. Nevertheless, the design of the model makes it easy to implement further modifications and improvements based on new scientific evidence. For instance, the use of less susceptible hosts can be easily addressed by incorporating modifiers (Loomis and Adams, 1983) accounting for resistance components, as previously implemented in similar model structures (Savary et al., 2012, 2015; Bove et al., 2021).

A daily time step was used for the main structure so that the rate of transfer (Rtrans) and rate of removal (Rrem) are calculated using the mean daily temperature. However, the use of daily weather data ignores the daily variations that may significantly affect infection and other epidemiological processes (Scherm and Van Bruggen, 1994). To avoid these inaccuracies, the model could be altered to assess infection rate (RI) as a function of hourly changes in temperature, wetness duration, and light regime. A time step of 1 h has been used to better account for the effect of fluctuating temperature and humidity, and of possible wetness interruptions during the day (Scherm and Van Bruggen, 1994; Narouei-Khandan et al., 2020).

Epidemics in the model begin on a given day (Onset), which depends on three weather factors (rain, wetness duration, and temperature) that are calculated hourly. As is the case for RI calculations, a time step of 1 h for Onset calculations ensures precise prediction of the first seasonal infection, based on the three conditions that initiate model calculations: (i) rain ≥1 mm h^–1; (ii) wet period following rain ≥3 h; and (iii) mean temperature during wetness (Tw) 15 < Tw < 32°C. The modeled pattern of epidemic initiation is another element that required assumptions about uredospore deposition. Deposition of airborne uredospores that are transported for long distance is known to be triggered by scrubbing rainfall (Rowell and Romig, 1966; Nagarajan et al., 1977, 1976; Singh et al., 2006). Because an inability to quantify uredospore dose is implicit in the model, the model assumes that the uredospore dose ranges from 0 to 1 (INOCP; how the value of this parameter is selected is described later in the Discussion as are the associated limitations) and that a rain of at least 1 mm h^–1 is able to cause uredospore deposition. This rain threshold was defined based on studies that related rain dynamics (duration and intensity) to spore concentration in the atmosphere (Rowell and Romig, 1966; Suffert, 1999). It is generally accepted that thunderstorms or rain showers usually require only a few minutes to remove the uredospores from the atmosphere (Eversmeyer et al., 1972; Suffert, 1999; Sache, 2000). Studies of rain duration (Suffert, 1999) showed that rapid scrubbing of airborne uredospores occurred during the first 10 min of a rain event. Rowell and Romig (1966) assessed spore concentrations in rain samples collected in the north-central United States during two seasons, and did not find any correlation between rain intensity and uredospores deposition; their data showed that uredospores were generally detected in rain samples of >1 mm.

The assumptions noted in the previous paragraph could result in false positive predictions of infection if no uredospores are deposited on the crop when predicted by the model, or could result in false negative predictions if uredospores are deposited on the crop when not predicted. Of the 30 cases used to validate the ability of the model to predict the first infection in the season, there were two cases in which the model predicted infections that were not observed (FPP = 0.091) and one case in which the model failed to predict infections that were observed (FNP = 0.125). Unjustified alarms (FPP) do not affect crop health but can lead to needless fungicide applications. To reduce this error, we require a better estimate of the presence of uredospores early in the season, i.e., better ways to estimate INOCP. Several authors (Rees, 1972; Nagarajan et al., 1976, 1977) proposed the use of spore traps or the sampling of rain water to monitor the presence of stem rust uredospores in the environment. The use of spore traps for monitoring airborne inoculum in support of epidemiological models has been suggested for other pathosystems (Rossi et al., 2007; Carisse et al., 2012).

False negative predictions (FNP) lead to missed real infections and reduce the model’s usefulness, because growers would fail to protect crops when necessary. This type of error occurred in only one case (at RAV18), and it was likely caused by a rain event of <1 mm h^–1 or a dry deposition of uredospores. To avoid this error, we also considered reducing the rainfall threshold used by the model to predict uredospore deposition (we considered using ≥0.4 or 0.6 mm h^–1), but this reduction led to an increase of FPP that significantly decreased the overall accuracy of the model (not shown). Further studies are needed on the effects of rain on the deposition of Pgt uredospores.

In this research, INOCP was estimated empirically: for each epidemic, different values of INOCP were initially considered and that value that resulted in the final disease severity closest to the real observation was selected and used for validation. This approach will not greatly affect the reliability of the model to predict disease progress because it modulates the final value of the disease severity but not its progress. Overall agreement of predicted and observed values was obtained, with high correlation between the fitted and prefect agreement line (CCC = 0.96) and little average distance between the real data and the fitted line (RMSE = 0.09), indicating good model accuracy (i.e., it provided predictions close to reality). Considering that the model was validated using independent data collected between 1968 and 1986 in the United States, further validation with recent data from sites with different climates (e.g., Mediterranean, temperate, and continental) should be performed to better evaluate the model’s robustness (i.e., its ability to provide accurate predictions in different environments and with different epidemiological conditions).

In spite of some shortcomings that mostly reflect its simplicity, the model seems to be useful for predicting epidemics of stem rust of wheat. In future, the model could be incorporated into existing decision support systems and used for scheduling fungicide applications to control the disease.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

VR and IS mainly contributed to the conceptualization of the model. VR provided the methodology and the resources for the study. IS and FB implemented the model in STELLA^® and performed model validation. All authors contributed to the analysis of results, collaborated in writing the manuscript, contributed to the article, and approved the submitted version.

Funding

This research was funded by the LIFE Programme of the European Union project LIFE AGRESTIC, grant number LIFE17 CCM/IT/000062.

Conflict of Interest

FB was employed by Horta Srl.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

IS conducted this study within the Doctoral School on the Agro-Food System (AgriSystem) at the Università Cattolica del Sacro Cuore, Piacenza, Italy. The authors thank P. Meriggi and M. Ruggeri (HORTA Srl, Piacenza, Italy) for providing the data on the disease outbreak at Ravenna, Emilia-Romagna, and Foggia, Apulia from 2017 to 2021. The authors also thank L. Mameli (Agris – Agenzia Regionale per la Ricerca in Agricoltura, Bonassai, Italy) for providing the data on the disease outbreak at Ussana, Sardinia, in 2016 and 2016.

Footnotes

1. ^ http://www.cabdirect.org
2. ^ https://www.scopus.com
3. ^ https://scholar.google.it
4. ^ https://www.r-project.org

References

Analytis, S. (1977). On the relation between biological development and temperature of some plant pathogenic fungi. Phytopathology 90, 64–76. doi: 10.1111/j.1439-0434.1977.tb02886.x

CrossRef Full Text | Google Scholar

Beard, C., Jayasena, K., Thomas, G., and Loughman, R. (2006). Managing Stem Rust of Wheat. Plant Pathology, Department of Agriculture, Western Australia. Farmnote 73. Available online at https://www.agric.wa.gov.au (accessed June 10, 2021).

Google Scholar

Bhattacharya, S. (2017). Deadly new wheat disease threatens Europe’s crops. Nat. News 542, 145-146. doi: 10.1038/nature.2017.21424

PubMed Abstract | CrossRef Full Text | Google Scholar

Bove, F., Savary, S., Willocquet, L., and Rossi, V. (2020). Simulation of potential epidemics of downy mildew of grapevine in different scenarios of disease conduciveness. Eur. J. Plant Pathol. 158, 599–614. doi: 10.1007/s10658-020-02085-8

CrossRef Full Text | Google Scholar

Bove, F., Savary, S., Willocquet, L., and Rossi, V. (2021). Modelling the effect of partial resistance on epidemics of downy mildew of grapevine. Eur. J. Plant Pathol. 161, 847–864. doi: 10.1007/s10658-021-02367-9

CrossRef Full Text | Google Scholar

Burnham, K. P., and Anderson, D. R. (2002). Model Selection and Multimodel Inference. A Practical Information-Theoretic Approach. New York: Springer-Verlag.

Google Scholar

Burrage, S. W. (1969). Dew and the growth of the uredospore germ tube of Puccinia graminis on the wheat leaf. Ann. Appl. Biol. 64, 495–501. doi: 10.1111/j.1744-7348.1969.tb02898.x

CrossRef Full Text | Google Scholar

Burrage, S. W. (1970). Environmental factors influencing the infection of wheat by Puccinia graminis. Ann. Appl. Biol. 66, 429–440. doi: 10.1111/j.1744-7348.1970.tb04622.x

CrossRef Full Text | Google Scholar

Caffi, T., Rossi, V., Cossu, A., and Fronteddu, F. (2007). Empirical vs. mechanistic models for primary infections of Plasmopara viticola. EPPO Bull. 37, 261–271. doi: 10.1111/j.1365-2338.2007.01120.x

CrossRef Full Text | Google Scholar

Carisse, O., Levasseur, A., and Van der Heyden, H. (2012). A new risk indicator for botrytis leaf blight of onion caused by Botrytis squamosa based on infection efficiency of airborne inoculum. Plant Pathol. 61, 1154–1164. doi: 10.1111/j.1365-3059.2012.02594.x

CrossRef Full Text | Google Scholar

Djurle, A., and Yuen, J. E. (1991). A simulation model for Septoria nodorum in winter wheat. Agric. Syst. 37, 193–218. doi: 10.1016/0308-521X(91)90005-U

CrossRef Full Text | Google Scholar

Durbin, R. D. (1984). Effects of rust on plant development in relation to the translocation of inorganic and organic solutes. Cereal Rusts 1, 509–528. doi: 10.1016/B978-0-12-148401-9.50022-4

CrossRef Full Text | Google Scholar

Duthie, J. A. (1997). Models of the response of foliar parasites to the combined effects of temperature and duration of wetness. Phytopathology 87, 1088–1095. doi: 10.1094/PHYTO.1997.87.11.1088

PubMed Abstract | CrossRef Full Text | Google Scholar

Eversmeyer, M. G., and Kramer, C. L. (1989). Survival and germination of urediniospores of Puccinia recondita and P. graminis. Trans. Kan. Acad. Sci. 1903, 159–175. doi: 10.2307/3628449

CrossRef Full Text | Google Scholar

Eversmeyer, M. G., and Kramer, C. L. (1992). Local dispersal and deposition of fungal spores from a wheat canopy. Grana 31, 53–59. doi: 10.1080/00173139209427826

CrossRef Full Text | Google Scholar

Eversmeyer, M. G., and Kramer, C. L. (2000). Epidemiology of wheat leaf and stem rust in the central great plains of the USA. Ann. Rev. Phytopathol. 38, 491–513. doi: 10.1146/annurev.phyto.38.1.491

PubMed Abstract | CrossRef Full Text | Google Scholar

Eversmeyer, M. G., Kramer, C. L., and Burleigh, J. R. (1972). Vertical spore concentrations of three wheat pathogens above a wheat field. Phytopathology 63, 211–218. doi: 10.1094/Phyto-63-211

CrossRef Full Text | Google Scholar

Forrester, J. W. (1961). Industrial dynamics. J. Oper. Res. Soc. 48, 1037–1041. doi: 10.1057/palgrave.jors.2600946

CrossRef Full Text | Google Scholar

Forrester, J. W. (1997). Industrial dynamics. J. Oper. Res. Soc. 48, 1037–1041. doi: 10.1057/palgrave.jors.2600946

CrossRef Full Text | Google Scholar

Givan, C. V., and Bromfield, K. R. (1963). Light inhibition of uredospore germination in Puccinia graminis var. tritici. Phytopathology 54, 382–384. doi: 10.21236/AD0410395

CrossRef Full Text | Google Scholar

Hirst, J. M. (1953). Changes in atmospheric spore content: diurnal periodicity and the effects of weather. Trans. Br. Mycol. Soc. 36:375. doi: 10.1016/S0007-1536(53)80034-3

CrossRef Full Text | Google Scholar

Hirst, J. M., Stedman, O. J., and Hogg, W. H. (1967). Long-distance spore transport: methods of measurement, vertical spore profiles and the detection of immigrant spores. Microbiology 48, 329–355. doi: 10.1099/00221287-48-3-329

PubMed Abstract | CrossRef Full Text | Google Scholar

Hovmøller, M. S., Patpour, M., Rodriguez Algaba, J., Thach, T., Justesen, A. F., and Hansen, J. G. (2021). GRRC Report of Yellow and Stem Rust Genotyping and Race Analyses 2020. Aarhus Universitet, Aarhus. Available online at. https://agro.au.dk/fileadmin/www.grcc.au.dk/International_Services/Pathotype_YR_results/GRRC_annual_report_2020.pdf (accessed May 25, 2021).

Google Scholar

Jin, Y. (2011). Role of Berberis spp. as alternate hosts in generating new races of Puccinia graminis and P. striiformis. Euphytica 179, 105–108. doi: 10.1007/s10681-010-0328-3

CrossRef Full Text | Google Scholar

Katsuya, K., and Green, G. J. (1967). Reproductive potentials of races 15B and 56 of wheat stem rust. Can. J. Bot. 45, 1077–1091. doi: 10.1139/b67-113

CrossRef Full Text | Google Scholar

Leffelaar, P. A., and Ferrari, T. J. (1989). “Some elements of dynamic simulation,” in Simulation and Systems Management in Crop Protection, eds R. Rabbinge, S. A. Ward, and H. H. van Laar (Netherlands: Pudoc), 19–45.

Google Scholar

Leonard, K. J., and Szabo, L. J. (2005). Stem rust of small grains and grasses caused by Puccinia graminis. Mol. Plant Pathol. 6, 99–111. doi: 10.1111/j.1364-3703.2005.00273.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lewis, C. M., Persoons, A., Bebber, D. P., Kigathi, R. N., Maintz, J., and Findlay, K. (2018). Potential for re-emergence of wheat stem rust in the United Kingdom. Commun. Biol. 1:13. doi: 10.1038/s42003-018-0013-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, L. (1989). A concordance correlation coefficient to evaluate reproducibility. Biometrics 45, 255–268. doi: 10.2307/2532051

CrossRef Full Text | Google Scholar

Littlefield, L. J. (1981). Biology of the Plant Rust: An Introduction. Iowa: Iowa State University Press.

Google Scholar

Littlefield, L. J., and Heath, M. C. (1979). Ultrastructure of Rust Fungi. New York: Academic Press. doi: 10.1016/B978-0-12-452650-1.50012-4

CrossRef Full Text | Google Scholar

Loomis, R. S., and Adams, S. S. (1983). Integrative analyses of host-pathogen relations. Annu. Rev. Phytopathol. 21, 341–362. doi: 10.1146/annurev.py.21.090183.002013

CrossRef Full Text | Google Scholar

Loughman, R., Jayasena, K., and Majewski, J. (2005). Yield loss and fungicide control of stem rust of wheat. Aust. J. Agric. Res. 56, 91–96. doi: 10.1071/AR04126

CrossRef Full Text | Google Scholar

Madden, L. V. (2006). Botanical epidemiology: some key advances and its continuing role in disease management. Eur. J. Plant Pathol. 115, 3–23. doi: 10.1007/s10658-005-1229-5

CrossRef Full Text | Google Scholar

McGrath, M. T., and Pennypacker, S. P. (1991). Reduction in the rate and duration of grain growth in wheat due to stem rust and leaf rust. Phytopathology 81, 778–787. doi: 10.1094/Phyto-81-778

CrossRef Full Text | Google Scholar

Mengesha, G. G. (2020). Management of yellow rust (Puccinia striiformis f. sp. tritici) and stem rust (Puccinia graminis f. sp tritici) of bread wheat through host resistance and fungicide application in Southern Ethiopia. Cogent Food Agric. 6:1739493. doi: 10.1080/23311932.2020.1739493

CrossRef Full Text | Google Scholar

Meyer, M., Cox, J. A., Hitchings, M. D. T., Burgin, L., Hort, M. C., Hodson, D. P., et al. (2017). Quantifying airborne dispersal routes of pathogens over continents to safeguard global wheat supply. Nat. Plants 3, 780–786. doi: 10.1038/s41477-017-0017-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Mortensen, K., and Green, G. J. (1978). Assessment of receptivity and urediospore production as components of wheat stem rust resistance. Can. J. Bot. 56, 1827–1839. doi: 10.1139/b78-221

CrossRef Full Text | Google Scholar

Mulatu, W. B., Robe, B., Robe, B., and Robe, B. (2020). Prediction of Wheat Rust Diseases Using Data Mining Application. Open Access Library J. 7:e6717. doi: 10.4236/oalib.1106717

CrossRef Full Text | Google Scholar

Nagarajan, S., and Joshi, L. M. (1975). Historic account of wheat rust epidemics in India and their significance. Cereal Rusts Bull. 3, 25–33.

Google Scholar

Nagarajan, S., Singh, H., Joshi, L. M., and Saari, E. E. (1976). Meteorological conditions associated with long-distance dissemination and deposition of Puccinia graminis tritici uredospores in India. Phytopathology 66, 198–203. doi: 10.1094/Phyto-66-198

CrossRef Full Text | Google Scholar

Nagarajan, S., Singh, H., Joshi, L. M., and Saari, E. E. (1977). Prediction of Puccinia graminis f. sp. tritici on wheat in India by trapping the uredospores in rain samples. Phytoparasitica 5, 104–108. doi: 10.1007/BF02981148

CrossRef Full Text | Google Scholar

Narouei-Khandan, H. A., Shakya, S. K., Garrett, K. A., Goss, E. M., Dufault, N. S., Andrade-Piedra, J. L., et al. (2020). BLIGHTSIM: A new potato late blight model simulating the response of Phytophthora infestans to diurnal temperature and humidity fluctuations in relation to climate change. Pathogens 9:659. doi: 10.3390/pathogens9080659

PubMed Abstract | CrossRef Full Text | Google Scholar

Nash, J. E., and Sutcliffe, J. V. (1970). River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 10, 282–290. doi: 10.1016/0022-1694(70)90255-6

CrossRef Full Text | Google Scholar

Nazareno, N. R. X., and Roelfs, A. P. (1981). Adult plant resistance of Thatcher wheat to stem rust. Phytopathology 71, 181–185. doi: 10.1094/Phyto-71-181

CrossRef Full Text | Google Scholar

Newcomb, M., Olivera, P. D., Rouse, M. N., Szabo, L. J., Johnson, J., Gale, S., et al. (2016). Kenyan isolates of Puccinia graminis f. sp. tritici from 2008 to 2014: Virulence to SrTmp in the Ug99 race group and implications for breeding programs. Phytopathology 106, 729–736. doi: 10.1094/PHYTO-12-15-0337-R

PubMed Abstract | CrossRef Full Text | Google Scholar

Newton, M. R., Wright, A. S., Kinkel, L. L., and Leonard, K. J. (1999). Competition alters temporal dynamics of sporulation in the wheat stem rust fungus. J. Phytopathol. 147, 527–534. doi: 10.1111/j.1439-0434.1999.tb03860.x

CrossRef Full Text | Google Scholar

Okoli, C., and Schabram, K. (2010). A guide to conducting a systematic literature review of information systems research. Papers Inf. Syst. 10, 1–46. doi: 10.2139/ssrn.1954824

CrossRef Full Text | Google Scholar

Prescott, J. M., Burnett, P. A., Saari, E. E., Ransom, J. K., Bowman, J. D., De Milliano, W., et al. (1986). Wheat Diseases and Pests: a Guide for Field Identification. Mexico, DF: International Maize and Wheat Improvement Center (CIMMYT).

Google Scholar

Pretorius, Z. A., Singh, R. P., Wagoire, W. W., and Payne, T. S. (2000). Detection of virulence to wheat stem rust resistance gene Sr31 in Puccinia graminis f. sp. tritici in Uganda. Plant Dis. 84, 203–203. doi: 10.1094/PDIS.2000.84.2.203B

PubMed Abstract | CrossRef Full Text | Google Scholar

Randazzo, B., Hansen, J. G., Justesen, A. F., Hovmøller, M. S., Patpour, M., Rodriguez-Algaba, J., et al. (2019). Wheat Rust Surveillance and Monitoring in Sicily 2016-2018. From Seed To Pasta III – A Sustainable Durum Wheat Chain for Food Security and Healthy Lives; Bologna, Italy, 19-21 September 2018. Available online at https://www.fromseedtopasta.com/wpcontent/uploads/2018/09/P4_37.pdf (accessed March 29).

Google Scholar

Rees, R. G. (1972). Uredospore movement and observations on the epidemiology of wheat rusts in northeast Australia. Aust. J. Agric. Res. 23, 215–223. doi: 10.1071/AR9720215

CrossRef Full Text | Google Scholar

Roelfs, A. P. (1977). Foliar fungal diseases of wheat in the People’s Republic of China. Plant Dis. Reptr. 61, 836–841.

Google Scholar

Roelfs, A. P. (1978). Estimated losses caused by rust in small grain cereals in the United States, 1918-76 (No. 1363). US. Dep. Agric. Misc. Publ. 1363, 1–85.

Google Scholar

Roelfs, A. P. (1982). Effects of barberry eradication on stem rust in the United States. Plant Dis. 66, 177–181. doi: 10.1146/annurev-phyto-080417-050133

PubMed Abstract | CrossRef Full Text | Google Scholar

Roelfs, A. P. (1985). “Wheat and rye stem rust,” in Diseases, Distribution, Epidemiology, and Control, eds A. P. Roelfs and W. R. Bushnell (New York: Academic Press), 3–37. doi: 10.1016/B978-0-12-148402-6.50009-2

CrossRef Full Text | Google Scholar

Roelfs, A. P. (2010). “Rusts,” in Compendium of Wheat Diseases and Pests, eds W. W. Bockus, R. L. Bowden, R. M. Hunger, T. D. Murray, and R. W. Smiley (St Paul: APS Press), 50–53.

Google Scholar

Roelfs, A. P., and Martell, L. B. (1984). Uredospore dispersal from a point source within a wheat canopy. Phytopathology 74, 1262–1267. doi: 10.1094/Phyto-74-1262

CrossRef Full Text | Google Scholar

Romig, R. W., and Calpouzos, L. (1970). The relationship between stem rust and loss in yield of spring wheat. Phytopathology 60, 1801–1805.

Google Scholar

Rossi, V., Giosue, S., and Bugiani, R. (2007). A-scab (Apple-scab), a simulation model for estimating risk of Venturia inaequalis primary infections. EPPO Bull. 37, 300–308. doi: 10.1094/PDIS-11-18-2046-RE

PubMed Abstract | CrossRef Full Text | Google Scholar

Rossi, V., Onesti, G., Legler, S. E., and Caffi, T. (2015). Use of systems analysis to develop plant disease models based on literature data: grape black-rot as a case-study. Eur. J. Plant Pathol. 141, 427–444.

Google Scholar

Rossi, V., Racca, P., Giosue, S., Pancaldi, D., and Alberti, I. (1997). A simulation model for the development of brown rust epidemics in winter wheat. Eur. J. Plant Pathol. 103, 453–465.

Google Scholar

Rowell, J. B., and Romig, R. W. (1966). Detection of urediospores of wheat rusts in spring rains. Phytopathology 56, 807–811.

Google Scholar

Sache, I. (2000). Short-distance dispersal of wheat rust spores. Agronomie 20, 757–767.

Google Scholar

Saunders, D. G. O., Pretorius, Z. A., and Hovmøller, M. S. (2019). Tackling the re-emergence of wheat stem rust in Western Europe. Commun. Biol. 2:51. doi: 10.1038/s42003-019-0294-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Savary, S., De Jong, P. D., Rabbinge, R., and Zadoks, J. C. (1990). Dynamic simulation of groundnut rust: a preliminary model. Agric. Syst. 32, 113–141. doi: 10.1016/0308-521X(90)90034-N

CrossRef Full Text | Google Scholar

Savary, S., Stetkiewicz, S., Brun, F., and Willocquet, L. (2015). Modelling and mapping potential epidemics of wheat diseases—examples on leaf rust and Septoria tritici blotch using EPIWHEAT. Eur. J. Plant Pathol. 142, 771–790. doi: 10.1007/s10658-015-0650-7

CrossRef Full Text | Google Scholar

Savary, S., Nelson, A. D., Djurle, A., Esker, P. D., Sparks, A., Amorim, L., et al. (2018). Concepts, approaches, and avenues for modelling crop health and crop losses. Eur. J. of Agron. 100, 4–18. doi: 10.1016/j.eja.2018.04.003

CrossRef Full Text | Google Scholar

Savary, S., Nelson, A., Willocquet, L., Pangga, I., and Aunario, J. (2012). Modeling and mapping potential epidemics of rice diseases globally. Crop Prot. 34, 6–17. doi: 10.1016/j.cropro.2011.11.009

CrossRef Full Text | Google Scholar

Scherm, H., and Van Bruggen, A. H. C. (1994). Effects of fluctuating temperatures on the latent period of lettuce downy mildew (Bremia lactucae). Phytopathology 84, 853–859.

Google Scholar

Schumann, G. L., and Leonard, K. J. (2011). Stem rust of wheat. Plant Health. Instr. 58, 1–12. doi: 10.1094/PHI-I-2000-0721-01

CrossRef Full Text | Google Scholar

Shamanin, V., Salina, E., Wanyera, R., Zelenskiy, Y., Olivera, P., and Morgounov, A. (2016). Genetic diversity of spring wheat from Kazakhstan and Russia for resistance to stem rust Ug99. Euphytica 212, 287–296. doi: 10.1007/s10681-016-1769-0

CrossRef Full Text | Google Scholar

Sharp, E. L., Schmitt, C. G., Staley, J. M., and Kingsolver, C. H. (1958). Some critical factors involved in establishment of Puccinia graminis var tritici. Phytopathology 48, 469–474.

Google Scholar

Signorell, A. (2020). DescTools: Tools for Descriptive Statistics. R package version 0.99. Available online at: https://cran.r-project.org/package=DescTools (accessed on 25 October 2020).

Google Scholar

Singh, R. P., Hodson, D. P., Jin, Y., Huerta-Espino, J., Kinyua, M. G., Wanyera, R., et al. (2006). Current status, likely migration and strategies to mitigate the threat to wheat production from race Ug99 (TTKS) of stem rust pathogen. CAB Rev. 54, 1–13. doi: 10.1079/PAVSNNR20061054

CrossRef Full Text | Google Scholar

Singh, R. P., Hodson, D. P., Jin, Y., Lagudah, E. S., Ayliffe, M. A., Bhavani, S., et al. (2015). Emergence and spread of new races of wheat stem rust fungus: continued threat to food security and prospects of genetic control. Phytopathology 105, 872–884. doi: 10.1094/PHYTO-01-15-0030-FI

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, R. P., Huerta-Espino, J., Roelfs, A. P., and Curtis, B. C. (2002). “The wheat rusts,” in Bread Wheat-Improvement and Production, eds B. C. Curtis, S. Rajaram, and H. G. Macherson (Rome: FAO Plant Production and Protection Series), 227–249.

Google Scholar

Stakman, E. C., and Christensen, C. M. (1946). Aerobiology in relation to plant disease. Bot. Rev. 12, 205–253. doi: 10.1007/BF02861523

CrossRef Full Text | Google Scholar

Steffenson, B. J., Case, A. J., Pretorius, Z. A., Coetzee, V., Kloppers, F. J., Zhou, H., et al. (2017). Vulnerability of barley to African pathotypes of Puccinia graminis f. sp. tritici and sources of resistance. Phytopathology 107, 950–962. doi: 10.1094/PHYTO-11-16-0400-R

PubMed Abstract | CrossRef Full Text | Google Scholar

Suffert, F. (1999). Effet du climat sur la progression au champ d’épidémies de rouille jaune (Puccinia striiformis Westend.) et de rouille brune (Puccinia recondite Rob. ex Desm. f. sp. tritici) sur blé. [Diplôme d’Agronomie Approfondie]. Rennes, FR: ENSA.

Google Scholar

Sun, P., and Zeng, S. (1994). On the measurement of the corrected basic infection rate. J. Plant Dis. Prot. 101, 297–302.

Google Scholar

Tadesse, K., Ayalew, A., and Badebo, A. (2010). Effect of fungicide on the development of wheat stem rust and yield of wheat varieties in highlands of Ethiopia. Afr. Crop Sci. J. 18, 23–33. doi: 10.4314/acsj.v18i1.54194

CrossRef Full Text | Google Scholar

Vanderplank, J. E. (1963). Plant Diseases: Epidemics and Control. New York: Academic Press Inc.

Google Scholar

Vanderplank, J. E. (1975). Principles of Plant Infection. New York: Academic Press Inc.

Google Scholar

Wanyera, R., Macharia, J. K., Kilonzo, S. M., and Kamundia, J. W. (2009). Foliar fungicides to control wheat stem rust, race TTKS (Ug99), in Kenya. Plant Dis. 93, 929–932. doi: 10.1094/PDIS-93-9-0929

PubMed Abstract | CrossRef Full Text | Google Scholar

Wickham, H. (2019). Modelr: Modelling Functions that Work with the Pipe. R Package Version 0.1, p. 4. Available online at: https://rdrr.io/cran/modelr/man/modelr-package.html (accessed on 20 October 2020).

Google Scholar

Willocquet, L., Rossi, V., and Savary, S. (2021). Simulation modelling of yield losses caused by wheat stem rust. Plant Pathol. 00, 1–12.

Google Scholar

Zadoks, J. C. (1963). Epidemiology of wheat rusts in Europe. FAO Plant Protection Bull. 13, 97–108.

Google Scholar

Zadoks, J. C. (1971). Systems analysis and the dynamics of epidemics. Phytopathology 61, 600–610.

Google Scholar

Zadoks, J. C., and Bouwman, J. J. (1985). “Epidemiology in Europe,” in The Cereal Rusts, eds A. P. Roelfs and W. R. Bushnell (Orlando, FL: Academic), 329–369. doi: 10.1016/B978-0-12-148402-6.50019-5

CrossRef Full Text | Google Scholar

Zillinsky, F. J. (1983). Common Diseases of Small Grain Cereals. A Guide to Identification. Mexico, DF: International Maize and Wheat Improvement Center (CIMMYT).

Google Scholar