Assessment of Canopy Conductance Responses to Vapor Pressure Deficit in Eight Hazelnut Orchards Across Continents

A remarkable increase in vapor pressure deficit (VPD) has been recorded in the last decades in relation to global warming. Higher VPD generally leads to stomatal closure and limitations to leaf carbon uptake. Assessing tree conductance responses to VPD is a key step for modeling plant performances and productivity under future environmental conditions, especially when trees are cultivated well outside their native range as for hazelnut (Corylus spp.). Our main aim is to assess the stand-level surface canopy conductance (G_surf) responses to VPD in hazelnut across different continents to provide a proxy for potential productivity. Tree sap flow (Fd) was measured by Thermal dissipation probes (TDP) probes (six per sites) in eight hazelnut orchards in France, Italy, Georgia, Australia, and Chile during three growing seasons since 2016, together with the main meteorological parameters. We extracted diurnal Fd to estimate the canopy conductance G_surf.. In all the sites, the maximum G_surf occurred at low values of VPD (on average 0.57 kPa) showing that hazelnut promptly avoids leaf dehydration and that maximum leaf gas exchange is limited at relatively low VPD (i.e., often less than 1 kPa). The sensitivity of the conductance vs. VPD (i.e., -dG/dlnVPD) resulted much lower (average m = −0.36) compared to other tree species, with little differences among sites. We identified a range of suboptimal VPD conditions for G_surf maximization (G_surf > 80% compared to maximum) in each site, named “VPD₈₀,” which multiplied by the mean G_surf might be used as a proxy for assessing the maximum gas exchange of the orchard with a specific management and site. Potential gas exchange appeared relatively constant in most of the sites except in France (much higher) and in the driest Australian site (much lower). This study assessed the sensitivity of hazelnut to VPD and proposed a simple proxy for predicting the potential gas exchange in different areas. Our results can be used for defining suitability maps based on average VPD conditions, thus facilitating correct identification of the potentially most productive sites.

Introduction

The role of the leaf to air vapor pressure deficit (VPD) is increasingly recognized as a leading limiting factor to determine plant gas exchange (Novick et al., 2016; Grossiord et al., 2020), while the influence of climate change on VPD rise becomes more and more evident. Anthropogenic-related global warming has increased unceasingly by 0.2°C every decade for more than 30 years (IPCC, 2018). A sharp increase of VPD was observed in the last decades (Yuan et al., 2019) and climatic projections show a future scenario where VPD increase is a diffuse phenomenon in many areas of the globe (Ficklin and Novick, 2017; Barkhordarian et al., 2019).

Higher VPD is in general detrimental for plant productivity because of the negative exponential response of stomatal conductance g_s to increasing VPD (Schulze et al., 1972; Jones, 1992; Oren et al., 1999). This response limits plant dehydration, but, at the same time, reduces carbon assimilation once stomata are partially closed. This explains why VPD was identified as a climatic factor related to tree mortality (McDowell et al., 2013) and limits crop productivity (Eamus et al., 2013). Prolonged periods of high VPD have been related to reduced growth (Sanginés de Cárcer et al., 2018) or large-scale forest die-off (Breshears et al., 2013; Will et al., 2013). Similarly, major crops such as maize, wheat, soybean, and fruit trees were reported to have decreased yields in response to high VPD (Challinor and Wheeler, 2008; Lobell et al., 2011; Zhao et al., 2017; Hsiao et al., 2019). Because plants are at the base of human life, the impact of changing climate and VPD rise on food provided by plants are a main issue in the upcoming future.

The response of plants to VPD variation has been extensively studied both at the leaf and at stand level. The latter is more suitable for assessing the effect of different management systems and structures in a specific site/orchard. At stand level, the surface canopy conductance G_surf (mol m^–2s^–1) refers to the capacity of gas exchange of the whole canopy expressed per unit of ground area, which includes a wide variety of heterogeneous leaf conditions (Medrano et al., 2015) and the community structure in terms of leaf area, roughness, soil properties, and species (Grossiord et al., 2020). In stands where the decoupling coefficient Ω is low (Jarvis and McNaughton, 1986), stomata experience a VPD close to the free atmosphere and the total canopy conductance is assumed to be driven largely by stomata aperture (Köstner et al., 1992; Hogg and Hurdle, 1997; Chapin et al., 2002). Thus, canopy conductance G_surf can be estimated from the rate of canopy transpiration (Ec) and VPD simply as: G_surf = k × Ec/VPD (Köstner et al., 1992; Arneth et al., 1996) where k is a temperature-dependent parameter (see below). G_surf includes two components: the stomatal component (average of different canopy leaves) and the aerodynamic component, which is a function of the orchard structure (i.e., density, height, roughness). Thus, when it is considered on a relatively long-term scale (weeks, months), G_surf can be a proxy for carbon uptake of the community, which, in turn, should also determine the carbon pool for reproductive allocation and seed production. In its turn, maximum value of G_surf (i.e., G_max) indicates the potential gas exchange of the whole canopy.

The potential conductance is reached under non-limiting conditions of soil water availability, light, and optimal temperature. In forests, these conditions are rarely met and G_max is generally estimated. Thus, Oren et al. (1999) proposed to use the G_surf reached at 1 kPa (G_surf@1kPa) as reference maximum conductance. G_surf@1kPa is highly variable across ecosystems because it depends both on the stand characteristics and species. In natural forest formations, it ranges from 0.2 to 0.7 mol m^–2s^–1 from savannah to deciduous forests (Grossiord et al., 2020). Tang et al. (2006) reported G_surf@1kPa 0.024 (mol m^–2s^–1) for some broad leaves of the genera Betula, Acer, and Ostrya and Fernández et al. (2009) from 0.28 to 0.44 in Nothofagus antarctica and Diostea juncea. On conifers, Köstner et al. (1996) and Köstner et al. (1996) reported G_surf@1kPa = 0.16–0.4 (mol m^–2s^–1) in Pinus sylvestris.

At the same time, some studies showed that many species, including hazelnut, present G_max occurring before 1 kPa (Tang et al., 2006; Herbst et al., 2008). Some other species reach G_max even above 1 kPa such as for example Pseudotsuga menziesii, where the G_max = 0.64 (mol m^–2s^–1) is reached at about 1.8 kPa (Fernández et al., 2009). Also some studies on leaves of fruit trees as olive (Rodriguez-Dominguez et al., 2019), walnut (Rosati et al., 2006), and different apple cultivars (Massonnet et al., 2007) show that G_max is reached between 1.5 and 2 kPa, probably related to the incidence of the fruit load in the whole tree physiology. Indeed, a correct approach to define the maximum potential gas exchange would be to consider the actual G_max, which may occur at different VPD according to the species or stand management.

Still, the reference G_surf@1kPa is often used to determine the sensitivity of a species. The sensitivity of stomatal response (even at canopy level) to VPD refers to the relative reduction in G with increasing VPD (i.e., -dG/dlnVPD). It is commonly believed that high G_surf@1kPa predicts high sensitivity (Oren et al., 1999). The sensitivity is measured as the slope (m) of the function G_surf = G_surf@1kPa – m lnVPD. G_surf@1kPa and m seem highly correlated (average R² = 0.75) with a slope of approximately 0.6 across species. In other words, the higher the G_surf@1kPa, the faster the stomata close with VPD increase, compared to species or individuals that present a lower G_surf@1kPa. However, it is likely that the sensitivity changes whether we consider G_surf@1kPa or G_max.

In this study, we explored the relationship between VPD and whole tree conductance G_surf as a contribution to understanding the limitations of potential productivity in eight commercial hazelnut orchards distributed in different countries. These sites have been considered as eight representative orchard conditions in a range of bearable climates for hazelnut growth, going from mild temperate to dry warm. Increasing VPD connected to global warming (IPCC, 2018; Barkhordarian et al., 2019) will certainly threaten these areas. Thus, we aimed at: (I) identifying the maximum canopy conductance and its sensitivity to VPD at each site and (II) providing a procedure to quantify the maximum potential gas exchange of a site by knowing the frequency of occurrence of VPD values.

The assessment of critical thresholds of VPD that guarantee optimal G_surf will become of great importance in defining suitability maps to locate new plantations and predict the responses of current crops to future climate change.

Materials and Methods

Study Areas, Orchard Characteristics, and Experimental Setting

This study occurred in eight different commercial orchards of European hazelnut (Corylus avellana, L.) distributed in both the hemispheres. In the northern hemisphere: in France (Cancon, 44°18′N, 0°34′E, named “F1”), Italy (Baldissero d’Alba, 44°45′N, 7°55′E, named “I1”), and Georgia (Gejeti, 42°19′N, 42°12′E, named “G2”); in the southern hemisphere: in Chile (Camarico, 35°18′S, 71°21′W, named “C1”; San Sebastian, 35°17′S, 71°32′W, named “C2”), and Australia (Glendale farm, 34°48′S, 146°40′E, named “A0”; Narrandera, 34°48′S, 146°40′E, named “A1”; Orange, 33°19′S, 149°5′E, named “A2”). The experiment included three main commercial cultivars: Tonda Trilobata (TT), Tonda di Giffoni (TG), and Ennies. Table 1 presents the biometrics and orchard features for all the study areas. The differences of orchard characteristics between sites are representative of diverse types of orchard management systems of the species. The total tree basal area refers to the sum of basal area of all the sprouts belonging to each single individual tree, which is normally grown as multistem. The leaf area index (LAI) derives from estimation of the tree leaf area (m²), which, in turn, is derived by a species-specific allometric equation, namely leaf area = 0.16 × D^2.22 (R² = 0.93), where D is the diameter (in cm) at the base of each stem. The relationship was established by using both the cultivars TT by Pisetta (2012) and TG (data not published). These orchards all entered the productive stage. Because hazelnut has a strong alternance in fruit bearing between years (almost two times of magnitude between years) and the fruit load (kg/tree) in Table 1 is the maximum value recorded in the three growing seasons in the parcel of the site where the trial was located. Thus, the data reported to the tree level shall be considered as an estimation of the maximum potential.

TABLE 1

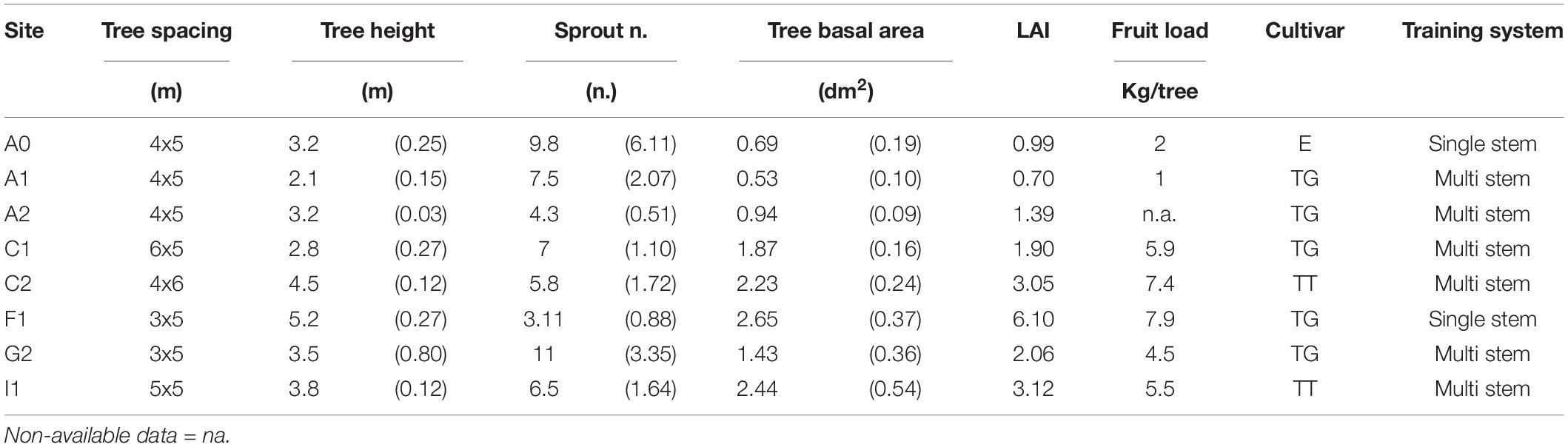
Table 1. Tree biometrics in the study areas: tree spacing, estimated tree height, sprout number per individual tree, total basal area (SD in brackets), estimated leaf area index (LAI), fruit load (maximum value recorded in the period), cultivar (TG, Tonda di Giffoni; TT, Tonda Trilobata; E, Ennies), and training system.

These orchards all entered the productive stage. Trees were in their productive stage in all the orchards (between 5 and 10 years old). Orchards are subjected to standard agronomic practices to support nut production (Roversi, 2014). Irrigation starts just before the nut cluster formation with about 3 mm of water per day distributed by a drip irrigation system. This study covered three growing seasons from 2016 to 2019. Sap flow was monitored by mean of thermal dissipation probes Granier type, 20 mm long (self-made in the Department of Territorio e Sistemi Agro-Forestali lab). Details on the construction and installation of Thermal dissipation probes (here after TDPs) are given in Pasqualotto et al. (2019). TDPs were installed in six trees per site in the phenological phase V03–V04 (bud brake and leaf emergence). Hazelnut phenology was collected at the orchard level according to a protocol proposed by Ferrero Agri-Farms, built on the (Biologische Bundesanstalt, Bundessortenamt and Chemical Industry, i.e. the German scale used to identify the phenological development stages of a plant) and on Romano et al. (1998). TDPs were set north-east facing on one branch per tree at about 50 cm above the ground in order to avoid thermal disturbance or humidity from the soil and possible damages to the sensors from the mechanical removal of sprouts. Further, TDPs were thermally insulated with aluminum heat insulation foil and Styrofoam. Two soil water content probes measuring the volumetric water content (TDR probe, Mod. CS650, Campbell Scientific Incorporation, Logan, USA) were installed between monitored trees at 30 and 60 cm depth. A data logger (CR1000, Campbell Scientific Incorporation, Logan, United States) recorded all the data every 15 min over the entire growing season, i.e., up to V08, leaves senescence, and shedding. A solar panel and a battery provided constant power supply to the stations. Air temperature (°C) and relative humidity (RH%) were recorded right on top of tree crowns in the orchard. Sap flow probes were replaced at the beginning of each growing season to prevent signal decaying.

Data Elaboration

The sap flow density Fd (dm³ dm^–2 h^–1) was calculated by using the classic equation form Granier (1985):

$Fd=a\cdot k^b(1)$

k = (ΔT0–ΔT)/ΔT, where ΔT is the temperature difference between the two probes (the heated vs. the reference one), ΔT0 is the maximum temperature difference (i.e., the condition corresponding to zero flow). For this study, we used specific parameters calibrated for hazelnut b = 1.45 and the constant a = 13.86 (Pasqualotto et al., 2019). Canopy transpiration (E_C) (g m^–2 s^–1) was calculated from mean Fd by multiplying it with the total sapwood area (A_S) over the orchard ground surface (A_O) (Oren et al., 1998):

$E_C=Fd\cdot \frac{A_S}{Ao}(2)$

The total water vapor transfer capacity or conductance at stand/orchard level (G_surf) in mm s^–1 was estimated from the canopy transpiration E_C and air VPD (Tang et al., 2006):

$G_{surf}=k\cdot E_C/VPD(3)$

Where k = 115.8 + 0.4226 T (m³ kPa °C kg^–1), T is the temperature (°C), and VPD = es – ea = es – (RH × es/100), where ea is a function of the relative humidity expressed in percent (Monteith and Unsworth, 2013). This was converted to mol m^–2 s^–1 according to Jones (1999) to allow for comparisons with recent reports. We also calculate the same values per unit of leaf area as EL = E_c/LAI and G_surf per unit of leaf area. The data set were subset to obtain diurnal data from 6 a.m. to 6 p.m. for the growing season: May to August for the northern hemisphere and November to February for the southern hemisphere. This choice means to extract the transpiration values related to positive carbon dioxide (CO₂) assimilation condition. To compare the slopes of the response curve between G_surf and VPD, we calculated the relative value of canopy conductance G_rel:

$G_{rel}=G_{surf}/G_{max}(4)$

where G_max is the maximum value of G_surf that occurs in the interval VPD₈₀. For the sake of better understanding of the site dynamic, data have been aggregated per site by averaging the response of G_rel to VPD of multiple growing seasons. An ANOVA was applied to the dataset to check for differences of stomata sensitivity between sites. G_rel is averaged into VPD classes of 0.1 kPa to simplify the response analysis in a continuous pattern (Hogg and Hurdle, 1997). The response of G_rel to VPD site by site aims at defining which are the best conditions for gas exchange around the optimum (G_max) in each study area. To meet this target, values of G_rel > 80% were selected and the corresponding VPD values were defined in a specific range of VPD at site level (VPD₈₀). Every time trees experience VPD belonging to the VPD₈₀ range and we can assume that canopy gas exchange was relatively high.

Trees experience conditions of VPD₈₀ at different times during the day throughout the year. The frequency of VPD₈₀ over the growing season in a specific site is critical to determine the total achievable gas exchange capacity (GEC). In order to include the temporal factor, we calculated the integral of the daily G_surf curve only in the intervals of VPD₈₀ occurrence (e.g., in Figure 1 for day of the year 175 in site I1—Italy). The sum of these integrals at site level for the entire growing season gives the GEC:

FIGURE 1

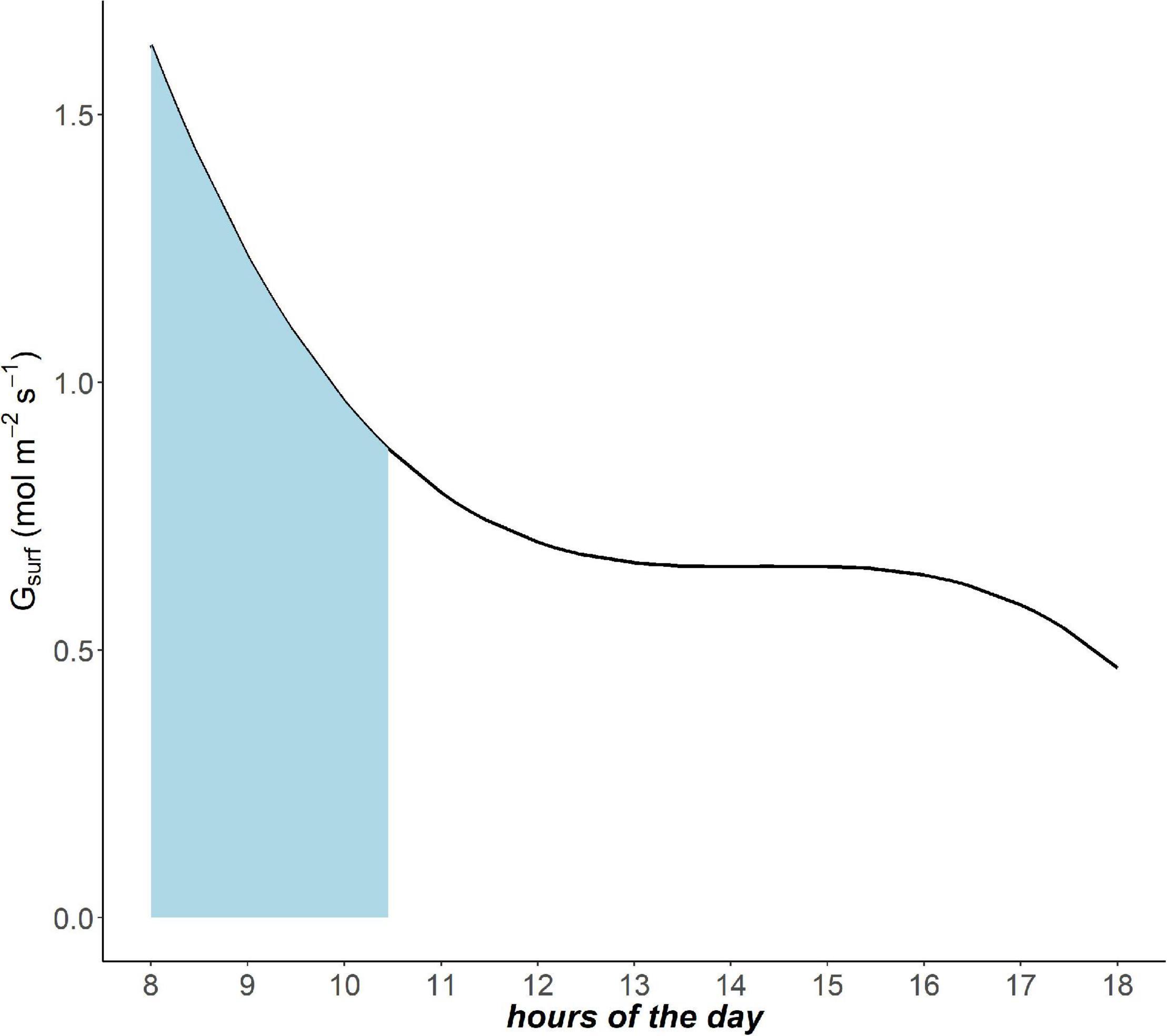
Figure 1. Example of daily pattern of canopy conductance G_surf (mol m^{– 2}s^{– 1}) in site I1 day of the year 175 (i.e., Italy 24th June). The light blue area underlies the time interval in which vapor pressure deficit (VPD)₈₀ occurs.

$GEC=n.VP{D}_{80}\cdot G_{surf80}$

Where n.VPD₈₀ is the number of occurrences (expressed in seconds) of VPD₈₀ per site during each growing season (mean occurrences per growing season) and G_surf80 is the mean value of G_surf recorded in the VPD₈₀ at each site. We obtained an estimation of the total GEC of a growing season at site level according to the orchard characteristics and to the average climatic conditions (Mmol m^–2).

Results

Climatic Conditions

The mean daily air VPD condition during the growing season ranged widely from 1.01 kPa day^–1 in site C1 and G2 to 1.93 and 2.66 kPa day^–1 in the Australian sites A0 and A1, respectively (Table 2) (Kruskal–Wallis nonparametric test, p < 0.001). Site A1 also resulted the warmest with peaks of 46°C, while C1 the coolest with minimum reaching −5°C during the growing season. The global radiation was higher in southern hemisphere sites, especially in Chile (sites C1 and C2) (about 30 MJ m^–2 day^–1), while in northern hemisphere sites, the global radiation was generally lower (about 20 MJ m^–2 day^–1). The volumetric water content (VWC) of the soil ranged between 0.09 and 0.45 m³ m^–3 and it is linearly correlated (R² = 0.75) with the mean VPD at site level, being highly dependent on the site temperature. The remaining difference can be explained by the soil texture, which is, for example, high in sandy soil in site A1.

TABLE 2

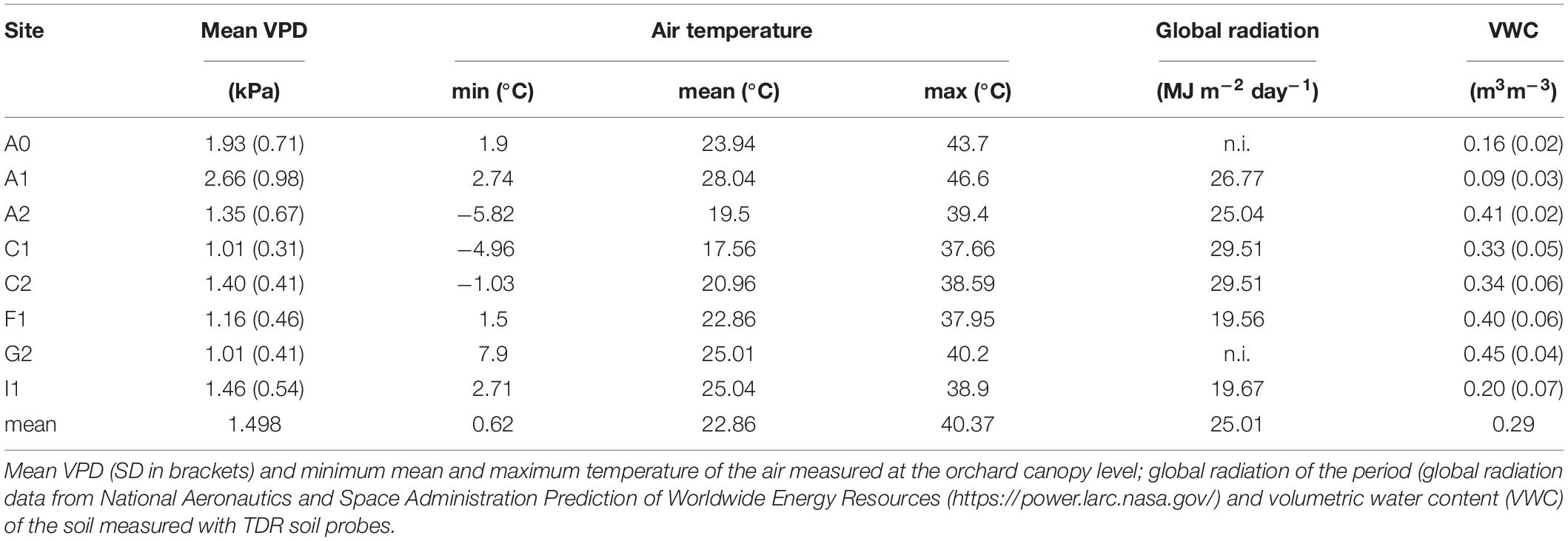
Table 2. Main climatic parameters at each site during the growing season (May to August or November to February).

Conductance of Orchard Systems

The response curve of G_surf to VPD classes (bin size 0.1 kPa) showed an initial increase of G_surf at very low VPD, followed by the typical exponential decrease with higher VPD (Figure 2). Different maximum values of G_surf were recorded at site level and explain the behavior of different orchard systems with different LAI: G_max was very low in site A1 (G_max = 0.094 mol m^–2s^–1), but much higher in site G2 (G_max = 0.586 mol m^–2s^–1) (Table 3). The maximum canopy conductance G_max (Table 3) occurred on average at VPD = 0.57 kPa across sites, ranging between 0.35 and 1.1 kPa (Table 4). In Supplementary Figure 1, the same response curve is presented with G_surf normalized by leaf area. In this case, G_max differences collapse to a range of 0.1 mol m^–2s^–1, while in some sites (e.g., F1), the response to VPD per leaf area unit is highly reduced (Figure 1).

FIGURE 2

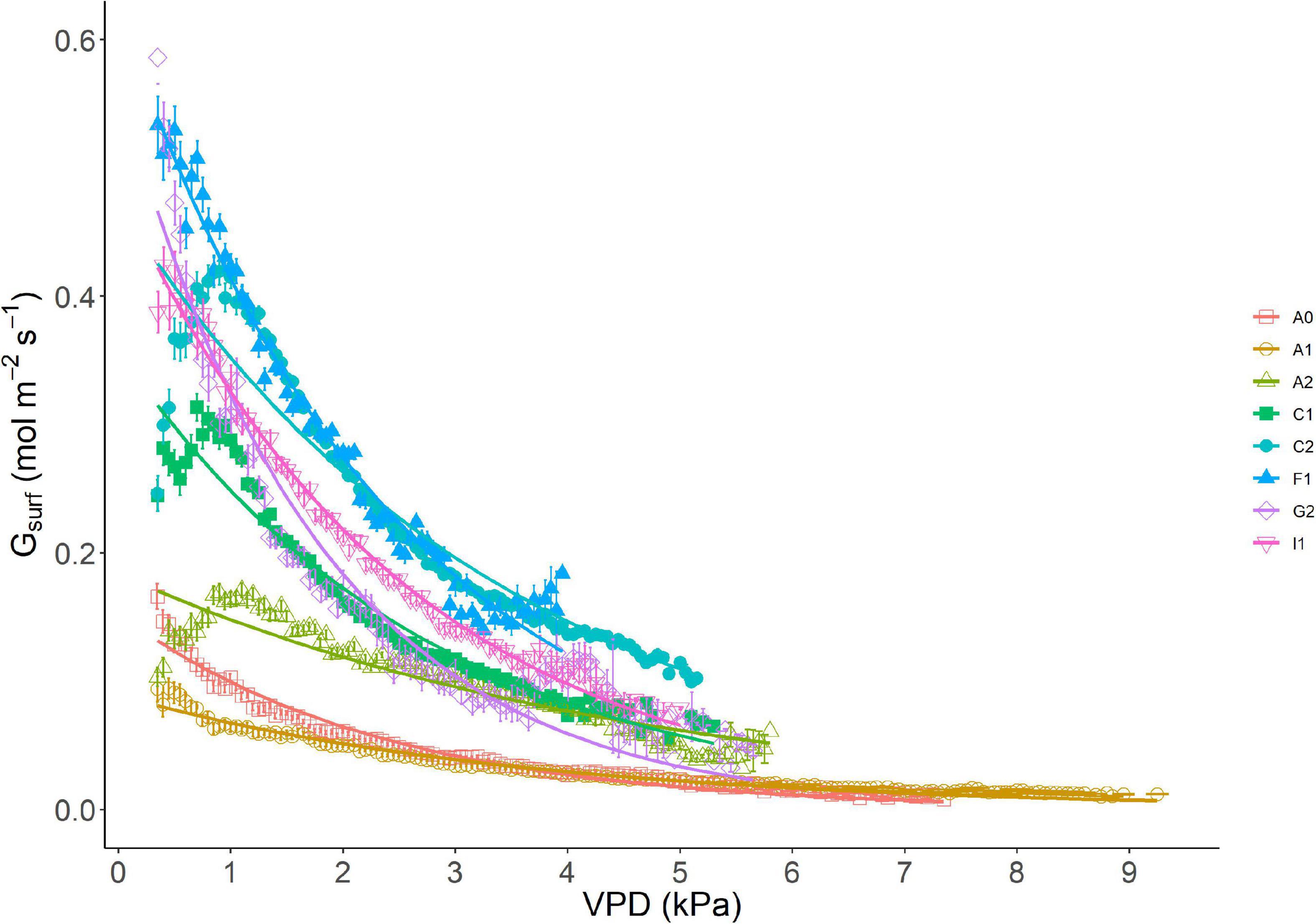
Figure 2. Response of G_surf to VPD in different sites (absolute values). Data are binned using 0.1 kPa bin size. SE per each interval of 0.1 kPa of VPD is shown on site-related markers.

TABLE 3

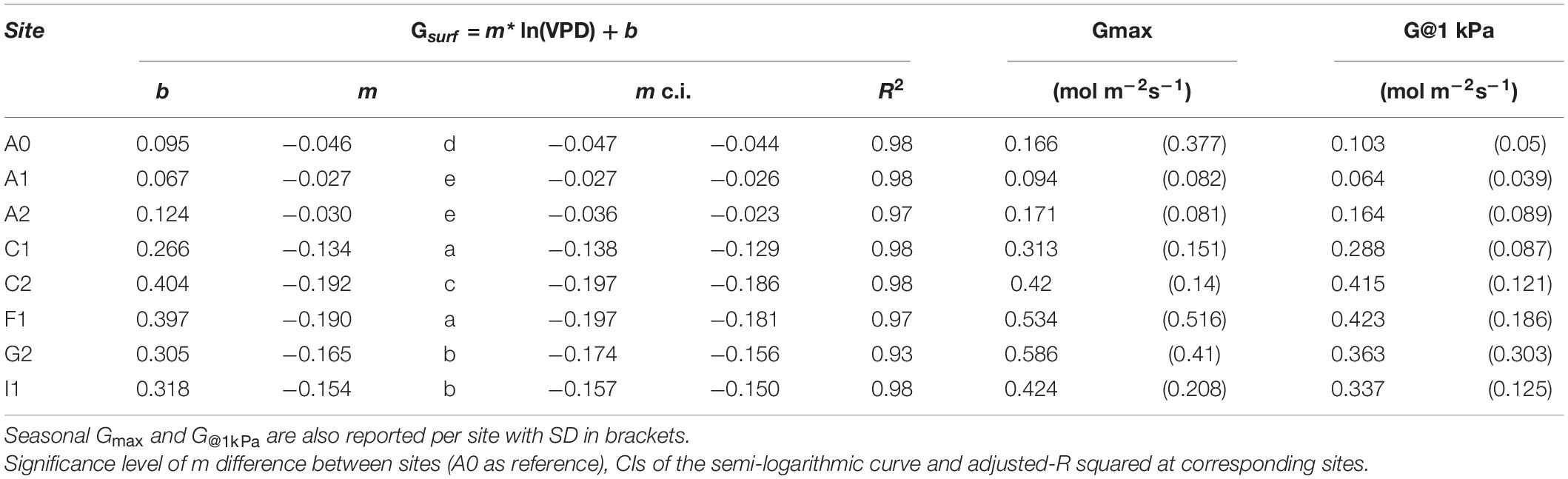
Table 3. Output of the linear model computed as lm = [Grel∼log(VPD) + log (VPD) × site, where b and m are the parameter of the equation G_rel = m × ln (VPD) + b.

TABLE 4

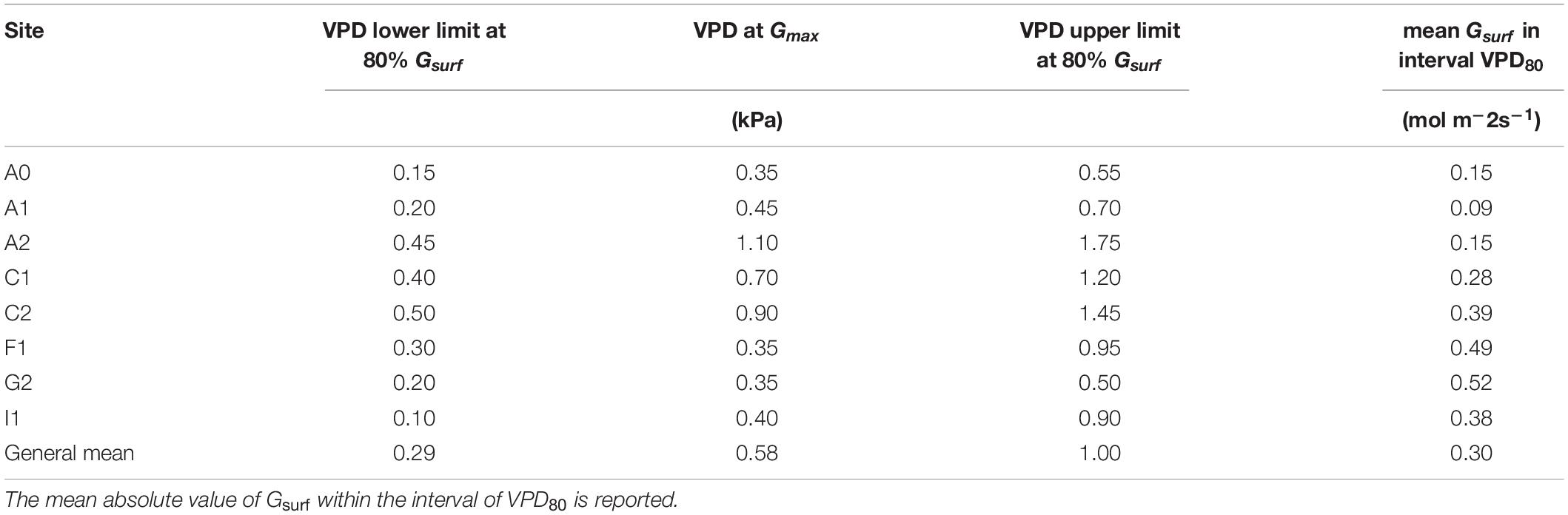
Table 4. Mean values of VPD at G_max and at the lower and upper limit of the VPD₈₀ interval, i.e., when G_surf = 80% of G_max.

The response of G_surf to VPD resulted well fitted in all the sites by a semi-log transformation of the type y = -m × log (x) + b as suggested in Oren et al. (1999). Globally, the regression between surface conductance (G_surf) and log (VPD) resulted highly significant (R² = 0.978) meaning that G_surf is strictly determined by the VPD measured at site level. The parameter m, i.e., the slope of the logarithmic function, was significantly different between sites (ANOVA, p < 0.01). Still, two main clusters were identified. The first included Australian sites A0, A1, and A2, where m values were between −0.027 and −0.046 describing a very low decrease of G_surf with VPD. The second cluster showed higher m values ranging from −0.134 in C1 to −0.192 in C2 (Table 3). Together with higher G_max, these orchard systems have a higher GEC of the canopy together with a faster decrease of G_rel with an increase in VPD.

The clustering of site sensitivity emerges clearly in the regression between –m and the maximum canopy conductance. We compared the variation of the sensitivity parameter –m to G_max and G_@1kPa (Figure 3). Even if a better correlation resulted from the linear regression of –m against G_@1kPa (R² = 0.96, p < 0.001) with respect to G_max (R² = 0.85, p < 0.01), the linear regressions are not significantly different from each other (p > 0.05). Thus, G_max can be used as reference value. Overall, lower sensitivity (lower –m values) corresponded to lower values of both the reference conductance G_max and G_@1kPa.

FIGURE 3

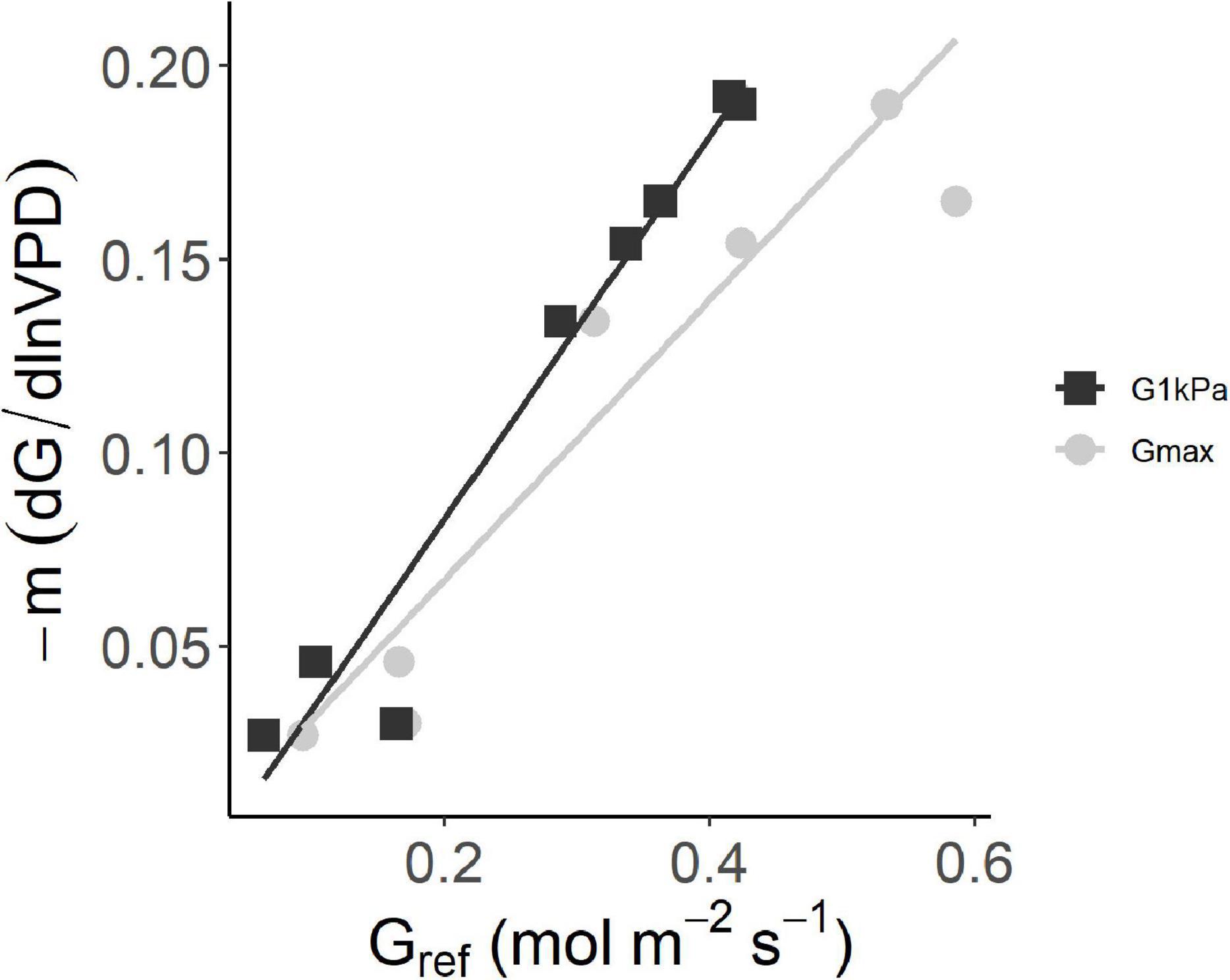
Figure 3. The sensitivity of average stomatal conductance at site level to increasing vapor pressure deficit (– dG/d lnVPD) as a function of the canopy stomatal conductance at VPD = 1 kPa and at its maximum value. The two axes represent the slope and intercept of the relationship G = – m ln(VPD) – b. G@1 kPa: y = 0.50X–0.016 (R² = 0.96; G_max: y = 0.36X–0.005 (R² = 0.85).

In addition, four sites with two different cultivars were selected to detect whether there was any clustering effect on the response of G_surf to VPD. Sites C2 and I1 were selected for cultivar TT and C1 and F1 for cultivar TG. However, we did not observe any difference related to the cultivar.

G_max was used to calculate the relative canopy conductance (G_rel) in order to compare the pattern of conductance response to VPD between sites (Figure 4). The interval width of the VPD₈₀, i.e., the interval of VPD in which G_rel is maintained ≥ 80% of its maximum was variable between sites. Even if the upper limit of VPD₈₀ occurred on average at 1 kPa, there was high variability between sites. Sites A0, A1, and G2 resulted as having a narrower interval of VPD₈₀ due to an initial pronounced peak in G_rel followed by a flatter decline; the upper limit of the VPD₈₀ remained within 0.75 kPa in these sites (Table 4), where we registered the highest maximum and minimum air temperature. On the contrary, the rest of the sites showed a wider interval of VPD₈₀ that reached the maximum value of 1.75 kPa in site A2, which is also the one with the lowest minimum temperature. These observations suggest that these plants might have acclimated to most extreme sites by changing their response to climate.

FIGURE 4

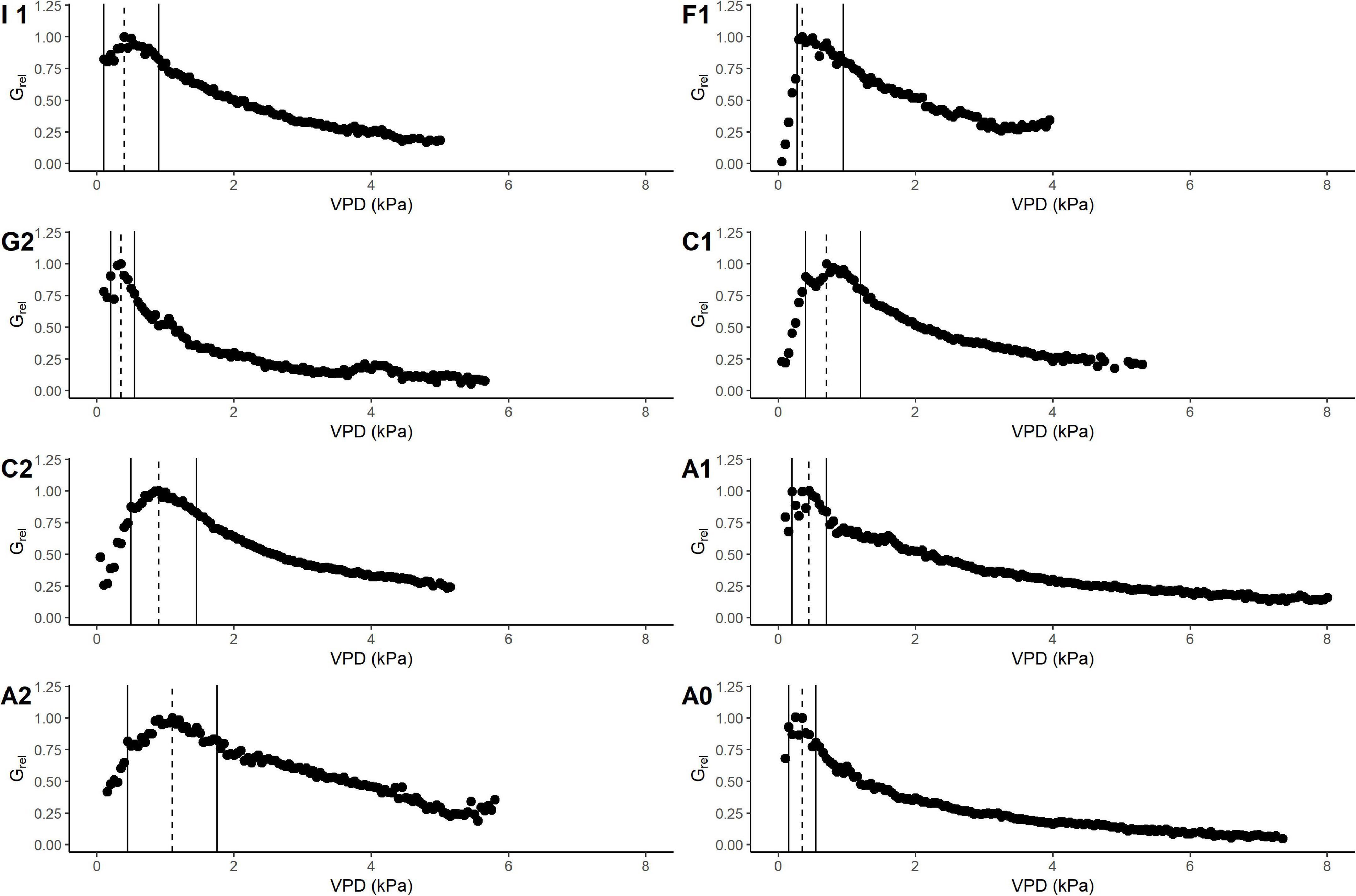
Figure 4. Response of G_rel to VPD class (kPa) in different sites. Study areas are marked with the corresponding site ID as described in “Materials and Methods” section. Markers refer to mean values of G_rel in each VPD class (0.1 kPa). Data are binned using 0.1 kPa bin size. Vertical dashed line shows the VPD value at maximum G_rel, while the solid line shows the limits of VPD value at 80% of the G_rel.

Finally, the mean G_surf value in each VPD₈₀ resulted well correlated (R² = 0.61) to interval with the fruit load per tree (maximum value over the 3 years) at site level (Supplementary Figure 2).

Maximum Gas Exchange Capacity

The sum of time with VPD₈₀ calculated over the 4 central months of the growing season (May to August and November to February) amounted to about 4 weeks in site A2 and 3.5 in site F1 (Figure 5A). Site A1 appeared the less suitable site in terms of climatic conditions with less than 1 week per growing season in which G_rel is above 80% of its potential. Even if some sites have a higher frequency of VPD₈₀ over the growing season, they might have low mean G_surf in this interval, as, for example, site A2 with 4 weeks of VPD₈₀ but only G_surf = 0.15 mol m^–2s^–1.

FIGURE 5

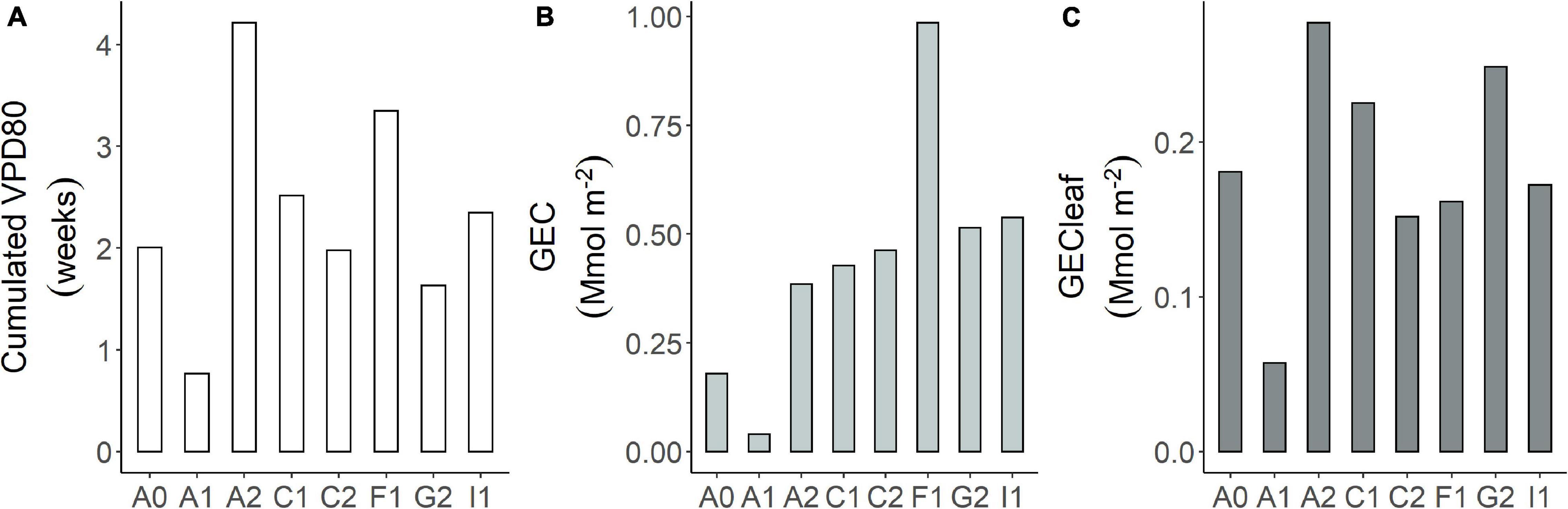
Figure 5. (A) Cumulated VPD₈₀ expressed as weeks per site during the main growing season. As the growing season, we considered the period from May to August in the northern hemisphere and from November to February in the southern; maximum gas exchange capacity (GEC) per site: (B) GEC = n.VPD₈₀ × G_surf; (C) GEC_leaf = n.VPD₈₀ × G_surf per unit of leaf area.

By combining these two characteristics per site, we obtained the maximum GEC of the orchard (Figure 5B). The GEC resulted the highest in site F1 because of the joint occurrence of high frequency of VPD₈₀ and high mean G_surf. Most of the other sites are similar in terms of GEC (about 0.45 Mmol m^–2) because the differences in mean G_surf are compensated by the width of the VPD₈₀ interval. Site A1 remains the site with the lowest GEC produced by the joint occurrence of very high VPD and very low mean G_surf. These results represent the whole orchard response. Due to this, they implicitly include the effect of the orchard structure (i.e., density, LAI, etc.). If we consider the GEC per unit of leaf area (Figure 5C), the differences decrease and they are parallel to variations of the mean VPD80.

Discussion

The comparative study of a species grown in different sites and under different orchard managements is a useful experimental setting to understand orchard responses under climate warming and VPD rise in the field. These study areas had different mean daily VPD during the growing season and despite irrigation, the soil water content was also affected. Australian sites A0 and A1 showed the most severe evaporative conditions with peaks of 5.2 kPa and daily mean temperature up to 46.6°C. These sites could represent the worst climatic scenario in which hazelnut can grow, together with a soil water content of 0.09 m³ m^–3. Italy was also an area with high VPD together with the Australian site A2 located at a higher altitude with respect to A0 and A1. All these regions combined with high daily global radiation in the southern hemisphere represent a very challenging environment for hazelnut that potentially limits the canopy conductance and growth. At present, France (F1) and Chile (C1 and C2) are in a milder condition, but climatic projections forecast increasing atmospheric water demand at global level (i.e., higher VPD) with extreme cases in the southern hemisphere related to the dry phase of El Niño cycles (Zhang et al., 2015; Barkhordarian et al., 2019). Thus, even milder sites may become challenging places to grow hazelnut and it is crucial to know how orchards will respond to these changes in order to adapt the cultivation systems.

The hazelnut response of G_surf to VPD across sites showed some differences between orchards in terms of both the pattern and G_max values. Differences in G_max are representative of wide range of LAI, which developed in orchards; thanks to different management strategies (spacing and training system). Different orchard managements were reported to have a significant effect also on grapevines gas exchanges (Prieto et al., 2020). Because the G_surf at the leaf area level is similar between sites, orchards with higher LAI have higher total G_max at the community level. Indeed, orchards with lower LAI, as, for example, A0 and A1 (0.99 and 0.70, respectively), responded to the VPD similarly to grassland or savannah species (Grossiord et al., 2020). In other words, in sites A0 and A1, the whole tree stomata are not only more tightly closed at low VPD with respect to other sites, but also the velocity to close further is low per unit of increase in VPD. This effect is further enhanced by the low soil water content in site A1, where despite irrigation being homogeneously distributed, the higher percentage of sandy soil together with high temperatures severely compromised the water uptake capacity of trees. In these areas, the orchard management shall favor higher orchard LAI. Most of the other sites present values that are closer to deciduous forests. Indeed, absolute G_max agrees with findings on other broad leaves reported in the literature (Barradas et al., 2005; Tang et al., 2006; Bourne et al., 2015; Grossiord et al., 2020). Another factor that we find linked to the differences in G_max between sites is the fruit load. Orchards with higher fruit load had also higher G_max. Accordingly, other studies on orange trees showed that low fruit loaded trees show < 40% stomatal conductance respect to fully loaded trees (Syvertsen et al., 2003). However, it has to be considered that fruit load and LAI, i.e., a proxy of the total photosynthetic capacity of the orchard, should be autocorrelated (Wünsche and Lakso, 2000).

The pattern of G_surf variation with VPD agrees with the theoretical framework presented by Oren et al. (1999) who described the response of G_surf to VPD by an exponential response curve, where the sensitivity is expressed by the parameter –m and higher G_max values predict higher sensitivity. Accordingly, Australian sites resulted in the less sensitive to increase in VPD and with very low G_max.(average m = −0.03 mol m^–2s^–1 kPa^–1), while the rest of the sites had an average m = −0.17 mol m^–2s^–1 kPa^–1. This latter is close to what found for broadleaved forests (including hazelnut understory) according to Herbst et al. (2008) and for Quercus alba (Oren et al., 1999). Still, these two clusters of sites (Figure 3) highlight differences in the sensitivity within the same species, suggesting a moderate capacity to acclimate. In this sense, this study represents one of the few examples of conductance sensitivity measurements on the same species (Oren et al., 2001; Addington et al., 2004) and the first to compare a single species across continents.

The maximum canopy conductance G_max is an important parameter to define the optimal gas exchange capacity of a stand. G_max should be defined under favorable conditions for the species, i.e., non-limiting light, water availability, and optimum temperature. In this study, we are analyzing trees under standard irrigation and fertilization regimes, thus we can assume that G_max values are as close as possible to the potential for the specific site. Thus, G_max can be a reference value to determine the species sensitivity to the increasing VPD. Often, the reference G is G_surf at 1 kPa because it is difficult to obtain continuous and reliable measurements for low VPD. However, in our data collection, we could benefit from a long and continuous data series from sap flow measurements. In this study, G_max was observed to range widely across sites from A1 (0.091 mol m^–2s^–1) to G2 (0.58 mol m^–2s^–1), occurring on average at 0.57 kPa, thus at a lower VPD compared to the reference of 1 kPa proposed by Oren et al. (1999). Other authors such as Tang et al. (2006) and Herbst et al. (2008) observed similar values of G_max at VPD < 1 kPa in few temperate broadleaves including forests with hazelnut understory, while many fruit trees as olive, walnut, and apple reach G_max at higher VPD (1.5–2 kPa) (Rosati et al., 2006; Massonnet et al., 2007; Rodriguez-Dominguez et al., 2019). In this perspective, hazelnut can be considered as a species with a water-saving behavior, which typically takes advantage of low VPD to maximize stomata opening and the carbon uptake.

This behavior is also confirmed by the pattern of relative canopy conductance. In this study, not only the slope, but also the value of VPD at which G_max occurs is important to assess the sensitivity of a species in a specific stand structure. Thus, the sensitivity described in this study is not exactly comparable with that calculated with the reference G_@1kPa reported by Oren et al. (1999). Indeed, if G_max occurs at 0.5, we will obtain a less negative slope (i.e., lower sensitivity) respect to the case in which we consider the same G_max value at 1 kPa (Figure 6). We simulated a case in which G_max occurs at 1 kPa and we found m = −0.53, while when G_max occurs at 0.5, m = −0.39. This shows that force comparisons with G_@1kPa may show different results suggesting sensitivity higher than it really is. This might be the reason behind the lower slope value in the linear regression between the parameter –m and reference conductance with respect to found by Oren et al. (1999).

FIGURE 6

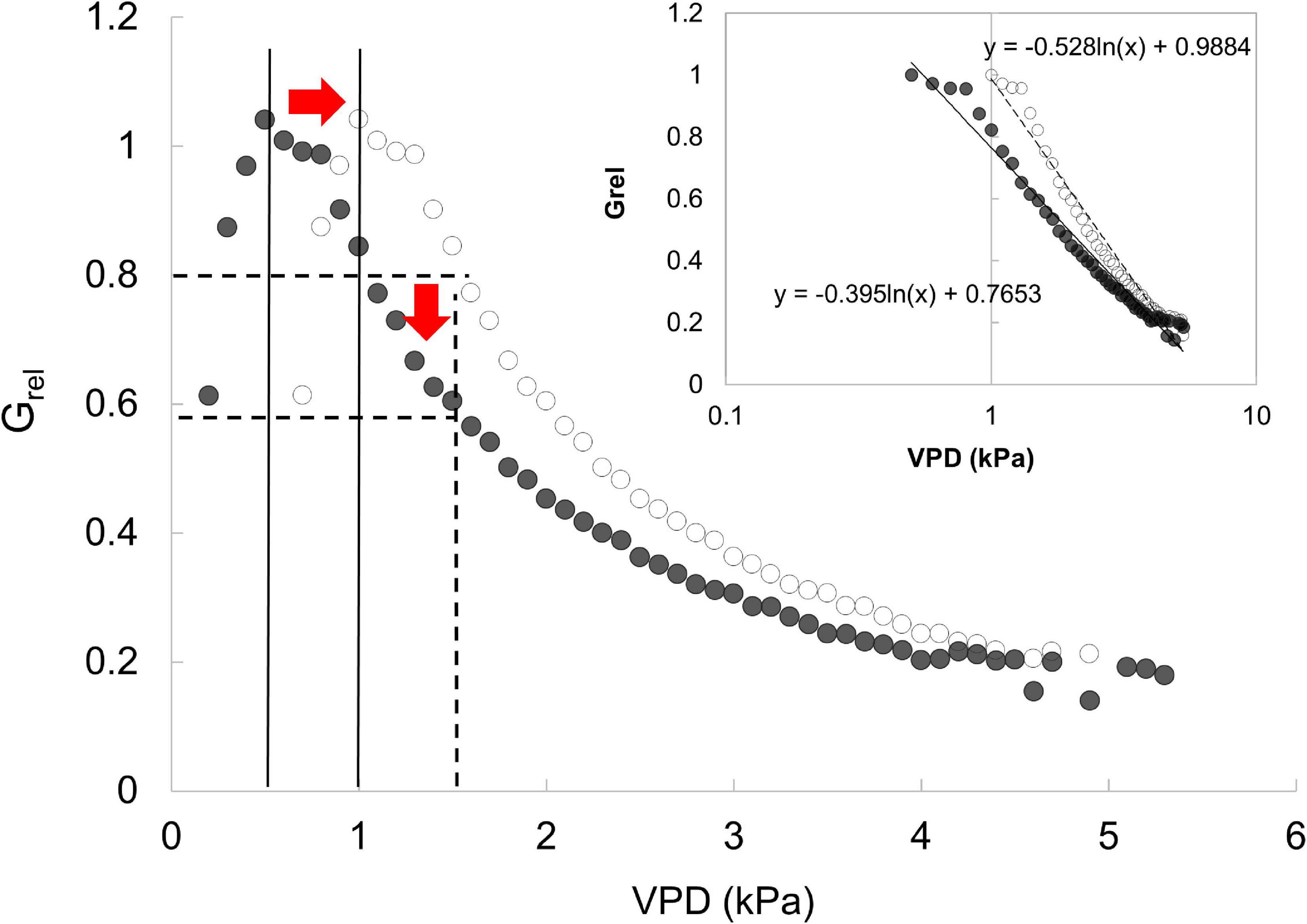
Figure 6. Simulation of the response of G_rel to VPD with G_rel calculated with two different maximum G. Inset presents the same data with x-axis log transformation. Black markers show the max G_rel at 0.5 kPa, the 0.8 × G_rel at 1 kPa and a slope of −0.39. White markers show max G_rel at 1 kPa, thus 0.8 × G_rel shifts toward the 1.5 kPa and the slope increases to about 0.13.

Indeed, the comparison of slopes between G_surf and dG_surf/dln VPD expresses the actual degree of sensitivity of the same species between orchard management. Sites A1 and A0 had the lowest sensitivity (less negative slope). These sites are also those with more extreme events of VPD (up to 8–9 kPa). Thus, we can hypothesize that the lowest sensitivity is related to acclimation in these sites and this acclimation capacity is cultivar independent. Despite the cultivar is different in sites A0 and A1, the pattern of G_surf to VPD has a steep increase at low VPD followed by a reduction suggesting that trees might have acclimate their leaf characteristics (e.g., number of stomata, size of the stomata, or others) across the growing seasons and this would maximize their gas exchange.

The interval of VPD in which trees could maintain over 80% of their maximum tree conductance in most of the sites is below 1.7 kPa. In all the sites, values above 5 kPa reduce the conductance to the minimum. In A0 and A1, the interval is particularly narrow. This, together with the low sensitivity in these sites, is a further clue that suggests an acclimation capacity of trees. In other words, hazelnut might have responded to the high site VPD by reducing stomata opening and improve the water use efficiency. Also, G2 resulted in a site with narrow interval of VPD. This has in common with A0 and A1 very high minimum temperatures of the air in this study period even at low VPD. This might have somehow forced the plants to further reduce their maximum canopy conductance capacity at low VPD. The chance that hazelnut can develop acclimation to extreme climates is of great interest for orchard managers and for the food industry, which relies on world nut supplies. Indeed, if the mechanism of stomatal acclimation would miss, VPD variation due to climate change could reduce stomatal conductance by 10–50% (Ficklin and Novick, 2017).

When we consider the implication of the higher or lower sensitivity to the carbon economy of the plant, it is also important to consider the temporal scale (Martínez-Vilalta and Garcia-Forner, 2017). To test what is the impact of the VPD₈₀ width on the total canopy conductance at the stand level, we estimated the total GEC of each orchard based on the occurrence of VPD₈₀ during the growing season and the corresponding mean G_surf in this interval.

Most of the sites had on average 2 weeks (cumulated hours) per growing season in favorable climatic conditions for conductance maximization, i.e., VPD₈₀ while for the rest of the season they are below the 80% of G_max. F1 and A2 had more than 3 weeks suggesting that from the climatic perspective, these are very promising sites for hazelnut, while A1 has a very limited amount of time during the growing season to optimize the conductance. The situation of site A1 is further worsened by the extremely low G_surf in the interval of VPD₈₀, which makes the total GEC of the site undesirable. While A1 remains an extreme case, the compensation between the occurrences of VPD₈₀ and G_surf supports the hypothesis of some acclimation capacity of the species, which leads to a quite even GEC at site level (about 0.45 Mmol m^–2). This acclimation might have been favored by the orchard management that favored a compensatory LAI through pruning and tree density. The extremely high GEC in site F1 is indeed related to the high LAI, close to a forest one, combined with very frequent VPD₈₀. When we normalize GEC by LAI, we get the leaf area unit gas exchange, independently to the orchard structure. What is clear is that the GEC_leaf is highly related to the frequency of VPD₈₀, but the orchard structures with higher LAI have, as a consequence, higher whole canopy gas exchange.

If the occurrence of VPD₈₀ remains stable in future growing seasons, we can expect most sites to maintain a good level of potential productivity at comparable growing conditions. Still changes in VPD might overturn the suitability of some areas. In this perspective, VPD must be monitored. At the same time, the orchard management shall favor high G_surf. This result can be achieved by increasing the LAI by favoring higher trees or by increasing the density where trees are small or still in the early productive stage. Indeed, the higher the fruit load, the higher the G_surf (Syvertsen et al., 2003). We believe that by collecting longer data series of fruit load combined with physiological and structural parameters of different orchards is a paramount goal to set in the future studies, perhaps toward modeling techniques as proposed by Prieto et al. (2020).

These results on suboptimal interval of VPD combined with the whole tree conductance (potential assimilation capacity) are the basis for a new global perspective on crop management. Indeed, they can be the basis for the construction of physiologically-based suitability maps: by using the projections of VPD conditions (Akpoti et al., 2019), it would be possible to roughly estimate the potential reduction of gas exchange and productivity in a given site.

Nonetheless, this study might provide guidelines for the management of existing orchards. We expect that the more the orchard is structured to maintain a range of favorable VPD conditions (within the VPD₈₀ range), the higher the carbon stocked in trees available for nut production will be. Indeed, the canopy structure variation may largely influence the water use efficiency of orchards (Cohen and Fuchs, 1987; Cohen and Naor, 2002).

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

TA and GP discussed and developed the idea and underlying rationale. GP elaborated the data, proposed the analytical approach, and wrote the first draft. VC was in charge of the technical support of all the devices from the installation phase to the maintenance and dismantling, created the thermal dissipation probes (Lab of the University of Padova, Department of Territorio e Sistemi Agro-Forestali), downloaded, and prepared the raw data. All the authors commented and revised the final version of the manuscript.

Funding

This study has been conducted thanks to the cooperation and the economic contribution through a Ph.D. grant (grant no. U-GOVANFO_COMM20_01, CUPC24I20-000350007) of the Hazelnut Company, Division of Ferrero Group, which promotes applied research in the agronomic field.

Conflict of Interest

This study received funding from Hazelnut Company, Division of Ferrero Group. The funder had the following involvement with this study: the study design and the location of study areas were agreed with the funder, besides the funder partly supported the field data collection.

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past co-authorship with one of the authors ES.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

For the collaboration on data collection, we thank the teams of Fruticola Agrichile, Agrigeorgia, Agriaustralis, and Unicoque France together with the Association National des Producteurs des Noisettes (ANPN) (France) and the Orange Agricultural Institute (New South Wales, Australia). We also thank Alison Garside for the revision of the English in the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpls.2021.767916/full#supplementary-material

References

Addington, R. N., Mitchell, R. J., Oren, R., and Donovan, L. A. (2004). Stomatal sensitivity to vapor pressure deficit and its relationship to hydraulic conductance in Pinus palustris. Tree Physiol. 24, 561–569. doi: 10.1093/treephys/24.5.561

PubMed Abstract | CrossRef Full Text | Google Scholar

Akpoti, K., Kabo-bah, A. T., and Zwart, S. J. (2019). Agricultural land suitability analysis: state-of-the-art and outlooks for integration of climate change analysis. Agric. Syst. 173, 172–208. doi: 10.1016/j.agsy.2019.02.013

CrossRef Full Text | Google Scholar

Arneth, A., Kelliher, F. M., Bauer, G., Hollinger, D. Y., Byers, J. N., Hunt, J. E., et al. (1996). Environmental regulation of xylem sap flow and total conductance of Larix gmelinii trees in eastern Siberia. Tree Physiol. 16, 247–255.

Google Scholar

Barkhordarian, A., Saatchi, S. S., Behrangi, A., Loikith, P. C., and Mechoso, C. R. (2019). A recent systematic increase in vapor pressure deficit over tropical South America. Sci. Rep. 9, 1–12. doi: 10.1038/s41598-019-51857-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Barradas, V. L., Nicolás, E., Torrecillas, A., and Alarcón, J. J. (2005). Transpiration and canopy conductance in young apricot (Prunus armenica L.) trees subjected to different PAR levels and water stress. Agric. Water Manag. 77, 323–333.

Google Scholar

Bourne, A. E., Haigh, A. M., and Ellsworth, D. S. (2015). Stomatal sensitivity to vapour pressure deficit relates to climate of origin in Eucalyptus species. Tree Physiol. 35, 266–278. doi: 10.1093/treephys/tpv014

PubMed Abstract | CrossRef Full Text | Google Scholar

Breshears, D. D., Adams, H. D., Eamus, D., McDowell, N. G., Law, D. J., Will, R. E., et al. (2013). The critical amplifying role of increasing atmospheric moisture demand on tree mortality and associated regional die-off. Front. Plant Sci. 4:266. doi: 10.3389/fpls.2013.00266

PubMed Abstract | CrossRef Full Text | Google Scholar

Challinor, A. J., and Wheeler, T. R. (2008). Crop yield reduction in the tropics under climate change: processes and uncertainties. Agric. For. Meteorol. 148, 343–356. doi: 10.1016/j.agrformet.2007.09.015

CrossRef Full Text | Google Scholar

Chapin, F. S. III, Matson, P. A., and Mooney, H. A. (2002). Principles of Terrestrial Ecosystem Ecology. New York, NY: Springer-Verlag, 298–300.

Google Scholar

Cohen, S., and Fuchs, M. (1987). The distribution of leaf area, radiation, photosynthesis and transpiration in a Shamouti orange hedgerow orchard. part I. leaf area and radiation. Agric. For. Meteorol. 40, 123–144. doi: 10.1016/0168-1923(87)90002-5

CrossRef Full Text | Google Scholar

Cohen, S., and Naor, A. (2002). The effect of three rootstocks on water use, canopy conductance and hydraulic parameters of apple trees and predicting canopy from hydraulic conductance. Plant Cell Environ. 25, 17–28.

Google Scholar

Eamus, D., Boulain, N., Cleverly, J., and Breshears, D. D. (2013). Global change-type drought-induced tree mortality: vapor pressure deficit is more important than temperature per se in causing decline in tree health. Ecol. Evol. 3, 2711–2729. doi: 10.1002/ece3.664

PubMed Abstract | CrossRef Full Text | Google Scholar

Fernández, M. E., Gyenge, J., and Schlichter, T. (2009). Water flux and canopy conductance of natural versus planted forests in Patagonia, South America. Trees Struct. Funct. 23, 415–427. doi: 10.1007/s00468-008-0291-y

CrossRef Full Text | Google Scholar

Ficklin, D. L., and Novick, K. A. (2017). Historic and projected changes in vapor pressure deficit suggest a continental-scale drying of the United States atmosphere. J. Geophys. Res. 122, 2061–2079. doi: 10.1002/2016JD025855

CrossRef Full Text | Google Scholar

Granier, A. (1985). Une nouvelle methode pour la measure du flux de seve brute dans le tronc des arbres. Ann. Des Sci. For. 42, 193–200. doi: 10.1051/forest:19850204

CrossRef Full Text | Google Scholar

Grossiord, C., Buckley, T. N., Cernusak, L. A., Novick, K. A., Poulter, B., Siegwolf, R. T. W., et al. (2020). Plant responses to rising vapor pressure deficit. New Phytol. 226, 1550–1566. doi: 10.1111/nph.16485

PubMed Abstract | CrossRef Full Text | Google Scholar

Herbst, M., Rosier, P. T. W., Morecroft, M. D., and Gowlng, D. J. (2008). Comparative measurements of transpiration and canopy conductance in two mixed deciduous woodlands differing in structure and species composition. Tree Physiol. 28, 959–970. doi: 10.1093/treephys/28.6.959

PubMed Abstract | CrossRef Full Text | Google Scholar

Hogg, E. H., and Hurdle, P. A. (1997). Sap flow in trembling aspen: implications for stomatal responses to vapor pressure deficit. Tree Physiol. 17, 501–509. doi: 10.1093/treephys/17.8-9.501

PubMed Abstract | CrossRef Full Text | Google Scholar

Hsiao, J., Swann, A. L. S., and Kim, S. H. (2019). Maize yield under a changing climate: the hidden role of vapor pressure deficit. Agric. For. Meteorol. 279:107692. doi: 10.1016/j.agrformet.2019.107692

CrossRef Full Text | Google Scholar

IPCC (2018). “Summary for policymakers,” in Global Warming of 1.5°C. An IPCC Special Report on the Impacts of Global Warming of 1.5°C Above Pre-industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty, eds V. Masson-Delmotte, P. Zhai, H.-O. Pörtner, D. Roberts, J. Skea, P. R. Shukla, (Geneva: World Meteorological Organization), 32.

Google Scholar

Jarvis, P. G., and McNaughton, K. G. (1986). Stomatal control of transpiration: scaling up from leaf to region. Adv. Ecol. Res. 15, 1–49. doi: 10.1016/S0065-2504(08)60119-1

CrossRef Full Text | Google Scholar

Jones, H. G. (1992). Plants and Microclimate?: A Quantitative Approach to Environmental Plant Physiology. Cambridge: Cambridge University Press.

Google Scholar

Jones, H. G. (1999). Use of thermography for quantitative studies of spatial and temporal variation of stomatal conductance over leaf surfaces. Plant Cell Environ. 22, 1043–1055. doi: 10.1046/j.1365-3040.1999.00468.x

CrossRef Full Text | Google Scholar

Köstner, B., Biron, P., Siegwolf, R., and Granier, A. (1996). Estimates of water vapor flux and canopy conductance of Scots pine at the tree level utilizing different xylem sap flow methods. Theor. Appl. Climatol. 53, 105–113. doi: 10.1007/BF00866415

CrossRef Full Text | Google Scholar

Köstner, B. M., Schulze, E. D., Kelliher, F. M., Hollinger, D. Y., Byers, J. N., Hunt, J. E., et al. (1992). Transpiration and canopy conductance in a pristine broad-leaved forest of Nothofagus: an analysis of xylem sap flow and eddy correlation measurements. Oecologia 91, 350–359. doi: 10.1007/BF00317623

PubMed Abstract | CrossRef Full Text | Google Scholar

Lobell, D. B., Schlenker, W., and Costa-Roberts, J. (2011). Climate trends and global crop production since 1980. Science 333, 616–620. doi: 10.1126/science.1204531

PubMed Abstract | CrossRef Full Text | Google Scholar

Martínez-Vilalta, J., and Garcia-Forner, N. (2017). Water potential regulation, stomatal behaviour and hydraulic transport under drought: deconstructing the iso/anisohydric concept. Plant Cell Environ. 40, 962–976. doi: 10.1111/pce.12846

PubMed Abstract | CrossRef Full Text | Google Scholar

Massonnet, C., Costes, E., Rambal, S., Dreyer, E., and Regnard, J. L. (2007). Stomatal regulation of photosynthesis in apple leaves: evidence for different water-use strategies between two cultivars. Ann. Bot. 100, 1347–1356.

Google Scholar

McDowell, N. G., Ryan, M. G., Zeppel, M. J. B., and Tissue, D. T. (2013). Feature: improving our knowledge of drought-induced forest mortality through experiments, observations, and modeling. New Phytol. 200, 289–293. doi: 10.1111/nph.12502

PubMed Abstract | CrossRef Full Text | Google Scholar

Medrano, H., Tomás, M., Martorell, S., Flexas, J., Hernández, E., Rosselló, J., et al. (2015). From leaf to whole-plant water use efficiency (WUE) in complex canopies: limitations of leaf WUE as a selection target. Crop J. 3, 220–228. doi: 10.1016/j.cj.2015.04.002

CrossRef Full Text | Google Scholar

Monteith, J. L., and Unsworth, M. H. (2013). Principles of Environmental Physics. Plants, Animals and the Atmosphere, 4th Edn. Cambridge, MA: Academic Press.

Google Scholar

Novick, K. A., Ficklin, D. L., Stoy, P. C., Williams, C. A., Bohrer, G., Oishi, A. C., et al. (2016). The increasing importance of atmospheric demand for ecosystem water and carbon fluxes. Nat. Clim. Chang. 6, 1023–1027. doi: 10.1038/nclimate3114

CrossRef Full Text | Google Scholar

Oren, R., Phillips, N., Katul, G., Ewers, B. E., and Pataki, D. E. (1998). Scaling xylem sap flux and soil water balance and calculating variance: a method for partitioning water flux in forests. Ann. Sci. For. 55, 191–216. doi: 10.1051/forest:19980112

CrossRef Full Text | Google Scholar

Oren, R., Sperry, J. S., Ewers, B. E., Pataki, D. E., Phillips, N., and Megonigal, J. P. (2001). Sensitivity of mean canopy stomatal conductance to vapor pressure deficit in a flooded Taxodium distichum L. forest: hydraulic and non-hydraulic effects. Oecologia 126, 21–29. doi: 10.1007/s004420000497

PubMed Abstract | CrossRef Full Text | Google Scholar

Oren, R., Sperry, J. S., Katul, G. G., Pataki, D. E., Ewers, B. E., Phillips, N., et al. (1999). Survey and synthesis of intra- and interspecific variation in stomatal sensitivity to vapour pressure deficit. Plant. Cell Environ. 22, 1515–1526. doi: 10.1046/j.1365-3040.1999.00513.x

CrossRef Full Text | Google Scholar

Pasqualotto, G., Carraro, V., Menardi, R., and Anfodillo, T. (2019). Calibration of granier-type (TDP) sap flow probes by a high precision electronic potometer. Sensors 19:2419. doi: 10.3390/s19102419

PubMed Abstract | CrossRef Full Text | Google Scholar

Pisetta, M. (2012). Relazioni Idriche in Nocciolo (Corylus avellana L.). Ph.D. thesis. Padova: University of Padova.

Google Scholar

Prieto, J. A., Louarn, G., Perez Peña, J., Ojeda, H., Simonneau, T., and Lebon, E. (2020). A functional-structural plant model that simulates whole- canopy gas exchange of grapevine plants (Vitis vinifera L.) under different training systems. Ann. Bot. 126, 647–660.

Google Scholar

Rodriguez-Dominguez, C. M., Hernandez-Santana, V., Buckley, T. N., Fernández, J. E., and Diaz-Espejo, A. (2019). Sensitivity of olive leaf turgor to air vapour pressure deficit correlates with diurnal maximum stomatal conductance. Agric. For. Meteorol. 27, 156–165.

Google Scholar

Romano, B., Mandrioli, P., Puppi, G., Zanotti, A., Botarelli, L., and Sacchetti, V. (1998). Guida al Rilevamento dei Giardini Fenologici Italiani. Progetto Finalizzato Phenagri: Fenologia per L’agricoltura; Sottoprogetto 2: Fenologia Delle Piante Arboree. Roma.

Google Scholar

Rosati, A., Metcalf, S., Buchner, R., Fulton, A., and Lampinen, B. (2015). Tree water status and gas exchange in walnut under drought, high temperature and vapour pressure deficit. J. Hortic. Sci. Biotechnol. 81, 415–420.

Google Scholar

Roversi, A. (2014). How many mineral nutrients does a hazelnut orchard take up annually from the soil? Acta Hortic. 1052, 201–206.

Google Scholar

Sanginés de Cárcer, P., Vitasse, Y., Peñuelas, J., Jassey, V. E. J., Buttler, A., and Signarbieux, C. (2018). Vapor–pressure deficit and extreme climatic variables limit tree growth. Glob. Chang. Biol. 24, 1108–1122. doi: 10.1111/gcb.13973

PubMed Abstract | CrossRef Full Text | Google Scholar

Schulze, E. D., Lange, O. L., Buschbom, U., Kappen, L., and Evenari, M. (1972). Stomatal responses to changes in humidity in plants growing in the desert. Planta 108, 259–270. doi: 10.1007/BF00384113

PubMed Abstract | CrossRef Full Text | Google Scholar

Syvertsen, J. P., Goñi, C., and Otero, A. (2003). Fruit load and canopy shading affect leaf characteristics and net gas exchange of ‘spring’ navel orange trees. Tree Physiol. 23, 899–906.

Google Scholar

Tang, J., Bolstad, P. V., Ewers, B. E., Desai, A. R., Davis, K. J., and Carey, E. V. (2006). Sap flux-upscaled canopy transpiration, stomatal conductance, and water use efficiency in an old growth forest in the Great Lakes region of the United States. J. Geophys. Res. Biogeosci. 111, 1–12. doi: 10.1029/2005JG000083

CrossRef Full Text | Google Scholar

Will, R. E., Wilson, S. M., Zou, C. B., and Hennessey, T. C. (2013). Increased vapor pressure deficit due to higher temperature leads to greater transpiration and faster mortality during drought for tree seedlings common to the forest-grassland ecotone. New Phytol. 200, 366–374. doi: 10.1111/nph.12321

PubMed Abstract | CrossRef Full Text | Google Scholar

Wünsche, J. N., and Lakso, A. N. (2000). The relationship between leaf area and light interception by spur and extension shoot leaves and apple orchard productivity. Hortscience 35, 1202–1206.

Google Scholar

Yuan, W., Zheng, Y., Piao, S., Ciais, P., Lombardozzi, D., Wang, Y., et al. (2019). Increased atmospheric vapor pressure deficit reduces global vegetation growth. Sci. Adv. 5:1396. doi: 10.1126/sciadv.aax1396

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, C., Liu, B., Piao, S., Wang, X., Lobell, D. B., Huang, Y., et al. (2017). Temperature increase reduces global yields of major crops in four independent estimates. Proc. Natl. Acad. Sci. U.S.A. 114, 9326–9331. doi: 10.1073/pnas.1701762114

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, K., Kimball, J. S., Nemani, R. R., Running, S. W., Hong, Y., Gourley, J. J., et al. (2015). Vegetation greening and climate change promote multidecadal rises of global land evapotranspiration. Sci. Rep. 5:15956. doi: 10.1038/srep15956

PubMed Abstract | CrossRef Full Text | Google Scholar