
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Plant Sci. , 23 December 2020
Sec. Technical Advances in Plant Science
Volume 11 - 2020 | https://doi.org/10.3389/fpls.2020.554905
This article is part of the Research Topic Artificial Intelligence Applications in Specialty Crops View all 33 articles
The design of plant tissue culture media remains a complicated task due to the interactions of many factors. The use of computer-based tools is still very scarce, although they have demonstrated great advantages when used in large dataset analysis. In this study, design of experiments (DOE) and three machine learning (ML) algorithms, artificial neural networks (ANNs), fuzzy logic, and genetic algorithms (GA), were combined to decipher the key minerals and predict the optimal combination of salts for hardy kiwi (Actinidia arguta) in vitro micropropagation. A five-factor experimental design of 33 salt treatments was defined using DOE. Later, the effect of the ionic variations generated by these five factors on three morpho-physiological growth responses – shoot number (SN), shoot length (SL), and leaves area (LA) – and on three quality responses - shoots quality (SQ), basal callus (BC), and hyperhydricity (H) – were modeled and analyzed simultaneously. Neurofuzzy logic models demonstrated that just 11 ions (five macronutrients (N, K, P, Mg, and S) and six micronutrients (Cl, Fe, B, Mo, Na, and I)) out of the 18 tested explained the results obtained. The rules “IF – THEN” allow for easy deduction of the concentration range of each ion that causes a positive effect on growth responses and guarantees healthy shoots. Secondly, using a combination of ANNs-GA, a new optimized medium was designed and the desired values for each response parameter were accurately predicted. Finally, the experimental validation of the model showed that the optimized medium significantly promotes SQ and reduces BC and H compared to standard media generally used in plant tissue culture. This study demonstrated the suitability of computer-based tools for improving plant in vitro micropropagation: (i) DOE to design more efficient experiments, saving time and cost; (ii) ANNs combined with fuzzy logic to understand the cause-effect of several factors on the response parameters; and (iii) ANNs-GA to predict new mineral media formulation, which improve growth response, avoiding morpho-physiological abnormalities. The lack of predictability on some response parameters can be due to other key media components, such as vitamins, PGRs, or organic compounds, particularly glycine, which could modulate the effect of the ions and needs further research for confirmation.
The process of designing protocols for successful plant tissue culture is a very complex task, since there are many potential interacting factors in this process (Figure 1). Plant materials, culture conditions, and culture media ingredients (inorganic and organic nutrients such as carbohydrates, vitamins, and plant growth regulators) are determining factors in the quality of the final product obtained in any plant cell culture protocol (micropropagated seedlings, somatic embryos, doubled haploids, etc.) (Figure 1).
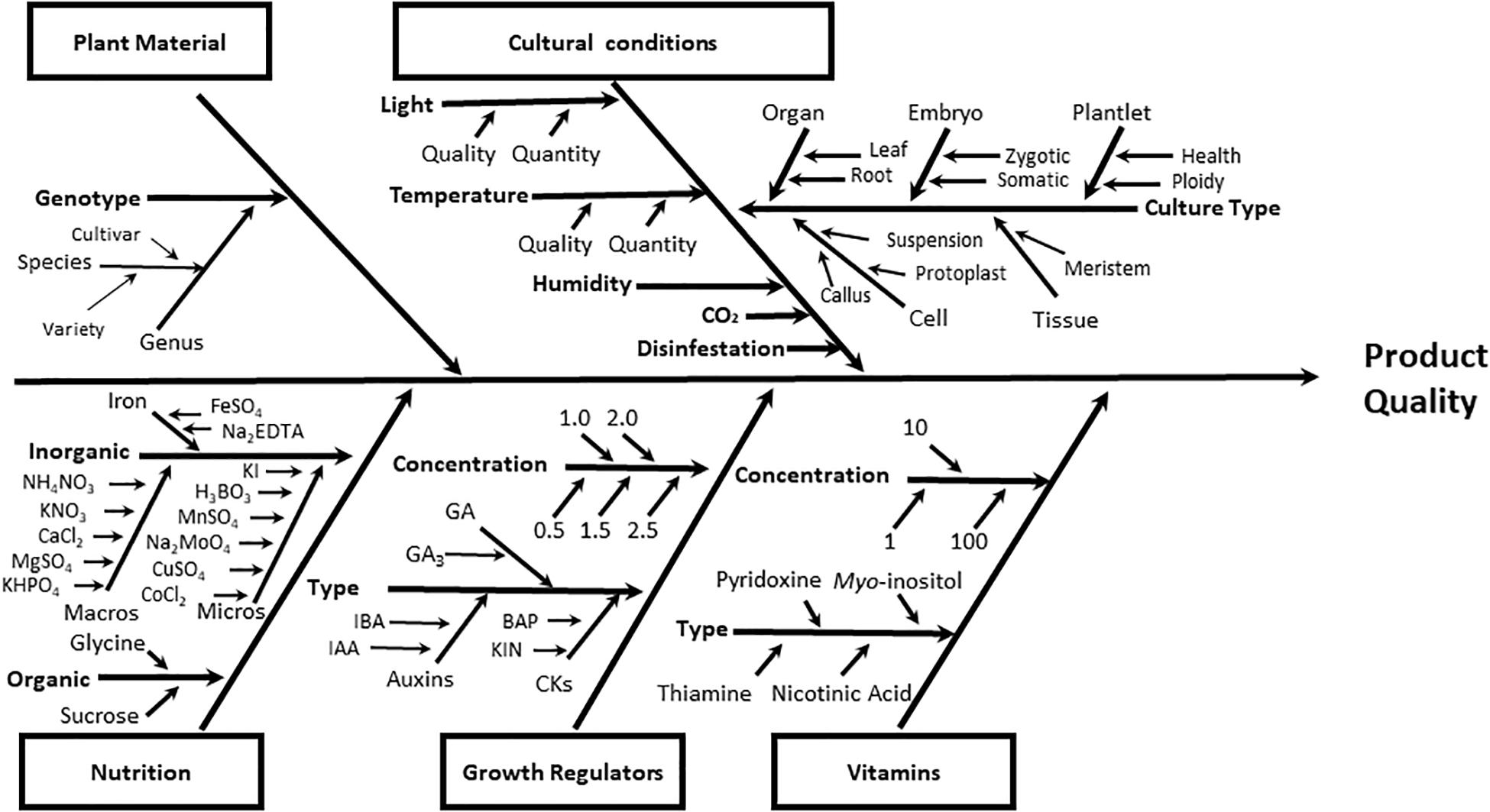
Figure 1. Ishikawa diagram for quick visualization of the main categories of causes (plant material, cultural conditions, nutrition, plant growth regulators, and vitamins) that affect the plant cell tissue culture. Each category grouped factors representing the root causes of variation on the final quality of the process. As example of plant growth regulators. the next auxins (IAA, indole acetic acid; IBA, indole-butiric acid); CKs, cytokinins (BAP, Benzyl adenine purine; KIN, kinetin), and GA, gibberellins (GA3, gibberellic acid) were included.
Achieving quality products during in vitro plant tissue culture, rather than low survival rates and/or occurrence of physiological disorders, is highly dependent on the mineral nutritional composition of the media, as they are essential for optimal morphogenesis and organogenesis (Ramage and Williams, 2002; George et al., 2008; Sonnewald, 2013). In fact, physiological disorders and/or toxicity due to their deficiency or excess in the culture media inorganic composition has been reported (Bresinsky et al., 2013; Nezami-Alanagh et al., 2019). The inorganic nutrients added into the plant tissue culture media can be differentiated in two groups (Figure 1): macronutrients, taken up in large amounts (>0.5 mM L–1) including nitrogen (N), potassium (K), calcium (Ca), phosphorus (P), magnesium (Mg) and sulfur (S); and those used in small quantities or micronutrients (<0.5 mM L–1) such as iron (Fe), chlorine (Cl), manganese (Mn), zinc (Zn), boron (B), copper (Cu), and molybdenum (Mo) (Epstein, 1972; George et al., 2008).
The most widely used basal medium, MS (Murashige and Skoog, 1962), although it constitutes a good starting point for the development of new protocols (Niedz and Evens, 2007), is often inadequate because it generates physiological disorders such as shoot tip necrosis and/or hyperhydricity (Nowak et al., 2007; Bhojwani and Dantu, 2013; Nezami-Alanagh et al., 2018). MS mineral composition has been considered as unideal for many fruit species and cultivars (Reed and Hummer, 1995) and even supra-optimal for in vitro culture of kiwifruit Actinidia sp. (Moncaleán et al., 1999, 2003).
Many strategies have been carried out to improve plant-specific genotypes’ tissue culture protocols by modifying the mineral composition of previously designed media. Initially, a trial and error strategy was employed by the pioneers of plant cell tissue culture (Gautheret, Heller and White’s media) by changing the levels of each factor (independent variable) at a time, named “one factor at time” (OFAT), keeping the rest of the factors constant. Later, Hildebrandt et al. (1946) used the “triangulation method” (three elements varied at time). Finally, Murashige and Skoog (1962) tested the effect of one single element on several concentrations (1, 2, 4, and 8× of the basal medium based on White’s nutrient solution) in the presence of several levels (3×, 8×, 16×, or even 32×) of the remaining elements. However, this strategy presented several disadvantages: (i) it does not give accurate information about the overall optimum, just partial optima for each factor; (ii) it ignores interactions between factors; and (iii) it increases the number of experiments (runs).
Currently, computer-based technologies are able to dramatically reduce the number of experiments and the associated cost (Nezami-Alanagh et al., 2018). As an example, the use of design of experiments (DOE) software facilitates the reduction of the optimal number of treatments to be performed, ensuring adequate sampling of the design space (Niedz and Evens, 2016; Nezami-Alanagh et al., 2019). The analysis of results with computer tools such as the response surface methodology (RSM) have been previously applied to study the composition of plant tissue culture media (Niedz and Evens, 2007; Poothong and Reed, 2016). However, the advantages of artificial intelligence tools, such as neurofuzzy logic, over some statistical analysis, including multiple regression analysis, has been described elsewhere (Landín et al., 2009; Gago et al., 2010a). Advantageously, algorithm-based machine learning (ML) tools provide the ability for autonomous learning and prediction of results without being explicitly programmed or with little human intervention (Gallego et al., 2011). In other words, algorithms can be trained to learn by themselves, generating a model that allows integrating and predicting results. ML approaches, such as artificial neural networks, fuzzy logic, and genetic algorithms, have been proposed as the most up-to-date methodology in the design of culture media (Gago et al., 2010a,c, 2011; Arteta et al., 2018; Nezami-Alanagh et al., 2018) to detect and understand the effect of several factors and their interactions (non-linear and multifactorial) and to predict the optimal combination of salts for the in vitro culture of plants (Gago et al., 2011; Gallego et al., 2011).
Due to the level of interest in the kiwi industry to introduce new kiwi genotypes (Kabaluk et al., 1997), our research group has pioneered the establishment of an in vitro culture protocol for kiwiberry, particularly for Actinidia arguta cv. Issai (Hameg et al., 2017). Firstly, based on successful results obtained for kiwifruit tissue culture (Revilla et al., 1992; Paradela et al., 2001), the media Cheng (1975) was used to establish in vitro kiwiberry explants (Hameg et al., 2018). Although good performance was achieved, the results suggested that additional research should be done to improve growth responses. To that end, several micropropagation media, previously used for in vitro kiwifruit culture, including B5 (Gamborg et al., 1968), Ha (Harada, 1975), Cheng (Cheng, 1975), Kh (Revilla et al., 1992), St (Standardi, 1981), and MS (Murashige and Skoog, 1962), were compared. The most appropriate medium for kiwiberry shoot proliferation was the St medium, but it caused some unwanted physiological disorders, such as basal callus formation (Hameg et al., 2018). For this reason, the challenge of designing a new basal medium that could avoid all these physiological disorders was considered (Hameg, 2019). In this work, we described how the combination of DOE and ML approaches were very useful, as a new strategy, in identifying the multifactorial and non-linear interactions between the culture media mineral nutrients and plant growth responses, and how it is possible to predict its optimal combination for the healthy in vitro proliferation of any plant, particularly kiwiberry, using these promising approaches.
Nodal segments from a stock culture of A. arguta (Sieb. and Zucc.) Planch. ex Miq. cv. ‘Issai’ were maintained in Cheng basal medium (Cheng, 1975) supplemented with 1 mg L–1 6-benzylaminopurine (BAP) and 1 mg L–1 gibberellic acid (GA3), 8 g L–1 agar, and 30 g L–1 sucrose. Media pH was set to 5.7 before autoclaving at 121°C for 15 min at 105 KPa (Hameg et al., 2017; Hameg, 2019).
Salts of MS medium (Murashige and Skoog, 1962) were classified into five independent factors (single salt or group of salts): (i) NH4NO3, (ii) KNO3, (iii) mesos, (iv) micros, and (v) iron. Each factor has several levels corresponding to different concentrations of the MS medium (Table 1). These levels were defined over a range (minimum and maximum) of concentrations expressed as × MS level (1× correspond to MS concentration). The experimental space was designed to decipher the effect of extreme concentrations (very low and high) of ions with levels from 0.1 to 5× MS levels on the morpho-physiological shoots growth and quality responses.
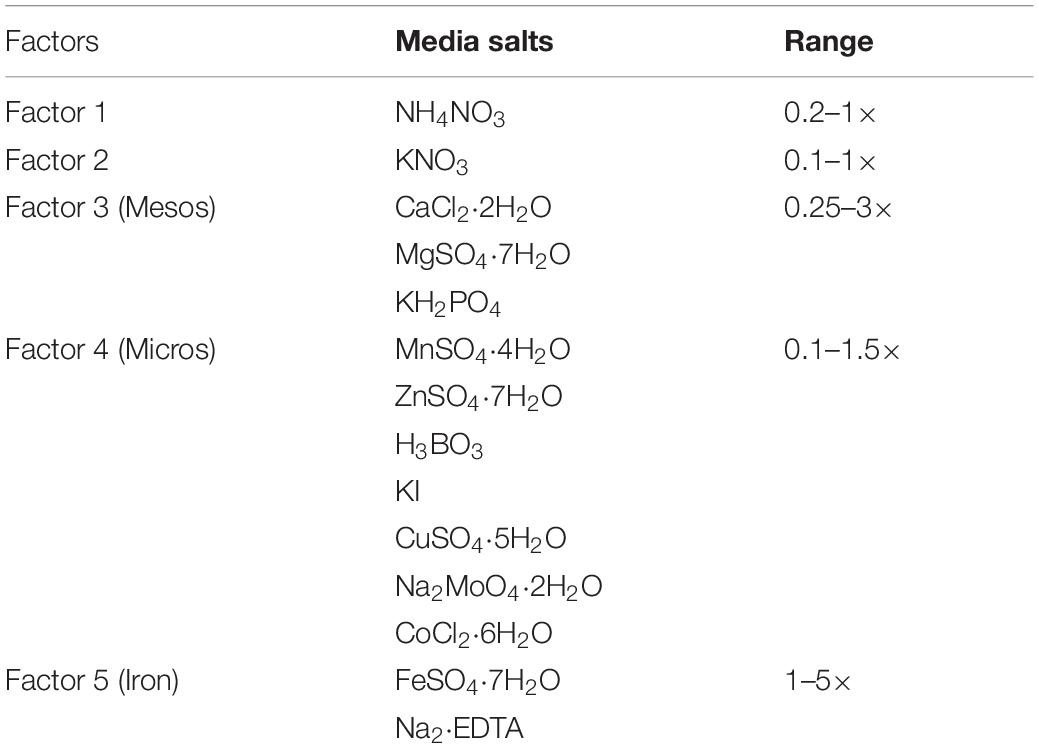
Table 1. Five factors used to define the five-dimensional design space based on MS medium salts and concentration range expressed as (× MS levels).
A five-dimensional experimental design (Niedz and Evens, 2007) was developed using the software Design-Expert® 8 (Design-Expert, 2010). The generated database included 36 treatments. 33 were generated by the software using modified D-optimal criteria (Reed et al., 2013b), while three additional points of MS media were used as controls (34–36; Table 2). All treatments contained MS medium vitamin composition and were supplemented with 2 mg L–1 glycine, 30 g L–1 sucrose, 8 g L–1 agar, ad 1 mg L–1 BAP, and 1 mg L–1 GA3.
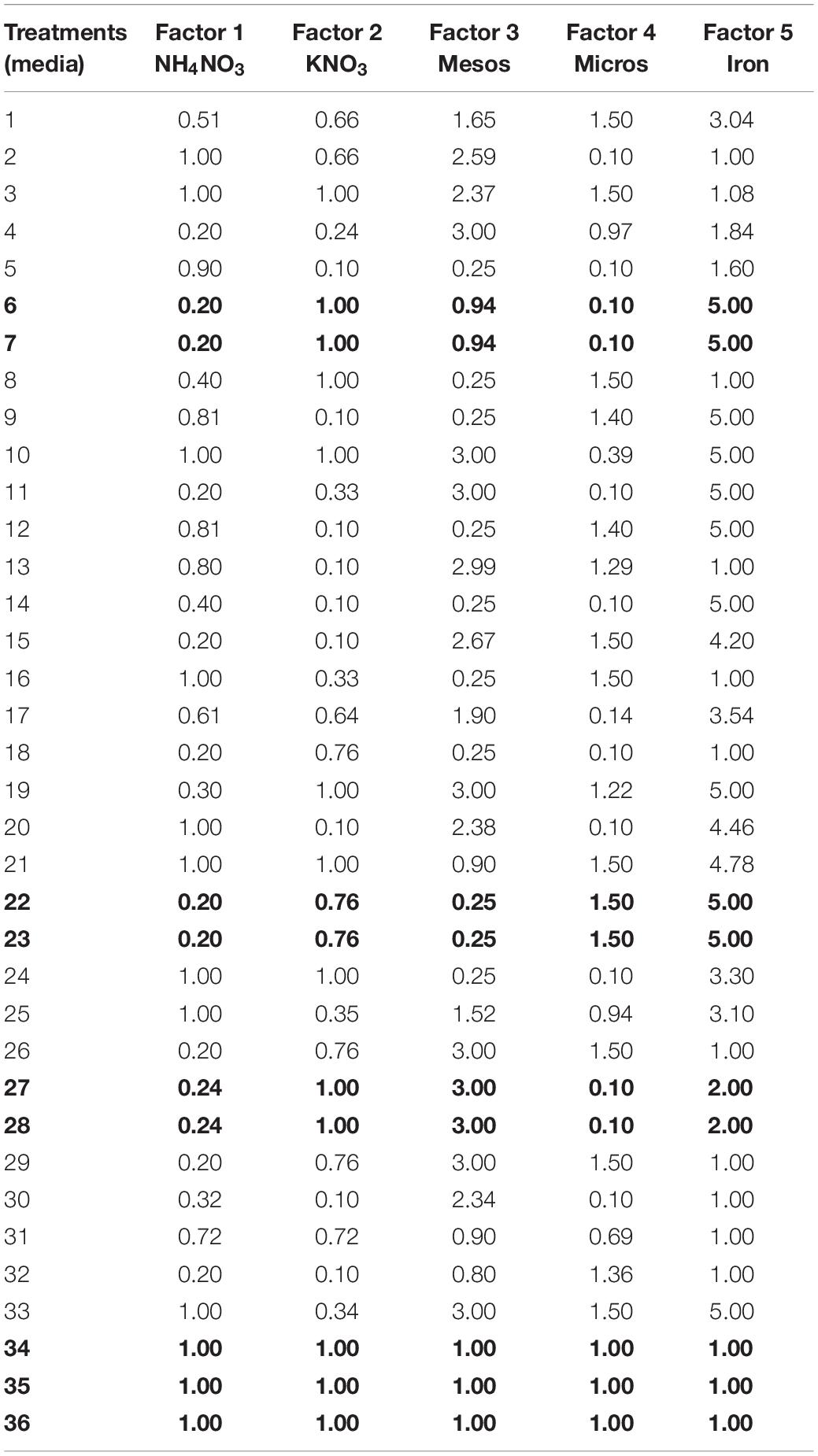
Table 2. Five-factor design with 33 treatments, including three replicates points (6–7, 22–23, and 27–28) plus another three replicates of MS medium (34–36), that are bolded.
Explants about 2 cm were cultured in 200 mL culture vessels containing 30 mL of each medium for 50 days. The cultures were maintained in a growth chamber at 25 ± 1°C under a 16 h photoperiod at 40 μmol m–2 s–1 irradiation provided by cool white fluorescent tubes (Hameg et al., 2017).
Each treatment included five glass culture vessels (used as replicates) containing three explants each, sealed with plastic caps. The experiments were carried out in triplicate. The explants were harvested after 50 days of culture, all followed, and the next six growth responses were evaluated (Hameg, 2019):
(1) Shoot number (SN), number of new regenerated shoots per explant.
(2) Shoot length (SL), length from the base of the shoot to the tip, per explant (cm).
(3) Leaf area (LA), the sum of areas (cm2) of the leaves >1.5 cm. Leaf area per explant was measured using a portable laser leaf area meter (Meter CI-202, CID biosciences, WA, United States).
As the MS mineral salts have been reported for promoting physiological disorders in some plants, the next three morpho-physiological quality responses were also evaluated:
(1) Shoot quality (SQ), as indicative of shoot vigor, was visually assessed and scored from 1 to 5 (1 very poor, 2 poor, 3 moderate, 4 good and 5 very good; Figure 2A).
(2) Basal callus (BC), callus formation at the cut edge of shoots was visually assessed and scored from 1 to 4 (1 necrotic, 2 big, 3 moderate, 4 absent; Figure 2B).
(3) Hyperhydricity (H), was visually assessed and scored from 1 to 3 (1 high, 2 low, 3 none; Figure 2C).

Figure 2. Shoot quality rating (A): 1 (very poor), 2 (poor), 3 (moderate), 4 (good), and 5 (very good); basal callus formation rating (B): 1 (necrotic), 2 (big), 3 (moderate), and 4 (absent) and hyperhydricity rating; (C): 1 (high), 2 (low), and 3 (absent).
Machine learning uses a wide range of algorithms to build mathematical models using databases as training data, helping humans to make predictions and decisions. Here, three artificial intelligence tools were used to build the mathematical models: neural networks (ANNs), fuzzy logic, and genetic algorithms (GA). The commercial neurofuzzy logic software, FormRules® v4.03, (Intelligensys Ltd., United Kingdom) which combines ANNs with fuzzy logic (Colbourn and Rowe, 2005; Landin and Rowe, 2013) was selected to model and decipher the effect of the mineral media composition on plant growth responses, while the commercial software INForm® v5.01 (Intelligensys Ltd., United Kingdom) that combines ANNs with GA (ANNs-GA), was used for the optimization of the mineral nutrition. Advantageously, those artificial intelligence tools allow for the modeling of large databases with an important number of inputs (factors studied) and outputs (plant response parameters determined), independently of the type of data or even if the data set is incomplete, vague, or noisy (Gago et al., 2011; Gallego et al., 2011).
The neurofuzzy logic model was built using 18 inputs (ion concentrations of each treatment) and six outputs (SN, SL, LA, SQ, BC, and H). The ion composition of each treatment (Table 3) was calculated from each salt concentration in the media (Supplementary Table 1). Each ionic concentration was used as an input for the model (Table 3). This procedure deeply facilitates the understanding of the specific effects of mineral elements (ions), avoiding the “ion confounding effect” as described elsewhere (Niedz and Evens, 2006, 2007; Nezami-Alanagh et al., 2017). Instead, the ANNs-GA model was built using 14 inputs corresponding to the MS salts and the same six outputs used for the neurofuzzy logic model (Supplementary Table 1) in order to optimize the salt composition and define a new optimal culture media for kiwiberry.
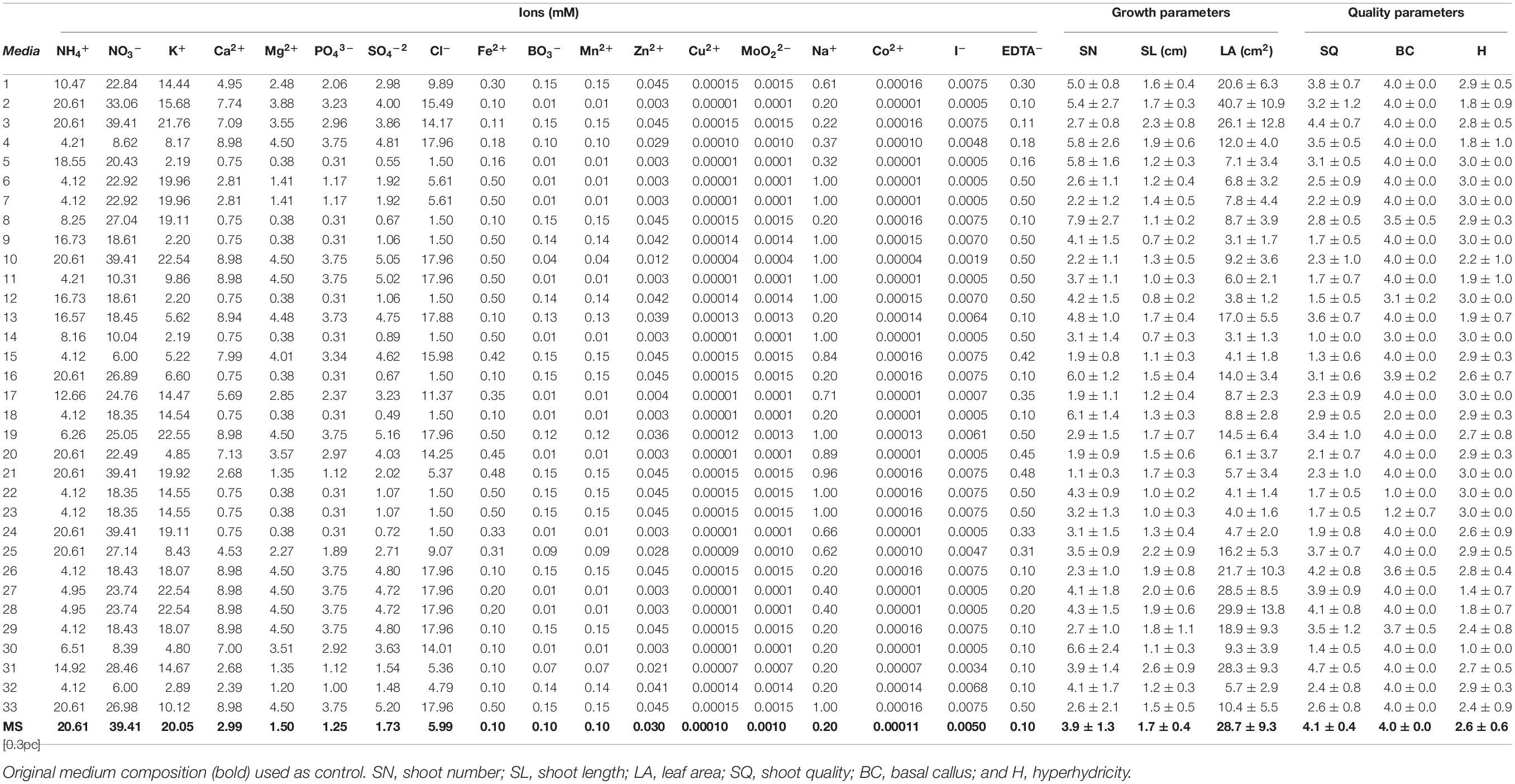
Table 3. Mineral nutrients’ (expressed as ions) composition of the different culture media based on the five-factor experimental design (0–33) and response values of the parameters (mean and standard deviation) used to characterize plant growth.
Machine learning algorithms were able to build empirical models using the training parameters presented in Table 4. The Adaptive Spline Modeling of Data (ASMOD algorithm) was used by FormRules for the parameter minimization, including in the model the relevant inputs, facilitating a more parsimonious and transparent model for users. Compared to other models of a general structure, ASMOD reduces the model complexity but improves its accuracy even with fewer parameters (Kavli and Weyer, 1994). Finally, ASMOD allows for dividing of the model obtained into submodels to easily interpret the results by generating a set of rules. Once the accuracy of the model was ensured, structural risk minimization (SRM) was selected to obtain models with the highest predictability along with the simplest rules. FormRules® presents the results obtained as a set of linguistic labels or IF-THEN rules with a degree of membership, which greatly facilitates their interpretation. The antecedent part (IF) expresses the conditions at the inputs, and the consequent part (THEN) describes the values of the outputs. The degree of membership represents a degree of truth, ranging from 0 to 1, with 1 meaning that the expected output value is always a complete member of the fuzzy set “low,” “medium,” or “high” (Shao et al., 2006; Gago et al., 2011; Gallego et al., 2011; Nezami-Alanagh et al., 2018).

Table 4. Train parameter settings for neurofuzzy logic (FormRules® v4.03) and artificial neural networks (INForm® v5.01) software.
The Back-Propagation (BP) for Multi-Layer Perceptron (MLP) was used as the training algorithm for InForm® software. To avoid overfitting during MLP training, the data set was split into two groups of data randomly: 80% for training and 20% for testing. Both training error and testing error were checked at every step to prevent overfitting, as described previously (Nezami-Alanagh et al., 2017).
For the optimization process, the software requires the definition of the desirability function for each output, together with their relative importance or weight, expressed on a scale of 0 to 10, 10 being the most important. For media optimization, only the measurable three growth parameters and shoot quality were included. The priority established was: SQ = 10, SN = 9, SL = 8, and LA = 7. As desired values to be achieved, SQ > 4.00, SN > 4.4, SL > 1.6 cm, LA > 28 cm2 were included. Finally, the model reveals the percentage of agreement between the predicted values with those desired by the researchers on a scale of 0–100%.
The predictability and accuracy for each parameter developed by both software was assessed using the Train Set R2 and the ANOVA f-ratios. Train Set R2 values are calculated by the following equation (Shao et al., 2006).
Where yi is the experimental point in the data set, yi′ is the predicted point calculated by the model, and yi′′ is the mean of the dependent variable. The higher the Train Set R2 value, the better the predictability of the model. In previous works, R2 values higher than 70% have shown good model prediction capacity. It is necessary to avoid R2 that are too high (>99%), which is indicative of over fitted models of low prediction capacity and should be readjusted as described elsewhere (Colbourn and Rowe, 2005; Landín et al., 2009; Nezami-Alanagh et al., 2017).
To assess statistically significant differences between experimental and predicted values from the model an analysis of variance (one-way ANOVA) was carried out. If the ANOVA f-ratio is higher than f-critical values for the degrees of freedom of the model, then there are no statistically significant differences between those groups (predicted and experimental values) and the model is accurate.
In order to validate the model, a new experiment including optimal predicted R medium was carried out in the laboratory. As controls, another six media generally used in kiwifruit tissue culture, such as MS, B5, St, and Ha, were also tested. A total of 45 explants per medium were cultivated in the same conditions as above. After 50 days, the growth parameters (SN, SL, and LA) and quality parameters (SQ, BC, and H) were recorded.
Statistical analysis was used to check the validity of the new optimized R medium and search for the significant differences between the new R medium and MS. Continuous data (SL and LA) were analyzed using ANOVA with Tukey’s Studentized range, (HSD) post hoc test at α = 0.001. Discrete (SQ, BC, and H) and categorical (SN) data were analyzed by the non-parametric Kruskal–Wallis test at α = 0.001. All the statistical analyses were performed using Statistica v.12 (StatSoft-Inc., 2014).
The computer-based software for optimal design was used to guarantee a well sampled design space, giving a database of 34 treatments combining all 18 mineral nutrients based on the MS medium composition (Table 3). To focus on the effect of the mineral composition, the other media ingredients were kept constant. The MS based treatments caused a great variety of physiological responses compared with the MS control (Table 3). As example, very good quality (#31: 4.7), large SN (#8: 7.9), long SL (#31: 2.6 cm), and very large LA (#2: 40.7 cm2) versus the MS (4.1, 3.9; 1.7 cm and 28.7 cm2, respectively) were obtained. On the contrary, very poor quality (#14: 1.0), few SN (#21: 1.1), short SL (#9: 0.7 cm), or LA (#9 and 14: 3.1 cm2) were also achieved.
Physiological disorders such as necrotic, big, or even moderate basal callus and hyperhydricity were also found (Figure 3). As an example, the treatments #18, 22, and 23 (Figures 3A1–A3) promoted the formation of big and necrotic callus at the cut edge of shoots, whereas the treatments #2, 3, and 30 (Figures 3B1–B3) promoted hyperhydricity. The MS medium, used as control, did not show basal callus formation (4.0) on kiwiberry, but some hyperhydricity (1.4) was detected.

Figure 3. Morpho-physiological abnormalities responses to some media treatments as basal callus (A): treatments 18 (A1), 22 (A2), and 23 (A3) and hyperhydricity (B): treatments 2 (B1) and 30 (B2,B3) versus high quality plants without symptoms (A4,B4).
Classical statistical techniques (ANOVA) are very useful in data analysis, but they do not help much in extracting valuable information about key mineral nutrients in these complex processes, or the right combination of minerals to promote ever-healthy plantlets. Currently, other advanced algorithm-based technologies like decision trees, SRM, or machine learning tools look promising for deciphering key minerals. Here, the latest technologies were used.
The neurofuzzy logic tool was able to successfully model the dataset (Table 3) with the training parameters described in Table 4. The results of the Train Set R2, higher than 70% for all parameters, indicated good performance and a high predictability of the neurofuzzy logic models (Table 5). Moreover, the ANOVA f ratio was always higher than the f critical value showing the quality and accuracy for prediction, since no statistically significant differences (α < 0.001) between experimental and predicted values were found (Table 5 and Supplementary Figure 1).
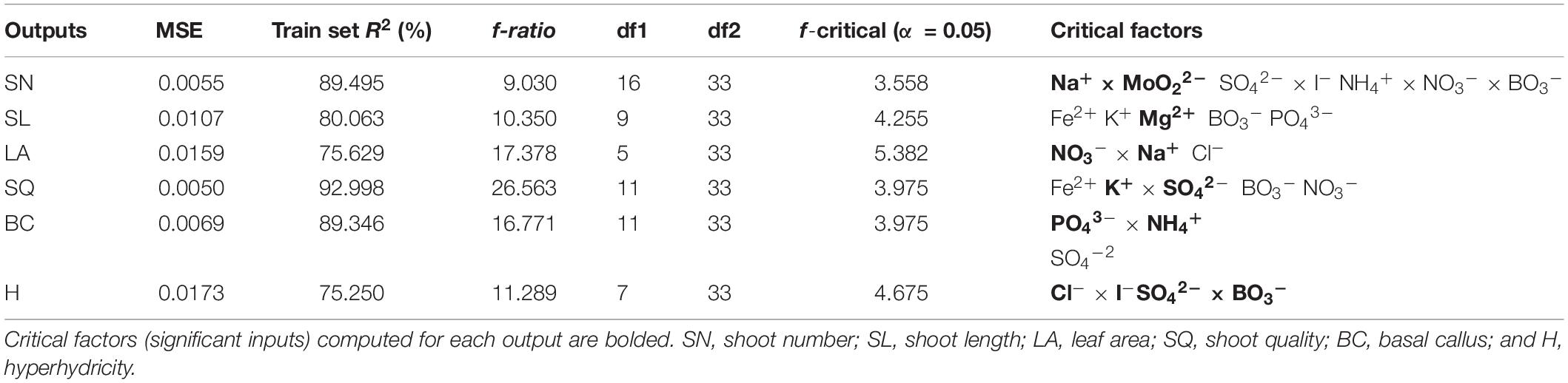
Table 5. Neurofuzzy logic model Mean Square Error (MSE), train set R2, ANOVA parameters for training [f-ratio, degrees of freedom (df1: model and df2: total), and f-critical value for α = 0.05].
Neurofuzzy logic approach also succeeded in identifying the key factors (inputs) for each parameter (outputs) studied. Among the 18 evaluated ions, just 11 were critical and explain variations among treatments (Table 5). Of these, five belong to macronutrients (N, K, P, Mg, and S) and six to micronutrients (Cl, Fe, B, Mo, Na, and I). While some ions caused independent effects, others interacted with each other. As an example, the variability of the SN parameter was explained as a function of the interactions of seven ions, Na+ × MoO22–; SO42– × I– and NH4+ × NO3– × BO3–, while the SL variability was independently affected by the following 5 ions: Fe2+, K+, Mg2+, BO3–, and PO43– (Table 5).
The variability on the new regenerated shoots per explant (SN parameter) is explained by three submodels showing three interactions of Na+ and MoO22– (strongest effect; submodel 1), the SO42– × I– interaction (submodel 2), and NH4+ × NO3– × BO3– (submodel 3; Table 5).
Through simple rules IF THEN the model pinpoints the negative effect of both Na+ and MoO22– ions at high concentrations on shoot proliferation (Table 6; rule 4), recommending their use at low concentrations to obtain the highest number of regenerated shoots (Table 6; rule 1). In both cases, the membership was 1.00 which means that if we combine low concentrations of both ions, we will obtain a truly high number of new shoots.
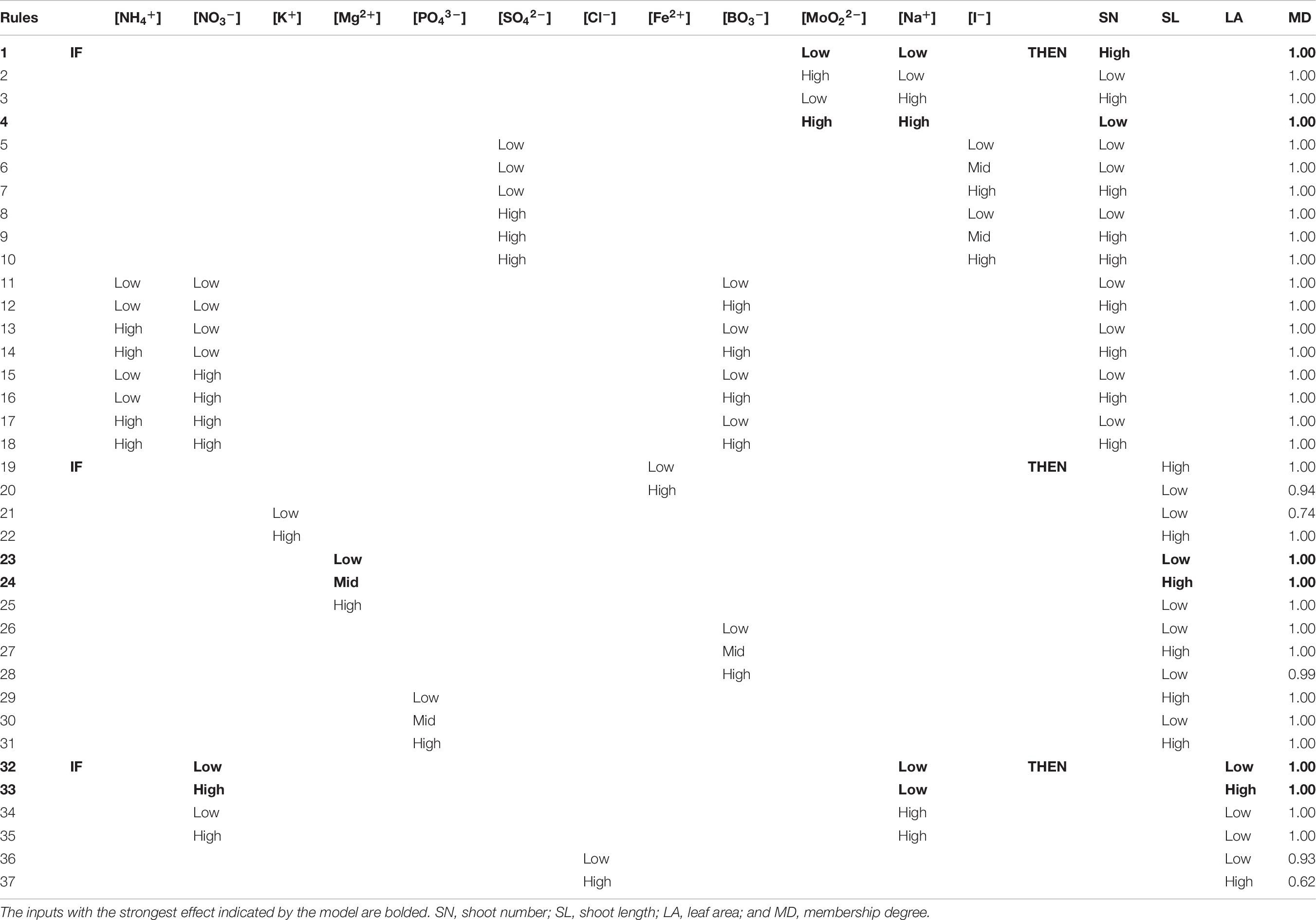
Table 6. Rules for morpho-physiological growth responses (SN, shoot number; SL, shoot length and LA, leaf area) with their membership degree (MD) generated by neurofuzzy logic.
Also, the presence of High SO42– concentrations in the medium in combination with mid or high I– concentration significantly increases the number of shoots (Table 6; rules 9–10). Finally, the model also pinpoints the key role of High concentrations of BO3– combined with either low or high concentrations of NH4+ × NO3– in the culture medium (Table 6; rules 12, 14, 16, and 18).
Shoots length (SL) of A. arguta is independently influenced by the effect of five ions: Fe2+, K+, Mg2+, BO3–, and PO43– (Table 5). The model selects Mid Mg2+ as the adequate concentration to obtain large (high) shoot length (Table 6; rules 24). When low (rule 23) or high (rule 25) concentrations are added to the media (membership 1.00) a truly short SL is achieved. Additionally, Low Fe2+, High K+, Mid BO3–, and Low or High PO43– concentrations in the culture media increases SL (Table 6; rules 19, 22, 27, 29, and 31).
Area of leaves in A. arguta were mainly influenced by the interaction of NO3– and Na+ concentrations and the single effect of Cl– concentration (Table 5). The greatest leaf area is achieved with the combination of High NO3– and Low Na+ concentrations (Table 6; rule 33). Other combinations promoted worse results for leaf area (Table 6, rules 32, 34–36). High values of LA are also obtained when high concentrations of Cl– were used (Table 6, rule 37).
Mineral nutrients had a great impact on the appearance of morpho-physiological abnormalities such as basal callus and hyperhydricity (Table 3 and Figure 3). Therefore, a parameter to establish the quality of the shoots was included as output and determined as explained previously (Figure 2A).
The neurofuzzy logic software selected just five ions as critical factors for the quality of the shoots: the interaction between K+ and SO42– as the stronger, and the independent effect of Fe2+, BO3–, and NO3 (Table 5). The best shoot quality is promoted (membership 1.00), if High K+ and Mid SO42– concentrations are added into the media (Table 7; rule 44), although High SO42– concentration also improves shoot quality with high membership (0.83; Table 7; rule 45). On the contrary, the high concentration of Fe2+ ion promotes a truly low quality of shoots (Table 7; rule 39). The same occurs when the concentrations of BO3– and NO3– are high (Table 7; rules 48 and 51). However, if mid concentration of BO3– and NO3– ion are used, a truly high shoot quality will be obtained (Table 7; rules 47 and 50) with the highest membership degree (1.00). As an example, these results agree with the treatments #3 and 26 (Table 3).
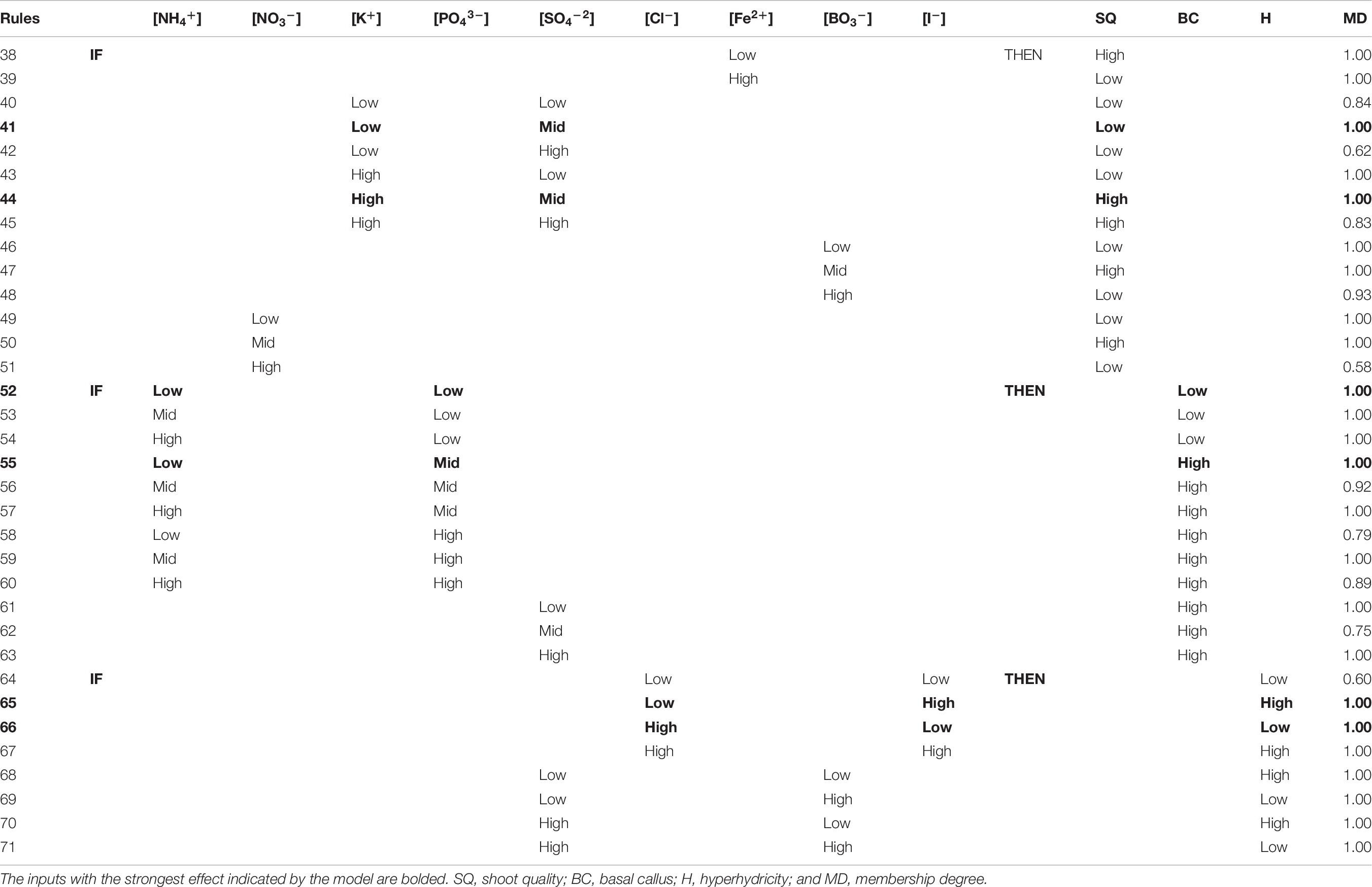
Table 7. Rules for morpho-physiological quality responses (SQ, shoot quality; BC, basal callus; H, hyperhydricity) with their membership degree (MD) generated by neurofuzzy logic.
The neurofuzzy model was also able to identify the key ions causing the physiological abnormalities described here (Table 5) and explain their effect using simple rules (Table 7). Thus, the model pinpoints the effect of only three ions on the development of basal callus: PO43– × NH4+ and SO42– (Table 5). The model highlights the positive effect of using Mid to High PO43– concentration (Table 7; Rules 55–60), which favor the production of healthy shoots that show moderate or absent callus formation (Figure 2B), particularly at Low NH4+ concentration (Table 7, rule 55; membership 1.00). If Low PO43– is added to the media, (membership 1.00) the formation of big and truly necrotic basal callus are promoted (Table 7; rules 52–54), independently of the NH4+ concentration. Finally, the rules 61–63 generated by the model shows that the presence of SO42– at any concentration within the design space reduces the basal callus formation, generating healthy shoots (Table 7).
The hyperhydricity, a well-described physiological disorder in plant tissue culture, is associated in A. arguta to the combined effect of four ions: Cl– × I– and SO42– × BO3– (Table 5). High I– concentration in the medium promoted no hyperhydricity (Table 7; rule 65 and 67), with a stronger effect if combined with low concentration of Cl– (rule 65). Interestingly, Low BO3– concentration also minimized the hyperhydricity (Table 7; rules 69 and 71), in interaction with any concentration of SO42–.
A database including as inputs the salt concentrations in the different culture media and as outputs all growth and quality parameter results (Supplementary Table 1) was modeled using INForm® software, achieving high predictability. Both the Train Set and Test Set R2 were above 70% (76.66 < R2 < 96.59) for all the parameters studied (Supplementary Table 2).
Genetic algorithms predicted the best combination of salts that would provide, simultaneously, the highest values for all parameters: 4.8, 2.6 cm, 39.5 cm2 and 4.4 for the SN, SL, LA, and SQ, respectively. The new optimized medium, named “R medium,” predicted higher values than MS medium used as control (Table 3).
The results from the experiment carried out in order to validate “R medium” are shown in Table 8. As can be seen, predicted and experimental (Table 8) are close for both R and MS medium. In fact, no significant differences (α < 0.001) between the data obtained in both experiments for MS media (Tables 3, 8), used as internal control, was detected.
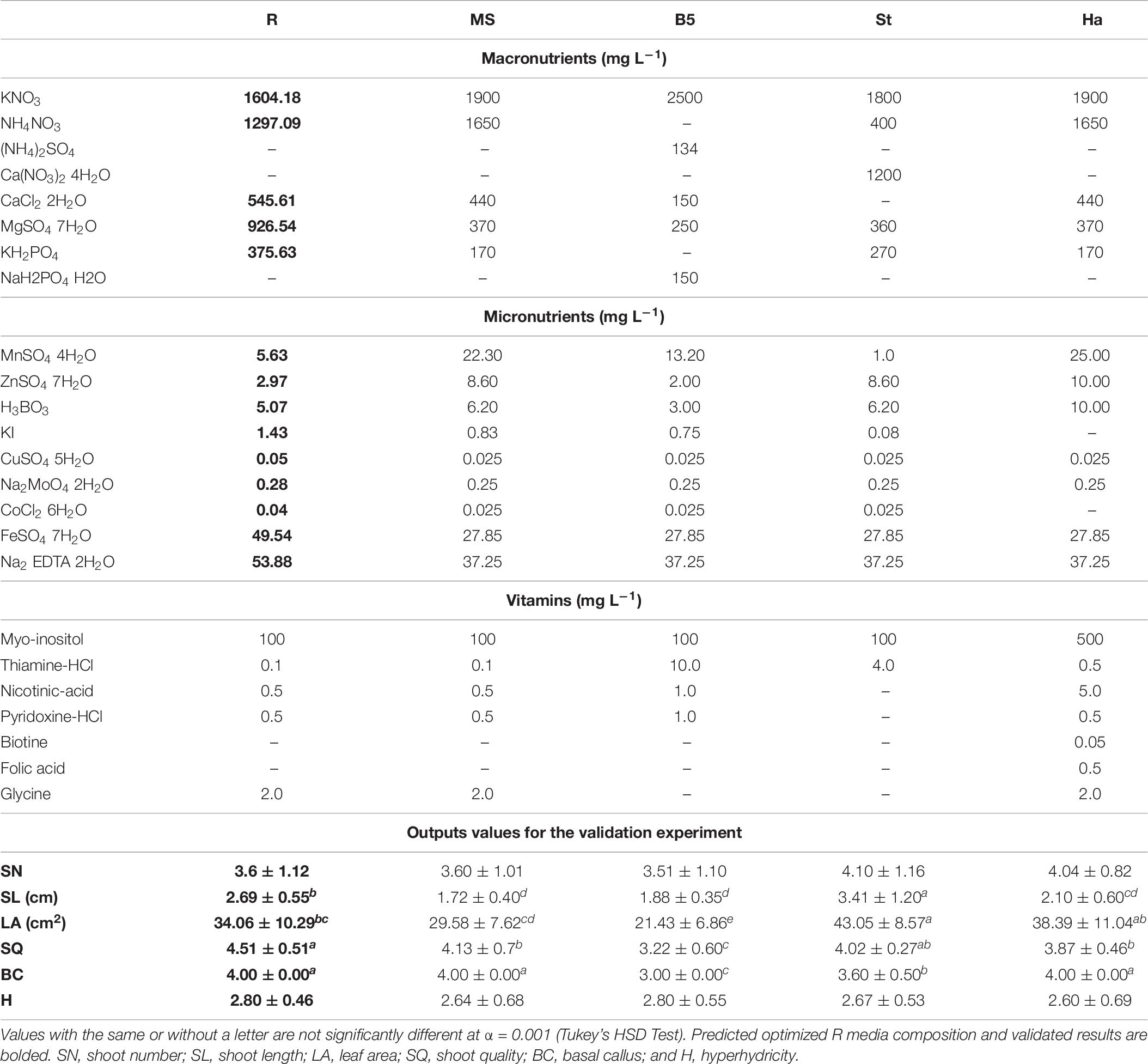
Table 8. Composition of the standard media (MS, Murashige and Skoog; B5, Gamborg; St, Standardi; Ha, -Harada) and the predicted optimized R medium together with output values obtained at validation experiment (mean ± standard deviation).
Compared to the MS medium, the optimized R medium significantly improved (α < 0.001) the two responses selected as important in the optimization process (SQ and SL) with a weight of 10 and 9, respectively (100% desirability), but not the other outputs (Table 8).
Regarding the other media used, the optimized R medium was surpassed by the St medium in promoting the growth parameters SL and LA (α < 0.001; Table 8), however, R medium obtained a better value for the SQ (α < 0.001) with less formation of basal calluses and hyperhydricity. On the contrary, medium B5 promoted the lowest values of SQ, BC, SL, and LA (α < 0.001). Finally, the Ha medium promoted lower SQ and SL than R medium (α < 0.001; Table 8).
Recently, algorithm-based approaches were introduced in plant tissue culture studies. Decision Trees, Chi-square Automatic Interaction Detector (CHAID), and adaptive regression splines were preferred to other ML methods such as ANNs, considering that ANNs generate “black box” models that are difficult to interpret and use (Olden et al., 2008; Akin et al., 2016, 2020). However, ANNs are powerful ML tools for plant tissue researchers, particularly when they are combined with other techniques that help in the interpretation of results or the use of the models (Gago et al., 2010b; Gallego et al., 2011). Some of their strengths are: (i) ANNs do not require a specific experimental design, so they can deal with incomplete factorial designs, trial-error series, or even historical data; (ii) they do not entail orthogonality or uniformity in the data; and (iii) subtle non-linear relationships in the data can be elucidated. The two major weakness of ANNs are the possibility of “overtraining” and the generation of “black box” models. The first limits the predictability and the second limits the possibility of using the model out of the computer used to generate it. Those limitations can be overcome by validating the model with unseen data before using it and combining the ANN model with other technology that allows knowledge to be extracted. Thus, systems that combine ANN with fuzzy logic or “neurofuzzy logic” systems allow for the obtaining of “gray box” models, providing sets of linguistic rules that help to generate knowledge about the process studied; and the combination of ANNs with GA is able to answer “How to get” questions to find the compromised solution to obtain simultaneously a set of desirable outputs. In the present work we take advantage of the use of two ML techniques, neurofuzzy logic and ANN-GA, to study the mineral nutrition of kiwiberry and address the development of an efficient in vitro protocol for this cultivar, as it has been carried out for other species by further innovative research groups (Zielińska and Kêpczyńska, 2013; Nezami-Alanagh et al., 2019).
The MS medium was the first and only medium described in the literature for kiwiberry in vitro culture (Seelye and Butcher, 1991; Matkowski and Przywara, 1995; Han et al., 2010). However, several authors have reported side effects and physiological disorders, such as shoot tip necrosis and hyperhydricity, when using it (Nowak et al., 2007; Bhojwani and Dantu, 2013; Nezami-Alanagh et al., 2018 and references therein). MS medium has also been considered supra optimal for other species of kiwifruit (Moncaleán et al., 1999, 2003), being necessary to reduce its composition by half or even more to improve performance (Monette, 1986; Akbas et al., 2007; Nasib et al., 2008).
Based on the salt composition of the MS medium, a reduced experimental design has been established (Tables 1, 2). MS medium includes a combination of 14 salts. It is almost impossible to develop a complete factorial design for all of them because of the number of treatments to be assayed (e.g., 14 factors at three levels give 4,782,969 treatments). Instead, MS media salts were grouped in to five factors, which were used to define a five-dimensional design space, including just 33 treatments.
The factors selection followed the strategy used by other authors to study the shoot quality of the hazelnut, raspberry, or apricot (Wada et al., 2013; Hand et al., 2014; Poothong and Reed, 2014; Kovalchuk et al., 2017). Factors were: (i) NH4NO3, (ii) KNO3, (iii) mesos, (iv) micros, and (v) iron (Reed et al., 2013a,b; Akin et al., 2017). The levels were chosen according to the maxima and minima found in the literature, in-house experience (Nezami-Alanagh et al., 2018, 2019), and the biological actions of the different nutrients (Hameg, 2019). This approach leads to more manageable and feasible research, ensuring adequate sampling of the design space (Niedz and Evens, 2006; Niedz and Evens, 2007).
The use of salts as factors creates the ion confounding effect, as has been demonstrated by some authors (Niedz and Evens, 2006), making it difficult to detect and explain the effects of individual ions on growth responses. However, it has been postulated that the specific control of some ions, such as K+, NH4+, and NO3–, is a critical aspect in the optimization of culture media (Akin et al., 2017). In order to study the effects of the specific ions on growth parameters and/or physiological disorders of in vitro kiwiberry culture, the ionic composition for the different treatments was calculated (Table 3) and modeled by a neurofuzzy logic software. For all parameters studied, the models showed high predictability (Train Set R2 > 70%) and good accuracy. Reading the simple “IF-THEN” rules allows the acquisition of knowledge about the ions that are critical for the response parameters of kiwiberry explants. Subsequently, the ANNs-GA modeling was also carried out using the salt database, which allowed for predicting of the mineral nutrients of an optimal R medium, specifically adapted to kiwiberry tissue culture.
Seven ions explain the variations in shoot number: NH4+, NO3–, SO42–, BO3–, MoO22–, Na+, and I–. Neurofuzzy rules (Table 6) state that a low MoO22– supplement (<0.0008 mM, Table 9) is necessary with all Na+ concentrations to promote a high number of shoots. Molybdate is generally added to the culture media up to 1 mM, and participates in NO3– catabolism (George et al., 2008). The R medium designed here is also proposed as 0.001 mM.
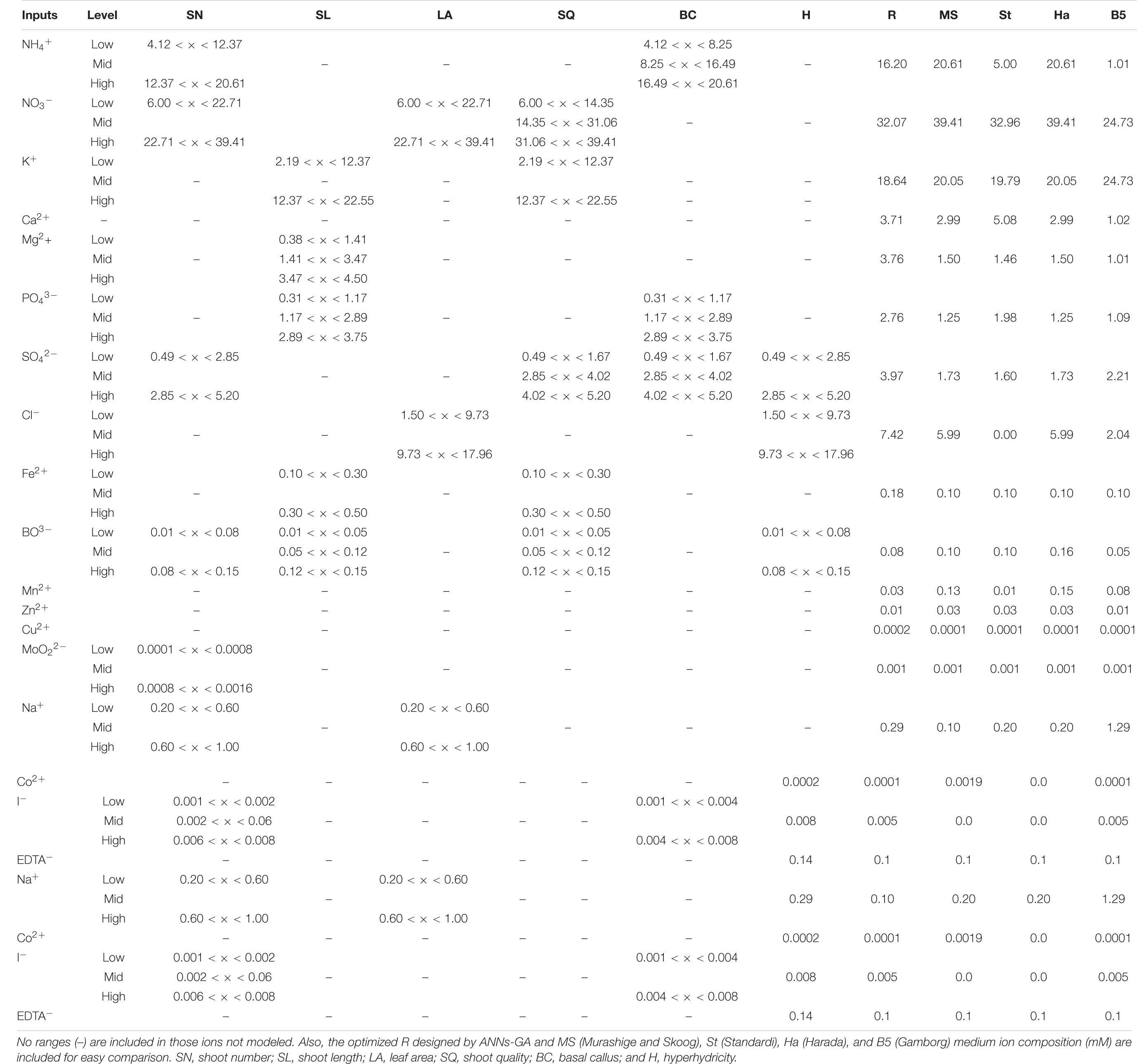
Table 9. Ranges (mM) and meaning of the levels (low, mid, and high) after fuzzification process by neurofuzzy logic software according to the rules Tables 6, 7 for each response parameter.
Na+ is considered a functional but inessential element, except for C4 plants, due to its relationship with CO2 fixation (George et al., 2008). Sotiropoulos and Dimassi (2004) have reported the beneficial effect of NaCl in the range of 10–20 mM on the in vitro proliferation of Actinidia deliciosa. Sodium is part of different salts added to the culture media, so it is usually difficult to establish its specific needs since it is affected by the ion confounding effect. However, the neurofuzzy logic model established that the Na+ concentration within the limits of the study (0.2–1 mM) is adequate to obtain a high number of shoots for kiwiberry, especially when the molybdate is in low concentration (<0.0008 mM, Table 9).
Iodine has not been recognized as an essential mineral for plant nutrition, but it is included in almost 65% of the media (George et al., 2008). Chée (1986) has suggested that I– interferes with lateral auxin transport and/or facilitates its catabolism. Generally, iodine is added to the culture media through the KI salt. The effect of adding KI to the media is controversial in the literature. Some authors (Da Silva et al., 2017) have pointed out that KI accelerates the development of plants. However, KI is not added to various media specifically designed for woody plants, such as DKW (Driver and Kuniyuki, 1984) or WPM (Lloyd and McCown, 1980). It is also not incorporated into the Ha medium, which is designed for kiwi. Neurofuzzy logic suggests that medium-high concentrations of iodine (>0.006 mM), whatever the concentration of SO42–, contributes to improving the number of shoots.
Sulfur is an essential component and plays an important role as ligand through the -SH groups. Most culture media contain this ion in the range of 1–2.5 mM. The available form of sulfur in plants is as SO42– ion and it is supplied in plant tissue cultures combined with other essential elements (Mg, Mn, Zn, Cu, and Fe) in at least five different salts, therefore its own role in mineral nutrition is still poorly understood due to the ion confounding effect. The neurofuzzy ML tool allows us to deduce its key role not only in the number of shoots, but in all the quality parameters studied (see below). Interestingly, the two most frequently cited media for woody plants, WPM and DKW, contain a high concentration of sulfate (7.45 and 12.39 mM, respectively). Our results demonstrate that the SO42–, per se, in concentrations higher than 2.85 mM (Table 9), is essential to improve the number of shoots in woody fruit tree plants, which is in agreement with other authors (Poothong and Reed, 2014) who have shown that the high level of mesos and micros, including MgSO4, MnSO4, ZnSO4, and CuSO4, promotes this effect on red raspberries.
Finally, the neurofuzzy model established the positive effect of the interaction among NH4+ × NO3– × BO3– on the regeneration of new shoots (SN). BO3– is generally supplemented in a range of 0.05–0.1 mM, being toxic at higher concentrations (0.185 mM; Bowen et al., 1979). As I–, BO3– also stimulates auxin catabolism and increases its translocation (George et al., 2008), the excess of boron counteracts these important morphogenetic PGRs. Other studies showed that boron deficiency affects cell elongation more than cell division in plant growth (Martín-Rejano et al., 2011). High concentrations of BO3–, within the range of the study (>0.08 mM; to avoid possible toxicity), should be added to the media for obtaining high SN, independently of the levels of both nitrogen and ammonium ions.
Nitrogen sources, mainly in form of NH4+ and NO3–, are constituents of proteins, nucleic acid, and chlorophyll, being essential to plant life (George et al., 2008). In general, in media design, NO3– and NH4+ are combined as the latter acidifies the medium. The addition of NO3– counteracts this effect buffering the pH (George et al., 2008). Although different NO3–/NH4+ ratios have been tested, most media, as MS, have twice as much nitrate as ammonium, as a useful control of media pH. Furthermore, while high NO3– levels are non-toxic, high NH4+ levels promote physiological abnormalities such as hyperhydricity (Lips et al., 1990; Nezami-Alanagh et al., 2019). The neurofuzzy logic model points out the importance of both nitrogen ions, in combination with BO3– whatever its concentration, suggesting that the main role of NH4+ and NO3– could also be related with their function as pH media control, rather than only nutrients.
The shoot elongation of A. arguta was significantly affected by five ions (Table 9). With the exception of BO3–, the ions that explain the variability in the elongation of the shoots are different from those that intervene in the appearance of new shoots. The model pinpointed the key positive effect of Mid Mg2+ (1.41 < X < 3.47 mM), Low Fe2+ (<0.3 mM), High K+ (>12.37 mM), and Mid BO3– (0.05 < X < 0.12 mM) (Table 9) on shoot length growth. Finally, Mid PO43– (1.17 < X < 2.89) reduced the SL.
Several studies have shown the importance of mesos salts on shoot length. Thus, it has been described that for apricot this parameter is affected by K2SO4 levels (Kovalchuk et al., 2017). Moreover, High mesos (MgSO4⋅7H2O, and KH2PO4) and Low iron are required to enhance red raspberries’ shoot length (Poothong and Reed, 2014, 2015). Accordingly, our results (Table 8), support the same pattern for another fruit tree species, A. arguta. The cause-effect of the specific ions is thus demonstrated, avoiding the ion confounding effect.
Within the limits of the study, to obtain a large leaf area, a combination of High NO3– (>22.71 mM) and Low Na+ (<0.60 mM) concentrations (Table 6, rule 33) should be added to the media. Some authors have demonstrated that High KNO3 and NH4NO3 levels improve the number and size of leaves in pear genotypes (Ibrahim et al., 2008; Reed et al., 2013a). Also, leaf area can be affected by NO3– factor as has been shown for red raspberry (Poothong and Reed, 2016). All these findings agree with our results (Table 8).
Morphophysiological disorders in in vitro cultures are caused by a wide variety of factors (Hazarika, 2006) and avoiding them is one of the greatest challenges in shoots micropropagation. In this study, important abnormalities such as BC and hyperhydricity were observed (Figure 3) and neurofuzzy logic was able to determine the ions that are directly related to the appearance of them.
The effect of three ions on the development of basal callus were pointed out; PO43– × NH4+ and SO42– were included in the factors nitrogen (NH4NO3) and mesos (MgSO4). The model highlighted the positive effect of Mid-High PO43– (>1.17 mM) to favor the production of healthy shoots with moderate or absent callus formation (Figure 2B), particularly when Low NH4+ (<8.25 mM) are used, in agreement with other reports (Niedz and Evens, 2007; Kovalchuk et al., 2018). If Low PO43– is added to the media, necrosis and the formation of big basal callus are significantly promoted, whatever the NH4+ concentration. Finally, SO42– at any concentration tested in this space of design reduces the basal callus formation, generating healthy shoots (High BC). The beneficial effect of high concentrations of these ions on callus formation has been previously demonstrated for other species, such as pear (Reed et al., 2013b), raspberries (Poothong and Reed, 2014), or hazelnut (Akin et al., 2017, 2020). MS medium promotes higher callus formation than WPM and DKV in pistachio culture (Nezami-Alanagh et al., 2019), probably due to its lower and higher levels of NH4+ and SO42–, respectively.
Hyperhydricity is one of the main morpho-physiological disorders in the micropropagation of plants that has been associated with alterations in mineral composition, hormonal imbalances, or the use of gelling agents (Pâques, 1991; Hazarika, 2006). Within the range of the study, kiwiberry also showed hyperhydricity for some treatments (Figure 3B). The hyperhydricity was caused by the interaction of four ions: Cl– × I– and SO42– × BO3–. The combination of High I– (>0.004 mM) and Low BO3– (<0.08 mM) concentrations in the medium avoided hyperhydricity formation, whatever the concentration of Cl– and SO42–, respectively. High percentages of hyperhydricity in Prunus and Dianthus caryophyllus cultures have been associated with high concentrations of Cl– in the culture medium (Quoirin and Lepoivre, 1977; Dantas et al., 2001). In contrast, high concentrations of mesos (CaCl2, KH2PO4, and MgSO4) in pear cultures reduce hyperhydricity (Reed et al., 2013b).
The shoot quality parameter integrates, in some way, both the growth parameters, and the absence of abnormalities and physiological disorders. The neurofuzzy logic model selected five ions as critical factors for the quality of the shoots: K+, SO42–, Fe2+, BO3–, and NO3–. All of them contribute in a way to the growth parameters (SN, SL, or LA), but some are also involved in the appearance of abnormalities as SO42– (BC and H) or BO3– (H).
Rules reveal that good shoot quality is achieved when a High K+ (>12.35 mM) concentration is supplied to the medium along with concentrations of Fe2+ and NO3– within the ranges of 0.10–0.30 mM and 14.35–31.06 mM, respectively, in agreement with other authors for other cultivars (Akin et al., 2017; Kovalchuk et al., 2017) and also with the predictions for the growth parameters of kiwiberry. Medium SO42– (2.85–4.02 mM) concentration is also necessary, since it promotes a high number of shoots and plantlets with low callus formation. Finally, BO3– must be in 0.05–0.12 mM due to its effect on the number of shoots and hyperhydricity (Table 9).
Different ML models based on artificial neural networks, fuzzy logic, genetic algorithms, or gene expression programming algorithms has been previously employed with success for predicting optimal in vitro culture media of fruit tree species such as Prunus (Nezami-Alanagh et al., 2014; Arab et al., 2016, 2018), pear (Jamshidi et al., 2016, 2019), or pistachio rootstocks (Nezami-Alanagh et al., 2017). In this study, ML tools, including ANNs-GA were selected to build a model based on salt composition of culture media for each growth parameter. All of them have good predictability (Train and Test Set R > 70%). The utility of GA allows the estimation of the best combination of salts to obtain a set of desired values for each parameter (maximal growth parameters). The model predicts for a medium of optimal composition (R medium) values of SN, SL, LA, and SQ of 4.8 shoots, 2.6 cm, 39.5 cm2, and 4.4, respectively.
The experimental values obtained for kiwiberry culture using the R medium composition validate those predicted by the model. Even more, the comparison of the results obtained with the R medium and the four media (MS, St, Ha, and B5), used as controls in the validation experiment, shows that the optimized R medium outperforms the others in terms of SL, LA, and SQ. However, the SN parameter appears to be a bit overestimated (4.8 versus 3.6). Only, St basal medium promoted statistically significant (α < 0.001) larger SL and LA.
Differences in mineral composition among all media (Table 9) reveals that St is the poorest media in NH4+ and Cl– but rich in Ca2+, as is other media used for woody plants such as DKW (Driver and Kuniyuki, 1984) and WPM (Lloyd and McCown, 1980), while B5 included low nitrogen but also the lowest mesos (Ca2+, Mg2+, and PO43–) concentration among the media tested, but the highest Na+ (Table 9; Hameg et al., 2018). However, the optimized R medium adjusted at total nitrogen of MS content, but increased 2× all mesos (Ca2+, Mg2+, PO43–, and SO42–) and also increased almost all micros (Cl–, Cu2+, Na+, Co2+, and I–) and iron (Fe2+ and EDTA–) with respect to MS (Table 9). The increasing levels of micronutrients over the level in MS promoted cell growth and morphogenesis in some species (George et al., 2008). With those adjustments, the medium R promoted better results than MS, particularly shoot quality. In conclusion, it is clear that it is the interactions among the ions, rather than their independent effect, that caused the described results. Thus, it is multivariable analysis, rather than single-factor analysis, that is required to really understand media component relationships. Finally, another important fact is that those media (St, Ha, and B5) included different vitamin contents and glycine, not included in this optimization. Furthermore, the PGR effect on organogenesis and growth was not studied, because all media were supplemented with the same PGRs.
The suitability of computer-based tools, such as DOE and ML, as a new strategy to design tissue culture media for kiwiberry has been stated. DOE allowed the plant cell tissue researchers to perform well sampled and efficient experiments in order to save time and plant material. ML tools allowed for the extraction of information to clarify the complex non-linear interactions between variables and understand the effects of single ions on growth parameters and morpho-physiological disorders. A new medium, named R medium, was established with excellent results. The designed R medium differs from MS by reducing up to 20% nitrogen, increasing almost 200% mesos, 100% micros, and 50% iron factor concentrations and performs better for kiwiberry. The R medium also performs better than the B5, Ha, and St media, since although some of them have slight advantages in terms of growth parameters, they also promote more physiological disorders. The R medium could be improved considering the effects of other key components of the media that have not been studied in this work, such as vitamins, PGR, or organic compounds, particularly glycine, that can modulate the effect of ions. They need further additional research.
The original contributions generated for this study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
RH and TA performed micropropagation experiments. RH, TA, and MB performed the statistical analysis. ML and PG contributed to machine learning models supervision. MB and PG conceived and designed the experiments. All authors equally contributed to the discussions for data interpretation and drawing the conclusions. All authors contributed to the writing and agreed to the published version of the manuscript.
The funding for this work was provided by Xunta de Galicia through “Red de Uso Sostenible de los Recursos Naturales y Agroalimentarios” (REDUSO, Grant number ED431D 2017/18) and CITACA Strategic Partnership, Grant number ED431E 2018/07).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors acknowledge the Erasmus Mundus GREENIT grant from the European Commission (reference 2012-2625/001-001-EMA) to RH and the Ph.D. grant from University of Vigo to TA.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpls.2020.554905/full#supplementary-material
Supplementary Figure 1 | Determination coefficient (R2) between the predicted values from the neurofuzzy logic versus experimental values for each factor expressed as determination coefficient (R2): (A) SN, shoot number; (B) SL, shoot length; (C) LA, leaf area; (D) SQ, shoot quality; (E) BC, basal callus formation; and (F) H, hyperhydricity.
Supplementary Figure 2 | Examples of graphical representation of the fuzzyfication process developed by neurofuzzy logic per NO3– (A) and K++ (B) and their respective domains Low–Mid–High and Low–High.
Supplementary Table 1 | Mineral nutrients’ (expressed as salt concentrations) composition of the different culture media based on the five-factor experimental design (0–33) and response values of the parameters (mean and standard deviation) used to characterize plant growth. Original medium composition (bold) used as control. SN, shoot number; SL, shoot length; LA, leaf area; SQ, shoot quality; BC, basal callus; and H, hyperhydricity.
Supplementary Table 2 | Artificial neural network model train set R2 and test set R2. MSE (Mean Squared Error).
Akbas, F. A., Isikalan, C., Namli, S., and Basaran, D. (2007). Micropropagation of kiwifruit (Actinidia deliciosa). Int. J. Agric. Biol. 9, 489–493.
Akin, M., Eyduran, E., Niedz, R. P., and Reed, B. M. (2017). Developing hazelnut tissue culture medium free of ion confounding. Plant Cell Tissue Organ Cult. 130, 483–494. doi: 10.1007/s11240-017-1238-z
Akin, M., Eyduran, E., and Reed, B. M. (2016). Use of RSM and CHAID data mining algorithm for predicting mineral nutrition of hazelnut. Plant Cell Tissue Organ Cult. 128, 303–316. doi: 10.1007/s11240-016-1110-6
Akin, M., Eyduran, S. P., Eyduran, E., and Reed, B. M. (2020). Analysis of macro nutrient related growth responses using multivariate adaptive regression splines. Plant Cell Tissue Organ Cult. 140, 661–670. doi: 10.1007/s11240-019-01763-8
Arab, M. M., Yadollahi, A., Eftekhari, M., Ahmadi, H., Akbari, M., and Khorami, S. S. (2018). Modeling and optimizing a new culture medium for in vitro rooting of G×N15 Prunus rootstock using artificial neural network-genetic algorithm. Sci. Rep. 8:9977. doi: 10.1038/s41598-018-27858-4
Arab, M. M., Yadollahi, A., Shojaeiyan, A., and Ahmadi, H. (2016). Artificial neural network genetic algorithm as powerful tool to predict and optimize in vitro proliferation mineral medium for G × N15 rootstock. Front. Plant Sci. 7:1526. doi: 10.3389/fpls.2016.01526
Arteta, T. A., Hameg, R., Landin, M., Gallego, P. P., and Barreal, M. E. (2018). Neural networks models as decision-making tool for in vitro proliferation of hardy kiwi. Eur. J. Hortic. Sci. 83, 259–265. doi: 10.17660/eJHS.2018/83.4.6
Bhojwani, S. S., and Dantu, P. K. (2013). “Micropropagation,” in Plant Tissue Culture: An Introductory Text, eds S. S. Bhojwani and K. P. Dantu (New Delhi: Springer), 245–274. doi: 10.1007/978-81-322-1026-9_17
Bowen, R. D., Williams, D. H., and Schwarz, H. (1979). The chemistry of isolated cations. Angew Chem. Int. Edit. 18, 451–461. doi: 10.1002/anie.197904511
Bresinsky, A., Körner, C., Kadereit, J. W., Neuhaus, G., and Sonnewald, U. (2013). Strasburger’s Plant Sciences: Including Prokaryotes and Fungi. Berlin: Springer.
Chée, R. (1986). In vitro culture of Vitis: the effects of light spectrum, manganese sulfate and potassium iodide on morphogenesis. Plant Cell Tiss Org Cult. 7, 121–134. doi: 10.1007/BF00043036
Cheng, T. Y. (1975). Adventitious bud formation in culture of Douglas fir (Pseudotsuga menziesii (MIRB.) Franco). Plant Sci. Lett. 5, 97–102. doi: 10.1016/0304-4211(75)90049-8
Colbourn, E., and Rowe, R. (2005). “Neural computing and pharmaceutical formulation,” in Encyclopaedia of Pharmaceutical Technology, eds J. Swarbrick and J. Boylan (New York, NY: Marcel Dekker), 145–157.
Da Silva, F., Nascimento, A., Barbosa, L., and Magalhães, H. (2017). In vitro cultivation of purple basil Ocimum basilicum L. ‘red rubin’ at different levels of salts, charcoal, sucrose and potassium iodine. Aust. J. Crop. Sci. 11, 1137–1145. doi: 10.21475/ajcs.17.11.09.pne624
Dantas, A. K., Majada, J. P., Fernández, B., and Cañal, M. J. (2001). Mineral nutrition in carnation tissue cultures under different ventilation conditions. Plant Growth Regul. 33, 237–243. doi: 10.1023/A:1017542106252
Driver, J. A., and Kuniyuki, A. H. (1984). In vitro propagation of Paradox walnut rootstock. HortScience 19, 507–509.
Epstein, E. (1972). Mineral Nutrition of Plants: Principles and Perspectives. London: John Wiley and Sons, Inc.
Gago, J., Landín, M., and Gallego, P. P. (2010a). Artificial neural networks modeling the in vitro rhizogenesis and acclimatization of Vitis vinifera L. J. Plant Physiol. 167, 1226–1231. doi: 10.1016/j.jplph.2010.04.008
Gago, J., Landín, M., and Gallego, P. P. (2010b). Strengths of artificial neural networks in modeling complex plant processes. Plant Signal Behav. 5, 743–745. doi: 10.4161/psb.5.6.11702
Gago, J., Martínez-Núñez, L., Landín, M., and Gallego, P. P. (2010c). Artificial neural networks as an alternative to the traditional statistical methodology in plant research. J. Plant Physiol. 167, 23–27. doi: 10.1016/j.jplph.2009.07.007
Gago, J., Pérez-Tornero, O., Landín, M., Burgos, L., and Gallego, P. P. (2011). Improving knowledge of plant tissue culture and media formulation by neurofuzzy logic: a practical case of data mining using apricot databases. J. Plant Physiol. 168, 1858–1865. doi: 10.1016/j.jplph.2011.04.008
Gallego, P. P., Gago, J., and Landín, M. (2011). “Artificial neural networks technology to model and predict plant biology process,” in Artificial Neural Networks-Methodological Advances and Biomedical Applications, ed. K. Suzuki (London: IntechOpen), 197–216. doi: 10.5772/14945
Gamborg, O. L., Miller, R. A., and Ojima, K. (1968). Nutrient requirements of suspension cultures of soybean root cells. Exp. Cell Res. 50, 151–158. doi: 10.1016/0014-4827(68)90403-5
George, E. F., Hall, M. A., and Klerk, G.-J. D. (2008). “The components of plant tissue culture media I: macro- and micro-nutrients,” in Plant Propagation by Tissue Culture, eds E. F. George, M. A. Hall, and G. J. D. Klerk (Dordrecht: Springer Netherlands), 65–113. doi: 10.1007/978-1-4020-5005-3_3
Hameg, R. (2019). Computer-Based Tools for Designing Plant Tissue Culture Media. Ph.D. thesis, University of Vigo, Vigo.
Hameg, R., Arteta, T., Gallego, P. P., and Barreal, M. E. (2018). Selecting an efficient proliferation medium for Actinidia arguta ‘Issai’ explants. Acta Hortic. 1218, 565–572. doi: 10.17660/ActaHortic.2018.1218.77
Hameg, R., Gallego, P. P., and Barreal, M. E. (2017). In vitro establishment and multiplication of hardy kiwi (Actinidia arguta ‘Issai’). Acta Hortic. 1187, 51–58. doi: 10.17660/ActaHortic.2017.1187.6
Han, M., Gleave, A. P., and Wang, T. (2010). Efficient transformation of Actinidia arguta by reducing the strength of basal salts in the medium to alleviate callus browning. Plant Biotechnol. Rep. 4, 129–138. doi: 10.1007/s11816-010-0128-1
Hand, C., Maki, S., and Reed, B. M. (2014). Modeling optimal mineral nutrition for hazelnut micropropagation. Plant Cell Tissue Organ Cult. 119, 411–425. doi: 10.1007/s11240-014-0544-y
Harada, H. (1975). In vitro organ culture of Actinidia chinensis PL as a technique for vegetative multiplication. J. Hortic. Sci. 50, 81–83. doi: 10.1080/00221589.1975.11514606
Hazarika, B. N. (2006). Morpho-physiological disorders in in vitro culture of plants. Sci. Hortic. 108, 105–120. doi: 10.1016/j.scienta.2006.01.038
Hildebrandt, A. C., Riker, A. J., and Duggar, B. M. (1946). The influence of the composition of the medium on growth in vitro of excised tobacco and sunflower tissue cultures. Am. J. Bot. 33, 591–597. doi: 10.2307/2437399
Ibrahim, I. A., Nasr, M. I., Mohammedm, B. R., and El-Zefzafi, M. M. (2008). Nutrient factors affecting in vitro cultivation of Stevia rebaudiana. Sugar Tech. 10, 248–253. doi: 10.1007/s12355-008-0044-7
Jamshidi, S., Yadollahi, A., Ahmadi, H., Arab, M. M., and Eftekhari, M. (2016). Predicting in vitro culture medium macro-nutrients composition for pear rootstocks using regression analysis and neural network models. Front. Plant Sci. 7:274. doi: 10.3389/fpls.2016.00274
Jamshidi, S., Yadollahi, A., Arab, M. M., Soltani, M., Eftekhari, M., Sabzalipoor, H., et al. (2019). Combining gene expression programming and genetic algorithm as a powerful hybrid modeling approach for pear rootstocks tissue culture media formulation. Plant Methods 15:136. doi: 10.1186/s13007-019-0520-y
Kabaluk, J., Kempler, C., and Toivonen, P. (1997). Actinidia arguta: Characteristics relevant to commercial production. Fruit Var J. 51, 117–122.
Kavli, T., and Weyer, E. (1994). ASMOD (Adaptive Spline Modelling of Observation Data): some theoretical and experimental results. IEE Colloq (Digest) 136, 1–7.
Kovalchuk, I. Y., Mukhitdinova, Z., Turdiyev, T., Madiyeva, G., Akin, M., Eyduran, E., et al. (2017). Modeling some mineral nutrient requirements for micropropagated wild apricot shoot cultures. Plant Cell Tissue Organ Cult. 129, 325–335. doi: 10.1007/s11240-017-1180-0
Kovalchuk, I. Y., Mukhitdinova, Z., Turdiyev, T., Madiyeva, G., Akin, M., Eyduran, E., et al. (2018). Nitrogen ions and nitrogen ion proportions impact the growth of apricot (Prunus armeniaca) shoot cultures. Plant Cell Tissue Organ Cult. (PCTOC) 133, 263–273. doi: 10.1007/s11240-018-1379-8
Landin, M., and Rowe, R. C. (2013). “Artificial neural networks technology to model, understand, and optimize drug formulations,” in Formulation Tools for Pharmaceutical Development, ed. J. E. Aguilar (Cambridge: Woodhead Publishing), 7–37. doi: 10.1533/9781908818508.7
Landín, M., Rowe, R. C., and York, P. (2009). Advantages of neurofuzzy logic against conventional experimental design and statistical analysis in studying and developing direct compression formulations. Eur. J. Pharm. Sci. 38, 325–331. doi: 10.1016/j.ejps.2009.08.004
Lips, S. H., Leidi, E. O., Silberbush, M., Soares, M. I. M., and Lewis, O. E. M. (1990). Physiological aspects of ammonium and nitrate fertilization. J. Plant. Nutr. 13, 1271–1289. doi: 10.1080/01904169009364151
Lloyd, G., and McCown, B. (1980). Commercially-feasible micropropagation of mountain laurel, kalmia latifolia, by use of shoot-tip culture. Proc. Int. Plant Prop. Soc. 30, 421–427.
Martín-Rejano, E. M., Camacho-Cristóbal, J. J., Herrera-Rodríguez, M. B., Rexach, J., Navarro-Gochicoa, M. T., and González-Fontes, A. (2011). Auxin and ethylene are involved in the responses of root system architecture to low boron supply in Arabidopsis seedlings. Physiol. Plant. 142, 170–178. doi: 10.1111/j.1399-3054.2011.01459.x
Matkowski, A., and Przywara, L. (1995). Callus induction and plant regeneration in vitro in Actinidia. Acta Soc. Bot. Pol. 64, 131–138. doi: 10.5586/asbp.1995.017
Moncaleán, P., Cañal, M. J., Feito, I., Rodríguez, A., and Fernández, B. (1999). Cytokinins and mineral nutrition in Actinidia deliciosa (Kiwi) shoots cultured in vitro. J. Plant Physiol. 155, 606–612. doi: 10.1016/S0176-1617(99)80061-3
Moncaleán, P., Cañal, M. J., Fernández, H., Fernández, B., and Rodríguez, A. (2003). Nutritional and gibberellic acid requirements in kiwifruit vitroponic cultures. In Vitro Cell Dev. Biol. Plant 39, 49–55. doi: 10.1079/IVP2002371
Monette, P. L. (1986). Micropropagation of kiwifruit using non-axenic shoot tips. Plant Cell Tissue Organ Cult. 6, 73–82. doi: 10.1007/BF00037760
Murashige, T., and Skoog, F. (1962). A revised medium for rapid growth and bio assays with tobacco tissue cultures. Physiol. Plant 15, 473–497. doi: 10.1111/j.1399-3054.1962.tb08052.x
Nasib, A., Ali, K., and Khan, S. (2008). An optimized and improved method for the in vitro propagation of kiwifruit (Actinidia deliciosa) using coconut water. Pak J. Bot. 40, 2355–2360.
Nezami-Alanagh, E., Garoosi, G. A., Haddad, R., Maleki, S., Landín, M., and Gallego, P. P. (2014). Design of tissue culture media for efficient Prunus rootstock micropropagation using artificial intelligence models. Plant Cell Tissue Organ Cult. 117, 349–359. doi: 10.1007/s11240-014-0444-1
Nezami-Alanagh, E., Garoosi, G. A., Landín, M., and Gallego, P. P. (2018). Combining DOE with neurofuzzy logic for healthy mineral nutrition of pistachio rootstocks in vitro culture. Front. Plant Sci. 9:1474. doi: 10.3389/fpls.2018.01474
Nezami-Alanagh, E., Garoosi, G.-A., Landín, M., and Gallego, P. P. (2019). Computer-based tools provide new insight into the key factors that cause physiological disorders of pistachio rootstocks cultured in vitro. Sci. Rep. 9:9740. doi: 10.1038/s41598-019-46155-2
Nezami-Alanagh, E., Garoosi, G. A., Maleki, S., Landín, M., and Gallego, P. P. (2017). Predicting optimal in vitro culture medium for Pistacia vera micropropagation using neural networks models. Plant Cell Tissue Organ Cult. 129, 19–33. doi: 10.1007/s11240-016-1152-9
Niedz, R. P., and Evens, T. J. (2006). A solution to the problem of ion confounding in experimental biology. Nat. Methods 3, 417–417. doi: 10.1038/nmeth0606-417
Niedz, R. P., and Evens, T. J. (2007). Regulating plant tissue growth by mineral nutrition. In Vitro Cell Dev. Biol. Plant 43, 370–381. doi: 10.1007/s11627-007-9062-5
Niedz, R. P., and Evens, T. J. (2016). Design of experiments (DOE)—history, concepts, and relevance to in vitro culture. In Vitro Cell Dev. Biol Plant 52, 547–562. doi: 10.1007/s11627-016-9786-1
Nowak, B., Miczyński, K., and Hudy, L. (2007). The effect of total inorganic nitrogen and the balance between its ionic forms on adventitious bud formation and callus growth of ‘Wêgierka Zwykła’ plum (Prunus domestica L.). Acta Physiol. Plant 29, 479–484. doi: 10.1007/s11738-007-0058-x
Olden, J. D., Lawler, J. J., and Poff, N. L. R. (2008). Machine learning methods without tears: a primer for ecologists. Q. Rev. Biol. 83, 171–193. doi: 10.1086/587826
Pâques, M. (1991). Vitrification and micropropagation: causes, remedies and prospects. Acta Hortic. 289, 283–290. doi: 10.17660/ActaHortic.1991.289.76
Paradela, M., De Paz, P., and Gallego, P. (2001). Variability in the organogenic response of kiwi from material undergoing micropropagation. Melhoramiento 37, 79–83.
Poothong, S., and Reed, B. M. (2014). Modeling the effects of mineral nutrition for improving growth and development of micropropagated red raspberries. Sci. Hortic. 165, 132–141. doi: 10.1016/j.scienta.2013.10.040
Poothong, S., and Reed, B. M. (2015). Increased CaCl2, MgSO4, and KH2PO4 improve the growth of micropropagated red raspberries. In Vitro Cell Dev. Biol. Plant 51, 648–658. doi: 10.1007/s11627-015-9720-y
Poothong, S., and Reed, B. M. (2016). Optimizing shoot culture media for Rubus germplasm: the effects of NH4+, NO3–, and total nitrogen. In Vitro Cell Dev. Biol Plant 52, 265–275. doi: 10.1007/s11627-016-9750-0
Quoirin, M., and Lepoivre, P. (1977). Improved media for in vitro culture of Prunus sp. Acta Hortic. 77, 437–442. doi: 10.17660/actahortic.1977.78.54
Ramage, C. M., and Williams, R. R. (2002). Mineral nutrition and plant morphogenesis. In Vitro Cell Dev. Biol. Plant 38, 116–124. doi: 10.1079/IVP2001269
Reed, B. M., and Hummer, K. E. (1995). “Conservation of germplasm of strawberry (Fragaria species),” in Cryopreservation of Plant Germplasm I Biotechnology in Agriculture and Forestry, ed. Y. P. S. Bajaj (Berlin: Springer), 354–370. doi: 10.1007/978-3-662-03096-7_25
Reed, B. M., Wada, S., DeNoma, J., and Niedz, R. P. (2013a). Improving in vitro mineral nutrition for diverse pear germplasm. In Vitro Cell Dev. Biol. Plant 49, 343–355. doi: 10.1007/s11627-013-9504-1
Reed, B. M., Wada, S., DeNoma, J., and Niedz, R. P. (2013b). Mineral nutrition influences physiological responses of pear in vitro. In Vitro Cell Dev. Biol. Plant 49, 699–709. doi: 10.1007/s11627-013-9556-2
Revilla, M. A., Rey, M. A., Gonzalez-Rio, F., Gonzalez, M. V., Diaz-Sala, C., and Rodriguez, R. (1992). “Micropropagation of Kiwi (Actinidia spp.),” in High-Tech and Micropropagation II, ed. Y. P. S. Bajaj (Berlin: Springer), 399–423. doi: 10.1007/978-3-642-76422-6_21
Seelye, J. F., and Butcher, S. M. (1991). In vitro response of Actinidia leaf and callus tissue to thidiazuron. N. Z. J. Crop. Hortic. Sci. 19, 447–450. doi: 10.1080/01140671.1991.10422891
Shao, Q., Rowe, R. C., and York, P. (2006). Comparison of neurofuzzy logic and neural networks in modelling experimental data of an immediate release tablet formulation. Eur. J. Pharm. Sci. 28, 394–404. doi: 10.1016/j.ejps.2006.04.007
Sonnewald, U. (2013). “Physiology of metabolism,” in Strasburger’s Plant Sciences: Including Prokaryotes and Fungi, eds A. Bresinsky, C. Körner, J. W. Kadereit, G. Neuhaus, and U. Sonnewald (Berlin: Springer), 239–409. doi: 10.1007/978-3-642-15518-5_5
Sotiropoulos, T. E., and Dimassi, K. N. (2004). Response to increasing rates of boron and NaCl on shoot proliferation and chemical composition of in vitro kiwifruit shoot cultures. Plant Cell Tissue Organ Cult. 79, 285–289. doi: 10.1007/s11240-004-4609-1
Standardi, A. (1981). Micropropagazione dell’ Actinidia chinensis Pl. mediante coltura in vitro di apici meristematici. Frutticoltura 43, 23–27.
Wada, S., Niedz, R. P., DeNoma, J., and Reed, B. M. (2013). Mesos components (CaCl2, MgSO4, KH2PO4) are critical for improving pear micropropagation. In Vitro Cell Dev Biol Plant. 49, 356–365. doi: 10.1007/s11627-013-9508-x
Keywords: algorithms, artificial intelligence, kiwiberry, modeling, mineral nutrition, plant tissue culture, physiological disorders
Citation: Hameg R, Arteta TA, Landin M, Gallego PP and Barreal ME (2020) Modeling and Optimizing Culture Medium Mineral Composition for in vitro Propagation of Actinidia arguta. Front. Plant Sci. 11:554905. doi: 10.3389/fpls.2020.554905
Received: 23 April 2020; Accepted: 01 December 2020;
Published: 23 December 2020.
Edited by:
Yiannis Ampatzidis, University of Florida, United StatesReviewed by:
Hamed Ahmadi, Tarbiat Modares University, IranCopyright © 2020 Hameg, Arteta, Landin, Gallego and Barreal. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pedro P. Gallego, cGdhbGxlZ29AdXZpZ28uZXM=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.