- 1College of Agriculture, Northeast Agricultural University, Harbin, China
- 2Institute of Crop Science, Chinese Academy of Agricultural Sciences, Beijing, China
Maize yield components including row number, kernel number per row, kernel thickness, kernel width, kernel length, 100-kernel weight, and volume weight affect grain yield directly. Previous studies mainly focused on dissecting the genetic basis of per se performances for yield-related traits, but the genetic basis of general combining ability (GCA) for these traits is still unclear. In the present study, 328 RILs were crossed as males to two testers according to the NCII mating design, resulting in a hybrid panel composed of 656 hybrids. Both the hybrids and parental lines were evaluated in four environments in 2015 and 2016. Correlation analysis showed the performances of GCA effects were significantly correlated to the per se performances of RILs for all yield-related traits (0.17 ≤ r ≤ 0.64, P > 0.01). Only 17 of 95 QTL could be detected for both per se performances of RILs and GCA effects for eight yield-related traits. The QTL qKN7-1 and qHKW1-3, which could explain more than 10% of the variation in the GCA effects of KN and HKW, were also detected for per se performances for the traits. The pleiotropic loci qRN3-1 and qRN6, which together explained 14.92% of the observed variation in GCA effects for RN, were associated with the GCA effects of KW and HKW, but not with per se performances for these traits. In contrast, Incw1, which was related to seed weight in maize, was mapped to the region surrounding MK2567 at the qHKW5-2 locus, but no GCA effect was detected. The QTL identified in present study for per se performances and corresponding GCA effects for yield-related traits might be useful for maize hybrid breeding.
Introduction
Maize (Zea mays L.), one of the most extensively grown crops worldwide, is important for both animal feed and as a bioenergy feedstock. Crop breeders and farmers face the daunting task of meeting increasing demand for food and feed. The improvement of maize yield depends mainly on the exploitation of heterosis in the F1 resulting from the hybridization of genetically diverse parents. However, the yield of hybrids cannot be predicted by the performance of their parents per se (Hallauer, 1990), but depends largely on their combining ability, or the potential to generate progenies exhibiting high heterosis. Thus, understanding the genetic basis of their combining ability is essential for utilizing heterosis and selecting elite inbred lines in hybrid breeding.
Combining ability can be divided into general combining ability (GCA) and specific combining ability (SCA). The genetic variances of GCA and SCA were first estimated using a diallel cross-mating design (Griffing, 1956). GCA is estimated by the average performance of parents, while SCA is measured as the deviations of hybrid performance from that predicted from the GCA of the parents (Sprague and Tatum, 1942; Xu, 2010). GCA is primarily the result of additive allelic effects of high-heritability traits, and SCA mainly results from non-additive effects including dominance and epistasis (Reif et al., 2007). Due to their low heritability and interactions with the environment, the non-additive effects usually are difficult to resolve in progeny (Lu, 1999). Therefore, during the crop breeding process, the contribution of GCA to test-cross hybrid values and inbred line development is greater than that of SCA (Schrag et al., 2006; Fischer et al., 2010; Grieder et al., 2012).
Combining ability estimates have been used to anticipate improvement due to hybridization and selection in maize breeding (Khalil et al., 2010; Issa et al., 2018), but further exploration will be required to dissect the genetic basis of combining ability (Gichuru et al., 2017). With the development of molecular markers (e.g., AFLP, RFLP, SSR), the genetic basis of combining ability effects was estimated by QTL mapping (Liu et al., 2004; Basbag et al., 2007; Shukla and Pandey, 2010; Giraud et al., 2017; Zhou Q. et al., 2017; Seye et al., 2019). In maize, 23 QTL related to the GCA effects of 10 yield-related traits were identified using a linkage map constructed from 146 pairs of SSR primers using a double haploid (DH) population (Gu, 2007). A total of 21 loci for SCA and 56 significant loci for GCA have been identified for five yield-related traits in multiple environments using a set of testcrosses with introgression lines (ILs) (Qi et al., 2013). Ghd7 and OsPRR37 were confirmed to affect the GCA effects of three yield-related traits in rice by linkage analysis (Liu et al., 2015). These studies indicated that using molecular markers to construct linkage maps was an effective way to dissect the genetic basis of combining ability. However, the resolution of those genetic maps based on traditional molecular markers was relatively low. Fine-scale mapping was more time-consuming, identifying QTL with minimal effects was more challenging (Holland, 2007). Next-generation sequencing technologies for constructing high-density genetic maps for large QTL mapping population are more efficient and improve mapping accuracy (Chen et al., 2014; Zhou et al., 2016). For example, qPH5-1 and qPH10, which are located on chromosomes 5 and 10, respectively, were validated for maize plant height-related traits using a high-density genetic linkage map containing 4602 bin markers developed using genotyping by sequencing (GBS). The genotype at the qPH10 locus was only associated with GCA effects, while that at qPH5-1 was associated with both per se performances and corresponding GCA effects for the traits (Zhou et al., 2018). A recent genome-wide association study (GWAS) identified 34 significant associations between GCA and SCA, and agronomic traits in rice, and suggested the accumulation of desirable Ghd8, GS3, and qSSR4 alleles in parental lines with high GCA (Chen et al., 2019). Chromosome segment substitution lines (CSSLs) were elite genetic resources for identifying naturally occurring favorable alleles. A total of 40 significant GCA loci were identified for 14 grain and stover yield-related traits in millet using testcross hybrid populations of 85 CSSLs (Basava et al., 2019). Differing from the trait values obtained by observation and measurement, GCA effects were statistical values, and the feasibility of analyzing the genetic basis of GCA effects by molecular markers has been proved theoretically and practically.
Grain yield is a complex quantitative trait that cannot be improved by directly selecting individual plants with excellent performance. This is especially true for heterozygous maize, for which yield gains largely depend on the utilization of heterosis (Messmer et al., 2009). Previous studies have identified highly significant genetic correlations between grain yield and yield components, including kernel number per ear, kernel weight, and volume weight (Ahmed et al., 1992; Zhang et al., 2007; Li C.H. et al., 2013; Liu et al., 2014; Liu C.L. et al., 2016; Liu et al., 2015). The factors, kernel number per row (KN) and kernel row number (RN), are the two components of kernel number per ear. Kernel weight is mainly determined by kernel thickness (KT), kernel width (KW), and kernel length (KL). Comparing with grain yield, these yield components exhibit higher heritability (Messmer et al., 2009; Li C.H. et al., 2013; Raihan et al., 2016). Although numerous QTL have been identified to associate with per se performances for yield-related traits in maize, few studies concentrate on the genetic basis of the GCA for yield-related traits (Zhang et al., 2017; Zhou Q. et al., 2017; Lan et al., 2018). Therefore, it is essential to study the genetic basis of yield components and their combining abilities, especially GCA, for the improvement of grain yield.
In the present study, a NCII mating design was used to analysis the GCA effects of eight yield-related traits in 328 RILs and two test cross-populations by linkage analysis across four environments. The objectives of this study were to (a) analyze the correlation between per se performances and GCA effects for yield-related traits; (b) identify stable QTL for GCA of these traits; (c) compare the genetic basis of per se performances and GCA effects for these traits and discuss the utility of these QTL for maize breeding.
Materials and Methods
Materials
A set of 365 RILs and two testers were analyzed in the present study. These RILs were derived from a cross between Ye478 (as female) and Qi319 (as male). Ye478 and Qi319, two elite inbred lines, were selected from the PA (Partner A) and PB (Partner B) heterotic groups, respectively. The two testers were Chang7-2 and Mo17, which belong to the SPT and Lancaster heterotic groups, respectively. Chang7-2, an inbred line derived from Huangzao4, was extensively used in the Yellow and Huai River maize-growing zone of China. Mo17, an elite inbred line derived from Lancaster Sure Crop, has been used widely in commercial maize breeding. Each RIL was crossed as male to the two testers according to the NCII mating design. A hybrid panel composed of 656 hybrids was thus obtained by 328 RILs that were successfully crossed with both Chang7-2 and Mo17, as sufficient seed was not produced from 74 crosses. The Chang7-2 testcross population and Mo17 testcross population were defined as TC and TM, respectively. The four F1 hybrids that were produced by crossing the Ye478 and Qi319 to the two testers were used as controls.
Field Experiments
Phenotypic performance was evaluated in 2015 and 2016 at Shijiazhuang (37.27°N, 113.30°E) and Xinxiang (35.19°N, 113.53°E) in China. Both of the locations for evaluating the phenotypic performance of the parental lines and hybrids were located in the summer maize-growing regions of China. All of the experimental materials were arranged in a randomized incomplete block design with two-row plots and two replicates at each location. In each row, 17 plants were planted with 25 cm of space between each plant, 60 cm of space between rows, and a final density of 60,000 plants/ha. RILs and testcrosses were planted separately to avoid the competitive effects. Fields were managed according to the standard agronomic practices for maize.
Evaluation of Phenotypes
At harvest stage, the middle 10 open-pollinated ears in the central row of each plot were sampled for phenotypic evaluation using standard procedures after air-drying. Eight agronomic traits were measured in this study, including kernel thickness (KT, mm), kernel width (KW, mm), kernel length (KL, mm), 100-kernel weight (HKW, g), row number (RN), kernel number per row (KN), volume weight (VW), and yield per plot (YP, g). An electronic digital caliper with a precision of 0.1 mm was used to measure the former three traits, and these traits were scored by randomly selecting 10 kernels from the middle of each ear. HKW was measured as three repeated measurements of 100 kernels mixed from 10 ears per plot. RN, KN, VW, and YP were determined from 10 randomly selected ears. The average measured value of three replications for each trait in each environment represents the performance for each plot.
Statistical Analysis of Phenotypic Data
The “‘lme” function in the R package “lme4” was applied to correct the raw phenotypic data using best linear unbiased estimation (BLUE) using the formula: Pheno ∼1 + Line + (1| Year) + (1| Loc) + (1| Line: Year) + (1| Line: Loc) + (1| Rep), where Pheno represents trait data; Line represents the phenotypic data of inbred lines or hybrids; Year represents the planting year; Loc represents the planting location; and Rep represents the replications in each environment. Line is considered a fixed effect, while the other factors are considered random effects: indicates an interaction between factors, and | separates the model matrix and grouping factors. Estimates of phenotypic distributions, correlations, and part of these QTL analyses were based on BLUE.
The broad-sense heritability (H2) for each of the traits analyzed in the RILs across multiple environments was estimated according to Knapp (Knapp et al., 1985) using the modified formula: H2 = σ2G/(σ2G + σ2GL/L + σ2GY/Y + σ2GLY/L × Y + σ2E/L × Y × R), where σ2G is the genotypic variance; σ2GL,σ2GY and σ2GLY are estimates of genotype × location interaction variance, genotype × year interaction variance, and genotype × location × year interaction variance; σ2E is the error variance; L is the number of location; Y is the number of year; and R refers to the number of replications per location, respectively. All of these variances were estimated using the “ASReml” R package. The genetic variance effects of GCA and SCA of both testcross populations in four environments were evaluated using a joint linear mixed model (Butler et al., 2007), as follows:
where Yijklm indicates the phenotypic value of the hybrid derived from the kth female and the lth male evaluated in the jth block and the ith location of the mth year; μ refers to the overall mean, Li is the ith location effect; Ym is the mth year effect; and Bj(im) indicates the jth block within the ith location and mth year. GCAk and GCAl are the effects of kth female and the lth male, respectively; SCAkl is the effect of the kth and the lth parents; L × GCAik, L × GCAil, L × SCAikl indicates the location interaction effect by GCAik, GCAil, and SCAikl, respectively; Y × GCAik, Y × GCAil, Y × SCAikl indicates the year interaction effect by GCAik, GCAil, and SCAikl, respectively; L × Y × GCAik, L × Y × GCAil, L × Y × SCAikl indicates the location and the year interaction effect by GCAik, GCAil, and SCAikl, respectively; and Eijklm is random error. Li and the remaining factors are considered random effects.
Linkage Mapping and QTL Detection
A high-density linkage map was constructed for a population of 365 F11 RILs using genotyping by sequencing (GBS) technology on an Illumina 2500 platform and the raw sequence reads of these lines are public on NCBI (Accession: PRJNA627044)1. We developed a total of 88,268 SNP markers from SNP sites that were heterozygous between parental lines and used them to genotype this population. Finally, 4602 high-quality bin markers were obtained using the sliding window (Zhou et al., 2016). The map spanned total genetic distance of 1533.72 cM with an average distance between markers of 0.33 cM (Supplementary Figure S1). The QTL locations of the per se performances and GCA effects for eight yield-related traits in each of four environments were determined using a composite-interval mapping (CIM) method with the R/qtl package (Broman et al., 2003), and a joint analysis across all environments was performed using BLUE. The threshold for identifying a significant QTL was defined by a logarithm of the odds (LOD) score of 3.0 calculated using 1000 permutations (P < 0.05). The QTL confidence interval was considered as genomic regions within a 1.5-LOD drop from the peak LOD scores. The proportion of phenotypic variation explained by each QTL was calculated using the fitqtl function in the R “qtl” package. QTL detected in different environments for different traits with overlapping confidence intervals or whose peaks were within 20 Mb of each other were considered as pleiotropic QTL (Frascaroli et al., 2007).
Results
Performance of RILs and Testcross Populations for Yield-Related Traits
The means and ranges of eight yield-related traits measured in the RILs and their testcross progenies were shown in Figure 1. The TC and TM values for most of the traits except for KT and VW were significantly higher than the corresponding values in the RIL population (P < 0.01). The percentages of testcross progenies were with higher values than RILs for these traits ranged from −22.98% (KT) to 141.46% (YP) for TC and −12.36% (KT) to 130.13% (YP) for TM. Notably, the percentages for KN and YP were 61.55% and 141.46% for TC and 66.48% and 130.13% for TM (Figure 1A), indicating that KN and YP showed apparent heterosis in these two testcross populations. In addition, percentages for KT were −22.98% for TC and −12.36% for TM, suggesting that the average performances of RILs were higher than testcross progenies for KT. The GCA effects of eight yield-related traits in RILs were normally distributed with the average around zero, and the variations for the GCA effects of YP and VW were larger than those for the GCA effects of other traits (Supplementary Table S1). The value of all the traits in the RIL population also showed a continuous and normal distribution (Figure 1B), indicating the presence of complex underlying genetic mechanisms for per se performances and GCA effects for yield-related traits.
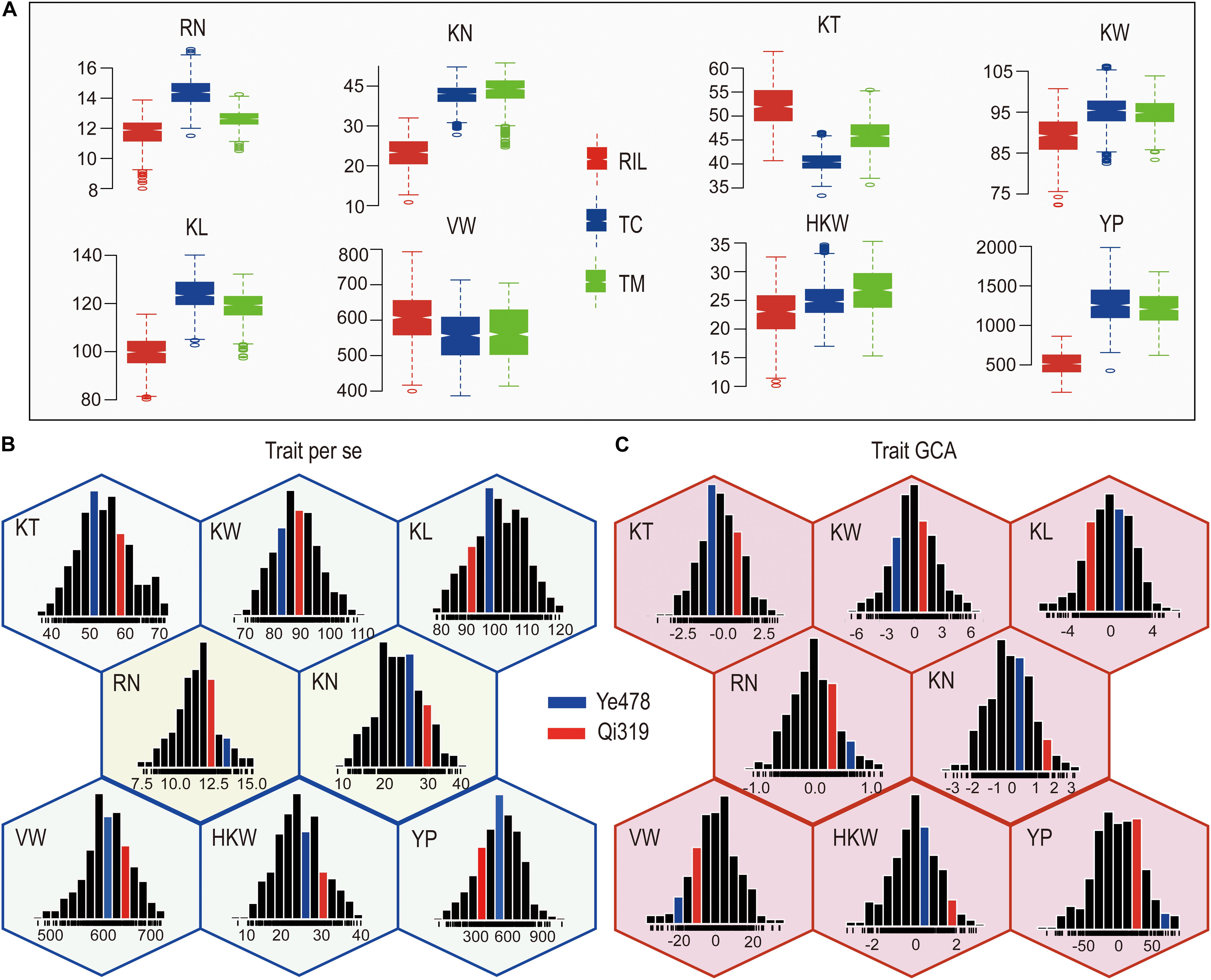
Figure 1. Phenotypic variation in eight traits in different populations. (A) The means and ranges of eight yield-related traits in the RILs and their testcross progenies. (B,C) Phenotypic variation of per se performances and their GCA effects for eight yield-related traits. The histograms inside each hexagon indicate the distribution of phenotypic values for each trait. RN, Row number; KN, Kernel number per row; KT, Kernel thickness; KW, Kernel width; KL, Kernel length; HKW, 100-kernel weight; VW, Volume weight; YP, Yield per plot.
Correlation Analysis Between per se Performance and Corresponding GCA Effects for Yield-Related Traits and Variance Analysis of Combining Ability
The correlations between the phenotypic values of per se performances and the corresponding GCA effects for yield-related traits were shown in Table 1. Most of the traits in RILs were significantly correlated with each other. HKW was significantly positively correlated with KT (0.56, P < 0.01), KW (0.77, P < 0.01), and KL (0.42, P < 0.01), suggesting that kernel size was a major component of kernel weight. However, HKW was significantly negatively correlated with RN and KN, which indicated tradeoffs between HKW and RN or KN. YP was significantly positively correlated with all of the other traits (0.15–0.71, P < 0.01) except for KT (-0.37, P < 0.01), but especially with RN (0.41, P < 0.01), KN (0.71, P < 0.01), and KL (0.55, P < 0.01). The correlations between the GCA effects of YP and the GCA effects of KN, KL, and HKW were relatively strong, indicating that it was important to select inbred lines with relatively high GCA effects for these traits. In addition, significant positive correlations were observed between GCA effects and per se performances for all eight yield-related traits (0.17–0.64, P < 0.01) (Table 2), for which strong correlations were detected for RN (0.64, P < 0.01), KT (0.54, P < 0.01), KW (0.62, P < 0.01), and HKW (0.53, P < 0.01).
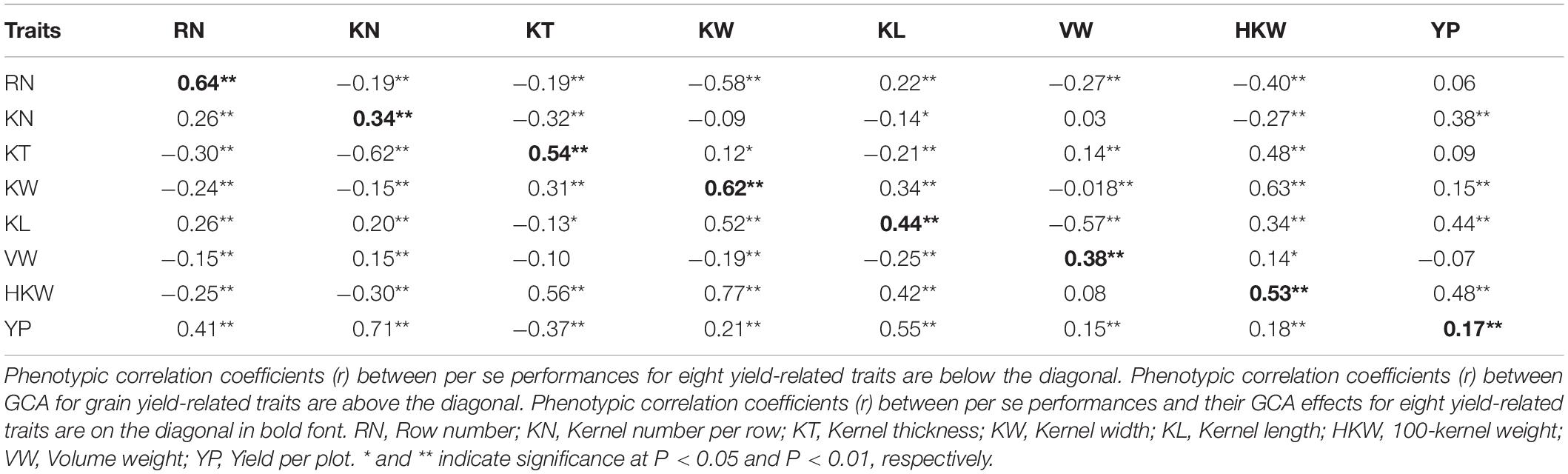
Table 1. Phenotypic correlation coefficients (r) between per se performances and GCA effects for eight yield-related traits.
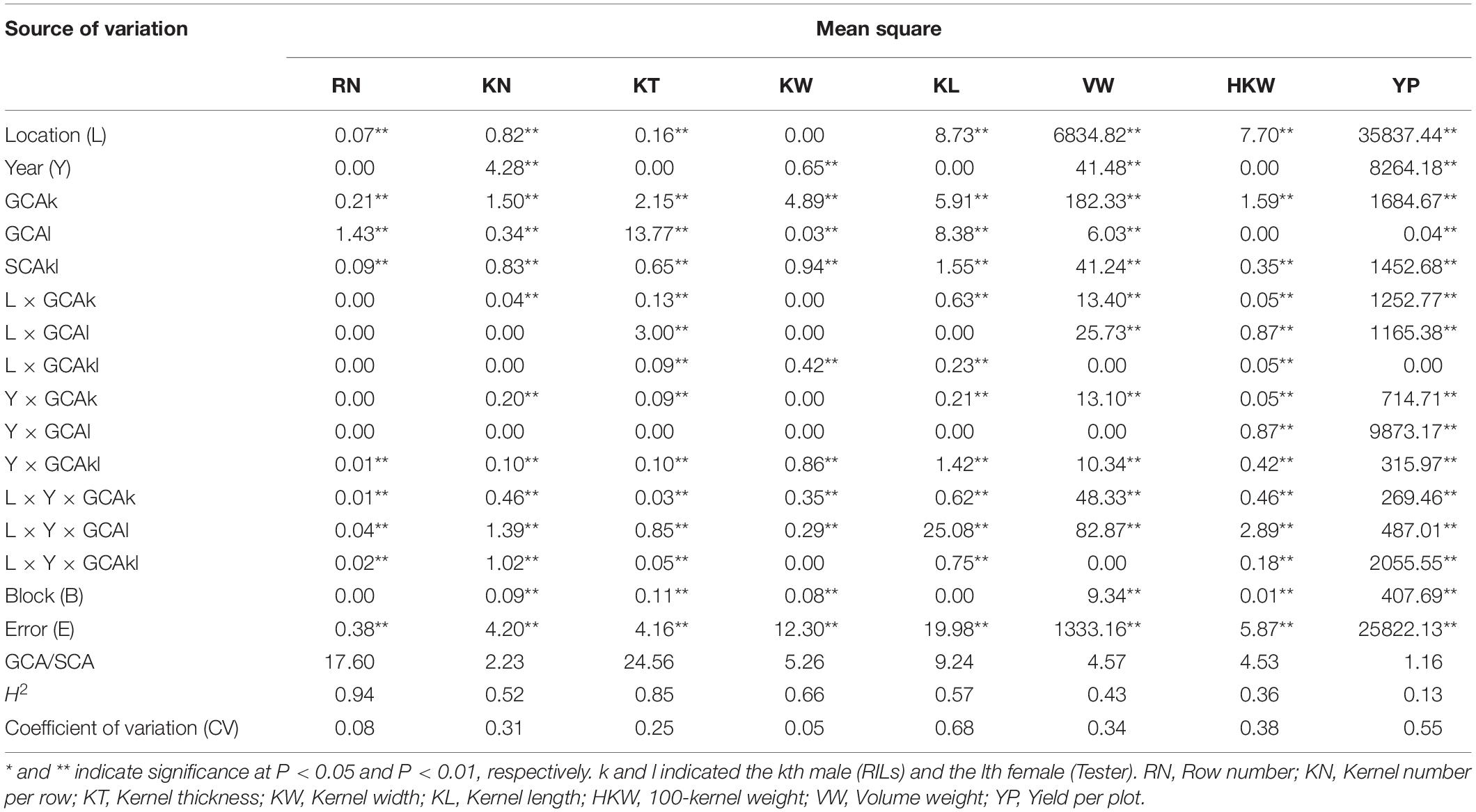
ANOVA revealed highly significant differences among genotypes, environments, and the genotype-by-environment interactions for these eight yield-related traits (Table 2). Broad-sense heritability (H2) was high for most of the yield-related traits [ranging from 0.74 (HKW) to 0.86 (RN, KT)], suggesting high heritability for these traits, except for VW and YP. The variances for GCAk and SCAkl were significant for all of the traits, suggesting that both of these genetic effects were important for controlling the inheritance of the traits (Table 3). Higher ratios of σ2GCA/σ2SCA [1.16 (YP) to 24.56 (KT)] suggesting that the predominance of additive gene action was more important for the expression of these yield-related traits, especially for RN (17.60) and KT (24.56).
QTL Detection
QTL for per se Performances for Eight Grain Yield Related Traits
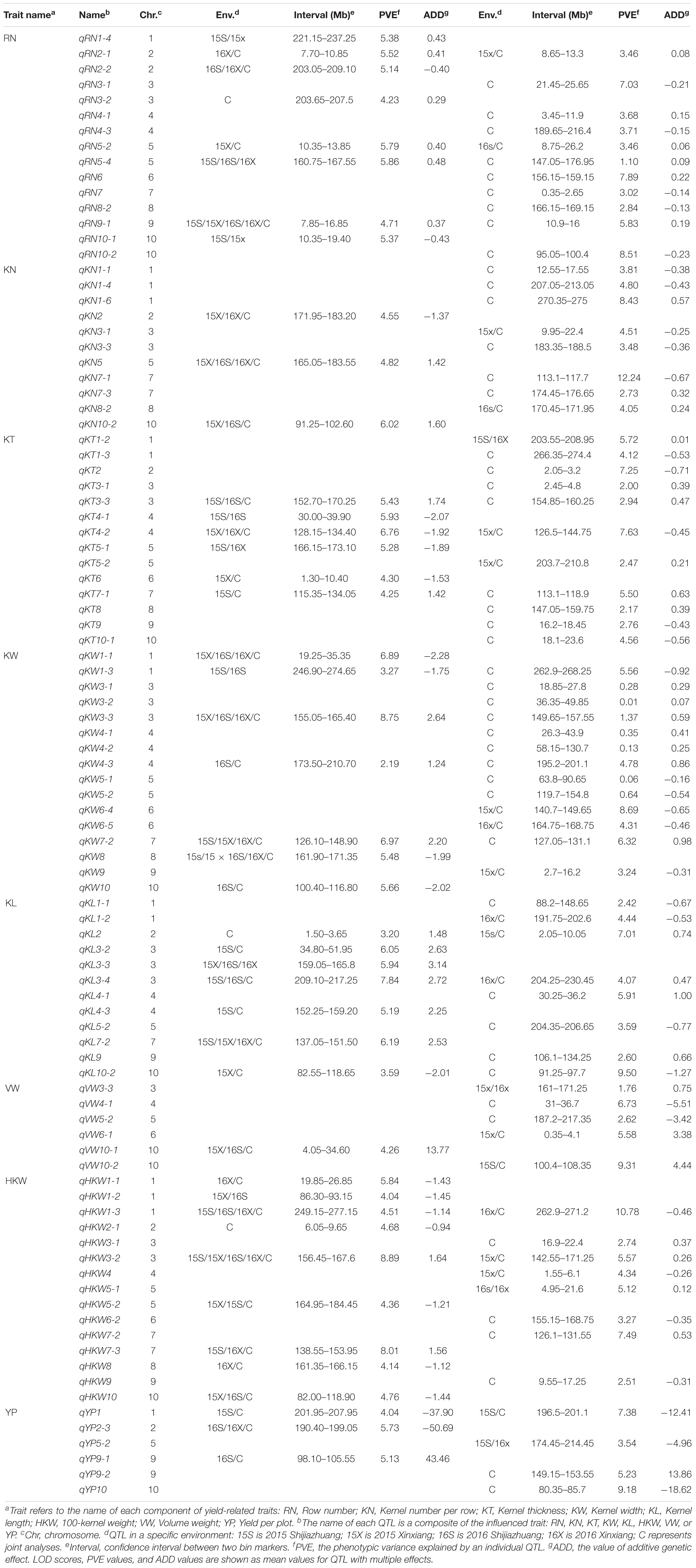
To better understand the genetic basis of per se performances and GCA effects for eight yield-related traits, QTL mapping in four environments (Supplementary Tables S3, S4) and joint analyses were performed in the present study (Table 4). The results of the joint analyses showed that a total of 36 loci were identified for per se performances for eight yield-related traits (Table 4). A total of 121 significant QTL were associated with per se performances for these traits in four environments, and 26 of these QTL were detected in multiple environments (Figure 2A). The QTL were distributed over all 10 maize chromosomes, ranging from six on chromosome 9–19 on chromosome 3 (Figure 2B). Between 11 and 23 significant QTL were identified for RN, KN, KT, KW, KL, and HKW, while only 10 significant QTL were detected for VW, which might be due to the low heritability of VW. All of these QTL could individually explain between 2.46 and 12.71% of the variation in particular traits (Figure 2C). The confidence intervals for these QTL spanned physical distances ranging from 2.15 to 18.85 Mb, with an average of 5.52 Mb, with a mode for physical distance of about 5 Mb (Figure 2C). Notably, qHKW3-2 explained the greatest proportion of phenotypic variation for HKW and co-localized with QTL for three grain morphological traits, including qKT3-3, qKW3-3, qKL3-3, and all of these QTL were identified in at least two environments. Qi319 alleles had positive effects on performance for KT, KL, KW, and HKW (Supplementary Table S3).
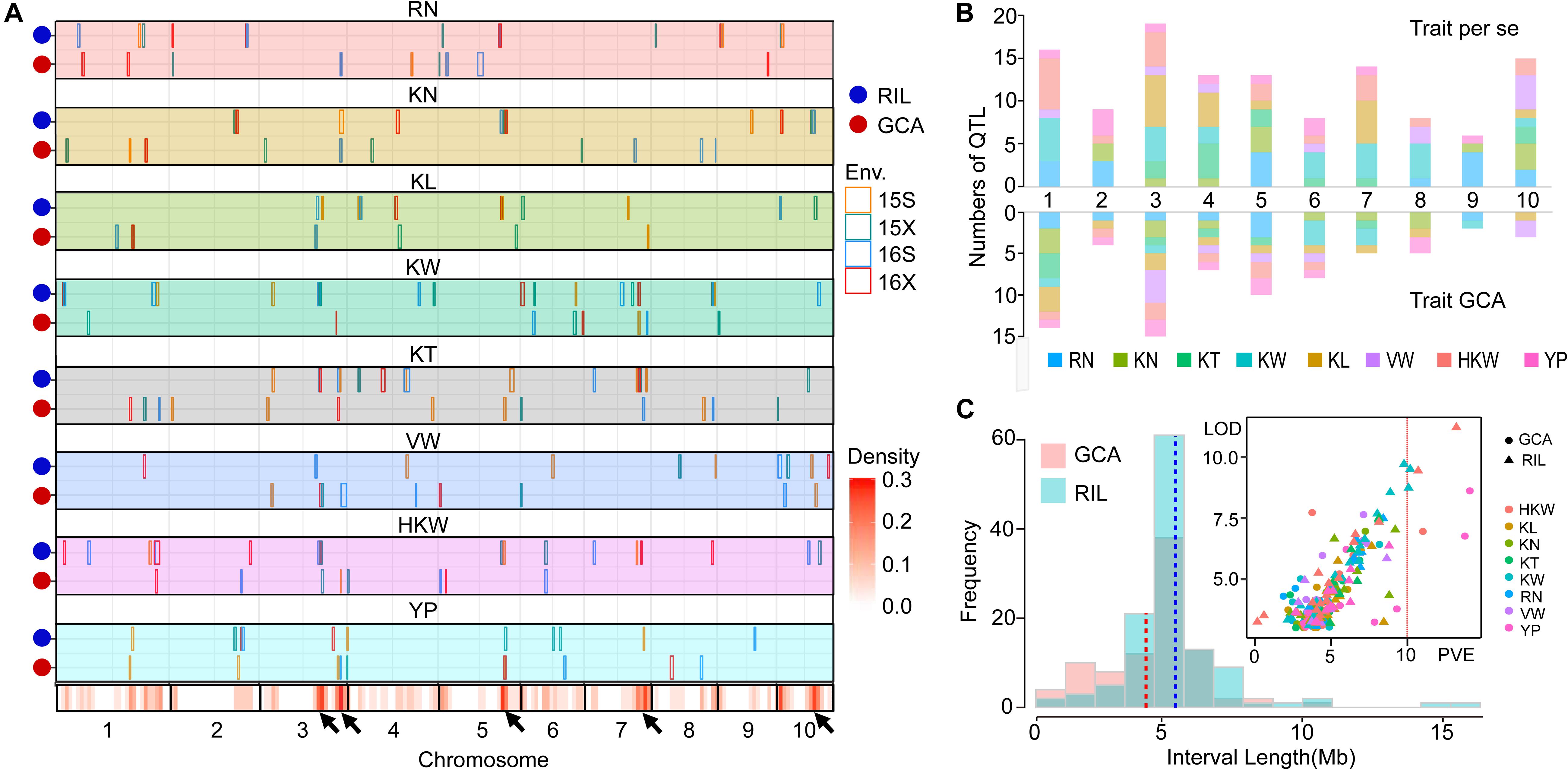
Figure 2. Chromosomal distributions of yield-related QTL identified in the present study. (A) QTL regions represented by the confidence intervals for linkage mapping across the maize genome from each dataset are shown as boxes. The width of the boxes reflects the length of the confidence interval. The different colors of the boxes indicate the four environments, respectively. Orange, 2015 Shijiazhuang; green, 2015 Xinxiang; blue, 2016 Shijiazhuang; and red, 2016 Xinxiang. The x-axis indicates genetic positions across the maize genome in Mb. The heatmap under the x-axis illustrates the density of grain yield-related related QTL across the genome. The black arrows point out the QTL hotspots. RN, Row number; KN, Kernel number per row; KT, Kernel thickness; KW, Kernel width; KL, Kernel length; HKW, 100-kernel weight; VW, Volume weight; YP, Yield per plot. (B) The numbers of QTL distributed on each chromosome for the eight yield-related traits identified for per se performances of traits (above) and their GCA effects (below). (C) Frequency distribution of QTL interval length and the variance explained by each QTL identified for per se performances of traits and their GCA effects. PVE, phenotypic variation explained.
QTL for GCA Effects of Eight Grain Yield-Related Traits
Joint analyses identified a total of 64 loci associated with GCA effects of eight grain yield-related traits. A total of 74 significant QTL for eight yield-related traits were associated with GCA effects in four environments, but only four of them were detected in multiple environments (Figure 2A). These QTL were distributed over all 10 maize chromosomes, and two (chromosome 9) to 15 (chromosome 3) QTL were detected on each chromosome. Seven to 11 significant QTL for GCA effects were identified for each trait (Figure 2B). All of these QTL could individually explain from 0.04 to 9.10% of the observed variation in a single environment (Figure 2C). The confidence intervals for these QTL spanned physical distances from 0.70 to 14.55 Mb, with an average of 4.72 Mb, a mode near 5 Mb (Figure 2C). The two QTL qKN7-1 and qHKW1-3 could explain more than 10% of the variation in GCA effects for KN and HKW, respectively (Table 4). Notably, the stable QTL qHKW1-3 explained 10.78% of the phenotypic variation in the GCA effects of HKW and co-localized with the QTL for the GCA effects of four grain morphological traits: qKT1-3, qKW1-3, qKL1-4, and qKN1-6. Qi319 alleles had a negative effect on KT, KW, KL, and HKW GCA effects, but had a positive effect on GCA effects for KN. These results also confirmed the close genetic correlations observed between the GCA effects of grain morphological traits, which might result from pleiotropy.
Comparison of the Genetic Basis Between per se Performances and GCA of Traits
In order to improve the reliability of our results, only the loci identified in multiple environments and the results of the joint analyses were used for subsequent analysis. A total of 95 QTL were identified that affected the per se performances and corresponding GCA effects for eight yield-related traits in Figure 3A and Table 4. A total of 17 of these QTL were detected for both per se performances and corresponding GCA effects for these traits. Zero (KN, VW) to four (RN, KW) QTL were detected for both per se performances and corresponding GCA effects of the traits. The numbers of QTL that co-localized for per se performances and corresponding GCA effects of traits corresponded to the results of correlation analysis (Tables 1, 4). For example, qHKW3-2, which associated with KT, KW, and HKW, was identified for both per se performances and corresponding GCA effects for the traits. In addition, the direction of the parental contribution was identical for the 17 co-localized QTL for the per se performances and corresponding GCA effects for these traits (Figure 3B). This result validated the positive correlation between the genetic basis of per se performances and corresponding GCA effects for these traits.
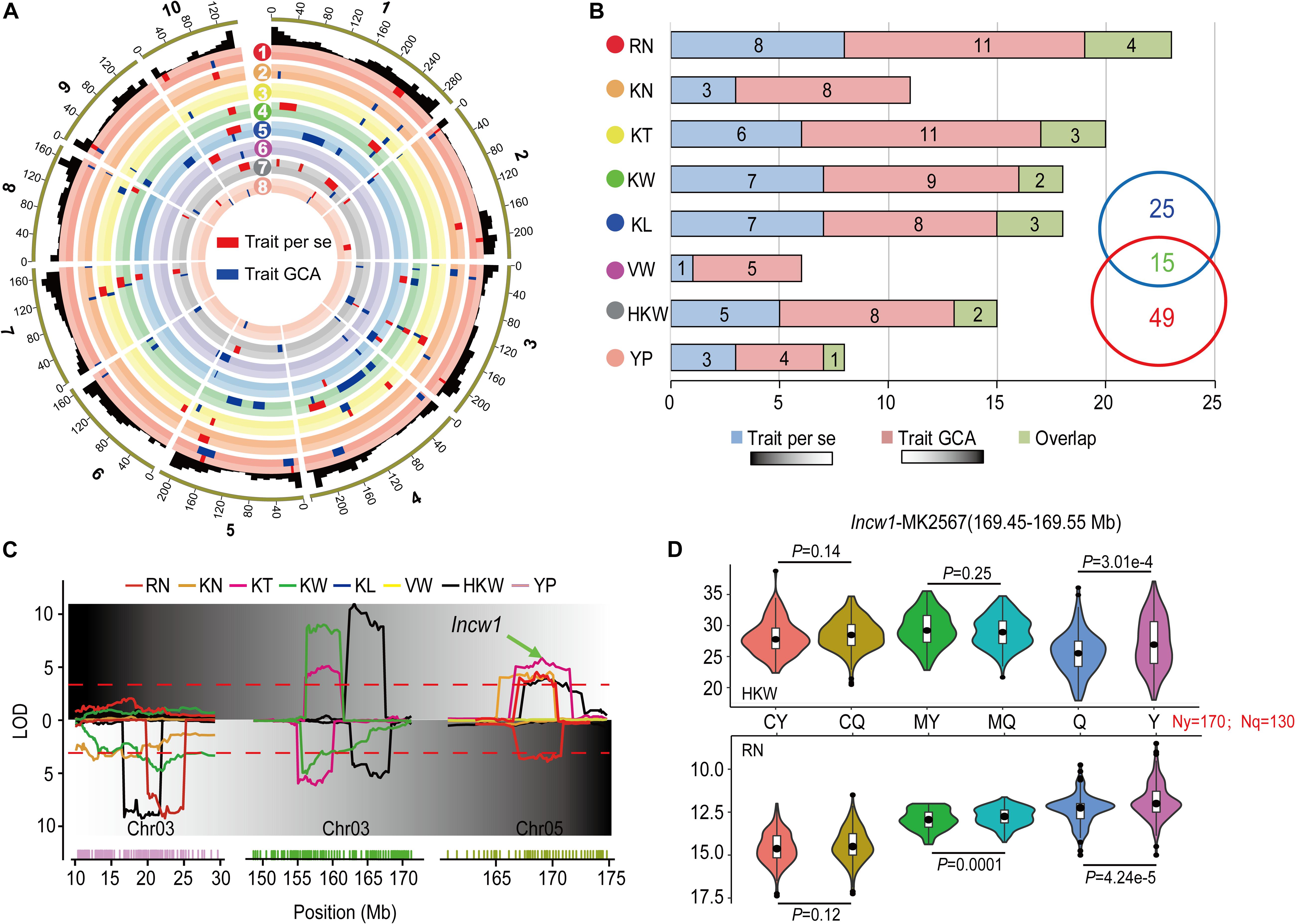
Figure 3. Comparison of the QTL distributions associated with per se performances and their GCA effects for eight yield-related traits. (A) Integrated QTL on the 10 maize chromosomes for eight yield-related traits across multiple environments and the joint analyses. RN (red), Row number; KN (orange), Kernel number per row; KT (yellow), Kernel thickness; KW (green), Kernel width; KL (blue), Kernel length; VW (purple), Volume weight; HKW (gray), 100-kernel weight; YP (pink), Yield per plot. The red and blue boxes indicate the QTL results in per se performances and their GCA effects for the traits, respectively. The width of the boxes reflects the length of the confidence intervals for each QTL. (B) QTL numbers distributed on each dataset for eight yield-related traits across multiple environments and joint analyses. Green boxes show the number of QTL overlapping between per se performances and their GCA effects for the traits. (C) A typical pleiotropic locus on chromosomes 3 and 5. The x-axis indicates the genetic positions across the maize genome in Mb. The y-axis indicates the LOD score of the detected QTL. The green arrow shows the position of Incw1, which influences HKW. (D) Tests for differences among phenotypic values for HKW and RN associated with MK2567 in the parental inbred lines, Ye478 and Qi319, of RILs and the corresponding hybrids obtained by crossing with testers. CY and CQ represent the phenotypic values of the hybrids of Chang7-2 × Ye478 and Chang7-2 × Qi319. MY and MQ represent phenotypic values of the hybrids of Mo17 × Ye478 and Mo17 × Qi319. Y and Q represent phenotypic values of Ye478 and Qi319. P < 0.05 represents the level of significance for differences in the performance HKW (above) and RN (below) in CY and CQ, MY and MQ, and Y and Q, respectively.
Of the 27 and 51 QTL were characteristically detected in the per se performances and corresponding GCA effects of traits, respectively. Two QTL, qRN3-1 and qRN6, together explained 14.92% of the observed variation for the GCA effect of RN (Table 4). qHKW3-1 was associated with GCA effects of HKW, KW, and KN. However, no significant loci were detected for the respective per se performances of the traits (Figure 3C). In addition, qKT1-2 and qHKW5-1 explained 5.72 and 5.12% of the observed variation for GCA effects of KT and HKW individually rather than per se performances for the traits in multiple environments. In contrast, the stable qHKW5-2 locus that was associated with RN, KN, KT, and HKW per se, was only associated with the GCA effects of RN and explained only 1.10% of the observed variation in the GCA effects of RN. The results reflected the distinct genetic bases of per se performances and corresponding GCA effects for these traits.
The maize gene annotation database at MaizeGDB2 was used to predict candidate genes in the qHKW5-2 region. Incw1, which encodes cell-wall invertase in the developing endosperm of maize, was located in the region surrounding MK2567 (169.45–169.55) at the qHKW5-2 locus (Figure 3D). SNPs between Ye478 and Qi319 located around MK2567 were calculated and categorized according to parental allele. A total of 170 SNPs match the Ye478 parental genotype and 130 match the Qi319 genotype. The phenotypic values for HKW in the Ye478 × Qi319 RIL population differed significantly (P = 3.01e-4). Nevertheless, there was no significant difference in HKW between either the Chang7-2 × Ye478 and Chang7-2 × Qi319 F1 hybrid groups (P = 0.14) or the Mo17 × Ye478 and Mo17 × Qi319 F1 hybrid groups (P = 0.25). There were significant phenotypic differences in RN in the RIL population (P = 4.24e-5). However, there was no significant difference in phenotypic values for RN between the Chang7-2 × Ye478 and Chang7-2 × Qi319 F1 hybrid groups (P = 0.12), but there was a significant difference in phenotypic values of RN between Mo17 × Ye478 and Mo17 × Qi319 F1 hybrid groups (P = 0.0001).
Pleiotropy of Quantitative Trait Loci for Eight Grain Yield-Associated Traits
The results of single environment analysis in the present study showed that five QTL hotspots were located on chromosomes 3, 5, 7, and 10 (Figure 2A). Integrating the results of QTL detected in multiple environments and during the joint analyses indicated that the most densely distributed QTL were highly concentrated in several chromosomal regions on chromosomes 1, 2, 3, 7, and 10 (Figure 3A). These QTL hotspots were likely responsible for pleiotropy. The non-random distribution of these pleiotropic loci might explain the correlation between some of these traits.
A total of 11 pleiotropic loci were detected for per se performances of the traits, and five, two, and four loci were simultaneously associated with two, three, and four traits, respectively, in the RILs. Loci affecting four traits each were located on chromosome 3, 5, 7, and 10, respectively. For instance, qHKW3-2 and qHKW7-3 were simultaneously associated with KW, KT, KL, and HKW. These results suggested that the qHKW3-2 and qHKW7-3 loci might affect grain yield via the development of grain morphology. Further, the qHKW5-2 locus was simultaneously associated with RN, KN, KT, and HKW. These results suggested that qHKW5-2 might affect grain yield by exerting effects on the differentiation and development of maize ears (Table 4). A total of 16 pleiotropic loci were identified that were associated with GCA effects, with four, five, and seven loci were simultaneously associated with the GCA effects of two, three, and four traits. These loci that were simultaneously detected for four traits were located on chromosomes 1, 3, 5, 7, 9, and 10, respectively. In general, these pleiotropic loci were associated with the GCA effects of YP or HKW. Most of the pleiotropic loci were detected for both per se performances and corresponding GCA effects of traits. Notably, qHKW10, which was associated with eight traits, was detected for the per se performances for the traits KN, KL, KW, and HKW per se, but was associated with the GCA effects of KL, RN, VW, and YP. This suggested that the genetic bases of these traits in RILs and their corresponding GCA effects could either be similar or different. Thus, these pleiotropic loci could be used to improve the GCA of traits while also simultaneously improving per se performances for yield-related traits.
Discussion
Comparative Mapping of QTL for Yield-Related Traits in the Spring and Summer Maize-Growing Region of China
The present QTL analysis of yield-related traits in the same population in different areas of the maize-growing region in China was helpful for adequately exploring the genetic basis of yield-related traits in maize. Earlier, the identical RIL population was planted in 2013 and 2014 in the spring maize-growing regions of Beijing and Gongzhuling, China (Zhang et al., 2017). Those results revealed three stable QTL associated with HKW located on chromosomes 1, 7, and 9, respectively. Among those loci, the qHKW7 locus located on chromosome 7 from position 133.60 to 139.25 Mb, explained the greatest proportion of phenotypic variation (7.13%) for HKW in this population and environment. We also found that qHKW7 was a polymorphic QTL that also influences kernel size. In the present study, the same RILs were planted in the summer maize-growing region of Shijiazhuang and Xinxiang, China, in 2015 and 2016. About 41.27% of the QTL detected in the present study were consistent with those identified in the previous study for six yield-related traits (Supplementary Table S3). Here, the major QTL qHKW3-2 with the major effects on HKW was located on chromosome 3 from position 156.45–167.6 Mb. Other significant QTL related to HKW were also detected on chromosomes 1 and 7, in the same intervals as in our previous studies, except for the qHKW9 locus. The current results showed that the loci on chromosomes 1 and 7 were the main QTL controlling HKW in both spring and summer maize-growing regions. However, the QTL on chromosome 3 only affected HKW in the summer maize-growing region, and that on chromosome 9 only affected HKW in the spring maize-growing region. The spring maize-growing region has a shorter maize growing season than the summer maize-growing region does, and growing season length was significantly correlated with HKW. This difference might explain the distinct genetic effects on yield-related traits in the spring and the summer maize-growing regions in the present study. qRN3-1, a major QTL that explained 7.03% of the observed variation in the GCA effects of RN, could not be detected for per se performances of the traits in both of these maize-growing regions. Thus, MAS for qRN3-1 will also be promoted for breeding hybrid combinations with optimal row number.
Correlation Between the Basis of General Combining Ability and per se Performances and GCA for Yield-Related Traits
Parental inbred lines with high combining ability were considered essential for the superior performance of hybrids (Duvick et al., 2004). Although GCA effects might be predicted based on the yield performance of inbred lines, the correlation between the yield performance of inbreds and that of their hybrid progeny was still not adequate for direct selection of inbred lines with high combining ability based on the per se yield of RILs (Lv et al., 2012). In general, although the correlations between the yield performance of inbred lines and their corresponding GCA effects in maize are positive, they are generally not strong. Previous studies have suggested that GCA effects were not significantly (r ≤ 0.44) correlated to their corresponding GCA effects for the yield-related traits YP, RN, KN, HKW, and PH (Huang et al., 2013). Similar results were found with another set of ILs whose performance for GCA effects were weakly (-0.01 ≤ r ≤ 0.49) correlated to the per se performances for the traits YP, KN, HKW, EL, PH, and EH. However, strong correlations have been detected between RN and its corresponding GCA effects (Qi et al., 2013). Positive and strong (0.55 ≤ r ≤ 0.77) correlations were identified between the three plant height related traits PH, EH, and IN in RILs (Zhou et al., 2018). These results suggest that correlations between traits have been influenced by genetic selection during the gathering of germplasm genetic resources and by environmental selection in planting locations.
In the present study, performances of GCA effects were significantly correlated to the per se performances of RILs for all yield-related traits (0.17 ≤ r ≤ 0.64, P > 0.01). The correlation between RN and its GCA effects was the strongest (r = 0.64), and was consistent with the results of previous studies (Qi et al., 2013). However, the performances of GCA effects were also strongly correlated to the per se performances for the traits KT, KW, and HKW. This agreed well with the results of QTL co-localization. The consistent genetic basis of the traits could be used to improve the GCA while improving the per se performances for these traits. However, the correlations between GCA effects and their corresponding per se performances for the traits KN, KL, VW, and YP were weak and indicated different genetic bases of the per se performances and their corresponding GCA effects for these traits. Due to diverse genetic backgrounds, various QTL populations can perform differently for specific traits. The selection of testers affected the performance of testcrosses directly, and was essential for the evaluation of GCA effects and the selection of elite inbred lines (Zhou H. et al., 2017). Non-genetic components, such as the environmental sensitivities of quantitative traits, can also affect phenotypes. Thus, it is necessary to study the genetic basis of quantitative traits and combining ability in multiple environments for many years with multiple populations.
The Reliability and Validity of QTL for GCA Effects
GCA was generally estimated by the method of variance analysis based on diallel crossing design (Griffing, 1956). With a large number of inbred lines, the huge workload was generated by the design of diallel cross design. In contrast, combinations with high GCA and parental lines with high SCA could be identified with ease by utilizing mating designs like incomplete diallel crossing or NCII (Comstock and Robinson, 1948), and the efficiency was similar to that of diallel crossing design (Dhillon and Singh, 1978). In rice, QTL analyses for 10 agronomic traits were conducted in a backcross recombinant inbred lines population and three testcross lines, and the results indicated similarities between the genetic characteristics of per se performances and corresponding GCA effects for these traits (Qu et al., 2012). Combining abilities for seven bioenergy and biomass related traits were predicated by 285 diverse dent inbred lines crossing with two flint testers. The prediction accuracies ranged from 0.60 to 0.80 for metabolites and 0.72–0.81 for SNPs with metabolic and whole-genome prediction models (Riedelsheimer et al., 2012). 365 F11 RILs using genotyping by a high-density linkage map with 4602 high-quality bin markers in the present study had provided the precision for QTL (Zhou et al., 2016). In the previous study, the power of QTL detection for grain yield and other agronomical important traits were estimated in maize using two independent samples (N = 107 and 344) of F2 plants with two testers in four environments. A total of 39 QTL with N = 107 and 107 QTL with N = 344 were detected for all traits and both testers. It also showed that QTL accounting for at least 10.2% of phenotypic variation in Experiment 2 (N = 107) could be detected, but as little as 3.3% of phenotypic variation in Experiment 1 (N = 344) with a LOD threshold of 2.5 (Melchinger et al., 1998). A set of 365 RILs and two testers were analyzed in the present study. The genetic bases of GCA for eight yield-related traits were dissected using a hybrid panel composed of 656 hybrids obtained by 328 RILs, which were successfully crossed both with Chang7-2 and Mo17. The amount of progeny was sufficient to identify more minor QTL for per se performances and corresponding GCA effects for the traits. Identification of marker-QTL associations also depended upon the magnitude of allele contrasts (Kerns et al., 1999). Consistency of QTL effects across testers was in agreement with corresponding genotypic correlations between the two testcross series (Melchinger et al., 1998). The power of combining ability detection can be improved by using the elite inbred lines in the opposite heterosis group as the tester (Lu et al., 2009). The influence on GCA effect estimation caused by testers can be eliminated by using standard testers. The two testers were Chang7-2 and Mo17, which belong to the SPT and Lancaster heterotic groups, respectively. Both of the testers were elite inbred lines and used widely in commercial maize breeding. Thus, the two testers in present study could provide abundant favorable alleles for identified variety QTL for traits GCA effects. In addition, the QTL × Environment interactions contributed to the lack of congruency of QTL found for multiple experiments (Melchinger et al., 1998; Kramer et al., 2009). In present study, the specific QTL locations of the per se performances and corresponding GCA effects for yield-related traits in each of four environments were determined (Supplementary Tables S3, S4), and a joint analysis across all environments was performed using BLUE. In order to improve the reliability of our results, only the loci identified in multiple environments and the results of the joint analyses were used for comparing the genetic bases of per se performances and corresponding GCA effects for the traits (Table 4). Therefore, the QTL identified in the present study for per se performances and corresponding GCA effects for eight yield-related traits could be reliable and efficient for marker-assisted selection (MAS) in breeding.
Potential Utilization of Main QTL for GCA Effects in Maize Hybrid Breeding
The genetics of combining ability were complex and greatly influenced by environments (Rojas and Sprague, 1952; Walejko and Russell, 1977). Marker-assisted selection offers an efficient way to dissect the genetic basis of combining ability (Yousef and Juvik, 2001; Eathington et al., 2007). Heterosis in F1 was caused by combination of different alleles at a specific locus of crossing parents (Liu et al., 2012; Zaid et al., 2017; Chen et al., 2019). Although some studies on the application of heterosis and combining ability have been published in several crops such as tomatoes (Kalloo et al., 1974), soybeans (Cerna et al., 1997), wheat (Singh et al., 2004), rice (Joshi et al., 2001), and maize (Ertiro et al., 2017), only few such studies related to the genetic dissections of combining abilities have been reported in maize (Gu, 2007; Lv et al., 2012; Qi et al., 2013; Huang et al., 2013; Giraud et al., 2017; Zhou et al., 2018). Comparing the genetic basis of per se performances and corresponding GCA effects for yield-related traits could improve the yields of maize inbred lines without affecting their corresponding combining ability.
In the present study, we detected some loci that only influence per se performances or their corresponding GCA effects for the traits. For instance, Incw1, which encodes a cell wall invertase in the developing endosperm of maize, was confirmed to have conserved influence on seed weight in Arabidopsis and maize (Liu et al., 2017). AtcwINV1, OsGIF1, and Mn1, which have similar functions as Incw1, were also associated with grain yield improvement (Li B. et al., 2013). Incw1 was identified at the stable qHKW5-2 locus in the present study. The qHKW5-2 locus, which was associated with per se performances for traits RN, KN, KT, and HKW traits per se, was only associated with the GCA effects of RN and was considered a minor QTL for that trait. Our results indicated that the Incw1 gene might affect the 100-grain weight through its effects on differentiation and development of maize ears.
qRN3-1 and qRN6, two pleiotropic loci, were associated with the GCA effects of RN, KW, and HKW rather than these per se performances for the traits. The two loci were not been identified in previous study (Qi et al., 2013), the specificities in additive effects might be caused by diverse testers (Qu et al., 2012), the identified loci occurred due to the presence of potential GCA coverage in the potential genomic regions (Zaid et al., 2019). Furthermore, qKT1-2 and qHKW5-1 were two stable loci for GCA effects of KT and HKW respectively, but no significant loci were detected for corresponding per se performances for the traits in multiple environments. This suggested that some genes or loci differ as to per se performances and/or corresponding GCA effects for these traits. Previous study also revealed the different genetic basis between per se performances and corresponding GCA effects for the traits (Eltahawy et al., 2020). Due to heterotic effects, differences between individuals in the testcross population were significantly reduced. In addition, the maternal genetic effects due to the selection of testers strongly influenced the variation in F1 performance and population structure (Chen et al., 2019). These factors might explain why some loci could only be detected in a single dataset. qKT1-2 and qHKW5-1 explained only 5.72 and 5.12% of the observed variation for GCA effects of KT and HKW individually. Previous studies suggested that traits GCA effects were mainly related with poly-genes rather than with major gene controlling the per se performances for the traits (Basava et al., 2019; Eltahawy et al., 2020), further loci associated with GCA effects should be explored in maize.
Some previous studies have shown that per se performances and corresponding GCA effects for the traits shared the same set of genetic loci. Nevertheless, the location and number of dominant QTL for GCA effects were affected by the allele frequency of testers (Austin et al., 2000; Frascaroli et al., 2009). The performances of GCA effects were also strongly correlated to the per se performances for the traits KT, KW, and HKW. This agreed well with the results of QTL co-localization. In addition, the QTL qKN7-1 and qHKW1-3, which could explain more than 10% of the variation in the GCA effects of KN and HKW, were also detected for per se performances for these traits. The direction of the parental contribution was identical. In a previous study, four QTL (qEH1-2, qEH5, qEH6-2, and qEH9-2) were simultaneously detected in per se performances and corresponding GCA effect, and together explained 18.16 and 19.70% of the observed variation for EH and EH GCA effects (Zhou et al., 2018). Therefore, the application of phenotypic or maker-assisted selection for improving inbred lines and GCA effects simultaneously could be evaluated economically and effectively (Mihaljevic et al., 2005; Qu et al., 2012).
Conclusion
In conclusion, we have compared the genetic basis of per se performances and corresponding GCA effects for eight grain yield-related traits. A total of 95 QTL were identified that affected per se performances and corresponding GCA effects for eight yield-related traits, and 17 of these QTL were detected for both per se performances and corresponding GCA effects of traits in multiple environments and the results of the joint analyses datasets. The genetic characteristics of the traits GCA effects were consistent or inconsistent with per se performances for the traits. Therefore, the congruous and diverse QTL identified in the present study for per se performances and corresponding GCA effects for yield-related traits should be effective for maize hybrid breeding.
Data Availability Statement
The datasets generated for this study can be found in the http://www.ncbi.nlm.nih.gov/bioproject/627044, Accession: PRJNA627044.
Ethics Statement
We claim that the experiments described herein comply with the ethical standards in China. Informed consent was obtained from all individual participants included in the study.
Author Contributions
XLu and ZZ performed the experiments and wrote the manuscript. ZY, CZ, ZH, ZW, ML, DZ, HY, and JH performed the experiments and revised the manuscript. XLi and JW designed the experiments. All authors contributed to the article and approved the submitted version.
Funding
This research was jointly funded by the National Key Research and Development Program (2016YFD0100303) and the National Natural Science Foundation of China (31471509).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpls.2020.00788/full#supplementary-material
Abbreviations
GCA, general combining ability; HKW, 100-kernel weight; KL, Kernel length; KN, Kernel number per row; KT, Kernel thickness; KW, Kernel width; QTL, quantitative trait loci; RILs, recombinant inbred lines; RN, row number; SCA, specific combining ability; VW, volume weight; YP, yield per plot.
Footnotes
References
Ahmed, S., Mian, M. A., and Gill, A. R. (1992). Correlation studies between yield, yield components and oil content in maize single crosses. Pak. J. Agric. Res. 13, 132–135.
Austin, D. F., Lee, M., Veldboom, L. R., and Hallauer, A. R. (2000). Genetic mapping in maize with hybrid progeny across testers and generations: grain yield and grain moisture. Crop Sci. 40, 30–39. doi: 10.2135/cropsci2000.40130x
Basava, R. K., Hash, C. T., Mahendrakar, M. D., Kishor, P. B. K., Satyavathi, C. T., Kumar, S., et al. (2019). Discerning combining ability loci for divergent environments using chromosome segment substitution lines (CSSLs) in pearl millet. PLoS One 14:e0218916. doi: 10.1371/journal.pone.0218916
Basbag, S., Ekinci, R., and Gencer, O. (2007). Combining ability and heterosis for earliness characters in line × tester population of Gossypium hirsutum L. Hereditas 144, 185–190. doi: 10.1111/j.2007.0018-0661.01998.x
Broman, K. W., Wu, H., Sen, S., and Churchill, G. A. (2003). R/qtl: QTL mapping in experimental crosses. Bioinformatics 19, 889–890. doi: 10.1093/bioinformatics/btg112
Butler, D., Cullis, B. R., Gilmour, A. R., and Gogel, B. J. (2007). ASReml-R Reference Manual. Brisbane: State of Queensland Department of Primary Industries and Fisheries.
Cerna, F. J., Cianzio, S. R., Rafalski, A., Tingey, S., and Dyer, D. (1997). Relationship between seed yield heterosis and molecular marker heterozygosity in soybean. Theor. Appl. Genet. 95, 460–467. doi: 10.1007/s001220050583
Chen, J., Zhou, H., Xie, W., Xia, D., Gao, G., Zhang, Q., et al. (2019). Genome-wide association analyses reveal the genetic basis of combining ability in rice. Plant Biotechnol. J. 17, 2211–2222. doi: 10.1111/pbi.13134
Chen, Z. L., Wang, B. B., Dong, X. M., Liu, H., Ren, L. H., Chen, J., et al. (2014). An ultra-high density bin-map for rapid QTL mapping for tassel and ear architecture in a large F2 maize population. BMC Genom. 15:433. doi: 10.1186/1471-2164-15-433
Comstock, R. E., and Robinson, H. F. (1948). The components of genetic variance in populations of biparental progenies and their use in estimating the average degree of dominance. Biomereics 4, 254–266. doi: 10.2307/3001412
Dhillon, B. S., and Singh, J. (1978). Evaluation of circulant partial diallel crosses in maize. Theor. Appl. Genet. 52, 29–37. doi: 10.1007/bf00273763
Duvick, D. N., Smith, J. S. C., and Cooper, M. (2004). Long-term selection in a commercial hybrid maize breeding program. Plant Breed Rev. 24, 109–152. doi: 10.1002/9780470650288.ch4
Eathington, S. R., Crosbie, T. M., Edwards, M. D., Reiter, R. S., and Bull, J. K. (2007). Molecular markers in a commercial breeding program. Crop Sci. 47, S154–S163. doi: 10.2135/cropsci2007.04.0015IPBS
Eltahawy, M. S., Ali, N., Zaid, I. U., Li, D., Abdulmajid, D., Bux, L., et al. (2020). Association analysis between constructed SNPLDBs and GCA effects of 9 quality-related traits in parents of hybrid rice (Oryza sativa L.). BMC Genomics 21:31. doi: 10.1186/s12864-019-6428-0
Ertiro, B. T., Beyene, Y., Das, B., Mugo, S., Olsen, M., Oikeh, S., et al. (2017). Combining ability and testcross performance of drought-tolerant maize inbred lines under stress and non-stress environments in Kenya. Plant Breed 136, 197–205. doi: 10.1111/pbr.12464
Fischer, S., Möhring, J., Schön, C. C., Piepho, H. P., Klein, D., Schipprack, W., et al. (2010). Trends in genetic variance components during 30 years of hybrid maize breeding at the University of Hohenheim. Plant Breed 127, 446–451. doi: 10.1111/j.1439-0523.2007.01475.x
Frascaroli, E., Canè, M. A., Landi, P., Pea, G., Gianfranceschi, L., Villa, M., et al. (2007). Classical genetic and quantitative trait loci analyses of heterosis in a maize hybrid between two elite inbred lines. Genetics 176, 625–644. doi: 10.1534/genetics.106.064493
Frascaroli, E., Canè, M. A., Pè, M. E., Pea, G., Morgante, M., and Landi, P. (2009). QTL detection in maize testcross progenies as affected by related and unrelated testers. Theor. Appl. Genet. 118, 993–1004. doi: 10.1007/s00122-008-0956-3
Gichuru, L., Derera, J., Tongoona, P., and Murenga, M. (2017). Combining ability and molecular genetic distances in tropical maize lines for grain yield and agronomic traits. S. Afr. J. Plant Soil 34, 1–9. doi: 10.1080/02571862.2016.1213323
Giraud, H., Bauland, C., Falque, M., Madur, D., Combes, V., Jamin, P., et al. (2017). Reciprocal Genetics: identifying QTLs for general and specific combining abilities in hybrids between multiparental populations from two maize (Zea mays L.) Heterotic Groups. Genetics 207, 1167–1180. doi: 10.1534/genetics.117.300305
Grieder, C., Dhillon, B. S., Schipprack, W., and Melchinger, A. E. (2012). Breeding maize as biogas substrate in Central Europe: I. Quantitative-genetic parameters for testcross performance. Theor. Appl. Genet. 124, 971–980. doi: 10.1007/s00122-011-1761-y
Griffing, B. (1956). Concept of general and specific combining ability in relation to diallel crossing systems. Aust. J. Biol. Sci. 9, 463–493. doi: 10.1071/BI9560463
Gu, L. X. (2007). General Combining Ability Analysis and its QTL Mapping of Maize DH Lines. Thesis for Master’s Degree, Heibei Agricultural University, Baoding.
Hallauer, A. R. (1990). Methods used in developing maize inbreds. Maydica 35, 1–16. doi: 10.1111/j.1439-037X.1990.tb00786.x
Holland, J. B. (2007). Genetic architecture of complex traits in plants. Curr. Opin. Plant Biol. 10, 156–161. doi: 10.1016/j.pbi.2007.01.003
Huang, J., Qi, H., Feng, X., Huang, Y., Zhu, L., and Yue, B. (2013). General combining ability of most yield-related traits had a genetic basis different from their corresponding traits per se in a set of maize introgression lines. Genetica 141, 453–461. doi: 10.1007/s10709-013-9744-3
Issa, Z. M. M., Nyadanu, D., Richard, A., Sangare, A. R., Adejumobi, I. I., and Ibrahim, D. (2018). Inheritance and combining ability study on drought tolerance and grain yield among early maturing inbred lines of maize (Zea mays L.). J. Plant Breed. Crop Sci. 10, 115–127. doi: 10.5897/JPBCS2017.0703
Joshi, S. P., Bhave, S. G., Chowdari, K. V., Apte, G. S., Dhonukshe, B. L., Lalitha, K., et al. (2001). Use of DNA markers in prediction of hybrid performance and heterosis for a three-line hybrid system in rice. Biochem. Genet. 39, 179–200. doi: 10.1023/A:1010293325482
Kalloo, Singh, R. K., and Bhutani, R. D. (1974). Combining ability studies in tomato (Lycopersicon esculentum Mill.). Theor. Appl. Genet. 44, 358–363. doi: 10.1007/BF00303477
Kerns, M. R., Dudley, J. W., and Ii, G. K. R. (1999). Tester and type of progeny affect QTL detection in maize. Maydica 44, 69–83.
Khalil, I. A., Rahman, H., Saeed, N., Khan, N. U., Nawaz, I., Ali, F., et al. (2010). Combining ability in maize single cross hybrids for grain yield: a graphical analysis. Sarhad J. Agric. 26, 374–379.
Knapp, S. J., Stroup, W. W., and Ross, W. M. (1985). Exact confidence intervals for heritability on a progeny mean basis. Crop Sci. 25, 192–194. doi: 10.2135/cropsci1985.0011183X002500010046x
Kramer, C. C., Polewicz, H., and Osborn, T. C. (2009). Evaluation of QTL alleles from exotic sources for hybrid seed yield in the original and different genetic backgrounds of spring-type Brassica napus L. Mol. Breed. 24, 419–431. doi: 10.1007/s11032-009-9303-x
Lan, T. R., He, K. H., Chang, L. G., Cui, T. T., Zhao, Z. X., Xue, J. Q., et al. (2018). QTL mapping and genetic analysis for maize kernel size and weight in multi-environments. Euphytica 214, 119–130. doi: 10.1007/s00122-014-2276-0
Li, B., Liu, H., Zhang, Y., Kang, T., Zhang, L., Tong, J., et al. (2013). Constitutive expression of cell wall invertase genes increases grain yield and starch content in maize. Plant Biotechnol. J. 11, 1080–1091. doi: 10.1111/pbi.12102
Li, C. H., Li, Y. X., Peng, B., Liu, Z. Z., and Yang, Z. Z. (2013). Quantitative trait loci mapping for yield components and kernel-related traits in multiple connected RIL populations in maize. Euphytica 193, 303–316. doi: 10.1007/s10681-013-0901-7
Liu, C., Song, G. Y., Zhou, Y. H., Qu, X. F., Guo, Z. B., Liu, Z. W., et al. (2015). OsPRR37 and Ghd7 are the major genes for general combining ability of DTH. PH and SPP in rice. Sci. Rep. 5, 12803–12813. doi: 10.1038/srep12803
Liu, C. L., Hua, J. G., Liu, C., Zhang, D. G., Hao, Z. F., Yong, H. J., et al. (2016). Fine mapping of a quantitative trait locus conferring resistance to maize rough dwarf disease. Theor. Appl. Genet. 129, 1–10. doi: 10.1007/s00122-016-2770-7
Liu, Z., Garcia, A., McMullen, M. D., and Flint-Garcia, S. A. (2016). Genetic analysis of kernel traits in maize-teosinte introgression populations. G3 6, 2523–2530. doi: 10.1534/g3.116.030155
Liu, J., Huang, J., Guo, H., Lan, L., Wang, H., Xu, Y., et al. (2017). The conserved and unique genetic architecture of kernel size and weight in maize and rice. Plant Physiol. 175, 774–785. doi: 10.1104/pp.17.00708
Liu, J., Zhang, F., Zhou, J., Chen, F., Wang, B., and Xie, X. (2012). Phytochrome B control of total leaf area and stomatal density affects drought tolerance in rice. Plant Mol. Biol. 78, 289–300. doi: 10.1007/s11103-011-9860-3
Liu, X., Chen, S., Chen, J., Ishiki, K., Wang, W., and Yu, L. (2004). Improvement of combining ability for restorer lines with the identified SSR markers in hybrid rice breeding. Breed Sci. 54, 341–346. doi: 10.1270/jsbbs.54.341
Liu, Y., Wang, L. W., Sun, C. L., Zhang, Z. X., Zheng, Y. L., and Qiu, F. Z. (2014). Genetic analysis and major QTL detection for maize kernel size and weight in multi-environments. Theor. Appl. Genet. 127, 1019–1037. doi: 10.1007/s00122-014-2276-2270
Lu, Y., Yan, J., Guimares, C. T., Taba, S., Hao, Z., Gao, S., et al. (2009). Molecular characterization of global maize breeding germplasm based on genome-wide single nucleotide polymorphisms. Theor. Appl. Genet. 120, 93–115. doi: 10.1007/s00122-009-1162-7
Lu, Z. M. (1999). On the combining ability selection in hybrid rice breeding. Chin. J. Rice Sci. 13, 1–5.
Lv, A. Z., Zhang, H., Zhang, Z. X., Tao, Y. S., Yue, B., and Zheng, Y. L. (2012). Conversion of the statistical combining ability into a genetic concept. J. Integr. Agric. 11, 43–52. doi: 10.1016/S1671-2927(12)60781-0
Melchinger, A. E., Utz, H. F., and Schön, C. C. (1998). Quantitative trait locus (QTL) mapping using different testers and independent population samples in maize reveals low power of QTL detection and large bias in estimates of QTL effects. Genetics 149, 383–403. doi: 10.1016/1369-5266(88)80015-3
Messmer, R., Fracheboud, Y., Banziger, M., Vargas, M., Stamp, P., and Ribaut, J. M. (2009). Drought stress and tropical maize: QTL-by-environment interactions and stability of QTLs across environments for yield components and secondary traits. Theor. Appl. Genet. 119, 913–930. doi: 10.1007/s00122-009-1099-x
Mihaljevic, R., Schön, C. C., Utz, H. F., and Melchinger, A. E. (2005). Correlations and QTL correspondence between line per se and testcross performance for agronomic traits in four populations of European maize. Crop Sci. 45, 114–122.
Qi, H. H., Huang, J., Zheng, Q., Huang, Y. Q., Shao, R. X., Zhu, L. Y., et al. (2013). Identification of combining ability loci for five yield-related traits in maize using a set of testcrosses with introgression lines. Theor. Appl. Genet. 126, 369–377. doi: 10.1007/s00122-012-1985-5
Qu, Z., Li, L., Luo, J., Wang, P., Yu, S., Mou, T., et al. (2012). QTL mapping of combining ability and heterosis of agronomic traits in rice backcross recombinant inbred lines and hybrid crosses. PLoS One 7:e28463. doi: 10.1371/journal.pone.0028463
Raihan, M. S., Liu, J., Huang, J., Guo, H., Pan, Q., and Yan, J. (2016). Multi-environment QTL analysis of grain morphology traits and fine mapping of a kernel-width QTL in Zheng58 × SK maize population. Theor. Appl. Genet. 129, 1465–1477. doi: 10.1007/s00122-016-2717-z
Reif, J. C., Gumpert, F. M., Fischer, S., and Melchinger, A. E. (2007). Impact of interpopulation divergence on additive and dominance variance in hybrid populations. Genetics 176, 1931–1934. doi: 10.1534/genetics.107.074146
Riedelsheimer, C., Czedik-Eysenberg, A., Grieder, C., Lisec, J., Technow, F., Sulpice, R., et al. (2012). Genomic and metabolic prediction of complex heterotic traits in hybrid maize. Nat. Genet. 44, 217–220. doi: 10.1038/ng.1033
Rojas, B. A., and Sprague, G. F. (1952). A comparison of variance components in corn yield trials: III. general and specific combining ability and their interaction with locations and years. Agron. J. 44, 462–466. doi: 10.2134/agronj1952.00021962004400090002x
Schrag, T. A., Melchinger, A. E., Sørensen, A. P., and Frisch, M. (2006). Prediction of single-cross hybrid performance for grain yield and grain dry matter content in maize using AFLP markers associated with QTL. Theor. Appl. Genet. 113, 1037–1047. doi: 10.1007/s00122-006-0363-6
Seye, A. I., Bauland, C., Giraud, H., Mechin, V., Reymond, M., Charcosset, A., et al. (2019). Quantitative trait loci mapping in hybrids between Dent and Flint maize multiparental populations reveals group-specific QTL for silage quality traits with variable pleiotropic effects on yield. Theor. Appl. Genet. 132, 1523–1542. doi: 10.1007/s00122-019-03296-2
Shukla, S. K., and Pandey, M. P. (2010). Combining ability and heterosis over environments for yield and yield components in two-line hybrids involving thermosensitive genic male sterile lines in rice (Oryza sativa L.). Plant Breed. 127, 28–32. doi: 10.1111/j.1439-0523.2007.01432.x
Singh, H., Sharma, S. N., and Sain, R. S. (2004). Heterosis studies for yield and its components in bread wheat over environments. Hereditas 141, 106–114. doi: 10.1111/j.1601-5223.2004.01728.x
Sprague, G. F., and Tatum, L. A. (1942). General vs. specific combining ability in single crosses of corn. J. Am. Soc. Agron. 34, 923–932. doi: 10.2134/agronj1942.00021962003400100008x
Walejko, R. N., and Russell, W. A. (1977). Evaluation of recurrent selection for specific combining ability in two open-pollinated maize cultivars. Crop Sci 17, 647–651. doi: 10.2135/cropsci1977.0011183X001700040043x
Yousef, G. G., and Juvik, J. A. (2001). Comparison of phenotypic and marker-assisted selection for quantitative traits in sweet corn. Crop Sci. 41, 645–655. doi: 10.2135/cropsci2001.413645x
Zaid, I. U., Tang, W., He, J., Khan, S. U., and Hong, D. (2019). Association analysis uncovers the genetic basis of general combining ability of 11 yield-related traits in parents of hybrid rice. AoB Plants 11:ly077. doi: 10.1093/aobpla/ply077
Zaid, I. U., Tang, W., Liu, E., Khan, S. U., Wang, H., Mawuli, E. W., et al. (2017). Genome-wide single-nucleotide polymorphisms in CMS and restorer lines discovered by genotyping using sequencing and association with marker-combining ability for 12 yield-related traits in Oryza sativa L. subsp. Japonica. Front. Plant Sci. 8:143. doi: 10.3389/fpls.2017.00143
Zhang, C., Zhou, Z., Yong, H., Zhang, X., Hao, Z., Zhang, F., et al. (2017). Analysis of the genetic architecture of maize ear and grain morphological traits by combined linkage and association mapping. Theor. Appl. Genet. 130, 1011–1029. doi: 10.1007/s00122-017-2867-7
Zhang, L., Dong, S. T., Liu, C. H., Wang, K. J., Zhang, J. W., and Liu, P. (2007). Correlation analysis on maize test weight, yield and quality. Sci. Agric. Sin. 40, 405–411.
Zhou, H., Xia, D., Zeng, J., Jiang, G., and He, Y. (2017). Dissecting combining ability effect in a rice NCII-III population provides insights into heterosis in indica-japonica cross. Rice 10, 39–47. doi: 10.1186/s12284-017-0179-9
Zhou, Q., Dong, Y. B., Shi, Q., Zhang, L., Chen, H. Q., Hu, C. H., et al. (2017). Verification and fine mapping of qGW1.05, a major QTL for grain weight in maize (Zea mays L.). Mol. Genet. Genom. 292, 871–881. doi: 10.1007/s00438-017-1318-0
Zhou, Z. Q., Zhang, C. S., Lu, X. H., Wang, L. W., Hao, Z. F., Li, M. S., et al. (2018). Dissecting the genetic basis underlying combining ability of plant height related traits in maize. Front. Plant Sci. 9:1117. doi: 10.3389/fpls.2018.01117
Keywords: maize, yield-related traits, NCII mating design, combining ability, QTL
Citation: Lu X, Zhou Z, Yuan Z, Zhang C, Hao Z, Wang Z, Li M, Zhang D, Yong H, Han J, Li X and Weng J (2020) Genetic Dissection of the General Combining Ability of Yield-Related Traits in Maize. Front. Plant Sci. 11:788. doi: 10.3389/fpls.2020.00788
Received: 17 February 2020; Accepted: 18 May 2020;
Published: 22 July 2020.
Edited by:
Hanwei Mei, Shanghai Agrobiological Gene Center, ChinaReviewed by:
Bing Yue, Huazhong Agricultural University, ChinaMahesh Damodhar Mahendrakar, International Crops Research Institute for the Semi-Arid Tropics (ICRISAT), India
Copyright © 2020 Lu, Zhou, Yuan, Zhang, Hao, Wang, Li, Zhang, Yong, Han, Li and Weng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xinhai Li, bGl4aW5oYWlAY2Fhcy5jbg==; Jianfeng Weng, d2VuZ2ppYW5mZW5nQGNhYXMuY24=
†These authors have contributed equally to this work
 Xin Lu
Xin Lu Zhiqiang Zhou
Zhiqiang Zhou Zhaohui Yuan1
Zhaohui Yuan1 Zhuanfang Hao
Zhuanfang Hao Hongjun Yong
Hongjun Yong Jianfeng Weng
Jianfeng Weng