- 1School of Agricultural Forest Food and Environmental Sciences, University of Basilicata, Potenza, Italy
- 2Pyrenean Institute of Ecology – Consejo Superior de Investigaciones Científicas, Zaragoza, Spain
Hydraulic theory suggests that tall trees are at greater risk of drought-triggered death caused by hydraulic failure than small trees. In addition the drop in growth, observed in several tree species prior to death, is often interpreted as an early-warning signal of impending death. We test these hypotheses by comparing size, growth, and wood-anatomy patterns of living and now-dead trees in two Italian oak forests showing recent mortality episodes. The mortality probability of trees is modeled as a function of recent growth and tree size. Drift-diffusion-jump (DDJ) metrics are used to detect early-warning signals. We found that the tallest trees of the anisohydric Italian oak better survived drought contrary to what was predicted by the theory. Dead trees were characterized by a lower height and radial-growth trend than living trees in both study sites. The growth reduction of now-dead trees started about 10 years prior to their death and after two severe spring droughts during the early 2000s. This critical transition in growth was detected by DDJ metrics in the most affected site. Dead trees were also more sensitive to drought stress in this site indicating different susceptibility to water shortage between trees. Dead trees did not form earlywood vessels with smaller lumen diameter than surviving trees but tended to form wider latewood vessels with a higher percentage of vessel area. Since living and dead trees showed similar competition we did not expect that moderate thinning and a reduction in tree density would increase the short-term survival probability of trees.
Introduction
Drought-induced tree mortality is becoming a major ecological concern as the planet becomes warmer and mortality episodes increase worldwide (Allen et al., 2010). Nevertheless, many research gaps still exist concerning the patterns of drought-related tree death and the reason why some trees are more prone to die than other coexisting individuals (McDowell et al., 2008). This has fostered the investigation of dieback mechanisms caused by hydraulic failure (substantial xylem embolism) and carbon starvation (carbon losses greatly exceed carbon gains) (Sevanto et al., 2014). In addition, the search for early-warning signals of tree death, particularly using retrospective proxies, such as tree-ring or wood-anatomy data, has been stimulated in connection with dieback mechanisms (Dobbertin, 2005; Camarero et al., 2015; Cailleret et al., 2016; Pellizzari et al., 2016).
In this study, we focus on such early-warning signals of tree death and we model the mortality probability as a function of recent growth and tree height. Further, we focus on a sub-Mediterranean ring-porous oak (Quercus frainetto) because in the Allen et al. (2010) global review, only 11% of the mortality cases involved similar oak species, which are the dominant hardwood trees in many drought-prone areas. In addition, Bennett et al. (2015) report in their review that, drought-related mortality increased with tree height in 65% of the cases examined, where few or none involved oak species.
Published reviews (Bennett et al., 2015; McDowell and Allen, 2015) have lead to predict that tall and dominant trees of isohydric species (characterized by strict control of water loss by closing stomata) are at greater risk of dying due to heat and drought stress; whereas smaller trees of anisohydric species (with less control of water loss and high stomatal conductance rates, i.e., showing variable maximum values of xylem tension depending on changes in soil water availability and vapor pressure deficit - hereafter VPD; cf. Klein, 2014) are predicted to better survive under drought conditions (McDowell and Allen, 2015). This does not agree with some field data showing that anisohydric species as oaks are not able to tolerate severe droughts showing growth decline and increased mortality rates (Klos et al., 2009).
In theory, anisohydric is expected to be linked to an enhanced hydraulic conductivity (Martínez-Vilalta and Garcia-Forner, 2016). However, recent studies show that there is a continuum between isohydric and anisohydric behavior rather than a clear threshold between these two functional strategies (Klein, 2014). Therefore, we can expect that coexisting oak trees display different wood-anatomical features reflecting contrasting xylem hydraulics and vulnerabilities to drought-induced dieback, connected with more or less anisohydric behavior (Rosner et al., 2016).
In trees the probability of tree death is usually related to size (height or diameter) (Grote et al., 2016), since empirical evidence shows that small trees are slow growing and have higher death probability than bigger ones (Monserud and Sterba, 1999; Das et al., 2007; Holzwarth et al., 2013). Overall, tree size, growth rate, and competition seem reasonable predictors of tree mortality (Cailleret et al., 2016). Some mortality models use relative growth rates to consider the influence of tree size (sometimes relative to the neighboring trees’ size) on the likelihood of tree death; whilst other models directly employ tree diameter and rarely height as predictors of mortality since these are the most widely measured variables in forestry (Yao et al., 2001; Ruiz-Benito et al., 2013). However, few studies have addressed if tree size is related to the probability of tree death after dry spells (but see Camarero et al., 2016).
In addition to static variables, such as tree size, mortality models are usually formulated as a function of growth rates or trends (based either on ring-width or on basal area increment – BAI) calculated over time periods (often between 5 and 50 years) prior to tree death (Pedersen, 1998; Wyckoff and Clark, 2000; Bigler and Bugmann, 2003, 2004; Bigler et al., 2004; Bircher et al., 2015). In selecting the growth variable, BAI reflects well long-term changes in tree vigor (Phipps and Whiton, 1988; Duchesne et al., 2003), and it is a better proxy of changes in biomass increment than tree-ring width (Bowman et al., 2013). However, establishing robust growth-mortality associations is challenging because dead and decaying trees can present elevated growth rates prior to tree death (Wunder et al., 2008; Levanic et al., 2011; Voltas et al., 2013; Sangüesa-Barreda et al., 2015). Mortality models depend on the selection and calculation of explanatory growth variables, such as growth rates or growth trends (see a recent review by Cailleret et al., 2016). Therefore, since growth and tree height are closely related, a biologically meaningful model of tree mortality should consider both variables.
In the specific case of oaks, low rates of radial growth and negative growth trends often precede tree death (Pedersen, 1998, 1999; Drobyshev et al., 2007; Stojanović et al., 2015), as it happens in other tree species (Dwyer et al., 1995; Ogle et al., 2000; Haavik et al., 2011; Gea-Izquierdo et al., 2014; Kane and Kolb, 2014; Mamet et al., 2015). However, a high year-to-year variability of growth, the occurrence of abrupt growth declines or an increase in lag-1 autocorrelation have also been associated to high mortality rates (Suarez et al., 2004; Das et al., 2007; Camarero et al., 2015). In addition, increased growth sensitivity to climate stressors (e.g., drought severity) has recently been detected in dead trees as compared with living trees (Linares and Camarero, 2012).
In this study, we employ tree size, growth, and wood-anatomy data and estimate recent competition intensity to understand if drought differently affected mortality rates in coexisting individuals of two decaying Mediterranean oak (Q. frainetto) forests. Specifically, we quantified wood anatomy to evaluate if dead trees formed a less xylem with more potential hydraulic conductivity characterized by latewood vessels with wider lumen areas (corresponding to a more anisohydric behavior during the dry summer season) than surviving trees; whilst, these latter should produce a xylem characterized by vessels with narrower lumen areas. Moreover, we employed a modeling approach to investigate mortality probability as a function of recent growth and tree size. We hypothesize those taller trees with wider vessels will be more prone to drought-induced tree death than smaller trees forming vessels with narrower lumen.
Materials and Methods
Study Sites
We selected two forests showing recent drought-induced canopy dieback and mortality located near the San Paolo Albanese (40° 01′ 20′ N, 16° 20′ 46′ E, 950 m a.s.l., mean slope 25–30%; hereafter SP site) and Oriolo (40° 00′ 10″ N, 16° 23′ 30″ E; 770 m a.s.l., mean slope 25%; hereafter OR site) villages situated in the Basilicata region, southern Italy. The SP site is a pure high forest located in the Pollino National Park and it has a density of 348 stems ha-1. The mean diameter at 1.3 m (dbh) and age are 40 cm and 145 years, respectively. The OR site is also a high forest with density of 444 stems ha-1, and mean dbh and age are 35 cm and 138 years. The soil in both study sites is sandy or silty clay. No silvicultural treatment has been applied for the past 40 years.
Since the early 2000s both forests presented trees with dieback symptoms (shoot dieback, leaf loss and withering, growth decline, high mortality, and epicormic shoot formation).
Climate and Drought Data
Climate in the study area is Mediterranean characterized by dry and warm summers (summer precipitation is 79 mm) and wet and mild winters (winter precipitation is 257 mm) with mean annual temperature of 16.4°C and annual precipitation of 742 mm (data from Oriolo station, 40° 03′ 11″ N, 16° 26′ 47″ E, 445 m a.s.l., 1950–2015 period). The warmest and coldest months are July (mean maximum temperature of 33.5°C) and January (mean minimum temperature of 4.0°C), respectively, whereas the driest and wettest months are July (22 mm) and December (99 mm). Drought occurs from June to September.
To evaluate drought-growth associations since 1950 we downloaded the Standardized Precipitation Evapotranspiration Index (SPEI) for the 0.5° grid where the study sites are located using the Global SPEI database webpage1. The SPEI is a multiscalar drought index, i.e., it expresses monthly cumulative drought stress at different time scales (e.g., a 10-month May SPEI considers drought stress from previous August to May). The SPEI considers the effects of temperature and evapotranspiration on drought severity and indicates wet (positive SPEI values) and dry (negative SPEI values) conditions (Vicente-Serrano et al., 2010).
Study Species
The Italian oak (Q. frainetto Ten.) is native to southern Italy, the Balkans, and north-west Turkey. It is a winter deciduous, shade-intolerant and sub-Mediterranean oak species forming ring-porous wood and reaching heights of at least 30 m (Chatziphilippidis and Spyroglou, 2004). Radial growth of the Italian oak is very sensitive to dry conditions in late spring and summer (Sanders et al., 2014).
Field Sampling and Competition Index
We sampled couples of coexisting and dominant living and dead trees located at less than 20 m apart within each couple, and sampled at the SP and OR sites. Firstly, seven and four circular plots (radius of 15 m) were randomly located in the SP and OR sites, respectively, to obtain estimates of density of dead trees at each site. Recently dead trees were characterized by the almost complete absence of green leaves or the presence of dead shoots and brown leaves remaining in the crown. In the SP site, 24 couples randomly selected of living and dead trees were sampled (n = 24 living and n = 24 dead trees), whilst at the OR sites 18 couples were sampled plus additional six living trees (n = 24 living and n = 18 dead trees). First, the tree dbh and height of each tree were measured using dbh tapes and a laser rangefinder, respectively. Second, to study growth and wood anatomy we extracted three increment cores per tree at breast height (1.3 m) separated by 120° using a Pressler increment borer. Two cores were used for dendrochronological analyses and the remaining core was used for wood anatomy.
The recent competition experienced by each focal tree i was calculated as a function of the tree size (DBH) and proximity of the three nearest j neighbors following Forrester et al. (2013) and using the following formula:
where CIi is the competition intensity experienced by the focal tree i, BAj is the basal area of neighboring j trees, and dij is the distance between the tree i and the j neighbors. We assume that choosing the three nearest neighbors provides a reasonable estimate of the tree-to-tree competition in the neighborhood of the focal trees since the samples stands correspond to relatively open high forests where most trees are dominant.
Tree-Ring Data
Wood samples were air-dried and the surface of the cores was cut using a sledge core microtome (Gärtner and Nievergelt, 2010). Tree rings were visually cross-dated and tree-ring widths were measured to the nearest 0.01 mm using a binocular microscope coupled to a computer with the LINTAB package (Rinntech, Heidelberg, Germany). To estimate tree age at 1.3 m, when a core did not reach the pith, the total missing width and the number of missing rings were estimated by interpolating the distance to the pith using the curvature of the innermost rings of the sample. The COFECHA program (Holmes, 1983) was used to evaluate the visual cross-dating of tree-ring series. To quantify growth we transformed the tree-ring widths into BAI using the following formula:
where R is the radius of the tree and t is the year of tree–ring formation.
Since BAI values are often not normally distributed, we used the median. In addition, we calculated: the BAI coefficient of variation (CV) as a measure of its dispersion; the slope of the BAI linear trend with time (Trend); and the BAI lag-1 autocorrelation (A1). Following Cailleret et al. (2016), these variables were calculated for several periods representing long, mid and short-term BAI changes previous to tree death: 1980–2014 (35 years prior to tree death), 2000–2014 (15 years prior to tree death), and 2005–2014 (10 years prior to tree death).
Wood Anatomy
We selected five couples of living-dead trees per site to perform wood-anatomical analyses. These trees were selected because they show the highest correlations between their BAI series and the mean BAI series of living or dead trees from each site. Wood anatomy was analyzed for the 1980–2013 period because several dead trees did not form the complete 2014 tree ring. Transversal sections (thickness of 20 mm) were prepared from each core tree by dividing it into pieces of approximately 2 cm length. Sections were cut using a sliding microtome (Microm HM 400, Thermo Sci., Walldorf, Germany) and then stained with safranin (1%) and astra blue (2%), dehydrated with ethanol (70, 95, and 100%) and xylol, and fixed on microscope slides using Eukitt® mounting medium. Images were captured at 20–40 × magnification using a light microscope (Zeiss Axiophot, Carl Zeiss Microscopy, Jena, Germany). Earlywood (EW) and latewood (LW) vessels were analyzed in tangential windows of 2 and 0.3 mm, respectively. EW vessels were considered those with lumen diameters larger than 50 mm. Transversal vessel diameters (along the radial direction) and areas were measured using the ImageJ software for image analysis (Schneider et al., 2012). We obtained the following wood-anatomical variables following Scholz et al. (2013): ring area, EW and LW areas, absolute and relative (%) areas occupied by vessels in the EW and LW, EW and LW vessel areas (mean, minimum, and maximum values), EW and LW vessel density. We also calculated the hydraulic diameter (Dh) for all vessels measured within each ring by weighting individual conduit diameters to correspond to the average Hagen–Poiseuille lumen theoretical hydraulic conductivity for a vessel size (Tyree and Zimmermann, 2002). The Dh was calculated as the average of Sd5/Sd4, where d is the diameter of each vessel (Sperry et al., 1994).
Statistical Analyses
Differences between living and dead trees in tree features (size, age, and competition index), growth and wood anatomy were assessed using Mann–Whitney U tests. The relationships between BAI and the SPEI were evaluated using Pearson correlations considering a 32-year long period previous to the dieback onset (1950–1981) and another period of similar duration encompassing the dieback process (1982–2013). Following Hentschel et al. (2014), we used the Wilcoxon signed-rank test to check if growth (BAI) and wood-anatomical variables differed between living and dead trees. To compare BAI-SPEI relationships between living and dead trees we used Mann–Whitney U tests. We chose these non-parametric tests because they are robust against deviations from standard distributions (Gibbons and Chakraborti, 2011).
Logistic Models of Tree Mortality
We evaluated if tree mortality is related to short and long-term growth characteristics by examining the variables of the selected logistic regression models. Generalized linear models (GLMs) with binomial error distribution (i.e., logistic regressions) were used to predict the survival probability of a tree i at time t, hereafter labeled Pr (Yi,t = 1), and to analyze the corresponding growth-mortality relationships (Bigler and Bugmann, 2004). Logistic regression models with fixed effects were used as trees were growing at one single site and most of them died on the same year following this equation:
where Pr (Yi,t) follows a binomial distribution with Yi,t = 0 indicating that tree i is dead at time t, while Yi,t = 1 indicates that the tree is alive; α0 is the intercept, β0 are tree variables (height, dbh, age); and δ0 is the coefficient for growth variables calculated over a period of length p (Gi,t,p).
Models were fitted using a combination of several variables. In the SP site, the evaluated models included the following variables height, dbh, age, CIi and variables derived from BAI (BAI2005-2014, CV BAI2005-2014, BAI Trend 1980-2014, and BAI A12005-2014). In the OR site, the evaluated models included the following variables height, dbh, age, CIi and the following variables derived from BAI (BAI2005-2014, CV BAI1980-2014, BAI Trend 2000-2014, and BAI A12005-2014).
Model performance was assessed using an information-theoretic approach (Burnham and Anderson, 1998). We calculated Akaike information criterion (AIC), the change in AIC for each model relative to the best model (DAIC), and Akaike weights (Wi) which evaluate the relative importance of the model. These metrics are commonly used to assess model performance, but the AIC is strongly positively correlated to the number of samples used to calibrate the model, and depends on the equitability of the sampling (Lawson et al., 2014). This is problematic when comparing the performance of models fitted on different sample sizes as in this study. Discrimination metrics may be more suitable in this case because they reflect the ability to separate survival and death observations (Lawson et al., 2014). Here, we employ the Area Under the Receiver Operating Characteristic Curve (AUC) which is not dependent on the equitability of the sampling. AUC values range from 0 to 1, with 0.5 indicating a random model. A model providing an excellent prediction and showing a notable amount of discrimination has AUC ≥ 0.9 (Fielding and Bell, 1997; Hosmer et al., 2013). Selected models had the highest Wi and AUC values. We present the three models with the highest Wi. We presented the AUC of the best-fitted model and its McFadden pseudo-R2 which is a likelihood ratio comparing a model without any predictor to a model including all predictors (Hosmer et al., 2013). GLMs were fitted using the function “glm” of the software R (R Core Team, 2015), and their AUC was calculated using the package ROCR (Sing et al., 2013).
Non-parametric Drift-Diffusion-Jump Metrics
Since BAI series provide a summary of the tree growth history, characteristics of these BAI series (Dakos et al., 2012) can be investigated to detect early-warning signals of tree death (Camarero et al., 2015). A sharp growth decline is often a discrete indicator of portending tree death (Pedersen, 1998), but BAI series represent continuous data whose underlying processes are unknown, possibly nonlinear and occur at short and long-term scales (Kane and Kolb, 2014). In the case of growth data, critical transitions may be detected using tools as non-parametric drift-diffusion-jump (DDJ) metrics which fit a general DDJ model as a surrogate for the unknown nonlinear processes generating the data (Brock and Carpenter, 2012; Mamet et al., 2015). Using these methods, estimates of the drift (deterministic) and diffusion (stochastic) components of underlying processes, as well as an indicator of the conditional variance, can be computed (Brock and Carpenter, 2012). Briefly, these DDJ metrics include: the drift which measures instantaneous changes due to deterministic trends corresponding to local rates of change; the diffusion which measures the standard deviation of relatively small shocks that occur every year; the jumps which are large intermittent shocks due to uncorrelated changes; the conditional variance that rises to infinity at a critical point and it is estimated as the difference between the second conditional moment and the square of the first conditional moment; and the total variance which combines the contributions of diffusion and jumps (Carpenter and Brock, 2011). The DDJ model is able to assess both high- and low-frequency patterns in BAI data estimating the probability of a range shift (Mamet et al., 2015). We expect rises in the conditional and total variances and a decrease in diffusion and an increase in jump intensity prior to a sharp BAI drop portending tree death. Following Mamet et al. (2015), we calculated the DDJ metrics on log+1-transformed BAI series for dying and living trees at both study sites. In this regard, the 1970–2014 period was considered, when BAI started stabilizing in terms of growth and age. The DDJ metrics were calculated with the earlywarnings R package (Dakos et al., 2012).
Results
Differences in Tree Size between Living and Dead Trees and Mortality Incidence
At both study sites, dead trees presented lower height than living trees (Table 1; Figure 1). At SP site, this difference was also observed in dbh, whereas the rest of the analyzed variables (age, CIi) did not show significant differences. Considering dead trees, dbh and height were not significantly related neither at the SP site (r = 0.31, P = 0.14) nor at the OR site (r = 0.38, P = 0.07). In contrast, in living trees dbh and height were significantly related at both study sites (SP, r = 0.70, P = 0.0001; OR, r = 0.62, P = 0.006).

TABLE 1. Characteristics of the living (L) and recently dead (D) oak trees sampled in the two study sites (OR and SP).
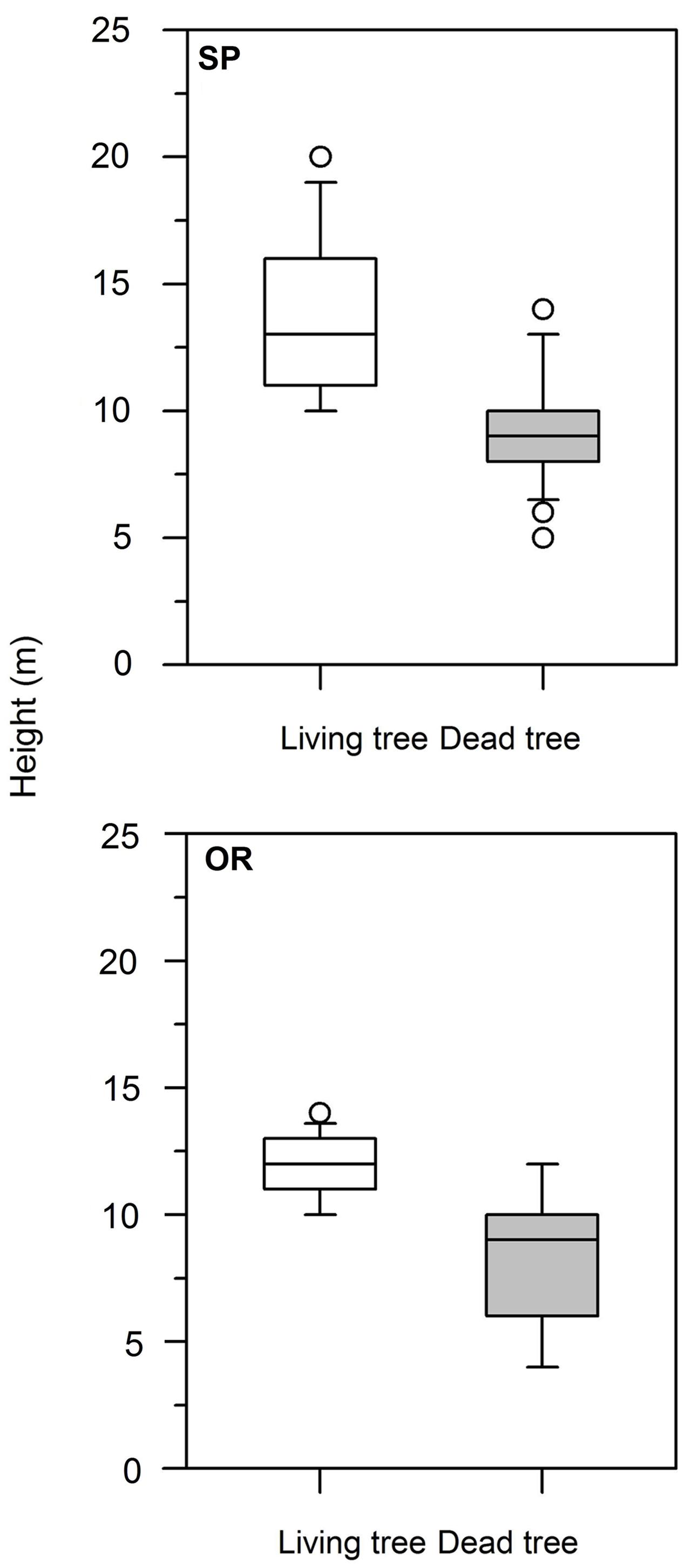
FIGURE 1. Box plots showing the significant differences in tree height between living (white boxes) and dead (gray boxes) Italian oak trees at the SP and OR study sites.
The densities of dead trees at the SP and OR sites were 35 (8%) and 25 stems ha-1 (5%), respectively, suggesting a greater impact of drought at SP than at OR site. Overall, 70 and 83% of the trees sampled at the SP and OR sites, respectively, died in 2014 (Figure 2).
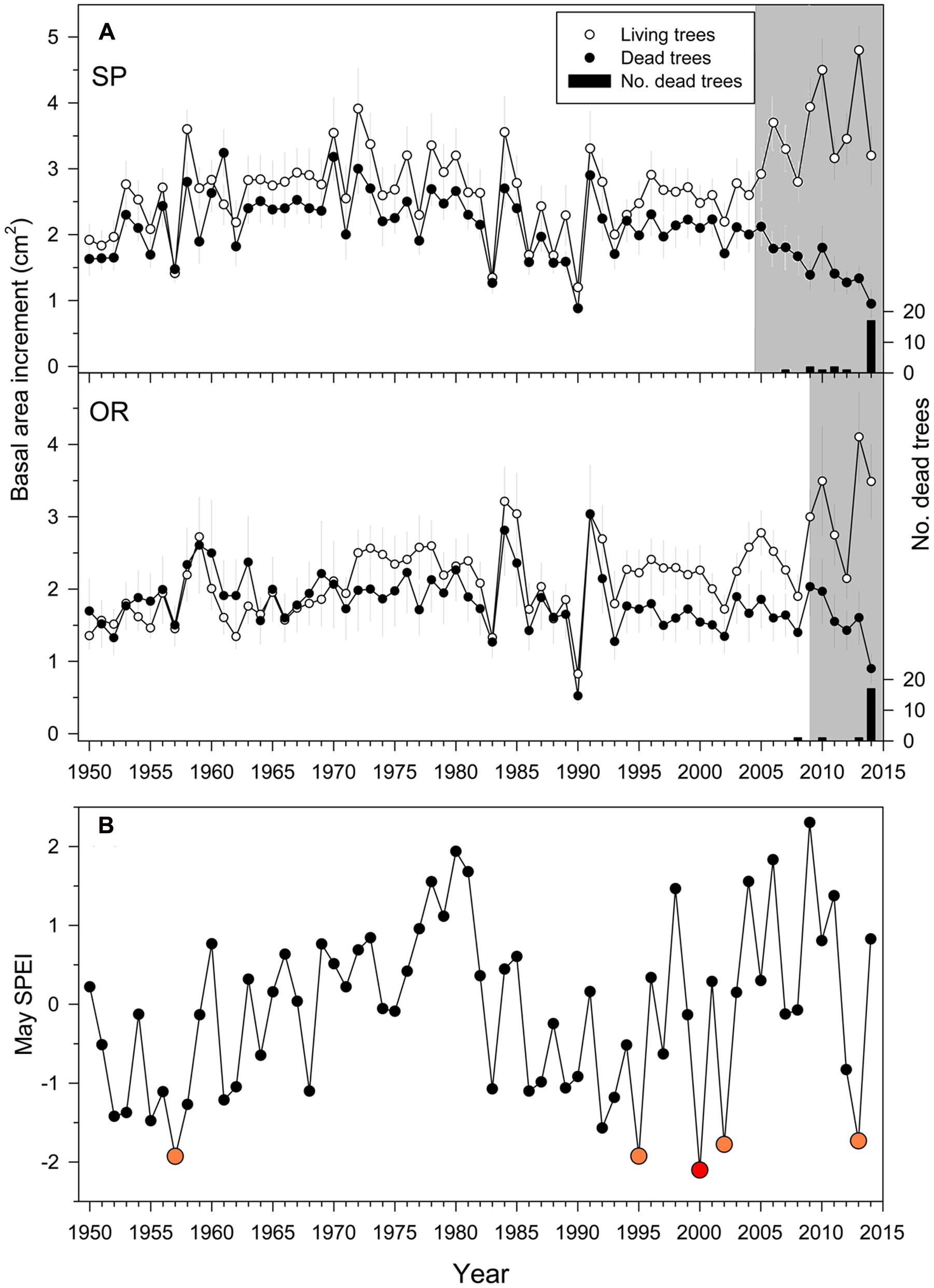
FIGURE 2. Growth (A) quantified as basal area increment (BAI) of living (white symbols) and dead (filled symbols) Italian oak trees at the SP and OR study sites and growing-season drought severity (B). In the uppermost plots, the black bars show the number of dead trees classified according to their last formed ring which was considered the death year (right y axes). The drought severity was quantified using the May SPEI drought index calculated at a 10-month long scale (big red and yellow symbols show very dry years; the 2000 year is highlighted with a red symbol because it showed the driest May). The gray filled areas indicate periods when the BAI of dead trees was significantly (P < 0.05) lower than that of living trees Values are means ± SE.
Growth Patterns and Trends of Living and Dead Trees
Trends in BAI were always significantly lower in dead than in living trees regardless of the compared period and the study site; such differences were magnified from 2000 onwards (Table 2). Observed BAI values corresponded to narrow rings and low growth rates (SP, mean ring width of 0.79 mm; OR, mean ring width of 0.72 mm) At both sites, median BAI values were also lower in dead than in living trees for the 2000–2014 and 2005–2014 periods. The BAI CV of living trees from the OR site was higher than in dead trees for all periods, except in the shortest one (2005–2104). Lastly, at the SP site, BAI A1 was higher in living than in dead trees during the 1980–2014 period but it was more negative in living trees when only the shorter period from 2000 onwards was considered.
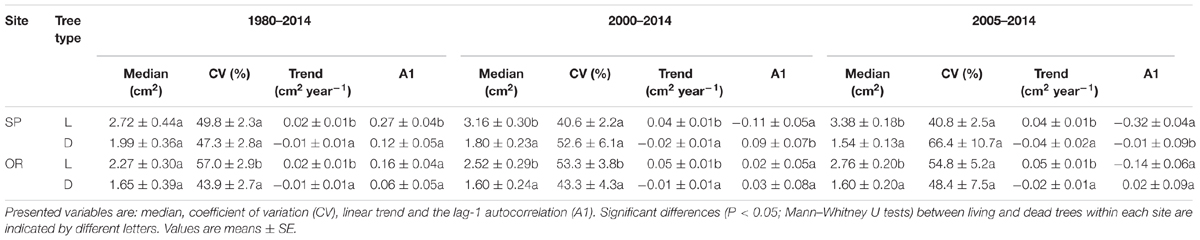
TABLE 2. Selected values of basal-area increment of living (L) and recently dead (D) trees sampled at the two study sites (SP and OR) and calculated for three different periods (1980–2014, 35 years prior to tree death; 2000–2014, 15 years prior to tree death; and 2005–2014, 10 years prior to tree death).
The BAI differences in single years between living and dead trees were significant from 2005 onwards at the SP site, and from 2009 onwards at the OR site (Figure 2A). Since then, BAI dropped in dead trees with some BAI increases corresponding to wet years (2009–2010) and steadily increased in living trees. Note that the divergence in BAI between living and dead trees started after severe spring droughts, which occurred in 1995, 2000, 2002, and 2013 (Figure 2). According to the calculated 10-month long May SPEI, droughts of similar severity since 1950 only occurred before in 1957 (Figure 2B).
Drought-Growth Relationships in Living and Dead Trees
The positive correlations between BAI and the 10-month long May SPEI were significantly higher in living than dead trees at the SP site for the 1950–1981 and 1982–2013 periods, i.e., during a period previous to the dieback onset and during the dieback process (Figure 3). Contrastingly, these differences were not significant at the OR site. Overall, living trees from the SP site showed higher BAI increases to wet conditions than living trees from the OR site.
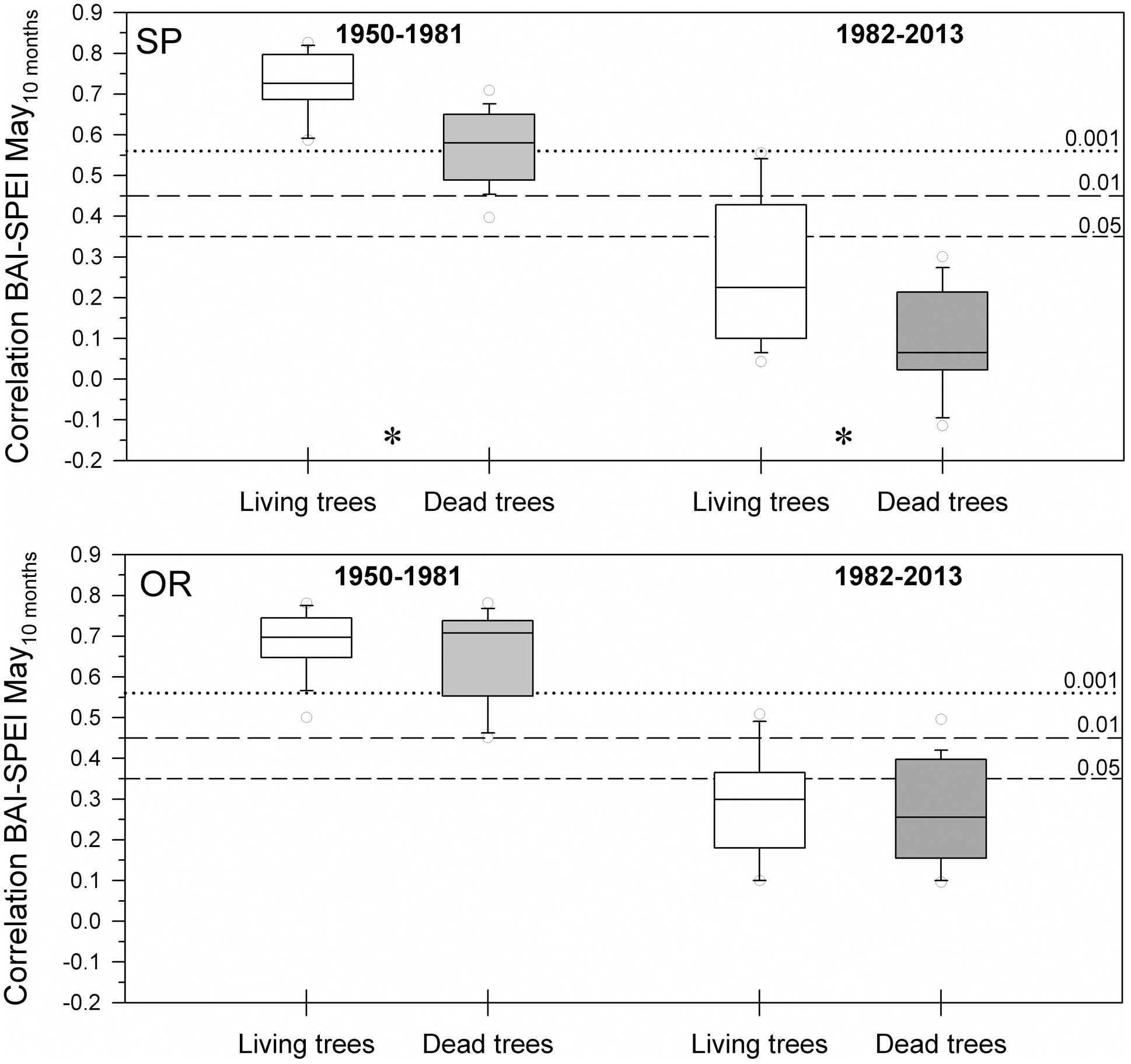
FIGURE 3. Drought-growth associations differed between living and dead trees at the SP site but not at the OR site. The box plots show the correlations between BAI and the May SPEI drought index calculated at 10-months long time scales. Correlations were calculated for 32-year long periods prior (1950–1981) and overlapping (1982–2013) with the drought-induced growth decline and increase in mortality rate of the studied Italian oaks. Asterisks indicate significant (P < 0.05) differences found between living and dead trees at the SP site. Empty and filled boxes correspond to living and dead trees, respectively. The dashed and dotted horizontal lines indicate significance levels.
Wood Anatomy
When comparing living and dead trees, we found no significant differences neither in hydraulic terms (Dh) nor in EW anatomical features (Table 3). However, LW vessel diameter tended to be wider for dead trees at the SP site (Table 3; Figure 4). In both sites, the LW vessel density of dead trees was also reduced as compared with living trees and the percentage of LW area occupied by vessels increased in now-dead trees.
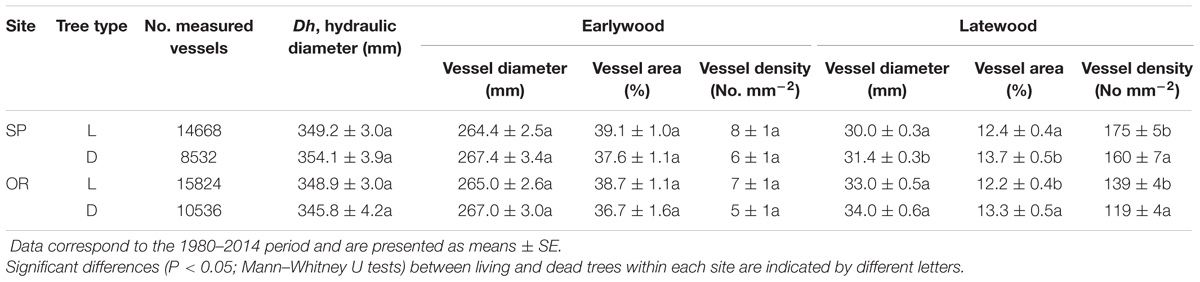
TABLE 3. Wood-anatomical variables obtained for living (L) and recently dead (D) trees in the two study sites (SP and OR).
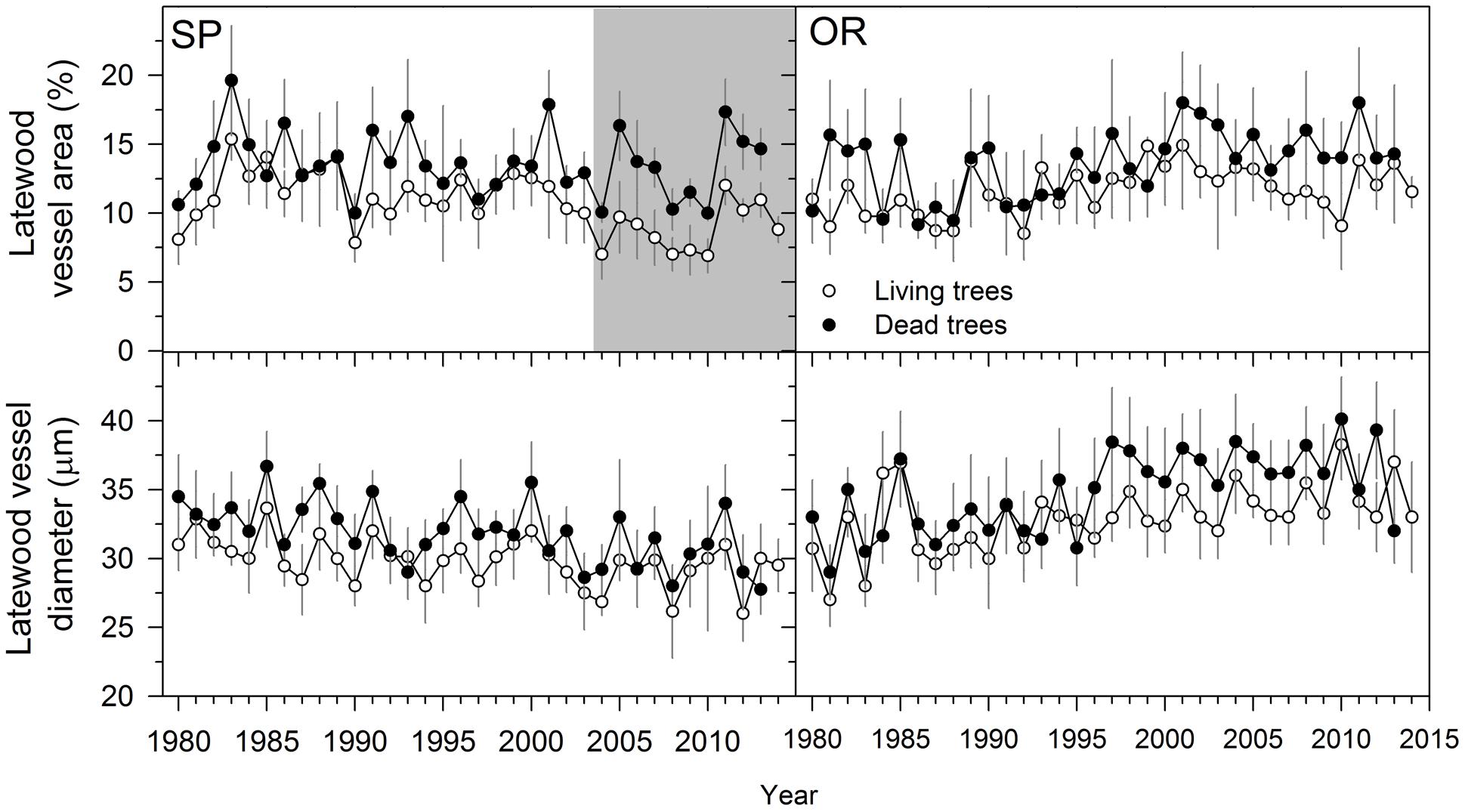
FIGURE 4. Latewood anatomical variables measured in living (empty symbols) and dead (filled symbols) Italian oak trees at SP and OR study sites. The gray filled areas indicate periods when the variables significantly (P < 0.05) differ between living and dead trees (Wilcoxon signed-rank test). Since most dead trees did not form the 2014 ring we did not present values for them and for this year. Values are means ± SE.
Logistic Models of Tree Mortality: Tree Height Matters
The selected models indicated that the probability of tree death increased at both sites for trees with lower height and presenting a sharper growth reduction (BAI trend) for the 2000–2014 period. At the SP site, the most parsimonious model also selected a lower median BAI for the 2005–2014 period, associated to an increasing chance of mortality; whereas at the OR site, the lower BAI CV, which occurred during the 1980–2014 period, was also selected as a characteristic of dead trees (Tables 2 and 4).
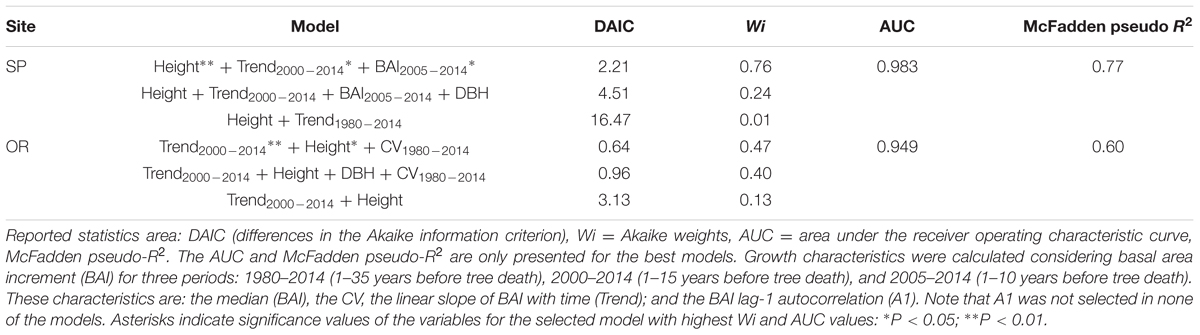
TABLE 4. Logistic regression results of the top three performing logistic models of tree survival for Italian oaks sampled at each of the two study sites (SP, OR) based on tree age, size (DBH, height) and growth characteristics.
Early-Warning Signals of Tree Death: DDJ Metrics of BAI Series
The DDJ metrics of the dead trees from the SP site showed a peak of conditional variance around 1995 and a sharp decrease in diffusion in the early 2000s. This coincided with an increase in total variance and jump intensity; whereas living trees did not present similar patterns, particularly concerning conditional variance and diffusion (Figure 5). The conditional variance of dead trees from the OR site peaked in the early 1990s and the diffusion fell around 2005, whilst living trees did not show these changes in DDJ metrics (Figure 5). The years when diffusion rapidly dropped in the case of dead trees roughly coincided with those when BAI of living trees was significantly higher than BAI of now-dead trees (compare Figures 2A and 5).
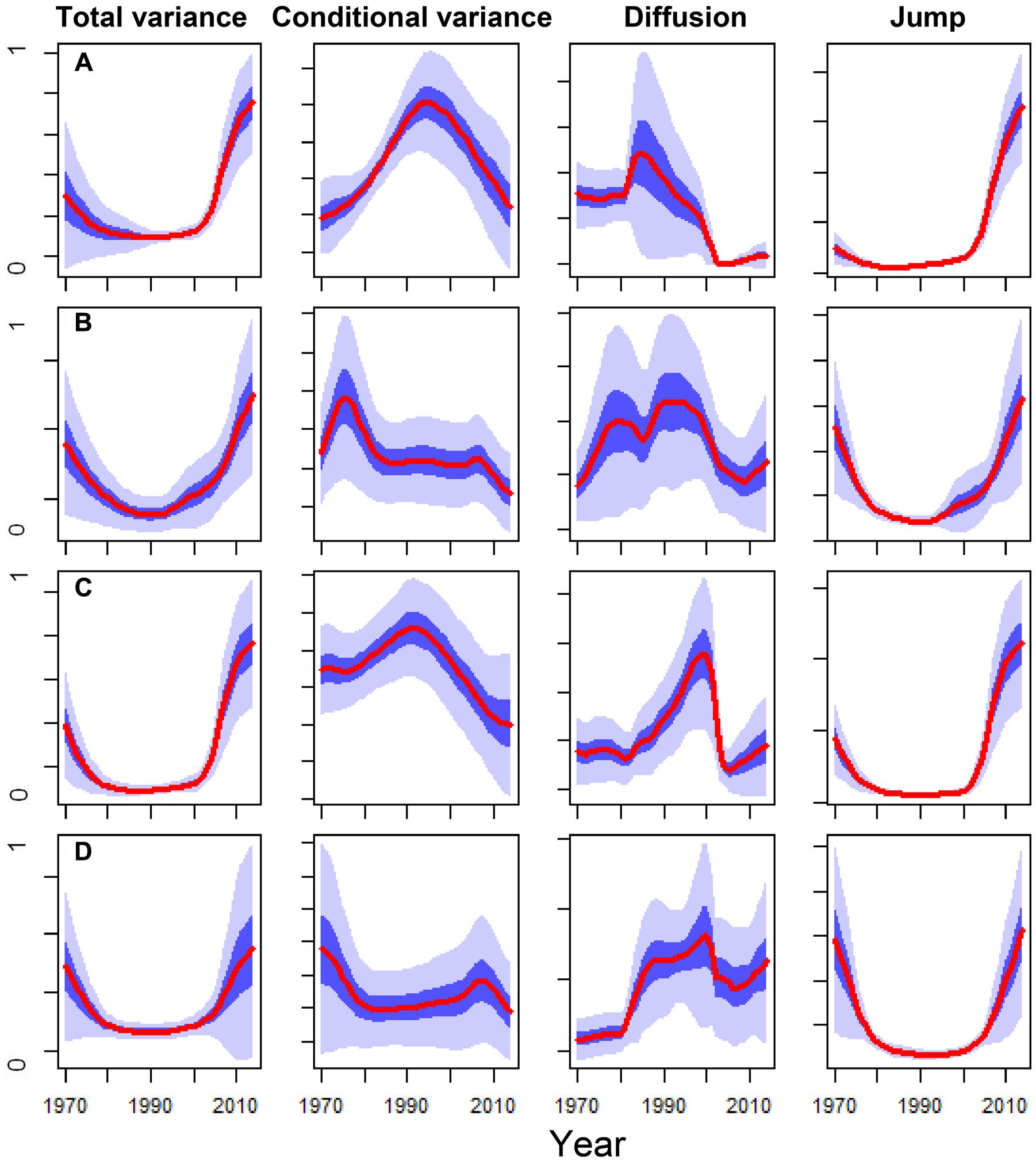
FIGURE 5. Comparison of the main non-parametric drift-diffusion-jump (DDJ) metrics calculated for the basal-area increment series (1970–2014 period) of the Italian oak dead trees sampled at the SM (A) and OR (C) sites vs. the living trees from SM (B) and OR (D) sites. The DDJ metrics include the total variance, the conditional variance, the diffusion and the jump. The red lines show the variance medians among trees and light and dark blue shadings indicate the 10–90% and 40–60% confidence intervals, respectively. The y axes show variance components and they were standardized to the 0–1 range.
Discussion
In contrast with Bennett et al. (2015), we observed that now-dead trees were smaller than living trees (Table 1), which agrees with a previous report on dieback of Mediterranean oaks showing a smaller size and a greater crown leaf loss (Camarero et al., 2016). This difference in height may have predisposed to the conspicuous and rapid leaf loss of recently dead trees associated to apical shoot dieback (F. Ripullone, personal observation).
Our findings do not imply that height and above ground competition are the most relevant variables to predict tree death in similar drought-prone sites. Alternatively, belowground competition for water and nutrients could constrain the vertical development of the trees most vulnerable to drought. Tree size per se (i.e., diameter; height; leaf, stem, and root volumes) might be more important to explain long-term changes in tree vigor (Mencuccini et al., 2005). Since tree diameter and height often covary, a bigger sample size may be helpful in future studies to discern the most relevant explanatory variable (diameter or height) of tree mortality.
The smaller size of dead trees and the lack of differences in the lumen diameter of the wider earlywood vessels between living and dead trees (Table 3) lead to refute our main hypotheses. It is likely that initial genetic or phenotypic differences or contrasting topoedaphic restrictions bring to distinct capacities of height and root depth among coexisting trees. Larger and taller trees with deeper root systems are able to explore more soil volume, especially in sandy or silty soils, which can make them less vulnerable to intense and prolonged drought conditions.
However, in contrast with our results, Bennett et al. (2015) in their global review report that tall trees have higher mortality rates than small ones. According to this review, larger trees are at higher risk of drought-induced hydraulic failure because they experience greater resistance in transporting water upwards (i.e., higher potential gradient, conduit resistance). Drought-induced dieback preferentially affected tall Neotropical tree species because large trees were more vulnerable to drought, due to their lower capacity to buffer the negative effects of soil water deficit (Zhang et al., 2009). Therefore, associations between tree height and the probability of death do not seem to be so simple. In addition, many drought-induced dieback cases involve dry regions (Allen et al., 2010), where trees mainly compete for water (e.g., southwestern USA, southern Europe) and do not grow as tall as in wet sites where resources abound (e.g., California redwood forests). Obviously, Italian oak trees are not expected to show similar limitations to those experienced by very tall redwood trees, whose leaves and shoots show increasing turgor limitation with increasing height, even without soil moisture deficit (Woodruff et al., 2004). Our findings indicate that in drought-prone areas where trees do not become very tall as in most Mediterranean oak forests, a small height is a drawback to withstand dry spells.
The best-performing models of tree mortality did not select the competition index, in agreement with the similar values found for living and dead trees (Tables 1 and 4). In boreal, subalpine and temperate forests, a curvilinear U-shaped relationship between tree mortality and size (usually dbh) has often been observed, indicating that a small tree size relative to the stand neighbors increases the probability of mortality due to competition for light (Monserud and Sterba, 1999; Yao et al., 2001; Chen et al., 2008). Since big and old dying trees are often absent on those mortality-size analyses, the negative associations between mortality rate and tree size are also expected to occur in mature forests showing advanced successional stages (Oliver and Larson, 1996). This could be applied to the presented study case, where both sites were relatively old forests (Table 1). In temperate forests, competition for light strongly influences the growth of small trees, whereas competition for nutrients affects trees of diverse sizes (Coomes and Allen, 2007). Under those conditions, the small size and low growth rates of dying trees usually correspond to suppressed trees forming the understorey (Kobe et al., 1995; Wyckoff and Clark, 2002). However, in more open stands from dry areas, the competition for water and nutrients overrides this competition for light and affects growth rates and tree mortality (Linares et al., 2010). In the study drought-prone area, aboveground competition, in terms of radial growth, did not seem to drive tree death.
Considering whole-tree water storage capacity (capacitance) aids to explain our findings because the contribution of water stored in the stem (sapwood and bark) to canopy transpiration during dry periods is considerable and increases with tree size (Phillips et al., 2003). Therefore, the time to reach critical levels of drought stress should increase with tree size, as stem volume increases relative to leaf area (Scholz et al., 2011). This suggests that larger trees should be less susceptible to drought-triggered mortality than smaller trees as we found. Other studies have also found a larger size of living trees as compared with now-dead coexisting trees, as in this study. For instance, in the case of aspen forests, living trees showed a larger size than trees which did not survive (Hanna and Kulakowski, 2012; but see Worrall et al., 2008). In a Bishop pine forest in southern California, tree survivorship increased for the tallest trees, because they intercept more fog than smaller trees, thus counteracting drought stress (Carbone et al., 2012; Baguskas et al., 2014). A simplified soil-plant-atmosphere-continuum model, applied on decaying piñon pines in southwestern USA, predicted that smaller trees were more prone to die after drought, which was in agreement with field observations of larger surviving pines on steep slopes where soil water content is low (Gentine et al., 2016). The pattern of larger size in living than in dead trees would correspond to a higher growth rate in living rather than dead trees, i.e., prior to the stress-induced dieback, which is opposite to what has been observed in some dieback studies (Levanic et al., 2011; Voltas et al., 2013).
Regarding growth data, dead trees showed lower growth rates than living trees 10 years prior to tree death at both study sites, albeit differences were significant 5 years prior to death (Figure 2). Our findings agree with previous studies indicating that a reduced growth in the 5–50 years preceding death is a reliable predictor of tree mortality (e.g., Pedersen, 1998; Ogle et al., 2000; Bigler and Bugmann, 2004; Das et al., 2007; Hereş et al., 2012; Ireland et al., 2014). We also observed that the growth of dead trees was less reduced by drought stress than living trees at the most affected SP site (Figure 3), suggesting that dead trees were less sensitive to water shortage. This lower responsiveness of dead trees prior to the dieback onset could be explained by their lower growth rates or because their growth was more constrained by other site (poor access to soil water due to a less developed root system) or climatic factors (warmer summer temperatures; see Camarero et al., 2016). The uncoupling between growth and the SPEI drought index observed since 1982 in SP dead trees could indicate that other climatic stressors (e.g., warmer temperatures) override the effects of water deficit on growth or that stressed trees are losing responsiveness to water deficit. Contrastingly, increased early growth rates of dead trees have been described in subalpine conifers, which were characterized by a direct association between fast early growth, large size and decreased longevity (Bigler and Veblen, 2009). In other studies, trees dying after dry spells showed intensified growth responsiveness to water shortage, associated to canopy dieback and to a lower whole crown gas exchange relative to living trees (McDowell et al., 2010; Hereş et al., 2012).
The severe 2000s droughts triggered an irreversible growth decline in the dead oak trees (Figure 2). The usefulness of such sharp or gradual drops in growth after drought, as early-warning signals of tree death, has been proven either by utilizing widely employed tools, such as logistic models (Table 4) or non-parametric DDJ metrics (Figure 5). The maximum of conditional variance occurred prior to the drop in diffusion (Figure 5) which, according to Dakos et al. (2012), indicates the onset of a negative growth trend and could be used to determine the trend timespan in the logistic model. Accordingly, the selected mortality models included the growth trend for the 2000–2014 period (Table 4). Therefore, the drop in diffusion coincides with the timespan of BAI selected by the model. This suggests that both methods could be combined, i.e., DDJ could help to predefine the relevant timespans for logistic mortality models.
One methodological caveat of tree-ring data is their retrospective base. For example, it is possible that part of the sharp BAI increase of living trees observed during the 2010s was a growth release caused by a reduced competition for water and nutrients with dying trees (Figure 2A). This could represent a limitation of the sampling method based on the selection of “living-dead tree” couples, which assumes that neighboring trees are subjected to similar environmental constraints through time (e.g., competition); but tree death could generate a biased growth response of surviving trees. A similar release effect was observed in tropical forests, where drought caused a preferential death of large trees, which were more vulnerable to hydraulic deterioration. This lead to a competitive release of small suppressed trees whose growth rates increased after big trees died (Rowland et al., 2015). In that tropical forest, taller trees were predisposed to greater atmospheric water demand and loss in xylem functionality due to their longer hydraulic path lengths (Mencuccini et al., 2005); whereas smaller trees could avoid hydraulic deterioration through leaf water uptake. However, this seems not to be the case of the sub-Mediterranean oak forests subjected to seasonal droughts and reaching much lower heights than tropical trees.
Since dead trees did not form earlywood vessels with wider lumen areas than surviving trees, but tended to form wider latewood vessels occupying more xylem area (Table 3), their xylem would not be more vulnerable to cavitation. The severe droughts during the early 2000s occurred mainly in spring, but the latewood was more affected because in Mediterranean ring-porous oaks the enlargement of earlywood vessels depends more on winter temperature conditions prior to their formation, whereas the development of latewood is driven by spring to summer cumulative water deficit (Alla and Camarero, 2012). It could be described as a “latewood-biased” xylem providing more hydraulic conductivity during the mid to late growing season (Corcuera et al., 2006), and possibly corresponding to a more anisohydric behavior. An increase in VPD caused by warmer conditions, as those observed at the study area during the recorded 2000s droughts (Figure 2B), could have triggered a decrease in the leaf transpiring surface, which is a way to reduce the canopy evaporative water loss (DeLucia et al., 2000). However, such a sharp decrease in leaf biomass did not avoid tree death, which started to occur in 2007 and 2008 (Figure 2A). At the shoot level, winter-deciduous Mediterranean oaks often show a reduction in transpiring leaf area as compared with similar oak species from temperate areas. However, their anisohydric behavior, particularly when VPD is not elevated and soil water is available, may compensate for the loss in carbon gain caused by a lower leaf area (Peguero-Pina et al., 2016). In addition, Mediterranean anisohydric oaks such as Quercus faginea present premature leaf withering in response to drought. This reduction in carbon gain has been linked to xylem hydraulic failure (Peguero-Pina et al., 2015). Leaf loss could thus be seen as a mechanism of drought avoidance in winter-deciduous Mediterranean species such as the Italian oak. This punctual reduction in carbon uptake could be offset by elevated gas-exchange rates, but also by high primary-growth rates, allowing a rapid development of shoots and leaves in spring (Alla et al., 2012). Further research could also compare the patterns of growth, as related to those of carbon storage (non-structural carbohydrates) in coexisting Mediterranean oak species, showing drought-induced dieback. A higher dependence of carbohydrates stored in leaves could make some evergreen oak species (e.g., Quercus ilex) very sensitive to dry spells, whilst deciduous species could tolerate drought by preferentially storing carbohydrates in shoot wood (Camarero et al., 2016).
Conclusion
The probability of oak death was negatively related to tree height, which is contrary to what hydraulic theory predicted. We interpret this result as increased drought sensitivity of small individuals compared to tall trees, suggesting that tall trees are better able than small trees to obtain soil water with their deeper root system under intense and prolonged drought stress. The more intense leaf shedding in recently dead oaks characterized the dieback process, which started during the early 2000s, when a strong decline in BAI began. This growth decline occurred about 10 years before most declining oaks died in 2014. The presented mortality models indicate that growth prior to tree death can be used as early-warning signal of impending tree mortality. Considering forest management, tree-to-tree competition did not predispose to tree death. In temperate forests competition in dense stands can contribute to drought-induced mortality (Pedersen, 1998), but at dry sites forest patches with low tree density also show high mortality rates (Dorman et al., 2015). This observation questions the validity of moderate thinning as a tool to increase the survival probability of trees facing prolonged droughts (McDowell et al., 2006), and indicates that intense thinning may be a better tool in some cases (Calev et al., 2016).
Author Contributions
MC, JC, MB, TG, and FR conceived the idea and contributed to the writing of research project. MC, TG, and FR contributed to the field work. The dataset was analyzed by JC, MC, and AG. All authors contributed to the interpretation of the results. JC and MC wrote the first draft of the manuscript; thereafter all authors revised the first draft by rewriting, discussing and commenting. All authors read and approved the final draft.
Funding
This research was financially supported by the project “Alarm of forest mortality in Southern Italy” (Gorgoglione Administration, Basilicata Region, Italy) and by the CGL2015-69186-C2-1-R project (Spanish Ministry of Economy).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acnowledgments
AG was supported by a Postdoctoral grant from MINECO (Contrato Formación Postdoctoral MINECO – FPDI 2013-16600, FEDER funds). MC was supported by the PhD program in Agricultural, Forest and Food Science (University of Basilicata, Italy). We thank the framework of the COST network STReESS for facilitating collaborative work. We acknowledge the E-OBS dataset from the EU-FP6 project ENSEMBLES (http://ensembles-eu.metoffice.com) and the data providers in the ECA&D project (http://www.ecad.eu).
Footnotes
References
Alla, A. Q., and Camarero, J. J. (2012). Contrasting responses of radial growth and wood anatomy to climate in a Mediterranean ring-porous oak: implications for its future persistence or why the variance matters more than the mean. Eur. J. For. Res. 131, 1537–1550. doi: 10.1007/s10342-012-0621-x
Alla, A. Q., Camarero, J. J., and Montserrat-Martí, G. (2012). Seasonal and inter-annual variability of bud development as related to climate in two co-existing Mediterranean Quercus species. Ann. Bot. 111, 261–270. doi: 10.1093/aob/mcs247
Allen, C. D., Macalady, A. K., Chenchouni, H., Bachelet, D., McDowell, N., Vennetier, M., et al. (2010). A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manage. 259, 660–684. doi: 10.1016/j.foreco.2009.09.001
Baguskas, S. A., Peterson, S. H., Bookhagen, B., and Still, C. J. (2014). Evaluating spatial patterns of drought-induced tree mortality in a coastal California pine forest. For. Ecol. Manage. 315, 43–53. doi: 10.1016/j.foreco.2013.12.020
Bennett, A. C., McDowell, N. G., Allen, C. D., and Anderson-Teixeira, K. J. (2015). Larger trees suffer most during drought in forests worldwide. Nat. Plants 1:15139. doi: 10.1038/nplants.2015.139
Bigler, C., and Bugmann, H. (2003). Growth-dependent tree mortality models based on tree rings. Can. J. For. Res. 33, 210–221. doi: 10.1139/x02-180
Bigler, C., and Bugmann, H. (2004). Predicting the time of tree death using dendrochronological data. Ecol. Appl. 14, 902–914. doi: 10.1890/03-5011
Bigler, C., Gričar, J., Bugmann, H., and Čufar, K. (2004). Growth patterns as indicators of impending tree death in silver fir. For. Ecol. Manage. 199, 183–190.
Bigler, C., and Veblen, T. T. (2009). Increased early growth rates decrease longevities of conifers in subalpine forests. Oikos 118, 1130–1138. doi: 10.1111/j.1600-0706.2009.17592.x
Bircher, N., Cailleret, M., and Bugmann, H. (2015). The agony of choice: different empirical models lead to sharply different future forest dynamics. Ecol. Appl. 25, 1303–1318. doi: 10.1890/14-1462.1
Bowman, D. M. J. S., Brienen, R. J. W., Gloor, E., Phillips, O. L., and Prior, L. D. (2013). Detecting trends in tree growth: not so simple. Trends Plant Sci. 18, 11–17. doi: 10.1016/j.tplants.2012.08.005
Brock, W. A., and Carpenter, S. R. (2012). Early warnings of regime shift when the ecosystem structure is unknown. PLoS ONE 7:e45586. doi: 10.1371/journal.pone.0045586
Burnham, K. P., and Anderson, D. R. (1998). Model Selection and Inference: A Practical Information-Theoretic Approach. New York, NY: Springer.
Cailleret, M., Bigler, C., Bugmann, H., Camarero, J. J., Cufar, K., Davi, H., et al. (2016). Towards a common methodology for developing logistic tree mortality models based on ring-width data. Ecol Appl. 26, 1827–1841. doi: 10.1890/15-1402.1
Calev, A., Zoref, C., Tzukerman, M., Moshe, Y., Zangy, E., and Osem, Y. (2016). High-intensity thinning treatments in mature Pinus halepensis plantations experiencing prolonged drought. Eur. J. For. Res. 135, 551–563. doi: 10.1007/s10342-016-0954-y
Camarero, J. J., Gazol, A., Sangüesa-Barreda, G., Oliva, J., and Vicente-Serrano, S. M. (2015). To die or not to die: early warnings of tree dieback in response to a severe drought. J. Ecol. 103, 44–57. doi: 10.1111/1365-2745.12295
Camarero, J. J., Sangüesa-Barreda, G., and Vergarechea, M. (2016). Prior height, growth, and wood anatomy differently predispose to drought-induced dieback in two Mediterranean oak species. Ann. For. Sci. 73, 341–351. doi: 10.1007/s13595-015-0523-4
Carbone, M. S., Williams, A. P., Ambrose, A. R., Boot, C. M., Bradley, E. S., Dawson, T. E., et al. (2012). Cloud shading and fog drip influence the metabolism of a coastal pine ecosystem. Glob. Chang. Biol. 19, 484–497. doi: 10.1111/gcb.12054
Carpenter, S. R., and Brock, W. A. (2011). Early warnings of unknown nonlinear shifts: a nonparametric approach. Ecology 92, 2196–2201. doi: 10.1890/11-0716.1
Chatziphilippidis, G., and Spyroglou, G. (2004). “Sustainable management of coppice forests in Greece,” in Towards the Sustainable Use of Europe’s Forests - Forest Ecosystem and Landscape Research: Scientific Challenges and Opportunities, EFI Proceedings No, 49, eds F. Andersson, Y. Birot, and R. Paivinen (Joensuu: European Forest Institute), 51–60.
Chen, H. Y. H., Fu, S., Monserud, R. A., and Gillies, I. C. (2008). Relative size and stand age determine Pinus banksiana mortality. For. Ecol. Manage. 255, 3980–3984. doi: 10.1016/j.foreco.2008.03.040
Coomes, D. A., and Allen, R. B. (2007). Effects of size, competition and altitude on tree growth. J. Ecol. 95, 1084–1097. doi: 10.1016/j.scitotenv.2016.08.115
Corcuera, L., Camarero, J. J., Sisó, S., and Gil-Pelegrín, E. (2006). Radial-growth and wood-anatomical changes in overaged Quercus pyrenaica coppice stands: functional responses in a new Mediterranean landscape. Trees 20, 91–98. doi: 10.1007/s00468-005-0016-4
Dakos, V., Carpenter, S. R., Brock, W. A., Ellison, A. M., Guttal, V., Ives, A. R., et al. (2012). Methods for detecting early warnings of critical transitions in time series illustrated using simulated ecological data. PLoS ONE 7:e41010. doi: 10.1371/journal.pone.0041010
Das, A., Battles, J., Stephenson, N., and van Mantgem, P. (2007). The relationship between tree growth patterns and likelihood of mortality: a study of two tree species in the Sierra Nevada. Can. For. J. Res. 37, 580–597. doi: 10.1139/X06-262
DeLucia, E. H., Maherali, H., and Carey, E. V. (2000). Climate-driven changes in biomass allocation in pines. Glob. Chang. Biol. 6, 587–593. doi: 10.1046/j.1365-2486.2000.00338.x
Dobbertin, M. (2005). Tree growth as indicator of tree vitality and of tree reaction to environmental stress: a review. Eur. J. For. Res. 124, 319–333. doi: 10.1007/s10342-005-0085-3
Dorman, M., Svoray, T., Perevolotsky, A., Moshe, Y., and Sarris, D. (2015). What determines tree mortality in dry environments? A multi-perspective approach. Ecol. Appl. 25, 1054–1071.
Drobyshev, I., Linderson, H., and Sonesson, K. (2007). Temporal mortality pattern of pedunculate oaks in southern Sweden. Dendrochronologia 24, 97–108. doi: 10.1016/j.dendro.2006.10.004
Duchesne, L., Ouimet, R., and Morneau, C. (2003). Assessment of sugar maple health based on basal area growth pattern. Can. J. For. Res. 33, 2074–2080. doi: 10.1139/x03-141
Dwyer, J. P., Cutter, B. E., and Wetteroff, J. J. (1995). A dendrochronological study of black and scarlet oak decline in the Missouri Ozarks. For. Ecol. Manage. 75, 69–75. doi: 10.1016/0378-1127(95)03537-K
Fielding, A. H., and Bell, J. F. (1997). A review of methods for the assessment of prediction errors in conservation presence/absence models. Environ. Conserv. 24, 38–49. doi: 10.1017/S0376892997000088
Forrester, D. I., Kohnle, U., Albrecht, A. T., and Bauhus, J. (2013). Complementarity in mixed-species stands of Abies alba and Picea abies varies with climate, site quality and stand density. For. Ecol. Manage. 304, 233–242. doi: 10.1016/j.foreco.2013.04.038
Gärtner, H., and Nievergelt, D. (2010). The core-microtome: a new tool for surface preparation on cores and time series analysis of varying cell parameters. Dendrochronologia 28, 85–92. doi: 10.1016/j.dendro.2009.09.002
Gea-Izquierdo, G., Viguera, B., Cabrera, M., and Cañellas, I. (2014). Drought induced decline could portend widespread pine mortality at the xeric ecotone in managed mediterranean pine-oak woodlands. For. Ecol. Manage. 320, 70–82. doi: 10.1016/j.foreco.2014.02.025
Gentine, P., Guérin, M., Uriarte, M., McDowell, N. G., and Pockman, W. T. (2016). An allometry-based model of the survival strategies of hydraulic failure and carbon starvation. Ecohydrology 9, 529–546. doi: 10.1002/eco.1654
Gibbons, J. D., and Chakraborti, S. (2011). Nonparametric Statistical Inference, 5th Edn. New York, NY: CRC Press.
Grote, R., Gessler, A., Hommel, R., Poschenrieder, W., and Priesack, E. (2016). Importance of tree height and social position for drought-related stress on tree growth and mortality. Trees 30, 1467–1482. doi: 10.1007/s00468-016-1446-x
Haavik, L. J., Stahle, D. W., and Stephen, F. M. (2011). Temporal aspects of Quercus rubra decline and relationship to climate in the Ozark and Ouachita Mountains. Arkansas. Can. J. For. Res. 41, 773–781. doi: 10.1139/x11-018
Hanna, P., and Kulakowski, D. (2012). The influences of climate on aspen dieback. For. Ecol. Manage. 274, 91–98. doi: 10.1111/gcb.12805
Hentschel, R., Rosner, S., Kayler, Z. E., Andreassen, K., Børja, I., Solverg, S., et al. (2014). Norway spruce physiological and anatomical predisposition to dieback. For. Ecol. Manage. 322, 27–36. doi: 10.1016/j.foreco.2014.03.007
Hereş, A. M., Martínez-Vilalta, J., and Claramunt, B. (2012). Growth patterns in relation to drought-induced mortality at two Scots pine (Pinus sylvestris L.) sites in NE Iberian Peninsula. Trees 26, 621–630. doi: 10.1007/s00468-011-0628-9
Holmes, R. L. (1983). Computer–assisted quality control in tree–ring dating and measurement. Tree Ring Bull. 43, 69–78.
Holzwarth, F., Kahl, A., Bauhus, J., and Wirth, C. (2013). Many ways to die – partitioning tree mortality dynamics in a near-natural mixed deciduous forest. J. Ecol. 101, 220–230. doi: 10.1111/1365-2745.12015
Hosmer, D. W., Lemeshow, S., and Sturdivant, R. X. (2013). Applied Logistic Regression. New York, NY: Wiley and Sons, Inc.
Ireland, K. B., Moore, M. M., Fulé, P. Z., Zegler, T. J., and Keane, R. E. (2014). Slow lifelong growth predisposes Populus tremuloides trees to mortality. Oecologia 175, 847–859. doi: 10.1007/s00442-014-2951-5
Kane, J. M., and Kolb, T. E. (2014). Short- and long-term growth characteristics associated with tree mortality in southwestern mixed-conifer forests. Can. J. For. Res. 44, 1227–1235. doi: 10.1139/cjfr-2014-0186
Klein, T. (2014). The variability of stomatal sensitivity to leaf water potential across tree species indicates a continuum between isohydric and anisohydric behaviours. Funct. Ecol. 28, 1313–1320. doi: 10.1111/1365-2435.12289
Klos, R. J., Wang, G. G., Bauerle, W. L., and Rieck, J. R. (2009). Drought impact on forest growth and mortality in the southeast USA: an analysis using Forest Health and Monitoring data. Ecol. Appl. 19, 699–708. doi: 10.1890/08-0330.1
Kobe, R. K., Pacala, S. W., Silander, J. A., and Canham, C. D. (1995). Juvenile tree survivorship as a component of shade tolerance. Ecol. Appl. 5, 517–532. doi: 10.2307/1942040
Lawson, C. R., Hodgson, J. A., Wilson, R. J., and Richards, S. A. (2014). Prevalence, thresholds and the performance of presence-absence models. Methods Ecol. Evol. 5, 54–64. doi: 10.1111/2041-210X.12123
Levanic, T., Cater, M., and McDowell, N. G. (2011). Associations between growth, wood anatomy, carbon isotope discrimination and mortality in a Quercus robur forest. Tree Physiol. 31, 298–308. doi: 10.1093/treephys/tpq111
Linares, J. C., and Camarero, J. J. (2012). Growth patterns and sensitivity to climate predict silver fir decline in the Spanish Pyrenees. Eur. J. For. Res. 131, 1001–1012. doi: 10.1007/s10342-011-0572-7
Linares, J. C., Camarero, J. J., and Carreira, J. A. (2010). Competition modulates the adaptation capacity of forests to climatic stress: insights from recent growth decline and death in relict stands of the Mediterranean fir Abies pinsapo. J. Ecol. 185, 471–480.
Mamet, S. D., Chun, K. P., Metsaranta, J. M., Barr, A. G., and Johnstone, J. F. (2015). Tree rings provide early warning signals of jack pine mortality across a moisture gradient in the southern boreal forest. Environ. Res. Lett. 10:084021. doi: 10.1088/1748-9326/10/8/084021
Martínez-Vilalta, J., and Garcia-Forner, N. (2016). Water potential regulation, stomatal behaviour and hydraulic transport under drought: deconstructing the iso/anisohydric concept. Plant Cell Environ. doi: 10.1111/pce.12846
McDowell, N., Pockman, W. T., Allen, C. D., Breshears, D. D., Cobb, N., Kolb, T., et al. (2008). Mechanisms of plant survival and mortality during drought: why do some plants survive while others succumb to drought? New Phytol. 178, 719–739. doi: 10.1111/j.1469-8137.2008.02436.x
McDowell, N. G., Adams, H. D., Bailey, J. D., Hess, M., and Kolb, T. E. (2006). Homeostatic maintenance of ponderosa pine gas exchange in response to stand density changes. Ecol. Appl. 16, 1164–1182. doi: 10.1890/1051-07612006016[1164:HMOPPG]2.0.CO;2
McDowell, N. G., and Allen, C. D. (2015). Darcy’s law predicts widespread forest mortality under climate warming. Nat. Clim. Chang. 5, 669–672. doi: 10.1038/nclimate2641
McDowell, N. G., Allen, C. D., and Marshall, L. (2010). Growth, carbon-isotope discrimination, and drought-associated mortality across a Pinus ponderosa elevational transect. Glob. Change Biol. 16, 399–415. doi: 10.1111/j.1365-2486.2009.01994.x
Mencuccini, M., Martínez-Vilalta, J., Vanderklein, D., Hamid, H. A., Korakaki, E., Lee, S., et al. (2005). Size-mediated ageing reduces vigour in trees. Ecol. Lett. 8, 1183–1190. doi: 10.1111/j.1461-0248.2005.00819.x
Monserud, R. A., and Sterba, H. (1999). Modeling individual tree mortality for Austrian forest species. For. Ecol. Manage. 113, 109–123. doi: 10.1016/S0378-1127(98)00419-8
Ogle, K., Whitham, T. G., and Cobb, N. S. (2000). Tree-ring variation in pinyon predicts likelihood of death following severe drought. Ecology 81, 3237–3243. doi: 10.1890/0012-9658(2000)081[3237:TRVIPP]2.0.CO;2
Pedersen, B. S. (1998). The role of stress in the mortality of Midwestern oaks as indicated by growth prior to death. Ecology 79, 79–93. doi: 10.1890/0012-9658(1998)079[0079:TROSIT]2.0.CO;2
Pedersen, B. S. (1999). The mortality of midwestern overstory oaks as a bioindicator of environmental stress. Ecol. Appl. 9, 1017–1027. doi: 10.1890/1051-07611999009[1017:TMOMOO]2.0.CO;2
Peguero-Pina, J. J., Sancho-Knapik, D., Martín, P., Saz, M. A., Gea-Izquierdo, G., Cañellas, I., et al. (2015). Evidence of vulnerability segmentation in a deciduous Mediterranean oak (Quercus subpyrenaica E. H. del Villar). Trees 29, 1917–1927. doi: 10.1007/s00468-015-1273-5
Peguero-Pina, J. J., Sisó, S., Sancho-Knapik, D., Díaz-Espejo, A., Flexas, J., Galmés, J., et al. (2016). Leaf morphological and physiological adaptations of a deciduous oak (Quercus faginea Lam.) to the Mediterranean climate: a comparison with a closely related temperate species (Quercus robur L.). Tree Physiol. 36, 287–299. doi: 10.1093/treephys/tpv107
Pellizzari, E., Camarero, J. J., Gazol, A., Sangüesa-Barreda, G., and Carrer, M. (2016). Wood anatomy and carbon-isotope discrimination support long-term hydraulic deterioration as a major cause of drought-induced dieback. Glob. Change Biol. 22, 2125–2137. doi: 10.1111/gcb.13227
Phillips, N. G., Ryan, M. G., Bond, B. J., McDowell, N. G., Hinckley, T. M., and Cermak, J. (2003). Reliance on stored water increases with tree size in three species in the Pacific Northwest. Tree Physiol. 23, 237–245. doi: 10.1093/treephys/23.4.237
Phipps, R. L., and Whiton, J. C. (1988). Decline in long-term growth trends of white oak. Can. J. For. Res. 18, 24–32. doi: 10.1139/x88-005
R Core Team (2015). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
Rosner, S., Svìtlík, J., Andreassen, K., Børja, I., Dalsgaard, L., Evans, R., et al. (2016). Novel hydraulic vulnerability proxies for a boreal conifer species reveal that opportunists may have lower survival prospects under extreme climatic events. Front. Plant. Sci. 7:831. doi: 10.3389/fpls.2016.00831
Rowland, L., da Costa, A. C. L., Galbraith, D. R., Oliveira, R. S., Binks, O. J., Oliveira, A. A. R., et al. (2015). Death from drought in tropical forests is triggered by hydraulics not carbon starvation. Nature 528, 119–122. doi: 10.1038/nature15539
Ruiz-Benito, P., Lines, E. R., Gómez-Aparicio, L., Zavala, M. A., and Coomes, D. A. (2013). Patterns and drivers of tree mortality in Iberian forests: climatic effects are modified by competition. PLoS ONE 8:e56843. doi: 10.1371/journal.pone.0056843
Sanders, T. G. M., Pitman, R., and Broadmeadow, M. S. J. (2014). Species-specific climate response of oaks (Quercus spp.) under identical environmental conditions. iForests 7, 61–69. doi: 10.3832/ifor0911-007
Sangüesa-Barreda, G., Camarero, J. J., Oliva, J., Montes, F., and Gazol, A. (2015). Past logging, drought and pathogens interact and contribute to forest dieback. Agric. For. Meteorol. 208, 85–94. doi: 10.1016/j.agrformet.2015.04.011
Schneider, C. A., Rasband, W. S., and Eliceiri, K. W. (2012). NIH image to ImageJ: 25 years of image analysis. Nat. Methods 9, 671–675. doi: 10.1038/nmeth.2089
Scholz, A., Klepsch, M., Karimi, Z., and Jansen, S. (2013). How to quantify conduits in wood? Front. Plant Sci. 4:56. doi: 10.3389/fpls.2013.00056
Scholz, F. G., Phillips, N., Bucci, S. J., Meinzer, F. C., and Goldstein, G. (2011). “Hydraulic capacitance: biophysics and functional significance of internal water sources in relation to tree size,” in Size- and Age-related Changes in Tree Structure and Function, eds F. C. Meinzer, B. Lachenbruch, and T. E. Dawson (Dordrecht: Springer), 341–361.
Sevanto, S., McDowell, N. G., Dickman, L. T., Pangle, R., and Pockman, W. T. (2014). How do trees die? A test of the hydraulic failure and carbon starvation hypotheses. Plant Cell Environ. 37, 153–161. doi: 10.1111/pce.12141
Sing, T., Sander, O., Beerenwinkel, N., and Lengauer, T. (2013). Package ‘ROCR’: Visualizing the Performance of Scoring Classifiers. Available at: http://rocr.bioinf.mpi-sb.mpg.de/
Sperry, J. S., Nichols, K. L., Sullivan, J. E. M., and Eastlack, S. E. (1994). Xylem embolism in ring-porous, diffuse-porous, and coniferous trees of Northern Utah and Interior Alaska. Ecology 75, 1736–1752. doi: 10.2307/1939633
Stojanović, D., Levanić, T., Matović, B., and Bravo-Oviedo, A. (2015). Climate change impact on a mixed lowland oak stand in Serbia. Ann. Silv. Res. 39, 94–99.
Suarez, M. L., Ghermandi, L., and Kitzberger, T. (2004). Factors predisposing episodic drought-induced tree mortality in Nothofagus – site, climatic sensitivity and growth trends. J. Ecol. 92, 954–966. doi: 10.1111/j.1365-2745.2004.00941.x
Tyree, M. T., and Zimmermann, M. H. (2002). Xylem Structure and the Ascent of Sap. Berlin: Springer.
Vicente-Serrano, S. M., Beguería, S., and López-Moreno, J. I. (2010). A multiscalar drought index sensitive to global warming: the standardized precipitation evapotranspiration index. J. Clim. 23, 1696–1718. doi: 10.1175/2009JCLI2909.1
Voltas, J., Camarero, J. J., Carulla, D., Aguilera, M., Oriz, A., and Ferrio, J. P. (2013). A retrospective, dual-isotope approach reveals individual predispositions to winter-drought induced tree dieback in the southernmost distribution limit of Scots pine. Plant Cell Environ. 36, 1435–1448. doi: 10.1111/pce.12072
Woodruff, D. R., Bond, B. J., and Meinzer, F. C. (2004). Does turgor limit growth in tall trees? Plant Cell Environ. 27, 229–236. doi: 10.1111/j.1365-3040.2003.01141.x
Worrall, J. J., Egeland, L., Eager, E., Mask, R. A., Johnson, E. W., Kemp, P. A., et al. (2008). Rapid mortality of Populus tremuloides in southwestern Colorado, USA. For. Ecol. Manage. 255, 686–696. doi: 10.1016/j.foreco.2007.09.071
Wunder, J., Brzeziecki, B., Żybura, H., Reineking, B., Bigler, C., and Bugmann, H. (2008). Growth–mortality relationships as indicators of life-history strategies: a comparison of nine tree species in unmanaged European forests. Oikos 117, 815–828. doi: 10.1111/j.0030-1299.2008.16371.x
Wyckoff, P. H., and Clark, J. S. (2000). Predicting tree mortality from diameter growth: a comparison of maximum likelihood and Bayesian approaches. Can. J. For. Res. 30, 156–167. doi: 10.1139/x99-198
Wyckoff, P. H., and Clark, J. S. (2002). The relationship between growth and mortality for seven co-occurring tree species in the southern Appalachian Mountains. J. Ecol. 90, 604–615. doi: 10.1046/j.1365-2745.2002.00691.x
Yao, X. H., Titus, S. J., and MacDonald, S. E. (2001). A generalized logistic model of individual tree mortality for aspen, white spruce, and lodgepole pine in Alberta mixedwood forests. Can. J. For. Res. 31, 283–291. doi: 10.1139/x00-162
Zhang, Y. J., Meinzer, F. C., Hao, G. Y., Scholz, F. G., Bucci, S. J., Takahashi, F. S. C., et al. (2009). Size-dependent mortality in a Neotropical savanna tree: the role of height-related adjustments in hydraulic architecture and carbon allocation. Plant Cell Environ. 32, 1456–1466. doi: 10.1111/j.1365-3040.2009.02012.x
Keywords: anisohydric species, drought-induced dieback, growth, mortality, Quercus frainetto, tree rings, wood anatomy
Citation: Colangelo M, Camarero JJ, Borghetti M, Gazol A, Gentilesca T and Ripullone F (2017) Size Matters a Lot: Drought-Affected Italian Oaks Are Smaller and Show Lower Growth Prior to Tree Death. Front. Plant Sci. 8:135. doi: 10.3389/fpls.2017.00135
Received: 12 September 2016; Accepted: 23 January 2017;
Published: 21 February 2017.
Edited by:
Sebastian Leuzinger, Auckland University of Technology, New ZealandReviewed by:
Eryuan Liang, Chinese Academy of Sciences, ChinaIgnacio García-González, University of Santiago de Compostela, Spain
Copyright © 2017 Colangelo, Camarero, Borghetti, Gazol, Gentilesca and Ripullone. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jesús J. Camarero, ampjYW1hcmVyb0BpcGUuY3NpYy5lcw==
 Michele Colangelo
Michele Colangelo Jesús J. Camarero
Jesús J. Camarero Marco Borghetti1
Marco Borghetti1 Francesco Ripullone
Francesco Ripullone