- 1Department of Computational and Systems Biology, John Innes Centre, Norwich, UK
- 2Botanical Institute and Cluster of Excellence on Plant Sciences, University of Cologne, Cologne Biocenter, Cologne, Germany
The key role of sulfur metabolites in response to biotic and abiotic stress in plants, as well as their importance in diet and health has led to a significant interest and effort in trying to understand and manipulate the production of relevant compounds. Metabolic engineering utilizes a set of theoretical tools to help rationally design modifications that enhance the production of a desired metabolite. Such approaches have proven their value in bacterial systems, however, the paucity of success stories to date in plants, suggests that challenges remain. Here, we review the most commonly used methods for understanding metabolic flux, focusing on the sulfur assimilatory pathway. We highlight known issues with both experimental and theoretical approaches, as well as presenting recent methods for integrating different modeling strategies, and progress toward an understanding of flux at the whole plant level.
Introduction
Sulfur is an essential nutrient; available in the soil as sulfate, plants are able to reduce inorganic sulfur, for use in a large number of primary and secondary metabolites.
Unsurprisingly, the study of reductive sulfur assimilation by plants is often pragmatically motivated; Brassicaceae especially have large sulfur requirements, and the quality and yield of oilseed rape is known to be affected by low sulfur availability (De Pascale et al., 2008). Furthermore, the importance of sulfur metabolites in diet and health (Sekiz et al., 1975; Tawfiq et al., 1995; Tripathi and Mishra, 2007; Traka and Mithen, 2011), their intrinsic economic value (Li et al., 2004), and conferred tolerance to abiotic or biotic stresses in the plant (Gatehouse, 2002; Bednarek et al., 2009; Yadav, 2010) has led to an interest in manipulating their production.
A tenet of metabolic engineering is that with sufficient understanding of the components, reactions, and fluxes through a pathway we can rationally design modifications that improve, for instance, the production of a desired metabolite. This interest in, and comparative lack of examples of successful sulfur pathway engineering in plants suggests that approaches thus far have failed to significantly advance our understanding of sulfur assimilation at some level.
For plants, all is flux; all biological responses are ultimately to direct the movement of molecules and energy through the metabolic network in the most appropriate way, often acting to buffer changes in metabolite levels (Mugford et al., 2011). Consequently, understanding the control of flux is a pre-requisite for successful metabolic engineering. Unfortunately, this dynamic property is comparatively difficult to measure and interpret, and thus requires the integrated involvement of theoretical biology. Mathematical modeling has developed a number of approaches to understand control of flux through metabolism, ranging from theoretical frameworks to integrate experimental results, to highly detailed kinetic models of small fragments of a pathway, to constraint-based methods which can encompass the entire reactome.
Here, we review the most commonly used methods for studying flux, focusing on the sulfur assimilatory pathway, not just because of the commercial and scientific importance of sulfur, but because it illustrates well the more general challenges and weaknesses of each approach. Starting with the difficulties of experimental attempts to partition control of flux among the enzymes of the pathway, we then consider small scale kinetic models of several pathway branches, and flux balance analysis (FBA), as well as recent approaches to integrate different modeling strategies, and progress toward an understanding of flux at the whole plant level.
Sulfur Assimilatory Pathway
The sulfur assimilatory pathway has been recently reviewed (Takahashi et al., 2011). In summary; sulfate is taken up from the environment, facilitated by specialized transporters. A large fraction of the sulfate is stored in the vacuole, while sulfate in chloroplasts or the cytosol is activated by ATP sulfurylase, forming adenosine 5′-phosphosulfate (APS). APS may then either be further phosphorylated by APS Kinase (APK) or reduced by APS Reductase (APR). Phoshorylation of APS forms 3′-phosphoadenosine 5′-phosphosulphate (PAPS), which acts as a promiscuous donor of activated sulfate, and is involved in the modification of a variety of proteins, saccharides, and secondary metabolites, including desulfo-glucosinolates. In primary assimilation, APS is instead reduced in the plastid to sulfite by APR, and then to sulfide by sulfite reductase (SiR). Sulfide in chloroplasts, mitochondria and the cytosol, is incorporated into O-acetylserine (OAS) to form cysteine, the precursor of all organic compounds containing reduced sulfur. Cysteine in the plastid may be converted into glutathione (GSH) via γ-glutamyl-cysteine, or reacts with phosphohomoserine, to form cystathionine, which can then be converted to methionine via homocysteine. Excess sulfite can be oxidized in the peroxisome back to sulfate by sulfite oxidase (Figure 1).
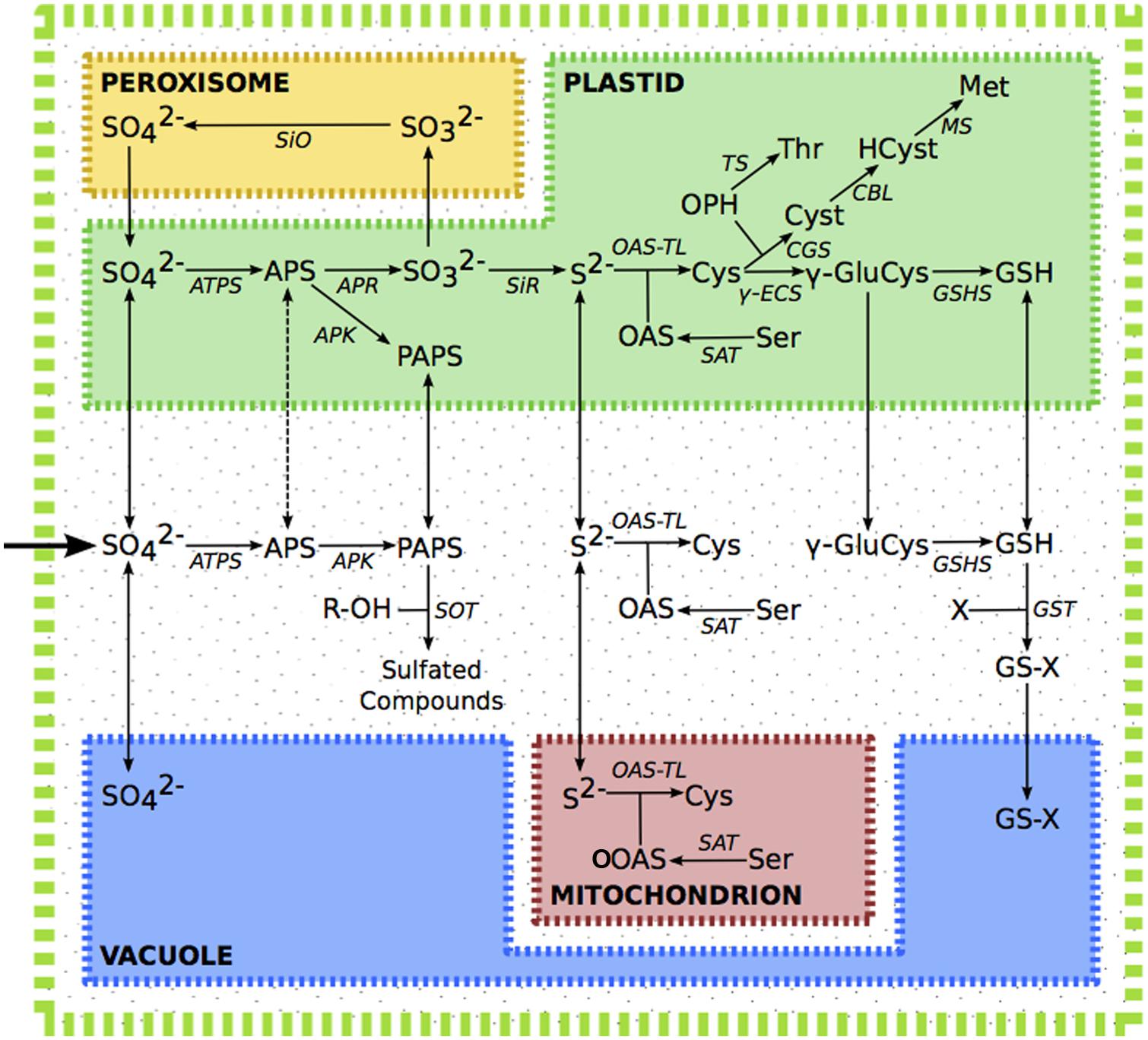
FIGURE 1. The sulfur assimilation pathway. Dashed line indicates putative transport of APS. Metabolite abbreviations; APS, adenosine 5′-phosphosulfate; Cys, cysteine; Cyst, cystathionine; γ-GluCys, γ-glutamyl-cysteine; GSH, glutathione; GS-X, glutathione conjugate; Hcy, homocysteine; Met, methionine; OAS, O-acetylserine; OPH, O-phosphohomoserine; PAPS, 3′-phosphoadenosine 5′-phosphosulfate; R-OH, hydroxylated precursor; Ser, serine; Thr, threonine. Enzyme abbreviations; APK, APS kinase; APR, APS reductase, ATPS, ATP sulfurylase; CBL, cystathionine β-lyase; CGS, cystathionine γ-synthase; γ-ECS, γ-glutamyl-cysteine synthetase; GSHS, glutathione synthetase; GST, glutathione-S-transferase; MS, methionine synthase; OAS-TL, OAS(thiol)lyase; SAT, serine acetyltransferase; SiO, sulphite oxidase; SiR, sulphite reductase; TS, threonine synthase.
Sulfur Flux Control – Measure by Measure
Efforts to experimentally characterize flux through the assimilation pathway are based on accumulation of radiolabelled 35S, from 35SO4, into various metabolite pools (Koprivova et al., 2000; Vauclare et al., 2002; Mugford et al., 2011). Assuming that over the timescale considered there is no significant turnover of the most downstream metabolites measured, this allows calculation of sulfur flux from SO4 through the pathway. By measuring alterations to flux distribution under genetically (Khan et al., 2010; Mugford et al., 2011), and environmentally (Koprivova et al., 2000; Vauclare et al., 2002; Scheerer et al., 2010) perturbed conditions it was hoped that insights could be gained into the control of flux through the sulfur assimilation pathway, and into various organic molecules.
Control is Distributed
To quantify control of flux, Vauclare et al. (2002) applied the metabolic control analysis (MCA) framework (for a comprehensive introduction to MCA, see Fell, 1992). Based on flux correlation with decreased APR activity, they calculated that APR has a large proportion of the total control of flux through the assimilatory pathway. From this, and several qualitative studies (Tsakraklides et al., 2002; Loudet et al., 2007), the hypothesis arose that APR is the key enzyme, controlling flux through the reductive assimilation pathway (Vauclare et al., 2002; Yoshimoto et al., 2007; Davidian and Kopriva, 2010; Scheerer et al., 2010). Consistent with this idea, APR has been shown to be highly regulated by demand for reduced sulfur products (Lappartient et al., 1999; Kopriva, 2006; Davidian and Kopriva, 2010; Takahashi et al., 2011), internal sulfate levels (Lee et al., 2012), and other environmental signals (Jost et al., 2005; Koprivova et al., 2008; Lee et al., 2011; Huseby et al., 2013).
More recently, however, a number of different enzymes have also been implicated in altered flux through the sulfur reduction pathway; Khan et al. (2010) found that SiR knockdown plants have a strongly reduced flux to thiols, variation in ATPS has been shown to cause altered flux of sulfur into primary metabolism (Koprivova et al., 2013), and reduction in APK increased flux through primary assimilation (Mugford et al., 2011). These results suggest that flux control is more complicated than had been previously thought, and extends beyond the APR enzyme. This distribution of control among multiple enzymes is a common feature of metabolic pathways (Thomas and Fell, 1998).
Difficulty of Applying MCA Framework to Experiments
Distributed control of flux means that a quantitative understanding, as attempted by Vauclare et al. (2002), becomes increasingly important for successfully engineering overproduction of metabolites. However, the results of this kind of perturbation experiment, in which the activity of an enzyme is artificially increased or decreased, are difficult to interpret within the MCA framework due to regulatory interactions, and non-linear changes in control coefficients with enzyme activity.
Metabolic control analysis defines flux control coefficients (FCCs) as the sensitivity of flux through the pathway to an infinitesimal change in a given enzyme activity from the reference state (Figure 2). These coefficients can be interpreted as a measure of the ‘rate limitingness’ of the enzyme to flux though the pathway, and potentially used to identify targets for overexpression to increase flux to metabolites of interest.
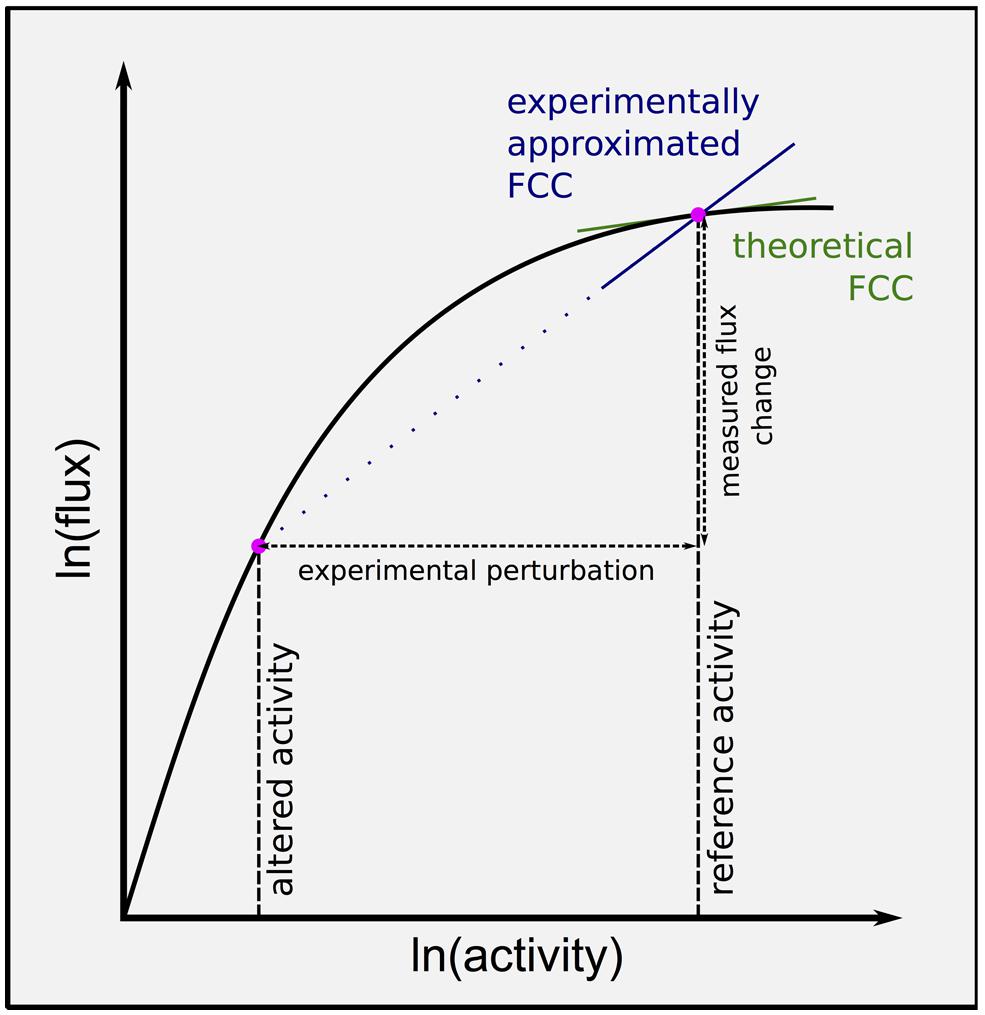
FIGURE 2. Flux control coefficient varies non-linearly with enzyme activity, confounding experimental approximations. Flux control coefficients (FCCs) can be computed from the gradient of the ln(flux) versus ln(activity) curve for a given enzyme. Most experimental attempts to approximate the FCC at the reference state measure the change in flux through the pathway with change in an enzyme activity. Larger experimental perturbations result in less accurate estimates, and knock down experiments can be expected to overestimate FCC at the reference state. Ideally multiple perturbations should be made, and the curve fitted to the data, allowing a point estimate of FCC at the reference state.
To determine FCCs experimentally, by measuring the effect of a genetic perturbation on flux through the pathway requires the assumption that no other enzyme activities change in compensation (Fell, 1992). However, demonstrating that this is the case is challenging (Vauclare et al., 2002; Scheerer et al., 2010), and given the complex regulation of the pathway by a number of metabolites (Takahashi et al., 2011) is generally unlikely to be true. Although for some simple purposes this may not matter, it does hinder an understanding the root causes of changes of flux through the network, limiting the applicability of any findings.
Flux control coefficients vary non-linearly with enzyme activity. Therefore although a large experimental change in enzyme activity may result in significantly altered flux through the pathway, this does not mean that the enzyme actually has a high control coefficient in the unperturbed state (Figure 2). Ideally several magnitudes of perturbation would be made, and used to estimate the control coefficient in unperturbed conditions, however, this has not been done to date within the sulfur community (Vauclare et al., 2002; Khan et al., 2010). Furthermore, this means that experimentally approximated control coefficients cannot be directly compared to each other, as genetic perturbations vary in magnitude (Vauclare et al., 2002; Khan et al., 2010). It is therefore still not quantitatively clear which reactions have how much control of sulfur assimilation, even under controlled experimental conditions.
This non-linearity also means that MCA is not a robust predictive framework for engineering; control coefficients at the reference state are not necessarily likely to reflect control coefficients under genetically altered conditions. Interestingly, Scheerer et al. (2010) found that distribution of FCCs through the sulfur assimilation pathway varied with environmental conditions and organism, likely due to altered enzyme expression levels. This highlights the importance of a predictive understanding of the controlling steps through the pathway, not only to more robustly predict the effect of genetic alterations, but also due to the impracticality of experimentally determining control distributions under all environments of interest.
Small is Beautiful – Kinetic Modeling
Although experimental investigations into control of flux through the pathway have been useful in qualitatively identifying important enzymes, this approach is limited, as multiple controlling enzymes and non-linear dynamics make predicting behavior away from measured conditions difficult. This was clearly seen in the analysis of poplar roots, where despite an increase in APR activity in many conditions, only few resulted in higher flux (Scheerer et al., 2010). Furthermore, the data generated experimentally is not easily integrated into a formal framework for analysis. In contrast, the MCA framework is easily applied to kinetic models of the pathway, which can be used not only to calculate control coefficients at the reference state more accurately than is possible experimentally, but also to simulate altered conditions. The difficulty lies, however, in producing an appropriate model.
Kinetic modeling of metabolic pathways is well established (see Curien et al., 2014 for a practical introduction). Models comprise a coupled system of ordinary non-linear, differential equations, functions of metabolite concentrations and kinetic parameters, which specify the rate of a reaction. A given pathway system can be mapped onto these equations, and solved numerically using a range of freely available software (Copeland et al., 2012).
In sulfur metabolism, this has allowed not only dissection of flux control distribution at several points (Curien et al., 2003; Mendoza-Cózatl and Moreno-Sánchez, 2006), but also predictions about how environmental perturbation changes control of flux to GSH (Mendoza-Cózatl and Moreno-Sánchez, 2006), and suggested engineering interventions to modify levels of sulfur metabolites. For example Curien et al. (2003) were able to predict that overexpressing cystathionine-γ-synthase would allow overproduction of methionine, without compromising threonine production, and that this was therefore a better strategy than knocking down threonine synthase (TS).
However, although kinetic models have yielded useful insights into flux through the sulfur assimilation pathway, the rarity of models published in this area hints at the difficulties of the approach.
Problems with Kinetic Models
Kinetic models require detailed understanding of the biological pathway under study, at the structural, thermodynamic, and kinetic levels. In many instances the pathway structure is well known, and thermodynamic data are either available (Goldberg et al., 2004), or can be calculated approximately (Jankowski et al., 2008), however, incomplete knowledge of enzyme kinetic parameters remains as the biggest hurdle to model building, particularly given that isoenzymes in different tissues or compartments often display different kinetics. Strategies for determining parameter values can be broadly split into measurement, and estimation approaches.
Parameter measurement
For small models, it may be possible to measure all kinetic parameters required. Curien et al. (2003) were able to measure the kinetic parameters of TS and cystathionine-γ-synthase for their model of the branch point of methionine and threonine biosynthesis in vitro, however, the large experimental effort required (Stitt and Gibon, 2014; Tummler et al., 2014; van Eunen and Bakker, 2014) makes this a comparatively rare example; it is more common to search the literature to recover the majority of parameters required (Rohwer, 2014). Several databases (Schomburg et al., 2004; Wittig et al., 2012) facilitate the search for previously determined kinetic parameters, however, generally poor coverage, particularly for allosteric regulation, means that it is accepted practice to use whichever parameters are available, either from experiments under differing conditions, or from orthologous proteins (Rohwer, 2014). The validity of transferring parameters in this way is generally unclear (Stitt and Gibon, 2014), the exception being enzyme activity parameters, which are acknowledged to vary so greatly with environment, that they should be measured under the condition of interest (Curien et al., 2014). There has been some speculation that advances in robotics, and microfluidics could lead to ‘omics style investigations’ into enzyme kinetics (Gibon et al., 2004; Sjostrom et al., 2013), however, a reliable high throughput pipeline has not to our knowledge been developed, and poor coverage is likely to remain a problem in the immediate future.
Kinetics databases highlight a further shortcoming of kinetic parameters measured in vitro; the assay conditions used are typically far from the in vivo environment seen by the enzyme. This problem of non-physiological in vitro assay media can be seen in Curien et al. (2003), where the use of high phosphohomoserine media, likely contributed to a poor initial model fit to data. Initiatives to design more in vivo like in vitro media, are underway for several microorganisms (Garcia-Contreras et al., 2012; Goel et al., 2012; Leroux et al., 2013), but to the best of our knowledge, no such effort has been reported in plants, where the problem is exacerbated by the presence of multiple subcellular compartments, each with a unique environment. In the sulfur assimilation pathway, three out of the five reactions converting sulfate to cysteine occur in multiple compartments (Takahashi et al., 2011) and thus likely require multiple sets of kinetic parameters.
Parameter estimation
The difficulties of obtaining experimentally measured kinetic parameters mean that in the vast majority of published models, at least some parameters are fitted by minimizing the difference between model predictions (e.g. of flux through the path), and experimental measurements (Tummler et al., 2014). Aside from the experimental difficulties of acquiring data, especially within subcellular compartments, one problem with this approach is overfitting; assigning parameter values to fit the data more precisely than is justified. As a result, many models parameterized using a top down approach lose predictive accuracy as conditions move away from those at which the parameters were fitted (Hawkins, 2004).
A number of approaches have been developed based on sensitivity of model predictions to parameter values to analyze parameter identifiability, and calculate confidence intervals for parameters and predictions (Cotten and Reed, 2013; Kravaris et al., 2013). However, these problems have not always been rigorously considered in the literature. Mendoza-Cózatl and Moreno-Sánchez (2006) ignored possible interaction terms between parameters in their sensitivity analysis, and Curien et al. (2003) provide no indication of the robustness of their predictions to error in measured parameter values.
Parameter reduction
Given the problem of estimating a large number of unknown parameters with limited data, most models tend to use lumped, empirical rate laws, which aim to capture the salient kinetic features, whilst minimizing the number of parameters required, rather than complicated, mechanistic laws (Heijnen, 2005; Curien et al., 2014; Rohwer, 2014). However, although this simplification can be useful (Costa et al., 2011), it inevitably leads to a loss in model fidelity. Curien et al. (2003) found that even replacing a ping-pong rate law with relatively complex Michaelis–Menten kinetics led to their model losing the experimentally identified insensitivity to cysteine concentration of cystathionine γ-synthase.
Small May not be Sufficient
A minimal model of a subsystem should include everything that affects the internal variables of the model (Curien et al., 2014), however, in practice, lack of biological knowledge can make it difficult to know what has to be included. Within the sulfur assimilation pathway, it is still often unclear which metabolites regulate enzyme activity allosterically, although it seems that many potentially can (Vauclare et al., 2002; Hopkins et al., 2005; Rouached et al., 2009; Hubberten et al., 2012; Lee et al., 2012). This means that, for example, even a small model of the APR, APK branch point must be large enough to consider the reduction pathway at least as far as GSH production, as this feeds back to regulate APR (Vauclare et al., 2002; Hacham et al., 2014) and possibly APK through changes in redox environment (Ravilious et al., 2012). This results in the requirement for a large number of kinetic parameters.
The extent to which models can be simplified and still remain useful is unclear, as an overly reduced model system can result in inaccurate predictions. For example ignoring phosphohomoserine production meant that Curien et al. (2003) were only able to identify a subset of the intervention steps that have since been experimentally shown to increase methionine production Lee et al. (2005) and Mendoza-Cózatl and Moreno-Sánchez (2006) demonstrated the importance of considering demand for GSH, as well as its production by finding that including demand results in large changes in the control coefficients of synthesizing reactions.
It is possible that a much larger metabolic network has to be considered when modeling sulfur assimilation than just the pathway itself, for example, GSH production at night is limited by availability of glycine, as its major source is photorespiration (Noctor et al., 1999). Integration of sulfur assimilation within the wider metabolic network is demonstrated by the tight coordination of sulfur uptake with nitrogen and carbon availability (Koprivova et al., 2000; Kopriva and Rennenberg, 2004; Nero et al., 2009), and the broad range of conditions which have been shown to alter enzyme activities in the pathway (Kopriva et al., 1999; Koprivova et al., 2008; Huseby et al., 2013). For instance cysteine links both nitrogen and carbon metabolism to sulfur assimilation via OAS. OAS availability is likely a dominant factor in regulating the production of cysteine by controlling formation of the cysteine synthase complex (Birke et al., 2012), and so its availability has to be considered in models of cysteine synthesis. Furthermore, as at least under some conditions, cysteine availability limits production of downstream metabolites such as methionine and GSH (Noctor et al., 1996), and these downstream metabolites can regulate upstream components (Vauclare et al., 2002; Hacham et al., 2014), therefore this link to wider metabolism should be acknowledged whichever part of the sulfur pathway is being studied.
The Difficulty with Larger Models
Unfortunately, as model size increases, the problems of unknown parameters, and rate laws become extremely difficult to overcome. To generate a large kinetic model, simplifying assumptions about parameter values (Smallbone and Mendes, 2013), and rate laws (Alves et al., 2008), are frequently made, but this often results in poor model quality away from the fitted conditions (Chakrabarti et al., 2013) and so is of limited predictive value.
Other kinetic modeling frameworks acknowledge the inherently greater unknowns of a large system, and use the available data to define a cadre of related models, or sample feasible parameter space, reflecting either structural, or parameter and rate law uncertainty in their predictions (Famili et al., 2005; Steuer et al., 2006; Tran et al., 2008; Miskovic and Hatzimanikatis, 2011). Some of these approaches have resulted in the production of large kinetic models, in the order of 200 metabolites and reactions (Khodayari et al., 2014), but do not scale well to bigger models. As model size increases, parameter space expands enormously (Zamora-Sillero et al., 2011), resulting in prohibitive computational requirements (Link et al., 2014). As such, kinetic modeling currently does not scale to the size that is likely to be required to gain a holistic understanding of flux through sulfur related pathways.
Bigger is Better – Genome Scale Models
In contrast, constraint-based modeling provides a number of hugely scalable, largely parameter free methods for understanding flux through large metabolic networks (Lewis et al., 2012; Bordbar et al., 2014a). Here we focus on FBA as the most commonly used constraint-based method, the only method currently applicable to the genome scale, and a foundation for of many closely related variants.
Flux balance analysis (Varma and Palsson, 1994) is a powerful technique to estimate internal flux distributions within a large-scale network using only the structure of the reaction network, an objective function, and a small number of measured nutrient uptake fluxes as constraints, (for a practical introduction, to the method, see Grafahrend-Belau et al., 2014). By assuming metabolic steady state, and that fluxes are distributed so as to maximize some cellular objective, feasible flux space is reduced, and a subset of biologically likely internal flux distributions are predicted.
Flux balance analysis can be directly used in a number of areas, including understanding metabolic efficiency (Chen and Shachar-Hill, 2012), interpreting ‘omics data’ (Toepfer et al., 2013; Simons et al., 2014b), and predicting novel metabolic pathways (Hay and Schwender, 2011; Bordbar et al., 2014b). Furthermore extensions to the method interpret structural properties related to control of flux (Notebaart et al., 2008; Sajitz-Hermstein and Nikoloski, 2013), predict how flux distribution changes in response to genetic and environmental changes (Segre et al., 2002; Cheung et al., 2014), and suggest optimal intervention strategies to engineer metabolite production (Zomorrodi et al., 2012; Tomar and De, 2013; Ohno et al., 2014), as well as having a number of other applications (Papp et al., 2011; Bordbar et al., 2014a). This array of methods has been recently reviewed (Lewis et al., 2012), but continues to rapidly expand.
Problems with Genome Scale Models
In spite of a profligacy of analytical methods and well-documented metabolic engineering case studies in microbes, application of FBA based methods to plants has been limited to date. This is likely due to challenges in genome scale model construction, and the assumptions of the FBA method, as will be discussed below.
Model construction
Despite a large number of available tools (Kim et al., 2012), construction of a genome scale model is not a facile task, and particularly in plants remains a laborious undertaking (Saha et al., 2014; Simons et al., 2014a). Here we highlight some of the difficulties biological unknowns cause in creating even single cell type models of plants.
Although primary metabolism is well understood, the generally poorer understanding of the huge plant secondary metabolism (Shachar-Hill, 2013), is reflected in the focus of models published to date (Poolman et al., 2009; Williams et al., 2010; Cheung et al., 2013). The problem of unknown metabolites was recently highlighted for sulfur metabolites in particular (Glaeser et al., 2014), and the potentially large numbers of missing reactions suggested by the large proportion of genome content with unknown function (Seaver et al., 2012) could also adversely affect prediction quality.
All published genome scale models of plant metabolism include compartmentalization to some extent, but the problem of biological unknowns again raises concern over the quality of some of the assignations. Wide variation between models in which compartments reactions occur (Poolman et al., 2009; Masakapalli et al., 2010; Mintz-Oron et al., 2012) suggests that despite databases of subcellular enzyme location (Heazlewood et al., 2007; Sun et al., 2009), and parsimony based methods for extending database coverage (Mintz-Oron et al., 2012), the number of reactions which can be confidently assigned to particular compartments, and in particular to the vacuole, is probably much lower than occur in reality (Krueger et al., 2011). This reflects the current difficulty of experimentally determining subcellular reaction location.
Additionally, transport between compartments is often poorly understood; even in well-studied parts of metabolism, it is not always clear which metabolites can move between compartments, and the energetic costs of transport reactions are rarely known. This is shown in the sulfur assimilatory pathway by the only recent identification of PAPS transport between the plastid and cytosol (Gigolashvili et al., 2012).
FBA analysis
Objective functions. In addition to defining network structure, some biological knowledge of the system is required to choose an appropriate objective function. One commonly used objective is maximization of biomass production (Feist and Palsson, 2010), which is equivalent to finding the most efficient way of generating biomass from nutrients taken up by the cell (Zarecki et al., 2014). Although maximization of biomass is generally accepted as a good objective function for bacteria in log phase, the accuracy of fluxes predicted using it vary with environment, growth phase, and species, suggesting that this is not always appropriate (Schuster et al., 2008; Feist and Palsson, 2010).
A number of other objective functions have been considered in the literature, most often tied either explicitly or implicitly to efficiency in some regard (Chen and Shachar-Hill, 2012), although recently other objectives have been proposed which either aim to maximize growth rate (Zarecki et al., 2014) or minimize conflict with ‘omic data’ (Becker and Palsson, 2008; Collins et al., 2012). Much literature assessing the performance of these various different objective functions in correctly predicting observed growth, gene essentiality or flux states in bacteria (Burgard and Maranas, 2003; Schuetz et al., 2007; Feist and Palsson, 2010), and plants (Cheung et al., 2013) has been produced, however, it is not clear that organisms act to optimize a single objective function, even under constant conditions (Nagrath et al., 2007; Schuetz et al., 2012; Harcombe et al., 2013).
Combined objectives give the most accurate predicted flux distributions, and both in bacteria (Schuetz et al., 2012), and Eukaryotes (Nagrath et al., 2007), cell fluxes apparently occupy a Pareto surface, at which several objectives trade-off against each other, as further increase in one objective leads to a decrease in another. It is not obvious how this problem of competing objectives can be addressed by FBA; defining an appropriate objective function becomes much more difficult, because although frameworks for optimizing multiple objectives are well established (Oh et al., 2009; Zomorrodi and Maranas, 2012; Zomorrodi et al., 2014), the lack of a predictive understanding of which trade-offs are likely to apply, limits their application, as it is likely to vary with species, environment, and developmental state.
Degeneracy. Another problem is degeneracy, FBA is often unable to distinguish between a number of flux distributions, which all maximize the objective function. Although this degeneracy of predicted distributions is often considered undesirable (Pozo et al., 2014), it is in fact likely to reflect biological reality. Degenerate optimal solutions are consistent with robustness, which seems to be a common feature of biological networks (Kitano, 2004), and a population of cells is unlikely to be adequately described by a single flux distribution (Labhsetwar et al., 2013).
The real difficulty associated with degenerate flux distributions is that experimentally measured fluxes in bacteria often actually exist in suboptimal regions, which allow large flux variation (Schuetz et al., 2012; Harcombe et al., 2013; Roman et al., 2014) without further compromising the best combination of assumed objectives. Although the extent to which apparent sub-optimal distributions arise through the averaging of measured fluxes in a heterogeneous population, rather than sub-optimality in a single cell is unclear, the FBA assumption that flux is distributed in order to maximize an objective function may only be a useful approximation in specific cases. FBA based methods are beginning to appear that address the need to consider only partially optimized distributions (Wintermute et al., 2013), but sub-optimal distributions are a major challenge for the FBA framework, which given the sophistication and size of plant metabolic networks, and numerous differentiated cell types, is likely to be particularly relevant to their study.
In spite of these difficulties, an increasing number of studies have accurately predicted flux distributions in plants cells using FBA (Dal’Molin et al., 2010a; Williams et al., 2010; Hay and Schwender, 2011; Saha et al., 2011; Cheung et al., 2013). Precise external flux measurements have been shown to be more important for accurately predicting internal fluxes than the objective function used (Cheung et al., 2013), and although current approaches to use transcriptomics data to improve flux prediction accuracy have been recently questioned (Machado and Herrgard, 2014), fluxomics data generated by metabolic flux analysis [recently reviewed from a sulfur perspective by Rennenberg and Herschbach (2014)] can be used to add additional constraints, and further improve prediction accuracy (Hay and Schwender, 2011). It seems only a matter of time before FBA is used to facilitate engineering outcomes in plant cell cultures.
Sulfur and Beyond – Toward Whole Plant Flux Models
There is great interest in bridging the gap between the long tradition of eco-physiological agronomic models (Keurentjes et al., 2013), and molecular models. Combined, these two approaches could provide an integrated understanding of control of economically important traits (Baldazzi et al., 2012; Poorter et al., 2013). This fusion requires the ability to model differentiated tissue, at least at the organ level, and consider dynamic changes to flux.
Genome scale plant models to date have generally focused on cell cultures grown in suspension (Williams et al., 2010; Cheung et al., 2013) and so bypassed the problem of differentiation, but a particular challenge in whole plant models is the large number of cell types present. Although attempts to address this remain fairly crude, and restricted to models of only a few cell types or organs, the framework, in which proteomics data is integrated into constraint-based models to generate tissue, or organ specific sub-models (Mintz-Oron et al., 2012), which can then be coupled together, and used to predict fluxes through heterogeneous material (Dal’Molin et al., 2010b; Grafahrend-Belau et al., 2013) is established.
The greatest limitation of the FBA method is that it can only consider a steady state snapshot of flux distribution, especially as the extent to which metabolism at the whole plant level is ever in steady state remains unclear. Although recent work in plants has studied responses to light–dark cycles using a purely FBA approach (Cheung et al., 2014), and FBA metrics have been identified which correlate with metabolite concentration dynamics (Reznik et al., 2013), the application of a purely FBA based methodology to study dynamic systems is limited. In bacteria, there has been a movement toward integrating FBA models within a kinetic model. This is used to dynamically modify the exchange reaction constraints while FBA is repeatedly performed, allowing internal flux dynamics to be approximated (Varma and Palsson, 1994; Mahadevan et al., 2002). Output from the FBA simulation may then be fed back, to modify the kinetic model, or not (Feng et al., 2012). This hybrid modeling approach allows prediction of genome scale fluxes over time (Vargas et al., 2011; Jouhten et al., 2012), with only a few parameters required to capture input and output fluxes, biomass prerequisites, and maintenance costs.
This dynamic flux balance analysis (dFBA) approach makes a pseudo steady state assumption, that intracellular metabolism equilibrates several orders of magnitude faster than extracellular changes. Although it is likely that the pseudo steady state assumption might not be justified in all aspects of plant metabolism, a recent extension to the method potentially relaxes this requirement (Birch et al., 2014). Grafahrend-Belau et al. (2013) recently used dFBA to link a multi organ model of barley metabolism with an agronomic model, and provide insight into the dynamic interaction of source and sink organs in relation to senescence. Although fairly unsophisticated in the models used and interaction framework considered, the first steps toward a whole plant model have been taken, and dFBA is likely to find wider application in the coming years.
Concluding Remarks
Flux is perhaps the most important metric to determine for a practical, applied understanding of plant biology. Through the study of sulfur metabolism we have seen that to understand flux requires a fusion of experimental and modeling approaches, but that to date, no integration of the two satisfactorily solves the problem to provide an accurate predictive framework. Each approach considered continues to advance independently both theoretically and experimentally, but currently perhaps most promising is the joining of kinetic and constraint-based approaches, which although an immature field, has the potential to finally deliver a useful facet of the famous ‘virtual plant.’
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by the Biotechnology and Biological Sciences Research Council (BBSRC) grant BB/J004561/1 and the John Innes Foundation.
References
Alves, R., Vilaprinyo, E., Hernandez-Bermejo, B., and Sorribas, A. (2008). Mathematical formalisms based on approximated kinetic representations for modeling genetic and metabolic pathways. Biotechnol. Genet. Eng. Rev. 25, 1–40. doi: 10.5661/bger-25-1
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Baldazzi, V., Bertin, N., De Jong, H., and Genard, M. (2012). Towards multiscale plant models: integrating cellular networks. Trends Plant Sci. 17, 728–736. doi: 10.1016/j.tplants.2012.06.012
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Becker, S. A., and Palsson, B. O. (2008). Context-specific metabolic networks are consistent with experiments. PLoS Comput. Biol. 4:e1000082. doi: 10.1371/journal.pcbi.1000082
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Bednarek, P., Pislewska-Bednarek, M., Svatos, A., Schneider, B., Doubsky, J., Mansurova, M.,et al. (2009). A glucosinolate metabolism pathway in living plant cells mediates broad-spectrum antifungal defense. Science 323, 101–106. doi: 10.1126/science.1163732
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Birch, E. W., Udell, M., and Covert, M. W. (2014). Incorporation of flexible objectives and time-linked simulation with flux balance analysis. J. Theor. Biol. 345, 12–21. doi: 10.1016/j.jtbi.2013.12.009
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Birke, H., Mueller, S. J., Rother, M., Zimmer, A. D., Hoernstein, S. N. W., Wesenberg, D.,et al. (2012). The relevance of compartmentation for cysteine synthesis in phototrophic organisms. Protoplasma 249, 147–155. doi: 10.1007/s00709-012-0411-9
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Bordbar, A., Monk, J. M., King, Z. A., and Palsson, B. O. (2014a). Constraint-based models predict metabolic and associated cellular functions. Nat. Rev. Genet. 15, 107–120. doi: 10.1038/nrg3643
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Bordbar, A., Nagarajan, H., Lewis, N. E., Latif, H., Ebrahim, A., Federowicz, S.,et al. (2014b). Minimal metabolic pathway structure is consistent with associated biomolecular interactions. Mol. Syst. Biol. 10:737. doi: 10.15252/msb.20145243
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Burgard, A. P., and Maranas, C. D. (2003). Optimization-based framework for inferring and testing hypothesized metabolic objective functions. Biotechnol. Bioeng. 82, 670–677. doi: 10.1002/bit.10617
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Chakrabarti, A., Miskovic, L., Soh, K. C., and Hatzimanikatis, V. (2013). Towards kinetic modeling of genome-scale metabolic networks without sacrificing stoichiometric, thermodynamic and physiological constraints. Biotechnol. J. 8, 1043–1057. doi: 10.1002/biot.201300091
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Chen, X., and Shachar-Hill, Y. (2012). Insights into metabolic efficiency from flux analysis. J. Exp. Bot. 63, 2343–2351. doi: 10.1093/jxb/ers057
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Cheung, C. Y. M., Poolman, M. G., Fell, D. A., Ratcliffe, R. G., and Sweetlove, L. J. (2014). A diel flux balance model captures interactions between light and dark metabolism during day-night cycles in C-3 and crassulacean acid metabolism leaves. Plant Physiol. 165, 917–929. doi: 10.1104/pp.113.234468
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Cheung, C. Y. M., Williams, T. C. R., Poolman, M. G., Fell, D. A., Ratcliffe, R. G., and Sweetlove, L. J. (2013). A method for accounting for maintenance costs in flux balance analysis improves the prediction of plant cell metabolic phenotypes under stress conditions. Plant J. 75, 1050–1061. doi: 10.1111/tpj.12252
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Collins, S. B., Reznik, E., and Segre, D. (2012). Temporal expression-based analysis of metabolism. PLoS Comput. Biol. 8:e1002781. doi: 10.1371/journal.pcbi.1002781
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Copeland, W. B., Bartley, B. A., Chandran, D., Galdzicki, M., Kim, K. H., Sleight, S. C.,et al. (2012). Computational tools for metabolic engineering. Metab. Eng. 14, 270–280. doi: 10.1016/j.ymben.2012.03.001
Costa, R. S., Machado, D., Rocha, I., and Ferreira, E. C. (2011). Critical perspective on the consequences of the limited availability of kinetic data in metabolic dynamic modelling. IET Syst. Biol. 5, 157–163. doi: 10.1049/iet-syb.2009.0058
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Cotten, C., and Reed, J. L. (2013). Mechanistic analysis of multi-omics datasets to generate kinetic parameters for constraint-based metabolic models. BMC Bioinformatics 14:32. doi: 10.1186/1471-2105-14-32
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Curien, G., Cardenas, M. L., and Cornish-Bowden, A. (2014). Analytical kinetic modeling: a practical procedure. Methods Mol. Biol. 1090, 261–280. doi: 10.1007/978-1-62703-688-7_16
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Curien, G., Ravanel, S., and Dumas, R. (2003). A kinetic model of the branch-point between the methionine and threonine biosynthesis pathways in Arabidopsis thaliana. Eur. J. Biochem. 270, 4615–4627. doi: 10.1046/j.1432-1033.2003.03851.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Dal’Molin, C. G. D. O., Quek, L.-E., Palfreyman, R. W., Brumbley, S. M., and Nielsen, L. K. (2010a). AraGEM, a genome-scale reconstruction of the primary metabolic network in Arabidopsis. Plant Physiol. 152, 579–589. doi: 10.1104/pp.109.148817
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Dal’Molin, C. G. D. O., Quek, L.-E., Palfreyman, R. W., Brumbley, S. M., and Nielsen, L. K. (2010b). C4GEM, a genome-scale metabolic model to study C-4 plant metabolism. Plant Physiol. 154, 1871–1885. doi: 10.1104/pp.110.166488
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Davidian, J. C., and Kopriva, S. (2010). Regulation of sulfate uptake and assimilation-the same or not the same? Mol. Plant 3, 314–325. doi: 10.1093/mp/ssq001
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
De Pascale, S., Maggio, A., Orsini, F., Bottino, A., and Barbieri, G. (2008). Sulphur fertilisation affects yield and quality in friarielli (Brassica rapa L. subsp. sylvestris L. Janch. var. esculenta Hort.) grown in a floating system. J. Hortic. Sci. Biotechnol. 83, 743–748.
Famili, I., Mahadevan, R., and Palsson, B. O. (2005). k-cone analysis: determining all candidate values for kinetic parameters on a network scale. Biophys. J. 88, 1616–1625. doi: 10.1529/biophysj.104.050385
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Feist, A. M., and Palsson, B. O. (2010). The biomass objective function. Curr. Opin. Microbiol. 13, 344–349. doi: 10.1016/j.mib.2010.03.003
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Fell, D. A. (1992). Metabolic control analysis – a survey of its theoretical and experimental development. Biochem. J. 286, 313–330.
Feng, X., Xu, Y., Chen, Y., and Tang, Y. J. (2012). Integrating flux balance analysis into kinetic models to decipher the dynamic metabolism of Shewanella oneidensis MR-1. PLoS Comput. Biol. 8:e1002376. doi: 10.1371/journal.pcbi.1002376
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Garcia-Contreras, R., Vos, P., Westerhoff, H. V., and Boogerd, F. C. (2012). Why in vivo may not equal in vitro – new effectors revealed by measurement of enzymatic activities under the same in vivo-like assay conditions. FEBS J. 279, 4145–4159. doi: 10.1111/febs.12007
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Gatehouse, J. A. (2002). Plant resistance towards insect herbivores: a dynamic interaction. New phytol. 156, 145–169. doi: 10.1046/j.1469-8137.2002.00519.x
Gibon, Y., Blaesing, O. E., Hannemann, J., Carillo, P., Hohne, M., Hendriks, J. H. M.,et al. (2004). A robot-based platform to measure multiple enzyme activities in Arabidopsis using a set of cycling assays: comparison of changes of enzyme activities and transcript levels during diurnal cycles and in prolonged darkness. Plant Cell 16, 3304–3325. doi: 10.1105/tpc.104.025973
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Gigolashvili, T., Geier, M., Ashykhmina, N., Frerigmann, H., Wulfert, S., Krueger, S.,et al. (2012). The Arabidopsis thylakoid ADP/ATP carrier TAAC has an additional role in supplying plastidic phosphoadenosine 5′-phosphosulfate to the cytosol. Plant Cell 24, 4187–4204. doi: 10.1105/tpc.112.101964
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Glaeser, K., Kanawati, B., Kubo, T., Schmitt-Kopplin, P., and Grill, E. (2014). Exploring the Arabidopsis sulfur metabolome. Plant J. 77, 31–45. doi: 10.1111/tpj.12359
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Goel, A., Santos, F., Vos, W. M., Teusink, B., and Molenaar, D. (2012). Standardized assay medium to measure Lactococcus lactis enzyme activities while mimicking intracellular conditions. Appl. Environ. Microbiol. 78, 134–143. doi: 10.1128/aem.05276-11
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Goldberg, R. N., Tewari, Y. B., and Bhat, T. N. (2004). Thermodynamics of enzyme-catalyzed reactions – a database for quantitative biochemistry. Bioinformatics 20, 2874–2877. doi: 10.1093/bioinformatics/bth314
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Grafahrend-Belau, E., Junker, A., Eschenroeder, A., Mueller, J., Schreiber, F., and Junker, B. H. (2013). Multiscale metabolic modeling: dynamic flux balance analysis on a whole-plant scale. Plant Physiol. 163, 637–647. doi: 10.1104/pp.113.224006
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Grafahrend-Belau, E., Junker, A., Schreiber, F., and Junker, B. H. (2014). Flux balance analysis as an alternative method to estimate fluxes without labeling. Methods Mol. Biol. 1090, 281–299. doi: 10.1007/978-1-62703-688-7_17
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hacham, Y., Koussevitzky, S., Kirma, M., and Amir, R. (2014). Glutathione application affects the transcript profile of genes in Arabidopsis seedling. J. Plant Physiol. 171, 1444–1451. doi: 10.1016/j.jplph.2014.06.016
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Harcombe, W. R., Delaney, N. F., Leiby, N., Klitgord, N., and Marx, C. J. (2013). The ability of flux balance analysis to predict evolution of central metabolism scales with the initial distance to the optimum. PLoS Comput. Biol. 9:e1003091. doi: 10.1371/journal.pcbi.1003091
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hawkins, D. M. (2004). The problem of overfitting. J. Chem. Inf. Comput. Sci. 44, 1–12. doi: 10.1021/ci0342472
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hay, J., and Schwender, J. (2011). Computational analysis of storage synthesis in developing Brassica napus L. (oilseed rape) embryos: flux variability analysis in relation to C-13 metabolic flux analysis. Plant J. 67, 513–525. doi: 10.1111/j.1365-313X.2011.04611.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Heazlewood, J. L., Verboom, R. E., Tonti-Filippini, J., Small, I., and Millar, A. H. (2007). SUBA: the Arabidopsis subcellular database. Nucleic Acids Res. 35, D213–D218. doi: 10.1093/nar/gkl863
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Heijnen, J. J. (2005). Approximative kinetic formats used in metabolic network modeling. Biotechnol. Bioeng. 91, 534–545. doi: 10.1002/bit.20558
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hopkins, L., Parmar, S., Baszczyk, A., Hesse, H., Hoefgen, R., and Hawkesford, M. J. (2005). O-acetylserine and the regulation of expression of genes encoding components for sulfate uptake and assimilation in potato. Plant Physiol. 138, 433–440. doi: 10.1104/pp.104.057521
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hubberten, H.-M., Klie, S., Caldana, C., Degenkolbe, T., Willmitzer, L., and Hoefgen, R. (2012). Additional role of O-acetylserine as a sulfur status-independent regulator during plant growth. Plant J. 70, 666–677. doi: 10.1111/j.1365-313X.2012.04905.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Huseby, S., Koprivova, A., Lee, B.-R., Saha, S., Mithen, R., Wold, A.-B.,et al. (2013). Diurnal and light regulation of sulphur assimilation and glucosinolate biosynthesis in Arabidopsis. J. Exp. Bot. 64, 1039–1048. doi: 10.1093/jxb/ers378
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Jankowski, M. D., Henry, C. S., Broadbelt, L. J., and Hatzimanikatis, V. (2008). Group contribution method for thermodynamic analysis of complex metabolic networks. Biophys. J. 95, 1487–1499. doi: 10.1529/biophysj.107.124784
Jost, R., Altschmied, L., Bloem, E., Bogs, J., Gershenzon, J., Hahnel, U.,et al. (2005). Expression profiling of metabolic genes in response to methyl jasmonate reveals regulation of genes of primary and secondary sulfur-related pathways in Arabidopsis thaliana. Photosynth. Res. 86, 491–508. doi: 10.1007/s11120-005-7386-8
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Jouhten, P., Wiebe, M., and Penttila, M. (2012). Dynamic flux balance analysis of the metabolism of Saccharomyces cerevisiae during the shift from fully respirative or respirofermentative metabolic states to anaerobiosis. FEBS J. 279, 3338–3354. doi: 10.1111/j.1742-4658.2012.08649.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Keurentjes, J. J. B., Molenaar, J., and Zwaan, B. J. (2013). Predictive modelling of complex agronomic and biological systems. Plant Cell Environ. 36, 1700–1710. doi: 10.1111/pce.12156
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Khan, M. S., Haas, F. H., Samami, A. A., Gholami, A. M., Bauer, A., Fellenberg, K.,et al. (2010). Sulfite reductase defines a newly discovered bottleneck for assimilatory sulfate reduction and is essential for growth and development in Arabidopsis thaliana. Plant Cell 22, 1216–1231. doi: 10.1105/tpc.110.074088
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Khodayari, A., Zomorrodi, A. R., Liao, J. C., and Maranas, C. D. (2014). A kinetic model of Escherichia coli core metabolism satisfying multiple sets of mutant flux data. Metab. Eng. 25, 50–62. doi: 10.1016/j.ymben.2014.05.014
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kim, T. Y., Sohn, S. B., Kim, Y. B., Kim, W. J., and Lee, S. Y. (2012). Recent advances in reconstruction and applications of genome-scale metabolic models. Curr. Opin. Biotechnol. 23, 617–623. doi: 10.1016/j.copbio.2011.10.007
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kitano, H. (2004). Biological robustness. Nat. Rev. Genet. 5, 826–837. doi: 10.1038/nrg1471
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kopriva, S. (2006). Regulation of sulfate assimilation in Arabidopsis and beyond. Ann. Bot. 97, 479–495. doi: 10.1093/aob/mc1006
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kopriva, S., Muheim, R., Koprivova, A., Trachsel, N., Catalano, C., Suter, M.,et al. (1999). Light regulation of assimilatory sulphate reduction in Arabidopsis thaliana. Plant J. 20, 37–44. doi: 10.1046/j.1365-313X.1999.00573.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kopriva, S., and Rennenberg, H. (2004). Control of sulphate assimilation and glutathione synthesis: interaction with N and C metabolism. J. Exp. Bot. 55, 1831–1842. doi: 10.1093/jxb/erh203
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Koprivova, A., Giovannetti, M., Baraniecka, P., Lee, B.-R., Grondin, C., Loudet, O.,et al. (2013). Natural variation in the ATPS1 Isoform of ATP sulfurylase contributes to the control of sulfate levels in Arabidopsis. Plant Physiol. 163, 1133–1141. doi: 10.1104/pp.113.225748
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Koprivova, A., North, K. A., and Kopriva, S. (2008). Complex signaling network in regulation of adenosine 5′-phosphosulfate reductase by salt stress in Arabidopsis roots. Plant Physiol. 146, 1408–1420. doi: 10.1104/pp.107.113175
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Koprivova, A., Suter, M., Op Den Camp, R., Brunold, C., and Kopriva, S. (2000). Regulation of sulfate assimilation by nitrogen in Arabidopsis. Plant Physiol. 122, 737–746. doi: 10.1104/pp.122.3.737.
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kravaris, C., Hahn, J., and Chu, Y. (2013). Advances and selected recent developments in state and parameter estimation. Comput. Chem. Eng. 51, 111–123. doi: 10.1016/j.compchemeng.2012.06.001
Krueger, S., Giavalisco, P., Krall, L., Steinhauser, M.-C., Buessis, D., Usadel, B.,et al. (2011). A topological map of the compartmentalized Arabidopsis thaliana leaf metabolome. PLoS ONE 6:e17806, doi: 10.1371/journal.pone.0017806
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Labhsetwar, P., Cole, J. A., Roberts, E., Price, N. D., and Luthey-Schulten, Z. A. (2013). Heterogeneity in protein expression induces metabolic variability in a modeled Escherichia coli population. Proc. Natl. Acad. Sci. U.S.A. 110, 14006–14011. doi: 10.1073/pnas.1222569110
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Lappartient, A. G., Vidmar, J. J., Leustek, T., Glass, A. D. M., and Touraine, B. (1999). Inter-organ signaling in plants: regulation of ATP sulfurylase and sulfate transporter genes expression in roots mediated by phloem-translocated compound. Plant J. 18, 89–95. doi: 10.1046/j.1365-313X.1999.00416.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Lee, B.-R., Huseby, S., Koprivova, A., Chetelat, A., Wirtz, M., Mugford, S. T.,et al. (2012). Effects of fou8/fry1 mutation on sulfur metabolism: is decreased internal sulfate the trigger of sulfate starvation response? PLoS ONE 7:e39425. doi: 10.1371/journal.pone.0039425
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Lee, B.-R., Koprivova, A., and Kopriva, S. (2011). The key enzyme of sulfate assimilation, adenosine 5′-phosphosulfate reductase, is regulated by HY5 in Arabidopsis. Plant J. 67, 1042–1054. doi: 10.1111/j.1365-313X.2011.04656.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Lee, M., Martin, M. N., Hudson, A. O., Lee, J., Muhitch, M. J., and Leustek, T. (2005). Methionine and threonine synthesis are limited by homoserine availability and not the activity of homoserine kinase in Arabidopsis thaliana. Plant J. 41, 685–696. doi: 10.1111/j.1365-313X.2004.02329.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Leroux, A. E., Haanstra, J. R., Bakker, B. M., and Krauth-Siegel, R. L. (2013). Dissecting the catalytic mechanism of Trypanosoma brucei trypanothione synthetase by kinetic analysis and computational modeling. J. Biol. Chem. 288, 23751–23764. doi: 10.1074/jbc.M113.483289
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Lewis, N. E., Nagarajan, H., and Palsson, B. O. (2012). Constraining the metabolic genotype-phenotype relationship using a phylogeny of in silico methods. Nat. Rev. Microbiol. 10, 291–305. doi: 10.1038/nrmicro2737
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Li, Y., Wei, G. Y., and Chen, J. (2004). Glutathione: a review on biotechnological production. Appl. Microbiol. Biotechnol. 66, 233–242. doi: 10.1007/s00253-004-1751-y
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Link, H., Christodoulou, D., and Sauer, U. (2014). Advancing metabolic models with kinetic information. Curr. Opin. Biotechnol. 29, 8–14. doi: 10.1016/j.copbio.2014.01.015
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Loudet, O., Saliba-Colombani, V., Camilleri, C., Calenge, F., Gaudon, V., Koprivova, A.,et al. (2007). Natural variation for sulfate content in Arabidopsis thaliana is highly controlled by APR2. Nat. Genet. 39, 896–900. doi: 10.1038/ng2050
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Machado, D., and Herrgard, M. (2014). Systematic evaluation of methods for integration of transcriptomic data into constraint-based models of metabolism. PLoS Comput. Biol. 10:e1003580. doi: 10.1371/journal.pcbi.1003580
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Mahadevan, R., Edwards, J. S., and Doyle, F. J. III. (2002). Dynamic flux balance analysis of diauxic growth in Escherichia coli. Biophys. J. 83, 1331–1340. doi: 10.1016/s0006-3495(02)73903-9
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Masakapalli, S. K., Le Lay, P., Huddleston, J. E., Pollock, N. L., Kruger, N. J., and Ratcliffe, R. G. (2010). Subcellular flux analysis of central metabolism in a heterotrophic Arabidopsis cell suspension using steady-state stable isotope labeling. Plant Physiol. 152, 602–619. doi: 10.1104/pp.109.151316
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Mendoza-Cózatl, D. G., and Moreno-Sánchez, R. (2006). Control of glutathione and phytochelatin synthesis under cadmium stress. Pathway modeling for plants. J. Theor. Biol. 238, 919–936. doi: 10.1016/j.jtbi.2005.07.003
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Mintz-Oron, S., Meir, S., Malitsky, S., Ruppin, E., Aharoni, A., and Shlomi, T. (2012). Reconstruction of Arabidopsis metabolic network models accounting for subcellular compartmentalization and tissue-specificity. Proc. Natl. Acad. Sci. U.S.A. 109, 339–344. doi: 10.1073/pnas.1100358109
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Miskovic, L., and Hatzimanikatis, V. (2011). Modeling of uncertainties in biochemical reactions. Biotechnol. Bioeng. 108, 413–423. doi: 10.1002/bit.22932
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Mugford, S. G., Lee, B.-R., Koprivova, A., Matthewman, C., and Kopriva, S. (2011). Control of sulfur partitioning between primary and secondary metabolism. Plant J. 65, 96–105. doi: 10.1111/j.1365-313X.2010.04410.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Nagrath, D., Avila-Elchiver, M., Berthiaume, F., Tilles, A. W., Messac, A., and Yarmush, M. L. (2007). Integrated energy and flux balance based multiobjective framework for large-scale metabolic networks. Ann. Biomed. Eng. 35, 863–885. doi: 10.1007/s10439-007-9283-0
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Nero, D., Krouk, G., Tranchina, D., and Coruzzi, G. M. (2009). A system biology approach highlights a hormonal enhancer effect on regulation of genes in a nitrate responsive “biomodule.” BMC Syst. Biol. 3:59. doi: 10.1186/1752-0509-3-59
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Noctor, G., Arisi, A. C. M., Jouanin, L., and Foyer, C. H. (1999). Photorespiratory glycine enhances glutathione accumulation in both the chloroplastic and cytosolic compartments. J. Exp. Bot. 50, 1157–1167. doi: 10.1093/jexbot/50.336.1157
Noctor, G., Strohm, M., Jouanin, L., Kunert, K. J., Foyer, C. H., and Rennenberg, H. (1996). Synthesis of glutathione in leaves of transgenic poplar overexpressing gamma-glutamylcysteine synthetase. Plant Physiol. 112, 1071–1078.
Notebaart, R. A., Teusink, B., Siezen, R. J., and Papp, B. (2008). Co-regulation of metabolic genes is better explained by flux coupling than by network distance. PLoS Comput. Biol. 4:e26. doi: 10.1371/journal.pcbi.0040026
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Oh, Y.-G., Lee, D.-Y., Lee, S. Y., and Park, S. (2009). Multiobjective flux balancing using the NISE method for metabolic network analysis. Biotechnol. Prog. 25, 999–1008. doi: 10.1002/btpr.193
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Ohno, S., Shimizu, H., and Furusawa, C. (2014). FastPros: screening of reaction knockout strategies for metabolic engineering. Bioinformatics 30, 981–987. doi: 10.1093/bioinformatics/btt672
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Papp, B., Notebaart, R. A., and Pal, C. (2011). Systems-biology approaches for predicting genomic evolution. Nat. Rev. Genet. 12, 591–602. doi: 10.1038/nrg3033
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Poolman, M. G., Miguet, L., Sweetlove, L. J., and Fell, D. A. (2009). A genome-scale metabolic model of Arabidopsis and some of its properties. Plant Physiol. 151, 1570–1581. doi: 10.1104/pp.109.141267
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Poorter, H., Anten, N. P. R., and Marcelis, L. F. M. (2013). Physiological mechanisms in plant growth models: do we need a supra-cellular systems biology approach? Plant Cell Environ. 36, 1673–1690. doi: 10.1111/pce.12123
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Pozo, C., Miró, A., Guillén-Gosálbez, G., Sorribas, A., Alves, R., and Jiménez, L. (2014). Gobal optimization of hybrid kinetic/FBA models via outer-approximation. Comput. Chem. Eng. 72, 325–333. doi: 10.1016/j.compchemeng.2014.06.011
Ravilious, G. E., Amelia, N., Francois, J. A., and Jez, J. M. (2012). Structural basis and evolution of redox regulation in plant adenosine-5′-phosphosulfate kinase. Proc. Natl. Acad. Sci. U.S.A. 109, 309–314. doi: 10.1073/pnas.1115772108
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Rennenberg, H., and Herschbach, C. (2014). A detailed view on sulphur metabolism at the cellular and whole-plant level illustrates challenges in metabolite flux analyses. J. Exp. Bot. 65, 5711–5724. doi: 10.1093/jxb/eru315
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Reznik, E., Mehta, P., and Segre, D. (2013). Flux imbalance analysis and the sensitivity of cellular growth to changes in metabolite pools. PLoS Comput. Biol. 9:e1003195. doi: 10.1371/journal.pcbi.1003195
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Rohwer, J. M. (2014). Applications of kinetic modeling to plant metabolism. Methods Mol. Biol. 1083, 275–286. doi: 10.1007/978-1-62703-661-0_16
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Roman, M. S., Cancela, H., and Acerenza, L. (2014). Source and regulation of flux variability in Escherichia coli. BMC Syst. Biol. 8:67. doi: 10.1186/1752-0509-8-67
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Rouached, H., Secco, D., and Arpat, A. B. (2009). Getting the most sulfate from soil: regulation of sulfate uptake transporters in Arabidopsis. J. Plant Physiol. 166, 893–902. doi: 10.1016/j.jplph.2009.02.016
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Saha, R., Chowdhury, A., and Maranas, C. D. (2014). Recent advances in the reconstruction of metabolic models and integration of omics data. Curr. Opin. Biotechnol. 29, 39–45. doi: 10.1016/j.copbio.2014.02.011
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Saha, R., Suthers, P. F., and Maranas, C. D. (2011). Zea mays iRS1563: a comprehensive genome-scale metabolic reconstruction of maize metabolism. PLoS ONE 6:e21784. doi: 10.1371/journal.pone.0021784
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Sajitz-Hermstein, M., and Nikoloski, Z. (2013). Structural control of metabolic flux. PLoS Comput. Biol. 9:e1003368. doi: 10.1371/journal.pcbi.1003368
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Scheerer, U., Haensch, R., Mendel, R. R., Kopriva, S., Rennenberg, H., and Herschbach, C. (2010). Sulphur flux through the sulphate assimilation pathway is differently controlled by adenosine 5′-phosphosulphate reductase under stress and in transgenic poplar plants overexpressing gamma-ECS, SO, or APR. J. Exp. Bot. 61, 609–622. doi: 10.1093/jxb/erp327
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Schomburg, I., Chang, A., Ebeling, C., Gremse, M., Heldt, C., Huhn, G.,et al. (2004). BRENDA, the enzyme database: updates and major new developments. Nucleic Acids Res. 32, D431–D433. doi: 10.1093/nar/gkh081
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Schuetz, R., Kuepfer, L., and Sauer, U. (2007). Systematic evaluation of objective functions for predicting intracellular fluxes in Escherichia coli. Mol. Syst. Biol. 3:119. doi: 10.1038/msb4100162
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Schuetz, R., Zamboni, N., Zampieri, M., Heinemann, M., and Sauer, U. (2012). Multidimensional optimality of microbial metabolism. Science 336, 601–604. doi: 10.1126/science.1216882
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Schuster, S., Pfeiffer, T., and Fell, D. A. (2008). Is maximization of molar yield in metabolic networks favoured by evolution? J. Theor. Biol. 252, 497–504. doi: 10.1016/j.jtbi.2007.12.008
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Seaver, S. M. D., Henry, C. S., and Hanson, A. D. (2012). Frontiers in metabolic reconstruction and modeling of plant genomes. J. Exp. Bot. 63, 2247–2258. doi: 10.1093/jxb/err371
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Segre, D., Vitkup, D., and Church, G. M. (2002). Analysis of optimality in natural and perturbed metabolic networks. Proc. Natl. Acad. Sci. U.S.A. 99, 15112–15117. doi: 10.1073/pnas.232349399
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Sekiz, S. S., Scott, M. L., and Nesheim, M. C. (1975). The effect of methionine deficiency on body weight, food and energy utilization in the chick. Poult. Sci. 54, 1184–1188. doi: 10.3382/ps.0541184
Shachar-Hill, Y. (2013). Metabolic network flux analysis for engineering plant systems. Curr. Opin. Biotechnol. 24, 247–255. doi: 10.1016/j.copbio.2013.01.004
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Simons, M., Misra, A., and Sriram, G. (2014a). Genome-scale models of plant metabolism. Methods Mol. Biol. 1083, 213–230. doi: 10.1007/978-1-62703-661-0_13
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Simons, M., Saha, R., Guillard, L., Clement, G., Armengaud, P., Canas, R.,et al. (2014b). Nitrogen-use efficiency in maize (Zea mays L.): from ’omics’ studies to metabolic modelling. J. Exp. Bot. 65, 5657–5671. doi: 10.1093/jxb/eru227
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Sjostrom, S. L., Joensson, H. N., and Svahn, H. A. (2013). Multiplex analysis of enzyme kinetics and inhibition by droplet microfluidics using picoinjectors. Lab Chip 13, 1754–1761. doi: 10.1039/c3lc41398e
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Smallbone, K., and Mendes, P. (2013). Large-scale metabolic models: from reconstruction to differential equations. Ind. Biotechnol. 9, 179–184. doi: 10. 1089/ind.2013.0003
Steuer, R., Gross, T., Selbig, J., and Blasius, B. (2006). Structural kinetic modeling of metabolic networks. Proc. Natl. Acad. Sci. U.S.A. 103, 11868–11873. doi: 10.1073/pnas.0600013103
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Stitt, M., and Gibon, Y. (2014). Why measure enzyme activities in the era of systems biology? Trends Plant Sci. 19, 256–265. doi: 10.1016/j.tplants.2013.11.003
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Sun, Q., Zybailov, B., Majeran, W., Friso, G., Olinares, P. D. B., and Van Wijk, K. J. (2009). PPDB, the plant proteomics database at cornell. Nucleic Acids Res. 37, D969–D974. doi: 10.1093/nar/gkn654
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Takahashi, H., Kopriva, S., Giordano, M., Saito, K., and Hell, R. (2011). “Sulfur assimilation in photosynthetic organisms: molecular functions and regulations of transporters and assimilatory enzymes,” in Annual Review of Plant Biology, Vol. 62, eds S. S. Merchant, W. R. Briggs, and D. Ort (Palo Alto, CA: Annual Reviews), 157–184.
Tawfiq, N., Heaney, R. K., Plumb, J. A., Fenwick, G. R., Musk, S. R., and Williamson, G. (1995). Dietary glucosinolates as blocking agents against carcinogenesis: glucosinolate breakdown products assessed by induction of quinone reductase activity in murine hepa1c1c7 cells. Carcinogenesis 16, 1191–1194. doi: 10.1093/carcin/16.5.1191
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Thomas, S., and Fell, D. A. (1998). The role of multiple enzyme activation in metabolic flux control. Adv. Enzyme Regul. 38, 65–85. doi: 10.1016/S0065-2571(97)00012-5
Toepfer, N., Caldana, C., Grimbs, S., Willmitzer, L., Fernie, A. R., and Nikoloski, Z. (2013). Integration of genome-scale modeling and transcript profiling reveals metabolic pathways underlying light and temperature acclimation in Arabidopsis. Plant Cell 25, 1197–1211. doi: 10.1105/tpc.112.108852
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Tomar, N., and De, R. K. (2013). Comparing methods for metabolic network analysis and an application to metabolic engineering. Gene 521, 1–14. doi: 10.1016/j.gene.2013.03.017
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Traka, M. H., and Mithen, R. F. (2011). Plant science and human nutrition: challenges in assessing health-promoting properties of phytochemicals. Plant Cell 23, 2483–2497. doi: 10.1105/tpc.111.087916
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Tran, L. M., Rizk, M. L., and Liao, J. C. (2008). Ensemble modeling of metabolic networks. Biophys. J. 95, 5606–5617. doi: 10.1529/biophysj.108.135442
Tripathi, M., and Mishra, A. (2007). Glucosinolates in animal nutrition: a review. Anim. Feed Sci. Technol. 132, 1–27. doi: 10.1016/j.anifeedsci.2006.03.003
Tsakraklides, G., Martin, M., Chalam, R., Tarczynski, M. C., Schmidt, A., and Leustek, T. (2002). Sulfate reduction is increased in transgenic Arabidopsis thaliana expressing 5′-adenylylsulfate reductase from Pseudomonas aeruginosa. Plant J. 32, 879–889. doi: 10.1046/j.1365-313X.2002.01477.x
Tummler, K., Lubitz, T., Schelker, M., and Klipp, E. (2014). New types of experimental data shape the use of enzyme kinetics for dynamic network modeling. FEBS J. 281, 549–571. doi: 10.1111/febs.12525
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
van Eunen, K., and Bakker, B.M. (2014). The importance and challenges of in vivo-like enzyme kinetics. Perspect. Sci. 1, 126–130. doi: 10.1016/j.pisc.2014.02.011
Vargas, F. A., Pizarro, F., Ricardo Perez-Correa, J., and Agosin, E. (2011). Expanding a dynamic flux balance model of yeast fermentation to genome-scale. BMC Syst. Biol. 5:75. doi: 10.1186/1752-0509-5-75
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Varma, A., and Palsson, B. O. (1994). Stoichiometric flux balance models quantitatively predict growth and metabolic by-product secretion in wild-type Escherichia coli w3110. Appl. Environ. Microbiol. 60, 3724–3731.
Vauclare, P., Kopriva, S., Fell, D., Suter, M., Sticher, L., Von Ballmoos, P.,et al. (2002). Flux control of sulphate assimilation in Arabidopsis thaliana: adenosine 5′-phosphosulphate reductase is more susceptible than ATP sulphurylase to negative control by thiols. Plant J. 31, 729–740. doi: 10.1046/j.1365-313X.2002.01391.x
Williams, T. C. R., Poolman, M. G., Howden, A. J. M., Schwarzlander, M., Fell, D. A., Ratcliffe, R. G.,et al. (2010). A genome-scale metabolic model accurately predicts fluxes in central carbon metabolism under stress conditions. Plant Physiol. 154, 311–323. doi: 10.1104/pp.110.158535
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Wintermute, E. H., Lieberman, T. D., and Silver, P. A. (2013). An objective function exploiting suboptimal solutions in metabolic networks. BMC Syst. Biol. 7:98. doi: 10.1186/1752-0509-7-98
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Wittig, U., Kania, R., Golebiewski, M., Rey, M., Shi, L., Jong, L.,et al. (2012). SABIO-RK-database for biochemical reaction kinetics. Nucleic Acids Res. 40, D790–D796. doi: 10.1093/nar/gkr1046
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Yadav, S. (2010). Heavy metals toxicity in plants: an overview on the role of glutathione and phytochelatins in heavy metal stress tolerance of plants. S. Afr. J. Bot. 76, 167–179. doi: 10.1016/j.sajb.2009.10.007
Yoshimoto, N., Inoue, E., Watanabe-Takahashi, A., Saito, K., and Takahashi, H. (2007). Posttranscriptional regulation of high-affinity sulfate transporters in Arabidopsis by sulfur nutrition. Plant Physiol. 145, 378–388. doi: 10.1104/pp.107.105742
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Zamora-Sillero, E., Hafner, M., Ibig, A., Stelling, J., and Wagner, A. (2011). Efficient characterization of high-dimensional parameter spaces for systems biology. BMC Syst. Biol. 5:142. doi: 10.1186/1752-0509-5-142
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Zarecki, R., Oberhardt, M. A., Yizhak, K., Wagner, A., Segal, E. S., Freilich, S.,et al. (2014). Maximal sum of metabolic exchange fluxes outperforms biomass yield as a predictor of growth rate of microorganisms. PLoS ONE 9:e98372. doi: 10.1371/journal.pone.0098372
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Zomorrodi, A. R., Islam, M. M., and Maranas, C. D. (2014). d-OptCom: dynamic multi-level and multi-objective metabolic modeling of microbial communities. ACS Synth. Biol. 3, 247–257. doi: 10.1021/sb4001307
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Zomorrodi, A. R., and Maranas, C. D. (2012). OptCom: a multi-level optimization framework for the metabolic modeling and analysis of microbial communities. PLoS Comput. Biol. 8:e1002363. doi: 10.1371/journal.pcbi.1002363
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Zomorrodi, A. R., Suthers, P. F., Ranganathan, S., and Maranas, C. D. (2012). Mathematical optimization applications in metabolic networks. Metab. Eng. 14, 672–686. doi: 10.1016/j.ymben.2012.09.005
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Keywords: sulfur, flux, genome scale, flux balance analysis, kinetic modeling, metabolic control analysis
Citation: Calderwood A, Morris RJ and Kopriva S (2014) Predictive sulfur metabolism – a field in flux. Front. Plant Sci. 5:646. doi: 10.3389/fpls.2014.00646
Received: 24 September 2014; Paper pending published: 25 October 2014;
Accepted: 02 November 2014; Published online: 18 November 2014.
Edited by:
Stanislaus Francis D’Souza, Bhabha Atomic Research Centre, IndiaCopyright © 2014 Calderwood, Morris and Kopriva. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alexander Calderwood, Department of Computational and Systems Biology, John Innes Centre, Norwich Research Park, Colney Lane, Norwich NR14 6AG, UK e-mail:YWxleGFuZGVyLmNhbGRlcndvb2RAamljLmFjLnVr
 Alexander Calderwood
Alexander Calderwood Richard J. Morris
Richard J. Morris Stanislav Kopriva
Stanislav Kopriva