- Department of Plant Sciences, University of Oxford, Oxford, UK
Flux-balance modeling of plant metabolic networks provides an important complement to 13C-based metabolic flux analysis. Flux-balance modeling is a constraints-based approach in which steady-state fluxes in a metabolic network are predicted by using optimization algorithms within an experimentally bounded solution space. In the last 2 years several flux-balance models of plant metabolism have been published including genome-scale models of Arabidopsis metabolism. In this review we consider what has been learnt from these models. In addition, we consider the limitations of flux-balance modeling and identify the main challenges to generating improved and more detailed models of plant metabolism at tissue- and cell-specific scales. Finally we discuss the types of question that flux-balance modeling is well suited to address and its potential role in metabolic engineering and crop improvement.
Introduction
Metabolism is a prerequisite for life. Hundreds of chemical reactions, mostly catalyzed by enzymes, define a metabolic network that supports all biological activity. In particular, the coupling of energy-releasing processes to energy-consuming anabolic reactions drives the biosynthesis of the polymers and metabolites that constitute the fabric of the cell. The rates of all the enzyme-catalyzed reactions, including the associated relocation of ions and metabolites across membranes, are tightly controlled through the regulation of enzyme activity, allowing metabolic outputs to be adjusted according to varying environmental conditions and growth patterns.
Plant metabolic networks are arguably the most complex of any organism, both because of the tremendous variation in their metabolic output and because of the range of environmental conditions that they encounter. Nevertheless, because the growth and survival of plants is intimately connected to metabolism (Smith and Stitt, 2007; Stitt et al., 2010) there is a need to understand and predict metabolic behavior. In particular, there is a need to connect genotype to specific metabolic outputs so that plant breeders and metabolic engineers can generate new varieties of crops with increased yield or altered chemical composition (Fernie and Schauer, 2009).
Although there have been some notable successes in engineering plant metabolism (Butelli et al., 2008; Naqvi et al., 2009), these are mainly related to the production of secondary metabolites. In contrast, there are few examples where the synthesis of the main biomass polymers has been manipulated in a predictive manner. At the heart of this contrasting ability to engineer the metabolic network is the difference in connectivity of primary and secondary metabolism. Many secondary metabolites are synthesized by reactions that occur at the periphery of the metabolic network with relatively few interconnections to other parts of the network. As a result, there are fewer regulatory constraints on the flux through these essentially linear pathways and control may be disproportionately resident in a single enzyme, providing a single target for genetic manipulation (Fraser et al., 2002; Enfissi et al., 2005). Where control is more evenly distributed, it is often possible to identify transcription factors that co-ordinately affect the expression of genes encoding enzymes in a pathway (Schwinn et al., 2006; Memelink and Gantet, 2007). In contrast, the main growth components of the cell are synthesized through a highly connected set of reactions that is commonly referred to as “central metabolism.” Not only is control of flux generally shared amongst many, if not all, enzymes of central metabolism (Raines, 2003; Geigenberger et al., 2004; Araujo et al., 2011), but because of the degree of connectivity, a perturbation of one part of the network has consequences for other parts of the network.
So in central metabolism, the functioning of individual enzymes and even pathways is dependent on the operational state of the whole metabolic network (Kruger and Ratcliffe, 2008; Sweetlove et al., 2008). As a result, efforts to understand the regulation of the central metabolic network in the last few years have focused on measuring the metabolic phenotype – flux – at a network level. Much of this work has centered on the development of approaches to determine network fluxes based on the steady-state redistribution of isotopically labeled carbon (Libourel and Shachar-Hill, 2008; Allen et al., 2009a; Kruger and Ratcliffe, 2009). This approach, known as steady-state metabolic flux analysis (MFA), has matured into a powerful technique whereby it is possible to reliably quantify both net and exchange fluxes of tens of reactions across the central metabolic network. MFA has been applied to several different plant species and tissue types and has yielded some significant insights into the behavior and organization of plant metabolism. For example, MFA was used to establish that Rubisco can function without the Calvin cycle to recycle carbon lost as CO2 during lipid synthesis in green oilseeds in the light, substantially increasing the carbon conversion efficiency (Schwender et al., 2004; Allen et al., 2009b). MFA has also revealed a variety of different flux modes in the TCA cycle (Sweetlove et al., 2010) as well as demonstrating the inherent stability of central metabolism to environmental perturbation (Iyer et al., 2008; Williams et al., 2008), and the complex, non-intuitive relationship between fluxes, metabolite levels, and enzyme activities (Junker et al., 2007; Kruger and Ratcliffe, 2009).
However, despite the undoubted power of steady-state MFA for defining the metabolic phenotype, it does have some limitations. In particular, the requirement to supply a labeled organic carbon substrate to isotopic steady-state limits the approach to heterotrophic or mixotrophic tissues in culture. The method is also entirely dependent on the correctness of the user-defined metabolic network because it is often possible to fit the labeling data to more than one network structure with little statistical power to discriminate between the alternatives (Masakapalli et al., 2010). MFA is, moreover, a relatively low throughput technique and this limits its use as a comparative tool since comparison of multiple samples (e.g., different genotypes) requires substantial effort (Lonien and Schwender, 2009).
These limitations have driven the search for alternative, complementary approaches to characterize and explore the plant metabolic network. Following the lead of the microbial field (Borodina and Nielsen, 2005), flux-balance modeling has emerged as an alternative to MFA. Like MFA, flux-balance analysis (FBA) is a constraints-based modeling approach in which steady-state fluxes in a metabolic network are predicted by applying mass-balance constraints to a model of the network based on the matrix of reaction stoichiometries. Typically, simple and easy to measure mass-balance information, such as growth rate, biomass composition, and substrate-consumption rate, is used to place boundaries on the flux solution space (Reed and Palsson, 2003). However, in contrast to MFA, isotopic labeling information is not used. As a result, the network fluxes are underdetermined and a range of feasible flux solutions are obtained that satisfy the constraints. Within this range, flux solutions that are optimal with respect to a specific objective function (such as maximizing growth rate or minimizing substrate consumption) can be identified with optimization algorithms such as linear programming (Edwards and Palsson, 2000).
Several flux-balance models of different plant species have been published in the last 2 years. These include models for Arabidopsis (Poolman et al., 2009; de Oliveira Dal’Molin et al., 2010a; Radrich et al., 2010), barley seeds (Grafahrend-Belau et al., 2009), Brassica napus seeds (Hay and Schwender, 2011b; Pilalis et al., 2011), maize (Saha et al., 2011), Chlamydomonas (Boyle and Morgan, 2009; Cogne et al., 2011), and photoautotrophic bacteria (Knoop et al., 2010; Montagud et al., 2010). The aim of this article is to review what has been learnt from these models, to discuss the advantages and limitations of flux-balance modeling and to look to the future. What insights into plant metabolic networks can we expect to obtain from flux-balance modeling and what are the main challenges for the biologically informative application of flux-balance modeling?
Genome-Scale Metabolic Modeling
One of the main advantages of flux-balance modeling is that it is relatively easy to scale up to cover very large networks. Indeed, metabolic models can be constructed at a genome-scale, using all the reactions catalyzed by the enzymes encoded in an annotated genome. However this remains a non-trivial task: Arabidopsis and maize are the only higher plants with genome-scale metabolic models (Poolman et al., 2009; de Oliveira Dal’Molin et al., 2010a; Radrich et al., 2010; Saha et al., 2011) – all the other plant models have been constructed using metabolic databases, biochemical textbooks, and the primary literature, and are essentially confined to the well known pathways of central metabolism. Several problems arise in the construction of metabolic models from genome-annotation databases, including network gaps caused by incomplete or imprecise genome annotation, mass-balance errors caused by reaction stoichiometry errors in the annotation database, and the presence of excess, non-functional reactions. However, working practices and computational approaches are emerging to help deal with such issues (Fell et al., 2010; Henry et al., 2010; Soh and Hatzimanikatis, 2010).
An additional challenge is that genome-annotation databases contain no information about reaction directionality. In smaller models of primary metabolism, it is possible to manually constrain reactions to a defined direction based on standard Gibbs free energy changes (and sometimes the in planta concentration of the reaction substrates and products). However, in genome-scale models, reaction directionality is often left unconstrained, with the result that flux solutions may contain thermodynamically infeasible reactions. A comprehensive standard Gibbs free energy of formation database is urgently required for metabolites to allow thermodynamic constraints to be included in genome-scale FBA. However, because experimentally measured free energies are not available for many reactions, theoretical approaches for estimating standard free energies such as the group contribution method (Jankowski et al., 2008) will need to be implemented.
Given the challenges inherent in constructing and analyzing such large models (the current Arabidopsis genome-scale models contain around 1500 reactions), it is relevant to ask whether this effort is worthwhile. Indeed, only 232 of the available 1406 reactions in the Arabidopsis genome-scale model constructed by Poolman et al. (2009) are required to synthesize the main biomass components and account for maintenance costs of heterotrophic Arabidopsis. The model may be genome-scale, but the flux solution is of similar size and considers similar reactions to FBA models of primary metabolism. It is also worth pointing out that most flux-balance models to date consider a similar span of the metabolic network to previous plant MFA models, although due to reaction lumping and network simplification the actual number of reactions in the MFA models is generally considerably lower.
A genome-scale metabolic network is, of course, not a biological reality. It is unlikely that every enzyme is expressed in a single cell type and under a single condition. Much of secondary metabolism, for example, is induced upon abiotic or biotic stress. Nevertheless, a genome-scale metabolic network has significant value as a foundation for investigating condition-specific scenarios. Thus, cell type-specific sub-models can be constructed based on transcriptomic or proteomic datasets (Lewis et al., 2010) although this has not yet been done to any significant degree for plant metabolism. Similarly, with the inclusion of appropriate constraints, it should be possible to model the consequences of the synthesis of a range of secondary metabolites. For example, in a recent genome-scale flux-balance model of maize, lignin metabolism was explicitly included as part of the biomass function (Saha et al., 2011).
The Issue of Multiple Flux Solutions
Although boundaries are imposed on the flux solution space, it will often still be possible to accommodate multiple solutions that satisfy the chosen objective function. Thus, when linear programming provides a flux solution that minimizes or maximizes a particular objective function, it is not necessarily a unique solution (Lee et al., 2000; Mahadevan and Schilling, 2003). The ability to uniquely define fluxes is dependent both on the structure of the metabolic network and the objective function being considered. For example, the objective function “minimization of total intracellular fluxes” will select metabolic routes that contain the fewest steps since this will result in a lower sum of fluxes. However, the metabolic network may contain equivalent alternative routes for the production of a given metabolite. For example in Figure 1A, both routes lead to the conversion of input substrate to output metabolite via an equal number of steps, meaning that there is no basis by which to select one over the other when minimization of total intracellular flux is used as an objective function. Other commonly used objective functions such as maximization of biomass per unit substrate (and the equivalent minimization of substrate consumed per unit biomass produced) which optimize the molar yield of the system would also fail to discriminate between the two routes if they are stoichiometrically equivalent with respect to carbon.
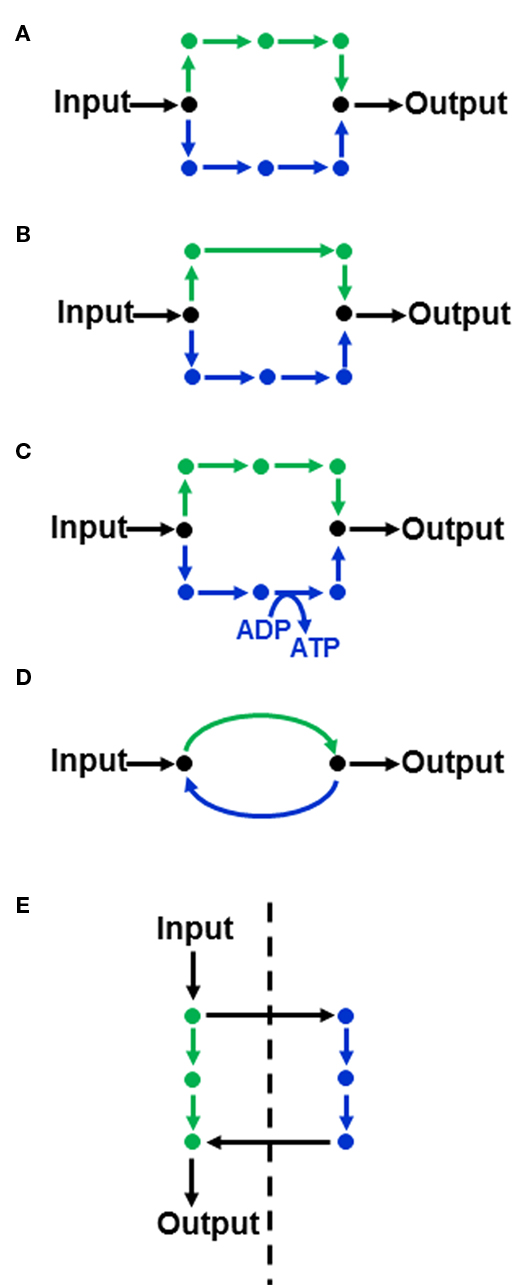
Figure 1. Features of a metabolic network than can lead to flux variability in FBA(A) Two equivalent routes (shown in green and blue) for converting an input substrate into an output metabolite. (B,C) illustrate non-equivalent routes that may be discriminated in FBA, depending on the objective function. (D) A substrate cycle. (E) Equivalent routes in different subcellular compartments (the dashed line indicating a membrane separating two subcellular compartments).
In contrast, if the two routes contain a different number of steps (Figure 1B) then the route with the fewest steps will be utilized under the minimization of flux objective function. Other differences between parallel pathways relate to energy production (Figure 1C). If the objective function is to maximize ATP yield then the objective function would select the ATP-producing pathway in Figure 1C. Another source of alternative solutions can be the presence of substrate cycles (Figure 1D). The minimization of flux objective function will eliminate such cycles, but other objective functions, such as maximization of biomass production, will not because substrate cycles do not influence the net flux from input to output. Accordingly the flux through the cycle is not defined by the objective function and it can hold any value. Subcellular compartmentation, especially the presence of equivalent pathways in different compartments (Figure 1E), can also lead to alternative flux solutions.
This issue of alternative optima can be dealt with in two ways: either, additional optimization criteria can be applied such that a unique flux solution is reached; or, flux variability can be viewed as a potentially informative aspect of network behavior that can be explicitly quantified and explored. A model of barley seed metabolism took the former approach (Grafahrend-Belau et al., 2009). First a conventional linear optimization was applied (with the objective function to maximize growth) and then a non-linear quadratic optimization was applied using the objective value (growth rate) of the first optimization as an additional constraint to the second optimization (with the objective function to minimize the overall sum of fluxes). This two-step procedure provided a unique solution because of the nature of the quadratic optimization. Similarly, a two-step linear optimization procedure can be used in which a “maximization” objective function (e.g., maximization of biomass) is followed by a “minimization” objective function (e.g., minimization of photon use). This approach led to a unique flux solution in an flux-balance model of photoautotrophic metabolism in Synechocystis (Shastri and Morgan, 2005, 2007).
In contrast, a recent FBA analysis of oilseed rape seed metabolism (Hay and Schwender, 2011a,b) made a virtue of flux variability. An explicit analysis of the extent of variability was performed using a linear programming routine based on a secondary minimization and maximization of the flux through each reaction (Mahadevan and Schilling, 2003). In a 572-reaction network of primary metabolism solved by minimization of substrate consumption, it was found that 75 reactions, mainly in the central core of the network, were variable. Flux variability was classified according to the direction and magnitude of the flux change, and it was found that the variability type of 57 reactions altered when different external substrates were used in the model. Flux variability is essentially a modeling issue that arises because the available constraints do not produce a unique solution with the chosen objective function. Nevertheless, changes in variability type can supplement the information that can be deduced from the changes that occur in the fluxes that are uniquely defined. It was also found that 51 reactions varied with infinite bounds and these were largely due to metabolite cycles in which there was no net consumption of carbon or energy. The flux through these reactions can hold any value if the constraints applied only relate to carbon or energy use. Most of the variable fluxes are substitutable, meaning that a solution to the flux optimization problem can be found using alternative reactions. This is a clear demonstration of metabolic redundancy. This work illustrates the utility of flux variability analysis in providing an additional layer of information about the behavior of the network and the nature of the flux solution, and this is particularly valuable when dealing with large networks in which it is not possible to manually inspect the entire flux solution. A similar analysis of flux variability was used to ascertain flux differences between bundle sheath and mesophyll cells in a model of C4 photosynthesis, although in this case, only four reactions were not uniquely defined by the optimality criterion and imposed constraints (de Oliveira Dal’Molin et al., 2010b). To date, only these two studies and a model of Synechocystis (Knoop et al., 2010) have explicitly analyzed flux variability in plant flux-balance models, but one would expect it to be a standard component of FBA in future work.
Validation of Flux-Balance Models
When a flux-balance solution is generated it is important to establish how closely it reflects the actual behavior of the metabolic network. One way of doing this is to look for the operation of metabolic pathways that are known to be physiologically important. Thus, when photosynthetic metabolism was modeled in an Arabidopsis genome-scale model (de Oliveira Dal’Molin et al., 2010a), the classical photorespiratory cycle was observed to support a flux when a 3:1 ratio of the carboxylation:oxygenation reaction of Rubisco was imposed and the photon-use efficiency was optimized. Moreover, the model predicted that 30–50% of the carbon fixed by photosynthesis would be lost through the photorespiratory cycle, a range consistent with experimental measurements.
However, while the recapitulation of known metabolic behavior is reassuring, FBA is unlikely to give a completely faithful representation of the actual flux distribution, and consideration of areas in which the flux-balance model diverges from known metabolic behavior is potentially more informative. For example, the oxidative reactions of the oxidative pentose phosphate pathway typically carry no flux in flux-balance solutions of heterotrophic plant metabolism (Williams et al., 2010; Hay and Schwender, 2011a). This is in contrast to the known importance of the oxidative pentose phosphate pathway in heterotrophic tissues (Averill et al., 1998) and to the fact that the oxidative reactions carry considerable flux in MFA-based flux maps (Kruger and von Schaewen, 2003; Schwender et al., 2003; Sriram et al., 2004; Alonso et al., 2007, 2010; Masakapalli et al., 2010). The discrepancy arises because in the flux-balance models the provision of NADPH, a likely role for the oxidative pentose phosphate pathway, can be met by plastidial NADP-dependent dehydrogenases, such as glyceraldehyde 3-phosphate dehydrogenase, malate dehydrogenase, and malic enzyme. Production of NADPH by these routes is marginally more efficient in terms of either carbon use or overall flux, and so the models predict that the oxidative branch of the pentose phosphate pathway is not required. Two points are worth making here. First, neither of the flux-balance models include thermodynamic constraints beyond specification of reaction directions, and there may be thermodynamic limitations to the establishment of a high NADPH:NADP ratio using these dehydrogenases. Secondly, the NADPH requirement specified in both models is only that required for synthesis of biomass components. There are several other known NADPH requirements in the cell including antioxidant enzyme activity (Apel and Hirt, 2004) and membrane NADPH oxidase activity (Torres, 2010). Thus, the actual NADPH demand in the cell is certainly higher than that specified in the model and would require NADPH to be produced in different subcellular compartments.
Perhaps the most rigorous way to validate an FBA flux solution is to compare it to fluxes estimated independently by 13C-MFA, and this has been done for both B. napus and Arabidopsis flux-balance models (Williams et al., 2010; Hay and Schwender, 2011b). Two points need to be borne in mind in making such comparisons. First, the metabolic networks that are used during 13C-MFA are projections of the real network that provide an explanation of the redistribution of 13C that occurs during the steady-state labeling experiment (Roscher et al., 2000). Steps between branch-points are represented as single steps, since the net flux carried by each intermediate step must be the same, and the model is usually constructed to eliminate indeterminable fluxes, i.e., fluxes that cannot be defined from the labeling data and which would therefore show infinite flux variability if included in the model. In contrast, a flux is assigned to every step in the complete network in FBA, even though many of them are the same, and indeterminable fluxes are not grouped to eliminate flux variability. Thus, many reactions in the FBA solution do not have a direct counterpart in the MFA model. It is also simpler to restrict the comparison to reactions that do not show flux variability in the FBA solutions, although statistical comparisons are possible that include a weighting factor to account for flux variability (Schuetz et al., 2007). Secondly, both FBA and MFA constrain the fluxes that lead directly to synthesis of biomass in the same manner, so these reactions will necessarily hold the same values in the FBA and MFA solutions. When these factors are taken into account, only a relatively small number of fluxes can be directly compared between the two approaches (24 reactions in the Arabidopsis genome-scale model and 19 reactions in the B. napus seed primary metabolism model). Nevertheless, for these few reactions (which are mainly from the core backbone of the network) a reasonable correlation with the predicted fluxes and those estimated by 13C-MFA was found, suggesting that FBA is able to predict realistic values for plant metabolic network fluxes. Moreover, FBA was able to successfully predict changes in flux under two environmental stress conditions in Arabidopsis (Williams et al., 2010).
Subcellular Compartmentation in Flux-Balance Models
Most of the published flux-balance models of plant metabolism make some attempt to take subcellular compartmentation into account, which is clearly desirable if the model is to reflect biological reality (Lunn, 2007). However, inclusion of subcellular compartmentation is problematic and at present, there is insufficient information to assess whether inclusion of compartmentation improves the models. One of the biggest problems is how to place reactions in the correct compartment. While the compartmentation of the core pathways of central metabolism is well established, this only accounts for a small percentage of a genome-scale network. Similarly, while databases such as SUBA (Heazlewood et al., 2007) are excellent inventories of subcellular compartmentation supported by experimental evidence mainly drawn from organellar proteome studies, they only represent a relatively small proportion of the metabolic network. Ideally subcellular location of reactions would be assigned automatically in a genome-scale model, perhaps on the basis of predicted protein sequences, but current algorithms are too unreliable (Heazlewood et al., 2004) and there is currently no alternative to manual curation.
Thus, the assignment of subcellular compartmentation is usually done manually. As a result, particularly in genome-scale models, the extent of compartmentation is patchy and may contain errors. For example, in the AraGEM genome-scale model of Arabidopsis metabolism (de Oliveira Dal’Molin et al., 2010a), the vast majority of reactions are assigned to the cytosol (1265 reactions in the cytosol, with 60, 159, and 98 reactions assigned to mitochondria, plastid, and peroxisome, respectively). This is almost certainly not a true reflection of the situation in the cell, and indeed many reactions assigned to cytosol in the model are known to occur in other compartments. For example, most reactions of amino acid biosynthesis and secondary metabolism were assigned a cytosolic location even though it is well established that both occur extensively in the plastid. By way of comparison, only 20% of the reactions in a model of Chlamydomonas primary metabolism were cytosolic and nearly half were plastidic (Boyle and Morgan, 2009). This was despite the use of the cytosol as a “default” location where the subcellular localization of an enzyme was unclear.
Another issue with introducing compartmentation into metabolic models is the lack of information about metabolite transport. This means that intracellular transporters are often added to metabolic models based on their necessity to allow the synthesis of biomass within the compartmented model (de Oliveira Dal’Molin et al., 2010a). It is also generally the case that no attempt is made to account explicitly for the energetic cost of transport, so by default this is included in the energy cost attributed to cell maintenance.
The functional significance of subcellular compartmentation is not necessarily obvious, and steady-state MFA has drawn attention to the importance of transmembrane metabolite exchange rates in determining the extent to which the intermediates in physically compartmented pathways are able to function indistinguishably from an uncompartmented pathway (Schwender et al., 2003; Ratcliffe and Shachar-Hill, 2006; Masakapalli et al., 2010). Thus in principle it would be useful if the problems identified above could be resolved to allow FBA to explore the functionality of subcellular compartmentation. However, it might be well to consider whether flux-balance models are sufficiently constrained to define compartmented fluxes. The addition of compartmentation, and especially the addition of parallel pathways in more than one compartment, effectively increases the solution space and it seems likely that increased compartmentation in a model will simply increase the number of alternate solutions to the optimization problem. There have been too few attempts to include the necessary level of subcellular compartmentation in plant models to reach a conclusion on this point, and the extent to which flux-balance models can usefully analyze highly compartmented networks requires further investigation.
Flux-Balance Modeling of Specific Cell Types or Tissues
Almost all of the flux-balance models of plant metabolism, compartmented or not, consider only a single cell type, either by modeling single-celled organisms such as Chlamydomonas (Boyle and Morgan, 2009; Cogne et al., 2011) or Synechocystis (Knoop et al., 2010; Montagud et al., 2010), modeling cell suspension cultures (Poolman et al., 2009; Williams et al., 2010) or simply ignoring the presence of multiple cell types in models of specific organs or tissues (Grafahrend-Belau et al., 2009; de Oliveira Dal’Molin et al., 2010a; Hay and Schwender, 2011a,b; Pilalis et al., 2011; Saha et al., 2011). To an extent this is justifiable because the measured biomass composition used to constrain these models are whole tissue biomass compositions. However, it follows that the resulting metabolic network flux solution represents an average of the different cell types in that tissue or organ. Given that different cell types have very different metabolic capacities (Brady et al., 2007; Lee et al., 2011), it is likely that there will be major differences in both the structure of their metabolic networks and in the fluxes through them. Ultimately, if a flux model is going to be useful in explaining the metabolic phenotype in detail, it will be necessary to provide information about flux at a cell-type level (Sweetlove et al., 2010).
The challenge goes beyond simply constructing specific models for specific cell types, but also in joining up these models to form multi-layered representations of complete tissues. This has been achieved in a sophisticated model of metabolic interactions between different cell types in the human brain (Lewis et al., 2010). This study used transcriptomic and proteomic data to define cell type specific metabolic networks for three different neuronal cell types, astrocytes, and blood/endothelium. Subcellular compartmentation was introduced into each cell-type model and transporters were included to allow transport of specific metabolites between the cell types. The model was able to generate possible explanations for the differential effects of Alzheimer’s disease on different cell types and regions of the brain.
This flux-balance model of brain metabolism is state-of-the-art and in principle there is no reason why such detailed large-scale models should not be constructed for plant metabolism. To date, only one study has attempted to account for the interaction of more than one cell type. Based on their previous genome-scale model of Arabidopsis metabolism, de Oliveira Dal’Molin et al. (2010b) constructed a flux-balance model describing the interaction between bundle sheath and mesophyll cells in C4 photosynthesis. The metabolic network was restricted in each cell type to reflect the known distribution of carbon fixation in C4 photosynthesis, with primary fixation of carbon through PEP carboxylase in mesophyll cells, transport of aspartate or malate to the bundle sheath cells, and subsequent decarboxylation by NADP-malic enzyme, NAD-malic enzyme or phosphoenolpyruvate carboxykinase. Flux solutions were generated using optimization of photon use as an objective function. While this objective function could not reproduce every aspect of C4 metabolism, for example the preferential accumulation of starch in bundle sheath cells, the model could be used to examine the energetic implications of the three C4 sub-types. For example, the ATP/NADPH ratio required in NAD-malic enzyme species is higher in mesophyll cells than in bundle sheath cells, but the opposite is true for NADP-malic enzyme species. The flux distribution in the models of the different sub-types confirmed the hypothesis that the additional ATP demand in the different cell types is met by cyclic photophosphorylation.
Another interesting observation from this study was that the relative fluxes between bundle sheath and mesophyll cells correlated well with the relative abundance of the enzymes estimated from proteomic studies (de Oliveira Dal’Molin et al., 2010b). It is clear that enzyme abundance does not relate directly to flux, partly because of post-translational regulation of enzyme activity and partly because of the impact of the thermodynamic poise of a reaction on the ability of an enzyme to support a net flux. However, what this correlation shows is that changes in flux are reflected in proteome-wide adjustments in enzyme amount. The implication is that relative enzyme abundance might be a useful proxy for the change in flux between two conditions or cell types. That said, there are many reasons why such a correlation might break down. For example, it has been shown in yeast that while some Vmax values correlate positively with flux changes, others show an inverse correlation and some show no correlation at all (Rossell et al., 2006). And during stress, many enzymes are inhibited by oxidative damage (Taylor et al., 2004; Lehmann et al., 2009), but this is not necessarily reflected at the protein level. An alternative way of exploiting the correlation between changes in flux and enzyme amount would be to use the enzyme abundance data as a constraint when predicting changes in flux, although the effort required to establish proteomic measurements of sufficient enzymes to cover a significant proportion of the metabolic network would be substantial.
Accounting for Cell Maintenance Energy Costs
In modeling the central metabolic network, the published flux-balance models have exclusively considered the conversion of carbon and nitrogen inputs into biomass. Biosynthesis of the precursors that constitute the main biomass polymers (cell wall, protein, lipid, starch) requires both ATP and NAD(P)H and thus, the energy costs of biomass synthesis are explicitly taken into account. However, there are several other cellular drains on ATP and NAD(P)H apart from the synthesis of biomass. These other energy costs are often bracketed together under the term “maintenance,” implying that these are growth-independent costs that are required just to keep the cell ticking over. This distinction is not strictly accurate because the maintenance costs in metabolic models often include some growth-associated costs.
Other energy costs are associated with the need to replace polymers as they turn over, with the costs of maintaining plasma membrane and tonoplast electrochemical potential gradients through ATP- and PPi-dependent proton pumps, and with the consumption of reductant during antioxidant metabolism (Amthor, 2000). The usual approach to dealing with these maintenance costs in flux-balance modeling is to include a fixed value for maintenance costs based on experimental measures (e.g., Grafahrend-Belau et al., 2009). However, there is a wide variation in reported values for maintenance respiration for plant tissues, and maintenance costs are likely to increase during environmental stress, which may be one explanation for the observed reduction in carbon conversion efficiency under stress (Williams et al., 2010). The importance of an accurate measure of maintenance costs is revealed by the observation that the maximum yield of ATP generated by the metabolic network of heterotrophic Arabidopsis cells is over seven times that required for the synthesis of the main biomass components (Masakapalli et al., 2010), the implication being that maintenance costs account for the majority of ATP consumed by the cell.
Poolman et al. (2009) used an alternative approach for the estimation of maintenance costs. Initially, fluxes in the network were estimated, with the synthesis of biomass components as constraints and minimization of total flux as an objective function, without taking maintenance into account. Subsequently, a generic ATPase reaction was added to the model to represent the maintenance ATP requirement. The flux value of this ATPase was iteratively varied and the linear programming optimization repeated. As the ATPase was increased, glucose consumption, glycolysis, and oxidative phosphorylation increased to meet the increased ATP demand. This allowed the maintenance ATP cost to be set to the ATPase reaction flux that led to a glucose consumption rate equal to the value measured experimentally in the cell suspension cultures (Williams et al., 2010). Effectively, the maintenance cost was estimated from the carbon balance of the system by assuming that consumed carbon that was not accounted for by biomass synthesis must have been for maintenance. A similar approach was used in a recent FBA model of oilseed rape, with the slight modification that carbon conversion efficiency was used as the parameter to set the value for the generic ATPase flux (Hay and Schwender, 2011b). The use of a generic ATPase flux in this way provides a convenient method for accounting for ATP costs that are additional to those required for biosynthesis of biomass components. However, it should be pointed out that the accuracy of the predicted maintenance ATP cost will be dependent on how close the flux-balance solutions are to the actual metabolic flux state.
Exploring Metabolic Efficiency with Flux-Balance Models
Flux-balance modeling is well equipped for the analysis of metabolic efficiency because FBA is based on the discovery of flux solutions that are optimal with respect to a specific objective function. Several of the published FBA studies of plant metabolism explore issues that relate to metabolic efficiency. For example photorespiration was non-zero in a model of photoautotrophic metabolism in Synechocystis optimized for maximal biomass production (Knoop et al., 2010). This is surprising because Rubisco oxygenase was not forced to operate and one would expect that reactions leading to loss of carbon as CO2 would have zero flux when maximization of biomass production is the objective function This is because when the carbon input rate is fixed, maximization of biomass equates to a maximization of carbon conversion efficiency. The fact that photorespiration carried flux under these circumstances means that the requirement for production of intermediates by this route outweighed the loss of carbon. Part of the explanation appears to be a lack of alternative routes to serine in the Synechocystis model. However, it is noteworthy that a flux-balance model of heterotrophic Arabidopsis metabolism also contains a non-zero flux for the Rubisco oxygenase reaction and subsequent reactions of photorespiration as far as glycine. (Poolman et al., 2009). In this model, this was the main route for synthesis of glycine. Transcript and proteomic data both suggest the presence of photorespiratory enzymes in non-photosynthetic tissues in Arabidopsis (Zimmermann et al., 2004; Baerenfaller et al., 2008). The precise role of the photorespiratory reactions in non-photosynthetic tissues, and their requirement for optimal growth of photosynthetic tissues, requires further investigation, highlighting the power of FBA in the identification of non-intuitive flux behavior in metabolic networks.
Flux-balance modeling can also be used to explore the efficiency of different modes of carbon assimilation within realistic growth constraints. Because the carbon conversion efficiency of photosynthesis is directly related to crop yield, there is a great deal of interest in the possibility of alternative photo-assimilatory pathways that might operate at higher efficiency (Bar-Even et al., 2010). The efficiency of six carbon assimilation pathways (Calvin–Benson–Bassham cycle, reductive TCA cycle, 3-hydroxypropionate/malyl-CoA cycle, reductive acetyl-CoA pathway, 3-hydroxypropionate/4-hydroxybutyrate cycle, and the dicarboxylate/4-hydroxybutyrate cycle) was compared by establishing flux-balance solutions for six different bacteria (Boyle and Morgan, 2011). Based on comparisons of either photon requirement or the energy demand for conversion of photoassimilate into biomass, it was found that photoautotrophic pathways are more efficient than chemoautotrophic carbon assimilation pathways (unless there is a free source of hydrogen) and that the reductive TCA cycle is the most efficient way of generating biomass from solar energy. However, the reductive TCA cycle is only marginally more efficient than the Calvin–Benson–Bassham cycle (25.3 and 24.9% efficiency, respectively, where efficiency is calculated as the heat of combustion of biomass divided by the total amount of energy used to create biomass).
The calculation of theoretical optimal yields of metabolic networks is relatively straightforward from flux-balance models, but more biologically informed assessments of metabolic efficiencies can be made by comparison of computed optimal flux distributions against those that actually occur. Two studies have found that flux-balance models can replicate experimentally determined flux distributions in heterotrophic Arabidopsis cells (Williams et al., 2010) and B. napus seeds (Hay and Schwender, 2011b). In both of these studies objective functions were used that equate to carbon conversion efficiency: minimization of total intracellular flux or minimization of substrate consumption, per unit biomass produced. The fact that these objective functions produce flux solutions that match the measured in vivo flux distributions suggests that the metabolic network in these tissues is functioning close to optimal carbon conversion efficiency. A similar conclusion can be reached from a flux-balance model of barley seed in which maximization of growth rate for a fixed substrate-consumption rate was able to predict the growth rate of barley seeds (Grafahrend-Belau et al., 2009). Maximization of growth (biomass) for a fixed amount of substrate is effectively a maximization of molar yield (Schuster et al., 2008). In other words, this objective function is closely related to objective functions that minimize substrate consumption or overall intracellular flux for a fixed biomass output.
The conclusion that plant metabolic networks may already be operating close to maximal carbon conversion efficiency is important, because improvement of carbon conversion efficiency is often cited as a key breeding target for improved crop yield (Hauben et al., 2009; Parry et al., 2010). However, the conclusion, as it stands, requires substantial qualification. The main issue is that the carbon conversion efficiency in the Arabidopsis and B. napus models is forced to match the measured value and this to a large extent dictates the good match between the modeled and measured fluxes in the central metabolic network. Moreover, only a small fraction of the flux distribution can be legitimately validated for the reasons discussed earlier, and systematic assessments of different objective functions (Schuetz et al., 2007) have not yet been reported for plant models. It is entirely possible that the differences in the flux solutions obtained with different objective functions may fall within the statistical error of the flux determinations, and thus provide no real discriminatory power to investigate metabolic network efficiency. Nevertheless the conclusion is in line with previous estimates of the theoretical efficiencies of plant energy metabolism based on less sophisticated pathway analysis (Penning de Vries, 1974; Penning de Vries et al., 1974).
Future Challenges for Flux-Balance Modeling of Plant Metabolism
The flux-balance models of plant metabolism that have been published in the last 2 years have been steadily gaining in sophistication. The inclusion of subcellular compartmentation, the analysis of multiple cell types, and the analysis of flux variability are significant developments that increase the utility and predictive capacity of the models. Technical challenges remain, for example in the analysis of subcellular compartmentation, but it is clear that FBA is a useful addition to the toolbox for analyzing plant metabolic networks. Moreover the ease of implementation in comparison to stable isotope-based MFA, and the availability of metabolic compendia (Zhang et al., 2010) based on genomic information, suggest that flux-balance models will continue to be developed for a variety of plant species and tissue types. Given the growing popularity of the approach, and the potential for genome-scale models to be used in tandem with computational analysis of genomes (Bekaert et al., 2011) it is pertinent to try and identify the areas in which FBA could be most usefully deployed as the technique develops.
Ultimately, the goal toward which metabolic modeling must advance is a reconstruction of metabolism at the whole-plant level. While in principle FBA is well suited to dealing with interacting cell types, considering whole plants raises the problem of temporal differences in metabolism during the development of the tissues (Walton and de Jong, 1990). A particular issue is that the pattern of growth of most plant tissues is not uniform with time: cells are initiated by division at the meristem and subsequently grow by expansion. This represents two very different modes of growth that will not be fully captured by constraints derived from biomass composition of mature cells. This is because such constraints assume that each component of biomass accumulates in a linear fashion and in the same proportion over the history of the cell. This is unlikely to be true since the nature of biomass accumulation during cell expansion is different to that during division (Thornley and Johnson, 1990). Moreover mature organs can make a significant contribution to whole-plant metabolism while not growing at all. Thus, the growth-based objective functions that currently tend to dominate flux-balance modeling would not be appropriate. On the other hand, differentiation and secondary growth can occur after organs have reached maturity, especially the synthesis of lignins and hemicelluloses prior to senescence (Amthor, 2000); and at the whole-plant scale, remobilization of resources during senescence can be quantitatively important for sink metabolism (Taylor et al., 2010). There is also the issue of environment to consider: acclimation to changing conditions is often associated with altered growth and composition (Armstrong et al., 2006) and leaves, in particular, are especially sensitive to diurnal fluctuations in light intensity. While none of these problems are insurmountable, it is obvious that careful consideration of objective functions and constraints that can usefully bound the flux space will be required. Additional experimental measures of growth and composition on a finer-grained scale will surely be necessary (Pramanik and Keasling, 1997). Computational approaches, such as dynamic FBA (Mahadevan et al., 2002), will also have to be developed to allow steady-state models to be concatenated along a developmental time axis.
Given the considerable effort that will be required to develop such sophisticated metabolic models, it is worth establishing at the outset the type of biological insights that might be expected from the approach. As we have already discussed, flux-balance modeling can highlight non-intuitive metabolic routes that may be worthy of subsequent experimental investigation. Flux-balance modeling can also be a useful means of predicting changes in flux under different conditions and with different nutrient sources, providing a deeper understanding of the metabolic demands of a varying environment. And because of the optimization algorithms at the heart of FBA, it is inherently good at examining the theoretical yield limits and energetic efficiencies of the metabolic networks under consideration.
Perhaps the ultimate driving force of most metabolic modeling is the lure of metabolic engineering; the aim being to identify the most appropriate target enzymes for genetic manipulation with respect to a desired metabolic output. However, in contrast to enzyme-kinetic modeling which provides a quantitative measure of the extent to which each enzyme controls pathway flux (Heinzle et al., 2007; Schallau and Junker, 2010), flux-balance models contain no intrinsic information about enzyme regulation or the control of flux. Nevertheless, flux-balance modeling can be used to identify optimal flux distributions that maximize the synthesis of a desired metabolic end-product. Commonly this takes the form of a systematic analysis of reaction deletions (either singly or combinations of multiple reaction deletions) while setting maximization of product yield as the objective function (Burgard et al., 2003; Alper et al., 2005). Unfortunately the solution usually involves a significant reduction in growth, reflecting the diversion of carbon into the desired product, and this is not particularly useful from a biotechnological viewpoint. Therefore, more recent attempts have incorporated combined objective functions of maximizing the production of the target compound while still maximizing biomass production (Montagud et al., 2010). This allows flux distributions to be identified that lead to over-production of the target compound without a drastic reduction in growth rate. Identifying the ideal flux distribution is only the first step and engineering that flux state into organisms, even bacteria, is a formidable challenge. But it can be done. In an impressive demonstration of metabolic engineering prowess, information from flux analysis was used to guide a total of 12 genetic interventions in Corynebacterium glutamicum (Becker et al., 2011) to generate a lysine-overproducing strain of similar performance to those produced industrially.
Summary
In summary, flux-balance modeling of plant metabolic networks provides an important complement to 13C-based MFA and an alternative to smaller scale mechanistic models based on enzyme kinetics. While flux-balance modeling has its limitations, stemming from the underdetermined nature of the problem and the lack of enzyme regulatory information or kinetic responses, it is capable of generating novel insights into metabolic behavior, capacities, and efficiency and it can be used as a framework for metabolic engineering. Future efforts toward multi-cell, multi-tissue, and ultimately whole-plant models will form an important component of computational models of plant growth and development (Christophe et al., 2008) and are likely to play a major role in efforts to improve crop yield and quality.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Allen, D. K., Libourel, I. G. L., and Shachar-Hill, Y. (2009a). Metabolic flux analysis in plants: coping with complexity. Plant Cell Environ. 32, 1241–1257.
Allen, D. K., Ohlrogge, J. B., and Shachar-Hill, Y. (2009b). The role of light in soybean seed filling metabolism. Plant J. 58, 220–234.
Alonso, A. P., Dale, V. L., and Shachar-Hill, Y. (2010). Understanding fatty acid synthesis in developing maize embryos using metabolic flux analysis. Metab. Eng. 12, 488–497.
Alonso, A. P., Goffman, F. D., Ohlrogge, J. B., and Shachar-Hill, Y. (2007). Carbon conversion efficiency and central metabolic fluxes in developing sunflower (Helianthus annuus L.) embryos. Plant J. 52, 296–308.
Alper, H., Jin, Y. S., Moxley, J. F., and Stephanopoulos, G. (2005). Identifying gene targets for the metabolic engineering of lycopene biosynthesis in Escherichia coli. Metab. Eng. 7, 155–164.
Amthor, J. S. (2000). The McCree-de Wit-Penning de Vries-Thornley respiration paradigms: 30 years later. Ann. Bot. 86, 1–20.
Apel, K., and Hirt, H. (2004). Reactive oxygen species: metabolism, oxidative stress, and signal transduction. Annu. Rev. Plant Biol. 55, 373–399.
Araujo, W. L., Nunes-Nesi, A., Nikoloski, Z., Sweetlove, L. J., and Fernie, A. R. (2011). Metabolic control and regulation of the tricarboxylic acid cycle in photosynthetic and heterotrophic plant tissues. Plant Cell Environ. 10.1111/j.1365-3040.2011.02332.x. [Epub ahead of print].
Armstrong, A. F., Logan, D. C., Tobin, A. K., O’Toole, P., and Atkin, O. K. (2006). Heterogeneity of plant mitochondrial responses underpinning respiratory acclimation to the cold in Arabidopsis thaliana leaves. Plant Cell Environ. 29, 940–949.
Averill, R. H., Bailey-Serres, J., and Kruger, N. J. (1998). Co-operation between cytosolic and plastidic oxidative pentose phosphate pathways revealed by 6-phosphogluconate dehydrogenase-deficient genotypes of maize. Plant J. 14, 449–457.
Baerenfaller, K., Grossmann, J., Grobei, M. A., Hull, R., Hirsch-Hoffmann, M., Yalovsky, S., Zimmermann, P., Grossniklaus, U., Gruissem, W., and Baginsky, S. (2008). Genome-scale proteomics reveals Arabidopsis thaliana gene models and proteome dynamics. Science 320, 938–941.
Bar-Even, A., Noor, E., Lewis, N. E., and Milo, R. (2010). Design and analysis of synthetic carbon fixation pathways. Proc. Natl. Acad. Sci. U.S.A. 107, 8889–8894.
Becker, J., Zelder, O., Hafner, S., Schroder, H., and Wittmann, C. (2011). From zero to hero-design-based systems metabolic engineering of Corynebacterium glutamicum for l-lysine production. Metab. Eng. 13, 159–168.
Bekaert, M., Edger, P. P., Pires, J. C., and Conant, G. C. (2011). Two-phase resolution of polyploidy in the arabidopsis metabolic network gives rise to relative and absolute dosage constraints. Plant Cell, 23, 1719–1728.
Borodina, I., and Nielsen, J. (2005). From genomes to in silico cells via metabolic networks. Curr. Opin. Biotechnol. 16, 350–355.
Boyle, N. R., and Morgan, J. A. (2009). Flux balance analysis of primary metabolism in Chlamydomonas reinhardtii. BMC Syst. Biol. 3, 4. doi: 10.1186/1752-0509-3-4
Boyle, N. R., and Morgan, J. A. (2011). Computation of metabolic fluxes and efficiencies for biological carbon dioxide fixation. Metab. Eng. 13, 150–158.
Brady, S. M., Orlando, D. A., Lee, J. Y., Wang, J. Y., Koch, J., Dinneny, J. R., Mace, D., Ohler, U., and Benfey, P. N. (2007). A high-resolution root spatiotemporal map reveals dominant expression patterns. Science 318, 801–806.
Burgard, A. P., Pharkya, P., and Maranas, C. D. (2003). OptKnock: a bilevel programming framework for identifying gene knockout strategies for microbial strain optimization. Biotechnol. Bioeng. 84, 647–657.
Butelli, E., Titta, L., Giorgio, M., Mock, H. P., Matros, A., Peterek, S., Schijlen, E. G. W. M., Hall, R. D., Bovy, A. G., Luo, J., and Martin, C. (2008). Enrichment of tomato fruit with health-promoting anthocyanins by expression of select transcription factors. Nat. Biotechnol. 26, 1301–1308.
Christophe, A., Letort, V., Hummel, I., Cournede, P. H., de Reffye, P., and Lecoeur, J. (2008). A model-based analysis of the dynamics of carbon balance at the whole-plant level in Arabidopsis thaliana. Funct. Plant Biol. 35, 1147–1162.
Cogne, G., Rugen, M., Bockmayr, A., Titica, M., Dussap, C. G., Cornet, J. F., and Legrand, J. (2011). A model-based method for investigating bioenergetic processes in autotrophically growing eukaryotic microalgae: application to the green algae Chlamydomonas reinhardtii. Biotechnol. Prog. 27, 631–640.
de Oliveira Dal’Molin, C. G., Quek, L. E., Palfreyman, R. W., Brumbley, S. M., and Nielsen, L. K. (2010a). Aragem, a genome-scale reconstruction of the primary metabolic network in Arabidopsis. Plant Physiol. 152, 579–589.
de Oliveira Dal’Molin, C. G., Quek, L. E., Palfreyman, R. W., Brumbley, S. M., and Nielsen, L. K. (2010b). C4gem, a genome-scale metabolic model to study C4 plant metabolism. Plant Physiol. 154, 1871–1885.
Edwards, J. S., and Palsson, B. O. (2000). The Escherichia coli mg1655 in silico metabolic genotype: its definition, characteristics, and capabilities. Proc. Natl. Acad. Sci. U.S.A. 97, 5528–5533.
Enfissi, E. M., Fraser, P. D., Lois, L. M., Boronat, A., Schuch, W., and Bramley, P. M. (2005). Metabolic engineering of the mevalonate and non-mevalonate isopentenyl diphosphate-forming pathways for the production of health-promoting isoprenoids in tomato. Plant Biotechnol. J. 3, 17–27.
Fell, D. A., Poolman, M. G., and Gevorgyan, A. (2010). Building and analysing genome-scale metabolic models. Biochem. Soc. Trans. 38, 1197–1201.
Fernie, A. R., and Schauer, N. (2009). Metabolomics-assisted breeding: a viable option for crop improvement? Trends Genet. 25, 39–48.
Fraser, P. D., Romer, S., Shipton, C. A., Mills, P. B., Kiano, J. W., Misawa, N., Drake, R. G., Schuch, W., and Bramley, P. M. (2002). Evaluation of transgenic tomato plants expressing an additional phytoene synthase in a fruit-specific manner. Proc. Natl. Acad. Sci. U.S.A. 99, 1092–1097.
Geigenberger, P., Stitt, M., and Fernie, A. R. (2004). Metabolic control analysis and regulation of the conversion of sucrose to starch in growing potato tubers. Plant Cell Environ. 27, 655–673.
Grafahrend-Belau, E., Schreiber, F., Koschutzki, D., and Junker, B. H. (2009). Flux balance analysis of barley seeds: a computational approach to study systemic properties of central metabolism. Plant Physiol. 149, 585–598.
Hauben, M., Haesendonckx, B., Standaert, E., Van Der Kelen, K., Azmi, A., Akpo, H., Van Breusegem, F., Guisez, Y., Bots, M., Lambert, B., Laga, B., and De Block, M. (2009). Energy use efficiency is characterized by an epigenetic component that can be directed through artificial selection to increase yield. Proc. Natl. Acad. Sci. U.S.A. 106, 20109–20114.
Hay, J., and Schwender, J. (2011a). Computational analysis of storage synthesis in developing rape Brassica napus L. (oilseed rape) embryos: flux variability analysis in relation to 13C-metabolic flux analysis. Plant J. 67, 513–525.
Hay, J., and Schwender, J. (2011b). Metabolic network reconstruction and flux variability analysis of storage synthesis in developing oilseed rape (Brassica napus L.) embryos. Plant J. 67, 526–541.
Heazlewood, J. L., Tonti-Filippini, J. S., Gout, A. M., Day, D. A., Whelan, J., and Millar, A. H. (2004). Experimental analysis of the Arabidopsis mitochondrial proteome highlights signaling and regulatory components, provides assessment of targeting prediction programs, and indicates plant-specific mitochondrial proteins. Plant Cell 16, 241–256.
Heazlewood, J. L., Verboom, R. E., Tonti-Filippini, J., Small, I., and Millar, A. H. (2007). SUBA: the Arabidopsis subcellular database. Nucleic Acids Res. 35, D213–D218.
Heinzle, E., Matsuda, F., Miyagawa, H., Wakasa, K., and Nishioka, T. (2007). Estimation of metabolic fluxes, expression levels and metabolite dynamics of a secondary metabolic pathway in potato using label pulse-feeding experiments combined with kinetic network modelling and simulation. Plant J. 50, 176–187.
Henry, C. S., Dejongh, M., Best, A. A., Frybarger, P. M., Linsay, B., and Stevens, R. L. (2010). High-throughput generation, optimization and analysis of genome-scale metabolic models. Nat. Biotechnol. 28, 977–982.
Iyer, V. V., Sriram, G., Fulton, D. B., Zhou, R., Westgate, M. E., and Shanks, J. V. (2008). Metabolic flux maps comparing the effect of temperature on protein and oil biosynthesis in developing soybean cotyledons. Plant Cell Environ. 31, 506–517.
Jankowski, M. D., Henry, C. S., Broadbelt, L. J., and Hatzimanikatis, V. (2008). Group contribution method for thermodynamic analysis of complex metabolic networks. Biophys. J. 95, 1487–1499.
Junker, B. H., Lonien, J., Heady, L. E., Rogers, A., and Schwender, J. (2007). Parallel determination of enzyme activities and in vivo fluxes in Brassica napus embryos grown on organic or inorganic nitrogen source. Phytochemistry 68, 2232–2242.
Knoop, H., Zilliges, Y., Lockau, W., and Steuer, R. (2010). The metabolic network of Synechocystis sp. PCC 6803: systemic properties of autotrophic growth. Plant Physiol. 154, 410–422.
Kruger, N. J., and Ratcliffe, R. G. (2008). Metabolic organization in plants: a challenge for the metabolic engineer. Adv. Plant Biochem. Mol. Biol. 1, 1–27.
Kruger, N. J., and Ratcliffe, R. G. (2009). Insights into plant metabolic networks from steady-state metabolic flux analysis. Biochimie 91, 697–702.
Kruger, N. J., and von Schaewen, A. (2003). The oxidative pentose phosphate pathway: structure and organisation. Curr. Opin. Plant Biol. 6, 236–246.
Lee, C. P., Eubel, H., O’Toole, N., and Millar, A. H. (2011). Combining proteomics of root and shoot mitochondria and transcript analysis to define constitutive and variable components in plant mitochondria. Phytochemistry 72 1092–1108.
Lee, S., Chan, P., Domach, M. M., and Grossman, I. E. (2000). Recursive MILP model for finding all the alternate optima in LP models for metabolic networks. Comput. Chem. Eng. 24, 711–716.
Lehmann, M., Schwarzlander, M., Obata, T., Sirikantaramas, S., Burow, M., Olsen, C. E., Tohge, T., Fricker, M. D., Moller, B. L., Fernie, A. R., Sweetlove, L. J., and Laxa, M. (2009). The metabolic response of arabidopsis roots to oxidative stress is distinct from that of heterotrophic cells in culture and highlights a complex relationship between the levels of transcripts, metabolites, and flux. Mol. Plant 2, 390–406.
Lewis, N. E., Schramm, G., Bordbar, A., Schellenberger, J., Andersen, M. P., Cheng, J. K., Patel, N., Yee, A., Lewis, R. A., Eils, R., König, R., and Palsson, B. Ø. (2010). Large-scale in silico modeling of metabolic interactions between cell types in the human brain. Nat. Biotechnol. 28, 1279–1285.
Libourel, I. G. L., and Shachar-Hill, Y. (2008). Metabolic flux analysis in plants: from intelligent design to rational engineering. Annu. Rev. Plant Biol. 59, 625–650.
Lonien, J., and Schwender, J. (2009). Analysis of metabolic flux phenotypes for two Arabidopsis mutants with severe impairment in seed storage lipid synthesis. Plant Physiol. 151, 1617–1634.
Mahadevan, R., Edwards, J. S., and Doyle, F. J. III (2002). Dynamic flux balance analysis of diauxic growth in Escherichia coli. Biophys. J. 83, 1331–1340.
Mahadevan, R., and Schilling, C. H. (2003). The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab. Eng. 5, 264–276.
Masakapalli, S. K., Le Lay, P., Huddleston, J. E., Pollock, N. L., Kruger, N. J., and Ratcliffe, R. G. (2010). Subcellular flux analysis of central metabolism in a heterotrophic Arabidopsis cell suspension using steady-state stable isotope labeling. Plant Physiol. 152, 602–619.
Memelink, J., and Gantet, P. (2007). Transcription factors involved in terpenoid indole alkaloid biosynthesis in Catharanthus roseus. Phytochem. Rev. 6, 353–362.
Montagud, A., Navarro, E., Fernandez de Cordoba, P., Urchueguia, J. F., and Patil, K. R. (2010). Reconstruction and analysis of genome-scale metabolic model of a photosynthetic bacterium. BMC Syst. Biol. 4, 156. doi: 10.1186/1752-0509-4-156
Naqvi, S., Zhu, C., Farre, G., Ramessar, K., Bassie, L., Breitenbach, J., Perez Conesa, D., Ros, G., Sandmann, G., Capell, T., and Christou, P. (2009). Transgenic multivitamin corn through biofortification of endosperm with three vitamins representing three distinct metabolic pathways. Proc. Natl. Acad. Sci. U.S.A. 106, 7762–7767.
Parry, M. A., Reynolds, M., Salvucci, M. E., Raines, C., Andralojc, P. J., Zhu, X. G., Price, G. D., Condon, A. G., and Furbank, R. T. (2010). Raising yield potential of wheat. II. Increasing photosynthetic capacity and efficiency. J. Exp. Bot. 62, 453–467.
Penning de Vries, F. W. T. (1974). Substrate utilization and respiration in relation to growth and maintenance in higher plants. Neth. J. Agric. Sci. 22, 40–44.
Penning de Vries, F. W. T., Brunsting, A. H. M., and Van Laar, H. H. (1974). Products, requirements and efficiency of biosynthesis – quantitative approach. J. Theor. Biol. 45, 339–377.
Pilalis, E., Chatziioannou, A., Thomasset, B., and Kolisis, F. (2011). An in silico compartmentalized metabolic model of Brassica napus enables the systemic study of regulatory aspects of plant central metabolism. Biotechnol. Bioeng. 108, 1673–1682.
Poolman, M. G., Miguet, L., Sweetlove, L. J., and Fell, D. A. (2009). A genome-scale metabolic model of Arabidopsis and some of its properties. Plant Physiol. 151, 1570–1581.
Pramanik, J., and Keasling, J. D. (1997). Stoichiometric model of Escherichia coli metabolism: incorporation of growth-rate dependent biomass composition and mechanistic energy requirements. Biotechnol. Bioeng. 56, 398–421.
Radrich, K., Tsuruoka, Y., Dobson, P., Gevorgyan, A., Swainston, N., Baart, G., and Schwartz, J. M. (2010). Integration of metabolic databases for the reconstruction of genome-scale metabolic networks. BMC Syst. Biol. 4, 114. doi: 10.1186/1752-0509-4-114
Ratcliffe, R. G., and Shachar-Hill, Y. (2006). Measuring multiple fluxes through plant metabolic networks. Plant J. 45, 490–511.
Reed, J. L., and Palsson, B. O. (2003). Thirteen years of building constraint-based in silico models of Escherichia coli. J. Bacteriol. 185, 2692–2699.
Roscher, A., Kruger, N. J., and Ratcliffe, R. G. (2000). Strategies for metabolic flux analysis in plants using isotope labelling. J. Biotechnol. 77, 81–102.
Rossell, S., van der Weijden, C. C., Lindenbergh, A., van Tuijl, A., Francke, C., Bakker, B. M., and Westerhoff, H. V. (2006). Unraveling the complexity of flux regulation: a new method demonstrated for nutrient starvation in Saccharomyces cerevisiae. Proc. Natl. Acad. Sci. U.S.A. 103, 2166–2171.
Saha, R., Suthers, P., and Maranas, C. (2011). Zea mays irs1563: a comprehensive genome-scale metabolic reconstruction of maize metabolism. PLoS ONE 6, e21784. doi: 10.1371/journal.pone.0021784
Schallau, K., and Junker, B. H. (2010). Simulating plant metabolic pathways with enzyme-kinetic models. Plant Physiol. 152, 1763–1771.
Schuetz, R., Kuepfer, L., and Sauer, U. (2007). Systematic evaluation of objective functions for predicting intracellular fluxes in Escherichia coli. Mol. Syst. Biol. 3, 119.
Schuster, S., Pfeiffer, T., and Fell, D. A. (2008). Is maximization of molar yield in metabolic networks favoured by evolution? J. Theor. Biol. 252, 497–504.
Schwender, J., Goffman, F., Ohlrogge, J. B., and Shachar-Hill, Y. (2004). Rubisco without the Calvin cycle improves the carbon efficiency of developing green seeds. Nature 432, 779–782.
Schwender, J., Ohlrogge, J. B., and Shachar-Hill, Y. (2003). A flux model of glycolysis and the oxidative pentosephosphate pathway in developing Brassica napus embryos. J. Biol. Chem. 278, 29442–29453.
Schwinn, K., Venail, J., Shang, Y., Mackay, S., Alm, V., Butelli, E., Oyama, R., Bailey, P., Davies, K., and Martin, C. (2006). A small family of myb-regulatory genes controls floral pigmentation intensity and patterning in the genus antirrhinum. Plant Cell 18, 831–851.
Shastri, A. A., and Morgan, J. A. (2005). Flux balance analysis of photoautotrophic metabolism. Biotechnol. Prog. 21, 1617–1626.
Shastri, A. A., and Morgan, J. A. (2007). A transient isotopic labeling methodology for 13C metabolic flux analysis of photoautotrophic microorganisms. Phytochemistry 68, 2302–2312.
Smith, A. M., and Stitt, M. (2007). Coordination of carbon supply and plant growth. Plant Cell Environ. 30, 1126–1149.
Sriram, G., Fulton, D. B., Iyer, V. V., Peterson, J. M., Zhou, R., Westgate, M. E., Spalding, M. H., and Shanks, J. V. (2004). Quantification of compartmented metabolic fluxes in developing soybean embryos by employing biosynthetically directed fractional 13C labeling, two-dimensional [13C, 1H] nuclear magnetic resonance, and comprehensive isotopomer balancing. Plant Physiol. 136, 3043–3057.
Stitt, M., Sulpice, R., and Keurentjes, J. (2010). Metabolic networks: how to identify key components in the regulation of metabolism and growth. Plant Physiol. 152, 428–444.
Sweetlove, L. J., Beard, K. F., Nunes-Nesi, A., Fernie, A. R., and Ratcliffe, R. G. (2010). Not just a circle: flux modes in the plant TCA cycle. Trends Plant Sci. 15, 462–470.
Sweetlove, L. J., Fell, D., and Fernie, A. R. (2008). Getting to grips with the plant metabolic network. Biochem. J. 409, 27–41.
Taylor, L., Nunes-Nesi, A., Parsley, K., Leiss, A., Leach, G., Coates, S., Wingler, A., Fernie, A. R., and Hibberd, J. M. (2010). Cytosolic pyruvate, orthophosphate dikinase functions in nitrogen remobilization during leaf senescence and limits individual seed growth and nitrogen content. Plant J. 62, 641–652.
Taylor, N. L., Day, D. A., and Millar, A. H. (2004). Targets of stress-induced oxidative damage in plant mitochondria and their impact on cell carbon/nitrogen metabolism. J. Exp. Bot. 55, 1–10.
Thornley, J. H. M., and Johnson, I. R. (1990). Plant and Crop Modeling Oxford: Oxford University Press.
Walton, E. F., and de Jong, T. M. (1990). Estimating the bioenergetic cost of a developing kiwifruit berry and its growth and maintenance respiration components. Ann. Bot. 66, 417–424.
Williams, T. C. R., Miguet, L., Masakapalli, S. K., Kruger, N. J., Sweetlove, L. J., and Ratcliffe, R. G. (2008). Metabolic network fluxes in heterotrophic Arabidopsis cells: stability of the flux distribution under different oxygenation conditions. Plant Physiol. 148, 704–718.
Williams, T. C. R., Poolman, M. G., Howden, A. J., Schwarzlander, M., Fell, D. A., Ratcliffe, R. G., and Sweetlove, L. J. (2010). A genome-scale metabolic model accurately predicts fluxes in central carbon metabolism under stress conditions. Plant Physiol. 154, 311–323.
Zhang, P., Dreher, K., Karthikeyan, A., Chi, A., Pujar, A., Caspi, R., Karp, P., Kirkup, V., Latendresse, M., Lee, C., Mueller, L. A., Muller, R., and Rhee, S. Y. (2010). Creation of a genome-wide metabolic pathway database for Populus trichocarpa using a new approach for reconstruction and curation of metabolic pathways for plants. Plant Physiol. 153, 1479–1491.
Keywords: flux-balance modeling, metabolism, flux
Citation: Sweetlove LJ and Ratcliffe RG (2011) Flux-balance modeling of plant metabolism. Front. Plant Sci. 2:38. doi: 10.3389/fpls.2011.00038
Received: 16 May 2011;
Accepted: 28 July 2011;
Published online: 11 August 2011.
Edited by:
Alisdair Fernie, Max Planck Institute for Plant Physiology, GermanyReviewed by:
Jörg Schwender, Brookhaven National Laboratory, USAJohn Morgan, Purdue University, USA
Copyright: © 2011 Sweetlove and Ratcliffe. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Lee J. Sweetlove, Department of Plant Sciences, University of Oxford, South Parks Road, Oxford OX1 3RB, UK. e-mail:bGVlLnN3ZWV0bG92ZUBwbGFudHMub3guYWMudWs=

