Towards verifiable cancer digital twins: tissue level modeling protocol for precision medicine

Cancer exhibits substantial heterogeneity, manifesting as distinct morphological and molecular variations across tumors, which frequently undermines the efficacy of conventional oncological treatments. Developments in multiomics and sequencing technologies have paved the way for unraveling this heterogeneity. Nevertheless, the complexity of the data gathered from these methods cannot be fully interpreted through multimodal data analysis alone. Mathematical modeling plays a crucial role in delineating the underlying mechanisms to explain sources of heterogeneity using patient-specific data. Intra-tumoral diversity necessitates the development of precision oncology therapies utilizing multiphysics, multiscale mathematical models for cancer. This review discusses recent advancements in computational methodologies for precision oncology, highlighting the potential of cancer digital twins to enhance patient-specific decision-making in clinical settings. We review computational efforts in building patient-informed cellular and tissue-level models for cancer and propose a computational framework that utilizes agent-based modeling as an effective conduit to integrate cancer systems models that encode signaling at the cellular scale with digital twin models that predict tissue-level response in a tumor microenvironment customized to patient information. Furthermore, we discuss machine learning approaches to building surrogates for these complex mathematical models. These surrogates can potentially be used to conduct sensitivity analysis, verification, validation, and uncertainty quantification, which is especially important for tumor studies due to their dynamic nature.

Introduction

Cancer is a heterogeneous disease with malignant cells that dynamically change their molecular signatures. The tumor tissue thus has a diverse collection of genetically distinct tumor sub-populations in a non-uniform spatial distribution. Each genotype exhibits different sensitivity to treatments. Spatial and temporal heterogeneity contribute to the development of resistance against therapies, complicating the effectiveness of treatments (Zhu et al., 2021; Vitale et al., 2021). In addition to genetic diversity, epigenetic modifications like DNA methylation, histone modifications, and chromatin remodeling can also drive therapeutic resistance (Vitale et al., 2021; Sadida et al., 2024). Combinatorial therapies targeting not only the drug/treatment sensitive tumor sub-clones but also the other drug-resistant subclones are likely to improve therapeutic responses (Zhu et al., 2021).

The tumor microenvironment also plays an important role in driving the evolution of cancer cells. It can lead to metabolic reprogramming in response to the availability of growth factors, oxygen, nutrients, drug exposure, and even mechanical cues such as cell density and extracellular matrix stiffness (Demicco et al., 2024). In the tumor microenvironment, stromal cells and immune cells exhibit substantial heterogeneity (Vitale et al., 2021), which further affects overall cancer heterogeneity.

Advances in single-cell sequencing (Baslan and Hicks, 2017; Lei et al., 2021) and multiomics (He et al., 2023; Menyhárt and Győrffy, 2021) techniques have enabled genetic, epigenetic, and even metabolic profiling of cancer cells at a cellular resolution, helping to delineate intratumoral heterogeneity (Lee et al., 2021; Schmidt et al., 2021; Ortega et al., 2017). Extensive multimodal data analysis on sequencing data has successfully identified biomarkers and stratifying risk in clinical settings (Lee et al., 2021; Schmidt et al., 2021; Ortega et al., 2017; Subramanian et al., 2020). Several multi-omic data repositories have been instrumental in furthering data-driven research to study cancer heterogeneity (Subramanian et al., 2020). (TCGA (NCI, 2022), TARGET (dbGaP, 2024), CPTAC (NCI, 2024), CCLE (CCLE, 2024), EUREKA (Peyser et al., 2022), AllofUs (Denny et al., 2019)) They are essential in guiding patient-specific treatment choices based on individual tumor profiles. However, these techniques on their own are not enough to decipher mechanisms or pathways that lead to the observed subclones. Moreover, these techniques are insufficient to characterize chemical or physical gradient-induced extrinsic spatial tissue heterogeneity. Physics-driven mechanistic systems biology modeling, which includes models of biochemical and genetic pathways using ordinary or partial differential equations, boolean networks, and even spatiotemporal models like hybrid cellular automaton and agent-based simulations, is essential. There is, however, a need to establish a verifiable computational framework that can utilize multi-modal patient-specific clinical information at different scales - molecular, single-cell sequencing, multi-omics, tissue histology, etc., in addition to physics-based and systems biology models to make tissue-level predictions. Such models can be used to explore model parameter space, simulate different treatments and compare model outcomes, formulate and test hypotheses to explore mechanisms of sub-clonal evolution, and elucidate pathways for tumor malignancy, sub-clonal evolution, resistance, and metastases.

A digital twin, as defined by the National Academies of Sciences, Engineering, and Medicine, is a set of virtual information constructs that mimics the structure, context, and behavior of a natural or engineered system, dynamically updated with data from its physical counterpart, with predictive capabilities to inform decision-making (National Academies, 2024). Cancer, as a complex and adaptive disease, requires personalized treatment strategies tailored to each patient’s genetic and environmental factors. Cancer cells’ ability to evolve and resist therapies further complicates treatment. To address this, an in-silico tumor simulator is needed, capable of capturing tumor complexity and updating with changes in the patient’s condition. Digital twin frameworks should incorporate mechanistic models at the cellular and tissue levels, continuously updated with real-time clinical and multiomics data. These cancer digital twins enable virtual patient simulations, allowing clinicians to test clinical hypotheses and refine therapeutic strategies in a predictive and personalized manner.

Multiscale hybrid digital twin models (virtual replicas of real-world entities) can facilitate personalized therapeutic strategies that are finely tuned to the unique characteristics of each patient. Agent-based modeling can serve as an effective conduit for integrating cancer systems models that encode signaling at the cellular scale into digital twin models that predict tissue-level responses in a tumor microenvironment customized to patient cohorts. Agent-based modeling (ABM) operates on a fundamental principle that each agent (e.g., a cell in a tumor) is programmed to follow a set of user-defined rules. These rules dictate how agents interact with each other and respond to their environment, thereby capturing the complex, dynamic behaviors observed in biological systems (Bonabeau, 2002). ABM frameworks are useful for cancer tissue systems because they can in corporate diversity at the single-cell level and predict the collective complex behavior of the tumor tissue spatiotemporally (West et al., 2023). These tissue-level spatiotemporal agent-based models can be powered by physics-based cellular systems biology models specific to different types of tumors, leveraging patient-specific clinical information. In this review, we examine various mechanistic cellular models and tissue-level agent-based models documented in the cancer research literature. We cite representative examples and explore potential strategies for integrating cellular-scale models with tissue-level frameworks.

Though such a hybrid modeling framework can be extremely useful for capturing the complexity of a tumor, the computational expense can grow exponentially as one increases the number of cells in the agent-based simulation. Machine learning approaches can reduce the computational expense of ABMs, conduct feature ranking, global sensitivity analysis, and uncertainty quantification (UQ) leveraging data-driven methods. Such a framework is outlined in Figure 1. While ML can help manage stochasticity and heterogeneity in ABMs and generate statistical measures for complex systems, the integration can result in limited interpretability due to the “black box” nature of ML models (Sivakumar et al., 2022). The synergy between ML and ABM leverages their respective strengths, but finding the right balance and integration strategy is complex and requires careful consideration of each approach’s limitations.

Figure 1

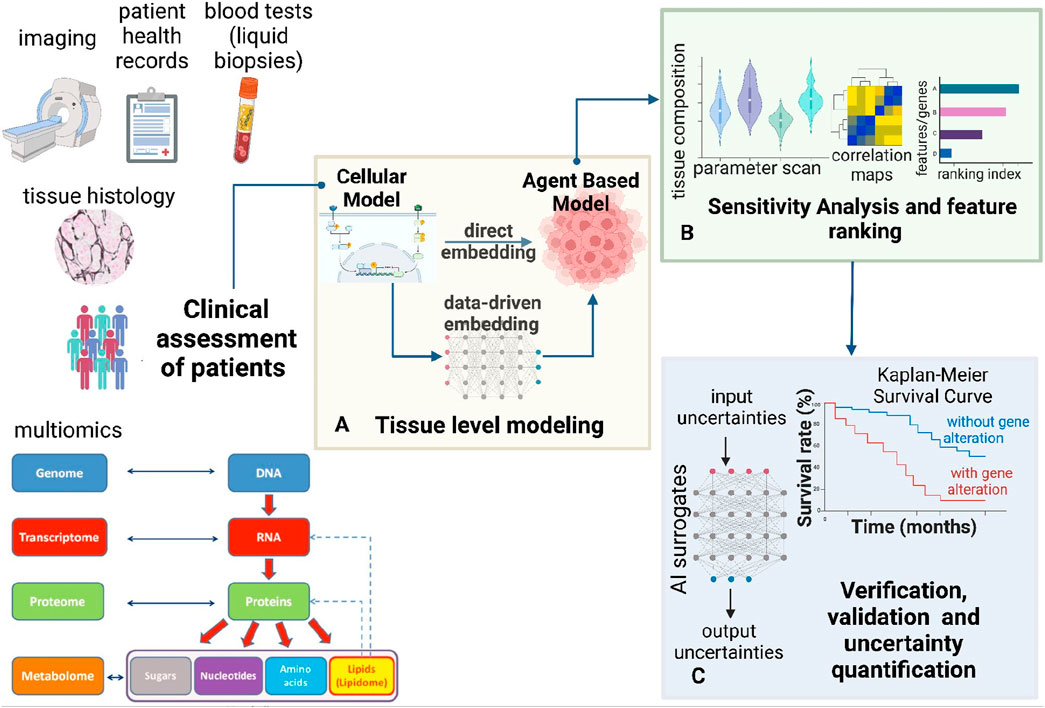
Figure 1. Modeling framework for multi-scale multi-agent spatiotemporal models. This figure presents a comprehensive bottom-up framework for hybrid multi-scale modeling. (A) This framework integrates cellular systems biology models with multi-agent simulations to predict tissue-level spatiotemporal dynamics. Cellular models, including ODE-based and Boolean approaches, can be embedded within the multi-agent framework to inform agent decisions. Cellular models can be constrained using patient-specific clinical information. Machine learning techniques can replace massive cellular models to enhance the efficiency of multi-agent simulations. Thus, the cellular models can also be embedded by training ML surrogates on data from the mechanistic cellular models. (B) Once the model is built, sensitivity analysis and feature importance assessment can be conducted (C) To ensure the robustness of the multi-scale framework, verification, validation, and uncertainty quantification (VVUQ) can be incorporated using AI surrogates. Clinical exploration using Kaplan-Meier survival analysis can help validate observations from the constructed hybrid model (A) and sensitivity analysis (B).

Cellular systems biology models to encode cell behavior

Cancer cells undergo multi-faceted changes in the complex network of pathways, thus differentiating them from normal cells. These networks involve gene regulation, signaling, metabolism, and other dynamic pathways (Laubenbacher et al., 2009) responsible for cancer cells’ superior replicative potential, sufficiency in growth signals, insensitivity to growth signals, evading apoptosis, and even improved angiogenesis (Hanahan and Weinberg, 2000). Additional hallmarks that are generic to all cancer types include reprogramming of energy metabolism and evading immune destruction (Hanahan and Weinberg, 2011). Mathematical models have been built for these pathways in the past couple of decades, and rigorous analyses have been conducted to delineate mechanisms and simulate and test hypotheses. With the influx of multi-omics data, such models can be customized to patient information to improve predictability.

At the most fundamental level, cell behavior is governed by growth-inducing pathways and their counterpart apoptotic pathways. These two mechanisms work together to maintain normal cellular growth conditions. Alterations in these pathways are the most prominent indications of malignancy. A common pathway frequently studied in cancers is mitogenic signaling. The ErbB signaling pathways (ErbB receptor-mediated Ras-MAPK and PI3K-AKT pathways) have been modeled using mass action kinetics to study the effect of epidermal growth factor (EGF), heregulin (HRG) and other ligands in cancer cell mitogenesis (Chen et al., 2009; Ebata et al., 2022; Kirouac et al., 2013). A cell cycle progression and apoptotic pathway frequently implicated in several cancers is the p53-Mediated DNA damage response pathway. Multiple studies have conducted boolean network modeling and molecular state transition dynamics to understand oscillatory behavior, regulation and identify potential therapeutic strategies (Choi et al., 2012; Wang, 2013; Gao et al., 2020). In addition to these competing mitogenic and apoptotic pathways, certain additional pathways can become important to study in specific cancer types. For instance, the cross-talk between PI3K and androgen receptor (AR) signaling pathways promotes pathogenesis and treatment resistance in prostate cancer (Crumbaker et al., 2017). Moreover, as understanding of cancer mechanisms has advanced, phenotypic plasticity and epigenetic reprogramming have emerged as additional factors responsible for malignant transformation (Hanahan, 2022). Newer hallmarks highlight the need for models that incorporate these additional pathways, which are crucial for predicting cancer cell behavior.

It has become increasingly apparent that single pathway-specific models are insufficient for high-fidelity cell fate predictions. Combining these models and enabling dynamic interaction/cross-talk can be useful in predicting the cellular macrostates from the individual microstates of pathway-specific species (e.g., growth factors, tumor suppressors, etc.,) concentrations. Hybrid modeling protocols are gaining traction in building multi-pathway informed cancer cell state models. A recent publication from the CHIC Project Consortium (CHIC, 2017) describes a molecular model (as a plug-in component of a cancer digital twin) that combines the ErbB Receptor-Mediated Ras/Raf/MAPK and PI3K/AKT pathways (Chen et al., 2009) with p53-Mediated DNA damage-response module (Choi et al., 2012) by establishing interaction between the two models via the state of the common nodes, namely, Erk, Akt and PTEN (Kolokotroni et al., 2024).

Cellular models can predict phenotypes like cell growth and death probabilities, and cell growth in response to radiotherapy, chemotherapy, and hormonal therapy treatments. They can be tailored to patient-specific clinical data for personalized modeling. These models can help develop insights into individual cancer cell behavior but are not enough to gain insight into the collective behavior of tissues with heterogeneous cell types and cell-cell interactions. These models can, however, power tissue-level spatiotemporal models to build a holistic representation of a complex tumor microenvironment.

Multi-agent models for simulating tissue-level spatiotemporal dynamics

The dynamics of cancer makes it important to capture and predict the spatiotemporal trends in tumor growth to develop effective treatment strategies. There has been an increasing interest in building agent-based models for cancer systems. Agent-based models consist of individual entities called agents in a shared environment. Agents can represent cells in a tissue or sections of blood vessels that reside in a space. These agents (cells) are programmed to act according to the rules set by the modeler (Cogno et al., 2024). Such rules encompass the cell-cell, cell-environment, and intra-cellular interactions. Cellular (i.e., agent) decisions can be based on physics-based models or probabilistic rules. When multi-cellular systems are allowed to evolve spatiotemporally based on these governing rules, the collective complex behavior of the system can be captured.

Agent-based models can be simulated using lattice-based or off-lattice methods. On-lattice (Lattice-based) models are spatially discrete models, where agent positions are asynchronously updated using simple migration rules. Such modeling style could lead to restrictions in simulating biologically close population dynamics. Lattice-based (On-lattice) methods include cellular automata models (where each lattice is occupied by one agent), lattice gas cellular automaton models (where each lattice site can contain multiple agents), and Cellular Potts models (CPMs) (use multiple lattice sites to represent each cell) (Metzcar et al., 2019). Off-lattice models usually simulate dynamics of individual agents using Newton equations of motion. These models provide more freedom in simulating behaviors like cell motility and chemotaxis. However, simulating these models is computationally expensive and the computational complexity increases with the number of agents. Off-lattice methods involve models that track the center of mass/volume of each agent and cell boundary-tracking methods (Metzcar et al., 2019). The latter is better suited for coupling detailed cell mechanics to fluid and solid tissue mechanics (Metzcar et al., 2019). Nava-Sedeno et al. (2020) and Metzcar et al. (2019) review these cell-based ABM methods with specific applications in cancer biology.

ABMs can simulate cancer initiation and progression by incorporating mechanistic cellular models informing each cell’s fate. They can also model tumor-host interactions, nutrient diffusion, hypoxia, angiogenesis, immune cell dynamics, and tumor-immune interaction (Cogno et al., 2024). It is extremely difficult to have mechanistic models to simulate all cellular behaviors. While constructing a multiscale hybrid model, one would need to approximate certain behaviors for which mechanistic models do not exist. ABMs thus become a powerful framework in complex multi-scale systems. ABMs can combine physics-based models (e.g., cell growth rate, death rate) with stochastic rule-based processes (where mechanistic molecular pathway-based models are currently non-existent). Examples of such phenotypes could be cell-cell adhesion, cell-matrix adhesion, chemotaxis, cellular uptake of drugs, hypoxia, angiogenesis, etc.

In the past two decades, numerous in-house and adapted ABMs have been developed to simulate tumor progression (Wang et al., 2015; Enderling et al., 2009; Norton et al., 2017; Yu and Bagheri, 2020; Rejniak, 2007) and its dependence on intra-tumor genetic diversity (Anderson et al., 2006), vasculature (Mehdizadeh et al., 2013; Yu and Bagheri, 2021; Cai et al., 2011; Duswald et al., 2024; de Montigny et al., 2021), nutrient (Kuznetsov and Kolobov, 2023) and oxygen (Anderson et al., 2006; de Montigny et al., 2021; Bull et al., 2020) (hypoxia and necrosis) gradients, solid stress (Kuznetsov and Kolobov, 2023), tumor-immune interactions (Heidary et al., 2020; van Genderen et al., 2024; Cess and Finley, 2020; Norton et al., 2019; Bergman et al., 2021), therapies like radiation therapy (Powathil et al., 2016; Chaudhuri et al., 2023), immunotherapy (Ruiz-Martinez et al., 2022; Gong et al., 2017) and even pre-clinical preventative vaccination studies (Palladini et al., 2010). Available open-source ABM software include PhysiCell (Ghaffarizadeh et al., 2018) (an off-lattice ABM framework that uses BioFVM (Ghaffarizadeh et al., 2016) to simulate diffusion partial differential equations for chemical substrates), BioDynaMo (Breitwieser et al., 2022), Chaste (Mirams et al., 2013; Cooper et al., 2020), CompuCell3D (Swat et al., 2012), and EPISIM (Sütterlin et al., 2013). These have been instrumental in improving the accessibility of multi-agent, multi-scale simulations for the computational biology modeling community.

Embedding cellular models for decision-making in a multi-agent modeling framework

Differential equation based and boolean approaches for cellular modeling

Most systems biology models that simulate intracellular or molecular processes in a cell include continuous time, nonlinear and coupled deterministic or stochastic ordinary differential equations (ODEs). These can be solved using numerical discretization methods. COPASI (Hoops et al., 2006) is a commonly used open-source complex pathway simulator that supports systems biology markup language (SBML) representation of cellular biochemical networks. Many ABM packages (e.g., Chaste (Mirams et al., 2013), CompuCell3D (Swat et al., 2012), and EPISIM (Sütterlin et al., 2013)) support SBML to include systems of ODEs that simulate molecular pathways in individual cells (Metzcar et al., 2019). Thus, each cell/agent can have embedded cellular models informing cellular behavior (Rikard et al., 2019; Corti et al., 2021; Schuetz et al., 2013). In pathways where quantitative kinetic data of the constituent chemical species and reactions is unavailable or large-scale networks need to be modeled that are computationally expensive, a discrete boolean approach (Hemedan et al., 2022) is more feasible to extract qualitative insights. PhysiCell (Ghaffarizadeh et al., 2018) has an auxiliary boolean modeling package, MaBoSS (Stoll et al., 2017), that simulates intracellular pathways or molecular mechanistic models at a single-cell level.

Machine learning approaches to speed up multi-agent simulations

ABMs informed by cellular mechanistic models can be used to understand how intracellular changes can influence tissue-level behavior in individual cells. Complex intracellular models can have tens to hundreds of equations with hundreds to thousands of parameters. Thus, embedding mechanistic ODE-based or boolean models to inform the decisions of every agent at each time step in the dynamic simulation can be computationally very expensive. Surrogate models are data-driven models trained on data generated from high fidelity models that are computationally expensive to run. Surrogates can produce new simulation data faster and at a very little computational cost as compared to the original high-fidelity models. Such techniques might be extremely valuable in our hybrid modeling framework. The cellular mechanistic models can be used to generate data for training ML surrogates. Such surrogates can be used for predicting agent behavior instead of running the expensive mechanistic cellular models. An example of such use case in cancer agent-based modeling has been proposed by Cess and Finley (2020) proposed a novel data-driven technique to replace mechanistic models with pre-trained neural networks. They used an intracellular signaling model that informs macrophage phenotypes to produce simulation data. This generated data was used to train a simple input/output model using a neural network with cytokine concentrations in the microenvironment as input and macrophage differentiation state (M1 or M2) as output. In the ABM simulation, each macrophage agent samples the local cytokine concentrations (solved by diffusion PDEs coupled with the ABM) and decides its phenotypic fate based on the neural network. Such data-driven cellular embedding can significantly increase the computational speed. In case of absence of mechanistic models, machine learning models trained on clinical data can also be used to inform agent behavior (Sivakumar et al., 2022).

Sensitivity analysis and feature importance in the multi-scale hybrid model

Predictive models are invaluable in biological research; however, they often lack sufficient experimental data to determine model parameters or initial conditions accurately (Zi, 2011). Building robust patient-specific predictive models requires longitudinal data from multi-omics, tissue imaging, and biopsies. However, in retrospective modeling efforts, access to such comprehensive data is often limited. Even when predictive modeling runs alongside clinical trials, challenges persist. These include uncertain data acquisition due to patient dropouts, failure to capture long-term post-trial data, and variability in data collection caused by non-standardized protocols across trial sites. These issues hinder the ability to create accurate and reliable models. In many instances, these values are estimated, thus leading to uncertainties that propagate through the model and affect its predictions. Sensitivity analysis techniques quantify the effect on fluctuations in the model output as caused by changes/uncertainties in the model inputs (Zi, 2011; Global Sensitivity Analysis, 2008). In the hybrid modeling context, these model inputs include model parameters, boundary conditions and initial conditions for cellular and tissue level models. Sensitivity analysis is used for evaluating robustness of mathematical surrogates of biological systems (Streif et al., 2016), parameter estimation (Linden et al., 2022), and rank the most important model parameter subsets that have the greatest impact on model outputs (Li et al., 2010). Such insights can also be used to design better experimental studies for the given biological system (Zi, 2011; Qian and Mahdi, 2020). Two types of sensitivity analyses exist - local and global (Table 1). Local sensitivity analysis (LSA) assesses the effect of small changes in individual model parameters on the output, varying one parameter at a time. On a wide range of values, parametric sensitivity analyses can be done on the multiscale hybrid agent-based model by scanning a few orders of magnitude for the parameter of interest. Global sensitivity analysis (GSA) evaluates the impact of varying all parameters simultaneously across their entire ranges, providing a comprehensive understanding of parameter influence and interactions. This method is more suited for highly nonlinear and coupled systems. Parameter sampling methods like Monte-carlo sampling and Latin hypercube sampling are required to conduct GSA. GSA includes variety of techniques - Multi-parametric sensitivity analysis (MPSA), Partial rank correlation coefficient (PRCC) analysis, Morris sensitivity analysis, Weighted average of local sensitivities (WALS), Sobol sensitivity analysis, Random sampling high-dimensional model representation (RS-HDMR), Fourier amplitude sensitivity test (FAST) (Zi, 2011). Zi (2011) discusses the advantages and disadvantages of all sensitivity analysis methods in the context of systems biology models. Global sensitivity methods are computationally expensive, even for simple models. They are extremely difficult to implement on hybrid models. Thus, there is scope for developing novel approaches to conducting global sensitivity analysis on complex hybrid multiscale models.

Table 1

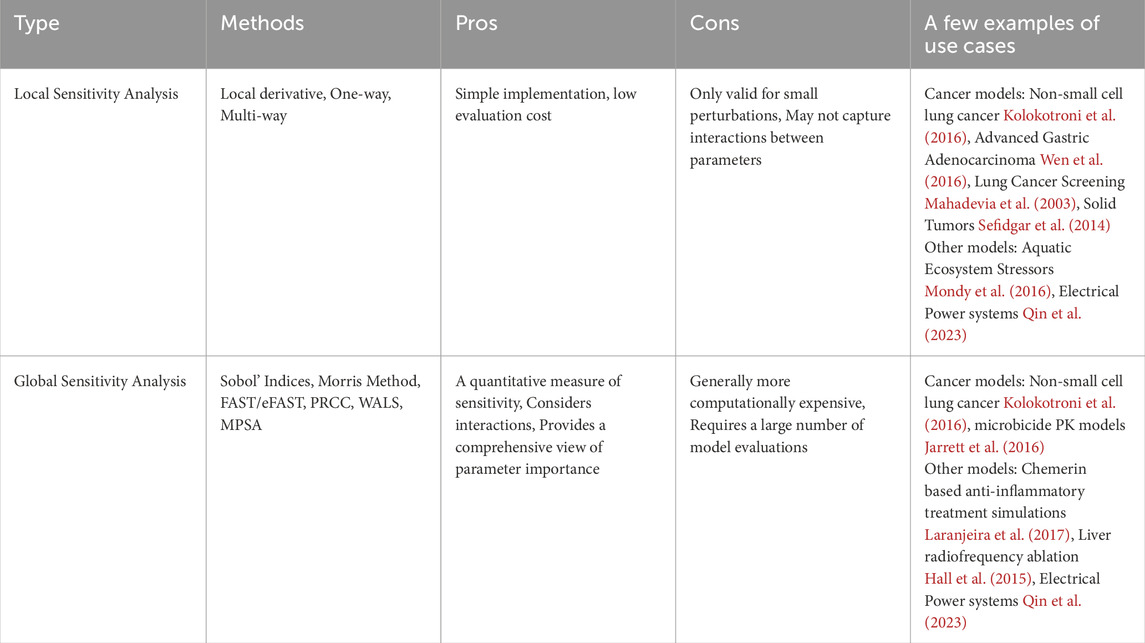
Table 1. Summary of sensitivity analysis types, including relevant methods, pros and cons of each analysis type, and a few examples of method use cases.

Surrogate models for sensitivity analysis and feature importance

Surrogate models are data-driven approximations trained on outputs from high-fidelity models, which are often computationally expensive to execute. By providing rapid predictions with minimal computational effort, surrogate models offer a more efficient alternative to the original high-fidelity simulations. Traditionally, GSA requires sampling of points in the model input parameter space. The complex models need to be evaluated at these sampled points. The corresponding outputs are used to define a measure of sensitivity. Direct use of such sampling methods for GSA on complex models is often unaffordable due to high computational costs. Surrogates offer a practical alternative (Cheng et al., 2020). Surrogate models can approximate complex mechanistic models, thus reducing the computational costs associated with global sensitivity analysis (Cheng et al., 2020). They are developed using machine learning data-driven regression techniques (Tsokanas et al., 2022). The traditional surrogate models include polynomial regression and response surface models, Kriging/Gaussian process, polynomial chaos expansion, and Multivariate Adaptive Regression Splines (Cheng et al., 2020; Alizadeh et al., 2020). Supervised learning algorithms like neural networks (Liu et al., 2021; Li et al., 2016; Yang et al., 2021), random forests (Dasari et al., 2019), and support vector machines (Pruett and Hester, 2016) have also been used to build surrogate models and conduct sensitivity analysis.

One of the major goals of global sensitivity analysis techniques is selecting the most important model features that have the most impact on the model output. Traditionally, feature selection has long been used as a pre-processing step while building large multi-parametric data-driven models. The objectives of feature selection include building simpler and more comprehensible models, improving data-mining performance, and preparing clean, understandable data (Li et al., 2017). Li et al. (2017) classify feature selection methods into these categories: similarity-based, information-theoretical-based, sparse-learning-based, and statistical-based. In addition to data-driven models, these methods can also be exploited to extract important features from complex mechanistic models like ODE systems, boolean networks or even hybrid tissue-level agent-based models. Identifying such features can provide meaningful insights into the important pathways for malignancy represented in the model. Since all feature selection algorithms require sampling through large input parameter spaces, computations can get very expensive with the complex multiscale hybrid models. Surrogates of these complex models can be used to perform feature selection. The variance-based Sobol global sensitivity method is among the most popular feature ranking methods. This variance-based technique determines the contribution of each model (or surrogate model) feature and their interactions with the overall variance of the target variable. It has been implemented for purely data-driven models as well (Zouhri et al., 2022; Fel et al., 2021; Efimov et al., 2017).

A game theoretic approach to feature ranking is Shapley value analysis. Shapley value (Winter, 2002) is a cooperative game theory approach used to distribute the total gain (or cost) among players based on their individual contributions. For feature attribution in machine learning models, each feature is considered a player in a coalition, and the Shapley value assigns a value to each feature representing its contribution to the model’s prediction. Features with higher Shapley values can be considered more important, aiding in selecting the most relevant features (Chen et al., 2023). Though this method is a straightforward check for global sensitivity, there are a few downsides: assumption of feature independence, difficulties with scalability, and high computational expense (Aas et al., 2021).

Clinical exploration of feature importance predictions

Sensitivity analysis methods can predict the top model parameter subsets that are responsible for aggressive tumor proliferation and metastatic tendencies, thus leading to poor patient prognosis. Once the most important model parameter subsets are identified, a simple check for clinical significance can be done by conducting Kaplan-Meier survival analysis on available clinical data. Worse survival in patient cohorts with alteration in the identified most sensitive model species would corroborate the model ranking results from the multiscale model.

Verification, validation, and uncertainty quantification (VVUQ) of the multi-scale hybrid-modeling framework

Experimental data for validation are available in cancer data repositories like TCGA (NCI, 2022), TARGET (dbGaP, 2024), EUREKA (Peyser et al., 2022), and AllofUs (Denny et al., 2019). These sources have clinical information like mutations, RNA sequencing, or other forms of liquid biopsies such as ctDNA, miRNA, or exosome profiling. Relevant data from these repositories can be used to calibrate different sub-modules (cellular models, tissue level diffusion, cell-population ABM) in the hybrid model. The key predictions from the multi-scale hybrid model can be compared against or regressed with the measured biomarkers. The time evolution of key biomarker concentrations in the hybrid level model can be compared against experimental and clinical data where possible (eg., comparing predicted PSA levels with available patient PSA level data for prostate cancer studies) Spatial tissue-level ABM results can be compared with tumor imaging results, particularly, tumor spheroid diameters and aspect ratio measurements. Spatial tissue-level ABM results can be compared with tumor imaging results, particularly, tumor spheroid diameters and aspect ratio measurements. A caveat here is that most spatiotemporal modeling studies might not find enough relevant clinical information including imaging, multi-omics and biopsies, to sufficiently validate the models.

Hybrid multi-scale models can have high fidelity but can be computationally expensive owing to several sub-modules capturing the complexities of the system. Heterogeneous multiscale approaches can be used for cost-effective linking of the submodules via information transfer at specific time intervals (Ee et al., 2007; Kevrekidis et al., 2004). However, increasing model complexity complicates model validations and inferential understanding (Cogno et al., 2024). Additionally, there is a scarcity of patient-specific clinical data for training or validation of such complex models. To ensure these models are viable in a clinical setting, extensive validation of their predictions is necessary, along with quantification of the uncertainty in the predicted outputs based on the model inputs. Verified and validated GenAI-based digital twins can increase the size of the data cohort and improve the robustness of uncertainty analysis, providing reliable predictions (Kamruzzaman et al., 2024).

Mathematical models inherently provide approximations of real-world phenomena, necessitating verification processes to quantify numerical errors and ensure model accuracy. Uncertainty Quantification (UQ) goes a step further by assessing the range of possible values that a quantity of interest may take within a given problem. UQ accounts for inherent variability and uncertainties in model inputs, parameters, and structure, offering a more comprehensive understanding of the model’s predictive capabilities and the reliability of its outcomes. Roy and Oberkampf (2011) classify uncertainty in model predictions arising from three broad categories: (1) model inputs, (2) numerical approximations, and (3) assumptions in the mathematical model. Input uncertainties encompass variability in data and parameters. (1) Model input uncertainties encompass inherent variability in data and parameters. They can be classified as aleatory or epistemic. Aleatory uncertainties refer to the variability in model input due to inherent random effects. In cellular or tissue level systems biology models, aleatory uncertainties can include experimentally derived kinetic parameters for ODEs, and physiologically relevant initial conditions to simulate diffusion of nutrients, oxygen in the tissues. Epistemic uncertainty stems from incomplete knowledge about the system, particularly, input data or model parameters. Such uncertainties are usually explored through alternative assumptions. In systems biology models, unknown mechanisms can be treated as epistemic uncertainties, and the range of assumptions used to bridge each epistemic uncertainty can be evaluated. (2) Numerical approximation errors assess simulation accuracy associated with computational solving techniques (verification). (3) Assumptions in the mathematical model are usually made to keep the model tractable. These assumptions contribute to model form uncertainty.

Roy and Oberkampf (2011) present a practical approach for quantifying uncertainty using probability boxes (P-boxes). To generate the P-boxes, both aleatory and epistemic uncertainties are propagated through the model to generate an ensemble of cumulative distribution functions of model output quantity of interest. For model validation, model predictions are compared with experimental data to estimate model form uncertainties. These are treated as epistemic uncertainties. The final step in this approach involves determining the total uncertainty in the system response by combining P-boxes derived from input uncertainties, extrapolated model form uncertainties, and uncertainties due to numerical approximations (Roy and Oberkampf, 2011). This comprehensive approach delineates confidence in model predictions, ensuring robust and reliable assessments of the system’s performance. Even though this method is valuable for UQ in complex models, it can get computationally expensive with increase in number of uncertain model input parameters and model form complexity. Hybrid multiscale models in cancer are built using several approximations and simplifications of tumor heterogeneity, tumor–microenvironment interactions. All these could contribute to epistemic uncertainty. Moreover, calibration of certain cellular or tissue models to clinical and experimental data involves significant aleatoric uncertainty. This would lead to a huge computational burden. ML surrogates offer a promising avenue for enhancing VVUQ by efficiently approximating complex models and providing rapid sampling. There is considerable scope for improvement with further research into the mathematics of VVUQ and the use of ML surrogates to enhance VVUQ for complex models.

There is a critical need for benchmarks to ensure the safe and reliable use of computational models in real-world settings. These benchmarks would provide standardized criteria for model verification, validation, and performance, ensuring models meet the necessary requirements before deployment. The ASME V&V 40 standard (ASME, 2018), recognized by the FDA, offers a risk-based framework to establish the credibility of computational models used in medical device development. ASME also has VVUQ standards for various modeling techniques, including Computational Fluid Dynamics, Computational Solid Mechanics, and machine learning models. There are verification and validation benchmarks for digital twins for manufacturing applications as well (Bitencourt et al., 2024). However, a similar benchmark for physiological models developed for clinical applications has not yet been established. In clinical contexts, the development of a robust Verification, Validation, and Uncertainty Quantification (VVUQ) benchmark is crucial to ensure that these models are trustworthy and safe for use, as patient safety becomes the paramount concern.

Discussion

Building verifiable cancer digital twins for precision medicine

Cancer is characterized by its dynamic and evolving nature. As the disease progresses, the diversity within cancer cell populations typically increases (Jacquemin et al., 2022). Such diversity can lead to uneven distributions of genetically varied tumor cells across different areas of the tissue (known as spatial heterogeneity). It can also cause changes over time in the genetic composition of these cells (temporal heterogeneity). This heterogeneity is a key factor in developing treatment resistance, making precise evaluation of tumor heterogeneity crucial for effective treatments (Dagogo-Jack and Shaw, 2018). Technologies like multi-region sequencing, single-cell sequencing, autopsy sample analysis, and longitudinal liquid biopsy are advancing rapidly and hold significant promise for unraveling the intricate clonal structure of tumors (Lee et al., 2021; Ortega et al., 2017; Gilson et al., 2022). Nevertheless, the complexity of the data gathered from these methods cannot be fully interpreted through multimodal data analysis alone. Data-driven techniques can help uncover important pathways and give insights into important biomarkers of malignancy (Sathyanarayanan et al., 2020; Vaske et al., 2010). This crucial information can be leveraged to build relevant mathematical models incorporating the identified pathways. Mathematical models can incorporate physical laws and dynamic behaviors, allowing for more detailed insights into the mechanisms of cancer growth, treatment response and resistance. The predictive capability of mathematical models are superior to purely data-driven models as the former allow hypothesis testing via insilico clinical trials, leading to more informed decision making. Mathematical modeling is critical in integrating personalized data, providing the groundwork for creating verifiable cancer digital twin (VCDT) models that could revolutionize our approach to understanding and treating cancer (National Academies, 2024; Strobl et al., 2023). Physics based models can be informed using clinical or experimental data. In context of our proposed hybrid modeling framework, data can be integrated in different the sub-modules. For example, tissue imaging information can help initialized cell-population agent-based models (Cess and Finley, 2023); genomics, proteomics and other omics data can be used to identify, model and calibrate cellular pathways (Kolokotroni et al., 2024; Byrne et al., 2016). Physics-based modeling has effectively integrated data across different scales and physics to reveal mechanisms underlying functional emergence. In addition to the genetic spatial and temporal heterogeneity, physics-based spatiotemporal models are well-suited to represent extrinsic heterogeneity in the tissue microenvironment due to substrate gradients, signal gradients, etc., (Bray et al., 2019)

Integrating physics-based hybrid models with multi-modal data can increase the computational complexity of the system, thus increasing computational costs. The recent emergence of machine learning as a powerful method to integrate diverse data types and uncover correlations among complex phenomena offers significant potential. However, relying solely on machine learning can overlook fundamental physical laws, leading to poorly defined problems or unrealistic solutions. Machine learning can be used to enhance physics-based hybrid models by facilitating better data integration. Generative AI methods can produce synthetic data for physics-based model calibration and validation, in cases where real-world data is sparse (Kamruzzaman et al., 2024). ML methods can also be used to create simplified surrogates of physics-based hybrid models (Peng et al., 2021). Consequently, a multidisciplinary approach to creating a digital twin by integrating machine learning with physics-based modeling can provide new insights into disease mechanisms, identifying new targets and treatment strategies (Alber et al., 2019).

This review discusses physics driven methods to encode the mechanisms driving an evolving primary tumor personalized to the genotype of a real-world patient. We underline the importance of mechanistic, multiscale hybrid cellular models that can integrate core biological pathways universally connected to cancer hallmarks of continued proliferation and evasion of cell cycle checkpoints common to several tumors. In addition to these core modules, several tumor-specific and patient-specific pathways can also be added to drive context-specific cell decision-making in the tumor microenvironment. Such cellular physics-based models can be embedded in a tissue-level framework. ABMs are modular and can embed many physics-based, stochastic, or data-driven models to enhance biological accuracy. ABMs can be spatially initialized using high-resolution imaging and tissue histology information (Cess and Finley, 2023). They can leverage patient-specific omics data to calibrate models for patient-representative prediction. ABMs can thus provide insights into cancer biology that can guide experimental designs and patient-specific therapeutic strategies (Cogno et al., 2024).

In addition to the bottom-up, cancer biology-driven digital twin development, a top-down, clinical medicine-driven approach has emerged in the literature (Kolokotroni et al., 2024; Kolokotroni et al., 2016; Stamatakos, 2010; Ouzounoglou et al., 2017; Stamatakos et al., 2014). This approach aims to create digital twins designed to answer specific clinical questions, such as the optimal sequencing of chemotherapy and surgery for individual patients. A careful hybridization of both approaches can be highly effective for certain cases. Some recent examples of top-down digital twin models include Oncosimulator developed by Stamatakos (2014). It is an information technology system that simulates tumor responses to therapies. This system includes modules for multiscale data handling, image processing, and spatiotemporal simulations. It combines clinical data with advanced modeling techniques to predict tumor evolution and optimize personalized treatment strategies. Using similar principles, Oncosimulator (Ouzounoglou et al., 2017) for acute lymphoblastic leukemia was created using hybridization of discrete entity-discrete event-based (Stamatakos, 2010) spatiotemporal modeling with machine learning. This model leverages extensive patient transcriptomics data to enhance predictive accuracy.

Sensitivity analysis is a fundamental tool in studying biological systems. It quantifies the influence of parameter changes on system responses, aiding in identifying key model inputs driving output variations. In precision medicine, this understanding is instrumental in assessing disease prognosis and designing more effective therapies by elucidating critical factors influencing disease progression and treatment response. Global sensitivity analysis methods are conducted on mechanistic models to identify the most important model parameters and conduct robustness analysis (Whitacre, 2012) to determine stiff and sloppy modes in the system. In addition to the traditional methods, data-driven approaches are becoming increasingly popular for GSA and feature importance.

The Digital Twin of a tumor of a real-world cancer patient aims to encode the dynamic, bidirectional interaction of the patient and a digital twin to inform clinical decisions regarding interventions, treatments, and assessments, which in turn updates the digital twin (National Academies, 2020). Data is gathered from the patient and the tumor through various clinical assessments to inform the digital twin, creating a virtual representation comprised of models that describe the temporal and spatial characteristics of the patient and tumor, with dynamic updates from real-world data (National Academies, 2020). Integrating interpretability through physics, biomarker alignment, cohort stratification, and cell state dynamics represents an aspirational approach to advancing precision medicine via digital twins. As the patient and tumor constantly evolve and the data collection can change over time, VVUQ must occur continually for digital twins (National Academies, 2020), see Figure 2. The VVUQ framework for the digital twin model consists of identifying and quantifying aleatory and epistemic uncertainties in the model inputs, verifying numerical approximation errors associated with the solvers, and quantifying uncertainties originating from the chosen form of the model by comparing model outputs with experimental data. It is essential to address UQ comprehensively, covering all aspects of the digital twin, including patient data, modeling and simulation, and decision-making processes (National Academies, 2020). There is a compelling need to develop novel methods to perform VVUQ in multiscale, dynamic digital twins. By addressing UQ comprehensively across patient data, modeling and simulation, and decision-making processes (National Academies, 2020), we can enhance the reliability and clinical viability of digital twin models.

Figure 2

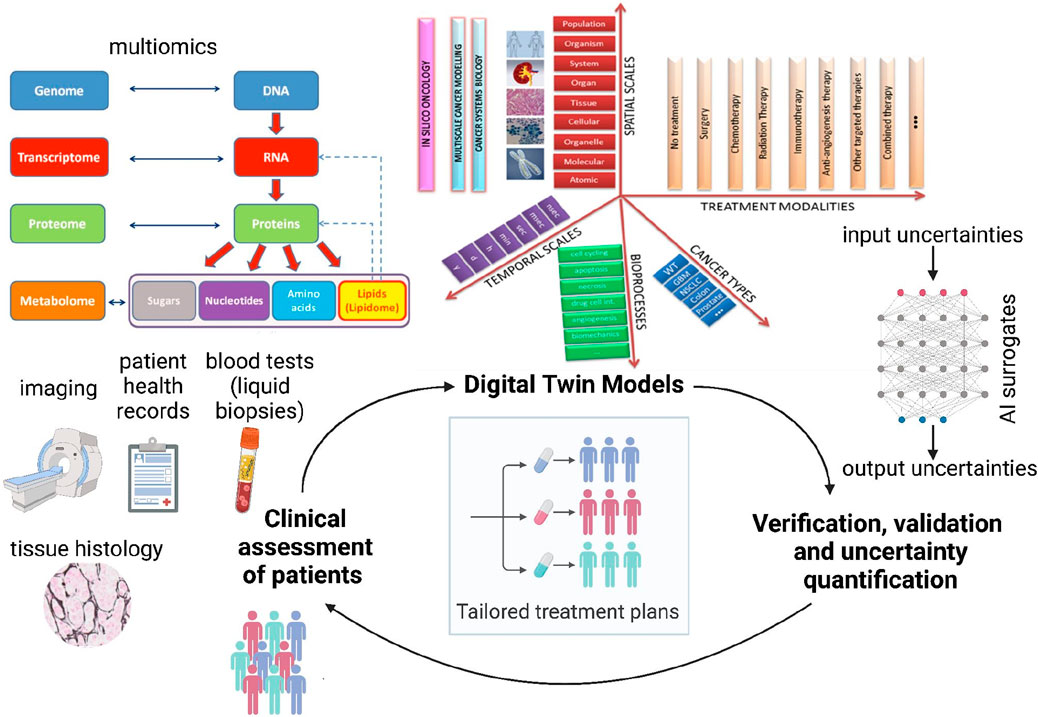
Figure 2. Proposed schematic of the Verifiable Cancer Digital Twin (VCDT) framework. The VCDT will enable dynamic, bidirectional information exchange between the patient and the digital twin, continuously updating with new clinical data. Digital twin models [illustration adapted from CHIC consortium (CHIC, 2017) final report] can span across temporal and spatial scales, include relevant bioprocesses, incorporate different treatment modalities, and simulate several cancer types. This adaptive physics-based model will integrate physical and data-driven approaches to represent the evolving tumor, generating synthetic data to enhance AI surrogate model training. Continuous Verification, Validation, and Uncertainty Quantification (VVUQ) will ensure robustness and reliability, supporting informed clinical decisions for personalized treatments.

Data-driven methods for multi-modal model interpretability and forecasting

Digital twins are invaluable in simulating virtual tumor dynamics and treatment. In the process, these models can vigorously generate high-dimensional data, owing to the tissue-level ABMs and embedded cellular models. For every patient, the digital twin can provide temporal tumor evolution information, spatial tumor-immune or tumor-drug interactions, temporal concentrations of important biomarkers and much more. Sensitivity analysis and large parametric studies on digital twins can result in a treasure trove of synthetic training data for building supervised machine learning surrogates. This data can be used to drive several machine learning methods for improving VVUQ, risk-stratifying patient cohorts and predicting important cancer system dynamics (illustrated in Figure 3). The recent advancements in multi-modal (Baltrusaitis et al., 2019; Stahlschmidt et al., 2022; Ektefaie et al., 2023) and physics-informed (Cuomo et al., 2022; Jabbari Zideh et al., 2023) machine learning have significantly enhanced the ability to analyze complex, multimodal scientific datasets summarized in Figure 3. Physics-informed neural networks (PINNs) operate by embedding physical laws, expressed as partial differential equations (PDEs), into the training process of neural networks. This integration allows PINNs to leverage both observational data and underlying physical principles to infer solutions to complex problems (Cuomo et al., 2022; Karniadakis et al., 2021). In systems biology (Yazdani et al., 2020), PINNs are particularly useful for modeling biological processes by providing robust predictions even with limited and noisy data, facilitating the understanding of high-dimensional biological systems, and improving the accuracy of simulations. The extensive spatiotemporal data generated through parametric, aleatoric, and epistemic variations in the digital twin can provide an opportunity to implement innovative approaches to capture data-informed dynamics effectively. Computationally efficient data-driven models can be built to simulate tumor dynamics by utilizing sparse identification of nonlinear dynamics (Brunton et al., 2016) integrated with neural ordinary differential equations. Neural ordinary differential equations (Chen et al., 2019) (ODEs) can learn black-box dynamics and structure-preserving formalisms to capture key dynamics of course-grained variables like surface area, circularity, aspect ratio, and clustering index. For our suggested digital twin architecture, Neural ODES could conform to the physics of reaction, diffusion, and convection powering the core ABM and preserve the fluctuation-dissipation relationship when coupling the agent dynamics with the dynamics of fields.

Figure 3

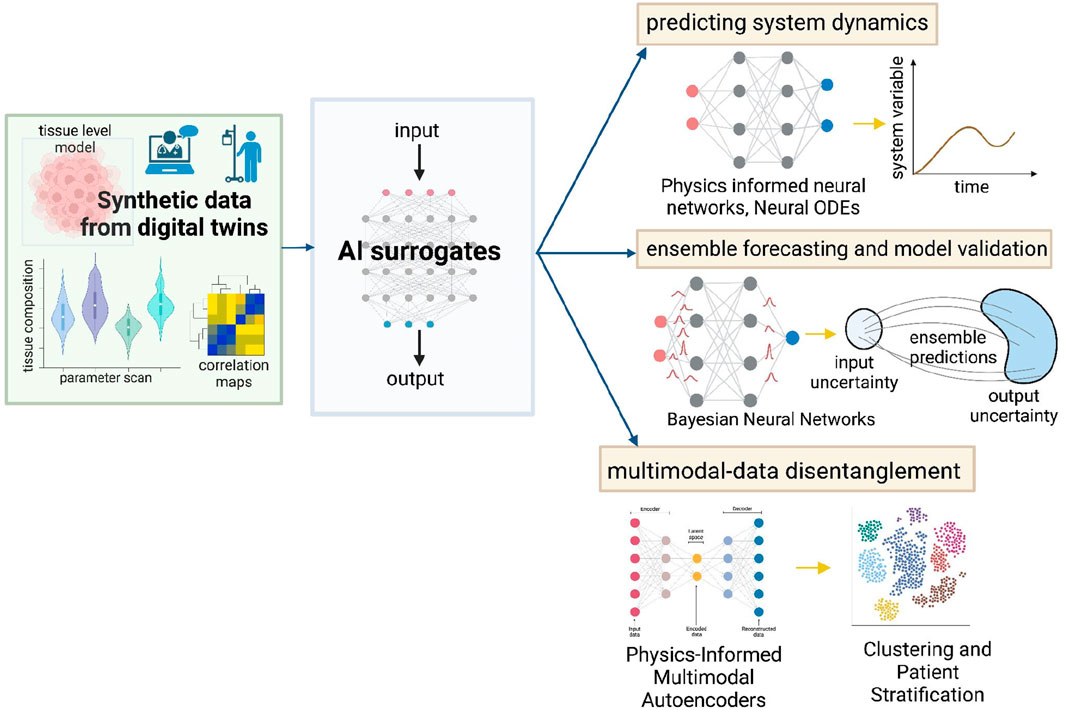
Figure 3. Data-driven methods to enhance utility and reliability of digital twins. Synthetic data generated from the digital twins can be used to construct AI surrogate models that capture data-informed dynamics while preserving the system physics - PINNs, Neural ODEs. Bayesian Neural Networks can enable ensemble forecasting and aid model validation. Additionally, Physics-Informed Multimodal Autoencoders can be used to disentangle multi-modal data and stratify patients. These techniques can improve personalized treatment strategies.

Developing AI-enabled computationally efficient surrogate models will reduce computational overload while also aiding the implementation of robust methodologies for VVUQ. McCulloch et al. (2022) propose a novel framework for calibrating agent-based models (ABMs) by integrating History Matching (HM) and Approximate Bayesian Computation (ABC) (Toni et al., 2009). By first employing HM, the parameter space is reduced by ruling out implausible models, thus decreasing the computational burden. This is followed by using ABC to generate a detailed posterior distribution of parameters, incorporating quantified uncertainties. Bayesian Neural Networks (BNNs) (Neal, 1996) integrate Bayesian inference into neural networks to quantify uncertainties in model predictions. By treating the weights and biases of the neural network as probability distributions rather than fixed values, BNNs can account for both aleatoric uncertainty (inherent noise in the data) and epistemic uncertainty (uncertainty due to limited data). Such models can be used for reliable ensemble forecasting (Olivier et al., 2021). Additionally, multiple trajectory simulations can be done by direct sampling of multiple neural network parameters. The simulated data statistics can be validated by comparison with real data summary statistics and quantifying the residuals.

Multimodal synthetic data generated from the digital twin and available real-world clinical data can be disentangled and mapped to clinical stratification of patients based on risk, genetic footprint, and other drivers of population heterogeneity. One notable framework, the Physics-Informed Multimodal Autoencoders (PIMA) (Walker et al., 2024), presents a solution for disentangling multimodal data. PIMA fuses data into a multimodal posterior by embedding individual modalities into a shared latent space and utilizing a product-of-experts formulation. Integrating a Gaussian mixture model (GMM) prior further identifies shared features across different data modalities, while a mixture-of-experts decoder incorporates prior scientific knowledge (in the form of digital twin synthetic data), ensuring structured disentanglement of the latent space. This approach enables cross-modal generative modeling and inference and facilitates the discovery of high-dimensional features, overcoming traditional limitations related to high-fidelity measurement and characterization (Walker et al., 2024).

These advancements can significantly enhance the interpretability, forecasting capability, and mechanism identification of cancer digital twin models. AI-enabled verifiable cancer digital twins will facilitate the development of personalized treatment strategies across various cancer types, ultimately leading to more effective and tailored healthcare solutions. This integration of cutting-edge technologies holds the promise of revolutionizing cancer treatment and patient outcomes.

From a clinical perspective, emphasizing comprehensive and individualized data collection from single patients is crucial to ensure accurate computational modeling and avoid artificial or amalgamated data. Educating clinicians on necessary data during the patient journey, and ensuring collaboration among hospital information systems and external providers, is vital. Integrating diverse data sources such as social media, wearables, ePROs (electronic Patient-Reported Outcomes), and ePROMs (electronic Patient-Reported Outcome Measures) enhances data quality. Ensuring data privacy and security through federated learning, and addressing trust through clinical validation and randomized trials comparing digital twin model predictions with standard treatments, can foster acceptance and utilization in clinical decision support.

Current limitations and future perspectives

Digital twins in oncology hold significant promise but face several challenges that need to be addressed before they can be widely adopted in clinical settings. In the past few years, there have been National Cancer Institute and US Department of Energy initiated collaborative exploratory projects to promote development of patient-specific cancer digital twins (Stahlberg et al., 2022). Hadjicharalambous et al. (2021) review recent cancer mathematical models in literature, with the potential for utility for insilico-clinical trials. Including image-driven models, radio/chemo-therapeutic planning models and tumor vasculature models. These models have demonstrated the potential of digital twins in oncology, while also highlighting key challenges that need to be addressed. One major limitation is the sparse and incomplete multimodal data currently available, which hinders the effective integration of patient-specific information into models. Advancements in AI could potentially help resolve this problem. Furthermore, continuously updating digital twins with real-time patient data remains a challenge. This requires the development of novel dynamic calibration methods to maintain accuracy and adaptability of digital twins in clinical applications.

Validation of digital twin model predictions is crucial and will need to be done through randomized clinical trials that compare these predictions with standard treatments. Additionally, for reliably exploring hypotheses and conducting in-vivo clinical trials, advancements in gaps in applicability of VVUQ methods to digital twins need to be addressed. As highlighted in this review, recent machine learning advancements, and others still emerging, will play a critical role in refining digital twin models and utilizing digital twin derived synthetic data to answer important clinical questions.

For digital twins to support clinical decision-making effectively, collaborations between cancer modelers, bioinformaticians, machine learning experts, mathematicians, and clinicians are essential. Clinicians must be educated on the necessary data required during a patient’s treatment journey, ensuring seamless data collection and integration. Hospital information systems, along with external medical service providers, need to work together to compile comprehensive and individualized data. In addition, the integration of diverse data sources, such as social media, wearables, ePROs (electronic Patient-Reported Outcomes), and ePROMs (electronic Patient-Reported Outcome Measures), will help enhance data quality and better support cancer modeling. However, concerns around data privacy and ownership must be addressed, requiring stringent benchmarks and regulatory frameworks to ensure patient data protection.

Similar to the ASME V&V40 guidelines for model verification and validation in medical devices, there is a need for standardized frameworks to ensure the safe and effective deployment of cancer digital twin models in clinical settings. Such guidelines will help establish clear protocols for verifying the accuracy, reliability, and clinical relevance of digital twins, ensuring their safe integration into patient care. Regulatory bodies like the FDA (US) and EMA (Europe) will need to develop clear guidelines for using digital twins in clinical trials, with the regulatory landscape likely to evolve continuously (Li, 2024). The scientific community must remain adaptable to these changes. Despite all these challenges, cancer digital twin technology has the potential to transform cancer medicine by accelerating drug development and reducing clinical costs. It could potentially become a cornerstone of future cancer treatment.

Concise Summary

Cancer’s heterogeneity often undermines the efficacy of conventional treatments. Advances in multiomics and sequencing have provided insights, but the complexity of the data requires robust mathematical models for full interpretation. This review highlights recent advancements in computational methodologies for precision oncology, emphasizing the potential of cancer digital twins to enhance patient-specific decision-making. We propose a framework that integrates agent-based modeling with cellular systems biology models, utilizing patient-specific data to predict tissue-level responses. Additionally, we discuss machine learning approaches to build surrogates for these models, facilitating sensitivity analysis, verification, validation, and uncertainty quantification. These advancements are crucial for improving the accuracy and reliability of clinical predictions.

Author contributions

RR: Writing–review and editing, Writing–original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal Analysis, Data curation, Conceptualization. SK: Writing–review and editing, Writing–original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal Analysis, Data curation, Conceptualization. MT: Writing–review and editing, Writing–original draft. AG: Writing–review and editing, Writing–original draft. GS: Writing–review and editing, Writing–original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal Analysis, Data curation, Conceptualization. NG: Writing–review and editing, Writing–original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal Analysis, Data curation, Conceptualization. KP: Writing–review and editing, Writing–original draft. UB: Writing–review and editing, Writing–original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal Analysis, Data curation, Conceptualization. NT: Writing–review and editing, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. CA250044 National Institutes of Health.

Acknowledgments

All figures created with biorender.com.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aas K., Jullum M., Løland A. (2021). Explaining individual predictions when features are dependent: more accurate approximations to Shapley values. Artif. Intell. 298, 103502. doi:10.1016/j.artint.2021.103502

CrossRef Full Text | Google Scholar

Alber M., Tepole A. B., Cannon W. R., De S., Dura-Bernal S., Garikipati K., et al. (2019). Integrating machine learning and multiscale modeling—perspectives, challenges, and opportunities in the biological, biomedical, and behavioral sciences. npj Digit. Med. 2, 115. doi:10.1038/s41746-019-0193-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Alizadeh R., Allen J. K., Mistree F. (2020). Managing computational complexity using surrogate models: a critical review. Res. Eng. Des. 31, 275–298. doi:10.1007/s00163-020-00336-7

CrossRef Full Text | Google Scholar

Anderson A. R. A., Weaver A. M., Cummings P. T., Quaranta V. (2006). Tumor morphology and phenotypic evolution driven by selective pressure from the microenvironment. Cell 127, 905–915. doi:10.1016/j.cell.2006.09.042

PubMed Abstract | CrossRef Full Text | Google Scholar

ASME (2018). Assessing credibility of computational modeling through verification and validation: application to medical devices.

Google Scholar

Baltrusaitis T., Ahuja C., Morency L.-P. (2019). Multimodal machine learning: a survey and taxonomy. IEEE Trans. Pattern Anal. Mach. Intell. 41, 423–443. doi:10.1109/TPAMI.2018.2798607

PubMed Abstract | CrossRef Full Text | Google Scholar

Baslan T., Hicks J. (2017). Unravelling biology and shifting paradigms in cancer with single-cell sequencing. Nat. Rev. Cancer 17, 557–569. doi:10.1038/nrc.2017.58

PubMed Abstract | CrossRef Full Text | Google Scholar

Bergman D. R., Karikomi M. K., Yu M., Nie Q., MacLean A. L. (2021). Modeling the effects of EMT-immune dynamics on carcinoma disease progression. Commun. Biol. 4, 983–1014. doi:10.1038/s42003-021-02499-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Bitencourt J., Wooley A., Harris G. (2024). Verification and validation of digital twins: a systematic literature review for manufacturing applications. Int. J. Prod. Res., 1–29. doi:10.1080/00207543.2024.2357741

CrossRef Full Text | Google Scholar

Bonabeau E. (2002). Agent-based modeling: methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. 99, 7280–7287. doi:10.1073/pnas.082080899

PubMed Abstract | CrossRef Full Text | Google Scholar

Bray N. J., Hutmacher D. W., Bock N. (2019). Addressing patient specificity in the engineering of tumor models. Front. Bioeng. Biotechnol. 7, 00217. doi:10.3389/fbioe.2019.00217

PubMed Abstract | CrossRef Full Text | Google Scholar

Breitwieser L., Hesam A., de Montigny J., Vavourakis V., Iosif A., Jennings J., et al. (2022). BioDynaMo: a modular platform for high-performance agent-based simulation. Bioinformatics 38, 453–460. doi:10.1093/bioinformatics/btab649

PubMed Abstract | CrossRef Full Text | Google Scholar

Brunton S. L., Proctor J. L., Kutz J. L. (2016). Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. U. S. A. 113, 3932–3937. doi:10.1073/pnas.1517384113

PubMed Abstract | CrossRef Full Text | Google Scholar

Bull J. A., Mech F., Quaiser T., Waters S. L., Byrne H. M. (2020). Mathematical modelling reveals cellular dynamics within tumour spheroids. PLOS Comput. Biol. 16, e1007961. doi:10.1371/journal.pcbi.1007961

PubMed Abstract | CrossRef Full Text | Google Scholar

Byrne K. M., Monsefi N., Dawson J. C., Degasperi A., Bukowski-Wills J. C., Volinsky N., et al. (2016). Bistability in the Rac1, PAK, and RhoA signaling network drives actin cytoskeleton dynamics and cell motility switches. Cell Syst. 2, 38–48. doi:10.1016/j.cels.2016.01.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Cai Y., Xu S., Wu J., Long Q. (2011). Coupled modelling of tumour angiogenesis, tumour growth and blood perfusion. J. Theor. Biol. 279, 90–101. doi:10.1016/j.jtbi.2011.02.017

PubMed Abstract | CrossRef Full Text | Google Scholar

CCLE (2024). Cancer cell line encyclopedia (CCLE). Available at: https://sites.broadinstitute.org/ccle/.

Google Scholar

Cess C. G., Finley S. D. (2020). Multi-scale modeling of macrophage—T cell interactions within the tumor microenvironment. PLOS Comput. Biol. 16, e1008519. doi:10.1371/journal.pcbi.1008519

PubMed Abstract | CrossRef Full Text | Google Scholar

Cess C. G., Finley S. D. (2023). Calibrating agent-based models to tumor images using representation learning. PLOS Comput. Biol. 19, e1011070. doi:10.1371/journal.pcbi.1011070

PubMed Abstract | CrossRef Full Text | Google Scholar

Chaudhuri A., Pash G., Hormuth D. A., Lorenzo G., Kapteyn M., Wu C., et al. (2023). Predictive digital twin for optimizing patient-specific radiotherapy regimens under uncertainty in high-grade gliomas. Front. Artif. Intell. 6. doi:10.3389/frai.2023.1222612

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen H., Covert I. C., Lundberg S. M., Lee S.-I. (2023). Algorithms to estimate Shapley value feature attributions. Nat. Mach. Intell. 5, 590–601. doi:10.1038/s42256-023-00657-x

CrossRef Full Text | Google Scholar

Chen R. T. Q., Rubanova Y., Bettencourt J., Duvenaud D. (2019). “Neural ordinary differential equations,” in 32nd conference on neural information processing systems (NeurIPS 2018), Montréal, Canada.

Google Scholar

Chen W. W., Schoeberl B., Jasper P. J., Niepel M., Nielsen U. B., Lauffenburger D. A., et al. (2009). Input–output behavior of ErbB signaling pathways as revealed by a mass action model trained against dynamic data. Mol. Syst. Biol. 5, 239. doi:10.1038/msb.2008.74

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheng K., Lu Z., Ling C., Zhou S. (2020). Surrogate-assisted global sensitivity analysis: an overview. Struct. Multidiscip. Optim. 61, 1187–1213. doi:10.1007/s00158-019-02413-5

CrossRef Full Text | Google Scholar

CHIC (2017). Consortium. Available at: http://chic-vph.eu/consortium/.

Google Scholar

Choi M., Shi J., Jung S. H., Chen X., Cho K.-H. (2012). Attractor landscape analysis reveals feedback loops in the p53 network that control the cellular response to DNA damage. Sci. Signal. 5, ra83. doi:10.1126/scisignal.2003363

PubMed Abstract | CrossRef Full Text | Google Scholar

Cogno N., Axenie C., Bauer R., Vavourakis V. (2024). Agent-based modeling in cancer biomedicine: applications and tools for calibration and validation. Cancer Biol. Ther. 25, 2344600. doi:10.1080/15384047.2024.2344600

PubMed Abstract | CrossRef Full Text | Google Scholar

Cooper F. R., Baker R. E., Bernabeu M. O., Bordas R., Bowler L., Bueno-Orovio A., et al. (2020). Chaste: cancer, heart and soft tissue environment. J. Open Source Softw. 5, 1848. doi:10.21105/joss.01848

PubMed Abstract | CrossRef Full Text | Google Scholar

Corti A., Colombo M., Migliavacca F., Rodriguez Matas J. F., Casarin S., Chiastra C. (2021). Multiscale computational modeling of vascular adaptation: a systems biology approach using agent-based models. Front. Bioeng. Biotechnol. 9. doi:10.3389/fbioe.2021.744560

PubMed Abstract | CrossRef Full Text | Google Scholar

Crumbaker M., Khoja L., Joshua A. M. (2017). AR signaling and the PI3K pathway in prostate cancer. Cancers 9, 34. doi:10.3390/cancers9040034

PubMed Abstract | CrossRef Full Text | Google Scholar

Cuomo S., Di Cola V. S., Giampaolo F., Rozza G., Raissi M., Piccialli F. (2022). Scientific machine learning through physics–informed neural networks: where we are and what’s next. J. Sci. Comput. 92, 88. doi:10.1007/s10915-022-01939-z

CrossRef Full Text | Google Scholar

Dagogo-Jack I., Shaw A. T. (2018). Tumour heterogeneity and resistance to cancer therapies. Nat. Rev. Clin. Oncol. 15, 81–94. doi:10.1038/nrclinonc.2017.166

PubMed Abstract | CrossRef Full Text | Google Scholar

Dasari S. K., Cheddad A., Andersson P. (2019). “Random forest surrogate models to support design space exploration in aerospace use-case,” in Artificial intelligence applications and innovations. Editors J. MacIntyre, I. Maglogiannis, L. Iliadis, and E. Pimenidis (Cham: Springer International Publishing), 532–544. doi:10.1007/978-3-030-19823-7_45

CrossRef Full Text | Google Scholar

dbGaP (2024). National cancer Institute (NCI) TARGET: therapeutically applicable research to generate effective treatments. Available at: https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000218.v26.p8.

Google Scholar

Demicco M., Liu X.-Z., Leithner K., Fendt S.-M. (2024). Metabolic heterogeneity in cancer. Nat. Metab. 6, 18–38. doi:10.1038/s42255-023-00963-z

PubMed Abstract | CrossRef Full Text | Google Scholar

de Montigny J., Iosif A., Breitwieser L., Manca M., Bauer R., Vavourakis V. (2021). An in silico hybrid continuum-/agent-based procedure to modelling cancer development: interrogating the interplay amongst glioma invasion, vascularity and necrosis. Methods 185, 94–104. doi:10.1016/j.ymeth.2020.01.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Denny J. C., Rutter J. L., Goldstein D. B., Philippakis A., Smoller N., Jenkins G. (2019). The “all of us” research program. N. Engl. J. Med. 381, 668–676. doi:10.1056/nejmsr1809937

PubMed Abstract | CrossRef Full Text | Google Scholar

Duswald T., Lima E. A. B. F., Oden J. T., Wohlmuth B. (2024). Bridging scales: a hybrid model to simulate vascular tumor growth and treatment response. Comput. Methods Appl. Mech. Eng. 418, 116566. doi:10.1016/j.cma.2023.116566

CrossRef Full Text | Google Scholar

Ebata K., Yamashiro S., Iida K., Okada M. (2022). Building patient-specific models for receptor tyrosine kinase signaling networks. FEBS J. 289, 90–101. doi:10.1111/febs.15831

PubMed Abstract | CrossRef Full Text | Google Scholar

Ee W., Engquist B., Li X., Ren W., Vanden-Eijnden E. (2007). Heterogeneous multiscale methods: a review. Commun. Comput. Phys. 2.

Google Scholar

Efimov D., Sulieman H. (2017). “Sobol sensitivity: a strategy for feature selection,” in Mathematics across contemporary Sciences. Editors T. Abualrub, A. S. Jarrah, S. Kallel, and H. Sulieman (Cham: Springer International Publishing), 57–75. doi:10.1007/978-3-319-46310-0_4

CrossRef Full Text | Google Scholar

Ektefaie Y., Dasoulas G., Noori A., Farhat M., Zitnik M. (2023). Multimodal learning with graphs. Nat. Mach. Intell. 5, 340–350. doi:10.1038/s42256-023-00624-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Enderling H., Hlatky L., Hahnfeldt P. (2009). Migration rules: tumours are conglomerates of self-metastases. Br. J. Cancer 100, 1917–1925. doi:10.1038/sj.bjc.6605071

PubMed Abstract | CrossRef Full Text | Google Scholar

Fel T., Cadène R., Chalvidal M. (2021). Look at the variance! Efficient black-box explanations with sobol-based sensitivity analysis.

Google Scholar

Gao C., Liu H., Yan F. (2020). Dynamic behavior of p53 driven by delay and a microrna-34a-mediated feedback loop. Int. J. Mol. Sci. 21, 1271. doi:10.3390/ijms21041271

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghaffarizadeh A., Friedman S. H., Macklin P. (2016). BioFVM: an efficient, parallelized diffusive transport solver for 3-D biological simulations. Bioinforma. Oxf. Engl. 32, 1256–1258. doi:10.1093/bioinformatics/btv730

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghaffarizadeh A., Heiland R., Friedman S. H., Mumenthaler S. M., Macklin P. (2018). PhysiCell: an open source physics-based cell simulator for 3-D multicellular systems. PLOS Comput. Biol. 14, e1005991. doi:10.1371/journal.pcbi.1005991

PubMed Abstract | CrossRef Full Text | Google Scholar

Gilson P., Merlin J.-L., Harlé A. (2022). Deciphering tumour heterogeneity: from tissue to liquid biopsy. Cancers 14, 1384. doi:10.3390/cancers14061384

PubMed Abstract | CrossRef Full Text | Google Scholar

Global Sensitivity Analysis (2008). The primer. Chichester, England, Hoboken, NJ: John Wiley.

Google Scholar

Gong C., Milberg O., Wang B., Vicini P., Narwal R., Roskos L., et al. (2017). A computational multiscale agent-based model for simulating spatio-temporal tumour immune response to PD1 and PDL1 inhibition. J. R. Soc. Interface 14, 20170320. doi:10.1098/rsif.2017.0320

PubMed Abstract | CrossRef Full Text | Google Scholar

Hadjicharalambous M., Wijeratne P. A., Vavourakis V. (2021). From tumour perfusion to drug delivery and clinical translation of in silico cancer models. Methods 185, 82–93. doi:10.1016/j.ymeth.2020.02.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Hall S. K., Ooi E. H., Payne S. J. (2015). Cell death, perfusion and electrical parameters are critical in models of hepatic radiofrequency ablation. Int. J. Hyperth. 31, 538–550. doi:10.3109/02656736.2015.1032370

PubMed Abstract | CrossRef Full Text | Google Scholar

Hanahan D. (2022). Hallmarks of cancer: new dimensions. Cancer Discov. 12, 31–46. doi:10.1158/2159-8290.CD-21-1059

PubMed Abstract | CrossRef Full Text | Google Scholar

Hanahan D., Weinberg R. A. (2000). The hallmarks of cancer. Cell 100, 57–70. doi:10.1016/s0092-8674(00)81683-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Hanahan D., Weinberg R. A. (2011). Hallmarks of cancer: the next generation. Cell 144, 646–674. doi:10.1016/j.cell.2011.02.013

PubMed Abstract | CrossRef Full Text | Google Scholar

He X., Liu X., Zuo F., Shi H., Jing J. (2023). Artificial intelligence-based multi-omics analysis fuels cancer precision medicine. Semin. Cancer Biol. 88, 187–200. doi:10.1016/j.semcancer.2022.12.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Heidary Z., Ghaisari J., Moein S., Javanmard S. H. (2020). The double-edged sword role of fibroblasts in the interaction with cancer cells; an agent-based modeling approach. PLOS ONE 15, e0232965. doi:10.1371/journal.pone.0232965

PubMed Abstract | CrossRef Full Text | Google Scholar

Hemedan A. A., Niarakis A., Schneider R., Ostaszewski M. (2022). Boolean modelling as a logic-based dynamic approach in systems medicine. Comput. Struct. Biotechnol. J. 20, 3161–3172. doi:10.1016/j.csbj.2022.06.035

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoops S., Sahle S., Gauges R., Lee C., Pahle J., Simus N., et al. (2006). COPASI—a COmplex PAthway SImulator. Bioinformatics 22, 3067–3074. doi:10.1093/bioinformatics/btl485

PubMed Abstract | CrossRef Full Text | Google Scholar

Jabbari Zideh M., Chatterjee P., Srivastava A. (2023). Physics-informed machine learning for data anomaly detection, classification, localization, and mitigation: a review, challenges, and path forward. IEEE Access 12, 4597–4617. doi:10.1109/ACCESS.2023.3347989

CrossRef Full Text | Google Scholar

Jacquemin V., Antoine M., Dom G., Detours V., Maenhaut C., Dumont J. E. (2022). Dynamic cancer cell heterogeneity: diagnostic and therapeutic implications. Cancers 14, 280. doi:10.3390/cancers14020280

PubMed Abstract | CrossRef Full Text | Google Scholar

Jarrett A. M., Gao Y., Hussaini M. Y., Cogan N. G., Katz D. F. (2016). Sensitivity analysis of a pharmacokinetic model of vaginal anti-HIV microbicide drug delivery. J. Pharm. Sci. 105, 1772–1778. doi:10.1016/j.xphs.2016.02.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Kamruzzaman M., Salinas J., Kolla H., Sale K., Uma B., Poorey K., et al. (2024). GenAI based digital twins aided data augmentation increases accuracy in real-time cokurtosis based anomaly detection of wearable data. Preprint. doi:10.21203/rs.3.rs-4427255/v1

CrossRef Full Text | Google Scholar

Karniadakis G. E., Kevrekidis I. G., Lu L., Perdikaris P., Wang S., Yang L. (2021). Physics-informed machine learning. Nat. Rev. Phys. 3, 422–440. doi:10.1038/s42254-021-00314-5

CrossRef Full Text | Google Scholar

Kevrekidis I. G., Gear C. W., Hummer G. (2004). Equation-free: the computer-aided analysis of complex multiscale systems. AIChE J. 50, 1346–1355. doi:10.1002/aic.10106

CrossRef Full Text | Google Scholar

Kirouac D. C., Du J. Y., Lahdenranta J., Overland R., Yarar D., Paragas V., et al. (2013). Computational modeling of ERBB2-amplified breast cancer identifies combined ErbB2/3 blockade as superior to the combination of MEK and AKT inhibitors. Sci. Signal. 6, ra68. doi:10.1126/scisignal.2004008

PubMed Abstract | CrossRef Full Text | Google Scholar

Kolokotroni E., Abler D., Ghosh A., Tzamali E., Grogan J., Georgiadi E., et al. (2024). A multidisciplinary hyper-modeling scheme in personalized in silico oncology: coupling cell kinetics with metabolism, signaling networks and biomechanics as plug-in component models of a cancer digital twin. Preprint. doi:10.20944/preprints202403.0490.v1

CrossRef Full Text | Google Scholar

Kolokotroni E., Dionysiou D., Veith C., Kim Y. J., Sabczynski J., Franz A., et al. (2016). In silico oncology: quantification of the in vivo antitumor efficacy of cisplatin-based doublet therapy in non-small cell lung cancer (NSCLC) through a multiscale mechanistic model. PLoS Comput. Biol. 12, e1005093. doi:10.1371/journal.pcbi.1005093

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuznetsov M., Kolobov A. (2023). Agent-based model for studying the effects of solid stress and nutrient supply on tumor growth. Mathematics 11, 1900. doi:10.3390/math11081900

CrossRef Full Text | Google Scholar

Laranjeira S., Regan-Komito D., Iqbal A. J., Greaves D. R., Payne S. J., Orlowski P. (2017). A model for the optimization of anti-inflammatory treatment with chemerin. Interface Focus 8, 20170007. doi:10.1098/rsfs.2017.0007

PubMed Abstract | CrossRef Full Text | Google Scholar

Laubenbacher R., Hower V., Jarrah A., Torti S. V., Shulaev V., Mendes P., et al. (2009). A systems biology view of cancer. Biochim. Biophys. Acta BBA - Rev. Cancer 1796, 129–139. doi:10.1016/j.bbcan.2009.06.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee D., Park Y., Kim S. (2021). Towards multi-omics characterization of tumor heterogeneity: a comprehensive review of statistical and machine learning approaches. Brief. Bioinform. 22, bbaa188. doi:10.1093/bib/bbaa188

PubMed Abstract | CrossRef Full Text | Google Scholar

Lei Y., Tang R., Xu J., Wang W., Zhang B., Liu J., et al. (2021). Applications of single-cell sequencing in cancer research: progress and perspectives. J. Hematol. Oncol.J Hematol. Oncol. 14, 91. doi:10.1186/s13045-021-01105-2

CrossRef Full Text | Google Scholar

Li G. (2024). New regulatory road in clinical trials: digital twins. Appl. Clin. Trials 33.

Google Scholar

Li G., Rabitz H., Yelvington P. E., Oluwole O. O., Bacon F., Kolb C. E., et al. (2010). Global sensitivity analysis for systems with independent and/or correlated inputs. J. Phys. Chem. A 114, 6022–6032. doi:10.1021/jp9096919

PubMed Abstract | CrossRef Full Text | Google Scholar

Li J., Cheng K., Wang S., Morstatter F., Trevino R. P., Tang J., et al. (2017). Feature selection: a data perspective. ACM Comput. Surv. 50, 1–45. doi:10.1145/3136625

CrossRef Full Text | Google Scholar

Li S., Yang B., Qi F. (2016). Accelerate global sensitivity analysis using artificial neural network algorithm: case studies for combustion kinetic model. Combust. Flame 168, 53–64. doi:10.1016/j.combustflame.2016.03.028

CrossRef Full Text | Google Scholar

Linden N. J., Kramer B., Rangamani P. (2022). Bayesian parameter estimation for dynamical models in systems biology. PLOS Comput. Biol. 18, e1010651. doi:10.1371/journal.pcbi.1010651

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu Y.-C., Nagawkar J., Leifsson L., Koziel S., Pietrenko-Dabrowska A. (2021). “Iterative global sensitivity analysis algorithm with neural network surrogate modeling,” in Computational science – ICCS 2021. Editors M. Paszynski, D. Kranzlmüller, V. V. Krzhizhanovskaya, J. J. Dongarra, and P. M. A. Sloot (Cham: Springer International Publishing), 298–311. doi:10.1007/978-3-030-77970-2_23

CrossRef Full Text | Google Scholar

Mahadevia P. J., Fleisher L. A., Frick K. D., Eng J., Goodman S. N., Powe N. R. (2003). Lung cancer screening with helical computed tomography in older adult smokers: a decision and cost-effectiveness analysis. JAMA 289, 313–322. doi:10.1001/jama.289.3.313

PubMed Abstract | CrossRef Full Text | Google Scholar

McCulloch J., Ge J., Ward J. A., Heppenstall A., Polhill J. G., Malleson N. (2022). Calibrating agent-based models using uncertainty quantification methods. J. Artif. Soc. Soc. Simul. 25, 1. doi:10.18564/jasss.4791

CrossRef Full Text | Google Scholar

Mehdizadeh H., Sumo S., Bayrak E. S., Brey E. M., Cinar A. (2013). Three-dimensional modeling of angiogenesis in porous biomaterial scaffolds. Biomaterials 34, 2875–2887. doi:10.1016/j.biomaterials.2012.12.047

PubMed Abstract | CrossRef Full Text | Google Scholar

Menyhárt O., Győrffy B. (2021). Multi-omics approaches in cancer research with applications in tumor subtyping, prognosis, and diagnosis. Comput. Struct. Biotechnol. J. 19, 949–960. doi:10.1016/j.csbj.2021.01.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Metzcar J., Wang Y., Heiland R., Macklin P. (2019). A review of cell-based computational modeling in cancer biology. JCO Clin. Cancer Inf. 3, 1–13. doi:10.1200/CCI.18.00069

CrossRef Full Text | Google Scholar

Mirams G. R., Arthurs C. J., Bernabeu M. O., Bordas R., Cooper J., Corrias A., et al. (2013). Chaste: an open source C++ library for computational physiology and biology. PLOS Comput. Biol. 9, e1002970. doi:10.1371/journal.pcbi.1002970

PubMed Abstract | CrossRef Full Text | Google Scholar

Mondy C., Muñoz I., Dolédec S. (2016). Life-history strategies constrain invertebrate community tolerance to multiple stressors: a case study in the Ebro basin. Sci. Total Environ. 572, 196–206. doi:10.1016/j.scitotenv.2016.07.227

PubMed Abstract | CrossRef Full Text | Google Scholar

National Academies (2020). Digital twin of a cancer patient and tumor. Available at: https://nap.nationalacademies.org/resource/26894/infographic-digital-twin.pdf.

Google Scholar

National Academies (2024). Foundational research gaps and future directions for digital twins. Available at: https://www.nationalacademies.org/our-work/foundational-research-gaps-and-future-directions-for-digital-twins.

Google Scholar

Nava-Sedeno J. M., Voss-Bohme A., Hatzikirou H., Deutsch A., Peruani F. (2020). Modelling collective cell motion: are on- and off-lattice models equivalent? Philosophical Trans. R. Soc. B Biol. Sci. 375, 20190378. doi:10.1098/rstb.2019.0378

PubMed Abstract | CrossRef Full Text | Google Scholar

NCI (2022). The cancer genome atlas program (TCGA). Available at: https://www.cancer.gov/ccg/research/genome-sequencing/tcga.

Google Scholar

NCI (2024). Proteomic data commons. Available at: https://pdc.cancer.gov/pdc/browse.

Google Scholar

Neal R. M. (1996). Bayesian learning for neural networks volume 118. New York, NY: Springer.

Google Scholar

Norton K.-A., Gong C., Jamalian S., Popel A. S. (2019). Multiscale agent-based and hybrid modeling of the tumor immune microenvironment. Processes 7, 37. doi:10.3390/pr7010037

PubMed Abstract | CrossRef Full Text | Google Scholar

Norton K.-A., Wallace T., Pandey N. B., Popel A. S. (2017). An agent-based model of triple-negative breast cancer: the interplay between chemokine receptor CCR5 expression, cancer stem cells, and hypoxia. BMC Syst. Biol. 11, 68. doi:10.1186/s12918-017-0445-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Olivier A., Shields M. D., Graham-Brady L. (2021). Bayesian neural networks for uncertainty quantification in data-driven materials modeling. Comput. Methods Appl. Mech. Eng. 386, 114079. doi:10.1016/j.cma.2021.114079

CrossRef Full Text | Google Scholar

Ortega M. A., Poirion O., Zhu X., Huang S., Wolfgruber T. K., Sebra R., et al. (2017). Using single-cell multiple omics approaches to resolve tumor heterogeneity. Clin. Transl. Med. 6, 46. doi:10.1186/s40169-017-0177-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Ouzounoglou E., Kolokotroni E., Stanulla M., Stamatakos G. S. (2017). A study on the predictability of acute lymphoblastic leukaemia response to treatment using a hybrid oncosimulator. Interface Focus 8, 20160163. doi:10.1098/rsfs.2016.0163

PubMed Abstract | CrossRef Full Text | Google Scholar

Palladini A., Nicoletti G., Pappalardo F., Murgo A., Grosso V., Stivani V., et al. (2010). In silico modeling and in vivo efficacy of cancer-preventive vaccinations. Cancer Res. 70, 7755–7763. doi:10.1158/0008-5472.CAN-10-0701

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng G. C. Y., Alber M., Tepole A. B., Cannon W. R., De S., Dura-Bernal S., et al. (2021). Multiscale modeling meets machine learning: what can we learn? Arch. Comput. Methods Eng. 28, 1017–1037. doi:10.1007/s11831-020-09405-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Peyser N. D., Marcus G. M., Beatty A. L., Olgin J. E., Pletcher M. J. (2022). Digital platforms for clinical trials: the Eureka experience. Contemp. Clin. Trials 115, 106710. doi:10.1016/j.cct.2022.106710

PubMed Abstract | CrossRef Full Text | Google Scholar

Powathil G. G., Munro A. J., Chaplain M. A. J., Swat M. (2016). Bystander effects and their implications for clinical radiation therapy: insights from multiscale in silico experiments. J. Theor. Biol. 401, 1–14. doi:10.1016/j.jtbi.2016.04.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Pruett W. A., Hester R. L. (2016). The creation of surrogate models for fast estimation of complex model outcomes. PLOS ONE 11, e0156574. doi:10.1371/journal.pone.0156574

PubMed Abstract | CrossRef Full Text | Google Scholar

Qian G., Mahdi A. (2020). Sensitivity analysis methods in the biomedical sciences. Math. Biosci. 323, 108306. doi:10.1016/j.mbs.2020.108306

PubMed Abstract | CrossRef Full Text | Google Scholar

Qin C., Jin Y., Tian M., Ju P., Zhou S. (2023). Comparative study of global sensitivity analysis and local sensitivity analysis in power system parameter identification. Energies 16, 5915. doi:10.3390/en16165915

CrossRef Full Text | Google Scholar

Rejniak K. A. (2007). An immersed boundary framework for modelling the growth of individual cells: an application to the early tumour development. J. Theor. Biol. 247, 186–204. doi:10.1016/j.jtbi.2007.02.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Rikard S. M., Athey T. L., Nelson A. R., Christiansen S. L. M., Lee J. J., Holmes J. W., et al. (2019). Multiscale coupling of an agent-based model of tissue fibrosis and a logic-based model of intracellular signaling. Front. Physiol. 10, 1481. doi:10.3389/fphys.2019.01481

PubMed Abstract | CrossRef Full Text | Google Scholar

Roy C. J., Oberkampf W. L. (2011). A comprehensive framework for verification, validation, and uncertainty quantification in scientific computing. Comput. Methods Appl. Mech. Eng. 200, 2131–2144. doi:10.1016/j.cma.2011.03.016

CrossRef Full Text | Google Scholar

Ruiz-Martinez A., Gong C., Wang H., Sové R. J., Mi H., Kimko H., et al. (2022). Simulations of tumor growth and response to immunotherapy by coupling a spatial agent-based model with a whole-patient quantitative systems pharmacology model. PLOS Comput. Biol. 18, e1010254. doi:10.1371/journal.pcbi.1010254

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadida H. Q., Abdulla A., Marzooqi S. A., Hashem S., Macha M. A., Akil A. S. A. S., et al. (2024). Epigenetic modifications: key players in cancer heterogeneity and drug resistance. Transl. Oncol. 39, 101821. doi:10.1016/j.tranon.2023.101821

PubMed Abstract | CrossRef Full Text | Google Scholar

Sathyanarayanan A., Gupta R., Thompson E. W., Nyholt D. R., Bauer D. C., Nagaraj S. H. (2020). A comparative study of multi-omics integration tools for cancer driver gene identification and tumour subtyping. Brief. Bioinform. 21, 1920–1936. doi:10.1093/bib/bbz121

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmidt D. R., Patel R., Kirsch D. G., Lewis C. A., Vander Heiden M. G., Locasale J. W. (2021). Metabolomics in cancer research and emerging applications in clinical oncology. Ca. Cancer J. Clin. 71, 333–358. doi:10.3322/caac.21670

PubMed Abstract | CrossRef Full Text | Google Scholar

Schuetz T. A., Becker S., Mang A., Toma A., Buzug T. M. (2013). Modelling of glioblastoma growth by linking a molecular interaction network with an agent-based model. Math. Comput. Model. Dyn. Syst. 19, 417–433. doi:10.1080/13873954.2013.777748

CrossRef Full Text | Google Scholar

Sefidgar M., Soltani M., Raahemifar K., Bazmara H., Nayinian S. M. M., Bazargan M. (2014). Effect of tumor shape, size, and tissue transport properties on drug delivery to solid tumors. J. Biol. Eng. 8, 12. doi:10.1186/1754-1611-8-12

PubMed Abstract | CrossRef Full Text | Google Scholar

Sivakumar N., Mura C., Peirce S. M. (2022). Innovations in integrating machine learning and agent-based modeling of biomedical systems. Front. Syst. Biol. 2. doi:10.3389/fsysb.2022.959665

CrossRef Full Text | Google Scholar

Stahlberg E. A., Abdel-Rahman M., Aguilar B., Asadpoure A., Beckman R. A., Borkon L. L., et al. (2022). Exploring approaches for predictive cancer patient digital twins: opportunities for collaboration and innovation. Front. Digit. Health 4, 1007784. doi:10.3389/fdgth.2022.1007784

PubMed Abstract | CrossRef Full Text | Google Scholar

Stahlschmidt S. R., Ulfenborg B., Synnergren J. (2022). Multimodal deep learning for biomedical data fusion: a review. Brief. Bioinform. 23, bbab569. doi:10.1093/bib/bbab569

PubMed Abstract | CrossRef Full Text | Google Scholar

Stamatakos G., Dionysiou D., Lunzer A., Belleman R., Kolokotroni E., Georgiadi E., et al. (2014). The technologically integrated oncosimulator: combining multiscale cancer modeling with information technology in the in silico oncology context. IEEE J. Biomed. Health Inf. 18, 840–854. doi:10.1109/JBHI.2013.2284276

PubMed Abstract | CrossRef Full Text | Google Scholar

Stamatakos G. (2010). “In silico oncology Part I: clinically oriented cancer multilevel modeling based on discrete event simulation,” in Multiscale cancer modeling, 2010. Editor T. Deisboeck, and G. S. Stamatakos (CRC Press) 18, 407–436.

Google Scholar

Stoll G., Caron B., Viara E., Dugourd A., Zinovyev A., Naldi A., et al. (2017). MaBoSS 2.0: an environment for stochastic Boolean modeling. Bioinformatics 33, 2226–2228. doi:10.1093/bioinformatics/btx123

PubMed Abstract | CrossRef Full Text | Google Scholar

Streif S., Kim K. K. K., Rumschinski P., Kishida M., Shen D. E., Findeisen R., et al. (2016). Robustness analysis, prediction, and estimation for uncertain biochemical networks: an overview. J. Process Control 42, 14–34. doi:10.1016/j.jprocont.2016.03.004

CrossRef Full Text | Google Scholar

Strobl M. A. R., Gallaher J., Robertson-Tessi M., West J., Anderson A. R. A. (2023). Treatment of evolving cancers will require dynamic decision support. Ann. Oncol. 34, 867–884. doi:10.1016/j.annonc.2023.08.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Subramanian I., Verma S., Kumar S., Jere A., Anamika K. (2020). Multi-omics data integration, interpretation, and its application. Bioinforma. Biol. Insights 14, 1177932219899051. doi:10.1177/1177932219899051

PubMed Abstract | CrossRef Full Text | Google Scholar

Sütterlin T., Kolb C., Dickhaus H., Jäger D., Grabe N. (2013). Bridging the scales: semantic integration of quantitative SBML in graphical multi-cellular models and simulations with EPISIM and COPASI. Bioinformatics 29, 223–229. doi:10.1093/bioinformatics/bts659

PubMed Abstract | CrossRef Full Text | Google Scholar

Swat M. H., Thomas G. L., Belmonte J. M., Shirinifard A., Hmeljak D., Glazier J. A. (2012). Multi-scale modeling of tissues using CompuCell3D. Methods Cell Biol. 110, 325–366. doi:10.1016/b978-0-12-388403-9.00013-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Toni T., Welch D., Strelkowa N., Ipsen A., Stumpf M. P. H. (2009). Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems. J. R. Soc. Interface 6, 187–202. doi:10.1098/rsif.2008.0172

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsokanas N., Pastorino R., Stojadinović B. A. (2022). A comparison of surrogate modeling techniques for global sensitivity analysis in hybrid simulation. Mach. Learn. Knowl. Extr. 4, 1–21. doi:10.3390/make4010001

CrossRef Full Text | Google Scholar

van Genderen M. N. G., Kneppers J., Zaalberg A., Bekers E. M., Bergman A. M., Zwart W., et al. (2024). Agent-based modeling of the prostate tumor microenvironment uncovers spatial tumor growth constraints and immunomodulatory properties. Npj Syst. Biol. Appl. 10, 20–13. doi:10.1038/s41540-024-00344-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Vaske C. J., Benz S. C., Sanborn J. Z., Earl D., Szeto C., Zhu J., et al. (2010). Inference of patient-specific pathway activities from multi-dimensional cancer genomics data using PARADIGM. Bioinformatics 26, i237–i245. doi:10.1093/bioinformatics/btq182

PubMed Abstract | CrossRef Full Text | Google Scholar

Vitale I., Shema E., Loi S., Galluzzi L. (2021). Intratumoral heterogeneity in cancer progression and response to immunotherapy. Nat. Med. 27, 212–224. doi:10.1038/s41591-021-01233-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Walker E., Trask N., Martinez C., Lee K., Actor J. A., Saha S., et al. (2024). Unsupervised physics-informed disentanglement of multimodal data. Found. Data Sci. 2024019. doi:10.3934/fods.2024019

CrossRef Full Text | Google Scholar

Wang W. (2013). Therapeutic hints from analyzing the attractor landscape of the p53 regulatory circuit. Sci. Signal. 6, pe5. doi:10.1126/scisignal.2003820

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang Z., Butner J. D., Kerketta R., Cristini V., Deisboeck T. S. (2015). Simulating cancer growth with multiscale agent-based modeling. Semin. Cancer Biol. 30, 70–78. doi:10.1016/j.semcancer.2014.04.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Wen F., Zheng H., Wu Y., Wheeler J., Zeng X., Fu P., et al. (2016). Cost-effectiveness analysis of fluorouracil, leucovorin, and irinotecan versus epirubicin, cisplatin, and capecitabine in patients with advanced gastric adenocarcinoma. Sci. Rep. 6, 36060. doi:10.1038/srep36060

PubMed Abstract | CrossRef Full Text | Google Scholar

West J., Robertson-Tessi M., Anderson A. R. A. (2023). Agent-based methods facilitate integrative science in cancer. Trends Cell Biol. 33, 300–311. doi:10.1016/j.tcb.2022.10.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Whitacre J. M. (2012). Biological robustness: paradigms, mechanisms, and systems principles. Front. Genet. 3, 67. doi:10.3389/fgene.2012.00067

PubMed Abstract | CrossRef Full Text | Google Scholar

Winter E. (2002). “Chapter 53 the shapley value,” in Handbook of game theory with economic applications (Elsevier), 2025–2054.

CrossRef Full Text | Google Scholar

Yang Y., Chen L., Xiong Y., Li S., Meng X. (2021). Global sensitivity analysis based on BP neural network for thermal design parameters. J. Thermophys. Heat. Transf. 35, 187–199. doi:10.2514/1.t5955

CrossRef Full Text | Google Scholar

Yazdani A., Lu L., Raissi M., Karniadakis G. E. (2020). Systems biology informed deep learning for inferring parameters and hidden dynamics. PLOS Comput. Biol. 16, e1007575. doi:10.1371/journal.pcbi.1007575

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu J. S., Bagheri N. (2020). Agent-based models predict emergent behavior of heterogeneous cell populations in dynamic microenvironments. Front. Bioeng. Biotechnol. 8, 249. doi:10.3389/fbioe.2020.00249

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu J. S., Bagheri N. (2021). Modular microenvironment components reproduce vascular dynamics de novo in a multi-scale agent-based model. Cell Syst. 12, 795–809.e9. doi:10.1016/j.cels.2021.05.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu L., Jiang M., Wang H., Sun H., Zhu J., Zhao W., et al. (2021). A narrative review of tumor heterogeneity and challenges to tumor drug therapy. Ann. Transl. Med. 9, 1351. doi:10.21037/atm-21-1948

PubMed Abstract | CrossRef Full Text | Google Scholar

Zi Z. (2011). Sensitivity analysis approaches applied to systems biology models. IET Syst. Biol. 5, 336–346. doi:10.1049/iet-syb.2011.0015

PubMed Abstract | CrossRef Full Text | Google Scholar

Zouhri W., Homri L., Dantan J.-Y. (2022). Handling the impact of feature uncertainties on SVM: a robust approach based on Sobol sensitivity analysis. Expert Syst. Appl. 189, 115691. doi:10.1016/j.eswa.2021.115691

CrossRef Full Text | Google Scholar