
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
HYPOTHESIS AND THEORY article
Front. Physiol., 07 August 2023
Sec. Clinical and Translational Physiology
Volume 14 - 2023 | https://doi.org/10.3389/fphys.2023.1230654
This article is part of the Research TopicCardiorespiratory Interactions in DiseaseView all 9 articles
While both cardiac output (Qcirculatory) and right atrial pressure (PRA) are important measures in the intensive care unit (ICU), they are outputs of the system and not determinants. That is to say, in a model of the circulation wherein venous return and cardiac function find equilibrium at an ‘operating point’ (OP, defined by the PRA on the x-axis and Qcirculatory on the y-axis) both the PRA and Qcirculatory are, necessarily, dependent variables. A simplified geometrical approximation of Guyton’s model is put forth to illustrate that the independent variables of the system are: 1) the mean systemic filling pressure (PMSF), 2) the pressure within the pericardium (PPC), 3) cardiac function and 4) the resistance to venous return. Classifying independent and dependent variables is clinically-important for therapeutic control of the circulation. Recent investigations in patients with acute respiratory distress syndrome (ARDS) have illuminated how PMSF, cardiac function and the resistance to venous return change when placing a patient in prone. Moreover, the location of the OP at baseline and the intimate physiological link between the heart and the lungs also mediate how the PRA and Qcirculatory respond to prone position. Whereas turning a patient from supine to prone is the focus of this discussion, the principles described within the framework apply equally-well to other more common ICU interventions including, but not limited to, ventilator management, initiating vasoactive medications and providing intravenous fluids.
Though evidence of benefit has existed for placing patients with moderate-to-severe acute respiratory distress syndrome (ARDS) in the prone position for some time, the coronavirus pandemic raised clinical awareness of this maneuver (Guérin et al., 2020). Guidelines currently recommend prone position for patients with ARDS and a partial pressure-to-fraction of inspired oxygen (PaO2/FiO2) ratio of not more than 150 mmHg (Papazian et al., 2019). Furthermore, with this ARDS severity, patients should maintain the prone position for at least 12 h per day for optimal benefit (Guérin et al., 2013).
Turning a patient from the supine to prone position has salutary benefits on gas exchange as oxygenation and carbon dioxide elimination are both enhanced (Guérin et al., 2020). The mechanisms by which the prone position exerts its salubrious effects are manifold. When the dorsal, de-gassed ‘sponge lung’ (Bone, 1993) is no longer gravity-dependent, it is recruited and the surface area for gas exchange increased. Critically, the newly-enlisted alveoli see no significant change in pulmonary blood flow (Henderson et al., 2013); as a consequence, the burden of low ventilation-to-perfusion (V/Q) lung units is reduced. In addition to alveolar recruitment, shifting to the prone position improves ‘shape matching’ between the pulmonary parenchyma and the chest wall (Gattinoni et al., 2013). In total, the result is that there is less pulmonary inhomogeneity (Cressoni et al., 2014; Cressoni et al., 2015) and, therefore, fewer ‘stress-raisers’ (Mead et al., 1970) that amplify radial traction forces upon the lungs and pulmonary vasculature (Broccard et al., 1998; Marini et al., 2003; Repessé et al., 2016). Furthermore, stiffening the chest wall with improved pulmonary compliance diminishes trans-pulmonary pressure (PTP) as the pleural pressure is raised for any given airway pressure (Marini and Gattinoni, 2021). This reduces the mechanical power applied to the pulmonary parenchyma and mitigates West zone 1 and 2 conditions (Gattinoni and Quintel, 2016). All of the aforementioned changes in pulmonary physiology (i.e., improved oxygenation and carbon dioxide elimination, optimized perivascular pulmonary mechanics, diminished PTP) minimize the afterload experienced by the right ventricle (RV), giving weight to the motto: ‘what’s good for the lung is good for the RV (Repessé et al., 2016).’
While the literature is replete with elegant investigations into the mechanical pulmonary pathophysiology of ARDS in both supine and prone positions, comparatively little is known about the hemodynamic effects. With a recent investigation exploring the determinants of venous return in the prone position (Lai et al., 2021) and an excellent related review (Lai et al., 2023), this overview will expand upon relevant concepts in clinical hemodynamics, propose a simplified geometrical model clarifying the determinants of cardiac output and right atrial pressure and then relate this to what is currently known about prone position in the ARDS patient (Table 1).
Many excellent reviews connecting Guyton’s model of the circulatory system to critical-illness are available (Sylvester et al., 1983; Bressack and Raffin, 1987; Fessler, 1997; Jacobsohn et al., 1997; Magder, 2004; Gelman, 2008; Parkin and Leaning, 2008; Feihl and Broccard, 2009a; Feihl and Broccard, 2009b; Magder, 2012; Berlin and Bakker, 2015; Berger and Takala, 2018; Persichini et al., 2022). Though this model has been criticized and debated (Brengelmann, 2003; Beard and Feigl, 2011; Moller et al., 2017; Berger et al., 2019; Brengelmann, 2019; Werner-Moller et al., 2020; Kenny, 2021), these controversies are beyond the scope of this review. Guyton’s contributions to hemodynamics are many and may be parsed into: 1.) the explication of venous return (Guyton et al., 1955) and 2.) the graphical superposition of the venous return and Starling-Sarnoff curves (Guyton, 1955).
The determinants of venous return from the peripheral circulation are, from Guyton’s experiments: 1.) the mean circulatory filling pressure (PMCF), 2.) right atrial pressure (PRA) and 3.) the resistance to venous return (RVR) (Guyton, 1955; Sylvester et al., 1983; Jacobsohn et al., 1997; Feihl and Broccard, 2009a). Together the PMCF and the PRA define the pressure gradient for venous return.
If blood flow were ceased, arterial pressure would fall and venous pressure would rise to a weighted recoil pressure reflecting the portion of the circulation with greatest blood volume (Sylvester et al., 1983; Jacobsohn et al., 1997). As the small veins and venules comprise this circulatory segment, the PMCF is a ‘pivot pressure’ found downstream of the capillary beds but upstream from the larger veins (Magder, 2012). The ‘pivot pressure’ description arises from the sense that when the heart recommences circulatory flow, pressure in the arteries rise up from the PMCF while the pressure in the downstream veins fall below it; thus, the PMCF acts as a quasi-static ‘pivot’ around which pressures upstream and downstream rise and fall, respectively (Broccard, 2012). As discussed below, the PMCF is similar, but not equivalent to, the mean systemic filling pressure (PMSF). The PMSF excludes the contributions of intrathoracic blood volume and compliance.
The PMCF (or PMSF) is determined by two related–and often confused–biophysical properties: capacitance and compliance (Rothe, 1986; Rothe, 1993; Tyberg, 2002). To understand capacitance, the reader must appreciate that the total circulatory volume is comprised of two distinct (though dynamic) ‘types’ of volume–the unstressed (VUS) and stressed (VS) volumes (Gelman, 2008; Magder, 2012). The VUS does not create a vascular elastic recoil pressure while the VS does. As an analogy, filling a waterbed requires water volume before the walls are stretched (i.e., the VUS); further volume generates a recoil pressure from the elastic walls (i.e., the VS). As compared to a water balloon, a waterbed has a much larger capacitance because its VUS is greater than the VUS of the balloon. Compliance and its inverse, elastance, describe the relationship between changing vascular volume and changing recoil pressure (Rothe, 1993). It follows that compliance (or elastance) pertain to the VS; the VUS, by definition, generates no change in pressure (i.e., the VUS has infinite compliance or zero elastance). Continuing with the analogy above, were the waterbed made from a poorly elastic (i.e., stiff) material, it would have a large capacitance, but low compliance (or high elastance). If the water balloon was made of a highly elastic material, it would have a low capacitance, but high compliance (or low elastance). Mathematically, the PMCF is determined by the volume of blood generating a recoil pressure (i.e., the VS, which is determined by total vascular volume and capacitance) divided by the vascular compliance (Tyberg, 2002; Magder, 2012) (Figure 1).
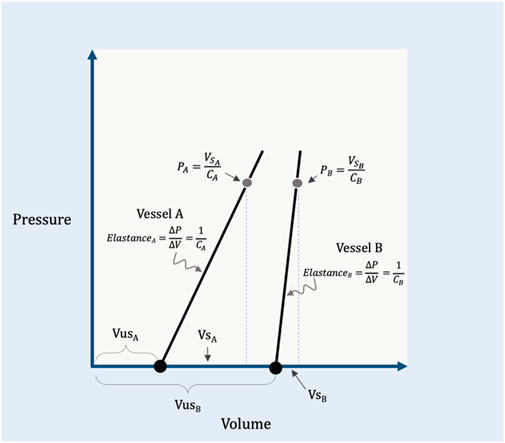
FIGURE 1. Illustration of capacitance and compliance. Vessel A has a relatively small capacitance because its unstressed volume (VUSA) is small. The compliance of the vessel (CA) is the inverse of elastance on this graph; by rearrangement, the recoil pressure generated in this vessel (PA) is equal to its stressed volume (VSA) divided by its compliance. Vessel B shows a larger capacitance, but an increased elastance (i.e., reduced compliance, CB) relative to vessel A. Vessel A and B are analogous to the ‘water balloon’ and ‘waterbed,’ respectively, described within the text. VSB is the stressed volume, VUSB is the unstressed volume and PB is the recoil pressure of vessel B.
As noted above, the PMCF includes the cardiac and pulmonary vascular volumes and compliances (i.e., the total circulation) while the PMSF measures only the extra-thoracic, systemic, circulation (Rothe, 1993); they are very similar in value and often used interchangeably. In clinical practice, the methods for estimating this static, ‘pivot pressure’ reflect the systemic pressure (i.e., PMSF) and this measure will be used throughout this review (Berger et al., 2016). For patients, there are three methods to estimate the PMSF: 1.) extrapolation to zero flow of the PRA–cardiac output relationship altered by ventilator-hold maneuvers (Pinsky, 1984; Maas et al., 2009), 2.) extremely rapid cuff insufflation on the arm with an ipsilateral arterial line (Maas et al., 2012) and 3.) mathematical modelling by the method of Parkin and Leaning (Parkin and Leaning, 2008). Though beyond the scope of this discussion, the ventilator-hold and arm-occlusion methods over-estimate PMSF (Maas et al., 2012; Berger et al., 2016) for a variety of reasons (Moller and Berger, 2023) whereas the mean systemic filling pressure analogue (PMSA) (i.e., the method of Parkin and Leaning) accurately estimated absolute and changing values of PMSF in a porcine model (Werner-Moller et al., 2022). Because it is simply calculated from PRA, cardiac output and mean arterial pressure (Parkin and Leaning, 2008; Moller and Parkin, 2022), the PMSA is an attractive tool for guiding both prospective and retrospective research as well as clinical therapy (Moller and Parkin, 2022; Moller and Berger, 2023). Given the above, the importance of understanding and, arguably, measuring the PMSF is that it is a hemodynamic variable the clinician can target therapeutically. For example, a low PMSF intimates low VS which could be due to diminished total blood volume (e.g., hypovolemia, hemorrhage) and/or high venous capacitance (e.g., venodilation, sepsis). The clinician might rectify these pathological states by giving volume and/or administering alpha-agonists, respectively (Parkin and Leaning, 2008). Thus, the PMSF and its determinants are independent variables that can be adjusted for therapeutic control of the circulation; increasing PMSF raises venous return for any given right atrial pressure (PRA) (Figure 2).
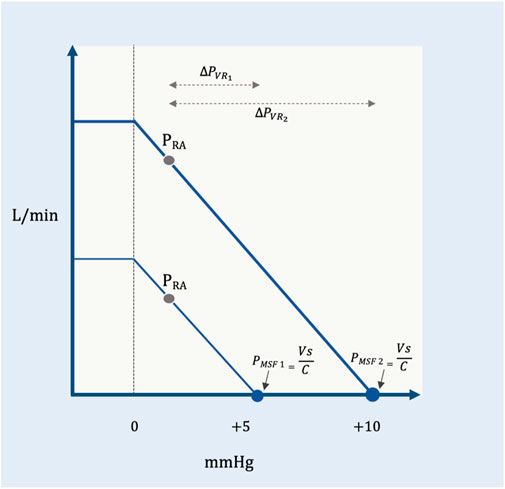
FIGURE 2. Pressure gradient for venous return. The effect of changing mean systemic filling pressure (in millimeters of mercury, mmHg) from a low (PMSF1) to a higher value (PMSF2) (e.g., volume infusion, decreased capacitance). The slope of the venous return curve is constant between the two curves meaning that the resistance to venous return is constant (see below). For a given right atrial pressure (PRA), the lower PMSF1 (i.e., reduced pressure gradient for venous return,
Downstream from the PMSF is the PRA. In Guyton’s original experimental set-up, PRA was studied as an independent variable, altered via the height of a collapsible tube (Guyton et al., 1957). Guyton observed that the PRA was inversely related to venous return; in other words, decreasing PRA increased venous return, linearly (Figure 2). Consequently, the difference between PMSF and PRA is the pressure gradient for venous return (
Guyton began with a mathematical approximation of the circulation, modeled after a system of distensible tubes (Jacobsohn et al., 1997). In this representation, the forces that resist total blood flow back to the heart are termed the ‘resistance to venous return’ (RVR). While the RVR is often considered to be a purely Poiseuillean description of the venous circulation, this is not correct. The RVR, like the PMSF, is a weighted average of the system (i.e., including arterial components) (Jacobsohn et al., 1997). Each vascular bed faces a downstream resistance and has a unique compliance; the RVR is a summation of the downstream resistance encountered by each vascular bed, multiplied by its individual compliance relative to the total compliance of the system (Figure 3).
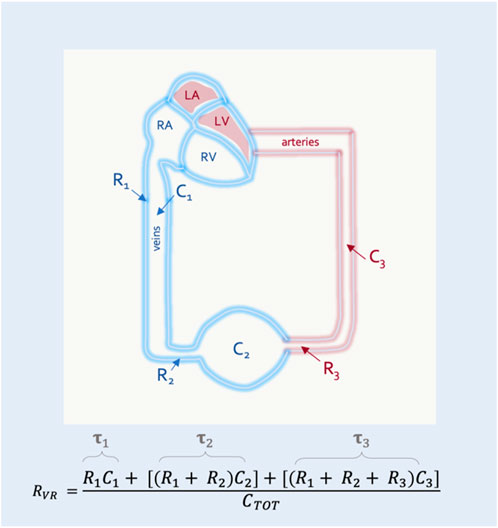
FIGURE 3. The resistance to venous return (RVR). RVR is composed of resistances (Rx) and compliances (Cx) for the entire circulation. This simplified model shows 3 vascular segments in series. The RVR is the sum of the resistance and compliance for each segment divided by the total compliance of the circulatory system (CTOT). Resistance multiplied by compliance is the time constant (
In this way the RVR can also be described by the time constant (i.e., the resistance multiplied by the compliance) of each vascular segment (Magder, 2016). This is clinically-important because diverting blood volume towards or away from a vascular bed with a long time constant (e.g., the splanchnic circulation) will increase or decrease the RVR, respectively (Caldini et al., 1974). The converse is true for vascular beds with a short time constant (e.g., kidneys, muscle) (Magder, 2016) (Figure 4). Accordingly, should an intervention in the ICU (e.g., prone position) alter the fraction of flow to vascular beds of differing time constants, RVR will be affected.
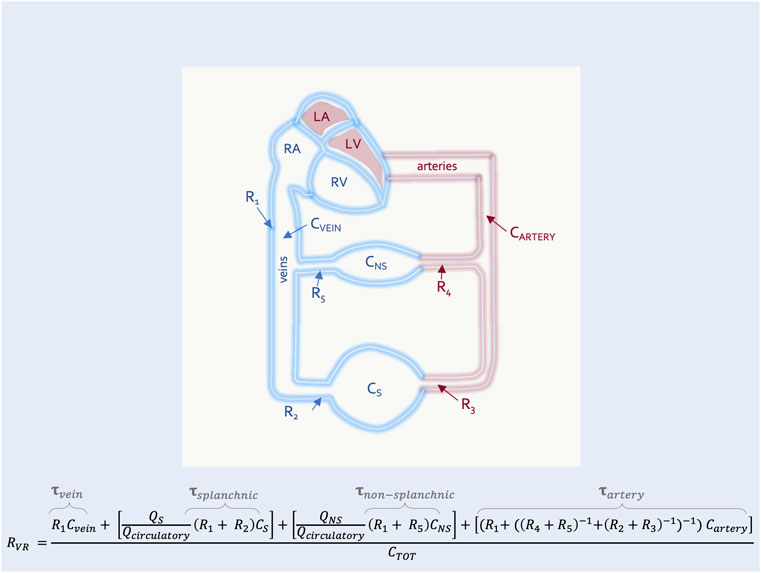
FIGURE 4. The resistance to venous return with high and low time-constant segments in parallel. This is an expansion of Figure 3 with two representative segments in parallel–the non-splanchnic (NS) (i.e., low time constant,
On the venous return curve, change in the RVR alters the slope for a given pressure gradient (Figure 5). An increase in RVR reduces the slope, while a decrease in RVR steepens the slope.
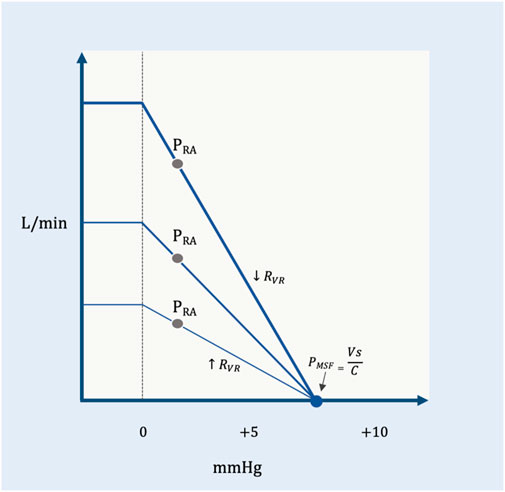
FIGURE 5. The RVR and the venous return curve. PMSF is constant, but the resistance to venous return changes. The shallow curve is a higher resistance (
In summary, venous return is directly proportional to the PMSF less the PRA and indirectly proportional to the RVR. If the PMSF increases and/or PRA falls, then venous return rises (Figure 2). Similarly, decreased RVR facilitates blood return to the heart and vice versa (Figure 5). The Ohmic representation of this relationship is as follows (Berger and Takala, 2018):
In addition to detailing the peripheral vascular determinants of blood returning to the heart, Guyton expanded our understanding of hemodynamics by adding to his analysis the cardiac determinants of blood flow from the heart. He did so by superimposing the venous return and Starling-Sarnoff curves (Guyton, 1955); this depiction is commonly referred to as the ‘Guyton diagram.’ These curves can be placed over each other because they both have PRA on the x-axis and blood flow on the y-axis (Figure 6). Though it will be developed in more detail below, the Guyton diagram introduces an important distinction between intravascular and transmural pressures. The PRA and PMSF measured on the Guyton diagram are intravascular pressures. Thus, the pressure gradient for venous return is directly related to the difference between the intravascular PMSF and PRA (Equation 1). The Starling mechanism, however, is related to right atrial transmural pressure which is the pressure within the right atrium less its ambient pressure (i.e., the pericardial pressure). The transmural right atrial pressure is a static pressure that determines cardiac myocyte stretch which servo-controls the ejected stroke volume to match the venous return inflow.
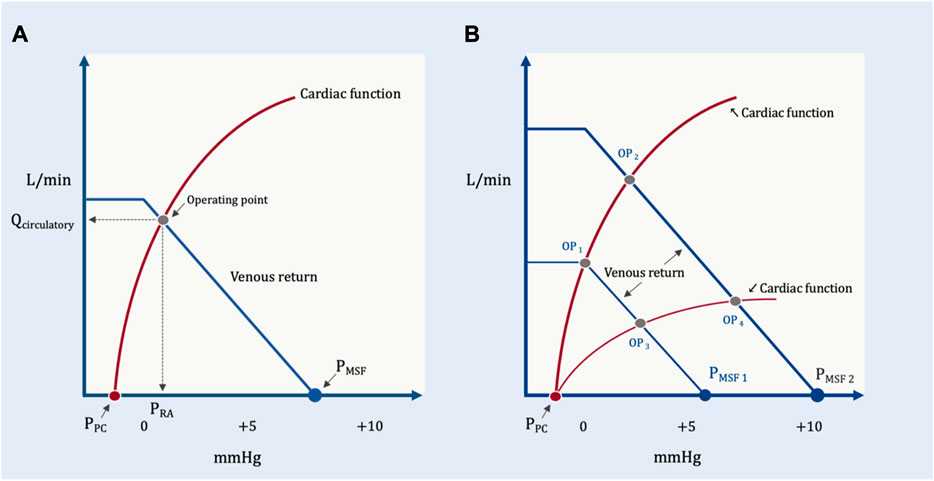
FIGURE 6. The Guyton diagram. (A) The circulation in its resting state; as in Figure 2, the x-axis is right atrial pressure in millimeters of mercury (mmHg) and y-axis is total blood flow in liters per minute (L/min). The PMSF is approximately 8 mmHg at the x-intercept of the venous return curve (in blue). The Starling-Sarnoff (or cardiac function) curve is in red in a normal, upright position; its x-intercept is the pressure around the right atrium, the pericardial pressure (PPC). In this model, the dependent variable is the operating point, at the intersection of the venous return and cardiac function curves at equilibrium. Accordingly, both the x- (i.e., PRA) and y- (i.e., Qcirculatory) coordinates defined by the operating point are also dependent variables. (B) How the PRA and Qcirculatory are determined by the system. Normal cardiac function but diminished PMSF1 (e.g., volume loss, venodilation) results in operating point 1 (OP1), diminished PRA and Qcirculatory. Normal cardiac function with increased PMSF2 (e.g., volume expansion, decreased venous capacitance from adrenergic agents) causes OP2 (i.e., increased PRA and Qcirculatory). Reduced PMSF and diminished cardiac function (e.g., acute cor pulmonale with tricuspid regurgitation) leads to OP3. Elevated PMSF with reduced cardiac function leads to OP4. Both Qcirculatory and PRA are dependent variables in this system. The independent variables are reflected in the position and slopes of the venous return and cardiac function curves.
Like any model, the value of the Guyton diagram is that it makes explicit the system’s independent and dependent variables. Independent variables are those things the clinician can change or control (e.g., vascular volume and capacitance, airway pressure), whereas dependent variables are what the clinician wants to predict or study (e.g., cardiac output) by manipulating the independent variables. These distinctions are critical when considering the effects of any intervention in the ICU (e.g., prone position).
Nestled within the venous return curve are some of the independent variables of the circulatory system touched upon above: 1.) vascular capacitance, 2.) total vascular volume and 3.) the RVR. Thus, increasing total vascular volume via intravenous fluids and/or decreasing vascular capacitance via alpha-agonists both augment the VS and, therefore, PMSF. On the Guyton diagram, raising PMSF right-shifts the venous return curve such that there is increased blood flow to the heart for any given PRA. Similarly, beta-agonists (Green, 1977) and/or shunting blood from long to short time-constant vascular beds decreases the RVR (Caldini et al., 1974); this also enhances venous return for any given PRA. On the Guyton diagram, diminished RVR is manifested by an increased slope of the venous return curve (Figure 6). The converse also holds, diminished blood volume, increased capacitance and/or increased RVR all reduce venous return for any given PRA. One clinically-important scenario wherein vascular capacitance rises (i.e., which decreases PMSF) is reduced adrenergic tone (e.g., sedation, anesthesia, relief of hypoxemia) (Bressack and Raffin, 1987).
Found within the cardiac function curve are additional independent variables: heart rate, rhythm, valve function, afterload, inotropic and lusitropic states (Feihl and Broccard, 2009a; Feihl and Broccard, 2009b). Consequently, rate and rhythm control (e.g., cardioversion), afterload reduction (e.g., vasodilator therapy, pulmonary vascular recruitment), enhanced contractility and improved relaxation (e.g., epinephrine infusion) all increase the slope of the Starling-Sarnoff curve. With this, blood flow from the heart is enhanced for any given PRA. The converse also holds, for example, rapid atrial dysrhythmia coupled with torrential tricuspid regurgitation and severe pulmonary arterial hypertension decreases the slope of the cardiac function curve, that is to say, reduce cardiac output for any given PRA (Figure 6).
But what about the PRA itself? Is it an independent variable? In Guyton’s experimental work on venous return, PRA was studied as an independent variable. However, on the Guyton diagram, which considers both venous return and cardiac function simultaneously, PRA is not independent. This was clearly stated by Guyton in his initial proposal: “right atrial pressure is not one of the primary determinants of cardiac output but, instead, is itself determined simultaneously with cardiac output” (Guyton, 1955). Later, Fiehl and Broccard expanded upon PRA as a dependent variable in their excellent review (Feihl and Broccard, 2009a). Accordingly, when analyzing venous return and cardiac function simultaneously, the dependent variable is the equilibrium formed at their intersection–the operating point. Thus, both the x- (i.e., PRA) and y- (i.e., cardiac output) Cartesian coordinates are equally dependent upon the system. This may be counterintuitive given the convention of placing the independent variable on the x-axis, however, with the Guyton diagram this is a vestige of his initial work on venous return. When it is understood that the operating point is the dependent variable, the circular and specious reasoning that the concept of venous return is incorrect because ‘raising PRA reduces venous return per Guyton but augments cardiac output by Starling’ becomes moot. Rather, at any given time (or in response to an intervention, such as the prone position) there are characteristics of the peripheral circulation and heart that, in tandem, produce a unique cardiac output and PRA (Guyton, 1955). To clarify this, a modified Guyton model is proposed below to disclose the clinically-relevant independent variables.
This is a simplified geometric approximation of the principles discussed above. If we consider the intersection of cardiac function and venous return as two directly-opposed right triangles, then we can solve for the height of their shared apex at equilibrium (i.e., cardiac output or venous return presently identified as Qcirculatory) as a function of their bases and hypotenuse slopes (Figure 7). Qcirculatory is numerically equivalent to cardiac output and/or venous return. It is used in the geometrical model to emphasize that total blood flow (i.e., Qcirculatory) is determined by the operating point–the intersection of both peripheral venous and cardiac function. This avoids the confusion that sometimes arises when ‘cardiac output’ is thought to be determined only by cardiac factors or when ‘venous return’ is thought entirely due to peripheral factors; ‘Qcirculatory’ circumvents this ambiguity.
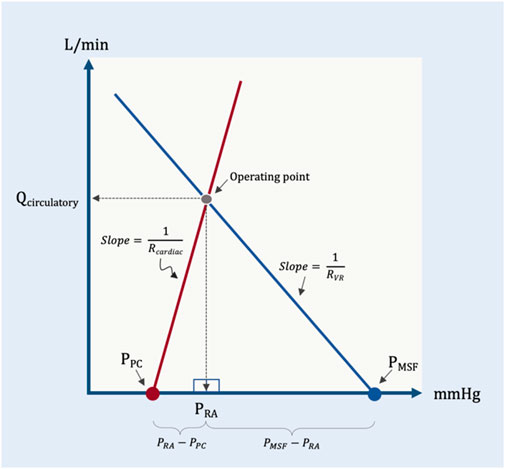
FIGURE 7. Simplified geometrical model. This model borrows from the Guyton diagram where the red line represents cardiac function and the blue line venous return. Two right triangles are formed as described in the text; the operating point is the apex of the two right triangles. Note that the slope (change in flow per unit pressure) is conductance, G. The inverse of conductance is resistance. As in previous figures, PPC is pericardial pressure, PMSF is mean systemic filling pressure, Rcardiac and RVR are cardiac and venous resistance, respectively. Qcirculatory is blood flow of the system with right atrial pressure (PRA) in millimeters of mercury (mmHg) on the x-axis and blood flow in liters per minute (L/min) on the y-axis.
The base of the left triangle rests on the x-axis and is defined by the pressure immediately surrounding the heart, within the pericardium (i.e., the PPC) and the PRA; this is the transmural pressure of the right atrium. The slope (i.e., hypotenuse) of this triangle is the change in cardiac output per mmHg of transmural right atrial pressure, or cardiac conductance (Gcardiac). This value is estimated to be 35 mL/min/kg per 1 mmHg (Rothe, 1993). Multiplying the base of this triangle (i.e., PRA–PPC) by the slope of the hypotenuse (Gcardiac) gives the height of this triangle (i.e., total circulatory flow, Qcirculatory).
Equation 2 is solved for PRA
Similarly, the base of the rightmost triangle is defined by the PMSF and the PRA; this is the pressure gradient for venous return (the difference between two intravascular pressures along a hypothetical length of vessel), as above. The slope of this triangle is the change in cardiac output per the gradient for venous return, or venous conductance (GVR). Based on a PMSF of 8 mmHg, this value is estimated to be 10 mL/kg/min per 1 mmHg. Multiplying the base of this triangle (i.e., PMSF–PRA) by the slope of its hypotenuse (GVR) gives the height of this triangle, which is also total circulatory flow, Qcirculatory.
Equation 4 is solved for PRA
Setting equation 3 equal to equation 5, we can reduce the equation to Qcirculatory as follows:
Because the inverse of conductance, G, is resistance, this equation can be written as:
Accordingly, in this model the shared apex of the two triangles (i.e., the operating point, which defines Qcirculatory) is a function of the total base of the two triangles (i.e., PMSF less PPC) and the inverse of the slopes of their respective hypotenuses (i.e., RVR and Rcardiac). More concretely, if RVR and Rcardiac remain constant, increased PMSF and/or decreased pressure surrounding the heart (PPC) raise the height of their shared apex (Figure 8). A concomitant decrease in Rcardiac (i.e., increased slope of the Starling-Sarnoff curve) or RVR (i.e., increased slope of the venous return curve) would further elevate their shared apex (Figure 8).
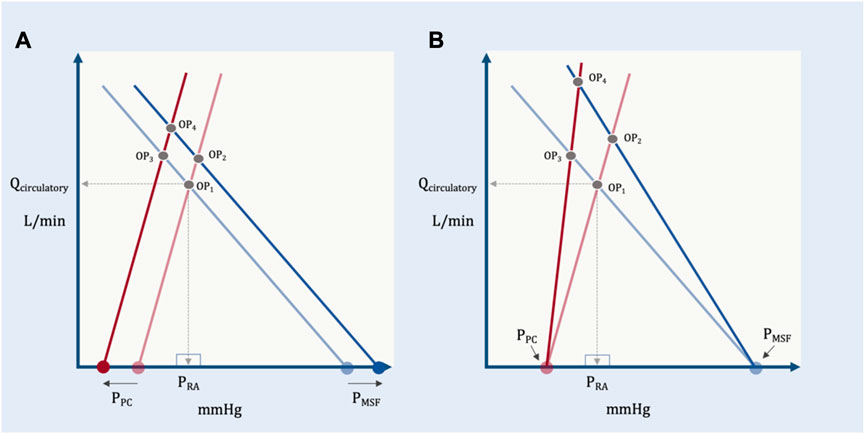
FIGURE 8. The independent and dependent variables of the geometric model. (A) The effect of changing the independent variables, PPC and PMSF on the dependent variable (operating point, OP). OP1 depicts baseline conditions, its x- (PRA) and y-(Qcirculatory) coordinates are shown. A solitary increase in PMSF (e.g., volume infusion) results in OP2, that is, increased PRA and Qcirculatory. A selective decrease in PPC (e.g., spontaneous inspiration) leads to OP3 which increases Qcirculatory, but decreases PRA. If PMSF rises and PPC falls, the result is OP4, increased Qcirculatory at a slightly reduced PRA relative to baseline. (B) The effect of changing the independent variables, RVR and Rcardiac on the dependent variable (operating point, OP). A selective decrease in venous resistance (e.g., shunting blood away from the splanchnic circulation) leads to OP2 (i.e., both PRA and Qcirculatory rise). A selective decrease in cardiac resistance (i.e., improving cardiac function by, for example, reducing pulmonary vascular resistance) leads to OP3 (i.e., PRA falls, while Qcirculatory rises). Reducing venous and cardiac resistance together leads to OP4 (i.e., little PRA change with large Qcirculatory augmentation).
In this model, PRA plays no role in cardiac output because the operating point (i.e., the shared apex) is the dependent variable; Qcirculatory and PRA both fall out from this equilibrium (Feihl and Broccard, 2009a). The equations above could have equally been solved for PRA instead of Qcirculatory; PRA, nevertheless, would still be dependent upon PMSF, PPC, Rcardiac and RVR.
To further develop this model with an emphasis on heart-lung interaction, the determinants of PPC are included. Doing so reveals additional, clinically-relevant independent variables when placing an ARDS patient in the prone position. The PPC is the x-intercept of the hypotenuse defined by Rcardiac (i.e., the cardiac function curve) (Magder, 2004; Feihl and Broccard, 2009a). As originally hypothesized by Guyton (Feihl and Broccard, 2009a) and demonstrated by Marini and colleagues (Marini et al., 1981), increasing PPC initiates a parallel, right-shift of the cardiac function curve. Consequently, increased PPC decreases the shared apex (i.e., the operating point) and Qcirculatory is diminished but only if there is no simultaneous change in PMSF, Rcardiac or RVR.
Given that the PPC is a summation of: 1.) pleural pressure (PPL), 2.) pressure added by mechanical ventilation (i.e., estimated as the mean airway pressure, PAW, multiplied by the ratio of the chest wall to respiratory system elastances, ECW/ERS) (Gattinoni et al., 2004) and 3.) the elastic recoil pressure of the pericardium (PPCEL) (Cabrera et al., 1989), we can expand equation 10 above.
Accordingly, increased pleural (e.g., thoracic supports) and/or elastic recoil pressure from the pericardium (e.g., right ventricular dilatation in acute cor pulmonale), raise the pressure surrounding the heart, PPC. Furthermore, elevated PAW (e.g., increasing positive end-expiratory pressure, PEEP) or a stiffened chest wall (e.g., prone position increases the ECW/ERS ratio) both amplify PPC; from equation 11, we see that increasing PPC reduces Qcirculatory but only if PMSF, Rcardiac and RVR are constant. It should not escape the reader’s attention that including PPC in this model is a crucial link between cardiac and respiratory physiologies.
While the proposed model is meant to illuminate the clinically-relevant independent variables determining Qcirculatory, equation 11 has important caveats (Magder, 2012). The most important is that it is predicated upon the intersection of two hypotenuses; in vivo, both the venous return and cardiac function curves have portions that flatten out. When the operating point falls upon the flat portion of the cardiac function curve, Qcirculatory depends only upon the independent variables of cardiac function: PPC, the right atrial pressure at which the cardiac function curve begins to plateau, PRAplat and the Rcardiac (Figure 9).
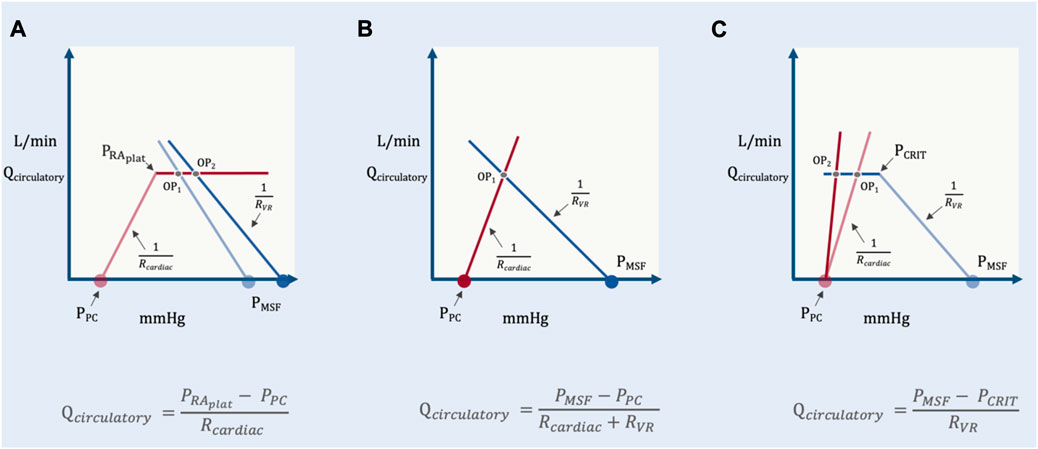
FIGURE 9. Operating point positions in the geometrical model. (A) reveals cardiac limitation where the operating point (OP) is on the flat portion of the cardiac function curve. Change in PMSF or RVR change only PRA and not Qcirculatory (OP1 versus OP2). (B) is when the system is neither venous nor cardiac limited. Qcirculatory is changed by PMSF, PPC, Rcardiac and RVR (see Figure 5). (C) shows venous limitation or ‘waterfall’ physiology. Changes in cardiac function alter only PRA and not Qcirculatory (OP1 versus OP2).
Fundamentally, this equation relays that Qcirculatory is no longer determined by peripheral factors when the operating point is above the PRAplat. Changing PMSF or RVR only alter PRA with fixed Qcirculatory.
In a manner similar to cardiac function, the venous return curve also flattens when the PRA falls below venous collapse pressure, PCRIT (Magder, 2012). This is the formation of a Starling resistor when the great veins enter the thorax and is observed with ultrasound as collapse of the great veins. This phenomenon is also termed ‘waterfall’ physiology because the pressure below PCRIT has no bearing on flow, just as the height of a waterfall does not mediate its flow (Permutt and Riley, 1963). Consequently, when the operating point lies to the left of PCRIT (i.e., on the “flat portion” of the venous return curve) Qcirculatory becomes independent of cardiac function or PPC; the independent variables are PCRIT, PMSF and RVR (Figure 9).
In other words, when venous limited, reducing Rcardiac (i.e., improving cardiac function) or changing PPC has no bearing on Qcirculatory; only changing PMSF, RVR or PCRIT might alter total flow.
With a Guyton-based circulatory model proposed above, anticipating the change in Qcirculatory follows the independent variables of the system: PMSF, PPC, Rcardiac and RVR. At present there are three key studies that have elucidated interactions between the circulation and prone position in ARDS (Vieillard-Baron et al., 2007; Jozwiak et al., 2013; Lai et al., 2021). Much of the discussion below is taken from these investigations.
Recently, Lai and colleagues studied the effect of prone position on the determinants of venous return (Lai et al., 2021). They measured PMSF by extrapolating to zero flow a series of PRA–cardiac output pairings in response to increasing airway pressure. Though this method overestimated PMSF in a porcine model (Berger et al., 2016), this observation was restricted to euvolemic conditions which are less likely in ARDS patients in the ICU. Nevertheless, considering the discussion on PMSF measurement above, a retrospective calculation of PMSA would be of great interest given that the average PMSF measured by Lai et al. was clinically quite high, especially in the prone position. Irrespective of absolute values, Lai and colleagues observed that PMSF increased significantly from the semi-recumbent to prone position; they hypothesized that this was due to increased intra-abdominal pressure (IAP). However, the baseline value and change in IAP had no bearing on PMSF behavior. This is unsurprising given what is known about the mechanisms by which PEEP increase PMSF. Initially, it was also hypothesized that IAP mediated PMSF augmentation with PEEP application and/or stiffening of the chest wall (i.e., akin to prone position) in early canine models (Scharf et al., 1977). However, IAP had no role in raising PMSF, instead, adrenergic reflexes (i.e., changing vascular capacitance) and redistribution of blood volume from the central to peripheral circulation were the main drivers of PMSF rise (Scharf and Ingram, 1977; Fessler, 1995; Fessler, 1997). Accordingly, central blood volume, adrenergic reserve and exogenous vasoactive agents all undoubtedly mediate the change in PMSF upon pronation, rather than IAP. Parenthetically, this could also explain hemodynamic differences noted between elective surgical and critically-ill ARDS patients when prone position is employed (Edgcombe et al., 2008). The latter are more likely to be on vasoactive agents and volume-loaded, while the former more likely euvolemic; as well, anesthetic agents may blunt reflexive changes in vascular capacitance which would limit PMSF rise in the operating room. As described above, PMSF is directly related to Qcirculatory when the patient is not cardiac limited and without concurrent changes in PPC, Rcardiac or RVR.
There are no known direct measurements of PPC in humans with ARDS placed in the prone position. Yet, inferences can be made given the mathematical approximation of PPC presented above. The prone position increases the elastance (i.e., stiffness) of the chest wall (ECW) (Pelosi et al., 1998). To the extent that pronation also decreases the elastance (i.e., improves compliance) of the lungs by alveolar recruitment, the ECW relative to the elastance of the respiratory system (i.e., the lungs and the chest wall together, ERS) rises. Multiplying the mean airway pressure generated by mechanical ventilation by the ECW/ERS ratio approximates PPC augmentation when a patient is passive with the ventilator. For example, if the mean airway pressure is 10 mmHg with an ECW/ERS ratio of 0.3 in the supine position, then 3 mmHg is added to the PPC. If mean airway pressure remains constant and prone position increases the ECW/ERS ratio to 0.5, then 5 mmHg is added to the PPC.
Additionally, pericardial restraint could play an important role determining PPC, especially if there is comorbid acute cor pulmonale (ACP). Typically, when right atrial volume is low (i.e., estimated by a transmural pressure below 5 mmHg (Hamilton et al., 1994)), there is little recoil pressure generated by the pericardium around it. As atrial volume increases beyond this, the pericardial sac is engaged and moves up its volume-pressure relationship. This leads to an increasingly large elastic recoil pressure from the pericardium, which raises the PPC. Elevated PPC, therefore, restricts right ventricular filling and ‘protects’ from overdistention; however, this blunts Qcirculatory by narrowing the PMSF–PPC gradient.
In the setting of ACP, often seen in moderate-to-severe ARDS (Guérin and Matthay, 2016; Mekontso Dessap et al., 2016), pericardial recoil may play an important role upon prone position. With ACP, co-existent right atrial distension elevates PPC by pericardial recoil; this is especially true with PRA above 10–12 mmHg (Hamilton et al., 1994). While prone position is expected to further increase PPC (i.e., by increasing PPL), to the extent that the elevated PPL shrinks cardiac volume, PPC may remain constant, or even fall, as the elastic recoil pressure imparted by the pericardium is reduced. More simply, the rising PPL experienced by the pericardial space is offset by falling recoil pressure of the pericardium. This was originally observed in models of continuous positive airway pressure in heart failure (Huberfeld et al., 1995). Were this to occur upon prone position in a patient with ACP, PPC would remain constant or fall. Taken with the effect of prone position on PMSF noted above, the PMSF–PPC gradient would be maintained (or enhanced) and so too would Qcirculatory if Rcardiac and RVR remain constant.
Finally, some have argued for the execution of prone position with thoracoabdominal supports that allow the abdomen to hang freely (Chiumello et al., 2006). These supports are typically placed mid-sternum and below the pelvis. Chiumello and colleagues compared these supports to the abdomen flush with the bed in prone ARDS patients (Chiumello et al., 2006). They found that the supports accentuated local pressure without any benefit to gas exchange while diminishing stroke volume. Given support placement directly at the sternum, it is possible that PPC is accentuated, reducing the PMSF–PPC gradient and Qcirculatory barring a concomitant decrease in Rcardiac or RVR.
While not a commonly-employed term within the sphere of clinical hemodynamics, ‘cardiac resistance’ (Rcardiac) is analogous to RVR. Graphically and mathematically, Rcardiac is simply the inverse slope of the cardiac function curve. A decrease in Rcardiac (i.e., a steeper slope of the cardiac function curve) represents improved cardiac function and raises the operating point (i.e., Qcirculatory) unless the system is venous limited. In an elegant ultrasonographic study, Vieillard-Baron and colleagues illuminated the salubrious effects on the RV prompted by prone position (Vieillard-Baron et al., 2007). In 21 patients with PaO2/FiO2 ratio of less than 100 mmHg and ACP defined as RV enlargement and septal dyskinesia, 18 h of prone position led to a significant reduction in heart rate and increase in cardiac output. Furthermore, RV end-diastolic area fell while LV end-diastolic area increased and tricuspid regurgitation was reduced. Taken together, the rise in cardiac output with diminished RV size strongly implies reduced Rcardiac as a mechanism of improved Qcirculatory, at least in patients with ACP. The mechanism for this improvement (detailed at the outset of this review and by others (Repessé et al., 2016)) was reduced pulmonary vascular impedance to flow facilitating RV ejection (Jardin and Vieillard-Baron, 2003; Vieillard-Baron et al., 2007) which improves stroke volume and cardiac output for any given PRA.
Recent studies also imply reduced Rcardiac. Ruste and colleagues investigated the hemodynamic effects of prone position in over 100 patients (Ruste et al., 2018). 25% of prone sessions led to significantly increased cardiac output, while 23% had a significant decrease; the remainder showed no change. Importantly, of those sessions where cardiac output rose, 56% had no change or a decrease in global end-diastolic volume (GEDV) measured by transpulmonary thermodilution. Rising cardiac output without an increase in end-diastolic volume infers reduced Rcardiac. Importantly, static GEDV with prone position could signify a shrinking RV end diastolic volume with enlarging LV end diastolic volume consistent with the reduced RV-to-LV end-diastolic area ratio observed with echocardiography by Vieillard-Baron et al. (Vieillard-Baron et al., 2007). Finally, Boesing and colleagues recently published on different PEEP titration strategies and their interaction with prone position (Boesing et al., 2022). In this study, esophageal pressure (PES) was used as a surrogate for PPL. Curiously, the PEEP titration strategy that led to the greatest increase in cardiac output from supine to prone was associated with the smallest rise in transmural PRA (i.e., PRA less PES), in other words, the least preload augmentation. Similar to the observations by Ruste and colleagues, this finding suggests, but does not prove, enhanced cardiac function (i.e., reduced Rcardiac).
In the study of Lai and colleagues (Lai et al., 2021), the RVR was calculated from semi-recumbent to prone position in ARDS patients. In total, RVR increased in the vast majority, though there were a few with stable or slightly diminished RVR. Like PMSF, the change in RVR was not related to IAP and like PMSF, this is unsurprising given the foundational work of Takata and Robotham (Takata et al., 1990). In their original model, Takata and Robotham proposed that the relationship between great vein pressure and IAP would behave analogously to West zones in the lung. That is, if the IAP is much greater than inferior vena cava (IVC) pressure (i.e., zone 2), then venous return is impaired when the abdomen is pressurized by diaphragmatic descent and, in theory, prone position. However, if IAP is much less than IVC pressure (i.e., zone 3), then increased IAP generated by diaphragmatic descent (or prone position) enhances venous return. Their initial work confirmed this model, however, they later found that the model held even with an open abdomen and evisceration, that is, constant IAP (Takata and Robotham, 1992). Thus, the ambient pressure of import was more likely focal subcostal, crural, or intra-hepatic pressure, rather than general IAP. This was observed by Decramer and colleagues (Decramer et al., 1984) and explored further by Brienza et al. in a porcine model (Brienza et al., 1995) and Jellinek et al. in humans (Jellinek et al., 2000). Accordingly, diaphragmatic shape-matching between the liver and upper abdomen, active versus passive diaphragm displacement, intra-hepatic compliance (e.g., intrinsic liver disease) and the use of focal thoracoabdominal supports, among other factors might affect hepatic pressure (Phepatic) upon pronation. Diminished venous pressure (e.g., hypovolemia, venodilation) relative to Phepatic might increase RVR. By contrast, elevated venous pressure (e.g., high blood volume, low venous capacitance) relative to Phepatic might blunt a rise in RVR with prone positioning.
Another possible mechanism for increased RVR with prone position follows that of PMSF. As described above, reflex sympathetic tone is a key mediator of increased PMSF. However, when alpha agonists act upon veins to increase the VS, resistance necessarily rises. This is because change in volume is proportional to the second power of vessel diameter but resistance is related to the fourth power. More concretely, if the diameter of a vein falls by 20% from its baseline, its volume is diminished by 36% (i.e., this reduces its capacitance, increases PMSF) but its resistance rises by 244% (Rothe, 1993). Because the splanchnic circulation is a crucial reservoir for venous blood, the rise in resistance in response to VS recruitment can be offset by beta-agonism (Green, 1977) in the hepatic veins, or redistribution of blood flow to short time constant vascular beds, as noted above (Magder, 2016) (Figure 4). Nevertheless, hepatosplanchnic blood flow during prone position in ARDS changes little (Hering et al., 2002; Matejovic et al., 2002). Interestingly, one study found decreased renal blood flow (Hering et al., 2001)—a fast time-constant bed; diversion of blood in this manner contributes to increased RVR. A final, potential mechanism for RVR augmentation with prone position lies in the superior vena cava (SVC). Fessler found that the rise in total RVR following PEEP application was predominantly due to the veins draining into the SVC rather than the IVC (Fessler et al., 1992). Because PPL is the pressure that surrounds SVC and prone tends to raise PPL for any given PAW (see equation 11 above), it is possible that mechanical compression of the SVC contributes to RVR (Lansdorp et al., 2014; Berger et al., 2016). Regardless of the mechanism, RVR is a critical determinant of Qcirculatory (Pinsky, 2021).
Taking the above into consideration, a key factor when predicting the hemodynamic response to prone position is the location of the operating point whilst semi-recumbent; is the operating point ‘cardiac limited’, ‘venous limited’ or ‘unlimited’ (Figure 6) (Magder, 2012)? Knowing this focuses the clinician on the independent variables most likely affecting Qcirculatory. For instance, if the operating point is cardiac limited (Figure 6) we see that changes in PMSF and RVR play no role, while changes in cardiac characteristics (e.g., Rcardiac) mediate Qcirculatory. Of course, this depends on how close the operating point is to the PRA at which the cardiac function curve flattens out, but this is, nevertheless, a reasonable clinical heuristic. Jozwiak and colleagues studied 18 ARDS patients with elevated right ventricular-to-left ventricular end-diastolic areas (RVEDA/LVEDA), but without ACP (Jozwiak et al., 2013). Prior to prone position, the change in cardiac output in response to a passive leg raise was evaluated. By the model above, ‘cardiac limitation’ is detected when a patient is preload unresponsive. In this state, only improved cardiac function during pronation (i.e., reduced Rcardiac) increases Qcirculatory; changes in PMSF and RVR shift the operating point along the x-axis, but not the y-axis. In other words, PRA changes but not blood flow. Jozwiak and colleagues found that in ‘cardiac limited’ patients, prone position significantly reduced pulmonary vascular resistance and the RVEDA/LVEDA which should diminish Rcardiac and improve Qcirculatory. However, these patients were also found to have depressed left ventricular ejection fraction. Furthermore, in the face of prone position, systemic afterload increased; total Rcardiac, therefore, did not improve.
When patients are not ‘cardiac limited,’ the operating point may be either ‘unlimited’ or ‘venous limited.’ In the study of Jozwiak and colleagues, imaging of the great veins was not reported, but those patients who were preload responsive were unlikely to have great vein collapse (i.e., venous ‘waterfall’) given that their average, baseline PRA was relatively high (i.e., 15 mmHg) with increased RVEDA/LVEDA ratios. Thus, based on equation 11 above, the change in Qcirculatory was probably subject to all of: PMSF, PPC, Rcardiac and RVR. Given what we know from Lai and colleagues, prone position likely increased PMSF; PPC may have increased less than the rise in PPL because of reduced pericardial restraint and Rcardiac fell due to diminished pulmonary vascular resistance. Each of these effects raise Qcirculatory, presumably offsetting heightened RVR with prone (Figure 10).
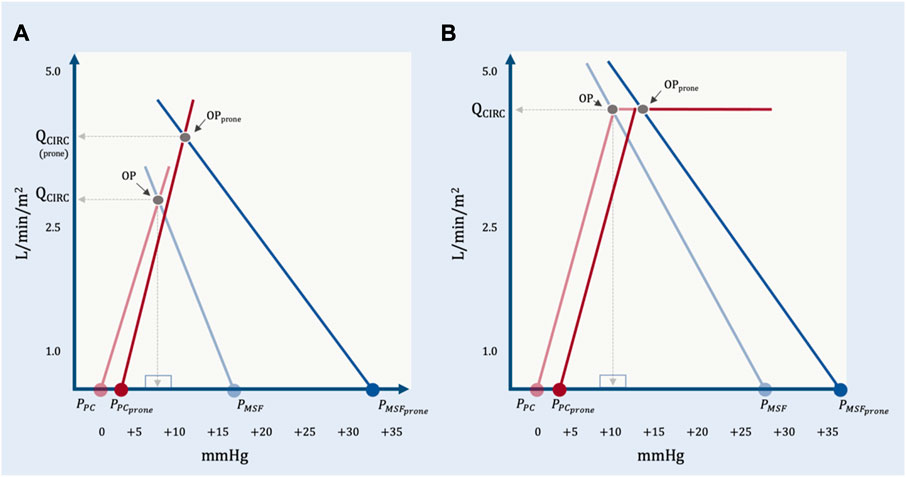
FIGURE 10. The geometrical model applied to representative data from Lai et al. (A) The effect of prone position on a preload responsive patient. At baseline, PPC is estimated by assuming a mean airway pressure of 15 mmHg, an ECW/ERS ratio of 0.2 and a pleural pressure (PPL) at functional residual capacity of—2.5 mmHg. With prone position, the PMSF rises much more than PPC. There is an increase in RVR and an assumed decrease in Rcardiac due to reduced pulmonary vascular resistance. The operating point with prone position (OPprone) leads to an increase in total blood flow (QCIRC) and increased right atrial pressure (PRA). By this model, PRA does not determine QCIRC; both PRA and QCIRC are determined by PMSF, PPC, Rcardiac and RVR. (B) Prone position in a preload unresponsive patient at baseline. PPC in prone is estimated by assuming a mean airway pressure of 15 mmHg, and ECW/ERS ratio of 0.5 and a PPL at functional residual capacity of—2.5 mmHg. With cardiac limitation, only a significant change in Rcardiac would increase QCIRC.
It is also possible for preload responsive patients to be ‘venous limited’ as described by equation 13 above. When the operating point lies on the flat portion of the venous return curve (i.e., below PCRIT) then Rcardiac ceases to affect Qcirculatory. Said another way, blood flow is determined solely by peripheral venous factors. When ‘venous limited’, volume status is likely a crucial determinant of the hemodynamic response to prone position based on the model of Takata and Robotham described above (Takata et al., 1990). A zone 3 abdomen might have a stable or enhanced PMSF relative to PCRIT and blunt any increase in RVR (i.e., stable or increased Qcirculatory), while a zone 2 abdomen would diminish PMSF relative to PCRIT and favour elevated RVR (i.e., stable or reduced Qcirculatory). There is little data on ‘venous limited’ ARDS patients being placed in prone. In the study by Lai and colleagues, there were four ‘preload responsive’ patients who had no change (n = 3) or a decrease (n = 1) in Qciculatory when placed in prone position. These patients may have been venous limited, but this data was not collected. Given that at low trans-mural pressure, the great veins are very compliant (Bodson and Vieillard-Baron, 2012), generation of a hemodynamically-significant Starling resistor, i.e., ‘venous limitation,’ should lead to great vein collapse throughout most of the respiratory cycle. In a patient passive with the ventilator, collapse is an inspiratory event for the SVC and expiatory event for the IVC. Collecting this data with ultrasound before and after pronation could help delineate this hemodynamic phenotype.
Finally, it is possible to be both venous and cardiac limited simultaneously, in other words, the operating point is on both the flat portion of the venous return and cardiac function curves concurrently. This might happen in states of high PCRIT (e.g., high PEEP, high subdiaphragmatic pressure) coupled with depressed cardiac function. In the setting of ARDS, this could be a syndrome of alveolar over-distension (Jardin and Vieillard-Baron, 2003). Prone position in such a patient might reduce Qcirculatory, especially if the patient is hypovolemic. Managing this hemodynamic phenotype might involve PEEP titration to reduce PCRIT and enhance cardiac function as this could move the operating point onto steep portions of the venous return and cardiac function curves.
At equilibrium, the intersection of venous return and cardiac function generates the hemodynamic operating point. The operating point and both of its coordinates (i.e., PRA and Qcirculatory) are dependent variables. The independent variables of the system are the PMSF, resistance to venous return, cardiac function and the pressure surrounding the right atrium. These are not new principles; however, clinical physiology can be muddied in terms of how dependent and independent variables are discussed. A simplified geometrical model was presented to clarify the mechanisms of blood flow at equilibrium founded on Guyton’s model of the circulation; this focuses the clinician on how interventions in the ICU (e.g., prone position) might affect hemodynamics. Recent mechanistic investigations into the circulatory consequences of prone position have been reported. These findings were incorporated into the simplified geometrical model with emphasis on the link between cardiac and respiratory physiologies. The pericardial pressure is one nexus binding the heart and the lungs; so too are changes in cardiac function from pulmonary vascular recruitment. Measuring ‘preload responsiveness’ locates the system’s operating point; this helps predict the hemodynamic response to any intervention in the ICU, including the decision to prone a patient with ARDS.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
The author confirms being the sole contributor of this work and has approved it for publication.
Pietro Verrecchia for review of Figures 3 and 4.
J-ESK is the cofounder and Chief Medical Officer of Flosonics Medical.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Beard, D. A., and Feigl, E. O. (2011). Understanding Guyton's venous return curves. Am. J. Physiol. Heart Circ. Physiol. 301 (3), H629–H633. doi:10.1152/ajpheart.00228.2011
Berger, D., Moller, P. W., and Takala, J. (2019). Reply to "Is the Guytonian framework justified in explaining heart lung interactions?" and "Venous return, mean systemic pressure and getting the right answer for the wrong reason. Ann. Transl. Med. 7 (8), 186. doi:10.21037/atm.2019.04.50
Berger, D., Moller, P. W., Weber, A., Bloch, A., Bloechlinger, S., Haenggi, M., et al. (2016). Effect of PEEP, blood volume, and inspiratory hold maneuvers on venous return. Am. J. physiology-heart circulatory physiology 311 (3), H794–H806. doi:10.1152/ajpheart.00931.2015
Berger, D., and Takala, J. (2018). Determinants of systemic venous return and the impact of positive pressure ventilation. Ann. Transl. Med. 6 (18), 350. doi:10.21037/atm.2018.05.27
Berlin, D. A., and Bakker, J. (2015). Starling curves and central venous pressure. Crit. Care 19 (1), 55. doi:10.1186/s13054-015-0776-1
Bodson, L., and Vieillard-Baron, A. (2012). Respiratory variation in inferior vena cava diameter: Surrogate of central venous pressure or parameter of fluid responsiveness? Let the physiology reply. Crit. Care 16 (6), 181. doi:10.1186/cc11824
Boesing, C., Graf, P. T., Schmitt, F., Thiel, M., Pelosi, P., Rocco, P. R. M., et al. (2022). Effects of different positive end-expiratory pressure titration strategies during prone positioning in patients with acute respiratory distress syndrome: A prospective interventional study. Crit. Care 26 (1), 82. doi:10.1186/s13054-022-03956-8
Bone, R. C. (1993). The ARDS lung. New insights from computed tomography. Jama 269 (16), 2134–2135. doi:10.1001/jama.269.16.2134
Brengelmann, G. L. (2003). A critical analysis of the view that right atrial pressure determines venous return. J. Appl. Physiol. (1985) 94 (3), 849–859. doi:10.1152/japplphysiol.00868.2002
Brengelmann, G. L. (2019). Venous return and the physical connection between distribution of segmental pressures and volumes. Am. J. Physiol. Heart Circ. Physiol. 317 (5), H939–h953. doi:10.1152/ajpheart.00381.2019
Bressack, M. A., and Raffin, T. A. (1987). Importance of venous return, venous resistance, and mean circulatory pressure in the physiology and management of shock. Chest 92 (5), 906–912. doi:10.1378/chest.92.5.906
Brienza, N., Ayuse, T., O'Donnell, C. P., Permutt, S., and Robotham, J. L. (1995). Regional control of venous return: Liver blood flow. Am. J. Respir. Crit. care Med. 152 (2), 511–518. doi:10.1164/ajrccm.152.2.7633700
Broccard, A. F. (2012). Cardiopulmonary interactions and volume status assessment. J. Clin. Monit. Comput. 26 (5), 383–391. doi:10.1007/s10877-012-9387-4
Broccard, A. F., Hotchkiss, J. R., Kuwayama, N., Olson, D. A., Jamal, S., Wangensteen, D. O., et al. (1998). Consequences of vascular flow on lung injury induced by mechanical ventilation. Am. J. Respir. Crit. care Med. 157 (6), 1935–1942. doi:10.1164/ajrccm.157.6.9612006
Cabrera, M. R., Nakamura, G. E., Montague, D. A., and Cole, R. P. (1989). Effect of airway pressure on pericardial pressure. Am. Rev. Respir. Dis. 140 (3), 659–667. doi:10.1164/ajrccm/140.3.659
Caldini, P., Permutt, S., Waddell, J. A., and Riley, R. L. (1974). Effect of epinephrine on pressure, flow, and volume relationships in the systemic circulation of dogs. Circulation Res. 34 (5), 606–623. doi:10.1161/01.res.34.5.606
Chiumello, D., Cressoni, M., Racagni, M., Landi, L., Li Bassi, G., Polli, F., et al. (2006). Effects of thoraco-pelvic supports during prone position in patients with acute lung injury/acute respiratory distress syndrome: A physiological study. Crit. Care 10 (3), R87. doi:10.1186/cc4933
Cressoni, M., Cadringher, P., Chiurazzi, C., Amini, M., Gallazzi, E., Marino, A., et al. (2014). Lung inhomogeneity in patients with acute respiratory distress syndrome. Am. J. Respir. Crit. care Med. 189 (2), 149–158. doi:10.1164/rccm.201308-1567OC
Cressoni, M., Chiurazzi, C., Gotti, M., Amini, M., Brioni, M., Algieri, I., et al. (2015). Lung inhomogeneities and time course of ventilator-induced mechanical injuries. Anesthesiology 123 (3), 618–627. doi:10.1097/ALN.0000000000000727
Decramer, M., De Troyer, A., Kelly, S., Zocchi, L., and Macklem, P. T. (1984). Regional differences in abdominal pressure swings in dogs. J. Appl. Physiol. Respir. Environ. Exerc Physiol. 57 (6), 1682–1687. doi:10.1152/jappl.1984.57.6.1682
Edgcombe, H., Carter, K., and Yarrow, S. (2008). Anaesthesia in the prone position. Br. J. Anaesth. 100 (2), 165–183. doi:10.1093/bja/aem380
Feihl, F., and Broccard, A. F. (2009a). Interactions between respiration and systemic hemodynamics. Part I: Basic concepts. Intensive Care Med. 35 (1), 45–54. doi:10.1007/s00134-008-1297-z
Feihl, F., and Broccard, A. F. (2009b). Interactions between respiration and systemic hemodynamics. Part II: Practical implications in critical care. Intensive Care Med. 35 (2), 198–205. doi:10.1007/s00134-008-1298-y
Fessler, H. E., Brower, R. G., Wise, R. A., and Permutt, S. (1992). Effects of positive end-expiratory pressure on the canine venous return curve. Am. Rev. Respir. Dis. 146 (1), 4–10. doi:10.1164/ajrccm/146.1.4
Fessler, H. E. (1995). Effects of CPAP on venous return. J. Sleep. Res. 4 (S1), 44–49. doi:10.1111/j.1365-2869.1995.tb00185.x
Fessler, H. E. (1997). Heart-lung interactions: Applications in the critically ill. Eur. Respir. J. 10 (1), 226–237. doi:10.1183/09031936.97.10010226
Gattinoni, L., Chiumello, D., Carlesso, E., and Valenza, F. (2004). Bench-to-bedside review: Chest wall elastance in acute lung injury/acute respiratory distress syndrome patients. Crit. Care 8 (5), 350–355. doi:10.1186/cc2854
Gattinoni, L., and Quintel, M. (2016). How ARDS should be treated. Crit. Care 20, 86. doi:10.1186/s13054-016-1268-7
Gattinoni, L., Taccone, P., Carlesso, E., and Marini, J. J. (2013). Prone position in acute respiratory distress syndrome. Rationale, indications, and limits. Am. J. Respir. Crit. care Med. 188 (11), 1286–1293. doi:10.1164/rccm.201308-1532CI
Gelman, S. (2008). Venous function and central venous pressure: A physiologic story. Anesthesiology 108 (4), 735–748. doi:10.1097/ALN.0b013e3181672607
Green, J. F. (1977). Mechanism of action of isoproterenol on venous return. Am. J. Physiol. 232 (2), H152–H156. doi:10.1152/ajpheart.1977.232.2.H152
Guérin, C., Albert, R. K., Beitler, J., Gattinoni, L., Jaber, S., Marini, J. J., et al. (2020). Prone position in ARDS patients: Why, when, how and for whom. Intensive Care Med. 46 (12), 2385–2396. doi:10.1007/s00134-020-06306-w
Guérin, C., and Matthay, M. A. (2016). Acute cor pulmonale and the acute respiratory distress syndrome. Intensive Care Med. 42 (5), 934–936. doi:10.1007/s00134-015-4197-z
Guérin, C., Reignier, J., Richard, J. C., Beuret, P., Gacouin, A., Boulain, T., et al. (2013). Prone positioning in severe acute respiratory distress syndrome. N. Engl. J. Med. 368 (23), 2159–2168. doi:10.1056/NEJMoa1214103
Guyton, A. C. (1955). Determination of cardiac output by equating venous return curves with cardiac response curves. Physiol. Rev. 35 (1), 123–129. doi:10.1152/physrev.1955.35.1.123
Guyton, A. C., Lindsey, A. W., Abernathy, B., and Richardson, T. (1957). Venous return at various right atrial pressures and the normal venous return curve. Am. J. Physiol. 189 (3), 609–615. doi:10.1152/ajplegacy.1957.189.3.609
Guyton, A. C., Lindsey, A. W., and Kaufmann, B. N. (1955). Effect of mean circulatory filling pressure and other peripheral circulatory factors on cardiac output. Am. J. Physiol. 180 (3), 463–468. doi:10.1152/ajplegacy.1955.180.3.463
Hamilton, D. R., Dani, R. S., Semlacher, R. A., Smith, E. R., Kieser, T. M., and Tyberg, J. V. (1994). Right atrial and right ventricular transmural pressures in dogs and humans. Effects of the pericardium. Circulation 90 (5), 2492–2500. doi:10.1161/01.cir.90.5.2492
Henderson, A. C., Sá, R. C., Theilmann, R. J., Buxton, R. B., Prisk, G. K., and Hopkins, S. R. (2013). The gravitational distribution of ventilation-perfusion ratio is more uniform in prone than supine posture in the normal human lung. J. Appl. Physiol. (1985) 115 (3), 313–324. doi:10.1152/japplphysiol.01531.2012
Hering, R., Vorwerk, R., Wrigge, H., Zinserling, J., Schröder, S., von Spiegel, T., et al. (2002). Prone positioning, systemic hemodynamics, hepatic indocyanine green kinetics, and gastric intramucosal energy balance in patients with acute lung injury. Intensive Care Med. 28 (1), 53–58. doi:10.1007/s00134-001-1166-5
Hering, R., Wrigge, H., Vorwerk, R., Brensing, K. A., Schröder, S., Zinserling, J., et al. (2001). The effects of prone positioning on intraabdominal pressure and cardiovascular and renal function in patients with acute lung injury. Anesth. analgesia 92 (5), 1226–1231. doi:10.1097/00000539-200105000-00027
Huberfeld, S. I., Genovese, J., Tarasiuk, A., and Scharf, S. M. (1995). Effect of CPAP on pericardial pressure and respiratory system mechanics in pigs. Am. J. Respir. Crit. care Med. 152 (1), 142–147. doi:10.1164/ajrccm.152.1.7599813
Jacobsohn, E., Chorn, R., and O'Connor, M. (1997). The role of the vasculature in regulating venous return and cardiac output: Historical and graphical approach. Can. J. Anaesth. 44 (8), 849–867. doi:10.1007/BF03013162
Jardin, F., and Vieillard-Baron, A. (2003). Right ventricular function and positive pressure ventilation in clinical practice: From hemodynamic subsets to respirator settings. Intensive Care Med. 29 (9), 1426–1434. doi:10.1007/s00134-003-1873-1
Jellinek, H., Krenn, H., Oczenski, W., Veit, F., Schwarz, S., and Fitzgerald, R. D. (2000). Influence of positive airway pressure on the pressure gradient for venous return in humans. J. Appl. Physiol. (1985) 88 (3), 926–932. doi:10.1152/jappl.2000.88.3.926
Jozwiak, M., Teboul, J. L., Anguel, N., Persichini, R., Silva, S., Chemla, D., et al. (2013). Beneficial hemodynamic effects of prone positioning in patients with acute respiratory distress syndrome. Am. J. Respir. Crit. care Med. 188 (12), 1428–1433. doi:10.1164/rccm.201303-0593OC
Kenny, J. S. (2021). Letter to the editor: The venous circulation actively alters flow: A brief evolutionary perspective. Am. J. Physiol. Heart Circ. Physiol. 320 (1), H469–h470. doi:10.1152/ajpheart.00862.2020
Lai, C., Adda, I., Teboul, J. L., Persichini, R., Gavelli, F., Guérin, L., et al. (2021). Effects of prone positioning on venous return in patients with acute respiratory distress syndrome. Crit. Care Med. 49 (5), 781–789. doi:10.1097/CCM.0000000000004849
Lai, C., Monnet, X., and Teboul, J. L. (2023). Hemodynamic implications of prone positioning in patients with ARDS. Crit. Care 27 (1), 98. doi:10.1186/s13054-023-04369-x
Lansdorp, B., Hofhuizen, C., van Lavieren, M., van Swieten, H., Lemson, J., van Putten, M. J., et al. (2014). Mechanical ventilation-induced intrathoracic pressure distribution and heart-lung interactions*. Crit. Care Med. 42 (9), 1983–1990. doi:10.1097/CCM.0000000000000345
Maas, J. J., Geerts, B. F., van den Berg, P. C., Pinsky, M. R., and Jansen, J. R. (2009). Assessment of venous return curve and mean systemic filling pressure in postoperative cardiac surgery patients. Crit. Care Med. 37 (3), 912–918. doi:10.1097/CCM.0b013e3181961481
Maas, J. J., Pinsky, M. R., Geerts, B. F., de Wilde, R. B., and Jansen, J. R. (2012). Estimation of mean systemic filling pressure in postoperative cardiac surgery patients with three methods. Intensive Care Med. 38 (9), 1452–1460. doi:10.1007/s00134-012-2586-0
Magder, S. (2012). Bench-to-bedside review: An approach to hemodynamic monitoring--Guyton at the bedside. Crit. Care 16 (5), 236. doi:10.1186/cc11395
Magder, S. (2004). Clinical usefulness of respiratory variations in arterial pressure. Am. J. Respir. Crit. care Med. 169 (2), 151–155. doi:10.1164/rccm.200211-1360CC
Magder, S. (2016). Volume and its relationship to cardiac output and venous return. Crit. Care 20 (1), 271. doi:10.1186/s13054-016-1438-7
Marini, J. J., Culver, B. H., and Butler, J. (1981). Effect of positive end-expiratory pressure on canine ventricular function curves. J. Appl. Physiol. Respir. Environ. Exerc Physiol. 51 (6), 1367–1374. doi:10.1152/jappl.1981.51.6.1367
Marini, J. J., and Gattinoni, L. (2021). Improving lung compliance by external compression of the chest wall. Crit. Care 25 (1), 264. doi:10.1186/s13054-021-03700-8
Marini, J. J., Hotchkiss, J. R., and Broccard, A. F. (2003). Bench-to-bedside review: Microvascular and airspace linkage in ventilator-induced lung injury. Crit. Care 7 (6), 435–444. doi:10.1186/cc2392
Matejovic, M., Rokyta, R., Radermacher, P., Krouzecky, A., Sramek, V., and Novak, I. (2002). Effect of prone position on hepato-splanchnic hemodynamics in acute lung injury. Intensive Care Med. 28 (12), 1750–1755. doi:10.1007/s00134-002-1524-y
Mead, J., Takishima, T., and Leith, D. (1970). Stress distribution in lungs: A model of pulmonary elasticity. J. Appl. Physiol. 28 (5), 596–608. doi:10.1152/jappl.1970.28.5.596
Mekontso Dessap, A., Boissier, F., Charron, C., Bégot, E., Repessé, X., Legras, A., et al. (2016). Acute cor pulmonale during protective ventilation for acute respiratory distress syndrome: Prevalence, predictors, and clinical impact. Intensive Care Med. 42 (5), 862–870. doi:10.1007/s00134-015-4141-2
Moller, P. W., and Berger, D. C. (2023). Commentary: Feasibility to estimate mean systemic filling pressure with inspiratory holds at the bedside. Front. Physiology 14, 1135769. doi:10.3389/fphys.2023.1135769
Moller, P. W., and Parkin, W. G. (2022). Correct calculation of the mean systemic pressure analogue. Intensive Care Med. 48 (11), 1679–1680. doi:10.1007/s00134-022-06862-3
Moller, P. W., Winkler, B., Hurni, S., Heinisch, P. P., Bloch, A., Sondergaard, S., et al. (2017). Right atrial pressure and venous return during cardiopulmonary bypass. Am. J. Physiol. Heart Circ. Physiol. 313 (2), H408–h420. doi:10.1152/ajpheart.00081.2017
Papazian, L., Aubron, C., Brochard, L., Chiche, J. D., Combes, A., Dreyfuss, D., et al. (2019). Formal guidelines: Management of acute respiratory distress syndrome. Ann. Intensive Care 9 (1), 69. doi:10.1186/s13613-019-0540-9
Parkin, W. G., and Leaning, M. S. (2008). Therapeutic control of the circulation. J. Clin. Monit. Comput. 22 (6), 391–400. doi:10.1007/s10877-008-9147-7
Pelosi, P., Tubiolo, D., Mascheroni, D., Vicardi, P., Crotti, S., Valenza, F., et al. (1998). Effects of the prone position on respiratory mechanics and gas exchange during acute lung injury. Am. J. Respir. Crit. care Med. 157 (2), 387–393. doi:10.1164/ajrccm.157.2.97-04023
Permutt, S., and Riley, R. L. (1963). Hemodynamics of collapsible vessels with tone: The vascular waterfall. J. Appl. Physiol. 18, 924–932. doi:10.1152/jappl.1963.18.5.924
Persichini, R., Lai, C., Teboul, J. L., Adda, I., Guérin, L., and Monnet, X. (2022). Venous return and mean systemic filling pressure: Physiology and clinical applications. Crit. Care 26 (1), 150. doi:10.1186/s13054-022-04024-x
Pinsky, M. R. (2021). Cardiovascular effects of prone positioning in acute respiratory distress syndrome patients: The circulation does not take it lying down. Crit. Care Med. 49 (5), 869–873. doi:10.1097/CCM.0000000000004858
Pinsky, M. R. (1984). Instantaneous venous return curves in an intact canine preparation. J. Appl. Physiol. Respir. Environ. Exerc Physiol. 56 (3), 765–771. doi:10.1152/jappl.1984.56.3.765
Repessé, X., Charron, C., and Vieillard-Baron, A. (2016). Acute respiratory distress syndrome: The heart side of the moon. Curr. Opin. Crit. Care 22 (1), 38–44. doi:10.1097/MCC.0000000000000267
Rothe, C. F. (1993). Mean circulatory filling pressure: Its meaning and measurement. J. Appl. Physiol. (1985) 74 (2), 499–509. doi:10.1152/jappl.1993.74.2.499
Rothe, C. F. (1986). Physiology of venous return. An unappreciated boost to the heart. Arch. Intern Med. 146 (5), 977–982. doi:10.1001/archinte.146.5.977
Ruste, M., Bitker, L., Yonis, H., Riad, Z., Louf-Durier, A., Lissonde, F., et al. (2018). Hemodynamic effects of extended prone position sessions in ARDS. Ann. Intensive Care 8 (1), 120. doi:10.1186/s13613-018-0464-9
Scharf, S. M., Caldini, P., and Ingram, R. H. (1977). Cardiovascular effects of increasing airway pressure in the dog. Am. J. Physiol. 232 (1), H35–H43. doi:10.1152/ajpheart.1977.232.1.H35
Scharf, S. M., and Ingram, R. H. (1977). Influence of abdominal pressure and sympathetic vasoconstriction on the cardiovascular response to positive end-expiratory pressure. Am. Rev. Respir. Dis. 116 (4), 661–670. doi:10.1164/arrd.1977.116.4.661
Sylvester, J. T., Goldberg, H. S., and Permutt, S. (1983). The role of the vasculature in the regulation of cardiac output. Clin. Chest Med. 4 (2), 333–348. doi:10.1016/s0733-8651(18)30629-5
Takata, M., and Robotham, J. L. (1992). Effects of inspiratory diaphragmatic descent on inferior vena caval venous return. J. Appl. Physiol. (1985) 72 (2), 597–607. doi:10.1152/jappl.1992.72.2.597
Takata, M., Wise, R. A., and Robotham, J. L. (1990). Effects of abdominal pressure on venous return: Abdominal vascular zone conditions. J. Appl. Physiol. (1985) 69 (6), 1961–1972. doi:10.1152/jappl.1990.69.6.1961
Tyberg, J. V. (2002). How changes in venous capacitance modulate cardiac output. Pflugers Arch. 445 (1), 10–17. doi:10.1007/s00424-002-0922-x
Vieillard-Baron, A., Charron, C., Caille, V., Belliard, G., Page, B., and Jardin, F. (2007). Prone positioning unloads the right ventricle in severe ARDS. Chest 132 (5), 1440–1446. doi:10.1378/chest.07-1013
Werner-Moller, P., Berger, D., and Takala, J. (2020). Letter to the Editor: Venous return and the physical connection between distribution of segmental pressures and volumes. Am. J. Physiol. Heart Circ. Physiol. 318 (1), H203–h204. doi:10.1152/ajpheart.00698.2019
Keywords: heart-lung interactions, hemodynamics, prone position, acute respiratory distress syndrome, venous return, fluid responsiveness
Citation: Kenny J-ES (2023) A framework for heart-lung interaction and its application to prone position in the acute respiratory distress syndrome. Front. Physiol. 14:1230654. doi: 10.3389/fphys.2023.1230654
Received: 29 May 2023; Accepted: 24 July 2023;
Published: 07 August 2023.
Edited by:
Antoine Vieillard-Baron, Assistance Publique Hopitaux De Paris, FranceReviewed by:
Arnoldo Santos, University Hospital Fundación Jiménez Díaz, SpainCopyright © 2023 Kenny. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jon-Emile S. Kenny, am9uLWVtaWxlQGhlYXJ0LWx1bmcub3Jn
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.