A modified formula using energy system contributions to calculate pure maximal rate of lactate accumulation during a maximal sprint cycling test

Purpose: This study aimed at comparing previous calculating formulas of maximal lactate accumulation rate (^ν_La.max) and a modified formula of pure ^ν_La.max (P^ν_La.max) during a 15-s all-out sprint cycling test (ASCT) to analyze their relationships.

Methods: Thirty male national-level track cyclists participated in this study (n = 30) and performed a 15-s ASCT. The anaerobic power output (W_peak and W_mean), oxygen uptake, and blood lactate concentrations (La⁻) were measured. These parameters were used for different calculations of ^ν_La.max and three energy contributions (phosphagen, W_PCr; glycolytic, W_Gly; and oxidative, W_Oxi). The P^ν_La.max calculation considered delta La⁻, time until W_peak (t_PCr−peak), and the time contributed by the oxidative system (t_Oxi). Other ^ν_La.max levels without t_Oxi were calculated using decreasing time by 3.5% from W_peak (t_{PCr −3.5%}) and t_PCr−peak.

Results: The absolute and relative W_PCr were higher than W_Gly and W_Oxi (p < 0.0001, respectively), and the absolute and relative W_Gly were significantly higher than W_Oxi (p < 0.0001, respectively); ^ν_La.max (t_{PCr −3.5%}) was significantly higher than P^ν_La.max and ^ν_La.max (t_PCr−peak), while ^ν_La.max (t_PCr−peak) was lower than P^ν_La.max (p < 0.0001, respectively). P^ν_La.max and ^ν_La.max (t_PCr−peak) were highly correlated (r = 0.99; R² = 0.98). This correlation was higher than the relationship between P^ν_La.max and ^ν_La.max (t_{PCr −3.5%}) (r = 0.87; R² = 0.77). ^ν_La.max (t_PCr−peak), P^ν_La.max, and ^ν_La.max (t_{PCr −3.5%}) were found to correlate with absolute W_mean and W_Gly.

Conclusion: P^ν_La.max as a modified calculation of ^ν_La.max provides more detailed insights into the inter-individual differences in energy and glycolytic metabolism than ^ν_La.max (t_PCr−peak) and ^ν_La.max (t_{PCr −3.5%}). Because W_Oxi and W_PCr can differ remarkably between athletes, implementing their values in P^ν_La.max can establish more optimized individual profiling for elite track cyclists.

Introduction

Three human energy systems (phosphagen, glycolytic, and oxidative systems) are simultaneously used during different exercises (Beneke et al., 2002; Yang et al., 2020; Yang et al., 2022a; Yang et al., 2022b). However, their relative energy contribution, particularly the energy systems that are predominantly utilized at a given moment, depends critically on the exercise intensity and duration (Beneke et al., 2002; Yang et al., 2022b). Therefore, precise determinations of energetic contributions during specific sports are crucial for a better understanding of physiological responses to enhance exercise prescriptions (Julio et al., 2017; Franchini, 2020; Yang et al., 2022b).

Among various Olympic disciplines, there are sections such as football, handball, basketball, rugby, and track cycling (Hettinga et al., 2007; Wackerhage et al., 2022), in which maximal anaerobic power and capacity are essential to achieve a highly competitive performance. For instance, the anaerobic capacity of track cyclists is exploited during a 1,500-m Keirin race over approximately 90–120 s (Foster et al., 1993; Hettinga et al., 2007). A crucial factor that determines the winner of such races is particularly the final all-out sprint to the finish line (Fujii et al., 2018). Although a high aerobic performance is absolutely necessary, these athletes also require high anaerobic power (Hettinga et al., 2007; Fujii et al., 2018). The anaerobic performance of athletes (e.g., 100-m sprint) is proportional to their individual anaerobic energy capacity (Yang et al., 2020; Park et al., 2021; Yang et al., 2022b). The phosphagen system (adenosine triphosphate and phosphocreatine, ATP-PCr) ensures the highest metabolic power or energy flux rate, which is reflected by the rate of energy transfer per unit of time. Although the energy flux rate is very high, the general capacity is low because of limited substrate stores that lasts for only a few muscle contractions (Gastin, 2001; Robergs et al., 2004). The glycolytic system can re-synthesize ATP through the non-aerobic degradation of carbohydrates and supports the metabolic energy requirements during intense exercise. This system, when compared to the phosphagen system, is characterized by an intermediate energy flux rate and metabolic power because of the higher number of reactions and greater overall capacity from a large amount of stored carbohydrates (Gastin, 2001; Robergs et al., 2004; Franchini, 2023). In this regard, the Mader’s (1984) model proposed considering individual maximal glycolytic rates (^ν_La.max) to be utilized while determining the maximal glycolysis and power after an all-out sports-specific sprint test (Hauser et al., 2014; Quittmann et al., 2020; Quittmann et al., 2021; Wackerhage et al., 2022). Accordingly, athletes in sprint sports can maximally produce over 1.0 mmol lactate per liter per second (i.e., ≥1.0 mmol·L⁻¹·s⁻¹) (Wackerhage et al., 2022).

The formula of ^ν_La.max (Mader, 1984) is considered the delta lactate concentration (∆La⁻) between maximal blood La⁻ accumulation after exercising and resting blood La⁻ levels are divided by the difference between the total exercise time (t_exer) and phosphagen system–contributed time (t_PCr). Here, t_PCr is assumed as the period in which no La⁻ formation (“fictitiously”) takes place, beginning from the start of the maximal power output until it is reduced by 3.5% (the point of −3.5% from the peak watt, t_{PCr −3.5%}). Previous studies have used the t_{PCr −3.5%} definition without providing an in-depth explanation on why the reduced 3.5% time point of the maximal power output was determined as t_PCr (Hauser et al., 2014; Adam et al., 2015; Nitzsche et al., 2018; Quittmann et al., 2020; Quittmann et al., 2021). However, this assumption likely originates from the precision of power measurement of an early SRM cycle ergometer (Weber, 2003). Another t_PCr definition was determined as the time until peak watt (t_PCr−peak) during the ^ν_La.max test (Manunzio et al., 2016).

Indeed, the determination of ^ν_La.max via these calculations may further have imprecisions with the involvement of oxidative energy metabolism, also in short time frames of exercising, when it is not separately subtracted from the total energy demand. Interestingly, previous studies have reported that oxidative energy metabolism is not considered in the ^ν_La.max formula, which contributes to a total energy expenditure of approximately 10% during the 100-m sprint (Heck et al., 2003; Quittmann et al., 2020; Park et al., 2021).

Also, calculations of the Mader’s model include the oxidative contribution timespan and not subtracting the energy contribution of oxidative metabolism. When considering an approximate contribution of 10% during short sprints, a “pure” ^ν_La.max determination during the maximal anaerobic cycling test cannot be precisely calculated. To determine ^ν_La.max, we minimize the oxidative contribution and lactate elimination during the aftermath of the test; its duration should be limited between 10 and 15 s (Heck et al., 2003; Quittmann et al., 2020). In this context, the PCr-La⁻-O₂ method is yet another well-established methodology involving all three energy system contributions when calculating exercise-induced energy turnover (Beneke et al., 2004; de Moraes Bertuzzi et al., 2007; de Campos Mello et al., 2009; Hausen et al., 2017; Julio et al., 2017; Yang et al., 2018; Park et al., 2021; Yang et al., 2022b; Kaufmann et al., 2022). This method can easily be incorporated into the ^ν_La.max formula as the time ratio of relative oxidative contribution (%) and then be used to calculate an optimized ^ν_La.max (Beneke et al., 2004; de Moraes Bertuzzi et al., 2007; de Campos Mello et al., 2009; Campos et al., 2012; Hausen et al., 2017; Julio et al., 2017; Lopes-Silva et al., 2018; Yang et al., 2018; Franchini, 2020; Park et al., 2021; Yang et al., 2022b).

Therefore, this study compares three different ^ν_La.max calculations based on the differences in determining the phosphagen-contributed time and incorporation of the oxidative energy system: first, ^ν_La.max by using t_{PCr −3.5%}; second, ^ν_La.max by using t_PCr−peak determinations; and third, by subtracting the contribution of the oxidative energy metabolism during a 15-s maximal sprint cycling test. The latter is substituted with a modified pure ^ν_La.max (P^ν_La.max) formula using the analysis of the PCr-La⁻-O₂ method. Finally, the relationships among the different ^ν_La.max calculations, mean power output, and glycolytic energy contribution are analyzed.

Materials and methods

Participants

With an effect size of 0.32, an alpha error probability of 0.05, and statistical power of 0.95, the sample size was calculated using the G*Power software, version 3.1.9.4 (Heinrich Heine University, Düsseldorf, Germany). The effect size was considered based on previous studies (Hauser et al., 2014; Manunzio et al., 2016; Fujii et al., 2018; Quittmann et al., 2020; Quittmann et al., 2021). Considering a 10% dropout rate, 30 male national-level track cyclists were enrolled in this study. All participants were track cyclists (main discipline: Keirin) who train for 18–20 h per week. They have been enrolled in the Korean national championships over the last 8 years. The anthropometric parameters of these participants are age: 30 ± 6 years; height: 177.30 ± 6.21 cm; body mass: 85.11 ± 9.89; and body fat: 19.16% ± 4.78%. The participants had rested for 2 h after lunchtime and performed a 15-s all-out sprint cycling test (ASCT). They were instructed not to take any coffee, neuro stimulants, or medication immediately before the test. Alcohol and nicotine was not consumed at least 24 h before the experiment. The Institutional Review Board of CHA University approved this study (No. 1044308-202206-HR-032-02). Study protocols followed the ethical standards in the Declaration of Helsinki. All participants had signed an informed consent form.

Study procedure

All participants attended a single laboratory session. The test procedure was conducted and controlled in the same laboratory environment throughout testing (temperature: 23°C and relative humidity: 50%). The anthropometric parameters were measured with an eight-electrode segmental multi-frequency bioelectrical impedance analysis (20–100 kHz; InBody 270; InBody Co., Ltd., Seoul, Republic of Korea). Before the 15-s ASCT, the latest SRM ergometer (No. 2203, 04/2022, Schoberer Rad Messtechnik, GmbH, Jülich, Germany) was set up to fit each participant’s track bicycle position (i.e., crank length, saddle height, handle height, and saddle fore–aft position). An initial warm-up was performed for 10 min at 2 W·kg⁻¹. They further rested passively in the sitting position on the ergometer was for 5 min (Figure 1). The 15-s ASCT was performed according to the manufacturer’s guidelines in an isokinetic mode set to a cadence of 120 rpm (Manunzio et al., 2016) in the ninth gear and with a 9.1 kg flywheel. The start and end of the 15-s ASCT were verbally announced by countdown. These settings enabled a reduction in the pedal force in a linear fashion during the initial acceleration phase and achieving a target pedaling rate of 120 rpm after ∼4 s (Manunzio et al., 2016; Dunst et al., 2023). The participants performed the test in the sitting position on the ergometer. They were verbally encouraged by the investigator to generate the maximum possible power output. Afterward, the absolute and relative peak and mean power outputs in watt and W·kg⁻¹ were determined (W_peak and W_mean, respectively) (Hauser et al., 2014; Manunzio et al., 2016; Quittmann et al., 2020; Quittmann et al., 2021). Oxygen uptake (resting oxygen uptake, $\dot{\mathrm{V}}$O_2rest; average oxygen uptake during the 15-s ASCT, $\dot{\mathrm{V}}$O_2mean; highest oxygen uptake during the 15-s ASCT, $\dot{\mathrm{V}}$O_2peak; and fast component of excess oxygen consumption [EPOC_fast], off $\dot{\mathrm{V}}$O₂ kinetics) at 5-min rest, and during and after the 15-s ASCT (6 min) were measured using the breath-by-breath method with a portable gas analyzer (METAMAX 3B, Cortex Biophysik, Leipzig, Germany) that was placed on the back of the participants. The portable gas analyzer was calibrated with the calibration gas (15% O₂ and 5% CO₂; Cortex Biophysik, Leipzig, Germany), and the turbine volume transducer was calibrated using a 3-L syringe (Hans Rudolph, Kansas, United States). $\dot{\mathrm{V}}$O_2mean and $\dot{\mathrm{V}}$O_2peak were calculated as the average and highest values during the 15-s ASCT, respectively. Capillary blood was collected from the earlobe (20 μL) before and, in minute intervals (1st to 10th), after the 15-s ASCT to determine rest and maximal lactate concentrations (La_rest and La_max; the maximal value of La⁻ among the 10 values) using an enzymatic–amperometric sensor chip system (Biosen C-line; EKF diagnostics sales, GmbH, Barleben, Germany).

FIGURE 1

FIGURE 1. Study procedure. An initial warm-up was performed for 10 min at 2 W·kg⁻¹. A further passive rest for 5 min followed. A 15-s all-out sprint cycling test was performed in the isokinetic mode set to a cadence of 120 rpm. Participants performed the test in the sitting position on the ergometer. Oxygen uptake at 5-min rest, and during as well as up to 6 min after 15-s all-out sprint cycling test was measured. Capillary blood was collected from the earlobe (20 μL) before and in minutes' interval (1st to 10th) after the 15-s all-out sprint cycling test. $\dot{\mathrm{V}}$O₂, oxygen uptake.

Calculations of energetic contributions (PCr-La⁻-O₂ method)

Phosphagen (W_PCr), glycolytic (W_Gly), and oxidative (W_Oxi) contributions in kilojoules, and their percentages were calculated by measuring $\dot{\mathrm{V}}$O₂ and La⁻ (PCr-La⁻-O₂) before, during, and after the 15-s ASCT (Julio et al., 2017; Yang et al., 2018; Yang et al., 2022b; Kaufmann et al., 2022).

W_PCr was calculated using $\dot{\mathrm{V}}$O₂ after the 15-s ASCT and the fast component of excess post-exercise after the 15-s ASCT (Gastin, 2001; Beneke et al., 2004; Yang et al., 2022b). $\dot{\mathrm{V}}$O₂ kinetics after the 15-s ASCT was fitted by mono-exponential and bi-exponential models using the OriginPro 2021 software (OriginLab Corp, Northampton, United States). The slow component of the bi-exponential model was negligible. Thus, $\dot{\mathrm{V}}$O₂ data after the 15-s ASCT were fitted using a mono-exponential model, and W_PCr was obtained by calculating the integral of the exponential area (Beneke et al., 2004; Campos et al., 2012; Julio et al., 2017; Yang et al., 2018; Yang et al., 2022b; Kaufmann et al., 2022).

The W_Gly calculation was performed by determining La⁻ before and after the 15-s ASCT (La_rest and La_max), assuming that the production of 1 mmol·L⁻¹ was equivalent to 3 mL O₂·kg⁻¹ of body mass (di Prampero and Ferretti, 1999). The difference in La⁻ (∆La⁻) was determined by La⁻ after the 15-s ASCT minus La⁻ before the 15-s ASCT (Beneke et al., 2004; Campos et al., 2012; Yang et al., 2018; Yang et al., 2022b).

The W_Oxi contribution was calculated by subtracting $\dot{\mathrm{V}}$O_2rest from $\dot{\mathrm{V}}$O₂ during the 15-s ASCT by the trapezoidal method in which the area under the curve was divided into sections and the sum of the trapezoid was used to calculate the integral (de Campos Mello et al., 2009; Yang et al., 2022b). The $\dot{\mathrm{V}}$O_2rest value was determined in the sitting position on the cycle ergometer in the last 30 s of the 5-min phase used as a reference (di Prampero and Ferretti, 1999; Beneke et al., 2002; Beneke et al., 2004; Julio et al., 2017; Yang et al., 2018; Kaufmann et al., 2022; Yang et al., 2022b). A caloric quotient of 20.92 kJ was used in the three energy system calculations (Gastin, 2001). The total energy expenditure was determined as the sum of the three energy systems in kilojoules (W_PCr, W_Gly, and W_Oxi) (Campos et al., 2012). The relative contribution of each of the three energy systems was calculated in percentage and compared with the total energy expenditure.

Different formulas of ^ν_La.max calculations

^ν_La.max (t_{PCr −3.5%}) was calculated as ∆La⁻ between La_rest and La_max, which was divided by the difference between the total exercise time (t_Exer) and the −3.5% time point from the peak watt (t_{PCr −3.5%}) (Mader, 1984; Weber, 2003) (Eq. 1):

${}^{\mathit{v}}\mathbf{L}\mathbf{a}.\mathbf{max}\left({\mathbf{t}}_{\mathbf{P}\mathbf{C}\mathbf{r}-\mathbf{3.5}\%}\right)\left[\mathrm{m}\mathrm{m}\mathrm{o}\mathrm{l}·{\mathrm{L}}^{-1}·{\mathrm{s}}^{-1}\right]=\frac{{\mathbf{L}\mathbf{a}}_{\mathbf{max}}-{\mathbf{L}\mathbf{a}}_{\mathbf{r}\mathbf{e}\mathbf{s}\mathbf{t}}}{{\mathbf{t}}_{\mathbf{E}\mathbf{x}\mathbf{e}\mathbf{r}}-{\mathbf{t}}_{\mathbf{P}\mathbf{C}\mathbf{r}-\mathbf{3.5}\%}}.(1)$

Furthermore, only t_PCr was differently determined according to previous studies (Serresse et al., 1988; Beneke et al., 2002; Manunzio et al., 2016) (Eq. 2):

${}^{\mathit{v}}\mathbf{L}\mathbf{a}.\mathbf{max}\left({\mathbf{t}}_{\mathbf{P}\mathbf{C}\mathbf{r}-\mathbf{p}\mathbf{e}\mathbf{a}\mathbf{k}}\right)\left[\mathrm{m}\mathrm{m}\mathrm{o}\mathrm{l}·{\mathrm{L}}^{-1}·{\mathrm{s}}^{-1}\right]=\frac{{\mathbf{L}\mathbf{a}}_{\mathbf{max}}-{\mathbf{L}\mathbf{a}}_{\mathbf{r}\mathbf{e}\mathbf{s}\mathbf{t}}}{{\mathbf{t}}_{\mathbf{E}\mathbf{x}\mathbf{e}\mathbf{r}}-{\mathbf{t}}_{\mathbf{P}\mathbf{C}\mathbf{r}-\mathbf{p}\mathbf{e}\mathbf{a}\mathbf{k}}}.(2)$

The accuracy of the latest SRM cycle ergometer (power meter in the science system) is reported to be ± 0.5–1% according to the manufacturer and previous studies (Bouillod et al., 2017; Nimmerichter et al., 2017; Montalvo-Pérez et al., 2021). Therefore, a representation of t_PCr−peak was determined as the time until W_peak during the 15-s ASCT because energy was influenced by the ATP-PCr system until peak power during the initial seconds of a maximal short-term exercise (Serresse et al., 1988; Beneke et al., 2002).

A modified pure ^ν_La.max was calculated as ∆La⁻ divided by the difference between t_Exer and t_PCr−peak plus relative W_Oxi in percentage of the PCr-La⁻-O₂ method during the 15-s ASCT. This percentage was converted to time in seconds (t_Oxi) related to the total ASCT time (Eq. 3):

$\mathbf{P}{}^{\mathit{v}}\mathbf{L}\mathbf{a}.\mathbf{max}\left[\mathrm{m}\mathrm{m}\mathrm{o}\mathrm{l}·{\mathrm{L}}^{-1}·{\mathrm{s}}^{-1}\right]=\frac{{\mathbf{L}\mathbf{a}}_{\mathbf{max}}-{\mathbf{L}\mathbf{a}}_{\mathbf{r}\mathbf{e}\mathbf{s}\mathbf{t}}}{{\mathbf{t}}_{\mathbf{E}\mathbf{x}\mathbf{e}\mathbf{r}}-\left({\mathbf{t}}_{\mathbf{P}\mathbf{C}\mathbf{r}-\mathbf{p}\mathbf{e}\mathbf{a}\mathbf{k}}+{\mathbf{t}}_{\mathbf{O}\mathbf{x}\mathbf{i}}\right)}.(3)$

Statistical analyses

All collected data were analyzed using GraphPad Prism 9.4.1. (GraphPad Prism Software Inc., La Jolla, CA, United States). The data of collected parameters are presented as mean ± standard deviation (SD). The normal distribution of all data was performed using the Shapiro−Wilk test. The contributions of the three energy systems and different ^ν_La.max values were compared using a repeated-measures analysis of variance (ANOVA) with the Bonferroni post hoc test. The Mauchly’s sphericity test was used to determine whether the assumption of sphericity was being violated by the data. The Greenhouse−Geisser correction was required when necessary. A comparison between t_{PCr −3.5%} and t_PCr−peak was conducted using a paired t-test. The significance level was set at p < 0.05. The effect sizes (partial eta squared [$\left.{\eta }_p^2\right]$ and Cohen’s [d]) were calculated for the main effect. The thresholds for small, medium, and large effects were 0.01, 0.06, and 0.14 for partial eta squared [${\eta }_p^2$] and 0.2, 0.5, and 0.8 for Cohen’s [d], respectively (Fritz et al., 2012). The relationships were analyzed with a two-tailed Pearson’s correlation [^ν_La.max (t_{PCr −3.5%}) vs. P^ν_La.max, ^ν_La.max (t_PCr−peak) vs. P^ν_La.max, and W_mean and W_Gly vs. different ^ν_La.max]. The Bland–Altman plots were determined to analyze the bias, difference, average, and 95% limit agreements among the ^ν_La.max (t_{PCr −3.5%}), the ^ν_La.max (t_PCr−peak), and the P^ν_La.max (Bland and Altman, 1995).

Results

Energetic contributions during 15-s ASCT

The repeated-measures ANOVA indicated significant differences in energetic contributions in kilojoules and their percentages (p < 0.0001, effect size [${\eta }_p^2$]: 0.90; p < 0.0001, [${\eta }_p^2$]: 0.98, respectively). The value of W_PCr was significantly higher than that of W_Gly and W_Oxi in kilojoules as well as in percentage (p < 0.0001, [d]: 1.45, 2.96, and 5.13 in kJ; p < 0.0001, [d]: 3.53, 7.72, and 4.37 in percentage, respectively) (Figure 2A).

FIGURE 2

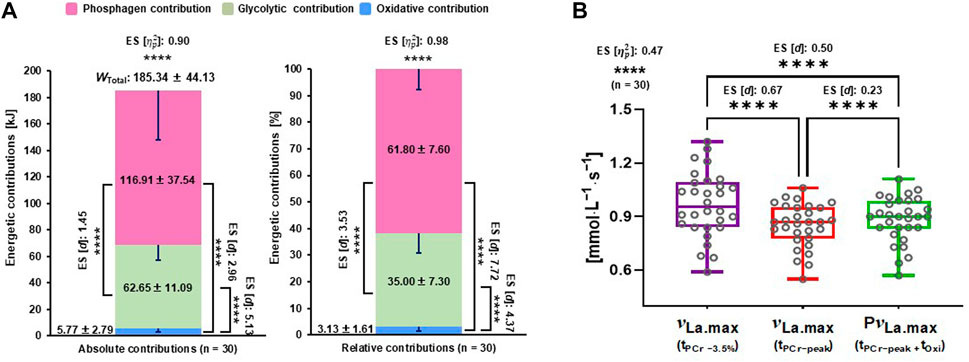
FIGURE 2. Energetic contributions and different calculations of ^ν_La.max. (A) Comparisons of three energy contributions in kilojoules and percentage, and (B) comparisons of three different ^ν_La.max calculations. ES, effect sizes; ^ν_La.max, maximal rate of lactate accumulation; P^ν_La.max, pure maximal rate of lactate accumulation; t_Oxi, time of oxidative energy system contribution; t_PCr−peak, phosphagen energy system–contributed time until the peak power output; t_{PCr −3.5%}, phosphagen energy system contributed −3.5% time point from the peak power output; W_Total, total energy demand. Significant difference; ****p < .0001.

Physiological parameters and relationships between different calculations of ^ν_La.max

The time duration (s) of the ^ν_La.max-related t_{PCr −3.5%} was significantly higher than t_PCr−peak (p < 0.0001, [d]: 1.42; Table 1). The data of the other physiological parameters of anaerobic performance are presented as mean ± SD in Table 1.

TABLE 1

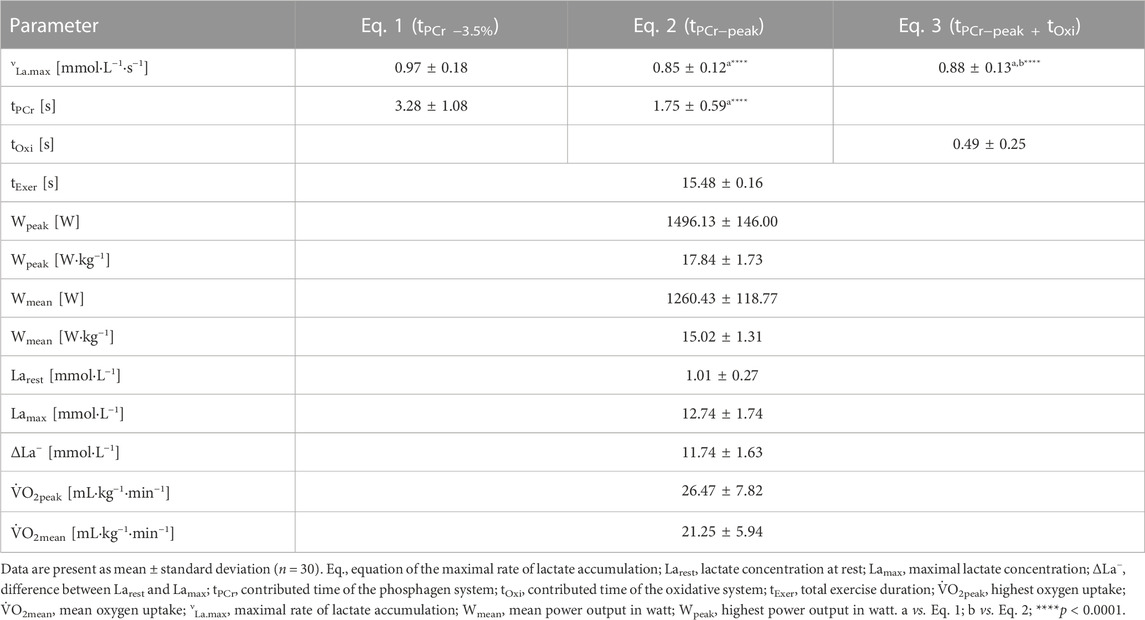
TABLE 1. Anaerobic performances and physiological parameters during a 15-s all-out sprint cycling test.

The repeated-measures ANOVA showed significant differences of the three ^ν_La.max values (p < 0.0001, [${\eta }_p^2$]: 0.47). The level of ^ν_La.max (t_{PCr −3.5%}) was significantly higher than that of ^ν_La.max (t_PCr−peak) and P^ν_La.max (p < 0.0001, [d]: 0.67 and 0.50, respectively). A significantly lower value of ^ν_La.max (t_PCr−peak) than that of P^ν_La.max (p < 0.0001, [d]: 0.23) was observed (Table 1; Figure 2B).

A very strong correlation was found between P^ν_La.max and ^ν_La.max (t_PCr−peak) (r = 0.99; R² = 0.98; 95% confidence interval [CI]: 0.98–0.99; p < 0.0001) (Figure 3A). A further high positive correlation between P^ν_La.max and ^ν_La.max (t_{PCr −3.5%}) was observed (r = 0.87; R² = 0.77; 95% CI: 0.75–0.94; p < 0.0001) (Figure 3B). The Bland–Altman analysis showed that the bias between P^ν_La.max and ^ν_La.max (t_PCr−peak) calculations was 0.031 ± 0.017. Another bias between ^ν_La.max (t_{PCr −3.5%}) and P^ν_La.max calculations was 0.087 ± 0.092. P^ν_La.max and ^ν_La.max (t_PCr−peak) calculations indicated a smaller 95% limit of agreement (−0.002 to 0.066) followed by ^ν_La.max (t_{PCr −3.5%}) and P^ν_La.max (−0.095 to 0.269) (Figures 3C, D).

FIGURE 3

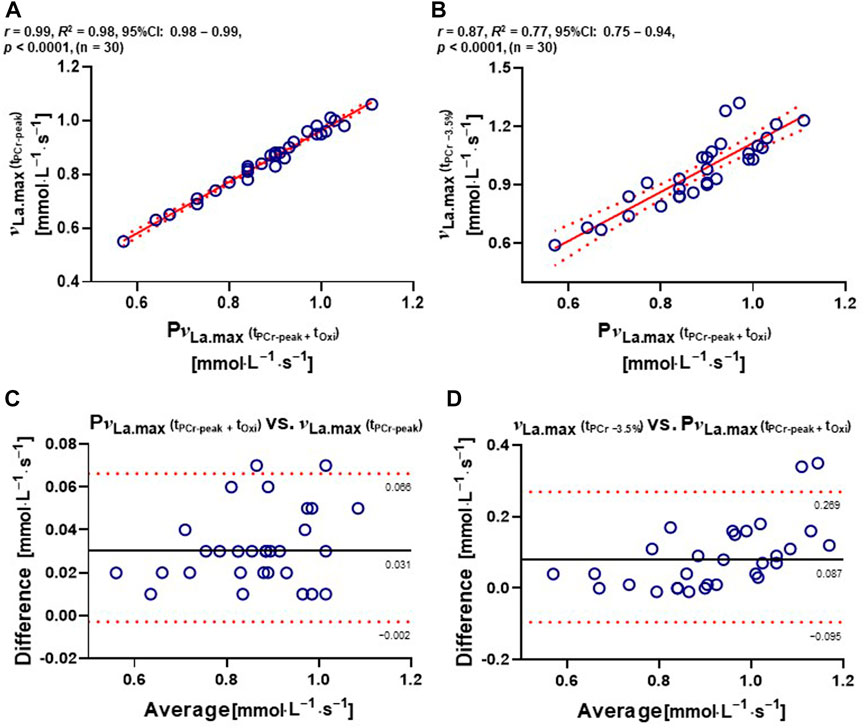
FIGURE 3. Relationships and Bland–Altman plots between different calculations of ^ν_La.max. (A) Two-tailed Pearson’s correlation between P^ν_La.max and ^ν_La.max (t_PCr−peak). (B) Two-tailed Pearson’s correlation between P^ν_La.max and ^ν_La.max (t_{PCr −3.5%}). (C and D) Bland–Altman plots of differences between P^ν_La.max and ^ν_La.max (t_PCr−peak) and between ^ν_La.max (t_{PCr −3.5%}) and P^ν_La.max. The dashed line represents bias. The dotted line represents 95% limit of agreements. CI, confidence interval; ES, effect sizes; ^ν_La.max, maximal rate of lactate accumulation; P^ν_La.max, pure maximal rate of lactate accumulation; t_Oxi, time of oxidative energy system contribution; t_PCr−peak, phosphagen energy system–contributed time until the peak power output; t_{PCr −3.5%}, phosphagen energy system contributed −3.5% time point from the peak power output. Significant difference; ****p < .0001.

Relationships between anaerobic performance and different ^ν_La.max

Low positive correlations between ^ν_La.max (t_PCr−peak) and absolute W_mean, P^ν_La.max and absolute W_mean, and ^ν_La.max (t_{PCr −3.5%}) and absolute W_mean were observed (r = 0.48, R² = 0.23, 95% CI: 0.14–0.72, and p = 0.0075; r = 0.45, R² = 0.21, 95% CI: 0.11–0.70, and p = 0.0120; r = 0.43, R² = 0.19, 95% CI: 0.08–0.69, and p = 0.0173, respectively) (Figures 4A−C). Furthermore, moderate to high positive correlations between ^ν_La.max (t_PCr−peak) and W_Gly, P^ν_La.max and W_Gly, and ^ν_La.max (t_{PCr −3.5%}) and W_Gly in kilojoules were found (r = 0.73, R² = 0.53, 95% CI: 0.49–0.86, and p < 0.0001; r = 0.70, R² = 0.49, 95% CI: 0.46–0.85, and p < 0.0001; r = 0.61, R² = 0.37, 95% CI: 0.31–0.79, and p = 0.0004, respectively) (Figures 4D−F).

FIGURE 4

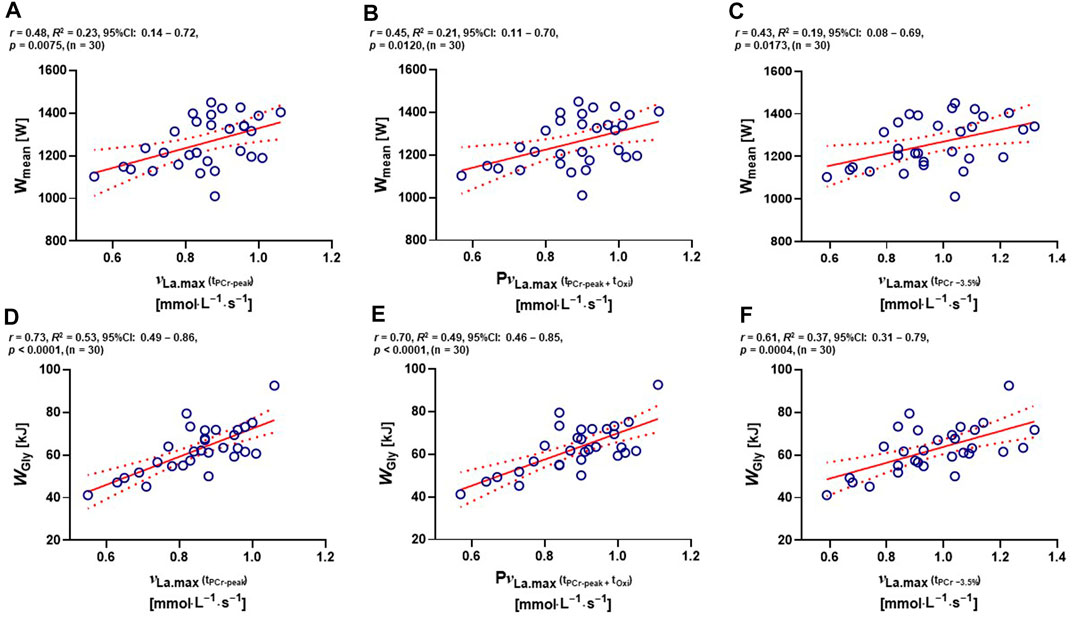
FIGURE 4. Two-tailed Pearson’s correlations (A) between ^ν_La.max (t_PCr−peak) and W_mean, (B) between P^ν_La.max and absolute W_mean, (C) between ^ν_La.max (t_{PCr −3.5%}) and absolute W_mean, (D) between ^ν_La.max (t_PCr−peak) and absolute W_Gly, (E) between P^ν_La.max and absolute W_Gly, and (F) between ^ν_La.max (t_{PCr −3.5%}) and absolute W_Gly. CI, confidence interval; ^ν_La.max, maximal rate of lactate accumulation; P^ν_La.max, pure maximal rate of lactate accumulation; t_Oxi, time of oxidative energy system contribution; t_PCr−peak, phosphagen energy system contribution time until peak power output; t_{PCr −3.5%}, phosphagen energy system contribution at −3.5% time point from peak power output; W_Gly, absolute glycolytic energy contribution in kilohoules; W_mean, absolute mean power output in watt.

Discussion

In previous studies, calculations of ^ν_La.max for the maximal glycolytic capacity after the 15-s ASCT were limited because t_PCr and aerobic energy contribution were not considered. To the best of our knowledge, this study is the first to integrate the oxidative energy contribution and contributions of the three energy systems during the 15-s ASCT via a modified P^ν_La.max calculation. This modified P^ν_La.max was compared with previous ^ν_La.max calculations for glycolytic performance and their correlations were determined.

The main findings of this study confirm that phosphagen and glycolytic systems are predominantly utilized, while the oxidative energy metabolism contributes to 3.13% ± 1.61% during the 15-s ASCT. The t_PCr−peak and t_Oxi- subtracted P^ν_La.max values were lower than ^ν_La.max (t_{PCr −3.5%}) but higher than ^ν_La.max (t_PCr−peak) values. Moreover, very strong and high correlations between P^ν_La.max and ^ν_La.max (t_PCr−peak) and between P^ν_La.max and ^ν_La.max (t_{PCr −3.5%}) were found. Three different ^ν_La.max values were positively associated with absolute W_mean and W_Gly values.

The phosphagen energy system has the highest absolute energetic contribution during the 15-s ASCT, followed by glycolytic and oxidative energy metabolism, thus being in agreement with the results of a previous study by Park et al. (2021). In this study, all three energy systems were analyzed using the same PCr-La⁻-O₂ method during a 100-m sprint and the oxidative energy system contributed over 10% here to the total energy requirements. In comparison to this outcome, the oxidative contribution in the present study was lower (∼3%) during the 15-s ASCT (Figure 2A). These different results might be because 100-m sprint and sprint cycling are differently characterized by maximal anaerobic performances, which include different movements of the upper extremities. Previous studies have reported that smaller muscles such as those in the upper extremities do not significantly contribute to total lactate accumulation (Julio et al., 2017; Yang et al., 2022b). Therefore, glycolytic energy contribution during the 15-s ASCT likely had a higher percentage (35% ± 7%) than during a 100-m sprint (∼25 ± 7%) as obtained in a previous study outcome (Park et al., 2021), which in turn reduced the relative oxidative contribution.

Regarding the different calculations of ^ν_La.max, the level of ^ν_La.max (t_{PCr −3.5%}) showed significantly higher values than ^ν_La.max (t_PCr−peak) and P^ν_La.max (Figure 2B) because the t_{PCr −3.5%} value calculated was 3.2 ± 1.0 s during the 15-s ASCT (Table 1) such that the denominator (∆time) of the formula was smaller than the others. Due to the same reason, in including t_PCr−peak + t_Oxi, P^ν_La.max showed higher values than ^ν_La.max (t_PCr−peak). According to our results, the calculation of ^ν_La.max (t_{PCr −3.5%}) was unsuitable to determine the glycolytic capacity or ^ν_La.max because the determined t_PCr time of −3.5% from W_peak was based on an error of the early SRM cycle ergometer (Weber, 2003). On the other hand, previous researchers suggested no lactate production during t_PCr which was incorrectly (fictitiously) assumed (Heck et al., 2003; Hauser et al., 2014; Adam et al., 2015; Nitzsche et al., 2018; Quittmann et al., 2020; Quittmann et al., 2021). In this regard, it is well known that all three energy systems start to work simultaneously and lactate production occurs independently of O₂ availability such as under anoxic, hypoxic, and normoxic conditions (Gastin, 2001; Philp et al., 2005; Brooks, 2018; Yang et al., 2020; Brooks et al., 2022; Yang et al., 2022b). La⁻ might be accumulated at a relatively low level during the initial seconds of the 15-s ASCT because ATP-PCr is a dominant energy contribution until the achievement of W_peak (Serresse et al., 1988; Beneke et al., 2002; Park et al., 2021). Moreover, Heck et al. (2003) have suggested that aerobic power and contribution are of minor significance during maximal short-term exercise testing. However, this interpretation is based on the results of a computer simulation that originated from systems biology (Wackerhage et al., 2022). The calculated ^ν_La.max values with and without t_Oxi show significant differences in our study's outcomes (Table 1; Figure 2B). Therefore, oxidative metabolism should be considered when aiming to analyze a pure maximal glycolytic rate. Considering the abovementioned factors, the accuracies of ^ν_La.max (t_PCr−peak) and P^ν_La.max calculations seem to be higher because the durations of t_PCr−peak and t_Oxi are additionally involved in calculating formulas by subtracting them from the total exercise time. Accordingly, P^ν_La.max was very strongly correlated with ^ν_La.max (t_PCr−peak), and this correlation was higher than that of P^ν_La.max with ^ν_La.max (t_{PCr −3.5%}). The Bland–Altman plot between P^ν_La.max and ^ν_La.max (t_PCr−peak) also showed a smaller limit of agreement than the limit of agreement between ^ν_La.max (t_{PCr −3.5%}) and P^ν_La.max (Figures 3C, D). Furthermore, P^ν_La.max and ^ν_La.max (t_PCr−peak) were associated with absolute W_mean and W_Gly. Such associations were higher than those of ^ν_La.max (t_{PCr −3.5%}), with absolute W_mean and W_Gly (Figures 4A−F). These results indicate that P^ν_La.max and ^ν_La.max (t_PCr−peak) are better calculating methods for glycolytic capacity/power.

To determine the anaerobic performance, the 30-s Wingate anaerobic test is often used in related studies (Bar-Or, 1987; Gastin, 2001; Zupan et al., 2009; Jaafar et al., 2014). However, this time frame will likely increase the oxidative contribution to the total energy demand and may also lead to an inhibition of phosphofructokinase activity because of accumulated hydrogen ions from increased ATP hydrolysis and reduced pH-levels (Gastin, 2001; Heck et al., 2003; Robergs et al., 2004; Yang et al., 2022b). This increased oxidative contribution may then reduce lactate accumulation and increase lactate elimination, which results in a reduced likelihood of measuring the maximal lactate accumulation (Heck et al., 2003; Yang et al., 2020; Yang et al., 2022b; Wackerhage et al., 2022). Thus, the ^ν_La.max determination combining the 15-s ASCT with the P^ν_La.max formula using the PCr-La⁻-O₂ method is more suitable to limit the activation of oxidative metabolism as much as possible in decreasing intracellular lactate oxidation (Heck et al., 2003; Wackerhage et al., 2022).

In the current study, the levels of ^ν_La.max (t_{PCr −3.5%}) were higher than those of P^ν_La.max and ^ν_La.max (t_PCr−peak), while a very strong relationship between P^ν_La.max and ^ν_La.max (t_PCr−peak) was observed, one that was better than the relationship between P^ν_La.max and ^ν_La.max (t_{PCr −3.5%}). Therefore, the calculation of P^ν_La.max using the analysis of energetic contributions should be considered in scientific research to precisely analyze the maximal rate of lactate accumulation and anaerobic capacity/power. In practical diagnostics, the calculation of ^ν_La.max (t_PCr−peak) may be useful without a complicated analysis of energetic contributions or if it is not possible to be available for gas analyzer equipment eventually. Otherwise, the use of ^ν_La.max (t_{PCr −3.5%}) calculation is only suggested if the early version of the SRM cycle ergometer is available to perform the 15-s ASCT.

This study successfully identified the differences of three possible ^ν_La.max calculations during the 15-s ASCT. However, the current study has some limitations. Because a spiroergometry system processing a dynamic micro-mixing chamber mode was not available during the test, the $\dot{\mathrm{V}}$O₂ data were measured with the breath-by-breath method using a portable gas analyzer during the 15-s ASCT, which was converted to calculate W_Oxi. This measurement mode during a maximal effort exercise has some errors (2–4%, approximately). Thus, the outcomes might be influenced by this factor. Moreover, although the t_PCr−peak determination is the physiologically acceptable method using the peak power output in sports science, the direct measuring of t_PCr is very difficult or impossible. It has never been measured using biomarkers/sensors such as the isotopic tracers or fluorescent protein sensors during a maximal short-term effort in humans. Actual direct measurements for t_PCr and exact metabolic contributions have to be determined in future studies. Further studies might also have to develop sport-specific P^ν_La.max testing in other high-intensity intermittent sports disciplines such as football, handball, basketball, rugby, and combat sports as anaerobic performance profiling.

Regarding the possible gender differences in energetic contributions, Yang et al. (2022a) recently calculated the energy system contributions during increasing exercise intensities. The results found different W_PCr and W_Gly levels between males and females that were attributed to the differences in skeletal muscle mass and all fiber types. Therefore, there may be a need for further research into gender differences in the P^ν_La.max calculation. Furthermore, the distribution of muscle fiber types might be considered when interpreting high or low ^ν_La.max values in individual athletes with higher muscle mass and more glycolytic type IIA and IIX fibers who show generally higher lactate production during aerobic and anaerobic exercises (Ivy et al., 1980; Wackerhage et al., 2022). Future studies must show to what extent ^ν_La.max might shift during a training year in track athletes with a different ^ν_La.max.

Moreover, there are currently no clear data available about which specific individual training sessions are helpful in improving ^ν_La.max. A recent study by Schünemann et al. (2023) suggests that sprint training, resistance training, and hypoxic training may increase glycolytic capacity and anaerobic performance. However, direct interventional approaches related to improving maximal glycolytic metabolism as P^ν_La.max should be investigated further.

Conclusion

The findings of the current study indicate that a modified calculation of P^ν_La.max with the additional incorporation of further energetic contributions is precision enhancing and therefore valuable for determining the maximal glycolytic rate or ^ν_La.max. Our modified calculation therefore allows for a more detailed input of individual characteristics of energy metabolism to becoming an increasingly popular method for determining differences in maximal rates of lactate accumulation. In light of inter-individual differences in maximal force generation, phosphagen levels, and oxidative capacity, our method allows for compensating this interaction during ^ν_La.max measurements when compared to previous methods. According to our results, the calculated formula of P^ν_La.max should be used for scientific research in exercise sciences to determine the maximal anaerobic capacity/power more precisely and with the exclusion of the aerobic component. This is supported by a small limit of agreement (a small variation) and very high correlation with ^ν_La.max (t_PCr−peak). Furthermore, the calculation of ^ν_La.max (t_PCr−peak) might be recommended for a faster analysis of the practical approach in the field.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Ethics statement

The studies involving human participants were reviewed and approved by the Institutional Review Board of CHA University, along with this study (No. 1044308-202206-HR-032-02). The patients/participants provided their written informed consent to participate in this study.

Author contributions

W-HY, S-YP, TK, H-JJ, OH, and SG were involved in the conception and design of the research. W-HY, S-YP, TK, and H-JJ collected the data. W-HY and S-YP analyzed the data. W-HY wrote the first draft of the manuscript. W-HY, OH, and SG revised and edited the manuscript. All authors approved the final manuscript.

Acknowledgments

The authors would like to thank all participants for participating in this study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, editors, and reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adam J., Öhmichen M., Öhmichen E., Rother J., Müller U. M., Hauser T., et al. (2015). Reliability of the calculated maximal lactate steady state in amateur cyclists. Biol. Sport 32 (2), 97–102. doi:10.5604/20831862.1134311

PubMed Abstract | CrossRef Full Text | Google Scholar

Bar-Or O. (1987). The Wingate anaerobic test. An update on methodology, reliability and validity. Sports Med. 4 (6), 381–394. doi:10.2165/00007256-198704060-00001

PubMed Abstract | CrossRef Full Text | Google Scholar

Beneke R., Beyer T., Jachner C., Erasmus J., Hütler M. (2004). Energetics of karate kumite. Eur. J. Appl. Physiol. 92 (4-5), 518–523. doi:10.1007/s00421-004-1073-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Beneke R., Pollmann C., Bleif I., Leithäuser R. M., Hütler M. (2002). How anaerobic is the wingate anaerobic test for humans? Eur. J. Appl. Physiol. 87 (4-5), 388–392. doi:10.1007/s00421-002-0622-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Bland J. M., Altman D. G. (1995). Comparing methods of measurement: Why plotting difference against standard method is misleading. Lancet 346 (8982), 1085–1087. doi:10.1016/s0140-6736(95)91748-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouillod A., Pinot J., Soto-Romero G., Bertucci W., Grappe F. (2017). Validity, sensitivity, reproducibility, and robustness of the PowerTap, stages, and garmin vector power meters in comparison with the SRM device. Int. J. Sports Physiol. Perform. 12 (8), 1023–1030. doi:10.1123/ijspp.2016-0436

PubMed Abstract | CrossRef Full Text | Google Scholar

Brooks G. A. (2018). The science and translation of lactate shuttle theory. Cell Metab. 27 (4), 757–785. doi:10.1016/j.cmet.2018.03.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Brooks G. A., Curl C. C., Leija R. G., Osmond A. D., Duong J. J., Arevalo J. A. (2022). Tracing the lactate shuttle to the mitochondrial reticulum. Exp. Mol. Med. 54 (9), 1332–1347. doi:10.1038/s12276-022-00802-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Campos F. A. D., Bertuzzi R., Dourado A. C., Santos V. G. F., Franchini E. (2012). Energy demands in taekwondo athletes during combat simulation. Eur. J. Appl. Physiol. 112 (4), 1221–1228. doi:10.1007/s00421-011-2071-4

PubMed Abstract | CrossRef Full Text | Google Scholar

de Campos Mello F., de Moraes Bertuzzi R. C., Grangeiro P. M., Franchini E. (2009). Energy systems contributions in 2,000 m race simulation: A comparison among rowing ergometers and water. Eur. J. Appl. Physiol. 107 (5), 615–619. doi:10.1007/s00421-009-1172-9

PubMed Abstract | CrossRef Full Text | Google Scholar

de Moraes Bertuzzi R. C., Franchini E., Kokubun E., Kiss M. A. P. D. M. (2007). Energy system contributions in indoor rock climbing. Eur. J. Appl. Physiol. 101 (3), 293–300. doi:10.1007/s00421-007-0501-0

PubMed Abstract | CrossRef Full Text | Google Scholar

di Prampero P. E., Ferretti G. (1999). The energetics of anaerobic muscle metabolism: A reappraisal of older and recent concepts. Respir. Physiol. 118 (2), 103–115. doi:10.1016/s0034-5687(99)00083-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunst A. K., Hesse C., Ueberschär O., Holmberg H. C. (2023). A novel approach to the determination of time- and fatigue-dependent efficiency during maximal cycling sprints. Sports (Basel) 11 (2), 29. doi:10.3390/sports11020029

PubMed Abstract | CrossRef Full Text | Google Scholar

Foster C., Snyder A. C., Thompson N. N., Green M. A., Foley M., Schrager M. (1993). Effect of pacing strategy on cycle time trial performance. Med. Sci. Sports Exerc 25 (3), 383–388. doi:10.1249/00005768-199303000-00014

PubMed Abstract | CrossRef Full Text | Google Scholar

Franchini E. (2023). Energy system contributions during olympic combat sports: A narrative Review. Metabolites 13 (2), 297. doi:10.3390/metabo13020297

PubMed Abstract | CrossRef Full Text | Google Scholar

Franchini E. (2020). High-intensity interval training prescription for combat-sport athletes. Int. J. Sports Physiol. Perform. 15 (6), 767–776. doi:10.1123/ijspp.2020-0289

PubMed Abstract | CrossRef Full Text | Google Scholar

Fritz C. O., Morris P. E., Richler J. J. (2012). Effect size estimates: Current use, calculations, and interpretation. J. Exp. Psychol. Gen. 141 (1), 2–18. doi:10.1037/a0024338

PubMed Abstract | CrossRef Full Text | Google Scholar

Fujii N., Nishida Y., Ogawa T., Tanigawa S., Nishiyasu T. (2018). Effects of work-matched moderate- and high-intensity warm-up on power output during 2-min supramaximal cycling. Biol. Sport 35 (3), 223–228. doi:10.5114/biolsport.2018.74633

PubMed Abstract | CrossRef Full Text | Google Scholar

Gastin P. B. (2001). Energy system interaction and relative contribution during maximal exercise. Sports Med. 31 (10), 725–741. doi:10.2165/00007256-200131100-00003

PubMed Abstract | CrossRef Full Text | Google Scholar

Hausen M., Soares P. P., Araújo M. P., Porto F., Franchini E., Bridge C. A., et al. (2017). Physiological responses and external validity of a new setting for taekwondo combat simulation. PloS One 12 (2), e0171553. doi:10.1371/journal.pone.0171553

PubMed Abstract | CrossRef Full Text | Google Scholar

Hauser T., Adam J., Schulz H. (2014). Comparison of calculated and experimental power in maximal lactate-steady state during cycling. Theor. Biol. Med. Model 11, 25–12. doi:10.1186/1742-4682-11-25

PubMed Abstract | CrossRef Full Text | Google Scholar

Heck H., Schulz H., Bartmus U. (2003). Diagnostics of anaerobic power and capacity. Eur. J. Sport Sci. 3 (3), 1–23. doi:10.1080/17461390300073302

CrossRef Full Text | Google Scholar

Hettinga F. J., De Koning J. J., Meijer E., Teunissen L., Foster C. (2007). Biodynamics. Effect of pacing strategy on energy expenditure during a 1500-m cycling time trial. Med. Sci. Sports Exerc 39 (12), 2212–2218. doi:10.1249/mss.0b013e318156e8d4

PubMed Abstract | CrossRef Full Text | Google Scholar

Ivy J. L., Withers R. T., Van Handel P. J., Elger D. H., Costill D. L. (1980). Muscle respiratory capacity and fiber type as determinants of the lactate threshold. J. Appl. Physiol. Respir. Environ. Exerc Physiol. 48 (3), 523–527. doi:10.1152/jappl.1980.48.3.523

PubMed Abstract | CrossRef Full Text | Google Scholar

Jaafar H., Rouis M., Coudrat L., Attiogbé E., Vandewalle H., Driss T. (2014). Effects of load on wingate test performances and reliability. J. Strength Cond. Res. 28 (12), 3462–3468. doi:10.1519/jsc.0000000000000575

PubMed Abstract | CrossRef Full Text | Google Scholar

Julio U. F., Panissa V. L. G., Esteves J. V., Cury R. L., Agostinho M. F., Franchini E. (2017). Energy-system contributions to simulated judo matches. Int. J. Sports Physiol. Perform. 12 (5), 676–683. doi:10.1123/ijspp.2015-0750

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaufmann S., Latzel R., Beneke R., Hoos O. (2022). Reliability of the 3-component model of aerobic, anaerobic lactic, and anaerobic alactic energy distribution (PCr-la-O2) for energetic profiling of continuous and intermittent exercise. Int. J. Sports Physiol. Perform. 17, 1642–1648. doi:10.1123/ijspp.2022-0115

PubMed Abstract | CrossRef Full Text | Google Scholar

Lopes-Silva J. P., Da Silva Santos J. F., Artioli G. G., Loturco I., Abbiss C., Franchini E. (2018). Sodium bicarbonate ingestion increases glycolytic contribution and improves performance during simulated taekwondo combat. Eur. J. Sport Sci. 18, 431–440. doi:10.1080/17461391.2018.1424942

PubMed Abstract | CrossRef Full Text | Google Scholar

Mader A. (1984). Eine Theorie zur Berechnung der Dynamik und des steady state von Phosphorylierungszustand und Stoffwechselaktivität der Muskelzelle als Folge des Energiebedarfs. Cologne: German Sport University Cologne.

Google Scholar

Manunzio C., Mester J., Kaiser W., Wahl P. (2016). Training intensity distribution and changes in performance and Physiology of a 2nd place finisher team of the race across America over a 6 Month preparation period. Front. Physiol. 7, 642. doi:10.3389/fphys.2016.00642

PubMed Abstract | CrossRef Full Text | Google Scholar

Montalvo-Pérez A., Alejo L. B., Valenzuela P. L., Castellanos M., Gil-Cabrera J., Talavera E., et al. (2021). Validity of the favero assioma duo power pedal system for measuring power output and cadence. Sensors 21 (7), 2277. doi:10.3390/s21072277

PubMed Abstract | CrossRef Full Text | Google Scholar

Nimmerichter A., Schnitzer L., Prinz B., Simon D., Wirth K. (2017). Validity and reliability of the garmin vector power meter in laboratory and field cycling. Int. J. Sports Med. 38 (6), 439–446. doi:10.1055/s-0043-101909

PubMed Abstract | CrossRef Full Text | Google Scholar

Nitzsche N., Baumgärtel L., Maiwald C., Schulz H. (2018). Reproducibility of blood lactate concentration rate under isokinetic force loads. Sports 6 (4), 150. doi:10.3390/sports6040150

PubMed Abstract | CrossRef Full Text | Google Scholar

Park S. B., Park D. S., Kim M., Lee E., Lee D., Jung J., et al. (2021). High-intensity warm-up increases anaerobic energy contribution during 100-m sprint. Biology 10 (3), 198. doi:10.3390/biology10030198

PubMed Abstract | CrossRef Full Text | Google Scholar

Philp A., Macdonald A. L., Watt P. W. (2005). Lactate–a signal coordinating cell and systemic function. J. Exp. Biol. 208 (24), 4561–4575. doi:10.1242/jeb.01961

PubMed Abstract | CrossRef Full Text | Google Scholar

Quittmann O. J., Appelhans D., Abel T., Strüder H. K. (2020). Evaluation of a sport-specific field test to determine maximal lactate accumulation rate and sprint performance parameters in running. J. Sci. Med. Sport 23 (1), 27–34. doi:10.1016/j.jsams.2019.08.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Quittmann O. J., Schwarz Y. M., Mester J., Foitschik T., Abel T., Strüder H. K. (2021). Maximal lactate accumulation rate in all-out exercise differs between cycling and running. Int. J. Sports Med. 42 (4), 314–322. doi:10.1055/a-1273-7589

PubMed Abstract | CrossRef Full Text | Google Scholar

Robergs R. A., Ghiasvand F., Parker D. (2004). Biochemistry of exercise-induced metabolic acidosis. Am. J. Physiol. Regul. Integr. Comp. Physiol. 287 (3), R502–R516. doi:10.1152/ajpregu.00114.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Schünemann F., Park S.-Y., Wawer C., Theis C., Yang W.-H., Gehlert S. (2023). Diagnostics of νLa. Max and glycolytic energy contribution indicate individual characteristics of anaerobic glycolytic energy metabolism contributing to rowing performance. Metabolites 13 (3), 317. doi:10.3390/metabo13030317

PubMed Abstract | CrossRef Full Text | Google Scholar

Serresse O., Lortie G., Bouchard C., Boulay M. R. (1988). Estimation of the contribution of the various energy systems during maximal work of short duration. Int. J. Sports Med. 9 (6), 456–460. doi:10.1055/s-2007-1025051

PubMed Abstract | CrossRef Full Text | Google Scholar

Wackerhage H., Gehlert S., Schulz H., Weber S., Ring-Dimitriou S., Heine O. (2022). Lactate thresholds and the simulation of human energy metabolism: Contributions by the cologne sports medicine group in the 1970s and 1980s. Front. Physiol. 13, 899670. doi:10.3389/fphys.2022.899670

PubMed Abstract | CrossRef Full Text | Google Scholar

Weber S. (2003). Berechnung leistungsbestimmender Parameter der metabolischen Aktivität auf zellulärer Ebene mittels fahrradergometrischer Untersuchungen. Dipl.-Thesis. Cologne: German Sport University Cologne.

Google Scholar

Yang W.-H., Heine O., Grau M. (2018). Rapid weight reduction does not impair athletic performance of Taekwondo athletes–A pilot study. PloS One 13 (4), e0196568. doi:10.1371/journal.pone.0196568

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang W.-H., Park H., Grau M., Heine O. (2020). Decreased blood glucose and lactate: Is a useful indicator of recovery ability in athletes? Int. J. Environ. Res. Public Health 17 (15), 5470. doi:10.3390/ijerph17155470

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang W.-H., Park J.-H., Park S.-Y., Park Y. (2022a). Energetic contributions including gender differences and metabolic flexibility in the general population and athletes. Metabolites 12 (10), 965–1014. doi:10.3390/metabo12100965

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang W.-H., Park J.-H., Shin Y.-C., Kim J. (2022b). Physiological profiling and energy system contributions during simulated epée matches in elite fencers. Int. J. Sports Physiol. Perform. 17 (6), 943–950. doi:10.1123/ijspp.2021-0497

PubMed Abstract | CrossRef Full Text | Google Scholar

Zupan M. F., Arata A. W., Dawson L. H., Wile A. L., Payn T. L., Hannon M. E. (2009). Wingate Anaerobic Test peak power and anaerobic capacity classifications for men and women intercollegiate athletes. J. Strength Cond. Res. 23 (9), 2598–2604. doi:10.1519/JSC.0b013e3181b1b21b

PubMed Abstract | CrossRef Full Text | Google Scholar