- 1Department of Sport Sciences, University of Beira Interior, Covilhã, Portugal
- 2Research Center in Sports Health and Human Development (CIDESD), University of Beira Interior, Covilhã, Portugal
- 3Department of Sport Sciences, Instituto Politécnico de Bragança, Bragança, Portugal
Introduction: In swimming, it is necessary to understand and identify the main factors that are important to reduce active drag and, consequently, improve the performance of swimmers. However, there is no up-to-date review in the literature clarifying this topic. Thus, a systematic narrative review was performed to update the body of knowledge on active drag in swimming through numerical and experimental methods.
Methods: To determine and identify the most relevant studies for this review, the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) approach was used.
Results: 75 studies related to active drag in swimming and the methodologies applied to study them were analyzed and kept for synthesis. The included studies showed a high-quality score by the Delphi scale (mean score was 5.85 ± 0.38). Active drag was included in seven studies through numerical methods and 68 through experimental methods. In both methods used by the authors to determine the drag, it can be concluded that the frontal surface area plays a fundamental role. Additionally, the technique seems to be a determining factor in reducing the drag force and increasing the propulsive force. Drag tends to increase with speed and frontal surface area, being greater in adults than in children due to body density factors and high levels of speed. However, the coefficient of drag decreases as the technical efficiency of swimming increases (i.e., the best swimmers (the fastest or most efficient) are those with the best drag and swimming hydrodynamics efficiency).
Conclusion: Active drag was studied through numerical and experimental methods. There are significantly fewer numerical studies than experimental ones. This is because active drag, as a dynamical phenomenon, is too complex to be studied numerically. Drag is greater in adults than in children and greater in men than in women across all age groups. The study of drag is increasingly essential to collaborate with coaches in the process of understanding the fundamental patterns of movement biomechanics to achieve the best performance in swimming. Although most agree with these findings, there is disagreement in some studies, especially when it is difficult to define competitive level and age. The disagreement concerns three main aspects: 1) period of the studies and improvement of methodologies; 2) discrimination of methodologies between factors observed in numerical vs. experimental methods; 3) evidence that drag tends to be non-linear and depends on personal, technical, and stylistic factors. Based on the complexity of active drag, the study of this phenomenon must continue to improve swimming performance.
Introduction
Swimming performance concerning humans is poor compared to species whose habitat is aquatic. In fact, the maximum swimming speed performed by humans represents about 16% of the maximum speed obtained by aquatic species (Toussaint et al., 2004). One of the reasons for this difference in speed is the greater resistance humans encounter when moving through the water (Toussaint et al., 2004).
A swimmer’s displacement relies on the net balance between propulsion and drag (Zamparo et al., 2020):
In which
In which D is the drag force (in N), ρ is the density of water (in kg/m3), v is the swimming speed (in m/s), S is the projected frontal surface area (FSA) of the swimmers (in m2) and Cd is the coefficient of drag (changing according to shape, orientation, and Reynolds number).
The total drag consists of three components: 1) friction drag (depends on the friction between the skin and the water); 2) pressure drag (depends on body surface area); 3) wave drag (depends on the water surface deformation) (Toussaint and Beek, 1992). Based on these components, total drag can be computed as:
In which F (in N) is the total drag force, Ff is the friction component (in N), Fp is the pressure component (in N), and Fw is the wave component (in N). Overall, it is generally accepted that frictional drag is the component with the smallest contribution to total drag, especially at higher swimming velocities (Bixler et al., 2007). Nonetheless, friction drag should not be disregarded in elite level swimmers. On the other hand, pressure drag and wave drag represent the most important part of the total drag, especially when performing a swimming stroke (Toussaint and Beek, 1992). Therefore, swimmers must intensify the most hydrodynamic postures during swimming.
Indeed, the literature reports two types of drag: 1) passive drag; 2) active drag. Passive drag (Dp) is the evaluation of the drag produced during the displacement of a towed body (i.e., without relative movement of the body segments in the aquatic environment) (Pendergast et al., 2006). Active drag (Da) is the water resistance induced to a body while swimming (Kolmogorov and Duplishcheva, 1992). Studies on Da are more common because during a race swimmers spend most of their time performing strokes (Morais et al., 2019).
In 1974, di Prampero et al., developed and used a method to evaluate drag during real swimming conditions through an energetic approach. All recent overviews of a swimmer’s drag have confirmed this statement (Keys and Lyttle, 2007; Sacilotto et al., 2014; Morais et al., 2019; Zamparo et al., 2020; González-Ravé et al., 2022). Both types of drag and its components can be measured by numerical and experimental methods. The former (i.e., numerical methods) is a virtual prototype of the product of interest represented by a system of equations based on a mathematical theory, such as computational fluid dynamics (CFD) (Takagi et al., 2016). The latter (i.e., experimental methods) is a method in which the variables are manipulated in a pre-established way and their effects are sufficiently controlled and known by the researcher for the observation of the study (Takagi et al., 2016). CFD is one of several methods that have been applied in sports research to observe and understand the water flow activity around the human body and its application to improve swimming technique, equipment, and performance (Keys and Lyttle, 2007; Marinho et al., 2011). Smooth particle hydrodynamics (SPH) is a numerical method without a Lagrangian mesh, which allows a detailed quantitative analysis of swimming stroke variations and kinanthropometric variations. It is important to mention that there are few studies that use numerical methods to study Da. Bixler and Schloder (1996) introduced two-dimensional CFD applied to swimming science. More recently, Cohen et al. have made progress in this method as they are the authors of some studies on numerical methodology that provide some interesting data (Cohen et al., 2015; Cohen et al., 2018; Cohen et al., 2020). However, in one of their studies, they mention that the angles of attack of the hands were compared with the contribution of lifting and dragging the hands to generate thrust in the direction of the current. This study allowed the investigation of possible connections between performance and asymmetries during swimming. Efficiency is negatively affected because periods of very high velocity consume exaggerated amounts of energy, considering that drag is non-linearly dependent on instantaneous velocity. Thus, a greater coefficient of variation of the swimmer’s speed suggests a lower swimming efficiency (Cohen et al., 2018; Cohen et al., 2020).
Based on experimental methods, Da can be measured through three approaches: 1) measurement of active drag (MAD) (Hollander et al., 1986); 2) velocity perturbation method (VPM) (Kolmogorov and Duplishcheva, 1992); 3) assisted towing method (ATM) (Alcock and Mason 2007), and; 4) measurement of residual thrust (MRT) (Narita et al., 2017). To determine Da through experimental studies, it was found that MAD, VPM, and ATM are now commonly used to obtain Da values accurately to assess swimmer technique (Toussaint et al., 2004; Formosa et al., 2012; Hazrati et al., 2016). The MAD system consists of pushing pads while the swimmer moves in the water performing the natural swimming movement (as much as possible) (Hollander et al., 1986). The thrust pads fixed below the water allow for the generation of propulsion without loss of energy (Formosa et al., 2012). The ATM system is relatively new compared to the MAD and VPM systems (Hazrati et al., 2016). The ATM system was developed identically to the bases of the VPM, except that it uses assisted towing and resisted swimming (Toussaint et al., 2004), as similar conditions are required in both tests. The main difference between the two is that the ATM produces Da profiles and intra-course propulsion, rather than just an average measure of Da (Formosa et al., 2012). The MRT method, which was recently developed, allows the estimation of drag in swimming using measured values of residual thrust (Narita et al., 2017; Narita et al., 2018b; Gonjo et al., 2020). Through this method, it is possible to investigate Da at various speeds without neglecting the influence of stroke length.
As stated by Toussaint et al., 2004, it is known that human performance in water is dependent on many variables in addition to innate ones. In this way, we must consider all the variables that can compromise a better performance. Thus, these variables depend not only on their propulsive abilities but also on their ability to reduce to a minimum the drag forces that involve the body in a hydrodynamic way (Taı̈ar et al., 1999). Studying active drag becomes relevant simply because it corresponds to the very act of swimming in a cyclical way, which consists almost of the entire race in high competition (Kolmogorov and Duplishcheva, 1992). Considering the importance that the measurement of drag has on swimming performance, it can be said that the evidence in the literature has not been systematically or narratively summarized, specially including studies based on both numerical and experimental measurements. It must be mentioned that Sacilotto et al. (2014) underwent a literature review on drag that also included numerical studies. The authors performed a biomechanical review of the techniques used to estimate or measure resistive forces in swimming. Therefore, the aim of this study was to carry out a systematic narrative review focusing on Da (and its components) measured by numerical and experimental methods.
Methods
Literature search and article selection
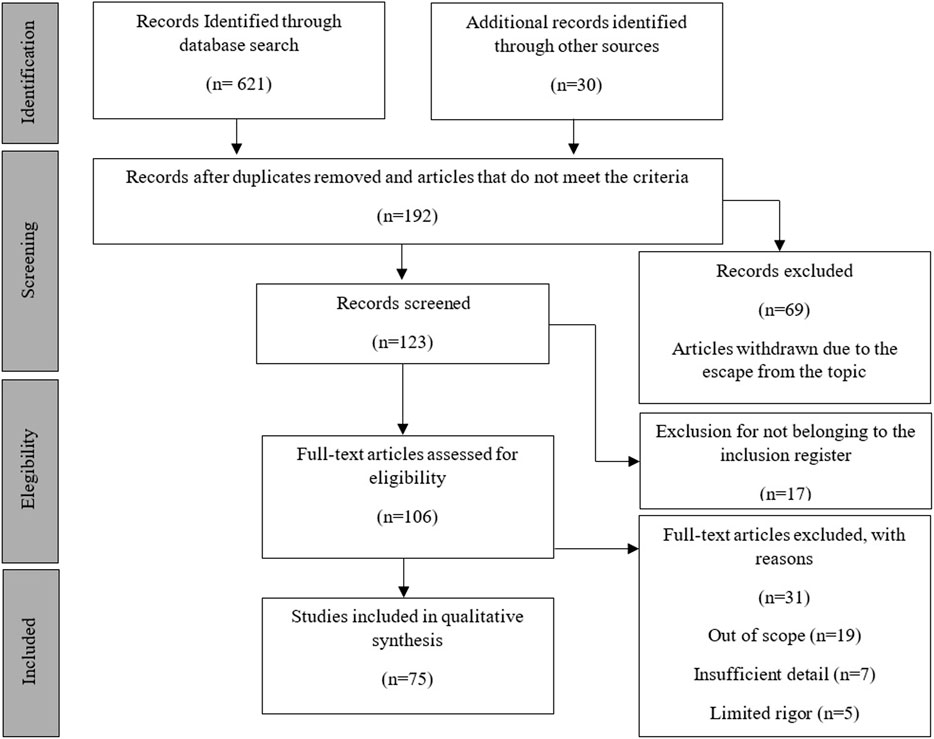
Studies that analyzed Da in swimming were searched in the following databases: Web of Science, Scopus, PubMed, and Science Direct. These electronic search databases were chosen as the most common databases related to methodological approaches in biomechanics applied to sport (framework, methodology, performance, and engineering). The studies that were selected met the following pre-defined inclusion criteria: 1) follow the criteria defined in Table 1; 2) are observational or intervention studies, 3) are written in English, 4) are published in a peer-reviewed journal; 5) involve fully healthy real human swimmers (or their three dimensional scans – 3D); 6) include tests performed to determine Da in swimming; 7) are related to the analysis of human movement in the aquatic environment; 8) use numerical and experimental methods. Review articles, conference articles and books, studies including animals, and publications not related to the topic in question were excluded from the analysis. Studies with disabled swimmers were also excluded from this review. The Preferred Reporting Items for Systematic Reviews flow diagram (PRISMA in Figure 1) characterizes the identification, screening, verification of eligibility, and inclusion of the studies. PRISMA describes the flow of information through the different phases of a systematic review and includes maps or number of identified, included, and excluded records and reasons for exclusion.
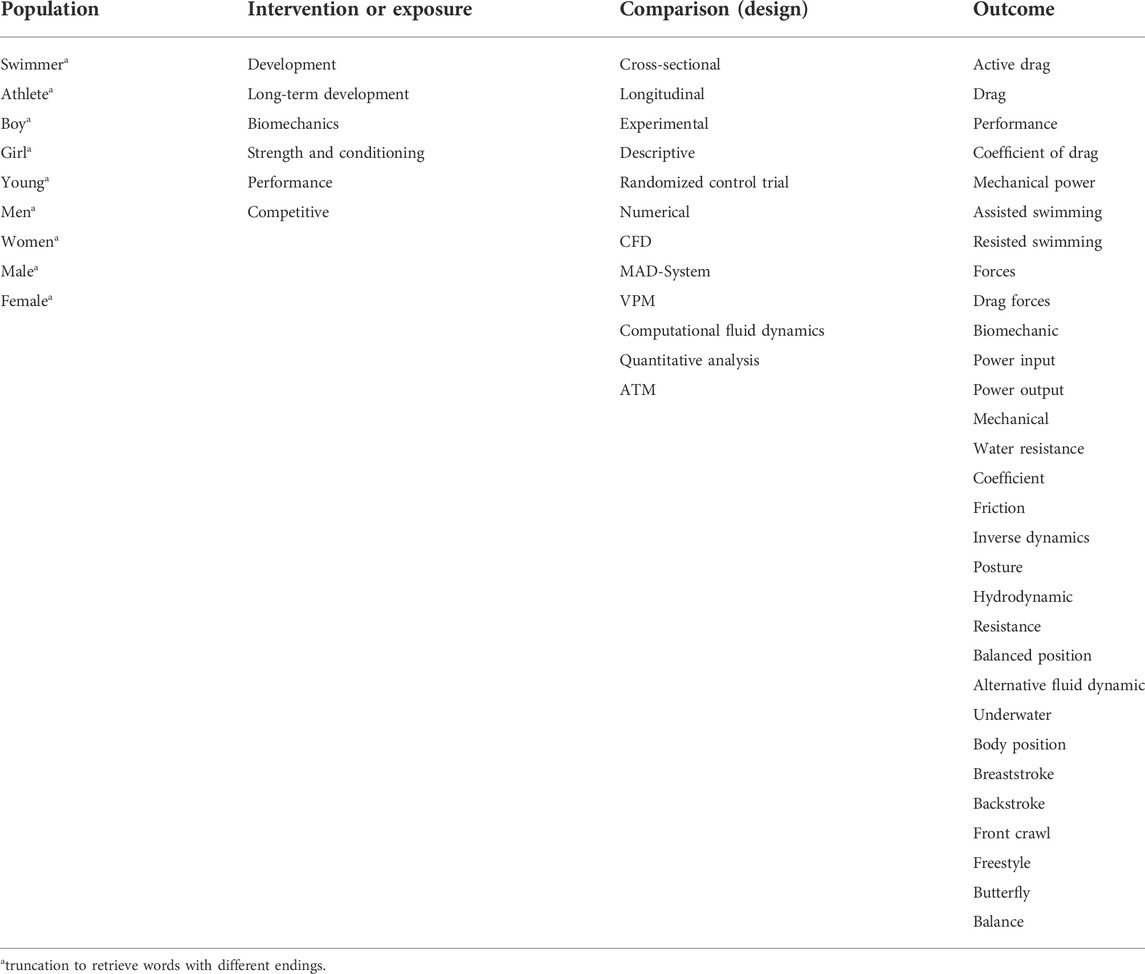
TABLE 1. PI(E)CO (P – patient, problem or population; I – intervention; E – exposure; C – comparison, control, or comparator; O – outcomes) search strategy.
The Patient/Problem, Intervention, Comparison and Outcome (PICO) search strategy is shown in Table 1. It presents the words used to carry out the research, supported by the words most used by the authors to describe their studies. Each title, abstract, and keyword field of the text was identified and carefully read for the first selection of journal articles. If any of these fields (title, abstract, and keywords) was not clear on the topic under analysis, it was necessary to read and review the entire article in question to ensure its inclusion. For the initial research, a Boolean search strategy was used based on a combination of keywords that can be seen in Table 1. After excluding all unrelated and duplicate articles, 75 articles were selected for the final published review (Figure 1), comprising studies from 1986 until the end of the review research on 31 January 2022, as this was the latest study framed within the pre-defined selection model. From the selected articles, the reviewers extracted information about the aim of the study, the participants, the methods to measure the Da in swimming, the characteristics of the numerical and experimental method (s), the measured variables, and the data analysis used.
Quality assessment
The Delphi method was used to assess the quality of the selected articles (knowing that Delphi is a process to develop a scale suitable for the purpose). It was noted that this approach (i.e., applying and creating a group scale) is an indicator of methodological quality (de Meyrick, 2003; de Morton, 2009). The Delphi method aims to structure a process of collective communication allowing a group of researchers to deal with a complex problem (de Meyrick, 2003). This method allows the creation of an evaluation scale for the articles selected for this study (de Meyrick, 2003; de Morton, 2009). Particularly when accessing numerical studies, there is a need to create a specific questionnaire and scale. Thus, it was agreed among the authors to create a questionnaire that would make the decision on the classification of the studies selected for this narrative review unanimous. In this way, through the Delphi method, the authors attempted to evaluate the following questions: 1) Does the contemplated content meet the objective?; 2) Was there a logic in the used methods?; 3) Were the methods and subjects well defined?; 4) Was there writing, language and clarity in the presentation of the contents covered?; 5) Was the presentation of the results clear?; 6) Are the results consistent with the culture of the study? Two independent reviewers read all articles and scored according to the items on the scale (poor quality if scored ≤2; fair quality if scored 3 to 4; high quality if scored 5–6) (de Meyrick, 2003; de Morton, 2009). Subsequently, Cohen’s Kappa (K) was calculated to assess agreement between reviewers. It was interpreted as 1) no agreement if K ≤ 0; 2) none to slight if 0.01 < K ≤ 0.20; 3) fair if 0.21 < K ≤ 0.40; 4) moderate if 0.41 < K ≤ 0.60; 5) substantial if 0.61 < K ≤ 0.80; 6) almost perfect if 0.81 < K ≤ 1.00 (McHugh, 2012). After reviewing all articles, the Delphi scale showed a mean score of 5.85 ± 0.38 (i.e., high quality if scored), and Cohen’s Kappa an almost perfect agreement between reviewers (K = 0.651, p < 0.001). The Delphi scores are presented in Table 2 for each article.

TABLE 2. Summary of the objective, sample demographics, and main results of the studies related with Da for numerical methods.
Results
A total of 75 studies met the inclusion criteria, of which seven used the numerical method and 68 the experimental method. The criterion for defining which studies to include was unanimous, and so it was decided to consider all studies regardless of their type of method. However, it was essential that the topic of the study followed the needs described in Table 1.
Table 2 present a summary of the included studies, indicating the authors, year of publication, objective, number of participants, if applicable, and main results, for studies based on numerical and experimental methods, respectively.
Seven studies analyzed Da based on numerical methods (including five studies on front crawl, two on backstroke, four on butterfly, and one on breaststroke (considering front crawl and dolphin kick), in which some studies include several techniques) (Table 2). All studies used swimmers as a sample, despite being models (scans of athletes or three-dimensional programming of at least one or more swimmers as their sample). Sixty-eight studies analyzed Da based on experimental methods (including 64 studies on front crawl, six on backstroke, two on butterfly, and six studies on breaststroke (considering front crawl and dolphin kick)) (Supplementary Table S1). They used human swimmers in their entire sample, all with effective experience in the modality and training.
Discussion
The aim of this study was to perform a systematic narrative review on the up-to-date body of knowledge on Da and its components through numerical and experimental methods. In the studies that used numerical methods for the Da analysis, it was found that the main focus was to: 1) confirm whether the drag measured the same force throughout the entire path; 2) verify the variation within the stroke cycle or between stroke cycles. Overall, the studies that focused on the experimental methods to assess Da tended to: 1) present the comparison between the determining factors of performance; 2) emphasize the comparison between the drag variation at different swimming speeds and between sexes and age groups.
Numerical methods – Da
Most studies were focused on the front crawl stroke for submaximal speeds (Cohen et al., 2012; Cohen et al., 2018; Yuan et al., 2019). It was found that the ratio of arm thrust to leg thrust increases with a higher stroke rate (Cohen et al., 2018). However, the attempt at specificity is also evident, i.e., they investigate specific movements such as kicks and arm strokes (cycles). Another study also analyzed the effects of buoyancy during swimming and the drafting as a parameter performance for competition (Cohen et al., 2014). Additionally, the authors observed that at different flow velocities, the hydrodynamic coefficients considered were not constant, knowing that the variation for different hand positions was examined for different phases of the path (Cohen et al., 2018). Regarding Da using numerical methods (Table 2), it was noted that the coefficient of variation (CoV) decreases from 4.8% at the lowest frequency to 3.9% at the highest frequency, indicating that velocity fluctuations decrease with the stroke rate (Cohen et al., 2018). It also highlights the asymmetries in the duration of the different phases of the strokes. The right arm had a 33% shorter impulse period and a 14% longer recovery period than the corresponding periods of the left arm. The duration of the traction phase was similar for both arms (Cohen et al., 2018). There are differences between the use of the underwater flutter kick over the large/slow kick or small/fast kick at 2.18 m/s (Keys and Lyttle, 2007), confirming that the Da, in relation to all these variables, is entirely influenced by the great variation between asymmetries, type of stroke, type of kick, and considering the type of style the swimmer is performing.
During the movements, vortex structures are generated by the arms, which then pass along the body towards the movement of the legs (using a female swimmer at submaximal speed in front crawl). These structures dissipate quickly due to the high-frequency kicking of the legs. There are earlier and more recent references (Cohen et al., 2018; Cohen et al., 2020) that suggest that generated vortices can be used to increase propulsion through vortex recapture. Another study that determined the pitching effects of buoyancy during all competitive swimming strokes (front crawl, backstroke, breaststroke, and butterfly) with a male swimmer and a female swimmer at constant submaximal speed verified that the average thrust torque tended to increase in the legs and decrease in the head (Cohen et al., 2014). However, the instantaneous torque had an opposite effect during part of the throttle stroke. In addition, the alternating techniques (front crawl and backstroke) showed smaller variations in the positions of the center of mass, thrust torques and positions of the center of thrust (Cohen et al., 2014). The simultaneous techniques (butterfly and breaststroke) showed greater variations in buoyancy torques, directly influencing the swimmer’s ability to maintain a horizontal inclination to perform the strokes. This helps athletes swim efficiently by minimizing their frontal areas and the consequent pressure drag (Cohen et al., 2014). The CoV values were moderate for front crawl (53% for women and 26% for men, respectively, this order will be used from now on) and backstroke (52% and 28%), with female values being approximately twice than those of males. The CoV values for butterfly (132% and 133%) and breaststroke (130% and 127%) were significantly higher than for the other strokes. The CoV is higher for strokes with synchronized limb movement. The CoV, and consequently Da, change depending on the movement or swimming phase, being different between kicks and strokes (Cohen et al., 2015). Regarding dolphin kicks, it was observed that the CoV of swimming velocity remains small (7–9%) in experiments with dolphin kicks even when the frequency increases. The amplitude of velocity fluctuations increases, which turns out to be much lower than other intracycle simulations (28–59%). The extension kick proved to be more important than the flexion kick (extension can also be known as down in prone swim and up in dorsal swim) for generating momentum (Cohen et al., 2012). The study by Keys and Lyttle (2007) also demonstrated that it is beneficial to use the underwater flutter kick over the large/slow kick or the small/fast kick using the CFD method.
In all techniques, but mostly in front crawl, swimmers should focus on maximizing their leg extension (it can be called the whiplash effect), as this generates most of the impulse (Cohen et al., 2012). Additionally, they should focus on decreasing Da, even knowing that these values change according to important multivariable and that they derive from the variation of swimming along the swimming path. For example, the full dolphin kick strikes a balance between minimizing drag and maximizing thrust while minimizing the physical effort required of the swimmer (Cohen et al., 2012). The periods before course reversals correspond to the maximum drag forces in the direction of the current, so swimmers should be aware of rapid reversals of direction (turns). After starting and turning, increasing stroke frequency (SF) automatically results in a linear increase in speed. All these recommendations described can be useful to optimize the swimmer’s stroke technique (Cohen et al., 2012). It can be assumed that studies with numerical methods have a higher percentage of studies variability (83.3% focus on the front crawl technique), despite a low number of articles that consider Da. Most studies that focus on front crawl try to evaluate multivariable (strokes, kicks, and stroke frequency), but always at constant speed (submaximal). In a way, studying the drag while considering these variables has become crucial in these studies. In butterfly, studies focused on the analysis of underwater dolphin kicks concluded that cases of higher kick frequency produced higher peaks of both thrust and drag, as already mentioned in a study by the same author that focuses on the front crawl technique. The extension kick proved to be more important for generating momentum than the flexion kick. The only study that showed a greater range of study was the one by Cohen et al., 2014 in which they compared all swimming techniques for a constant submaximal speed. The authors confirmed that the variation in buoyancy torque is much greater during breaststroke and butterfly than during front crawl and backstroke, having a peak of Da in this phase compared to the other techniques.
It should be noted that numerical methods that measure Da have some limitations. A main limitation of the laser body scanned method is that the volume enveloped by the triangular surface mesh is assumed to be of uniform density on the entire swimmer’s internal volume, which requires a very detailed reproduction of the swimmer’s body, as well as specific kinematics to be accurate (Cohen et al., 2012; Cohen et al., 2015). Another limitation is the approximation of the free surface as a horizontal plane (Cohen et al., 2012; Cohen et al., 2015). Swimming involves rapid accelerations and decelerations of the limbs and the estimates obtained are highly limited (Cohen et al., 2015). Regarding the numerical methods, the body position was limited to a single angle to prevent the swimmer’s model from deviating from its course, which ended up conditioning the trajectory, and the results obtained (Cohen et al., 2020). These limitations constitute a solid basis to be considered in future studies (Cohen et al., 2015; Yuan et al., 2019).
Experimental methods – Da
Effects of Da on elite/adult swimmers
Historically, Da was first measured in adult swimmers (e.g., di Prampero et al., 1974; Kolmogorov et al., 1997). Overall, studies noted that drag and Cd are about 1.5–2 times greater in Da than in passive conditions (di Prampero et al., 1974; Kolmogorov and Duplishcheva, 1992). In addition, such studies confirmed that better swimming technique reduced Da essentially due to reduced Cd. Indeed, Kolmogorov et al. (1997) supported the idea that elite swimmers have a greater ability to reduce Da than non-elite swimmers. More recently, Neiva et al. (2021) analyzed the effects of a swimming training mesocycle on the performance and Da of master swimmers in front crawl. The authors concluded that there is an improvement in the performance of master swimmers after 4 weeks of aerobic training. This also resulted in the reduction of Da while swimming mainly at submaximal speeds. Therefore, based on the literature, it can be stated that technical training plays a key role on reducing Da. Nonetheless, adult/elite swimmers tend to present greater Da and power needed to overcome drag, especially when the competitive level increases (Zamparo et al., 1996; Takagi et al., 1999; Toussaint et al., 2004; Zamparo et al., 2009; Seifert et al., 2010; Morais et al., 2020a; Kolmogorov et al., 2021). Furthermore, it is known that there are several variables that can directly influence the drag of a swimmer, as expressed in Eq. 3. Such variables are also dependent on external variables and in adults become even more important (Kolmogorov et al., 1997; Kjendlie and Stallman, 2008). Adult/elite swimmers tend to have a larger FSA and a fastest swimming speed than other age groups (Gatta et al., 2015; Kolmogorov et al., 2021; González-Ravé et al., 2022). Body position may also affect the hydrodynamic position and, consequently, Da. For example, Formosa et al. (2014) aimed to quantify the influence of the breathing action on Da during swimming. This variation is reported to be large when compared to non-breathing, with a 16%–26% difference in drag force during swimming. The simple act of breathing changes Da, so this variable must also be considered. Others aimed to study Da in a completely different way, examining relationships between IdC and Da assuming that at a constant speed, the average drag is equal to the average propulsion, expressing the idea presented in Eq. 1 (Seifert et al., 2015). In front crawl swimmers, changes in inter-arm coordination were linked to changes in resistance forces when swimming at different speeds. A significant and positive linear regression between IdC and Da was observed (Seifert et al., 2015). Overall, adult/elite swimmers present greater values of Da, mainly based on the assumption that they generate a greater metabolic power and mechanical power (Gatta et al., 2016; Kolmogorov et al., 2021).
Effects of Da on young swimmers
Active drag has been largely studied in young swimmers over the last decade, specifically in front-crawl (Kjendlie et al., 2004; Barbosa et al., 2010b; Marinho et al., 2010a; Morais et al., 2012; Morais et al., 2021). In studies on this topic, the authors noted that the best performers were also those with the highest Da and CDa (Morais et al., 2015; Barbosa et al., 2019). As expressed in Eq. 2, drag variables are highly dependent on swimming velocity and FSA. This indicates that bigger and faster swimmers are more likely to be under more drag (Barbosa et al., 2019; Silva et al., 2019; Morais et al., 2021). For example, top performers in freestyle sprinting events (front-crawl swim) not only had faster swimming velocity and better kinematics and swimming efficiency but also higher Da (Barbosa et al., 2013; Ribeiro et al., 2017; Barbosa et al., 2019). Thus, Da should be analyzed with some caution in young swimmers. That is, not always an increase in Da can be related to a decrease in performance. As young swimmers go through growth and maturation processes, they increase their body features, more specifically their FSA (Morais et al., 2020a; Morais et al., 2021). Therefore, an increase in body features leads to an increase in swimming velocity as well as in Da. Indeed, even in detraining periods this phenomenon occurs. It was noted that during an 11-week detraining period, swimmers increased their FSA (as well as other anthropometric features), and their swimming velocity and Da (Morais et al., 2020a). This highlights the importance that anthropometrics have on swimming velocity and Da. On the other hand, performing specific training to improve swimming technique may have a positive impact on the swimmers’ Da. For instance, Marinho et al. (2010a) aimed to assess the effects of 8-week of training in young swimmers’ Da. Although non-significant differences were found over time, the authors observed that later on, Da and CDa decreased in both genders. Authors argued that 8 weeks of specific swimming training were not sufficient to allow significant improvements on swimming technique (Marinho et al., 2010a). A reason for this non-significant effect can be the anthropometric factor, as young swimmers tend to increase their body dimensions. Furthermore, others aimed to understand the effect of Da on swimming performance during an entire competitive season (Morais et al., 2014). It was noted that depending on the season moment and training periodization, the effect of Da on swimming performance changes. At the beginning of the season, when the main aim is to increase energy, Da is the main determinant of performance. Again, as Da is strongly related to swimming velocity, an increase in swimming velocity will lead to an increase in Da. This indicates that coaches of young swimmers should be aware that when the goal is to build energy quickly, this can lead to an increase in Da and CDa (variables related to swimming technique).
Sex effect
Studies have compared Da between genders, whether among adults (Pendergast et al., 1977; Kolmogorov et al., 2021) or young swimmers (Barbosa et al., 2013; Barbosa et al., 2015a). In adults, Da and the hydrodynamic coefficient at maximum speed in front crawl showed significant differences between genders (Xin-Feng et al., 2007; Kjendlie and Stallman, 2008; Marinho et al., 2010b). Based on the literature, it can be stated that front crawl is the most analyzed stroke and boys/men are more studied than girls/women. In any case, studies corroborate the idea that the values presented by men compared to women are always higher, in regard to strength and Da (Kolmogorov and Duplishcheva, 1992; Kolmogorov et al., 1997). Initially, Toussaint et al. (1988), who analyzed Da in relation to speed in male and female swimmers, observed that differences in drag force and Cd are significant regardless of the speed in question. In addition these differences are also strongly present when all techniques other than front crawl are evaluated, ranging from 48.57 N to 105.88 N in men and 36.25 N–77.01 N (Xin-Feng et al., 2007). In another recent study, in all swimming techniques regarding metabolic power, men showed higher values of metabolic power and greater mechanical efficiency than women (Pai = 3346–3560 W and eg = 0.062–0.068 vs. Pai = 2248–2575 W and eg = 0.049–0.052, correspondingly in this order) (Kolmogorov et al., 2021). In all swimming techniques and for both sexes, values of metabolic power and mechanical power increased with exercise intensity (Pendergast et al., 1977; Kolmogorov et al., 2021). The opposite effect can be observed when technical components are analyzed, namely the influence of breathing on the effect of Da during swimming. Formosa et al. (2014) demonstrated that male participants who exhibited a breathing action caused a greater net drag force (26%) compared to females (16%). This confirms once again that these authors agree with others who state that the increase in Da is not synonymous with worse performance, but simply a natural increase in Da when the performance is also better (Seifert et al., 2010).
In an approach aimed at young swimmers, in relation to all swimming techniques but mostly front crawl, studies show that several anthropometric, kinematic and efficiency variables were significantly higher in boys than in girls (Morais et al., 2012; Barbosa et al., 2013; Barbosa et al., 2015a). Comparing both sexes, Barbosa et al., 2015a indicated that most of the studied variables showed non-significant differences (controlled for sprint performance). Nonetheless, boys performed better than girls due to their larger constitution and natural physical development at these ages (Barbosa et al., 2015a; Barbosa et al., 2015b). Thus, it is evident that adults present much more solid results regarding the comparison between genders because young swimmers are in the process of maturation and growth. These changes in the morphology of young swimmers can constantly affect their hydrodynamics (Morais et al., 2015; Morais et al., 2020a). Likewise, Barbosa et al. (2015b) when analyzing the changes in the hydrodynamic profile of young swimmers throughout a season, realized that no variable had a significant sex effect, due to the fact that throughout the season the hydrodynamic changes occurred in a non-existent linear way. This is clear when analyzing the differences between the beginning and the end of the epoch, as the drag decreased when comparing these moments (−4.37 ± 39.36%). Additionally, the study by Morais et al. (2014) corroborates this statement, confirming that the latent growth curve shows high variability in performance growth and that there is a significant effect on performance growth between genders.
Determinants of Da
As shown in Eq. 2, Da is dependent of speed, FSA, and Cd (in water density, which is constant). Initially di Prampero et al. (1974), pioneered the study of body drag and mechanical efficiency during swimming at speeds of 0.55 and 0.9 m/s. It was shown that the basic approach and the quantitative analysis of swimming proficiency were promising for the study of different forms of locomotion on and under the water surface. The studies by Zamparo et al. (1996) and Clarys (1985) found out that drag in the prone position under the water surface was greater than on the water surface, but the Da reached twice the values of drag in relation to passive drag during swimming. The actual strategy implemented by swimmers to neutralize underwater torque tolerates a large increase in Da (Zamparo et al., 1996; Zamparo et al., 2009). Lyttle et al. (1999) and Lyttle et al. (2000) aimed to analyze the variability and amount of drag at different speeds and depths. They showed that for speeds between 1.6 and 3.1 m/s there were no significant differences in drag forces recorded between the speeds indicated in front crawl, although the coefficient of the measures of variation for these tests indicated high reliability. However, although the differences are not significant, there is a tendency for the drag force to present a difference between the speeds, and it is evident that this force constantly increases (Lyttle et al., 1999; Lyttle et al., 2000). This may be because the applications of the towing device for swimming trawl research are widespread (Lyttle et al., 1999). It is necessary to take specific variables such as establishing the improved speed to start the underwater movement (Lyttle et al., 2000), in which results show that experienced swimmers should glide after pushing the wall until they decelerate to speeds between 2.2 and 1.9 m/s for maximum Da reduction benefits at higher glide speeds.
When comparing the drag/velocity relationship, it was shown that greater drag forces promoted a greater intracycle variation of horizontal velocity (di Prampero et al., 1974; Lyttle et al., 1999). However, as drag depends on the square of velocity, a comparison between swimmers is only relevant when: 1) it is done at the same absolute velocity, or 2) the effect of velocity is somehow controlled later (Barbosa et al., 2014). The same authors revealed that there were positive and moderate to strong associations between Da and velocity (intracycle variation) when controlling for the effect of swimming velocity alone in each test (i.e., slip decay velocity method and perturbation velocity method) and swimming speeds in young swimmers as well. Thus, empirical research confirms the theoretical relationship defined for the intracycle variation of horizontal velocity and drag. It can be mentioned that this topic was first argued in the study by di Prampero et al. (1974). The authors reinforced the idea that a change in velocity affects mechanical efficiency because a change in velocity leads to a change in the body’s reaction to water and similar variations in the mechanical efficiency and strength of the body. Another study indicated one relevant technique to estimate Da (Shimonagata et al., 1999). The aim was to clearly show the relationship between swimming speed and Da in front crawl swimming. This study was innovative at the time because the subjects were towed with the Da system (a towing device like the ATM and VPM) in a hydrodynamic position and the subjects swam several attempts at maximum speed (with additional resistance and with towing by the Da system) (Shimonagata et al., 1999). The propulsion, Da, and swimming speed present a significant correlation, showing that swimming performance depends both on propulsion and Da. Thus, it was essential to verify the existence of a balance between the power generated by the thrust forces and the power needed to overcome the drag forces in front crawl, evaluating the thrust and estimating Da at maximum speed (Gatta et al., 2016). The authors noted that the swimmer’s buoyancy force is very close to the force needed to reduce Da (Gatta et al., 2016; Gatta et al., 2018). Furthermore, another study by Gatta et al. (2018) explored the relationships between mechanical power, thrust power, propulsion efficiency and sprint performance in elite swimmers, reporting that maximum speed in sprint swimming depends on the interaction between power in dry conditions (using a full-body swimming ergometer) and propulsion efficiency. Furthermore, the relationship between maximum velocity and power data was observed with the first method used (in the pool by measuring full tethered swimming force and maximum swimming velocity). The propulsion efficiency is about 40% and the drag is about 1.5 times greater than the values generally reported during passive drag measurements (Gatta et al., 2018). Furthermore, studies such as the one by Shimonagata et al. (1999) showed that swimming speed progresses with increasing propulsion and decreasing Da (Seifert et al., 2010; Gatta et al., 2016; Gatta et al., 2018).
Frontal surface area is another major determinant of Da. Knowing that FSA can dynamically change (i.e., variation) during the swimming stroke, researchers set out to assess whether a single FSA measure is adequate to obtain estimates of Da and mechanical power (Morais et al., 2020b; González-Ravé et al., 2022). The authors noted that, in addition to FSA, swimming speed also changes during arm pull in front crawl, in young swimmers of both sexes (Morais et al., 2020b). There was a significant effect on the variation of the two variables of mechanical power and total input power, as well as on the measure of Da (Morais et al., 2020b). Thus, it is worth mentioning that the variation of the FSA throughout the course cycle must be considered in the assessment of Da (Gatta et al., 2015; Morais et al., 2020b; González-Ravé et al., 2022). Furthermore, Kolmogorov et al. (2021) recently determined that the FSA as a component of Da force is the main reason for the differences in maximum speed among the swimming techniques, as there were no relevant differences for the mechanical and propulsion efficiencies. The body position and swimming coordination parameters have an important influence on performance in different swimming strokes (Zamparo et al., 2009; Stosic et al., 2021). In addition, the body position and coordination between the limbs of competitive swimmers during the transition from underwater to surface swimming represented important factors in swimming speed, explaining 15–30% of the variation during the first stroke cycle (Stosic et al., 2021). This reinforces the idea that swimmers must carefully control the inclination and depth of the body and its coordination between the limbs, especially in the first stroke cycle after swimming underwater. Another study showed that waist indentation and buttock curvature can result in greater drag force and influence swimming performance. When differences in Cd exist, it may be due to the assumption used in Da methodologies that a swimmer’s velocity remains constant throughout the stroke cycle, rather than fluctuating, particularly in front crawl (Papic et al., 2020). Da and Cd had a negative effect on performance, being related to the increase in speed during the act of swimming (Morais et al., 2021). There are also significant correlations between anthropometric variables and Da (Barbosa et al., 2019). In addition, this also happens in front crawl, which results in 69% of the performance in young swimmers, for kinematic variables (efficiency), power in the water and strength on dry land (Morais et al., 2016). After a 10-week break, young swimmers show biomechanical improvements that are mainly explained by their normal growth. SF, Da, and CDa remained unchanged, however, improving performance while maintaining Da is a success factor (Moreira et al., 2014). An earlier study by Sharp and Costill (1989) found that the removal of body hair when swimming in breaststroke reduces the Da, and, thus, the physiology cost of swimming. which directly influences the biomechanical performance of swimming.
Checking the external determinants that directly influence the performance and Da of swimmers, Benjanuvatra et al. (2002) concluded that Da values are lower in swimmers who wear competitive suits (Fastskin ™) when compared to traditional swimwear (p < 0.01), not adopting a specific swimming technique, but a prone position. This variation occurred between 4.8% and 10.2%, and when the underwater flutter kick condition was excluded, all these differences were significant (p < 0.05). Moriyama et al. (2021) showed that Jammer-type race swimsuits improve sprint performance to accompany the increase in maximum swimming speed compared to the conventional training swimsuit, in front crawl. In a relatively recent and innovative study, researchers showed that the AquaTrainer® snorkel does not lead to an increase in Da during the front crawl performed over a wide range of speeds (Ribeiro et al., 2016). In addition, other studies have highlighted the importance of analyzing Da as an important variable to be considered in training (Supplementary Table S1), since the most advantageous pulling distance between members of the same team is between 0 and 50 cm from the lead swimmer, where drag is reduced by 21% and 20%, and in which 6% and 7% represent 50 and 100 cm from the lead swimmer. This is true for front crawl, in which maximal and submaximal speeds were analyzed (Kjendlie et al., 2004; Kjendlie and Stallman, 2008; Barbosa et al., 2013).
Drafting is certainly an underdeveloped subject in the literature, but it is known that the effect of distance between swimmers directly influences metabolic and hydrodynamic responses (Chatard and Wilson, 2003). A 4% body difference in underwater volume (p < 0.001) between the two techniques in the 3D motion analysis also confirmed that the pressure drag and the friction drag were higher between the techniques (Gonjo et al., 2020). In a pioneering study by Yuan et al. (2019), it was shown that the hydrodynamic interaction between human swimmers can best be described and explained in terms of the interference effect of the wave on the surface of free water.
Overview and practical applications
It is important to mention that all experimental methods that exist to measure and evaluate Da indicate that there is no agreement among each other regarding the values presented (Toussaint et al., 2004; Formosa et al., 2012). Nonetheless, all authors stated that all equipment measure the same phenomenon, and it can be said that none is more effective than the other (i.e., no gold-standard exists). They simply measure the effects differently and give different results. Some of the methods used were not completely reliable, as there is some margin of error; however, they highlight some issues that coaches should keep in mind not to apply in training or even to apply in an improved way, putting into practice some of the positive points applied in these studies, even if they present some margin of error. For example, the error in the Kolmogorov method can be attributed to the theoretical basis of the equal power assumption (Toussaint et al., 1988; Strojnik et al., 1999). Another analysis corroborated this by showing that the methods used measured essentially the same phenomenon of Da (Toussaint et al., 1988; Toussaint et al., 2004; Formosa et al., 2012). It is probably more appropriate to state that these methods coincidentally underestimate the Da coefficient by a similar magnitude.
Da is defined by the change in characteristics resulting from the flow around different parts of the body following the movement performed. That is why it is essential to have a strategic notion of body movements throughout the stroke cycles, performing in continuous, active and less passive movements. This confirms the need of Da to be further studied and transmitted to coaches. It is also necessary to understand the implications of Da on performance in a homogeneous way. However, it is believed that decomposing total drag into pressure drag, friction drag and wave drag is useful to understand the physical mechanisms that determine drag.
The study of drag is increasingly essential to collaborate with coaches in the process of understanding the fundamental patterns of movement biomechanics to achieve the best performance in swimming (Pendergast et al., 1977). Thus, through the Da research, it was possible to perceive that most studies present very important aspects of swimming technique, more practical movements and easy-to-maneuver variables, such as the distance between swimmers in a training session (aspiration cone), which can be changed depending on the group and type of work considered (Kjendlie et al., 2004; Kjendlie and Stallman, 2008; Barbosa et al., 2013). Furthermore, it will be essential to understand the drag variables regarding each of the four swimming techniques (Xin-Feng et al., 2007; Kjendlie and Stallman, 2008; Marinho et al., 2010b), observing that the values of drag and drag coefficient change completely (highlighting their oscillation and main difference).
Morais et al. (2011) showed that swimming performance in young swimmers is influenced by their swimming efficiency. Therefore, coaches and practitioners of young swimmers should design training programs with a focus on improving technical training (i.e., improving swimming efficiency), indicating that there are data showing that swimming performance is dependent on the SI (an efficiency estimator) and this, in turn, on dv, SL, AS, and Da (Morais et al., 2011). Considering the performance, latent modeling (modeling a latent growth curve) is a comprehensive way of collecting information about the performance of young swimmers over time. The performance improvement was influenced by the different variables, as well as showing an intra and inter subject variability between genders (Morais et al., 2014; Morais et al., 2015). Otherwise, cluster stability is a feasible, comprehensive and informative method of obtaining information about changes in young swimmers over time. Swimmers can be classified into different clusters based on their performance and determinant factors (Morais et al., 2015).
Finally, it can be confirmed that the resistive or drag images found during swimming greatly influence the swimming performance of swimmers of different age groups, including those in elite competition. The benefits of understanding the factors that affect drag are found to improve performance in this sport in different ways that can be analyzed (Sacilotto et al., 2014). However, current techniques used to measure or experimentally estimate drag values are questioned as to their consistency, thus limiting investigations to certain factors. A recent problem is to understand the best method to be applied to study and analyze the variables considered and to determine a context and purpose. Knowing that the range of methodology is wide but not specific, it can bring some confusion to the process, despite being multifaceted (Sacilotto et al., 2014).
Conclusion
Regarding numerical studies, considering all swimming strokes for a constant submaximal and maximum speed, it was found that the variation in buoyancy torque is much greater during breaststroke and butterfly than during front crawl and backstroke. Experimental studies observed that Da is greater in adults than in children. It is also meaningfully different between sexes with greater values achieved by males. Furthermore, it is evident that speed and FSA are the biggest contributors to the increase in Da (adults have a higher Da value because males and adults tend to have higher speed and FSA). Finally, the technical training dedicated for this purpose makes it possible to reduce Da and CDa and thus improving performance. Through longitudinal studies with pre and post-test it is possible to understand the variability of drag throughout the season and to understand the progression and changes in performance. The intensity of the drag force depends on some factors, among which it is possible to highlight the swimming technique and the morphological characteristics of the subject. The FSA appears as the main morphological characteristic of the subject, having a preponderant role in the determination of the drag force intensity.
It is necessary to understand how the resistive forces in swimming are measured and calculated, because like any method they demonstrate strengths and weaknesses in the evaluation of the techniques described in swimming. Furthermore, it can be indicated that Da is higher in men than in women, while CDa is not clear in the literature as to its significance between genders. Nevertheless, it is known that the CDa between the sexes cannot behave in a different way, because swimming efficiency depends on the drag coefficient. In this sense, the drag coefficient will also show a significant result. Notwithstanding, it should be mentioned that these results and outputs are based on discrete variables measured during an entire trial. Future studies should be conducted to understand how Da and CDa can change within a stroke cycle in all four swimming strokes.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
TL, JM, and DM conceived and designed the study. TL and JM performed the search and data analysis. JM and DM performed the quality assessment. TL and MP carried out the drafting of the manuscript. All authors reviewed the manuscript and approved the submitted version.
Funding
This work is supported by national funds (FCT -Portuguese Foundation for Science and Technology) with the reference 2020.07194.BD and the project UIDB/DTP/04045/2020.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2022.938658/full#supplementary-material
References
Alcock A., Mason B. (2007). “Biomechanical analysis of active drag in swimming,” in Proceedings of the 25th international symposium on biomechanics in sports. Editors H. J. Menzel, and M. H. Chagas (Brazil: Ouro Preto), 212–215.
Barbosa T. M., Bartolomeu R., Morais J. E., Costa M. J. (2019). Skillful swimming in age-groups is determined by anthropometrics, biomechanics and energetics. Front. Physiol. 10, 73. doi:10.3389/fphys.2019.00073
Barbosa T. M., Costa M. J., Marques M. C., Silva A. J., Marinho D. A. (2010b). Modeling the links between young swimmers' performance: Energetic and biomechanic profiles. Pediatr. Exerc. Sci. 22, 379–391. doi:10.1123/pes.22.3.379
Barbosa T. M., Costa M. J., Morais J. E., Morouco P., Moreira M., Garrido N. D., et al. (2013). Characterization of speed fluctuation and drag force in young swimmers: A gender comparison. Hum. Mov. Sci. 32 (6), 1214–1225. doi:10.1016/j.humov.2012.07.009
Barbosa T. M., Morais J. E., Costa M. J., Goncalves J., Marinho D. A., Silva A. J. (2014). Young swimmers' classification based on kinematics, hydrodynamics, and anthropometrics. J. Appl. Biomech. 30 (2), 310–315. doi:10.1123/jab.2013-0038
Barbosa T. M., Morais J. E., Marques M. C., Costa M. J., Marinho D. A. (2015a). The power output and sprinting performance of young swimmers. J. Strength Cond. Res. 29 (2), 440–450. doi:10.1519/JSC.0000000000000626
Barbosa T. M., Morais J. E., Marques M. C., Silva A. J., Marinho D. A., Kee Y. H. (2015b). Hydrodynamic profile of young swimmers: Changes over a competitive season. Scand. J. Med. Sci. Sports 25 (2), e184–e196. doi:10.1111/sms.12281
Benjanuvatra N., Dawson G., Blanksby B. A., Elliott B. C. (2002). Comparison of buoyancy, passive and net active drag forces between Fastskin and standard swimsuits. J. Sci. Med. Sport 5 (2), 115–123. doi:10.1016/S1440-2440(02)80032-9
Bixler B. S., Pease D., Fairhurst F. (2007). The accuracy of computational fluid dynamics analysis of the passive drag of a male swimmer. Sports Biomech. 6, 81–98. doi:10.1080/14763140601058581
Bixler B. S., Schloder M. (1996). Computational fluid dynamics: An analytical tool for the 21st century swimming scientist. J. Swim. Res. 11, 4–22.
Chatard J-C., Wilson B. (2003). Drafting distance in swimming. Med. Sci. Sports Exerc. 35 (7), 1176–1181. doi:10.1249/01.MSS.0000074564.06106.1F
Clarys J. P. (1985). Hydrodynamics and electromyography: Ergonomics aspects in aquatics. Appl. Ergon. 16 (1), 11–24. doi:10.1016/0003-6870(85)90143-7
Cohen R. C. Z., Cleary P. W., Harrison S. M., Mason B. R., Pease D. L. (2014). Pitching effects of buoyancy during four competitive swimming strokes. J. Appl. Biomech. 30 (5), 609–618. doi:10.1123/jab.2013-0260
Cohen R. C. Z., Cleary P. W., Mason B. R., Pease D. L. (2018). Forces during front crawl swimming at different stroke rates. Sports Eng. 21 (1), 63–73. doi:10.1007/s12283-017-0246-x
Cohen R. C. Z., Cleary P. W., Mason B. R., Pease D. L. (2020). Studying the effects of asymmetry on freestyle swimming using smoothed particle hydrodynamics. Comput. Methods Biomech. Biomed. Engin. 23 (7), 271–284. doi:10.1080/10255842.2020.1718663
Cohen R. C. Z., Cleary P. W., Mason B. R., Pease D. L. (2015). The role of the hand during freestyle swimming. J. Biomech. Eng. 137 (11), 111007. doi:10.1115/1.4031586
Cohen R. C. Z., Cleary P. W., Mason B. R. (2012). Simulations of dolphin kick swimming using smoothed particle hydrodynamics. Hum. Mov. Sci. 31 (3), 604–619. doi:10.1016/j.humov.2011.06.008
de Meyrick J. (2003). The Delphi method and health research. Health Educ. (Lond). 103 (1), 7–16. doi:10.1108/09654280310459112
de Morton N. A. (2009). The PEDro scale is a valid measure of the methodological quality of clinical trials: A demographic study. Aust. J. Physiother. 55 (2), 129–133. doi:10.1016/S0004-9514(09)70043-1
di Prampero P. E., Pendergast D. R., Wilson D. W., Rennie D. W. (1974). Energetics of swimming in man. J. Appl. Physiol. 37 (1), 1–5. doi:10.1152/jappl.1974.37.1.1
Formosa D. P., Sayers M. G. L., Burkett B. (2014). The influence of the breathing action on net drag force production in front crawl swimming. Int. J. Sports Med. 35 (13), 1124–1129. doi:10.1055/s-0034-1372636
Formosa D. P., Toussaint H. M., Mason B. R., Burkett B. (2012). Comparative analysis of active drag using the MAD system and an assisted towing method in front crawl swimming. J. Appl. Biomech. 28 (6), 746–750. doi:10.1123/jab.28.6.746
Gatta G., Cortesi M., Fantozzi S., Zamparo P. (2015). Planimetric frontal area in the four swimming strokes: Implications for drag, energetics and speed. Hum. Mov. Sci. 39, 41–54. doi:10.1016/j.humov.2014.06.010
Gatta G., Cortesi M., Swaine I., Zamparo P. (2018). Mechanical power, thrust power and propelling efficiency: Relationships with elite sprint swimming performance. J. Sports Sci. 36 (5), 506–512. doi:10.1080/02640414.2017.1322214
Gatta G., Cortesi M., Zamparo P. (2016). The relationship between power generated by thrust and power to overcome drag in elite short distance swimmers. PLoS One 11 (9), e0162387. doi:10.1371/journal.pone.0162387
Gonjo T., Narita K., McCabe C., Fernandes R. J., Vilas-Boas J. P., Takagi H., et al. (2020). Front crawl is more efficient and has smaller active drag than backstroke swimming: Kinematic and kinetic comparison between the two techniques at the same swimming speeds. Front. Bioeng. Biotechnol. 8, 570657–657. doi:10.3389/fbioe.2020.570657
González-Ravé J. M., Moya-Fernández F., Hermosilla-Perona F., Castillo-García F. J. (2022). Vision-based system for automated estimation of the frontal area of swimmers: Towards the determination of the instant active drag: A pilot study. Sensors (Basel, Switz. 22 (3), 955. doi:10.3390/s22030955
Hazrati P., Sinclair P. J., Ferdinands R. E., Mason B. R. (2016). Reliability of estimating active drag in swimming using the assisted towing method with fluctuating speed. Sports Biomech. 15 (3), 283–294. doi:10.1080/14763141.2016.1161064
Hazrati P., Sinclair P. J., Spratford W., Ferdinands R. E., Mason B. R. (2018). Contribution of uncertainty in estimation of active drag using assisted towing method in front crawl swimming. J. Sports Sci. 36 (1), 7–13. doi:10.1080/02640414.2016.1276295
Hollander A. P., de Groot G., Schenau G. J. V., Toussaint H. M., de Best H., Peeters W., et al. (1986). Measurement of active drag during crawl arm stroke swimming. J. Sports Sci. 4 (1), 21–30. doi:10.1080/02640418608732094
Keys M., Lyttle A. (2007). “Computational fluid dynamics–a tool for future swimming technique prescription,” in The impact of Technology on sport II (London: CRC Press), 633–638.
Kjendlie P. L., Ingjer F., Stallman R. K., Stray-Gundersen J. (2004). Factors affecting swimming economy in children and adults. Eur. J. Appl. Physiol. 93 (1-2), 65–74. doi:10.1007/s00421-004-1164-8
Kjendlie P. L., Stallman R. K. (2008). Drag characteristics of competitive swimming children and adults. J. Appl. Biomech. 24 (1), 35–42. doi:10.1123/jab.24.1.35
Kolmogorov S. V., Duplishcheva O. A. (1992). Active drag, useful mechanical power output and hydrodynamic force coefficient in different swimming strokes at maximal velocity. J. Biomech. 25 (3), 311–318. doi:10.1016/0021-9290(92)90028-Y
Kolmogorov S. V., Rumyantseva O. A., Gordon B. J., Cappaert J. M. (1997). Hydrodynamic characteristics of competitive swimmers of different genders and performance levels. J. Appl. Biomech. 13 (1), 88–97. doi:10.1123/jab.13.1.88
Kolmogorov S. V., Vorontsov A., Vilas-Boas J. P. (2021). Metabolic power, active drag, mechanical and propelling efficiency of elite swimmers at 100 meter events in different competitive swimming techniques. Appl. Sci. (Basel). 11 (18), 8511. doi:10.3390/app11188511
Lyttle A. D., Blanksby B. A., Elliott B. C., Lloyd D. G. (2000). Net forces during tethered simulation of underwater streamlined gliding and kicking techniques of the freestyle turn. J. Sports Sci. 18 (10), 801–807. doi:10.1080/026404100419856
Lyttle A. D., Elliott B. C., Blanksby B. A., Lloyd D. G. (1999). An instrument for quantifying the hydrodynamic drag of swimmers - a technical note. J. Hum. Mov. Stud. 37 (5), 261–270.
Marinho D. A., Barbosa T. M., Costa M. J., Figueiredo C., Reis V. M., Silva A. J., et al. (2010a). Can 8-weeks of training affect active drag in young swimmers? J. Sports Sci. Med. 9 (1), 71–78.
Marinho D. A., Garrido N., Barbosa T. M., Reis V. M., Silva A. J., Costa A. M., et al. (2010b). Can 8 weeks of training in female swimmers affect active drag? Open Sports Sci. J. 3, 36–37. doi:10.2174/1875399x010030100036
Marinho D. A., Silva A. J., Reis V. M., Barbosa T. M., Vilas-Boas J. P., Alves F. B., et al. (2011). Three-dimensional CFD analysis of the hand and forearm in swimming. J. Appl. Biomech. 27 (1), 74–80. doi:10.1123/jab.27.1.74
Masset J. B., Rouard A. H., Taiar R. (1999). 3-D analysis of the backstroke style. J. Hum. Mov. Stud. 36 (6), 253–271.
McHugh M. L. (2012). Interrater reliability: The kappa statistic. Biochem. Med. 22, 276–282. doi:10.11613/bm.2012.031
Morais J. E., Costa M. J., Mejias E. J., Marinho D. A., Silva A. J., Barbosa T. M. (2011). Morphometric study for estimation and validation of trunk transverse surface area to assess human drag force on water. J. Hum. Kinet. 28, 5–13. doi:10.2478/v10078-011-0017-x
Morais J. E., Forte P., Silva A. J., Barbosa T. M., Marinho D. A. (2021). Data modeling for inter- and intra-individual stability of young swimmers' performance: A longitudinal cluster analysis. Res. Q. Exerc. Sport 92 (1), 21–33. doi:10.1080/02701367.2019.1708235
Morais J. E., Jesus S., Lopes V., Garrido N., Silva A., Marinho D., et al. (2012). Linking selected kinematic, anthropometric and hydrodynamic variables to young swimmer performance. Pediatr. Exerc. Sci. 24 (4), 649–664. doi:10.1123/pes.24.4.649
Morais J. E., Lopes V. P., Barbosa T. M., Moriyama S. I., Marinho D. A. (2020a). How does 11-week detraining affect 11-12 years old swimmers' biomechanical determinants and its relationship with 100 m freestyle performance? Sports Biomech. 21, 1107–1121. doi:10.1080/14763141.2020.1726998
Morais J. E., Marinho D. A., Arellano R., Barbosa T. M. (2019). Start and turn performances of elite sprinters at the 2016 European Championships in swimming. Sports Biomech. 18 (1), 100–114. doi:10.1080/14763141.2018.1435713
Morais J. E., Marques M. C., Marinho D. A., Silva A. J., Barbosa T. M. (2014). Longitudinal modeling in sports: Young swimmers' performance and biomechanics profile. Hum. Mov. Sci. 37, 111–122. doi:10.1016/j.humov.2014.07.005
Morais J. E., Sanders R. H., Papic C., Barbosa T. M., Marinho D. A. (2020b). The influence of the frontal surface area and swim velocity variation in front crawl active drag. Med. Sci. Sports Exerc. 52 (11), 2357–2364. doi:10.1249/MSS.0000000000002400
Morais J. E., Silva A. J., Marinho D. A., Marques M. C., Batalha N., Barbosa T. M. (2016). Modelling the relationship between biomechanics and performance of young sprinting swimmers. Eur. J. Sport Sci. 16 (6), 661–668. doi:10.1080/17461391.2016.1149227
Morais J. E., Silva A. J., Marinho D. A., Seifert L., Barbosa T. M. (2015). Cluster stability as a new method to assess changes in performance and its determinant factors over a season in young swimmers. Int. J. Sports Physiol. Perform. 10 (2), 261–268. doi:10.1123/ijspp.2013-0533
Moreira M. F., Morais J. E., Marinho D. A., Silva A. J., Barbosa T. M., Costa M. J. (2014). Growth influences biomechanical profile of talented swimmers during the summer break. Sports Biomech. 13 (1), 62–74. doi:10.1080/14763141.2013.865139
Moriyama S. I., Mankyu H., Tsunokawa T., Kurono T., Mizukoshi H., Ogita F. (2021). Does a jammer-type racing swimsuit improve sprint performance during maximal front-crawl swimming? Sports Biomech. 2021, 1–13. doi:10.1080/14763141.2021.1878263
Narita K., Nakashima M., Takagi H. (2017). Developing a methodology for estimating the drag in front-crawl swimming at various velocities. J. Biomech. 54, 123–128. doi:10.1016/j.jbiomech.2017.01.037
Narita K., Nakashima M., Takagi H. (2018a). Effect of leg kick on active drag in front-crawl swimming: Comparison of whole stroke and arms-only stroke during front-crawl and the streamlined position. J. Biomech. 76, 197–203. doi:10.1016/j.jbiomech.2018.05.027
Narita K., Ogita F., Nakashima M., Takagi H. (2018b). Comparison of active drag using the MRT-method and the MAD-system in front crawl swimming. Proceedings 2 (6), 287. doi:10.3390/proceedings2060287
Neiva H. P., Fernandes R. J., Cardoso R., Marinho D. A., Abraldes J. A. (2021). Monitoring master swimmers' performance and active drag evolution along a training mesocycle. Int. J. Environ. Res. Public Health 18 (7), 3569. doi:10.3390/ijerph18073569
Papic C., McCabe C., Gonjo T., Sanders R. (2020). Effect of torso morphology on maximum hydrodynamic resistance in front crawl swimming. Sports Biomech. 2020, 1–15. doi:10.1080/14763141.2020.1773915
Pendergast D. R., Capelli C., Craig A. B., di Prampero P. E., Minetti A. E., Mollendorf J., et al. (2006). “Biophysics in swimming,” in Biomechanics and medicine in swimming X. Porto: Portuguese journal of sport science. Editors J. P. Vilas-Boas, F. Alves, and A. Marques (Porto: Faculdade de Desporto da Universidade do Porto), 185–189.
Pendergast D. R., Di Prampero P. E., Craig A. B., Wilson D. R., Rennie D. W. (1977). Quantitative analysis of the front crawl in men and women. J. Appl. Physiol. Respir. Environ. Exerc. Physiol. 43 (3), 475–479. doi:10.1152/jappl.1977.43.3.475
Peterson Silveira R., Soares S. M., Zacca R., Alves F. B., Fernandes R. J., de Souza Castro F. A., et al. (2019). A biophysical analysis on the arm stroke efficiency in front crawl swimming: Comparing methods and determining the main performance predictors. Int. J. Environ. Res. Public Health 16 (23), E4715. doi:10.3390/ijerph16234715
Poizat G., Ade D., Seifert L., Toussaint H., Gal-Petitfaux N. (2010). Evaluation of the measuring active drag system usability: An important step for its integration into training sessions. Int. J. Perform. Anal. Sport 10 (2), 170–186. doi:10.1080/24748668.2010.11868512
Ribeiro J., Figueiredo P., Guidetti L., Alves F., Toussaint H., Vilas-Boas J. P., et al. (2016). AquaTrainer® snorkel does not increase hydrodynamic drag but influences turning time. Int. J. Sports Med. 37 (4), 324–328. doi:10.1055/s-0035-1555859
Ribeiro J., Figueiredo P., Morais S., Alves F., Toussaint H., Vilas-Boas J. P., et al. (2017). Biomechanics, energetics and coordination during extreme swimming intensity: Effect of performance level. J. Sports Sci. 35 (16), 1614–1621. doi:10.1080/02640414.2016.1227079
Sacilotto G., Ball N., Mason B. (2014). A biomechanical review of the techniques used to estimate or measure resistive forces in swimming. J. Appl. Biomech. 30 (1), 119–127. doi:10.1123/jab.2013-0046
Schreven S., Toussaint H. M., Smeets J. B. J., Beek P. J. (2013). The effect of different inter-pad distances on the determination of active drag using the Measuring Active Drag system. J. Biomech. 46 (11), 1933–1937. doi:10.1016/j.jbiomech.2013.05.020
Seifert L., Schnitzler C., Bideault G., Alberty M., Chollet D., Toussaint H. M. (2015). Relationships between coordination, active drag and propelling efficiency in crawl. Hum. Mov. Sci. 39, 55–64. doi:10.1016/j.humov.2014.10.009
Seifert L., Toussaint H. M., Alberty M., Schnitzler C., Chollet D. (2010). Arm coordination, power, and swim efficiency in national and regional front crawl swimmers. Hum. Mov. Sci. 29 (3), 426–439. doi:10.1016/j.humov.2009.11.003
Sharp R. L., Costill D. L. (1989). Influence of body hair removal on physiological responses during breaststroke swimming. Med. Sci. Sports Exerc. 21 (5), 576–580. doi:10.1249/00005768-198910000-00013
Shimonagata S., Taguchi M., Taba S., Aoyagi M. (1999). “Estimation of propulsion and drag force in front crawls stroke,” in Biomech. Med. Swimming VIII. Editors K. L. Keskinen, P. V. Komi, and A. P. Hollander (Jyväskylä: Gummerus Printing), 107–112.
Silva A. F., Figueiredo P., Ribeiro J., Alves F., Vilas-Boas J. P., Seifert L., et al. (2019). Integrated analysis of young swimmers’ sprint performance. Mot. Control 23 (3), 354–364. doi:10.1123/mc.2018-0014
Silva A. J., Reis V. M., Guidetti L., Alves F. B., Mota P., Freitas J., et al. (2007). Effect of creatine on swimming velocity, body composition and hydrodynamic variables. J. Sports Med. Phys. Fit. 47 (1), 58–64.
Silveira R. P., Soares S. M., Zacca R., Alves F. B., Fernandes R. J., Castro F. A. D., et al. (2019). A biophysical analysis on the arm stroke efficiency in front crawl swimming: Comparing methods and determining the main performance predictors. Int. J. Environ. Res. Public Health 16 (23), E4715. doi:10.3390/ijerph16234715
Stosic J., Veiga S., Trinidad A., Navarro E. (2021). How should the transition from underwater to surface swimming be performed by competitive swimmers? Appl. Sci. (Basel). 11 (1), 122. doi:10.3390/app11010122
Strojnik V., Bednarik J., Strumbelj B. (1999). “Active and passive drag in swimming,” in Biomech med swimming VIII. Editors K. L. Keskinen, P. V. Komi, and A. P. Hollander (Jyvaskyla, Finland: University of Jyvaskyla), 113–117.
Taıär R., Sagnes P., Henry C., Dufour A. B., Rouard A. H. (1999). Hydrodynamics optimization in butterfly swimming: Position, drag coefficient and performance. J. Biomech. 32 (8), 803–810. doi:10.1016/S0021-9290(99)00066-4
Takagi H., Nakashima M., Sato Y., Matsuuchi K., Sanders R. H. (2016). Numerical and experimental investigations of human swimming motions. J. Sports Sci. 34 (16), 1564–1580. doi:10.1080/02640414.2015.1123284
Takagi H., Shimizu Y., Kodan N. (1999). A hydrodynamic study of active drag in swimming. JSME Int. J. Ser. B Fluids. Therm. Eng. 42 (2), 171–177. doi:10.1299/jsmeb.42.171
Toussaint H. M., Beek P. J. (1992). Biomechanics of competitive front crawl swimming. Sports Med. 13 (1), 8–24. doi:10.2165/00007256-199213010-00002
Toussaint H. M., de Groot G., Savelberg H. H., Vervoorn K., Hollander A. P., van Ingen Schenau G. J. (1988). Active drag related to velocity in male and female swimmers. J. Biomech. 21 (5), 435–438. doi:10.1016/0021-9290(88)90149-2
Toussaint H. M., Roos P. E., Kolmogorov S. (2004). The determination of drag in front crawl swimming. J. Biomech. 37 (11), 1655–1663. doi:10.1016/j.jbiomech.2004.02.020
Toussaint H. M., Truijens M., Elzinga M. J., van de Ven A., de Best H., Snabel B., et al. (2002). Effect of a Fast-skin 'body' suit on drag during front crawl swimming. Sports Biomech. 1 (1), 1–10. doi:10.1080/14763140208522783
Toussaint H. M., Vervoorn K. (1990). Effects of specific high resistance training in the water on competitive swimmers. Int. J. Sports Med. 11 (3), 228–233. doi:10.1055/s-2007-1024797
van der Vaart A. J., Savelberg H. H., de Groot G., Hollander A. P., Toussaint H. M., van Ingen Schenau G. J. (1987). An estimation of drag in front crawl swimming. J. Biomech. 20 (5), 543–546. doi:10.1016/0021-9290(87)90254-5
Vilas-Boas J. P., Costa L., Fernandes R. J., Ribeiro J., Figueiredo P., Marinho D., et al. (2010). Determination of the drag coefficient during the first and second gliding positions of the breaststroke underwater Stroke. J. Appl. Biomech. 26 (3), 324–331. doi:10.1123/jab.26.3.324
Xin-Feng W., Lian-Ze W., Wei-Xing Y., De-Jian L., Xiong S. (2007). A new device for estimating active drag in swimming at maximal velocity. J. Sports Sci. 25 (4), 375–379. doi:10.1080/02640410600812021
Yuan Z. M., Li M. X., Ji C. Y., Li L., Jia L. B., Incecik A. (2019). Steady hydrodynamic interaction between human swimmers. J. R. Soc. Interface 16 (150), 20180768. doi:10.1098/rsif.2018.0768
Zamparo P., Capelli C., Termin B., Pendergast D. R., diPrampero P. E. (1996). Effect of the underwater torque on the energy cost, drag and efficiency of front crawl swimming. Eur. J. Appl. Physiol. Occup. Physiol. 73 (3-4), 195–201. doi:10.1007/BF02425476
Zamparo P., Cortesi M., Gatta G. (2020). The energy cost of swimming and its determinants. Eur. J. Appl. Physiol. 120 (1), 41–66. doi:10.1007/s00421-019-04270-y
Zamparo P., Gatta G., Pendergast D., Capelli C. (2009). Active and passive drag: The role of trunk incline. Eur. J. Appl. Physiol. 106 (2), 195–205. doi:10.1007/s00421-009-1007-8
Glossary
ρ density of water
a acceleration
AIS assisted towing method
AP pitch angle
AS arm span
ATM assistant towing method
Cd coefficient of drag
CDa coefficient of active drag
CFD computational fluid dynamics
CoV coefficient of variation
Cx hydrodynamic coefficient
D drag force
Da active drag
Dp passive drag
dv speed fluctuation
EM experimental method
F total drag force
Fd active drag force
Ff friction component
Fp pressure component
Fr froude number
FSA frontal surface area
Fw wave component
ICC intra-class correlation coefficients
IdC coordination index
IVV intra-cyclic velocity variations
K Cohen’s Kappa
M total mass
MAD measuring Da system
MRT residual thrust measured values
NM numerical method
Pai metabolic power (power input)
Pk mechanical power to transfer
S projected frontal surface area
SB sweep-back angle
SE stroke efficiency
SF stroke frequency
SI stroke index
SL stroke length
SPH Coupled biomechanical-smoothed particle hydrodynamics
T total propulsive force
TDI technique drag index
TTSA trunk transverse surface
v swimming speed
VO2max maximal oxygen uptake
VPM speed perturbation method
WS whole stroke
Keywords: active drag, water resistance, biomechanics, assisted swimming, resisted swimming
Citation: Lopes TJ, Morais JE, Pinto MP and Marinho DA (2022) Numerical and experimental methods used to evaluate active drag in swimming: A systematic narrative review. Front. Physiol. 13:938658. doi: 10.3389/fphys.2022.938658
Received: 07 May 2022; Accepted: 03 October 2022;
Published: 20 October 2022.
Edited by:
Carla McCabe, Ulster University, United KingdomReviewed by:
Guilherme Tucher, Federal University of Rio de Janeiro, BrazilDaniel J. Daly, KU Leuven, Belgium
Matteo Cortesi, University of Bologna, Italy
Copyright © 2022 Lopes, Morais, Pinto and Marinho. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tiago J. Lopes, dGlhZ29fbG9wZXNfMTdAaG90bWFpbC5jb20=
 Tiago J. Lopes
Tiago J. Lopes Jorge E. Morais
Jorge E. Morais Mafalda P. Pinto
Mafalda P. Pinto Daniel A. Marinho
Daniel A. Marinho