Spatiotemporal Patterns in a General Networked Hindmarsh-Rose Model

Neuron modelling helps to understand the brain behavior through the interaction between neurons, but its mechanism remains unclear. In this paper, the spatiotemporal patterns is investigated in a general networked Hindmarsh-Rose (HR) model. The stability of the network-organized system without delay is analyzed to show the effect of the network on Turing instability through the Hurwitz criterion, and the conditions of Turing instability are obtained. Once the analysis of the zero-delayed system is completed, the critical value of the delay is derived to illustrate the profound impact of the given network on the collected behaviors. It is found that the difference between the collected current and the outgoing current plays a crucial role in neuronal activity, which can be used to explain the generation mechanism of the short-term memory. Finally, the numerical simulation is presented to verify the proposed theoretical results.

Introduction

Neuron modelling plays a vital role in understanding the brain behavior with its dynamic mechanisms Sun et al. (2018); Wang et al. (2021a),Wang et al. (2021b), Wang et al. (2022); Perc (2006). The HR model is the extended Fitzhugh–Nagumo model, which could exhibit various firing activities (periodic, chaotic, bursting firings, etc.) of the membrane potential Hindmarsh and Rose (1982), Hindmarsh and Rose (1984); Gu and Pan (2015). The dynamic bifurcation of the HR model was calculated and analyzed to illustrate the effects of different parameters on the dynamic behavior Wu et al. (2016). And the HR model with electromagnetic induction by analyzing the stability of equilibrium points was studied to show that electromagnetic induction could regularize chaotic regimes by the number of spikes Goulefack et al. (2022). The HR model with the slow intracellular exchange of calcium ions was investigated to present the effects of the coupling strength and the forcing current on the network behavior Rajagopal et al. (2019). Then the role of delay in the bifurcation behavior was considered in the fractional-order HR model with delay, and the condition for the existence of Hopf bifurcation was present Shi et al. (2020). Also, noise-induced resonances were obtained to describe the response of the HR model to noisy signals and intrinsic oscillations Baltanas and Casado (2002). A networked-organized HR model with delay was developed to explain the spatial relations between neurons and model the process of neural migration Lepek and Fronczak (2018). Although the phenomenon of spatiotemporal patterns was often considered to show the firing activities in a general networked HR model with the delay Umesh and Ambika (2021); Shi et al. (2022); Santos et al. (2017), the interaction mechanism of network nodes remains unclear.

Turing instability is a kind of collective spatial behavior, and the pattern formation could describe the interaction between species in a reaction-diffusion system and explain the biological mechanism (the formation of zebra and zebrafish skin, the nonlocal synaptic interactions) Turing (1990); Kolodina et al. (2021); Kondo et al. (2021). A nonlocal evolution equation was developed to explain color patterns on a guppy fish skin through the bifurcation theory Cygan (2021). The effect of landscape heterogeneity on pattern formation is studied to find the mechanisms of diffusion-driven instabilities in the predator-prey interactions Zaker et al. (2021). And the firing behavior of neurons can be represented by the pattern formation in the network-organized FitzHugh-Nagumo model Zheng and Shen (2020). The elimination of spiral waves is investigated to prevent some brain disorders by the transition between pattern formations in an HR model Eteme et al. (2019). Pattern formation is a well-studied phenomenon in neural field models, which describes the collected groups of neurons and presents the generation of spatial distribution in a dynamical system Kriener et al. (2013). Sometimes, the collective behavior is easier to keep the network in activity Erichsen and Brunnet (2009). Also, short-term memory is a kind of the collective behavior of neurons Zheng et al. (2020). Meanwhile, the network topology is predominant in the critical features of Turing systems Diego et al. (2018). Therefore, the general networked HR model should be considered to show the dynamical mechanism of neuronal activity.

It is well known that the neurons link each other through a network, and the brain activity is the collective behavior of the neurons rather than a single neuron. Pattern formation and bifurcation Tian et al. (2021); Yang (2022); Ma et al. (2021) is a crucial tool to elaborate on the dynamic and biological mechanism of the collective behavior of the neurons. In this paper, an HR model with a random network is considered to show the spatiotemporal patterns of collective behaviors. The effect of the network on pattern formation is presented through the Hurwitz criterion, and the conditions of Turing instability are derived. Then, Hopf bifurcation illustrates the profound impact of network and delay on the collected behavior. It is found that the difference in network topology plays a vital role in neuronal activity. Finally, the numerical simulation explains the generation mechanism of the short-term memory.

Model Description

In this paper, we consider the following HR model on networks,

$\begin{array}{c}\frac{d{x}_i}{dt}=y_i-a{x}_i^3+b{x}_i^2+I-z_i\left(t-\tau \right)+d_1\sum _{j=1}^n{A}_{ij}\left(t\right)f\left(x_j,x_i\right),\hfill \\ \frac{d{y}_i}{dt}=c-d{x}_i^2-y_i+d_2\sum _{j=1}^n{A}_{ij}\left(t\right)g\left(y_j,y_i\right),\hfill \\ \frac{d{z}_i}{dt}=r\left(s\left(x_i-x_r\right)-z_i\right),\hfill \end{array}(1)$

where x_i, y_i and z_i (i = 1, … , n) denote the membrane potential, recovery variable and bursting variable at node (neuron) i, respectively. I is the external stimulus, A is the adjacent matrix of the interaction between nodes, f (x_j, x_i), g (y_j, y_i) is the diffusive function. The equilibrium point of system (1) can be derived from the following Equation 2

$\begin{array}{c}{y}_0-a{x}_0^3+b{x}_0^2+I-z_0=0,\hfill \\ c-d{x}_0^2-y_0=0,\hfill \\ r\left(s\left(x_0-x_r\right)-z_0\right)=0.\hfill \end{array}(2)$

The linear term of system (1) at (x₀, y₀, z₀) can be expressed as

$\begin{array}{c}\frac{d{x}_i}{dt}=y_i-3a{x}_0^2{x}_i+2b{x}_0{x}_i-z_i\left(t-\tau \right)+d_1\sum _{j=1}^n{A}_{ij}\left(x_j-q{x}_i\right),\hfill \\ \frac{d{y}_i}{dt}=-2d{x}_0{x}_i-y_i+d_2\sum _{j=1}^n{A}_{ij}\left(y_j-q{y}_i\right),\hfill \\ \frac{d{z}_i}{dt}=rs{x}_i-r{z}_i,\hfill \end{array}(3)$

where A_ij is the symmetric adjacent matrix to show the interaction of nodes on network. x_j − qx_i, y_j − qy_i is the linear part of f (x_j, x_i), g (y_j, y_i), respectively. q can be treated as the difference between the collected current and the outgoing current. $L_{ij}=A_{ij}-q\sum _{j=1}^n{A}_{ij}$ and $\sum _{j=1}^n{L}_{ij}{v}_j^k={\mathrm{\Lambda }}_k{v}_i^k$, ${\mathrm{\Lambda }}_k,v^k={(v_1^k,\dots ,v_n^k)}^T$ are the kth eigenvalue of L and the corresponding eigenvector, respectively Zheng and Shen (2020). If the coefficient of x_j does not equal to 1, it simplifies to 1 by extracting the common factors.

A general solution of system (3) is

$\begin{array}{c}{x}_i=\sum _{k=1}^n{c}_k^1{e}^{{\lambda }_{k}t}{v}_i^k,\hfill \\ y_i=\sum _{k=1}^n{c}_k^2{e}^{{\lambda }_{k}t}{v}_i^k,\hfill \\ z_i=\sum _{k=1}^n{c}_k^3{e}^{{\lambda }_{k}t}{v}_i^k.\hfill \end{array}(4)$

Substituting system (4) into system (3), one has

${\lambda }_k\left(\begin{array}{c}\hfill c_k^1\hfill \\ \hfill c_k^2\hfill \\ \hfill c_k^3\hfill \end{array}\right)=J\left(\begin{array}{c}\hfill c_k^1\hfill \\ \hfill c_k^2\hfill \\ \hfill c_k^3\hfill \end{array}\right),$

where

$J=\left[\begin{array}{ccc}\hfill -3a{x_0}^2+d_1\mathrm{\Lambda }+2b{x}_0\hfill & \hfill 1\hfill & \hfill -e^{-{\lambda }_k\tau }\hfill \\ \hfill \hfill \\ \hfill -2d{x}_0\hfill & \hfill d_2\mathrm{\Lambda }-1\hfill & \hfill 0\hfill \\ \hfill \hfill \\ \hfill \hfill \\ \hfill rs\hfill & \hfill 0\hfill & \hfill -r\hfill \end{array}\right]$

Then the characteristic equation is

$\begin{array}{c}|{\lambda }_{k}E-J|={\lambda }^3+a_1{\lambda }^2+\left(a_2+a_3{e}^{-\lambda \tau }\right)\lambda +a_4+a_5{e}^{-\lambda \tau }=0,\hfill \end{array}(5)$

where

$\begin{array}{c}{a}_1=3a{x_0}^2-2b{x}_0-{\mathrm{\Lambda }}_k{d}_1-{\mathrm{\Lambda }}_k{d}_2+r+1,\hfill \\ a_2=-3a{x_0}^2{\mathrm{\Lambda }}_k{d}_2+3ar{x_0}^2+2b{x}_0{\mathrm{\Lambda }}_k{d}_2+{{\mathrm{\Lambda }}_k}^2{d}_1{d}_2+3a{x_0}^2-2br{x}_0-r{\mathrm{\Lambda }}_k{d}_1-r{\mathrm{\Lambda }}_k{d}_2-2b{x}_0+2d{x}_0-{\mathrm{\Lambda }}_k{d}_1+r,\hfill \\ a_3=rs,\hfill \\ a_4=-3ar{x_0}^2{\mathrm{\Lambda }}_k{d}_2+2br{x}_0{\mathrm{\Lambda }}_k{d}_2+r{{\mathrm{\Lambda }}_k}^2{d}_1{d}_2+3ar{x_0}^2-2br{x}_0+2d{x}_{0}r-r{\mathrm{\Lambda }}_k{d}_1,\hfill \\ a_5=-rs{\mathrm{\Lambda }}_k{d}_2+rs.\hfill \end{array}$

When τ = 0, the characteristic equation is,

$\begin{array}{c}p\left(\lambda \right)={\lambda }^3+a_1{\lambda }^2+\left(a_2+a_3\right)\lambda +a_4+a_5=0.\hfill \end{array}(6)$

According to Hurwitz criterion, the sufficient and necessary conditions for stable system (1) are,

$\begin{array}{c}{a}_1>0,a_2+a_3>0,a_4+a_5>0,a_1\left(a_2+a_3\right)-\left(a_4+a_5\right)>0.\hfill \end{array}(7)$

The converse-negative proposition is the condition of Turing instability, namely, Turing instability induced by network when one of H_i(i = 1, 2, 3) holds.

$\begin{array}{c}{H}_1:a_2+a_3<0,\hfill \\ H_2:a_4+a_5<0,\hfill \\ H_3:a_1\left(a_2+a_3\right)-\left(a_4+a_5\right)<0.\hfill \end{array}$

More precisely, for H₁, Turing instability occurs when

$\begin{array}{c}{p}_1\left({\mathrm{\Lambda }}_k\right)=a_2+a_3=b_1{\mathrm{\Lambda }}_k^2+b_2{\mathrm{\Lambda }}_k+b_3<0\hfill \end{array}$

where

$\begin{array}{c}{b}_1=d_1{d}_2,b_2=-3a{d}_2{x_0}^2+2b{d}_2{x}_0-r{d}_1-r{d}_2-d_1,\hfill \\ b_3=3ar{x_0}^2+3a{x_0}^2-2br{x}_0-2b{x}_0+2d{x}_0+rs+r.\hfill \end{array}$

According to the properties of quadratic equations of one variable, the minimum value of p₁ (Λ_k) is $p_1(-\frac{b_2}{2b_1})$; if $-\frac{b_2}{2b_1}>0$ and p₁ (0) < 0, Turing instability occurs; if $-\frac{b_2}{2b_1}<0$ and $p_1(-\frac{b_2}{2b_1})<0$, Turing instability occurs and the critical value is ${\mathrm{\Lambda }}_k=-\frac{b_2}{2b_1}$.

For H₂, Turing instability occurs when

$\begin{array}{c}{p}_2\left({\mathrm{\Lambda }}_k\right)=a_4+a_5=c_1{\mathrm{\Lambda }}_k^2+c_2{\mathrm{\Lambda }}_k+c_3<0\hfill \end{array}$

where, the analysis process refers to p₁ (Λ_k), and

$\begin{array}{c}{c}_1=r{d}_1{d}_2,c_2=-3ar{d}_2{x_0}^2+2br{d}_2{x}_0-rs{d}_2-r{d}_1,\hfill \\ c_3=3ar{x_0}^2-2br{x}_0+2d{x}_{0}r+rs.\hfill \end{array}$

For H₃, Turing instability occurs when

$\begin{array}{c}{p}_3\left({\mathrm{\Lambda }}_k\right)=-\left[a_1\left(a_2+a_3\right)-a_4+a_5\right]=q_1{\mathrm{\Lambda }}_k^3+q_2{\mathrm{\Lambda }}_k^2+q_3{\mathrm{\Lambda }}_k+q_4>0\hfill \end{array}$

where

$\begin{array}{cc}\hfill q_1& ={d_1}^2{d}_2+d_1{d_2}^2,\hfill \\ \hfill q_2& =-6a{d}_1{d}_2{x_0}^2-3a{d_2}^2{x_0}^2+4b{d}_1{d}_2{x}_0+2b{d_2}^2{x}_0-r{d_1}^2-2r{d}_1{d}_2-r{d_2}^2-{d_1}^2-2d_1{d}_2,\hfill \\ \hfill q_3& =9a^2{d}_2{x_0}^4-12ab{d}_2{x_0}^3+6ar{d}_1{x_0}^2+6ar{d}_2{x_0}^2+4b^2{d}_2{x_0}^2+6a{d}_1{x_0}^2\hfill \\ \hfill & +6a{d}_2{x_0}^2-4br{d}_1{x}_0-4br{d}_2{x}_0-4b{d}_1{x}_0-4b{d}_2{x}_0+2d{d}_1{x}_0\hfill \\ \hfill & +2d{d}_2{x}_0+rs{d}_1+r^2{d}_1+r^2{d}_2+2r{d}_1+2r{d}_2+d_1,\hfill \\ \hfill q_4& =-9a^{2}r{x_0}^4-9a^2{x_0}^4+12abr{x_0}^3+12ab{x_0}^3-6ad{x_0}^3-3ars{x_0}^2\hfill \\ \hfill & -3a{r}^2{x_0}^2-4b^{2}r{x_0}^2-6ar{x_0}^2-4b^2{x_0}^2+4bd{x_0}^2+2brs{x}_0+2b{r}^2{x}_0\hfill \\ \hfill & -3a{x_0}^2+4br{x}_0-s{r}^2+2b{x}_0-2d{x}_0-r^2-r.\hfill \end{array}$

Suppose r₁, r₂ (r₁ ≤ r₂) is the roots of $p_3^{\prime }({\mathrm{\Lambda }}_k)$,

$\begin{array}{c}{p}_3^{\prime }\left({\mathrm{\Lambda }}_k\right)=3q_1{\mathrm{\Lambda }}_k^2+2q_2{\mathrm{\Lambda }}_k+q_3\hfill \end{array}$

where p₃ (r₁), p₃ (r₂) are local maximum and minimum respectively. According to the properties of cubic equations of one variable, Turing instability occurs when r₁ < 0 and p₃ (r₁) > 0; Turing instability occurs when r₁ > 0 and p₃ (0) > 0.

Finally, we consider the stability of system (1), namely,

$\begin{array}{c}{p}_4\left(\lambda \right)={\lambda }^3+a_1{\lambda }^2+\left(a_2+a_3{e}^{-\lambda \tau }\right)\lambda +a_4+a_5{e}^{-\lambda \tau }=0.\hfill \end{array}(8)$

Suppose that the pure imaginary root λ = j ω (j represents the imaginary unit) exists and we substitute it into the above characteristic equation, we have

$-a_1{\omega }^2+\sin \left(\omega \tau \right)\omega a_3+a_4+\cos \left(\omega \tau \right)a_5+\left(-{\omega }^3+\left(a_2+\cos \left(\omega \tau \right)a_3\right)\omega -\sin \left(\omega \tau \right)a_5\right)j=0.$

Separating the real and imaginary parts

$\begin{array}{c}-a_1{\omega }^2+\sin \left(\omega \tau \right)\omega a_3+a_4+\cos \left(\omega \tau \right)a_5=0,\hfill \\ -{\omega }^3+\left(a_2+\cos \left(\omega \tau \right)a_3\right)\omega -\sin \left(\omega \tau \right)a_5=0.\hfill \end{array}$

Solving cos (ωτ), sin (ωτ) to get

$\begin{array}{c}\mathit{cos}\left(\omega \tau \right)=\frac{{\omega }^4{a}_3+{\omega }^2{a}_1{a}_5-{\omega }^2{a}_2{a}_3-a_4{a}_5}{{\omega }^2{a_3}^2+{a_5}^2},\hfill \\ \mathit{sin}\left(\omega \tau \right)=\frac{\omega \left({\omega }^2{a}_1{a}_3-{\omega }^2{a}_5+a_2{a}_5-a_3{a}_4\right)}{{\omega }^2{a_3}^2+{a_5}^2}.\hfill \end{array}$

Due to cos (ωτ)² + sin (ωτ)² = 1, one has

$\begin{array}{c}{s}_1{x}^4+s_2{x}^3+s_3{x}^2+s_{4}x+s_5=0,\hfill \end{array}(9)$

where

$\begin{array}{c}x={\omega }^2,s_1={a_3}^2,\hfill \\ s_2={a_1}^2{a_3}^2-2a_2{a_3}^2+{a_5}^2,\hfill \\ s_3={a_1}^2{a_5}^2-2a_1{a_3}^2{a}_4+{a_2}^2{a_3}^2-{a_3}^4-2a_2{a_5}^2,\hfill \\ s_4=-2a_1{a}_4{a_5}^2+{a_2}^2{a_5}^2+{a_3}^2{a_4}^2-2{a_5}^2{a_3}^2,\hfill \\ s_5={a_4}^2{a_5}^2-{a_5}^4.\hfill \end{array}$

If a positive root exists x_i (i = 1, 2, 3, 4) at least in system (9), one has

$\begin{array}{c}{\tau }_i=\frac{1}{{\omega }_i}\mathit{arccos}\left(\frac{{\omega }^4{a}_3+{\omega }^2{a}_1{a}_5-{\omega }^2{a}_2{a}_3-a_4{a}_5}{{\omega }^2{a_3}^2+{a_5}^2}\right)+\frac{2\pi }{{\omega }_i},\hfill \end{array}$

where ${\omega }_i=\sqrt{x_i}$ is the solution of system (9) and the critical value τ₀ = min{τ_i} when d₁ = d₂ = 0, and τ_c = min{τ_i} when d₁ ≠ 0 or d₂ ≠ 0. Also, the corresponding ω of τ₀, τ_c is ω₀, ω_c.

The transversality condition

$\begin{array}{c}\frac{d\lambda }{d\tau }=\frac{t_{3}cos\left(\omega \tau \right)+t_{4}sin\left(\omega \tau \right)+t_5}{t_1^2+t_2^2}\ne 0,\hfill \end{array}$

where

$\begin{array}{c}{t}_1=-\sin \left(\omega \tau \right)\omega \tau a_3+\cos \left(\omega \tau \right)\tau a_5+3{\omega }^2,\hfill \\ t_2=\cos \left(\omega \tau \right)\omega \tau a_3+\sin \left(\omega \tau \right)\tau a_5-2a_1\omega ,\hfill \\ t_3=-3a_3{\omega }^4-2{\omega }^2{a}_1{a}_5-3a_3{\omega }^2-\tau a_2{a}_5,\hfill \\ t_4=2{\omega }^3{a}_1{a}_3-3{\omega }^3{a}_5+\omega \tau a_2{a}_3+2\omega a_1{a}_3,\hfill \\ t_5=-3a_2{\omega }^2-a_3\tau a_5.\hfill \end{array}$

If

$\begin{array}{c}\frac{d\lambda }{d\tau }{|}_{\tau ={\tau }_c,\omega ={\omega }_c}>0,\hfill \end{array}$

Turing instability occurs when τ₀ > τ > τ_c. τ₀ > τ make system (1) without network stable, and network induce Turing instability, namely, τ₀ > τ > τ_c.

Through the above analysis, we can draw the following sufficient conditions for Turing instability.

Theorem 1. Turing instability occurs in the network-organized system when a H_i (i = 1, 2, 3) holds; Turing instability occurs in the network-organized system with delay when τ ∈ (τ₀, τ_c).

Proof 1. The proof process can refer to the above analysis.

Results and Discussion

In this section, these parameters a = 1, b = 3, c = 1, d = 5, r = 0.01, s = 4, I = 1, x_r = −1.6 Hindmarsh and Rose (1984) and d₁ = 0.1, d₂ = 0.3 are set. The adjacent matrix A is generated by random network Zheng and Shen (2020); Erdos and Renyi (1959) and the link probability p and nodes n = 100 is the initial value. For node i and node j, if the random number $<p$, A_ij = A_ji = 1, or else A_ij = A_ji = 0. Suppose the special form f (x_j, x_i) = x_j − qx_i, g (y_j, y_i) = y_j − qy_i in system (1). Also, x represent 100 neuron nodes in the pattern formation.

From Figure 1, system (1) is stable when d₁ = 0, d₂ = 0, τ = 0, which is the precondition of Turing instability induced by network and delay. Namely, H_i > 0 when Λ_i = 0 (Figure 1A,B,C) and the current values below the activity threshold of the single neuron. Also, Λ_i can not lead to Turing instability when Λ_i < 0, which means it is difficult to keep the network in activity when the collected current is the same as the outgoing current. Let’s take H₃ (H₁ and H₂ are relatively simple, and H₃ is more representative.) as an example to illustrate the stability of system (1) (Figure 2–6). Although system (1) without delay is periodic behavior (Figure 2B) under the initial stimulus, it ultimately tends to the rest state (Figure 2A) when no stimulus is added. Short-term memory attributes to a fixed point attractor Wang (2001), which could persistent neuronal activity when the remembered stimulus is removed Goldman (2009). The above results bring into correspondence with our results (Figure 2). When the collected current is larger than the outgoing currentq = 0.96, H₃ < 0 holds (Figure 3A) and Turing instability occurs (Figure 3B). In general, most of the neurons will be in the rest state. Meanwhile, a few persistent neuronal activities because of the constant external stimuli (Figure 3B). When the link probability p increases and the difference q becomes larger, H₃ < 0 holds (Figure 4A) and the corresponding pattern formation (Figure 4B) shows the periodic neural activity. Namely, constant external stimulation from other neurons is necessary to keep the neural activity. For the short-term memory, noise could induce the switch of different memories Zheng et al. (2020), and the constant external stimulation from other neurons can also leads to the switch of different memories. Only the link probability could not causes instability (Figure 5A), but it could keep the neural activity longer (Figure 5B). When the difference between the collected current and the outgoing current exceeds the threshold value of the neural activity (Figure 6A), Turing instability occurs (Figure 6B). Namely, the short-term memory generation requires enough stimulation, which is in line with the actual situation. Also, these above results can be verified by the bifurcation (Figure 7):system (1) is always stable when q = 0 (Figure 7A) and q could induce Turing instability (Figure 7B).

FIGURE 1

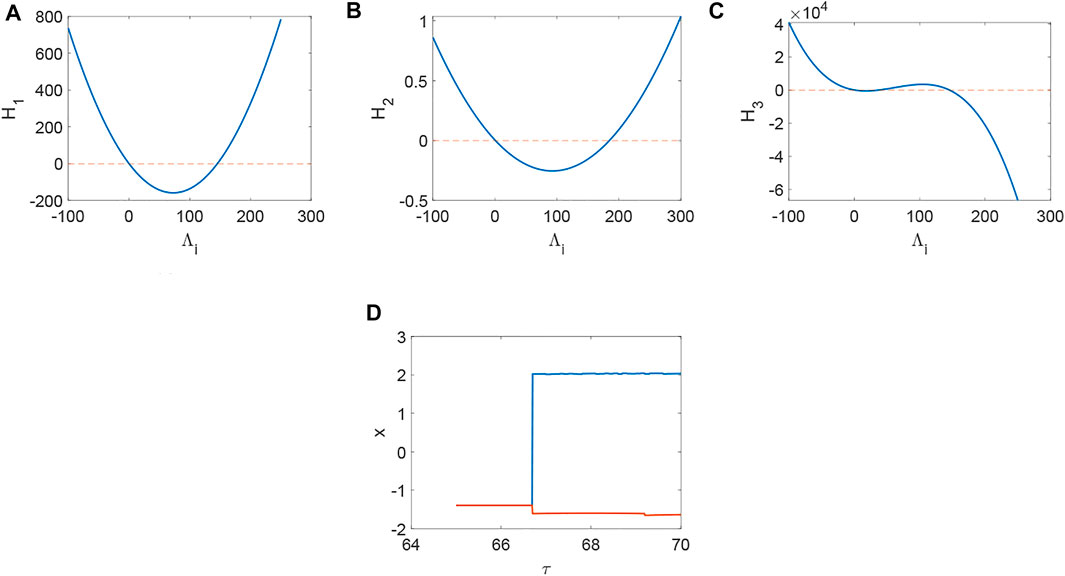
FIGURE 1. The distribution of H_i(i = 1, 2, 3) when a = 1, b = 3, c = 1, d = 5, r = 0.01, s = 4, I = 1, x_r = −1.6, d₁ = 0.1, d₂ = 0.3, τ = 0. (A) Turing instability occurs when H₁ < 0, or else stable. (B) Turing instability occurs when H₂ < 0, or else stable. (C) Turing instability occurs when H₃ < 0, or else stable. (D) The bifurcation about τ when d₁ = d₂ = 0.

FIGURE 2

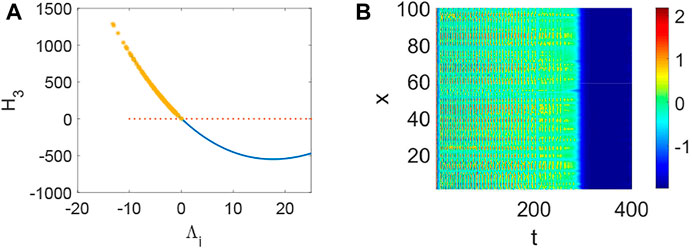
FIGURE 2. The stability of system (1) when p = 0.05, τ = 0. (A) The distribution of eigenvalues Λ_i (labeled by *) when q = 0. (B) The corresponding pattern formation is stable in system (1) when no eigenvalue Λ_i make H₃ < 0 hold.

FIGURE 3

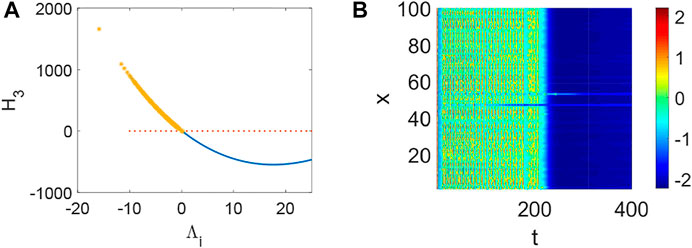
FIGURE 3. The stability of system (1) when p = 0.05, q = 0.96, τ = 0. (A) The distribution of eigenvalues Λ_i (labeled by *). (B) Turing instability occurs in system (1) when some eigenvalue Λ_i make H₃ < 0 hold.

FIGURE 4

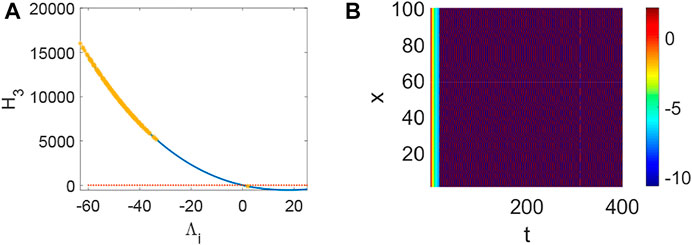
FIGURE 4. The stability of system (1) when p = 0.5, q = 0.96, τ = 0. (A) The distribution of eigenvalues Λ_i (labeled by *). (B) Turing instability occurs in system (1) when a eigenvalue Λ_i make H₃ < 0 hold.

FIGURE 5

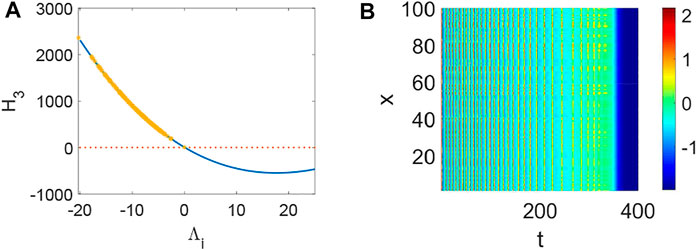
FIGURE 5. The stability of system (1) when p = 0.1, q = 0, τ = 0. (A) The distribution of eigenvalues Λ_i (labeled by *). (B) The corresponding pattern formation is stable in system (1) when no eigenvalue Λ_i make H₃ < 0 hold.

FIGURE 6

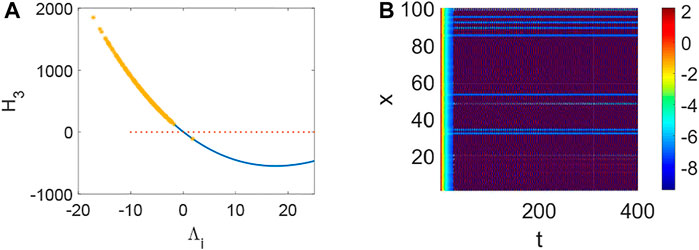
FIGURE 6. The stability of system (1) when p = 0.1, q = 0.82, τ = 0. (A) The distribution of eigenvalues Λ_i (labeled by *). (B) Turing instability occurs in system (1) when some eigenvalue Λ_i make H₃ < 0 hold.

FIGURE 7

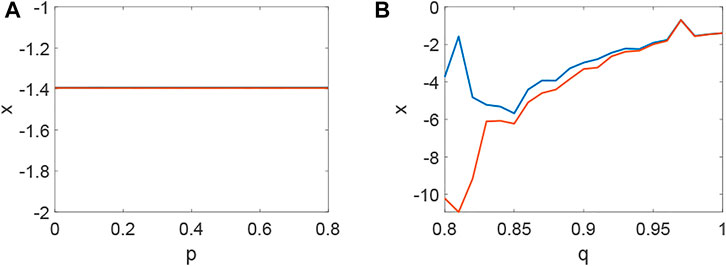
FIGURE 7. The bifurcation about p, q when τ = 0. (A) The inexistence bifurcation about p when q = 0. (B) The bifurcation about q when p = 0.1.

Delay plays a vital role in the rise or fall of neural activity. From Figure 8, the dynamic behavior (Figure 8A) is different from system (1) without delay (Figure 2), but the link probability nearly has no effect on the stability of system (1) (Figure 8B), because the collected current always equal to the outgoing current when q = 0. When q ≠ 0, the periodic behavior of the neuron may occur (Figure 8C,D). Meanwhile, the periodic behavior of the neuron under different p (Figure 8C,D). It is found that the link probability p could make system (1) network synchronization and the synchronicity becomes stronger with the increase of p, but the neuronal activity is low (Figure 9A,B,C, Figure 10A). Of course, q could increases neuronal activity (Figure 9D), which can also be represented in the bifurcation (Figure 10B). The phenomenon of spatiotemporal patterns Lepek and Fronczak (2018); Umesh and Ambika (2021); Shi et al. (2022); Santos et al. (2017) was often considered in the network-organized system when q = 1. The difference q < 1 between the collected current and the outgoing current plays a vital role in the neuronal activity through the above analysis, which may further show the firing mechanism in a general networked HR model with delay. Meanwhile, short-term memory results from external stimuli Zheng et al. (2020), but not all stimuli result in short-term memory. The difference q < 1 may theoretically explain why some stimuli can’t lead to short-term memory.

FIGURE 8

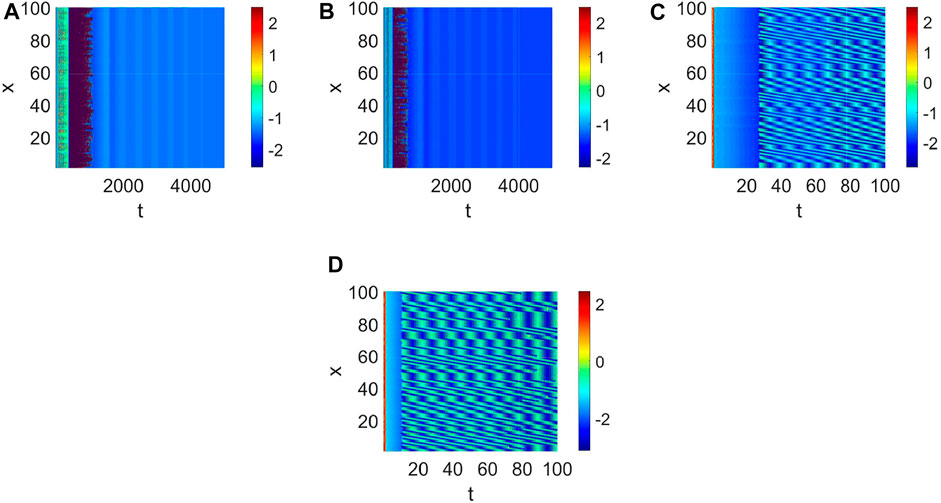
FIGURE 8. The pattern formation of system (1) when τ = 65. (A) The pattern formation when p = 0.05, q = 0. (B) The pattern formation when p = 0.1, q = 0. (C) The pattern formation when p = 0.1, q = 0.96. (D) The pattern formation when p = 0.15, q = 0.96.

FIGURE 9

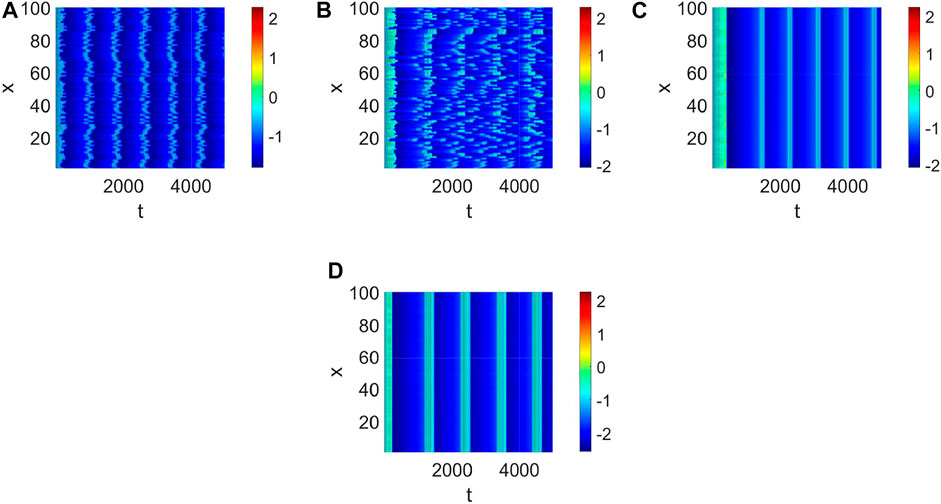
FIGURE 9. The pattern formation of system (1) when τ = 68. (A) The pattern formation when p = 0, q = 0. (B) The pattern formation when p = 0.01, q = 0. (C) The pattern formation when p = 0.1, q = 0. (D) The pattern formation when p = 0.1, q = 0.96.

FIGURE 10

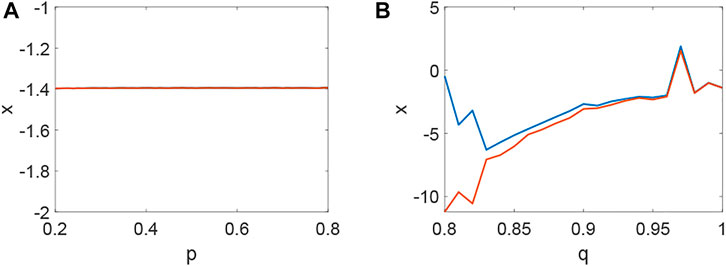
FIGURE 10. The bifurcation about p, q when τ = 65. (A) The inexistence bifurcation about p when q = 0. (B) The bifurcation about q when p = 0.1.

Conclusion

In this paper, spatiotemporal patterns are investigated to illustrate the collected behavior of neurons and the generation mechanism of short-term memory. We obtain the algebraic expressions for Turing instability to occur in any HR network setup. Then, we derive the critical value of Hopf bifurcation to present a profound impact of both network and delay on the Turing instability. Also, we find that the collected current and outgoing current play a vital role in neuronal activity, especially in the generation mechanism of the short-term memory. Meanwhile, the collected behavior may fire when the input to the neuron is below a certain threshold, and the output reaches a stationary regime. Finally, we try to explain the generation mechanism of the short-term memory through the theoretical results and numerical simulation.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author (Some related code can be found: https://github.com/zhengqianqian35).

Author Contributions

YX and JS conceived of the study, designed the study. The remaining authors contributed to refining the ideas, carrying out additional analyses and finalizing this paper. All authors contributed to the writing and revisions.

Funding

This work is supported by National Natural Science Foundation of China (12002297), Basic research Project of Universities in Henan Province (21zx009), Program for Science& Technology Innovation Talents in Universities of Henan Province (22HASTIT018), The Scientific Research Innovation Team of Xuchang University (2022CXTD002), Key scientific research projects of Henan Institutions of Higher learning in 2021 (21B130004), Outstanding Young Backbone Teacher of Xuchang University (2022).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Baltanás J. P., Casado J. M. (2002). Noise-induced Resonances in the Hindmarsh-Rose Neuronal Model. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 65, 041915. doi:10.1103/PhysRevE.65.041915

PubMed Abstract | CrossRef Full Text | Google Scholar

Cygan S. (2021). Pattern Formation in Nonlocal Kondo Model. Math. Meth Appl. Sci. 44, 10804–10822. doi:10.1002/mma.7448

CrossRef Full Text | Google Scholar

Diego X., Marcon L., Muller P., Sharpe J. (2018). Key Features of Turing Systems Are Determined Purely by Network Topology. Phys. Rev. X 8, 021071. doi:10.1103/physrevx.8.021071

CrossRef Full Text | Google Scholar

Erdos P., Renyi A. (1959). On Random Graphs. Publ. Math. 6, 290–297.

Google Scholar

Erichsen R., Brunnet L. G. (2009). Multistability in Networks of Hindmarsh-Rose Neurons. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 78, 061917. doi:10.1103/PhysRevE.78.061917

PubMed Abstract | CrossRef Full Text | Google Scholar

Etémé A. S., Tabi C. B., Mohamadou A., Kofané T. C. (2019). Elimination of Spiral Waves in a Two-Dimensional Hindmarsh-Rose Neural Network under Long-Range Interaction Effect and Frequency Excitation. Phys. A Stat. Mech. its Appl. 533, 122037. doi:10.1016/j.physa.2019.122037

CrossRef Full Text | Google Scholar

Goldman M. S. (2009). Memory without Feedback in a Neural Network. Neuron 61, 621–634. doi:10.1016/j.neuron.2008.12.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Goulefack L. M., Chamgoue A. C., Anteneodo C., Yamapi R. (2022). Stability Analysis of the Hindmarsh-Rose Neuron under Electromagnetic Induction. Nonlinear Dyn. 108, 2627–2642. doi:10.1007/s11071-022-07331-8

CrossRef Full Text | Google Scholar

Gu H., Pan B. (2015). A Four-Dimensional Neuronal Model to Describe the Complex Nonlinear Dynamics Observed in the Firing Patterns of a Sciatic Nerve Chronic Constriction Injury Model. Nonlinear Dyn. 81, 2107–2126. doi:10.1007/s11071-015-2129-7

CrossRef Full Text | Google Scholar

Hindmarsh J. L., Rose R. M. (1984). A Model of Neuronal Bursting Using Three Coupled First Order Differential Equations. Proc. R. Soc. Lond B Biol. Sci. 221, 87–102. doi:10.1098/rspb.1984.0024

PubMed Abstract | CrossRef Full Text | Google Scholar

Hindmarsh J. L., Rose R. M. (1982). A Model of the Nerve Impulse Using Two First-Order Differential Equations. Nature 296, 162–164. doi:10.1038/296162a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Kolodina K., Wyller J., Oleynik A., Sørensen M. P. (2021). Pattern Formation in a 2-population Homogenized Neuronal Network Model. J. Math. Neurosci. 11, 9–38. doi:10.1186/s13408-021-00107-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Kondo S., Watanabe M., Miyazawa S. (2021). Studies of Turing Pattern Formation in Zebrafish Skin. Philosophical Trans. R. Soc. A 379, 20200274. doi:10.1098/rsta.2020.0274

CrossRef Full Text | Google Scholar

Kriener B., Helias M., Rotter S., Diesmann M., Einevoll G. T. (2013). How Pattern Formation in Ring Networks of Excitatory and Inhibitory Spiking Neurons Depends on the Input Current Regime. Front. Comput. Neurosci. 7, 187. doi:10.3389/fncom.2013.00187

PubMed Abstract | CrossRef Full Text | Google Scholar

Lepek M., Fronczak P. (2018). Spatial Evolution of Hindmarsh-Rose Neural Network with Time Delays. Nonlinear Dyn. 92, 751–761. doi:10.1007/s11071-018-4088-2

CrossRef Full Text | Google Scholar

Ma J., Xu Y., Li Y., Tian R., Ma S., Kurths J. (2021). Quantifying the Parameter Dependent Basin of the Unsafe Regime of Asymmetric Lévy-Noise-Induced Critical Transitions. Appl. Math. Mech.-Engl. Ed. 42, 65–84. doi:10.1007/s10483-021-2672-8

CrossRef Full Text | Google Scholar

Perc M. (2006). Thoughts Out of Noise. Eur. J. Phys. 27, 451–460. doi:10.1088/0143-0807/27/2/026

CrossRef Full Text | Google Scholar

Rajagopal K., Khalaf A. J. M., Parastesh F., Moroz I., Karthikeyan A., Jafari S. (2019). Dynamical Behavior and Network Analysis of an Extended Hindmarsh-Rose Neuron Model. Nonlinear Dyn. 98, 477–487. doi:10.1007/s11071-019-05205-0

CrossRef Full Text | Google Scholar

Santos M., Szezech J., Borges F., Iarosz K., Caldas I., Batista A., et al. (2017). Chimera-like States in a Neuronal Network Model of the Cat Brain. Chaos, Solit. Fractals 101, 751–761. doi:10.1016/j.chaos.2017.05.028

CrossRef Full Text | Google Scholar

Shi M., Yu Y., Xu Q. (2020). Hopf Bifurcation of the Fractional-Order Hindmarsh-Rose Neuron Model with Time-Delay. Rocky Mt. J. Math. 50, 2213–2222. doi:10.1216/rmj.2020.50.2213

CrossRef Full Text | Google Scholar

Shi X., Wang Z., Wang Z., Zhuang L. (2022). Spatiotemporal Pattern in a Neural Network with Non-smooth Memristor. era 30, 715–731. doi:10.3934/era.2022038

CrossRef Full Text | Google Scholar

Sun X., Perc M., Kurths J., Lu Q. (2018). Fast Regular Firings Induced by Intra- and Inter-time Delays in Two Clustered Neuronal Networks. Chaos 28, 106310. doi:10.1063/1.5037142

PubMed Abstract | CrossRef Full Text | Google Scholar

Tian R., Zhao Z., Xu Y. (2021). Variable Scale-Convex-Peak Method for Weak Signal Detection. Sci. China Technol. Sci. 64, 331–340. doi:10.1007/s11431-019-1530-4

CrossRef Full Text | Google Scholar

Turing A. (1990). The Chemical Basis of Morphogenesis. Bull. Math. Biol. 52, 153–197. doi:10.1016/s0092-8240(05)80008-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Umesh K. V., Ambika G. (2021). Emergent Dynamics and Spatio Temporal Patterns on Multiplex Neuronal Networks. Front. Comput. Neurosci. 15, 774969. doi:10.3389/fncom.2021.774969

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang X.-J. (2001). Synaptic Reverberation Underlying Mnemonic Persistent Activity. Trends Neurosci. 24, 455–463. doi:10.1016/s0166-2236(00)01868-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang Z., Li Y., Xu Y., Kapitaniak T., Kurths J. (2022). Coherence-resonance Chimeras in Coupled Hr Neurons with Alpha-Stable Levy Noise. J. Stat. Mech. Theory Exp. 2022, 1–15. doi:10.1088/1742-5468/ac6254

CrossRef Full Text | Google Scholar

Wang Z., Xu Y., Li Y., Kapitaniak T., Kurths J. (2021a). Chimera States in Coupled Hindmarsh-Rose Neurons with α-stable Noise. Chaos, Solit. Fractals 148, 110976. doi:10.1016/j.chaos.2021.110976

CrossRef Full Text | Google Scholar

Wang Z., Xu Y., Li Y., Kurths J. (2021b). The Probability Density Function of Interspike Intervals in an Fhn Model with α-stable Noise. Eur. Phys. J. Plus 136, 1–14. doi:10.1140/epjp/s13360-021-01245-x

CrossRef Full Text | Google Scholar

Wu K., Luo T., Lu H., Wang Y. (2016). Bifurcation Study of Neuron Firing Activity of the Modified Hindmarsh-Rose Model. Neural Comput. Applic 27, 739–747. doi:10.1007/s00521-015-1892-1

CrossRef Full Text | Google Scholar

Yang W. (2022). Bifurcation and Dynamics in Double-Delayed Chua Circuits with Periodic Perturbation. Chin. Phys. B 31, 020201. doi:10.1088/1674-1056/ac1e0b

CrossRef Full Text | Google Scholar

Zaker N., Cobbold C. A., Lutscher F. (2021). The Effect of Landscape Fragmentation on Turing-Pattern Formation. Math. Biosci. Eng. 19, 2506–2537. doi:10.3934/mbe.2022116

CrossRef Full Text | Google Scholar

Zheng Q., Shen J. (2020). Turing Instability Induced by Random Network in Fitzhugh-Nagumo Model. Appl. Math. Comput. 381, 125304. doi:10.1016/j.amc.2020.125304

CrossRef Full Text | Google Scholar

Zheng Q., Shen J., Xu Y. (2020). Spontaneous Activity Induced by Gaussian Noise in the Network-Organized Fitzhugh-Nagumo Model. Neural Plast. 2020, 1–12. doi:10.1155/2020/6651441

PubMed Abstract | CrossRef Full Text | Google Scholar