The Application of Artificial Intelligence in Predicting Embryo Transfer Outcome of Recurrent Implantation Failure

Background: Recurrent implantation failure (RIF) refers to that infertile patients have undergone multiple in vitro fertilization (IVF) or intracytoplasmic sperm injection (ICSI) cycles and transferred multiple embryos without embryo implantation or clinical pregnancy. Due to the lack of clear evidence-based medical guidelines for the number of embryos to be transferred in RIF patients, how to obtain the highest single cycle pregnancy success rate with as few embryos transferred as possible while avoiding multiple pregnancy as much as possible, that is, how to balance the pregnancy success rate and multiple pregnancy rate, is a great challenge for clinicians and RIF patients. We urgently need an effective and reliable assisted decision-making method to help clinicians find this balance, and an artificial intelligence (AI) system will provide an efficient solution.

Design and Methods: In this research, we filtered out the RIF data set (n = 45,921) from the Human Fertilisation and Embryology Authority (HFEA) database from 2005 to 2016. The data set was divided into two groups according to the number of embryos transferred, Group A and B. Group A included 34,175 cycles with two embryos transferred, while Group B included 11,746 cycles with only one embryo transferred, each containing 44 features and a prediction label (pregnancy). Four machine learning algorithms (RF, GBDT, AdaBoost, and MLP) were used to train Group A and Group B data set respectively and 10-folder cross validation method was used to validate the models.

Results: The results revealed that the AdaBoost model of Group A obtained the best performance, while the GBDT model in Group B was proved to be the best model. Both models had been proved to provide accurate prediction of transfer outcome.

Conclusion: Our research provided a new approach for targeted and personalized treatment of RIF patients to help them achieve efficient and reliable pregnancy. And an AI-assisted decision-making system will be designed to help clinicians and RIF patients develop personalized transfer strategies, which not only guarantees efficient and reliable pregnancy, but also avoids the risk of multiple pregnancy as much as possible.

1 Introduction

Since the first test tube baby was born in 1978, in vitro fertilization-embryo transfer (IVF-ET) has become one of the most important methods to treat infertility. So far, pregnancy rate following one IVF-ET cycle can be as high as 60%. But even in the very successful units, about 10% of women undergoing in vitro fertilization (IVF) treatment fail repeatedly (Margalioth et al., 2006; Busnelli et al., 2020). Recurrent implantation failure (RIF) refers to that infertile patients have undergone multiple IVF or intracytoplasmic sperm injection (ICSI) cycles and transferred multiple embryos without embryo implantation or clinical pregnancy.

Currently, there is no consensus on the definition of RIF (Coughlan et al., 2014). Disputes mainly exist in the number of embryo transfer cycles, the number and quality of embryos transferred, the age of patients and so on. Stern et al. defined patients with accumulative transfer of more than 10 embryos without clinical pregnancy as RIF (Stern et al., 2003). With the development of IVF-ET technology, the total number of embryo transfer cycles and the cumulative number of embryos transferred for diagnosing RIF have also changed accordingly. At present, the definition of RIF recognized by most clinicians was proposed by Simon et al., in 2012, that is, receiving three or more embryo transfer cycles (including fresh or frozen cycles), and transferring one or two high-quality embryos each cycle without clinical pregnancy (Simon and Laufer, 2012). In addition, in 2018, Cao et al. (2018) believed that RIF can be identified as receiving ≥2 transfer cycles, with high-quality embryos in each cycle and no pregnancy. In 2021, the ESHRE survey results opinion on RIF was no more than two failed ETs (Cimadomo et al., 2021).

In order to ensure a better clinical pregnancy rate for RIF patients, the current routine transfer strategies of many reproductive centers around the world include increasing the number of embryos transferred in a single cycle to improve the success rate of single cycle pregnancy or accumulating multiple single embryo transfer (SET) cycles to obtain a final clinical pregnancy (Calhaz-Jorge et al., 2016; Penzias et al., 2017). However, these two transfer strategies have some limitations and disadvantages.

Although increasing the number of embryos transferred in a single transfer cycle can improve the clinical pregnancy rate, it will also increase the multiple pregnancy rate (Pandian et al., 2004; de Mouzon et al., 2012). Multiple pregnancy will significantly increase the possibility of maternal and infant complications, such as: miscarriage, premature birth, fetal distress, low birth weight infants, serious obstetric complications (such as postpartum hemorrhage and gestational hypertension, etc.) (Pinborg, 2005; Santana et al., 2016; Calhaz-Jorge et al., 2017). In addition, it will greatly increase the expenditure of patients and bring them a huge economic burden (Lee et al., 2016). Just as the optimal goal of assisted reproductive technologies (ART) to treat infertility should be one healthy baby at a time, multiple pregnancy is one of the most important adverse pregnancy outcomes that should be strictly prevented in this field. Therefore, improving the pregnancy success rate of RIF patients by increasing the number of embryos transferred in a single transfer cycle is actually a risk-benefit strategy, not the best one.

On the other hand, the strategy of accumulating multiple SET cycles to obtain a clinical pregnancy completely avoids the risk of multiple pregnancy caused by iatrogenic factors, but significantly increases the time cost, economic burden, and family pressure of RIF patients. For example, just as female age is closely related to pregnancy success and maternal complications, a lengthy treatment process is bound to carry great risks. The strategy is a conservative and inefficient strategy, not the best one.

Due to the lack of clear evidence-based medical guidelines for the number of embryos to be transferred in RIF patients, how to obtain the highest single cycle pregnancy success rate with as few embryos transferred as possible while avoiding multiple pregnancy as much as possible, that is, how to balance the pregnancy success rate and multiple pregnancy rate, is a great challenge for clinicians and RIF patients (Tobias et al., 2016; Kamath et al., 2020; Ma et al., 2022). We urgently need an effective and reliable assisted decision-making method to help clinicians find this balance, and the computer-aided decision-making system will provide an efficient solution.

At present, based on big data, advanced algorithms and computing power (hash rate), artificial intelligence (AI) has been rapidly developed and widely used in various fields. AI has proved its strong strength in the application of pattern recognition technologies such as speech recognition and face recognition. The connection between medical health and AI is also getting closer (Deo, 2015; Obermeyer and Emanuel, 2016). More and more applications appear in intelligent diagnosis, virtual assistant, medical imaging, drug mining, nutrition, biotechnology, hospital management, health management, mental health, wearable devices and other application scenarios. Moreover, AI, especially machine learning has rapidly demonstrated its ability to predict human fertility.

A perfect embryo transfer strategy should have at least two elements: (ⅰ) to ensure a high level of clinical pregnancy rate; (ⅱ) to reduce the multiple pregnancy rate as much as possible. For a long time, a large number of studies have been devoted to exploring appropriate embryo transfer strategies (Practice Committee of the American Society for Reproductive Medicine, 2017; Practice Committee of the American Society for Reproductive Medicine and Practice Committee of the Society for Assisted Reproductive Technology, 2017). Our aim is to use this new technology of AI to find the best embryo transfer strategy. We included the data of patients receiving ART treatment from the Human Fertilisation and Embryology Authority (HFEA), which is a world-class expert organization collecting data and statistics about the fertility treatment cycles performed each year in the United Kingdom. The data of RIF patients between 2005–2016 were filtered out to construct the data set for model training. We further divided the data set into two groups according to the embryo transfer strategy, i.e., Group A: double embryo transfer (DET) group; Group B: single embryo transfer (SET) group. Finally, two prediction models were trained and built separately using machine learning algorithms. The two models will predict the pregnancy outcome after embryo transfer (SET or DET) based on the clinical variables before embryo transfer in RIF patients who are starting a new IVF cycle. Then, the prediction results will help clinicians develop transfer strategies to achieve the best pregnancy outcome.

2 Materials and Methods

2.1 Data Set Construction

The Human Fertilisation and Embryology Authority (HFEA) is the UK’s independent regulator of fertility treatment and research using human embryos. It is a world-class expert organization in the fertility sector, and the first statutory body of this type in the world. HFEA collects data and statistics about the fertility treatment cycles performed each year in the United Kingdom to improve patient care and help researchers to conduct world-class research, whilst ensuring very strong protection of patient, donor and offspring confidentiality.

In this research, we are allowed to access a large and rich anonymized data set from HFEA. The data set cannot help to identify any patients, or children born as a result of treatment. So, no ethics approval is required for this research.

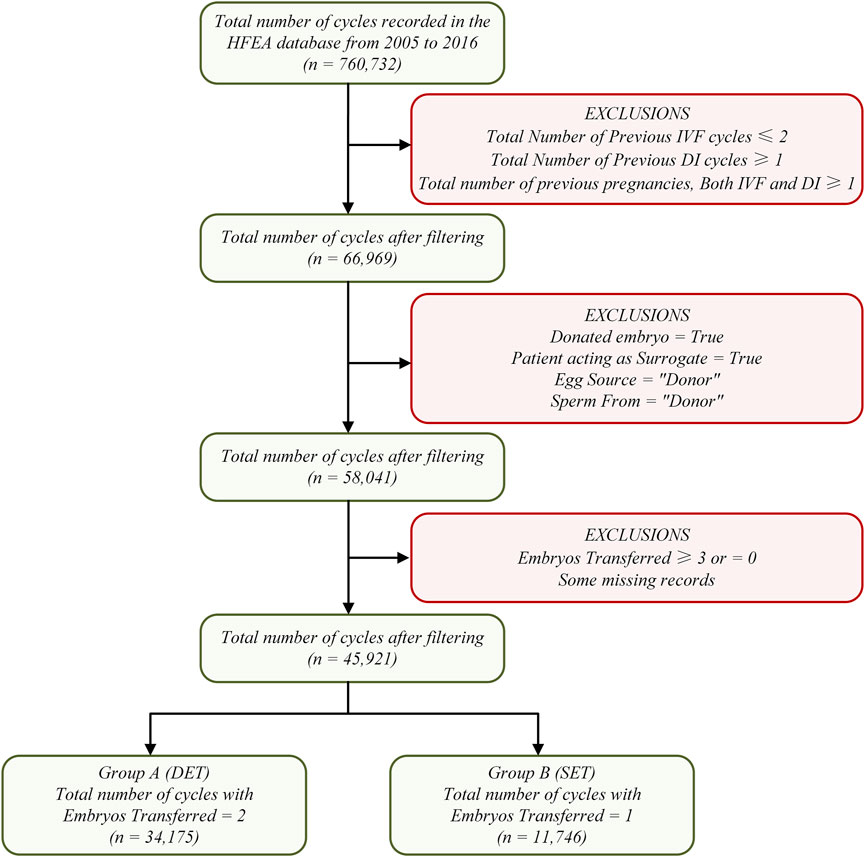
The raw data set in this research contains 760,732 patient records with 95 fields on treatment cycles started between 2005 and 2016. We used more stringent criteria to filter RIF samples to avoid research errors as much as possible, that is, having received at least three transfer cycles (fresh or frozen), with high-quality embryos in each cycle, without pregnancy, and undergoing IVF treatment again (at least the fourth cycle). Data set filtering mainly includes four steps. Step 1: cycles unrelated to RIF cases were excluded. Step 2: cycles involving sperm, egg, or embryo donation, and cycles involving surrogacy were excluded. Step 3: cycles involving only one or two embryos transferred were reserved. Step 4: the remaining data were divided into two sub datasets: Group A and Group B; Group A contained 34,175 cycles with two embryos transferred and Group B contained 11,746 cycles with one embryo transferred. The entire data set filtering process is shown in Figure 1.

FIGURE 1

FIGURE 1. Data set construction flowchart.

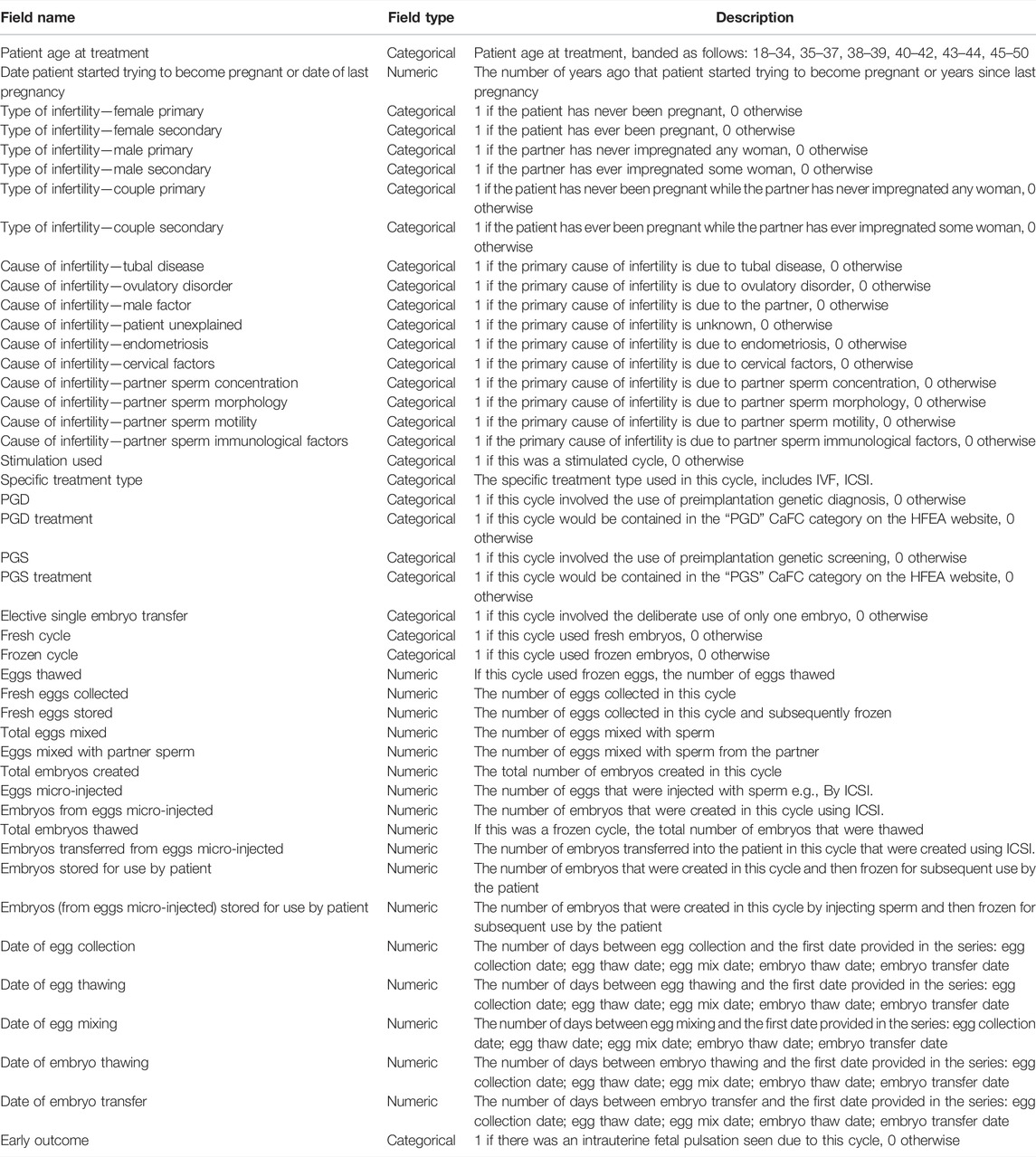
Focusing on the 95 fields of the raw data set, after the above data filtering steps, some fields containing exactly one value were eliminated, which are obviously meaningless to a machine learning algorithm. In addition, we also eliminated some fields that have nothing to do with RIF cases, such as fields involving donation, surrogacy, etc. Finally, 45 fields were retained. The detailed description of these 45 fields can be seen in Table 1.

TABLE 1

TABLE 1. Description of 45 fields in the data set.

The field “Early Outcome” indicates whether an intrauterine fetal pulsation was found, which was used as a prediction label, or output. The remaining 44 fields were defined as features, or inputs. Finally, the data set was constructed, that is, one 34,175 × 45 matrix for Group A and one 11,746 × 45 matrix for Group B.

2.2 Data Cleaning

In this process, our main purpose is to correct the data, eliminate the recording errors during data acquisition and standardize the data format so that the algorithm can recognize. It includes the following steps:

(ⅰ) Standardize the data format into two categories: numeric and categorical, e.g., “Patient Age at Treatment” was converted to categorical data (18–34: ‘0’, 35–37: ‘1’, 38–39: ‘2’, 40–42: ‘3’, 43–44: ‘4’, 45–50: ‘5’), “Eggs Thawed” was converted to numeric data (range from 0 to 21), “Total Embryos Thawed” was converted to numeric data (range from 0 to 26), etc.

(ⅱ) Check for missing values and outliers, e.g., all the blanks in “PGD treatment” and “PGS Treatment” were filled with 0, outliers in “Date of Egg Mixing” were deleted, etc.

(ⅲ) Apply Z-score normalization method to make the data have a mean of 0 and a standard deviation of 1, which can weaken the influence of the value range on the model (Shiffler, 1988).

In addition, due to the imbalance of the data set, that is, the number of negative cycles is greater than that of positive cycles, we randomly sampled the negative samples to ensure that the data set used for model training is a completely balanced one, which can greatly improve the classification performance.

2.3 Model Building

Our main purpose is to use machine learning algorithms to build a mapping from features to labels, which is similar to a specific function. Each set of features is used as the input of the function, and then the output of the function will be classified under a specific threshold. The algorithms obtain the best threshold in multiple iterations of classification and summary. At this time, the classification result is closest to the real label. That is the entire learning process. In this research, four machine learning algorithms were used to build the classification model (prediction model).

2.3.1 Random Forest

Random Forest (RF) is an averaging algorithm based on randomized decision trees (DT). The algorithm is a perturb-and-combine technique specifically designed for trees (Breiman, 1998). This means a diverse set of classifiers is created by introducing randomness in the classifier construction. The prediction of the ensemble is given as the averaged prediction of the individual classifiers (Breiman, 2001). In RF, each tree in the ensemble is built from a sample drawn with replacement (i.e., a bootstrap sample) from the training set. Furthermore, when splitting each node during the construction of a tree, the best split is found either from all input features or a random subset. The purpose of these two sources of randomness is to decrease the variance of the forest estimator. Indeed, individual decision trees typically exhibit high variance and tend to overfit. The injected randomness in forests yield decision trees with somewhat decoupled prediction errors. By taking an average of those predictions, some errors can cancel out. RF achieve a reduced variance by combining diverse trees, sometimes at the cost of a slight increase in bias. In practice the variance reduction is often significant, hence yielding an overall better model (Geurts et al., 2006).

2.3.2 AdaBoost

AdaBoost is to fit a sequence of weak learners (i.e., models that are only slightly better than random guessing, such as small decision trees) on repeatedly modified versions of the data (Freund and Schapire, 1997). The predictions from all of them are then combined through a weighted majority vote (or sum) to produce the final prediction. The data modifications at each so-called boosting iteration consist of applying weights ${\omega }_1,{\omega }_2,{\omega }_3,\dots ,{\omega }_N$ to each of the training samples. Initially, those weights are all set to ${\omega }_i=1/N$, so that the first step simply trains a weak learner on the original data. For each successive iteration, the sample weights are individually modified and the learning algorithm is reapplied to the reweighted data. At a given step, those training examples that were incorrectly predicted by the boosted model induced at the previous step have their weights increased, whereas the weights are decreased for those that were predicted correctly. As iterations proceed, examples that are difficult to predict receive ever-increasing influence. Each subsequent weak learner is thereby forced to concentrate on the examples that are missed by the previous ones in the sequence (Hastie et al., 2009).

2.3.3 Gradient Boosted Decision Tree

Gradient Tree Boosting or Gradient Boosted Decision Tree (GBDT) is a generalization of boosting to arbitrary differentiable loss functions (Friedman, 2002). GBDT is an accurate and effective off-the-shelf procedure that can be used for both regression and classification problems in a variety of areas including Web search ranking and ecology. GBRT is an additive model whose prediction $y_i$ for a given input $x_i$ is of the following form:

$\widehat{y_i}=F_M\left(x_i\right)={\displaystyle \sum _{m=1}^M{h}_m\left(x_i\right)}$

where the $h_m$ are estimators called weak learners in the context of boosting. GBDT uses DT of fixed size as weak learners. Similar to other boosting algorithms, GBRT is built in a greedy fashion:

$F_m\left(x\right)=F_{m-1}\left(x\right)+h_m\left(x\right)$

where the newly added tree $h_m$ is fitted in order to minimize a sum of losses $L_m$, given the previous ensemble $F_{m-1}$:

$h_m=\arg \underset{h}{\min }{L}_m=\arg \underset{h}{\min }{\displaystyle \sum _{i=1}^{n}l\left(y_i,F_{m-1}\left(x_i\right)+h\left(x_i\right)\right)}$

where $l\left(y_i,F\left(x_i\right)\right)$ is defined as loss function. Using a first-order Taylor approximation, the value of $l$ can be approximated as follows:

$l\left(y_i,F_{m-1}\left(x_i\right)+h_m\left(x_i\right)\right)\approx l\left(y_i,F_{m-1}\left(x_i\right)\right)+h_m\left(x_i\right){\left[\frac{\partial l\left(y_i,F\left(x_i\right)\right)}{\partial F\left(x_i\right)}\right]}_{F=F_{m-1}}$

Then, we will denote $g_i$ as follows:

$g_i={\left[\frac{\partial l\left(y_i,F\left(x_i\right)\right)}{\partial F\left(x_i\right)}\right]}_{F=F_{m-1}}$

Removing the constant terms, we have:

$h_m\approx \arg \underset{h}{\min }{\displaystyle \sum _{i=1}^{n}h\left(x_i\right)}{g}_i$

This is minimized if $h\left(x_i\right)$ is fitted to predict a value that is proportional to the negative gradient $-g_i$. Therefore, at each iteration, the estimator $h_m$ is fitted to predict the negative gradients of the samples. The gradients are updated at each iteration. This can be considered as some kind of gradient descent in a functional space.

2.3.4 Multi-layer Perceptron

Multi-layer Perceptron (MLP), also known as Artificial Neural Network (ANN), is a supervised learning algorithm that learns a function $f(\cdot ):R^m\to R^o$ by training on a data set, where $m$ is the number of dimensions for input and $o$ is the number of dimensions for output. It can learn a non-linear function approximator for either classification or regression. It is different from logistic regression, in that between the input and the output layer, there can be one or more non-linear layers, called hidden layers. Given a set of training examples $\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots \left(x_n,y_n\right)$ where $x_i\in R^n$ and $y_i\in \left\{\mathrm{0,1}\right\}$, a one hidden layer one hidden neuron MLP learns the function $f\left(x\right)=W_{2}g\left(W_1^{T}x+b_1\right)+b_2$ where $W_1\in R^m$ and $W_2,b_1,b_2\in R$ are model parameters. $W_1,W_2$ represent the weights of the input layer and hidden layer, respectively; and $b_1,b_2$ represent the bias added to the hidden layer and the output layer, respectively. $g(\cdot ):R\to R$ is the activation function. For binary classification, $f\left(x\right)$ passes through the logistic function $g\left(z\right)=1/\left(1+e^{-z}\right)$ to obtain output values between zero and one. A threshold, set to 0.5, would assign samples of outputs larger or equal 0.5 to the positive class, and the rest to the negative class. The loss function for classification is Cross-Entropy, which in binary case is given as,

$Loss\left(\widehat{y},y,W\right)=-y\ln \widehat{y}-\left(1-y\right)\ln \left(1-\widehat{y}\right)+\alpha \Vert W{\Vert }_2^2$

Starting from initial random weights, MLP minimizes the loss function by repeatedly updating these weights. After computing the loss, a backward pass propagates it from the output layer to the previous layers, providing each weight parameter with an update value meant to decrease the loss. The algorithm stops when it reaches a preset maximum number of iterations; or when the improvement in loss is below a certain, small number (Rumelhart et al., 1986; Widrow and Lehr, 2002).

2.4 Model Validation

Hold-out method: divide the data set $D$ into two mutually exclusive subsets, one as the training set $S$ and the other as the test set $T$, i.e., $D=S\cup T,S\cap T=\varnothing$. After training the model on $S$, use $T$ to evaluate its test error as an estimate of the generalization error. In this research, we used 70% of the data set as the training set and 30% as the test set.

K-folder cross validation method: randomly divide the data set $D$ into $K$ mutually exclusive subsets of the same size, i.e., $D=D_1\cup D_2\cup \dots \cup D_K,D_i\cap D_j=\varnothing \left(i\ne j\right)$. Each time randomly select $K-1$ subsets as the training set, and the remaining one as the test set. In each of these $K$ training and validation runs, the subset used to validate the model is different. Finally, we average the training error and validation error respectively for these $K$ runs. In this research, $K$ was set to 10, i.e., 10-folder cross validation (Kohavi, 1995; Rao and Fung, 2008).

We used hold-out method to pre-select the models, which can quickly eliminate some models that are not suitable for this research. 10-folder cross validation was used to conduct in-depth analysis of the model, which can make full use of the distribution characteristics of the data set.

2.5 Performance Measure

In machine learning research, confusion matrix is a visualization technique used to summarize the performance of classification algorithms, especially for supervised learning. In binary classification, the confusion matrix consists of four elements, which are true negatives (TN), true positives (TP), false positives (FP), and false negatives (FN). In a binary confusion matrix, upper left corner (TN) and lower right corner (TP) refer to correct classification performance; lower left corner (FN) and upper right (FP) corner refer to incorrect classification performance.

Accuracy is the ratio of the number of correctly predicted samples to the total number of samples, i.e.,

$Accuracy=\frac{TP+TN}{TP+FP+TN+FN}$

Accuracy seems to be a good evaluation metric, but in practice, it may hide a lot of details we need. which hinders a better understanding of the performance of the classification model. Therefore, we need to calculate more metrics from the four elements of the confusion matrix to obtain a more comprehensive performance measure (Stralen et al., 2009). At this time, we used the following metrics:

Precision indicates the ratio of samples correctly predicted as positive to the total samples predicted as positive, i.e.,

$Precision=\frac{TP}{TP+FP}$

Recall indicates the ratio of samples correctly predicted as positive to the total positive samples, i.e.,

$Recall=\frac{TP}{TP+FN}$

Sensitivity also represents the positive classification performance, which has the same formula as Recall. Specificity indicates the ratio of samples correctly predicted as negative to the total negative samples, i.e.,

$\begin{array}{cc}Sensitivity=\frac{TP}{TP+FN}& Specificity=\frac{TN}{TN+FP}\end{array}$

Precision and Recall are contradictory, and we cannot have them both. If both Precision and Recall are considered comprehensively, a new evaluation metric F1-score, also known as the comprehensive classification rate, can be obtained. The formula is as follows:

$F\mathit{1}score=2\ast \frac{Precision\times Recall}{Precision+Recall}$

The Precision-Recall curve (P-R curve) is actually a curve composed of two variables, Precision and Recall, in which the horizontal axis represents Recall, and the vertical axis represents Precision. A threshold corresponds to a point on the PR curve. By selecting an appropriate threshold, the samples are classified, and then calculate the corresponding Precision and Recall. The P-R curve can be drawn by connecting the points formed by many sets of Precision and Recall corresponding to different thresholds. The P-R curve is closer to the upper right corner (i.e., Precision = 1, Recall = 1), the better the performance of the classifier. Moreover, if the P-R curve of one classifier is completely enclosed by the P-R curve of another classifier, it can be asserted that the performance of the latter is better than that of the former (Mosley, 2013).

Receiver operating characteristic curve (ROC curve) was also used in this research. In the ROC curve, the horizontal axis is defined as false positive rate (FPR), and the vertical axis is defined as true positive rate (TPR). Similar to the P-R curve, the corresponding FPR and TPR are calculated after selecting an appropriate threshold, and the curve is drawn by connecting the points formed by different sets of FPR and TPR. The ROC curve is closer to the upper left corner (i.e., TPR = 1, FPR = 0), the better the performance of the classifier (Fawcett, 2005).

Moreover, area under receiver operating characteristic curve (AUC-ROC), which can intuitively evaluate the performance of the classifier, has a numerical value range from 0 to 1, where 1 represents the best performance, 0 is the worst, 0.5–1 means the model can predict by setting an appropriate threshold and AUC-ROC = 0.5 means no predictive value like random guessing. In the same way, we can also calculate the area under Precision-Recall curve (AUC-PR), that is, the larger the value, the better the performance (Hanley and Mcneil, 1982).

3 Results

3.1 Cycle Data Statistics

The data set included in this research was filtered from 760,732 cycle records in the HFEA database from 2005 to 2016. A total of 45,921 cycle records were used in the model training and validation process. They were divided into two groups according to the number of embryos transferred, Group A and Group B. Group A contained 34,175 cycles with two embryos transferred, while Group B contained 11,746 cycles with only one embryo transferred. “Early Outcome” (intrauterine fetal pulsation) was used as the prediction label (or output), and the remaining 44 fields were identified as features (or input). As mentioned above, the entire data set included one 34,175 × 45 matrix for Group A and one 11,746 × 45 matrix for Group B.

In Group A, the total number of cycles was 34,175, including 9,333 positive outcome cycles and 24,842 negative outcome cycles. Focusing on the feature “Patient Age at Treatment”, among all cycles, the patients aged 18–34 had the largest proportion (n = 12,784, 37.41%), followed by those aged 35–37 (n = 9,748, 28.52%). Focusing on the features “Type of Infertility”, “Couple Primary” cycles accounted for the largest proportion (n = 10,179, 29.78%), followed by the “Female Primary” cycles (n = 8,985, 26.29%) and “Male Primary” cycles (n = 8,699, 25.45%). Focusing on the features “Cause of Infertility”, “Male Factor” cycles accounted for the largest proportion (n = 13,501, 39.51%), and “Unexplained” cycles had the second largest proportion (n = 9,339, 27.33%). Moreover, “Stimulation used” cycles had a higher percentage (n = 21,936, 64.19%).

In Group B, the total number of cycles was 11,746, including 2,386 positive outcome cycles and 9,360 negative outcome cycles. The proportion of patients aged 18–34 was still the largest (n = 4,121, 35.08%), followed by those aged 35–37 (n = 3,025, 25.75%). Among the features “Type of Infertility”, “Couple Primary” cycles accounted for the largest proportion (n = 1844, 15.70%), followed by the “Female Primary” cycles (n = 1,624, 13.83%) and “Male Primary” cycles (n = 1,554, 13.23%). Among the features “Cause of Infertility”, “Male Factor” cycles accounted for the highest proportion (n = 4,340, 36.95%), and “Unexplained” cycles had the second highest proportion (n = 3,352, 28.54%). In this group, cycles without “Stimulation used” had a higher percentage (n = 6,824, 58.10%).

3.2 Model Evaluation and Analysis

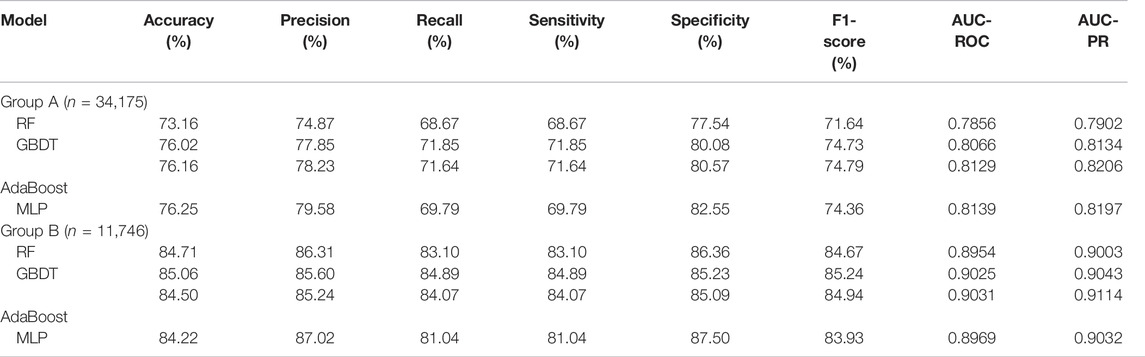
As shown in Table 2, a total of eight metrics were used to evaluate model performance, the specific definitions of these eight metrics have been introduced above. Eight metrics were divided into two groups: one group contains five separate performance metrics, i.e., Accuracy, Precision, Recall, Sensitivity, and Specificity; the other group contains 3 comprehensive performance metrics, i.e., F1-score, AUC-ROC and AUC-PR.

TABLE 2

TABLE 2. Evaluation metrics of all models.

In Group A, the MLP model got the highest Accuracy (76.25%) and Precision (79.58%), but the Recall (69.79%) was very low. The MLP model also obtained the highest Specificity (82.55%) and lower Sensitivity (69.79%), indicating that this model was not balanced. The RF model obtained the lowest scores in all five separate performance metrics. The GBDT model and the AdaBoost model got very balanced scores in all five separate performance metrics. Among the three comprehensive performance metrics, the AdaBoost model won the best F1-score (74.79%) as well as AUC-PR (0.8206), and also won the second-best AUC-ROC (0.8129). Figure 2 shows the ROC curves and P-R curves of the four models in Group A respectively, and the shaded part under the curve is the AUC. In Figures 4A,B, the ROC curves and P-R curves of the four models in Group A were superimposed together and the green curves (AdaBoost model) wrapped more of the other curves. After comprehensive comparison, we found that the AdaBoost model was the model with the most balanced performance, that is, the best model.

FIGURE 2

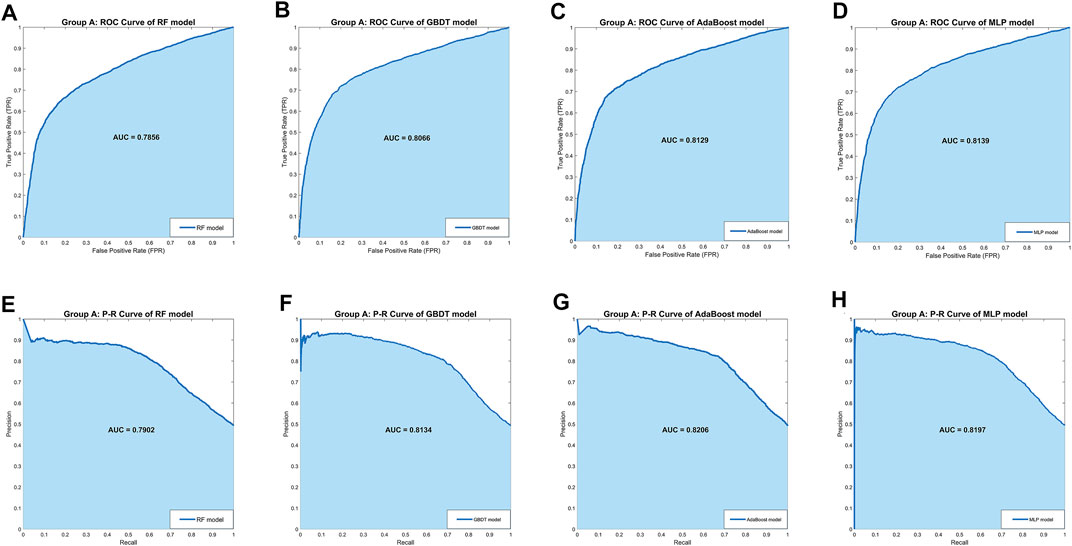
FIGURE 2. The ROC curves and P-R curves of the four models in Group A. (A–D) The ROC curves and AUC scores of four models in Group A: the dark blue curve refers to the ROC curve, the area under the curve is covered by light blue color and the AUC score is clearly marked. (E–H) The P-R curves and AUC scores of four models in Group A: the dark blue curve refers to the P-R curve, the area under the curve is covered by light blue color and the AUC score is clearly marked.

In Group B, the MLP model obtained the highest Precision (87.02%) and Specificity (87.50%), along with the lowest Recall (81.04%) and Sensitivity (81.04%), indicating that this model was still unbalanced in this group. The GBDT model obtained the best Accuracy (85.06%) and the RF model got the second-best Accuracy (84.71%). But in the other four separate performance metrics, the imbalance of the RF model was slightly larger than the GBDT model and the AdaBoost model, while the GBDT model was slightly better than the AdaBoost model. We turned our focus to the comprehensive performance metrics, where the GBDT model won the best F1-score (85.24%), but the AdaBoost model won the best AUC-ROC (0.9031) and AUC-PR (0.9114). In addition, Figure 3 shows more details of the curves and their shadow areas. In Figures 4C,D, the ROC curves and P-R curves of the four models in Group B were superimposed together and the green and blue curves (AdaBoost model and GBDT model) wrapped more of the other curves. The metrics and curves proved that the GBDT model obtained the best classification performance in Group B, that is, the best classifier.

FIGURE 3

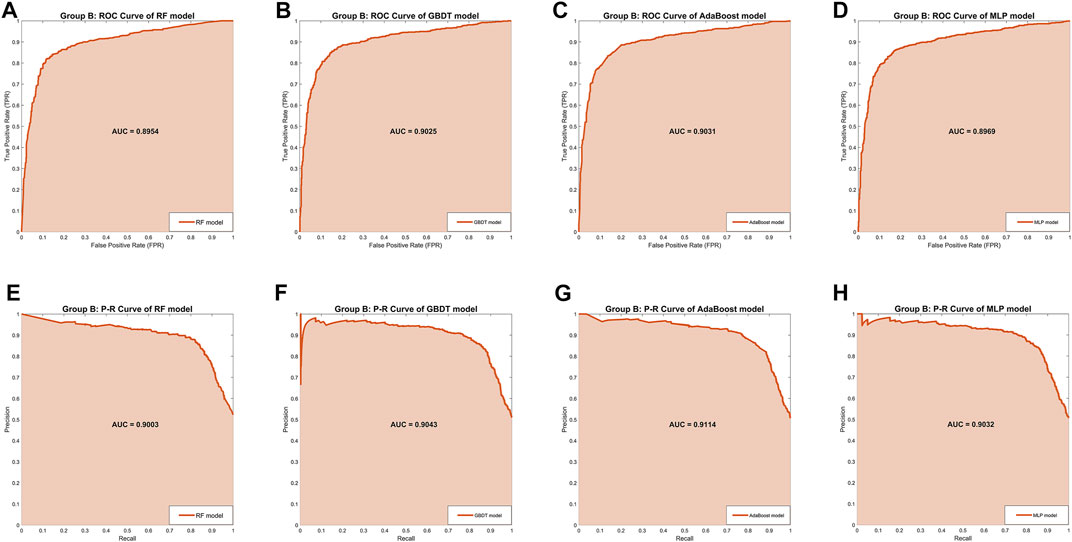
FIGURE 3. The ROC curves and P-R curves of the four models in Group B. (A–D) The ROC curves and AUC scores of four models in Group B: the dark orange curve refers to the ROC curve, the area under the curve is covered by light orange color and the AUC score is clearly marked. (E–H) The P-R curves and AUC scores of four models in Group A: the dark orange curve refers to the P-R curve, the area under the curve is covered by light orange color and the AUC score is clearly marked.

FIGURE 4

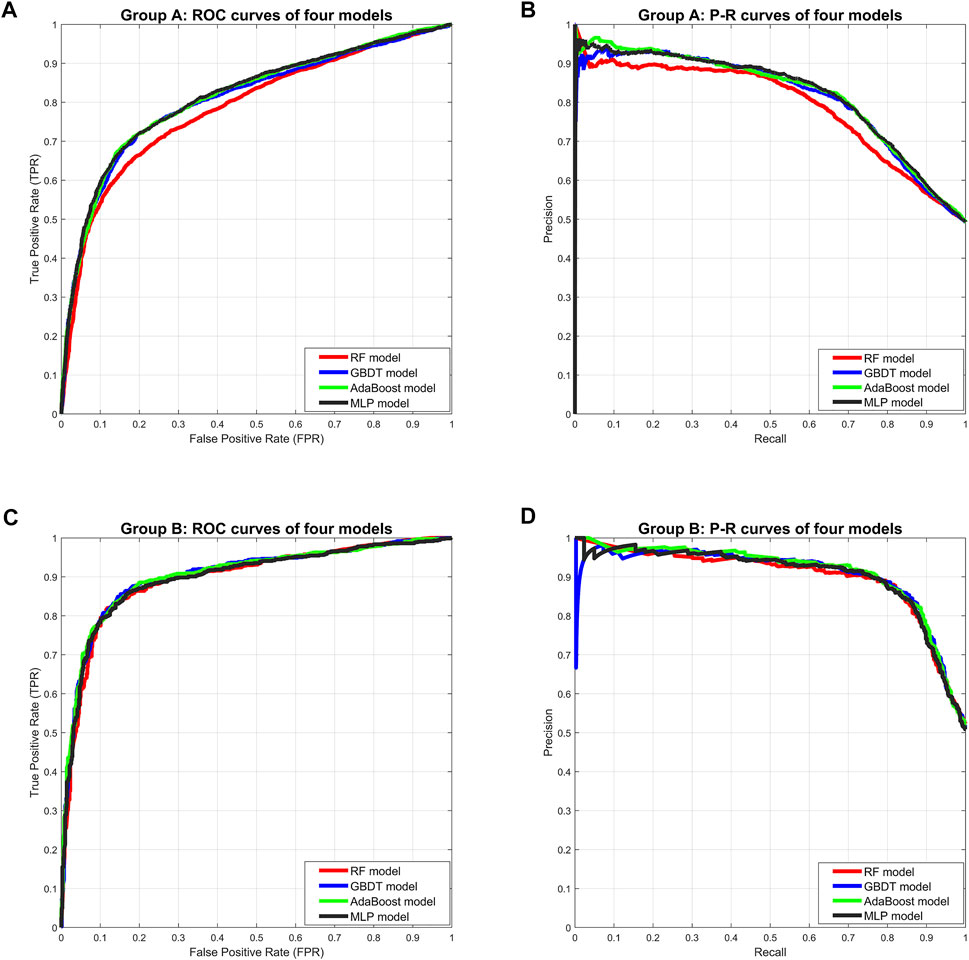
FIGURE 4. Comprehensive comparison of four models. (A) Comprehensive ROC curves of four models in Group A: the larger the area under the curve, the better the performance. (B) Comprehensive P-R curves of four models in Group A: the larger the area under the curve, the better the performance. (C) Comprehensive ROC curves of four models in Group B. (D) Comprehensive P-R curves of four models in Group B.

Although we strictly evaluated the models according to the metrics and curves, in fact, the performance difference of these four models is not large, especially the GBDT model and AdaBoost model.

4 Discussion

RIF patients, as a special group in the infertile population, are still unable to obtain pregnancy and live birth after multiple IVF-ET cycles. At present, it is believed that a personalized embryo transfer strategy may be the most direct and effective method to improve the success rate of embryo transfer and obtain a good pregnancy outcome (Patel et al., 2019). To ensure clinical pregnancy rates in RIF patients, transfer strategies in many reproductive centers include: (ⅰ) increasing the number of embryos transferred in a single cycle; (ⅱ) accumulating multiple single embryo transfer (SET) cycles. As we mentioned above, both strategies have limitations and disadvantages: the former will significantly increase the multiple pregnancy rate and the risk of pregnancy; the latter will significantly increase the time cost and economic burden, as well as the patients’ mental stress. However, it is currently impossible to carry out targeted operations and treatments for each individual or even each embryo and more often, we only rely on the experience of clinicians. Obviously, we urgently need a reliable, accurate and intelligent assisted decision-making method to help clinicians and RIF patients develop personalized transfer strategies, which not only guarantees efficient and reliable pregnancy, but also avoids the risk of multiple pregnancy as much as possible.

In this research, we focused on AI. AI is a new technical science that studies and develops theories, methods, technologies and application systems for simulating, extending and expanding human intelligence. AI is a branch of computer science that attempts to understand the essence of intelligence and produce a new type of intelligent machine that responds in a similar way to human intelligence. Research in this field includes robotics, language recognition, image recognition, natural language processing and expert systems, etc. Since the birth of AI, theories and technologies have become increasingly mature, and the application fields have been expanding. Currently, AI, especially machine learning has rapidly demonstrated its ability to predict human fertility (Curchoe and Bormann, 2019). The research indicated that machine learning models including patients’ data can assist clinicians to offering couples undergoing IVF personalized treatment strategies (Siristatidis et al., 2016). Barnett-Itzhaki et al. tested two machine learning algorithms, SVM and artificial neural network (ANN) to predict IVF outcomes (β-HCG, clinical pregnancies, live births, etc.) (Barnett-Itzhaki et al., 2020). Raef et al. examined six machine learning approaches based on the dataset containing 82 features of IVF cycles to predict outcome and concluded that random forest (RF) was the best classifier (Raef et al., 2020). Tran et al. created a deep learning model to predict the probability of pregnancy with fetal heart (FH) from time-lapse videos (Tran et al., 2019).

In this research, we filtered out the RIF data set (n = 45,921) from HFEA database containing 760,732 cycle records from 2005 to 2016, and far exceeding the currently known data set of RIF patients in other studies. We divided the data set into Group A (DET, n = 34,175) and Group B (SET, n = 11,746), each containing 44 features and a prediction label (pregnancy). Four machine learning algorithms (RF, GBDT, AdaBoost, and MLP) were used to train Group A and Group B data set respectively and 10-folder cross validation method was used to validate the models. The results revealed that the AdaBoost model of Group A obtained the best performance, while the GBDT model in Group B was proved to be the best model. Both models had been proved to provide accurate prediction of transfer outcome. Naturally, our research still has some limitations. Our data are all from the United Kingdom and are limited in terms of ethnic and geographic diversity. Some potential specific indicators may not be fully covered. In addition, natural-cycle IVF (NC-IVF) and stimulated IVF (SIVF) have a different basis for success. SET in NC-IVF, which is most commonly as being used in poor responders, and SET in SIVF, which is most commonly used in high responders, have a different basis. This factor should be taken into account when setting up future models.

In conclusion, our research provided a new approach for targeted and personalized treatment of RIF patients to help them achieve efficient and reliable pregnancy. In addition, As we first imagined, an AI-assisted decision-making system is being designed for clinical application. The clinical variables before embryo transfer stage of RIF patients undergoing a new cycle will be entered into the system. The date of embryo transfer (cleavage embryo or blastocyst) as an unknown variable can be finely set as an input option. Then, the two prediction models in the system start to work separately, and prediction results will be calculated, that is, results after SET and DET. When the success rate of SET is predicted to be high, the system suggests that SET is preferred to reduce the multiple pregnancy rate. When the predicted success rate of SET is much lower than that of DET, clinicians can choose whether to perform DET according to the patient’s own wishes. The AI-assisted decision-making system cannot replace the decision-making of clinicians. It only provides suggestions. Furthermore, we will also open the model upgrade interface. More samples or features can be incorporated for training with the goal to improve the prediction accuracy and to make the prediction results more multidimensional (not just predicting SET and DET).

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://www.hfea.gov.uk/about-us/our-data/#ar.

Ethics Statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.

Author Contributions

LS and YZ initiated and conceived the study. YZ were responsible for data acquisition and data preprocessing. LS were responsible for algorithm selection and model training. LS and YZ wrote the manuscript. WC and XY advised on the development of the study, revised and commented the draft. LS and WC are developing the software. All authors read and approved the final version of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank the Human Fertilisation and Embryology Authority for collecting and providing the data set.

References

Barnett-Itzhaki Z., Elbaz M., Butterman R., Amar D., Amitay M., Racowsky C., et al. (2020). Machine Learning vs. Classic Statistics for the Prediction of IVF Outcomes. J. Assist. Reprod. Genet. 37 (10), 2405–2412. doi:10.1007/s10815-020-01908-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Breiman L. (1998). Arcing Classifiers. Annals of Statistics.

Google Scholar

Breiman L. (2001). Random Forests. Mach. Learn. 45 (1), 5–32. doi:10.1023/a:1010933404324

CrossRef Full Text | Google Scholar

Busnelli A., Reschini M., Cardellicchio L., Vegetti W., Somigliana E., Vercellini P. (2020). How Common Is Real Repeated Implantation Failure? an Indirect Estimate of the Prevalence. Reprod. Biomed. Online 40 (1), 91–97. doi:10.1016/j.rbmo.2019.10.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Calhaz-Jorge C., Calhaz-Jorge C., De Geyter C., Kupka M. S., de Mouzon J., Erb K., et al. (2017). Assisted Reproductive Technology in Europe, 2013: Results Generated from European Registers by ESHRE†. Hum. Reprod. 32 (10), 1957–1973. doi:10.1093/humrep/dex264

PubMed Abstract | CrossRef Full Text | Google Scholar

Calhaz-Jorge C., de Geyter C., Kupka M. S., de Mouzon J., Erb K., Mocanu E., et al. (2016). Assisted Reproductive Technology in Europe, 2012: Results Generated from European Registers by ESHRE. Hum. Reprod. 31 (8), 1638–1652. doi:10.1093/humrep/dew151

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao H., You D., Yuan M., Xi M. (2018). Hysteroscopy after Repeated Implantation Failure of Assisted Reproductive Technology: A Meta-Analysis. J. Obstet. Gynaecol. Res. 44 (3), 365–373. doi:10.1111/jog.13571

PubMed Abstract | CrossRef Full Text | Google Scholar

Cimadomo D., Craciunas L., Vermeulen N., Vomstein K., Toth B. (2021). Definition, Diagnostic and Therapeutic Options in Recurrent Implantation Failure: an International Survey of Clinicians and Embryologists. Hum. Reprod. 36 (2), 305–317. doi:10.1093/humrep/deaa317

PubMed Abstract | CrossRef Full Text | Google Scholar

Coughlan C., Ledger W., Wang Q., Liu F., Demirol A., Gurgan T., et al. (2014). Recurrent Implantation Failure: Definition and Management. Reprod. Biomed. Online 28 (1), 14–38. doi:10.1016/j.rbmo.2013.08.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Curchoe C. L., Bormann C. L. (2019). Artificial Intelligence and Machine Learning for Human Reproduction and Embryology Presented at ASRM and ESHRE 2018. J. Assist. Reprod. Genet. 36 (4), 591–600. doi:10.1007/s10815-019-01408-x

PubMed Abstract | CrossRef Full Text | Google Scholar

de Mouzon J., Goossens V., Bhattacharya S., Castilla J. A., Ferraretti A. P., Korsak V., et al. (2012). Assisted Reproductive Technology in Europe, 2007: Results Generated from European Registers by ESHRE. Hum. Reprod. 27 (4), 954–966. doi:10.1093/humrep/des023

PubMed Abstract | CrossRef Full Text | Google Scholar

Deo R. C. (2015). Machine Learning in Medicine. Circulation 132 (20), 1920–1930. doi:10.1161/CIRCULATIONAHA.115.001593

PubMed Abstract | CrossRef Full Text | Google Scholar

Fawcett T. (2005). An Introduction to ROC Analysis. Pattern Recognit. Lett. 27 (8), 861–874. doi:10.1016/j.patrec.2005.10.010

CrossRef Full Text | Google Scholar

Freund Y., Schapire R. E. (1997). A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 55, 119. doi:10.1006/jcss.1997.1504

CrossRef Full Text | Google Scholar

Friedman J. H. (2002). Stochastic Gradient Boosting. Comput. Statistics Data Analysis 38, 369. doi:10.1016/s0167-9473(01)00065-2

CrossRef Full Text | Google Scholar

Geurts P., Ernst D., Wehenkel L. (2006). Extremely Randomized Trees. Mach. Learn 63 (1), 3–42. doi:10.1007/s10994-006-6226-1

CrossRef Full Text | Google Scholar

Hanley J. A., Mcneil B. J. (1982). The Meaning and Use of the Area under a Receiver Operating Characteristic (ROC) Curve. Radiology 143 (1), 29–36. doi:10.1148/radiology.143.1.7063747

PubMed Abstract | CrossRef Full Text | Google Scholar

Hastie T., Tibshirani R., Friedman J. (2009). The Elements of Statistical Learning. Data Mining, Inference, and Prediction. 2nd ed. New York: Springer.

Google Scholar

Kamath M. S., Mascarenhas M., Kirubakaran R., Bhattacharya S. (2020). Number of Embryos for Transfer Following In Vitro Fertilisation or Intra-cytoplasmic Sperm Injection. Cochrane Database Syst. Rev. 8, CD003416. doi:10.1002/14651858.CD003416.pub5

PubMed Abstract | CrossRef Full Text | Google Scholar

Kohavi R. (1995). “A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection,” in International joint conference on Artificial intelligence.

Google Scholar

Lee M. S., Evans B. T., Stern A. D., Hornstein M. D. (2016). Economic Implications of the Society for Assisted Reproductive Technology Embryo Transfer Guidelines: Healthcare Dollars Saved by Reducing Iatrogenic Triplets. Fertil. Steril. 106 (1), 189–195. doi:10.1016/j.fertnstert.2016.03.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma S., Peng Y., Hu L., Wang X., Xiong Y., Tang Y., et al. (2022). Comparisons of Benefits and Risks of Single Embryo Transfer versus Double Embryo Transfer: a Systematic Review and Meta-Analysis. Reprod. Biol. Endocrinol. 20 (1), 20. doi:10.1186/s12958-022-00899-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Margalioth E. J., Ben-Chetrit A., Gal M., Eldar-Geva T. (2006). Investigation and Treatment of Repeated Implantation Failure Following IVF-ET. Hum. Reprod. 21 (12), 3036–3043. doi:10.1093/humrep/del305

PubMed Abstract | CrossRef Full Text | Google Scholar

Mosley L. (2013). A Balanced Approach to the Multi-Class Imbalance Problem Doctoral Dissertation. Ames, Iowa,: Iowa State University.

Google Scholar

Obermeyer Z., Emanuel E. J. (2016). Predicting the Future - Big Data, Machine Learning, and Clinical Medicine. N. Engl. J. Med. 375 (13), 1216–1219. doi:10.1056/NEJMp1606181

PubMed Abstract | CrossRef Full Text | Google Scholar

Pandian Z., Bhattacharya S., Ozturk O., Serour G., Templeton A. (2004). Number of Embryos for Transfer Following In-Vitro Fertilisation or Intra-cytoplasmic Sperm Injection. Cochrane Database Syst. Rev. 4, CD003416. doi:10.1002/14651858.CD003416.pub2

PubMed Abstract | CrossRef Full Text | Google Scholar

Patel J., Patel A., Banker J., Shah S., Banker M. (2019). Personalized Embryo Transfer Helps in Improving In Vitro Fertilization/ICSI Outcomes in Patients with Recurrent Implantation Failure. J. Hum. Reprod. Sci. 12 (1), 59–66. doi:10.4103/jhrs.JHRS_74_18

PubMed Abstract | CrossRef Full Text | Google Scholar

Penzias A., Bendikson K., Butts S., Coutifaris C., Falcone T., Fossum G., et al. (2017). ASRM Standard Embryo Transfer Protocol Template: a Committee Opinion. Fertil. Steril. 107 (4), 897–900. doi:10.1016/j.fertnstert.2017.02.108

PubMed Abstract | CrossRef Full Text | Google Scholar

Pinborg A. (2005). IVF/ICSI Twin Pregnancies: Risks and Prevention. Hum. Reprod. Update 11 (6), 575–593. doi:10.1093/humupd/dmi027

PubMed Abstract | CrossRef Full Text | Google Scholar

Practice Committee of the American Society for Reproductive Medicine (2017). Performing the Embryo Transfer: a Guideline. Fertil. Steril. 107 (4), 882–896. doi:10.1016/j.fertnstert.2017.01.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Practice Committee of the American Society for Reproductive Medicine, and Practice Committee of the Society for Assisted Reproductive Technology (2017). Guidance on the Limits to the Number of Embryos to Transfer: a Committee Opinion. Fertil. Steril. 107 (4), 901–903. doi:10.1016/j.fertnstert.2017.02.107

PubMed Abstract | CrossRef Full Text | Google Scholar

Raef B., Maleki M., Ferdousi R. (2020). Computational Prediction of Implantation Outcome after Embryo Transfer. Health Inf. J. 26 (3), 1810–1826. doi:10.1177/1460458219892138

PubMed Abstract | CrossRef Full Text | Google Scholar

Rao R. B., Fung G. (2008). “On the Dangers of Cross-Validation. An Experimental Evaluation,” in Proceedings of the SIAM International Conference on Data Mining, SDM 2008, Georgia, USA, April 24-26, 2008. doi:10.1137/1.9781611972788.54

CrossRef Full Text | Google Scholar

Rumelhart D. E., Hinton G. E., Williams R. J. (1986). Learning representations by back-propagating errors. Nature 323 (6088), 533–536. doi:10.1038/323533a0

CrossRef Full Text | Google Scholar

Santana D. S., Cecatti J. G., Surita F. G., Silveira C., Costa M. L., Souza J. P., et al. (2016). Twin Pregnancy and Severe Maternal Outcomes. Obstet. Gynecol. 127 (4), 631–641. doi:10.1097/AOG.0000000000001338

PubMed Abstract | CrossRef Full Text | Google Scholar

Shiffler R. E. (1988). Maximum Z scores and outliers. Am. Statistician 42, 79–80. doi:10.1080/00031305.1988.10475530

CrossRef Full Text | Google Scholar

Simon A., Laufer N. (2012). Assessment and treatment of repeated implantation failure (RIF). J. Assist. Reprod. Genet. 29 (11), 1227–1239. doi:10.1007/s10815-012-9861-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Siristatidis C., Vogiatzi P., Pouliakis A., Trivella M., Papantoniou N., Bettocchi S. (2016). Predicting IVF Outcome: A Proposed Web-based System Using Artificial Intelligence. Vivo 30 (4), 507–512. doi:10.21873/invivo.11018

PubMed Abstract | CrossRef Full Text | Google Scholar

Stern C., Chamley L., Norris H., Hale L., Baker H. W. G. (2003). A randomized, double-blind, placebo-controlled trial of heparin and aspirin for women with In Vitro fertilization implantation failure and antiphospholipid or antinuclear antibodies. Fertil. Steril. 80 (2), 376–383. doi:10.1016/s0015-0282(03)00610-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Tobias T., Sharara F. I., Franasiak J. M., Heiser P. W., Pinckney-Clark E. (2016). Promoting the use of elective single embryo transfer in clinical practice. Fertil Res Pract 2, 1. doi:10.1186/s40738-016-0024-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Tran D., Cooke S., Illingworth P. J., Gardner D. K. (2019). Deep learning as a predictive tool for fetal heart pregnancy following time-lapse incubation and blastocyst transfer. Hum. Reprod. 34 (6), 1011–1018. doi:10.1093/humrep/dez064

PubMed Abstract | CrossRef Full Text | Google Scholar

van Stralen K. J., Stel V. S., Reitsma J. B., Dekker F. W., Zoccali C., Jager K. J. (2009). Diagnostic methods I: sensitivity, specificity, and other measures of accuracy. Kidney Int. 75 (12), 1257–1263. doi:10.1038/ki.2009.92

PubMed Abstract | CrossRef Full Text | Google Scholar

Widrow B., Lehr M. A. (2002). 30 years of adaptive neural networks: perceptron, Madaline, and backpropagation. Proc. IEEE 78 (9), 1415–1442. doi:10.1109/5.58323

CrossRef Full Text | Google Scholar