Refining Our Understanding of the Flow Through Coronary Artery Branches; Revisiting Murray’s Law in Human Epicardial Coronary Arteries

Background: Quantification of coronary blood flow is used to evaluate coronary artery disease, but our understanding of flow through branched systems is poor. Murray’s law defines coronary morphometric scaling, the relationship between flow (Q) and vessel diameter (D) and is the basis for minimum lumen area targets when intervening on bifurcation lesions. Murray’s original law (Q α D^P) dictates that the exponent (P) is 3.0, whilst constant blood velocity throughout the system would suggest an exponent of 2.0. In human coronary arteries, the value of Murray’s exponent remains unknown.

Aim: To establish the exponent in Murray’s power law relationship that best reproduces coronary blood flows (Q) and microvascular resistances (Rmicro) in a bifurcating coronary tree.

Methods and Results: We screened 48 cases, and were able to evaluate inlet Q and Rmicro in 27 branched coronary arteries, taken from 20 patients, using a novel computational fluid dynamics (CFD) model which reconstructs 3D coronary anatomy from angiography and uses pressure-wire measurements to compute Q and Rmicro distribution in the main- and side-branches. Outputs were validated against invasive measurements using a Rayflow™ catheter. A Murray’s power law exponent of 2.15 produced the strongest correlation and closest agreement with inlet Q (zero bias, r = 0.47, p = 0.006) and an exponent of 2.38 produced the strongest correlation and closest agreement with Rmicro (zero bias, r = 0.66, p = 0.0001).

Conclusions: The optimal power law exponents for Q and Rmicro were not 3.0, as dictated by Murray’s Law, but 2.15 and 2.38 respectively. These data will be useful in assessing patient-specific coronary physiology and tailoring revascularisation decisions.

Introduction

First described in 1926, Murray’s law describes the physical principles for fluid flow through branched transfer networks across a wide range of biological systems. The diameters of branched vessels obey a scaling relation such that total viscous dissipation and material storage energy costs are minimised. In human arteries, Murray’s law characterises the optimal counterpoise between frictional and metabolic forces. Thus, the energy required to drive blood through the coronary circulation (overcoming vascular resistance) is balanced against the energy required to produce and maintain the blood volume such that overall energy costs are minimised (Murray, 1926). Murray’s law characterises the tapering of the arterial diameter (D) as daughter-branches (DB) arise from a parent vessel (PV) and where k is a constant, the proportionality of volumetric flow rate (Q) to diameter:

${\mathrm{D}}_{\mathrm{P}\mathrm{V}}^3 = {\mathrm{D}}_{\mathrm{D}\mathrm{B}1}^3+{\mathrm{D}}_{\mathrm{D}\mathrm{B}2}^3$

and

$\mathrm{Q}=\mathrm{k}{\mathrm{D}}^3$

A consequence of the exponent of 3.0 in Murrays’ Law, is that wall shear stress (the frictional force per unit area acting on the endothelium) is constant throughout the branching tree. Murray’s law however, assumes steady, laminar flow of a Newtonian fluid through rigid tubes of constant volume. In contrast, flow in human coronary arteries is pulsatile and may be disturbed in the context of atherosclerotic stenoses. Arteries are also distensible vessels, carrying a fluid whose mechanical properties vary with vessel radius. Theoretical derivations of turbulent flow suggest the exponent of proportionality that Murray originally proposed (3.0) may range from 2.33 to 3.0, with lower values being appropriate in more disturbed flow (Uylings, 1977). Furthermore, a range of studies, based on prototypical geometries in a wide range of practical networks, applied to Newtonian and non-Newtonian fluids largely recover the essential form of Murray’s law with varying exponent values (Bejan et al., 2000; Revellin et al., 2009; Miguel, 2019; Soni et al., 2020; Miguel, 2021). Morphometric analyses of coronary arterial trees suggest that the exponent may even lie outside theoretical limits, with reported values ranging from 2.06 to 3.20 (Hutchins et al., 1976; Zhou et al., 1999; Kassab, 2006, 2007; van der Giessen et al., 2011; Li et al., 2021).

In human coronary arteries, Murray’s law is central to all analyses of anatomy, physiology, morphometric scaling, shear-stress, wave and pressure-transmission mechanics, and predictive modelling. It is therefore relevant in clinical cardiology, even if many practitioners are unaware of it. In the cardiac catheter laboratory, the appropriate size of parent and daughter branches is deduced from a number of cues; often, pragmatically, the diameter of “normal” segments of downstream branches, but Murray’s law and Finet’s rule (Finet et al., 2008) (a derivation of Murray’s law) are also used. Decisions regarding stent sizing at bifurcation points, for example, can be made on that basis. Furthermore, the minimum diseased lumen area (MLA) triggering ischemia of a diseased left main coronary artery (≥6 mm²) recommended by current guidelines for lesion assessment (Neumann et al., 2019) was derived from Murray’s law (de la Torre Hernández et al., 2007; de la Torre Hernandez et al., 2011).

Recently, we developed a novel computational fluid dynamics (CFD)-based method for simulating human coronary artery physiology called virtuQ™, capable of quantifying absolute coronary blood flow (Q_CFD) and microvascular resistance (Rmicro_CFD) (Morris et al., 2020). In this study, we adapted the 3D CFD method to simulate side branch (SB) flow, the magnitude of which was dependent upon the exponent used in Murray’s law (Gosling et al., 2020).

The aim of this study was to apply our novel CFD-based physiological method to determine the most accurate exponent of Murray’s law in human epicardial coronary arteries and validate this against invasive clinical measurements.

Materials and Methods

This was a retrospective analysis of clinical data collected at the Catharina Hospital, Eindhoven, NL. Computational analysis was performed at the University of Sheffield, United Kingdom. Patients provided informed consent and the study was approved by the research and ethics boards. All supporting data are provided in this manuscript or in the Supplementary Material.

Clinical Data Collection

Adult patients undergoing clinically-indicated invasive angiography for the assessment of chest pain were included. During angiography, fractional flow reserve (FFR) and absolute coronary blood flow (Q_CIT) and microvascular resistance (Rmicro_CIT) were assessed in the artery of interest, with the PressureWire™ X (Abbott, MN, United States) and the continuous infusion thermodilution (CIT) method using the Rayflow™ infusion catheter (Hexacath, Paris, Fr) and the Coroventis™ (Abbott, Plymouth, MN) system (Aarnoudse et al., 2007; van ‘t Veer et al., 2016). Pseudonymised clinical imaging (DICOM) and physiological data were exported to the University of Sheffield for analysis. Cases were excluded if the physiological data were incomplete, the angiogram quality was insufficient for arterial reconstruction, or if there were major arterial SBs within 3.0 cm of the Rayflow™ infusion port. The latter exclusion is recommended by the manufacturer because significant SBs can affect the Q_CIT result (Aarnoudse et al., 2007). A recommended correction for the haemodynamic effect of the infusion catheter is detailed in the Supplementary Material S1. The angiographic requirements for reconstruction have been published (Ghobrial et al., 2021). Percentage stenosis was graded visually by a panel of interventional-cardiologists and additionally, with 2D- and 3D-quantitative coronary angiography (QCA).

Simulating Coronary Blood Flow

The virtuQ method for reconstructing 3D coronary anatomy and simulating Q_CFD and Rmicro_CFD has been validated and published (Morris et al., 2020; Ghobrial et al., 2021; Solanki et al., 2021). In brief, 3D arterial anatomy of a single vessel is reconstructed from two angiographic planes, acquired ≥30° apart, using an epipolar line transection method. The relatively gentle taper of vessels means that recirculation regions are not encountered and the proximal and distal outlet manifolds to accommodate profile development are deemed unnecessary. Simulations applied standard blood parameters (density 1,056 kg/m³; viscosity 0.0035 Pa s). A 3D CFD simulation was then performed with the invasively measured pressures as inlet and outlet boundary conditions, which corresponded to the locations of proximal and distal pressure and temperature measurements. Simulations modelled incompressible, laminar, steady Newtonian flow in the reconstructed artery. The suitability of the steady flow approximation has previously been demonstrated in Morris’ 2015 examination (Morris, 2015) and was confirmed via analysis of Reynolds number at each model inlet, outlet and point of maximal stenosis. Furthermore, the epicardial arteries are of sufficiently large diameter to reliably model blood as a Newtonian fluid (Huckabe and Hahn, 1968). Principal model outputs were inlet and outlet Q_CFD and Rmicro_CFD.

Simulating Side Branch Flow

In this study, the virtuQ™ method was adapted to additionally simulate SB blood flow across the wall of arterial reconstructions, so that Q_inlet > Q_outlet and Q_SB = Q_inlet-Q_outlet. In a CFD analysis of a tube of varying cross section, conservation of mass dictates that the flow at every cross section is the same. If a vessel is tapered, the velocity and the wall shear stress increase as the vessel diameter reduces. A consequence of Murray’s Law is constant wall shear stress. At an arterial bifurcation the proximal flow must be shared between the two distal vessels depending on their diameters. A simple analysis protocol to compensate for branches that are clearly visible, but not included in the 3D arterial model, is to remove flow through the vessel wall at the bifurcation according to a power law representation (a generalisation of Murray’s Law) of the flow at the bifurcation. The same approach can readily be extended to smaller vessel branches that are not visible on the angiogram if it is assumed that the tapering of the primary vessel under analysis has developed, in the healthy state, according to a power law relationship between flow and diameter. Thus, it is assumed that flow must be leaking from the vessel wall to feed the myocardium through the small vessels that are not visible on the angiogram, with the remaining flow in the vessel under analysis reducing consistently as the vessel tapers. This can be handled in the CFD analysis in exactly the same way as the visible bifurcations, by prescribing a wall leak that is a function of the taper. Our model of vessel leakage therefore represented some average of the bifurcations and is intended to describe effects in real coronary arteries. The collection of unresolved SBs was therefore, characterised by a distribution of radii and geometry, ranging from the small calibre vasa vasorum (Gössl et al., 2003) to the largest, named arterial branches, and no single homothety relationship applies. The mathematical derivation of the porous wall method is described in the Supplementary Material S2.

Reconstructions with a total taper (D_outlet-D_inlet) less than one pixel (0.265 mm) were excluded because such small diameter changes cannot be accurately discerned, and so SB flow cannot be modelled reliably. Simulations were performed applying Murray’s exponents of 1.0, 1.5, 2.0, 2.5, 3.0, 3.5. The magnitude of SB flow was then plotted against the relevant exponent and an exponential function was used to fit the relationship. The optimal exponent was then interpolated from this function as the value associated with the best agreement between the CFD method and the invasive CIT measurements. All processing was performed blind to the invasive clinical results.

Statistical Analysis

Categorical variables are presented as frequency (percentage). Continuous variables with a normal distribution are presented as mean (standard deviation) and those with a non-normal distribution as median (interquartile range). The Shapiro-Wilk test was used to assess the normality of data distribution. Between-variable correlation was assessed with Pearson’s correlation coefficient (r) and agreement with Bland Altman plots, calculating the 95% limits of agreement. The optimal value for Murray’s exponent was considered as the value with the smallest bias (mean delta) and narrowest 95% limits of agreement when comparing CFD-derived and invasive measurements of Q and Rmicro. Log transformation was used for skewed datasets.

Results

Case Exclusions

Forty-eight separate patient cases were assessed. Two had insufficient angiographic data and one case had incomplete pressure data. Of the remaining 45 cases, 16 were excluded due to: insufficient angiographic views (n = 11), percutaneous coronary intervention had been performed before Q_CIT measurement (n = 2), major arterial SBs being present within ≤3.0 cm of the CIT infusion port (n = 2), and arterial anatomy precluding reconstruction (n = 1). Twenty-nine arterial cases were successfully processed, and two of these were excluded due to insufficient arterial taper. Twenty-seven cases were therefore included in the final analysis (Figure 1).

FIGURE 1

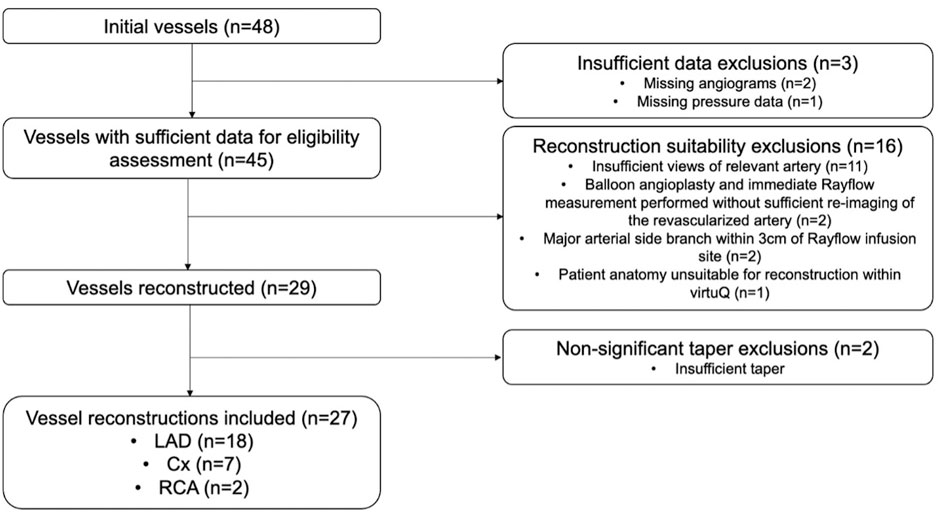
FIGURE 1. Flow diagram showing case exclusions. Cx, Left circumflex artery; LAD, Left anterior descending artery; RCA, Right coronary artery.

Patient Characteristics

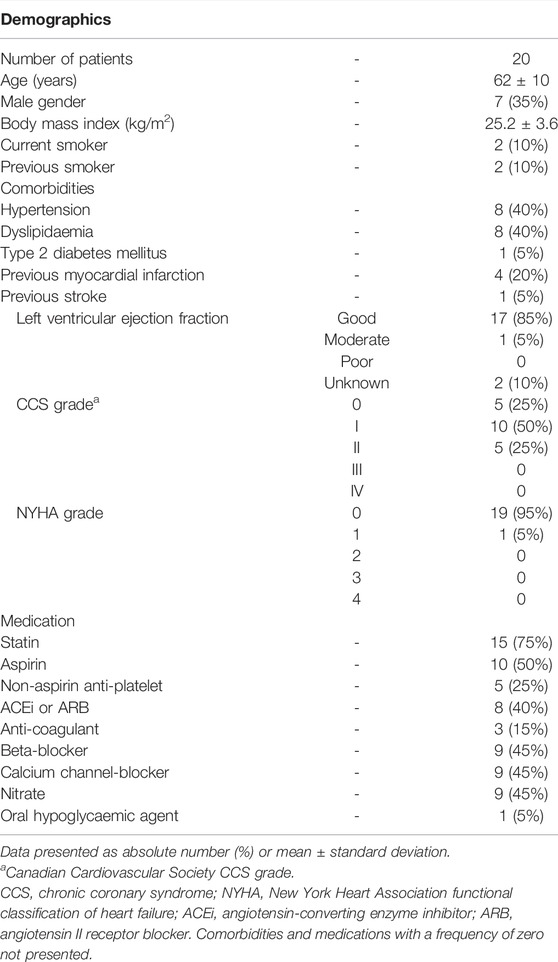
Mean age was 62 (±10) years, 35% were male, mean body mass index (BMI) was 25.2 (±3.6) kg/m² and four (20%) were current or ex-smokers. Full details, including demographics, comorbid conditions, and medical therapy are summarised in Table 1.

TABLE 1

TABLE 1. Recruited patient characteristics.

Baseline Arterial, Lesion and Physiological Characteristics

The 27 arterial cases comprised 18 left anterior descending (LAD) arteries, seven left circumflex (LCX) arteries and two right coronary arteries (RCA). Mean Q_CIT was 219 ml/min (±61 ml/min) and median Rmicro_CIT was 360 mmHg min/L (IQR 290–450 mmHg min/L). Characteristics of individual vessels reported in Supplementary Table S1.

Optimal Murray’s Exponent Based on Absolute Coronary Blood Flow

Murray’s exponent was first optimised for Q between the CIT and CFD methods. The exponent associated with the lowest mean delta, strongest correlation and best agreement (narrowest 95% limits of agreement) between Q_CFD and Q_CIT was 2.15. Differences between Q_CFD and Q_CIT were normally distributed (p = 0.966). When an exponent of 2.15 was applied to the CFD method, the mean delta (bias) between the methods were -168 to +168 ml/min (Figure 2) (Reconstruction measurements, flow rates and Reynolds numbers reported in Supplementary Table S2).

FIGURE 2

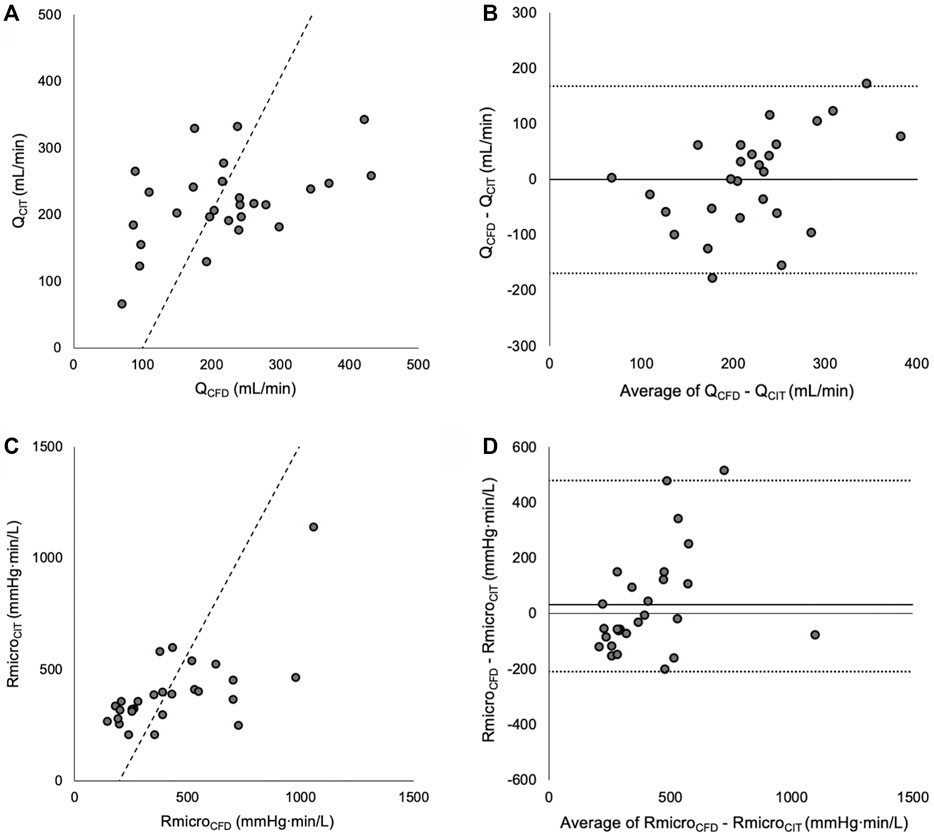
FIGURE 2. (A) Correlation between Q_CFD and Q_CIT (Line of best fit is Passing and Bablok). (B) Bland Altman plot showing mean bias and 95% limits of agreement between Q_CFD and Q_CIT. (C) Scatter plot showing correlation between Rmicro_CFD and Rmicro_CIT. (D) Bland Altman plot of reverse-transformed data, showing mean bias and 95% limits of agreement.

Optimal Murray’s Exponent Based on Absolute Microvascular Resistance

Murray’s exponent was then optimised for Rmicro. The exponent associated with the lowest mean delta, strongest correlation and best agreement between log-transformed Rmicro_CFD and Rmicro_CIT was 2.38. Differences between log-transformed RmicroCFD and RmicroCIT were normally distributed (p = 0.662). When an exponent of 2.38 was applied to the CFD method, the mean delta (bias) between Rmicro_CFD and Rmicro_CIT was +30 mmHg min/L, there was a statistically significant correlation between the methods (r = 0.65, p < 0.001) and the 95% Bland Altman limits of agreement were -210 to +480 mmHg min/L (Figure 2).

Discussion

In this study, we have derived the value for Murray’s exponent that best fits human epicardial coronary anatomical and physiological data. The optimum value was 2.15 based upon Q data, and 2.38 based upon Rmicro data. This is the first study to derive Murray’s exponent using a physiological approach, based upon optimised CFD analysis of absolute Q and Rmicro.

Deviation From Theoretical Estimates

The optimum exponent of 2.15 deviates from Murray’s original law (Murray, 1926) and other analyses of geometries, homotheties and flow as related to bifurcations (Uylings, 1977; Sherman, 1981; Bejan et al., 2000; Revellin et al., 2009; Miguel, 2018; Soni et al., 2020). However, the clinical data used in this physiological-based approach captures the combined effects of numerous known and unknown factors that influence the exponent. The coronary circulation is a network of vessels that continually adapts to a multitude of factors on both the macro and microscopic level. Therefore, it is currently unclear what factor(s) contribute to this lower exponent. It is hypothesised the cyclical variation in shear forces exerted on endothelium, generated by the pulsatility of flow, may play a role, but further research is required on this area.

Previous Estimates of Murray’s Exponent

Previous investigations of Murray’s exponent within human epicardial arteries have relied almost exclusively upon morphometric analysis of parent and daughter vessel diameters. Porcine and murine studies derived values for Murray’s exponent ranging from 2.06 to 2.72 (Zhou et al., 1999; Kassab, 2006, 2007; Li et al., 2021). However, this value may overestimate the true value in epicardial arteries, which tends to be lower than that derived from the penetrating and arteriolar branches (Zamir et al., 2015). Four studies have attempted to validate a Murray’s exponent of three in human epicardial arteries with limited success (Hahn et al., 2008; van der Waal et al., 2009; Schoenenberger et al., 2012; Chen et al., 2020). These studies suffer from large uncertainties, introduced through comparison of cubed values. Two studies have specifically aimed to quantify Murray’s exponent in human epicardial coronary arteries. The first used post-mortem angiographic imaging of 110 left main coronary artery bifurcations (Hutchins et al., 1976). Results were stratified by coronary artery stenosis grades 0–4, but the grading criteria was not reported. Exponent values for bifurcations graded 0, 1.0, 2.0, 3.0 and 4.0 were 3.2 ± 1.6, 2.8 ± 1.3, 2.6 ± 1.5 and 2.2 ± 2.1 respectively. The second and more recent study analysed Doppler ultrasound velocity and angiographic data in 18 un-diseased epicardial bifurcations, associated with an exponent of 2.27 (van der Giessen et al., 2011). The exponent derived from the most normally distributed data is considered the most reliable result. Applied to the current study, the Shapiro Wilk test as test of normality would support that the optimal exponent in human epicardial coronary arteries was 2.15. This is consistent with the findings of similar studies in the literature, derived from morphometric analysis, differing by only 0.12 compared with the most similar study (van der Giessen et al., 2011).

Implications for Clinical Practice

In the context of human coronary arteries, Murray’s law (and exponent) is clinically relevant around bifurcations, with current treatment guidelines (Neumann et al., 2019) grounded in research underpinned by Murray’s law (de la Torre Hernández et al., 2007; de la Torre Hernandez et al., 2011). It is, therefore, important to understand and apply the appropriate value of Murray’s exponent for human epicardial coronary arteries. As an example, Murray’s original law (D_PV³ = D_DB1³ + D_DB2³) dictates that, for a typical 3.5 mm downstream LAD artery and a 3.0 mm circumflex artery, the (parent) left main stem (LMS) should be 4.1 mm in diameter (MLA 13.3 mm²). Applying an exponent of 2.15 instead of 3.0 means that the LMS would need to be 4.5 mm in diameter (MLA 15.9 mm²) (Figure 3) (comment on homothety ratios detailed in Supplementary Material S3).

FIGURE 3

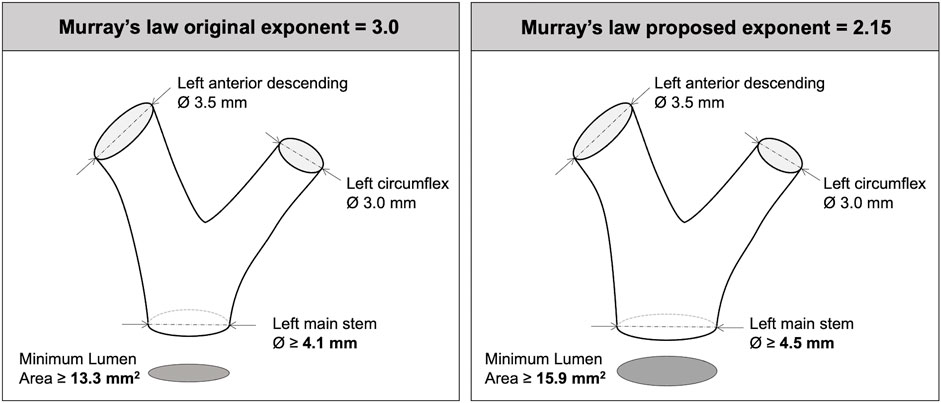
FIGURE 3. Implications of Murray’s exponent when interpreting left main bifurcation anatomy and parent daughter branch scaling.

Limitations

The sample size in this study was modest, but is larger than most studies in this area. More importantly, the arteries in this study were minimally diseased (INOCA cases), as assessed by FFR and percentage diameter stenosis. This has implications for the accuracy of the CFD method, which requires a pressure drop for accuracy and this may explain poorer correlation in these cases. A disproportionately high number of LAD arteries were included. The results may, therefore, not reflect the best value of Murray’s exponent in other arteries. Cases with significant SBs within 3.0 cm of the Rayflow™ infusion port were excluded as per the manufacturer’s instructions for use. These cases are likely to have had more significant taper and may have been valuable for Murray’s exponent determination. Finally, this was a retrospective analysis and so angiograms were not acquired according to the optimised protocols for 3D reconstruction; this is reflected in the percentage of case exclusions.

Conclusion

Using a novel CFD model and invasive physiological data, we have identified the optimal exponent for Murray’s law was 2.15 for Q and 2.38 for Rmicro. This is lower than that proposed in Murray’s original law, is consistent with recent derivations based on theoretical and morphometric analyses and has clinically relevant implications.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Ethics Statement

The studies involving human participants were reviewed and approved by the MEC-U, Medical Research Ethics Committees United, St. Antonius Ziekenhuis. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.

Author Contributions

PM conceived the original study. PM, DT, and JG generated the study protocol. DH, IH, JF, and MR developed the CFD methodology. Mv‘tV, DK, and PT collected the clinical data and analysed the invasive flow data. DT reconstructed the arteries and modelled physiology. DT, PM, and IH performed the statistical analysis. PM, DT, JG, DH, IH, RG, LA-R, Mv‘tV, DK, PT, JF, and MR contributed to drafting, revising and approval of the submitted version.

Funding

PM was funded by the Wellcome Trust (214567/Z/18/Z). For the purpose of Open Access, the author has applied a CC BY public copyright license to any Author Accepted Manuscript version arising from this submission. RG (NIHR clinical lecturer) is funded by Health Education England (HEE)/National Institute for Health Research (NIHR). The views expressed in this publication are those of the authors and not necessarily those of the NIHR, NHS or the United Kingdom Department of Health and Social Care.

Conflict of Interest

PM is named as an inventor on a University of Sheffield patent that describes elements of the CFD method.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2022.871912/full#supplementary-material

References

Aarnoudse W., van’t Veer M., Pijls N. H. J., Ter Woorst J., Vercauteren S., Tonino P., et al. (2007). Direct Volumetric Blood Flow Measurement in Coronary Arteries by Thermodilution. J. Am. Coll. Cardiol. 50 (24), 2294–2304. doi:10.1016/j.jacc.2007.08.047

PubMed Abstract | CrossRef Full Text | Google Scholar

Bejan A., Rocha L. A. O., Lorente S. (2000). Thermodynamic Optimization of Geometry: T- and Y-Shaped Constructs of Fluid Streams. Int. J. Therm. Sci. 39, 949–960. doi:10.1016/s1290-0729(00)01176-5

CrossRef Full Text | Google Scholar

Chen X., Dai J., Lin J., Wu Y., Ouyang J., Huang M., et al. (2020). Image-based Morphometric Studies of Human Coronary Artery Bifurcations With/without Coronary Artery Disease. Comp. Methods Biomech. Biomed. Eng. 24, 740–752. doi:10.1080/10255842.2020.1850702

PubMed Abstract | CrossRef Full Text | Google Scholar

de la Torre Hernandez J. M., Hernández Hernandez F., Alfonso F., Rumoroso J. R., Lopez-Palop R., Sadaba M., et al. (2011). Prospective Application of Pre-defined Intravascular Ultrasound Criteria for Assessment of Intermediate Left Main Coronary Artery Lesions. J. Am. Coll. Cardiol. 58 (4), 351–358. doi:10.1016/j.jacc.2011.02.064

PubMed Abstract | CrossRef Full Text | Google Scholar

de la Torre Hernández J. M., Ruiz-Lera M., Fernández-Friera L., Ruisanchez C., Sainz-Laso F., Zueco J., et al. (2007). Prospective Use of an Intravascular Ultrasound-Derived Minimum Lumen Area Cut-Off Value in the Assessment of Intermediate Left Main Coronary Artery Lesions. Rev. Esp Cardiol. 60 (8), 811–816.

PubMed Abstract | Google Scholar

Finet G., Gilard M., Perrenot B., Rioufol G., Motreff P., Gavit L., et al. (2008). Fractal Geometry of Arterial Coronary Bifurcations: a Quantitative Coronary Angiography and Intravascular Ultrasound Analysis. EuroIntervention 3 (4), 490–498. doi:10.4244/eijv3i4a87

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghobrial M., Haley H. A., Gosling R., Rammohan V., Lawford P. V., Hose D. R., et al. (2021). The New Role of Diagnostic Angiography in Coronary Physiological Assessment. Heart 107 (10), 783–789. doi:10.1136/heartjnl-2020-318289

PubMed Abstract | CrossRef Full Text | Google Scholar

Gosling R. C., Sturdy J., Morris P. D., Fossan F. E., Hellevik L. R., Lawford P., et al. (2020). Effect of Side branch Flow upon Physiological Indices in Coronary Artery Disease. J. Biomech. 103, 109698. doi:10.1016/j.jbiomech.2020.109698

PubMed Abstract | CrossRef Full Text | Google Scholar

Gössl M., Rosol M., Malyar N. M., Fitzpatrick L. A., Beighley P. E., Zamir M., et al. (2003). Functional Anatomy and Hemodynamic Characteristics of Vasa Vasorum in the walls of Porcine Coronary Arteries. Anat. Rec. A. Discov. Mol. Cell Evol Biol 272 (2), 526–537. doi:10.1002/ar.a.10060

PubMed Abstract | CrossRef Full Text | Google Scholar

Hahn J.-Y., Gwon H.-C., Kwon S. U., Choi S.-H., Choi J.-H., Lee S. H., et al. (2008). Comparison of Vessel Geometry in Bifurcation between normal and Diseased Segments: Intravascular Ultrasound Analysis. Atherosclerosis 201 (2), 326–331. doi:10.1016/j.atherosclerosis.2008.02.021

PubMed Abstract | CrossRef Full Text | Google Scholar

Huckabe C. E., Hahn A. W. (1968). A Generalized Approach to the Modeling of Arterial Blood Flow. Bull. Math. Biophys. 30 (4), 645–662. doi:10.1007/BF02476681

PubMed Abstract | CrossRef Full Text | Google Scholar

Hutchins G. M., Miner M. M., Boitnott J. K. (1976). Vessel Caliber and branch-angle of Human Coronary Artery branch-points. Circ. Res. 38 (6), 572–576. doi:10.1161/01.res.38.6.572

PubMed Abstract | CrossRef Full Text | Google Scholar

Kassab G. S. (2007). Design of Coronary Circulation: A Minimum Energy Hypothesis. Comp. Methods Appl. Mech. Eng. 196 (31), 3033–3042. doi:10.1016/j.cma.2006.09.024

CrossRef Full Text | Google Scholar

Kassab G. S. (2006). Scaling Laws of Vascular Trees: of Form and Function. Am. J. Physiology-Heart Circulatory Physiol. 290 (2), H894–H903. doi:10.1152/ajpheart.00579.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Li J., Wu H., Kassab G. S., Tan W., Huo Y. (2021). Intra- and Inter-specific Scaling Laws of Plants and Animals. Acta Mech. Sin. 37, 321–330. doi:10.1007/s10409-020-01013-7

CrossRef Full Text | Google Scholar

Miguel A. F. (2021). A Constructal View of Prefractal Dendritic Flow Networks Using an Exergy Analysis. Ijex 36 (1), 56–75. doi:10.1504/ijex.2021.117604

CrossRef Full Text | Google Scholar

Miguel A. F. (2018). A General Model for Optimal Branching of Fluidic Networks. Physica A: Stat. Mech. its Appl. 512, 665–674. doi:10.1016/j.physa.2018.07.054

CrossRef Full Text | Google Scholar

Miguel A. F. (2019). Optimal Y-Shaped Constructs Heat Sinks under Different Size Constraints. Int. J. Heat Mass Transfer 131, 64–71. doi:10.1016/j.ijheatmasstransfer.2018.11.033

CrossRef Full Text | Google Scholar

Morris P. D. (2015). Computational Fluid Dynamics Modelling of Coronary Artery Disease. Sheffield, United Kingdom: PhD, University of Sheffield.

Google Scholar

Morris P. D., Gosling R., Zwierzak I., Evans H., Aubiniere-Robb L., Czechowicz K., et al. (2020). A Novel Method for Measuring Absolute Coronary Blood Flow and Microvascular Resistance in Patients with Ischaemic Heart Disease. Cardiovasc. Res. 117, 1567–1577. doi:10.1093/cvr/cvaa220

PubMed Abstract | CrossRef Full Text | Google Scholar

Murray C. D. (1926). The Physiological Principle of Minimum Work. Proc. Natl. Acad. Sci. U.S.A. 12 (3), 207–214. doi:10.1073/pnas.12.3.207

PubMed Abstract | CrossRef Full Text | Google Scholar

Neumann F. J., Sousa-Uva M., Ahlsson A., Alfonso F., Banning A. P., Benedetto U., et al. (2019). 2018 ESC/EACTS Guidelines on Myocardial Revascularization. The Task Force on Myocardial Revascularization of the European Society of Cardiology (ESC) and European Association for Cardio-Thoracic Surgery (EACTS). G Ital. Cardiol. (Rome) 20 (2), 1S–61S. doi:10.1714/3203.31801

PubMed Abstract | CrossRef Full Text | Google Scholar

Revellin R., Rousset F., Baud D., Bonjour J. (2009). Extension of Murray's Law Using a Non-newtonian Model of Blood Flow. Theor. Biol. Med. Model. 6 (1), 7. doi:10.1186/1742-4682-6-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Schoenenberger A. W., Urbanek N., Toggweiler S., Seelos R., Jamshidi P., Resink T. J., et al. (2012). Deviation from Murray's Law Is Associated with a Higher Degree of Calcification in Coronary Bifurcations. Atherosclerosis 221 (1), 124–130. doi:10.1016/j.atherosclerosis.2011.12.040

PubMed Abstract | CrossRef Full Text | Google Scholar

Sherman T. F. (1981). On Connecting Large Vessels to Small. The Meaning of Murray's Law. J. Gen. Physiol. 78 (4), 431–453. doi:10.1085/jgp.78.4.431

PubMed Abstract | CrossRef Full Text | Google Scholar

Solanki R., Gosling R., Rammohan V., Pederzani G., Garg P., Heppenstall J., et al. (2021). The Importance of Three Dimensional Coronary Artery Reconstruction Accuracy when Computing Virtual Fractional Flow reserve from Invasive Angiography. Sci. Rep. 11 (1), 19694. doi:10.1038/s41598-021-99065-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Soni B., Miguel A. F., Kumar Nayak A. (2020). A Mathematical Analysis for Constructal Design of Tree Flow Networks under Unsteady Flow. Proc. R. Soc. A. 476 (2240), 20200377. doi:10.1098/rspa.2020.0377

CrossRef Full Text | Google Scholar

Uylings H. (1977). Optimization of Diameters and Bifurcation Angles in Lung and Vascular Tree Structures. Bull. Math. Biol. 39 (5), 509–520. doi:10.1007/bf0246119810.1016/s0092-8240(77)80054-2

PubMed Abstract | CrossRef Full Text | Google Scholar

van der Giessen A. G., Groen H. C., Doriot P.-A., de Feyter P. J., van der Steen A. F. W., van de Vosse F. N., et al. (2011). The Influence of Boundary Conditions on wall Shear Stress Distribution in Patients Specific Coronary Trees. J. Biomech. 44 (6), 1089–1095. doi:10.1016/j.jbiomech.2011.01.036

PubMed Abstract | CrossRef Full Text | Google Scholar

van der Waal E. C., Mintz G. S., Garcia-Garcia H. M., Bui A. B., Pehlivanova M., Girasis C., et al. (2009). Intravascular Ultrasound and 3D Angle Measurements of Coronary Bifurcations. Cathet. Cardiovasc. Intervent. 73 (7), 910–916. doi:10.1002/ccd.21965

CrossRef Full Text | Google Scholar

van ’t Veer M., Adjedj J., Wijnbergen I., Tóth G. G., Rutten M. C. M., Barbato E., et al. (2016). Novel Monorail Infusion Catheter for Volumetric Coronary Blood Flow Measurement in Humans: In Vitro Validation. EuroIntervention 12 (6), 701–707. doi:10.4244/eijv12i6a114

PubMed Abstract | CrossRef Full Text | Google Scholar

Zamir M., Vercnocke A. J., Edwards P. K., Anderson J. L., Jorgensen S. M., Ritman E. L. (2015). Myocardial Perfusion: Characteristics of Distal Intramyocardial Arteriolar Trees. Ann. Biomed. Eng. 43 (11), 2771–2779. doi:10.1007/s10439-015-1325-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou Y., Kassab G. S., Molloi S. (1999). On the Design of the Coronary Arterial Tree: a Generalization of Murray's Law. Phys. Med. Biol. 44 (12), 2929–2945. doi:10.1088/0031-9155/44/12/306

PubMed Abstract | CrossRef Full Text | Google Scholar