Influence of Step Frequency on the Dynamic Characteristics of Ventilation and Gas Exchange During Sinusoidal Walking in humans

We tested the hypothesis that restricting either step frequency (SF) or stride length (SL) causes a decrease in ventilatory response with limited breath frequency during sinusoidal walking. In this study, 13 healthy male and female volunteers (mean ± SD; age: 21.5 ± 1.8 years, height: 168 ± 7 cm, weight: 61.5 ± 8.3 kg) participated. The walking speed was sinusoidally changed between 50 and 100 m⋅min^–1 with periods from 10 to 1 min. Using a customized sound system, we fixed the SF at 120 steps⋅min^–1 with SL variation (0.83–0.41 m) (SF_fix) or fixed the SL at 0.7 m with SF variation (143–71 steps⋅min^–1) (SL_fix) during the subjects’ sinusoidal walking. Both the subjects’ preferred locomotion pattern without a sound system (Free) and the unprompted spontaneous locomotor pattern for each subject (Free) served as the control condition. We measured breath-by-breath ventilation [tidal volume (VT) and breathing frequency (Bf)] and gas exchange [CO₂ output ($\stackrel{.}{\text{V}}$CO₂), O₂ uptake ($\stackrel{.}{\text{V}}$O₂)]. The amplitude (Amp) and the phase shift (PS) of the fundamental component of the ventilatory and gas exchange variables were calculated. The results revealed that the SF_fix condition decreased the Amp of the Bf response compared with SL_fix and Free conditions. Notably, the Amp of the Bf response under SF_fix was reduced by less than one breath at the periods of 5 and 10 min. In contrast, the SL_fix condition resulted in larger Amps of Bf and $\stackrel{.}{\text{V}}$_E responses as well as Free. We thus speculate that the steeper slope of the $\stackrel{.}{\text{V}}$_E-$\stackrel{.}{\text{V}}$CO₂ relationship observed under the SL_fix might be attributable to the central feed-forward command or upward information from afferent neural activity by sinusoidal locomotive cadence. The PSs of the $\stackrel{.}{\text{V}}$_E, $\stackrel{.}{\text{V}}$O₂, and $\stackrel{.}{\text{V}}$CO₂ responses were unaffected by any locomotion patterns. Such a sinusoidal wave manipulation of locomotion variables may offer new insights into the dynamics of exercise hyperpnea.

Introduction

Humans’ sinusoidal exercising is clearly voluntary rhythmic movement in response to the stress of a varying work rate or speed. The resulting exercise-induced hyperpnea is expected to be integrated with chemical feedback from both central (Bell, 2006) and peripheral chemoreceptors (Forster et al., 2012; Ebine et al., 2018), afferent neural activity from working muscles (Eldridge et al., 1982; Eldridge, 1994; Amann et al., 2010; Forster et al., 2012), and feedforward signals from the motor cortex (Comroe and Schmidt, 1943; Dejours, 1959; Eldridge et al., 1981).

Several previous studies have used sinusoidal work forcing to define the resulting kinetics of cardiac, ventilatory, and gas exchange responses (Casaburi et al., 1977, 1978; Fukuoka et al., 2017; Ebine et al., 2018), and it is well established that these responses to a sinusoidal workload will have a consistent fundamental frequency component, which can be characterized by a mean value (Mx), an amplitude (Amp), and a phase shift (PS) on gas exchange kinetics (Casaburi et al., 1977). Moreover, several investigators have observed that for the same increase in metabolic rate, the hyperpnea is greater when the treadmill speed or pedaling frequency during cycling is increased, as opposed to an increase in the treadmill grade or cycling resistance (Bechbache and Duffin, 1977; Bramble and Carrier, 1983; Casey et al., 1987; Lafortuna et al., 1996). During sinusoidal exercise, greater Amps and lower PSs for pulmonary ventilation ($\stackrel{.}{\text{V}}$_E) were observed when the limb-movement frequency was varied sinusoidally by alterations in cycling work rates (Casaburi et al., 1977) or in treadmill speed (Wells et al., 2007). The PS of $\stackrel{.}{\text{V}}$_E dynamics during a sinusoidal leg-cycling exercise was less for the cadence variation than for the sinusoidal pedal forcing variation (Duffin, 2014). It may also be possible that the sinusoidal step frequency (SF) of walking accelerates the ventilatory dynamics as the SF is equivalent to pedaling cadence.

Sinusoidal exercise protocols can be considered a robust method to investigate multiple factors that affect the ventilatory response (Caterini et al., 2016), and these protocols may be suitable for avoiding the entrainment of breath frequency to limb movement (Bechbache and Duffin, 1977). In this study, the SF was forced sinusoidally to minimize contributions from locomotor-respiratory entrainment even at a constrained stride length (SL) during sinusoidal walking (Caterini et al., 2016). The variation in the SF would induce sufficient exercise hyperpnea, possibly involving muscle reflex drives from type III and IV afferent neural activities (Bruce et al., 2019; Ward, 2019).

The synchronization of limb movement and breathing rhythms has been observed in locomoting animals (Bechbache and Duffin, 1977; Bramble and Carrier, 1983; Lafortuna et al., 1996; Boggs, 2002) as locomotor-respiratory entrainment. A limb movement-related afferent signal can entrain the ongoing respiratory rhythm (Giraudin et al., 2012). We thus speculated that during sinusoidal walking, a constrained SF could reinforce locomotor-respiratory entrainment and consequentially the breath frequency (Bf) would remain constant.

Accordingly, we addressed two specific aims in this study: (i) the locomotive cadence (i.e., the SF) may be a significant factor to cause exercise-induced hyperpnea, possibly involving muscle reflex drives from type III and IV afferents (Haouzi et al., 2004; Haouzi, 2006; Bruce et al., 2019) or the central feed-forward command (i.e., feedforward mechanism from the higher central nervous system to locomotor and respiratory neurons) (Eldridge and Waldrop, 1991; Waldrop et al., 1996; Bell, 2006); and (ii) locomotion with a fixed SF may cause dynamic ventilatory depression (i.e., Amp depression in ventilation) as a secondary result of constrained Bf due to a respiratory-locomotor network (Le Gal et al., 2020). To test this hypothesis, we investigated whether the ventilatory and gas exchange responses showed different dynamics in conditions with different locomotion patterns during walking with sinusoidal speed changes.

Materials and Methods

Subjects

The subjects were 13 healthy young male (n = 7) and female (n = 6) volunteers [age: 21.5 ± 1.8 years, height: 168 ± 7 cm, weight: 61.5 ± 8.3 kg; mean ± standard deviation (SD)] who were not taking any medication that could affect cardiovascular responses. The subjects were fully informed of any risks and discomforts associated with these experiments before giving their written, informed consent to participate in the study, which was approved by the ethics committees of the Institutional Review Board of Doshisha University (no. 1045).

Protocols

All experimental tests were completed in a temperature-controlled laboratory (25 ± 0.4°C with 50 ± 3% relative humidity), and all subjects wore underwear, shorts, and a T-shirt, as well as socks and shoes. The protocols used herein are based on our previous work (Fukuoka et al., 2017). The treadmill speed was changed in a sinusoidal pattern from 50 to 100 m⋅min^–1 at periods (T) of 10, 5, 2, and 1 min. A warm-up session consisted of steady-state walking for 4 or 6 min, which preceded each recording sinusoidal exercise session. In Protocol I, after 50, 100, and 75 m⋅min^–1 for 5, 3, and 4 min of warm-up walking, the sinusoidal loading was repeated for five cycles at 1-min periods, followed by three cycles at 2-min periods (Figure 1A). In Protocol II, after 75 m⋅min^–1 for 6 min of warm-up walking, the sinusoidal loading was repeated for three cycles at 5-min periods, followed by two cycles at 10-min periods (Figure 1E). A microcomputer transmitted the signal controlling the speed of the motor driving the treadmill (modified TMS 2200, Nihon Koden, Tokyo) through a digital-analog converter.

FIGURE 1

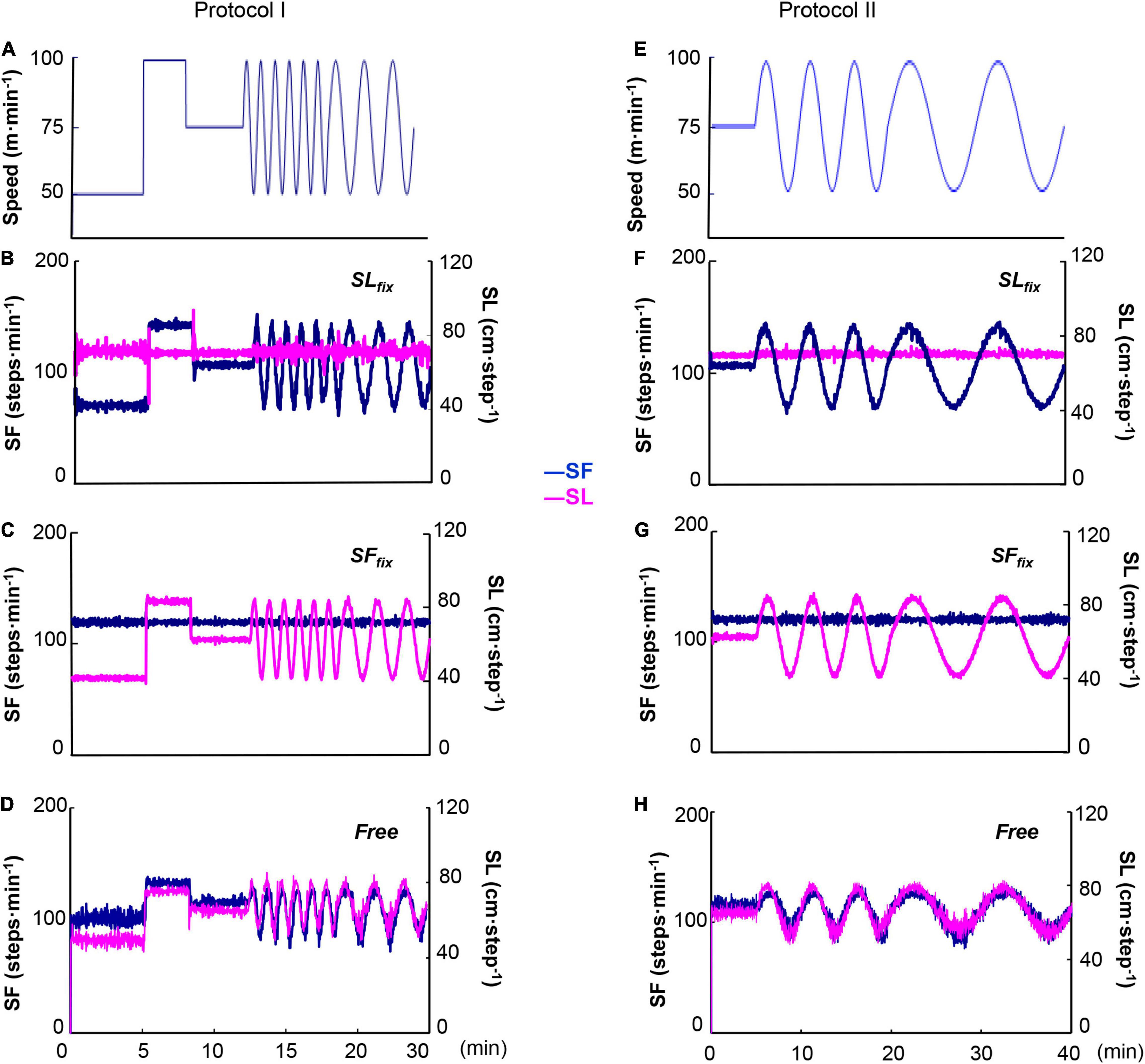
Figure 1. Two sinusoidal locomotion protocols at a sinusoidal speed between 50 and 100 m⋅min^–1 at the period of 1⋅2 min (A) and 5⋅10 min (E). The stride length (SL) was fixed at 0.7 m with step frequency (SF) variation (143–71 step⋅min^–1) (SL_fix) (B,F) and the SF was fixed at 120 steps⋅min^–1 with stride variation (0.83–0.41 m) (SF_fix) (C,G). The control (Free) condition was the subjects’ preferred locomotion pattern (D,H).

Using a customized personal computer sound cueing system (Arco Metronome, Ver.2.00, Arco System, Chiba, Japan), we set two locomotion patterns. In the fixed SL (SL_fix) condition, the SL was fixed at 0.7 m and the SF varied between 143 and 71 steps⋅min^–1 in coordination with the sinusoidal changes in treadmill speed (Figures 1B,F; Latt et al., 2008). In the fixed SF (SF_fix) condition, the SF was set at 120 steps⋅min^–1 with SL variation (0.83–0.41 m) during sinusoidal walking (Figures 1C,G; Casaburi et al., 1978). The subjects were instructed to synchronize their locomotion to the sound. In addition, the subjects were allowed to breathe freely, so breathing and walking were not intentionally synchronized. The subject’s preferred locomotion pattern without the sound was used as the control condition (Free) (Figures 1D,H). The subjects performed each protocol on six separate occasions metricconverterProductID0.7 m(one session at a time, three sessions per week for each individual).

Measurements

A mass-flow sensor (type AB, Minato Medical Sciences, Osaka) was fit to the expiratory port of the valve of the face mask worn by the subject to continuously record the subject’s expiratory airflow, which was calibrated before each measurement with a 3-L syringe at three different flow rates. We calculated the ventilation ($\stackrel{.}{\text{V}}$_E) values by integrating the tidal volume (VT; L) and breathing frequency (Bf; breaths⋅min^–1). The end-tidal oxygen pressure (P_ETO₂; mmHg) and carbon dioxide pressure (P_ETCO₂; mmHg) were determined using mass spectrometry (Arco-2000, Arco System, Chiba, Japan) from a sample drawn continuously from the inside of the face mask at 1 ml⋅s^–1. This loss of gas volume was not examined in this study, because the loss of 1 ml⋅s^–1 was much smaller than the inspired and expired airflows. Three reference gases of known concentrations (O₂: 15.04%, CO₂: 2.92%, and N₂: 82.04%; O₂: 11.93%, CO₂: 6.96%, and N₂: 81.11%) and room air (O₂: 20.93%, CO₂: 0.03%, Ar: 0.94%, and N₂: 78.10%) were used to calibrate the mass spectrometer.

The volumes, flows, partial pressure of carbon dioxide (PCO₂), and partial pressure of oxygen (PO₂) at the subject’s mouth were recorded in real time with a 50-Hz sampling frequency using a computerized online breath-by-breath system (AE-280, Minato Medical Sciences, Osaka) from the time-aligned gas volume and concentration signals. Breath-by-breath $\stackrel{.}{\text{V}}$_E (BTPS), $\stackrel{.}{\text{V}}$O₂ (STPD), and $\stackrel{.}{\text{V}}$CO₂ (STPD), VT, Bf, P_ETCO₂, and P_ETO₂ were determined. An electrocardiogram (ECG) was recorded using a bioamplifier (AB 621G, Nihon Kohden, Tokyo). Heart rate (HR) was measured by beat-by-beat counting from the R spike of the ECG. The signals from the treadmill were fed into a data acquisition system (PowerLab system, A/D Instruments, Castle Hill, NSW, Australia) and temporally aligned to the ventilatory and ECG data.

In all subjects, the SF and SL were measured using a switch activated by the subject stepping on a sensor on the sole of the right foot of the right leg in each protocol. The signals from the treadmill and the stepping sensor were fed into the PowerLab data acquisition system and temporally aligned with the ventilatory data.

Data Analysis

All the cardiorespiratory and locomotive data were analyzed using a Fourier analysis as previously reported (Wigertz, 1971; Haouzi et al., 1992, 2004; Fukuoka et al., 2017). The breath-by-breath ventilatory and gas exchange data were interpolated into a 1-s interval value before Fourier analysis (Supplementary Figure 1). The repeated cardiorespiratory responses to sinusoidal walking speed were superimposed in correspondence with the cycle period, and we obtained the average cardiorespiratory data at each respective cycle. The variation in the speed of the treadmill was regarded as the input function. The Amp (i.e., mean to peak) and the PS of the fundamental component (the same frequency as the input function) of the $\stackrel{.}{\text{V}}$_E, $\stackrel{.}{\text{V}}$O₂, $\stackrel{.}{\text{V}}$CO₂, HR, and end-tidal PCO₂ (P_ETCO₂) responses as well as the locomotion responses (locomotion SF and SL) were computed as follows:

$Amp=\sqrt{R{e}^2+I{m}^2}(1)$

and

$PS=tan{}^{-}{}^1(\frac{Re}{Im})(2)$

where the Re and Im are the real and imaginary components; these were calculated as follows. The larger the PS, the slower the response. The larger the Amp, the higher the responsiveness.

$Re=\frac{2}{NT}\sum _{t=0}^{NT}\left[(x\left(t\right)-Mx)\cos (2\mathrm{\pi }f\text{t})\right](3)$

and

$Im=\frac{2}{NT}\sum _{t=0}^{NT}\left[(x(t)-Mx)\sin (2\mathrm{\pi }f\text{t})\right](4)$

where x(t) is the response value at time t (in s), Mx is the mean value of x for an integer number of cycles (N), T is the period of the input signal (in s), and f ( = 1/T) is its frequency in cycles per second.

We normalized the ratios of Amp of the respiratory and locomotion variables against sinusoidal change in walking speed by dividing the magnitude of variables from 50 to 100 m min^–1 during each steady-state exercise, and the results are presented as the Amp ratio (%) (Fukuoka et al., 2017).

The R-R intervals during sinusoidal work were calculated beat-by-beat by the computer, and 1-s interval HR data were measured from the calculated R-R intervals (R-R) and converted as HR values (60/R-R). The subject’s locomotion SF and SL were measured with a switch activated by stepping on a sensor on the sole of the right foot in each protocol (Fukuoka et al., 2017).

Statistical Analyses

All values are presented as mean ± SD. The significance of differences in each variable ($\stackrel{.}{\text{V}}$E, VT, Bf, $\stackrel{.}{\text{V}}$O₂, $\stackrel{.}{\text{V}}$CO₂, and HR) was determined by a two-way repeated-measures analysis of variance (ANOVA) in the comparison of the three locomotion patterns (SF_fix, SL_fix, and Free) × oscillation frequency period (T; 1 to 10 min). Bonferroni’s test was applied for the appropriate datasets if a significant F-value was obtained. We compared the regression coefficients of the independent variables of $\stackrel{.}{\text{V}}$_E of the three locomotion patterns (SF_fix, SL_fix, and Free). The level of significance was set at p < 0.05.

Results

Figure 2 shows the representative smoothing SL_fix, SF_fix, and Free locomotion patterns at the period of 5 min. The SL_fix and SF_fix were strictly controlled (Figures 2A,B). In Free locomotion, both the SL and SF responded almost synchronously with the sinusoidal walking speed (Figure 2C).

FIGURE 2

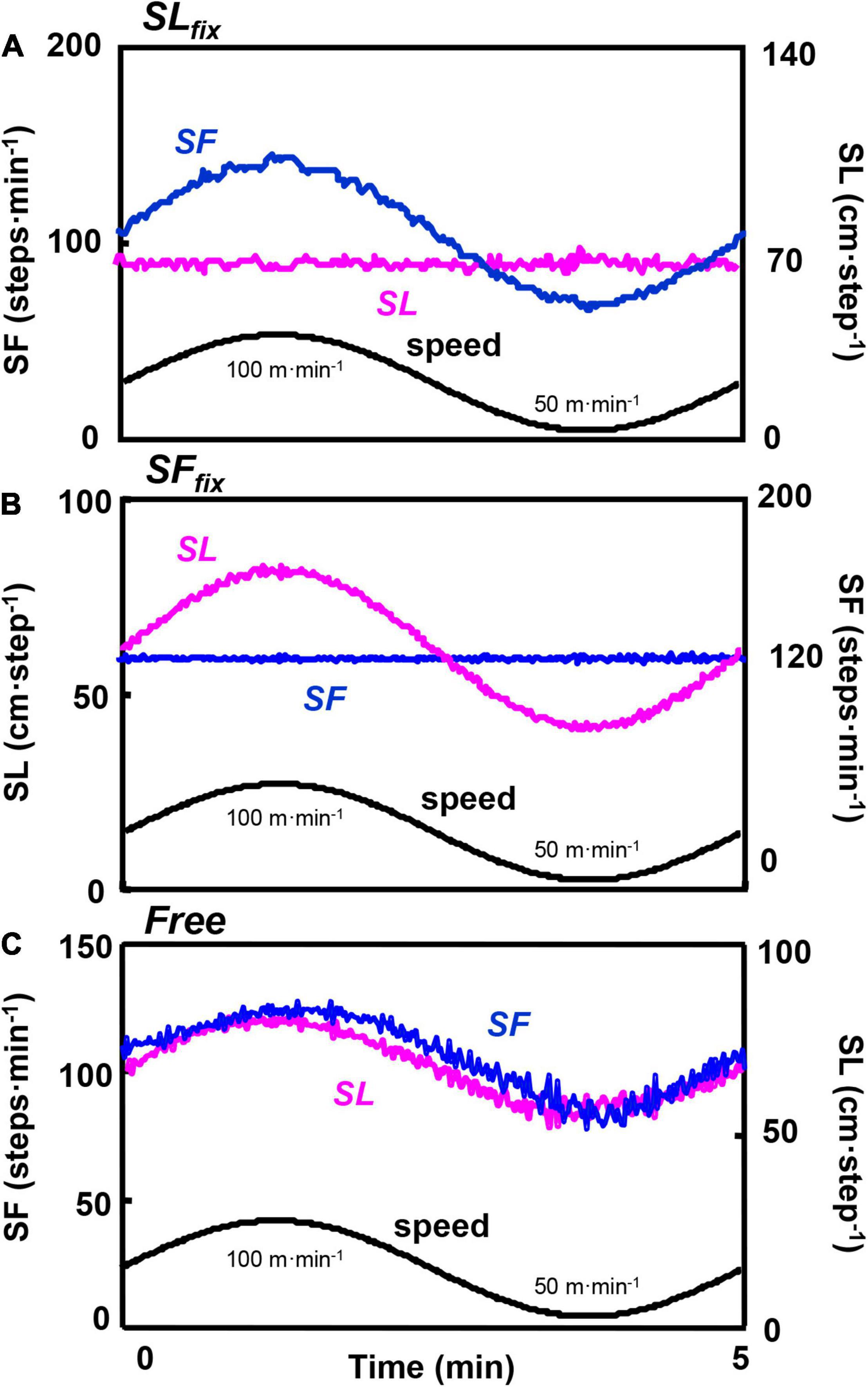
Figure 2. Time course of the locomotion responses at a 5-min period. Example from a representative subject of the locomotion pattern of the step frequency (SF) and the stride length (SL) divided under SL_fix (A), SF_fix (B), and Free (C). The oscillating line is the superimposed SL and SF for a 5-min period. The lower sinusoidal curve is the sinusoidal change of the speed between 50 and 100 m⋅min^–1.

The Amp, PS, and Mx under the SF_fix or SL_fix conditions at all periods (T: 1, 2, 5, and 10 min) are given in Figure 3. Compared with the Free locomotion, the Amp of the SF under the SL_fix condition was significantly greater at all periods (pattern effect: p < 0.001, η² = 0.983) (Figure 3A). The Mx value for SF tended to be greater in the Free conditions than in the SL_fix condition (pattern effect: p = 0.065, η² = 0.255) (Figure 3C). The PS for SF was not significantly different between the Free and SL_fix conditions except at the 5-min period (p < 0.01) (Figure 3B).

FIGURE 3

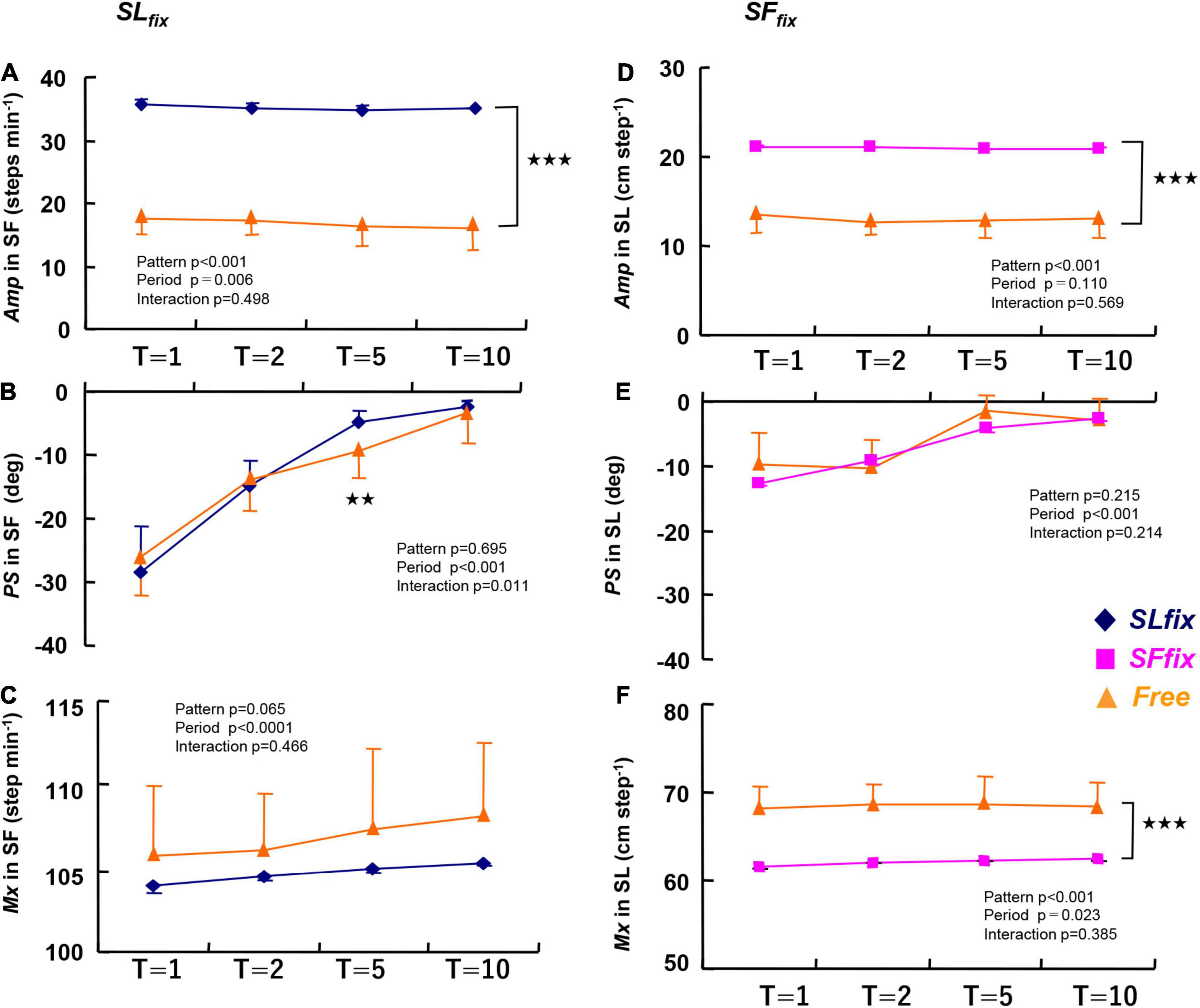
Figure 3. The amplitude (Amp), phase shift (PS), and mean (Mx) values in the step frequency under SL_fix (A–C) and in the stride length under SF_fix (D–F) compared with Free. The Amp under both SL_fix and SF_fix became significantly higher compared with those at Free at any period (p < 0.001). The PS values for SL were quite small and virtually close to zero at each period (E). The Mx under SL_fix tended to be lower and the Mx under SF_fix was significantly lower than that under the Free condition at each period. **p < 0.01, ***p < 0.001 vs. Free. T, time periods (1, 2, 5, and 10 min). Data are mean ± SD.

The Amp of the SL under the SF_fix condition was significantly larger than that under Free at all periods (pattern effect: p < 0.001, η² = 0.965) (Figure 3D). In contrast, the Mx for the SL became significantly lower under SF_fix compared to Free (pattern effect: p < 0.001, η² = 0.877) (Figure 3F). There were no significant differences in the PS for the SL at any period (Figure 3E).

Dynamic Responses of Ventilatory Variables

Figure 4 illustrates the responses of ventilatory variables at the 5-min period for a representative single same subject, revealing that the VT and Bf showed markedly different responses. Specifically, under the SL_fix condition, the PS for the Bf response was preceded by a delay in VT (i.e., a late appearance of the peak in VT), whereas under the SF_fix condition, the PS for the VT response was preceded by a delay in the Bf (i.e., a late appearance of the peak of Bf or an almost constant).

FIGURE 4

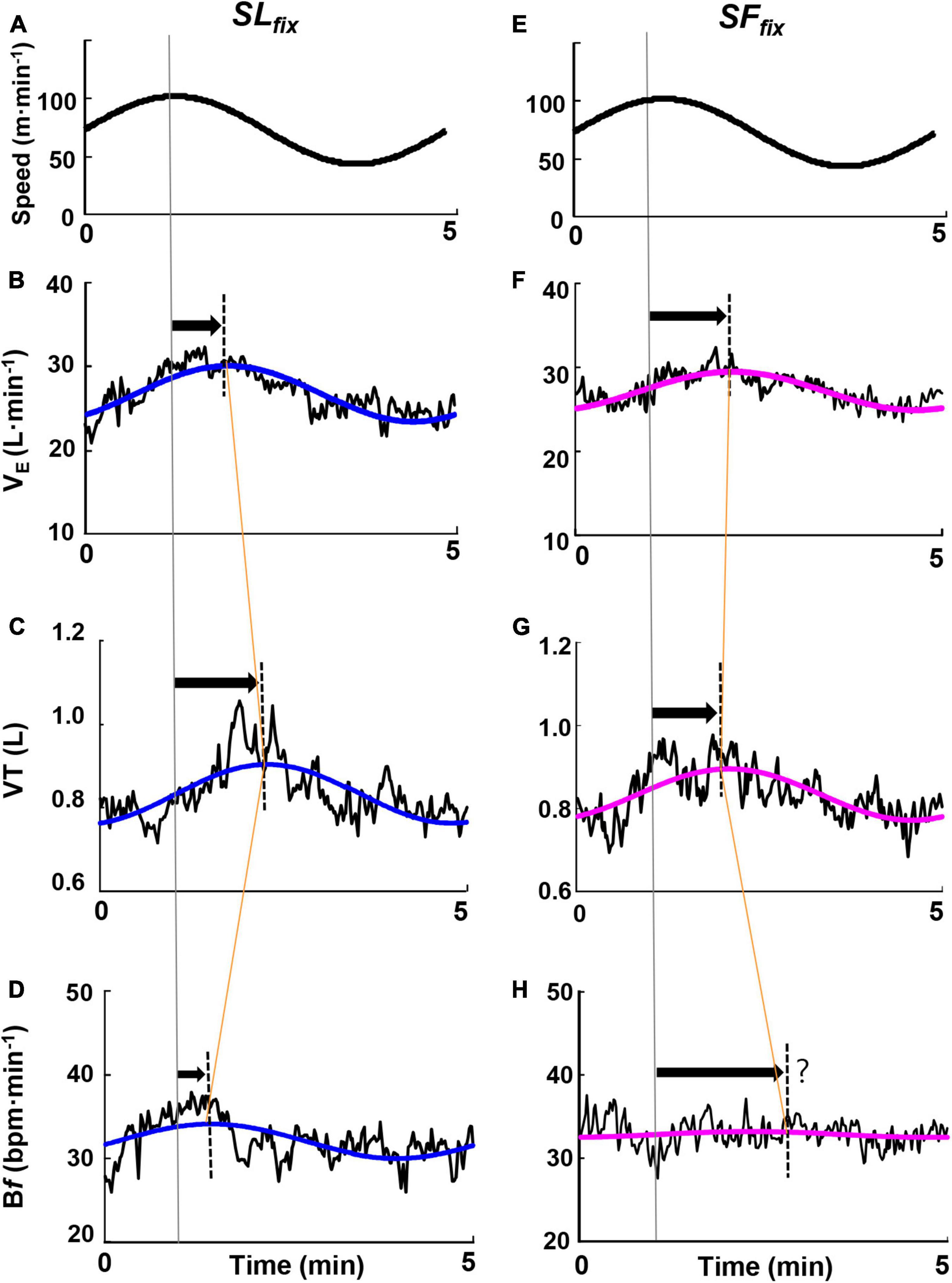
Figure 4. Time course of the ventilatory responses to the sinusoidal change in treadmill speed at the period of 5 min. Examples highlighting characteristic responsiveness of the ventilatory variables of ventilation ($\stackrel{.}{\text{V}}$_E), breath frequency (Bf), and tidal volume (VT) responses under SL_fix locomotion (A–D) and SF_fix locomotion (E–H) in a representative subject. The oscillating line is the superimposed gas exchange variables data. The smooth blue and red lines are the sine-wave fundamental component of these dynamics.

The SF_fix condition induced significantly lower Amps in $\stackrel{.}{\text{V}}$_E and P_ETCO₂ at allmetricconverterProductID1 A of the periods compared with the SL_fix condition, with similar values between the SL_fix and Free conditions (Figures 5A,D). The Amp response for the Bf remained unchanged (<1.0 breath⋅min^–1) under SF_fix (Figure 5B), with a pattern effect among the three patterns (pattern effect: p = 0.006, η² = 0.348). The Amp of the VT response tended to be larger under SL_fix compared with SF_fix and Free at all periods (p = 0.064, η² = 0.204) (Figure 5C). With respect to the PS, a significant main effect of patterns was observed in the VT (pattern effect: p = 0.021, η² = 0.275) (Figure 5G). A Bonferroni post-hoc test further revealed that the PS for the VT at the 2-min period under the SL_fix condition was significantly lower than under the SF_fix condition (p < 0.05).

FIGURE 5

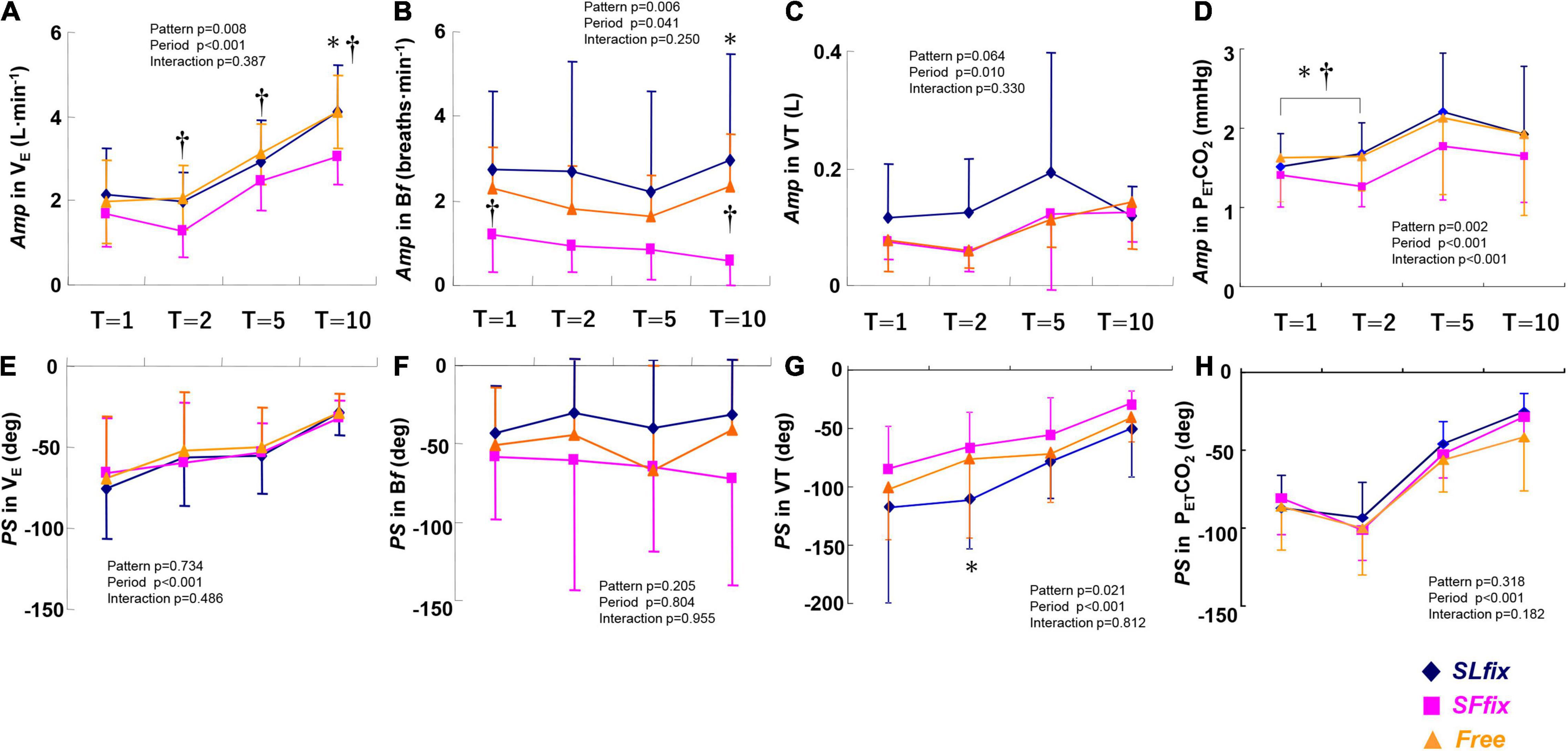
Figure 5. Comparisons of Amp and PS in $\stackrel{.}{\text{V}}$_E (A,E), Bf (B,F), VT (C,G), and end-tidal PCO₂ (P_ETCO₂) (D,H) dynamics under SL_fix, SF_fix, and Free. *p < 0.05 between SL_fix vs. SF_fix within the same period. ^†p < 0.05 between Free vs. SF_fix within the same period. T, time periods (1, 2, 5, and 10 min). Data are mean ± SD.

However, we did not observe any effects of the patterns on the PS in $\stackrel{.}{\text{V}}$_E, Bf, or P_ETCO₂metricconverterProductID1 C, with period effects for $\stackrel{.}{\text{V}}$_E and P_ETCO₂ (Figures 5E,F,H). In addition, a significant main effect of the pattern was observed on the Mx in $\stackrel{.}{\text{V}}$_E (pattern effect: p = 0.012, η² = 0.309), with a significant difference between the Free and SL_fix conditions at only the 5-min period (Supplementary Table 1, p = 0.015). There were no significant main effects of the locomotion patterns or frequency period, and no interaction effect in the Mx for VT, Bf, and P_ETCO₂ (all p > 0.05, Supplementary Table 1).

Dynamic Responses of Gas Exchange and Heart Rate Variables

The Amp values of the HR, $\stackrel{.}{\text{V}}$O₂, and $\stackrel{.}{\text{V}}$CO₂ variables were significantly lower under SF_fix compared with SL_fix and Free (pattern effect: p = 0.001, 0.002, and 0.004, and η² = 0.446, 0.408, and 0.370, respectively, Figures 6A–C). Although the period had significant main effects on the PS of HR, $\stackrel{.}{\text{V}}$O₂, and $\stackrel{.}{\text{V}}$CO₂ (Figures 6D–F), those values were similar irrespective of the locomotion patterns, with the exception of a greater PS in the HR at 5 min under SF_fix. We also observed no significant main effects of the locomotion patterns and frequency period, and no interaction effect in the Mx of $\stackrel{.}{\text{V}}$CO₂, $\stackrel{.}{\text{V}}$O₂, and HR (all p > 0.05, Supplementary Table 2).

FIGURE 6

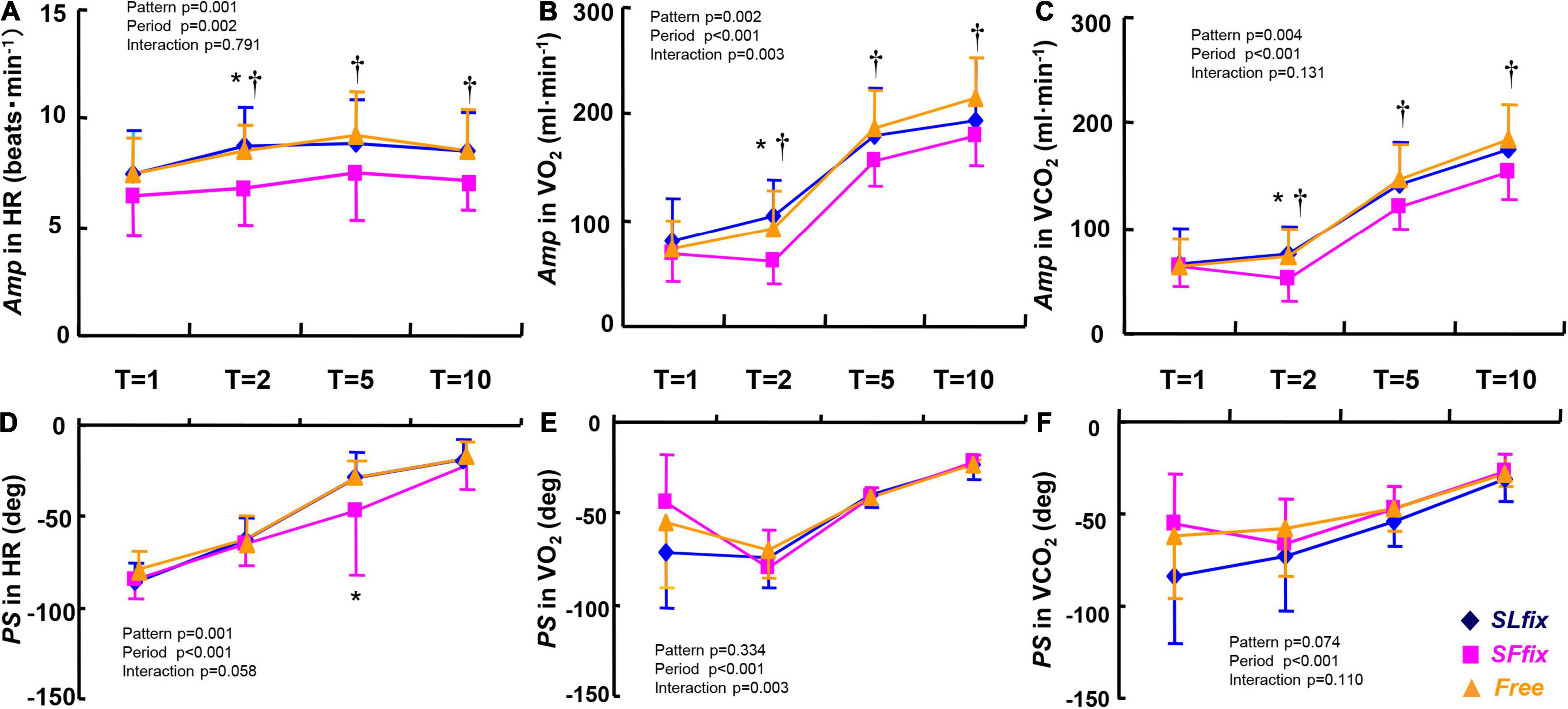
Figure 6. Comparisons of Amp and PS in heart rate (HR) (A,D), O₂ uptake ($\stackrel{.}{\text{V}}$O₂) (B,E), and CO₂ output ($\stackrel{.}{\text{V}}$CO₂) (C,F) dynamics under SL_fix, SF_fix, and Free. *p < 0.05 between SL_fix vs. SF_fix within the same period. ^†p < 0.05 between Free vs. SF_fix within the same period. T, time periods (1, 2, 5, and 10 min). Data are shown in mean ± SD.

Relationship Between the Amp Ratio in $\stackrel{.}{\text{V}}$_E and $\stackrel{.}{\text{V}}$CO₂

The Amp ratio in the $\stackrel{.}{\text{V}}$_E (i.e., Amp ratio of sinusoidal forcing variations to constant) was closely related to the Amp ratio in the $\stackrel{.}{\text{V}}$CO₂ when the data from all periods were pooled (SL_fix: r = 0.83, SF_fix: r = 0.88, and Free: r = 0.91, p < 0.01) (Figure 7). The slope of the regression lines of the $\stackrel{.}{\text{V}}$_E−$\stackrel{.}{\text{V}}$CO₂ relationship was steeper under SL_fix (s: 1.19) than under SF_fix (s: 0.70) and Free conditions (s: 0.97).

FIGURE 7

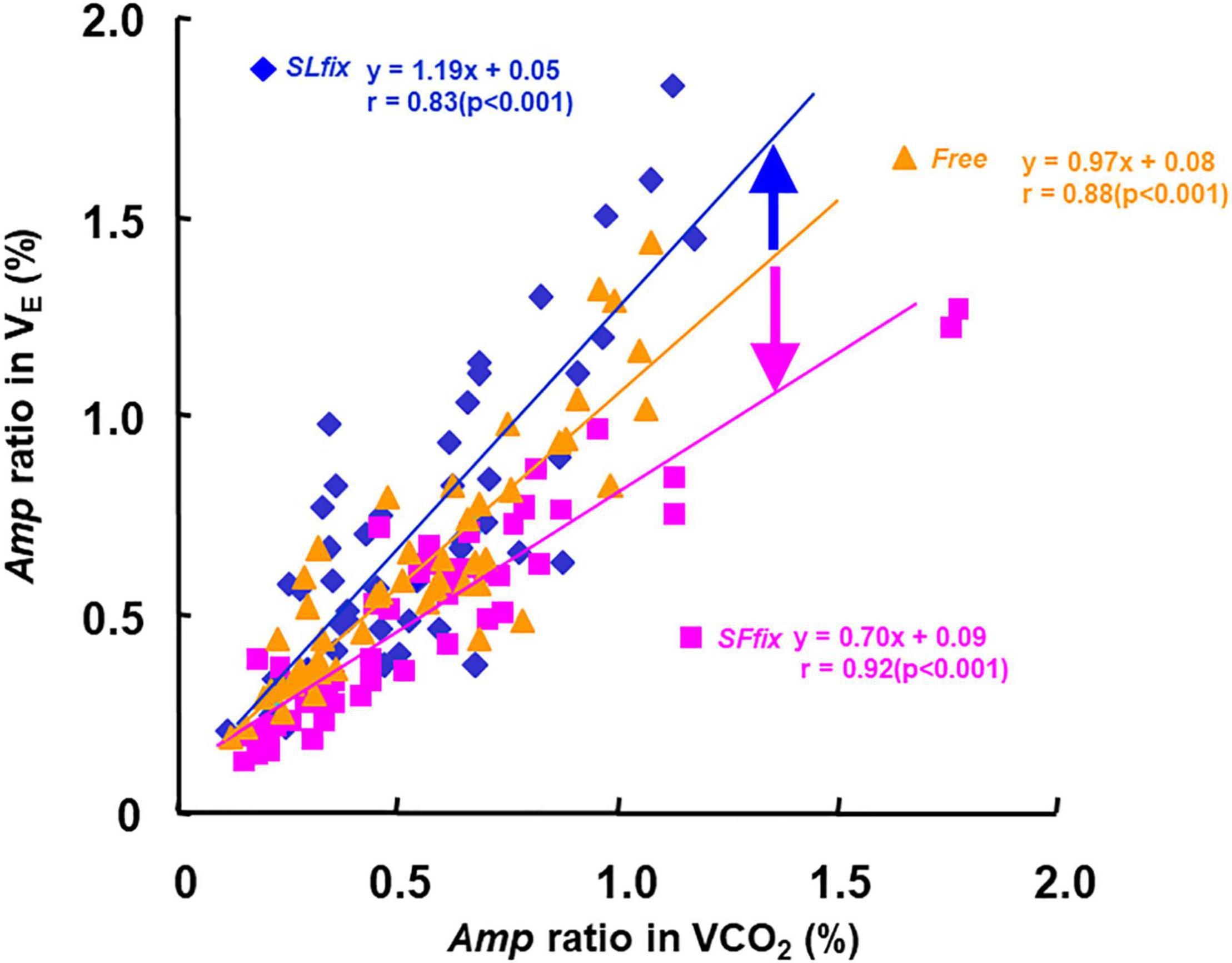
Figure 7. Relationship between the Amp ratio in $\stackrel{.}{\text{V}}$_E and $\stackrel{.}{\text{V}}$CO₂ under SL_fix, SF_fix, and Free, respectively. The slope of the regression lines of the $\stackrel{.}{\text{V}}$_E-$\stackrel{.}{\text{V}}$CO₂ relationship was steeper at SL_fix than SF_fix. SL_fix: y = 1.19x + 0.05, r = 0.83 (p < 0.001). SL_fix: y = 0.70x + 0.09, r = 0.92 (p < 0.001). Free: y = 0.97x + 0.08, r = 0.88 (p < 0.001).

Discussion

The three major findings of this study are as follows: (i) the SL_fix locomotion pattern increased the Amp of $\stackrel{.}{\text{V}}$_E (Figure 5A) and metabolic responses ($\stackrel{.}{\text{V}}$O₂ and $\stackrel{.}{\text{V}}$CO₂; Figures 6B,C) compared with the SF_fix (i.e., 120 steps⋅min^–1); (ii) the Amp of the Bf under the SF_fix locomotion pattern remained unchanged (i.e., <1.0 breath⋅min^–1); and (iii) when the slope of the $\stackrel{.}{\text{V}}$_E−$\stackrel{.}{\text{V}}$CO₂ relationship under the Free condition was used as the reference (1.0), the slope under SL_fix was steeper than that under Free, and the slope under SF_fix was lower than that under Free. These phenomena may be explained as follows: afferent feedback from the limb is important for locomotor-respiratory entrainment, whereby the discharge rhythm of sensory inputs can entrain a central respiratory pattern generator (Potts et al., 2005; Shevtsova et al., 2019; Le Gal et al., 2020).

Locomotor-Respiratory Entrainment Irrespective of the Sinusoidal Change in Speed

In human studies, locomotor-respiratory entrainment has been observed when the locomotion speed is kept constant during walking (Bramble and Carrier, 1983; Bernasconi et al., 1995; McDermott et al., 2003; O’Halloran et al., 2012). Our locomotion protocol used the sinusoidal change in speed between 50 and 100 m⋅min^–1. We thus considered the following possibilities: locomotor-respiratory entrainment forcing the synchronization of step movement and breathing rhythms is more likely to occur when the sinusoidal change in speed is synchronized with the sinusoidal change in SF (i.e., the SL_fix condition). According to our hypothesis, the SF_fix condition provided an unchanged Bf (i.e., <1.0 breath⋅min^–1), with the Mx for the Bf approximately 24 breaths⋅min^–1 at all periods (Supplementary Table 1 and Figure 4). Thus, the Amp of $\stackrel{.}{\text{V}}$_E depended mostly on that for VT, which was characterized as the faster phasic response under the SF_fix condition (Figure 5G).

Apparently, the constrained Bf under the SF_fix condition induced smaller Amps of $\stackrel{.}{\text{V}}$_E and P_ETCO₂ (Figures 5A,B,D), despite the absence of differences in the Mx for $\stackrel{.}{\text{V}}$_E and P_ETCO₂ between the SF_fix and SL_fix conditions (Supplementary Table 1). Therefore, respiratory entrainment might be achieved by the same exercise hyperpnea without hypoventilation and lower P_ETCO₂ even under SF_fix. These phenomena suggest the physiological significance of afferent feedback from the hindlimb locomotor generators for locomotor-respiratory coupling, whereby the discharge rhythm of sensory inputs can entrain a central respiratory pattern generator (Potts et al., 2005; Shevtsova et al., 2019; Le Gal et al., 2020). It was also reported that respiratory entrainment can be achieved by lumbar and/or cervical proprioceptive input stimulations in an isolated rat or mice brain stem-spinal cord preparation (Morin and Viala, 2002; Giraudin et al., 2012; Le Gal et al., 2020). Even though the Amp of the SL under the SF_fix condition was significantly (two times) larger than that under the control Free condition in all of the periods used herein, the SF_fix locomotion induced the sluggish dynamics of the Amp of $\stackrel{.}{\text{V}}$_E, $\stackrel{.}{\text{V}}$O₂, and $\stackrel{.}{\text{V}}$CO₂. Thus, the contribution of sinusoidal variation in SL to the adjustment in $\stackrel{.}{\text{V}}$_E would be less than that in a Free condition.

The Physiological Implications of Sinusoidal Cadence for Ventilation

Several research groups have compared the PS of $\stackrel{.}{\text{V}}$_E dynamics under different experimental conditions during leg cycling, namely, between sinusoidal cadence with a constant pedal force and sinusoidal pedal force with a constant pedal cadence (Casaburi et al., 1978; Duffin, 2014; Caterini et al., 2016), and they observed that the PS of $\stackrel{.}{\text{V}}$_E dynamics was much less for the cadence variation than for the sinusoidal pedal forcing variation. These studies used the fundamental concept that changing the frequency of limb movement during exercise would affect ventilation.

In contrast to those findings, our present investigation demonstrated that the SL_fix condition induced a significantly larger Amp of $\stackrel{.}{\text{V}}$_E with similar PS and Mx values compared with the SF_fix condition (Figures 4, 5A and Supplementary Table 1). The larger Amp of $\stackrel{.}{\text{V}}$_E was equal to that in the Free condition, even though the Amp of Bf and VT tended to be larger under SL_fix compared with Free (Figures 5B,C). The smaller PS values for Bf and the larger PS value for VT were specifically characterized under the SL_fix condition. The increased muscle contraction of sinusoidal cadence may thus be competitively related to the faster ventilatory drive to breathe (Takano, 1988; Caterini et al., 2016; Girardi et al., 2021). Notably, this specific adaptation was to the PS rather than the magnitude (Casaburi et al., 1977; 1978; Wells et al., 2007).

In this study, the phasic responses of $\stackrel{.}{\text{V}}$_E, Bf, and P_ETCO₂ were not significantly different among the three locomotion patterns. The discrepancies between our results and those of the studies reported by Casaburi et al. (1978), Duffin (2014), and Caterini et al. (2016) may be explained by the different study settings (e.g., leg cycling vs. walking, and/or the mode of sinusoidal changes).

We also observed that the Amp of $\stackrel{.}{\text{V}}$_E under the SL_fix condition was similar to that under the Free condition, even though the Amp of SF was sinusoidally altered (two times larger) compared with the Free condition (Figure 3A). Irrespective of the larger variation in SF during sinusoidal locomotion, the sinusoidal cadence under the present SL_fix condition inherently seemed to play a dominant role in the Amp responses of the ventilatory variables.

Considering the physiological mechanisms underlying these observations, it has been shown that the groups III and IV afferents in exercising limbs are stimulated by muscle contraction (Kaufman et al., 1983; Mense and Stahnke, 1983; Bruce et al., 2019). In this study, a greater Mx of $\stackrel{.}{\text{V}}$_E under the SL_fix condition was manifested compared with the Free condition, which supports the concept that the limb movement frequency is a significant factor in the greater increase of $\stackrel{.}{\text{V}}$_E during sinusoidal locomotion (Eldridge et al., 1981; Eldridge, 1994).

Influence on $\stackrel{.}{\text{V}}$_E-$\stackrel{.}{\text{V}}$CO₂ Linkage During Three Locomotion Patterns

When we used the slope of the $\stackrel{.}{\text{V}}$_E-$\stackrel{.}{\text{V}}$CO₂ relationship under the Free condition as the reference (1.0), the slope under SL_fix (1.2) was steeper than that under Free, and the slope under SF_fix was gentler than that in Free (Figure 7). The gait pattern for a sinusoidal variation of the SF may cause greater exercise hyperpnea, which can be interpreted as an overreaction of the additional stimulation on the respiratory center via the supraspinal locomotor center (DiMarco et al., 1983; Fukuoka et al., 2017). In other words, the greater $\stackrel{.}{\text{V}}$_E at a given $\stackrel{.}{\text{V}}$CO₂ under SL_fix locomotion suggests that the central feed-forward command (Bell, 2006) or upward information from the afferent neural activity was stimulated by the sinusoidal locomotive cadence. Therefore, these neural drives could be partly related to the steeper slope of the $\stackrel{.}{\text{V}}$_E−$\stackrel{.}{\text{V}}$CO₂ relationship under SL_fix rather than the humoral outcome via the equivalent metabolic demand under Free (Eldridge and Waldrop, 1991; Waldrop et al., 1996; Forster et al., 2012; Fukuoka et al., 2017).

Considering Free locomotion, our subjects’ preferred SL was likely to have a lower metabolic demand (Supplementary Table 2), and a significant main effect of the locomotion patterns was observed on the Mx for $\stackrel{.}{\text{V}}$_E, and there was a significant difference between the Free and SL_fix conditions in the 5-min period (p = 0.015, Supplementary Table 1). Thus, the steeper slope of the $\stackrel{.}{\text{V}}$_E−$\stackrel{.}{\text{V}}$CO₂ relationship under SL_fix might be attributed to a greater Mx for $\stackrel{.}{\text{V}}$_E. The observed differences in the ventilatory response between our SL_fix and Free conditions would be attributed to the larger Amp of SF, which contributed to the neuromuscular afferent flow into the medial brain and respiratory-locomotor generation center (Eldridge et al., 1981, 1982; Eldridge, 1994).

In contrast, the slope under SF_fix (0.7) was lower than that under Free even though the Mx of $\stackrel{.}{\text{V}}$_E, $\stackrel{.}{\text{V}}$O₂, and $\stackrel{.}{\text{V}}$CO₂ were not significantly different between the SL_fix and SF_fix conditions (Figure 7 and Supplementary Table 2). The remarkable difference in the slope of the $\stackrel{.}{\text{V}}$_E−$\stackrel{.}{\text{V}}$CO₂ relationship was due to the Amp of the SF. The lower slope was caused by the depressed $\stackrel{.}{\text{V}}$_E, which we attribute to the entrained breath frequency under SF_fix. The neural stimulus related to locomotion appeared to interact with the chemical stimulus in a predominantly “additive” manner (DiMarco et al., 1983). This finding may support our hypothesis that the modification of respiratory changes occurs indirectly via the gait pattern generator by maintaining the constrained SF (Le Gal et al., 2020).

We speculate that the very close association between $\stackrel{.}{\text{V}}$_E and $\stackrel{.}{\text{V}}$CO₂ at all locomotion patterns (r = 0.83−0.92, Figure 7) provides a rationale for considering mechanisms unrelated to the motor act (such as humoral factors) to explain the link between $\stackrel{.}{\text{V}}$_E and $\stackrel{.}{\text{V}}$CO₂ (Whipp et al., 1982). A major question in the physiological interpretation of the strong linkage between $\stackrel{.}{\text{V}}$_E and $\stackrel{.}{\text{V}}$CO₂ is that the CO₂ amount is an adjustment factor, but the chemoreceptor does not sense the CO₂ amount and respond to the partial pressure of CO₂ (Forster et al., 2012). Considering that chemoreceptors are always involved, the alteration of P_ETCO₂ could be involved as a derivative signal to the arterial and central chemoreceptors, which are further related to $\stackrel{.}{\text{V}}$_E (Forster et al., 2012; Ebine et al., 2018).

It has been recognized that a sinusoidal exercise protocol would indicate a lesser contribution to the ventilatory changes from the neural signals through the motor activity and/or central command (Forster et al., 2012). Wells et al. (2007) chose the shorter period of 1 or 2 min of sinusoidal change in walking speed between 3.2 and 6.4 km⋅h^–1 (approximately 53 and 107 m⋅min^–1) to emphasize the faster $\stackrel{.}{\text{V}}$_E response against locomotion. Contrary to their observations, the Amp values of $\stackrel{.}{\text{V}}$_E in this study were tightly coupled to those of $\stackrel{.}{\text{V}}$CO₂ during sinusoidal walking. The contribution of limb movement to exercise hyperpnea has thus been a matter of debate (Casaburi et al., 1978; Duffin, 2014; Ward, 2019). Moreover, exercise training can affect exercise hyperpnea through attenuation of a neural drive that is either feedforward or feedback in nature (Miyamoto et al., 2012).

Limitations

We set up three locomotive patterns based on the assumption of a sine wave speed, and thus we did not experiment with changing the SF sinusoidally at a fixed load (in this case, speed), which has been treated in leg cycling (Casaburi et al., 1978; Wells et al., 2007). Further studies using sinusoidal changing of the SF may be necessary.

It remains difficult to determine the relative contributions of the mechanoreflex vs. the metaboreflex to ventilatory control in humans (Olson et al., 2010, 2014). The novel findings of our present investigation possibly demonstrate that the afferent feedback from skeletal muscle triggers a marked increase in the slope of the $\stackrel{.}{\text{V}}$_E−$\stackrel{.}{\text{V}}$CO₂ relationship under SL_fix locomotion. However, we were unable to differentiate the involvements of peripheral afferent feedback from central command without the direct measures. The individual contribution of both neural factors to the ventilatory response in humans cannot be evidently stated from the experimental results in this study.

Conclusion

In summary, the SL_fix locomotion pattern enlarged the Amp of $\stackrel{.}{\text{V}}$_E and metabolic responses ($\stackrel{.}{\text{V}}$O₂ and $\stackrel{.}{\text{V}}$CO₂, and HR) compared with the SF_fix pattern (i.e., 120 steps⋅min^–1). Moreover, the Amp of Bf remained unchanged (<1.0 beats/min) under SF_fix. The slope of the $\stackrel{.}{\text{V}}$_E−$\stackrel{.}{\text{V}}$CO₂ relationship was steeper by 1.23 times under SL_fix and was gentler by 0.72 times under SF_fix when the slope under the control (Free) condition was used as the reference. These results are explained as follows: afferent feedback from the limb is important in locomotor-respiratory entrainment, whereby the discharge rhythm of sensory inputs can entrain central respiratory-pattern generation. The PSs of $\stackrel{.}{\text{V}}$_E, $\stackrel{.}{\text{V}}$O₂, and $\stackrel{.}{\text{V}}$CO₂ responses were unaffected at any of the locomotion patterns. Such sinusoidal wave manipulation of locomotion variables may offer new insights into the dynamics of exercise hyperpnea.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by the Ethics Committees of the Institutional Review Board of Doshisha University (no. 1045). The patients/participants provided their written informed consent to participate in this study.

Author Contributions

MF, TA, and YF conceived and design of the study. MF, TA, and KK collected the data. MF, MH, KK, and YF interpreted of the data. MF, MH, and YF wrote, reviewed, and approved the final manuscript. All authors contributed to the collection of data.

Funding

This study was financially supported by the Grant-in-Aid for Scientific Research from the Japan Society for the Promotion of Science (22370091 to YF, 26440268 to MH, and 19K06874 to TA).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank all participants for their participation in this study.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2022.820666/full#supplementary-material

References

Amann, M., Blain, G. M., Proctor, L. T., Sebranek, J. J., Pegelow, D. F., and Dempsey, J. A. (2010). Group III and IV muscle afferents contribute to ventilatory and cardiovascular response to rhythmic exercise in humans. J. Appl. Physiol. 109, 966–976. doi: 10.1152/japplphysiol.00462.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Bechbache, R. R., and Duffin, J. (1977). The entrainment of breathing frequency by exercise rhythm. J. Physiol. 272, 553–561. doi: 10.1113/jphysiol.1977.sp012059

PubMed Abstract | CrossRef Full Text | Google Scholar

Bell, H. J. (2006). Respiratory control at exercise onset: an integrated system perceptive. Respir. Physiol. Neurobiol. 152, 1–15. doi: 10.1016/j.resp.2006.02.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Bernasconi, P., Bürki, P., Bührer, A., Koller, E. A., and Kohl, J. (1995). Running training and co-ordination between breathing and running rhythms during aerobic and anaerobic conditions in humans. Eur. J. Appl. Physiol. Occup. Physiol. 70, 387–393. doi: 10.1007/BF00618488

PubMed Abstract | CrossRef Full Text | Google Scholar

Boggs, D. F. (2002). Interactions between locomotion and ventilation in tetrapods. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 133, 269–288. doi: 10.1016/s1095-6433(02)00160-5

CrossRef Full Text | Google Scholar

Bramble, D. M., and Carrier, D. R. (1983). Running and breathing in mammals. Science 219, 251–256. doi: 10.1126/science.6849136

PubMed Abstract | CrossRef Full Text | Google Scholar

Bruce, R. M., Jolley, C., and White, M. J. (2019). Control of exercise hyperpnoea: contributions from thin-fibre skeletal muscle afferents. Exp. Physiol. 104, 1605–1621. doi: 10.1113/EP087649

PubMed Abstract | CrossRef Full Text | Google Scholar

Casaburi, R., Whipp, B. J., Wasserman, K., Beaver, W. L., and Koyal, S. N. (1977). Ventilatory and gas exchange dynamics in response to sinusoidal work. J. Appl. Physiol. 42, 300–301. doi: 10.1152/jappl.1977.42.2.300

PubMed Abstract | CrossRef Full Text | Google Scholar

Casaburi, R., Whipp, B. J., Wasserman, K., and Koyal, S. N. (1978). Ventilatory and gas exchange responses to cycling with sinusoidally varying pedal rate. J. Appl. Physiol. 44, 97–103. doi: 10.1152/jappl.1978.44.1.97

PubMed Abstract | CrossRef Full Text | Google Scholar

Casey, K., Duffin, J., Kelsey, C. J., and McAvoy, G. V. (1987). The effect of treadmill speed on ventilation at the start of exercise in man. J. Physiol. 391, 13–24. doi: 10.1113/jphysiol.1987.sp016722

PubMed Abstract | CrossRef Full Text | Google Scholar

Caterini, J. E., Duffin, J., and Wells, G. D. (2016). Limb movement frequency is a significant modulator of the ventilatory response during submaximal cycling exercise in humans. Respir. Physiol. Neurobiol. 220, 10–16. doi: 10.1016/j.resp.2015.09.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Comroe, J. H., and Schmidt, C. F. (1943). Reflexes from the limbs as a factor in the hyerpnea of muscular exercise. Am. J. Physiol. 138, 536–547. doi: 10.1152/ajplegacy.1943.138.3.536

CrossRef Full Text | Google Scholar

Dejours, P. (1959). Regulation of ventilation during muscular exercise in man. J. Physiol. (Paris) 51, 163–261.

Google Scholar

DiMarco, A. F., Romaniuk, J. R., Von Euler, C., and Yamamoto, Y. (1983). Immediate changes in ventilation and respiratory pattern associated with onset and cessation of locomotion in the cat. J. Physiol. 343, 1–16. doi: 10.1113/jphysiol.1983.sp014878

PubMed Abstract | CrossRef Full Text | Google Scholar

Duffin, J. (2014). The fast exercise drive to breathe. J. Physiol. 592, 445–451. doi: 10.1113/jphysiol.2013.258897

PubMed Abstract | CrossRef Full Text | Google Scholar

Ebine, N., Aoki, T., Itoh, M., and Fukuoka, Y. (2018). Differential kinetics of the cardiac, ventilatory, and gas exchange variables during walking under moderate hypoxia. PLoS One 13:e0200186. doi: 10.1371/journal.pone.0200186

PubMed Abstract | CrossRef Full Text | Google Scholar

Eldridge, F. L. (1994). Central integration of mechanisms in exercise hyperpnea. Med. Sci. Sports Exerc. 26, 319–327.

PubMed Abstract | Google Scholar

Eldridge, F. L., Millhorn, D. E., and Waldrop, T. G. (1981). Exercise hyperpnea and locomotion: parallel activation from the hypothalamus. Science 211, 844–846. doi: 10.1126/science.7466362

PubMed Abstract | CrossRef Full Text | Google Scholar

Eldridge, F. L., Millhorn, D. E., and Waldrop, T. G. (1982). Input—output relationships of the central respiratory controller during peripheral muscle stimulation in cats. J. Physiol. 324, 285–295. doi: 10.1113/jphysiol.1982.sp014113

PubMed Abstract | CrossRef Full Text | Google Scholar

Eldridge, F. L., and Waldrop, T. G. (1991). “Neural control of breathing during exercise,” in Lung Biology in Health and Disease, vol. 52, Exercise Pulmonary Physiology and Pathophysiology, eds B. J. Whipp and K. Wasserman (New York, NY: Dekker Inc), 309–370.

Google Scholar

Forster, H. V., Haouzi, P., and Dempsey, J. A. (2012). Control of breathing during exercise. Compr. Physiol. 2, 743–777. doi: 10.1002/cphy.c100045

PubMed Abstract | CrossRef Full Text | Google Scholar

Fukuoka, Y., Iihoshi, M., Nazunin, J. T., Abe, D., and Fukuba, Y. (2017). Dynamic characteristics of ventilatory and gas exchange during sinusoidal walking in humans. PLoS One 12:e0168517. doi: 10.1371/journal.pone.0168517

PubMed Abstract | CrossRef Full Text | Google Scholar

Girardi, M., Gattoni, C., Mauro, L., and Capelli, C. (2021). The effects of sinusoidal linear drifts on the estimation of cardiorespiratory dynamic parameters during sinusoidal workload forcing: a simulation study. Respir. Physiol. Neurobiol. 289:103652. doi: 10.1016/j.resp.2021.103652

PubMed Abstract | CrossRef Full Text | Google Scholar

Giraudin, A., Le Bon-Jégo, M., Cabirol, M. J., Simmers, J., and Morin, D. (2012). Spinal and pontine relay pathways mediating respiratory rhythm entrainment by limb proprioceptive inputs in the neonatal rat. J. Neurosci. 32, 11841–11853. doi: 10.1523/JNEUROSCI.0360-12.2012

PubMed Abstract | CrossRef Full Text | Google Scholar

Haouzi, P. (2006). Theories on the nature of the coupling between ventilation and gas exchange during exercise. Respir. Physiol. Neurobiol. 151, 267–279. doi: 10.1016/j.resp.2005.11.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Haouzi, P., Chenuel, B., and Chalon, B. (2004). The control of ventilation is dissociated from locomotion during walking in sheep. J. Physiol. 559, 315–325. doi: 10.1113/jphysiol.2003.057729

PubMed Abstract | CrossRef Full Text | Google Scholar

Haouzi, P., Fukuba, Y., Peslin, R., Chalon, B., Marchal, F., and Crance, J. P. (1992). Ventilatory dynamics in children and adults during sinusoidal exercise. Eur. J. Appl. Physiol. Occup. Physiol. 64, 410–418. doi: 10.1007/BF00625059

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaufman, M. P., Longhurst, J. C., Rybicki, K. J., Wallach, J. H., and Mitchell, J. H. (1983). Effects of static muscular contraction on impulse activity of groups III and IV afferents in cats. J. Appl. Physiol. Respir. Environ. Exerc. Physiol. 55, 105–112. doi: 10.1152/jappl.1983.55.1.105

PubMed Abstract | CrossRef Full Text | Google Scholar

Lafortuna, C. L., Reinach, E., and Saibene, F. (1996). The effects of locomotor-respiratory coupling on the pattern of breathing in horses. J. Physiol. 492, 587–596. doi: 10.1113/jphysiol.1996.sp021331

PubMed Abstract | CrossRef Full Text | Google Scholar

Latt, M. D., Menz, H. B., Fung, V. S., and Lord, S. R. (2008). Walking speed, cadence and step length are selected to optimize the stability of head and pelvis accelerations. Exp. Brain Res. 184, 201–209. doi: 10.1007/s00221-007-1094-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Le Gal, J. P., Colnot, E., Cardoit, L., Bacqué-Cazenave, J., Thoby-Brisson, M., Juvin, L., et al. (2020). Modulation of respiratory network activity by forelimb and hindlimb locomotor generators. Eur. J. Neurosci. 52, 3181–3195. doi: 10.1111/ejn.14717

PubMed Abstract | CrossRef Full Text | Google Scholar

McDermott, W. J., Van Emmerik, R. E., and Hamill, J. (2003). Running training and adaptive strategies of locomotor-respiratory coordination. Eur. J. Appl. Physiol. 89, 435–444. doi: 10.1007/s00421-003-0831-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Mense, S., and Stahnke, M. (1983). Responses in muscle afferent fibres of slow conduction velocity to contractions and ischaemia in the cat. J. Physiol. 342, 383–397. doi: 10.1113/jphysiol.1983.sp014857

PubMed Abstract | CrossRef Full Text | Google Scholar

Miyamoto, T., Inagaki, M., Takaki, H., Kawada, T., Shishido, T., Kamiya, A., et al. (2012). Adaptation of the respiratory controller contributes to the attenuation of exercise hyperpnea in endurance-trained athletes. Eur. J. Appl. Physiol. 112, 237–251. doi: 10.1007/s00421-011-1968-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Morin, D., and Viala, D. (2002). Coordinations of locomotor and respiratory rhythms in vitro are critically dependent on hindlimb sensory inputs. J. Neurosci. 22, 4756–4765. doi: 10.1523/JNEUROSCI.22-11-04756.2002

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Halloran, J., Hamill, J., McDermott, W. J., Remelius, J. G., and Van Emmerik, R. E. (2012). Locomotor-respiratory coupling patterns and oxygen consumption during walking above and below preferred stride frequency. Eur. J. Appl. Physiol. 112, 929–940. doi: 10.1007/s00421-011-2040-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Olson, T. P., Joyner, M. J., Eisenach, J. H., Curry, T. B., and Johnson, B. D. (2014). Influence of locomotor muscle afferent inhibition on the ventilatory response to exercise in heart failure. Exp. Physiol. 99, 414–426. doi: 10.1113/expphysiol.2013.075937

PubMed Abstract | CrossRef Full Text | Google Scholar

Olson, T. P., Joyner, M. J., and Johnson, B. D. (2010). Influence of locomotor muscle metaboreceptor stimulation on the ventilatory response to exercise in heart failure. Circ. Heart Fail. 3, 212–219. doi: 10.1161/CIRCHEARTFAILURE.109.879684

PubMed Abstract | CrossRef Full Text | Google Scholar

Potts, J. T., Rybak, I. A., and Paton, J. F. R. (2005). Respiratory rhythm entrainment by somatic afferent stimulation. J. Neurosci. 25, 1965–1978. doi: 10.1523/JNEUROSCI.3881-04

CrossRef Full Text | Google Scholar

Shevtsova, N. A., Marchenko, V., and Bezdudnaya, T. (2019). Modulation of respiratory system by limb muscle afferents in intact and injured spinal cord. Front. Neurosci. 13:289. doi: 10.3389/fnins.2019.00289

PubMed Abstract | CrossRef Full Text | Google Scholar

Takano, N. (1988). Effects of pedal rate on respiratory responses to incremental bicycle work. J. Physiol. 396,389–397. doi: 10.1113/jphysiol.1988.sp016968

PubMed Abstract | CrossRef Full Text | Google Scholar

Waldrop, T. G., Eldridge, F., Iwamoto, G. A., and Mitchel, J. (1996). “Central neural control of respiration and circulation during exercise,” in Handbook of Physiology, Exercise: Regulation and Integration of Multiple Systems, eds L. Rowell and J. Shepherd (New York, NY: The American Physiological Society), 332–380.

Google Scholar

Ward, S. A. (2019). Exercise physiology: exercise hyperpnea. Curr. Opin. Physiol. 10, 166–172. doi: 10.1016/j.cophys.2019.05.010

CrossRef Full Text | Google Scholar

Wells, G. D., Diep, T., and Duffin, J. (2007). The ventilatory response to sine wave variation in exercise loads and limb movement frequency. Respir. Physiol. Neurobiol. 158, 45–50. doi: 10.1016/j.resp.2007.03.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Whipp, B. J., Ward, S. A., Lamarra, N., Davis, J. A., and Wasserman, K. (1982). Parameters of ventilatory and gas exchange dynamics during exercise. J. Appl. Physiol. 52, 1506–1513. doi: 10.1152/jappl.1982.52.6.1506

PubMed Abstract | CrossRef Full Text | Google Scholar

Wigertz, O. (1971). Dynamics of respiratory and circulatory adaptation to muscular exercise in man. A systems analysis approach. Acta Physiol. Scand. Suppl. 363, 1–32.

PubMed Abstract | Google Scholar