
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Physiol. , 04 March 2022
Sec. Computational Physiology and Medicine
Volume 13 - 2022 | https://doi.org/10.3389/fphys.2022.760404
This article is part of the Research Topic Machine Learning in Systems Quantitative Biology View all 4 articles
Cryo-electron tomography (Cryo-ET) has been regarded as a revolution in structural biology and can reveal molecular sociology. Its unprecedented quality enables it to visualize cellular organelles and macromolecular complexes at nanometer resolution with native conformations. Motivated by developments in nanotechnology and machine learning, establishing machine learning approaches such as classification, detection and averaging for Cryo-ET image analysis has inspired broad interest. Yet, deep learning-based methods for biomedical imaging typically require large labeled datasets for good results, which can be a great challenge due to the expense of obtaining and labeling training data. To deal with this problem, we propose a generative model to simulate Cryo-ET images efficiently and reliably: CryoETGAN. This cycle-consistent and Wasserstein generative adversarial network (GAN) is able to generate images with an appearance similar to the original experimental data. Quantitative and visual grading results on generated images are provided to show that the results of our proposed method achieve better performance compared to the previous state-of-the-art simulation methods. Moreover, CryoETGAN is stable to train and capable of generating plausibly diverse image samples.
Cryo-electron tomography (Cryo-ET) has emerged as a powerful 3D imaging tool with unprecedented quality in capturing structural and spatial organization information of macromolecules inside single cells. Analysis of macromolecules in a Cryo-ET image (i.e., a tomogram, usually of size 6,000 × 6,000 × 1,500 voxels) is done at subtomogram level. A subtomogram is a small 3D cubic sub-image of a tomogram that generally contains one macromolecule extracted from tomograms. Deep-learning-based classification has been successfully applied and achieved high accuracy on Cryo-ET subtomogram identification. Plenty of previous works have been devoted to separating structurally highly heterogeneous macromolecules captured by Cryo-ET data into structurally homogeneous subgroups (Bartesaghi et al., 2008; Scheres et al., 2009; Xu and Alber, 2011, 2012; Xu et al., 2012; Chen et al., 2014; Bharat et al., 2015; Che et al., 2018). Nevertheless, the main bottleneck for these deep learning methods is a lack of training data. Since various subtomogram datasets may be collected under different experimental conditions, directly applying the knowledge learned from one dataset to the other will result in a decrease in performance such as classification accuracy due to domain shift. Therefore, part of the dataset must be manually labeled in order to predict the rest of the data, which is a highly time consuming process. To automate this process and reduce domain shift, training the network on realistically generated subtomogram datasets becomes an ideal approach. Simulation can provide an unlimited number of training instances with pre-specified labels.
Conventional image simulation methods for Cryo-ET use atomic models in Protein DataBank (PDB) (Bernstein et al., 1977), using a specified resolution and voxel spacing together with low-pass data filtering. Gaussian-distributed noise and Modulation Transfer Function noise (MTF) are applied for the realistic electron optical effect to match a certain signal-to-noise ratio (SNR). Random rotation and translation operations are performed to synthesize more samples. Yet, simulating realistic data presents challenges due to high degree of structural complexity, irregular noise, and tomographic distortions. Neural networks trained on them result in poor testing performance when applied to experimental data. By inferring from real image data, machine learning methods potentially overcome common restrictions such as infeasible interactive use and substantial computational resources.
The recent explosion in the Generative Adversarial Networks (GANs) field have shown great success in tasks such as image synthesis, image-to-image translation (Yang et al., 2017; Schlemper et al., 2018; Seitzer et al., 2018; Wang et al., 2019, 2021; Guo et al., 2020; Yuan et al., 2020; Chen J. et al., 2021; Chen Y. et al., 2021; Jiang et al., 2021; Li et al., 2021; Lv et al., 2021a,b,c). Recent advances have used GANs to formulate biomedical image simulation as an image-to-image translation task and arouse a wide interest in biomedical area (Bi et al., 2017; Calimeri et al., 2017; Nie et al., 2017; Wolterink et al., 2017; Zhao et al., 2017; Liu et al., 2021a,b). In most cases, 3D images do not have paired data; as a result, learning from unpaired data becomes crucial. The cycle-consistent generative adversarial network (Zhu et al., 2017) successfully performed unpaired image-to-image translations, only requiring two unpaired datasets and is capable of preserving semantics. In the same spirit, we formulate a framework called CryoETGAN to simulate subtomograms indiscriminable from real data on given structures from density map which shows electron density occupancies and distribution of the particle (Kaur et al., 2021). We conduct experiments to demonstrate the effectiveness of our method qualitatively and quantitatively. The generated datasets can serve as training datasets for future subtomogram study.
We are the first to propose an image translation based simulation method for cryo-ET 3D images. Although image translation has been used to simulate cryo-EM 2D images (Gupta et al., 2020b, 2021; Miolane et al., 2020), they are not directly comparable to our method as 3D cryo-ET and 2D cryo-EM images capture different kinds of information. One prior work applying GANs in a related space is Gupta et al. (2020a), in which a GAN is trained to perform single-particle cryogenic electron microscopy (Cryo-EM) reconstruction given a large number of Cryo-EM images. We note this work differs in many aspects including the task and the nature of the data. First, Gupta et al. (2020a) trains a generative simulator using many Cryo-EM images of a specific particle, not a general image-to-image translation model. In addition, 2D single-particle cryogenic electron microscopy (Cryo-EM) images and 3D cryo-electron tomography (Cryo-ET) images are different media: single-particle Cryo-EM typically uses noisy images of many copies of a macromolecular structure, while Cryo-ET operates on a single cell sample (Marx, 2018). As noted in Marx (2018), Cryo-ET shines where it is not feasible to make “tens of thousands” of copies of a structure of interest, and has led to discoveries such as Basler et al. (2012). In essence, Gupta et al. (2020a) solves an important but distinct task in a related field.
Thus, our main contributions are as follows:
1. We propose the use of a GAN-based image translation method in order to augment the training datasets of Cryo-ET models using density maps.
2. We develop a GAN framework to robustly generate diverse Cryo-ET images from density maps. We propose several architectural modifications to incorporate priors on Cryo-ET data to stabilize training.
3. We demonstrate the effectiveness of these techniques on traditional metrics of generative model performance as well as downstream classification performance.
Our proposed framework for Cryo-ET image synthesis: CryoETGAN is presented in Figure 1. In the following paragraphs, we will elaborate on CryoETGAN and its network architecture starting with preliminary details.
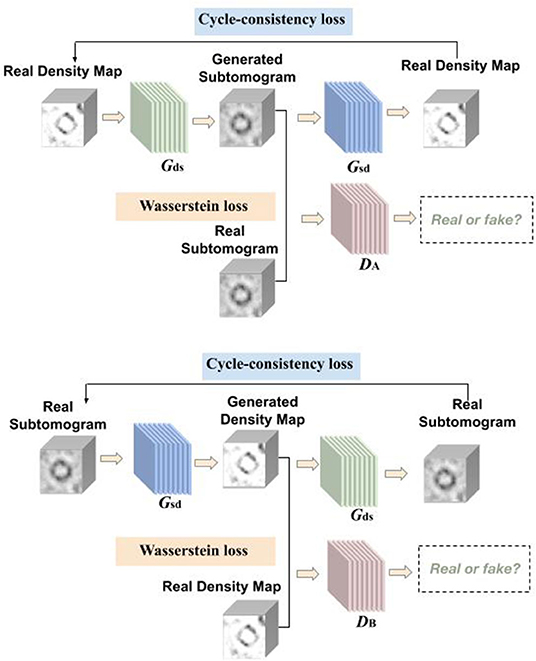
Figure 1. Overview of CryoETGAN: with adversarial loss, cycle-consistency loss, and Wasserstein loss, our method is capable of learning mapping between domain and with unpaired data.
We first introduce our notations. Macromolecular complexes and cellular components which can be extracted from tomograms of cells using template-free methods such as Difference of Gaussian, are densely packed in small 3D volume of cubic shape (3D analog of a 2D image patch). Those experimental subtomograms are represented as where si ∈ S (i.e., 3D gray scale images of size n × n × n).
Another domain we use contains density maps which are simulated from proteins using EMAN2 (Tang et al., 2007), which is a image processing package with a focus on single particle reconstruction. Those experimental density maps are denoted as where di ∈ D, our goal is to learn two mapping functions, Gds : D → S and Gsd : S → D. The generators are guided by the discriminators to learn the mappings between the subtomograms and density maps in order to preserve the edges and details.
As shown in Figure 1, our CryoETGAN model has four main components: two generators Gds and Gsd to capture the data distribution from two domains, two discriminators DA and DB that estimate the probability of the generated samples whether they are from the experimental datasets or generated ones. Discriminator DA aims to distinguish between experimental subtomograms and generated ones , and DB aims to discriminate between experimental density map and generated ones . Two generators are trained to produce realistic data to fool the adversarially trained discriminators DA and DB. The training loss of CryoETGAN contains three types of terms: adversarial loss for matching the distribution of generated data to corresponding D or S domain; cycle-consistent loss to make sure the generated images in target domain can be generated back to the source domain and enable the mapping between these two domains; and Wasserstein loss to prevent mode collapse.
The adversarial losses are applied to both mapping directions. Given a distribution s ~ pdata, generators define the probability distribution as the distribution of the sample Gds(d) and Gsd(s) For the generator Gds : D → S and its discriminator DA, the objective is defined as:
In this setting, we train the generators Gds, Gsd, and discriminators DA, DB together. Without paired data, we conduct a min-max training between the generators and discriminators. Ideally the image Gds(d) generated by Gds will be visually similar to images in S domain. Meanwhile the discriminators distinguish between generated images and real images. Similarly, the adversarial loss for the mapping function Gsd : S → D and its discriminator DB is defined as below:
To further guarantee that the mapping function can map an input di to its ideal output si, also from si to di. Inspired by Zhu et al. (2017), we use cycle-consistent loss to enable the image translation cycle to force d back to the original image, i.e., d → Gds(d) → Gsd(Gds(d)) ≈ d. Similarly, for each image s from domain S, Gsd and Dd should also make the reconstructed image Gds[Gsd(s)] to be identical to input s. The cycle-consistent loss is written as:
During preliminary testing, expressions of density maps were frequently transferred to the same pose and to the same subtomogram expression. Moreover, the standard discriminator loss uses cross-entropy loss and suffers from vanishing gradients. Instead of the Jensen-Shannon divergence, Wasserstein GAN (Arjovsky et al., 2017) adopts the Earth Mover distance to measure the distance between real and generated samples:
Following the notation from Arjovsky et al. (2017) Π(ℙr, ℙg) represents for the set of all joint distributions. γ(x, y) represents for the transporting cost from x to y in order to transform the distributions ℙr to ℙg. In practice, this is accomplished by replacing the discriminator with a critic and using the difference between the critic predictions on real and fake images as the critic's loss, and the negated version for the generator, and then enforcing a constraint on the discriminator to enforce 1-Lipschitz continuity. Inspired by Wasserstein GAN, we adopted the following improvements in order to deal with the model collapse problem in adversarial training and to achieve more stable results.
• Clip the weight ofs D.
• Use RMSProp instead of ADAM.
• Lower learning rate. The rate in the paper is α = 0.0005.
The scenario of mode collapse refers to the generator produces similar data every time and still able to successfully fool the discriminator. We pass random noise vectors to the generator in order to deal with mode collapse. To learn the distribution over subtomogram, the generator builds a mapping function from a distribution density map to subtomogram. Between convolutional layers and deconvolutional layers, we concatenate a noise vector to it so that it can generate different pattern according to the style. On the other side of the cycle translation, another generator builds a mapping function from subtomogram to density map.
Given the formulations of adversarial loss, cycle-consistent loss, and wasserstein loss above, our full objective is formulated as follows:
where λ adjusts the importance of the cycle-consistency objective.
Solving the min-max optimization problem has long been known for a challenging task. Previous work proposed careful designed network architectures and objective functions in order to achieve good performance—we adopt the spectral normalization layer proposed by Miyato et al. (2018) to normalize weights, regulating the scale of feature response values and stabilizing the training process.
Following the CycleGAN paper notation (Zhu et al., 2017), the generator architecture is c7s1-d32, d64, d128, R128, R128, R128, R128, R128, R128, u64, u32, c7s1-u1. The output after downsampling is concatenated along the filter dimension with a one-channel Gaussian noise vector of the same shape, so the input to the u32 layer has 129 channels. Note dk denotes a k-filter 3 × 3 × 3 and stride-2 convolution followed by instance norm and ReLU, uk denotes the same with stride and fractional-strided-convolution, and Rk is a k-filter residual block. The last convolutional layer has tanh without InstanceNorm. The discriminator has an architecture of C64, C128, C256. Note Ck corresponds to a 4 × 4 × 4 convolution with stride 1 followed by InstanceNorm and a Leaky ReLU with slope of 0.2. Spectral Normalization is applied to each convolutional layer of the discriminator.
We tested our CryoETGAN on two experimental datasets Se1 and Se2. Dataset Se1 contains 1,600 subtomograms of size 403 from four classes of macromolecules, the four classes are Proteasome (5MPA), Ribosome (5T2C), TRiC (4V94), and Membrane. Each class has 400 images. For the density maps, We simulated 3D noise free density maps using EMAN2 corresponding to the subtomogram classes. The proteins are from Protein Data Bank (Berman et al., 2000) which is a database for the three-dimensional structural data of large biological molecules, such as proteins and nucleic acids. Dataset Se2 contains 2,800 subtomograms from seven classes of macromolecules, which were extracted from Noble Single Particle Dataset collected by Noble et al. (2018), each class has 400 subtomograms from EMPIAR. Subtomograms were extracted and about 20 macromolecules were manually picked. The 20 subtomograms were averaged to generate the structural template. Structural template was aligned to all subtomograms extracted and produces cross-correlation scores. Each particle is consisted of 283 voxels, and the size of each voxel is 0.94 nm. The SNR is 0.5 and missing wedge angle is 30°. For each tomogram in the original set, subtomograms of size 283 were extracted using a Difference of Gaussian(DOG) particle picking process (Pei et al., 2016) with the parameters of s1 = 7.0 and k = 1.1. We applied a template search approach as described in Zeng et al. (2018) to select the top 1,000 subtomograms according to the cross-correlation scores. Four hundred subtomograms are manually selected for each class which contain macromolecule structures. In our experiments, we select 2,000 subtomograms for training and the remaining 800 for testing.
Figure 2 displays simulation results of applying CryoETGAN, and each section of the image represents for a slice of the generated subtomogram data. We can observe that the reconstructed images Gsd[Gds(d)] end up matching closely to the input images d as shown in Figure 3.
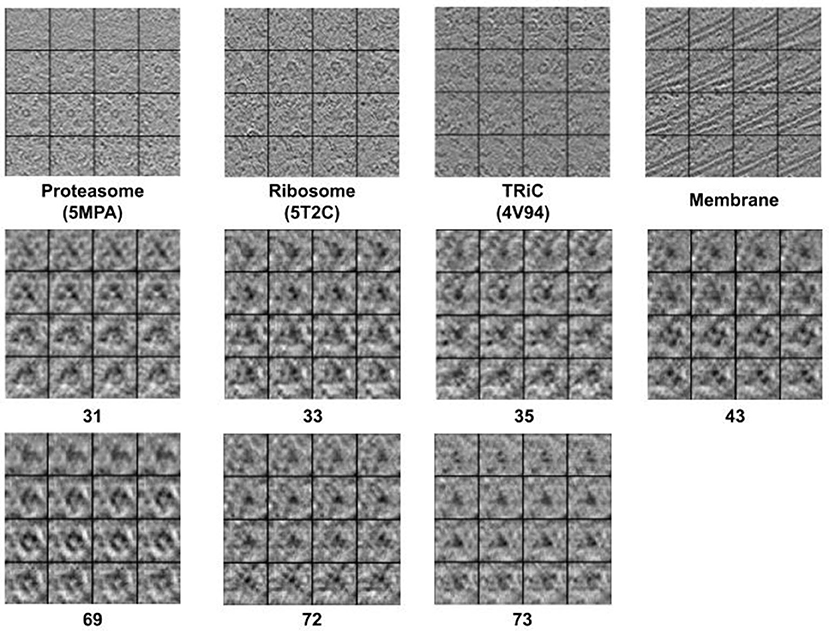
Figure 2. The 2D slide visualization of generated subtomograms (Top: Se1, Middle and Bottom: Se2). In general, we find CryoETGAN retrieval produces qualitatively similar subtomogram compared to the ground truth and is capable of producing various classes without mode collapse.
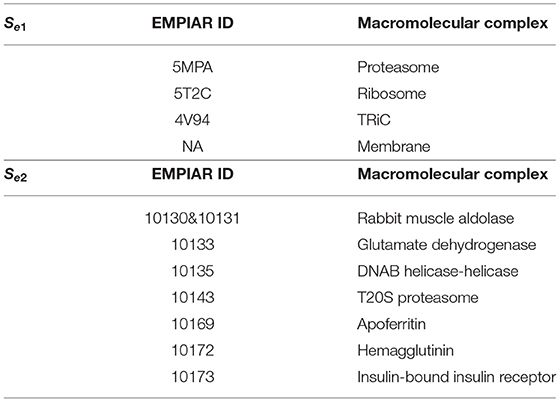
Table 1. For domain S, we use two datasets for training Se1 and Se2 separately, which contains four classes subtomograms and seven classes subtomograms, with 400 images in each class.

Figure 3. The 2D slide visualization of real subtomogram samples from every class (Top: Se1, Middle and Bottom: Se2), the sequence of those subtomograms is corresponding to the sequence in Table 1.
We use several common GAN evaluation metrics (Borji, 2019) as the quality evaluation criteria for the Cryo-ET data generated in our experiments as shown in Figures 5, 6.
IS was originally proposed by Salimans et al. (2016) to quantitatively evaluate the quality of the generated images (shown in Equation 6). The intuition behind Inception Score is that a generator with high performance should generate samples with low entropy in the class distribution of a single generated data while producing high entropy in the classes across all generated samples. In our experiments, we adopted CB3D (Che et al., 2018) as our “Inception V3” to calculate an IS-equivalent for Cryo-ET.
FID has been widely used in measuring the similarity between real and generated images. Unlike IS, FID (Heusel et al., 2017) compares the distance between two multivariate Gaussian distributions as shown in (Equation 7)
s where and are the 4,096 dimensional activation inputs of the CB3D model's dense layer for real and generated data, respectively.
Single-value metrics such as IS and FID evaluate the generative model, yet they are not perfect for diagnostic purposes (Naeem et al., 2020). Fidelity and diversity attribute are usually considered as a trade-off in the design strategy of generative models, which represents for how realistic the inputs are and how well those generated data capture the variations in real data (Naeem et al., 2020). We use precision and recall proposed by Sajjadi et al. (2018) to measure these two characteristics, we use the same notations as in Naeem et al. (2020), B(X, r): the ball around the point x with radius r, NNDk(Xi): the distance to the kth-nearest neighbor. Xi are the real embedded samples and Yj are the fake embedded samples.
Precision:
Recall:
Density and coverage are proposed by Naeem et al. (2020) as alternatives to precision and recall, respectively, to be more robust to outliers. Density emphasizes not only whether the samples generated are close to a real sample, but also how many spheres around real-samples contain the generated example. It counts how many real-sample neighborhood contains fake samples.
Coverage is a metric evaluating recall in terms of the real manifold rather than the fake manifold. This penalizes sparse coverage of the real space, where generators may benefit in terms of the recall metric by simply having few examples in some part of the real space. It builds the nearest neighbor manifolds around the real samples instead of the fake samples due to more outliers.
Deep Neural networks are able to capture global and local information from image data. Therefore, we use the state-of-the-art deep learning-based classification model for Cryo-ET data: CB3D (Che et al., 2018) to objectively quantify the generated subtomogram generated from density map data. We consider this as a way to interpret the generative ability of our model.
Compared to the traditional method (Bernstein et al., 1977) which has the testing classification accuracy 19.7% on a well-trained CB3D for Se1 and 28.9% for Se2, our method outperforms the traditional method by achieving the classification accuracy of 76.4 and 67.3%.
We believe that the fact that the coverage result is much better than the recall result is a consequence of a few factors: first, the relatively small size of the real dataset means that the original recall metric will penalize the model for generating anything except exactly the correct test set examples. Using the real manifold, as in coverage, rather than the fake manifold, as in recall, is more forgiving. Since these metrics were not developed with an emphasis on small real datasets and the evaluation of precision and recall of generative models is an ongoing topic of research, there may be a better metric to be proposed, but this is outside the scope of our article. The evaluation results are shown in Table 2.
Uncertainty estimation is a common approach to check the generative model's performance, we build on Gal and Ghahramani (2016) and combine their contributions in order to get an uncertainty map using Monte Carlo dropout as an implicit representation of the underlying subnetworks.
The detailed description of our uncertainty estimation method is: we apply dropout in the generator, sample 20 times using the same density map, calculate the standard deviation per pixel, and then we can overlay them to have an uncertainty map over the pixel wise of the model per given input for visualization. Then we compare the result of using Dropout and not using dropout. In this way we will be able to measure the generator uncertainty from pixel level. We show the uncertainty maps in Figure 4.
In Table 3, we compare CryoETGAN's performance under various standard deviations of noise during training. The performance of our CryoETGAN substantially improved when we applied zero-mean Gaussian noise to the density maps in the experiment relative to training without noise. From Figures 5, 6, we can see improvements in Inception Score and faster convergence in Frechet Inception Distance.
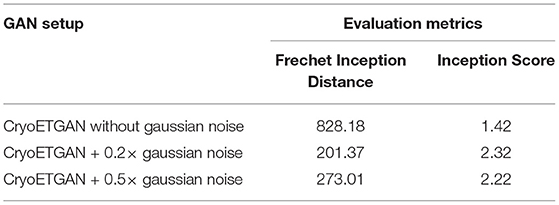
Table 3. Ablation study to demonstrate the performance impact of applying zero-mean Gaussian noise applied on density maps w.r.t. Frechet Inception Distance and Inception Score.
We further evaluated the presence of the Wasserstein loss and the Spectral normalization. The results are shown below. Here we evaluated on Se1 four classes dataset. We find that without the Wasserstein loss there is clear indication of mode collapse, and without the spectral norm a significant penalty on downstream performance. The ablation study results are shown in Table 4.
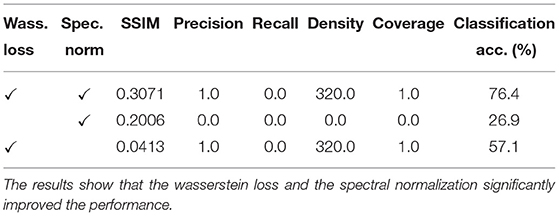
Table 4. Ablation study to demonstrate the performance impact of using Wasserstein loss and Spectral normalization.
We proposed a machine learning based method: CryoETGAN to synthesize Cryo-ET images and therefore to enable the realistic simulation of protein density maps consistent with the Cryo-ET data. Our generated images performed competitively when trained for classification and this approach potentially increases the available training data for further new Cryo-ET based algorithms which depends on large data collection. This new data provides a way to investigate new methods for object detection, segmentation, domain adaptation tasks, etc. Our approach can also be extended to support other multimodal nanoparticles image synthesis in fluorescence/soft X-ray/tomography of nucleoplasmic reticulum and apoptosis in mammalian cells, which serves as a way to study images and resolve tasks limited by insufficient available data.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
MX conceived the study. XW and XZ proposed CryoETGAN. XW designed and implemented the methods and ran analysis. CL and HW evaluated the methods and did the ablation studies. XW, CL, and HW analyzed the results. XZ processed the data. XW wrote the article with suggestions from MX, XZ, H-WD, and JZ. All authors contributed to the article and approved the submitted version.
This work was supported in part by U.S. NIH grants R01GM134020 and P41GM103712, NSF grants DBI-1949629 and IIS-2007595, and Mark Foundation For Cancer Research 19-044-ASP. We thank the computational resources support from AMD COVID-19 HPC Fund. XZ was supported in part by a fellowship from CMU CMLH. JZ was supported in part by U.S. NIH grant K01MH123896.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Arjovsky, M., Chintala, S., and Bottou, L. (2017). Wasserstein GAN. arXiv [Preprint] arXiv:1701.07875.
Bartesaghi, A., Sprechmann, P., Liu, J., Randall, G. E., Sapiro, G., and Subramaniam, S. (2008). Classification and 3D averaging with missing wedge correction in biological electron tomography. J. Struct. Biol. 162, 436–450. doi: 10.1016/j.jsb.2008.02.008
Basler, á., Pilhofer, á., Henderson, G., Jensen, G., and Mekalanos, J. (2012). Type VI secretion requires a dynamic contractile phage tail-like structure. Nature 483, 182–186. doi: 10.1038/nature10846
Berman, H. M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T. N., Weissig, H., et al. (2000). The protein data bank. Nucleic Acids Res. 28, 235–242. doi: 10.1093/nar/28.1.235
Bernstein, F. C., Koetzle, T. F., Williams, G. J., Meyer, E. F. Jr, Brice, M. D., Rodgers, J. R., et al. (1977). The protein data bank: a computer-based archival file for macromolecular structures. Eur. J. Biochem. 80, 319–324. doi: 10.1111/j.1432-1033.1977.tb11885.x
Bharat, T. A., Russo, C. J., Löwe, J., Passmore, L. A., and Scheres, S. H. (2015). Advances in single-particle electron cryomicroscopy structure determination applied to sub-tomogram averaging. Structure 23, 1743–1753. doi: 10.1016/j.str.2015.06.026
Bi, L., Kim, J., Kumar, A., Feng, D., and Fulham, M. (2017). “Synthesis of positron emission tomography (PET) images via multi-channel generative adversarial networks (GANs),” in Molecular Imaging, Reconstruction and Analysis of Moving Body Organs, and Stroke Imaging and Treatment, eds M. J. Cardoso, T. Arbel, F. Gao, B. Kainz, T. van Walsum, K. Shi, K. K. Bhatia, R. Peter, T. Vercauteren, A. Reyes, A. Dalca, R. W. W. Niessen, and B. J. Emmer (Springer), 43–51. doi: 10.1007/978-3-319-67564-0_5
Borji, A. (2019). Pros and cons of gan evaluation measures. Comput. Vis. Image Understand. 179, 41–65. doi: 10.1016/j.cviu.2018.10.009
Calimeri, F., Marzullo, A., Stamile, C., and Terracina, G. (2017). “Biomedical data augmentation using generative adversarial neural networks,” in International Conference on Artificial Neural Networks (Alghero: Springer), 626–634. doi: 10.1007/978-3-319-68612-7_71
Che, C., Lin, R., Zeng, X., Elmaaroufi, K., Galeotti, J., and Xu, M. (2018). Improved deep learning-based macromolecules structure classification from electron cryo-tomograms. Mach. Vis. Appl. 29, 1227–1236. doi: 10.1007/s00138-018-0949-4
Chen, J., Yang, G., Khan, H., Zhang, H., Zhang, Y., Zhao, S., et al. (2021). JAS-GAN: generative adversarial network based joint atrium and scar segmentation on unbalanced atrial targets. IEEE J. Biomed. Health Inform. doi: 10.1109/JBHI.2021.3077469
Chen, X., Chen, Y., Schuller, J. M., Navab, N., and Förster, F. (2014). “Automatic particle picking and multi-class classification in cryo-electron tomograms,” in 2014 IEEE 11th International Symposium on Biomedical Imaging (ISBI) (Beijing: IEEE), 838–841. doi: 10.1109/ISBI.2014.6868001
Chen, Y., Firmin, D., and Yang, G. (2021). “Wavelet improved GAN for MRI reconstruction,” in Medical Imaging 2021: Physics of Medical Imaging, Vol. 11595 (Remote: International Society for Optics and Photonics), 1159513 doi: 10.1117/12.2581004
Gal, Y., and Ghahramani, Z. (2016). “Dropout as a Bayesian approximation: representing model uncertainty in deep learning,” in International Conference on Machine Learning (New York, NY: PMLR), 1050–1059.
Guo, Y., Wang, C., Zhang, H., and Yang, G. (2020). “Deep attentive wasserstein generative adversarial networks for MRI reconstruction with recurrent context-awareness,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (Strasbourg: Springer), 167–177. doi: 10.1007/978-3-030-59713-9_17
Gupta, H., McCann, M. T., Donati, L., and Unser, M. (2020a). CryoGAN: a new reconstruction paradigm for single-particle cryo-em via deep adversarial learning. BioRxiv [Preprint]. doi: 10.1101/2020.03.20.001016
Gupta, H., Mccann, M. T., Donati, L., and Unser, M. (2021). CryoGAN: a new reconstruction paradigm for single-particle cryo-EM via deep adversarial learning. IEEE Trans. Comput. Imaging. 7, 759–774. doi: 10.1109/TCI.2021.3096491
Gupta, H., Phan, T. H., Yoo, J., and Unser, M. (2020b). “Multi-cryoGAN: Reconstruction of continuous conformations in cryo-EM using generative adversarial networks,” in European Conference on Computer Vision (Remote: Springer), 429–444. doi: 10.1007/978-3-030-66415-2_28
Heusel, M., Ramsauer, H., Unterthiner, T., Nessler, B., and Hochreiter, S. (2017). GANs trained by a two time-scale update rule converge to a local nash equilibrium. arXiv [Preprint] arXiv:1706.08500. doi: 10.5555/3295222.3295408
Jiang, M., Zhi, M., Wei, L., Yang, X., Zhang, J., Li, Y., et al. (2021). FA-GAN: Fused attentive generative adversarial networks for MRI image super-resolution. Comput. Med. Imaging Graph. 92:101969. doi: 10.1016/j.compmedimag.2021.101969
Kaur, S., Gomez-Blanco, J., Khalifa, A. A., Adinarayanan, S., Sanchez-Garcia, R., Wrapp, D., et al. (2021). Local computational methods to improve the interpretability and analysis of cryo-EM maps. Nat. Commun. 12, 1–12. doi: 10.1038/s41467-021-21509-5
Li, G., Lv, J., Tong, X., Wang, C., and Yang, G. (2021). High-resolution pelvic MRI reconstruction using a generative adversarial network with attention and cyclic loss. IEEE Access 9, 105951–105964. doi: 10.1109/ACCESS.2021.3099695
Liu, Q., Chen, S., Jiang, R., and Wong, W. H. (2021a). Simultaneous deep generative modelling and clustering of single-cell genomic data. Nat. Mach. Intell. 3, 536–544. doi: 10.1038/s42256-021-00333-y
Liu, Q., Xu, J., Jiang, R., and Wong, W. H. (2021b). Density estimation using deep generative neural networks. Proc. Natl. Acad. Sci. U.S.A. 118:e2101344118. doi: 10.1073/pnas.2101344118
Lv, J., Li, G., Tong, X., Chen, W., Huang, J., Wang, C., et al. (2021a). Transfer learning enhanced generative adversarial networks for multi-channel MRI reconstruction. Comput. Biol. Med. 2021:104504. doi: 10.1016/j.compbiomed.2021.104504
Lv, J., Wang, C., and Yang, G. (2021b). Pic-GAN: a parallel imaging coupled generative adversarial network for accelerated multi-channel MRI reconstruction. Diagnostics 11:61. doi: 10.3390/diagnostics11010061
Lv, J., Zhu, J., and Yang, G. (2021c). Which GAN? A comparative study of generative adversarial network-based fast MRI reconstruction. Philos. Trans. R. Soc. A 379:20200203. doi: 10.1098/rsta.2020.0203
Marx, V. (2018). Calling cell biologists to try cryo-et. Nat. Methods 15, 575–578. doi: 10.1038/s41592-018-0079-y
Miolane, N., Poitevin, F., Li, Y.-T., and Holmes, S. (2020). “Estimation of orientation and camera parameters from cryo-electron microscopy images with variational autoencoders and generative adversarial networks,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (Remote), 970–971. doi: 10.1109/CVPRW50498.2020.00493
Miyato, T., Kataoka, T., Koyama, M., and Yoshida, Y. (2018). Spectral normalization for generative adversarial networks. arXiv preprint arXiv:1802.05957.
Naeem, M. F., Oh, S. J., Uh, Y., Choi, Y., and Yoo, J. (2020). “Reliable fidelity and diversity metrics for generative models,” in International Conference on Machine Learning (Remote), 7176–7185.
Nie, D., Trullo, R., Lian, J., Petitjean, C., Ruan, S., Wang, Q., et al. (2017). “Medical imag synthesis with context-aware generative adversarial networks,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (Quebec City, QC), 417–425. doi: 10.1007/978-3-319-66179-7_48
Noble, A. J., Dandey, V. P., Wei, H., Brasch, J., Chase, J., Acharya, P., et al. (2018). Routine single particle cryoem sample and grid characterization by tomography. Elife 7:e34257. doi: 10.7554/eLife.34257
Pei, L., Xu, M., Frazier, Z., and Alber, F. (2016). Simulating cryo electron tomograms of crowded cell cytoplasm for assessment of automated particle picking. BMC Bioinformatics 17:405. doi: 10.1186/s12859-016-1283-3
Sajjadi, M. S., Bachem, O., Lucic, M., Bousquet, O., and Gelly, S. (2018). Assessing generative models via precision and recall. arXiv [Preprint] arXiv:1806.00035. doi: 10.5555/3327345.3327249
Salimans, T., Goodfellow, I., Zaremba, W., Cheung, V., Radford, A., and Chen, X. (2016). Improved techniques for training gans. arXiv [Preprint] arXiv:1606.03498. doi: 10.5555/3157096.3157346
Scheres, S. H., Melero, R., Valle, M., and Carazo, J.-M. (2009). Averaging of electron subtomograms and random conical tilt reconstructions through likelihood optimization. Structure 17, 1563–1572. doi: 10.1016/j.str.2009.10.009
Schlemper, J., Yang, G., Ferreira, P., Scott, A., McGill, L.-A., Khalique, Z., et al. (2018). “Stochastic deep compressive sensing for the reconstruction of diffusion tensor cardiac MRI,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (Granada: Springer), 295–303. doi: 10.1007/978-3-030-00928-1_34
Seitzer, M., Yang, G., Schlemper, J., Oktay, O., Würfl, T., Christlein, V., et al. (2018). “Adversarial and perceptual refinement for compressed sensing MRI reconstruction,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (Granada: Springer), 232–240. doi: 10.1007/978-3-030-00928-1_27
Tang, G., Peng, L., Baldwin, P. R., Mann, D. S., Jiang, W., Rees, I., et al. (2007). EMAN2: an extensible image processing suite for electron microscopy. J. Struct. Biol. 157, 38–46. doi: 10.1016/j.jsb.2006.05.009
Wang, C., Dong, S., Zhao, X., Papanastasiou, G., Zhang, H., and Yang, G. (2019). SaliencyGAN: deep learning semisupervised salient object detection in the fog of IOT. IEEE Trans. Indus. Inform. 16, 2667–2676. doi: 10.1109/TII.2019.2945362
Wang, C., Yang, G., Papanastasiou, G., Tsaftaris, S. A., Newby, D. E., Gray, C., et al. (2021). DiCyc: GAN-based deformation invariant cross-domain information fusion for medical image synthesis. Inform. Fus. 67, 147–160. doi: 10.1016/j.inffus.2020.10.015
Wolterink, J. M., Dinkla, A. M., Savenije, M. H., Seevinck, P. R., van den Berg, C. A., and Išgum, I. (2017). “Deep MR to CT synthesis using unpaired data,” in International Workshop on Simulation and Synthesis in Medical Imaging (Quebec City, QC), 14–23. doi: 10.1007/978-3-319-68127-6_2
Xu, M., and Alber, F. (2011). “Gradient-based high precision alignment of cryo-electron subtomograms,” in 2011 IEEE International Conference on Systems Biology (ISB) (Zhuhai), 279–284. doi: 10.1109/ISB.2011.6033166
Xu, M., and Alber, F. (2012). High precision alignment of cryo-electron subtomograms through gradient-based parallel optimization. BMC Syst. Biol. 6:S18. doi: 10.1186/1752-0509-6-S1-S18
Xu, M., Beck, M., and Alber, F. (2012). High-throughput subtomogram alignment and classification by fourier space constrained fast volumetric matching. J. Struct. Biol. 178, 152–164. doi: 10.1016/j.jsb.2012.02.014
Yang, G., Yu, S., Dong, H., Slabaugh, G., Dragotti, P. L., Ye, X., et al. (2017). Dagan: Deep de-aliasing generative adversarial networks for fast compressed sensing MRI reconstruction. IEEE Trans. Med. Imaging 37, 1310–1321. doi: 10.1109/TMI.2017.2785879
Yuan, Z., Jiang, M., Wang, Y., Wei, B., Li, Y., Wang, P., et al. (2020). SARA-GAN: self-attention and relative average discriminator based generative adversarial networks for fast compressed sensing MRI reconstruction. Front. Neuroinform. 14:611666. doi: 10.3389/fninf.2020.611666
Zeng, X., Leung, M. R., Zeev-Ben-Mordehai, T., and Xu, M. (2018). A convolutional autoencoder approach for mining features in cellular electron cryo-tomograms and weakly supervised coarse segmentation. J. Struct. Biol. 202, 150–160. doi: 10.1016/j.jsb.2017.12.015
Zhao, H., Li, H., and Cheng, L. (2017). Synthesizing filamentary structured images with GANs. arXiv preprint arXiv:1706.02185.
Keywords: Cryo-ET, image synthesis, image translation, generative model, generative adversarial network
Citation: Wu X, Li C, Zeng X, Wei H, Deng H-W, Zhang J and Xu M (2022) CryoETGAN: Cryo-Electron Tomography Image Synthesis via Unpaired Image Translation. Front. Physiol. 13:760404. doi: 10.3389/fphys.2022.760404
Received: 18 August 2021; Accepted: 17 January 2022;
Published: 04 March 2022.
Edited by:
Tetsuya J. Kobayashi, The University of Tokyo, JapanReviewed by:
Guang Yang, Imperial College London, United KingdomCopyright © 2022 Wu, Li, Zeng, Wei, Deng, Zhang and Xu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Min Xu, bXh1MUBjcy5jbXUuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.