
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Physiol. , 06 December 2022
Sec. Exercise Physiology
Volume 13 - 2022 | https://doi.org/10.3389/fphys.2022.1052449
This article is part of the Research Topic Oxygen Delivery:Demand Matching in Exercising Skeletal Muscle View all 7 articles
Objectives: We aimed to quantify the magnitude and time transients of capillary blood flow responses to acute changes in local oxygen concentration ([O2]), and carbon dioxide concentration ([CO2]) in skeletal muscle. Additionally, we sought to quantify the combined response to both low [O2] and high [CO2] to mimic muscle microenvironment changes at the onset of exercise.
Methods: 13 Sprague Dawley rats were anaesthetized, mechanically ventilated, and instrumented with indwelling catheters for systemic monitoring. The extensor digitorum longus muscle was blunt dissected, and reflected over a microfluidic gas exchange chamber in the stage of an inverted microscope. Four O2 challenges, four CO2 challenges, and a combined low O2 (7–2%) and high CO2 (5–10%) challenges were delivered to the surface with simultaneous visualization of capillary blood flow responses. Recordings were made for each challenge over a 1-min baseline period followed by a 2-min step change. The combined challenge employed a 1-min [O2] challenge followed by a 2-min change in [CO2]. Mean data for each sequence were fit using least-squared non-linear exponential models to determine the dynamics of each response.
Results: 7–2% [O2] challenges decreased capillary RBC saturation within 2 s following the step change (46.53 ± 19.56% vs. 48.51 ± 19.02%, p < 0.0001, τ = 1.44 s), increased RBC velocity within 3 s (228.53 ± 190.39 μm/s vs. 235.74 ± 193.52 μm/s, p < 0.0003, τ = 35.54 s) with a 52% peak increase by the end of the challenge, hematocrit and supply rate show similar dynamics. 5–10% [CO2] challenges increased RBC velocity within 2 s following the step change (273.40 ± 218.06 μm/s vs. 276.75 ± 215.94 μm/s, p = 0.007, τ = 79.34s), with a 58% peak increase by the end of the challenge, supply rate and hematocrit show similar dynamics. Combined [O2] and [CO2] challenges resulted in additive responses to all microvascular hemodynamic measures with a 103% peak velocity increase by the end of the collection period. Data for mean responses and exponential fitting parameters are reported for all challenges.
Conclusion: Microvascular level changes in muscle [O2] and [CO2] provoked capillary hemodynamic responses with differing time transients. Simulating exercise via combined [O2] and [CO2] challenges demonstrated the independent and additive nature of local blood flow responses to these agents.
The microcirculation across all tissues is responsible for delivering nutrients, such as oxygen (O2), while simultaneously removing waste products such as carbon dioxide (CO2), produced from aerobic metabolism (Duling & Berne, 1970; Segal, 2005). Accordingly, it has been well established that blood flow within the microcirculation increases to match local oxygen demand in response to hypoxia or elevated oxidative metabolism during exercise (Hudlicka, 1985; Segal, 2005; Jackson et al., 2010). Under resting and moderate exercise conditions, energy is produced in skeletal muscle via oxidative phosphorylation that requires sufficient O2 for production of ATP, while simultaneously producing CO2 as a waste product. There is a significant positive correlation between the rate of increase in blood flow and the calculated muscle O2 uptake (V̇O2) at the onset of exercise (Hughson et al., 1996). Extensive data support the principle that increases in blood flow to working muscle during exercise are directly coupled to oxidative demand for production of ATP through vasomotor responses that promote O2 transport and delivery (Nuutinen et al., 1982). The dynamics of V̇O2 at the onset of exercise, and the accompanying bulk blood flow response, has been a major area of investigation focused on elucidating the limitations to exercise performance, and the underlying mechanisms that govern regional blood flow responses (Murias et al., 2014). At the microvascular level, local changes in arteriolar tone modulate conductance which serves as the key driver of blood flow responses during exercise. Conventional studies that logically employ exercise in humans, or stimulated contractions in animal models, to dynamically increase aerobic muscle metabolism and provoke regional blood flow responses are inherently confounded by a myriad of simultaneous microvascular vasomotor mechanisms. Indeed, multiple metabolic stimuli are integrated within the microcirculation to determine the magnitude and time course of local blood flow (Walløe & Wesche, 1988; Shoemaker and Hughson, 1999; Boushel et al., 2000; Herspring et al., 2008). In the context of exercise, it is difficult to separate the specific contributions that O2 and CO2 concentrations have on blood flow supply and demand matching from other vasoactive metabolites that regulate blood flow.
Microvascular blood flow responses at the onset of exercise result from the cumulative stimulus of multiple vasoactive stimuli and mechanical factors. Within the first 1-2 muscular contractions, blood flow increases precede changes in V̇O2 as measured at the mouth. This sudden increase in blood flow has been attributed to rapid onset vasodilation (Corondilas et al., 1964; Shoemaker and Hughson, 1999; Mihok et al., 2004; VanTeeffelen, 2006; Jackson et al., 2010). Additionally, this increase in blood flow at the arteriolar level increases the shear stress experienced by these vessels, promoting the release of nitric oxide (NO) from the endothelium which stimulates vasodilation in arterioles and feed arteries (Wray et al., 2011). Experimentally it has been shown that the onset of exercise also reduces availability of superoxide, due to an increase in oxygen consumption, leading to an increase in the concentration of NO in the interstitium, resulting in vasodilation (Golub et al., 2014).
Electrically coupled conducted responses have been implicated across multiple levels of microvessels. Changes in electrical potential in both endothelial and vascular smooth muscle cells (VSMC) have been shown to propagate upstream and ultimately modulate arteriolar tone (Cohen et al., 2000; Segal and Jacobs, 2001). Multiple transmembrane channels have been associated with blood flow responses during exercise. Arteriolar VSMC within skeletal muscle depend on Ca2+ influx through voltage-gated Ca2+ channels and release from internal stores through inositol 1,4,5-triphosphate receptors to regulate myogenic tone (Jackson & Boerman, 2018). During muscle contractions, K+ channels located in capillary endothelium are exposed to an accumulation of K+ ions and subsequently transduce a signal resulting in endothelial cell hyperpolarization that is transmitted upstream to stimulate arteriole vasodilation (Jackson, 2017).
Exercise decreases the local availability of O2 in working skeletal muscle, this increase in demand for O2 stimulates an increase in O2 supply for metabolic matching. In exercising muscle, increased aerobic metabolism and a lower capillary SO2 leads to ATP release from red blood cells (RBC), which is believed to trigger a conducted response that travels upstream causing vasodilation of arterioles and subsequently increase blood flow to areas of muscle with decreased O2 availability, thereby matching the high oxygen demand of active skeletal muscle (Jackson, 1987, 2016; Ellis et al., 2012; Ellsworth et al., 2016). An increase in lactate during exercise decreases pH in the muscle; this increase in lactate occurs in heavy exercise, yet muscle blood flow and oxygen uptake increase linearly with work loads (Andersen & Saltin, 1985; Berg et al., 1997). There have been several suggested O2 dependent mechanisms involved for local blood flow regulation in active skeletal muscle; however, mechanisms underlying the response to increased CO2 have yet to be elucidated.
Changing O2 and CO2 concentrations in skeletal muscle during exercise have been shown to elicit local blood flow responses, and several potential mechanisms responsible for these responses have been identified. The release of ATP from RBCs has been shown to elicit an increase in blood flow by dilating upstream arterioles providing support for RBCs as both a sensor and stimulus to regulate oxygen concentration in skeletal muscle. RBCs release ATP when hemoglobin desaturates in response to low oxygen environments such as that found in exercise (Jagger et al., 2001; Ellsworth et al., 2016). Arteriolar smooth muscle cells and endothelial cells have also been demonstrated, in ex vivo studies, to play a role in O2 mediated blood flow responses, however this has not been similarly observed in vivo using intravital microscopy methods (reviewed in Jackson, 2016). Furthermore, during exercise, as aerobic metabolism increases, and the rate of CO2 production increases proportionally with O2 consumption causing elevated tissue partial pressure of carbon dioxide (PCO2). Higher tissue CO2 concentration on its own, and in combination with the resulting decrease in tissue pH, has been shown to provoke vasodilation in striated muscle (Duling, 1973; Charter et al., 2018).
Targeted manipulation of [O2] and [CO2] while simultaneously measuring the resulting capillary blood flow response is possible when coupled with intravital video microscopy and precisely controlled gas conditions. The microcirculation is essential in the transport of O2 from the blood delivering it into tissue while simultaneously removing CO2. Direct manipulation of local O2 and CO2 concentrations has been previously achieved by employing microfluidic gas exchange chambers that can maintain a constant gas partial pressure in the tissue while simultaneously measuring capillary blood flow in skeletal muscle (Ghonaim, 2011; Ghonaim, 2013; Sové 2021). The use of a gas exchange chamber allows dynamic manipulation of [O2] and [CO2] both individually and in combination with one another. Previous work manipulating [O2] and [CO2] have largely focused on steady state flow conditions and as a result, dynamic characterization of capillary level blood flow in response to acute changes in [O2] and [CO2] have yet to be thoroughly described. Characterizing the time course of [O2] and [CO2] mediated microvascular blood flow responses is essential to understanding the broader dynamics of conduit artery flow at the onset of exercise. Furthermore, examining the dynamics of microvascular responses under various conditions can provide mechanistic insights which may be masked by overlapping or redundant mechanisms. In this study, we aim to quantify the magnitude and time transient of capillary blood flow responses to acute changes in local [O2] and [CO2] in skeletal muscle. Additionally, we sought to quantify the additive response to both [O2] and [CO2] to mimic muscle microenvironment conditions similar to those found following the onset of moderate exercise.
13 male Sprague Dawley rats (170 g–211 g) were obtained from Charles River Laboratories and were allowed to acclimatize in animal care for 1 week before use. Rats were fed Teklad 2018 (Envigo, Indianapolis, IND, United States) standard rodent chow and allowed water ad libitum. All animal protocols were approved by Memorial University Animal Care Committee.
On the day of testing, animals were anesthetized with a 65 mg/kg intraperitoneal injection of sodium pentobarbital (Euthanyl, Bimeda, Cambridge, ON, Canada). Following induction, depth of anesthesia was assessed with palpebral reflex and toe pinch prior to the start of surgery to verify the animal was sufficiently anesthetized. Once in the surgical plane, a rectal temperature probe was inserted to monitor the body temperature of the animal throughout the experiment. Physiological temperatures were maintained between 36–37°C using a heated mat and/or heat lamp as necessary.
The common carotid artery was cannulated to allow continuous monitoring of blood pressure and heart rate (400a Blood Pressure Analyzer, Micro-Med, Louisville, KY, United States). The right jugular vein was cannulated to provide fluid resuscitation (0.5 ml/kg/hr) and maintenance anaesthetic as required. The animal’s heart rate and blood pressure were monitored continuously for variability as well as regular testing the palpebral reflexes and toe pinch to ensure acceptable depth of anaesthesia. Maintenance doses of sodium pentobarbital (22 mg/kg) were administered intravenously when the animal’s mean arterial pressure exceeded 110 mmHg or if the animal responded to adverse stimuli. Animals were tracheotomized and mechanically ventilated (Inspira ASV, Harvard Apparatus, Holliston, MA, United States) with an initial gas mixture of ∼30% O2 and 70% N2. Respiratory rates and volumes were automatically determined by the ventilator’s built in software based on the animal’s weight. The right extensor digitorum longus (EDL), a muscle of the lower hind limb, was blunt dissected and isolated as previously described (Tyml and Budreau, 1991; Fraser et al., 2012). The distal tendon was cut, the muscle was lifted and cleared from the remaining tissue without damaging the feed artery and vein. The EDL muscle was reflected over the gas exchange chamber on the stage of an inverted microscope (IX73, Olympus, Tokyo, Japan). The EDL was fixed under slight tension at approximately in situ length, covered with a polyvinylidene chloride film, bathed in warm saline, and gently compressed with a glass coverslip and microscope slide to isolate the EDL from room air, and to aid in establishing a uniform optical interface that is orthogonal to the incident light path. The animal was allowed to acclimatize on the stage for 30 min following positioning. Following the acclimatization, and with the animal’s body temperature between 36–37°C, an arterial blood sample was collected to measure blood gases (VetScan iSTAT, Abbott Point of Care Inc. Princeton, NJ, United States). Arterial PCO2 and PO2 were maintained within normal physiological range by adjusting ventilation rate and volume as needed prior to data collection.
The microscopy imaging setup was composed of an Olympus IX73 microscope (Olympus, Tokyo, Japan) fitted for transillumination with a 300 W Xenon light source (Lambda LS-30, Sutter Instruments, Novato, CA, United States). A parfocal beam splitter (Optosplit II Bypass, Cairn Research Ltd. Faversham, United Kingdom) directed light through 420 nm (isosbestic wavelength) and 438 nm (oxygen-sensitive) bandpass filters. Simultaneous and parfocal capture of video sequences were recorded for both wavelengths, with each wavelength on separate halves of the camera chip. Video recordings were made at 16 bit depth 2048 × 2048 resolution using a 10× objective (NA 0.40, Olympus, Tokyo, Japan) using an Orca Flash 4.0 v3 scientific digital camera (Hamamatsu, Hamamatsu City, Japan) and controlled by HCImage Live software (Hamamatsu, Hamamatsu City, Japan) on a desktop computer.
To evaluate O2 and CO2 dependence on blood flow in the microcirculation both independently and simultaneously, a series of gas perturbations were imposed on the surface of the EDL muscle in contact with the gas exchange chamber membrane similar to those described previously (Sové et al., 2021). The series of 9 perturbations were conducted on multiple fields of view across the muscle at a focal depth within ∼60 µm of the surface. Each field was recorded during the following four O2 perturbations: 1) 1 min 7% O2 followed by 2 min 12% O2, 2) 1 min 7% O2 followed by 2 min 2% O2, 3) 1 min 12% O2 followed by 2 min of 7% O2, 4) 1 min 2% O2 followed by 2 min of 7% O2. CO2 was maintained at 5% throughout the O2 challenges, N2 made up the balance of the gasses delivered via the exchange chamber. Following completion of O2 challenges, recordings were made during the following four CO2 challenges: 5) 1 min of 5% CO2 then 2 min of 10% CO2, 6) 1 min of 5% CO2 then 2 min of 0% CO2, 7) 1 min of 10% CO2 then 2 min of 5% CO2, and 8) 1 min of 0% CO2 then 2 min of 5% CO2. [O2] was maintained at 7% throughout the duration of the CO2 challenges. The combined perturbation was as follows: 1 min of 7% O2 and 5% CO2, then 1 min of 2% O2 and 5% CO2, and lastly 2 min of 2% O2 and 10% CO2 with N2 being the balance of gasses delivered. Prior to the start of each perturbation the muscle was allowed to equilibrate for 1–2 min at the baseline O2 and CO2 concentrations for the next perturbation. Following the full series of 9 challenges the muscle was allowed to re-equilibrate at 7% [O2] and 5% [CO2] for 10 min prior to repeating the sequence in the next field of view.
Gas perturbations were imposed on the surface of the muscle using a three-dimensionally (3D) printed gas exchange chamber as described previously (Sové et al., 2021). The device in the present study employed an exchange window (5 mm × 3.5 mm) fitted with a 50 µm thick gas permeable membrane fabricated by spin coating polydimethylsiloxane onto a standard glass slide. The assembled device was connected by plastic tubing to a triple-inlet manifold supplied by three computer-controlled mass flow meters (SmartTrak100, Sierra Instruments, Monterey, CA, United States) for each gas channel, with a frequency response of <300 ms. The EDL muscle was placed over the exchange window of the device and isolated from room air as described above. Gas concentrations from the mass flow meters were dynamically controlled by custom MATLAB software allowing changes in O2 and CO2 concentrations to be triggered automatically at the appropriate time and sequence.
Offline analysis was conducted using custom software written in MATLAB (Mathworks, Natick, MA, United States). The software generated mp4 videos of captured sequences and functional images including variance and sum of absolute difference images used to facilitate identification of in-focus vessel segments for analysis (Japee et al., 2004). In focus capillaries with single file RBC flow were semi-automatically selected for analysis and space time images (STIs) were generated at each wavelength as described previously (Ellis et al., 1990, 1992, 2002, 2012; Japee et al., 2004; Ghonaim et al., 2011; Fraser et al., 2012). STIs were analyzed using the custom software package written in MATLAB and 1 second means were calculated from frame-by-frame measurements of velocity, lineal density, RBC supply rate (SR), and RBC oxygen saturation (SO2). Resulting second-by-second means were used for statistical comparisons.
Statistical analysis of the resulting capillary hemodynamic data was completed using Prism (Graphpad, California, United States). Time constants and associated parameters were determined using a mono-exponential non-linear least-squared curve fitting implemented in Prism for O2, CO2, and combined O2 and CO2 challenges, similar to approaches used to quantify V̇O2 kinetics (Tschakovsky et al., 2006). O2 and CO2 responses were fit to the following mono-exponential model:
where Y(t) is the response over time, Yb is the magnitude at baseline, X0 is the time delay, Y0 is the asymptotic amplitude of the response, and τ is the time constant representing the time to reach 63% of the full response. Combined O2 and CO2 responses were fit to a multi-exponential model as follows:
where Y(t) is the response over time, Yb is the magnitude at baseline, X1 is the time delay, Y1 is the amplitude of the response to O2, τ1 is the time constant for the O2 response, Y2 is the amplitude of the CO2 response, X2 is the time delay, and τ2 is the time constant for the CO2 response. Repeated measures one-way ANOVA (using a mixed effects model to account for missing values) and Dunnett’s multiple comparisons were used to evaluate differences in the baseline period and the second-by-second mean responses following gas changes in the 3- and 4-min challenges. A p-value of <0.05 was considered significant. Mean and standard deviation are reported unless otherwise noted.
Animal weight and systemic physiological animal monitoring data are shown in Table 1. Animal weights were measured immediately prior to the experiment. Reported mean arterial, systolic, and diastolic blood pressures represent the values recorded from the start of the capturing protocol and therefore include periods immediately following administration of anaesthetic. Mechanical ventilation respiratory rate and stroke volume are reported in Table 1. Arterial blood gasses are listed in Table 1.
On-transient O2 mediated flow responses were measured during the 1-min baseline period at 7% [O2] followed by 12% high and 2% low O2 challenges for the remaining 2 min with a constant 5% [CO2] throughout the sequence. Off-transient flow responses were measured over 1-min periods of 12% (high), and 2% (low) chamber [O2] followed by 2 min of baseline 7% [O2]. Modeled parameters determined by non-linear least-squared fitting to mono-exponential curves for hemodynamic and capillary RBC SO2 following oxygen perturbation curves are listed in Table 2, stable exponential fits were determined for each hemodynamic and saturation measure in response to the O2 challenges.
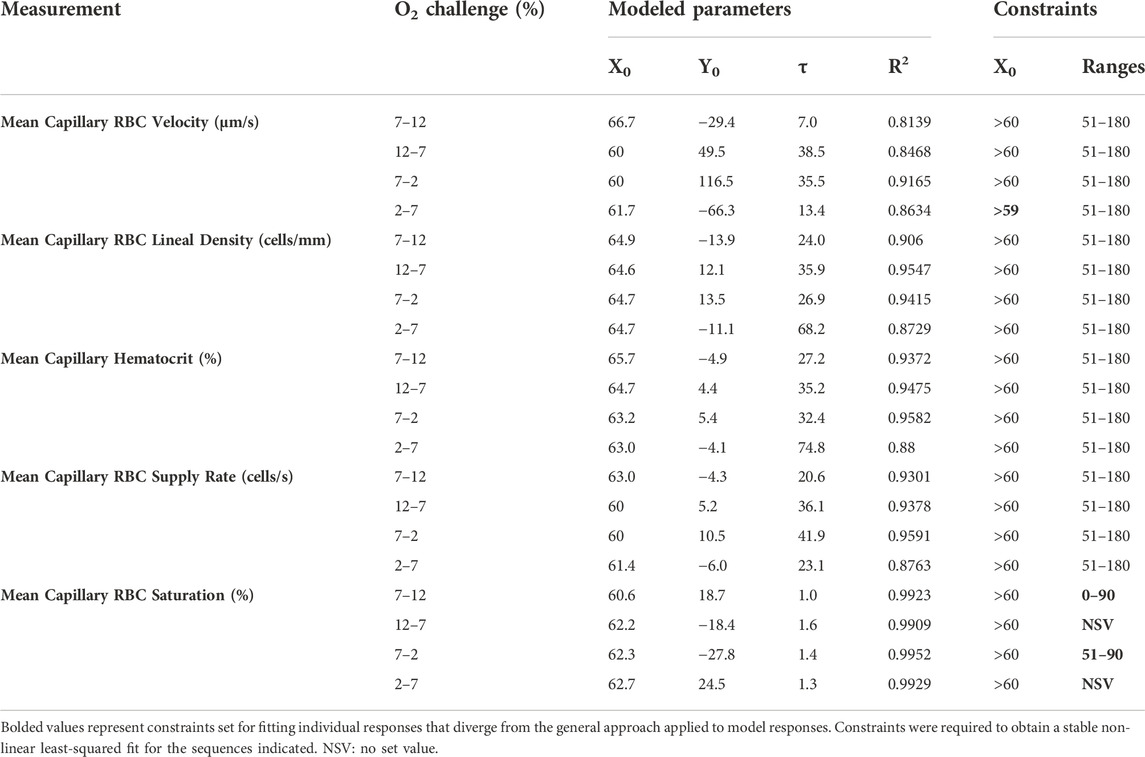
TABLE 2. Parameters and constraints for mono-exponential non-linear least squared fit modeling of oxygen challenge responses.
Increases in [O2] from 2–7% and 7–12% caused significant increases in RBC SO2 within 2 s of the step change, compared to the respective baseline periods (Table 3; Figures 1A,D). Significant decreases in RBC velocity, lineal density, capillary hematocrit, and RBC supply rate, were observed in response to increased [O2] (Table 3; Figures 2–5). Capillary RBC velocity decreased by 66 s following the 2–7% change in [O2]; whereas lineal density did not show significantly decreases until 79 s (Table 3; Figures 2–5). Decreasing [O2] from 12 to 7% and 7 to 2% resulted in significant decreases in RBC SO2 by 62 s after the step change in [O2] (Table 3; Figures 1B,C). Significant increases in all measured hemodynamic parameters were observed within 18 s following the decrease in [O2] (Table 3; Figures 2–5). Changes in RBC SO2 in response to increased [O2] from 7 to 12%, yielded the fastest time transient (τ = 1.009 s), while the slowest time constant was observed with capillary hematocrit in response to increases in [O2] from 2—7% (τ = 74.75 s). Time constants were fastest for saturation changes and slowest for lineal density and capillary hematocrit responses.
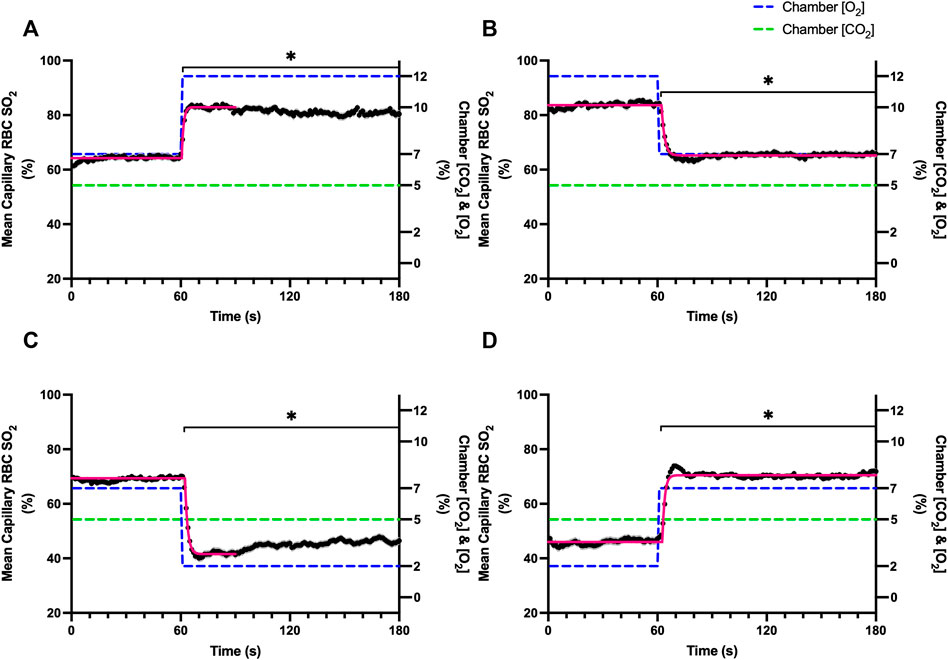
FIGURE 1. Mean capillary red blood cell oxygen saturation in response to O2 challenges. Second-by-second capillary red blood cell (RBC) oxygen saturation (SO2) measurements were made from intravital video microscopy of rat skeletal muscle microcirculation, recorded during four different stepwise O2 challenges. Each oxygen challenge began with a 1-min baseline period where chamber O2 concentration ([O2]) was set to a low (2%), normal (7%), or high (12%) concentration as the initial [O2]. Following the baseline period, the chamber [O2] was abruptly changed to the concentration of interest for the remaining 2-min so that hemodynamic responses could be quantified. The regime of [O2] challenges were 7–12% (A), 12–7% (B), 7–2% (C), and 2–7% (D) with a steady 5% [CO2] and the balance of the gas mixture being composed of N2. The mean SO2 at each time point consists of all capillaries measured during a given challenge, with the shaded region representing the standard error of the mean. Resulting mean responses were modeled to a mono-exponential using established non-linear least squared fitting methods to aid in describing the dynamics of responses. Time constants (τ) for each SO2 response were 1.01 s (Panel A, n = 167), 1.44 s (Panel B, n = 168), 1.64 s (Panel C, n = 221) and 1.27 s (Panel D, n = 214). A repeated measures one-way ANOVA (using a mixed effects model to account for missing values) was used to compare the last 10 s of the baseline period to the second-by-second mean responses following the step-change, the Dunnett’s multiple comparisons test was used. p < 0.05 (*) were considered to be significant.
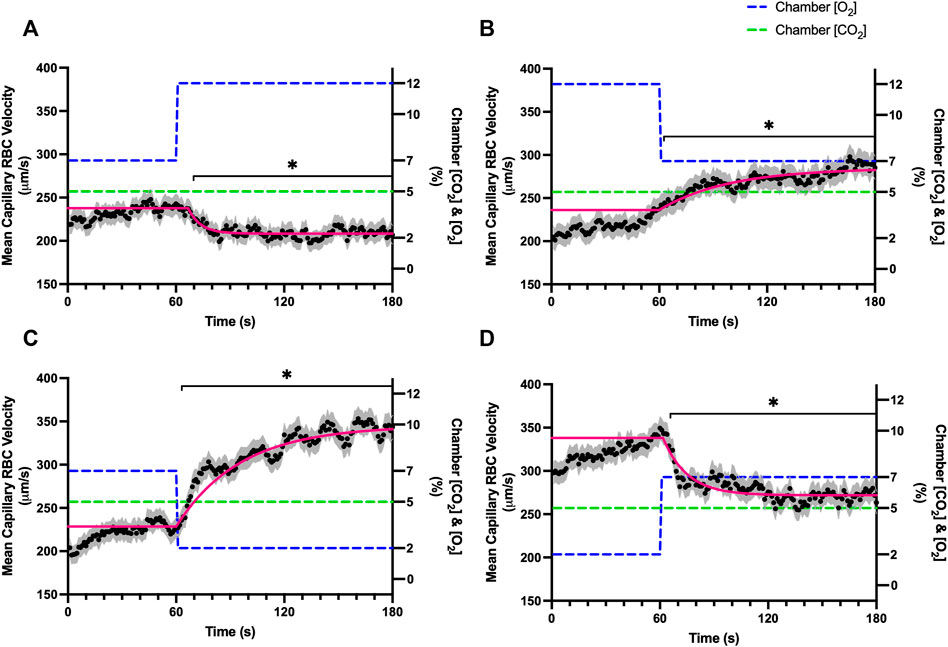
FIGURE 2. Mean capillary red blood cell velocity in response to O2 challenges. Second-by-second capillary red blood cell (RBC) velocity measurements were made from intravital video microscopy of rat skeletal muscle microcirculation, recorded during four different stepwise O2 challenges. Each oxygen challenge began with a 1-min baseline period where chamber O2 concentration ([O2]) was set to a low (2%), normal (7%), or high (12%) concentration as the initial [O2]. Following the baseline period, the chamber [O2] was abruptly changed to the concentration of interest for the remaining 2-min so that hemodynamic responses could be quantified. The regime of [O2] challenges were 7–12% (A), 12–7% (B), 7–2% (C), and 2–7% (D) with a steady 5% [CO2] and the balance of the gas mixture being composed of N2. The mean velocity at each time point consists of all capillaries measured for a given challenge, with the shaded region representing the standard error of the mean. Resulting mean responses were modeled to a mono-exponential using established non-linear least squared fitting methods to aid in describing the dynamics of responses. Time constants (τ) for each velocity response were 6.96 s (Panel A, n = 272 capillaries), 35.54 s (Panel B, n = 294), 38.54 s (Panel C, n = 300) and 13.36 s (Panel D, n = 293). A repeated measures one-way ANOVA (using a mixed effects model to account for missing values) was used to compare the last 10s of the baseline period to the second-by-second mean responses following the step-change, the Dunnett’s multiple comparisons test was used. p < 0.05 (*) were considered to be significant.
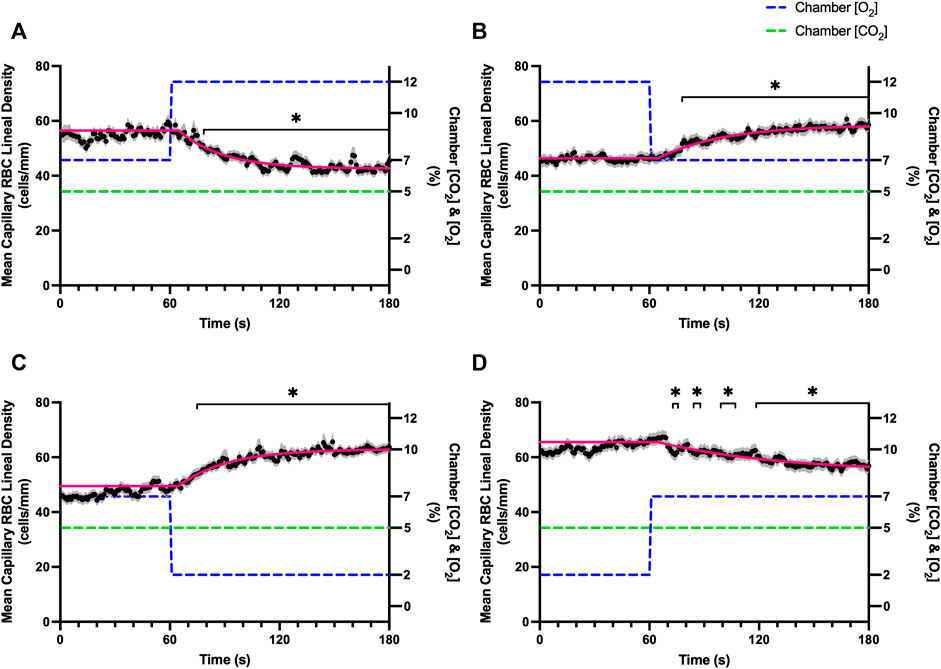
FIGURE 3. Mean capillary red blood cell lineal density in response to O2 challenges. Second-by-second capillary red blood cell (RBC) lineal density (LD) measurements were made from intravital video microscopy of rat skeletal muscle microcirculation, recorded during four different stepwise O2 challenges. Each oxygen challenge began with a 1-min baseline period where chamber O2 concentration ([O2]) was set to a low (2%), normal (7%), or high (12%) concentration as the initial [O2]. Following the baseline period, the chamber [O2] was abruptly changed to the concentration of interest for the remaining 2-min so that hemodynamic responses could be quantified. The regime of [O2] challenges were 7–12% (A), 12–7% (B), 7–2% (C), and 2–7% (D) with a steady 5% [CO2] and the balance of the gas mixture being composed of N2. The mean LD at each time point consists of all capillaries measured during a given challenge, with the shaded region representing the standard error of the mean. Resulting mean responses were modeled to a mono-exponential using established non-linear least squared fitting methods to aid in describing the dynamics of responses. Time constants (τ) for each LD response were 24.03 s (Panel A, n = 279), 26.93 s (Panel B, n = 298), 35.93 s (Panel C, n = 305) and 68.24 s (Panel D, n = 294). A repeated measures one-way ANOVA (using a mixed effects model to account for missing values) was used to compare the last 10 s of the baseline period to the second-by-second mean responses following the step-change, the Dunnett’s multiple comparisons test was used. p < 0.05 (*) were considered to be significant.
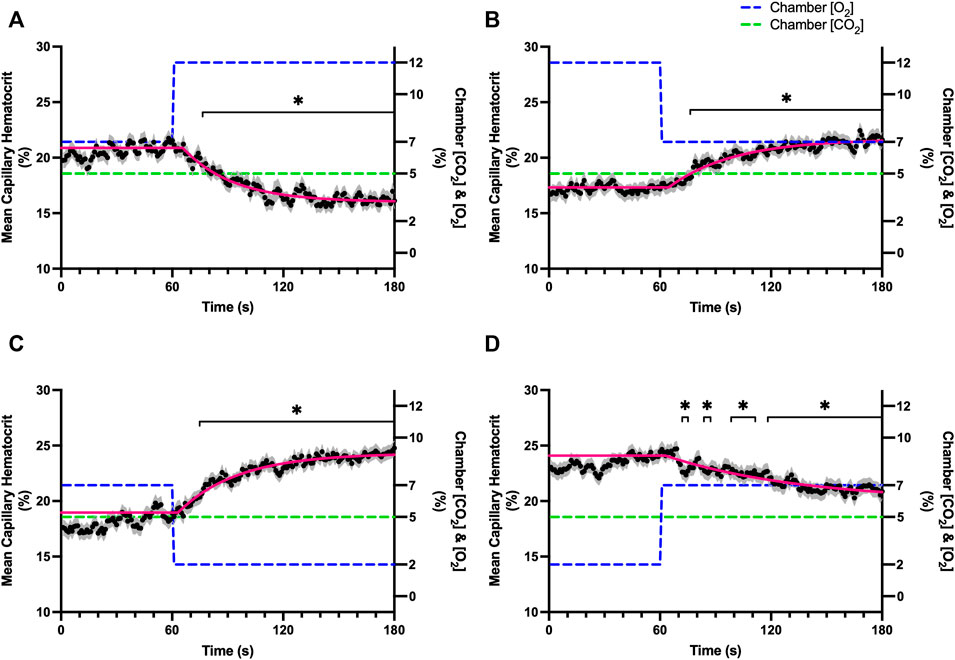
FIGURE 4. Mean capillary red blood cell hematocrit in response to O2 challenges. Second-by-second capillary red blood cell (RBC) hematocrit measurements were made from intravital video microscopy of rat skeletal muscle microcirculation, recorded during four different stepwise O2 challenges. Each oxygen challenge began with a 1-min baseline period where chamber O2 concentration ([O2]) was set to a low (2%), normal (7%), or high (12%) concentration as the initial [O2]. Following the baseline period, the chamber [O2] was abruptly changed to the concentration of interest for the remaining 2-min so that hemodynamic responses could be quantified. The regime of [O2] challenges were 7–12% (A), 12–7% (B), 7–2% (C), and 2–7% (D) with a steady 5% [CO2] and the balance of the gas mixture being composed of N2. The mean hematocrit at each time point consists of all capillaries measured during a given challenge, with the shaded region representing the standard error of the mean. Resulting mean responses were modeled to a mono-exponential using established non-linear least squared fitting methods to aid in describing the dynamics of responses. Time constants (τ) for each hematocrit response were 27.19 s (Panel A, n = 278), 32.42 s (Panel B, n = 298), 35.21 s (Panel C, n = 305) and 74.75 s (Panel D, n = 294). A repeated measures one-way ANOVA (using a mixed effects model to account for missing values) was used to compare the last 10 s of the baseline period to the second-by-second mean responses following the step-change, the Dunnett’s multiple comparisons test was used. p < 0.05 (*) were considered to be significant.
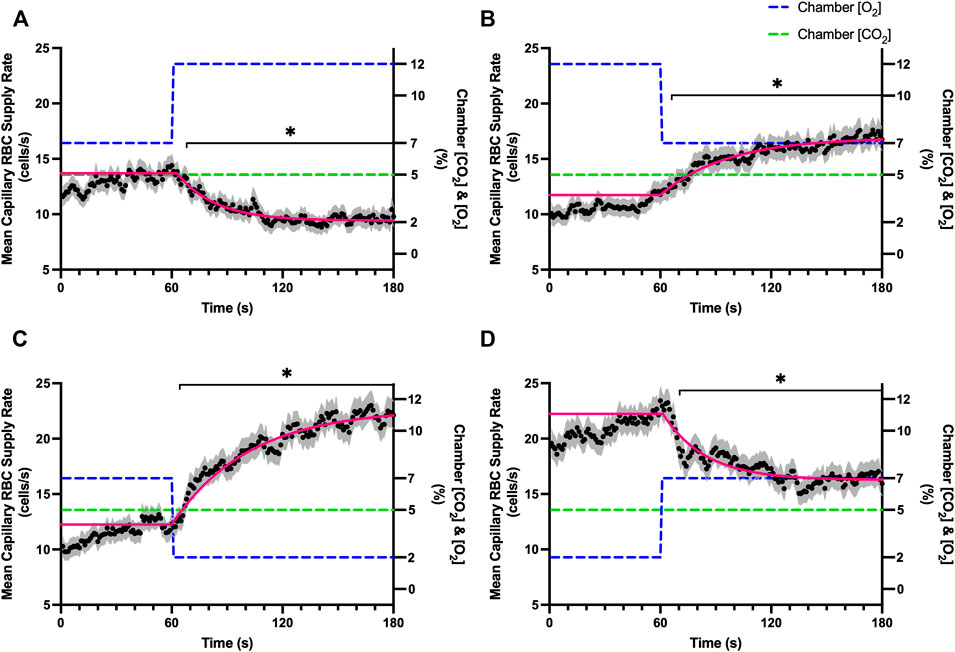
FIGURE 5. Mean capillary red blood cell supply rate in response to O2 challenges. Second-by-second capillary red blood cell (RBC) supply rate (SR) measurements were made from intravital video microscopy of rat skeletal muscle microcirculation, recorded during four different stepwise O2 challenges. Each oxygen challenge began with a 1-min baseline period where chamber O2 concentration ([O2]) was set to a low (2%), normal (7%), or high (12%) concentration as the initial [O2]. Following the baseline period, the chamber [O2] was abruptly changed to the concentration of interest for the remaining 2-min so that hemodynamic responses could be quantified. The regime of [O2] challenges were 7–12% (A), 12–7% (B), 7–2% (C), and 2–7% (D) with a steady 5% [CO2] and the balance of the gas mixture being composed of N2. The mean SR at each time point consists of all capillaries measured during a given challenge, with the shaded region representing the standard error of the mean. Resulting mean responses were modeled to a mono-exponential using established non-linear least squared fitting methods to aid in describing the dynamics of responses. Time constants (τ) for each SR response were 20.61 s (Panel A, n = 278), 41.87 s (Panel B, n = 298), 36.06 s (Panel C, n = 304) and 23.07 s (Panel D, n = 294). A repeated measures one-way ANOVA (using a mixed effects model to account for missing values) was used to compare the last 10s of the baseline period to the second-by-second mean responses following the step-change, the Dunnett’s multiple comparisons test was used. p < 0.05 (*) were considered to be significant.
On-transient CO2 mediated flow responses were measured during the 1-min baseline period at 5% followed by 0% low and 10% high [CO2] challenge for the remaining 2 min with stable 7% [O2] throughout. Off-transient challenges were measured by 1-min periods of 0% low and 10% high CO2 with sequential change to 5% CO2. Parameters defined for mono-exponential non-linear least squared fitting of CO2 perturbation curves are listed in Table 4.

TABLE 4. Parameters and constraints for mono-exponential non-linear least squared fit modeling of carbon dioxide challenge responses.
Reducing [CO2] from 5 to 0% and 10 to 5% lead to significant increases in RBC SO2 within 2 s compared to 51–60 s baseline period in both challenges (Table 5; Figures 6A,D). RBC velocity and RBC supply rate significantly decreased within 17 s of the step decrease in [CO2] (Figures 7A,D, 10A,D, respectively). Lineal density and capillary hematocrit were significantly decreased by 6 s after [CO2] was decreased from 5 to 0% (Figures 8A, 9A); however, lineal density and hematocrit did not significantly change in response to the 10–5% challenge (Figures 8D, 9D). Red blood cell SO2 significantly decreased in response to increased [CO2] both from 0 to 5% and 5–10% within 17 s following the change in [CO2] (Table 5; Figures 6B,C). There were significant increases in RBC velocity, lineal density, hematocrit, and RBC supply rate in response to increased [CO2] (Table 5; Figures 7–10). Increases in hemodynamic measurements occurred between 62 and 80 s following the change in gas conditions. The time constants for SO2 changes were among the fastest with tau ranging from 0.38 s to 5.3 s. The increased [CO2] from 5—10% resulted in the longest time constants for hemodynamic changes (τ = 30.3 s–88.1 s).
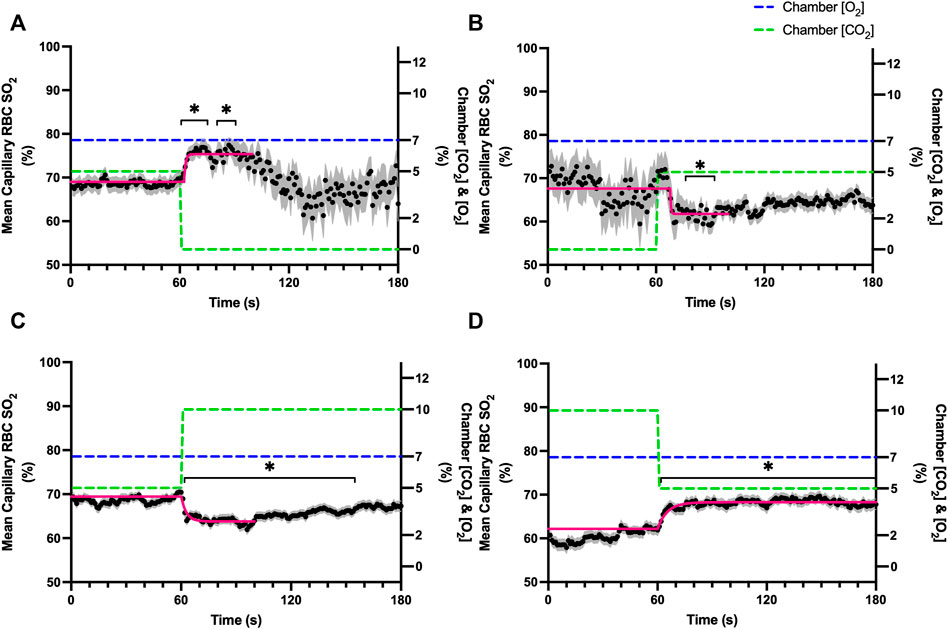
FIGURE 6. Mean capillary red blood cell oxygen saturation in response to CO2 challenges. Second-by-second capillary red blood cell (RBC) oxygen saturation (SO2) measurements were made from intravital video microscopy of rat skeletal muscle microcirculation, recorded during four different stepwise CO2 challenges. Each CO2 challenge began with a 1-min baseline period where chamber CO2 concentration ([CO2]) was set to a low (0%), normal (5%), or high (10%) concentration as the initial [CO2]. Following the baseline period, the chamber [CO2] was abruptly changed to the concentration of interest for the remaining 2-min so that hemodynamic responses could be quantified. The regime of [CO2] challenges were 5–0% (A), 0–5% (B), 5–10% (C), and 10–5% (D) with a steady 7% [O2] and the balance of the gas mixture being composed of N2. The mean SO2 at each time point consists of all capillaries measured during a given challenge, with the shaded region representing the standard error of the mean. Resulting mean responses were modeled to a mono-exponential using established non-linear least squared fitting methods to aid in describing the dynamics of responses. Time constants (τ) for each SO2 response were 0.84 s (Panel A, n = 82), 0.38 s (Panel B, n = 90), 2.887 s (Panel C, n = 197) and 5.339 s (Panel D, n = 183). A repeated measures one-way ANOVA (using a mixed effects model to account for missing values) was used to compare the last 10s of the baseline period to the second-by-second mean responses following the step-change, the Dunnett’s multiple comparisons test was used. p < 0.05 (*) were considered to be significant.
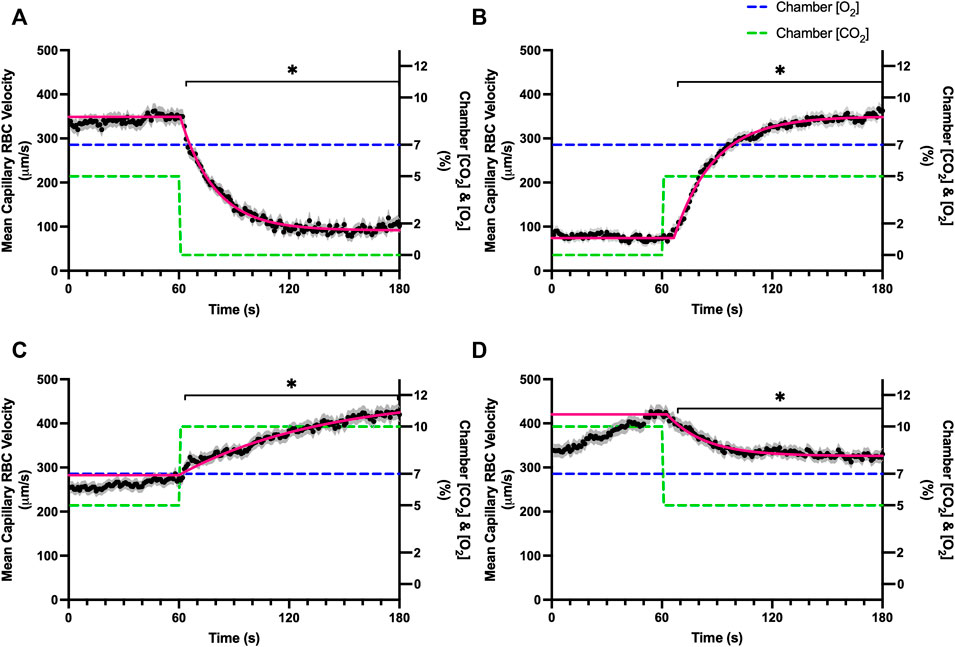
FIGURE 7. Mean capillary red blood cell velocity in response to CO2 challenges. Second-by-second capillary red blood cell (RBC) velocity measurements were made from intravital video microscopy of rat skeletal muscle microcirculation, recorded during four different stepwise CO2 challenges. Each CO2 challenge began with a 1-min baseline period where chamber CO2 concentration ([CO2]) was set to a low (0%), normal (5%), or high (10%) concentration as the initial [CO2]. Following the baseline period, the chamber [CO2] was abruptly changed to the concentration of interest for the remaining 2-min so that hemodynamic responses could be quantified. The regime of [CO2] challenges were 5–0% (A), 0–5% (B), 5–10% (C), and 10–5% (D) with a steady 7% [O2] and the balance of the gas mixture being composed of N2. The mean velocity at each time point consists of all capillaries measured during a given challenge, with the shaded region representing the standard error of the mean. Resulting mean responses were modeled to a mono-exponential using established non-linear least squared fitting methods to aid in describing the dynamics of responses. Time constants (τ) for each velocity response were 18.88 s (Panel A, n = 245), 21.79 s (Panel B, n = 242), 79.34 s (Panel C, n = 288) and 20.66 s (Panel D, n = 285). A repeated measures one-way ANOVA (using a mixed effects model to account for missing values) was used to compare the last 10s of the baseline period to the second-by-second mean responses following the step-change, the Dunnett’s multiple comparisons test was used. p < 0.05 (*) were considered to be significant.
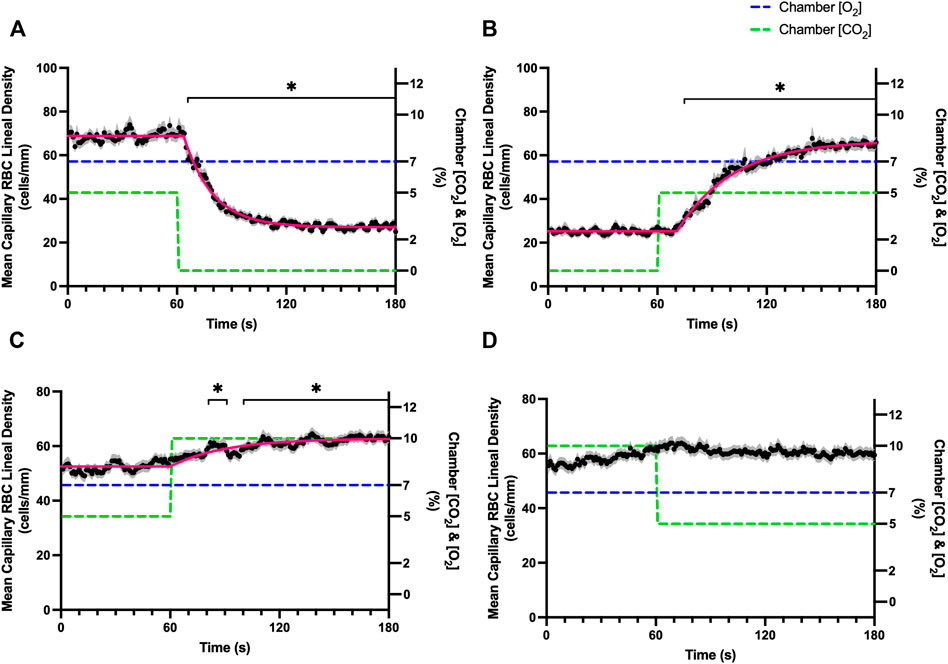
FIGURE 8. Mean capillary red blood cell lineal density in response to CO2 challenges. Second-by-second capillary red blood cell (RBC) lineal density (LD) measurements were made from intravital video microscopy of rat skeletal muscle microcirculation, recorded during four different stepwise CO2 challenges. Each CO2 challenge began with a 1-min baseline period where chamber CO2 concentration ([CO2]) was set to a low (0%), normal (5%), or high (10%) concentration as the initial ([CO2]). Following the baseline period, the chamber [CO2] was abruptly changed to the concentration of interest for the remaining 2-min so that hemodynamic responses could be quantified. The regime of [CO2] challenges were 5–0% (A), 0–5% (B), 5–10% (C), and 10–5% (D) with a steady 7% [O2] and the balance of the gas mixture being composed of N2. The mean LD at each time point consists of all capillaries measured during a given challenge, with the shaded region representing the standard error of the mean. Resulting mean responses were modeled to a mono-exponential using established non-linear least squared fitting methods to aid in describing the dynamics of responses. Time constants (τ) for each LD response were 15.89 s (Panel A, n = 255), 30.63 s (Panel B, n = 246) and 30.31 s (Panel C, n = 292); there was no time constant for 10–5% (Panel D, n = 289). A repeated measures one-way ANOVA (using a mixed effects model to account for missing values) was used to compare the last 10 s of the baseline period to the second-by-second mean responses following the step-change, the Dunnett’s multiple comparisons test was used. p < 0.05 (*) were considered to be significant.
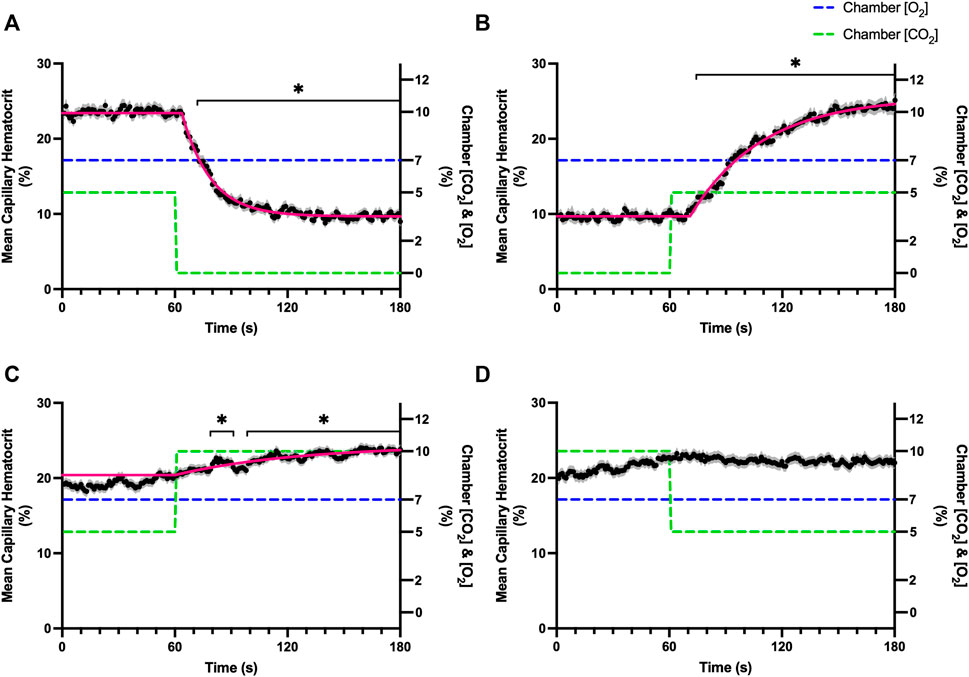
FIGURE 9. Mean capillary red blood cell hematocrit in response to CO2 challenges. Second-by-second capillary red blood cell (RBC) hematocrit measurements were made from intravital video microscopy of rat skeletal muscle microcirculation, recorded during four different stepwise CO2 challenges. Each CO2 challenge began with a 1-min baseline period where chamber CO2 concentration ([CO2]) was set to a low (0%), normal (5%), or high (10%) concentration as the initial ([CO2]). Following the baseline period, the chamber ([CO2]) was abruptly changed to the concentration of interest for the remaining 2-min so that hemodynamic responses could be quantified. The regime of ([CO2]) challenges were 5–0% (A), 0–5% (B), 5–10% (C), and 10–5% (D) with a steady 7% [O2] and the balance of the gas mixture being composed of N2. The mean hematocrit at each time point consists of all capillaries measured during a given challenge, with the shaded region representing the standard error of the mean. Resulting mean responses were modeled to a mono-exponential using established non-linear least squared fitting methods to aid in describing the dynamics of responses. Time constants (τ) for each hematocrit response were 15.27 s (Panel A, n = 250), 38.50 s (Panel B, n = 248) and 65.94 s (Panel C, n = 292); there was no time constant for 10–5% ([CO2]) (Panel D, n = 289). A repeated measures one-way ANOVA (using a mixed effects model to account for missing values) was used to compare the last 10s of the baseline period to the second-by-second mean responses following the step-change, the Dunnett’s multiple comparisons test was used. p < 0.05 (*) were considered to be significant.
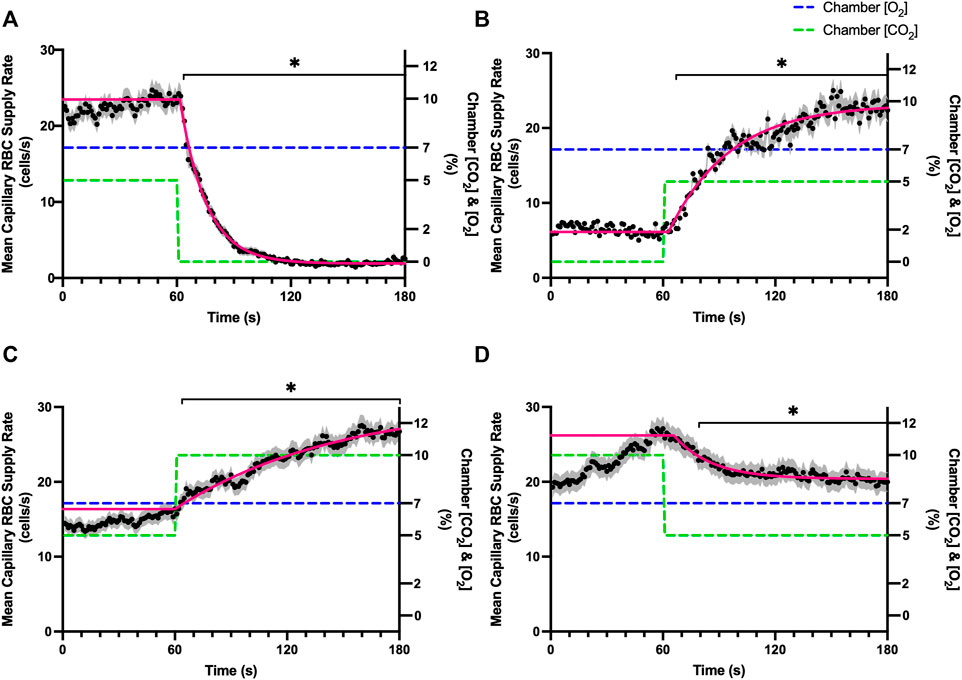
FIGURE 10. Mean capillary red blood cell supply rate in response to CO2 challenges. Second-by-second capillary red blood cell (RBC) supply rate (SR) measurements were made from intravital video microscopy of rat skeletal muscle microcirculation, recorded during four different stepwise CO2 challenges. Each CO2 challenge began with a 1-min baseline period where chamber CO2 concentration ([CO2]) was set to a low (0%), normal (5%), or high (10%) concentration as the initial ([CO2]). Following the baseline period, the chamber ([CO2]) was abruptly changed to the concentration of interest for the remaining 2-min so that hemodynamic responses could be quantified. The regime of ([CO2]) challenges were 5–0% (A), 0–5% (B), 5–10% (C), and 10–5% (D) with a steady 7% [O2] and the balance of the gas mixture being composed of N2. The mean SR at each time point consists of all capillaries measured during a given challenge, with the shaded region representing the standard error of the mean. Resulting mean responses were modeled to a mono-exponential using established non-linear least squared fitting methods to aid in describing the dynamics of responses. Time constants (τ) for each SR response were 13.84 s (Panel A, n = 250), 32.96 s (Panel B, n = 246), 88.08 s (Panel C, n = 290) and 20.18 s (Panel D, n = 287). A repeated measures one-way ANOVA (using a mixed effects model to account for missing values) was used to compare the last 10 s of the baseline period to the second-by-second mean responses following the step-change, the Dunnett’s multiple comparisons test was used. p < 0.05 (*) were considered to be significant.
Combined O2 and CO2 mediated flow responses were measured during a 4-min challenge. The 4-min sequence consisted of a 1-min baseline period with 7% [O2] and 5% [CO2], followed by a 1-min period with 2% [O2] and 5% [CO2], and lastly a 2-min period with 2% [O2] and 10% [CO2]. Parameters defined by mono-exponential non-linear least squared fitting hemodynamic and oxygen saturation responses to the combined O2 and CO2 perturbation are provided in Table 6. Stable exponential fits were achieved for all hemodynamic and saturation measures in response to the combined challenge.
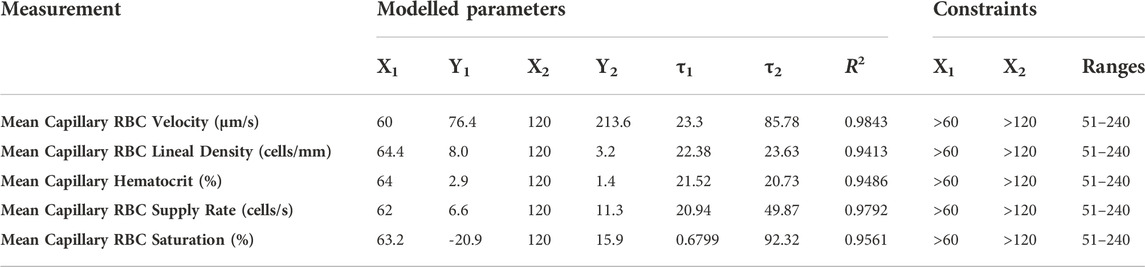
TABLE 6. Parameters and constraints for multi-exponential non-linear least squared fit modeling of combined oxygen and carbon dioxide responses.
A significant decrease in RBC SO2 was observed by 62 s in response to a decrease in gas exchange chamber [O2] from 7–2%; however, this decrease in SO2 was followed by an increase in RBC SO2 at 142 s in response to increased [CO2] from 5–10% compared to the last 10 s of the low O2 period (111–120 s) (Table 7; Figure 11A). The combined challenge caused significant increases in RBC velocity by 67 s following the step change to 2% [O2] compared to the mean of the baseline period between 51–60 s, and subsequently velocity significantly increased by 123 s following the change from 5 to 10% [CO2] when compared to the low O2 period (111–120 s) (Figure 11B). The step change in gas exchange chamber [O2] from 7 to 2% caused significant increases in lineal density and mean capillary hematocrit by 83 s (Figures 11C,D respectively). The [CO2] step change from 5 to 10% during the combined challenge caused significant increases in lineal density by 162 s compared to the 111–120 s time period of the initial [O2] step change (Figure 11C). Similarly, hematocrit significantly increased by 161 s following the change to 10% [CO2] (Figure 11D). Mean capillary RBC SR significantly increased by 68 and 124 s in response to the combined step change in [O2] and [CO2] respectively (Figure 11E).
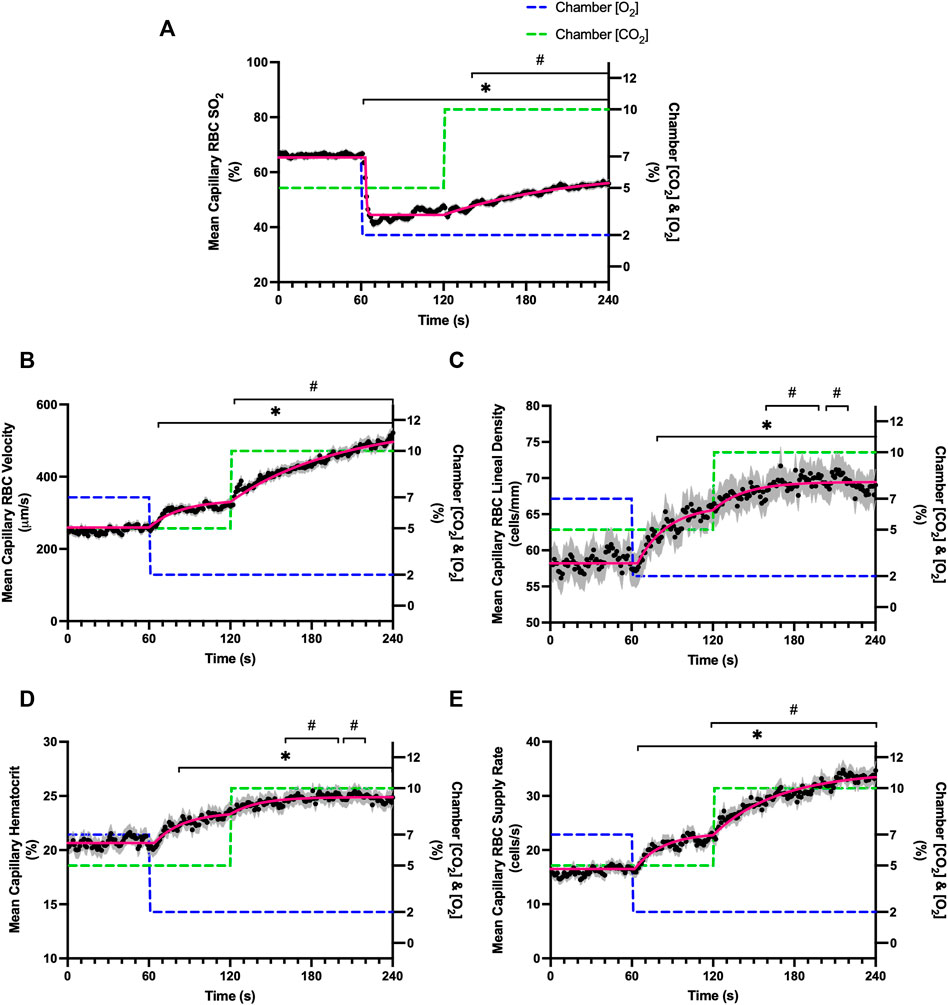
FIGURE 11. Mean hemodynamic measures in responses to combined O2 and CO2 challenges. Second-by-second capillary hemodynamic measurements were made from intravital video microscopy of rat skeletal muscle microcirculation, recorded during a 4-min combined O2 and CO2 stepwise challenge. For O2, the chamber O2 concentration ([O2]) was set to baseline 7% for 1-min, then decreased to 2% [O2] for the remaining 3 min. For CO2 concentrations ([CO2]), a 5% baseline period was set for 2 min, then [CO2] increased to 10% for the second 2 min period. During the 4-min sequence, the balance of the gas mixture was composed of N2. The hemodynamic parameters quantified were red blood cell (RBC) oxygen saturation (SO2) (A), RBC velocity (B), lineal density (LD) (C), hematocrit (D), and RBC supply rate (SR) (E). Each time point consists of all capillaries measured during the combined challenge, with the shaded region representing the standard error of the mean. Resulting mean responses were modeled to a mono-exponential using established non-linear least squared fitting methods to aid in describing the dynamics of responses. Time constants (τ) for each O2 response were 23.30 s (Panel A, n = 286 capillaries), 22.38 s (Panel B, n = 292), 21.52 s (Panel C, n = 292), 20.94 s (Panel D, n = 291) and 0.68 s (Panel E, n = 193). Time constants (τ) for each CO2 response were 85.78 s (Panel A), 23.63 s (Panel B), 20.73 s (Panel C), 49.87 s (Panel D) and 92.32 s (Panel E). A repeated measures one-way ANOVA (using a mixed effects model to account for missing values) was used to compare the 51–60 s of the baseline period and the 111–120 s period to the second-by-second mean responses following the O2 and CO2 step-change, respectively, and the Dunnett’s multiple comparisons test was used. *: p < 0.05, compared to 51–60 s #: p < 0.05, compared to 111–120 s.
The dynamics of V̇O2 uptake at the onset of exercise is coupled to the increased oxidative requirements of working skeletal muscle and the resulting time course of blood flow responses necessary to match oxygen demand (Andersen & Saltin, 1985). Measurements of conduit vessel blood flow during moderate exercise have demonstrated a two-phase blood flow response composed of a fast component attributed to mechanical factors, and a slower second phase driven by multiple agents produced or diminished during elevated aerobic metabolism (Shoemaker and Hughson, 1999; VanTeeffelen and Segal, 2006). While the full contribution of metabolic products to blood flow responses and their underlying mechanisms have not been fully elucidated, oxygen and carbon dioxide have long been understood to have independent vasoactive properties which act in a concentration dependent manner to increase blood supply during exercise. Indeed, there is evidence for multiple mechanisms governing vasoactive responses for both oxygen and carbon dioxide, though there is little data in the literature that describes the dynamics of these mechanisms or the overall time course of the resulting change in blood flow (reviewed in Jackson, 2016). To address this gap in our understanding, we quantified the microvascular blood flow responses to direct step changes in skeletal muscle PO2 and PCO2 in the absence of muscular contractions or other changes in aerobic metabolism. For the purposes of this discussion, we focus primarily on salient responses that are comparable with the decrease in skeletal muscle [O2] and increase in [CO2] seen at the onset of exercise and electrically stimulated contractions.
In this study we manipulated muscle oxygen concentration using a microfluidic gas exchange chamber that was directly interfaced with the EDL muscle via a gas permeable membrane. As expected, step changes in gas exchange chamber [O2] provoked rapid and profound alterations in capillary RBC SO2 that provides essential insight into the dynamics of our experimental method and important context for the resulting capillary blood flow responses (Figure 1). In each of the 4 oxygen challenges employed, significant changes in RBC SO2 were observed within 1–2 s of the step-change within the chamber with times to new steady state SO2 conditions ranging from 5—9 s. It is important to note that the dynamics of this imposed change in SO2 [τ = 1.4 s, for 7–2% (O2) challenge] is much faster than reported fast component decreases in microvascular (τ = 9.0 s) and interstitial (τ = 12.8 s) PO2 at the onset of electrically stimulated contractions using similar rat models (Behnke et al., 2001; Hirai et al., 2018). Step changes in chamber [O2] from 7–2% provoked a 52% peak increase in capillary RBC velocity, an 83% increase in RBC supply rate, and a 30% increase in capillary hematocrit over the course of the 2 min challenge, each of which are remarkably similar to previous observations of capillary hemodynamics during 1 Hz stimulated contractions in rat muscle (Kindig et al., 2002). The determined time transients of capillary RBC velocity (τ = 35.5 s), hematocrit (τ = 32.4 s), and supply rate (τ = 42.0 s) responses to 7–2% [O2] in our model were all of similar time scales and notably slower than responses during muscle contraction, particularly with respect to reported contraction induced supply rate response in animals (τ = 16 s) (Kindig et al., 2002; Poole et al., 2021) and early phase flow response in humans (τ < 7 s) (Shoemaker and Hughson, 1999). The discrepancy in dynamics with our model is almost certainly due to the absence of contraction that drives the early phase of exercise hyperemia via mechanical factors and rapid onset vasodilation (Tschakovsky et al., 1996; Laughlin et al., 1999; Mihok and Murrant, 2004; VanTeeffelen and Segal, 2006). Transient changes in capillary hematocrit in the present study suggest involvement of higher order arterioles that would be capable of affecting downstream hematocrit based on the Fåhræus-Lindqvist effect as also suggested by Kindig et al. (Fåhræus and Lindqvist, 1931; Barbee and Cokelet, 1971; Pries et al., 1986; Kindig et al., 2002). Further, in our model it is also likely that hematocrit and lineal density changes are driven, at least in part, by asymmetries in blood flow distribution between upstream arteriolar branches that supply the muscle volume influenced by our imposed gas perturbations, compared to other regions of the muscle which remain at basal conditions (Pries et al., 1989). Indeed, the hemodynamic changes observed during the 7–2% [O2] challenge likely integrate dilation of multiple levels of the arteriolar tree from terminal arterioles to higher order vessels via conducted signaling (reviewed in Bagher and Segal, 2011).
It is interesting to note that the dynamics of on and off transient responses to 12% and 2% oxygen challenges were not symmetrical, with faster capillary RBC velocity kinetics determined for 7–12% [O2] (τ = 7.0 s) and 2–7% [O2] (τ = 13.4 s) challenges (Table 2). However, the slower velocity dynamics based on the exponential fit to the 7–2% challenge does not describe the apparent multi-exponential nature of the response that includes a fast component evident over the first 20 s of the step change, and followed by a slower component that persists over the remainder of the 2 min challenge (Figure 2C). Similarly, this fast component is visible in the first 20 s of the velocity response to the 2–7% [O2] challenge (Figure 2D) and over the same time period in the 7–2% [O2] portion of the combined [O2] and [CO2] challenge (Figure 11B). The fast component of the velocity response to these challenges supports the role of rapid conducted signaling in oxygen mediated blood flow regulation, and provides further evidence of multiple mechanisms with distinct kinetics that overlap in time to produce the observed response. In contrast, the kinetics of hematocrit and lineal density responses were well represented by mono-exponential fits, and in the case of the 2–7% [O2] challenge showed profoundly slower dynamics (τ = 74.75 s) compared to the velocity response, with hematocrit changes likely driven by higher order arterioles as explained above.
Step changes in the gas exchange chamber [CO2] provoked robust blood flow responses in each of the 4 challenge sequences studied. Increasing [CO2] from the putative resting concentration in the 5–10% challenge resulted in a 58% peak increase in capillary RBC velocity, a 16% increase in capillary hematocrit, and a 63% increase in capillary RBC supply rate which were similar in proportion to the increases seen over 2 min during the 7–2% [O2] challenges. The dynamics of the 5–10% [CO2] capillary hemodynamic responses were markedly slower than other CO2 challenges studied. Capillary RBC velocity (τ = 79.3 s), hematocrit (τ = 65.9), and supply rate (τ = 88.1 s) demonstrated distinctly slower kinetics that were two-fold longer than the oxygen mediated responses in the 7–2% [O2] challenge. Charter et al. reported similarly slow dynamics in vivo in second order cremaster arterioles when exposed to superfusate equilibrated with 5 and 10% CO2 (with measured PCO2 = 43 and 62 mmHg respectively) which showed vasodilation that progressively increased throughout the 2-min observation period at each concentration (Charter et al., 2018). Importantly, micropipette application of buffer equilibrated to the 5 and 10% [CO2] in the same study failed to elicit conducted vasodilation when applied to downstream capillaries or arterioles (Charter et al., 2018). The slow vascular response to high CO2 coupled with the progressive increase in venous PCO2 over the first 4 min of exercise (Casaburi et al., 1989) likely contributes to the slow phase of blood flow responses during this period.
Surprisingly, the strongest responses to step changes in [CO2] were observed in the 5–0% and 0–5% [CO2] challenges. The transition from 5–0% [CO2] provoked a 71% decrease in capillary RBC velocity over the 2 min challenge with a rapid time constant (τ = 18.9 s) both of which were highly symmetrical with the 0–5% [CO2] challenge (Table 4; Figures 7A,B). Interestingly, although the magnitude of capillary hematocrit responses were very similar (Table 4), the time constant for the 0–5% [CO2] challenge was more than two-fold longer (τ = 38.50 s) compared to the 5–0% [CO2] transition (τ = 15.3 s). It is unclear why there is such a discrepancy between the on and off transient dynamics associated with 0% [CO2], though it may be a product of the very low flow state during the first minute of the 0–5% [CO2] challenge. It could be argued that examination of responses to 0% CO2 are non-physiological; however, we expect that tissue PCO2 during these challenges to be non-zero due to the gradient between the gas exchange chamber and the muscle where mean PCO2 at a distance within the muscle volume is assumed to be ∼38 mmHg. Regardless, the profound decrease in blood flow observed under 0% CO2 indicates strong arteriolar reactivity to these conditions, though it is unclear whether or not the underlying mechanisms overlap with vasodilatory pathways at play when tissue [CO2] is increased beyond 5%.
Imposed changes in [CO2] caused a rapid shift in capillary RBC SO2 that serendipitously provides an indirect reference for the time course of tissue [CO2] changes (Figure 6), which followed a similar time scale to those observed when manipulating oxygen with the τ of SO2 changes ranging from 0.8 s in the 5–0% [CO2] challenge to 5.3 s in the transition from 10–5% (Table 4). We expect that this [CO2] dependent change in RBC SO2 reflects a shift in the oxy-hemoglobin dissociation curve caused by allosteric interactions via the Bohr effect that result in conformational changes in hemoglobin molecules associated with both [CO2] and the resulting change in pH. Based on the model by Dash and Bassingthwaighte, in the absence of pH changes we would expect RBC SO2 to only vary by 1% between [CO2] of 0–5%, while a change in [CO2] from 5–10% would be expected to cause a 3% shift in RBC SO2 (Dash and Bassingthwaighte, 2010). By comparison these findings suggest that the observed 5–6% shift in RBC SO2 during CO2 challenges is driven in part by a change in tissue pH. The apparent change in pH is notable as previous work has shown that the vasoactive effects of CO2 are through [CO2] in and of itself, and via the resulting change in [H+] (Charter et al., 2018). Unfortunately, in the current study we lacked the means to measure tissue pH within our muscle preparation, or at the interface with the exchange chamber. Additionally, SO2 measurements were somewhat confounded during 0% [CO2] conditions due to the extremely low RBC supply rates (Figures 10A,B), with many capillaries experiencing close to zero RBC supply. As we maintain the same plane of focus during data acquisition, and our method requires in focus capillaries with flowing RBCs to measure SO2, the low RBC supply rates resulted in higher variability due to the sparse number of SO2 measurements under this 0% [CO2] condition (Figures 6A,B).
In order to study the combined effects of oxygen and carbon dioxide mediated blood flow responses we examined a step change in gas exchange chamber [O2] from 7–2% for 1 minute, followed by an additional step change in chamber [CO2] from 5–10% (Figure 11). Over the minute following the step change in chamber [O2] from 7–2%, peak capillary RBC velocity increased by 25% with similar, though faster, dynamics (τ = 23.3 s) compared to the same step change in the non-combined 7–2% [O2] challenge described above (τ = 35.5 s). Similarly, capillary hematocrit increased by 15% over the 1-min period with somewhat faster dynamics (τ = 21.5 s) compared to the non-combined 7–2% [O2] challenge (τ = 32.42 s). Capillary RBC supply rate increased by 40% over the 7–2% [O2] portion of the combined challenge compared to the baseline period. The addition of a 5–10% [CO2] step change caused a peak increase in capillary RBC velocity by a further 78% above baseline over the 2-min combined challenge. Peak capillary hematocrit response showed a small 9% increase over baseline levels, while capillary RBC supply rate increased a further 76% over baseline by the end of the 5–10% [CO2] portion of the combined challenge. The time constant for the velocity response for the 5–10% [CO2] portion of the combined challenge (τ = 85.8 s) was consistent with the dynamics from the non-combined 5–10% [CO2] challenge (τ = 79.3 s). These findings clearly illustrate that the oxygen and carbon dioxide mediated blood flow responses to challenges that mimic conditions in exercise, are additive and operate with distinctly different dynamics.
Exponential fit for the capillary RBC SO2 changes over the course of the combined challenge following the 7–2% [O2] showed similar rapid dynamics (τ = 0.7 s) to the non-combined 7–2% [O2] challenge (τ = 1.4 s). The 7–2% [O2] step change abruptly reduced capillary RBC SO2 from 66% to a nadir of 41%, similar to that observed during the non-combined 7–2% [O2]. Similarly, as was observed in the non-combined 7–2% [O2] challenge there was an upwards drift in capillary RBC SO2 beginning ∼20 s after the step change that increased mean SO2 to 47%. We expect this partial restoration of capillary RBC SO2 is due to the flow response where increased oxygen supply via higher RBC supply rate partially restores tissue PO2 (Figures 1C, 11A). Furthermore, following the 5–10% [CO2] portion of the combined challenge, SO2 continued to rise to 56% as capillary RBC velocity and supply rate progressively increased over the remainder of the collection period. Again, we expect that this upwards drift in SO2 to reflect a partial restoration of tissue PO2 resulting from increased oxygen supply via the flow response. Interestingly, the rapid drop in SO2 that was noted in the non-combined 5–10% [CO2] challenge that reflects a shift in the oxy-hemoglobin dissociation curve as described above, was not observed during the combined response, perhaps due to the already elevated flow state.
This approach used to study the dynamics of O2 and CO2 as a mimetic for exercise has some limitations. [O2] and [CO2] challenges for each field of view were completed in a fixed sequence as described above in order to limit the apparent hysteresis that was noted during pilot studies that caused an upward drift in basal blood flow state following repeated exposure of the muscle to high [CO2]. While not ideal, this sequence of challenges was deliberately chosen as a means to mitigate the effect of this hysteresis on blood flow responses; future studies could randomize the order of perturbations and limit observations to a single series of challenges per animal. Furthermore, following analysis of our experimental data we noted that in the case of the 10–5% [CO2] challenge, there appears to not have been sufficient time to fully reach steady state during the baseline period at 10% [CO2] (see panel D in Figures 7, 10). Future studies should extend the pre-baseline period to 5 min at the desired gas concentrations to ensure a stable baseline is established. Lastly, these experiments were conducted under resting conditions in anesthetized animals where the muscle was not contracted but rather exposed to precisely controlled gas conditions mimicking the low [O2] and high [CO2] environment that would be expected during exercise. The conditions under which our data were collected, and the absence of muscular contraction should be considered when interpreting our findings in the context of exercise.
In summary, we have provided a thorough quantification of the magnitude and dynamics of oxygen and carbon dioxide mediated blood flow responses in vivo following abrupt step changes in tissue [O2] and [CO2], imposed via a microfluidic gas exchange chamber. Importantly, we demonstrate that in several cases the dynamics of hemodynamic responses in terms of capillary RBC velocity, lineal density, hematocrit, and supply rate that differ in time, show elements of concentration dependence, and in some instances are not symmetrical for on and off transient responses. Furthermore, we clearly show that combined [O2] and [CO2] perturbations elicit additive microvascular hemodynamic responses with each agent contributing different magnitudes and dynamics to the overall change in blood flow. For future studies our method presents an opportunity to study how adaptations in the context of exercise training, aging, and disease models may alter the dynamics of microvascular responses to skeletal muscle [O2] and [CO2]. Finally, our approach can be extended to examine how specific mechanisms contribute to the dynamics of oxygen and carbon dioxide mediated responses, which presents exciting additional avenues for future mechanistic studies.
The data supporting the conclusions of this article will be made available by the authors, without undue reservation.
The animal study was reviewed and approved by the Memorial University of Newfoundland’s Animal Care and Use Committee.
GF conceptualized the study. GRM and BW contributed to experimental design with oversight from GF. GF completed animal surgeries with technical support by GRM, BW, MK, and KK. BW and GRM completed data collection. Data analysis and organization was completed by BW, GF, GRM, KK, and MK. Interpretation of results was completed equally by BW and GRM with support from GF. Preparation of the text was completed by GRM, BW, and GF. All authors provided critical review and approved of the final manuscript.
This work was supported by the Natural Sciences and Engineering Research Council of Canada Discovery grants RGPIN 2017-05205 to GF. NSERC funding supplied resources for experimental materials, equipment, technical support, and trainee stipends. GRM was supported by Memorial University’s President’s Doctoral Student Investment Fund. Publishing fees were supported by Memorial University of Newfoundland’s School of Graduate Studies and the Dean of Medicine Open–Access Publication Fund.
The authors would like to thank MUNMed3D for providing custom 3D printing services. We would also like to thank Meaghan A. McCarthy for her previous work on CO2 step changes which provided us with some initial insights into microvascular reactivity to CO2 in our model.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Andersen P., Saltin B. (1985). Maximal perfusion of skeletal muscle in man. J. Physiol. 366, 233–249. doi:10.1113/jphysiol.1985.sp015794
Bagher P., Segal S. S. (2011). Regulation of blood flow in the microcirculation: Role of conducted vasodilation. Acta Physiol. (Oxf) 202 (3), 271–284. doi:10.1111/j.1748-1716.2010.02244
Barbee J. H., Cokelet G. R. (1971). The Fahraeus effect. Microvasc. Res. 3 (1), 6–16. doi:10.1016/0026-2862(71)90002-1
Behnke B. J., Kindig C. A., Musch T. I., Koga S., Poole D. C. (2001). Dynamics of microvascular oxygen pressure across the rest-exercise transition in rat skeletal muscle. Respir. Physiol. 126 (1), 53–63. doi:10.1016/s0034-5687(01)00195-5
Berg B. R., Cohen K. D., Sarelius I. H. (1997). Direct coupling between blood flow and metabolism at the capillary level in striated muscle. Am. J. Physiol. 272 (6), H2693–H2700. doi:10.1152/ajpheart.1997.272.6.H2693
Boushel R., Langberg H., Olesen J., Nowak M., Simonsen L., Bulow J., et al. (2000). Regional blood flow during exercise in humans measured by near-infrared spectroscopy and indocyanine green. J. Appl. Physiol. 89 (5), 1868–1878. doi:10.1152/jappl.2000.89.5.1868
Casaburi R., Daly J., Hansen J. E., Effros R. M. (1989). Abrupt changes in mixed venous blood gas composition after the onset of exercise. J. Appl. Physiol. 67 (3), 1106–1112. doi:10.1152/jappl.1989.67.3.1106
Charter M. E., Lamb I. R., Murrant C. L. (2018). Arteriolar and capillary responses to CO2 and H+ in hamster skeletal muscle microvasculature: Implications for active hyperemia. Microcirculation 25 (7), e12494. doi:10.1111/micc.12494
Cohen K. D., Berg B. R., Sarelius I. H. (2000). Remote arteriolar dilations in response to muscle contraction under capillaries. Am. J. Physiol. Heart Circ. Physiol. 278 (6), H1916–H1923. doi:10.1152/ajpheart.2000.278.6.H1916
Corcondilas A., Koroxenidis G. T., Shepherd J. T. (1964). Effect of a brief contraction of forearm muscles on forearm blood flow. J. Appl. Physiol. 19, 142–146. doi:10.1152/jappl.1964.19.1.142
Dash R. K., Bassingthwaighte J. B. (2010). Erratum to: Blood HbO2 and HbCO2 dissociation curves at varied O2, CO2, pH, 2,3-DPG and temperature levels. Ann. Biomed. Eng. 38 (4), 1683–1701. doi:10.1007/s10439-010-9948-y
Duling B., Berne R. (1970). Longitudinal gradients in periarteriolar oxygen tension: A possible mechanism for the participation of oxygen in local regulation of blood flow. Circ. Res. 27 (5), 669–678. doi:10.1161/01.res.27.5.669
Duling B. R. (1973). Changes in microvascular diameter and oxygen tension induced by carbon dioxide. Circ. Res. 32 (3), 370–376. doi:10.1161/01.res.32.3.370
Ellis C. G., Ellsworth M. L., Pittman R. N. (1990). Determination of red blood cell oxygenation in vivo by dual video densitometric image analysis. Am. J. Physiol. 258 (4), 1216–1223. doi:10.1152/ajpheart.1990.258.4.H1216
Ellis C. G., Ellsworth M. L., Pittman R. N., Burgess W. L. (1992). Application of image analysis for evaluation of red blood cell dynamics in capillaries. Microvasc. Res. 44 (2), 214–225. doi:10.1016/0026-2862(92)90081-Y
Ellis C. G., Bateman R. M., Sharpe M. D., Sibbald W. J., Gill R. (2002). Effect of a maldistribution of microvascular blood flow on capillary O(2) extraction in sepsis. Am. J. Physiol. Heart Circ. Physiol. 282, H156–H164. doi:10.1152/ajpheart.2002.282.1.h156
Ellis C. G., Milkovich S., Goldman D. (2012). What is the efficiency of ATP signaling from erythrocytes to regulate distribution of O(2) supply within the microvasculature? Microcirculation 19 (5), 440–450. doi:10.1111/j.1549-8719.2012.00196
Ellsworth M. L., Ellis C. G., Sprague R. S. (2016). Role of erythrocyte-released ATP in the regulation of microvascular oxygen supply in skeletal muscle. Acta Physiol. 216 (3), 265–276. doi:10.1111/apha.12596
Fahraeus R., Lindqvist T. (1931). The viscosity of the blood in narrow capillary tubes. Am. J. Physiology-Legacy Content 96 (3), 562–568. doi:10.1152/ajplegacy.1931.96.3.562
Fraser G. M., Milkovich S., Goldman D., Ellis C. G. (2012). Mapping 3-D functional capillary geometry in rat skeletal muscle in vivo. Am. J. Physiol. Heart Circ. Physiol. 302 (3), H654–H664. doi:10.1152/ajpheart.01185.2010
Ghonaim N. W., Fraser G. M., Ellis C. G., Yang J., Goldman D. (2013). Modeling steady state SO2-dependent changes in capillary ATP concentration using novel O2 micro-delivery methods. Front. Physiol. 4, 260. doi:10.3389/fphys.2013.00260
Ghonaim N. W., Lau L. W. M., Goldman D., Ellis C. G., Yang J. (2011). A micro- delivery approach for studying microvascular responses to localized oxygen delivery. Microcirculation 18, 646–654. doi:10.1111/j.1549-8719.2011.00132.x
Golub A. S., Song B. K., Pittman R. N. (2014). Muscle contraction increases interstitial nitric oxide as predicted by a new model of local blood flow regulation. J. Physiol. 592 (6), 1225–1235. doi:10.1113/jphysiol.2013.267302
Herspring K. F., Ferreira L. F., Copp S. W., Snyder B. S., Poole D. C., Musch T. I. (2008). Effects of antioxidants on contracting spinotrapezius muscle microvascular oxygenation and blood flow in aged rats. J. Appl. Physiol. 105 (6), 1889–1896. doi:10.1152/japplphysiol.90642.2008
Hirai D. M., Craig J. C., Colburn T. D., Eshima H., Kano Y., Sexton W. L., et al. (2018). Skeletal muscle microvascular and interstitial PO2 from rest to contractions. J. Physiol. 596 (5), 869–883. doi:10.1113/JP275170
Hughson R. L., Shoemaker J. K., Tschakovsky M. E., Kowalchuk J. M. (1996). Dependence of muscle VO2 on blood flow dynamics at onset of forearm exercise. J. Appl. Physiol. 81 (4), 1619–1626. doi:10.1152/jappl.1996.81.4.1619
Jackson D. N., Moore A. W., Segal S. S. (2010). Blunting of rapid onset vasodilatation and blood flow restriction in arterioles of exercising skeletal muscle with ageing in male mice. J. Physiol. 588 (12), 2269–2282. doi:10.1113/jphysiol.2010.189811
Jackson W. F. (2016). Arteriolar oxygen reactivity: Where is the sensor and what is the mechanism of action? J. Physiol. 594 (18), 5055–5077. doi:10.1113/JP270192
Jackson W. F. (1987). Arteriolar oxygen reactivity: Where is the sensor? Am. J. Physiol. 253, H1120–H1126. doi:10.1152/ajpheart.1987.253.5.H1120
Jackson W. F., Boerman E. M. (2018). Voltage-gated Ca2+ channel activity modulates smooth muscle cell calcium waves in hamster cremaster arterioles. Am. J. Physiol. Heart Circ. Physiol. 315, H871–H878. doi:10.1152/ajpheart.00292.2018
Jackson W. F. (2017). Boosting the signal: Endothelial inward rectifier K+ channels. Microcirculation 24 (3). doi:10.1111/micc.12319doi:e12319
Jagger J. E., Bateman R. M., Ellsworth M. L., Ellis C. G. (2001). Role of erythrocyte in regulating local O2 delivery mediated by hemoglobin oxygenation. Am. J. Physiol. Heart Circ. Physiol. 280 (6), H2833–H2839. doi:10.1152/ajpheart.2001.280.6.H2833
Japee S. A., Ellis C. G., Pittman R. N. (2004). Flow visualization tools for image analysis of capillary networks. Microcirculation 11, 39–54. doi:10.1080/10739680490266171
Kindig C. A., Richardson T. E., Poole D. C. (2002)., 92. Bethesda, Md, 2513–2520. doi:10.1152/japplphysiol.01222.2001Skeletal muscle capillary hemodynamics from rest to contractions: Implications for oxygen transferJ. Appl. Physiol.6
Laughlin M. H. (1999). Cardiovascular response to exercise. Am. J. Physiol. 277 (6), S244–S259. doi:10.1152/advances.1999.277.6.S244
Mihok M. L., Murrant C. L. (2004). Rapid biphasic arteriolar dilations induced by skeletal muscle contraction are dependent on stimulation characteristics. Can. J. Physiol. Pharmacol. 82 (4), 282–287. doi:10.1139/y04-016
MuriasSpencer M. D., Paterson D. H. (2014). The critical role of O2 provision in the dynamic adjustment of oxidative phosphorylation. Exerc. Sport Sci. Rev. 42 (1), 4–11. doi:10.1249/JES.0000000000000005
Nuutinen E. M., Nishiki K., Erecińska M., Wilson D. F. (1982). Role of mitochondrial oxidative phosphorylation in regulation of coronary blood flow. Am. J. Physiol. 243 (2), 159–169. doi:10.1152/ajpheart.1982.243.2.H159
Poole D. C., Behnke B. J., Musch T. I. (2021). The role of vascular function on exercise capacity in health and disease. J. Physiol. 599 (3), 889–910. doi:10.1113/JP278931
Pries A. R., Ley K., Gaehtgens P. (1986). Generalization of the Fahraeus principle for microvessel networks. Am. J. Physiol. 251 (6), H1324–H1332. doi:10.1152/ajpheart.1986.251.6.H1324
Pries A. R., Ley K., Claassen M., Gaehtgens P. (1989). Red cell distribution at microvascular bifurcations. Microvasc. Res. 38 (1), 81–101. doi:10.1016/0026-2862(89)90018-6
Segal S. S., Jacobs T. L. (2001). Role for endothelial cell conduction in ascending vasodilatation and exercise hyperaemia in hamster skeletal muscle. J. Physiol. 536 (3), 937–946. doi:10.1111/j.1469-7793.2001.00937
Segal S. (2005). Regulation of blood flow in the microcirculation. Microcirculation 12, 33–45. doi:10.1080/10739680590895028
Shoemaker J. K., Hughson R. L. (1999). Adaptation of blood flow during the rest to work transition in humans. Med. Sci. Sports Exerc. 1931 (7), 1019–1026. doi:10.1097/00005768-199907000-00015
Sové R. J., Milkovich S., Nikolov H., Holdsworth D., Ellis C. G., Fraser G. M. (2021). Localized oxygen exchange platform for intravital video microscopy investigations of microvascular oxygen regulation. Front. Physiol. 12, 654928. doi:10.3389/fphys.2021.654928
Tschakovsky M. E., Saunders N. R., Webb K. A., O'Donnell D. E. (2006). Muscle blood-flow dynamics at exercise onset: Do the limbs differ? Med. Sci. Sports Exerc. 38 (10), 1811–1818. doi:10.1249/01.mss.0000230341.86870.4f
Tschakovsky M. E., Shoemaker J. K., Hughson R. L. (1996). Vasodilation and muscle pump contribution to immediate exercise hyperemia. Am. J. Physiol. 271 (4), H1697–H1701. doi:10.1152/ajpheart.1996.271.4.H1697
Tyml K., Budreau C. H. (1991). A new preparation of rat extensor digitorum longus muscle for intravital investigation of the microcirculation. Int. J. Microcirc. Clin. Exp. 10 (4), 335–343. PMID: 1778678
VanTeeffelen J. W., Segal S. S. (2006). Rapid dilation of arterioles with single contraction of hamster skeletal muscle. Am. J. Physiol. Heart Circ. Physiol. 290 (1), H119–H127. doi:10.1152/ajpheart.00197.2005
Walløe L., Wesche J. (1988). Time course and magnitude of blood flow changes in the human quadriceps muscles during and following rhythmic exercise. J. Physiol. 405 (1), 257–273. doi:10.1113/jphysiol.1988.sp017332
Wray D. W., Witman M. A. H., Ives S. J., McDaniel J., Fjeldstad A. S., Trinity J. D., et al. (2011). Progressive handgrip exercise: Evidence of nitric oxide- dependent vasodilation and blood flow regulation in humans. Am. J. Physiol. Heart Circ. Physiol. 300 (3), H1101–H1107. doi:10.1152/ajpheart.01115.2010
Keywords: microcirculation, oxygen mediated blood flow regulation, capillary, skeletal muscle, exercise, carbon dioxide
Citation: Russell McEvoy GM, Wells BN, Kiley ME, Kaur KK and Fraser GM (2022) Dynamics of capillary blood flow responses to acute local changes in oxygen and carbon dioxide concentrations. Front. Physiol. 13:1052449. doi: 10.3389/fphys.2022.1052449
Received: 23 September 2022; Accepted: 15 November 2022;
Published: 06 December 2022.
Edited by:
Ylva Hellsten, University of Copenhagen, DenmarkReviewed by:
Roland Pittman, Virginia Commonwealth University, United StatesCopyright © 2022 Russell McEvoy, Wells, Kiley, Kaur and Fraser. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Graham M. Fraser, Z3JhaGFtLmZyYXNlckBtZWQubXVuLmNh
†These authors contributed equally to this work and share first authorship
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.