Unraveling Aβ-Mediated Multi-Pathway Calcium Dynamics in Astrocytes: Implications for Alzheimer’s Disease Treatment From Simulations

The accumulation of amyloid β peptide (Aβ) in the brain is hypothesized to be the major factor driving Alzheimer’s disease (AD) pathogenesis. Mounting evidence suggests that astrocytes are the primary target of Aβ neurotoxicity. Aβ is known to interfere with multiple calcium fluxes, thus disrupting the calcium homeostasis regulation of astrocytes, which are likely to produce calcium oscillations. Ca²⁺ dyshomeostasis has been observed to precede the appearance of clinical symptoms of AD; however, it is experimentally very difficult to investigate the interactions of many mechanisms. Given that Ca²⁺ disruption is ubiquitously involved in AD progression, it is likely that focusing on Ca²⁺ dysregulation may serve as a potential therapeutic approach to preventing or treating AD, while current hypotheses concerning AD have so far failed to yield curable therapies. For this purpose, we derive and investigate a concise mathematical model for Aβ-mediated multi-pathway astrocytic intracellular Ca²⁺ dynamics. This model accounts for how Aβ affects various fluxes contributions through voltage-gated calcium channels, Aβ-formed channels and ryanodine receptors. Bifurcation analysis of Aβ level, which reflected the corresponding progression of the disease, revealed that Aβ significantly induced the increasing [Ca²⁺]_i and frequency of calcium oscillations. The influence of inositol 1,4,5-trisphosphate production (IP₃) is also investigated in the presence of Aβ as well as the impact of changes in resting membrane potential. In turn, the Ca²⁺ flux can be considerably changed by exerting specific interventions, such as ion channel blockers or receptor antagonists. By doing so, a “combination therapy” targeting multiple pathways simultaneously has finally been demonstrated to be more effective. This study helps to better understand the effect of Aβ, and our findings provide new insight into the treatment of AD.

Introduction

Alzheimer’s disease (AD) is currently the most common neurodegenerative disease and is the major dementia type, which accounts for 60–70% of cases (Prince, 2015; Canter et al., 2016). The Alzheimer Disease International estimated in 2019 that over 50 million people were living with dementia and this number is expected to exceed 150 million by 2050 (Lynch, 2020). The disease has already caused incalculable losses worldwide. Little is known about the complex pathophysiology of AD, and thus, there is no cure. Pathological characteristics of accumulation of amyloid β-peptide (Aβ), is considered to be drivers in AD pathogenesis (Hardy and Selkoe, 2002; Birch, 2014).

Astrocytes were historically considered to provide support for neurons (Carmignoto and Gómez-Gonzalo, 2010). Since they were found to be involved in many brain functions and neurodegenerative diseases such as AD and Parkinson’s disease etc., astrocytes have become a hot topic in neuroscience research over the past few decades (Tewari and Majumdar, 2012; Tewari and Parpura, 2013; Bazargani and Attwell, 2016). In cultures of mixed neurons and astrocytes treated with Aβ, astrocytes always exhibit pathological alterations before neuronal death suggesting that astrocytes appear to be the primary target of Aβ (Abramov et al., 2003). Their role as protector and housekeeper in central nervous system is universally acknowledged, however, Aβ impairs important supportive astrocyte functions in AD cases (Verkhratsky and Nedergaard, 2018).

Astrocytes do not generate electrical signals like neurons (Wu et al., 2015). However, the concept of “cellular excitability” in astrocytes has been recently formalized to describe the changes in cytosolic Ca²⁺ concentration in response to chemical or mechanical stimulation (Verkhratsky, 2019). For example, they encode synaptic information via the modulation of intracellular calcium dynamics in response to synaptic activity (De Pittà et al., 2009). However, this kind of Ca²⁺ homeostasis can be disrupted by Aβ, whether in neurons or astrocytes, especially its soluble oligomeric form is more harmful (Demuro et al., 2010). In an AD mouse model, astrocytes displayed higher basal astrocyte Ca²⁺ levels and increased transient Ca²⁺ signals (Kuchibhotla et al., 2009).

Aβ is known to interfere with multiple calcium fluxes in astrocytes. Aβ oligomers deposition not only form pores in the lipid bilayer permeable to cationic ions, but also directly or indirectly activate L-type Ca_V, which increases the concentration of intracellular Ca²⁺ (Alves et al., 2019). Additionally, the expression of astroglial mGluR₅ is up-regulated by exposure to Aβ (Lim et al., 2013). Inside astrocytes, Aβ can induce endoplasmic reticulum (ER) Ca²⁺ release through ryanodine receptors (RyRs) and inositol triphosphate receptors (IP₃Rs) (Alberdi et al., 2013). How to combine these different findings to understand the big picture is crucial for further research (Markowetz, 2017). However, it is experimentally very difficult to investigate the interactions of many mechanisms of Ca²⁺ dyshomeostasis (Cutsuridis and Moustafa, 2017), e.g., the limitations of Ca²⁺ indicators and imaging techniques.

Simulation based on the mathematical model has been an invaluable tool to investigate complex interactions. There are hundreds of computational models on astrocyte Ca²⁺ dynamics and homeostasis either in a single astrocyte or in astrocyte networks or in neuron-astrocyte synapses (Manninen et al., 2018). Here, we focus primarily on modeling efforts in single astrocyte. Most of them studied Ca²⁺ oscillations, while a small part of them modeled spontaneous Ca²⁺ activity (Lavrentovich and Hemkin, 2008; Riera et al., 2011b); some assessed neurotransmitter-evoked Ca²⁺ excitability (De Pittà et al., 2009; Dupont et al., 2011). These computational studies are mostly based on classic models, including components for calcium-induced calcium release (CICR) and the sarco-endoplasmic Ca²⁺ ATPase pump (SERCA). In astrocytes, intracellular Ca²⁺ oscillations depend mainly on CICR, while Ca²⁺ influx from extracellular space via receptors or channels on membrane such as voltage-gated calcium channels (VGCCs) has also been linked with Ca²⁺ oscillations (Lavrentovich and Hemkin, 2008; Zeng et al., 2009). Taheri et al. (2017) modeled capacitive Ca²⁺ entry, which is mediated via store-operated Ca²⁺ channels. Ding et al. (2018) constructed two stochastic models, one describing the VGCC channel noise and the other describing the stochastic IP₃R dynamics. Recently, some modeling work has addressed the effect of Aβ on Ca²⁺ dynamics in generic cells (Latulippe et al., 2018). We established an Aβ-mediated calcium signaling model in astrocytes for the pilot study (Gao et al., 2020). All the models have useful implications for understanding Ca²⁺ signaling. However, no model has integrated the abovementioned putative mechanisms (Abramov et al., 2003; Alberdi et al., 2013; Lim et al., 2013; Alves et al., 2019) to simulate Ca²⁺ dynamics in astrocytes. The synergistic effect of the different Ca²⁺ fluxes on Ca²⁺ dynamics is not well understood so far. In particular, the current development of the theme lacks results regarding restoring the Ca²⁺ homeostasis in astrocytes during the progression of AD.

To date, the treatment of AD has remained a challenge. Although some promising drugs are under continuous development, clinical trials in recent years fail to get satisfied results (Qian et al., 2015). The currently approved anti-AD drugs fall into two types: cholinesterase inhibitors (donepezil, rivastigmine and galantamine) and N-methyl-D-aspartic acid receptor antagonists (memantine) (Aupperle, 2006). On the one hand, these drugs can only relieve symptoms but do not prevent the progression of AD, suggesting that their targets might not be the disease origin (Liu et al., 2019). On the other hand, memantine can prevent NMDAR-mediated Ca²⁺ flux indicating that other Ca²⁺ mechanisms may be a potential target for the treatment of AD when they have been demonstrated to play a proximal role in AD.

Here, a comprehensive model integrating multiple Aβ-affected Ca²⁺ pathways is proposed. This model of astrocytes describes Ca²⁺ signals as individual Ca²⁺ transport pathways rather than a macroscopic flow of Ca²⁺, including both intracellular release and extracellular influx. With this computational model, we can begin to study how Aβ affects each source of Ca²⁺ through various pathways. Recent wet-lab data are also incorporated into modeling work to obtain insights into AD treatment (Sadick and Liddelow, 2019). The explicit intention is to test the specific treatment strategy for AD.

Materials and Methods

Biophysical Model

Intracellular Ca²⁺ levels are modulated by influx from the extracellular space or controlled release from intracellular Ca²⁺ stores such as the ER. Generally, Ca²⁺ entry into astrocytes includes active transport by different types of VGCCs distributed in the membrane and passive leakage. In astrocytes, however, IP₃-dependent CICR from the ER is considered the primary mechanism responsible for intracellular Ca²⁺ dynamics (Agulhon et al., 2008). CICR is essentially controlled by efflux from the ER to the cytoplasm that is mediated both by IP₃R and RyR and influx into the ER, which is due to the action of SERCA pumps. Aβ can interfere with some of these Ca²⁺ fluxes and the detailed modeling methods for Aβ are described in section “Aβ Assumption.” So, the whole-cell model is shown in Figure 1.

FIGURE 1

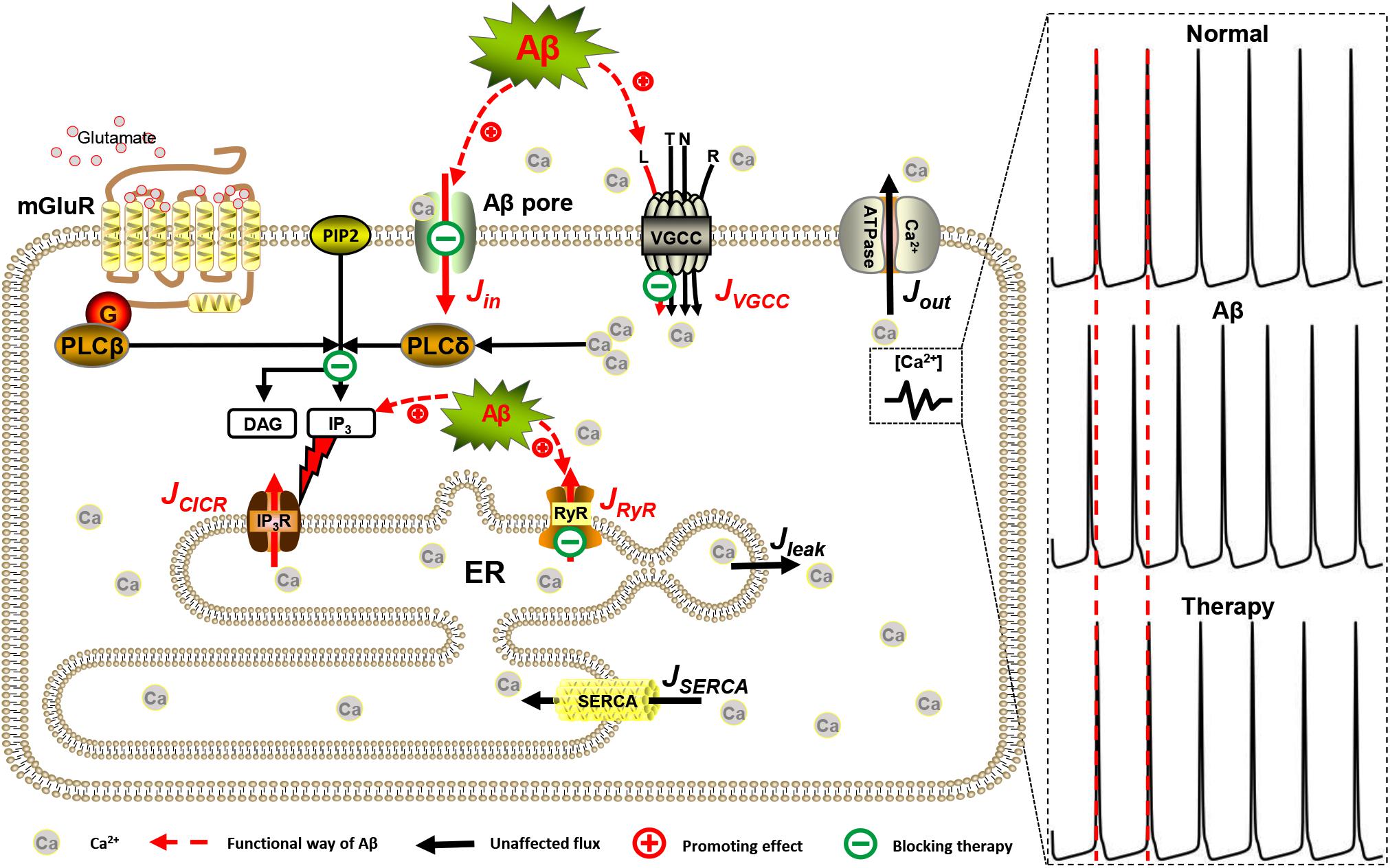
Figure 1. Mechanisms involved in intracellular Ca²⁺ dysregulation in AD. In this model, J_VGCC and J_in are Ca²⁺ influxes from the extracellular space. The two separate mechanisms involved in the process of Ca²⁺ release from the ER via IP₃Rs and RyRs are J_CICR and J_RyR, respectively. J_SERCA represents the SERCA pump of the ER refilling the ER by pumping Ca²⁺ back from the cytosol. J_leak is the leakage Ca²⁺ flux from the ER into the cytosol. J_out is Ca²⁺ efflux by Ca²⁺-ATPase pump. Red lines represent the functional pathway of Aβ, and green lines represent the inhibitory effects of drugs.

Intracellular Ca²⁺ Dynamics

We describe the model by tracking the flux in and out of the cytoplasm. Then, the change in intracellular Ca²⁺ is governed by

$$d{[C{a}^{2+}]}_i/dt=J_{VGCC}-J_{out}+J_{in}+J_{CICR}+J_{RyR}+J_{leak}-J_{SERCA},(1)$$

$$d{[C{a}^{2+}]}_{ER}/dt=(J_{SERCA}-J_{CICR}-J_{RyR}-J_{leak})/c_1,(2)$$

where [Ca^{2 +}]_i and [Ca^{2 +}]_ERdenote the concentration of Ca²⁺ in the cytoplasm and ER, respectively. c₁is the ratio of ER volume to the cytoplasmic volume. We assumed a spatially homogeneous astrocyte whose volume was fixed. As such, the ER and cytoplasm are simplified as two points of the cell for better quantifying and identifying key mechanisms behind certain Ca²⁺ fluxes.

The term J_VGCC represents the pathway of Ca²⁺ influx through four types of VGCCs, including L-, N-, T-, and R-types. When the volume of the cell is constant, the Ca²⁺ flux and current are related by the equations (Zeng et al., 2009):

$$J_{VGCC}=-\frac{I_{VGCC}}{zF{V}_{ast}},(3)$$

$$I_{VGCC}=I_{Ca,L}+I_{Ca,T}+I_{Ca,N}+I_{Ca,R},(4)$$

where I_VGCC is the VGCC-conducted Ca²⁺ current, and I_Ca,L, I_Ca,T, I_Ca,N, I_Ca,R represent the current through different types of channels. z is the valence of Ca²⁺, F is the Faraday constant and V_ast is the volume of the astrocyte. The concrete formula for every type of calcium current is given in detail in Table 1.

TABLE 1

Table 1. Details of the voltage-gated calcium channels.

J_in is a passive leakage from the extracellular space. Riera et al. (2011a) used a heuristic strategy to determine J_in = 0.036 μM/s for healthy astrocytes:

$$J_{in}=v_5.(5)$$

To represent the kinetics of the IP₃R, we used a simplification form (Ullah et al., 2006) described as

$$J_{CICR}=v_1{m}^3{n}^3{h}^3({\left[C{a}^{2+}\right]}_{ER}-{\left[C{a}^{2+}\right]}_i),(6)$$

where v₁ determines the maximal rate of transported Ca²⁺, m, n and h are gating variables of IP₃R. The first two are assumed to have instantaneous kinetics, m=m_∞, n=n_∞, while h obeys Hodgkin-Huxley formalism. They are specified as follows:

$$m_{\mathrm{\infty }}=\frac{[I{P}_3]}{[I{P}_3]+d_1},(7)$$

$$n_{\mathrm{\infty }}=\frac{{[C{a}^{2+}]}_i}{{\left[C{a}^{2+}\right]}_i+d_5},(8)$$

$$dh/dt=a_2{d}_2\frac{\left[I{P}_3\right]+d_1}{\left[I{P}_3\right]+d_3}\left(1-h\right)-a_2{\left[C{a}^{2+}\right]}_{i}h,(9)$$

d₁ and d₅ determine the dissociation of IP₃ and Ca²⁺ by the channel’s subunits, whereas d₂ and d₃ is the inactivation dissociation constant of Ca²⁺ and IP₃, respectively. a₂ determines the IP₃R binding rate for Ca²⁺ inhibition.

The SERCA pump rate can be taken as an instantaneous function of [Ca²⁺]_i by using a Hill-type kinetic model (Ullah et al., 2006):

$$J_{SERCA}=v_3\frac{{[C{a}^{2+}]}_i^2}{{[C{a}^{2+}]}_i^2+k_3^2},(10)$$

where v₃ represents the maximum SERCA pump flux and k₃ is the dissociation constant of Ca²⁺ to SERCA.

To model RyR, we modified the previous model (Friel, 1995) by increasing the effect of [Ca²⁺]_i and took the following form:

$$J_{RyR}=(k_0+\frac{k_2{[C{a}^{2+}]}_i^3}{k_d^3+{[C{a}^{2+}]}_i^3})({\left[C{a}^{2+}\right]}_{ER}-{\left[C{a}^{2+}\right]}_i),(11)$$

where k₀ is the zero calcium concentration level leak. This parameter is usually used to ensure a physiologically meaningful resting Ca²⁺ level (Dupont et al., 2016). Furthermore, k₂ is the maximal rate of the channel, k_d corresponds to the RyR channel sensitivity for the CICR.

The leakage flux from the ER is assumed to be proportional to the Ca²⁺ gradient across the ER membrane by v₂, the maximal rate of Ca²⁺ leakage (Ullah et al., 2006).

$$J_{leak}=v_2({\left[C{a}^{2+}\right]}_{ER}-{\left[C{a}^{2+}\right]}_i).(12)$$

Finally, we considered Ca²⁺ extrusion flux as described (Ullah et al., 2006):

$$J_{out}=k_1{\left[C{a}^{2+}\right]}_i,(13)$$

where k₁ is the rate constant of calcium extrusion.

Generation/Degradation of Cytosolic IP₃

IP₃ is the second messenger involved in G protein-coupled receptor-mediated signal transduction. In astrocytes, IP₃ is produced by hydrolysis of phosphatidylinositol 4,5-bisphosphate by two phosphoinositide-specific phospholipase C (PLC) isoenzymes, PLCβ and PLCδ (Rebecchi and Pentyala, 2000). Therefore, the IP₃ dynamic is described as:

$$d[I{P}_3]/dt=J_{PLC\mathrm{\beta }}+J_{PLC\mathrm{\delta }}-k_{deg}[I{P}_3],(14)$$

where J_PLCβ and J_PLCδ are PLCβ- and PLCδ-dependent IP₃ production, respectively. k_deg represents the rate of IP₃ degradation.

PLCβ is primarily controlled by external glutamate stimulation (De Pittà et al., 2009). So J_PLCβ can be modeled as follows (De Pittà et al., 2009):

$$J_{PLC\mathrm{\beta }}=v_{\mathrm{\beta }}\frac{g^{0.7}}{g^{0.7}+{(k_R+k_P\frac{{[C{a}^{2+}]}_i}{{[C{a}^{2+}]}_i+k_{\mathrm{\pi }}})}^{0.7}},(15)$$

where v_β is the maximal PLCβ rate, g is the concentration of glutamate, we set this value to be g = 1 μM. k_R is glutamate affinity and k_P is the Ca²⁺/PLC-dependent inhibition factor and k_π controls Ca²⁺ affinity of PLC.

In contrast, PLCδ is essentially activated by increased intracellular Ca²⁺ levels (Rhee and Bae, 1997) and is written as (De Young and Keizer, 1992):

$$J_{PLC\mathrm{\delta }}=v_4\frac{{[C{a}^{2+}]}_i+(1-\mathrm{\alpha })k_4}{{[C{a}^{2+}]}_i+k_4},(16)$$

where v₄ is the maximum rate of IP₃ production, and k₄ is the dissociation constant for Ca²⁺ stimulation of IP₃ production. Here α is used to investigate the relative effect of Ca²⁺ stimulation of PLCδ on IP₃ production. For example, if α = 0, the IP₃ production rate is v₄, which is independent of [Ca²⁺]_i.

Aβ Assumption

Exposure of astrocytes to Aβ was reported to trigger [Ca²⁺]_i transients and [Ca²⁺]_i oscillations (Alberdi et al., 2013). Such effects may involve various Ca²⁺ entry pathways as well as Ca²⁺ release from ER (Abramov et al., 2003; Alberdi et al., 2013). These experimental findings have provided useful insights for us to make our Aβ assumption. However, in the real condition, the accumulation of Aβ can occur over months, years, and even decades which does not match the short timescale of changes in Ca²⁺. To solve this issue, we assumed a fixed level of Aβ concentration in our model using the parameter a which corresponds to the certain stage of the progression of AD. For example, a small value of a may reflect a low level of Aβ representing the early stage of the disease. By changing a, we can easily investigate the effect of Aβ on different progressions of AD.

A study has demonstrated that L-type channels might be activated by Aβ, and increased expression of L-type channels is associated with Aβ-positive plaques (Alves et al., 2019). To do this, we altered the original form of I_Ca,L:

$$I_{Ca,L}=(g_L+k_{VGCC}a)m_L{h}_L(V_m-E_{Ca}),(17)$$

where k_VGCC controls the strength of the effect of Aβ on the channels.

Besides, Aβ-formed channels on the plasma membrane can also trigger additional Ca²⁺ influx into the cytoplasm (Demuro et al., 2010). In order to incorporate the possible influence, we included another term inJ_in:

$$J_{in}=v_5+k_{in}{a}^k,(18)$$

where k_in represents a rate constant (De Caluwé and Dupont, 2013), or, in other words, the strength of Aβ in this study, and k is the cooperativity coefficient.

Although some studies have elucidated the role of RyRs in regulating Ca²⁺ disruption in AD (Stutzmann et al., 2006; Goussakov et al., 2010; Briggs et al., 2013), data on the contributions of Ca²⁺ flux through the RyR in the presence of Aβ are minimal. Given that Aβ can increase the channel open probability, we decided to revise the expression as follows:

$$J_{RyR}=(k_0+\frac{k_2{[C{a}^{2+}]}_i^3}{{(k_d+k_{RyR}a)}^3+{[C{a}^{2+}]}_i^3})({\left[C{a}^{2+}\right]}_{ER}-{\left[C{a}^{2+}\right]}_i),(19)$$

where k_RyR represents the strength of Aβ.

In addition to the direct effect on Ca²⁺ fluxes, Aβ can also alter IP₃ levels. On the one hand, Aβ up-regulates the expression of astroglial mGluR₅, therefore, affects downstream IP₃ production (Renner et al., 2010). On the other hand, intracellular Aβ oligomers induce Ca²⁺ liberation from the ER via IP₃Rs by stimulating PLC-mediated IP₃ production (Demuro and Parker, 2013). Based on these findings, we adapted equations (15) and (16), assuming that the glutamate- and Ca²⁺-dependent IP₃ production would take the following forms:

$$J_{PLC\mathrm{\beta }}=(v_{\mathrm{\beta }}+k_{PLC\mathrm{\beta }}a)\frac{g^{0.7}}{g^{0.7}+{(k_R+k_P\frac{{[C{a}^{2+}]}_i}{{[C{a}^{2+}]}_i+k_{\mathrm{\pi }}})}^{0.7}},(20)$$

$$J_{PLC\mathrm{\delta }}=(v_4+k_{PLC\mathrm{\delta }}a)\frac{{\text{[Ca}}^{2+}]{}_{\text{i}}+(1-\mathrm{\alpha })k{}_4}{{\text{[Ca}}^{2+}]{}_{\text{i}}+k{}_4},(21)$$

where the parameters k_PLCβ and k_PLCδ control the strength of the linear influence of Aβ on each term, respectively.

All the parameters used in our model can be found in Table 2. In simulations, parameters are chosen under the principle that the oscillations obtained agree qualitatively with the experimental data. More details of the model can be found in the associated MATLAB code (R2020a, MathWorks; see in the Supporting Material).

TABLE 2

Table 2. Parameters used in the model.

Sensitivity and Robustness Analysis

Robustness characterizes the ability to maintain performance in the face of perturbations while sensitivity characterizes the ability of living organisms to adequately react to certain stimulus. The two concepts are interlinked. In deterministic modeling, robustness is usually quantified by calculating sensitivity, e.g., period and amplitude sensitivity in quantifying robustness of circadian rhythms (Dubitzky et al., 2013). In this study, our model is highly sensitive to certain parameters and the oscillatory responses presented here only occur under certain scenarios. Therefore, a simple local sensitivity analysis was performed to assess the sensitivity of the model output, i.e., [Ca²⁺]_i and frequency, to variation in parameters determining the contribution of various fluxes and those representing the effect of therapy. We followed the Morris screening method in which only one input parameter x_i is modified between two successive runs of the model. The change of the output induced onto the model objective function y(x)=(x₁,x₂,,x_n), can then be unambiguously attributed to such a modification of x_i. Therefore, the sensitivity S of an oscillatory amplitude and frequency to changes in model parameters P can be quantified by:

$$S=\frac{\mathrm{△}Output}{\mathrm{△}{P}_{change}},$$

where △Output represents the changes of the model output induced by the changes in input parameters, and △P_change is the changes in input parameters between two runs of the model. Each parameter was allowed to vary around its control value and the model was solved for each parameter change.

Results

Our simulations show that Aβ can trigger disruptions of cytosolic Ca²⁺ levels through interactions between various mechanisms, or, the single components. Each pathway exhibits different characteristics with the influence of Aβ. Changes in astrocyte resting membrane potential (RMP) were considered and incorporated into our model. With the intention of restoring dysregulated calcium signals, some therapeutic measures were tested, and the multi-pathway involved “combination therapy” gained effective recovery.

Aβ Impairs Ca²⁺ Homeostasis in Astrocytes

Calcium oscillations in astrocytes are crucial signaling pathways with multiple roles in several brain functions (Riera et al., 2011a). Charles et al. (1991) have reported the [Ca²⁺]_i oscillations in glial cells with the peak amplitude of 0.6–0.8 μM induced by mechanical and glutamate stimulations. Parri and Crunelli (2001) found a subset of spontaneously active thalamic astrocytes exhibits [Ca²⁺]_i oscillations with an average frequency of 0.019 Hz. Here, our model produced typical calcium oscillations of approximately 0.6 μM in amplitude and 0.03 Hz in frequency without Aβ (Figure 2) which is consistent with the experimental data suggesting the physiological agreement of our biophysical model.

FIGURE 2

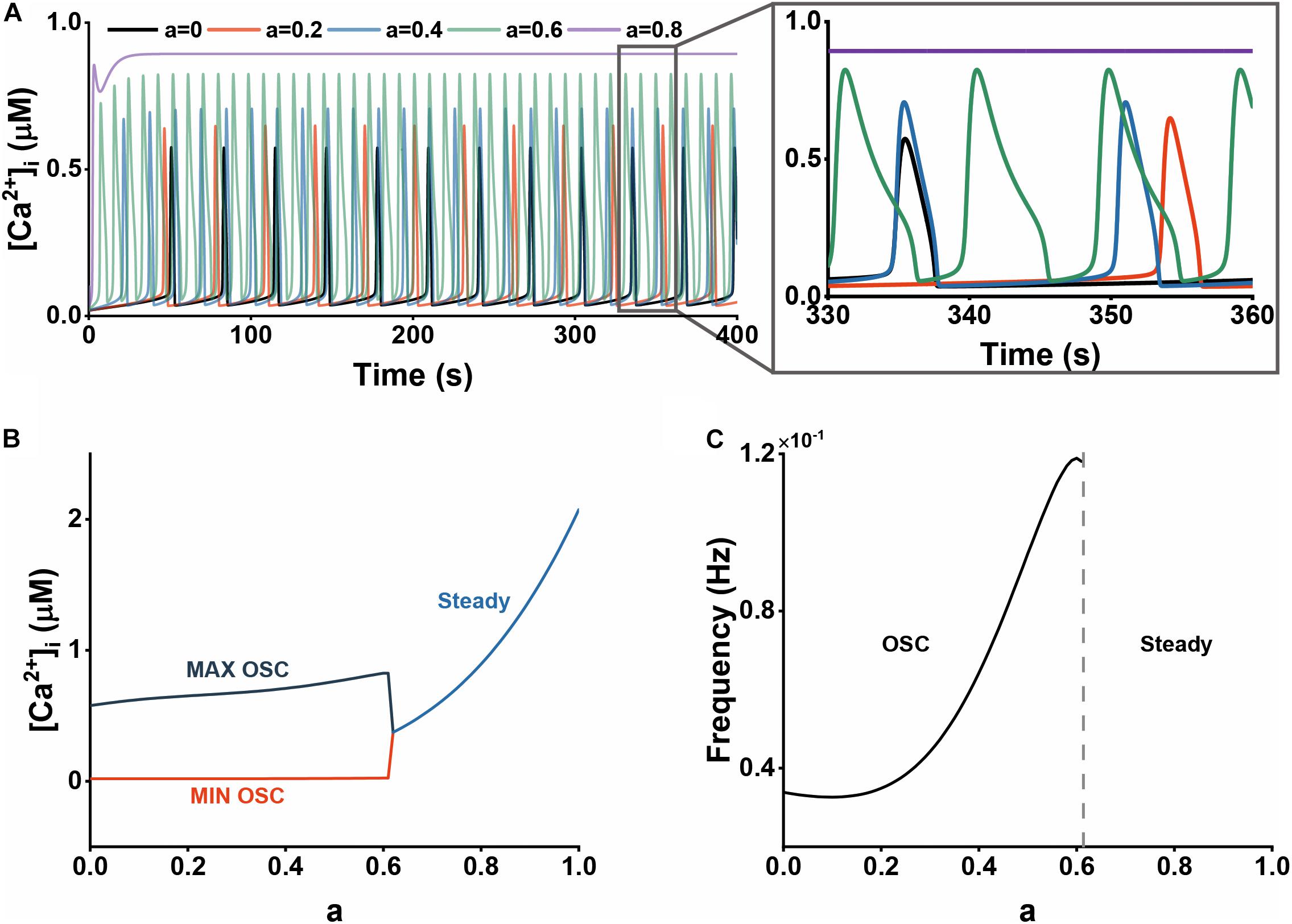
Figure 2. The effect of Aβ on cytosolic Ca²⁺ dynamics. (A) The time course of Ca²⁺ dynamics at different Aβ levels (0, 0.2, 0.4, 0.6, and 0.8). (B) Bifurcation diagram of [Ca²⁺]_i plotted against the Aβ level, a. (C) The frequency of Ca²⁺ oscillations plotted against the Aβ level, a.

Aβ has been shown to impair intracellular Ca²⁺ homeostasis in our simulations. Figure 2A describes the cytosolic Ca²⁺ with different Aβ levels. We can clearly observe the increasing amplitude and frequency with elevated Aβ. The intracellular calcium signals would change into a high steady state if there is excessive Aβ. In Figures 2B,C, we performed analyses on bifurcation features and variations of frequency to study the dynamical influence of Aβ on Ca²⁺. At a low level of Aβ, that is, 0 < a < 0.3, which we assumed to represent an early or milder state of the disease, the oscillation amplitude increases while the frequency changes little. At a middle Aβ level (0.3 < a < 0.6), the oscillation frequency has a rapid increase. For a higher level of Aβ (a > 0.6), which represents a later or more severe stage of the disease, astrocytic Ca²⁺ dynamics become the high steady state in which the calcium concentration has an explosive increase.

Since Aβ has such significant effects, we continued to test parameters representing the strength of Aβ on each pathway. Illustrated in Figures 3A–E are bifurcation analysis for this purpose. Regardless of the level of Aβ, the effect on VGCCs is minimal because both amplitude and frequency show good robustness against k_VGCC (Figure 3A). Nevertheless, Aβ channels makes an obvious influence with increasing Aβ. Both [Ca²⁺]_i and frequency markedly vary in oscillation or steady state (Figure 3B). Figure 3C displays the effect of k_RyR, showing that [Ca²⁺]_i is relatively robust against large k_RyR whereas the frequency is quite the opposite. On balance, k_RyR induced alterations are minor. Figures 3D,E are the effects of parameters related to IP₃ production and their influence is essentially similar. Increasing IP₃ can make elevated frequency but slightly decreased [Ca²⁺]_i. They both do not affect the steady state. Besides, we also considered other indirect parameters. Their sensitivities which are calculated for parameter variations of ± 10% are shown in Figures 3F,G. A small change in k₂ can cause a significant decrease in [Ca²⁺]_i and increase in frequency, while the rate of ER leakage (v₂) acts as the same role but is less sensitive than k₂. Another leak flux J_in has a positive effect on both sides. Some other parameters here with low sensitivity are not discussed further.

FIGURE 3

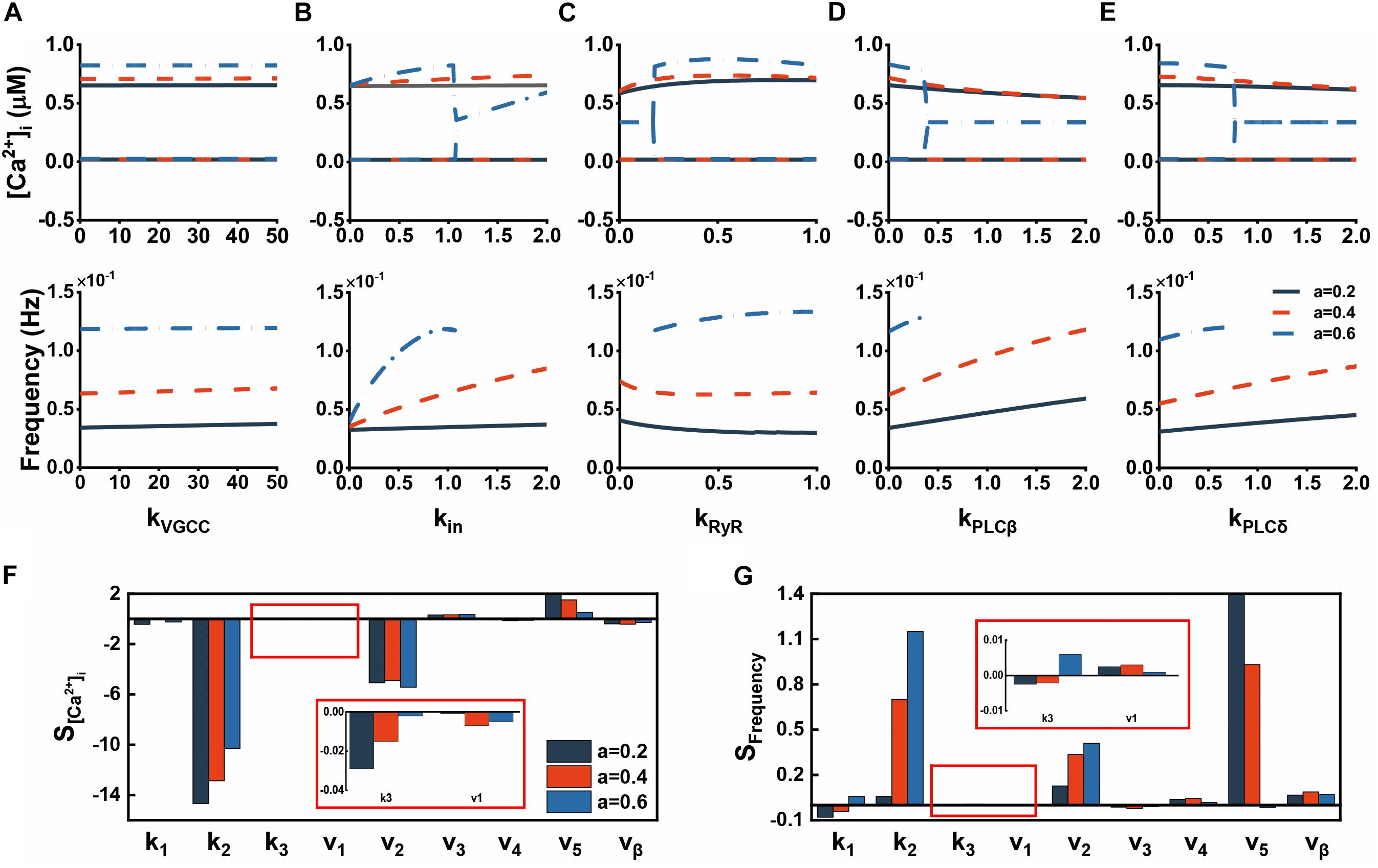
Figure 3. The effect of various parameters on cytosolic Ca²⁺ dynamics. (A–E) Bifurcation diagrams of [Ca²⁺]_i plotted against the strength of Aβ acting on different pathways. (F) Amplitude sensitivity of Ca²⁺ dynamics. The sensitivities are calculated for parameter variations of ± 10%. (G) Frequency sensitivity of Ca²⁺ dynamics. The sensitivities are calculated for parameter variations of ± 10%.

In general, various results suggest that Aβ triggers aberrant calcium signals by increasing [Ca²⁺]_i and frequency. In particular, high levels of Aβ are more hazardous and can be fatal. These disruptions of calcium oscillations make calcium signaling abnormal and raise the possibility of calcium intoxication (Mattson and Chan, 2003).

Contribution of Aβ on Ca²⁺ Dynamics Through Different Pathways

The above results have revealed how the multiple Aβ-affected pathways interact and collectively contribute to Ca²⁺ dysregulation. However, we remained curious about the alterations in these pathways, and therefore, we next separated these pathways and examined, in isolation, how Aβ alters these pathways and causes abnormalities in cytosolic Ca²⁺. So, we denoted whether Aβ affects calcium flux by changing the strength of the effect of Aβ on the individual pathways (i.e., k_VGCC, k_in, k_RyR, k_PLCβ and k_PLCδ) to 0 or 1 and described the dynamics of varying the parameter a, meaning how Aβ acts on a single pathway.

We examined the effect of each pathway on cytosolic Ca²⁺ dynamics by analyzing bifurcation and frequency. The results are shown in Figure 4. Diagram indicates that large amounts of Aβ are required to elicit changes in intracellular Ca²⁺ activity when acting on VGCCs; even at steady state, the effects of Aβ are slow (Figure 4A). This illustrates that [Ca²⁺]_i are robust to changes in J_VGCC. In contrast, slight Aβ acting on the formed channels is able to disrupt normal astrocytic calcium oscillations and enables [Ca²⁺]_i at steady state to grow rapidly as well. When a < 0.3, the frequency essentially exhibits unchanged behavior. Then the frequency increased significantly as Aβ became larger. Figure 4C illustrates the effect of J_RyR. We can observe the increased amplitude of oscillation, stable and unchanged low steady state concentration, and reduced frequency, especially when a > 0.3, where a sharp decrease in frequency occurs. Figure 4D shows that Aβ-mediated IP₃ production leads to the decrease of calcium oscillation amplitude and the increase of frequency, but this effect gradually disappears with the increase of the Aβ level. We analyzed the reason and found that when Aβ increases to a certain value, both m and n tend to be constant, resulting in no change of J_CICR affected by IP₃, so the whole dynamics gradually tend to be stable.

FIGURE 4

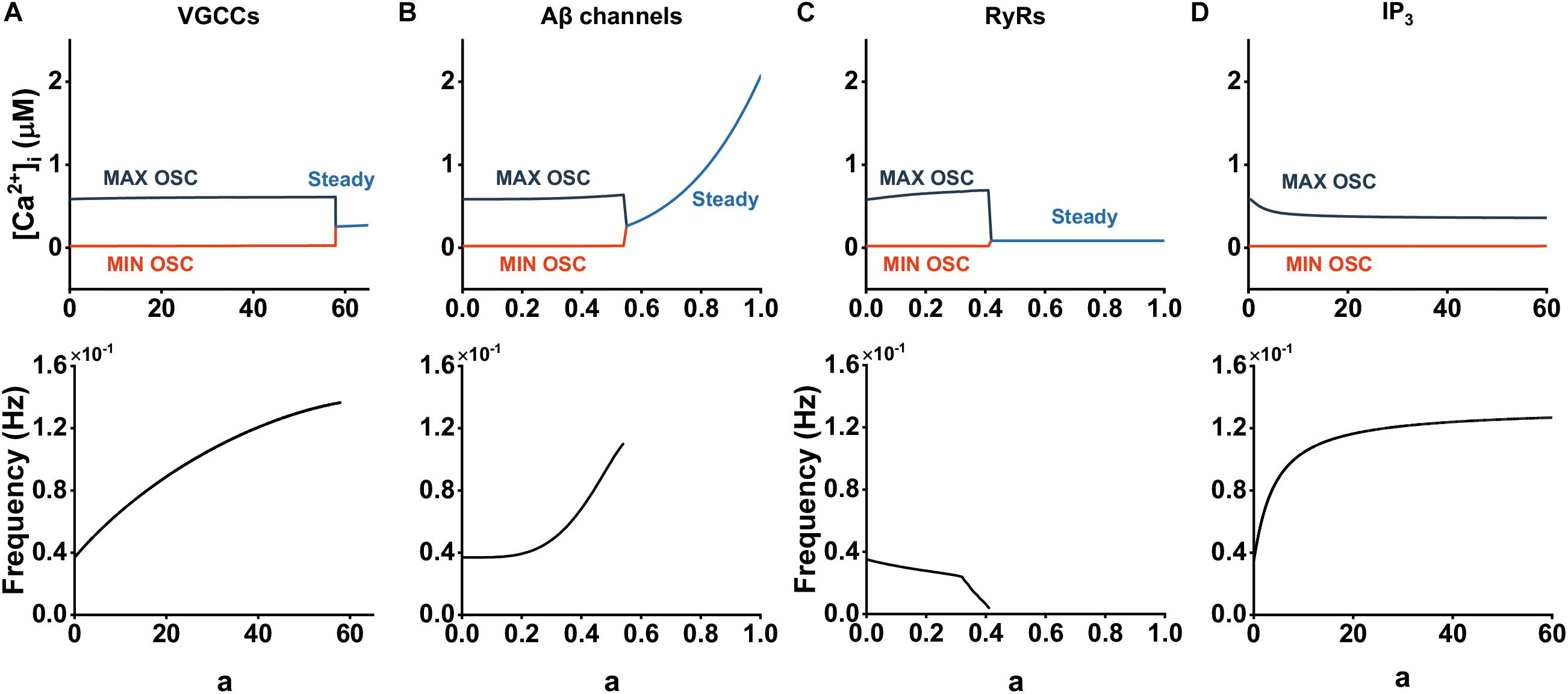
Figure 4. Contribution of Aβ on cytosolic Ca²⁺ dynamics through different pathways. (A–D) Bifurcation diagrams of [Ca²⁺]_i plotted against the Aβ level with affected pathways.

On the whole, we considered that Aβ channels and RyRs play a major role in the regulation of intracellular Ca²⁺ under the influence of Aβ, while the other two pathways have little effect.

The Influence of Resting Membrane Potential

Although astrocytes are non-excitable cells, values of RMP reported in different studies may vary in extension to some ones due differences in outside K⁺ concentration (Anderson et al., 1995). Thus, the changes in extracellular K⁺ concentration can depolarize the astrocyte and increase the open probability of VGCCs (Bellot-Saez et al., 2017). Therefore, we simulated how changes in RMP can affect the J_VGCC and intracellular Ca²⁺ dynamics.

The hyperpolarized RMP of mature astrocytes is set close to the K⁺ Nernst potential, approximately –80 mV (Verkhratsky and Nedergaard, 2018). So, we modeled V_m as the following form (Wu et al., 2019):

$$V_m=\frac{RT}{z_{K}F}\ln \frac{{[K^{+}]}_o}{{[K^{+}]}_i}+\mathrm{\epsilon },(22)$$

where R is the ideal gas constant, T is the absolute temperature, z_K is the valence of K⁺, and F is Faraday constant. [K⁺]_o and [K]_i are the extracellular and intracellular K⁺ concentrations, respectively. ε is a modulation factor.

Now we can examine the effects of changes to RMP by adjusting [K]_o. The impact of such changes in V_m and the resulting Ca²⁺ dynamics are shown in Figures 5, 6.

FIGURE 5

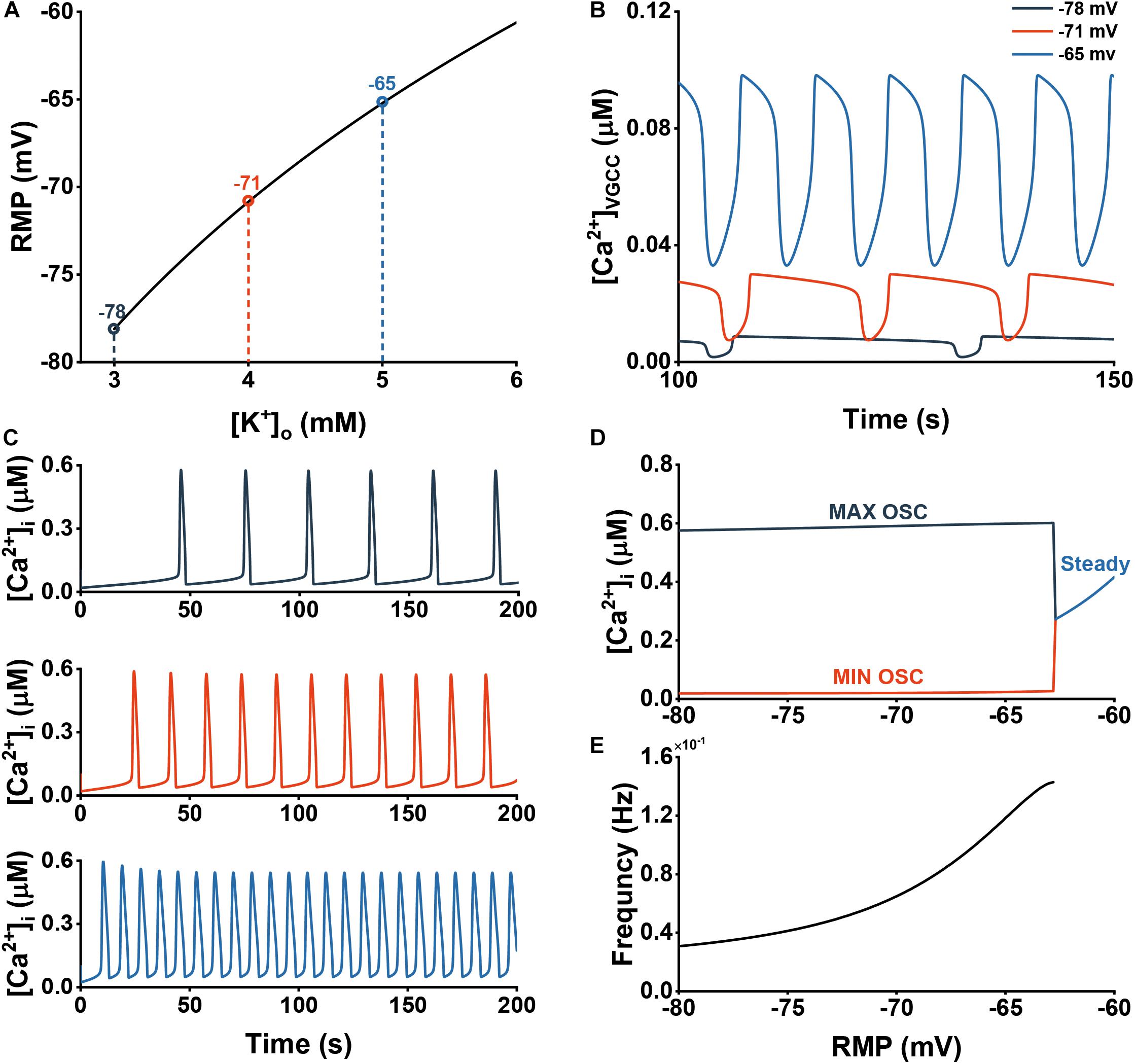
Figure 5. Extracellular K⁺ increases the frequency of Ca²⁺ oscillations through activation of VGCCs. (A) The dependency of the astrocytic RMP V_m of different [K⁺]_o. (B) Ca²⁺ influx through VGCCs at three different RMPs (–78, –71, and –65 mV). (C) Cytosolic Ca²⁺ dynamics at three different RMPs (–78, –71, and –65 mV). (D) Bifurcation diagram of the [Ca²⁺]_i in cytosol vs. RMP. (E) The frequency of the oscillations vs. RMP.

FIGURE 6

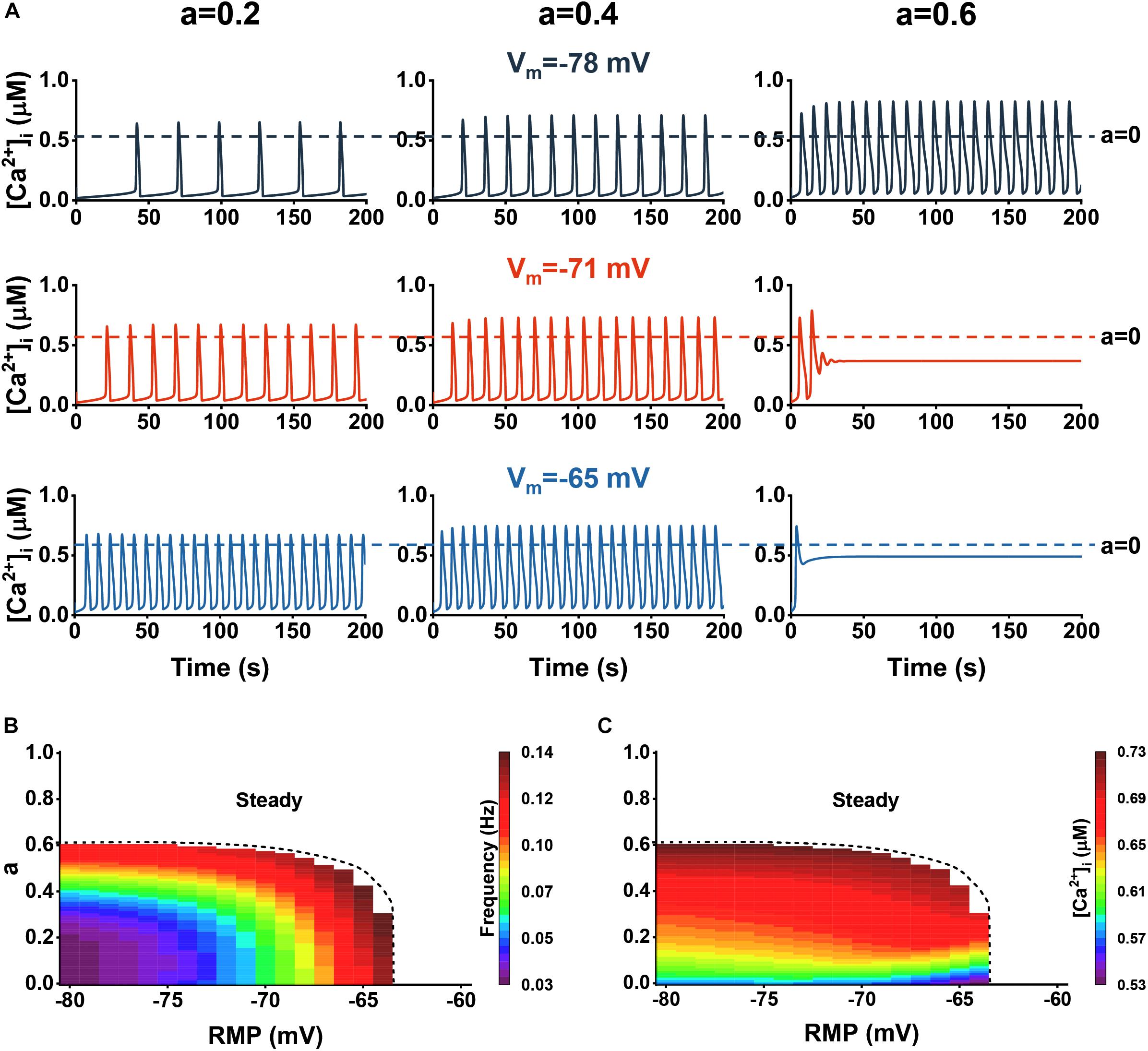
Figure 6. The influence of Aβ on Ca²⁺ dynamics with RMP. (A) Representative traces of Ca²⁺ dynamics within the three different Aβ levels (0.2, 0.4, and 0.6) at different V_m: –78, –71, and –65 mV. (B) The frequency of Ca²⁺ signals vs. Aβ levels and RMPs. (C) The amplitude of Ca²⁺ signals vs. Aβ levels and RMPs.

Figure 5A displays the dependence of V_m on [K]_o. We then chose three different values of V_m with [K]_o of 3, 4, and 5 mM for our following simulations. Figure 5B shows how RMP significantly affect the J_VGCC. Both the amplitude and frequency increase with depolarization. These alterations in J_VGCC similarly affected [Ca²⁺]_i (Figure 5C). Through the bifurcation and frequency diagrams in Figures 5D,E, we could observe that before reaching steady state, [Ca²⁺]_i is very robust to RMP, but after entering steady state, it increases dramatically. In contrast, the frequency consistently shows an increasing trend.

We induced Aβ and studied the interactions between the two factors. Figure 6A shows the cytosolic Ca²⁺ dynamics vs. three different RMP (−78, −71, and −65 mV) and three different Aβ levels (0.2, 0.4, and 0.6). In Figures 6B,C, we show the analysis of the frequency and amplitude of cytosolic Ca²⁺ dynamics, respectively. For the range where oscillation emerged (about −80 to −64 mV), the higher the RMP, the more profoundly affected by Aβ, since only a little Aβ is required to disrupt the oscillations. However, when at a high Aβ level, the range rapidly narrowed and eventually disappeared, indicating that the astrocytes will always be in the steady state with a high [Ca²⁺]_i. In the research scope, increasing Aβ and RMP will lead to the increase of amplitude and frequency, in which the influence of the two on the amplitude is close while Aβ has a more significant contribution to the increase of calcium amplitude than the RMP.

Blocking Aβ-Affected Pathways Benefits the Recovery of Calcium Homeostasis

At present, the treatment of AD remains a challenging research hotspot. There are four FDA-approved prescription drugs (Vaz and Silvestre, 2020) that show some effectiveness; however, they only relieve symptoms. Here, we tested the effects of blocking channels, receptors and products affected by Aβ as described above. We characterized the effect of recovery as a function of the blocking ratio of specific parameters and investigated their respective sensitivities at three different Aβ levels of a = 0.2, a = 0.4 and a = 0.6, which represented different stages of the disease. Results are shown in Figure 7.

FIGURE 7

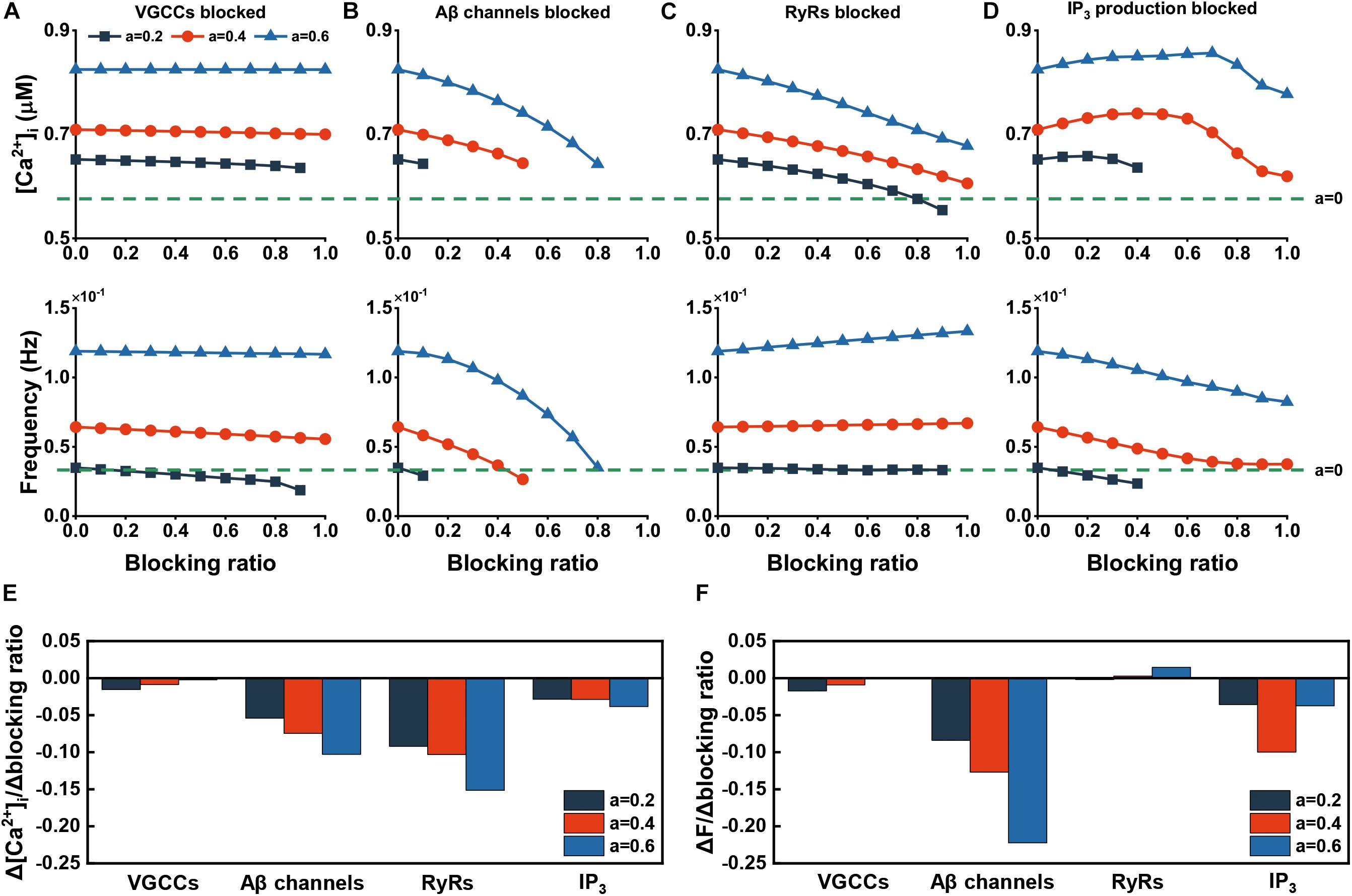
Figure 7. Effect of blocking channels, receptors, and products. (A–D) The changes in amplitude and frequency after different blocking ratios of related channels, receptors, and products. The green dashed line represents the absence of Aβ. (E) Amplitude sensitivity of recovery effect. The sensitivities are calculated by the slope in (A–D). (F) Frequency sensitivity of recovery effect. The sensitivities are calculated by the slope in (A–D).

If we blocked VGCCs, as you can see in Figure 7A, therapy of this pathway shows a weak effect to the recovery of [Ca²⁺]_i. For frequency, this method can restore the frequency to normal at the low level of Aβ (a = 0.2), but when at the high level, even the channel is completely blocked, it fails to do so. Inhibition of membrane leak flux obtains effective results with the ability to reduce the frequency and amplitude of abnormal rise (Figure 7B). Blocking RyRs has a certain effect on the recovery of elevated [Ca²⁺]_i, but the recovery is not obvious and even has an adverse effect at a higher Aβ level for frequency (Figure 7C). Reducing the production rate of IP₃ can help to low down the increased frequency. However, this way contributes to decreasing [Ca²⁺]_i only at high inhibition ratio (Figure 7D). Illustrated in Figures 7E,F are quantitative sensitivity analysis of the recovery of [Ca²⁺]_i and frequency, respectively. Overall, targeting J_in has the best effect, followed by RyR blockade, and blocking VGCCs has the least effect.

In Figure 8, different strategies based on our sensitivity analysis are applied to restore calcium homeostasis for two different situations (a = 0.2 and a = 0.6). When a = 0.2 representing the early stage of the disease, there exists significant variation in frequency. However, the abnormal signals can recover to some extent by simply inhibited the RyR pathway by 80% (Figure 8A). When a = 0.6 representing the advanced stage of the disease in which both frequency and [Ca²⁺]_i are markedly affected, targeting only one pathway is powerless. With the “combination therapy”, we can not only get the ideal recovery effect, but also carry out the treatment with more than one strategy (Figure 8B).

FIGURE 8

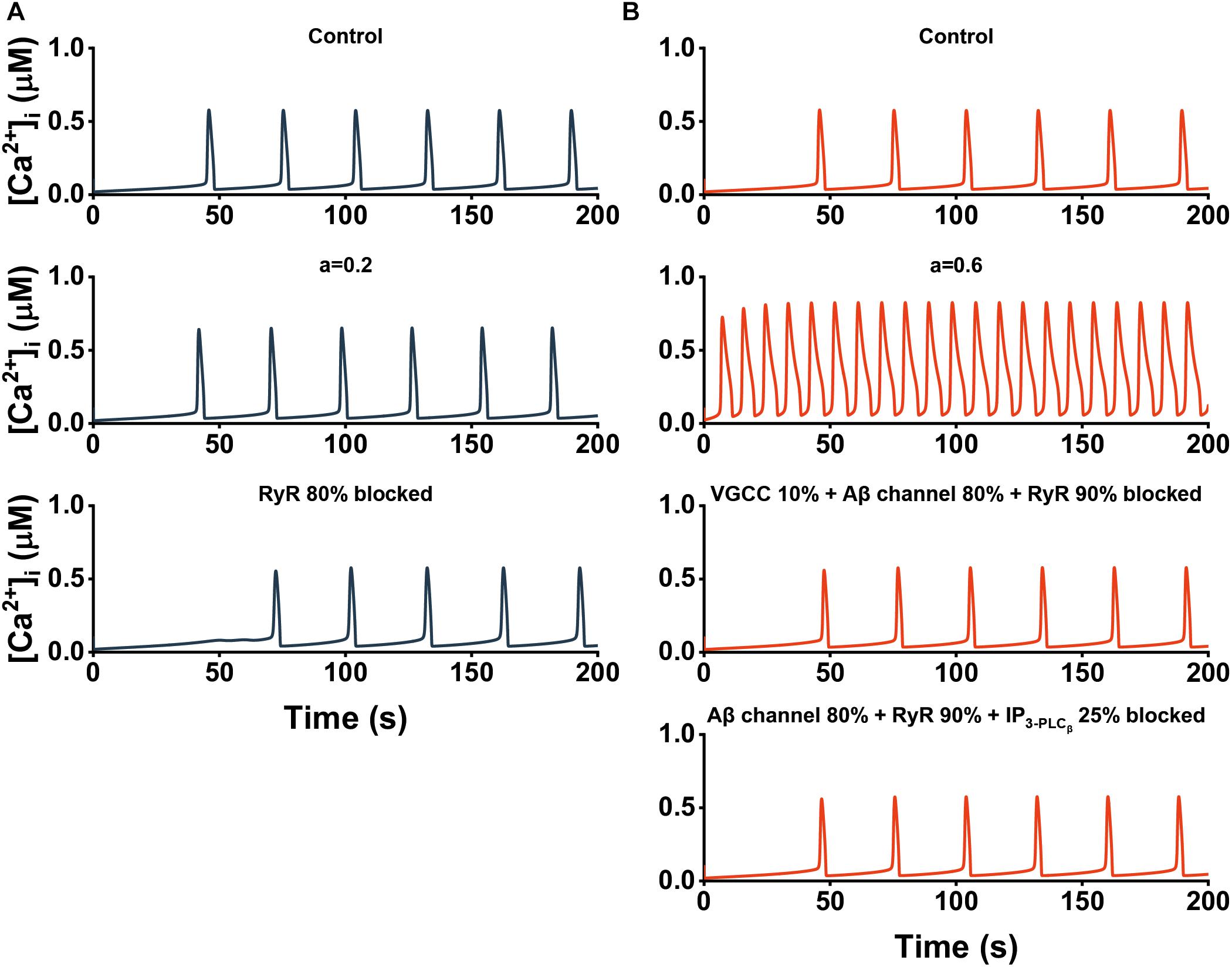
Figure 8. The cytosolic Ca²⁺ dynamics after treatment. (A) Effect of single therapy at the early stage of AD. Top, a = 0. Middle, a = 0.2. Bottom, a = 0.2 + single therapy. (B) Effect of “combination therapy” at the advanced stage of AD. Top, a = 0. Middle, a = 0.6. Bottom, a = 0.6 + two different “combination therapies.”

Discussion

With a rapidly aging population, AD has become a major public health concern. However, the causation of AD remains unclear. Dysregulation of astrocytic Ca²⁺ has been widely regarded as an important component of AD. While controversy still remains, because some researches have not found acute [Ca²⁺]_i responses to Aβ (Casley et al., 2009; Toivari et al., 2011), this could possibly be attributed to the variability of Aβ species (monomers, oligomers, fibrils) and astrocyte types (from different brain areas) (Lim et al., 2014). More experiments reported that Aβ triggered transient [Ca²⁺]_i increases or [Ca²⁺]_i oscillations in astrocytes (Jalonen et al., 1997; Abramov et al., 2003; Alberdi et al., 2013; Lim et al., 2014). Unfortunately, the interactions of various mechanisms make it difficult to precisely understand how Aβ impacts cytosolic Ca²⁺ levels and individual fluxes. Decoupling various components and integrating their contributions into a full view may help us better understand the complexity of Aβ mechanisms in intracellular calcium dysregulation.

Computational modeling is a powerful approach that provides great opportunities to study complex mechanisms since it is experimentally difficult to isolate each component for separate studies. Our previous work on bioRxiv (Gao et al., 2020) has proposed a model related to AD focusing on the effect of Aβ through four different pathways on cytosolic Ca²⁺. Although we have considered a multi-pathway model, there is still room for more in-depth study of the individual contribution of Aβ on each pathway and methods of restoring the disrupted signals. There are also some limitations to the model itself. Specifically, for example, our prior study has only included the PLCδ-dependent production while IP₃ is regulated by two entirely different pathways in astrocytes. Also, differences in volume of cytosol and ER, and changes in membrane potential were neglected. These all deserve rigorous consideration and continued refinement.

In this paper, we modified and extended the previous studies in conjunction with experimental data and a comprehensive model was proposed. Not only all the issues mentioned are considered, but also the model is more physiologically reasonable. Just as important, the brevity and universality of the modeling method are worth noting. We previously used Lavrentovich’s model (Lavrentovich and Hemkin, 2008) to describe CICR dynamics depended on [IP₃] and [Ca²⁺]_i from both the ER and cytosol. However, a form simplified from De Young’s model (De Young and Keizer, 1992) by Li (Li and Rinzel, 1994) based on the gating of IP₃R provides good agreement with experimental recordings of channel opening and is more suitable for biophysical modeling. These, then, make a model more compatible with physiological data, providing good foundations for simulation studies of AD-induced dysregulation of astrocytic Ca²⁺.

In the experimental studies, Jalonen et al. (1997) exposed astrocytes to 1 μM Aβ and found that transient increase in [Ca²⁺]_i rose from about 0.6 to 0.9 μM. Takano et al. (2007) reported that after the injection of Aβ in both Dutch/Iowa mice and controls, the frequency of astrocytic Ca²⁺ oscillations increased significantly and became approximately three times as the control group. In our model, similar results were observed. The [Ca²⁺]_i and frequency are about 0.83 μM and 0.12 Hz when a = 0.6, compared to 0.58 μM and 0.034 Hz when a = 0. This means that our model has a good physiological agreement. Besides, we also found that the accumulation of Aβ not only leads to the increase of [Ca²⁺]_i and frequency in astrocytes, but also makes a transition from oscillation to a high steady state after exceeding a certain threshold, in which, the intracellular [Ca²⁺]_i will remain at a very high level, and this level will continue to rise rapidly with the increase of Aβ. In AD, the high intracellular [Ca²⁺]_i directly impacts memory formation and consolidation (Berridge, 2014).

Upregulation of astrocytic VGCCs expression in astrocytes has been indicated in pathological conditions, especially the L-Type in AD. Our model shows that VGCCs may contribute less to the dysregulation of cytosolic Ca²⁺ levels. This is because [Ca²⁺]_i is very robust either under high strength of the effect of Aβ or a large amount of Aβ. Even when there is a clear change in frequency, the sensitivity is low relative to the changes in Aβ. In response to the disruptions, Anekonda et al. (2011) have demonstrated that L-type Ca²⁺ current blockers can protect cells from the inductive effect of Aβ. We did confirm the efficacy of blocking VGCCs, but the recovery was not significant enough.

Aβ has been shown to impair the membrane permeability, due to the Aβ-formed pores resulting in the increase of Ca²⁺ influx through the membrane (Demuro et al., 2010). This additional influx shows damage to astrocytic homeostasis in our simulations. Especially, when oscillations disappear and the astrocyte calcium level is at a high steady state, Aβ can cause dramatic increases in [Ca²⁺]_i. In fact, channel formation has been already proposed as a molecular mechanism for Aβ toxicity in the early 1990s (Arispe et al., 1993), and our model, in the light of physiology, has well reflected how ionic leakage strongly affects and rapidly disrupts the cellular homeostasis. This intense pathology can be treated with Zn²⁺ (Abramov et al., 2003). We demonstrated that blocking the channel achieves desirable effects and may serve as a promising therapeutic approach.

Although disruptions on the membrane by Aβ are believed to be an important mechanism, the intracellular signaling pathways also deserve attention. In this study, we reflect the toxic effects of Aβ by increasing the channel open probability of RyRs. Other studies also suggested that Aβ can directly increase the RyR expression (Supnet et al., 2006). The increasing [Ca²⁺]_i and unchanged low steady state were observed. Unlike the other pathways, Aβ caused a decrease in frequency, which was more rapid in the presence of large amounts of Aβ because of the occurrence of mixed oscillations. Research has reported that RyR-mediated Ca²⁺ release can be reduced after treatment with RyR inhibitor (Oulès et al., 2012). Results showed a significant therapeutic effect on abnormal high [Ca²⁺]_i in our study.

Accumulated evidence indicates that Aβ is involved in the regulation of IP₃ production in AD (Demuro and Parker, 2013; Jensen et al., 2013). In this paper, we considered both Aβ-mediated channels or receptors, as well as non-directly acting intermediates such as IP₃, which embodies the concept of “multi-pathway” in a true sense and illustrates the complexity of our model. According to the results of the simulation, increasing IP₃ levels can lead to the decrease of [Ca²⁺]_i but the increase of frequency. The recovery effect is stronger than the blockage of VGCCs but not as effective as the other two pathways. Reducing the intracellular IP₃ level has a certain effect on frequency recovery, but the recovery effect on [Ca²⁺]_i is not ideal. This may reveal that IP₃ mainly regulates the frequency of intracellular calcium signals.

The RMP of astrocytes is also a contributing factor within our consideration. Compared to their neuronal counterparts, astrocytes display a highly negative RMP (Bolton et al., 2006). Some studies have shown that [K⁺]_o is critical in establishing the RMP of astrocytes (Anderson et al., 1995; Bellot-Saez et al., 2017). However, defective extracellular K⁺ clearance mechanisms have also been observed in AD which led to the loss of astrocyte polarization (Olabarria et al., 2010). Our model shows that increasing [K⁺]_o contributes to astrocyte depolarization, which to some extent reflects the impairment of astrocyte polarization by abnormal accumulation of [K⁺]_o in AD. During the process of depolarization, the amplitude of transmembrane Ca²⁺ flow mediated by VGCCs, as well as frequency increases. The affected J_VGCC, in turn, will cause further damage to cytosolic Ca²⁺ dynamics, manifested primarily by a large increase in [Ca²⁺]_i at steady state and a marked increase in frequency. This finding suggests that the frequency of Ca²⁺ events can be increased by depolarization of astrocytes, through activating of VGCCs. On the other hand, the accumulation of Aβ can narrow the range of membrane potential where oscillations are triggered. This may indicate the destructive nature of Aβ to synchronization oscillation of astrocyte network. Besides, astrocyte RMP displays extensive heterogeneity in the central nervous system (McNeill et al., 2021). To a certain extent, our model also reflects the characteristics of astrocytes with different RMP.

Finding a cure for AD is one of the most urgent and difficult tasks in modern medicine. At present, the drugs that are used to treat AD can only relieve symptoms but cannot slow down or reverse the progression of the disease (Alzheimer’s Association, 2020). The recent development and FDA approval of the AD drug Aducanumab, which targets Aβ, caused a great controversy (Vaz and Silvestre, 2020). But there is no doubt that drug research targeting Aβ or Tau proteins has once fallen into a bottleneck (Congdon and Sigurdsson, 2018; Foroutan et al., 2019), so it is advisable to explore feasible therapies from the perspective of Ca²⁺ dynamics. Mounting evidence has demonstrated that calcium signals play an indispensable role in AD (Yu et al., 2009), but Ca²⁺-pathway therapeutics remain undeveloped. Our simulations suggested that therapy targeting a specific receptor, channel or product is efficacious but limited because of multiple targets of Aβ, particularly in the terminal stages of the disease. Meanwhile, combination therapy can perfectly compensate for the shortage of single therapy. Generally, restoring calcium homeostasis is useful and necessary (Lim et al., 2014). Memantine, approved for the treatment of AD, has been clinically proven to be effective in preventing NMDAR-mediated calcium flux for decades, and here, we have demonstrated that other Ca²⁺ pathways in astrocytes may also be potential therapeutic targets and unraveled which Ca²⁺ pathway is effective because it is also likely to bring significant side-effects if the pathway is not carefully chosen.

It is challenging to establish a model of Aβ-mediated multi-pathway calcium dynamics. Although several mechanisms by which Aβ affects astrocytes have been experimentally demonstrated, how some of these mechanisms occur remains unclear. But the ubiquitous Ca²⁺ regulatory fluxes used in our model make it easily applicable for studying various cell types with spatial components. In fact, astrocytes exhibit a very complex morphology suggesting the spatiotemporal characteristics of Ca²⁺ signals in different structures (Semyanov et al., 2020) while we considered a spatially homogeneous astrocyte for better quantifying. However, even by adopting some simplifications, our model includes a large number of parameters, some of which still lack the effectiveness of the verification experiment. Our deterministic model generated regular calcium oscillations, which is consistent with the situation in some reports (Parri and Crunelli, 2001; Tashiro et al., 2002), However, in most cases, the calcium signals observed in the experiments presented clear irregularities which revealed its stochastic nature, meaning that some level of stochasticity may be closer to the physiology. All the deficiencies can be altered in future follow-up work as we continue to improve our understanding of the effects of Aβ in the astrocytic system. Our codes are publicly available for reproducibility, assisting with fast, convenient, and accurate validation of the model. Moreover, continuous improvement of the model combined with experimental data helps to make the model more useful.

In general, we have presented a hypothetical AD-specific model regarding Ca²⁺ dysregulation in astrocytes. The proposed general model incorporates multiple critical individually modeled Ca²⁺ mechanisms into a single framework, which obtains a more comprehensive picture compared to present work, especially fewer models are containing VGCCs and RyRs in astrocytes. To our knowledge, this is one of the few computational models to investigate the contribution of various Ca²⁺ fluxes to Ca²⁺ dynamics including entry and release under the influence of Aβ. Furthermore, we tested methods of blocking affected pathways. The “combination therapy” was first proposed and showed the significant effects on restoring calcium homeostasis. This may provide factual predictions for future drug development. Our study can provide an in-depth understanding of AD and pave the way toward the development of much more effective treatment modalities.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

SC, HG, and AZ conceived and designed the research. LL and HG conducted literature research and wrote MATLAB code. LL, SC, and HG performed simulations and analyzed data and discussed the results and wrote the article with input from AZ. SC supervised the study. LL plotted pictures. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 91749209), and the Director Fund of WNLO. AZ thanks MRC grant MR/R02524X/1 and the Ministry of Science and Higher Education of the Russian Federation within the framework of state support for the creation and development of World-Class Research Centers “Digital biodesign and personalized healthcare” No. 075-15-2020-926.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to thank Dr. Yicheng Xie and Ms. Jinyu Li for helpful suggestions and revisions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2021.767892/full#supplementary-material

References

Abramov, A. Y., Canevari, L., and Duchen, M. R. (2003). Changes in intracellular calcium and glutathione in astrocytes as the primary mechanism of amyloid neurotoxicity. J. Neurosci. 23, 5088–5095. doi: 10.1016/S0361-9230(03)00055-8

CrossRef Full Text | Google Scholar

Agulhon, C., Petravicz, J., McMullen, A. B., Sweger, E. J., Minton, S. K., Taves, S. R., et al. (2008). What is the role of astrocyte calcium in neurophysiology? Neuron 59, 932–946. doi: 10.1016/j.neuron.2008.09.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Alberdi, E., Wyssenbach, A., Alberdi, M., Sánchez-Gómez, M. V., Cavaliere, F., Rodríguez, J. J., et al. (2013). Ca^{2 +}-dependent endoplasmic reticulum stress correlates with astrogliosis in oligomeric amyloid β-treated astrocytes and in a model of Alzheimer’s disease. Aging Cell 12, 292–302. doi: 10.1111/acel.12054

PubMed Abstract | CrossRef Full Text | Google Scholar

Alves, V. S., Alves-Silva, H. S., Orts, D. J., Ribeiro-Silva, L., Arcisio-Miranda, M., and Oliveira, F. A. (2019). Calcium signalling in neurons and glial cells: role of Ca_v1 channels. Neuroscience 421, 95–111. doi: 10.1016/j.neuroscience.2019.09.041

PubMed Abstract | CrossRef Full Text | Google Scholar

Alzheimer’s Association (2020). 2020 Alzheimer’s disease facts and figures. Alzheimers Dement. 16, 391–460. doi: 10.1002/alz.12068

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, S., Brismar, T., and Hansson, E. (1995). Effect of external K⁺, Ca^{2 +}, and Ba^{2 +} on membrane potential and ionic conductance in rat astrocytes. Cell Mol. Neurobiol. 15, 439–450. doi: 10.1007/BF02071879

PubMed Abstract | CrossRef Full Text | Google Scholar

Anekonda, T. S., Quinn, J. F., Harris, C., Frahler, K., Wadsworth, T. L., and Woltjer, R. L. (2011). L-type voltage-gated calcium channel blockade with isradipine as a therapeutic strategy for Alzheimer’s disease. Neurobiol. Dis. 41, 62–70. doi: 10.1016/j.nbd.2010.08.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Arispe, N., Rojas, E., and Pollard, H. B. (1993). Alzheimer disease amyloid beta protein forms calcium channels in bilayer membranes: blockade by tromethamine and aluminum. Proc. Natl. Acad. Sci. U.S.A. 90, 567–571. doi: 10.1073/pnas.90.2.567

PubMed Abstract | CrossRef Full Text | Google Scholar

Aupperle, P. M. (2006). Navigating patients and caregivers through the course of Alzheimer’s disease. J. Clin. Psychiatry. 67 Suppl 3, 8–23.

Google Scholar

Bazargani, N., and Attwell, D. (2016). Astrocyte calcium signalling: the third wave. Nat. Neurosci. 19, 182–189. doi: 10.1038/nn.4201

PubMed Abstract | CrossRef Full Text | Google Scholar

Bellot-Saez, A., Kekesi, O., Morley, J. W., and Buskila, Y. (2017). Astrocytic modulation of neuronal excitability through K⁺ spatial buffering. Neurosci. Biobehav. Rev. 77, 87–97. doi: 10.1016/j.neubiorev.2017.03.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Berridge, M. J. (2014). Calcium regulation of neural rhythms, memory and Alzheimer’s disease. J. Physiol. 592, 281–293. doi: 10.1113/jphysiol.2013.257527

PubMed Abstract | CrossRef Full Text | Google Scholar

Birch, A. M. (2014). The contribution of astrocytes to Alzheimer’s disease. Biochem. Soc. Trans. 42, 1316–1320. doi: 10.1042/BST20140171

PubMed Abstract | CrossRef Full Text | Google Scholar

Bolton, S., Greenwood, K., Hamilton, N., and Butt, A. M. (2006). Regulation of the astrocyte resting membrane potential by cyclic AMP and protein kinase A. Glia 54, 316–328. doi: 10.1002/glia.20384

PubMed Abstract | CrossRef Full Text | Google Scholar

Briggs, C. A., Schneider, C., Richardson, J. C., and Stutzmann, G. E. (2013). Beta amyloid peptide plaques fail to alter evoked neuronal calcium signals in APP/PS1 Alzheimer’s disease mice. Neurobiol. Aging 34, 1632–1643. doi: 10.1016/j.neurobiolaging.2012.12.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Canter, R. G., Penney, J., and Tsai, L.-H. (2016). The road to restoring neural circuits for the treatment of Alzheimer’s disease. Nature 539, 187–196. doi: 10.1038/nature20412

PubMed Abstract | CrossRef Full Text | Google Scholar

Carmignoto, G., and Gómez-Gonzalo, M. (2010). The contribution of astrocyte signalling to neurovascular coupling. Brain Res. Rev. 63, 138–148. doi: 10.1016/j.brainresrev.2009.11.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Casley, C. S., Lakics, V., Lee, H. G., Broad, L. M., Day, T. A., Cluett, T., et al. (2009). Up-regulation of astrocyte metabotropic glutamate receptor 5 by amyloid-β peptide. Brain Res. 1260, 65–75. doi: 10.1016/j.brainres.2008.12.082

PubMed Abstract | CrossRef Full Text | Google Scholar

Charles, A. C., Merrill, J. E., Dirksen, E. R., and Sanderson, M. J. (1991). Intercellular signalling in glial cells: calcium waves and oscillations in response to mechanical stimulation and glutamate. Neuron 6, 983–992. doi: 10.1016/0896-6273(91)90238-u

CrossRef Full Text | Google Scholar

Congdon, E. E., and Sigurdsson, E. M. (2018). Tau-targeting therapies for Alzheimer disease. Nat. Rev. Neurol. 14, 399–415. doi: 10.1038/s41582-018-0013-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Cutsuridis, V., and Moustafa, A. A. (2017). Computational models of Alzheimer’s disease. Scholarpedia 12:32144. doi: 10.4249/scholarpedia.32144

CrossRef Full Text | Google Scholar

De Caluwé, J., and Dupont, G. (2013). The progression towards Alzheimer’s disease described as a bistable switch arising from the positive loop between amyloids and Ca²⁺. J. Theor. Biol. 331, 12–18. doi: 10.1016/j.jtbi.2013.04.015

PubMed Abstract | CrossRef Full Text | Google Scholar

De Pittà, M., Goldberg, M., Volman, V., Berry, H., and Ben-Jacob, E. (2009). Glutamate regulation of calcium and IP₃ oscillating and pulsating dynamics in astrocytes. J. Biol. Phys. 35, 383–411. doi: 10.1007/s10867-009-9155-y

PubMed Abstract | CrossRef Full Text | Google Scholar

De Young, G. W., and Keizer, J. (1992). A single-pool inositol 1,4,5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca^{2 +} concentration. Proc. Natl. Acad. Sci. U.S.A. 89, 9895–9899. doi: 10.1073/pnas.89.20.9895

PubMed Abstract | CrossRef Full Text | Google Scholar

Demuro, A., and Parker, I. (2013). Cytotoxicity of intracellular aβ₄₂ amyloid oligomers involves Ca^{2 +} release from the endoplasmic reticulum by stimulated production of inositol trisphosphate. J. Neurosci. 33, 3824–3833. doi: 10.1523/JNEUROSCI.4367-12.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

Demuro, A., Parker, I., and Stutzmann, G. E. (2010). Calcium signalling and amyloid toxicity in Alzheimer disease. J. Biol. Chem. 285, 12463–12468. doi: 10.1074/jbc.R109.080895

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, X., Zhang, X., and Ji, L. (2018). Contribution of calcium fluxes to astrocyte spontaneous calcium oscillations in deterministic and stochastic models. Appl. Math. Model. 55, 371–382. doi: 10.1016/j.apm.2017.11.002

CrossRef Full Text | Google Scholar

Dubitzky, W., Wolkenhauer, O., Cho, K. H., and Yokota, H. (2013). Encyclopedia of Systems Biology. New York, NY: Springer.

Google Scholar

Dupont, G., Falcke, M., Kirk, V., and Sneyd, J. (2016). Models of Calcium Signalling. New York, NY: Springer.

Google Scholar

Dupont, G., Lokenye, E. F. L., and Challiss, R. A. J. (2011). A model for Ca^{2 +} oscillations stimulated by the type 5 metabotropic glutamate receptor: an unusual mechanism based on repetitive, reversible phosphorylation of the receptor. Biochimie 93, 2132–2138. doi: 10.1016/j.biochi.2011.09.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Foroutan, N., Hopkins, R. B., Tarride, J.-E., Florez, I. D., and Levine, M. (2019). Safety and efficacy of active and passive immunotherapy in mild-to-moderate Alzheimer’s disease: a systematic review and network meta-analysis. Clin. Invest. Med. 42:E53–E65. doi: 10.25011/cim.v42i1.32393

PubMed Abstract | CrossRef Full Text | Google Scholar

Friel, D. D. (1995). [Ca^{2 +}]_i oscillations in sympathetic neurons: an experimental test of a theoretical model. Biophys. J. 68, 1752–1766. doi: 10.1016/S0006-3495(95)80352-8

CrossRef Full Text | Google Scholar

Gao, H., Liu, L., and Chen, S. (2020). Simulation of Ca^{2 +} oscillations in astrocytes mediated by amyloid beta in Alzheimer’s disease. bioRxiv [Preprint] doi: 10.1101/2020.03.18.996843

CrossRef Full Text | Google Scholar

Goussakov, I., Miller, M. B., and Stutzmann, G. E. (2010). NMDA-mediated Ca^{2 +} influx drives aberrant ryanodine receptor activation in dendrites of young Alzheimer’s disease mice. J. Neurosci. 30, 12128–12137. doi: 10.1523/JNEUROSCI.2474-10.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Hardy, J., and Selkoe, D. J. (2002). The amyloid hypothesis of Alzheimer’s disease: progress and problems on the road to therapeutics. Science 297, 353–356. doi: 10.1126/science.1072994

PubMed Abstract | CrossRef Full Text | Google Scholar

Jalonen, T. O., Charniga, C. J., and Wielt, D. B. (1997). β-Amyloid peptide-induced morphological changes coincide with increased K⁺ and Cl^– channel activity in rat cortical astrocytes. Brain Res. 746, 85–97. doi: 10.1016/s0006-8993(96)01189-4

CrossRef Full Text | Google Scholar

Jensen, L. E., Bultynck, G., Luyten, T., Amijee, H., Bootman, M. D., and Roderick, H. L. (2013). Alzheimer’s disease-associated peptide Aβ₄₂ mobilizes ER Ca^{2 +} via InsP₃R-dependent and -independent mechanisms. Front. Mol. Neurosci. 6:36. doi: 10.3389/fnmol.2013.00036

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuchibhotla, K. V., Lattarulo, C. R., Hyman, B. T., and Bacskai, B. J. (2009). Synchronous hyperactivity and intercellular calcium waves in astrocytes in Alzheimer mice. Science 323, 1211–1215. doi: 10.1126/science.1169096

PubMed Abstract | CrossRef Full Text | Google Scholar

Latulippe, J., Lotito, D., and Murby, D. (2018). A mathematical model for the effects of amyloid beta on intracellular calcium. PLoS One 13:e0202503. doi: 10.1371/journal.pone.0202503

PubMed Abstract | CrossRef Full Text | Google Scholar

Lavrentovich, M., and Hemkin, S. (2008). A mathematical model of spontaneous calcium (II) oscillations in astrocytes. J. Theor. Biol. 251, 553–560. doi: 10.1016/j.jtbi.2007.12.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y. X., and Rinzel, J. (1994). Equations for InsP₃ receptor-mediated [Ca^{2 +}]_i oscillations derived from a detailed kinetic model: a hodgkin-huxley like formalism. J. Theor. Biol. 166, 461–473. doi: 10.1006/jtbi.1994.1041

PubMed Abstract | CrossRef Full Text | Google Scholar

Lim, D., Iyer, A., Ronco, V., Grolla, A. A., Canonico, P. L., Aronica, E., et al. (2013). Amyloid beta deregulates astroglial mGluR₅-mediated calcium signalling via calcineurin and Nf-kB. Glia 61, 1134–1145. doi: 10.1002/glia.22502

PubMed Abstract | CrossRef Full Text | Google Scholar

Lim, D., Ronco, V., Grolla, A. A., Verkhratsky, A., and Genazzani, A. A. (2014). Glial calcium signalling in Alzheimer’s disease. Rev. Physiol. Biochem. Pharmacol. 167, 45–65. doi: 10.1007/112

CrossRef Full Text | Google Scholar

Liu, P. P., Xie, Y., Meng, X. Y., and Kang, J. S. (2019). History and progress of hypotheses and clinical trials for Alzheimer’s disease. Signal. Transduct. Target Ther. 4:29. doi: 10.1038/s41392-019-0063-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Lynch, C. (2020). World Alzheimer report 2019-attitudes to dementia, global survey. Alzheimers Dement. 16:e038255.

Google Scholar

Manninen, T., Havela, R., and Linne, M.-L. (2018). Computational models for calcium-mediated astrocyte functions. Front. Comput. Neurosci. 12:14. doi: 10.3389/fncom.2018.00014

PubMed Abstract | CrossRef Full Text | Google Scholar

Markowetz, F. (2017). All biology is computational biology. PLoS Biol. 18:e2002050. doi: 10.1371/journal.pbio.2002050

PubMed Abstract | CrossRef Full Text | Google Scholar

Mattson, M. P., and Chan, S. L. (2003). Neuronal and glial calcium signalling in Alzheimer’s disease. Cell Calcium 34, 385–397. doi: 10.1016/j.biosystems.2015.05.003

PubMed Abstract | CrossRef Full Text | Google Scholar

McNeill, J., Rudyk, C., Hildebrand, M. E., and Salmaso, N. (2021). Ion channels and electrophysiological properties of astrocytes: implications for emergent stimulation technologies. Front. Cell Neurosci. 15:644126. doi: 10.3389/fncel.2021.644126

PubMed Abstract | CrossRef Full Text | Google Scholar

Olabarria, M., Noristani, H. N., Verkhratsky, A., and Rodríguez, J. J. (2010). Concomitant astroglial atrophy and astrogliosis in a triple transgenic animal model of Alzheimer’s disease. Glia 58, 831–838. doi: 10.1002/glia.20967

PubMed Abstract | CrossRef Full Text | Google Scholar

Oulès, B., Del Prete, D., Greco, B., Zhang, X., Lauritzen, I., Sevalle, J., et al. (2012). Ryanodine receptor blockade reduces amyloid-β load and memory impairments in Tg2576 mouse model of Alzheimer disease. J. Neurosci. 32, 11820–11834. doi: 10.1523/JNEUROSCI.0875-12.2012

PubMed Abstract | CrossRef Full Text | Google Scholar

Parri, H. R., and Crunelli, V. (2001). Pacemaker calcium oscillations in thalamic astrocytes in situ. Neuroreport 12, 3897–3900. doi: 10.1097/00001756-200112210-00008

PubMed Abstract | CrossRef Full Text | Google Scholar

Prince, M. J. (2015). World Alzheimer Report 2015: The Global Impact of Dementia: An Analysis of Prevalence, Incidence, Cost and Trends. London: Alzheimer’s Disease International.

Google Scholar

Qian, X., Hamad, B., and Dias-Lalcaca, G. (2015). The Alzheimer disease market. Nat. Rev. Drug Discov. 14, 675–676. doi: 10.1038/nrd4749

PubMed Abstract | CrossRef Full Text | Google Scholar

Rebecchi, M. J., and Pentyala, S. N. (2000). Structure, function, and control of phosphoinositide-specific phospholipase C. Physiol. Rev. 80, 1291–1335. doi: 10.1152/physrev.2000.80.4.1291

PubMed Abstract | CrossRef Full Text | Google Scholar

Renner, M., Lacor, P. N., Velasco, P. T., Xu, J., Contractor, A., Klein, W. L., et al. (2010). Deleterious effects of amyloid beta oligomers acting as an extracellular scaffold for mGluR5. Neuron 66, 739–754. doi: 10.1016/j.neuron.2010.04.029

PubMed Abstract | CrossRef Full Text | Google Scholar

Rhee, S. G., and Bae, Y. S. (1997). Regulation of phosphoinositide-specific phospholipase C isozymes. J. Biol. Chem. 272, 15045–15048. doi: 10.1074/jbc.272.24.15045

PubMed Abstract | CrossRef Full Text | Google Scholar

Riera, J., Hatanaka, R., Uchida, T., Ozaki, T., and Kawashima, R. (2011b). Quantifying the uncertainty of spontaneous Ca^{2 +} oscillations in astrocytes: particulars of Alzheimer’s disease. Biophys. J. 101, 554–564. doi: 10.1016/j.bpj.2011.06.041

PubMed Abstract | CrossRef Full Text | Google Scholar

Riera, J., Hatanaka, R., Ozaki, T., and Kawashima, R. (2011a). Modelling the spontaneous Ca^{2 +} oscillations in astrocytes: inconsistencies and usefulness. J. Integra. Neurosci. 10, 439–473. doi: 10.1142/S0219635211002877

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadick, J. S., and Liddelow, S. A. (2019). Don’t forget astrocytes when targeting Alzheimer’s disease. Br. J. Pharmacol. 176, 3585–3598. doi: 10.1111/bph.14568

PubMed Abstract | CrossRef Full Text | Google Scholar

Semyanov, A., Henneberger, C., and Agarwal, A. (2020). Making sense of astrocytic calcium signals–from acquisition to interpretation. Nat. Rev. Neurosci. 21, 551–564. doi: 10.1038/s41583-020-0361-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Stutzmann, G. E., Smith, I., Caccamo, A., Oddo, S., LaFerla, F. M., and Parker, I. (2006). Enhanced ryanodine receptor recruitment contributes to Ca^{2 +} disruptions in young, adult, and aged Alzheimer’s disease mice. J. Neurosci. 26, 5180–5189. doi: 10.1523/JNEUROSCI.0739-06.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Supnet, C., Grant, J., Kong, H., Westaway, D., and Mayne, M. (2006). Amyloid-beta-(1-42) increases ryanodine receptor-3 expression and function in neurons of TgCRND8 mice. J. Biol. Chem. 281, 38440–38447. doi: 10.1074/jbc.M606736200

PubMed Abstract | CrossRef Full Text | Google Scholar

Taheri, M., Handy, G., Borisyuk, A., and White, J. A. (2017). Diversity of evoked astrocyte Ca^{2 +} dynamics quantified through experimental measurements and mathematical modelling. Front. Syst. Neurosci. 11:79. doi: 10.3389/fnsys.2017.00079

PubMed Abstract | CrossRef Full Text | Google Scholar

Takano, T., Han, X., Deane, R., Zlokovic, B., and Nedergaard, M. (2007). Two-photon imaging of astrocytic Ca^{2 +} signalling and the microvasculature in experimental mice models of Alzheimer’s disease. Ann. N. Y. Acad. Sci. 1097, 40–50. doi: 10.1196/annals.1379.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Tashiro, A., Goldberg, J., and Yuste, R. (2002). Calcium oscillations in neocortical astrocytes under epileptiform conditions. J. Neurobiol. 50, 45–55. doi: 10.1002/neu.10019

PubMed Abstract | CrossRef Full Text | Google Scholar

Tewari, S., and Majumdar, K. (2012). A mathematical model for astrocytes mediated LTP at single hippocampal synapses. J. Comput. Neurosci. 33, 341–370. doi: 10.1007/s10827-012-0389-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Tewari, S., and Parpura, V. (2013). A possible role of astrocytes in contextual memory retrieval: an analysis obtained using a quantitative framework. Front. Comput. Neurosci. 7:145. doi: 10.3389/fncom.2013.00145

PubMed Abstract | CrossRef Full Text | Google Scholar

Toivari, E., Manninen, T., Nahata, A. K., Jalonen, T. O., and Linne, M. L. (2011). Effects of transmitters and amyloid-beta peptide on calcium signals in rat cortical astrocytes: fura-2AM measurements and stochastic model simulations. PLoS One 6:e17914. doi: 10.1371/journal.pone.0017914

PubMed Abstract | CrossRef Full Text | Google Scholar

Ullah, G., Jung, P., and Cornell-Bell, A. H. (2006). Anti-phase calcium oscillations in astrocytes via inositol (1, 4, 5)-trisphosphate regeneration. Cell Calcium. 39, 197–208. doi: 10.1016/j.ceca.2005.10.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Vaz, M., and Silvestre, S. (2020). Alzheimer’s disease: recent treatment strategies. Eur. J. Pharmacol. 887:173554. doi: 10.1515/revneuro-2013-0056

PubMed Abstract | CrossRef Full Text | Google Scholar

Verkhratsky, A. (2019). Astroglial calcium signalling in aging and Alzheimer’s disease. Cold Spring Harb. Perspect. Biol. 11:a035188. doi: 10.1101/cshperspect.a035188

PubMed Abstract | CrossRef Full Text | Google Scholar

Verkhratsky, A., and Nedergaard, M. (2018). Physiology of astroglia. Physiol. Rev. 98, 239–389. doi: 10.1152/physrev.00042.2016

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, K. C., Kuo, C. S., Chao, C. C., Huang, C. C., Tu, Y. K., Chan, P., et al. (2015). Role of voltage-gated K⁺ channels in regulating Ca^{2 +} entry in rat cortical astrocytes. J. Physiol. Sci. 65, 171–177. doi: 10.1007/s12576-015-0356-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y. W., Gordleeva, S., Tang, X., Shih, P. Y., Dembitskaya, Y., and Semyanov, A. (2019). Morphological profile determines the frequency of spontaneous calcium events in astrocytic processes. Glia 67, 246–262. doi: 10.1002/glia.23537

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, J.-T., Chang, R. C.-C., and Tan, L. (2009). Calcium dysregulation in Alzheimer’s disease: from mechanisms to therapeutic opportunities. Prog. Neurobiol. 89, 240–255. doi: 10.1016/j.pneurobio.2009.07.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeng, S., Li, B., Zeng, S., and Chen, S. (2009). Simulation of spontaneous Ca^{2 +} oscillations in astrocytes mediated by voltage-gated calcium channels. Biophys. J. 97, 2429–2437. doi: 10.1016/j.bpj.2009.08.030

PubMed Abstract | CrossRef Full Text | Google Scholar