Qingqing Li1†Wenhui Xie1†Liping Li1†
Lijing Wang2Qinyi You1Lu Chen1Jing Li1
Yilang Ke1Jun Fang1Libin Liu2*
Huashan Hong1*- 1Fujian Key Laboratory of Vascular Aging, Department of Geriatrics, Department of Cardiology, Department of Cardiac Surgery, Fujian Heart Disease Center, Fujian Institute of Geriatrics, Fujian Medical University Union Hospital, Fuzhou, China
- 2Department of Endocrinology, Fujian Medical University Union Hospital, Fuzhou, China
Background: Arterial stiffness assessed by pulse wave velocity is a major risk factor for cardiovascular diseases. The incidence of cardiovascular events remains high in diabetics. However, a clinical prediction model for elevated arterial stiffness using machine learning to identify subjects consequently at higher risk remains to be developed.
Methods: Least absolute shrinkage and selection operator and support vector machine-recursive feature elimination were used for feature selection. Four machine learning algorithms were used to construct a prediction model, and their performance was compared based on the area under the receiver operating characteristic curve metric in a discovery dataset (n = 760). The model with the best performance was selected and validated in an independent dataset (n = 912) from the Dryad Digital Repository (https://doi.org/10.5061/dryad.m484p). To apply our model to clinical practice, we built a free and user-friendly web online tool.
Results: The predictive model includes the predictors: age, systolic blood pressure, diastolic blood pressure, and body mass index. In the discovery cohort, the gradient boosting-based model outperformed other methods in the elevated arterial stiffness prediction. In the validation cohort, the gradient boosting model showed a good discrimination capacity. A cutoff value of 0.46 for the elevated arterial stiffness risk score in the gradient boosting model resulted in a good specificity (0.813 in the discovery data and 0.761 in the validation data) and sensitivity (0.875 and 0.738, respectively) trade-off points.
Conclusion: The gradient boosting-based prediction system presents a good classification in elevated arterial stiffness prediction. The web online tool makes our gradient boosting-based model easily accessible for further clinical studies and utilization.
Introduction
Cardiovascular disease (CVD) remains the leading cause of death worldwide (Zhao et al., 2019). Arterial stiffness is a vascular measure that has been reported to predict cardiovascular events (Munakata, 2014). It is the common pathological basis for CVD, such as hypertension, atherosclerosis, and stroke, and has been linked to the aging cardiovascular continuum (O’Rourke et al., 2010; Donato et al., 2018; Zhang and Hong, 2019). Arterial stiffness increases with vascular aging due to gradual loss of arterial elasticity and is accelerated by conditions that increase cardiovascular risk, including diabetes mellitus (DM) (Horton et al., 2021). Clinically, brachial-ankle pulse wave velocity (baPWV) is a unique measure of systemic arterial stiffness (Munakata, 2014). Individuals with baPWV > 1400 cm/s are considered to have vascular aging (VA) (Sang et al., 2020), indicating a moderate risk level of the Framingham Risk Score (Yamashina et al., 2003) and increased risk of hypertension (Tomiyama et al., 2009; Wang Y. et al., 2016; Chen et al., 2017; Yang et al., 2018). Although considerable effort has been made to reduce the CVD risk, the number of individuals with elevated arterial stiffness risk for CVD is large and the application of the baPWV measurement is limited. Thus, the necessity of a simple and convenient clinical tool to assess elevated arterial stiffness in daily clinical practice is highlighted.
The development of a risk scoring system based on simple predictors, i.e., clinical data, is an important step toward the monitoring and diagnosis of elevated arterial stiffness. SAGE based on a multiple logistic regression (LG) was introduced as a method to predict elevated arterial stiffness (Xaplanteris et al., 2019). However, the LG-based approach fails to consider the complex non-linear interactions between variables, which can be captured by more sophisticated model algorithms, thus improving the accuracy of risk prediction. Recently, machine learning has been widely applied to the development of clinical tools for disease diagnosis (Rajkomar et al., 2019; de Gonzalo-Calvo et al., 2020; Zhang Z. et al., 2021). Unlike the traditional LG-based approach, machine learning can recognize hidden patterns and non-linear interactions in complex data, allowing for a better assessment of clinical outcomes (Myszczynska et al., 2020).
In this study, to our knowledge, we have developed the first machine learning-based clinical scoring system for elevated arterial stiffness in patients with diabetes, validating the model in an independent dataset from a Japanese cohort. We have also developed a user-friendly web application using this risk scoring system, allowing for further study and application of this system.
Materials and Methods
Patients
The discovery dataset included a total of 760 patients recruited from Fujian Medical University Union Hospital (Fujian, China) from April 2017 to January 2019. The inclusion criteria were as follows: patients diagnosed with DM (American Diabetes Association, 2019), older than 18 years, first visited our clinic, and underwent a baPWV test. The exclusion criteria were as follows: patients with an ankle-brachial index (ABI) less than 0.9 (Ato, 2018); diagnosis of severe arrhythmia, pulmonary, renal, rheumatic diseases, heart valve disease, aortopathy, and myocarditis; and antibiotic and probiotic usage in the past 3 months. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Medical Faculty of Fujian Medical University Union Hospital Ethics Committee (NO.: 2020KY031) and individual consent for this retrospective analysis was waived.
The validation dataset from an existing study from the Dryad Digital Repository1 (Fukuda et al., 2014b) was used to further evaluate the performance of the predictive model. A total of 912 patients from Murakami Memorial Hospital in Japan from March 2004 to December 2012 were recruited in this study. Detailed information about this cohort is described in the original study publication (Fukuda et al., 2014a).
Assessment of Elevated Arterial Stiffness and Measurement of Other Covariants
The automatic artery stiffness tester BP203RPE-II (VP-1000; Omron, Kyoto, Japan) was used to measure baPWV, blood pressure, and ABI. The patients were divided into two groups: baPWV ≥ 1,400 cm/s as the elevated arterial stiffness (EAS) group and baPWV < 1,400 cm/s as the non-EAS group (non-EAS).
A standardized questionnaire regarding demographic characteristics, blood test indicators, arterial elasticity indicators, hemodynamic parameters, echocardiographic parameters, and carotid artery ultrasound parameters was administered by the same trained team of interviewers. The body mass index (BMI) was based on the height and weight: BMI (kg/m2) = weight (kg)/height2 (m2). The estimated glomerular filtration rate (eGFR) was calculated according to the CKD-EPI formula (Biljak et al., 2017). The ascending aortic diameter (AO) and other parameters were measured via echocardiography according to the American Society of Echocardiography guidelines (Mitchell et al., 2019). The internal diameter of the common carotid artery and other parameters were measured by carotid vascular ultrasound. Alcohol consumption was categorized into two groups: no alcohol and > 30 g/week beginning at least 1 year after drinking (Yang et al., 2010). The smoking status was classified into two groups: non-smoker and current smoker (continuously smoking one or more cigarettes a day for at least 6 months) (Qian et al., 2010). Postmenopausal state was defined as amenorrhea for 12 consecutive months, excluding other pathological or physiological causes (Hamaguchi et al., 2012). Coronary heart disease was diagnosed according to the European Society of Cardiology (ESC) guidelines (Taylor, 2013). Hypertension was diagnosed according to the ESC guidelines (Williams et al., 2018). Diabetes was diagnosed according to the American Diabetes Association guidelines (American Diabetes Association, 2019). Carotid artery plaque was diagnosed according to the European Mannheim consensus (Touboul et al., 2012). Carotid intima-media thickness (CIMT) was evaluated using ultrasound, and CIMT > 1 mm signified the thickening of carotid intima (Guo et al., 2020).
Feature Selection
Least absolute shrinkage and selection operator (LASSO) is a compression estimation algorithm, which adds a penalty parameter to least squares regression to compress the estimated variables, thereby improving the prediction accuracy and interpretation of a model (Cecelja et al., 2020; Zhang K. et al., 2021). Thus, we used LASSO to select candidate variables. In addition, a support vector machine-recursive feature elimination (SVM-RFE) analysis was performed for variable selection (Wang L. et al., 2016). Finally, we combined variables from either the LASSO or SVM-RFE algorithm and then selected variables that are easily available in clinical practice for subsequent model development. LASSO and SVM-RFE were performed using glmnet (version 3.0−2) and e1071 (version 1.7−3) R packages, respectively.
Machine Learning and Parameter Tuning
Accurate prediction of EAS is important for clinical treatment decisions and can avoid excessive medical treatment caused by false-positive prediction. Thus, in this study, we aimed to achieve a simple and high-accuracy predictive model. Machine learning algorithms, including decision tree (DT), support vector machine (SVM), random forest (RF), and gradient boosting (GB), were used to construct the model, and then their performances were compared to determine the best model.
Decision tree is a tree structure model that consists of a root node and several internal nodes and leaf nodes. The root node contains all samples, each internal node represents a decision point corresponding to a single attribute, and each leaf represents a single class label (Podgorelec et al., 2002; Krzywinski and Altman, 2017). The sample was classified based on the structure of the DT model level by level. Given that DT has a high degree of transparency and is not affected by data scaling, we first used DT to construct the model. Although DT can provide a complete decision-making process for clinical problems, it often suffers from overfitting, which increases the complexity of the model and may result in poor performance on generalization. Thus, the second algorithm, SVM, with excellent generalization capability, is also used to construct an optimal classification hyperplane in an N-dimensional feature space (N: the number of features) to separate the two classes of data points. SVM is a supervised learning method based on the principle of structural risk minimization for classification prediction and non-linear regression (Nedaie and Najafi, 2018). Finally, ensemble learning methods including RF and GB, which aim to reduce the variance in models and further improve the accuracy of predictions by combining multiple models instead of using a single model, were used to develop the models. The RF model is based on the DT method, which parallelly combines a large number of DTs using bootstrap resampling to generate a model with a lower variance and better generalization than a single DT (Friedman, 2001). GB goes one step further, improving performance over iterations rather than averaging predictive results from all DTs in an RF (Friedman, 2001). GB generates a new DT based on previous DTs by reducing prediction errors when blended with previous ones.
To obtain optimal hyperparameters, the area under the receiver operating characteristic curve (AUROC) was evaluated based on a 10-fold cross-validation with different parameters in the discovery cohort. We tuned the complexity parameter for the DT model, the ntree and mtry parameters for the RF model, and multiple parameters (interaction.depth, n.tree, shrinkage, and n.minobsinnode) for the GB model. The SVM, DT, RF, and GB models were constructed using svm (version 1.4.0), rpart (version 4.1−15), randomForest (version 4.6−14), and gbm (version 2.1.5) R packages, respectively. p < 0.05 indicates a statistically significant difference.
Assessment of the Model Performance and Model Validation
The discovery data were randomly split into two groups 100 times: training data (70%) and testing data (30%). Each time, we first developed the four different machine learning models on the training data based on the previous tuning parameters. We then calculated the AUROC and area under the precision-recall curve (AUPRC) of the four machine learning algorithms on the testing data. Finally, we compared the values of AUROC and AUPRC from the four models to determine which model performed best. After selecting the best-performing model as the final model, we constructed the GB model using the full discovery data. Youden’s index was calculated to determine the best cutoff value of the GB model. To further validate the classification capacity of the GB model, we applied our trained GB model on an independent validation cohort. The ROC and PRC were analyzed using pROC (version 1.16.2) and PRROC (version 1.3.1) R packages, respectively.
Web Application Development
To develop a web application for EAS assessment that is applicable in daily clinical practice, we designed a web-based tool, an EAS predictor, allowing access to our final trained model. Specifically, we used front-end development technologies, Node.js (v12.14.0), React (v16.13.1), and Ant Design (v4.5.4), to simplify the development process. RestRserve (v0.3.0) back-end development technology was used to load the final trained model. Data required for prediction were received by the model using the TCP/IP method, and then the predictive result was returned. This web tool is hosted on our server, which is freely accessible via http://vascularagingpredictor.top/.
Statistical Analysis
The Kolmogorov–Smirnov (K–S) test was used to assess the normality of data. Continuous data with a normal distribution are presented as mean values ± standard deviation (SD), whereas continuous data with non-normal distribution are presented as median values (quartile). Student’s t-test was used for the comparison of continuous data following a normal distribution, and Mann–Whitney U test was used for the comparison of data with a non-normal distribution. Categorical data are presented as frequency (percentage), and comparisons between two groups were performed using the χ2 test or Fisher’s exact test (if theoretical frequency T < 5). The above statistical analysis was performed using R software 3.6.22.
Results
Subject Characteristics
This study enrolled 760 subjects with a mean age of 56 ± 12 years (60.1% male, 39.9% female). Based on the dividing value of 1,400 cm/s of baPWV, the subjects were divided into two groups: non-EAS and EAS. The complete data of patients include demographic information, chemistry indicators, diseases, hemodynamic parameters, and echocardiographic and carotid artery ultrasound parameters in each group (Table 1 and Supplementary Tables 1–3). A total of 230 patients with a mean age ± SD of 48 ± 13 (66.5% male, 33.5% female) are in the non-EAS group, whereas a total of 530 patients with age of 60 ± 9 (57.4% male, 42.6% female) are in the EAS group. Significant differences in baPWV values were observed between the non-EAS and EAS groups.
Table 1. Clinical characteristics of the patients.
Feature Selection
Two different algorithms, LASSO and SVM-RFE, were applied to select the most significant features for classifying individuals with normal (<1,400 cm/s) or abnormally elevated baPWV (≥1,400 cm/s). First, all features (a total of 99 variables) were included in the LASSO regression analysis and narrowed down to 15 features with non-zero β coefficients in the LASSO regression model (Figures 1A,B and Supplementary Table 4). Second, SVM-RFE was analyzed to select the top 15 important features (Supplementary Table 5). We combined features from either the LASSO or SVM-RFE algorithm, and then we further selected four variables (age, SBP, DBP, and BMI) that are easily available in clinical practice for subsequent model construction.
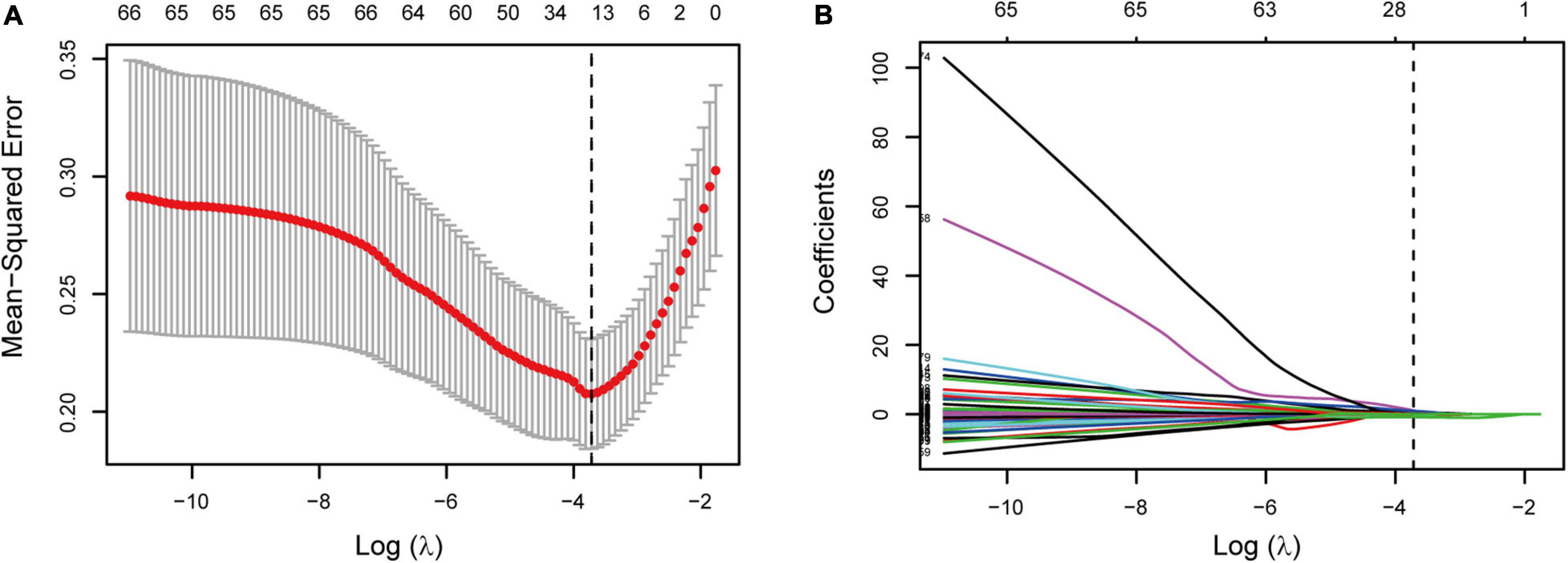
Figure 1. Feature selection based on the LASSO binary logistic regression analysis. (A) Optional lambda (λ) value of 0.024 with log(λ) of −3.72 was obtained based on a 10-fold cross-validation and minimum criteria. Dotted vertical line shows the optional λ value. (B) LASSO coefficient profiles of 15 features. Vertical line shows the optional λ value that resulted in 15 features with non-zero coefficients.
Parameter Optimization and Model Selection
Before the model construction using the full discovery dataset, we first tuned the parameters of the model based on a 10-fold cross-validation. We found that when the complexity parameter of the DT model was set as 0, the model achieved the highest AUC value, whereas when the RF ntree = 1,000 and mtry = 2, the model achieved the best performance. For the GB model, the best performance was obtained when interaction.depth = 2, n.trees = 400, shrinkage = 0.02, and n.minobsinnode = 5 (Supplementary Figures 1A–C).
Next, we randomly divided the discovery dataset into two groups 100 times: training data (70%) and testing data (30%). Each time, four cutting-edge machine learning algorithms with the optimized parameters were used to develop models on the training data. Based on the obtained models, we used the testing data to assess the probability of EAS of the testing population, and ROC and PRC analyses were performed, followed by calculating the AUC values on the testing data. We compared the models and observed that DT was associated with significantly lower AUROC and AUPRC values, whereas the GB approach has higher AUROC and AUPRC values (Figure 2). Moreover, the two ensemble learning algorithms (RF and GB), especially GB, have lower variances compared to DT and SVM (Figure 2). Altogether, the GB algorithm outperformed the other machine learning algorithms in terms of the classification capacity of EAS.
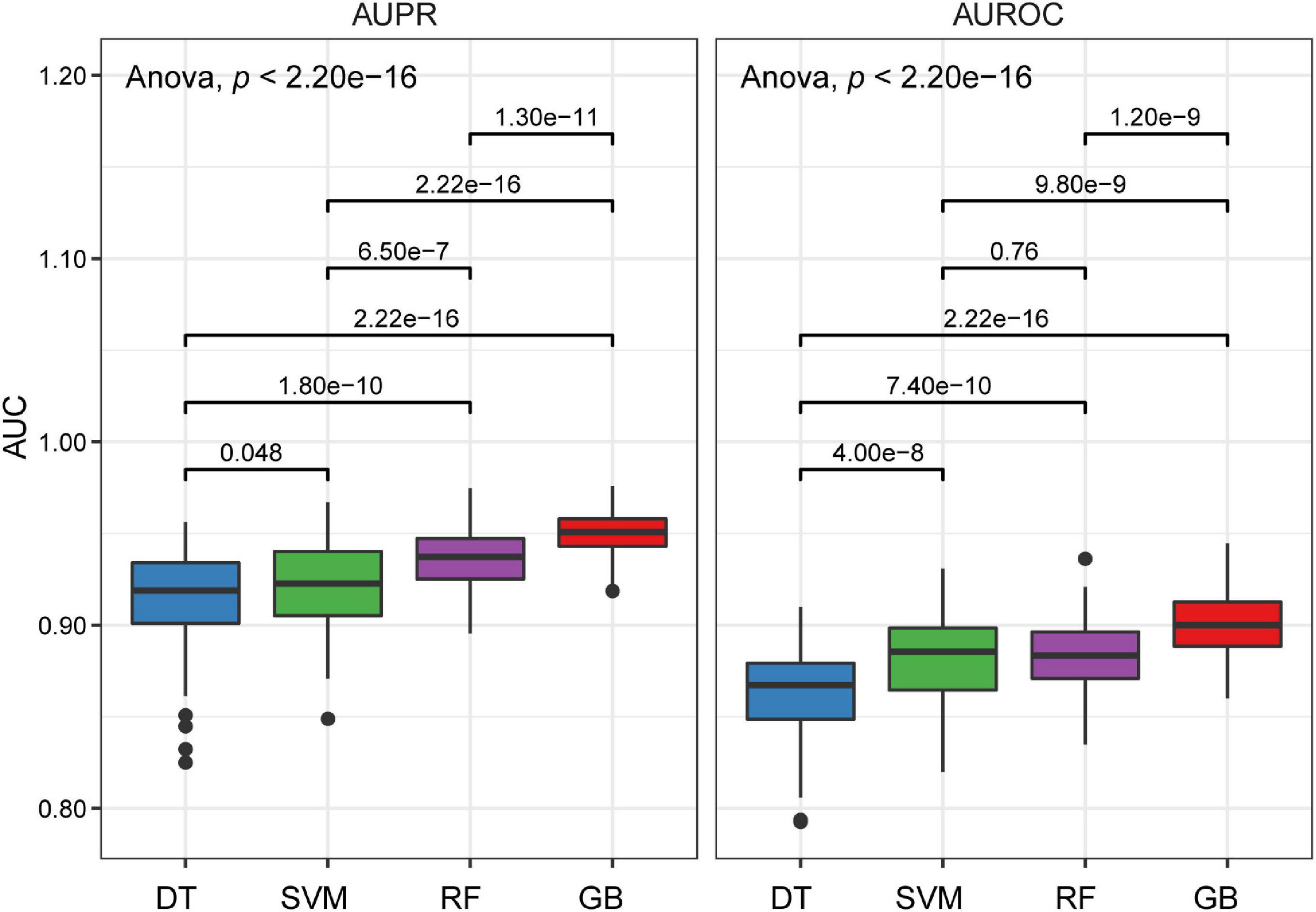
Figure 2. Boxplots of AUPRC and AUROC on the testing data for four different machine learning algorithms. P values were calculated through a one-way analysis of variance with Tukey’s post hoc test.
Predictive Model Construction and Validation
Based on the GB algorithm, we finalized our EAS predictive model by training the GB model on the full discovery data with optimized parameters and calculated GB-based risk scores. In addition, we applied the GB model to the validation data from an independent Japanese cohort. Each predictor and other demographic information for the discovery and validation data are shown in Table 2. The AUROC and AUPRC values were assessed in both cohorts. The results showed high AUROC values of 0.928 and 0.821 and AUPRC values of 0.964 and 0.798 in the discovery and validation datasets, respectively, for the classification between non-EAS and EAS (Figures 3A,B).
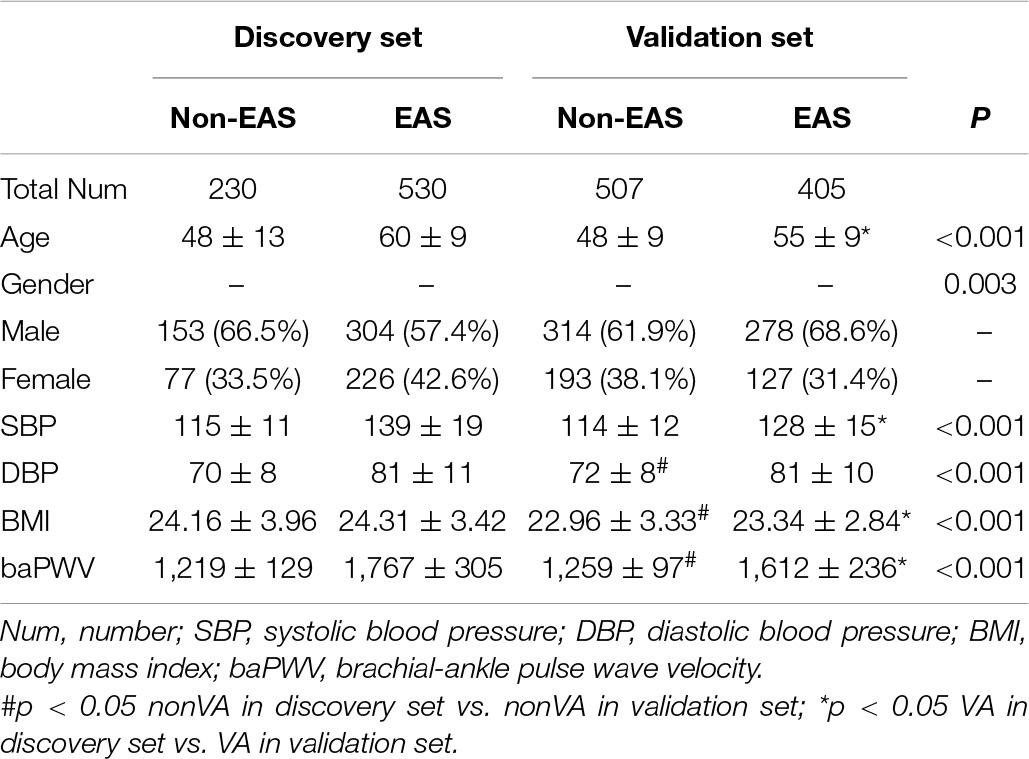
Table 2. Comparison of clinical and demographical characteristics between the discovery and validation cohorts.
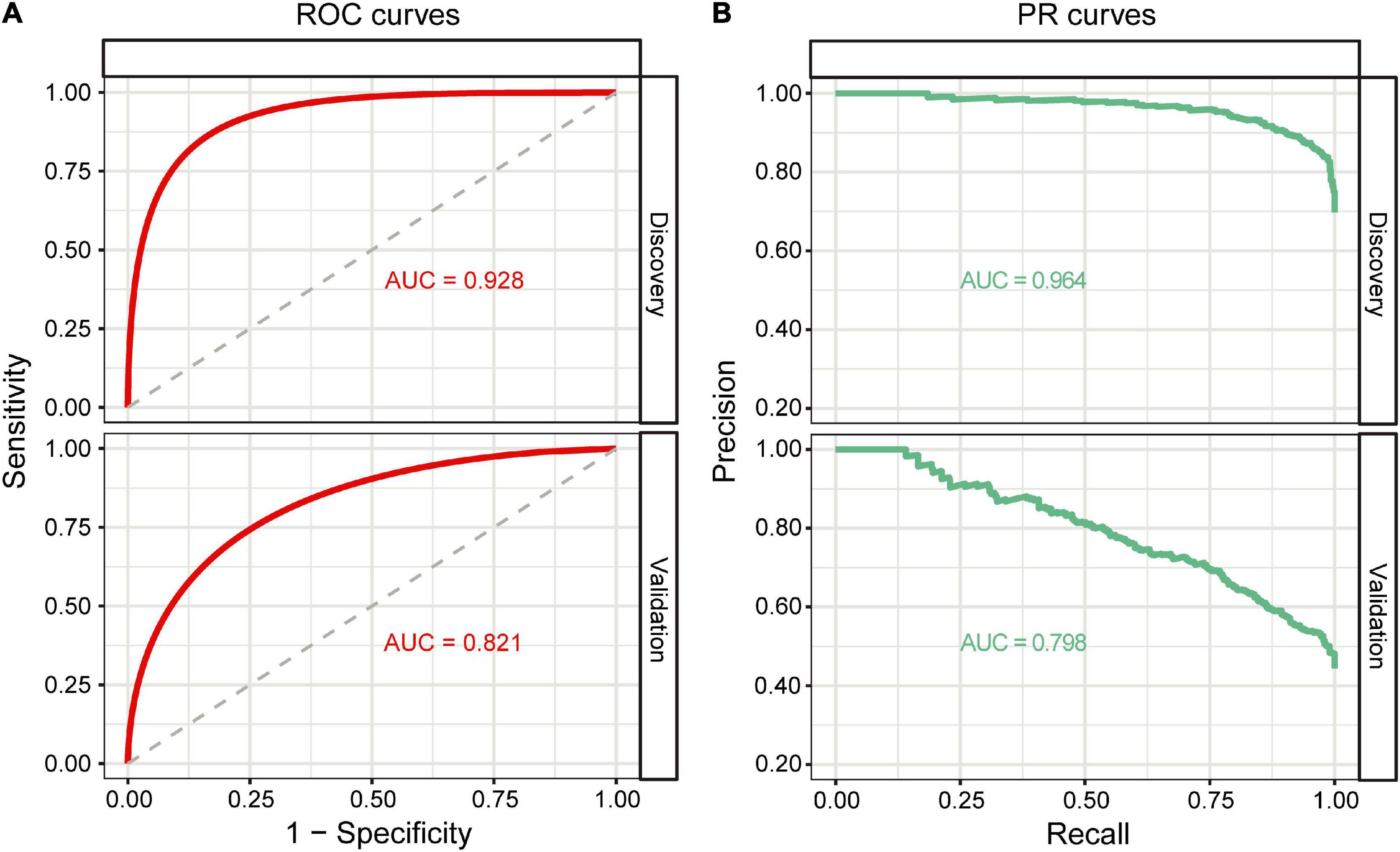
Figure 3. Classification performance of the GB model. (A) ROC curves of the GB model on the discovery and validation datasets. (B) PR curves of the GB model on the discovery and validation datasets.
To determine the best cutoff value of the GB model, Youden’s indexes were calculated in both cohorts. The cutoff value (0.75) built on the discovery cohort was higher than that (0.46) of the validation cohort (Figure 4), suggesting that the cutoff value derived from one cohort might not be ideal for other cohorts from different countries. Given that a cutoff value of 0.46 resulted in a better classification performance in both cohorts relative to a cutoff value of 0.75, which led to more false negative findings due to low sensitivity (0.677; Supplementary Table 6), we, therefore, selected 0.46 as a cutoff value for GB scores. The specificity/sensitivity in the discovery and validation cohorts at this cutoff value for the GB scoring system were 0.813/0.875 and 0.761/0.738, respectively (Supplementary Table 6).
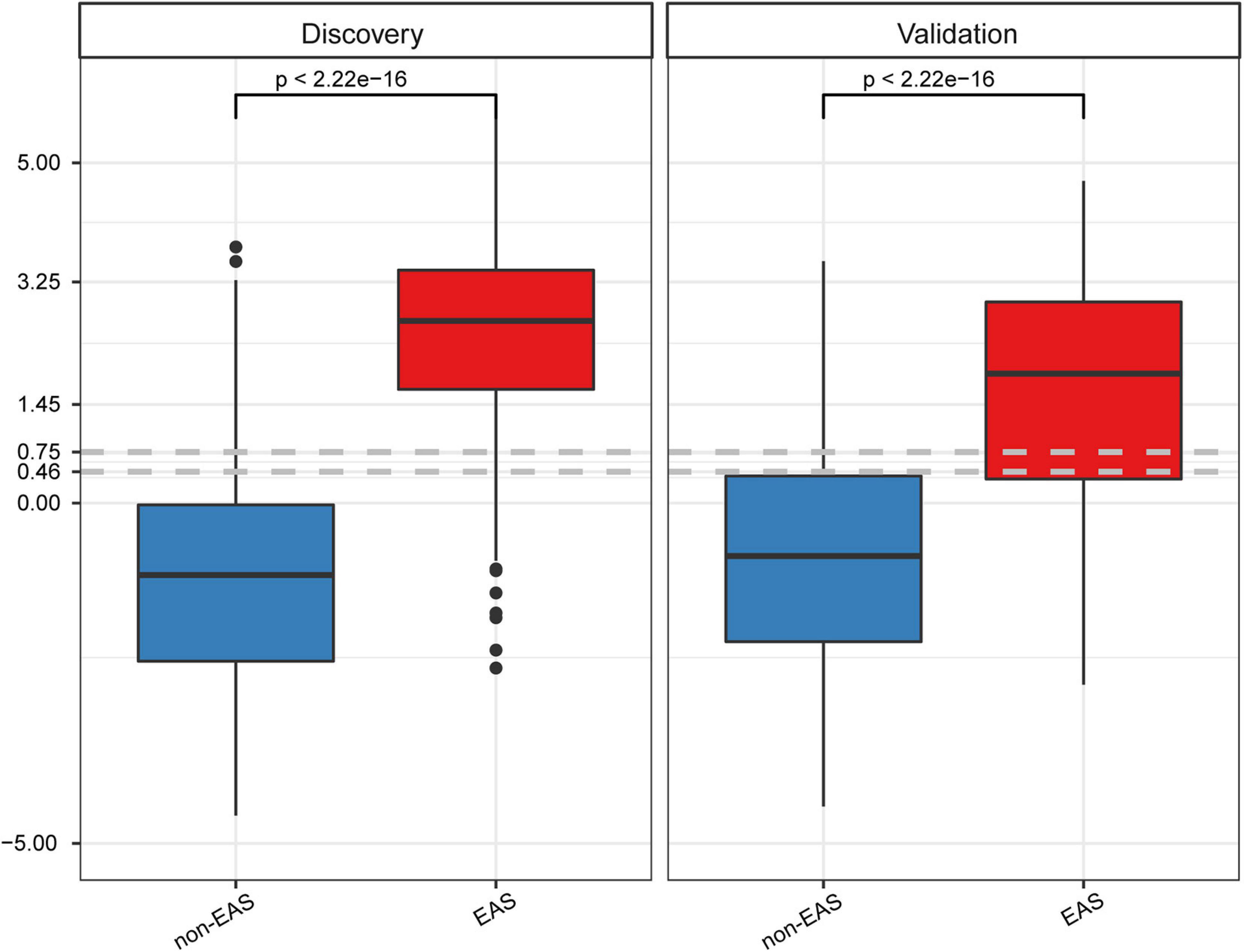
Figure 4. GB scores on the discovery and validation datasets between non-EAS and EAS. P values were calculated using Student’s t-tests.
Web Tool Development
To facilitate further study and use of this GB model for EAS prediction, we built a free and user-friendly online web-based tool (elevated arterial stiffness predictor:3). Figure 5 shows the user interface (UI) of the web tool. To use this web application, one only needs to input values for age, SBP, DBP, weight, and height, followed by clicking the “Predictor” button. Then, the UI will display the BMI and GB risk score value for this subject.
Figure 5. Screenshot of the web-based application (elevated arterial stiffness predictor).
Discussion
The increase in baPWV is considered a characteristic manifestation of EAS (Cunha et al., 2017). An increase of 1 m/s in baPWV will increase the mortality due to cardiovascular events, CVDs, and all-cause mortality by 12, 13, and 6%, respectively (Vlachopoulos et al., 2012). Thus, an affordable, reproducible, and accurate method for predicting EAS is desirable to support longitudinal surveillance and clinical decision making. In this study, we aim to construct a new EAS scoring system based on machine learning to identify EAS. To our knowledge, this is the first time that machine learning methods have been applied to develop an EAS predictor. Moreover, this model has been packaged into a user-friendly web application to encourage further study of its clinical utility.
Given that the clinical data we collected are relatively complete, including 99 features, we first narrowed down all features into 15 features based on the LASSO algorithm and 15 features based on the SVM-RFE algorithm. Four features (age, SBP, DBP, and BMI) from either the LASSO or SVM-RFE were further selected as the predictors in that they are easily accessible in clinical practice. Evidence suggests that the increase in age, SBP, and DBP are the important risk factors of artery stiffness (Papaioannou et al., 2019; Sang et al., 2020). Consistently, we observed a significant increase in age, SBP, and DBP in the EAS group compared to the non-EAS group. Furthermore, Baier et al. (2018) reported that age and SBP could explain 18% of the changes in PWV. Therefore, when predicting EAS and VA, age, SBP, and DBP are indispensable predictors. BMI was also determined as a diagnostic predictor of EAS by the SVM-RFE algorithm. Although no statistically significant difference in BMI between the EAS and non-EAS groups was observed, the multivariate logistic regression analysis with age, SBP, and DBP adjustments showed that BMI was an independent protective factor for EAS (p = 0.001, OR = 0.890; Supplementary Table 7). This result was similar to that of previous studies, which indicated that a high BMI was a protective factor for EAS and a higher BMI was associated with a lower baPWV (Lurbe et al., 2012; Huang et al., 2019; Yang et al., 2019).
Recently, the SAGE scoring system (including SBP, age, glycemia, and eGFR predictors) was established to predict EAS, which was an important step for the EAS surveillance and identification (Xaplanteris et al., 2019; Tomiyama et al., 2020). However, SAGE requires the predictors, i.e., glycemia and eGFR, to be obtained by an invasive blood test. Moreover, the LG-based SAGE system is not capable of obtaining interactions between predictors, which may affect the performance of SAGE. On the contrary, machine learning algorithms capable of capturing complicated interactions perform well in disease and prognosis prediction. For example, Alvin et al. pointed out that the predictive model based on machine learning could reliably identify patients who have high-risk diseases and increase the utilization of healthcare services (Rajkomar et al., 2019). David et al. used machine learning algorithms to improve the cardiovascular risk prediction of patients with end-stage renal disease on hemodialysis (de Gonzalo-Calvo et al., 2020). Michalis et al. also found that, based on machine learning algorithms, using volatile organic compounds in exhaled gas as predictors distinguishes lung cancer from other lung diseases or healthy individuals well (Zhang Z. et al., 2021). We used the four machine learning algorithms to develop the EAS predictive model. The results showed that all the models performed well with AUROC > 0.85 and AUPRC > 0.90, and particularly, GB outperformed other methods in terms of the AUROC, AUPRC, and variance. Owing to the limitations of the algorithm, DT constructs the model based on a single tree, and often suffers from overfitting (Katardjiev et al., 2019). Furthermore, if a certain correlation exists between the variables in the data, DT may cause a loss of associated information and reduction of accuracy. Thus, DT showed the relatively poor performance compared to other methods in this study. SVM maps data from low to high dimensional space using a kernel function to handle non-linearly separable data (Li et al., 2020). In the mapping process, if the kernel function does not discretize the data, that is, the data are sensitive to the kernel function, SVM may lead to a decrease in accuracy. However, ensemble learning algorithms such as RF and GB do not rely on a kernel function for data preprocessing, which integrate multiple prediction models that are trained on independent datasets and combined in a certain manner to make an overall prediction (Che et al., 2011). This yields more accurate results than those predicted by a single model. Therefore, these two methods performed better in this study. RF with a strong anti-interference ability can handle missing data especially in biomedical research. RF parallelly combines the results of multiple DTs to obtain the final model and does not further optimize the training results of different DTs, which may be the reason why the performance of RF is lower than that of GB. Unlike RF, which is based on bagging strategy and DT, GB is a combination of boosting strategy and DT. Boosting uses the residual value obtained in each iteration as the target value of the next iteration to further build the classification tree, whereas bagging parallelly trains multiple models based on training data randomly and independently sampled with replacement from the original dataset (Hall et al., 2011). GB keeps track of model’s errors, and assigns a higher weight to a good model. With the increase of number of iterations, the predictive ability of the GB model gradually improves and becomes stable. The advantages of the GB algorithm may be the reason why GB performed best in our dataset. Thus, we selected the GB model to predict EAS. The GB model showed good performance in the discovery and external verification datasets with AUROC and AUPRC values of 0.928/0.821 and 0.964/0.798, respectively. Compared to the SAGE, the GB scoring system not only has easier accessible predictors (age, SBP, DBP, and BMI vs. age, SBP, fasting glucose, and eGFR) but also higher AUROC values (0.928/0.821 vs. 0.85/0.77) in the discovery and external validation cohorts, respectively (Xaplanteris et al., 2019), further suggesting that the machine learning model outperforms the LG-based model.
Another point that needs to be discussed is the cutoff values of the GB model. Compared to the discovery cohort, there was a trend for lower GB scores in the EAS group of the validation cohort (Figure 4), which might be a result of the relatively higher age, SBP, and baPWV values in the EAS group of the discovery cohort than those of the validation cohort (Table 2). Differences in demographic and clinical characteristics may contribute to differences in the optional cutoff value, which prompted us to select a lower cutoff value to achieve a more rational classification performance. The first cutoff value (0.75) of the GB model was an optional trade-off point in the discovery cohort, whereas the second cutoff value (0.46) showed a better classification performance in the validation cohort. For the GB scoring system, we observed that the best trade-off point (0.75) for the discovery cohort showed biased classification in the validation cohort. After changing the trade-off point from 0.75 to 0.46, we observed better sensitivity (from 0.677 to 0.738; 6) without drastically decreasing the specificity (from 0.797 to 0.761; Supplementary Table 6). Thus, the demographic and clinical characteristics should be considered when determining the cutoff value.
Certain limitations of this study should be noted. First, the training sample size was limited. We plan to recruit more subjects from multiple center sites in the future to further increase the robustness of the model. Second, although this study was based on a Chinese cohort and validated using a Japanese cohort, prospective studies in different countries are required to further validate the results. Lastly, limitations in clinical data sharing infrastructure and mechanisms hinder further validation of cutting-edge machine learning methods (Geifman et al., 2015). We have packaged our GB model into a web-based application to encourage its dissemination for independent testing by other researchers.
In summary, we applied a cutting-edge machine learning method, GB, to establish an EAS scoring system for the identification of patients with EAS. We also validated the predictive performance of our GB model in an independent cohort from Japan. This GB model may help predict individual EAS risk and help clinicians manage patients with EAS.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.
Ethics Statement
The studies involving human participants were reviewed and approved by Medical Faculty of Fujian Medical University Union Hospital Ethics Committee. The ethics committee waived the requirement of written informed consent for participation.
Author Contributions
HH and LbL lead the study. QL, WX, and LpL performed the data analysis, implemented the methodology, and generated the web-based tool. LW, QY, LC, and JL collected the data and discussed the results. JF, WX, QL, and LpL prepared the original draft. HH, LL, WX, QL, and LpL reviewed and edited the final manuscript. All authors contributed to the article and approved the submitted version.
Funding
This study was supported by the National Natural Science Foundation of China (Grant No: 81800422 and 82071560); the Joint Funds of Scientific and Technological Innovation Program of Fujian Province (2017Y9055, 2017Y9060, and 2019Y9086); National Key Clinical Specialty Discipline Construction Programs (2013544); and Fujian Province’s Key Clinical Specialty Discipline Construction Programs (2012149).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2021.714195/full#supplementary-material
Footnotes
- ^ https://doi.org/10.5061/dryad.m484p
- ^ https://www.R-project.org
- ^ http://vascularagingpredictor.top/
References
American Diabetes Association (2019). 2. classification and diagnosis of diabetes: standards of medical care in diabetes-2019. Diab. Care 42, (Suppl. 1), S13–S28. doi: 10.2337/dc19-S002
Ato, D. (2018). Pitfalls in the ankle-brachial index and brachial-ankle pulse wave velocity. Vasc. Health Risk Manag. 14, 41–62. doi: 10.2147/VHRM.S159437
Baier, D., Teren, A., Wirkner, K., Loeffler, M., and Scholz, M. (2018). Parameters of pulse wave velocity: determinants and reference values assessed in the population-based study LIFE-Adult. Clin. Res. Cardiol. 107, 1050–1061. doi: 10.1007/s00392-018-1278-1273
Biljak, V. R., Honović, L., Matica, J., Krešić, B., and Vojak, S. Š (2017). The role of laboratory testing in detection and classification of chronic kidney disease: national recommendations. Biochem. Med. (Zagreb) 27, 153–176. doi: 10.11613/BM.2017.019
Cecelja, M., Keehn, L., Ye, L., Spector, T. D., Hughes, A. D., and Chowienczyk, P. (2020). Genetic aetiology of blood pressure relates to aortic stiffness with bi-directional causality: evidence from heritability, blood pressure polymorphisms, and mendelian randomization. Eur. Heart J. 41, 3314–3322. doi: 10.1093/eurheartj/ehaa238
Che, D., Liu, Q., Rasheed, K., and Tao, X. (2011). Decision tree and ensemble learning algorithms with their applications in bioinformatics. Adv. Exp. Med. Biol. 696, 191–199. doi: 10.1007/978-1-4419-7046-6_19
Chen, S., Li, W., Jin, C., Vaidya, A., Gao, J., Yang, H., et al. (2017). Resting heart rate trajectory pattern predicts arterial stiffness in a community-based Chinese cohort. Arterioscler. Thromb. Vasc. Biol. 37, 359–364. doi: 10.1161/ATVBAHA.116.308674
Cunha, P. G., Boutouyrie, P., Nilsson, P. M., and Laurent, S. (2017). Early Vascular Ageing (EVA): definitions and clinical applicability. Curr. Hypertens. Rev. 13, 8–15. doi: 10.2174/1573402113666170413094319
de Gonzalo-Calvo, D., Martínez-Camblor, P., Bär, C., Duarte, K., Girerd, N., Fellström, B., et al. (2020). Improved cardiovascular risk prediction in patients with end-stage renal disease on hemodialysis using machine learning modeling and circulating microribonucleic acids. Theranostics 10, 8665–8676. doi: 10.7150/thno.46123
Donato, A. J., Machin, D. R., and Lesniewski, L. A. (2018). Mechanisms of dysfunction in the aging vasculature and role in age-related disease. Circ. Res. 123, 825–848. doi: 10.1161/CIRCRESAHA.118
Friedman, J. H. (2001). Greedy function approximation: a gradient boosting machine. Ann. Statist. 29, 1189–1232. doi: 10.1214/aos/1013203451
Fukuda, T., Hamaguchi, M., Kojima, T., Ohshima, Y., Ohbora, A., Kato, T., et al. (2014a). Association between serum γ-glutamyltranspeptidase and atherosclerosis: a population-based cross-sectional study. BMJ Open 4:e005413. doi: 10.1136/bmjopen-2014-005413
Fukuda, T., Hamaguchi, M., Kojima, T., Ohshima, Y., Ohbora, A., Kato, T., et al. (2014b). Data from: association between serum γ-glutamyl-transpeptidase and atherosclerosis: a population-based cross-sectional study. Dryad Digital Repository doi: 10.5061/dryad.m484p
Geifman, N., Bollyky, J., Bhattacharya, S., and Butte, A. J. (2015). Opening clinical trial data: are the voluntary data-sharing portals enough? BMC Med. 13:280. doi: 10.1186/s12916-015-0525-y
Guo, C., Zhao, L., Ding, Y., Zhao, Z., Wang, C., Li, L., et al. (2020). Gene polymorphism rs2278426 is related to carotid intima-media thickness in T2DM. Diab. Metab. Syndr. Obes. 13, 4519–4528. doi: 10.2147/DMSO.S274759
Hall, M., Witten, I., and Frank, E. (2011). Data Mining: Practical Machine Learning Tools and Techniques. San Francisco: Margan Kaufmann.
Hamaguchi, M., Kojima, T., Ohbora, A., Takeda, N., Fukui, M., and Kato, T. (2012). Aging is a risk factor of nonalcoholic fatty liver disease in premenopausal women. World J. Gastroenterol. 18, 237–243. doi: 10.3748/wjg.v18.i3.237
Horton, W. B., Jahn, L. A., Hartline, L. M., Aylor, K. W., Patrie, J. T., and Barrett, E. J. (2021). Insulin increases central aortic stiffness in response to hyperglycemia in healthy humans: a randomized four-arm study. Diab. Vasc. Dis. Res. 18:14791641211011009. doi: 10.1177/14791641211011009
Huang, J., Chen, Z., Yuan, J., Zhang, C., Chen, H., Wu, W., et al. (2019). Association between Body Mass Index (BMI) and brachial-ankle pulse wave velocity (baPWV) in males with hypertension: a community-based cross-section study in North China. Med. Sci. Monit. 25, 5241–5257. doi: 10.12659/MSM.914881
Katardjiev, N., McKeever, S., and Hamfelt, A. (2019). “A machine learning-based approach to forecasting alcoholic relapses,” in Proceedings of the ITISE 2019 6th International Conference on Time Series and Forecasting, (Granada).
Krzywinski, M., and Altman, N. (2017). Classification and regression trees. Nat. Methods 14, 757–758. doi: 10.1038/nmeth.4370
Li, Q., Wen, Z., and He, B. (2020). Adaptive kernel value caching for SVM training. IEEE Trans. Neural. Netw. Learn. Syst. 31, 2376–2386. doi: 10.1109/TNNLS.2019.2944562
Lurbe, E., Torro, I., Garcia-Vicent, C., Alvarez, J., Fernández-Fornoso, J. A., and Redon, J. (2012). Blood pressure and obesity exert independent influences on pulse wave velocity in youth. Hypertension 60, 550–555. doi: 10.1161/HYPERTENSIONAHA.112.194746
Mitchell, C., Rahko, P. S., Blauwet, L. A., Canaday, B., Finstuen, J. A., Foster, M. C., et al. (2019). Guidelines for performing a comprehensive transthoracic echocardiographic examination in adults: recommendations from the american society of echocardiography. J. Am. Soc. Echocardiogr. 32, 1–64. doi: 10.1016/j.echo.2018.06.004
Munakata, M. (2014). Brachial-ankle pulse wave velocity in the measurement of arterial stiffness: recent evidence and clinical applications. Curr. Hypertens. Rev. 10, 49–57. doi: 10.2174/157340211001141111160957
Myszczynska, M. A., Ojamies, P. N., Lacoste, A. M. B., Neil, D., Saffari, A., Mead, R., et al. (2020). Applications of machine learning to diagnosis and treatment of neurodegenerative diseases. Nat. Rev. Neurol. 16, 440–456. doi: 10.1038/s41582-020-0377-378
Nedaie, A., and Najafi, A. A. (2018). Support vector machine with Dirichlet feature mapping. Neural. Netw. 98, 87–101. doi: 10.1016/j.neunet.2017.11.006
O’Rourke, M. F., Safar, M. E., and Dzau, V. (2010). The cardiovascular continuum extended: aging effects on the aorta and microvasculature. Vasc. Med. 15, 461–468. doi: 10.1177/1358863X10382946
Papaioannou, T. G., Oikonomou, E., Lazaros, G., Christoforatou, E., Vogiatzi, G., Tsalamandris, S., et al. (2019). The influence of resting heart rate on pulse wave velocity measurement is mediated by blood pressure and depends on aortic stiffness levels: insights from the corinthia study. Physiol. Meas. 40:055005. doi: 10.1088/1361-6579/ab165f
Podgorelec, V., Kokol, P., Stiglic, B., and Rozman, I. (2002). Decision trees: an overview and their use in medicine. J. Med. Syst. 26, 445–463. doi: 10.1023/a:1016409317640
Qian, J., Cai, M., Gao, J., Tang, S., Xu, L., and Critchley, J. A. (2010). Trends in smoking and quitting in China from 1993 to 2003: national health service survey data. Bull. World Health Organ. 88, 769–776. doi: 10.2471/BLT.09.064709
Rajkomar, A., Dean, J., and Kohane, I. (2019). Machine learning in medicine. N. Engl. J. Med. 380, 1347–1358. doi: 10.1056/NEJMra1814259
Sang, Y., Wu, X., Miao, J., Cao, M., Ruan, L., and Zhang, C. (2020). Determinants of brachial-ankle pulse wave velocity and vascular aging in healthy older subjects. Med. Sci. Monit. 26:e923112. doi: 10.12659/MSM.923112
Taylor, J. (2013). New ESC guidelines published on stable coronary artery disease. Eur. Heart J. 34, 2927–2928. doi: 10.1093/eurheartj/eht377
Tomiyama, H., Matsumoto, C., Yamada, J., Yoshida, M., Odaira, M., Shiina, K., et al. (2009). Predictors of progression from prehypertension to hypertension in Japanese men. Am. J. Hypertens. 22, 630–636. doi: 10.1038/ajh.2009.49
Tomiyama, H., Vlachopoulos, C., Xaplanteris, P., Nakano, H., Shiina, K., Ishizu, T., et al. (2020). Usefulness of the SAGE score to predict elevated values of brachial-ankle pulse wave velocity in Japanese subjects with hypertension. Hypertens. Res. 43, 1284–1292. doi: 10.1038/s41440-020-0472-477
Touboul, P. J., Hennerici, M. G., Meairs, S., Adams, H., Amarenco, P., Bornstein, N., et al. (2012). Mannheim carotid intima-media thickness and plaque consensus (2004-2006-2011). an update on behalf of the advisory board of the 3rd, 4th and 5th watching the risk symposia, at the 13th, 15th and 20th European Stroke Conferences, Mannheim, Germany, 2004, Brussels, Belgium, 2006, and Hamburg, Germany, 2011. Cerebrovasc. Dis. 34, 290–296. doi: 10.1159/000343145
Vlachopoulos, C., Aznaouridis, K., Terentes-Printzios, D., Ioakeimidis, N., and Stefanadis, C. (2012). Prediction of cardiovascular events and all-cause mortality with brachial-ankle elasticity index: a systematic review and meta-analysis. Hypertension 60, 556–562. doi: 10.1161/HYPERTENSIONAHA.112194779
Wang, L., Wang, Y., and Chang, Q. (2016). Feature selection methods for big data bioinformatics: a survey from the search perspective. Methods 111, 21–31. doi: 10.1016/j.ymeth.2016.08.014
Wang, Y., Yang, Y., Wang, A., An, S., Li, Z., Zhang, W., et al. (2016). Association of long-term blood pressure variability and brachial-ankle pulse wave velocity: a retrospective study from the APAC cohort. Sci. Rep. 6:21303. doi: 10.1038/srep21303
Williams, B., Mancia, G., Spiering, W., Agabiti Rosei, E., Azizi, M., Burnier, M., et al. (2018). 2018 ESC/ESH Guidelines for the management of arterial hypertension. Eur. Heart J. 39, 3021–3104. doi: 10.1093/eurheartj/ehy339
Xaplanteris, P., Vlachopoulos, C., Protogerou, A. D., Aznaouridis, K., Terentes-Printzios, D., Argyris, A. A., et al. (2019). A clinical score for prediction of elevated aortic stiffness: derivation and validation in 3943 hypertensive patients. J. Hypertens. 37, 339–346. doi: 10.1097/HJH.0000000000001904
Yamashina, A., Tomiyama, H., Arai, T., Hirose K-i, Koji, Y., Hirayama, Y., et al. (2003). Brachial-ankle pulse wave velocity as a marker of atherosclerotic vascular damage and cardiovascular risk. Hypertens Res. 26, 615–622. doi: 10.1291/hypres.26.615
Yang, H., Zhao, J., Deng, X., Tan, I., Butlin, M., Avolio, A., et al. (2019). Pulse wave velocity is decreased with obesity in an elderly Chinese population. J. Clin. Hypertens. (Greenwich) 21, 1379–1385. doi: 10.1111/jch.13659
Yang, W., Lu, J., Weng, J., Jia, W., Ji, L., Xiao, J., et al. (2010). Prevalence of diabetes among men and women in China. N. Engl. J. Med. 362, 1090–1101. doi: 10.1056/NEJMoa0908292
Yang, Y., Fan, F., Kou, M., Yang, Y., Cheng, G., Jia, J., et al. (2018). Brachial-Ankle pulse wave velocity is associated with the risk of new carotid plaque formation: data from a chinese community-based cohort. Sci. Rep. 8:7037. doi: 10.1038/s41598-018-25579-25572
Zhang, C., and Hong, H. (2019). Aging cardiovascular continuum. Chin. J. Geriatr. 38, 1180–1184. doi: 10.3760/cma.j.issn.0254-9026.2019.10.029
Zhang, K., Zhang, S., Cui, W., Hong, Y., Zhang, G., and Zhang, Z. (2021). Development and validation of a sepsis mortality risk score for Sepsis-3 patients in intensive care unit. Front. Med. (Lausanne). 7:609769. doi: 10.3389/fmed.2020.609769
Zhang, Z., Liu, J., Xi, J., Gong, Y., Zeng, L., and Ma, P. (2021). Derivation and validation of an ensemble model for the prediction of agitation in mechanically ventilated patients maintained under light sedation. Crit. Care Med. 49, e279–e290. doi: 10.1097/CCM.0000000000004821
Keywords: arterial stiffness, LASSO, machine learning, gradient boosting, web tool
Citation: Li Q, Xie W, Li L, Wang L, You Q, Chen L, Li J, Ke Y, Fang J, Liu L and Hong H (2021) Development and Validation of a Prediction Model for Elevated Arterial Stiffness in Chinese Patients With Diabetes Using Machine Learning. Front. Physiol. 12:714195. doi: 10.3389/fphys.2021.714195
Received: 26 May 2021; Accepted: 31 July 2021;
Published: 23 August 2021.
Edited by:
Liang Zhong, National Heart Centre Singapore, SingaporeReviewed by:
Steve McKeever, Uppsala University, SwedenAravind Rammohan, Corning Inc., United States
Copyright © 2021 Li, Xie, Li, Wang, You, Chen, Li, Ke, Fang, Liu and Hong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Huashan Hong, 15959159898@163.com; Libin Liu, Libinliu@fjmu.edu.cn
†These authors have contributed equally to this work and share first authorship