
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Physiol., 30 April 2020
Sec. Computational Physiology and Medicine
Volume 11 - 2020 | https://doi.org/10.3389/fphys.2020.00324
This article is part of the Research TopicComputational Biomechanics for Ventricle-arterial Dysfunction and Remodeling in Heart Failure, Volume IView all 11 articles
 Wenguang Li1
Wenguang Li1 Alan Lazarus1
Alan Lazarus1 Hao Gao1
Hao Gao1 Ana Martinez-Naharro2
Ana Martinez-Naharro2 Marianna Fontana2
Marianna Fontana2 Philip Hawkins2
Philip Hawkins2 Swethajit Biswas3
Swethajit Biswas3 Robert Janiczek3
Robert Janiczek3 Jennifer Cox3
Jennifer Cox3 Colin Berry4
Colin Berry4 Dirk Husmeier1
Dirk Husmeier1 Xiaoyu Luo1*
Xiaoyu Luo1*Deposition of amyloid in the heart can lead to cardiac dilation and impair its pumping ability. This ultimately leads to heart failure with worsening symptoms of breathlessness and fatigue due to the progressive loss of elasticity of the myocardium. Biomarkers linked to the clinical deterioration can be crucial in developing effective treatments. However, to date the progression of cardiac amyloidosis is poorly characterized. There is an urgent need to identify key predictors for disease progression and cardiac tissue function. In this proof of concept study, we estimate a group of new markers based on mathematical models of the left ventricle derived from routine clinical magnetic resonance imaging and follow-up scans from the National Amyloidosis Center at the Royal Free in London. Using mechanical modeling and statistical classification, we show that it is possible to predict disease progression. Our predictions agree with clinical assessments in a double-blind test in six out of the seven sample cases studied. Importantly, we find that multiple factors need to be used in the classification, which includes mechanical, geometrical and shape features. No single marker can yield reliable prediction given the complexity of the growth and remodeling process of diseased hearts undergoing high-dimensional shape changes. Our approach is promising in terms of clinical translation but the results presented should be interpreted with caution due to the small sample size.
Amyloidosis occurs when proteins that take abnormal forms known as amyloid deposits build up in the tissues. These deposits are composed of abnormal protein fibers that accumulate more quickly than they are cleared away, and thus interfere with the structure and function of affected organs throughout the body. These include the heart, liver, skin, lungs, kidneys, and nervous system (Gertz et al., 2013). When amyloid fibrils infiltrate in myocardium, the ventricles will show impaired contraction and relaxation. This is known as cardiac amyloidosis. The most prevalent forms of cardiac amyloidosis are known as Transthyretin-related (ATTR) and immunoglobulin light chain (AL) amyloidosis (formerly known as primary amyloidosis). Untreated cardiac amyloid, particularly the AL type, can be life-threatening, the median survival of patients is half a year from the onset of heart failure (Grogan et al., 2017).
The left ventricle (LV) with amyloid becomes firm, rubbery and stiff, similar to hypertrophic cardiomyopathy (Kholova and Niessen, 2005). Further, the ventricular wall is thickened (Carroll et al., 1982; Kholova and Niessen, 2005; Quarta et al., 2012; Martinez-NaharrO et al., 2018), particularly in the interventricular septum (Frenzel et al., 1986), but the ventricular cavity does not dilate much (Kholova and Niessen, 2005). Hence, the functional defect in amyloidosis is associated to the “stiff heart” syndrome, with the LV end-diastolic pressure rising to at least 10 mmHg higher than normal subjects (Chew et al., 1975; Swanton et al., 1977). As a result, the amyloidosis myocardium material properties also altered (Petre et al., 2005).
With effective treatments, it is hoped that amyloid deposits can gradually diminish in patients. However, although various anti-amyloid drugs are being researched, none has been introduced into routine clinical practice. A standing challenge in developing anti-amyloid drugs is the difficulty of reliably assessing the disease progression non-invasively and within in a short follow-up duration, because subtle changes inside tissues with reduced amyloid deposits are not always visible in clinical images, such as cardiac magnetic resonance (CMR) imaging.
Using Doppler echocardiography, Koyama et al. found that the early impairment in systolic function of a cardiac amyloidosis heart can be reflected by changed longitudinal strain and strain rate (Koyama et al., 2003). Both circumferential and longitudinal strains are found to be substantially lower in an amyloidosis LV, compared with a normal, or hypertrophic cardiomyopathy LV (Sun et al., 2009; Buss et al., 2012). CMR images are used to diagnose cardiac amyloid with late gadolinium enhancement (LGE) (Vogelsberg et al., 2008; Liu et al., 2013; Dungu et al., 2014) or delayed enhancement (White et al., 2014). Based on CMR basal and apical short-axis images, White et al. showed that the peak LV twist rate and untwist rates are significantly lower in patients with cardiac amyloid LV (White et al., 2014). Nucifora et al. (2014) measured the circumferential strain of 61 amyloidosis patients using tagging CMR and found the peak circumferential strain could be a potential clinical biomarker.
In previous studies, strain and material stiffness were found to be associated with cardiac amyloidosis. However, there is much to be done on understanding the disease progression of cardiac amyloid. Needless to say, finding a reliable classification based on suitable biomarkers is crucially important in assessing the effectiveness of amyloidosis treatments and any clinical trials for new drugs. Despite major research development of computational cardiac models, which can provide a rich set of biomarkers, it is perhaps surprising that very little modeling effort has focused on cardiac amyloidosis (Chapelle et al., 2015), and no studies considered the relation to amyloidosis disease progression.
The aim of this work is to carry out an image-derived mechanical and statistical modeling approach for LVs with amyloidosis progression. We systemically checked multiple factors, including the strains, stresses, p-V curve, LV shape, and volume of a group of amyloidosis patients before and after treatment. The biomechanical modeling analysis was blind to the clinical assessment, and the classification based on the multiple factors compares favorably with the clinical observation. To the best of the authors' knowledge, this is the first time that cardiac amyloidosis progression has been studied in a combined mechanical and statistical approach, based on longitudinal images of real patients during treatments.
The study consists of CMR images from seven cardiac amyloidosis patients before treatment (baseline) and at 6 or 9 months after the treatment (follow-up). The information of all patients is in Table 1. Each patient has been clinically classified as recovery, worsening, and stable (no obvious change). The assessment was based on the clonal response to chemotherapy and progression/regression on the extracellular volume. The biomechanical modeling analysis in this paper is blind to the clinical assessment and the CMR imaging acquisition, briefly summarized in Appendix A.1, has been described in detail elsewhere (Fontana et al., 2015).
A prolate spherical coordinate system is used to reconstruct the LV geometry following the steps in Liu et al. (2009). Short-axis and long-axis cine images (Figure A1) at a total of 13 time instants in diastole are used to warp the LV geometry. The LV wall boundaries are manually segmented using an in-house Matlab code (Gao et al., 2017), and all short-axis LV wall boundaries are aligned to the images of the horizontal long axis, the vertical long axis, and the left ventricular outflow tract, respectively. In order to align the LV geometries along the long-axis at different times, we first determine the distance between the most-basal short-axis image and the mitral annulus ring, denoted as dt at time t. Following this, the most-basal short-axis image is moved toward the annuls ring along the long axis with a distance of dt − min(di), (i = 1, …13, representing the ith short axis image at diastole). Note that the long axis is defined by connecting the center of the LV base and the apex. In order to align the LV geometries circumferentially, the angles of right ventricular insertion points are defined in the basal plane (corresponding to the most-basal short-axis image), v1 near the inferior segment, and v2 near the anterior segment, as shown in Figure 1 at two different time instances. Then, for LV geometries at different times, the basal plane is aligned by matching the insertion points at v1, and the same number of elements are assigned to the septum circumferentially when generating the layered hexhedron mesh. Figure 2 shows the reconstructed LV at early-diastole, right after isovolumetric relaxation when the mitral valve just opens and the ventricular pressure is the lowest, for all patients both before and after treatment. This choice of reference configuration has been used in the literature (Genet et al., 2014; Gao et al., 2017).
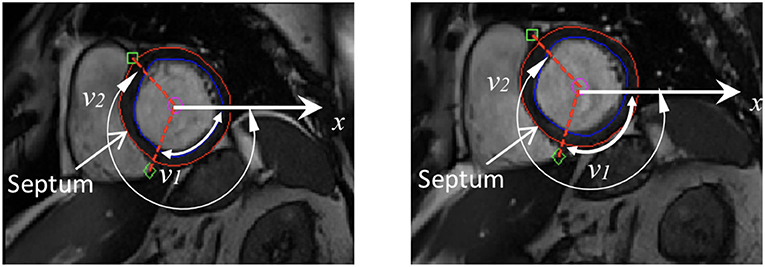
Figure 1. Definition of right ventricular insertion points at the basal plane in order to align LV geometries circumferentially at different time instances.
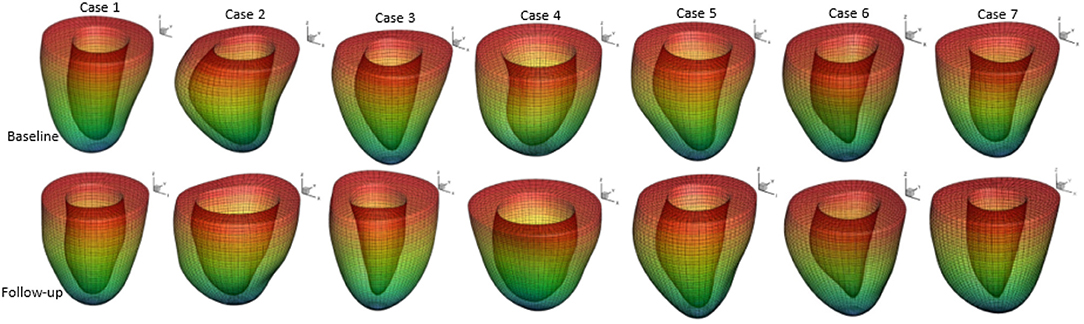
Figure 2. Generated LV geometrical models based on the CMR images and their meshes at early-diastole of seven patients in baseline and follow-up scans.
A rule-based approach (Potse et al., 2006) is adopted to generate myofiber structure within the LV wall, with fibers varied linearly from −60o at the epicardium to 60o at the endocardium, and the sheet angle from −45o at the epicardium to 45o at the endocardium (see Figure 3A). Because the reconstructed LV geometries are fitted to one standard template mesh after long-axis and circumferential alignment, we may reasonably assume that elements with the same index from LV models at different times are co-registered. As shown in Figure 3B, three short-axis planes are further defined for extracting strains. Within each selected plane, 20 regions distributed equally along the circumferential direction are selected to obtain regional-average strains. In total, 60 circumferential strains are measured from CMR derived LV models.
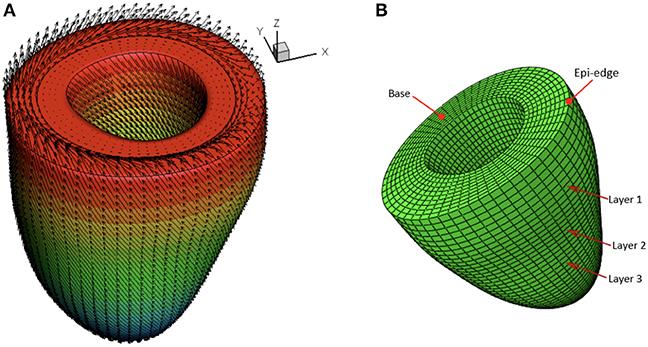
Figure 3. Schematic illustration of myofiber orientation (A) and selected three layers in the LV wall (B).
Since each LV geometry has the same mesh connectivity, after co-registration of all LV geometries, a mapping can be established for every element of the LV geometry at different time frames. The deformation gradient related to the first time frame (at early-diastole) can be readily calculated as , where X and x are position vectors at the first and later time frames, respectively. We further obtain the circumferential direction (c) locally with respect to the long axis, and the transmural direction (r) pointing from endocardium to epicardium, and then the local longitudinal direction l = r × c, which follows local geometrical curvature (Gao et al., 2014a). This enables us to compute the circumferential and longitudinal strains as and , in which I is the identity matrix. Note the reference state for strain calculation is early-diastole, not end-diastole which is usually adopted in clinics.
We use the Holzapfel-Ogden strain energy function to describe myocardial passive properties (Holzapfel and Ogden, 2009),
where a, b, af, bf, as, bs, afs, bfs are patient-dependent material parameters, and Ij (j = 1, 4f, 4s) are invariants of the right Cauchy-Green tensor. A more detailed description of the model (1) can be found in Holzapfel and Ogden (2009) and its applications in LV modeling should be referred to Göktepe et al. (2011), Wang et al. (2013), Gao et al. (2014b), and Wang et al. (2014). Differentiation of the strain energy function (1) with respect to the displacements and applying constraints related to various conservation laws leads to a set of equations that define the cardiac dynamics. These equations are solved numerically using finite element discretization, implemented in ABAQUS software 6.11.
Early-diastole is used as the reference configuration. The following boundary conditions are applied at the most basal plane (see Figure 3B),
where , , , are the displacements in the x and y directions determined from the model and the CMR images at the epicardial edge in the most basal plane (see Figure 3B).
The diastolic pressure profile is assumed to be linear between zero at early-diastole (t = 0 s) and PED at end-diastole (t = 1 s), following (Steendijk et al., 2004). t here is a pseudo simulation time. The values of PED should be patient-specific. However, as the pressure measurements are invasive, this information is not available from in vivo studies. On the other hand, the literature suggests that all amyloidosis patients have increased wall thickness and higher pressure compared with normal subjects (Kholova and Niessen, 2005; Quarta et al., 2012; Martinez-NaharrO et al., 2018). Hence, we assume PED is proportional to scaled LV wall volume as follows:
where PEDm is the mean end-diastolic pressure, taken to be 19 mmHg based on measurements in Plehn et al. (1992) and Boufidou et al. (2010). Vwall/VLV is the ratio of the LV wall volume to the LV chamber volume. Its mean value at early-diastole before treatment is 2.678. The scaled PED for each patient is listed in Table 2. This range of pressure values seems to be consistent with clinical observations of amyloidosis patients (Bhuiyan et al., 2011).
For each amyloidosis patient, the material parameters in Equation (1) are inferred by using an optimization algorithm through minimizing an objective function (the difference between the model and imaged-derived P-V curve and circumferential strains). Sensitivity analysis in our previous study (Gao et al., 2015) shows the ranking order of the parameters, from the most significant to the least, is
This allows us to divide the parameters in Equation (1) into two groups, the first group includes a, b, af, bf, afs, and the second group involves as, bs, bfs. The first group may be determined with higher accuracy than the second group because of the higher sensitivity to clinical measurements, although this may not be true all the time as the material model is strongly nonlinear. As such, a two-step approach is used. In the first step, parameters of the first group are determined by minimizing the following objective function with the parameters in the second group taking the values from Gao et al. (2015) for healthy volunteers estimated at PEDm = 8 mmHg (as = 0.5426 kPa, bs = 1.5998, bfs = 3.3900):
where nlayer is the number of layers considered, nlayer = 3 indexed by k; ntime is the number of time steps, ntime = 13 indexed by j; nreg is the number of regions in each layer considered, nreg = 20 indexed by i; , are the LV chamber volumes from the FEA and CMR images, respectively; , are the mean circumferential strains in 20 regions from the FEA and CMR images, respectively; wv, wE are the weights. Note we do not include the longitudinal strains in our objective function because the uncertainty of estimating longitudinal strains is much larger than the circumferential strains. This is because the simplified long-axial alignment we use does not account for the out-of-plane motion along the long axis. We are unable to quantify the out-of-plane motion due to the lack of necessary features in cine images. 3D strain imaging such as tagging allows one to include longitudinal strains (Nikou et al., 2016) or the displacement fields (Asner et al., 2016) in the objective function, but it is not used routinely in clinics. It is for this reason many published studies using in vivo cine images mainly used measured volume (Genet et al., 2014; Palit et al., 2018), or regional circumferential strains along with measured volume in the objective function (Gao et al., 2015).
After obtaining the optimal five constants in the first group, we proceed to infer all parameters but found as, bs, and bfs are insensitive to the optimization. Therefore we first focus on the ratios of parameters: as/afs, af/as, bs/bfs, bf/bs. A range of values for these ratios can be found from the literature (Gao et al., 2015; Palit et al., 2018) from which we derive the linear regressions,
The first equation of (6) shows that as is the only unknown after the first optimization step,
In the second equation of (6), two unknowns remain, bs bfs. Let ξ = bf/bfs, we write
It is easy to see that ξ ∈ [1.44, 2.96] from data in Gao et al. (2015) and Palit et al. (2018). Thus in the second step, ξ is optimized by minimizing the objective function FE in Equation (5).
The flowchart of the two-step optimization method and the inferred parameters are given in Appendix A.2. The uncertainties of these parameters are evaluated using the residual bootstrap method (Efron and Tibshirani, 1986), as described in Appendix A.2.
For feature comparison between the amyloidosis patients and control, we make use of the LV geometries of 26 healthy subjects from our previous study (Gao et al., 2017). Basic characteristics for the healthy volunteers are: ages: 45±15, sex (male: female): 15 : 11, systolic blood pressure (mmHg): 145.6 ± 31.4, diastolic blood pressure (mmHg): 83 ± 15, LV EF(%):57 ± 5, LV end-diastolic-volume (mL): 126 ± 21, LV end-systolic-volume (mL): 55±14. Geometry reconstruction follows the same procedure as for the amyloidosis patients (see section 2.1.2). All the LV geometries are fitted to one template LV mesh, with 5,792 vertices from the endocardial and epicardial surfaces, extracted from CMR images with the same imaging orientation as shown in Figure 4 (i.e., the chest wall in the left side of the short-axis images). Note the vertices inside the ventricular wall are excluded, and each vertex has three coordinate components. Thus, a Cartesian coordinate representation lies in the 17,376 dimensional space, necessitating the use of dimensionality reduction techniques for consideration of the geometry in the context of classification and data visualization (see Figure 4).
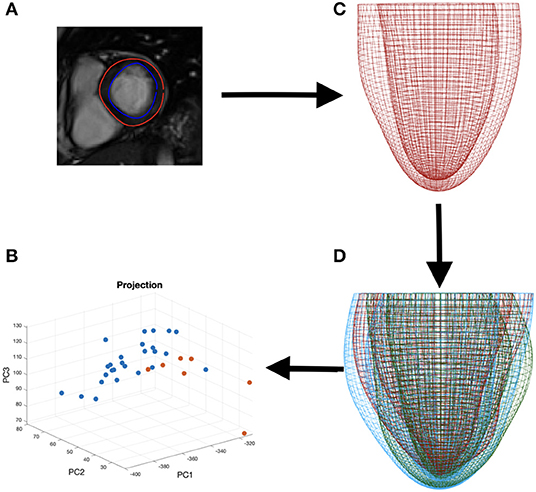
Figure 4. The process of data segmentation and dimensionality reduction. First we segment the outer and inner walls of the LV (A) allowing us to construct a mesh representation of the LV (C). We then extract the main variations in a sample of LVs (D) allowing us to represent the geometries in a lower dimensional space (B).
To analyse the LV shape change, we first need to represent the LV in a low dimensional space. Principal component analysis (PCA) relies on, successively, finding the principal directions of variation in the data where the amount of variation explained by the eigenvectors (principal components) can be quantified using the corresponding eigenvalues (Bishop, 2006). If we begin with data in n dimensions, then projecting onto the first m < n principal components provides us with a lower dimensional representation of the data while preserving variations in the data captured by these first m principal components. By construction, PCA assumes a linear mapping into the lower dimensional space and constrains the principal directions of variation to be orthogonal to one another (Shlens, 2014). Similarly, there is an implicit assumption of Gaussianity since we assume that dependence between data points is fully specified by the first two moments (mean and variance). These limitations of PCA can be overcome by considering a more flexible, non-linear, dimensionality reduction technique. Methods such as an autoencoding neural network could be considered however, for sparse data sets, as available in our study, parameter tuning will either lead to overfitting, or (if properly regularized) lose the non-linear model flexibility that motivated the method in the first place. For visualization purposes, t-Distributed Stochastic Neighbor Embedding (t-SNE) (van der Maaten and Hinton, 2008) provides a non-linear projection of the data into a lower dimensional space by minimizing a KL divergence between conditional probabilities of nearest neighbors in both spaces. However, since an explicit transformation is never learned, the method is limited to only data visualization. More details of dimensional reduction is given in Appendix A.3.
For the purpose of classification, we can first consider a supervised method similar to PCA, namely linear discriminant analysis (LDA) (Bishop, 2006). Whereas PCA finds the direction of maximal variation without taking classes into account, LDA attempts to find a lower dimensional projection for separation of the two classes (in this case, healthy volunteers and amyloidosis patients). LDA is restricted by assumptions of linearity and Gaussianity. To overcome these constraints, we will also consider a kernel support vector machine (SVM), which allows for the possibility of non-linear boundaries between the groups in the dataset by the introduction of a kernel function (Murphy, 2012).
The optimization procedure is given in Appendix A.2, followed by uncertainty quantification using the bootstrap method. The inferred material parameters for the seven patients and the corresponding errors are listed in Table 5, and Tables A2, A3. However, it is not easy to see the pattern of parameter changes directly given the potential correlations between these parameters, and the lack of uniqueness. To assess the mechanical features, below we analyze the mechanical response of the cardiac amyloidosis patients during the disease progression using our FE models with the inferred parameters.
Based on the wall-thickness scaled PED, the p-V curves estimated from the FE models are shown in Figure 5, which are compared with the corresponding results when the volume is estimated directly from CMR images. Figure 5 shows that there are little changes in the p-V curves of Cases 1, 4, 5, 7 from baseline to follow-up, but dramatic changes for Cases 2, 3, 6. The end-diastolic volumes of Cases 3, 5, and 7 increased compared to the baseline values, suggesting a ventricular dilation, while the end-diastolic volumes of Cases 1, 2, 4, and 6 decreased, especially for Case 2.
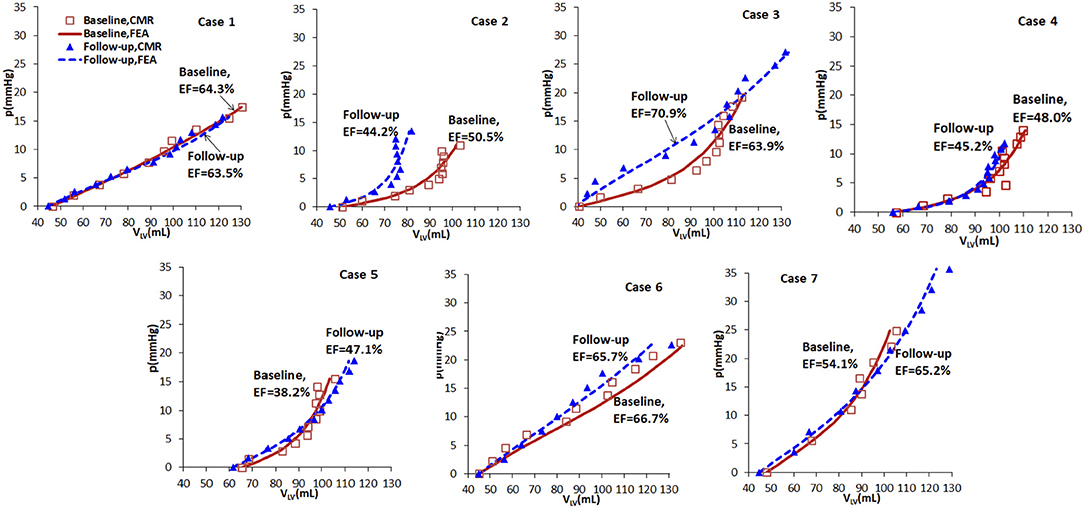
Figure 5. p-V curves of the seven cases in baseline (red) and follow-up (blue), from CMR images (symbols) and FE models (lines).
The myocardium stress-stretch response along the myofiber direction for each patient can now be obtained from a pseudo uni-axial test of the myocardium using the material parameters estimated with perfectly aligned myofibers in one direction. The results are plotted in Figure 6. The stress-stretch curves of Cases 1, 2, 4, 5, and 6 in the follow-up are less stiff than in the baseline, in contrast to Cases 3 and 7. Note that in Case 6, the difference in the baseline and follow-up is very small.
Figure 7 shows the first principal strain and stress of two different patients (Case 1 and Case 7) at baseline and follow-up. Clearly, the progression is very different in these two subjects. In Case 1, the first principal strain is slightly lower in the follow-up (Figure 7B) compared to the baseline (Figure 7A), particularly in the apical region. The strain patterns are somewhat different, but the maximum strain does not increase in the follow-up (Figure 7C vs. Figure 7D). However, for Case 7, there is a dramatic increase in the first principal stress level in the follow-up (Figure 7E) from the baseline Figure 7F. The strain patterns are also very different. In terms of the LV shape, not much change is seen in Case 1, but significant axial elongation is observed in Case 7.
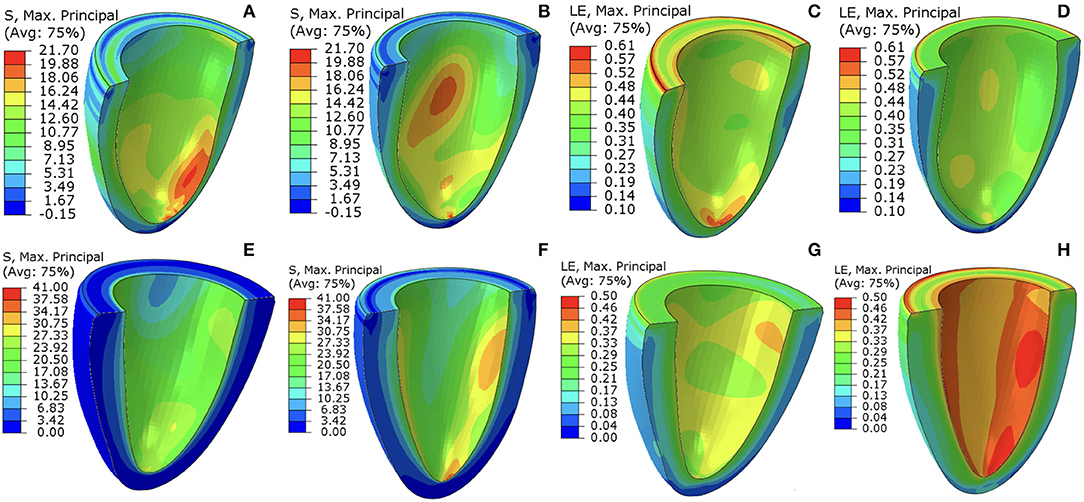
Figure 7. The first principal stress contours at baseline (A,E) and follow-up (B,F). The corresponding (logarithmic) strain contours are shown in (C,D,G,H). (A–D) are for Case 1, (E–H) are for Case 7. The unit of the stresses is kPa.
PCA permits an intuitive representation of the variations in the data via the modes of variation (See Appendix A.3, top of Figure A3), obtained by perturbing the mean LV shape along each of the principal components. For our dataset, mode 1 is clearly related to overall size of the LV, mode 2 appears to represent thickness of the LV wall and mode 3 is related to the horizontal shape. Considering the absence of group indicators in this method, it is interesting to observe the second mode of variation, showing that within the dataset one of the largest sources of LV variation appears to be wall thickness. In the central plot on the bottom of Figure A3 we see the projection of the data onto this second principal component where, as expected, there is some separation of the amyloidosis patients from the healthy volunteers once we isolate this source of variation. This separation can also be observed by considering the median distance (wall thickness) between points on the epicardium and endocardium of healthy volunteers and amyloidosis patients, found to be 0.77 and 1.11 cm for healthy volunteers and amyloidosis patients respectively. Letting wall thickness be taken as the median distance between the epicardium and endocardium walls, we obtain a p < 0.05 for a test of a difference between median wall thickness of healthy volunteers and amyloidosis patients using Mood's median test (these results are consistent with a t-test and a rank sum test).
Before studying amyloidosis progression prediction, we perform classification of the seven amyloidosis patients at baseline compared with a set of 26 healthy volunteers based on geometries alone, assessing the performance of LDA and a kernel SVM. Sensitivity (the ratio of the correctly predicted positive observations to all observations in the positive class) and specificity (the ratio of correctly predicted negative observations to all observations in the negative class) scores for these methods, obtained using a leave-one-out cross validation (LOOCV) procedure, are given in Table 3 along with an overall accuracy quantification obtained using the F1 score:
where TP is number of true positives, FP is number of false positives and FN is number of false negatives. The F1 score is the harmonic mean of the precision (the ratio of correctly predicted positive observations to the total predicted positive observations) and the recall (also called sensitivity). We use the harmonic rather than the arithmetic mean to penalize the improvement of one of the scores at the expense of the other.
Accuracy of both the linear and non-linear methods is encouraging, suggesting the discriminative properties of the LV geometry with regards to amyloidosis.
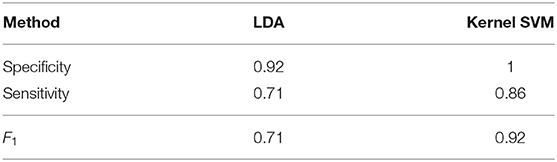
Table 3. Sensitivity, specificity, and F1 scores for classifying geometries using LDA and Kernel SVM.
The analysis above shows that no single marker provides a clear indication for disease progression. A combination of multiple features must be considered. To this end, we summarize the representative markers below that may contribute to the growth and remodeling of myocardium.
1. Vwall/VLV, which reflects the wall thickness change relative to the ventricular volume. A lower value of Vwall/VLV means the wall becomes thinner (recovery);
2. Ēcc, the circumferential strain at end-diastole averaged from the three planes. A larger value of Ēcc indicates that the LV is more compliant in the circumferential direction (recovery);
3. Ēll, the longitudinal strain at end-diastole averaged from the three planes. A larger value of Ēll indicates that the LV is more compliant in the longitudinal direction (recovery);
4. , the principal stress at end-diastole averaged from the three planes. A lower value of means the tissue is less stressed (recovery);
5. W, work done by pressure during diastolic filling, because it is not straightforward to compare different p-V curves, we compare the area-under-the-curve, which is defined as
A higher value of W in the follow-up means more work is required to maintain the heart function, corresponding to worsening.
6. The average slope of the stress-stretch curve σ − λ. A steeper σ − λ in the follow-up indicates the myocardium becomes stiffer (worsening).
7. Shape features, obvious shape changes compared to control indicate worsening.
The markers used for follow-up cardiac amyloidosis status prediction are divided into three classes: (1) geometrical markers (features 1–3), (2) biomechanical markers (features 4–6), and (3) LV shape markers (feature 7). Geometrical markers include normalized LV wall thickness, which has been applied clinically. Biomechanical markers are discussed in section 3.2.
We first study the amyloidosis patient recovery using shape features. As we do not know what is a “healthier” shape for LV, we make use of the control data from our previous study (Gao et al., 2017). The analysis is conducted by projecting the seven patients onto LDA components and measuring distances from the group of healthy volunteers before and after treatment. Pre-processing with PCA is necessary, removing collinearity and preventing singularities in the LDA calculations (this is the result of all meshes being formed by the same base LV mesh). Figure 8 presents these distances where a negative gradient is a sign of movement toward healthy volunteers. Only patients 1, 5, 6, and 7 appear to improve as a result of the treatment. This analysis is performed using leave-one-out-cross-validation where in each case one amyloidosis patient is left out of the training set. These movements toward or away from healthy volunteers provide the shape marker in Table 4 where values of the six markers in the previous section are also provided. Further details on computation of the first six markers are provided in Appendix A.2.
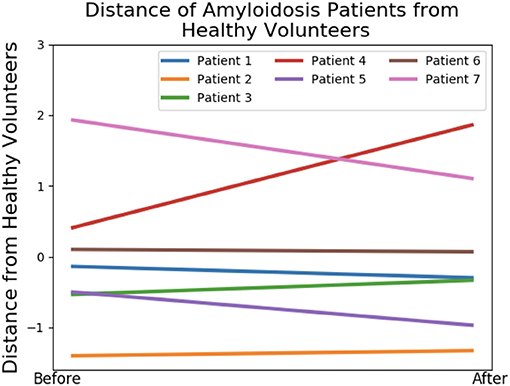
Figure 8. Shape analysis of the amyloidosis patients. This plot was produced using LDA during an initial analysis of the data, before any patient recovery labels were known. The y-axis provides a measure of distance from the group of healthy volunteers and the x-axis provides two timepoints: before and after treatment.
Now that we have quantified the shape features, we can summarize the changes of all the markers from our model in Table 4. The original values of these markers at the baseline and follow up as well as the uncertainty quantification are provided in Appendix A.4.
Using a modeling approach, we have studied the predictive power of the mechanical and geometric markers with respect to amyloidosis classification. Of great interest is the relation of amyloidosis progression with these markers, and which ones have greater predictive power. We find that, due to the complexity of the LV disease, no single marker can provide the whole picture of the disease progression. Indeed, as shown in Table 4, some markers give opposite predictions for the same case. To overcome this issue, we made use of the recovery score for each patient based on the predictions of all the markers studied.
Table 5 summarizes the results of predicting recovery of amyloidosis patients. The recovery score refers to a classification done based on Table 4, which was found before the patient labels were made available. The recovery score is obtained as the proportion of “better” predictions in Table 4. In other words, we take the number of recovery scores and divide by the total so if a patient is said to recover by 3 out of 7 markers, then the recovery score is 3/7. The small sample size here severely limits significance of these results, but by consulting a committee of weak classifiers we seek to obtain more conclusive results. All patients were diagnosed with heart failure and all of them had NYHA class 2 at presentation. However, some cases (e.g., Case 1) became class 1 after treatment, and others (e.g., case number 7) became class 3 on the second follow up. Hence, the clinical assessments can be made. This is used to compare to our recovery score in Table 4, with a good overall agreement, particularly in cases (1, 3, 4, 6, 7). Notice that although we have computed the recovery scores, we do not know the corresponding range of recovery scores to the clinical statuses (of recovery, stable or worsening). If we declare all scores above 0.5 correspond to stable or recovery, then 6 out of 7 predictions are accurate. Case 2 is predicted wrong, but the score is almost at the boundary.
Despite the encouraging results from the double blind test shown in Table 5, limitations of our work must be discussed. This is a proof of concept study in the goal of classifying disease progression after treatment in amyloidosis patients. Thus, although the concept of the approach is deemed to be rather promising, it is important to exercise caution when interpreting the statistical results presented in this paper, as the lack of data reduces significance of the statistical analysis, as well as the dimensionality reduction results.
There are two issues that can impact the stress values we estimate. The first is that it is known that the eight parameters in the HO model are coupled and not independent. Therefore, each parameter may not be uniquely determined. However, it is not the individual change of the parameters that we look for, but the collective effects of all the parameters. For example, it has been shown that the stress-strain curves can be more robustly estimated despite the inter-correlations of the parameters, as shown in our previous study (Gao et al., 2015), for different measurement noise levels or initial values. To quantify the parameter uncertainty in our paper, we have carried out a residual bootstrap analysis (Efron and Tibshirani, 1986). Our uncertainty quantification follows a three-tier approach. At the bottom tier, we apply the residual bootstrap analysis to estimate the estimation uncertainty of the biomechanical parameters, which are defined below Equation (1). The methodological details are described in Appendix A.2. Note that the bootstrap analysis takes two effects into consideration: intrinsic uncertainty as a consequence of measurement noise, and algorithmic uncertainty as a consequence of potential convergence of the optimization algorithm to local optima of the objective function. At the middle tier, we use the bootstrap distributions of the biomechanical parameter estimates from the bottom tier to obtain the corresponding distributions of the biomechanical markers, which were introduced in section 3.3.1. The results can be found in Appendix A.4. At the highest tier, we use the uncertainty of the biomechanical markers to determine the uncertainty of the recovery scores. The methodological details can be found in Appendix A.4, and the results are in Table 4.
The second issue is the significant assumption we made on the end-of-diastole pressure for the patients since invasive pressure measurements are not available. We assumed that there is a proportional relationship between the pressure and wall volume, inspired by data from the literature. This assumption increased the uncertainty of the final stress values we computed. However, we would like to state that it is not the absolute stress values, but the relative change (follow up vs. acute), that matters in our evaluations. Clearly, Table 4 shows that the recovery scores are not affected by the uncertainty intervals since, within the interval provided by the uncertainty propagation outlined in Appendix A.4, the recovery indicator does not change. We also estimated the recovery scores based on markers from the image-based strain and shape analysis alone, and found that the prediction is not as good, in that two cases (1 and 7) are predicted wrong if we exclude the stresses related markers. However, we noted that some of the individual scores give nearly opposite results. For example, in Table 4, two strain and shape indicators show that case 7 is getting better, but the three stress and wall thickness indicators show it is getting worse. Hence, not all indicators give a positive contribution to the overall score. This highlights the complexity of the pathological system, and indicates that no single biomarker studied is able to predict the amyloidosis progression. We tentatively suggest that competing mechanisms may be in play during patients' recovery. For instance, the increased strains (showing recovering) in Case 7 are accompanied by the increased stresses (showing worsening). This may imply that the more stiffened myocardium over-weights the benefits of the smaller strains. Therefore, it seems that multiple markers are required to give a balanced view for the overall picture. We remark again that our observations need to be supported by a larger sample size, as with a small sample size it is difficult to distinguish systematic effects from random fluctuations.
Other modeling limitations should also be mentioned. In this paper, amyloidosis LV is regarded as homogeneous material. The loaded early diastolic configuration is used as the reference configuration which excludes the effect of residual stresses. Our alignment of LV geometries at different times is based on a simplified linear registration approach. Nonlinear methods, such as deformable registration approaches (Rueckert et al., 1999), the large deformation deformetric metric mapping (Durrleman et al., 2014), may provide more accurate geometry co-registrations. These issues need to be addressed in future work.
A proof of concept analysis of cardiac amyloidosis progression has been obtained by projecting a group of amyloidosis patients onto linear discriminant analysis components and measuring distances from the group of healthy volunteers before and after treatment. Extensive mechanical, geometrical, and shape markers are included in the analysis for the first time for cardiac amyloidosis patients. A promising agreement with clinical observation is achieved in predicting disease progression following medical treatments in a double blind test. Although these results should be interpreted with caution due to a small sample size, the methodology of using statistical analysis and multiple markers, in particular the shape analysis, can play a powerful role in clinical translation in the future when used in large samples with new and automatic image segmentation methods.
All datasets generated for this study are included in the article/Supplementary Material.
Ethical approval was obtained from the Joint University College London/University College London Hospitals Research Ethics Committee (REC reference: 07/H0715/101). All research-related procedures were performed in accordance with local guidelines and regulations. The patients/participants provided their written informed consent to participate in this study.
XL, HG, and DH designed the study. WL and AL developed the mechanical and statistical models. AM-N, MF, and PH acquired the CMR scans. SB, RJ, and JC initiated the research idea and helped with image analysis. CB provided clinical insight. All participated in writing the manuscript.
This research was supported by the Engineering and Physical Sciences Research Council (EP/N014642/1, EP/S030875, EP/S020950/1), the British Heart Foundation Grant (Project Grant PG/14/64/31043, PG/11/2/28474), the National Health Service, and the Chief Scientist Office, and the British Heart Foundation Centre of Research Excellence Award (CoE RE/186134217). DH was supported by a grant from the Royal Society of Edinburgh, award no. 62335.
RJ and JC were employed by the company GlaxoSmithKline, plc, UK. The University of Glasgow holds research and/or consultancy agreements with Siemens Healthcare and GlaxoSmithKline plc for work done by XL, CB, and others.
We thank the patients who participated in this study.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2020.00324/full#supplementary-material
Asner, L., Hadjicharalambous, M., Chabiniok, R., Peresutti, D., Sammut, E., Wong, J., et al. (2016). Estimation of passive and active properties in the human heart using 3D tagged MRI. Biomech. Model. Mechanobiol. 15, 1121–1139. doi: 10.1007/s10237-015-0748-z
Bhuiyan, T., Helmke, S., Patel, A. R., Ruberg, F. L., Packman, J., Cheung, K., et al. (2011). Pressure-volume relationships in patients with transthyretin (ATTR) cardiac amyloidosis secondary to V122I mutations and wild-type transthyretin: Transthyretin cardiac amyloid study (TRACS). Circulation 4, 121–128. doi: 10.1161/CIRCHEARTFAILURE.109.910455
Bishop, C. M. (2006). Pattern Recognition and Machine Learning (Information Science and Statistics). Berlin; Heidelberg: Springer-Verlag.
Boufidou, A., Mantziari, L., Paraskevaidis, S., Karvounis, H., Nenopoulou, E., Manthou, M.-E., et al. (2010). An interesting case of cardiac amyloidosis initially diagnosed as hypertrophic cardiomyopathy. Hellenic J. Cardiol. 51, 552–557. Available online at: https://www.hellenicjcardiol.org/archive/full_text/2010/6/2010_6_552.pdf
Buss, S. J., Emami, M., Mereles, D., Korosoglou, G., Kristen, A. V., Voss, A., et al. (2012). Longitudinal left ventricular function for prediction of survival in systemic light-chain amyloidosis: incremental value compared with clinical and biochemical markers. J. Am. Coll. Cardiol. 60, 1067–1076. doi: 10.1016/j.jacc.2012.04.043
Carroll, J. D., Gaasch, W. H., and McAdam, K. P. (1982). Amyloid cardiomyopathy: characterization by a distinctive voltage/mass relation. Am. J. Cardiol. 49, 9–13. doi: 10.1016/0002-9149(82)90270-3
Chapelle, D., Felder, A., Chabiniok, R., Guellich, A., Deux, J.-F., and Damy, T. (2015). “Patient-specific biomechanical modeling of cardiac amyloidosis–a case study,” in International Conference on Functional Imaging and Modeling of the Heart (Maastricht: Springer), 295–303. doi: 10.1007/978-3-319-20309-6_34
Chew, C., Ziady, G. M., Raphael, M. J., and Oakley, C. M. (1975). The functional defect in amyloid heart disease: the “stiff heart” syndrome. Am. J. Cardiol. 36, 438–444. doi: 10.1016/0002-9149(75)90891-7
Dungu, J. N., Valencia, O., Pinney, J. H., Gibbs, S. D., Rowczenio, D., Gilbertson, J. A., et al. (2014). CMR-based differentiation of AL and ATTR cardiac amyloidosis. JACC 7, 133–142. doi: 10.1016/j.jcmg.2013.08.015
Durrleman, S., Prastawa, M., Charon, N., Korenberg, J. R., Joshi, S., Gerig, G., et al. (2014). Morphometry of anatomical shape complexes with dense deformations and sparse parameters. NeuroImage 101, 35–49. doi: 10.1016/j.neuroimage.2014.06.043
Efron, B., and Tibshirani, R. (1986). Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat. Sci. 1, 54–75. doi: 10.1214/ss/1177013815
Fontana, M., Pica, S., Reant, P., Abdel-Gadir, A., Treibel, T. A., Banypersad, S. M., et al. (2015). Prognostic value of late gadolinium enhancement cardiovascular magnetic resonance in cardiac amyloidosis. Circulation 132, 1570–1579. doi: 10.1161/CIRCULATIONAHA.115.016567
Frenzel, H., Schwartzkopff, B., Kuhn, H., Lösse, B., Thormann, J., Hort, W., et al. (1986). Cardiac amyloid deposits in endomyocardial biopsies: light microscopic, ultrastructural, and immunohistochemical studies. Am. J. Clin. Pathol. 85, 674–680. doi: 10.1093/ajcp/85.6.674
Gao, H., Aderhold, A., Mangion, K., Luo, X., Husmeier, D., and Berry, C. (2017). Changes and classification in myocardial contractile function in the left ventricle following acute myocardial infarction. J. R. Soc. Interface 14:20170203. doi: 10.1098/rsif.2017.0203
Gao, H., Carrick, D., Berry, C., Griffith, B. E., and Luo, X. (2014a). Dynamic finite-strain modelling of the human left ventricle in health and disease using an immersed boundary-finite element method. IMA J. Appl. Math. 79, 978–1010. doi: 10.1093/imamat/hxu029
Gao, H., Li, W., Cai, L., Berry, C., and Luo, X. (2015). Parameter estimation in a holzapfel–ogden law for healthy myocardium. J. Eng. Math. 95, 231–248. doi: 10.1007/s10665-014-9740-3
Gao, H., Wang, H., Berry, C., Luo, X., and Griffith, B. E. (2014b). Quasi-static image-based immersed boundary-finite element model of left ventricle under diastolic loading. Int. J. Numer. Methods Biomed. Eng. 30, 1199–1222. doi: 10.1002/cnm.2652
Genet, M., Lee, L. C., Nguyen, R., Haraldsson, H., Acevedo-Bolton, G., Zhang, Z., et al. (2014). Distribution of normal human left ventricular myofiber stress at end diastole and end systole: a target for in silico design of heart failure treatments. J. Appl. Physiol. 117, 142–152. doi: 10.1152/japplphysiol.00255.2014
Gertz, M., Dispenzieri, A., Grogan, M., Kumar, S., Leung, N., Maurer, M., et al. (2013). Amyloidosis Awareness. Amyloidosis Support Groups.
Göktepe, S., Acharya, S., Wong, J., and Kuhl, E. (2011). Computational modeling of passive myocardium. Int. J. Numer. Methods Biomed. Eng. 27, 1–12. doi: 10.1002/cnm.1402
Grogan, M., Dispenzieri, A., and Gertz, M. A. (2017). Light-chain cardiac amyloidosis: strategies to promote early diagnosis and cardiac response. Heart 103, 1065–1072. doi: 10.1136/heartjnl-2016-310704
Holzapfel, G. A., and Ogden, R. W. (2009). Constitutive modelling of passive myocardium: a structurally based framework for material characterization. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 367, 3445–3475. doi: 10.1098/rsta.2009.0091
Kholova, I., and Niessen, H. (2005). Amyloid in the cardiovascular system: a review. J. Clin. Pathol. 58, 125–133. doi: 10.1136/jcp.2004.017293
Koyama, J., Ray-Sequin, P. A., and Falk, R. H. (2003). Longitudinal myocardial function assessed by tissue velocity, strain, and strain rate tissue doppler echocardiography in patients with al (primary) cardiac amyloidosis. Circulation 107, 2446–2452. doi: 10.1161/01.CIR.0000068313.67758.4F
Liu, D., Hu, K., Niemann, M., Herrmann, S., Cikes, M., Störk, S., et al. (2013). Impact of regional left ventricular function on outcome for patients with al amyloidosis. PLoS ONE 8:e56923. doi: 10.1371/journal.pone.0056923
Liu, Y., Wen, H., Gorman, R. C., Pilla, J. J., Gorman, J. H. III., Buckberg, G., et al. (2009). Reconstruction of myocardial tissue motion and strain fields from displacement-encoded MR imaging. Am. J. Physiol. Heart Circul. Physiol. 297, H1151–H1162. doi: 10.1152/ajpheart.00074.2009
Martinez-NaharrO, A., Hawkins, P. N., and Fontana, M. (2018). Cardiac amyloidosis. Clin. Med. 18, s30–s35. doi: 10.7861/clinmedicine.18-2-s30
Nikou, A., Dorsey, S. M., McGarvey, J. R., Gorman, J. H., Burdick, J. A., Pilla, J. J., et al. (2016). Computational modeling of healthy myocardium in diastole. Ann. Biomed. Eng. 44, 980–992. doi: 10.1007/s10439-015-1403-7
Nucifora, G., Muser, D., Morocutti, G., Piccoli, G., Zanuttini, D., Gianfagna, P., et al. (2014). Disease-specific differences of left ventricular rotational mechanics between cardiac amyloidosis and hypertrophic cardiomyopathy. Am. J. Physiol. Heart Circul. Physiol. 307, H680–H688. doi: 10.1152/ajpheart.00251.2014
Palit, A., Bhudia, S. K., Arvanitis, T. N., Turley, G. A., and Williams, M. A. (2018). In vivo estimation of passive biomechanical properties of human myocardium. Med. Biol. Eng. Comput. 56, 1615–16317. doi: 10.1007/s11517-017-1768-x
Petre, R. E., Quaile, M. P., Wendt, K., Houser, S. R., Wald, J., Goldman, B. I., et al. (2005). Regionally heterogeneous tissue mechanics in cardiac amyloidosis. Amyloid 12, 246–250. doi: 10.1080/13506120500386824
Plehn, J. F., Southworth, J., and Cornwell III, G. G. (1992). Atrial systolic failure in primary amyloidosis. N. Engl. J. Med. 327, 1570–1573. doi: 10.1056/NEJM199211263272205
Potse, M., Dubé, B., Richer, J., Vinet, A., and Gulrajani, R. M. (2006). A comparison of monodomain and bidomain reaction-diffusion models for action potential propagation in the human heart. IEEE Trans. Biomed. Eng. 53, 2425–2435. doi: 10.1109/TBME.2006.880875
Quarta, C., Kruger, J., and Falk, R. (2012). Cardiac amyloidosis. Clin. Med. 126, e178–e182. doi: 10.1161/CIRCULATIONAHA.111.069195
Rueckert, D., Sonoda, L. I., Hayes, C., Hill, D. L., Leach, M. O., and Hawkes, D. J. (1999). Nonrigid registration using free-form deformations: application to breast MR images. IEEE Trans. Med. Imaging 18, 712–721. doi: 10.1109/42.796284
Steendijk, P., Tulner, S. A., Wiemer, M., Bleasdale, R. A., Bax, J. J., van der Wall, E. E., et al. (2004). Pressure–volume measurements by conductance catheter during cardiac resynchronization therapy. Eur. Heart J. Suppl. 6(Suppl. D), D35–D42. doi: 10.1016/j.ehjsup.2004.05.012
Sun, J. P., Stewart, W. J., Yang, X. S., Donnell, R. O., Leon, A. R., Felner, J. M., et al. (2009). Differentiation of hypertrophic cardiomyopathy and cardiac amyloidosis from other causes of ventricular wall thickening by two-dimensional strain imaging echocardiography. Am. J. Cardiol. 103, 411–415. doi: 10.1016/j.amjcard.2008.09.102
Swanton, R. H., Brooksby, A. I., Davies, M. J., Coltart, D. J., Jenkins, B. S., and Webb-Peploe, M. M. (1977). Systolic and diastolic ventricular function in cardiac amyloidosis: studies in six cases diagnosed with endomyocardial biopsy. Am. J. Cardiol. 39, 658–664. doi: 10.1016/S0002-9149(77)80125-2
Vogelsberg, H., Mahrholdt, H., Deluigi, C. C., Yilmaz, A., Kispert, E. M., Greulich, S., et al. (2008). Cardiovascular magnetic resonance in clinically suspected cardiac amyloidosis: noninvasive imaging compared to endomyocardial biopsy. J. Am. Coll. Cardiol. 51, 1022–1030. doi: 10.1016/j.jacc.2007.10.049
Wang, H., Gao, H., Luo, X., Berry, C., Griffith, B., Ogden, R., et al. (2013). Structure-based finite strain modelling of the human left ventricle in diastole. Int. J. Numer. Methods Biomed. Eng. 29, 83–103. doi: 10.1002/cnm.2497
Wang, H., Luo, X., Gao, H., Ogden, R., Griffith, B., Berry, C., et al. (2014). A modified holzapfel-ogden law for a residually stressed finite strain model of the human left ventricle in diastole. Biomech. Model. Mechanobiol. 13, 99–113. doi: 10.1007/s10237-013-0488-x
Keywords: cardiac amyloidosis, left ventricle, model-based markers, classification, strain and stress, shape analysis, MRI
Citation: Li W, Lazarus A, Gao H, Martinez-Naharro A, Fontana M, Hawkins P, Biswas S, Janiczek R, Cox J, Berry C, Husmeier D and Luo X (2020) Analysis of Cardiac Amyloidosis Progression Using Model-Based Markers. Front. Physiol. 11:324. doi: 10.3389/fphys.2020.00324
Received: 19 October 2019; Accepted: 20 March 2020;
Published: 30 April 2020.
Edited by:
Wenchang Tan, Peking University, ChinaReviewed by:
Vicky Y. Wang, The University of Auckland, New ZealandCopyright © 2020 Li, Lazarus, Gao, Martinez-Naharro, Fontana, Hawkins, Biswas, Janiczek, Cox, Berry, Husmeier and Luo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaoyu Luo, WGlhb3l1Lmx1b0BnbGFzZ293LmFjLnVr
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.