Multiple Dynamical Mechanisms of Phase-2 Early Afterdepolarizations in a Human Ventricular Myocyte Model: Involvement of Spontaneous SR Ca2+ Release

Early afterdepolarization (EAD) is known to cause lethal ventricular arrhythmias in long QT syndrome (LQTS). In this study, dynamical mechanisms of EAD formation in human ventricular myocytes (HVMs) were investigated using the mathematical model developed by ten Tusscher and Panfilov (Am J Physiol Heart Circ Physiol 291, 2006). We explored how the rapid (I_Kr) and slow (I_Ks) components of delayed-rectifier K⁺ channel currents, L-type Ca²⁺ channel current (I_CaL), Na⁺/Ca²⁺ exchanger current (I_NCX), and intracellular Ca²⁺ handling via the sarcoplasmic reticulum (SR) contribute to initiation, termination and modulation of phase-2 EADs during pacing in relation to bifurcation phenomena in non-paced model cells. Parameter-dependent dynamical behaviors of the non-paced model cell were determined by calculating stabilities of equilibrium points (EPs) and limit cycles, and bifurcation points to construct bifurcation diagrams. Action potentials (APs) and EADs during pacing were reproduced by numerical simulations for constructing phase diagrams of the paced model cell dynamics. Results are summarized as follows: (1) A modified version of the ten Tusscher-Panfilov model with accelerated I_CaL inactivation could reproduce bradycardia-related EADs in LQTS type 2 and β-adrenergic stimulation-induced EADs in LQTS type 1. (2) Two types of EADs with different initiation mechanisms, I_CaL reactivation–dependent and spontaneous SR Ca²⁺ release–mediated EADs, were detected. (3) Termination of EADs (AP repolarization) during pacing depended on the slow activation of I_Ks. (4) Spontaneous SR Ca²⁺ releases occurred at higher Ca²⁺ uptake rates, attributable to the instability of steady-state intracellular Ca²⁺ concentrations. Dynamical mechanisms of EAD formation and termination in the paced model cell are closely related to stability changes (bifurcations) in dynamical behaviors of the non-paced model cell, but they are model-dependent. Nevertheless, the modified ten Tusscher-Panfilov model would be useful for systematically investigating possible dynamical mechanisms of EAD-related arrhythmias in LQTS.

Introduction

Early afterdepolarization (EAD) is well known to trigger lethal ventricular arrhythmias, called Torsades de Pointes (TdP), in patients with long QT syndrome (LQTS) (Weiss et al., 2010; Shimizu and Horie, 2011; Shimizu, 2013). For prevention and treatment of ventricular arrhythmias in LQTS patients, therefore, elucidating the mechanisms of initiation and termination of EADs and how to suppress EADs is of crucial importance. There are many experimental studies regarding the mechanisms of EAD formation in cardiomyocytes, suggesting major contribution of reactivation of the L-type Ca²⁺ channel current (I_CaL) to the initiation of EADs during the action potential (AP) phase 2 (e.g., January et al., 1988; January and Riddle, 1989; Guo D. et al., 2007; Weiss et al., 2010; Xie et al., 2010; Milberg et al., 2012a; Shimizu, 2013). However, recent experimental studies suggested the major role in EAD formation of the spontaneous Ca²⁺ release from the sarcoplasmic reticulum (SR) (Volders et al., 2000; Choi et al., 2002; Zhao et al., 2012). In our recent theoretical study (Kurata et al., 2017) using two human ventricular myocyte (HVM) models developed by Kurata et al. (2005) and O’Hara et al. (2011), referred to as K05 and O11 models, respectively, we could find EAD formations resulting from the I_CaL reactivation, but not the spontaneous SR Ca²⁺ release-mediated EADs. With respect to the termination of EADs (AP repolarization), theoretical studies (Tran et al., 2009; Qu et al., 2013) using a guinea-pig ventricular myocyte model (Luo and Rudy, 1991) suggested the slowly activating delayed-rectifier K⁺ channel current (I_Ks) as a key current to cause termination of EADs. However, our preceding study (Kurata et al., 2017) suggested that the mechanisms of EAD termination were model-dependent, not necessarily requiring I_Ks. Thus, despite many experimental and theoretical studies, how individual membrane and intracellular components contribute to the initiation, termination and modulation of EADs remains controversial.

The aims of this study were (1) to determine whether the ten Tusscher and Panfilov model (ten Tusscher and Panfilov, 2006; referred to as the TP06 model) for HVMs, which has often been used for simulations of reentrant arrhythmias in the human ventricle (ten Tusscher et al., 2007; Adeniran et al., 2012; Zimik et al., 2015; Kazbanov et al., 2016), could reproduce EAD formation in LQTS (validation of the model cell for EAD reproducibility), and (2) to define the contributions of individual sarcolemmal and intracellular components to the initiation, termination, and modulation of phase-2 EADs in the TP06 model in comparison with those in other HVM models (evaluation of model dependence for EAD mechanisms). As in our preceding study (Kurata et al., 2017; Tsumoto et al., 2017), we examined parameter-dependent changes in stabilities of steady states and AP dynamics in the HVM model from the aspect of bifurcation phenomena, which are parameter-dependent qualitative changes in dynamical behaviors, in non-linear dynamical systems (Guckenheimer and Holmes, 1983; Parker and Chua, 1989; Kuznetsov, 2003). Conditions and dynamical mechanisms of EAD formation in the paced model cell were determined in relation to bifurcations of the non-paced model cell.

With respect to the dynamical mechanisms of EAD formation, we particularly focused on (1) whether and how contributions of each cellular component to occurrences of EADs and bifurcations in the TP06 model are different from those in the K05 and O11 models; (2) whether spontaneous SR Ca²⁺ release-mediated EAD initiation, which did not occur in the K05 or O11 model, can be reproduced by the TP06 model in connection with a bifurcation (destabilization) of intracellular Ca²⁺ dynamics; and (3) how slow I_Ks activation, as well as I_CaL inactivation and other slow factors, contributes to EAD termination. This study would further provide a theoretical background for experimental and simulation studies on mechanisms of EAD formation and EAD-triggered reentrant arrhythmias in the LQTS human ventricle, as well as for prevention and treatments of life-threatening arrhythmias, like TdPs, in LQTS.

Materials and Methods

Mathematical Modeling for HVMs

Base Mathematical Model

In this study, we tested the mid-myocardial (M) cell version of the TP06 model for HVMs (ten Tusscher and Panfilov, 2006), which could reproduce phase-2 EADs during inhibition of I_Ks and/or the rapidly activating delayed rectifier K⁺ channel current (I_Kr) or enhancement of I_CaL. The M cell version was chosen because it has smaller I_Kr and I_Ks and thus more vulnerable to EAD formation than the epicardial or endocardial version, as suggested experimentally as well (Antzelevitch et al., 1999), and a few modifications were made for the M cell version of the TP06 model. Figure 1 shows simulated behaviors of APs, sarcolemmal ionic currents and intracellular Ca²⁺ concentrations in the original and modified M cell versions of the TP06 model with various g_Ks and g_Kr values. Inconsistent with experiments for HVMs that observed only small prolongation of AP duration (APD) by I_Ks inhibition (Jost et al., 2005; O’Hara and Rudy, 2012), the original version of the TP06 model, which has relatively large I_Ks, exhibited marked APD prolongation during I_Ks inhibition, and failed to reproduce greater APD prolongation and phase-2 EADs during I_Kr inhibition (see Figure 1A). In addition, the Ca²⁺ concentration in the SR (Ca_SR) (3–4 mM during 1-Hz pacing) was higher than the experimentally observed values of 1–2 mM for rabbit ventricular myocytes (Shannon et al., 2003, 2004; Guo T. et al., 2007). Therefore, the modified version, referred to as the “mTP06a” model, underwent the following modifications: (1) 60% reduction of the maximum I_Ks conductance (g_Ks) with 50% increment of the maximum I_Kr conductance (g_Kr) to reproduce the I_Kr/I_Ks inhibition experiments, and (2) 40% reduction in the SR Ca²⁺ uptake rate (P_up) to reduce the Ca²⁺ concentration in the SR during pacing under control conditions. These modifications yielded the experimentally observed small APD prolongation by I_Ks inhibition and smaller Ca_SR of 1.3–2.6 mM during pacing at 0.5–1 Hz, but not EAD formation (Figure 1B). Therefore, we have developed another version of the modified TP06 model referred to as the “mTP06b” model with halved time constant of I_CaL inactivation (τ_fL) and doubled maximum I_CaL conductance (g_CaL) on the basis of a previous theoretical study by Vandersickel et al. (2014) that required acceleration of the voltage-dependent inactivation of I_CaL for reproducing EADs in the TP06 model. As shown in Figure 1C, the mTP06b model could reproduce the experimentally observed responses of HVMs to reductions of I_Kr or I_Ks, with EADs generated during I_Kr reductions. Maximum conductance of the ionic channels, densities of transporters, and SR Ca²⁺ uptake/release rates for the modified versions, as well as for the original version, are given in Supplementary Table S1.

FIGURE 1

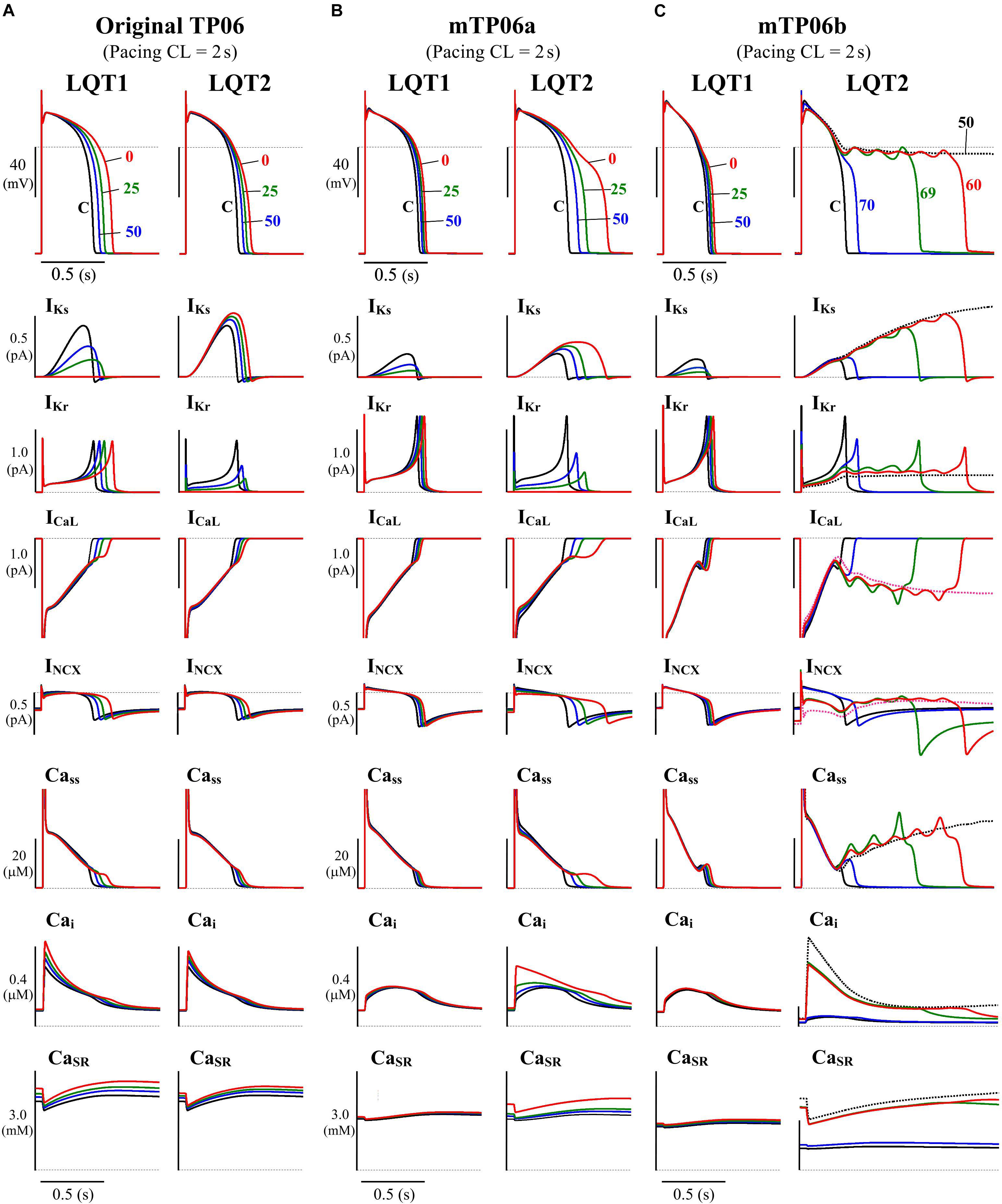
Figure 1. Simulated behaviors of APs (EADs), sarcolemmal ionic currents (I_Ks, I_Kr, I_CaL, I_NCX) and intracellular Ca²⁺ concentrations (Ca_ss, Ca_i, Ca_SR) in the M cell versions of the original TP06 (A), mTP06a (B), and mTP06b (C) models. To mimic the pathological conditions of LQT1 and LQT2, g_Ks and g_Kr values, respectively, were decreased by 30–100%; individual APs are labeled by the numbers representing the residual g_Ks or g_Kr (%Control), with ionic currents and Ca²⁺ concentrations for each g_Ks and g_Kr value shown by the same colors. The horizontal dashed lines denote the 0 mV, zero current and zero concentration levels. Current amplitudes for the y-axis scale bars are given in pA/pF. The model cells were paced at 0.5 Hz, i.e., with the cycle length (CL) of 2 s for 60 min; AP waveforms, ion currents and Ca²⁺ concentrations after the last stimulus are shown as steady-state behaviors under each condition.

The TP06 model for the normal activity of single HVMs is described as a non-linear dynamical system of 19 first-order ordinary differential equations. The membrane current system includes the Na⁺ channel current (I_Na), I_CaL, I_Kr, I_Ks, 4-aminopyridine-sensitive transient outward current (I_to), inward-rectifier K⁺ channel current (I_K1), background K⁺ (I_pK), Na⁺ (I_bNa) and Ca²⁺ (I_bCa) currents, Na⁺-K⁺ pump current (I_NaK), Na⁺/Ca²⁺ exchanger current (I_NCX), and Ca²⁺ pump current (I_pCa). Time-dependent changes in the membrane potential (V_m) are described by the equation,

$$\mathrm{dV}{}_{\text{m}}/\mathrm{dt}=\mathrm{I}{}_{\text{stim}}-(\mathrm{I}{}_{\text{Na}}+\mathrm{I}{}_{\text{CaL}}+\mathrm{I}{}_{\text{Kr}}+\mathrm{I}{}_{\text{Ks}}+\mathrm{I}{}_{\text{to}}+$$

$$\mathrm{I}{}_{\mathrm{K1}}+\mathrm{I}{}_{\text{pK}}+\mathrm{I}{}_{\text{b}}{}_{\text{Na}}+\mathrm{I}{}_{\text{b}}{}_{\text{Ca}}+\mathrm{I}{}_{\text{NaK}}+\mathrm{I}{}_{\text{NC}}{}_{\text{X}}+\mathrm{I}{}_{\text{pCa}})(1)$$

where I_stim represents the stimulus current (in pA/pF).

The basic model systems include material balance expressions to define the temporal variations in concentrations of myoplasmic K⁺ (K_i), Na⁺ (Na_i) and Ca²⁺ (Ca_i), and subspace Ca²⁺ (Ca_ss), while external concentrations of K⁺, Na⁺ and Ca²⁺ were fixed at 5.4, 140, and 2.0 mM, respectively. For bifurcation analyses, K_i was fixed at 140 mM for the removal of degeneracy (Krogh-Madsen et al., 2005; Kurata et al., 2008); effects of parameter-dependent changes in K_i (∼5 mM) on EAD formation and bifurcation phenomena in the model cell were much smaller than those of the same amount of changes in Na_i. Na_i was unfixed unless otherwise stated, but fixed at 6 mM in some cases (e.g., for the slow-fast decomposition analysis and for voltage-clamped cells, as described later); changes in Na_i during AP phase 2 and EAD formation in paced model cells were slow and relatively small.

Details on expressions, standard parameter values, and dynamics of the TP06 model are provided in the original article (ten Tusscher and Panfilov, 2006), and the original TP06 model has been implemented in a cellML-based open resource for public access¹. In addition, the original TP06, mTP06a, and mTP06b models have been implemented in PhysioDesigner as XML-based Physiological Hierarchy Markup Language (PHML)² models. These models can be referred from PHML database (ID938 to 940)³, and simulations of their temporal behaviors can be performed using the software, Flint⁴.

Modeling LQTS Cardiomyocytes With Simulated EADs

Mutations of I_Ks and I_Kr channels (Roden et al., 1996; Chouabe et al., 1997; Anderson et al., 2006; Wiener et al., 2008; Kondo et al., 2016), as well as their pharmacological inhibitions (e.g., Carmeliet, 1992; Volders et al., 2003; Jost et al., 2005), are known to cause a wide range of channel conductance changes, leading to congenital or acquired LQTS type 1 (LQT1) and type 2 (LQT2), respectively. We developed LQT1- and LQT2-type model cells by continuously reducing g_Ks and g_Kr, respectively, from unity to zero. As illustrated in Figure 1, the TP06b model, but not the original version (with larger I_Ks) or the mTP06a model, reproduced phase-2 EADs (and AP repolarization failure) when g_Kr became smaller as in LQT2 cardiomyocytes. In contrast, g_Ks-reduced LQT1 model cells did not exhibit EADs but showed only slight prolongation of APDs under the basal condition, consistent with the recent experimental results from HVMs (Jost et al., 2005; O’Hara and Rudy, 2012).

Simulating Conditions of β-Adrenergic Stimulation

To simulate the condition of β-adrenergic stimulation (β-AS) as a major trigger of EADs and TdP in LQT1 patients, we modified the maximum conductance of ion channels and density of transporters based on previous reports (Zeng and Rudy, 1995; Volders et al., 2003; Kuzumoto et al., 2008), as described in our preceding article (Kurata et al., 2017). g_CaL and g_Ks were increased up to 250% and 200%, respectively, according to previous reports for their changes during β-AS (Veldkamp et al., 2001; Saucerman et al., 2003; Himeno et al., 2008; Maltsev and Lakatta, 2010; Briston et al., 2014). Modifications of parameters for simulating β-AS are listed in Supplementary Table S2.

Numerical Methods for Dynamic Simulations

Basic Methods

Dynamic behaviors of the model cells were determined by numerically solving a set of non-linear ordinary differential equations including Eqn. 1. AP responses were elicited by 1-ms current stimuli of 60 pA/pF. When phase-2 EADs occurred at higher frequencies of the pacing, a complete AP repolarization was preceded by the next stimulus. Thus, the pacing cycle length (CL) was usually set to longer values of 2–5 s, except for analyses of the rate dependence. Numerical integration was performed by using MATLAB (The MathWorks, Inc., Natick, MA, United States) ODE solvers, ode15s and ode45, with the maximum relative error tolerance for the integration methods of 1 × 10^–8.

Initial values of the state variables for computation at a parameter set were their steady-state values at a resting V_m (see Supplementary Table S3 for the control conditions), which were perturbed by the current stimulus; the last values of the state variables in computation were used as initial conditions for the next computation at a new parameter set. The minimum V_m during AP phase 4 (V_min) and the maximum V_m during early phase 2 before emergence of an EAD (V_max), as well as APD at 90% repolarization (APD₉₀), were determined for individual APs or AP sets. Steady-state APs for the first parameter set were obtained by numerical integration for 30 min; subsequent numerical integration with each parameter set was continued until the differences in V_min, V_max and APD₉₀ between the newly calculated AP and the preceding one became <1 × 10^–3 of their preceding values.

Detection of EADs

EADs were detected as transient V_m oscillations which emerged during late AP phase 2 (200 ms or later from the AP peak) and eventually led to AP repolarization to a resting V_m. All the local minimum (EAD_min) and maximum (EAD_max) of V_m oscillations during EAD formation, as well as a set of V_min, V_max and APD₉₀, were determined for one AP cycle. When APs with EADs were irregular (arrhythmic), all the potential extrema (V_min, V_max, EAD_min, and EAD_max) and APD₉₀ values were sampled for APs evoked by the last 10 stimuli.

Stability and Bifurcation Analyses for HVMs

We performed bifurcation analysis to explore how dynamical properties of the HVM model cell systems alter with changes in parameters. Detailed procedures for bifurcation analyses, i.e., locating equilibrium points (EPs) and limit cycles (LCs), detecting bifurcation points by determination of their stabilities, were provided in our previous articles (Kurata et al., 2008, 2012, 2013, 2017; Tsumoto et al., 2017), as well as in textbooks (Guckenheimer and Holmes, 1983; Parker and Chua, 1989; Kuznetsov, 2003). In the present study, one- and two-parameter bifurcation diagrams for the non-paced cell model, as well as phase diagrams for the paced model cell, were constructed as functions of parameters, including (1) g_Ks, g_Kr, and g_CaL, (2) scaling factor for I_NCX, (3) P_up, and (4) pacing CL. The maximum conductance of the ionic channel currents and P_up were expressed as normalized values, i.e., ratios to the control values. Mechanisms of the initiation and termination of EADs were further examined by the slow-fast decomposition analysis, in which stability and bifurcations of a fast subsystem are determined as functions of a slow variable, i.e., the gating variable xs for I_Ks activation or Ca_SR (Tran et al., 2009; Qu et al., 2013; Xie et al., 2014). Basic concepts of bifurcation analysis, types of bifurcations, and methods for constructions of bifurcation/phase diagrams and slow-fast decomposition analysis are briefly described in Supplementary Materials.

Results

Validation and Characterization of the mTP06 Models for LQTS HVMs

We first determined whether the mTP06a/b models can mimic the electrophysiological properties of I_Kr-reduced LQTS type 2 (LQT2) and I_Ks-reduced LQTS type 1 (LQT1) HVMs, in which EADs occur mainly at lower heart rates (bradycardia), and under β-AS, e.g., during exercise (tachycardia), respectively.

Decreases in I_Kr and/or I_Ks Accelerated EAD Formation in the mTP06 Model

The mTP06b model, but not the original TP06 or mTP06a model, exhibited an AP with EADs when I_Kr was inhibited during 0.5-Hz pacing (Figure 1). Similarly, when g_Kr was reduced by 40% during 0.2-Hz pacing, we could observe the AP with EADs in the g_Kr-reduced mTP06b model, as shown in Figure 2A-a. This simulated AP with EADs was accompanied by oscillatory reactivation of I_CaL, and was terminated (i.e., V_m went back to the resting V_m) as I_Ks increased (blue arrows for I_Ks in Figure 2A-a). Further reducing g_Kr by 60% caused another type of EADs with I_Ks saturated before applying the second stimulus (Figure 2A-b); just before applying this second stimulus, the transient depolarization in plateau phase originating from the spontaneous SR Ca²⁺ release and resulting activation of inward I_NCX (red arrows in Figure 2A-b). In this case, repolarization did not occur without the next stimulus, i.e., repolarization failure occurred in the non-paced model cell after the cessation of pacing (Figure 2A-c).

FIGURE 2

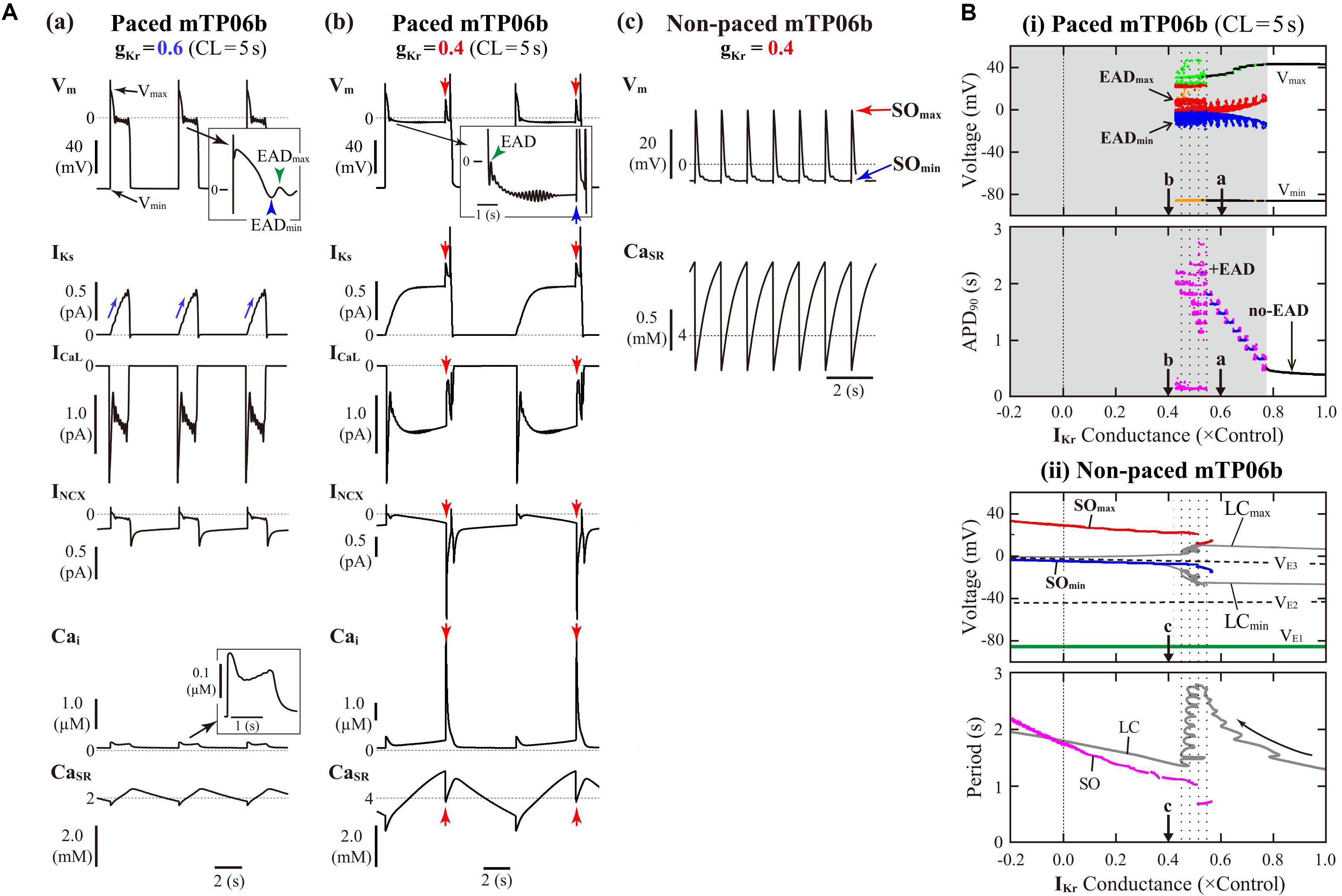
Figure 2. I_Kr-dependent EAD generation and bifurcations in the mTP06b model. (A) Simulated dynamics of V_m, I_Ks, I_CaL, I_NCX, Ca_i, and Ca_SR (from top to bottom) in the g_Kr-reduced model cells paced at 0.2 Hz, illustrating two types of EADs. Temporal behaviors of the variables were computed for 30 min; the behaviors elicited by additional 3-4 stimuli are shown. APs with EADs were terminated (V_m repolarized) by gradual increases in I_Ks (a) or the next stimulus as indicated by the blue arrow (b). Spontaneous SR Ca²⁺ releases and resulting increases of inward I_NCX to provoke EADs occurred at g_Kr = 0.4, as indicated by the red arrows (b). With the smaller g_Kr, sustained V_m oscillations driven by spontaneous SR Ca²⁺ releases were observed after cessation of pacing, i.e., in the non-paced model cell (c). (B) Potential extrema of APs and EADs, and the AP duration (APD) measured at 90% repolarization (APD₉₀) are plotted as functions of normalized g_Kr for the paced model cell (i). One-parameter bifurcation diagrams depicting steady-state V_m at equilibrium points (EPs), the extrema of limit cycles (LCs) and spontaneous oscillations (SOs), and the periods of LCs and SOs plotted against g_Kr are also shown for the non-paced model cell (ii). In the panel (i), AP dynamics during 0.2-Hz pacing were computed for 1 min at each g_Kr value, which was reduced from 1.0 to −0.2 at an interval of 0.001. The minimum V_m during AP phase 4 (V_min) and the maximum V_m during AP phase 2 before EAD formation (V_max) are indicated by black dots for rhythmic APs, and by orange (V_min) and light green (V_max) dots for arrhythmic APs. When EADs appeared, their local potential minimum (EAD_min) and maximum (EAD_max) were plotted by blue and red dots, respectively. In the panel for APD₉₀, the black, blue, and magenta dots represent APD₉₀ values for regular APs without EAD, regular APs with EADs, and arrhythmic APs with EADs, respectively (no-EAD: APs without EAD, + EAD: APs with EADs). The points labeled as “a” and “b” indicate g_Kr values for which AP behaviors are shown in Panel (A). In the panel (ii), the steady-state branches as loci of V_m at EPs (V_E1–3), periodic branches as the potential minimum (LC_min) and maximum (LC_max) of LCs, and potential extrema of SOs (SO_min, SO_max), as well as the periods of LCs and SOs, are plotted for the non-paced model cell. The steady-state branch V_E1 is stable (green solid lines), while V_E2 and V_E3 unstable (black dashed lines). The periodic branches represented by gray solid lines are always unstable. The point labeled as “c” indicates the g_Kr values for which SOs are shown in A-c.

Figure 2B-i shows switching of AP dynamics when g_Kr was gradually reduced during 0.2-Hz pacing. In this figure for the paced system, V_m extrema of APs (V_min/V_max) and EADs (EAD_min/EAD_max), were plotted against g_Kr. EADs emerged at g_Kr = 0.772, i.e., with 22.8% block of I_Kr (Figure 2B-i, top); the g_Kr reduction led to increases in the number of EADs, resulting in the discrete increase of APD₉₀ values (see Figure 2B-i, bottom). The AP repolarization dynamics in the paced cell model relates to the dynamical behavior of the non-paced cell model because there is no stimulation during the AP repolarization. Therefore, we investigated the dynamical behavior of the non-paced cell model using bifurcation analysis. Figure 2B-ii shows one-parameter bifurcation diagrams as functions of g_Kr, constructed for the non-paced mTP06b model (see also Supplementary Figure S1A showing those for the mTP06a model for comparison). In the non-paced mTP06b and mTP06a model, there existed three EPs as the steady states. The EP in the upper steady-state branch (V_E3 in Figure 2B-ii and Supplementary Figure S1A-ii) was always unstable at positive g_Kr values, while stable at negative g_Kr values in the mTP06a model. When g_Kr markedly reduced to a large negative value (out of range in Figure 2B-ii), the unstable EP (V_E3) underwent the supercritical Hopf bifurcation (HB), which changed it to a stable EP and led to a generation of LC oscillation. The LCs spawned from the HB point were always unstable in the positive g_Kr range (see gray lines in Figure 2B-ii and Supplementary Figure S1A-ii). On the one hand, we found small-amplitude spontaneous V_m oscillations (SOs) that occurred at depolarized V_m (red and blue lines in Figure 2B-ii, top) in the vicinity of the unstable LCs, as exemplified in Figure 2A-c. Just before the disappearance of SOs with increasing g_Kr, the period of unstable LC markedly prolonged (see the gray zigzag trace in Figure 2B-ii, bottom). This marked prolongation of LC periods and the emergence of SOs correlated with very long APD (long-lasting EADs) and irregularity of the repolarization time in the paced cell model (compare the dotted ranges in Figures 2B-i,ii).

In contrast, V_E3 in the I_Ks-eliminated (g_Ks = 0) non-paced model cells was stabilized via an occurrence of the subcritical HB when g_Kr was reduced (solid green lines to the left of the label “H” in Supplementary Figure S1B-ii). Thus, I_Ks inhibition caused drastic shift of HB points toward higher g_Kr values. Unstable LCs emerged via the subcritical HB, not changing their stability in the g_Kr range tested. In the I_Ks-eliminated paced mTP06a/b models (Supplementary Figure S1B-i), decreasing g_Kr did not yield EADs, but abruptly changed APs without EADs to local responses in the depolarized V_m range during pacing, i.e., arrest at stable EPs (V_E3) without pacing.

To evaluate the dependencies of EAD formation on g_Kr and g_Ks, we performed AP simulations using the mTP06b model with various sets of g_Kr and g_Ks. Figure 3A-i shows a phase diagram of AP behaviors for changes in g_Ks and g_Kr values with 0.2-Hz pacing. By characterizing AP behaviors observed in the paced mTP06b model, the g_Ks–g_Kr parameter plane was divided into three regions: (1) AP without EAD, (2) AP with EADs (colored regions; see examples of Figure 3B for the points “d” and “e” in Figure 3A-i), and (3) local response (dotted region; see an example of Figure 3C for the point “f” in Figure 3A-i). We further separated the region of the AP with EADs into two regions based on characteristics of the repolarization time in an AP with EADs: During 0.2-Hz pacing, further decreases in g_Kr (and/or g_Ks) in the EAD region altered an AP with shorter APD₉₀ of ≤5 s that repolarizes before the next stimulus to an AP with longer APD₉₀ of >5 s that is repolarized by the next stimulus, as shown in Figure 2A; then, the APs with EADs were defined as “fast repolarization (fR)” type for the former and “repolarization failure (RF)” type for the latter, which are exemplified in Figures 2A-a,b, respectively. The fR and RF types were distinguished by AP behaviors after an extra stimulus following the last test stimulus to cause AP repolarization, as illustrated in Figure 3B: The fR-type AP repolarized to resting V_m within 5 s (Figure 3B-i), while the RF-type one did not (Figure 3B-ii); in this case, APD₉₀ values of the RF-type AP were almost always more than 10 min.

FIGURE 3

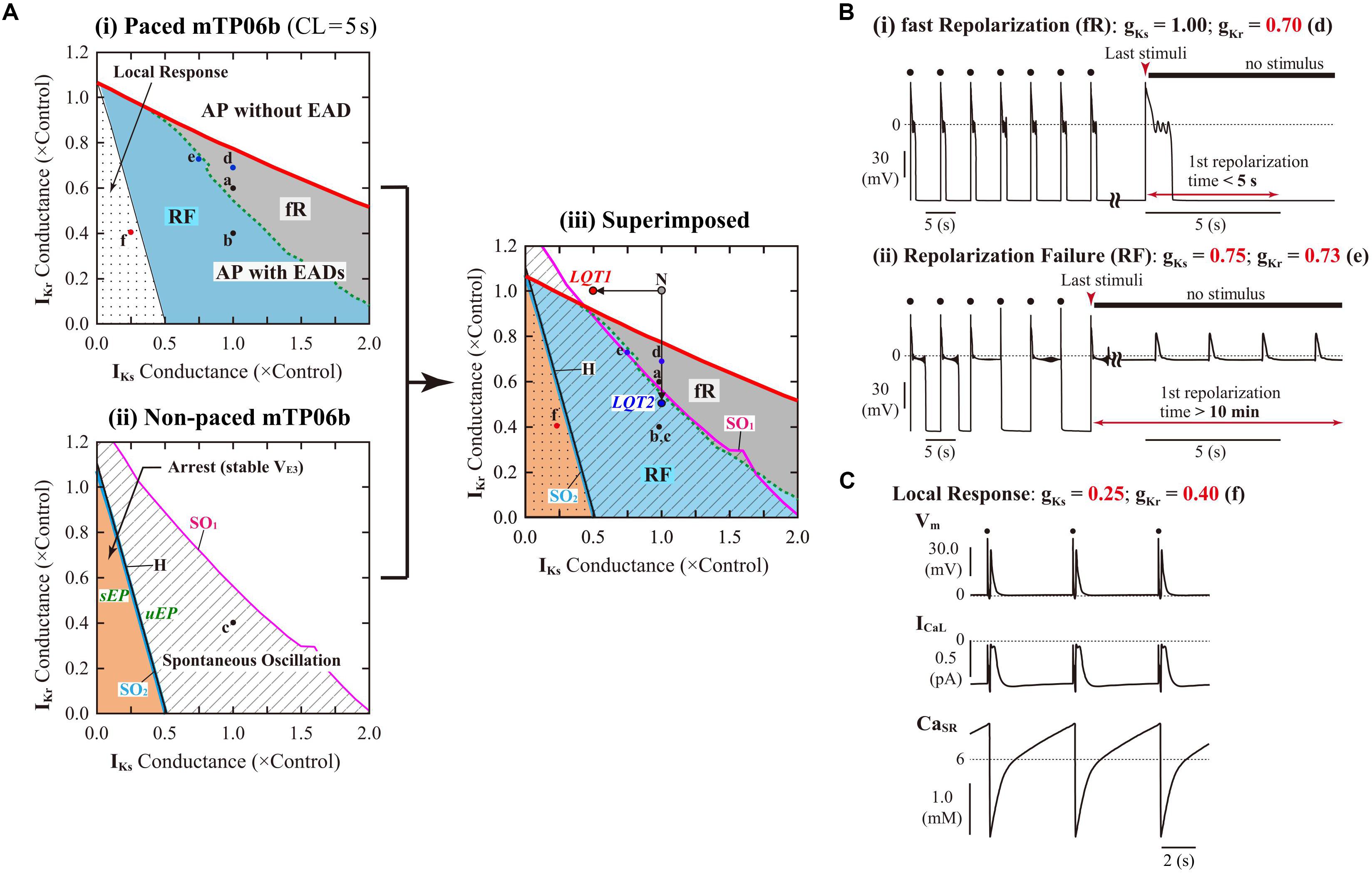
Figure 3. I_Kr/I_Ks-dependent EAD formation, dynamics and bifurcations of the mTP06b model. (A) A phase diagram indicating the region of EAD formation (and local responses) in the paced model cell (i) and two-parameter bifurcation diagrams for the non-paced model cell (ii) on the g_Ks–g_Kr parameter plane. In the diagram for the paced model cell (i), the thick red solid, black dashed and thin black solid lines, respectively, indicate parameter sets of critical points at which short-term EADs (APD₉₀ < 5 s, as in Figure 2A-a and [B-(i)], long-term or sustained EADs (APD₉₀ > 5 s, as in Figure 2A-b and [B-(ii)], and a local response (C) emerged; parameter regions in which short-term EADs, long-term or sustained EADs, and local responses occur are shown as the light-gray region labeled as “fR” (fast repolarization), blue region labeled as “RF” (repolarization failure), and dotted region, respectively. In the two-parameter bifurcation diagram for the non-paced model cell (ii), H, SO₁, and SO₂ indicate parameter sets of HB points, critical points at which SOs emerged, and critical points at which SOs switched into quiescence, respectively. The parameter regions in which SOs and convergence to the steady state (V_E3), i.e., arrest, can be observed are indicated as the shaded and orange regions, respectively. The labels “sEP” and “uEP” indicate the areas of stable and unstable EPs, respectively, divided by the HB curve. The panel (iii) is the diagram for which the phase diagram (i) is superimposed upon the two-parameter bifurcation diagram (ii). The points labeled as “N”, “LQT1” and “LQT2” denote the normal, LQT1, and LQT2 conditions, respectively. The points “a”–“f” indicate parameter sets for which AP behaviors are shown in Figures 2A-a–c, and [B (d,e)] [C (f)]. (B) Representative behaviors of APs with EADs during 0.2-Hz pacing at the points labeled as “d” and “e” in (A), which are classified into the fast repolarization type (d) and repolarization failure type (e) behaviors, respectively. (C) An example of the local response during 0.2-Hz pacing at the point “f” in (A).

Decreases in g_Kr and/or g_Ks required for EAD formation were much smaller in the mTP06b model than in the mTP06a model (compare Figure 3A-i and Supplementary Figure S2). The borderline of EAD initiation (the red solid line in Figure 3A-i) shifted in a g_Ks-dependent manner, with the g_Kr region of EADs broadening as g_Ks increased. Furthermore, two-parameter bifurcation analysis for the non-paced cell model (Figure 3A-ii) determined three areas with different behaviors: (1) quiescence at a stable EP (resting state; V_E1) with no stable EP or LC at depolarized V_m, (2) co-existence of quiescence at a stable EP (resting state) and a stable LC or SO at depolarized V_m (shaded area labeled as “Spontaneous Oscillation”), and (3) co-existence of two stable EPs at V_E1 and depolarized V_m (V_E3), i.e., the arrest at depolarized V_m (colored area labeled as “Arrest (stable V_E3)”).

To clarify relationships between AP responses observed in the paced cell model and bifurcations occurred in the non-paced cell model, we superimposed the phase diagram on the two-parameter bifurcation diagram (Figure 3A-iii). Most of the SO region in which SOs can be observed in the non-paced cell model was included in the RF region, suggesting the relation of spontaneous SR Ca²⁺ release-mediated sustained EADs to SOs (Figure 3B-ii). The borderline between local response and AP with EADs corresponded to the HB set in the non-paced cell model, indicating that V_m in the paced cell model converges to the stable EP (V_E3) in the area of local response.

Slow and Rapid Pacing Facilitated EAD Formation in the mTP06b Model

To further validate the mTP06b model as a LQT2 model, we next determined whether EAD formation in the g_Kr-reduced mTP06b model is facilitated at lower pacing rates (in bradycardia). Rate effects on EAD formation are shown in the diagrams depicting the g_Kr regions of EADs as functions of the pacing cycle length (Figure 4A). EAD formation in the g_Kr-reduced system was promoted at lower pacing rates in the Na_i-variable system, while prevented in the Na_i-fixed system. As in the K05 and O11 models (Kurata et al., 2017), the facilitation of EAD formation at lower pacing rates in the Na_i-variable mTP06b model was accompanied by the decrease in Na_i, which resulted in the decrease of outward I_NaK leading to delays in AP repolarization and EAD formation (Figure 4B-i). In the Na_i-fixed mTP06b model, the inhibition of EAD formation at lower pacing rates accompanied marked outward shift of I_NCX resulting from diminished Ca_i transients (Figure 4B-ii). In Supplementary Figure S3, two-parameter bifurcation diagrams on the g_Ks–g_Kr parameter plane are also shown for the Na_i-variable and Na_i-fixed mTP06b model cells paced at 0.2 and 1 Hz. In the Na_i-variable system (Supplementary Figure S3A), slower pacing promoted EAD formation during decreases of g_Kr and/or g_Ks and broadened the parameter region of EADs; in the Na_i-fixed system (Supplementary Figure S3B), however, the rate-dependent changes in the onset and region of EADs were opposite to those in the Na_i-variable system (compare the gray and blue areas in each panel of Supplementary Figure S3).

FIGURE 4

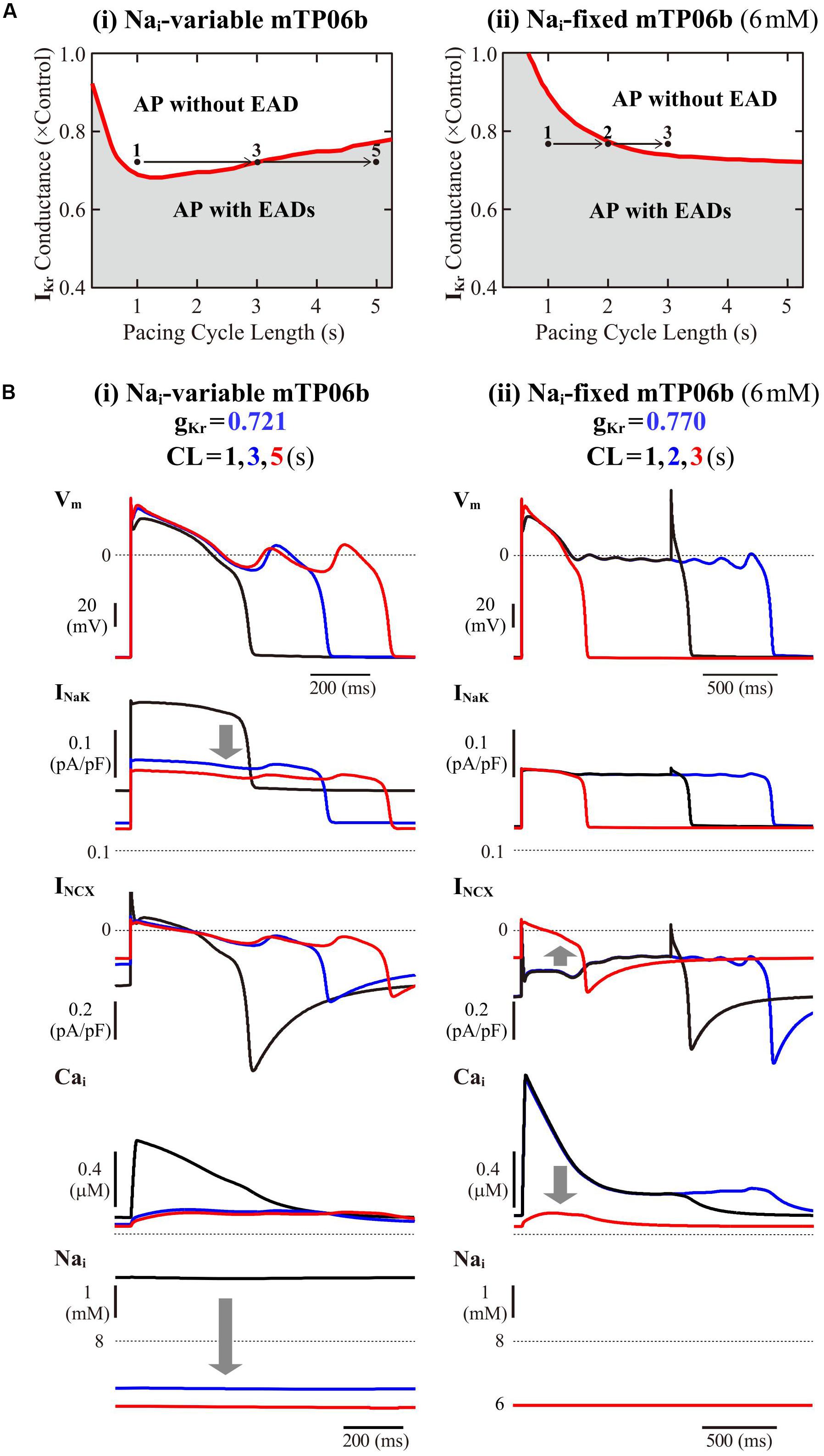
Figure 4. Rate dependence of EAD generation in the mTP06b model. (A) Two-parameter phase diagrams for the pacing cycle length (CL) and g_Kr depicted for the Na_i-variable (i) and Na_i-fixed (ii) model cells paced with various CLs of 0.75-5.25 s at 0.01-0.2 s intervals. The red solid lines and gray regions represent the parameter sets of critical points for occurrences of EADs and parameter region in which APs with EADs can be observed, respectively. (B) Simulated dynamics of the Na_i-variable (i) and Na_i-fixed (ii) g_Kr-reduced model cell paced at various frequencies (with CLs of 1, 3, and 5 s or 1, 2, and 3 s). Temporal behaviors of the model cell were computed for 30 min at each pacing rate; V_m, I_NaK, I_NCX, and Na_i for the last 1-2 s are shown as steady-state dynamics. The arrows indicate the directions of changes induced by increases in CL.

The rate dependence shown in Figure 4 and Supplementary Figure S3 was determined by quasi steady-state dynamics for each parameter set. In LQT2 patients, however, EADs and TdP may often be induced by abrupt pause or transient slowing of heartbeats (bradycardia) at rest or during sleep. Thus, we also determined how EADs emerge after sudden reductions of pacing rates (Supplementary Figure S4). When a pacing CL was increased from 1 s to 3, 4, and 5 s in the I_Kr-reduced mTP06b model (g_Kr = 0.721), EADs were first induced by 172nd, 74th, and 51st stimulus, respectively, after the reductions in pacing rates; pause-induced EAD or early onset of EADs after the increment in pacing CL was not observed, but long bradycardiac periods of more than 4 min were needed for EAD formation in this model cell.

In the mTP06b model, rapid pacing (CL < 1 s) also facilitated EAD formation via increases in Ca_i and Ca_SR, and resulting increases of inward I_NCX (data not shown). EADs are known to be inhibited at higher pacing rates by accumulation of slowly deactivating I_Ks as well as reductions in I_CaL due to slow recovery. Cumulative I_Ks increments and I_CaL reductions were certainly observed at the higher pacing rates in the mTP06b model as well; however, the enhanced inward I_NCX appeared to cause APD prolongation and EAD formation in this model cell.

Spontaneous SR Ca²⁺ Release-Medicated EADs Occurred During β-AS

To validate the mTP06b model as a LQT1 model, i.e., to determine whether the I_Ks-reduced model cell can exhibit EADs under the conditions of β-AS, we examined susceptibilities to EAD generation during β-AS of the normal and LQT1 versions of the mTP06b model. For the LQT1 model cell, g_Ks was reduced by 50% and 75%, following the reports for the KCNQ1 mutations M437V and A590W, respectively (see Sogo et al., 2016). Figure 5A shows simulated APs of the normal and LQT1 versions of the mTP06b model under the basal condition and conditions of β-AS with g_CaL increased to 140, 150, 160, and 180% of the control value. The LQT1 model cells exhibited longer APDs under the basal condition (APD₉₀ of 334 ms with the normal g_Ks vs. 348 ms with 50% g_Ks and 356 ms with 25% g_Ks) and EADs under β-AS with g_CaL increased by 60% or more for 50% g_Ks and 40% or more for 25% g_Ks, whereas the normal cell did not exhibit EAD. By constructing a two-parameter bifurcation diagram on the g_Ks–g_CaL plane for the Na_i-variable model cell paced at 1 Hz (Figure 5B), we could explain their EAD formation under the conditions of β-AS. As in the K05 model (Kurata et al., 2017), EAD formation during g_CaL increases under β-AS could be inhibited by concomitant g_Ks increases more effectively in the normal mTP06b model than in the LQT1 models: The LQT1 model cells entered the area of EAD formation with smaller increases in g_CaL (50.8% or more for the 50% g_Ks reduction and 31.0% or more for the 75% g_Ks reduction), while the normal cell with more than 87.7% increases in g_CaL. Thus, the mTP06b model could recapitulate EAD formation via enhancement of I_CaL during β-AS in the LQT1 cardiomyocyte. Under β-AS with higher g_CaL and P_up, spontaneous SR Ca²⁺ releases as evidenced by abrupt falls in Ca_SR without I_CaL reactivation often occurred, leading to Ca_i elevations (see Supplementary Figure S5), increments of inward I_NCX, and resultant EADs (or spontaneous V_m oscillations), as indicated by the dots in Figure 5A.

FIGURE 5

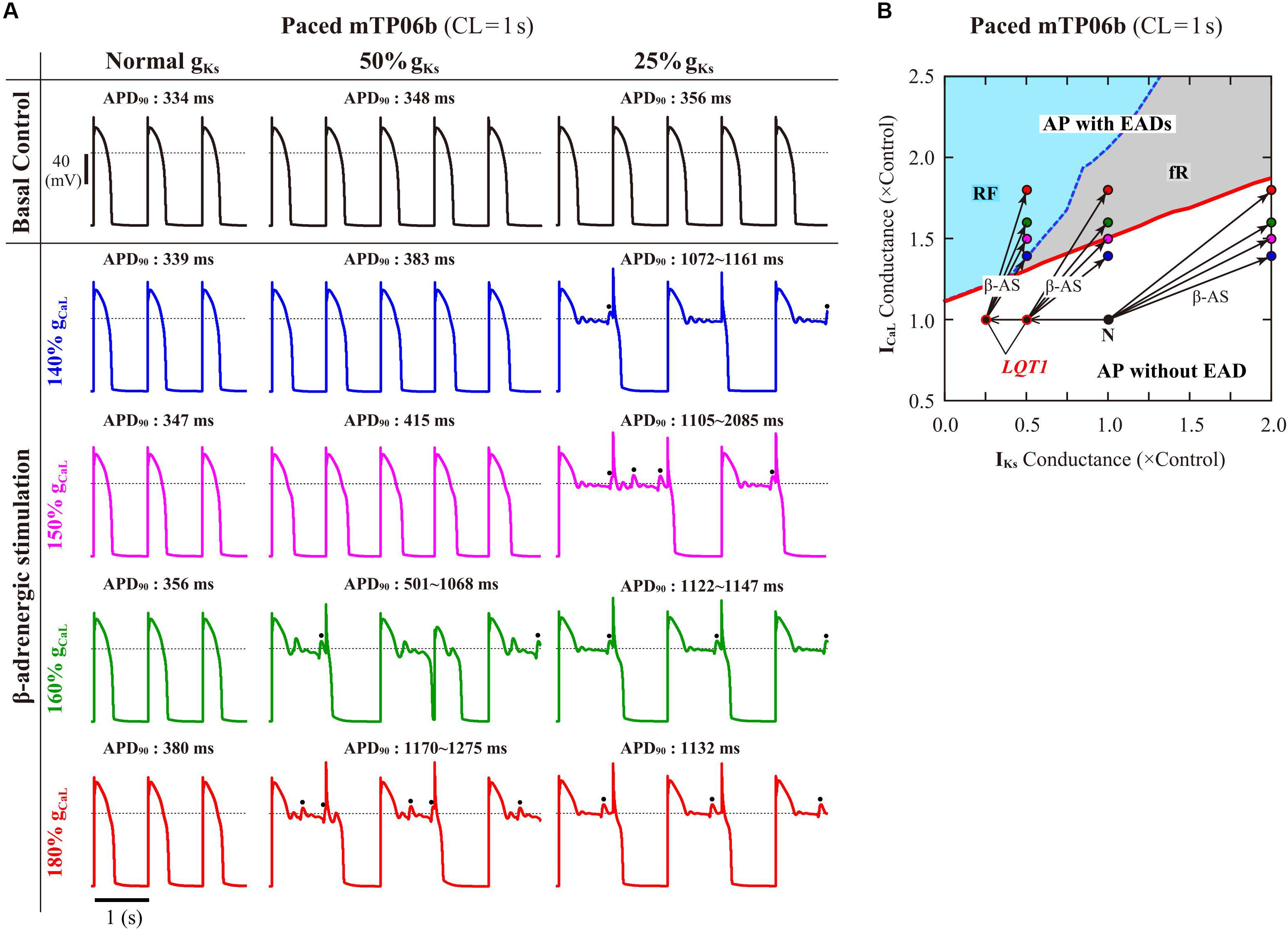
Figure 5. EAD generations during β-AS in the normal and LQT1 versions of the mTP06b model. (A) Simulated APs of the model cells under the basal condition (top) and conditions of β-AS as indicated by the points and arrows in (B). Model cells were paced at 1 Hz for 30 min. The dots denote EADs induced by spontaneous SR Ca²⁺ releases. (B) A phase diagram on the g_Ks–g_CaL parameter plane depicting displacements of critical points at which EADs emerged during 1-Hz pacing. The critical points were determined during g_CaL increases at an interval of 0.002 for individual g_Ks values increased at intervals of 0.02–0.1. For simulating the conditions of β-AS, the parameters other than g_CaL and g_Ks were modified as stated in the section “Materials and Methods” (see Supplementary Table S2). The LQT1 model cell was assumed to have reduced g_Ks of 50% or 25% of the control value. The points of the control (basal) conditions for cardiomyocytes with the normal and reduced g_Ks are labeled as “N” and “LQT1”, respectively. The arrows indicate the parameter shifts from the basal condition to the conditions of β-AS with g_Ks doubled and g_CaL increased to 140, 150, 160 and 180% of the control value.

Influences of SR Ca²⁺ Cycling, I_NCX and I_CaL on EAD Formation

Following the finding of spontaneous SR Ca²⁺ releases which occurred especially under β-AS with enhanced I_CaL and SR Ca²⁺ uptake, we next examined how SR Ca²⁺ uptake/release (intracellular Ca²⁺ dynamics) and I_NCX regulated by the intracellular Ca²⁺, as well as I_CaL regulated by the subspace Ca²⁺, affect EAD formation and bifurcations of dynamical behaviors in the mTP06b model by changing P_up, the scaling factor for I_NCX, or g_CaL. Figure 6A shows phase diagrams on the P_up–g_Kr and P_up–g_CaL parameter planes. P_up values were varied from zero to 2-times the control value, assuming the effects of SR Ca²⁺ pump inhibitors and β-AS (Maltsev and Lakatta, 2010; Briston et al., 2014). The region of EADs shrank with reducing P_up as in the K05 and O11 models (Kurata et al., 2017), while broadening at higher P_up; however, for the emergence of EADs (red solid lines in Figure 6A), the critical g_Kr value was not decreased but slightly increased (the critical g_CaL value was not increased but slightly decreased) as P_up reduced. The facilitated EAD formation at smaller P_up was associated with increased Ca_i and resulting inward shift in I_NCX as well as slight increases in I_CaL during AP late phase 2 (see Supplementary Figure S6A). The two-parameter bifurcation analysis offered further information on how the region of EADs depends on P_up and g_Kr. As shown in Supplementary Figure S7, the critical set of the emergence of EADs and the HB set were mostly parallel to the P_up and g_Kr axes, respectively, suggesting that alterations in P_up contributed not to EAD formation but to rather stability changes of EP (V_E3) in the non-paced mTP06b model; HB points disappeared with the emergence of spontaneous V_m and Ca²⁺ oscillations at higher P_up, indicating that the SR Ca²⁺ uptake/release machinery destabilizes EPs and thereby induces spontaneous oscillations. When g_Kr was markedly reduced in the mTP06b model, spontaneous SR Ca²⁺ releases to cause transient increases in intracellular Ca²⁺ concentrations (Ca_ss and Ca_i) and resulting activation of inward I_NCX occasionally occurred with prolonged APD (Figure 6B-a). Increasing P_up shortened the time to the emergence of the first spontaneous Ca²⁺ release and raised the incidence and frequency of spontaneous Ca²⁺ oscillations to yield EADs or V_m oscillations (Figure 6B-b).

FIGURE 6

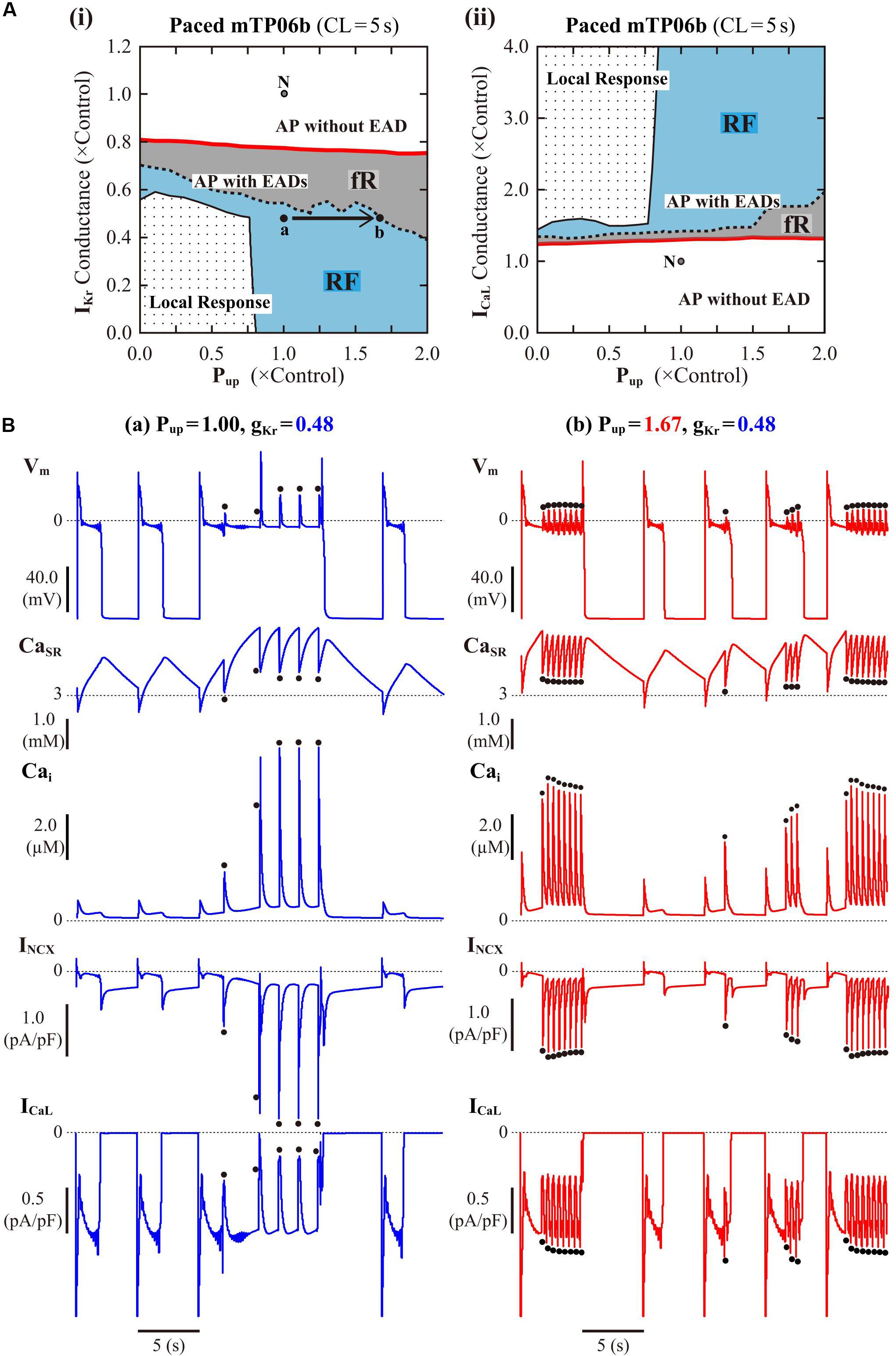
Figure 6. Influences of SR Ca²⁺ handling on EAD generation in the mTP06b model. (A) Phase diagrams on the P_up–g_Kr (i) and P_up–g_CaL (ii) parameter planes, depicting displacements of critical points for the occurrence of short-term EADs (red solid lines) and long-term or sustained EADs (dashed lines) as well as the emergence of local responses (black solid lines). By the parameter sets of these critical points, the parameter planes are divided into the areas of APs with short-term EADs (fR), APs with long-term or sustained EADs (RF) and local response, as described for Figure 3A. The points “a” and “b” in the panel (i) denote the parameter sets for simulations of the model cell dynamics shown in B-a,b, respectively. (B) Simulated dynamics of the model cells with the normal (1.00) or increased (1.67) P_up and the reduced g_Kr (0.48). Temporal behaviors of the model cells were computed for 30 min with pacing at 0.2 Hz; V_m, Ca_SR, Ca_i, I_NCX and I_CaL for additional 30 s are shown as steady-state dynamics. The dots indicate spontaneous SR Ca²⁺ releases as evidenced by abrupt falls of Ca_SR and resulting increases in Ca_i and inward I_NCX.

Contributions of I_NCX to bifurcations and EAD formation were also explored in relation to those of intracellular Ca²⁺ dynamics, SR Ca²⁺ cycling, and I_CaL. The scaling factor of I_NCX was varied from 0.1 to 10, within the range of experimental changes in Na⁺/Ca²⁺ exchanger densities or I_NCX (Milberg et al., 2008, 2012b; Pott et al., 2012). On the I_NCX–g_Kr and I_NCX–g_CaL parameter planes (Supplementary Figure S8), enhancement of I_NCX yielded the upward shift in the critical g_Kr and downward shift in the critical g_CaL for EAD formation (see red curves in Supplementary Figure S8). However, the TP06b model did not exhibit a significant shift in the critical g_Kr or g_CaL for EAD formation when I_NCX was reduced; only small (20–30%) inhibition of I_NCX was effective in shifting the critical points toward the prevention of EADs, with further inhibition resulting in the promotion of EADs. Whether EADs emerge or not depended mainly on the amplitude of inward I_NCX and I_CaL during the AP late phase 2: As exemplified in Supplementary Figure S6B, disappearance of EADs with lower I_NCX density was accompanied by a decrease of inward I_NCX and a slight reduction of I_CaL with increased inactivation during the preconditioning phase just before initiation of the first EAD (see the ellipses and inset in Supplementary Figure S6B).

We finally examined effects of I_CaL on EAD formation in the paced mTP06b model and bifurcations of dynamical behaviors in the non-paced mTP06b model by changing g_CaL. g_CaL-dependent changes in AP dynamics observed in the paced model cell when I_Ks was normal (g_Ks = 1) and one-parameter bifurcation diagrams as functions of g_CaL for the non-paced cell model are shown in Supplementary Figures S9A-i,ii, respectively. The one-parameter bifurcation diagrams for g_CaL (Supplementary Figure S9A-ii) suggest the scenario of EAD formation during enhancement of I_CaL, which is different from those in the K05 and O11 models (Kurata et al., 2017): Increments of g_CaL yielded unstable EPs via a saddle-node bifurcation (SNB) of EPs and unstable LCs via a SNB of LCs. With normal I_Ks (g_Ks = 1), an enhanced g_CaL of 1.298-fold the control value was high enough for EAD formation in the mTP06b model (Supplementary Figure S9A-i), whereas unrealistically large increases in g_CaL (to 4.248-fold the control value) were required in the mTP06a model (Supplementary Figure S10A). Supplementary Figure S9B shows a phase diagram of AP behaviors in the paced model cell (Supplementary Figure S9B-i) and a two-parameter bifurcation diagram for the non-paced model cell (Supplementary Figure S9B-ii), as well as the merged diagram (Supplementary Figure S9B-iii), on the g_CaL–g_Ks parameter planes. Decreasing g_Ks shifted the critical g_CaL value for EAD generation toward lower values and enlarged the g_CaL region of EADs (RF) in the mTP06b model. Larger g_CaL (going into the RF region in Supplementary Figures S9B-i,iii) led to the AP behavior classified into the RF type with small-amplitude spontaneous V_m oscillations around unstable LCs. EPs (V_E3) in the mTP06 models were unstable independent of g_CaL unless g_Ks was extremely low or high; no HB occurred for moderate variation of g_Ks value and consequently stability changes of the EP did not occur (see also Supplementary Figure S9B-ii). In the I_Ks-eliminated mTP06a/b models (g_Ks = 0), an EP (V_E3) was stabilized via supercritical HBs at relatively small g_CaL; stable LCs emerging from the HBs were immediately destabilized via a period-doubling bifurcation (PDB) or Neimark-Sacker bifurcation (NSB) (Supplementary Figure S10B). EAD did not occur at g_Ks = 0; larger I_CaL caused repolarization failure, in this case, local response.

Dynamical Mechanisms for Initiation and Termination of EADs in the mTP06 Model

I_Ks Activation-Dependent Bifurcations of the Fast Subsystem Associated With EAD Formation

To clarify the dynamical mechanisms of EAD formation in the I_Kr-reduced LQT2-type mTP06b model and why EADs emerge at larger g_Kr in the mTP06b model than in the mTP06a model (compare Figure 2 and Supplementary Figure S1), we further performed the slow-fast decomposition analysis (Tran et al., 2009; Qu et al., 2013; Xie et al., 2014). The I_Ks activation gating variable xs or I_Ks channel open probability (xs²) appears to be a slow variable yielding the termination of EADs (Figure 2A-a, the second from top). Thus, bifurcation diagrams for the fast subsystem composed of the state variables other than the slow variables xs, Na_i and Ca_SR were first constructed as functions of xs², with Na_i and Ca_SR fixed at constant values (Figure 7, left); then, trajectories of the full system (with fixed Na_i and Ca_SR) were superimposed on the diagrams (Figure 7, right). The quasi-EP (qEP), defined as a steady state of the fast subsystem, at depolarized quasi-V_m (qV_E3) has possessed a property of spiral sink in the mTP06b model (Figure 7A) but spiral source in the mTP06a model (Figure 7B) at xs² = 0. Stable qEP in the former was destabilized via an HB as xs² increased. The g_Kr reduction led to broadening of the xs² region of stable qEPs (compare green traces of qV_E3 in Figures 7A-i,ii, left). The g_Kr reduction-induced broadening of the xs² range of stable qEPs yielded a transient trapping of the full system trajectory in the attractor basin of the stable qEP (Figure 7A-ii, right). This trapping of the full system trajectory around the stable qEP as spiral sink sustained until the trajectory came across the steady-state xs² curve. This trapping phenomenon was not observed in the mTP06a model (Figure 7B, right) or the I_Kr-normal mTP06b model (Figure 7A-i, right), because the full system trajectories did not intersect with the stable steady-state branch (qV_E3) before intersecting the steady-state xs² curve. These results indicate that an acceleration of the voltage-dependent I_CaL inactivation to form the mTP06b model from the mTP06a model plays a critical role in the stabilization of qV_E3, consequently leading to the trapping of the full system trajectory.

FIGURE 7

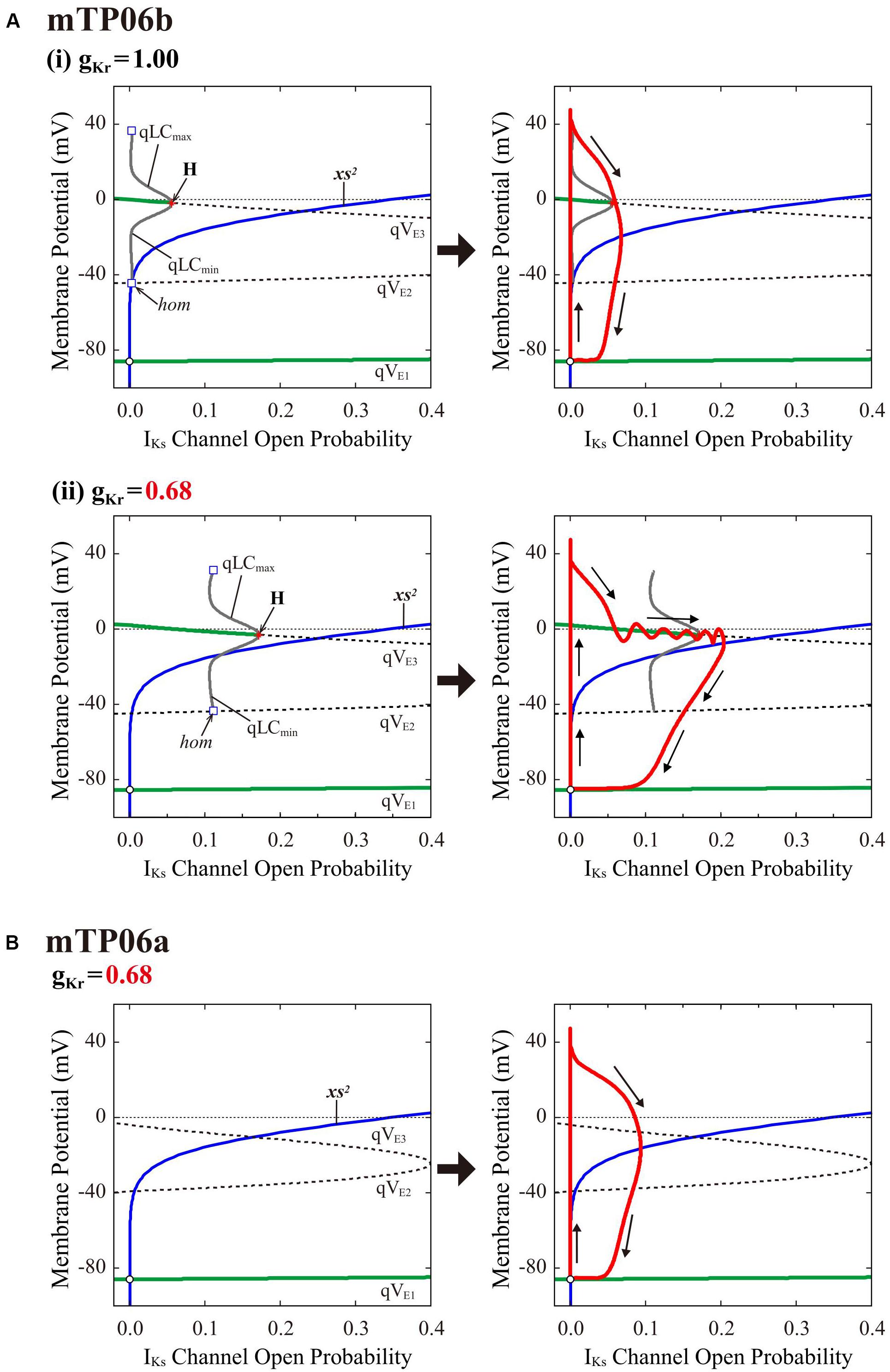
Figure 7. Dynamical mechanisms of EAD initiation and termination determined by the slow-fast decomposition analysis for the mTP06 models. Shown are one-parameter bifurcation diagrams of quasi-equilibrium points (qEPs) and quasi-limit cycles (qLCs), where the steady-state branches as loci of V_m at qEPs (qV_E1–3) and periodic branches as the potential minimum (qLC_min) and maximum (qLC_max) of qLCs are depicted as functions of the square of the I_Ks activation gating variable (xs²), i.e., I_Ks channel open probability for the fast subsystems of the g_Kr-normal [A-(i), left] and g_Kr-reduced [A-(ii), left] mTP06b model and g_Kr-reduced mTP06a model (B, left). Other slow variables, Na_i and Ca_SR, were fixed at constant values: Na_i = 6 mM for all cases; Ca_SR was fixed at the value which was reached just before occurrence of the first EAD or the maximum values during AP phase 2 (when no EAD occurred), i.e., at 0.5 mM and 1.5 mM for the normal and g_Kr-reduced mTP06b model, respectively, and at 0.5 mM for the g_Kr-reduced mTP06a model. The steady-state branches consist of the stable (green solid lines) and unstable (black dashed lines) segments. The periodic branches (gray solid lines) are all unstable. The blue lines indicate the steady-state xs² curve. Trajectories of the full system (with the fixed Ca_SR and Na_i) are superimposed on the bifurcation diagrams for the fast subsystems (red lines in each right panel). The arrows indicate the directions of changes in the state variables. H, Hopf bifurcation; hom, homoclinic bifurcation.

Dynamical Mechanisms of Spontaneous SR Ca²⁺ Release-Mediated EAD

To clarify the dynamical mechanisms of spontaneous SR Ca²⁺ release-mediated EAD formation, we further examined the stability, dynamics and bifurcations of the voltage-clamped mTP06 model. Ca²⁺ dynamics during a train of 1-s depolarizing test pulses to −10 mV (from the holding potential of −85 mV) applied at 2-s intervals to mimic APs evoked by 0.5 Hz pacing were first determined for the mTP06b model with different P_up (Figure 8A). Spontaneous SR Ca²⁺ releases occurred when Ca_SR increased at higher P_up, as indicated by the dots in Figure 8A; as P_up increased, the time to the first Ca²⁺ release and period of spontaneous Ca²⁺ releases shortened, and their frequency increased. Figure 8B shows one-parameter bifurcation diagrams of the steady-state stability and dynamics of Ca_i as functions of the clamped-V_m in the voltage-clamped mTP06b model. Steady-state intracellular Ca²⁺ concentrations (EPs) in the voltage-clamped model cell were stable at hyperpolarized and depolarized V_m (green traces in the right and middle panels of Figure 8B) but became unstable via supercritical HBs in the V_m range of AP phase 2 and early phase 3 (dashed traces in Figure 8B, middle). LCs emerging from the HB points were first stable but were destabilized via NSBs after small changes in V_m; spontaneous Ca²⁺ oscillations occurred in the V_m range of unstable LCs, i.e., between NS₁ and NS₂ (gray traces labeled as LC_min and LC_max for the minimum and maximum Ca_i during LC oscillations in Figure 8B). As shown in Figure 8C, the unstable V_m region (uEP) was enlarged by increasing P_up (see Figure 8C, left), decreasing I_NCX activity (Figure 8C, middle), and/or enhancing I_CaL (Figure 8C, right), all of which led to increases in Ca_SR.

FIGURE 8

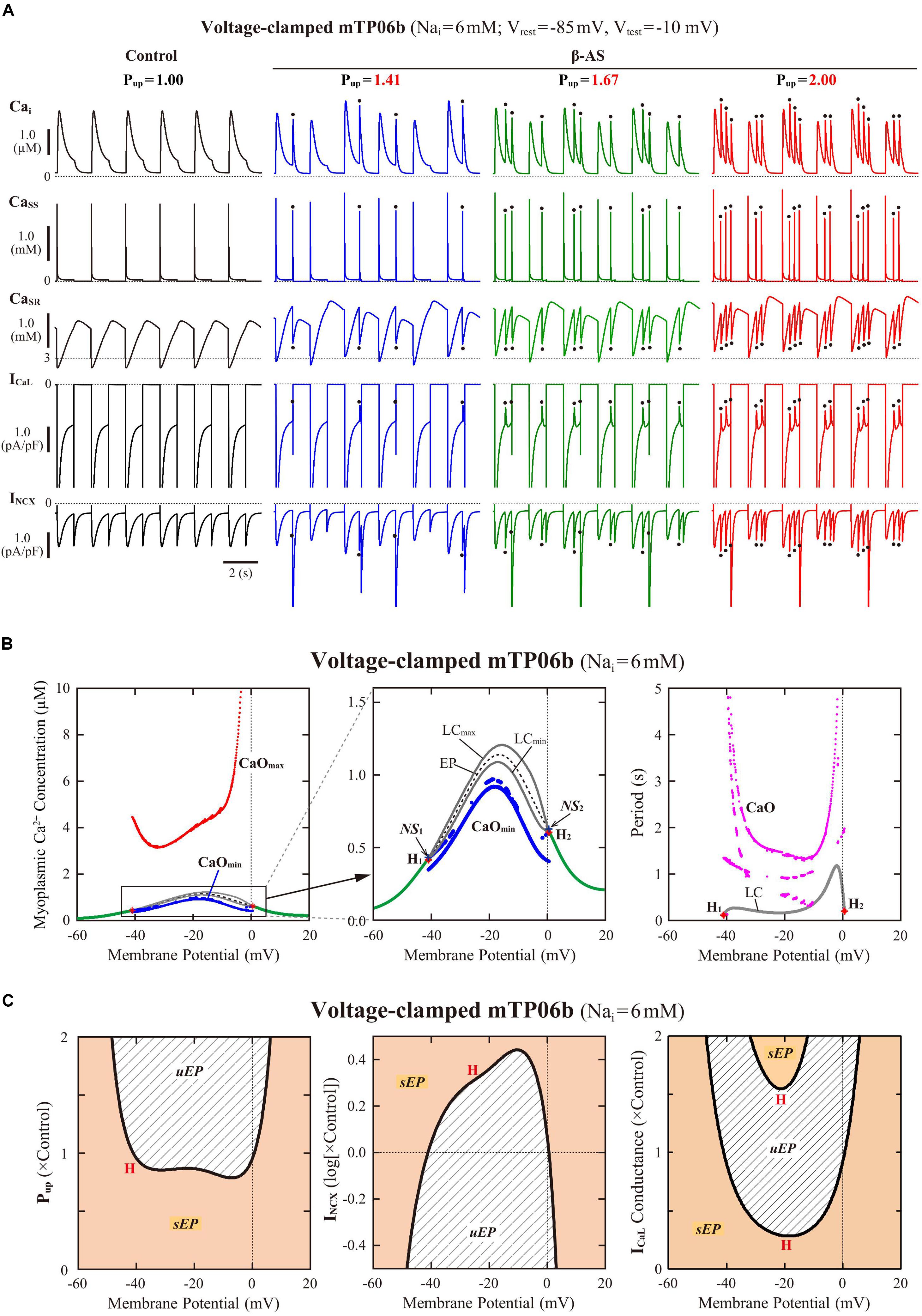
Figure 8. Stability and bifurcations of intracellular Ca²⁺ dynamics in voltage-clamped mTP06b model cell. (A) Dynamics of intracellular Ca²⁺ concentrations as well as Ca²⁺-dependent sarcolemmal currents in the Na_i-fixed voltage-clamped model cell under the control condition (P_up = 1) and the conditions of β-AS (P_up = 1.41, 1.67, and 2.00). Temporal behaviors of the voltage-clamped model cell during a train of 1-s step depolarization from −85 mV to −10 mV at 0.5 Hz were computed for 10 min; Ca_i, Ca_ss, Ca_SR, I_CaL and I_NCX for the last 12 s (6 pulses) are shown as steady-state dynamics. Spontaneous SR Ca²⁺ releases, as evidenced by abrupt falls of Ca_SR and increases in Ca_i, Ca_ss and inward I_NCX with attenuated I_CaL, occurred at higher P_up (indicated by the dots). (B) One-parameter bifurcation diagrams of the equilibrium point (EP) and extrema of limit cycles (LC_min/max) and spontaneous Ca_i oscillations (CaO_min/max) as functions of V_m for the voltage-clamped model cell (left and middle). The middle panel shows an enlarged diagram of the rectangular area in the left panel. The periods of spontaneous Ca²⁺ oscillations (CaO) and limit cycles (LC) are also plotted against V_m (right). H_1–2, Hopf bifurcations of the EP; NS_1–2, Neimark-Sacker bifurcations of the LC. (C) Two-parameter diagrams on the V_m–P_up (left), V_m–I_NCX (middle) and V_m–g_CaL (right) planes, indicating how the unstable V_m range changed depending on P_up, I_NCX and I_CaL. HB values, i.e., the critical V_m at which an EP is (de)stabilized are plotted as functions of P_up, I_NCX and I_CaL for the Na_i-fixed mTP06b model; the HB points were very close to the Neimark-Sacker bifurcation points at which LCs were destabilized with the emergence of CaOs.

To further clarify the Ca_SR-dependent mechanism of spontaneous SR Ca²⁺ releases in the P_up-increased mTP06b model and why SR Ca²⁺ release-mediated EADs emerge more frequently at larger P_up, we also performed the slow-fast decomposition analysis for the slow variable Ca_SR. Bifurcation diagrams were constructed as functions of Ca_SR for the voltage-clamped fast subsystem composed of the voltage-independent state variables f_CaL (Ca²⁺-dependent inactivation gate for I_CaL), R (proportion of closed SR Ca²⁺ release channels), Ca_ss, and Ca_i (Figure 9). Trajectories of the voltage-clamped full system dynamics as shown in Figure 8A for the normal (1) and enhanced (1.67) P_up were superimposed on the diagrams. The steady states of the fast subsystem, stable at lower Ca_SR (green traces in the middle and right panels of Figure 9), became unstable via an HB at higher Ca_SR (dashed traces in the middle and right panels of Figure 9). In the P_up-enhanced system, spontaneous SR Ca²⁺ releases as shown in blue trajectories in the middle and right panels of Figure 9B occurred when the full system trajectory, moving along the stable steady-state branch, passed through the HB point, i.e., when Ca_SR exceeded the HB value. In contrast, the P_up-normal system did not exhibit spontaneous SR Ca²⁺ release, because an increment of Ca_SR (Ca²⁺ refilling of the SR) during Ca²⁺ transient decay was too slow for the full system trajectory to reach the HB point for Ca_SR before V_m repolarization (Figure 9A, middle and right).

FIGURE 9

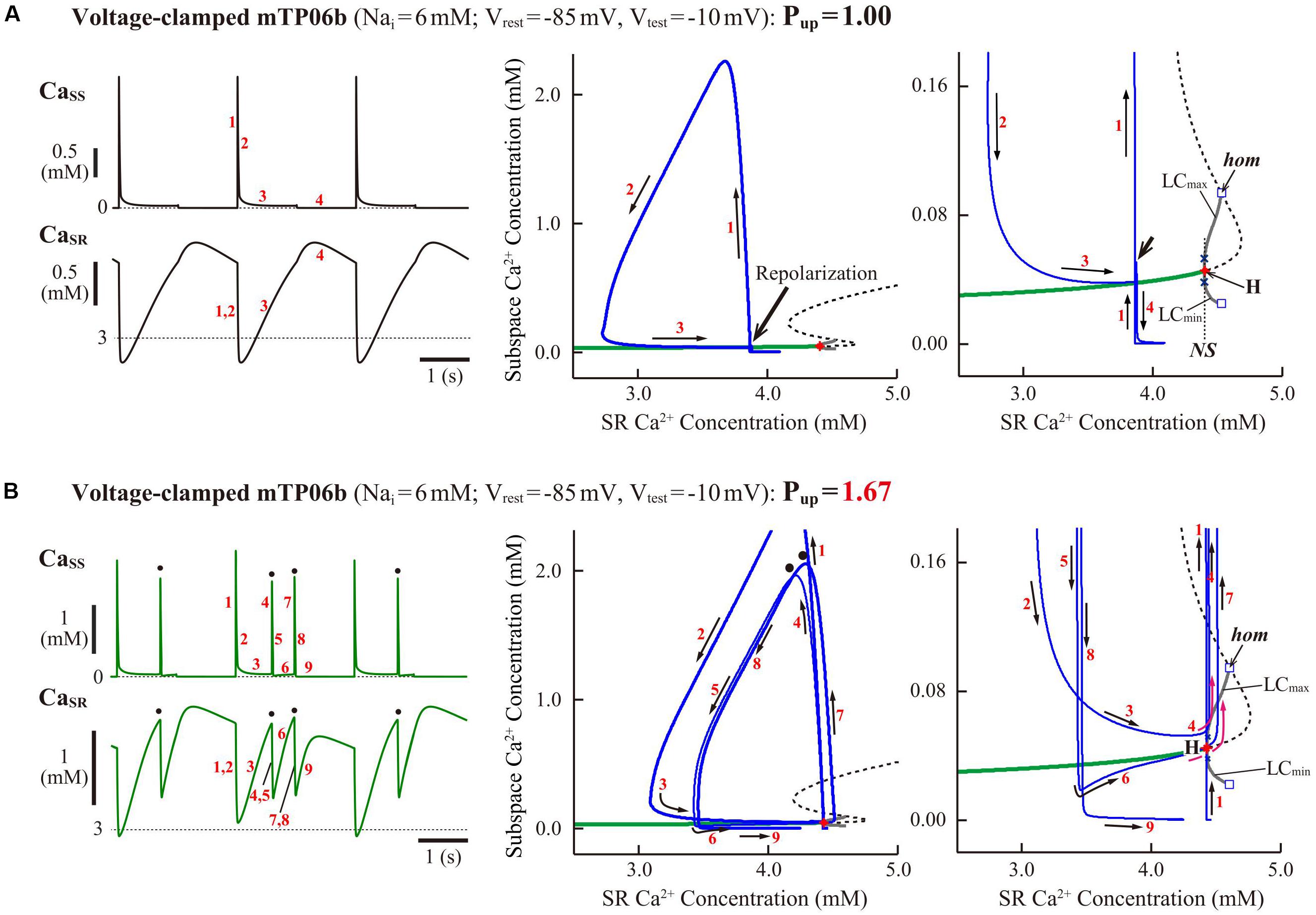
Figure 9. Slow-fast decomposition analysis for the slow variable Ca_SR of the voltage-clamped mTP06b model. Normal (middle) and expanded (right) scale views of one-parameter bifurcation diagrams, where the steady-state branch as a locus of Ca_ss at EPs, as well as periodic branches as the minimum (LC_min) and maximum (LC_max) of Ca_ss limit cycles (LCs) that were almost always unstable, are plotted as functions of Ca_SR for the fast subsystems of the voltage-clamped model cells with the normal (A) and increased (B) P_up. The green solid and black dashed lines represent stable and unstable steady-state branch, respectively. Subcritical HB (H) with the emergence of an unstable LC, NSB from a stable LC to an unstable one following a SNB of LCs (NS), and homoclinic bifurcation (hom) are located. Trajectories projected onto the Ca_SR-Ca_ss plane of the full system during a 1-s step depolarization to −10 mV (from −85 mV) and subsequent 1-s repolarization to −85 mV are superimposed on the diagrams; Ca_ss and Ca_SR dynamics in the full system during this voltage-clamp pulse are shown on the left. The labels “1”–“9” for the arrows on each diagram (middle, right) indicate the time course of changes in the state variables (Ca_ss and Ca_SR) along the trajectories, with the labels also given for the Ca_ss and Ca_SR dynamics (left).

Discussion

In this study, we theoretically investigated dynamical mechanisms of EAD formation in the TP06 model for HVMs, which has often been used for simulations and theoretical analyses of reentrant arrhythmias, automaticity, multi-stability and EAD formation in HVMs, in relation to the model cell dynamical behaviors and their bifurcations. In summary, EAD formation and its dynamics in the paced (non-autonomous) mTP06 model cell basically depended on stability and bifurcations of the non-paced (autonomous) model cell. Bifurcation phenomena and dynamical mechanisms of EAD formation in the mTP06 model were different from those in the K05 and O11 models tested previously (Kurata et al., 2017) in several respects (see also Supplementary Materials for additional discussions).

Validation of the mTP06 Model for EAD Reproducibility in LQT1 and LQT2 Conditions

EAD Formation in LQT1 and LQT2 Conditions (mTP06a vs. mTP06b)

Like the K05 model, the TP06b model with accelerated I_CaL inactivation could recapitulate EAD formation in the I_Ks-reduced LQT1-type and I_Kr-reduced LQT2-type HVMs. The mTP06b model was much more vulnerable to EAD formation than the mTP06a model, consistent with the previous experimental finding that slowing I_CaL inactivation eliminated EADs (Qu et al., 2013). As demonstrated by the slow-fast decomposition analysis (Figure 7), higher susceptibility of the mTP06b model to EAD development is attributable to the stabilization of qEPs at depolarized V_m close to the plateau V_m in the xs-parameterized fast subsystem by accelerating I_CaL inactivation.

EAD amplitudes in the mTP06b model (LQT1/2 versions) during pacing (∼30 mV) were smaller than those in the K05 and O11 models (Zimik et al., 2015; Kurata et al., 2017) as well as those in rabbit and guinea-pig ventricular myocyte models (Song et al., 2015; Zhong et al., 2018); however, they were comparable to those in many experimental reports for isolated HVMs (Verkerk et al., 2000; Veldkamp et al., 2001) and human iPS cell-derived LQT2 cardiomyocytes (Itzhaki et al., 2011) as well as for ferret, rabbit, and mouse ventricular myocytes (Marban et al., 1986; Liu et al., 2012; Edwards et al., 2014). Periods of EADs (∼200 ms) were shorter than those in the other HVM models, but comparable to the experimental data from HVMs (Verkerk et al., 2000).

Rate Dependence of EAD Formation (Validation for LQT2 Model)

In LQT2 patients, fatal cardiac events often occur during sleep or at rest, i.e., in bradycardia (Shimizu and Horie, 2011; Shimizu, 2013). The K05 and O11 models could partially reproduce the bradycardia-related EADs (Kurata et al., 2017). Like the other HVM models, the Na_i-variable mTP06b model could partly reproduce the rate-dependent EAD generation in LQT2 patients (Figure 4). In the I_Kr-reduced mTP06b model, however, EADs appeared only when pacing CLs increased to 3 s or more (i.e., pacing rates decreased to 20 beats/min or less) and extreme bradycardia continued for more than 4 min (Supplementary Figure S4). Although LQTS patients are known to exhibit sinus arrest or severe bradycardia due to coexisting sick sinus syndrome or atrio-ventricular block (Roden et al., 1996; Chiang and Roden, 2000), such long-lasting extreme bradycardia may be unlikely to occur often in LQT2 patients. Like the Luo-Rudy model for guinea-pig ventricular myocytes (Viswanathan and Rudy, 1999), the I_Kr-reduced O11 model could reproduce pause-induced EAD formation on increasing a pacing CL from 1 s to 2 s, which was attributable to a decrease in I_Ks and Ca_i increase-mediated enhancement of inward I_NCX at the lower pacing rate (data not shown). In contrast, the mTP06 model did not exhibit EADs by a single pause or transient bradycardia, which may be a limitation of this model cell.

In our previous study for the Na_i-variable K05 and O11 models (Kurata et al., 2017), the facilitation of EAD formation during lower rate pacing was accompanied by the decrease in Na_i and resulting reductions in outward I_NaK and inward shift of I_NCX. This study also demonstrated for the mTP06b model that the facilitation of EAD formation at lower pacing rates was mainly due to the decrease in Na_i and resultant changes in I_NaK (Figure 4B). Thus, the major mechanism for bradycardia-related EADs in the mTP06b model is essentially the same as that in the K05 model. Bradycardia-induced EADs are believed to be ascribable to a reduction of I_Ks (and increment of I_CaL). In the mTP06 model, however, I_Ks reduction (or I_CaL increment) did not occur when a pacing CL increased from 1 s to 2–5 s; deactivation of I_Ks was fast enough to complete before the next stimulus during 1-Hz pacing (Wang et al., 1994; Virág et al., 2001; Kurata et al., 2005; Jost et al., 2007).

EAD Formation During β-AS (Validation for LQT1 Model)

In LQT1 patients with smaller I_Ks, fatal cardiac events are exercise-induced (tachycardia-related), because adrenergic enhancement of I_CaL is no longer counterbalanced by the concomitant stimulation of I_Ks; the smaller increase in I_Ks leads to the occurrence of EADs that trigger ventricular tachyarrhythmia. The K05 model, but not the O11 model, could reproduce this I_Ks reduction-related EAD formation as a cause of ventricular tachycardia in LQT1 patients during β-AS (Sogo et al., 2016; Kurata et al., 2017). The mTP06b model was also capable of reproducing β-AS-related EAD formation in LQT1 cardiomyocytes, which could clearly be accounted for by the I_CaL- and I_Ks-dependent bifurcation properties of the model cell (Figure 5). I_CaL/I_Ks-dependent properties of EAD formation in the mTP06b model were very similar to those in the K05 model (Kurata et al., 2017), whereas I_CaL/I_Ks-dependent HB properties of the mTP06 models were totally different (Supplementary Figures S9B, S10). However, EAD formation in the mTP06b model during β-AS was different in a mechanism from that in the K05 model: EADs in the mTP06b model involved spontaneous SR Ca²⁺ releases and resulting increments of inward I_NCX (Figure 5A and Supplementary Figure S4), while those in the K05 model solely I_CaL-reactivation dependent, not involving spontaneous SR Ca²⁺ releases (Kurata et al., 2017). It is likely that the spontaneous SR Ca²⁺ release is implicated in EAD formation during β-AS; delayed afterdepolarizations (DADs), known to be induced by spontaneous SR Ca²⁺ releases, often accompanied EADs (Priori and Corr, 1990; Volders et al., 2000; Zhao et al., 2012). Amplitudes of spontaneous SR Ca²⁺ releases in the mTP06b model appeared to be comparable to or slightly larger than those observed in experimental studies during β-AS (Volders et al., 2000; Zhao et al., 2012) or for LQT2 cardiomyocytes (Choi et al., 2002; Němec et al., 2010, 2016; Parikh et al., 2012) unless AP phase 2 was extremely long (Figure 8A and Supplementary Figure S5), while much larger than those reproduced by another HVM model (Trenor et al., 2013) and rabbit ventricular myocyte models (Milberg et al., 2012b; Song et al., 2015; Wilson et al., 2017; Zhong et al., 2018). More sophisticated HVM models incorporating β-AS-related modulating factors, like those developed by Saucerman et al. (2003) and Kuzumoto et al. (2008), are required for further investigations of the mechanisms of exercise-induced EAD formation in LQT1 HVMs.

Comparisons With Other HVM Models for Bifurcation Phenomena and EAD Mechanisms

EAD Initiation Mechanisms (Roles of I_CaL, I_NCX, and SR Ca²⁺ Release)

At least two mechanisms appeared to underlie the initiation of phase-2 EADs in the mTP06b model: (1) I_CaL reactivation-dependent mechanism which operates and causes EADs even in the absence of spontaneous SR Ca²⁺ releases at lower P_up and lower pacing rates, and (2) spontaneous SR Ca²⁺ release-mediated mechanism activating inward I_NCX at higher P_up and higher pacing rates (Figures 2A-b, 6B). Coexistence of these two distinct mechanisms for EAD formation have been demonstrated experimentally as well (Zhao et al., 2012).

The major contribution of I_CaL to EAD formation was suggested in many previous experimental and theoretical studies for ventricular myocytes (January and Riddle, 1989; Ming et al., 1994; Guo D. et al., 2007; Yamada et al., 2008; Xie et al., 2010; Corrias et al., 2011; Madhvani et al., 2011; Chang et al., 2012a, b; Milberg et al., 2012a; Qu and Chung, 2012; Qu et al., 2013). EAD formation in the mTP06b model with lower P_up is also attributable to I_CaL reactivation in that reactivated I_CaL contributes to V_m depolarization (Figures 1C, 2A-a, and Supplementary Figure S6). In the K05 and O11 models, EADs often emerged in the vicinity of the critical point at which a stable LC appeared during I_CaL increases (Kurata et al., 2017), suggesting that EAD formation depends on I_CaL responsible for the instability of EPs and generation of stable LCs. EADs also occurred in the I_CaL-enhanced mTP06b model when unstable LCs emerged, but stable LCs were not detected (Supplementary Figure S9A). The slow-fast decomposition analysis of the guinea-pig ventricular myocyte model have suggested that the I_CaL-dependent destabilization of a qEP and formation of a stable quasi-LC (qLC) via an HB in the fast subsystem is required for EAD generation in the full system (Tran et al., 2009; Qu et al., 2013; Song et al., 2015). In the mTP06b model, however, transient trapping of the full system trajectory occurred around the stable and unstable qEPs without forming a stable qLC, indicating that the emergence of a stable qLC is not necessarily needed for EAD formation. This scenario for EAD formation is essentially the same as that in a two-current three-variable AP model (Xie et al., 2014). Nevertheless, the absence of a stable qLC may result in EADs of relatively small amplitudes, as demonstrated for the mTP06b model. As mentioned above, the initiation of EADs in the mTP06b model is attributable to the stabilization of qEPs at depolarized V_m in the xs-parameterized fast subsystem, which causes transient trapping of the full system trajectory around the stable qEP; I_Kr reduction promotes EAD formation by broadening the region of stable qEPs at depolarized V_m (Figure 7).

As another possible mechanism for EAD initiation, many recent experimental and simulation studies have strongly suggested the spontaneous SR Ca²⁺ release causing Ca_i oscillations, oscillatory increases in inward I_NCX, and resulting V_m depolarization during β-AS (Choi et al., 2002; Volders et al., 2003; Zhao et al., 2012; Song et al., 2015; Wilson et al., 2017; Zhong et al., 2018) and in I_Kr-reduced LQT2 cardiomyocytes (Choi et al., 2002; Kim et al., 2005; Němec et al., 2010, 2016), which is similar to the mechanism for DADs induced by spontaneous SR Ca²⁺ releases under Ca²⁺ overload conditions or β-AS (e.g., Volders et al., 2003; Zhao et al., 2012) and the Ca²⁺ clock mechanism for sinoatrial node cell pacemaking (Maltsev and Lakatta, 2009). The K05 or O11 model could not reproduce the spontaneous SR Ca²⁺ release as a cause of phase-2 EADs (Kurata et al., 2017). In contrast, the mTP06b model could clearly replicate this scenario in a Ca_SR-dependent manner (Figures 2A-b, 5A, 6B, 9), while it was not found in the previous study using a modified TP06 model (Vandersickel et al., 2014). Such SR Ca²⁺ release-mediated EADs under β-AS conditions (Figure 5) have also been reproduced by the rabbit ventricular myocyte model (Volders et al., 2000; Song et al., 2015; Zhong et al., 2018).

One of the prominent properties of the mTP06 model is the instability of steady-state intracellular Ca²⁺ concentrations resulting in the spontaneous SR Ca²⁺ release at higher P_up to increase Ca_SR (Figures 8, 9). The K05 or O11 model did not exhibit spontaneous SR Ca²⁺ releases even at higher P_up, because steady-state intracellular Ca²⁺ concentrations were always stable independently of V_m; although Ca_i oscillations occurred during EADs in the K05 and O11 models, these Ca_i oscillations were not induced by spontaneous SR Ca²⁺ releases but by oscillatory reactivation of I_CaL (Kurata et al., 2017). Thus, this study newly suggests that the occurrence of spontaneous SR Ca²⁺ releases and Ca²⁺ oscillations as a cause of phase-2 EADs are attributable to instability of intracellular Ca²⁺ concentrations in a steady state, destabilization of which leads to spontaneous Ca²⁺ oscillations (Figures 8, 9). This scenario, i.e., steady-state destabilization for spontaneous Ca²⁺ oscillations involving ryanodine or IP₃ receptors, has previously been suggested by bifurcation analyses for cardiac myocytes (Keizer and Levine, 1996; Tveito et al., 2012) and for other cells (Schuster et al., 2002; Higgins et al., 2006; Kusters et al., 2007). However, the Ca²⁺ oscillations reported in these previous studies were much longer in period than those observed in the mTP06b model, not relating to EAD formation. Wilson et al. (2017) demonstrated spontaneous SR Ca²⁺ releases and sustained Ca²⁺ oscillations in a voltage-clamped rabbit ventricular myocyte model, suggesting instability of intracellular Ca²⁺ dynamics; however, dynamical mechanisms for the Ca²⁺ oscillation were not clarified by bifurcation analysis. To the best of our knowledge, this is the first report demonstrating instability of steady-state intracellular Ca²⁺ concentrations and resulting spontaneous SR Ca²⁺ releases that cause EADs in the HVM model (Kurata et al., 2019). In the mTP06b model, enhanced I_CaL further contributed to spontaneous SR Ca²⁺ releases via the increment of SR Ca²⁺ contents and resultant enhancement of the instability of intracellular Ca²⁺ dynamics (Figure 8C). Elevations of Ca_ss by spontaneous SR Ca²⁺ releases caused transient I_CaL reductions due to Ca²⁺-dependent inactivation (Figures 2A-b, 6B, 8A), which may be regarded as a negative feedback mechanism leading to inhibition of EADs.

EAD Termination Mechanisms (Roles of I_Ks, I_Kr, and I_CaL)

The mTP06 model requires I_Ks for EAD termination, i.e., repolarization failure occurred abruptly during I_Kr inhibition or I_CaL enhancement when I_Ks was absent or small, whereas I_Ks was not necessarily needed in the K05 or O11 model. Thus, EADs in the mTP06b model during pacing appeared to terminate in an I_Ks activation-dependent (or stimulus-dependent) manner: The open probability of I_Ks channels (xs²) increased progressively in the model cell with relatively small I_Kr, i.e., LQT2-like cells (Figure 2A-a). Tran et al. (2009) suggested the major role of the slow I_Ks activation for the guinea-pig ventricular myocyte model by the slow-fast decomposition analysis in which the slow I_Ks activation gating variable was assumed to be a parameter for the fast subsystem. In the diagram for the slow gating variable-parameterized fast subsystem with a superimposed full system trajectory, gradual increases in the slow variable led the full system trajectory slowly across the stable steady-state branch of qEP and then into the region of the stable periodic branch of qLC through an HB point, resulting in the termination of EADs via a homoclinic bifurcation of qLC. This scenario is known as the Hopf-homoclinic bifurcation mechanism (Tran et al., 2009; Qu et al., 2013; Song et al., 2015; Huang et al., 2018). Consistent with these previous reports, the mTP06b model exhibited slow I_Ks activation-dependent EADs in the xs² regions of stable and unstable qEPs (Figure 7A); however, a stable qLC region or homoclinic bifurcation to yield EAD termination was not detected for the fast subsystem of the mTP06b model. EAD terminated simply via the destabilization of a qEP in the I_Kr-reduced mTP06b model, suggesting that the Hopf-homoclinic bifurcation scenario is not necessarily applicable.

In the I_Ks-eliminated system, EADs would not terminate unless there exist other slow components or factors, such as the slowly inactivating I_CaL or late I_Na and intracellular Na⁺ accumulation to increase outward I_NaK gently. Our previous study using the K05 and O11 models indicated that EAD termination might occur in a slow I_CaL inactivation-dependent manner when I_Ks was relatively small (Figure 3 in Kurata et al., 2017). However, I_CaL inactivation-dependent EAD termination was not clearly detected in the TP06 model. Other candidates for slow variables to cause EAD termination include the slow inactivation of late I_Na (Horvath et al., 2013; Trenor et al., 2013; Asakura et al., 2014) not incorporated into the TP06 model and gradual increases in Na_i (Chang et al., 2012a; Xie et al., 2015). After cessation of pacing, the I_Kr-reduced and/or I_CaL-enhanced mTP06b model could exhibit long-term EAD bursts the termination of which was induced by slow elevation of Na_i and resulting enhancement of outward I_NaK (data not shown). This Na_i-dependent mechanism has previously been demonstrated for a rabbit ventricular AP model as well (Chang et al., 2012a). Nevertheless, the slow Na_i elevation (intracellular Na⁺ accumulation) is unlikely as a termination mechanism for short-term EADs during pacing at 0.2–2 Hz in the mTP06b model.

As another termination mechanism, stimulus-induced repolarization was observed when APD became very long with stable AP phase 2 (Figures 2A-b, 3B-ii, 5, 6). In the mTP06b model, it was yielded mainly by the prolonged decrease (inactivation) of I_CaL due to its slow recovery and resulting outward shift in the total membrane current after the stimulus off. In terms of bifurcation theory, this phenomenon is related to bistability (co-existence of two stable EPs at resting V_m and depolarized V_m close to AP phase 2) and a transition between the two stable EPs by the stimulus; the transition occurs when following an application of the stimulus current a trajectory of a system starting from one stable EP at the depolarized V_m goes outside the attractor basin of the stable EP and enters the attractor basin of the other stable EP at the resting V_m (Vinet and Roberge, 1990). Bistability and the stimulus-induced transition between two stable states were found in other cardiomyocyte models (Landau et al., 1990; Vinet and Roberge, 1990). We could not find any experimental evidence for the AP repolarization induced by a stimulus current during stable AP phase 2, but it is theoretically possible. Experimental studies for wider ranges of channel conductance or other parameters may verify that the stimulus-induced repolarization really occurs.

Limitations and Perspectives of Study

As summarized in our preceding article (Kurata et al., 2017), bifurcation analyses have been used for elucidating the dynamical mechanisms of sinoatrial node pacemaking, abnormal automaticity in ventricular myocytes, generation of biological pacemaker activity, and EAD formation in ventricular myocytes. These theoretical studies have clearly demonstrated the significance of bifurcation analyses for general understanding and systematic description of the dynamical mechanisms of normal and abnormal oscillatory behaviors.

There are many limitations of our study including incompleteness of the model and inconsistency between model predictions and experimental observations, as well as the lack of experimental evidence for bifurcation phenomena in real HVMs. The aim of this study was not to refine but to validate the TP06 model. Nevertheless, more sophisticated HVM models have to be used or developed for more detailed theoretical investigations. As mentioned above, simulated Ca²⁺ transients induced by spontaneous SR Ca²⁺ releases during AP phase 2 were larger than those observed in many experimental studies. The larger Ca²⁺ transients in the model cell may be due to the one compartment SR with weak Ca²⁺ leak, which results in higher SR Ca²⁺ load and greater Ca²⁺ releases during AP phase 2; a two-compartment SR model may be required for reproducing experimentally observed smaller Ca²⁺ releases, as suggested previously (Wilson et al., 2017). Moreover, incorporation of more elaborate schemes for the mechanisms of SR Ca²⁺ release and intra-SR Ca²⁺ transfer (Laver, 2007, 2009; Chen et al., 2014; Song et al., 2015; Zhong et al., 2018) would also be crucial. Our preceding (Kurata et al., 2017; Tsumoto et al., 2017) and present studies have demonstrated that EAD mechanisms are different depending on models and parameter values. Therefore, we have to test as many models as possible for providing more profound understanding of EAD mechanisms.

In this study, bifurcation analysis was limited to a single cell model. However, EAD-related arrhythmias are suggested to be induced by synchronization of EADs in multiple cells (Sato et al., 2009; Xie et al., 2010) and also influenced by heterogeneity of ventricular myocytes; because of electrotonic interactions, EAD formation in multicellular or tissue models including epicardial, endocardial and M cell models may be very different in conditions from that in single cell models (Gibb et al., 1994; Huelsing et al., 2000; Weiss et al., 2010; Corrias et al., 2011). Therefore, we need investigations of the mechanisms for EAD formation and for triggering arrhythmias in human ventricles in vivo, which require multicellular (tissue) models, like those used in previous simulation studies (Weiss et al., 2010; de Lange et al., 2012; Vandersickel et al., 2014; Chang et al., 2015; Liu et al., 2018). Despite many limitations, our studies provide significant insights into the dynamical mechanisms of EAD generation in LQT1 and LQT2 HVMs by utilizing recently developed HVM models.

Author’s Note

This manuscript has been released as a Pre-Print at https://www.biorxiv.org/content/10.1101/613182v1 (Kurata et al., 2019).

Data Availability Statement

All datasets generated for this study are included in the article/Supplementary Material.

Author Contributions

YaK conception and design of the research and drafted the manuscript. YaK and KT performed the programing, simulations, bifurcation analyses, and analyzed the data. YaK, KT, and KH interpreted the results. YaK, KT, MT, and YuK prepared the figures. YaK, KT, KH, and IH edited and revised the manuscript. YaK, KT, KH, IH, MT, and YuK approved the final version of the manuscript.

Funding

This work was supported in part by the Grant-in-Aid for Scientific Research on Innovative Areas “HD Physiology (4203)” from the Ministry of Education, Culture, Sports, Science and Technology, Japan (25136720 to YaK); Grant-in-Aid for Scientific Research (C) from Japan Society for the Promotion of Science (26460303 to YaK; 22590806 to KH; 16KT0194 to KT); Grant from The Takeda Science Foundation, the Hiroshi and Aya Irisawa Memorial Promotion Award for Young Physiologists from the Physiological Society of Japan, and Grant for Promoted Research from Kanazawa Medical University (S2019-2) to KT; and Grant for Collaborative Research from Kanazawa Medical University (C2015-3 and C2016-1 to YaK and IH).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2019.01545/full#supplementary-material

Footnotes

1. ^ http://models.cellml.org/exposure/a7179d94365ff0c9c0e6eb7c6a787d3d
2. ^ http://physiodesigner.org/
3. ^ https://phdb.unit.oist.jp/modeldb/
4. ^ http://www.physiodesigner.org/simulation/flint/

References

Adeniran, I., El Harchi, A., Hancox, J. C., and Zhang, H. (2012). Proarrhythmia in KCNJ2-linked short QT syndrome: insights from modelling. Cardiovasc. Res. 94, 66–76. doi: 10.1093/cvr/cvs082

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, C. L., Delisle, B. P., Anson, B. D., Kilby, J. A., Will, M. L., Tester, D. J., et al. (2006). Most LQT2 mutations reduce Kv11.1 (hERG) current by a class 2 (trafficking-deficient) mechanism. Circulation 113, 365–373. doi: 10.1161/CIRCULATIONAHA.105.570200

PubMed Abstract | CrossRef Full Text | Google Scholar

Antzelevitch, C., Shimizu, W., Yan, G. X., Sicouri, S., Weissenburger, J., Nesterenko, V. V., et al. (1999). The M cell: its contribution to the ECG and to normal and abnormal electrical function of the heart. J. Cardiovasc. Electrophysiol. 10, 1124–1152. doi: 10.1111/j.1540-8167.1999.tb00287.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Asakura, K., Cha, C. Y., Yamaoka, H., Horikawa, Y., Memida, H., Powell, T., et al. (2014). EAD and DAD mechanisms analyzed by developing a new human ventricular cell model. Prog. Biophys. Mol. Biol. 116, 11–24. doi: 10.1016/j.pbiomolbio.2014.08.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Briston, S. J., Dibb, K. M., Solaro, R. J., Eisner, D. A., and Trafford, A. W. (2014). Balanced changes in Ca buffering by SERCA and troponin contribute to Ca handling during β-adrenergic stimulation in cardiac myocytes. Cardiovasc. Res. 104, 347–354. doi: 10.1093/cvr/cvu201

PubMed Abstract | CrossRef Full Text | Google Scholar

Carmeliet, E. (1992). Voltage- and time-dependent block of the delayed K+ current in cardiac myocytes by dofetilide. J. Pharmacol. Exp. Ther. 262, 809–817.

PubMed Abstract | Google Scholar

Chang, M. G., Chang, C. Y., de Lange, E., Xu, L., O’Rourke, B., Karagueuzian, H. S., et al. (2012a). Dynamics of early afterdepolarization-mediated triggered activity in cardiac monolayers. Biophys. J. 102, 2706–2714. doi: 10.1016/j.bpj.2012.05.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, M. G., Sato, D., de Lange, E., Lee, J. H., Karagueuzian, H. S., Garfinkel, A., et al. (2012b). Bi-stable wave propagation and early afterdepolarization-mediated cardiac arrhythmias. Heart Rhythm 9, 115–122. doi: 10.1016/j.hrthm.2011.08.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, P. C., Wo, H. T., Lee, H. L., Lin, S. F., Wen, M. S., Chu, Y., et al. (2015). Role of sarcoplasmic reticulum calcium in development of secondary calcium rise and early afterdepolarizations in long QT syndrome rabbit model. PLoS One 10:e0123868. doi: 10.1371/journal.pone.0123868

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, W., Wang, R., Chen, B., Zhong, X., Kong, H., Bai, Y., et al. (2014). The ryanodine receptor store-sensing gate controls Ca2+ waves and Ca2+-triggered arrhythmias. Nat. Med. 20, 184–192. doi: 10.1038/nm.3440

PubMed Abstract | CrossRef Full Text | Google Scholar

Chiang, C. E., and Roden, D. M. (2000). The long QT syndromes: genetic basis and clinical implications. J. Am. Coll. Cardiol. 36, 1–12. doi: 10.1016/s0735-1097(00)00716-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Choi, B. R., Burton, F., and Salama, G. (2002). Cytosolic Ca2+ triggers early afterdepolarizations and torsade de pointes in rabbit hearts with type 2 long QT syndrome. J. Physiol. 543, 615–631. doi: 10.1113/jphysiol.2002.024570

PubMed Abstract | CrossRef Full Text | Google Scholar

Chouabe, C., Neyroud, N., Guicheney, P., Lazdunski, M., Romey, G., and Barhanin, J. (1997). Properties of KvLQT1 K+ channel mutations in romano-ward and jervell and lange-nielsen inherited cardiac arrhythmias. EMBO J. 16, 5472–5479. doi: 10.1093/emboj/16.17.5472

PubMed Abstract | CrossRef Full Text | Google Scholar

Corrias, A., Giles, W., and Rodriguez, B. (2011). Ionic mechanisms of electrophysiological properties and repolarization abnormalities in rabbit Purkinje fibers. Am. J. Physiol. Heart Circ. Physiol. 300, H1806–H1813. doi: 10.1113/jphysiol.2002.024570

PubMed Abstract | CrossRef Full Text | Google Scholar

de Lange, E., Xie, Y., and Qu, Z. (2012). Synchronization of early afterdepolarizations and arrhythmogenesis in heterogeneous cardiac tissue models. Biophys. J. 103, 365–373. doi: 10.1016/j.bpj.2012.06.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Edwards, A. G., Grandi, E., Hake, J. E., Patel, S., Li, P., Miyamoto, S., et al. (2014). Nonequilibrium reactivation of Na+ current drives early afterdepolarizations in mouse ventricle. Circ. Arrhythm. Electrophysiol. 7, 1205–1213. doi: 10.1161/CIRCEP.113.001666

PubMed Abstract | CrossRef Full Text | Google Scholar

Gibb, W. J., Wagner, M. B., and Lesh, M. D. (1994). Effects of simulated potassium blockade on the dynamics of triggered cardiac activity. J. Theor. Biol. 168, 245–257. doi: 10.1006/jtbi.1994.1106

PubMed Abstract | CrossRef Full Text | Google Scholar

Guckenheimer, J., and Holmes, P. (1983). Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. New York, NY: Springer-Verlag.

Google Scholar

Guo, D., Zhao, X., Wu, Y., Liu, T., Kowey, P. R., and Yan, G. X. (2007). L-type calcium current reactivation contributes to arrhythmogenesis associated with action potential triangulation. J. Cardiovasc. Electrophysiol. 18, 196–203. doi: 10.1111/j.1540-8167.2006.00698.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, T., Ai, X., Shannon, T. R., Pogwizd, S. M., and Bers, D. M. (2007). Intra-sarcoplasmic reticulum free [Ca2+] and buffering in arrhythmogenic failing rabbit heart. Circ. Res. 101, 802–810. doi: 10.1161/CIRCRESAHA.107.152140

PubMed Abstract | CrossRef Full Text | Google Scholar

Higgins, E. R., Cannell, M. B., and Sneyd, J. (2006). A buffering SERCA pump in models of calcium dynamics. Biophys. J. 91, 151–163. doi: 10.1529/biophysj.105.075747

PubMed Abstract | CrossRef Full Text | Google Scholar

Himeno, Y., Sarai, N., Matsuoka, S., and Noma, A. (2008). Ionic mechanisms underlying the positive chronotropy induced by beta1-adrenergic stimulation in guinea pig sinoatrial node cells: a simulation study. J. Physiol. Sci. 58, 53–65. doi: 10.2170/physiolsci.RP015207

PubMed Abstract | CrossRef Full Text | Google Scholar

Horvath, B., Banyasz, T., Jian, Z., Hegyi, B., Kistamas, K., Nanasi, P. P., et al. (2013). Dynamics of the late Na+ current during cardiac action potential and its contribution to afterdepolarizations. J. Mol. Cell. Cardiol. 64, 59–68. doi: 10.1016/j.yjmcc.2013.08.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, X., Song, Z., and Qu, Z. (2018). Determinants of early afterdepolarization properties in ventricular myocyte models. PLoS Comput. Biol. 14:e1006382. doi: 10.1371/journal.pcbi.1006382

PubMed Abstract | CrossRef Full Text | Google Scholar

Huelsing, D. J., Spitzer, K. W., and Pollard, A. E. (2000). Electrotonic suppression of early afterdepolarizations in isolated rabbit purkinje myocytes. Am. J. Physiol. Heart Circ. Physiol. 279, H250–H259. doi: 10.1152/ajpheart.2000.279.1.H250

PubMed Abstract | CrossRef Full Text | Google Scholar

Itzhaki, I., Maizels, L., Huber, I., Zwi-Dantsis, L., Caspi, O., Winterstern, A., et al. (2011). Modelling the long QT syndrome with induced pluripotent stem cells. Nature 471, 225–229. doi: 10.1038/nature09747

PubMed Abstract | CrossRef Full Text | Google Scholar

January, C. T., and Riddle, J. M. (1989). Early afterdepolarizations: mechanism of induction and block; a role for L-type Ca2+ current. Circ. Res. 64, 977–990. doi: 10.1161/01.res.64.5.977

PubMed Abstract | CrossRef Full Text | Google Scholar

January, C. T., Riddle, J. M., and Salata, J. J. (1988). A model for early afterdepolarizations: induction with the Ca2+ channel agonist Bay K 8644. Circ. Res. 62, 563–571. doi: 10.1161/01.res.62.3.563

PubMed Abstract | CrossRef Full Text | Google Scholar

Jost, N., Papp, J. G., and Varró, A. (2007). Slow delayed rectifier potassium current (IKs) and the repolarization reserve. Ann. Noninvasive Electrocardiol. 12, 64–78. doi: 10.1111/j.1542-474X.2007.00140.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Jost, N., Virág, L., Bitay, M., Takács, J., Lengyel, C., Biliczki, P., et al. (2005). Restricting excessive cardiac action potential and QT prolongation: a vital role for IKs in human ventricular muscle. Circulation 112, 1392–1399. doi: 10.1161/CIRCULATIONAHA.105.550111

PubMed Abstract | CrossRef Full Text | Google Scholar

Kazbanov, I. V., ten Tusscher, K. H., and Panfilov, A. V. (2016). Effects of heterogeneous diffuse fibrosis on arrhythmia dynamics and mechanism. Sci. Rep. 6:20835. doi: 10.1038/srep20835

PubMed Abstract | CrossRef Full Text | Google Scholar

Keizer, J., and Levine, L. (1996). Ryanodine receptor adaptation and Ca2+-induced Ca2+ release-dependent Ca2+ oscillations. Biophys. J. 71, 3477–3487. doi: 10.1016/S0006-3495(96)79543-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, J. J., Němec, J., Li, Q., and Salama, G. (2005). Synchronous systolic subcellular Ca2+-elevations underlie ventricular arrhythmia in drug-induced long QT type 2. Circ. Arrhythm. Electrophysiol. 8, 703–712. doi: 10.1161/CIRCEP.114.002214

PubMed Abstract | CrossRef Full Text | Google Scholar

Kondo, T., Hisatome, I., Yoshimura, S., Mahati, E., Notsu, T., Li, P., et al. (2016). Characterization of the novel mutant A78T-HERG from a long QT syndrome type 2 patient: instability of the mutant protein and stabilization by heat shock factor 1. J. Arrhythm. 32, 433–440. doi: 10.1016/j.joa.2015.10.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Krogh-Madsen, T., Schaffer, P., Skriver, A. D., Taylor, L. K., Pelzmann, B., Koidl, B., et al. (2005). An ionic model for rhythmic activity in small clusters of embryonic chick ventricular cells. Am. J. Physiol. Heart Circ. Physiol. 289, H398–H413. doi: 10.1152/ajpheart.00683.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Kurata, Y., Hisatome, I., Matsuda, H., and Shibamoto, T. (2005). Dynamical mechanisms of pacemaker generation in IK1-downregulated human ventricular myocytes: insights from bifurcation analyses of a mathematical model. Biophys. J. 89, 2865–2887. doi: 10.1529/biophysj.105.060830

PubMed Abstract | CrossRef Full Text | Google Scholar

Kurata, Y., Hisatome, I., and Shibamoto, T. (2012). Roles of sarcoplasmic reticulum Ca2+ cycling and Na+/Ca2+ exchanger in sinoatrial node pacemaking: insights from bifurcation analysis of mathematical models. Am. J. Physiol. Heart Circ. Physiol. 302, H2285–H2300. doi: 10.1152/ajpheart.00221.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

Kurata, Y., Hisatome, I., Tanida, M., and Shibamoto, T. (2013). Effect of hyperpolarization-activated current If on robustness of sinoatrial node pacemaking: theoretical study on influence of intracellular Na+ concentration. Am. J. Physiol. Heart Circ. Physiol. 304, H1337–H1351. doi: 10.1152/ajpheart.00777.2012

PubMed Abstract | CrossRef Full Text | Google Scholar

Kurata, Y., Matsuda, H., Hisatome, I., and Shibamoto, T. (2008). Regional difference in dynamical property of sinoatrial node pacemaking: role of Na+ channel current. Biophys. J. 95, 951–977. doi: 10.1529/biophysj.107.112854

PubMed Abstract | CrossRef Full Text | Google Scholar

Kurata, Y., Tsumoto, K., Hayashi, K., Hisatome, I., Kuda, Y., and Tanida, M. (2019). Multiple dynamical mechanisms of phase-2 early afterdepolarizations in a human ventricular myocyte model: involvement of spontaneous SR Ca2+ release. BioRxiv [Preprint]. Available at: https://www.biorxiv.org/content/10.1101/613182v1 (accessed June 12, 2019).

Google Scholar

Kurata, Y., Tsumoto, K., Hayashi, K., Hisatome, I., Tanida, M., Kuda, Y., et al. (2017). Dynamical mechanisms of phase-2 early afterdepolarizations in human ventricular myocytes: insights from bifurcation analyses of two mathematical models. Am. J. Physiol. Heart Circ. Physiol. 312, H106–H127. doi: 10.1152/ajpheart.00115.2016

PubMed Abstract | CrossRef Full Text | Google Scholar

Kusters, J. M., Cortes, J. M., van Meerwijk, W. P., Ypey, D. L., Theuvenet, A. P., and Gielen, C. C. (2007). Hysteresis and bistability in a realistic cell model for calcium oscillations and action potential firing. Phys. Rev. Lett. 98:098107. doi: 10.1103/PhysRevLett.98.098107

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuznetsov, Y. A. (2003). Elements of Applied Bifurcation Theory, 3rd Edn, New York, NY: Springer-Verlag.

Google Scholar

Kuzumoto, M., Takeuchi, A., Nakai, H., Oka, C., Noma, A., and Matsuoka, S. (2008). Simulation analysis of intracellular Na+ and Cl- homeostasis during β1-adrenergic stimulation of cardiac myocyte. Prog. Biophys. Mol. Biol. 96, 171–186. doi: 10.1016/j.pbiomolbio.2007.07.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Landau, M., Lorente, P., Michaels, D., and Jalife, J. (1990). Bistabilities and annihilation phenomena in electrophysiological cardiac models. Circ. Res. 66, 1658–1672. doi: 10.1161/01.res.66.6.1658

PubMed Abstract | CrossRef Full Text | Google Scholar

Laver, D. R. (2007). Ca2+ stores regulate ryanodine receptor Ca2+ release channels via luminal and cytosolic Ca2+ sites. Biophys. J. 92, 3541–3555. doi: 10.1529/biophysj.106.099028

PubMed Abstract | CrossRef Full Text | Google Scholar

Laver, D. R. (2009). Luminal Ca2+ activation of cardiac ryanodine receptors by luminal and cytoplasmic domains. Eur. Biophys. J. 39, 19–26. doi: 10.1007/s00249-009-0417-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, G. X., Choi, B. R., Ziv, O., Li, W., de Lange, E., Qu, Z., et al. (2012). Differential conditions for early after-depolarizations and triggered activity in cardiomyocytes derived from transgenic LQT1 and LQT2 rabbits. J. Physiol. 590, 1171–1180. doi: 10.1113/jphysiol.2011.218164

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, W., Kim, T. Y., Huang, X., Liu, M. B., Koren, G., Choi, B. R., et al. (2018). Mechanisms linking T-wave alternans to spontaneous initiation of ventricular arrhythmias in rabbit models of long QT syndrome. J. Physiol. 596, 1341–1355. doi: 10.1113/JP275492

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, C., and Rudy, Y. (1991). A model of the ventricular cardiac action potential: depolarization, repolarization, and their interaction. Circ. Res. 68, 1501–1526. doi: 10.1161/01.res.68.6.1501

PubMed Abstract | CrossRef Full Text | Google Scholar

Madhvani, R. V., Xie, Y., Pantazis, A., Garfinkel, A., Qu, Z., Weiss, J. N., et al. (2011). Shaping a new Ca²⁺ conductance to suppress early afterdepolarizations in cardiac myocytes. J. Physiol. 589, 6081–6092. doi: 10.1113/jphysiol.2011.219600

PubMed Abstract | CrossRef Full Text | Google Scholar

Maltsev, V. A., and Lakatta, E. G. (2009). Synergism of coupled subsarcolemmal Ca²⁺ clocks and sarcolemmal voltage clocks confers robust and flexible pacemaker function in a novel pacemaker cell model. Am. J. Physiol. Heart Circ. Physiol. 296, H594–H615. doi: 10.1152/ajpheart.01118.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Maltsev, V. A., and Lakatta, E. G. (2010). A novel quantitative explanation for the autonomic modulation of cardiac pacemaker cell automaticity via a dynamic system of sarcolemmal and intracellular proteins. Am. J. Physiol. Heart Circ. Physiol. 298, H2010–H2023. doi: 10.1152/ajpheart.00783.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Marban, E., Robinson, S. W., and Wier, W. G. (1986). Mechanisms of arrhythmogenic delayed and early afterdepolarizations in ferret ventricular muscle. J. Clin. Invest. 78, 1185–1192. doi: 10.1172/JCI112701

PubMed Abstract | CrossRef Full Text | Google Scholar

Milberg, P., Fink, M., Pott, C., Frommeyer, G., Biertz, J., Osada, N., et al. (2012a). Blockade of ICa suppresses early afterdepolarizations and reduces transmural dispersion of repolarization in a whole heart model of chronic heart failure. Br. J. Pharmacol. 166, 557–568. doi: 10.1111/j.1476-5381.2011.01721.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Milberg, P., Pott, C., Frommeyer, G., Fink, M., Ruhe, M., Matsuda, T., et al. (2012b). Acute inhibition of the Na+/Ca2+ exchanger reduces proarrhythmia in an experimental model of chronic heart failure. Heart Rhythm 9, 570–578. doi: 10.1016/j.hrthm.2011.11.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Milberg, P., Pott, C., Fink, M., Frommeyer, G., Matsuda, T., Baba, A., et al. (2008). Inhibition of the Na+/Ca2+ exchanger suppresses torsades de pointes in an intact heart model of long QT syndrome-2 and long QT syndrome-3. Heart Rhythm 5, 1444–1452. doi: 10.1016/j.hrthm.2008.06.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Ming, Z., Nordin, C., and Aronson, R. S. (1994). Role of L-type calcium channel window current in generating current-induced early afterdepolarization. J. Cardiovasc. Electrophysiol. 5, 323–334. doi: 10.1111/j.1540-8167.1994.tb01169.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Němec, J., Kim, J. J., Gabris, B., and Salama, G. (2010). Calcium oscillations and T-wave lability precede ventricular arrhythmias in acquired long QT type 2. Heart Rhythm 7, 1686–1694. doi: 10.1016/j.hrthm.2010.06.032

PubMed Abstract | CrossRef Full Text | Google Scholar

Němec, J., Kim, J. J., and Salama, G. (2016). The link between abnormal calcium handling and electrical instability in acquired long QT syndrome–Does calcium precipitate arrhythmic storms? Prog. Biophys. Mol. Biol. 120, 210–221. doi: 10.1016/j.pbiomolbio.2015.11.003

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Hara, T., and Rudy, Y. (2012). Quantitative comparison of cardiac myocyte electrophysiology and response to drugs in human and nonhuman species. Am. J. Physiol. Heart Circ. Physiol. 302, H1023–H1030. doi: 10.1152/ajpheart.00785.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Hara, T., Virág, L., Varró, A., and Rudy, Y. (2011). Simulation of the undiseased human cardiac ventricular action potential: model formulation and experimental validation. PLoS Comput. Biol. 7:e1002061. doi: 10.1371/journal.pcbi.1002061

PubMed Abstract | CrossRef Full Text | Google Scholar

Parikh, A., Mantravadi, R., Kozhevnikov, D., Roche, M. A., Ye, Y., Owen, L. J., et al. (2012). Ranolazine stabilizes cardiac ryanodine receptors: a novel mechanism for the suppression of early afterdepolarization and torsades de pointes in long QT type 2. Heart Rhythm 9, 953–960. doi: 10.1016/j.hrthm.2012.01.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Parker, T. S., and Chua, L. O. (1989). Practical Numerical Algorithms for Chaotic Systems. New York, NY: Springer-Verlag.

Google Scholar

Pott, C., Muszynski, A., Ruhe, M., Bögeholz, N., Schulte, J. S., Milberg, P., et al. (2012). Proarrhythmia in a non-failing murine model of cardiac-specific Na+/Ca2+ exchanger overexpression: whole heart and cellular mechanisms. Basic Res. Cardiol. 107, 1–13. doi: 10.1007/s00395-012-0247-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Priori, S. G., and Corr, P. B. (1990). Mechanisms underlying early and delayed afterdepolarizations induced by catecholamines. Am. J. Physiol. 258, H1796–H1805. doi: 10.1152/ajpheart.1990.258.6.H1796

PubMed Abstract | CrossRef Full Text | Google Scholar

Qu, Z., and Chung, D. (2012). Mechanisms and determinants of ultralong action potential duration and slow rate-dependence in cardiac myocytes. PLoS One 7:e43587. doi: 10.1371/journal.pone.0043587

PubMed Abstract | CrossRef Full Text | Google Scholar

Qu, Z., Xie, L. H., Olcese, R., Karagueuzian, H. S., Chen, P. S., Garfinkel, A., et al. (2013). Early afterdepolarizations in cardiac myocytes: beyond reduced repolarization reserve. Cardiovasc. Res. 99, 6–15. doi: 10.1093/cvr/cvt104

PubMed Abstract | CrossRef Full Text | Google Scholar

Roden, D. M., Lazzara, R., Rosen, M., Schwartz, P. J., Towbin, J., and Vincent, G. M. (1996). Multiple mechanisms in the long-QT syndrome. Current knowledge, gaps, and future directions. the SADS foundation task force on LQTS. Circulation 94, 1996–2012. doi: 10.1161/01.cir.94.8.1996

PubMed Abstract | CrossRef Full Text | Google Scholar

Sato, D., Xie, L. H., Sovari, A. A., Tran, D. X., Morita, N., Xie, F., et al. (2009). Synchronization of chaotic early afterdepolarizations in the genesis of cardiac arrhythmias. Proc. Natl. Acad. Sci. U.S.A. 106, 2983–2988. doi: 10.1073/pnas.0809148106

PubMed Abstract | CrossRef Full Text | Google Scholar

Saucerman, J. J., Brunton, L. L., Michailova, A. P., and McCulloch, A. D. (2003). Modeling β-adrenergic control of cardiac myocytes contractility in silico. J. Biol. Chem. 278, 47997–48003. doi: 10.1074/jbc.M308362200

PubMed Abstract | CrossRef Full Text | Google Scholar

Schuster, S., Marhl, M., and Höfer, T. (2002). Modelling of simple and complex calcium oscillations. From single-cell responses to intercellular signalling. Eur. J. Biochem. 269, 1333–1355. doi: 10.1046/j.0014-2956.2001.02720.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Shannon, T. R., Guo, T., and Bers, D. M. (2003). Ca2+ scraps: local depletions of free [Ca2+] in cardiac sarcoplasmic reticulum during contractions leave substantial Ca2+ reserve. Circ. Res. 93, 40–45. doi: 10.1161/01.RES.0000079967.11815.19

PubMed Abstract | CrossRef Full Text | Google Scholar

Shannon, T. R., Wang, F., Puglisi, J., Weber, C., and Bers, D. M. (2004). A mathematical treatment of integrated Ca dynamics within the ventricular myocyte. Biophys. J. 87, 3351–3371. doi: 10.1529/biophysj.104.047449

PubMed Abstract | CrossRef Full Text | Google Scholar

Shimizu, W. (2013). Update of diagnosis and management inherited cardiac arrhythmias. Circ. J. 77, 2867–2872. doi: 10.1253/circj.cj-13-1217

PubMed Abstract | CrossRef Full Text | Google Scholar

Shimizu, W., and Horie, M. (2011). Phenotypic manifestations of mutations in genes encoding subunits of cardiac potassium channels. Circ. Res. 109, 97–109. doi: 10.1161/CIRCRESAHA.110.224600

PubMed Abstract | CrossRef Full Text | Google Scholar

Sogo, T., Morikawa, K., Kurata, Y., Li, P., Ichinose, T., Yuasa, S., et al. (2016). Electrophysiological properties of iPS cell-derived cardiomyocytes from a patient with long QT syndrome type 1 harboring the novel mutation M437V of KCNQ1. Regener. Ther. 4, 9–17. doi: 10.1016/j.reth.2015.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, Z., Ko, C. Y., Nivala, M., Weiss, J. N., and Qu, Z. (2015). Calcium-voltage coupling in the genesis of early and delayed afterdepolarizations in cardiac myocytes. Biophys. J. 108, 1908–1921. doi: 10.1016/j.bpj.2015.03.011

PubMed Abstract | CrossRef Full Text | Google Scholar

ten Tusscher, K. H., Hren, R., and Panfilov, A. V. (2007). Organization of ventricular fibrillation in the human heart. Circ. Res. 100, e87–e101. doi: 10.1161/CIRCRESAHA.107.150730

PubMed Abstract | CrossRef Full Text | Google Scholar

ten Tusscher, K. H., and Panfilov, A. V. (2006). Alternans and spiral breakup in a human ventricular tissue model. Am. J. Physiol. Heart Circ. Physiol. 291, H1088–H1100. doi: 10.1152/ajpheart.00109.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Tran, D. X., Sato, D., Yochelis, A., Weiss, J. N., Garfinkel, A., and Qu, Z. (2009). Bifurcation and chaos in a model of cardiac early afterdepolarizations. Phys. Rev. Lett. 102:258103. doi: 10.1103/PhysRevLett.102.258103

PubMed Abstract | CrossRef Full Text | Google Scholar

Trenor, B., Cardona, K., Saiz, J., Rajamani, S., Belardinelli, L., and Giles, W. R. (2013). Carbon monoxide effects on human ventricular action potential assessed by mathematical simulation. Front. Physiol. 4:282. doi: 10.3389/fphys.2013.00282

CrossRef Full Text | Google Scholar

Tsumoto, K., Kurata, Y., Furutani, K., and Kurachi, Y. (2017). Hysteretic dynamics of multi-stable early afterdepolarisations with repolarisation reserve attenuation: a potential dynamical mechanism for cardiac arrhythmias. Sci. Rep. 7:10771. doi: 10.1038/s41598-017-11355-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Tveito, A., Lines, G. T., Hake, J., and Edwards, A. G. (2012). Instabilities of the resting state in a mathematical model of calcium handling in cardiac myocytes. Math. Biosci. 236, 97–107. doi: 10.1016/j.mbs.2012.02.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Vandersickel, N., Kazbanov, I. V., Nuitermans, A., Weise, L. D., Pandit, R., and Panfilov, A. V. (2014). A study of early afterdepolarizations in a model for human ventricular tissue. PLoS One 9:e84595. doi: 10.1371/journal.pone.0084595

PubMed Abstract | CrossRef Full Text | Google Scholar

Veldkamp, M. W., Verkerk, A. O., van Ginneken, A. C., Baartscheer, A., Schumacher, C., de Jonge, N., et al. (2001). Norepinephrine induces action potential prolongation and early afterdepolarizations in ventricular myocytes isolated from human end-stage failing hearts. Eur. Heart J. 22, 955–963. doi: 10.1053/euhj.2000.2499

PubMed Abstract | CrossRef Full Text | Google Scholar

Verkerk, A. O., Veldkamp, M. W., de Jonge, N., Wilders, R., and van Ginneken, A. C. (2000). Injury current modulates afterdepolarizations in single human ventricular cells. Cardiovasc. Res. 47, 124–132. doi: 10.1016/s0008-6363(00)00064-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Vinet, A., and Roberge, F. A. (1990). A model study of stability and oscillations in the myocardial cell membrane. J. Theor. Biol. 147, 377–412. doi: 10.1016/s0022-5193(05)80495-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Virág, L., Iost, N., Opincariu, M., Szolnoky, J., Szécsi, J., Bogáts, G., et al. (2001). The slow component of the delayed rectifier potassium current in undiseased human ventricular myocytes. Cardiovasc. Res. 49, 790–797. doi: 10.1016/s0008-6363(00)00306-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Viswanathan, P. C., and Rudy, Y. (1999). Pause induced early afterdepolarizations in the long QT syndrome: a simulation study. Cardiovasc. Res. 42, 530–542. doi: 10.1016/s0008-6363(99)00035-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Volders, P. G., Stengl, M., van Opstal, J. M., Gerlach, U., Spatjens, R. L., Beekman, J. D., et al. (2003). Probing the contribution of IKs to canine ventricular repolarization: key role for beta-adrenergic receptor stimulation. Circulation 107, 2753–2760. doi: 10.1161/01.CIR.0000068344.54010.B3

PubMed Abstract | CrossRef Full Text | Google Scholar

Volders, P. G., Vos, M. A., Szabo, B., Sipido, K. R., de Groot, S. H., Gorgels, A. P., et al. (2000). Progress in the understanding of cardiac early afterdepolarizations and torsades de pointes: time to revise current concepts. Cardiovasc. Res. 46, 376–392. doi: 10.1016/s0008-6363(00)00022-5

CrossRef Full Text | Google Scholar

Wang, Z., Fermini, B., and Nattel, S. (1994). Rapid and slow components of delayed rectifier current in human atrial myocytes. Cardiovasc. Res. 28, 1540–1546. doi: 10.1093/cvr/28.10.1540

PubMed Abstract | CrossRef Full Text | Google Scholar

Weiss, J. N., Garfinkel, A., Karagueuzian, H. S., Chen, P. S., and Qu, Z. (2010). Early afterdepolarizations and cardiac arrhythmias. Heart Rhythm 7, 1891–1899. doi: 10.1016/j.hrthm.2010.09.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Wiener, R., Haitin, Y., Shamgar, L., Fernández-Alonso, M. C., Martos, A., Chomsky-Hecht, O., et al. (2008). The KCNQ1 (Kv7.1) COOH terminus, a multitiered scaffold for subunit assembly and protein interaction. J. Biol. Chem. 283, 5815–5830. doi: 10.1074/jbc.M707541200

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, D., Ermentrout, B., Němec, J., and Salama, G. (2017). A model of cardiac ryanodine receptor gating predicts experimental Ca2+-dynamics and Ca2+-triggered arrhythmia in the long QT syndrome. Chaos 27:093940. doi: 10.1063/1.5000711

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, Y., Izu, L. T., Bers, D. M., and Sato, D. (2014). Arrhythmogenic transient dynamics in cardiac myocytes. Biophys. J. 106, 1391–1397. doi: 10.1016/j.bpj.2013.12.050

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, Y., Sato, D., Garfinkel, A., Qu, Z., and Weiss, J. N. (2010). So little source, so much sink: requirements for afterdepolarizations to propagate in tissue. Biophys. J. 99, 1408–1415. doi: 10.1016/j.bpj.2010.06.042

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, Y., Liao, Z., Grandi, E., Shiferaw, Y., and Bers, D. M. (2015). Slow [Na]_i changes and positive feedback between membrane potential and [Ca]_i underlie intermittent early afterdepolarizations and arrhythmias. Circ. Arrhythm. Electrophysiol. 8, 1472–1480. doi: 10.1161/CIRCEP.115.003085

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamada, M., Ohta, K., Niwa, A., Tsujino, N., Nakada, T., and Hirose, M. (2008). Contribution of L-Type Ca2+ channels to early afterdepolarizations induced by IKr and IKs channel suppression in guinea pig ventricular myocytes. J. Membr. Biol. 222, 151–166. doi: 10.1007/s00232-008-9113-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeng, J., and Rudy, Y. (1995). Early afterdepolarizations in cardiac myocytes: mechanism and rate dependence. Biophys. J. 68, 949–964. doi: 10.1016/S0006-3495(95)80271-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Z., Wen, H., Fefelova, N., Allen, C., Baba, A., Matsuda, T., et al. (2012). Revisiting the ionic mechanisms of early afterdepolarizations in cardiomyocytes: predominant by Ca waves or Ca currents? Am. J. Physiol. Heart Circ. Physiol. 302, H1636–H1644. doi: 10.1152/ajpheart.00742.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhong, M., Rees, C. M., Terentyev, D., Choi, B. R., Koren, G., and Karma, A. (2018). NCX-mediated subcellular Ca2+ dynamics underlying early afterdepolarizations in LQT2 cardiomyocytes. Biophys. J. 115, 1019–1032. doi: 10.1016/j.bpj.2018.08.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Zimik, S., Vandersickel, N., Nayak, A. R., Panfilov, A. V., and Pandit, R. (2015). A comparative study of early afterdepolarization-mediated fibrillation in two mathematical models for human ventricular cells. PLoS One 10:e0130632. doi: 10.1371/journal.pone.0130632

PubMed Abstract | CrossRef Full Text | Google Scholar