
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Physiol. , 10 April 2012
Sec. Fractal Physiology
Volume 3 - 2012 | https://doi.org/10.3389/fphys.2012.00094
This article is part of the Research Topic Is life a globally critical phenomenon? And if so, why? View all 13 articles
Many attempts have been made to understand the origin of life and biological complexity both at the experimental and theoretical levels but neither is fully explained. In an influential work, Maynard Smith and Szathmáry (1995) argued that the majority of the increase in complexity is not gradual, but it is associated with a few so-called major transitions along the way of the evolution of life. For each major transition, they identified specific mechanisms that could account for the change in complexity related to information transmission across generations. In this work, I propose that the sudden and unexpected improvement in the functionality of an organism that followed a major transition was enabled by a phase transition in the network structure associated with that function. The increase in complexity following a major transition is therefore directly linked to the emergence of a novel structure–function relation which altered the course of evolution. As a consequence, emergent phenomena arising from these network phase transitions can serve as a common organizing principle for understanding the major transitions. As specific examples, I analyze the emergence of life, the emergence of the genetic apparatus, the rise of the eukaryotic cells, the evolution of movement and mechanosensitivity, and the emergence of consciousness. Finally, I discuss the implications of network associated phase transitions to issues that bear relevance to the history, the immediate present and perhaps the future, of life.
Life is the most intricate and complex phenomenon known to science. Over billions of years, diversity and complexity of the biological world have been increasing. Many attempts have been made to understand the evolution of organisms and the gradual increase of biological complexity both at the experimental and theoretical levels. The theory of evolution by natural selection predicts that organisms will change to improve their ability to survive and reproduce in a given environment. However, this gradual change does not have to come with increased complexity. In a groundbreaking work, Maynard Smith and Szathmáry (1995, 1999) argued that the majority of the increase in complexity is in fact associated with a few so-called major transitions along the way of the evolution of life. Different authors consider different transitions as major (Calcott et al., 2011) and some of these have been considered to be the great inventions of evolution (Lane, 2009). The most commonly accepted major transitions include the following: emergence of living matter, emergence of information carrying molecules, the rise of the eukaryotic cell, photosynthesis, the arrival of sex, the development of multicellular organisms, energy powered movement, the emergence of vision, the appearance of warm blooded species, the coming of language, the emergence of consciousness, and the formation of human culture and society.
Each of the major transitions brought about a new level of complexity by enabling certain behavior that was not possible before the transition. The emergence of such new behavior cannot be predicted from the properties of the components before the transition. The new kind of behavior post-transition is often accompanied by a rapid secondary adaption that makes it difficult or even prohibits the organism to return to the pre-transition state (Maynard Smith and Szathmáry, 1999). Examples of such irreversibility abound in nature. For example, once sexual reproduction appeared, the large majority of species never returned to asexual life. Also, cells in a multicellular organism cannot survive alone, except in the laboratory under artificial cell culture conditions. Maynard Smith and Szathmáry (1999) relate the major transitions to a qualitative change in the way information is stored, transmitted, and translated. However, information storing and processing always require some physical structure, just like software requires hardware as first suggested by von Neumann (1961–63) through the development of the self-replicating cellular automaton. Here I will argue that the basis of the new kind of behavior post-transition is a fundamental change in the structure pre-transition. If each major transition can be linked to the emergence of a novel structure, then there may be a common mechanism behind these transitions related to the complexity of the underlying structural organization.
The theory of complexity (Nicolis and Prigogine, 1989; Badii and Politi, 1997) has much to offer to understand life and its major transitions. Specifically, complexity deals with systems that show emergent behavior resulting from the interactions of many components or subunits of the system. A convenient way to discuss such systems is to consider the interactions among the units as a network. Examples include biochemical reaction networks (Klipp et al., 2004), the protein–protein interaction network (Yook et al., 2004), the cytoskeletal network (Pelletier et al., 2003; Silveira et al., 2009), or the neural network (Srahna et al., 2006). Various phenomena can then be associated with a given network such as information processing as electrical impulses flow through the neural network of the brain (Horwitz and Braun, 2004). As the interconnectedness of a network increases, the network can undergo a phase transition in its connectivity which in turn can lead to emergent phenomena allowing new functional features of the network (Stauffer and Aharony, 1992). If the structural basis of the major transitions of life is similar to a network phase transition, then it is easy to see that network effects are enabling in that they allow the emergence of new levels of biological complexity both in structure and function.
In this perspective, I will argue that biological complexity as we see it today cannot have evolved without networks. Specifically, I will examine several major transitions of life from the perspective of general network phenomena. I need to point out that some aspects of what I will present here have been said before. My purpose is not only to produce novel discoveries; rather, it is inclusiveness in an attempt to organize and possibly generalize thoughts from previous facts and knowledge as well as gain new insight into aspects of how the current level of biological complexity may have arisen. Before discussing the implications of network behavior for several of the major transitions, it is useful to first briefly describe networks, their relationship to complex systems and emergent network phenomena associated with phase transitions.
What is complexity and how to measure it? These questions have been addressed from various aspects (Adami, 2002) and many measures of complexity have been proposed such as algorithmic or Kolmogorov, statistical (Crutchfield and Young, 1989), physical (Huberman and Hogg, 1986), or thermodynamic (Llyod and Pagels, 1988) complexity. Biological systems certainly qualify as complex. Perhaps the most important aspect of their complexity is that they operate under non-equilibrium conditions and exhibit emergent properties that manifest in correlated spatial structure and temporal behavior (Suki et al., 2011). Without relying on any formal definition of complexity, the increase in complexity following a major transition will be taken to be the emergence of a novel structure–function relation for the organism that fundamentally alters the course of subsequent evolution.
To understand what is meant by emergence, we note that complex systems usually include many interacting units such as our economic system, the mammalian brain, a single cell, or the cytoskeletal protein network. The topological connectivity and the associated interactions among the units of a given system form a network. Interesting phenomena in a network are those that give rise to emergent behavior not seen at the level of the single unit and this is called a network phenomenon (Barabasi and Albert, 1999; Strogatz, 2001). The emergent behavior arises due to the interactions among the units which take place through the topological connectivity of the network. For example, the set of neurons arranged in a network constitutes the brain. Electrical impulses propagating through this network give rise to unexpected behavior; we call it thinking. However, the fact that neurons function in a network does not guarantee emergent behavior. Indeed, many species have brains with similar biophysical properties but coherent thinking as we know it has emerged only in one species and is considered a major transition. Since emergence cannot happen without interactions among the units, interconnectivity of the units has received substantial attention.
Interconnectivity, the way units are linked, allows the flow of agents including material, information or energy. The specific topology of how the units in a system are coupled defines the type of network (Albert and Barabasi, 2002). In a random network the links among nodes are added randomly (Erdös and Rényi, 1960). In a scale-free network, there are a few highly connected hubs and many nodes with a small number of links and the distribution of links follows a power law (Barabasi and Albert, 1999). Networks can also be clustered yet have small characteristic path lengths due to a few links that connect the different clusters and these are called small-world networks (Watts and Strogatz, 1998). Examples include the World Wide Web, the food chain, cell–cell communications, metabolic networks, elastic networks, and many more. One particular approach that studies network connectivity is percolation (Stauffer and Aharony, 1992). The beauty of percolation theory is that it can model various phenomena in terms of simple geometric considerations. In biology, percolation has been invoked for a better understanding of network behavior including intracellular mitochondrial signaling (Aon et al., 2004), percolation through the cytoskeleton (Forgacs, 1995; Silveira et al., 2009), or capillary formation (Coniglio et al., 2004).
As a brief introduction to percolation, consider a simple square lattice (Figure 1). Each bond (or site) in the lattice is occupied with probability p. A cluster of bonds is defined as the set of neighboring occupied bonds. For simplicity, we only consider bond percolation here because site percolation is similar in many respects. When p = 0, all bonds are empty. For small p, there is a sparse population of bonds resulting in only small clusters (top left). As p increases, the mean size of the clusters grows (top right, bottom left) and when p = 1, all bonds are occupied. Hence, as p increases from 0 to 1, there appears a specific value of p at which a large cluster, the incipient percolation cluster, emerges providing full connectivity of the network from one side to the other for the first time. The shortest contiguous path on the percolating cluster is traced with red (bottom left). If the size of the lattice approaches infinity, the transition from an unconnected to a connected lattice occurs sharply when p crosses a critical threshold called the percolation threshold, pc (Stauffer and Aharony, 1992). Whatever property a bond represents, this property percolates through the network and the emergence of the percolating cluster represents a phase transition.
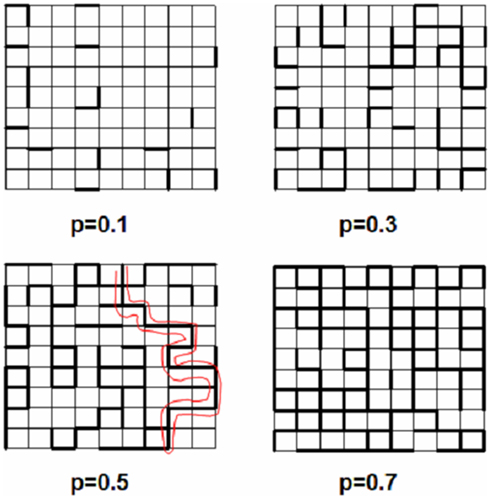
Figure 1. Bond percolation on a square lattice (thin lines) for different values of the probability p. Thick line segments are occupied with probability p. The red curve marks the shortest percolating pathway at p = pc = 0.5 (with permission from Suki et al., 2011).
Let us now consider the probability P that a bond belongs to the percolating cluster. It is easy to see that P itself also undergoes a phase transition, since P = 0 for p < pc (no connectivity across the lattice), while P increases continuously for p > pc, eventually approaching 1. Close to the transition, just above pc, P follows a power law, P ∼ (p − pc)β, a key ingredient of complex biological systems (Suki, 2002; Buldyrev, 2009). This transition is known as the percolation transition and it conveniently models, for example, fluid flow through a porous medium in which bonds present/absent in the lattice represent open/blocked channels. While the numerical value of pc depends on the type of lattice, the critical exponents such as β are independent of the microscopic details of the lattice and only depend on the dimension of the space (Stauffer and Aharony, 1992). The percolation transition is similar to other continuous phase transitions with P playing the role of the order parameter and β the critical exponent of the order parameter. As conceptually shown in Figure 2, the essence of a network associated phase transition is that it separates two regimes of network functionality and the transition between these two states occurs sharply at a critical organization of the network which, for the case of a simple percolation, happens when p = pc. At the critical point, phase transitions also generate fractals which are self-similar structures between the fully ordered and random configurations and exhibit long-range spatial correlations. The percolation cluster at p = pc is thus a fractal with a fractal dimension that is only a function of the dimension of the space and the critical exponents (Stauffer and Aharony, 1992). Since fractals are widespread in nature (Mandelbrot, 1983; Buldyrev, 2009), percolation has become a central tool in the understanding of complex structures and processes.
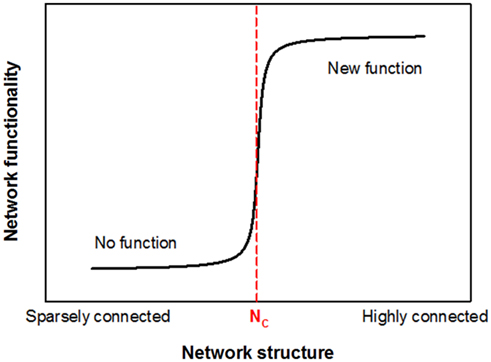
Figure 2. A conceptual representation of network associated phase transitions. The horizontal axis represents some measure of network structure that can range from “sparsely connected” to “highly connected” configuration. In percolation, this would represent the probability p that a bond is occupied. The vertical axis is related to some functional property of the network. For example, in percolation it can represent the fraction of networks in an ensemble that percolate the system or the probability that a bond belongs to the percolating cluster. If flow such as fluid or electrical current that can be carried by the network is of interest as a functional property, there would be essentially no function available for the network below a critical organization of its structure NC that corresponds to pc in percolation. It can be seen that the functionality of the network suddenly changes, once its structural organization reaches the critical configuration at NC which represents a phase transition.
Percolation can be applied to a wide variety of phenomena. Examples include the estimation of the amount of oil in oil fields from limited drilling (Stauffer and Aharony, 1992) or understanding gelation in bronchial mucus (McCullagh et al., 1995). Modeling the spreading of infectious diseases (Meyers et al., 2006) can be thought of as a model of the survival of the fittest in Darwinian evolution where a small advantage brought about by a random mutation results in spreading or percolating through the population. Indeed, a percolation model that incorporates species–species interactions and ancestral relationships has been successful in explaining the distributions of extinction events and the distribution of species and lifetimes, all of which display power-law type distributions (Klimek et al., 2009). Another important application is the error and attack tolerance of networks whereby the robustness of a network structure is tested against gradual removal nodes (Albert et al., 2000) which has implications for the evolution of biological networks discussed later. Percolation can also be used to explain dynamic phenomena occurring over a physiological structure within an individual including airway opening in the airway tree (Barabasi et al., 1996), capillary opening in the pulmonary vascular network (Wagner et al., 1999), the progression of symptoms in diseases such as pulmonary fibrosis and emphysema (Bates et al., 2007), or perhaps aiding tissue engineering (Suki et al., 2007).
Finally, I mention a few more general features of network behavior. An important application of network theory is related to the dynamics of mass or information transfer through networks (de Menezes and Barabasi, 2004). Directionality can also be associated with bonds which limits the transmission in one direction. These processes are called directed percolation and phase transitions on such networks belong to the non-equilibrium class which has also been applied to the emergence of life (Ferreira and Fontanari, 2002). Although non-equilibrium phase transitions are likely the dominant type in biology, their theory is not as well worked out as that of equilibrium transitions. Another area relevant for biology is the dynamics of network connectivity. For example, the stress-induced dynamic elimination or addition of network links can lead to phase transitions in the cell (Szalay et al., 2007) and similar approaches exhibit a rich variety of topological phase transitions (Palla et al., 2004). Often a major change in structure or function is associated with the transition from a poorly connected to a well-connected network or vice versa. Such cyclic phase transitions in connectivity underlie many complex emergent properties of adaptive biological systems (Paperin et al., 2011). Increase in species diversity often occurred in a relatively short time during evolution such as the Cambrian explosion. Such explosive diversifications may be a sign of a phase transition. Indeed, in a network with a fixed interaction density, there is a phase transition from a relatively unpopulated regime of “products” (e.g., species) to a highly populated and diverse regime of products (Hanel et al., 2005). Additionally, various networks often communicate with and depend on each other. The dynamics and failure of interdependent networks is different from those of single isolated networks (Buldyrev et al., 2010) and hence the concept of network of networks will surely find applications in biology.
In this section, I will discuss several of the major transitions of life. However, I will not discuss sex, vision, language, and human culture although population dynamics and network phenomena have been associated with other transitions (Santos et al., 2003; Palla et al., 2007). Instead, I will briefly discuss the implications of the network perspective to the emergence of life, the genetic apparatus, the eukaryotic cell, movement and mechanosensitivity, and finally the brain.
The very first major transition in evolution is the emergence of life. The smallest unit of living matter is currently considered the cell which exhibits high levels of complexity including intricate structure, metabolism with multiple embedded biochemical feedback loops, and replication with high accuracy. Consequently, a useful definition of life cannot be simple; it should include all of the essential characteristics of living entities such that neglecting a single feature from the list would not allow long-term biological evolution. As science progresses, the list of the essential features included in the definition of life may change and often it becomes longer and more convoluted. As of today, there is no consensus regarding what such a list should contain (Tirard et al., 2010). In fact, it has been proposed that what is needed is not even a list of such features, but understanding how the characteristics we consider essential for life were acquired by objects we call organisms (Tirard et al., 2010).
It is difficult to deal with this transition if there is no generally accepted agreement for the definition of life, and even the usefulness of a definition is questionable. One way to possibly overcome this difficulty is to seek to define the structural basis that can enable certain behaviors that we associate with life. In this sense, it is still useful to examine the various definitions of life because they often include elements from complexity and non-linear dynamics (Weber, 2010). For example, Macklem and Seely (2010) recently proposed the following definition: “Life is a self-organizing, self-regulating, self-reproducing, interconnected, open thermodynamic network of component parts existing in a complex regime in the phase transition between order and chaos as a plant, animal, microbe or fungus.” Obviously, one can argue about the details and a possible minimal set of the list (Trifonov, 2011) or the elusiveness of a convergent theme (Tirard et al., 2010). However, the concept that a “network” of some elements is involved seems to be essential since the above as well as many other definitions also directly include the word “network” or hint at a network behavior.
If we accept the notion that the structural basis of life is a network, then the “emergence” of living matter maybe associated with the emergence of a suitable network structure that allows processes associated with life. There are two main processes that have been considered: metabolism and replication. The metabolism first concept was originally proposed by Oparin in 1927 (Oparin and Synge, 1957) when virtually nothing was known about the structure and composition of genes. The replication first idea was proposed by Eigen (Eigen et al., 1981) and once evidence was found that RNA segments are capable of functioning as enzymes, the RNA world hypothesis became popular (Cech, 1986). Currently, there is little evidence as to which happened first or perhaps they emerged together. While my personal view is that some rude form of autocatalytic metabolism must have existed before accurate replication arrived on the scene, it is still possible to examine the implications of network phenomena without having to decide whether metabolism preceded or followed replication.
The RNA world concept is very popular. In the latest book by Richard Dawkins, “The Greatest Show on Earth”, he states that without genetic material, there is no inheritance and hence no evolution is possible (Dawkins, 2009). Thus, since RNA can carry information as well as function as an enzyme, it is likely that RNA was the first step in the origin of life. However, any complex system has memory and if a sufficiently large and complex network that acts as a non-linear dynamics system splits into two nearly identical systems, it is conceivable that each daughter systems will contain elements of the complexity reminiscent of the parent network. Once a network has information carrying capacity it is ready for natural selection if it has to share resources with other networks. Since not all new networks are conditioned best for a given environmental situation, those that do not function well will stop functioning and will not survive. Therefore, some inheritance, even if it’s crude, should be available in metabolic reaction networks. Furthermore, remarkably, proteins have been shown to be capable of replication (Lee et al., 1996). Kauffman (1986, 1995) showed that sufficiently rich polymer networks can undergo a phase transition and an autocatalytic network of reactions forms which in fact can evolve. The notion that an autocatalytic network is essential for turning a set of non-living but sufficiently rich soup of chemicals into something like a living metabolic network is attractive. The phase transition Kauffman talks about is a network related phase transition and it is in fact an emergent network phenomenon in the sense described above. It has been also suggested that once the primordial soup was sufficiently rich, some sort of a Krebs cycle could run in the reverse direction fueled by the hydrothermal vents of the ocean floor to produce amino acids and eventually more complex proteins and catalysts (Lane, 2009).
An interesting analytical model of the origin of life was proposed by Dyson (1999). He assumed that first some sort of a cell or isolated fluid droplet existed and considered a set of monomers inside the droplet. The monomers can be absorbed to an internal surface and be in an active state that catalyzes reactions and build new polymers. Since each chemical reaction changes the population of molecular species, a given population can be considered as a parent giving rise to a daughter population following the reaction. When the average catalytic activity of a daughter population is equal to that of the parent population, the system is in a quasi-stationary state. He showed that with respect to the fraction of active monomers, this molecular system, under the assumptions made, had two stable stationary states, or fixed points, separated by an unstable fixed point. The first stable fixed point corresponds to a low level of stationary catalytic activity with disorder and is considered as a “dead” cell. The other stable fixed point corresponds to a high level of catalytic activity, which means the cell is in an ordered state since most molecules are “working together in a collaborative fashion to maintain the catalytic cycles that keep them active.” Dyson calls this ordered homeostatic state of the cell “alive.” The transition from the low level of activity to the high level of activity represents the origin of life in this model system. Figure 3 illustrates the concept schematically. It is interesting to note that once the transition occurs by traversing an energy barrier, the system settles down by going downhill in free energy and becomes stabilized against a reverse transition. This is very similar to what Maynard Smith and Szathmáry (1999) suggest to occur after each of the major transitions. Dyson also calculated that transition to life would occur with a minimum of eight monomer species which is just a bit less than half of the current number of amino acids used by modern cells. The total number of molecules per droplet needed to be in the range between 2000 and 20000. The components of the model are monomers and polymers that form a network of reactions and the network undergoes a transition from low random activity to collective network behavior forming essentially an autocatalytic closure similar to Kauffman’s idea. It is thus remarkable how similar the final conclusion of the two theories is despite the differences in the details. Indeed, Kauffman (1995) predicted that such an autocatalytic closure is bound to happen with high probability as the network of interactions approaches a percolation-like phase transition.
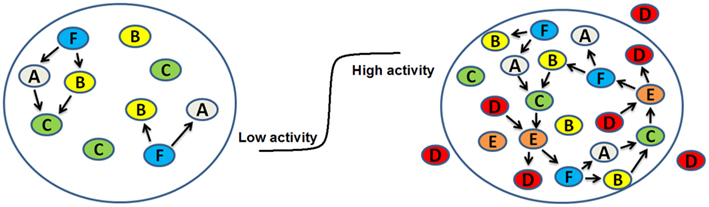
Figure 3. Schematic representation of the emergence of life in the Dyson model (Dyson, 1999). On the left is a droplet with only a few monomers. For example, F spontaneously breaks down to A and B which then recombine to form C, a slightly different molecular form of F. However, the variety of reactions is small and the activity of the reaction network is low; this represents the dead state. With the appearance of monomer D, which can come from outside or arise by chance inside, the situation suddenly changes (right panel). In this hypothetical model, D now catalyzes the reaction of C turning into E which then breaks down to D and F. Therefore, an autocatalytic cycle emerges and the reaction network undergoes a phase transition (middle panel) from a state of low activity to a state of high activity which represents life.
There are of course many newer approaches and models. For example, the protein interaction world assumes a dense network of protein–protein interactions before the RNA world (Andras and Andras, 2005). Dyson (1999) suggested that his model of the transition to life precedes evolution by natural selection. However, chemical reaction networks can store information and can evolve when encapsulated and provided with input matter (Ricard, 2010). In such networks, there can be selection and mutation but not accurate replication. Nevertheless, the conclusion from this overview is that whatever the original primordial soup was made of, eventually a transition must have occurred: from the set of random chemical reactions emerged an organized network of catalytic activity. In this organized network, there must have been a sufficiently rich activity of chemical reactions maintaining itself in the presence of steady energy supply. Thus, network phenomena under non-equilibrium conditions must have played a key role in the very first major transition, the origin of life, independent of the precise details of chemistry.
In his model, Dyson (1999) specifically addresses the question of inheritance and error tolerance. He speculates that following the transition to life, the droplet would grow and eventually become unstable and split into two with a high probability that both daughter droplets would inherit sufficient material to remain alive. The reproduction is not accurate; the corresponding error rate in catalyzing polymers would be ∼25%. However, it is exactly the high error rate that allows the model to make the first transition to become “alive” in reasonable time. Interestingly, the model does not transition to life with four monomer species such as the four modern nucleotides. Also, several recent works suggest that metabolism first in an encapsulated volume followed by the emergence of the genetic apparatus is a more likely scenario with more explanatory power than the so-called RNA world (Andras and Andras, 2005; Ricard, 2010). As the Dyson model suggests (Dyson, 1999), a crude inheritance in an autocatalytic polymer network is possible without RNA. In modern cells, RNA cannot be translated into larger proteins without the help of protein enzymes. An important experimental result supporting the RNA world hypothesis is that RNA segments can in fact self-replicate (Doudna and Szostak, 1989; Doudna et al., 1991). While the polymerization of nucleotides by RNA needed for replication remains limited to relatively short segments, this polymerization is highly accurate (Johnston et al., 2001). In an effort to link the inheritance via the metabolic networks and the genetic apparatus, it has been proposed that the appearance of RNA is a memory of the inheritance in the protein interaction world whereas the appearance of DNA is a memory of the RNA apparatus (Andras and Andras, 2005). Whether or not this is true, it is clear that the emergence of the genetic material produced a system that was much more capable in terms of accurate replication and hence increased survival of the proto-cells than what could be achieved via the metabolic networks.
Numerical models also produce interesting results suggesting that once the more accurate replication emerges, there will be a competition between high error inheritance through protein interactions and the RNA-based accurate replication and if the effective replication rate reaches a critical threshold, there will be a phase transition and in the new phase, systems with the ability of replication outcompete those without replication (Nowak and Ohtsuki, 2008). Obviously, the discovery of the genetic code by evolution is likely a necessary step in order to move beyond the complexity of simple metabolic networks and develop more complex and specific enzymes leading to the emergence of the first prototype of modern cells. Once the inheritance system became more efficient than the metabolic network, it must have spread through the population of proto-cells competing within the same environment via a percolation process. Again, following this major transition, the population stabilizes and returning to the simpler metabolic inheritance is no longer available for the cells.
The reading and transcribing of DNA to RNA and eventually translating the code into proteins need a lot of specific catalysts operating in a new and sophisticated biochemical network. Viewed in this way, the biochemical protein network of enzymes associated with the genetic code is enabling the genetic code to operate efficiently and hence the development of the bacterial cells from the simpler metabolic networks. This is an example of interacting biochemical networks in such a way that neither remains viable without the other. From now on, RNA and DNA are needed for coding proteins, which is the software of the cell, whereas in order to run the software, a network of enzymes is necessary playing the symbolic role of hardware. This is somewhat similar to building an arch bridge which requires assembling a falsework, a structure supporting the bridge during construction. Once the bridge is built, the falsework is eliminated. For observers arriving on the scene after the construction is finished, the functioning bridge appears as a miracle because it cannot be built alone, it would collapse under its own weight during the construction process. Without actually trying to build an arch bridge, one can only speculate or use computer models to figure out how the construction could have happened.
The transition from prokaryotes to eukaryotes has been suggested to be perhaps the most important major transition after the emergence of life because it took a long time, over a billion years and it appears to have happened only once (Lane, 2009). While bacteria have remained more or less the same ever since they first came to life, the emergence of eukaryotes opened up huge possibilities for complexity to increase both within the cell and among cells. The eukaryotic cell is a giant network of embedded loops of biochemical reactions. There are many cycles and signal transduction pathways that also communicate with each other so that they form a weakly linked super network of networks. There are several novel structural features of the eukaryotic cell compared to both bacteria and archaea including significant increases in cell volume and DNA size, the appearance of mitochondria or chloroplasts, the nucleus as well as the complex cytoskeletal network (Maynard Smith and Szathmáry, 1999). With the increase in size, the internal network structures were able to grow and become increasingly more complex. All these new structures facilitated new functions such as phagocytosis, sex, new ways of moving around and adhering to surfaces, etc. which in turn led to the development of multicellular organisms, specialized cells, organs, and eventually modern plants and animals including us.
The bacterial cell is almost empty compared to the eukaryotic cell. How did this enormous change in size, structure, and function come about in the eukaryotic cell? Maynard Smith and Szathmáry (1999) argue that the first step in the transition was that prokaryotes lost their rigid cell wall which enabled them to carry out phagocytosis and more efficient food digestion. This process could then allow these young eukaryotes to phagocytose bacteria which turned out to be a symbiotic advantage leading to the emergence of the mitochondria. On the other hand, Lane (2005) argues that it was the development of mitochondria that changed the entire energy budget of the cell allowing it to increase in size and complexity. A more recent theory proposes that eukaryogenesis and the development of sex must have occurred in a synergistic fashion in response to a metabolic crisis in the cell in order to cope with the repair of DNA damage induced by UV light and/or the accumulation of reactive oxygen species (Gross and Bhattacharya, 2010). Whatever the first trigger was, it is likely that the transition in fact was a series of smaller transitions as suggested by Maynard Smith and Szathmáry (1999). For example, in the Maynard Smith and Szathmáry scenario, the loss of the rigid cell wall in some bacteria was supposed to have happened by a digestion process in which enzymes produced by other bacteria eliminated the outer wall. Interestingly, the digestion and mechanical failure of a thin sheet of a network of proteins can be modeled as a percolation process (Black et al., 2008). Once the wall is partially or fully eliminated, there would be a strong selective pressure to develop a structural system that can stabilize the shape and integrity of these fragile and wall-less cells. Consequently, a novel and dynamic network, called the cytoskeleton, emerged. The cytoskeleton composed mainly of actin and microtubules is an interesting network in itself and its emergence is very likely a percolation process. Some early forms of actin and microtubules exist in bacteria (Frankel and Mooseker, 1996). Once the wall was lost, these proteins may have been modified randomly first and some of these modifications allowed efficient polymerization of these proteins to form local structural networks. The stiffness of a network is 0 below the percolation threshold (Stauffer and Aharony, 1992). Thus, shape and structural integrity would be available only for those cells that could produce a percolating cytoskeletal network. Cells that were successful in this would then be able to survive and gradually take over the population of wall-less cells. The end result is a remarkable dynamic percolating network of elastic fibers (Figure 4).
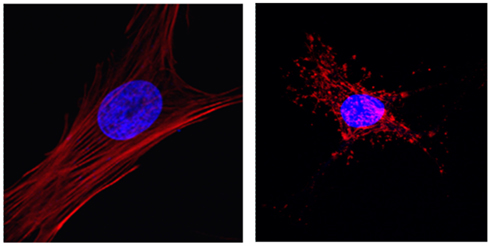
Figure 4. Fluorescent images of the actin network (red) and the nucleus (blue) in primary vascular smooth muscle cells in culture. The left panel demonstrates an intact percolating actin network. The straightness of stress fibers suggests that they are under mechanical tension generated by myosin motors. The right panel shows actin in the presence of cytochalasin D which inhibits the polymerization of the actin monomers to form stress fibers. The transmission of mechanical forces in the absence of a percolating network is highly limited.
The presence of such a network in the cell allows several novelties. For example, the polymerization state of microtubules, similar to the percolation probability, adds a negative feedback to control flux through some of the most basic metabolic pathways such as the Krebs cycle (Aon and Cortassa, 2002). The development of phagocytosis directly depends on the actin network (Yutin et al., 2009) and phagocytosis in turn might have allowed the development of the nucleus (Maynard Smith and Szathmáry, 1999). Another important function of the cytoskeletal network is to provide efficient intracellular transport of cargo including enzymes, signaling molecules or extracellular matrix molecules for general cell function and exocytosis, which invariably takes place along the microtubules (Hamm-Alvarez and Sheetz, 1998). Additionally, the cytoskeletal network allows the controlled maintenance and adaptation of cell shape and the emergence of mechanosensitivity (Ingber, 2006) that is separately discussed below. Many of these would in turn allow further novelties.
Clearly, without the dynamic structural network of the cytoskeleton, phagocytosis is not possible which in turn would make the emergence of mitochondria unlikely. Without mitochondria, the energy supply of the cell is limited and cell size and DNA complexity could not have increased. Thus, we see yet another example where the emergence of a new structural network allows the development and emergence of an array of novel functions. To conclude, the simpler reaction cycles and the lack of a dynamic cytoskeleton in bacteria do not lead to such increase in complexity as in the eukaryotic cell. Thus, the transition to eukaryotic cells is clearly associated with the emergence of structural networks working in unison with the embedded biochemical reaction networks which play a significant role in enabling new avenues toward increasing complexity and hence the evolution of higher levels of life form.
Movement is critically important in the evolution of higher levels of complexity. Indeed, movement has been considered as one of the major inventions of life (Lane, 2009). Cells can swim and crawl around and multicellular organisms can explore vast regions opening up new possibilities for species evolution and diversification forming large and intricate ecosystems. The sudden increase in the complexity of ecosystems – characterized by the number of species coexisting together in similar numbers – following the Permian extinction about 250 million years ago is likely due to the improved motility (Lane, 2009). The emergence of movement is also accompanied by a new kind of signaling that helps probe and map out the rigidity and texture of the external world. This signaling is called mechanotransduction by which an external mechanical perturbation is converted to electrical or biochemical signals within the cell. Mechanotransduction plays many roles in normal and pathological tissues from embryonic development to cardiac misfunction (Hoffman et al., 2011). Even though its evolutionary relation to movement is unclear, it is discussed here as part of the transition that involves mechanical forces.
The basic molecular mechanism behind movement is the generation of mechanical force by a motor protein, the myosin. A single myosin motor forms a cross-bridge between two neighboring actin filaments and in the presence of ATP, the energy currency of the cell, the myosin motor moves in discrete steps pulling the two filaments inward and generating a contractile force at the opposing ends of the filaments. The magnitude of the force coming from this single molecule force-generating unit is very small (Finer et al., 1994), not sufficient for movement. When these force-generating units form a network that percolates through the entire cell or at least between two adhesion receptors, the total contractile force significantly increases. The force outside the cell undergoes a phase transition related to the percolation of the intracellular actin network. Indeed, disrupting the actin network with inhibitors almost completely abolishes the measurable contractile force (Tseng et al., 1997). Thus, at the single cell level, a network of force-generating units is essential for all cellular functions that require mechanical forces. Furthermore, it is conceivable that once a network forms, further refinement of the network by evolutionary changes in the protein as well as the network structure becomes possible for more specific functional tasks. For example, skeletal muscle cells have a highly organized regular network of force-generating units with a coordinated contractile effort that allows generating large forces to move body parts. Smooth muscle cells, on the other hand, have different myosin motors (Srivastava et al., 1979) working in a diffuse network of actin and play different physiological roles such as peristaltic motion or controlling blood flow in organs. Hence network effects are not only important for function, but can feed back and influence the evolution of protein structure. In fact, it is the network formation of molecular motors along the actin that eventually allows the motility of the eukaryotic cells.
Following the emergence of multicellular organisms, which can be considered as a symbiotic fusion of many small cellular networks to form a super network, the contractile cells have become specialized and combined to form muscle groups serving different functions. These muscle groups are part of a larger network of the entire musculature which is densely interwoven with a network of nerve cells that control the activation of the muscle groups. All these networks allow the individual organisms to move around and interact much more with the environment, with other individuals and other species than before. Consequently, giant complex ecosystems emerged which form hierarchical interaction networks. As the inter-species interactions became richer and more complex, competition forced individuals and then the corresponding species to refine their capabilities in movement coordination, jumping, swimming, etc. Thus, network effects clearly have an impact on evolution at multiple length scales spanning some 15 orders of magnitude from the networks of force-generating units at the nanometer scale to the interaction network of species in ecosystems at a scale of hundreds of kilometers.
Mechanical forces such as gravity, fluid pressure, or shear stress acting on the cell membrane critically influence cell behavior. Interestingly, mechanosensitivity of ion channels evolved very early and exists even in eubacteria and archaebacteria perhaps to deal with harsh environments and to release osmotic pressure (Martinac and Kloda, 2003). The eukaryotic ion channels are quite similar to the bacterial ones. However, these channels in eukaryotic cells are strongly associated with the cytoskeletal network. For example, pharmacological disruption of the actin network inhibits the stretch-induced elevation of intracellular Ca++, a key signaling molecule, in endothelial cells (Ito et al., 2010). Eukaryotic cells also developed the ability to adhere to solid surfaces and new mechanotransductory pathways such as integrin-based signaling emerged (Ingber, 1991). The application of forces to cell adhesion points, the focal adhesions, results in the transmission of the forces into the cells. Along the chain of force transmission, some protein conformational change takes place which in turn elicits biochemical processes (Silver and Siperko, 2003) as well as direct effects on the nucleus leading to transcription and production of proteins (Dahl et al., 2008). The major load-bearing component of such responses is again the cytoskeleton (Hoffman et al., 2011) and hence force generation and mechanotransduction are intimately linked. Broken linkages in the cytoskeletal network cannot support the signaling (Figure 4), thus a percolation-like process is the basis of mechanotransduction (Forgacs, 1995).
In higher organisms, structural and hierarchal networks exist at multiple length scales that span from the macroscale to the nanoscale and mechanical forces across these networks lead to mechanotransduction (Ingber, 2006). The dynamic nature of the mechanical forces also seem to influence signal transduction (Hoffman et al., 2011). For example, in the lung, macroscopic mechanical forces of breathing generate mechanical stresses in the lung parenchyma which are transmitted through the alveolar septal walls to collagen fibers to which all resident cells are linked directly or indirectly (Suki et al., 2005). With every breath, the fluctuations in mechanical stresses at all levels of these multiscale networks are transmitted through the integrin receptors and the magnitude and apparent randomness of these force fluctuations play a fundamental role in the function of the lung and likely other organs such as blood pressure fluctuations in vessel walls. Indeed, random variations in stretch amplitude, which mimic the natural variability of tidal breathing, increase surfactant secretion in alveolar epithelial cells compared to monotonous stretch (Arold et al., 2009).
With regard to the implications of random variations in mechanical stimuli, we also note that the intracellular structures including the actin and microtubule networks that support mechanotransduction are dynamic undergoing assembly and disassembly (Cassimeris et al., 1988; Bretschneider et al., 2002) similar to the cyclic phase transition in connectivity (Paperin et al., 2011). An emerging picture then is that the physical basis of the transduction of mechanical forces into biochemical signals and cell responses is a dynamic network structure that operates near the percolation threshold. The dynamic nature of this structure allows selective signaling in the sense that fluctuations in the magnitude of mechanical forces can regulate different signaling pathways depending on the particular characteristics of the external force fluctuations. Since mechanosensing is almost as ancient as the cell, such signaling mechanisms operating on the dynamic network of the cytoskeleton must be deeply rooted within all eukaryotic cell types.
In the human brain, there are about 23 billion neurons which have an amazing 20 trillion connections. It is a super highway of information passing and processing. The brain controls many things in the body without which higher organisms would not be possible. The basis of brain function is that neurons talk to each other via action potentials through this enormous network. Neurons also form various subnetworks such as the respiratory rhythm generator which consists of five interacting neuron groups. The particular cross-talk among the groups within the respiratory center together with inputs from the periphery leads to the emergence of a new feature, a limit cycle firing pattern (Botros and Bruce, 1990) which drives the respiratory muscles enabling cyclic breathing, an essential life-support process. At an even higher level, the clusters of neuron groups are weakly linked forming a small-world type of network structure (Humphries et al., 2006). Many tasks corresponding to a given cluster are automatically performed and take place even during sleep. However, following some 3.5 billion years of evolution of life, the brain has evolved to do something remarkably new, conscious thinking.
Let us consider the mind. What is consciousness? While the answer is not known with much certainty, the science of complexity and networks will definitely contribute to a better understanding of it. In 1959, Hubel and Wiesel discovered that visual perception of shapes and colors requires breaking the image into simpler units then building up a brain image (Hubel and Wiesel, 2009). The process of building up the brain’s own images of the external world must occur in neural networks perhaps somewhat similarly as pattern recognition is achieved by neural networks in the computer. Surely, the interpretation of the outside world by the brain, which is the basis of thinking, requires network effects since a single neuron cannot do much more then random firing of action potentials. Moreover, memory itself is a reinforced pattern of neuronal firing activity by a set of neurons. The components of both the images and memories are stored and, via a synchronized firing of a cluster of neurons, these images and memories can re-emerge. This process of knitting the pieces together is reminiscent of the approach invoked in complexity science in which the goal is to understand function based on not just the properties of individual units, but their non-linear interactions. Taken together, it seems to be generally true that the many subtasks of consciousness require network function. How do these subtasks interact with each other? Low-frequency oscillations in human functional MRI time series obtained from regions of the brain exhibit a small-world architecture and it was argued that this probably reflects the underlying neuroanatomical connectivity (He et al., 2009). Thus, when the subtasks are put together, a super network of networks is formed in the brain which appears to have small-world characteristics that ensures enhanced signal-propagation speed, computational power, as well as synchronizability (Watts and Strogatz, 1998). Since a single neuron works the same way in a rabbit’s brain as in the human brain, differences in the functional abilities of the rabbit and human brains must be related to the differences in their network structure. Indeed, even the small and primitive brain of C. elegans has a small-world structure that is different from a random graph in that it exhibits high local connectivity with a few longer links bridging different modules (Watts and Strogatz, 1998). However, the complexity of the brain anatomical network increases in the cat and the macaque by exhibiting for example hubs, which are highly connected nodes that can link neurons within a module as well as among modules (Sporns et al., 2007). Moreover, in healthy humans, a higher intelligence score corresponds to a shorter characteristic path length and a higher overall efficiency of the underlying anatomical network, indicating a more efficient parallel information transfer (Li et al., 2009).
As discussed by Maynard Smith and Szathmáry (1999), even though the human brain size already reached that of the modern human about 100,000 years ago, real change in technical activity and inventiveness started to emerge only about 50,000 years ago. Perhaps, they argue, it was the emergence of language that allowed brain modules to access each other that resulted in the emergence of fully conscious creativity about 50,000 years ago. However, it is equally likely that not the size but the complexity of the connectivity of the brain increased gradually during this time period although language may have provided a feedback on the structural evolution. It is thus tempting to speculate that consciousness is a modular multiscale network phenomenon that emerged as a consequence of a phase transition in the connectivity of the underlying neural network structure of the brain. The particular connectivity allows subnetworks or modules to function in semi-autonomous ways such that only a coarse grained version of the information is passed on to the next higher level. Perhaps the modules are not even hardwired to a given set of neurons but form a synchronized pattern of correlated activity or dynamic coalition (Crick and Koch, 2003). How the neural subnetworks carry out this job is unclear. And how the super network integrates the information at the highest level is even less clear. What is obvious is that without the high level of connectivity of the brain neuronal network, it is impossible to achieve not only thinking but even much simpler tasks such as breathing.
The impact of the emergence of consciousness on the world cannot be overestimated. Indeed, consciousness brought with it many new and often emergent phenomena ranging from the possibility of forming social interactions, societies, industry, art, culture, war, and exploring and changing the world even outside the planet. While much of these issues can also be looked at through the microscope of the network perspective, this is beyond the scope of this assay.
I have argued that network phenomena are at the heart of several if not all major transitions of life. While the specifics differ, the essence may be similar: the components of a network gradually approach a critical level. When the critical point is reached, a phase transition brings about a sudden and substantial increase in complexity which corresponds to a new level of structural organization. The increased structural complexity in turn enables one or more novel functions for the organism not apparent before the transition. If such a transition increases the fitness of an individual in its niche, natural selection will spread it through the population.
It is likely that many smaller evolutionary changes also occurred via phase transitions. However, the majority of phase transitions did not lead to a major transition since most of them were not accompanied by a sufficiently large increase in complexity. The major transitions brought such significant increases in complexity that changed the course of evolution. What is the driving force behind the major transitions? Being open systems, biological organisms are constantly exposed to various external thermodynamic forces. Given that biological systems are non-linear and capable of reorganizing their internal structure, the overall direction of change is a new network organization with increasing internal order which allows exporting more entropy into the environment. These processes are likely governed by the principle of maximum entropy production which says that under the constraints of a system far from equilibrium, the path chosen from the possibilities maximizes entropy production (Jaynes, 1957; Martyushev and Seleznev, 2006). Indeed, metabolic networks naturally tend toward the maximum entropy production state (Unrean and Srienc, 2011). Furthermore, it has recently been hypothesized that maximum entropy production leads to fractal structures and correlated variabilities because they are able to break down energy gradients efficiently (Seely and Macklem, 2012). As mentioned earlier, fractal structures and long-range correlated fluctuations naturally appear at the critical point during phase transitions providing thus an intriguing link between non-equilibrium conditions, ordered structures and the corresponding novel functions related to the major transitions of life.
Experimentally it is difficult to study the major transitions. The mode of investigation has been limited to analyzing the fossil record, tracing back the genetic similarities among species and utilizing advanced modeling. With regard to the early events such as the origin of life, experiments can only limit the space of possibilities, but not prove how the emergence happened. On the other hand, any analytic and computer models necessarily have to invoke assumptions and the results obviously depend on both the model structure and the assumptions. Such modeling efforts can even lead to contradicting conclusions. The network associated phase transition on the other hand does not need any assumptions and should generally be valid. While this is a major advantage, the drawback of this approach is that it is not specific enough to pinpoint what chemicals might have been involved in the prebiotic autocatalytic reaction networks. While this argument probably holds for most of the other major transitions, in some cases the underlying network structure is better known, such as the brain neural network. The corresponding functional phase transition, consciousness, is therefore likely related to the increase in the complexity of the structure via increased connectivity that allows emergent novel features in the processing of information. Hence, in this case, the specificity is known and the generality of the network approach is not a drawback.
Although approaching a phase transition may require many small steps taking a long time, the transition itself can occur over a much shorter period perhaps in a sequence of correlated jumps similar to avalanches. Thus, the rate of change of increase in complexity can show sudden discontinuous jumps when considered over an evolutionary time scale. An example of this may be the Cambrian explosion. Consequently, the appearance of a new function does not have to be gradual and smooth as often assumed; rather, it is a sudden and unexpected property emerging from a phase transition.
An interesting implication of the network associated phase transition is that following the transition, additional small adaptations can follow that make it difficult for the organism to return to the pre-transition state. While in a few cases return is possible, it would be accompanied by a hysteresis on graphs similar to Figure 2. Nevertheless, the irreversible nature of this highly uni-directional process results in an apparent arrow of evolution from simple to complex. Furthermore, since the organism is no longer capable of using certain functional features that were available pre-transition, maintaining functionality requires superimposing smaller adjustments on the existing complexity which then further increases irreversibility and complexity. For example, a specific signaling cascade in the cell may have emerged from various chemicals reaching a critical level such as the percolation threshold to form a network. The network likely allowed some variation in certain components or structure and natural selection would fine tune the signaling cascade adding a new component or replacing an old perhaps to protect the cell from an invader or other stimuli. However, this new feature could also have a negative side effect. Once the signaling cascade exists, its advantages do not allow the cell to go back to its pre-transition state. Hence another compensatory layer is needed in order to actually compensate for the side effect of a new feature. Consequently, layer by layer, complexity of the system necessarily increases possibly reaching levels where some of the components would not even be needed, yet the entanglement of individual components in various nested networks prohibits simplification by natural selection. A salient example of such an entangled network of signaling is the hierarchical apoptotic signaling cascade in eukaryotic cells that involves a cascade of signaling events. A general consequence of such processes contributing to the increase in complexity is that using the reductionist approach, it may not be possible to identify a distinct role for every single protein in a signaling cascade. A full understanding requires a network approach.
Finally, a more general implication of network phenomena is related to the error and attack tolerance (Albert et al., 2000). Differently organized network structures tolerate breakdown differently (Liu et al., 2002). Nevertheless, a gradual breakdown of a network structure within an organism can lead to partial or full impairment of the corresponding function. For example, the loss of neuronal connectivity in Alzheimer’s disease leads to the gradual loss of consciousness (He et al., 2009). Another example is pulmonary emphysema where the alveolar network structure breaks down in a sequence of avalanches (Suki et al., 2011). The corresponding total surface area decreases and the associated function – gas exchange –, becomes seriously impaired. If one of the essential life-support networks is compromised sufficiently, network breakdown ultimately leads to death. In emphysema, complete loss of gas exchange is such an event. Serious bleeding is another example where the network structure of the circulatory system is compromised which leads to an impaired function, supplying oxygen to tissues, and possibly death. Alternatively, death itself may be associated with the breakdown of all essential network phenomena in the body. Whether death comes first or death is a consequence of the breakdown of network phenomena, is unclear and probably there are instances of both.
The network perspective discussed here provides a new opportunity to examine life as a critical phenomenon. Hence, before closing, I would like to reiterate some old and raise several new questions that bear relevance to the history, the immediate present and perhaps the future of life:
(1) If the major transitions are indeed a network associated phase transition, then, to some extent, they should be independent of the details of the system. With regard to the first transition, the origin of life, does this suggest that a transition is likely to occur in any sufficiently rich soup of raw materials largely independent of the specifics of chemistry? Given the steady discovery of Earth-like planets, an important implication of this would be that some sort of a self-sustaining primitive life should be abound in the universe as suggested by Kauffman (1995).
(2) If each transition mounts a barrier to reversing itself, then there is an irreversible increase in biological complexity providing a sense of arrow of time in biology. What is the relation of this arrow of time to the physical arrow of time? Except for Prigogine (Prigogine, 1997), most physicists hold that there is no arrow of time and at the fundamental level, time is reversible. However, non-biological chemical reaction networks can be sensitive to the direction of time too (Ricard, 2010). Is it then possible that the macroscopic arrow of time that pervades human experience is related to irreversibility associated with network behavior?
(3) If network phenomena are important, can we then expect a continued increase in complexity such that newer network associated phase transitions come about? While the answer to this question would require predictions of the future, looking back at the history of evolution implies that transitions are likely to occur in the future. Furthermore, it is likely that small changes have been accruing in many species which, depending on the environmental conditions and the interactions among the species, should eventually lead to transitions.
(4) What is the expected impact of a new transition, biological or other, on human society? It is evident that even over the short time period of human evolution, various new networks have emerged and transitions occurred. A recent and perhaps most revolutionizing network in terms of human experience is the internet. As the complexity of the internet increases, is it possible to live through a phase transition such that the internet acquires some form of intelligence or consciousness, a possibility already raised by Barabási (2002)? Also, consciousness is certainly an emergent phenomenon arising from the neural network connectivity of the brain. Could the human species undergo yet another phase transition?
(5) If a transition is likely, then what would the character of this transition be. It is of course impossible to accurately predict a new transition. The approach to a transition may take a long period. While a transition itself might seem rapid or even instantaneous in terms of evolutionary time, it may be comparable to the human life expectancy. In that case, can we develop means to anticipate a coming transition? Should we consider the direction of Craig Venter’s newly synthesized self-replicating biological system (Gibson et al., 2010) as a sign of a coming new transition? Will research in artificial intelligence lead to an unexpected phase transition?
(6) Evolutionary changes sometimes occur via symbiosis, a crash of two complex networks. If following the crash, new links form between the two networks such that the flow of information and/or material between them provides selective advantages, a new organism with unexpected potentials emerges. A salient example is the symbiotic development of the eukaryotic cell by the fusion of different bacteria. Since eventually the eukaryotic cells were able to spread through the world, we might wonder whether fusion of computers with humans or symbiosis of robotics, genetics and artificial intelligence can lead to the emergence of a new self-replicating species capable of evolution and spreading through the Earth and perhaps even replacing humanity.
(7) A transition does not have to represent a better function. For example, although death itself is necessary for evolution to work, at the level of an individual, it is an undesirable transition. More generally, at the level of human societies, a peaceful society may turn into an aggressive despotic system. Such malfunction at a node in the network of human societies, might lead to a local war. If the society in question is in fact a hub of the network, the war, like a virus, might rapidly percolate through the underlying network with the risk of an eventual world war. Thus, we might want to be able to interfere with a transition and depending on the actual condition and expected behavior, we may try to avoid or accelerate the transition. While certain networks can be controlled (Liu et al., 2011), the question is whether we can develop general tools based on the properties of networks to detect and influence the course of transitions. Could the knowledge of network properties and transitions be utilized in political decisions to avoid major catastrophes endangering humanity, the Earth’s ecology and potentially all life?
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This work was supported by NIH HL-098976. The author acknowledges Dr. Erzsébet Bartolák-Suki and Dr. Nuria Martinez for providing help with several figures and Dr. Matthew Nugent for helpful suggestions.
Albert, R., and Barabasi, A. L. (2002). Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97.
Albert, R., Jeong, H., and Barabasi, A. L. (2000). Error and attack tolerance of complex networks. Nature 406, 378–382.
Andras, P., and Andras, C. (2005). The origins of life – the ‘protein interaction world’ hypothesis: protein interactions were the first form of self-reproducing life and nucleic acids evolved later as memory molecules. Med. Hypotheses 64, 678–688.
Aon, M. A., and Cortassa, S. (2002). Coherent and robust modulation of a metabolic network by cytoskeletal organization and dynamics. Biophys. Chem. 97, 213–231.
Aon, M. A., Cortassa, S., and O’Rourke, B. (2004). Percolation and criticality in a mitochondrial network. Proc. Natl. Acad. Sci. U.S.A. 101, 4447–4452.
Arold, S. P., Bartolak-Suki, E., and Suki, B. (2009). Variable stretch pattern enhances surfactant secretion in alveolar type II cells in culture. Am. J. Physiol. Lung Cell Mol. Physiol. 296, L574–581.
Badii, R., and Politi, A. (1997). Complexity: Hierarchical Structures and Scaling in Physics. Cambridge: Cambridge University Press.
Barabasi, A. L., and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–512.
Barabasi, A. L., Buldyrev, S. V., Stanley, H. E., and Suki, B. (1996). Avalanches in the lung: a statistical mechanical model. Phys. Rev. Lett. 76, 2192–2195.
Bates, J. H., Davis, G. S., Majumdar, A., Butnor, K. J., and Suki, B. (2007). Linking parenchymal disease progression to changes in lung mechanical function by percolation. Am. J. Respir. Crit. Care Med. 176, 617–623.
Black, L. D., Allen, P. G., Morris, S. M., Stone, P. J., and Suki, B. (2008). Mechanical and failure properties of extracellular matrix sheets as a function of structural protein composition. Biophys. J. 94, 1916–1929.
Botros, S. M., and Bruce, E. N. (1990). Neural network implementation of a three-phase model of respiratory rhythm generation. Biol. Cybern. 63, 143–153.
Bretschneider, T., Jonkman, J., Kohler, J., Medalia, O., Barisic, K., Weber, I., Stelzer, E. H., Baumeister, W., and Gerisch, G. (2002). Dynamic organization of the actin system in the motile cells of Dictyostelium. J. Muscle Res. Cell. Motil. 23, 639–649.
Buldyrev, S. V. (2009). “Fractals in biology,” in Encyclopedia of Complexity and Systems Science, ed. R. A. Meyers (New York: Springer), 3779–3802.
Buldyrev, S. V., Parshani, R., Paul, G., Stanley, H. E., and Havlin, S. (2010). Catastrophic cascade of failures in interdependent networks. Nature 464, 1025–1028.
Calcott, B., Sterelny, K., and Szathmáry, E. (2011). The Major Transitions in Evolution Revisited. Cambridge, MA: MIT Press.
Cassimeris, L., Pryer, N. K., and Salmon, E. D. (1988). Real-time observations of microtubule dynamic instability in living cells. J. Cell Biol. 107, 2223–2231.
Cech, T. R. (1986). A model for the RNA-catalyzed replication of RNA. Proc. Natl. Acad. Sci. U.S.A. 83, 4360–4363.
Coniglio, A., De Candia, A., Di Talia, S., and Gamba, A. (2004). Percolation and Burgers’ dynamics in a model of capillary formation. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 69, 051910.
Crutchfield, J. P., and Young, K. (1989). Inferring statistical complexity. Phys. Rev. Lett. 63, 105–108.
Dahl, K. N., Ribeiro, A. J., and Lammerding, J. (2008). Nuclear shape, mechanics, and mechanotransduction. Circ. Res. 102, 1307–1318.
de Menezes, M. A., and Barabasi, A. L. (2004). Fluctuations in network dynamics. Phys. Rev. Lett. 92, 028701.
Doudna, J. A., Couture, S., and Szostak, J. W. (1991). A multisubunit ribozyme that is a catalyst of and template for complementary strand RNA synthesis. Science 251, 1605–1608.
Doudna, J. A., and Szostak, J. W. (1989). RNA-catalysed synthesis of complementary-strand RNA. Nature 339, 519–522.
Eigen, M., Gardiner, W., Schuster, P., and Winkler-Oswatitsch, R. (1981). The origin of genetic information. Sci. Am. 244, 88–92, 96, et passim.
Erdös, P., and Rényi, A. (1960). On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 5, 17–61.
Ferreira, C. P., and Fontanari, J. F. (2002). Nonequilibrium phase transitions in a model for the origin of life. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 65, 021902.
Finer, J. T., Simmons, R. M., and Spudich, J. A. (1994). Single myosin molecule mechanics: piconewton forces and nanometre steps. Nature 368, 113–119.
Forgacs, G. (1995). On the possible role of cytoskeletal filamentous networks in intracellular signaling: an approach based on percolation. J. Cell. Sci. 108(Pt 6), 2131–2143.
Frankel, S., and Mooseker, M. S. (1996). The actin-related proteins. Curr. Opin. Cell Biol. 8, 30–37.
Gibson, D. G., Glass, J. I., Lartigue, C., Noskov, V. N., Chuang, R. Y., Algire, M. A., Benders, G. A., Montague, M. G., Ma, L., Moodie, M. M., Merryman, C., Vashee, S., Krishnakumar, R., Assad-Garcia, N., Andrews-Pfannkoch, C., Denisova, E. A., Young, L., Qi, Z. Q., Segall-Shapiro, T. H., Calvey, C. H., Parmar, P. P., Hutchison, C. A. III, Smith, H. O., and Venter, J. C. (2010). Creation of a bacterial cell controlled by a chemically synthesized genome. Science 329, 52–56.
Gross, J., and Bhattacharya, D. (2010). Uniting sex and eukaryote origins in an emerging oxygenic world. Biol. Direct 5, 53.
Hamm-Alvarez, S. F., and Sheetz, M. P. (1998). Microtubule-dependent vesicle transport: modulation of channel and transporter activity in liver and kidney. Physiol. Rev. 78, 1109–1129.
Hanel, R., Kauffman, S. A., and Thurner, S. (2005). Phase transition in random catalytic networks. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 72, 036117.
He, Y., Chen, Z., Gong, G., and Evans, A. (2009). Neuronal networks in Alzheimer’s disease. Neuroscientist. 15, 333–350.
Hoffman, B. D., Grashoff, C., and Schwartz, M. A. (2011). Dynamic molecular processes mediate cellular mechanotransduction. Nature 475, 316–323.
Horwitz, B., and Braun, A. R. (2004). Brain network interactions in auditory, visual and linguistic processing. Brain Lang. 89, 377–384.
Hubel, D. H., and Wiesel, T. N. (2009). Republication of The Journal of Physiology (1959) 148, 574–591: receptive fields of single neurones in the cat’s striate cortex. 1959. J. Physiol. 587, 2721–2732.
Humphries, M. D., Gurney, K., and Prescott, T. J. (2006). The brainstem reticular formation is a small-world, not scale-free, network. Proc. Biol. Sci. 273, 503–511.
Ingber, D. E. (2006). Cellular mechanotransduction: putting all the pieces together again. FASEB J. 20, 811–827.
Ito, S., Suki, B., Kume, H., Numaguchi, Y., Ishii, M., Iwaki, M., Kondo, M., Naruse, K., Hasegawa, Y., and Sokabe, M. (2010). Actin cytoskeleton regulates stretch-activated Ca2+ influx in human pulmonary microvascular endothelial cells. Am. J. Respir. Cell Mol. Biol. 43, 26–34.
Johnston, W. K., Unrau, P. J., Lawrence, M. S., Glasner, M. E., and Bartel, D. P. (2001). RNA-catalyzed RNA polymerization: accurate and general RNA-templated primer extension. Science 292, 1319–1325.
Kauffman, S. A. (1995). At Home in the Universe: The Search for Laws of Self-Organization and Complexity. New York: Oxford University Press.
Klimek, P., Thurner, S., and Hanel, R. (2009). Pruning the tree of life: k-core percolation as selection mechanism. J. Theor. Biol. 256, 142–146.
Klipp, E., Liebermeister, W., and Wierling, C. (2004). Inferring dynamic properties of biochemical reaction networks from structural knowledge. Genome Inform. 15, 125–137.
Lane, N. (2005). Power, Sex, Suicide: Mitochondria and the Meaning of Life. Oxford: Oxford University Press.
Lee, D. H., Granja, J. R., Martinez, J. A., Severin, K., and Ghadri, M. R. (1996). A self-replicating peptide. Nature 382, 525–528.
Li, Y., Liu, Y., Li, J., Qin, W., Li, K., Yu, C., and Jiang, T. (2009). Brain anatomical network and intelligence. PLoS Comput. Biol. 5, e1000395. doi:10.1371/journal.pcbi.1000395
Liu, Y. Y., Slotine, J. J., and Barabasi, A. L. (2011). Controllability of complex networks. Nature 473, 167–173.
Liu, Z., Lai, Y. C., and Ye, N. (2002). Statistical properties and attack tolerance of growing networks with algebraic preferential attachment. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 66, 036112.
Macklem, P. T., and Seely, A. (2010). Towards a definition of life. Perspect. Biol. Med. 53, 330–340.
Martinac, B., and Kloda, A. (2003). Evolutionary origins of mechanosensitive ion channels. Prog. Biophys. Mol. Biol. 82, 11–24.
Martyushev, L. M., and Seleznev, V. D. (2006). Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 426, 1–45.
Maynard Smith, J., and Szathmáry, E. (1995). The Major Transitions in Evolution. Oxford: W.H. Freeman/Spektrum.
Maynard Smith, J., and Szathmáry, E. (1999). The Origins of Life: From the Birth of Life to the Origin of Language. Oxford: Oxford University Press.
McCullagh, C. M., Jamieson, A. M., Blackwell, J., and Gupta, R. (1995). Viscoelastic properties of human tracheobronchial mucin in aqueous solution. Biopolymers 35, 149–159.
Meyers, L. A., Newman, M. E., and Pourbohloul, B. (2006). Predicting epidemics on directed contact networks. J. Theor. Biol. 240, 400–418.
Nicolis, G., and Prigogine, I. (1989). Exploring Complexity: An Introduction. New York: W.H. Freeman.
Nowak, M. A., and Ohtsuki, H. (2008). Prevolutionary dynamics and the origin of evolution. Proc. Natl. Acad. Sci. U.S.A. 105, 14924–14927.
Palla, G., Barabasi, A. L., and Vicsek, T. (2007). Quantifying social group evolution. Nature 446, 664–667.
Palla, G., Derenyi, I., Farkas, I., and Vicsek, T. (2004). Statistical mechanics of topological phase transitions in networks. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 69, 046117.
Paperin, G., Green, D. G., and Sadedin, S. (2011). Dual-phase evolution in complex adaptive systems. J. R. Soc. Interface 8, 609–629.
Pelletier, O., Pokidysheva, E., Hirst, L. S., Bouxsein, N., Li, Y., and Safinya, C. R. (2003). Structure of actin cross-linked with alpha-actinin: a network of bundles. Phys. Rev. Lett. 91, 148102.
Prigogine, I. (1997). The End of Certainty: Time, Chaos, and the New Laws of Nature. New York: Free Press.
Ricard, J. (2010). Systems biology and the origins of life? Part I. Are biochemical networks possible ancestors of living systems? Reproduction, identity and sensitivity to signals of biochemical networks. C. R. Biol 333, 761–768.
Santos, M., Zintzaras, E., and Szathmary, E. (2003). Origin of sex revisited. Orig. Life Evol. Biosph. 33, 405–432.
Seely, A., and Macklem, P. T. (2012). Fractal variability: an emergent property of complex dissipative systems. Chaos 22, 013108.
Silveira, P. S. P., Alencar, A. M., Majumdar, A., Lemos, M., Fredberg, J. J., and Suki, B. (2009). Percolation in a network with long-range connections: implications for cytoskeletal structure and function. Physica A 388, 1521–1526.
Silver, F. H., and Siperko, L. M. (2003). Mechanosensing and mechanochemical transduction: how is mechanical energy sensed and converted into chemical energy in an extracellular matrix? Crit. Rev. Biomed. Eng. 31, 255–331.
Sporns, O., Honey, C. J., and Kotter, R. (2007). Identification and classification of hubs in brain networks. PLoS ONE 2, e1049. doi:10.1371/journal.pone.0001049
Srahna, M., Leyssen, M., Choi, C. M., Fradkin, L. G., Noordermeer, J. N., and Hassan, B. A. (2006). A signaling network for patterning of neuronal connectivity in the Drosophila brain. PLoS Biol. 4, e348. doi:10.1371/journal.pbio.0040348
Srivastava, S. K., Tonomura, Y., and Inoue, A. (1979). Modification of cardiac and smooth muscle myosins with 2,4,6-trinitrobenzenesulfonate. Evidence for differences in structure around the active sites of cardiac, smooth, and skeletal muscle myosin ATPase. J. Biochem. 86, 725–731.
Suki, B. (2002). Fluctuations and power laws in pulmonary physiology. Am. J. Respir. Crit. Care Med. 166, 133–137.
Suki, B., Bates, J. H., and Frey, U. (2011). “Complexity and emergent phenomena,” in Comprehensive Physiology, the Respiratory System, Respiration Mechanics: Organ, Cell, Molecule, eds J. J. Fredberg, G. C. Sieck, and W. T. Gerthoffer (Wiley-Blackwell), 995–1029.
Suki, B., Ito, S., Stamenovic, D., Lutchen, K. R., and Ingenito, E. P. (2005). Biomechanics of the lung parenchyma: critical roles of collagen and mechanical forces. J. Appl. Physiol. 98, 1892–1899.
Suki, B., Majumdar, A., Nugent, M. A., and Bates, J. H. (2007). In silico modeling of interstitial lung mechanics: implications for disease development and repair. Drug Discov. Today Dis. Models 4, 139–145.
Szalay, M. S., Kovacs, I. A., Korcsmaros, T., Bode, C., and Csermely, P. (2007). Stress-induced rearrangements of cellular networks: consequences for protection and drug design. FEBS Lett. 581, 3675–3680.
Tirard, S., Morange, M., and Lazcano, A. (2010). The definition of life: a brief history of an elusive scientific endeavor. Astrobiology 10, 1003–1009.
Trifonov, E. N. (2011). Vocabulary of definitions of life suggests a definition. J. Biomol. Struct. Dyn. 29, 259–266.
Tseng, S., Kim, R., Kim, T., Morgan, K. G., and Hai, C. M. (1997). F-actin disruption attenuates agonist-induced [Ca2+], myosin phosphorylation, and force in smooth muscle. Am. J. Physiol. 272, C1960–C1967.
Unrean, P., and Srienc, F. (2011). Metabolic networks evolve towards states of maximum entropy production. Metab. Eng. 13, 666–673.
von Neumann, J. (1961–63). The General and Logical Theory of Automata. Lecture Given in 1948. New York: Macmillan.
Wagner, W. W. Jr., Todoran, T. M., Tanabe, N., Wagner, T. M., Tanner, J. A., Glenny, R. W., and Presson, R. G. Jr. (1999). Pulmonary capillary perfusion: intra-alveolar fractal patterns and interalveolar independence. J. Appl. Physiol. 86, 825–831.
Watts, D. J., and Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature 393, 440–442.
Weber, B. H. (2010). What is life? Defining life in the context of emergent complexity. Orig. Life Evol. Biosph. 40, 221–229.
Yook, S. H., Oltvai, Z. N., and Barabasi, A. L. (2004). Functional and topological characterization of protein interaction networks. Proteomics 4, 928–942.
Keywords: phase transition, emergence, origin of life, genetic apparatus, eukaryotic cell, mechanotransduction, brain
Citation: Suki B (2012) The major transitions of life from a network perspective. Front. Physio. 3:94. doi: 10.3389/fphys.2012.00094
Received: 15 February 2012; Accepted: 26 March 2012;
Published online: 10 April 2012.
Edited by:
Zbigniew R. Struzik, The University of Tokyo, JapanReviewed by:
Andrew J. E. Seely, University of Ottawa, CanadaCopyright: © 2012 Suki. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Béla Suki, Department of Biomedical Engineering, Boston University, 44 Cummington Street, Boston, MA, USA. e-mail:YnN1a2lAYnUuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.