Increased non-Gaussianity of heart rate variability predicts cardiac mortality after an acute myocardial infarction

Non-Gaussianity index (λ) is a new index of heart rate variability (HRV) that characterizes increased probability of the large heart rate deviations from its trend. A previous study has reported that increased λ is an independent mortality predictor among patients with chronic heart failure. The present study examined predictive value of λ in patients after acute myocardial infarction (AMI). Among 670 post-AMI patients, we performed 24-h Holter monitoring to assess λ and other HRV predictors, including SD of normal-to-normal interval, very-low frequency power, scaling exponent α₁ of detrended fluctuation analysis, deceleration capacity, and heart rate turbulence (HRT). At baseline, λ was not correlated substantially with other HRV indices (|r| < 0.4 with either indices) and was decreased in patients taking β-blockers (P = 0.04). During a median follow-up period of 25 months, 45 (6.7%) patients died (32 cardiac and 13 non-cardiac) and 39 recurrent non-fatal AMI occurred among survivors. While all of these HRV indices but λ were significant predictors of both cardiac and non-cardiac deaths, increased λ predicted exclusively cardiac death (RR [95% CI], 1.6 [1.3–2.0] per 1 SD increment, P < 0.0001). The predictive power of increased λ was significant even after adjustments for clinical risk factors, such as age, diabetes, left ventricular function, renal function, prior AMI, heart failure, and stroke, Killip class, and treatment ([95% CI], 1.4 [1.1–2.0] per 1 SD increment, P = 0.01). The prognostic power of increased λfor cardiac death was also independent of all other HRV indices and the combination of increased λ and abnormal HRT provided the best predictive model for cardiac death. Neither λ nor other HRV indices was an independent predictor of AMI recurrence. Among post-AMI patients, increased λ is associated exclusively with increased cardiac mortality risk and its predictive power is independent of clinical risk factors and of other HRV predictors.

Introduction

Experimental models for sudden cardiac death after myocardial infarction (AMI) indicate that sympathetic stimulation under impaired reflex vagal antagonism provokes ventricular vulnerability to fibrillation during transient myocardial ischemia (Schwartz et al., 1984; Vanoli et al., 1991). Usefulness of the detection of autonomic dysfunction by heart rate variability (HRV) has been proposed for post-AMI risk stratification (Kleiger et al., 1987; La Rovere et al., 1998; Schmidt et al., 1999; Bauer et al., 2006). Most of HRV indices proposed, however, primarily reflect reduced or impaired vagal function (Camm et al., 1996; Marine et al., 2002; Bauer et al., 2006). In contrast, few HRV indices have been related to sympathetic function and their prognostic significance is still uncertain. For example, a decrease in low-frequency-to-high-frequency ratio, but not its increase, is associated with increased risk of mortality (Tsuji et al., 1994; Huikuri et al., 2000).

As a marker potentially related to sympathetic cardiac overdrive, we have recently proposed increased non-Gaussianity of HRV (Kiyono et al., 2008). Non-Gaussianity has been used in fluid dynamics for characterizing intermittency of turbulence (Castaing et al., 1990). When applied to analysis of HRV, it captures the occurrence of intermittent heart rate increments (Kiyono et al., 2004, 2007). In a cohort of chronic heart failure (Kiyono et al., 2008),we previously observed that the increased non-Gaussianity of HRV predicts increased risk of mortality, while none of the conventional HRV indices were predictive of death among these patients. In the present study, we sought to determine if increased non-Gaussianity of HRV in post-AMI patients is also associated with their increased mortality risk independent of clinical risk factors and of the established HRV predictors.

Materials and Methods

Study Patients

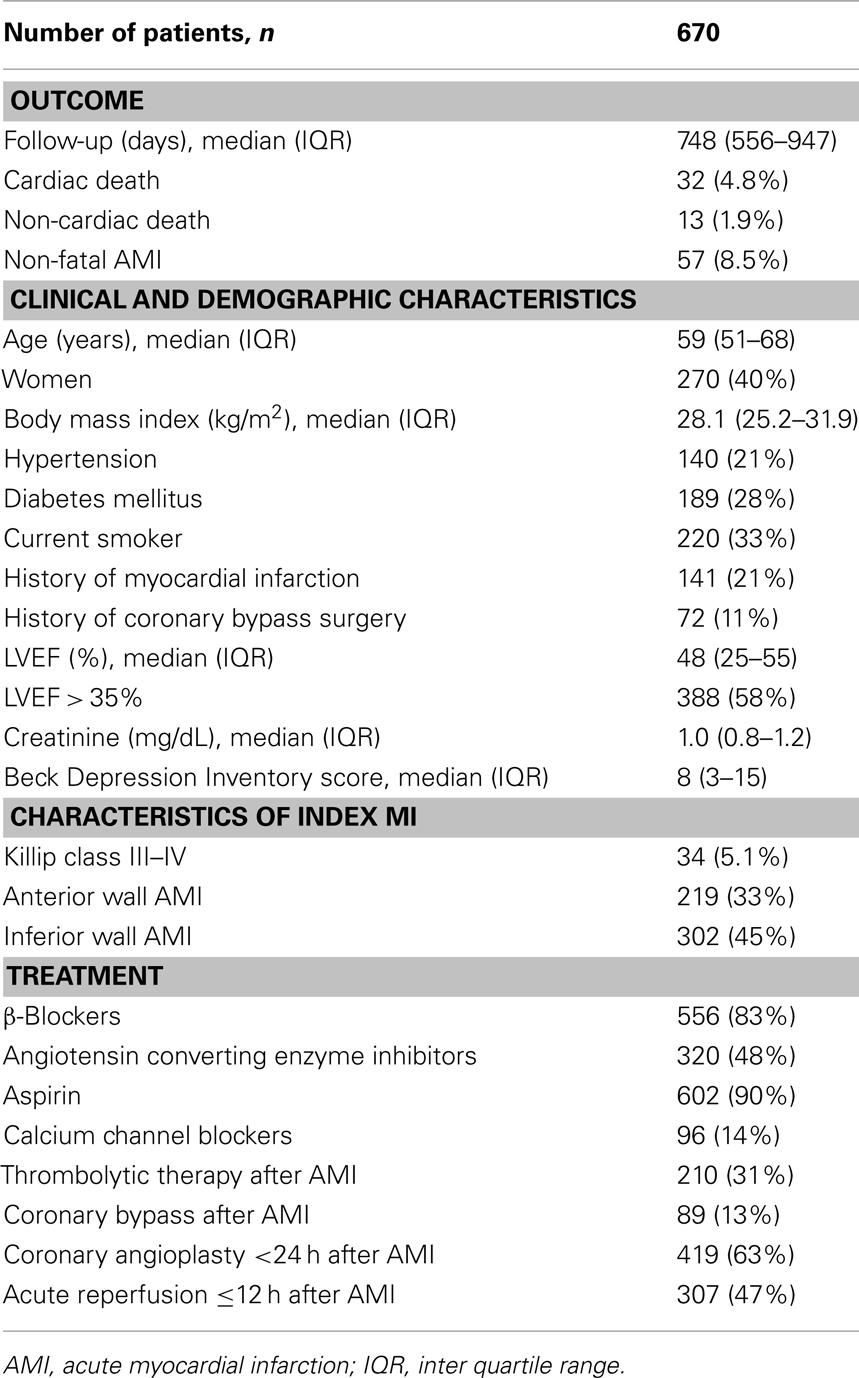
Patients admitted to the coronary care units of four of the eight clinical trial sites (Washington University, St. Louis, MO, USA; Duke University, Durham, NC, USA; Harvard University, Boston, MA, USA; Yale University, New Haven, CT, USA) of the enhancing recovery in coronary heart disease (ENRICHD) study (Berkman et al., 2003) for an attack of AMI between October 1997 and January 2000 were enrolled in this substudy. AMI was diagnosed if a patient had at least 2 of the following findings: chest pain for ≥20 min, creatine kinase >200 U/L, and ST-segment elevation of ≥0.1 mV in two or more limb leads or ≥0.2 mV in two or more contiguous precordial leads at the time of admission. The sample included 358 participants of the ENRICHD clinical trial who scored 10 or higher on the Beck Depression Inventory (BDI; Steeds et al., 2004) and 408 AMI control participants who were not randomized in the ENRICHD trial because they were not depressed (BDI < 10), but were otherwise medically eligible for the trial. Patients were excluded if they: (1) had other life-threatening illnesses; (2) were too ill or logistically unable to participate; (3) had analyzable electrocardiographic data <22 h or sinus rhythm <80% of total recorded beats in Holter monitoring; (4) had atrial fibrillation, atrial flutter, or animplanted pacemaker or defibrillator; or (5) declined to provide informed written consent.

Measurements

Holter electrocardiograms were recorded for 24 h within 28 (median [inter quartile range, IQR], 13 [6–19]) days after the index AMI. To assure standardization of the Holter recordings, we used Marquette Model 8500 monitors at each site. Holter recordings were scanned at the Heart Rate Variability Core laboratory at Washington University on a Marquette SXP Laser scanner with software version 5.8 (Marquette Electronics) using standard procedures. The labeled beat file was exported to a personal computer and a workstation for analysis of non-Gaussianity and other HRV indices.

Analysis of Non-Gaussianity Index

This analysis is designed to detect intermittency of heart rate increment. The intermittent behavior of HRV is related to non-Gaussian probability distribution with marked fat tails and a peak around the mean value, indicative of a higher probability of the interspersed appearance of large and small increments than the Gaussian fluctuations. To quantify such non-Gaussian behavior, we calculated a non-Gaussianity index. The background and a mathematical description of the non-Gaussianity index have been reported previously (Kiyono et al., 2004, 2007). Briefly, this index has been derived from a method for analyzing multi-scale statistics of complex fluctuations, originally used for characterizing intermittency of hydrodynamic turbulence (alternating transition of a fluid regime between laminar flow and its breakdown into bursty disorganized eddies, occurring in a seemingly random manner at a variety of scales; Castaing et al., 1990).

The analysis of non-Gaussianity of HRV is divided into four steps. In step 1, time series of normal-to-normal R–R intervals are interpolated with a cubic spline function and resampled at an interval (Δt) of 250 ms (4 Hz), yielding interpolated time series b(t) (Figure 1). After subtracting average interval b_ave, integrated time series B(t) are obtained by integrating b(t) over the entire length,

FIGURE 1

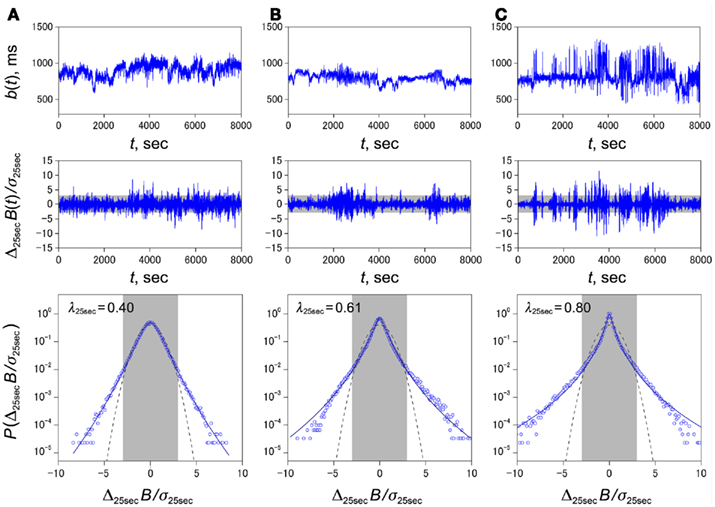
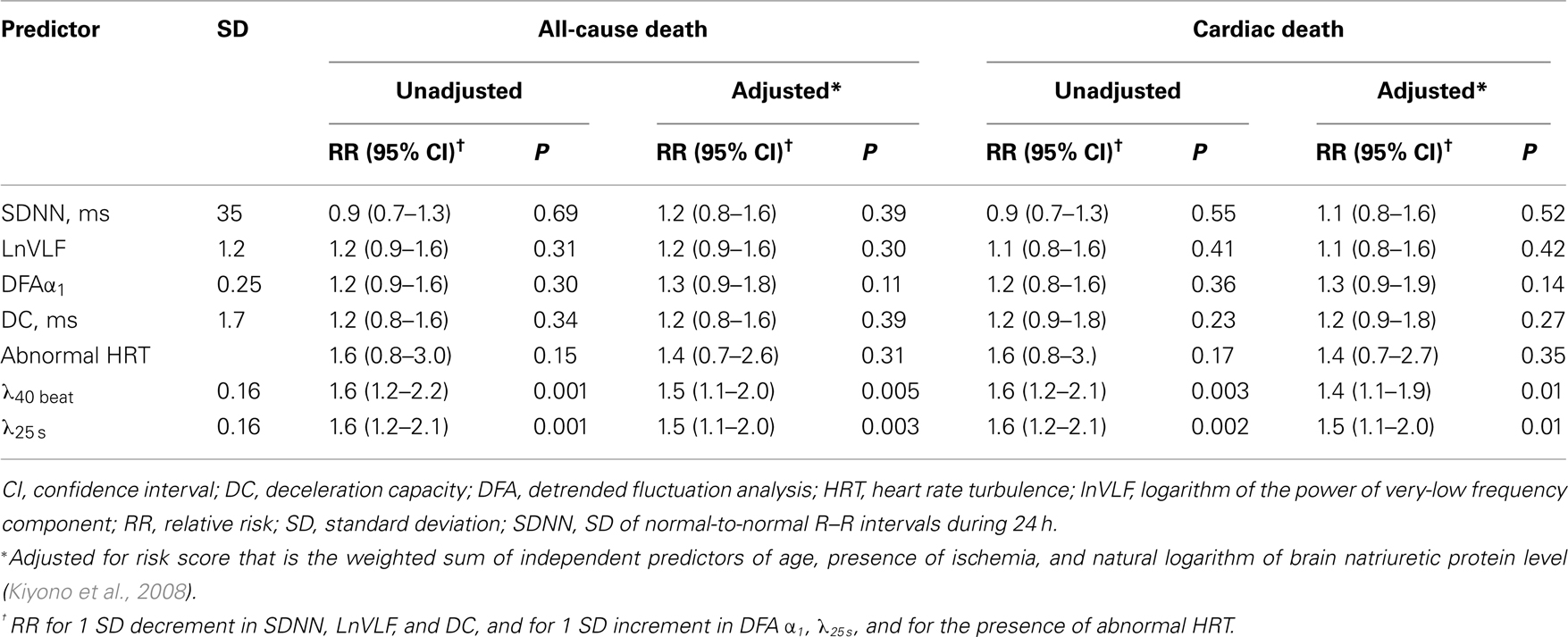
Figure 1. Representative examples of non-Gaussian heart rate fluctuations with different values of λ_{25 s} in post-AMI patients, survivor (A) and cardiac death (B, C). Trend graphs of normal-to-normal sinus rhythm interval (Top row), standardized time series of heart rate increments {Δ_{25 s}B(t)} (middle row), and standardized PDFs of heart rate increments {Δ_{25 s}B(t)} (bottom row). Estimated values of the non-Gaussianity index of λ_{25 s} are shown in each panel in the bottom row. In the solidline, we superimposed the PDF approximated by a non-Gaussian model (Kiyono et al., 2007) with the parameter λ_{25 s}. The non-Gaussian model provides an excellent approximation of the peaked PDF around center (particularly in the gray shaded area covering ±3 SD) of the observed distribution, caused mainly by intermittent alterations of quiet (laminar) phase and busty phase (middle row), because our non-Gaussianity index with q = 0.25 characterizes peaked shape of the observed non-Gaussian distribution and reduces the effects of extreme outliers, if any. The dashed lines represent the Gaussian distribution (λ_{25 s} → 0).

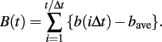
In step 2, the local trend of {B(t)} is eliminated by third-order polynomial that is fit to {B(t)} within moving windows of length 2s, where s is the scale of analysis. In step 3, intermittent deviation Δ_sB(t) is measured as the increment with a time lag s of the detrended time series {B^*(t)}. For instance, in a window from T − s to T + s, the increments are calculated as

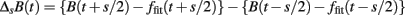
where T − s/2 ≤ t < T + s/2 and f_fit(t) is the polynomial representing the local trend of B(t), of which the elimination assures the zero-mean probability density function in the next step. In step 4, Δ_sB is normalized by the SD to quantify the probability density function (PDF). Then, the non-Gaussianity index λ_s is estimated as

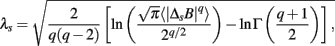
where <|Δ_sB|^q> denotes an estimated value of the q-th order absolute moment of {Δ_sB}. If the λ_s is close to zero, the observed PDF is close to a Gaussian distribution. On the other hand, a larger value of λ_s means that the observed PDF has fatter tails and a sharper peak in comparison with the Gaussian distribution. This λ_s was originally introduced as a parameter of a phenomenological model to describe non-Gaussian distributions in the study of intermittency of hydrodynamic turbulence (Castaing et al., 1990). Kiyono et al. (2007) further showed that the λ_s can be estimated by the above equation based on the q-th order absolute moment of a time series independently of q.

In the present study, we calculated the λ_s based on the 0.25th order moment (q = 0.25) to emphasize the center part of PDF and to reduce the effects of large outliers such as those by ectopic beats, if any, even after the correction. This implies that our non-Gaussianity index with q = 0.25 more strongly characterize speaked PDF around the center of the observed non-Gaussian distribution, differently from that with higher order moments, such as kurtosis based on the fourth moment, emphasizing heavy tails, and extreme deviations. Also, we previously showed that the accuracy of estimation of λ_s for typical Holter records (data points, n ≈ 10⁵) is much higher when using q < 2, as compared to q > 2 (see Figure 3 of Kiyono et al., 2007). The C source codes and executables for computing the non-Gaussianity index are available online at www.ge.ce.nihon-u.ac.jp/∼kiyono/app/.

In the present study, we set the scale s at 25 s. In a previous cohort study of chronic heart failure, we noted that λ_{40 beat} > 0.6 had the best predictive power for mortality (Kiyono et al., 2008). Because the λ_{40 beat} is based on beat scale, could be affected by both inter- and intra-individual differences in heart rate, we reanalyzed the previous data using time (s) as the unit of scale (see Appendix). Then, we found that λ_{25 s} was comparable to λ_{40 beat} in predictive power for mortality. We therefore used λ_{25 s} as the non-Gaussianity index and λ_{25 s} > 0.6 as the cutoff threshold in survival curve analyses.

Analysis of Conventional HRV Indices

We calculated the conventional indices of HRV that are recognized as post-AMI risk predictors by the Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology (Camm et al., 1996): mean N–N interval, SD of all N–N intervals (SDNN), the variances corresponding to ultra-low frequency (ULF; 0–0.0033 Hz), very-low frequency (VLF; 0.0033–0.04 Hz), low frequency (LF; 0.04–0.15 Hz) and high frequency (HF; 0.15–0.40 Hz) bands, and LF/HF. The variances of these frequency components were transformed in the natural logarithmic values (Ln). We examined the fractal correlation properties of heart rate dynamics using detrended fluctuation analysis (DFA) and calculated the short-term (4–11 beat) and long-term (≥11 beats) scaling exponents as α₁ and α₂, respectively (Peng et al., 1995). We also computed the deceleration and acceleration capacity (DC and AC) by the phase rectified signal averaging of the 24-h N–N interval time series (Bauer et al., 2006). Finally, we assessed indices of heart rate turbulence (HRT; Schmidt et al., 1999). In accordance with previous reports (Barthel et al., 2003; Bauer et al., 2009), we defined abnormal turbulence onset (TO) as ≥0%, abnormal turbulence slope (TS) as ≤2.5 ms/beat and abnormal HRT as an instance when both TO and TS were abnormal. If ventricular premature contractions suitable for calculating HRT were five or less in the 24-h recording, the patients were classified as having normal HRT.

Endpoint Analysis

The end points of the present study were all-cause mortality and recurrent non-fatal AMI. Patients underwent follow-up assessments 6 months after study enrollment and annually thereafter for up to 30 months. The end points were identified from follow-up visits, telephone calls, routine hospital surveillance, and contacts with patients’ physicians. The records of every identified hospitalization were obtained for review and confirmation. The ENRICHD ECG core laboratory classified electrocardiograms obtained during hospitalizations by the Minnesota code using serial change rules. Death certificates were obtained for all reported deaths. The mortality endpoints used for the present study were either cardiac deaths (AMI, cardiac failure, and sudden cardiac death) or non-cardiac deaths. Sudden cardiac death was defined as unexpected death within 1 h after the onset of a new symptom, or unexpected unwatched death.

Statistical Analysis

Cox proportional hazards regression analyses were used for determining the significant predictors of mortality and recurrent non-fatal AMI. The independent associations of predictors were evaluated with the multivariable hazards regression analysis adjusted for the ENRICHD risk score, which is a weighted sum of all independent risk factors for mortality in the ENRICHD trial (Jaffe et al., 2006). Potential risk factors that were considered included factors such as smoking, and medications, including beta blockers. The final risk score included age, diabetes, left ventricular ejection fraction, creatinine level, prior AMI, history of pulmonary disease, prior transient ischemic attack or stroke, history of congestive heart failure, Killip class at time of index AMI, and treatment with vasodilators. The predictors of mortality were determined in the entire subjects, while those of recurrent non-fatal AMI were determined within survivors. The survival curves were estimated by the Kaplan–Meier method and compared using the Mantel–Haenszel log-rank test.

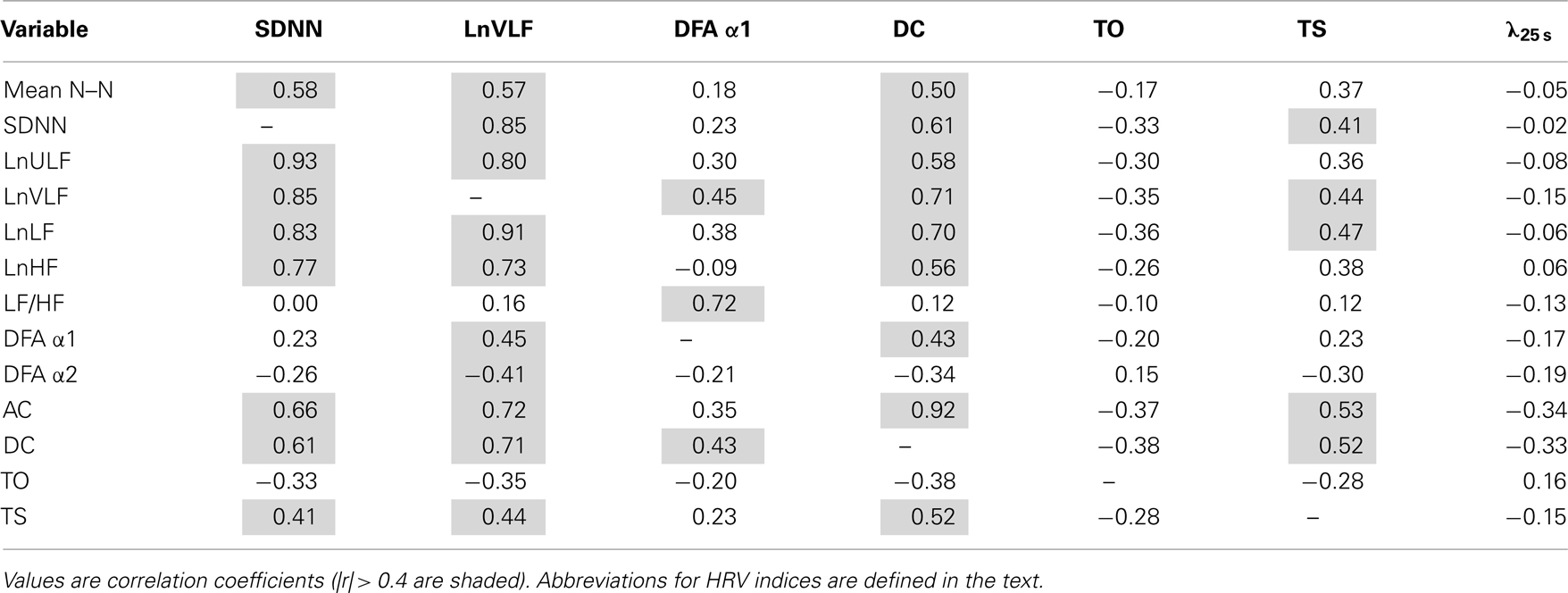
The data are reported as the median and IQR for continuous variables and counts and percentage for categorical variables unless otherwise noted. Comparisons between groups were performed by Chi-square test for categorical variables and one-way analysis of variance for continuous variables with Tukey’s Studentized range test for multiple comparisons. Pearson’s correlation coefficient (r) was used to evaluate correlations between different variables and an |r | ≥ 0.4 was interpreted to show a substantial correlation. We judged a P value of less than 0.05 to be significant.

Results

Holter electrocardiograms were analyzable in 670 out of 766 eligible patients (88%). The 96 excluded patients were medically and demographically similar to those included, except that they were more likely to have diabetes and less likely to be currently smoking. Table 1 shows the clinical characteristics of the 670 patients. β-Blockers were prescribed at the Holter monitoring in 556 patients (83%).

TABLE 1

Table 1. Characteristics of patients.

HRV and Non-Gaussianity Indices

The HRV indices that are considered as relating to cardiac vagal function were highly correlated with each other, while the non-Gaussianity index of λ_{25 s} showed no substantial correlations with these indices (Table 2). Also, λ_{25 s} correlated with neither the number of ventricular ectopies per 24 h (r = − 0.01) nor its products with TO or TS (r = 0.01, − 0.07), indicating that λ_{25 s} is unrelated to heart rate fluctuations accompanying ventricular arrhythmias (“HRT”). On the other hand, λ_{25 s} was lower in patients taking β blockers than in those not taking (mean [SD], 0.53 [0.12], and 0.56 [0.13], respectively, P = 0.04). No such effect on λ_{25 s} was observed for angiotensin converting enzyme inhibitors, aspirin, or calcium channel blockers.

TABLE 2

Table 2. Correlations among HRV indices, HRT, and λ_{25 s}.

Increased Non-Gaussianity and Prognosis

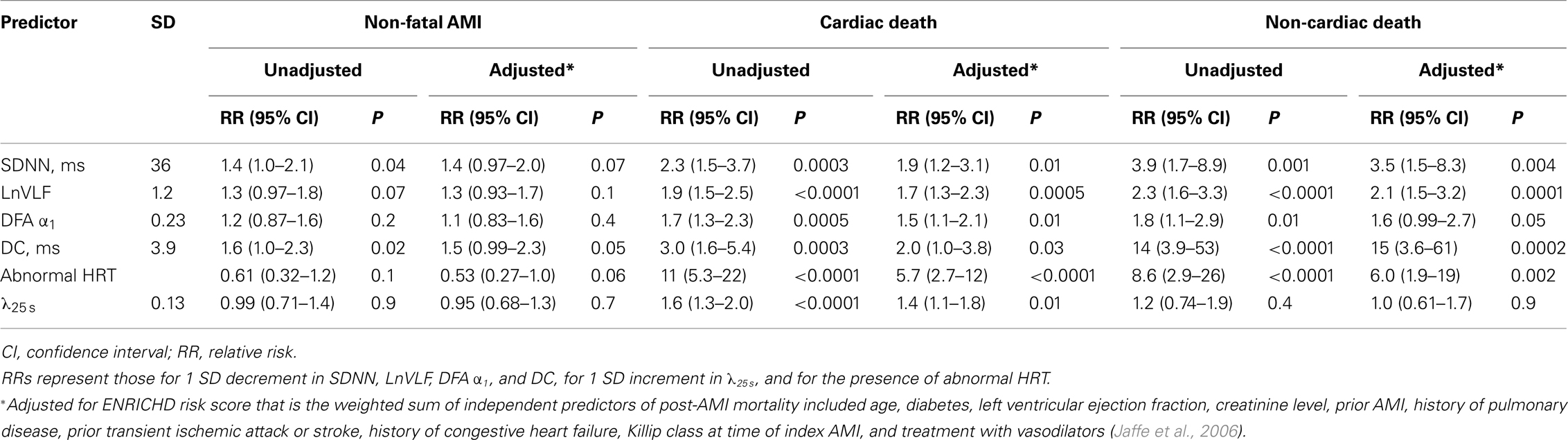
During follow-up for a median of 25 months, 45 (6.7%) patients died, with 32 deaths classified as cardiac and 13 as non-cardiac deaths, and 39(6.2%) patients among survivors had recurrent non-fatal AMI. On average, all HRV indices including λ_{25 s} and HRT category showed no significant difference between survivors with and without recurrent non-fatal AMI (Figure 2). SDNN, lnVLF, DFA α₁ and DC were lower and abnormal HRT was more prevalent in patients suffering both cardiac death and non-cardiac death compared to survivors, whereas λ_{25 s} was greater only in the cardiac death patients. The typical relationships between λ_{25 s} and other HRV indices are shown in Figure 3. The surviving patient (Figure 3A) showed large N–N interval variability, while both cardiac (Figure 3B) and non-cardiac (Figure 3C) death patients showed decreased variability. Figure 3D shows standardized PDFs of heart rate increment constructed from the same data. The surviving and non-cardiac death patients showed similar PDF curves and comparable λ_{25 s} (0.40 and 0.44, respectively) despite the large difference in absolute variability. In contrast, the cardiac death patient showed a PDF curve with a more tapered center and fatter tails with a λ_{25 s} of 0.80.

FIGURE 2

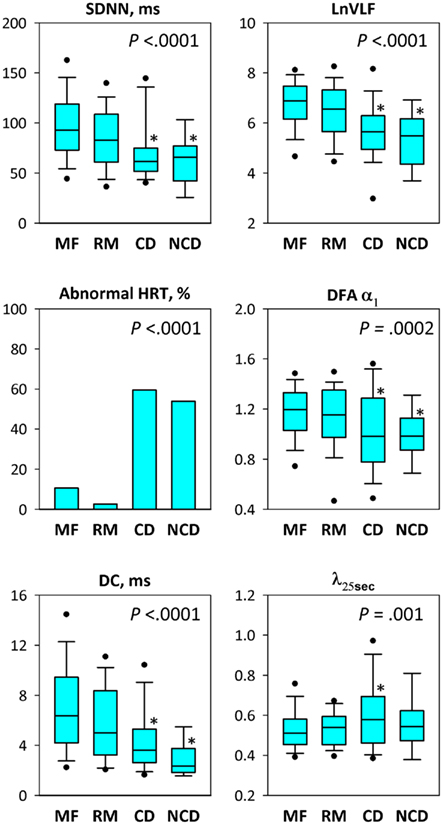
Figure 2. Heart rate variability indices, HRT, and non-Gaussianity index (λ_{25 s}) in post-AMI patients grouped by the endpoint of follow-up: MF, recurrent AMI-free survival; RM, recurrent non-fatal AMI; CD, cardiac death; and NCD, non-cardiac death. For box plots, upper and lower boundaries of the box indicate the 75th and 25th percentiles and a line within the box marks the median. Whiskers above and below the box indicate the 90th and 10th percentiles and dots above and below the whiskers indicate 95th and 5th percentiles. P values show significance of ANOVA except for abnormal HRT, for which bar graphs show percentage of patients who showed abnormal HRT and P value indicates the significance of chi-square test. *Significantly different from the value for recurrent AMI-free survivors (Tukey’s Studentized range test).

FIGURE 3

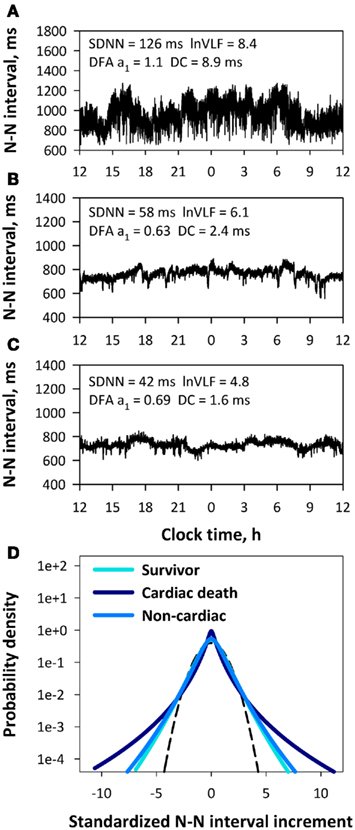
Figure 3. Trend graphs of 24-h N–N interval in three representative patients, recurrent AMI-free survivor (A), cardiac death (B) and non-cardiac death (C), and their standardized PDF of intermittent heart rate increments (D). Insets of panels (A–C) show values of HRV indices obtained from each N–N interval time series. In panel (D), the Gaussian distribution (λ_{25 s} = 0), an inverted parabola in this semi-log plot without “tapered” centers and “fat” tails, is shown as a dashed line. Abbreviations for HRV indices are defined in the text.

The unadjusted Cox hazards regression analysis revealed that decreases in SDNN and DC were increased risk of recurrent non-fatal AMI, while DFA α1, HRT, and λ_{25 s} had no predictive power for the recurrence (Table 3). All HRV indices but λ_{25 s} and abnormal HRT predicted increased risk of both cardiac and non-cardiac death, while increased λ_{25 s} predicted increased risk of only cardiac death but not of non-cardiac death. The associations of λ_{25 s} and other HRV indices with mortality risk remained significant even after adjustment for the ENRICHD risk score, while the associations of HRV indices with AMI recurrence were no longer significant (Table 3).

TABLE 3

Table 3. Unadjusted and adjusted mortality risk in post-AMI patients.

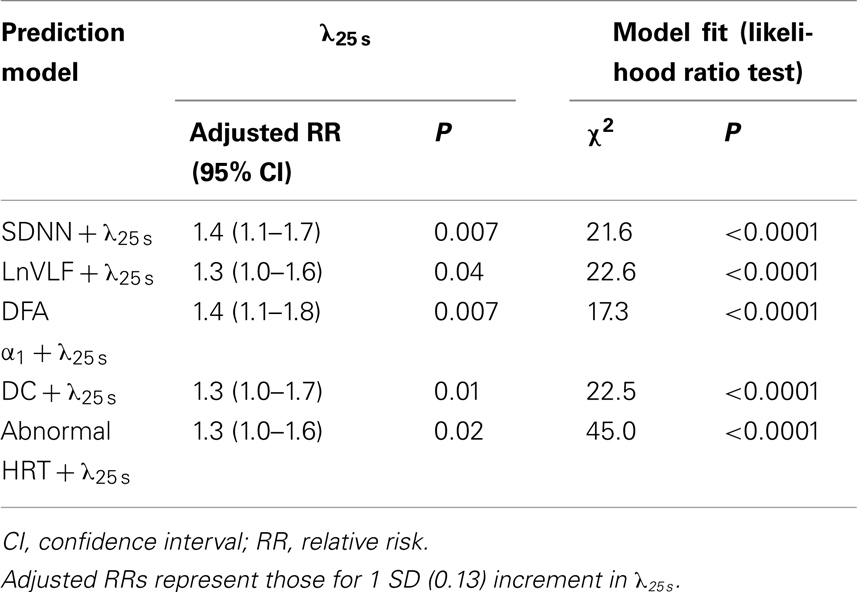
The predictive power of λ_{25 s} for cardiac death was independent of the other HRV indices. Increased λ_{25 s} was a significant predictor in the models including either HRV predictors (Table 4). Among these models, the risk of cardiac death was best predicted by the combination of increased λ_{25 s} and abnormal HRT (Table 4). We therefore generated Kaplan–Meier curves for this combination along with those for λ_{25 s} dichotomized at 0.6 (Figure 4). As expected, mortality was highest in the patients who had both increased λ_{25 s} and abnormal HRT. More importantly, however, mortality was low not only in patients who had neither of the two factors but also was low in those who had either one factor alone, suggesting that these factors acted synergistically.

TABLE 4

Table 4. Independent relative risk of λ_{25 s} for post-AMI cardiac mortality.

FIGURE 4

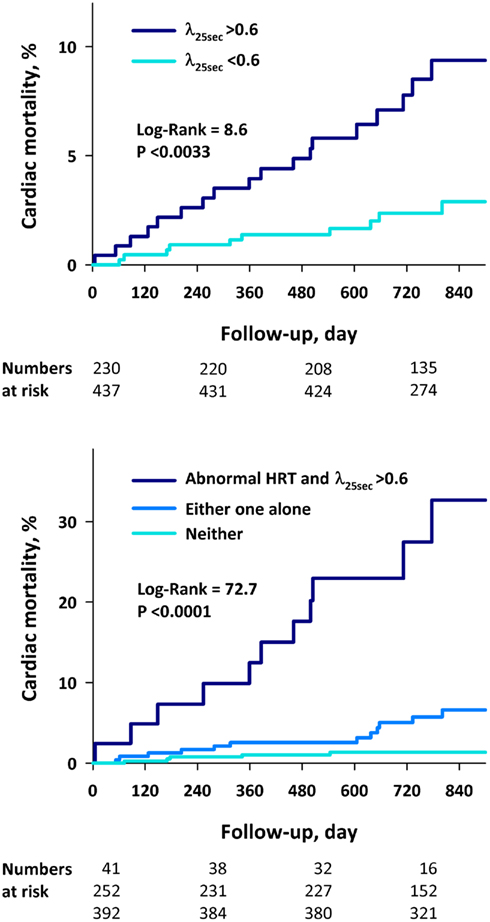
Figure 4. Kaplan–Meier curves for cardiac death after AMI. The patients were stratified by λ_{25 s} > 0.6 and by the combination of λ_{25 s} > 0.6 and abnormal HRT.

Discussion

We assessed non-Gaussianity of HRV in post-AMI patients and found that increased non-Gaussianity index of λ_{25 s} predicts risk of cardiac death in these patients. The λ_{25 s} showed no substantial correlation with HRV indices reflecting cardiac vagal functions and was decreased in patients taking β-blockers. While the other HRV indices were associated with both cardiac and non-cardiac deaths, the increased λ_{25 s} was associated exclusively with cardiac death but not with non-cardiac death. The predictive power of increased λ_{25 s} was independent of clinical risk factors and of the other HRV predictors. The survival curve analyses revealed that increased λ_{25 s} and abnormal HRT have a synergistic effect on the risk of cardiac mortality. Additionally, λ_{25 s} showed no predictive power for the recurrence of non-fatal AMI, suggesting that λ_{25 s} may not be associated with the mechanisms developing AMI itself.

The non-Gaussianity of heart rate has several unique features that had been undetected by conventional indices of HRV. First, λ_{25 s} is unrelated to the cardiac autonomic responsiveness reflected in the magnitude of HRV. As shown in Figure 3, surviving and non-cardiac death patients exhibited comparable λ_{25 s} despite a large difference in other HRV indices. Second, λ_{25 s} captures intermittent heart rate increments within a scale of 25 s. Although the heart rate fluctuations in this scale are mediated almost exclusively by neural autonomic activities (Camm et al., 1996), λ_{25 s} showed no substantial correlation with the HRV indices reflecting vagal heart rate regulation and was decreased in patients taking β blockers. Thus, λ_{25 s} is likely to capture heart rate fluctuation mediated by intermittent activations of cardiac sympathetic activity at least partly. Third, λ_{25 s} is independent of heart rate fluctuations caused by ectopic beats, i.e., HRT (Schmidt et al., 1999). Indeed, λ_{25 s} showed no significant correlation with the number of ventricular ectopies per 24 h or its products with TO or TS. Additionally, λ_{25 s} is also independent of erratic rhythms detected by Poincare plot (Woo et al., 1992; Stein et al., 2005), because beat-to-beat changes in N–N intervals are averaged out when calculating λ_{25 s} (Kiyono et al., 2008).

The present study indicates that the risk of mortality is particularly high in the presence of increased λ_{25 s} and abnormal HRT compared with the presence of only one alone. This synergistic effect between λ_{25 s} and HRT is compatible with a pathophysiologic paradigm for post-AMI sudden cardiac death; i.e., sympathetic stimulation under impaired reflex vagal antagonism precipitates ventricular fibrillation during transient myocardial ischemia in the heart with healed AMI (Schwartz et al., 1984; Vanoli et al., 1991). The increased λ_{25 s} appears to detect frequent sympathetic activations and the abnormal HRT to reflect impaired reflex vagal antagonism. The absence of the association of λ_{25 s} with the AMI recurrence also supports the hypothesis, suggesting that the increased λ_{25 s} maybe associated with the mechanisms precipitating cardiac death after AMI rather than those developing AMI.

The present findings also indicate that λ_{25 s} is unrelated to the risk of non-cardiac death. This finding was not observed for the other HRV indices. Decreased HRV is associated with various health conditions (Priori et al., 2001), including diabetes, uremia, alcoholism, obesity, smoking, depression, and aging (Malik and Camm, 2004) and with mortality among general elderly populations (Tsuji et al., 1994), which may explain the non-specific associations of decreased HRV with increased risk for all – cause mortality (Kleiger et al., 1987; La Rovere et al., 1998; Schmidt et al., 1999; Bauer et al., 2006). The selective associations of increased λ_{25 s} with cardiac death seems useful for predicting patients who would benefit from preventive approaches, such as those with implantable cardioverter defibrillators (Moss et al., 2002).

Study Limitations

Our study has several limitations. First, the sample included a subset of patients enrolled in the ENRICHD trial who had elevated symptoms of depression, which could affect the generalizability of our results. However, the proportion of the depressed patients with BDI scores ≥ 10 was 47%, which is comparable to the reported prevalence of depression (45–47%) in general post-AMI populations (Schleifer et al., 1989; Steeds et al., 2004). Second, we did not consider sudden cardiac death as a separate endpoint because the causes of cardiac death were not subcategorized in the record of ENRICHD study. Furthermore, the number of deaths, particularly that of non-cardiac death was small (13) and the power to detect a possible association between λ_{25 s} and non-cardiac death was inadequate. Finally, to establish the λ_{25 s} as a clinical risk factor of post-AMI cardiac death, it will be necessary to demonstrate that a reduction of this index improves clinical outcomes; however, our observations suggest a potential effect of β-blockers in reducing λ_{25 s}.

Conclusion

Among post-AMI patients, an increase in non-Gaussianity index of λ_{25 s} is independently associated with increased risk of cardiac death. Our observations suggest that the increased λ_{25 s} may reflect the deleterious effects of heightened sympathetic cardiac activation, which may contribute to the increased risk of cardiac death in post-AMI patients.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Dr Lisa Berkman of the Department of Epidemiology at the Harvard School of Public Health for providing data from the Yale University clinical site for our analysis. This research was supported by a Grant-in-Aid for Scientific Research(C) from the Japan Society for the Promotion of Science (JSPS), Japan, by a Research Grant (20B-7) for Nervous and Mental Disorders from the Ministry of Health, Labor and Welfare, Japan and by Grant HL 093374, HL080664, and HL58946 from the National Heart, Lung and Blood Institute, National Institutes of Health, Bethesda, MD, USA.

References

Barthel, P., Schneider, R., Bauer, A., Ulm, K., Schmitt, C., Schomig, A., and Schmidt, G. (2003). Risk stratification after acute myocardial infarction by heart rate turbulence. Circulation 108, 1221–1226.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bauer, A., Barthel, P., Schneider, R., Ulm, K., Muller, A., Joeinig, A., Stich, R., Kiviniemi, A., Hnatkova, K., Huikuri, H., Schomig, A., Malik, M., and Schmidt, G. (2009). Improved stratification of autonomic regulation for risk prediction in post-infarction patients with preserved left ventricular function (ISAR-Risk). Eur. Heart J. 30, 576–583.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bauer, A., Kantelhardt, J. W., Barthel, P., Schneider, R., Makikallio, T., Ulm, K., Hnatkova, K., Schomig, A., Huikuri, H., Bunde, A., Malik, M., and Schmidt, G. (2006). Deceleration capacity of heart rate as a predictor of mortality after myocardial infarction: cohort study. Lancet 367, 1674–1681.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Berkman, L. F., Blumenthal, J., Burg, M., Carney, R. M., Catellier, D., Cowan, M. J., Czajkowski, S. M., DeBusk, R., Hosking, J., Jaffe, A., Kaufmann, P. G., Mitchell, P., Norman, J., Powell, L. H., Raczynski, J. M., and Schneiderman, N. (2003). Effects of treating depression and low perceived social support on clinical events after myocardial infarction: the Enhancing recovery in coronary heart disease patients (ENRICHD) randomized trial. JAMA 289, 3106–3116.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Camm, A. J., Malik, M., Bigger, J. T. Jr., Breithardt, G., Cerutti, S., Cohen, R. J., Coumel, P., Fallen, E. L., Kleiger, R. E., Lombardi, F., Malliani, A., Moss, A. J., Rottman, J. N., Schmidt, G., Schwartz, P. J., and Singer, D. H. (1996). Task force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Heart rate variability: standards of measurement, physiological interpretation and clinical use. Circulation 93, 1043–1065.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Castaing, B., Gagne, Y., and Hopfinger, F. J. (1990). Velocity probability density-functions of high Raynolds-number turbulence. Physica D 46, 177–200.

CrossRef Full Text

Huikuri, H. V., Mäkikallio, T. H., Peng, C. K., Goldberger, A. L., Hintze, U., Moller, M., and Grp, D. S. (2000). Fractal correlation properties of R-R interval dynamics and mortality in patients with depressed left ventricular function after an acute myocardial infarction. Circulation 101, 47–53.

Pubmed Abstract | Pubmed Full Text

Jaffe, A. S., Krumholz, H. M., Catellier, D. J., Freedland, K. E., Bittner, V., Blumenthal, J. A., Calvin, J. E., Norman, J., Sequeira, R., O’Connor, C., Rich, M. W., Sheps, D., and Wu, C. (2006). Prediction of medical morbidity and mortality after acute myocardial infarction in patients at increased psychosocial risk in the enhancing recovery in coronary heart disease patients (ENRICHD) study. Am. Heart J. 152, 126–135.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kiyono, K., Hayano, J., Watanabe, E., Struzik, Z. R., and Yamamoto, Y. (2008). Non-Gaussian heart rate as an independent predictor of mortality in patients with chronic heart failure. Heart Rhythm 5, 261–268.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kiyono, K., Struzik, Z. R., Aoyagi, N., Sakata, S., Hayano, J., and Yamamoto, Y. (2004). Critical scale invariance in a healthy human heart rate. Phys. Rev. Lett. 93, 178103.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kiyono, K., Struzik, Z. R., and Yamamoto, Y. (2007). Estimator of a non-Gaussian parameter in multiplicative log-normal models. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 76, 041113.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kleiger, R. E., Miller, J. P., Bigger, J. T. Jr., and Moss, A. J. (1987). Decreased heart rate variability and its association with increased mortality after acute myocardial infarction. Am. J. Cardiol. 59, 256–262.

La Rovere, M. T., Bigger, J. T. Jr., Marcus, F. I., Mortara, A., and Schwartz, P. J. (1998). Baroreflex sensitivity and heart-rate variability in prediction of total cardiac mortality after myocardial infarction. Lancet 351, 478–484.

Malik, M., and Camm, A. J. (2004). “Heart rate variability,” in Dynamic Electrocardiography, eds M. Malik and A. J. Camm (New York: Blackwell), 3–213.

Marine, J. E., Watanabe, M. A., Smith, T. W., and Monahan, K. M. (2002). Effect of atropine on heart rate turbulence. Am. J. Cardiol. 89, 767–769.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Moss, A. J., Zareba, W., Hall, W. J., Klein, H., Wilber, D. J., Cannom, D. S., Daubert, J. P., Higgins, S. L., Brown, M. W., and Andrews, M. L. (2002). Prophylactic implantation of a defibrillator in patients with myocardial infarction and reduced ejection fraction. N. Engl. J. Med. 346, 877–883.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Peng, C. K., Havlin, S., Stanley, H. E., and Goldberger, A. L. (1995). Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 5, 82–87.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Priori, S. G., Aliot, E., Blomstrom-Lundqvist, C., Bossaert, L., Breithardt, G., Brugada, P., Camm, A. J., Cappato, R., Cobbe, S. M., Di Mario, C., Maron, B. J., McKenna, W. J., Pedersen, A. K., Ravens, U., Schwartz, P. J., Trusz-Gluza, M., Vardas, P., Wellens, H. J., and Zipes, D. P. (2001). Task force on sudden cardiac death of the European Society of Cardiology. Eur. Heart J. 22, 1374–1450.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schleifer, S. J., Macari-Hinson, M. M., Coyle, D. A., Slater, W. R., Kahn, M., Gorlin, R., and Zucker, H. D. (1989). The nature and course of depression following myocardial infarction. Arch. Intern. Med. 149, 1785–1789.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schmidt, G., Malik, M., Barthel, P., Schneider, R., Ulm, K., Rolnitzky, L., Camm, A. J., Bigger, J. T. Jr., and Schomig, A. (1999). Heart-rate turbulence after ventricular premature beats as a predictor of mortality after acute myocardial infarction. Lancet 353, 1390–1396.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schwartz, P. J., Billman, G. E., and Stone, H. L. (1984). Autonomic mechanisms in ventricular fibrillation induced by myocardial ischemia during exercise in dogs with healed myocardial infarction: an experimental preparation for sudden cardiac death. Circulation 69, 790–800.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Steeds, R. P., Bickerton, D., Smith, M. J., and Muthusamy, R. (2004). Assessment of depression following acute myocardial infarction using the Beck depression inventory. Heart 90, 217–218.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stein, P. K., Domitrovich, P. P., Hui, N., Rautaharju, P., and Gottdiener, J. (2005). Sometimes higher heart rate variability is not better heart rate variability: results of graphical and nonlinear analyses. J. Cardiovasc. Electrophysiol. 16, 954–959.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tsuji, H., Venditti, F. J. Jr., Manders, E. S., Evans, J. C., Larson, M. G., Feldman, C. L., and Levy, D. (1994). Reduced heart rate variability and mortality risk in an elderly cohort: the Framingham Heart Study. Circulation 90, 878–883.

Pubmed Abstract | Pubmed Full Text

Vanoli, E., De Ferrari, G. M., Stramba-Badiale, M., Hull, S. S. Jr., Foreman, R. D., and Schwartz, P. J. (1991). Vagal stimulation and prevention of sudden death in conscious dogs with a healed myocardial infarction. Circ. Res. 68, 1471–1481.

Pubmed Abstract | Pubmed Full Text

Woo, M. A., Stevenson, W. G., Moser, D. K., Trelease, R. B., and Harper, R. M. (1992). Patterns of beat-to-beat heart rate variability in advanced heart failure. Am. Heart J. 123, 704–710.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Appendix

Reanalysis of Previous Observations in a Cohort Study of Congestive Heart Failure Patients

In a previously study (Kiyono et al., 2008), we reported that non-Gaussian index λ_{40 beat} is an independent predictor of increased risk for mortality in patients with congestive heart failure (CHF). We studied 108 patients who were consecutively referred for evaluation or treatment of CHF. They underwent 24-h Holter ECG monitoring prior to hospital discharge and were subsequently followed up for 33 ± 17 months. The Holter ECG was analyzed to determine non-Gaussian index together with time and frequency domain indices of heart rate variability (HRV), fractal HRV measures, and heart rate turbulence.

In this previous study (Kiyono et al., 2008), we computed the non-Gaussian index λ based on beat scale and we found that the λ at a scale of 40 beats (λ_{40 beat}) showed the best predictive power for mortality. However, analyses based on beat scale could be affected by both inter- and intra-individual differences in heart rate. We therefore reanalyzed the same data based on time (s) scale. Time series of R–R intervals were interpolated with cubic spline function, resampled at 4 Hz, and submitted to the algorithm for estimating λ. Cox proportional hazards regression analysis was performed to determine the relative mortality risk of the indices. Then, we found that the λ at a scale of 25 s (λ_{25 s}) was the best independent predictor of both all-cause and cardiac mortality. The predictive power of λ_{25 s} was comparable to that of λ_{40 beat} for both all-cause and cardiac mortality and even after adjustment for other predictors (Table A1).

TABLE A1

Table A1. Associations of HRV indices with mortality risk in CHF patients.