- Departments of Physiology, Physics, and Institute of Biomedical Engineering, University of Toronto, Toronto, ON, Canada
Le Chatelier’s principle asserts that a disturbance, when applied to a resting system may drive the system away from its equilibrium state, but will invoke a countervailing influence that will counteract the effect of the disturbance. When applied to the field of sensation and perception, a generalized stimulus will displace the system from equilibrium, and a generalized adaptation process will serve as the countervailing influence tending to reduce the impact of the stimulus. The principle applies at all levels, from the behavioral to the neural, the larger enfolding the smaller in fractal-like form. Le Chatelier’s principle, so applied, leads to the unification of many concepts in sensory science. Ideas as diverse as sensory adaptation, reflex arcs, and simple deductive logic can be brought under the umbrella of a single orienting principle. Beyond unification, this principle allows us to approach many questions in pathophysiology from a different perspective. For example, we find new direction toward the reduction of phantom-limb pain and possibly of vertigo.
Introduction
Definition
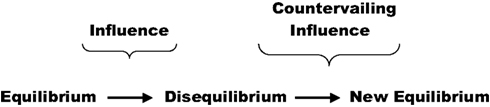
Although usually designated as “Le Chatelier’s principle”, this concept was, apparently, discovered independently by Henri Louis Le Chatelier and Karl Ferdinand Braun. Le Chatelier’s treatise was published in 1888. The Le Chatelier–Braun principle (LCB principle) states that when a system in dynamic equilibrium is acted on by an external stress, it will adjust in such a way as to relieve the stress and establish a new equilibrium. Although this principle was developed through the medium of chemistry, it found expression in many other scientific fields. There is a general tendency for influences that produce changes in an equilibrium state to induce countervailing influences that oppose the changes and establish a new state of equilibrium. Lenz’s law in electromagnetism is an example of the extension of the LCB into physics. Graphically we can express a generalized Le Chatelier–Braun principle as shown in Figure 1 .
Generalization of Le Chatelier’s Principle to Sensation and Perception
It is suggested in this paper that the generalized Le Chatelier principle governs the processes of sensation and perception, as illustrated in Figure 2 and it may be applied to advantage in sensory science. We begin on the left-hand side, with an initial state of sensory equilibrium. This initial state may be, for example, a state of quiescence for the visual system, where no light stimulus is applied to a light receptor. The stimulus may be a sudden bright light, introducing a transient state of disequilibrium. Perhaps unfamiliar in Figure 2 is the countervailing influence, which may also be referred to as a restoring influence. In the vision example given, the eye may simply rotate away from the visual stimulus, leading to a new state of sensory equilibrium which may or may not approximate the original state of quiescence. The countervailing influence tends to mute or turn off a stimulus. We shall see later that this countervailing or restoring influence assumes quite familiar psychophysical and physiological forms.
The concept that a restoring influence is an integral part of all perceptual processes is, perhaps, new, although sensory adaptation, which is discussed below, is familiar. It will be argued that such a restoring influence is the rule rather than the exception, and that violation of the rule leads to negative consequences. We shall develop the argument progressively.
Theoretical Development
Unification of the Units of Perceptual Stimuli: Introduction of Uncertainty
We consider perception as a term describing a broad range of cognitive functions, one of the simplest of which is sensation. That is, the set of sensory functions will be taken as a subset of the set of perceptual functions. Traditionally, the values of the stimulus that appears in Figure 2 are written with different units for each sensory modality. This tradition is quite natural. For example, the newton which is a unit of force can be used to measure a stretch stimulus, while units of molarity are used in the chemical senses, sound pressure for hearing, etc. More complex stimuli such as music or graphical art cannot be expressed in simple physical units yet they are, unquestionably perceptual stimuli, and each is discussed using its characteristic referent (e.g., harmony, contrast…). In order to apply the LCB principle most effectively in the field of sensation and perception, we shall find it advantageous to convert the “units” in which stimuli are expressed to a common, dimensionless form. We may lose some coloration by doing so but the result will be a simpler theoretical structure.
In order to carry out this unification of the units of perceptual stimuli, we must abstract a feature shared by all stimuli – not a simple task and perhaps one without a unique solution. However, it is suggested that such a feature, common to all psychological and physiological stimuli, is the “stimulus-evoked question”. For example, if the stimulus is light from an incandescent source, the implied, stimulus-invoked question may be: “What color is the light?” Or, if a stimulus set consists only of blue lights, the implied question may be: “How bright is the blue light?” In the case of simple sensation, the implied question can be regarded as asked by the sensory receptor (What color is the light?), and answered by the stimulus (Blue). There are similarities to the television game Jeopardy: each stimulus-answer implies a certain receptor-question. For example, if the stimulus-answer is “He was British prime minister 1940-1945”, the receptor-question provided by the contestant is “Who was Winston Churchill?”
The advantage of associating stimuli with implied questions is that it does seem to permit the expression of all stimuli in a common “unit”, namely uncertainty. “What color is the light?” expresses the a priori uncertainty of the perceiver about the color of the light: it could be red or yellow or blue … “How bright is the blue light?” expresses the a priori uncertainty that the blue light could assume many different levels of brightness. So we shall adopt uncertainty as the common unit or language into which all stimuli may be cast. In dealing with more complex perceptual stimuli, the questions, of course, are commensurately more complex.
When we apply this idea of the stimulus-evoked question to Figure 2 , it introduces a degree of symmetry. We recall that the “restoring influence” is the process that partially or totally nullifies the stimulus – turning off the stimulus, so to speak. Therefore in Figure 2 , in place of the word “stimulus”, we may now substitute “uncertainty established” (or “stimulus-evoked question asked”); and in place of the phrase “restoring influence”, it would seem natural to substitute “uncertainty resolved, partially or completely” (or “question answered, at least in part”). These changes are introduced later, in Figure 3 .
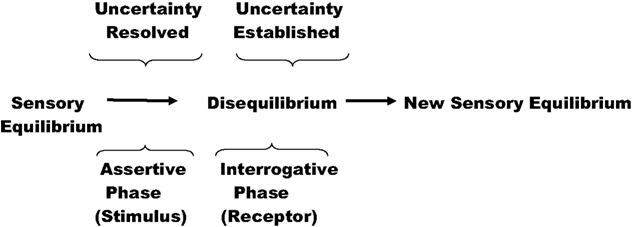
Figure 3. Evolution of Figure 2 to represent uncertainty set up by a receptor and resolved by receipt of a stimulus.
The Measurement of Uncertainty
It is all very well to convert stimuli into uncertainties, but can one assign a numerical measure to perceptual uncertainty, and is a numerical measure always possible? The answer seems to be that a Shannon measure of uncertainty can be applied to steady sensory stimuli, but that more complex perceptual inputs cannot be convincingly quantified. Simple sensory stimuli are examples of continuous stimuli: they may vary in intensity continuously from some threshold value to some physiological maximum. For example, a solution that is tasted may have concentration 0.500, 0.501 M, etc. A tone may have sound level 30.0, 30.1 dB, etc. These stimuli enjoy a continuum of values which we could designate by v. Then if p(v) is the corresponding probability density function for the stimulus, −∫p(v) log p(v) dv, is a differential entropy that can be used to express uncertainty (Shannon and Weaver, 1949 ). If v is normally distributed or uniformly distributed, the differential entropy will be a linear function of the logarithm of the variance of the distribution. Or, speaking casually, the greater the dispersion of the stimuli (reflecting uncertainty), the greater the differential entropy.
Everyday perceptual stimuli are often discrete stimuli (vis-à-vis the continuous sensory stimuli), whose Shannon entropy (uncertainty) can be calculated from −Σi pi log pi, where the pi are the probabilities of the possible discrete outcomes. For example the key that I am looking at is either the key to my car, to the front door of my home, to my office… a set of discrete possibilities. If there are equal probabilities that the key that I am withdrawing from my pocket fits any one of n locks, the entropy (uncertainty) is just equal to the logarithm of n. In this case, the numerical measure is very simple: the more locks that my key may possibly fit, the greater the entropy (uncertainty). The stimulus has the “quantity” log n.
However, more complex stimuli do not permit such simple numerical quantification.
The Resolution of Uncertainty: Incorporation of Time
After uncertainty is set up by a perceptual process, how then is this uncertainty resolved? A simple answer is that the perceiver executes a process which will select one of the possibilities as “true” or “extant”, and eliminates many of the others. Therefore, the steady auditory tone of uncertain intensity is perceived to have a level of about 50 dB – uncertainty resolved to the neighborhood of 50 dB (in the case of a continuous stimulus); or the key is perceived to be my office key in the case of a discrete stimulus. That is, there is some psychological or physiological action that carries out the process of resolving uncertainty. However, particularly in the case of the continuous stimulus, one cannot always remove all of the uncertainty. The tone is perceived to have a sound level of about 50 dB. Moreover, such perceptual events do not occur instantaneously; there is a certain processing time required. It may take milliseconds or seconds to resolve the intensity of an unknown tone. During this interval of time, the auditory system will take many samples of its unknown tone. Perhaps the perceptual system – the hearing system in this case – will avail itself of the mean of a set of these samples. The uncertainty or log (variance), of a single sample of a tone might then be replaced by the log (variance) of the mean of all the samples (dividing the mean by the number of samples). The variance of the mean will always be smaller than that of individual samples, and, hence, the uncertainty of a continuous sensory signal will be reduced, but not eliminated, by the active process of sampling. A physicist might say (and we’ll return to physics later) that uncertainty of a classical event is reduced by the process of observation.
Discrete events also require processing time. The mechanical process of examining my key is also time-consuming. When I look at the key in my hand, it is quickly apparent that it is too large for my filing cabinet, but could fit my house or office. A moment later, I have turned it over in my hand and looked at its shape and color, which identifies it as my office key. So a certain amount of time and perhaps motor activity is needed in order to reduce the uncertainty.
We may conclude, at least tentatively, that the countervailing influence in Figure 2 is one that reduces the initial uncertainty, requires a finite period of time, and constitutes part of the act of perception.
Collecting Ideas
Figure 2 has now evolved into Figure 3 . A receptor unit may be thought of as the interrogative or questioning portion of the perceptual process. It asks the question: “Of all the possibilities, which one or ones does this stimulus comprise?” establishing a level of uncertainty. The stimulus provides a unique answer to the question or narrows down the number possibilities. That is, speaking very generally, the Le Chatelier–Braun principle adapted to perception has two phases, the interrogative, or “sensory” phase, and the assertive, or “motor” phase. The “sensory” phase consists, at least in part, of the absorption of energy (e.g., light, heat, sound) from the external world; the “motor” phase is more generally described as an “energy expending phase”. In a much earlier publication (Norwich, 1982 ) these phases were described as active and passive phases respectively.
Adaptation
Sensory adaptation is the familiar process whereby steady sensory stimuli, such as steady taste or olfactory stimuli, fade progressively from our sensorium with the passage of time without conscious intervention. An odor that was perceived as being intense 5 min ago may be nearly imperceptible now. A solution held in the mouth that initially tasted sweet or salty will have very little taste after a minute or two.
Adaptation enters the sensory LCB principle at the level of the countervailing influence, or the process that tends to diminish the effect of a sensory stimulus by reducing its uncertainty value. We addressed the issue of progressively decreasing uncertainty induced by repeated sampling of the steady stimulus when we recalled that the sample mean is larger than the standard error of the mean. Our uncertainty about the population mean (read here the “mean value of the stimulus”) diminishes with the size of the sample (n-value). That is, the process of repeated sampling parallels the process of adaptation (Norwich, 1993 ). In this respect, sensory adaptation can be viewed as a process of reduction in stimulus uncertainty, or gaining information about the stimulus.
“Perception” Generalized
The process known as perception, then, consists of the dual function of establishing and disestablishing uncertainty. As we have seen, this process can occur from the behavioral level (such as everting the eyes or finding an object) down to the neural level (such as sensory adaptation). Uncertainty functions are nested from macroscopic to microscopic, in the manner of a fractal. Examples of this property will follow. The development and resolution of uncertainty is found in many functions of activity, including the process of deduction.
Perception through logical deduction
The LCB principle of perception is mirrored in the way we talk as well as in the logical manner in which we think.
“What are you carrying in that bag? Oh. I see. Oranges.”
(Question: uncertainty established, sensory. Answer: uncertainty resolved, motor).
Within symbolic logic: “If p then q. p therefore q”. Usually interpreted: “If statement p is true, then statement q is true. p is true, therefore q is true.” However, we may also interpret the logical code within a Le Chatelier paradigm. That is,
Interrogative or establishing uncertainty: Is q true (“sensory”)? q is true if p is true.
Assertive or resolving uncertainty: p has been found to be true (“motor”), therefore
q is true. Or, q has been perceived logically.
We note the generality conferred upon the concept of perception using LCB. We perceive when uncertainty is established and then removed, whether this process occurs directly by observation or logically by inference.
Perception viewed linguistically: Latin roots of the uncertainty concept
Irish philosopher George Berkeley has written in his Principles of Human Knowledge the expression for which he is, perhaps, best known: esse is percipi: to be is to be perceived. The Latin verb percipere has been used to refer to perception with the senses. However, to convey perception with understanding, Latin often used the infinitive intellegere, which is an interesting word, with direct links to our current study. It is synthesized from two simpler Latin words: inter, between, and legere to choose. To the Roman thinker, the process of perception with understanding was synonymous with making a choice from among a set of possibilities – the same idea we have used above in framing the general LCB principle for perception. Other early languages embody the same concept. The process from stimulus to response, from sensory to motor, is one of selecting one or few from among many possibilities. Plus ça change …
Links to Modern Physics
Quantum observation is, at least arguably, an extension of psychophysics, in that it relates a physical measure of the observed world (energy, momentum, geometrical structure) to the final observation (or perception) made by a human observer. It is then not surprising to find that some of the concepts of quantum physics apply, with appropriate changes, in the mesoscopic, or middle-sized, world of everyday sensation and perception. Among the enigmatic ideas of quantum physics is the concept of the wavefunction, which is a mathematical function defining the state of a portion of the world before it is observed directly. The wavefunction is really a superposition – or a piling on top of each other – of all the various ways in which the world could be observed, before it is actually observed. When this wavefunction is “collapsed”, which occurs when an observation (we may prefer perception) is made, the heap of possible ways that the world could be observed condenses to one or just a few of these ways. This scenario should now be familiar to the reader; it is very close to the process of “uncertainty established” and “uncertainty resolved” that form part of the sensory LCB principle. Turning the analogy around, the wavefunction of quantum mechanics is the sensory component of quantum perception, and the collapse of the wavefunction is the motor component.
Links to Physiology
Spinal reflexes are readily incorporated into the generalized LCB principle. Consider the simple knee-jerk. A peripheral stimulus, such as stretch to a tendon stretch receptor, acts directly through the spinal cord (perhaps through the medium of one interneuron), and activates a motor neuron which will produce muscle contraction. This is an example of a simple spinal reflex arc. The stretch stimulus, which is a force acting on a stretch receptor, displaces the system from equilibrium. A signal is relayed by means of a sensory afferent neuron to the central nervous system. A motor neuron then activates muscle fibers. The motor activity, which provides the restoring force, acts to remove, or at least minimize, the stretch stimulus, and we have cycled through a Le Chatelier process from one state of equilibrium to the next. The fact that a muscle contracts is not as important to us here as the fact that as contraction occurs, the stretch stimulus is effectively removed by a countervailing stimulus (Figures 1 and 2 ). The scale of action of LCB is here at the neuronal or cellular level, midway between the quantum and behavioral scales.
However, some rather unexpected consequences now emerge from the generalized LCB principle. New theoretical structures generate new ideas and, often, new consequences.
Philosophical Considerations Emerging from the Sensory Le Chatelier–Braun Principle
If the general process of perception is encoded by Figure 3 : uncertainty established (sensory) followed by uncertainty resolved or removed (motor, or at least energy consuming), what significance can then be attached to a sensory stimulus which resolves no uncertainty whatever? It is not immediately evident that there can exist a non-zero stimulus which resolves no uncertainty, and provides no answer. However, let us study the following experiment.
Consider an image, controlled by optical means to occupy a fixed position on the retina of a human participant. No matter how the eye may be moved, the image remains fixed in position on the retina. Initially, immediately after the image is initiated, it is sharply visible; however, after a few seconds the image peripheral to the fixation point begins to “gray-out”. The image fades from the sensorium of the perceiver (Ditchburn and Fender, 1955 ). This phenomenon, known as Troxler’s effect, can be easily demonstrated for oneself. If one stares at a large dot on a blank page, trying hard not to blink or move one’s eyes, the dot will fade and become invisible. The explanation for the phenomenon can be found, at least partially, in the perceptual LCP. When the visual system establishes complete certainty about the nature of a percept (the scene or object that produces a stabilized image), when no uncertainty remains about the nature of the object, and no question is posed, then no answer can be offered, and hence, no perception takes place. That is, once uncertainty about the image has been unequivocally removed, the process of perception ceases. In such a case, a non-zero stimulus (light continues to reach the retina) resolves no uncertainty, and, therefore, becomes “not perceivable”. Why do images not vanish from our field of vision during everyday life? Probably because the images are held in existence by the tiny eye movements called microsaccades that prevent these images from being fixed on the retina, and hence prevent perfect certainty. The fading of fixed images is an example of sensory adaptation (Clarke, 1957 ).
However, the general philosophical question remains: Is it possible to perceive “a certainty”? If I am absolutely certain that I have a quarter in my pocket, must I in some way re-establish doubt about its presence before I can detect its presence in my pocket sensorially? Looked at in this manner, the fixed retinal image discussed above evolved into a state of imperceptibility because the image simply had no more information to convey to the perceiver. The effect of microsaccades is to reinitialize the visual system, permitting a new Le Chatelier cycle to begin (new state of sensory equilibrium), which again asks the implicit question: “What is this image?” A second displacement of equilibrium from an incompletely adapted system is expressed by the second curve in Figure 4 on the right-hand side: New sensory equilibrium disturbed by second stimulus leads to second new sensory equilibrium, etc.
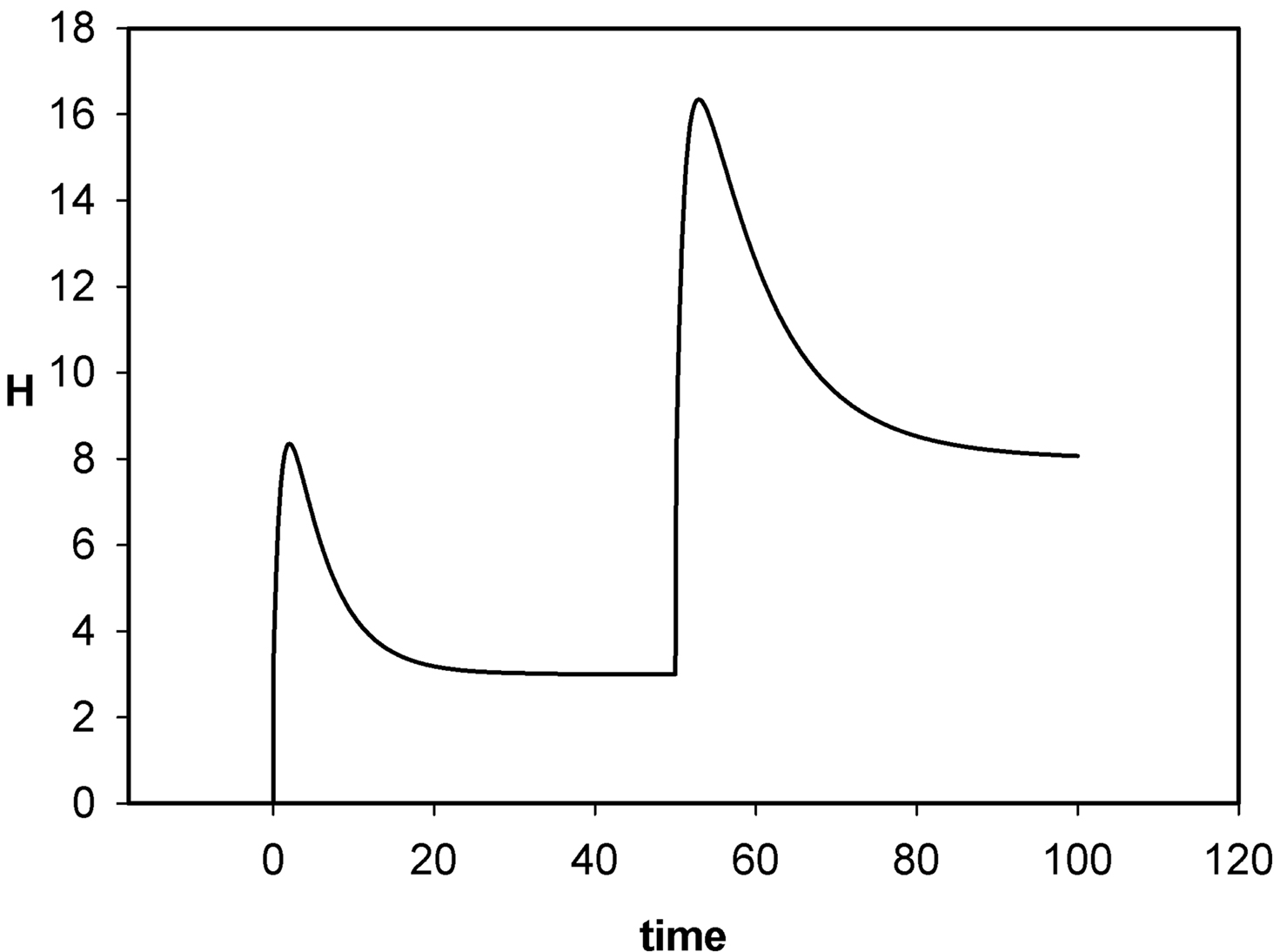
Figure 4. Change of uncertainty, H, with time in a sensory system in response to two sequential stimuli. H(0) = 0. In response to a steady stimulus applied at t = 0, H rises rapidly, then adapts to a value of about 3 as uncertainty declines, but does not vanish. A second stimulus greater in magnitude than the first, is applied at t = 50. Uncertainty rises again, and then adapts to a value of about 8.
Possibility of Incomplete Reduction of Uncertainty
We have seen above that the end result of the process of perception is not necessarily the total resolution of the uncertainty. I may not find my key, but I can reduce the number of locations in which it may be hiding; I may not discern your facial expression but I can see that you are not distressed. So the result of the process of perception may be the reduction, if not the total obliteration, of uncertainty. In simple cases, the reduction in uncertainty may be quantified as the initial uncertainty value minus the final value. Thus, for example, reduction in uncertainty may be expressed by the reduction in the number of locations for a missing key, or, in general, the reduction in the number of possible outcomes to an event. In simple cases, the Wiener–Shannon entropy provides a numerical measure of residual uncertainty. So for equally probable events, the reduction in uncertainty can be quantified by log (number of possibilities prior to perception) – log (number of possibilities after the act of perception).
It is significant that the quantum physical counterpart of the motor phase of perception, namely the collapse of the wavefunction, does not eliminate all uncertainty about the quantum event. There still remains a residual uncertainty that is expressed by Heisenberg’s celebrated Uncertainty Principle. It seems that at its very roots, nature places limits on the degree to which uncertainty can be reduced, both at the microscopic (quantum) and the mesoscopic (“everyday”) levels. We recognize the significance of Heisenberg’s Uncertainty Principle in cognitive science: if uncertainty could be reduced to zero, possibly the event would become unperceivable, as we have discovered philosophically before. Therefore, we come to recognize that in the final state of sensory equilibrium there must remain some level of uncertainty if the sensorium is to remain active or aware.
Discussion
Fractal-Like Nature of the Sensory LCB Principle
It is noteworthy that the sensory LCB principle acts behaviorally, in a manner involving whole movements of the organism (such as searching or puzzle-solving); organically (involving the senses); and neurally (such as reflex arcs). That is, the LCB operates in the same manner at different scales within the organism. In this way it emulates the structure of a fractal.
Uncertainty Reduction as Consummation
There is some evidence that the restoration phase, the uncertainty reduction component of the sensory LCP, can be regarded as “consummating” the perceptual process. The term consummation suggests that motor activity undertaken brings about a state of perfection or fulfillment to the sensory event. In some cases, this desirable conclusion may be self-evident. For example, the spinal reflex mediating withdrawal from a painful stimulus definitely leads to a desirable result. There are other cases, too, to support the use of this term, consummation. When one perceives the solution to a puzzle, the uncertainty engendered by the puzzle is reduced, the result is the desired result, or a consummation of the effort of solution. But is this effect universal? It may be argued that it is. Within a physiological context, the trigeminally mediated nasal stimulus is consummated by sneezing; the vagus-mediated bronchial reflex is consummated by coughing; bladder stimulation of pudendal afferents by micturition, etc. Even parturition brings about a consummation of the urge to push. We will not belabor the point here, but rather just plant the seed of the idea that the restoration phase of the sensory LCP may be associated with consummation of the effort. One can ponder this concept and its converse: Is failure to consummate a sensory activity by reducing uncertainty always unfulfilling, uncomfortable or painful?
Applications of the LCB Principle to Problems and Enigmas
The concept that the restoring influence reducing the displacement from equilibrium brings about a consummation of sorts casts some light on why certain activities are more pleasant than others. Trivially, we experience a degree of consternation before we solve the jigsaw puzzle; there is some uncertainty about how the pieces will interlock. When we reduce the uncertainty by interlocking the pieces, a motor activity, we consummate our search and experience some satisfaction. Failure to solve a puzzle can leave us in a state of dissatisfaction. Mellers (2000) has observed “… pain can arise from the frustration of not achieving a goal”.
Frustration of this nature can be decidedly non-trivial. Phantom-limb pain is pain experienced in limbs that have been removed (see, for example, Melzack, 2006 ). We can, perhaps, begin to understand this phenomenon when we realize that sensation mediated by sensory nerves from the amputated limb cannot “adapt”. Attempting to move a limb in an effort to alter or reduce the sensations issuing from it is a kind of “frustration”. That is, no motor function by the amputee can reduce the uncertainty that characterizes a sensory stimulus, which brings about a feeling of pain or discomfort.
This concept was illustrated dramatically (Ramachandran et al. 1995 ). By use of a mirror to “superimpose” a normal hand on a phantom, it became possible for the patient to “move” the phantom limb, and to unclench it from potentially painful positions. Once again, consummating the motor process in a Le Chatelier process brings about reduction in distress. Similarly vertigo can be a major medical problem. Vertigo is the sensation of dizziness or spinning experienced when a patient is completely stationary. Again, the sensation cannot be “reduced” by voluntary action by the patient. That is, the patient cannot reduce the sensation of vertigo by any motor action such as reducing the rotation of his or her head. The inability to “consummate” leads to gross discomfort. We might conjecture that movement of the afflicted person can be used here to simulate consummation and reduce vertigo.
Beyond the Sensory LCB Principle: Is the Uncertainty Reduction Phase Deterministic or Random?
The simple application of the LCB principle to sensation and perception mandates only that a restoration phase is present. We have classified this restoration phase as the phase of reduction in uncertainty about a stimulus. However, can we ascertain whether the restoration is deterministic or random in nature?
When uncertainty reduction is purely sensory, for example the sampling of an odorant by the nose, it may be embraced totally by the physiological process of adaptation, over which the perceiver has little if any control. Perhaps in such cases the system is largely deterministic in nature. However, when uncertainty reduction is brought about by conscious activity, such as the search for the best move in a chess game, the matter is less clear. Do we search randomly for a move or do we implement a logical process that is largely deterministic? Neural networks, for example, can evolve an optimal strategy by testing random changes to network components. If the randomly induced changes bring the network closer to its goal (in our case, reduction in uncertainty), the change is retained, otherwise it is abandoned. This method is sometimes called gradient descent. So it would seem that sometimes the process of uncertainty reduction is conducted using physiological processes that are, to a large extent, deterministic. However, sometimes this energy-expending phase evolves purely randomly, directed perhaps by a process akin to gradient descent.
The Peaks in the H vs. t curve in Figure 4
Referring to Figure 3 , it is seen that the peaks of the H vs. t curve in Figure 4 represent phase transitions, between an assertive and an interrogative phase. Such peaks can be regarded as critical points in the phase transition, and there has been a good deal of interest in these points in recent years. Haldeman and Beggs (2005) , for example, have shown in simulated neural networks that the number of metastable states in larger networks tended to peak at critical values, which can potentially store information. Perhaps even more relevant is the earlier paper, Beggs and Plenz (2003) , which shows that branching parameters near a critical point optimizes information transmission in feedforward networks. It is also significant (since psychophysical laws are often expressed as power laws) that propagation of activity in such networks are governed by a power law.
There may be some overlap between an LCB process and a system influenced by self-organized criticality (SOC). Within SOC, components are usually governed by simple rules. Pressure builds within the system until some threshold for change is traversed. This is a critical point. Up to this point, there is a parallel with an LCB process, which begins in some initial state of equilibrium, and remains there until external influences impel a change. However, in SOC, the system often progresses past the critical point to chaos or avalanche formation, while the LCB process usually progresses more classically to a new state of equilibrium.
Summary and Conclusions
The principle of Le Chatelier and Braun has been found to govern many systems. It asserts that a force or disturbance, when applied to a resting system will drive the system away from its equilibrium state, but will invoke a countervailing force or disturbance that will tend to mitigate or minimize the effect of the disturbance, leaving the system in a new and displaced state of equilibrium. Le Chatelier’s principle has been invoked many times in the past in a bid to understand reflex activity. One of the early papers dealt with the withdrawal response of the land snail (Humphrey, 1930 ), and has been often cited in recent years.
There is a caveat that should be invoked. The LCB is a principle not a law. LCB is a kind of rule of thumb which complements the laws of science. Le Chatelier’s principle provides a simple rule by which one can infer changes in chemical equilibria, but one can deduce these same changes using the known laws of physical chemistry. Similarly, Lenz’s law may exemplify the LCB principle, but one can deduce this law from the laws of electromagnetism. When we apply the LCB to biology, we are, in a sense, extrapolating its use beyond known laws of biochemistry, biophysics, etc. There remains the incumbency to discover these laws in detail, relegating LCB to its proper place as an adjunctive principle.
It should be emphasized that the LCB principle is not an expression of a closed loop control system, where a variable is brought as closely as possible to some reference level by means of a negative feedback loop. Powers (1973) extended the scope of closed loop control systems into sensory science, regarding behavior as “control of perception”. Perceptions, in Powers’ view, are controlled when they are kept as close as possible to internal reference levels. The approach taken in this paper is simpler, and takes us in quite a different direction. There is no internal reference level, no error signal, and no feedback loop.
We required a general unit with which to measure the state of sensory equilibrium and displacement from equilibrium and we chose uncertainty. Much of our discussion was confined to sensory systems operating between levels of equilibrium. Initial equilibrium may be represented as a state of complete certainty (no questions are asked). When a positive stimulus is applied, uncertainty increases, because the nature of the stimulus is not known instantaneously. The restoring influence is usually motor (or at least energy-expending) in quality, and guides the system in such a way that the uncertainty is reduced. The final, new state of equilibrium represents a new level of uncertainty.
We can extend the LCB principle to a generalized stimulus (a simple sensory stimulus, or more complex stimulus such as a visual scene, auditory landscape, etc.), and apply the same rules for changes in uncertainty with the passage of time. However, an important distinction should be made. All stimuli discussed in this paper are constant stimuli, in that they do not autonomously change; all time-varying changes brought about in the system may be regarded as due to the restoring influence. For example we do not consider a stimulus in the form of a light of diminishing intensity; if the light does diminish in brightness, it is due to sensory adaptation or movement of the organism away from the source of light.
What is the psychophysical significance of the reduction of uncertainty that attends a process of perception? As discussed in various other sources (Norwich, 1993 , 2001 , 2005 ), when the stimulus is a simple, sensory, prothetic stimulus, the magnitude of uncertainty is reflected by the subjective magnitude of the stimulus: a stimulus with greater uncertainty is attended by a greater subjective magnitude and vice versa. In this case, the restoring influence that reduces uncertainty is known as sensory adaptation. When these ideas applied to very simple stimuli are cast in mathematical form, one can derive using the uncertainty concept many psychophysical laws which had previously been largely empirical, such as Weber’s law, Fechner’s law, the power law of sensation, Piéron’s law for simple reaction times, the Blondel–Rey law, and many other familiar empirical equations (Norwich, 1993 ). When the stimuli are more complex, no simple mathematical structure will suffice, but the LCB principle still demonstrates the interrelationship between sensory and motor activity in the process of perception. One can perceive a degree of unity within the sciences: a principle borrowed from the physical sciences is seen to extend to the biological sciences. Conversely, the collapse of the wavefunction in quantum physics may be viewed as a special case of a principle of perception. Philosophically similar to fractal images, LCB functions are nested within other LCB functions. For example, reflex arcs operate locally as LCB functions, while the organism may carry out complex searching activity on LCB principles at the behavioral level.
The basic idea is that each stimulus will be met by an “anti-stimulus”, or something that will try to “turn it off”. When we append to the Le Chatelier–Braun principle the conjecture that within the field of sensation, “success” in turning off the stimulus brings about a feeling of satisfaction or pleasure, while “failure” will bring dissatisfaction or pain, we can embrace an additional set of psychological phenomena, such as the delight in solving a puzzle, as well as medical symptomatology such as the discomfort of phantom limbs and of vertigo.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work has been supported by a Discovery grant from the Natural Sciences and Engineering Research Council of Canada. I am extraordinarily grateful to Esteban Barrull of the University of Barcelona, for inaugurating a number of the lines of thought explored in this work, and to Lisa D’Alessandro of the Sensory Communications Group at the University of Toronto for her careful scrutiny of several drafts of this paper.
References
Beggs, J. M., and Plenz, D. (2003). Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11167–11177.
Clarke, F. J. J. (1957). Rapid light adaptation of localized areas of the extra-foveal retina. J. Mod. Opt. 4, 69–77.
Haldeman, C., and Beggs, J. M. (2005). Critical branching captures activity in living neural networks and maximizes the number of metastable states. Phys. Rev. Lett. 94, 05801.
Humphrey, G. (1930). Le Chatelier’s rule and the problem of habituation and dehabituation in helix albolabris. Psychol. Forsch. 13, 113–127.
Le Chatelier, H. (1888). Recherches Expérimentales et Théoriques sur les équilibres Chimiques, Vve Ch. Dunod, éditeur, Libraire des corps nationaux des ponts et chaussées, des mines et des télégraphes, Quai des Augustins, 49.
Norwich, K. H. (2001). Determination of saltiness from the laws of thermodynamics: estimating the gas constant from psychophysical experiments. Chem. Senses 26, 1015–1022.
Keywords: perceptual systems, fractals, sensory adaptation, concept of pain
Citation: Norwich KH (2010) Le Chatelier’s principle in sensation and perception: fractal-like enfolding at different scales. Front. Physio. 1:17. doi: 10.3389/fphys.2010.00017
Received: 16 April 2010;
Paper pending published: 21 May 2010;
Accepted: 10 June 2010;
Published online: 28 June 2010
Edited by:
John M. Beggs, Indiana University, USAReviewed by:
José M. Medina, University of Minho, PortugalCopyright: © 2010 Norwich. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Kenneth H. Norwich, Institute of Biomaterials and Biomedical Engineering, University of Toronto, 164 College Street, Toronto, ON, M5S 3G9, Canada. e-mail:ay5ub3J3aWNoQHV0b3JvbnRvLmNh