The Euclidean model of space and time, and the wave nature of matter

The aim of the paper is to show the fundamental advantage of the Euclidean Model of Space and Time (EMST) over Special Relativity (SR) in the field of wave description of matter. The EMST offers a unified description of all particles of matter as waves moving through four-dimensional Euclidean space at the speed of light. Unlike the usual description in three dimensions, where the group and phase velocities of a particle differ, in four-dimensional space the wave and the associated particle can be treated as a single object. The paper deepens understanding of the EMST as a viable alternative to SR. The EMST clarifies the origin of relativistic phenomena and at the same time explains the apparent mysteries associated with the wave nature of matter. From the broader perspective, the EMST has all the prerequisites to become the starting point for the mutual combination of “relativistic” and “quantum” physics into a single physical theory.

1 Introduction

The Euclidean Model of Space and Time (EMST) is a parallel theory to Special Relativity (SR) [1]. It is based on the assumption that physical space is four-dimensional space with Euclidean metrics. The EMST belongs to the group of theories referred to as Euclidean relativity [2–8], however, it differs significantly by a compact fourth dimension. Such solution solves the problem of space-time collisions [9], as well as unresolved questions regarding the wave nature of matter. The implications of the EMST in the later area are the subjects of this paper.

1.1 The wave nature of matter

The idea that all matter exhibits wave properties is not new in physics. Louis de Broglie is generally considered to be the father of this idea, as his dissertation thesis Recherches sur la théorie des quanta (Research on the Theory of Quanta, [10]) was the first work to present it comprehensively. In that work, de Broglie built on previous discoveries by Max Planck and Albert Einstein and extended the concept of wave-particle duality, which until then was only considered and accepted for light, to all particles of matter. De Broglie received a Nobel Prize for Physics in 1929 for his research in this area [11].

De Broglie used the theory of relativity as a starting point. Namely, it was Einstein’s equation $E=m{c}^2$, which relates the particle energy E to its mass m, and also the quantum “Planck-Einstein relation” $E=hf$, which relates the photon energy E to its frequency f. De Broglie concluded that the latter is generally valid and extended its use to all types of particles. In the above-mentioned relations, h is Planck’s constant.

For a particle at rest, de Broglie obtained the relation $h{f}_0=m_0{c}^2$, where f₀ and m₀ are the particle’s frequency and mass at rest. However, this relation cannot be easily modified for a particle in motion.

De Broglie designated the “theorem of phase harmony” as the basic hypothesis of his theory, which he formulated as [10]:

“A periodic phenomenon is seen by a stationary observer to move with velocity v and exhibit frequency $f_1=\left(m_0{c}^2/h\right)\sqrt{1-v^2/c^2}$ that appears constantly in phase with a wave having the frequency $f=\left(m_0{c}^2/h\right)/\sqrt{1-v^2/c^2}$ propagating in the same direction with velocity $v_f=c^2/v$.”

The application of this theorem to particles of matter in motion led Louise de Broglie to the conclusion that every particle of matter is accompanied by a specific “phase wave” (also known as a “de Broglie wave” or “matter wave”) which has the above-stated properties, i.e., direction, velocity and frequency. The energy and momentum of this wave is equal to the energy and momentum of the particle. The particle and the wave are mutually inseparable: they represent two forms of the same quantum of energy.

While the mathematical validation of the initial theorem is not difficult to provide, finding an acceptable physical interpretation of de Broglie waves turned out to be very difficult. A de Broglie wave has very unusual properties. It has a different frequency compared to the particle it represents, it moves at a different velocity, and this velocity is always superluminal. The only success that has been achieved in this field was finding that velocity v_f is the phase velocity, and this is not the velocity at which wave energy moves. Instead, it moves at group velocity, which equals the velocity of the particle v. The energy and the particle thus move at the same speed.

The question arises whether the strange properties of the de Broglie waves are not just due to an incorrect choice of the space in which they are described. Maybe it suffices to choose a different space dimension or metric and the seemingly incomprehensible properties disappear. Now, an interesting opportunity arises to try out the bounded Euclidean space E₄-B, in which the Euclidean model of space and time (EMST) is formulated.

1.2 The Euclidean model of space and time

The EMST is fully equivalent competitive theory to Einstein’s SR which, although based on different space-time metric, leads to the same predictions (time dilation, length contraction, Lorentz transformation…) in ordinary three-dimensional space. The theory uses a four-dimensional Euclidean space with a metric signature (+,+,+,+), where all four dimensions are space-like. In the EMST, time is not considered as a separate dimension, it is only a linear parameter of motion.

Since the theory of EMST is quite extensive, I will limit myself to a summary of the basic information necessary to understand the paper. A detailed description can be found in [9].

The EMST is based on three fundamental presumptions (postulates):

• Space is four-dimensional Euclidean, with all four dimensions being space-like.

• All particles of matter are restricted to a narrow layer in the fourth spatial dimension. This layer does not provide enough room for their mutual passing.

• In the stationary coordinate system, all particles of matter move with the same 4D speed which is equal to the speed of light.

Important features of the EMST:

• The methods of time interval measurement, distance measurement and clocks synchronization are the same as in Einstein’s SR. Time is measured by “ideal clocks,” distances are calculated from the transit times of two-way light signals, and the same light signals are used for clocks synchronization. As in Einstein’s SR, coordinate time is maintained by a set of mutually synchronized clocks.

• The bounded four-dimensional space of the EMST (abbreviated E₄-B) is a subset of four-dimensional Euclidean space E₄. E₄-B is composed of one restricted (w) and three unrestricted (x, y, z) spatial dimensions, so it forms a thin four-dimensional layer in E₄. Space E₄-B is bounded by pair of impenetrable planar mutually parallel barriers.

• Euclidean metrics is given by

$c\delta t=\sqrt{\delta x^2+\delta y^2+\delta z^2+\delta w^2}(1)$

where δx, δy, δz and δw are infinitesimal coordinate increments and δt infinitesimal increment of coordinate time.

• The coordinate w of all particles is in the range from w_min to w_max, so the usable width $\overline{w}$/2 of space in the fourth dimension is given by $\overline{w}$/2 = w_max − w_min. The value $\overline{w}$/2 is the distance between the barriers bounding the space in the fourth dimension (value $\overline{w}$ is equal to the full cycle of particles). The particles reflect from the barriers without loss of energy and momentum during their motion. The usable width $\overline{w}$/2 is not determined in [9]. At this stage of research, it is not necessary to determine its exact value. For the purpose of this article, we should anticipate that $\overline{w}$/2 is smaller than the Bohr radius (5.3 × 10⁻¹¹ m).

• The coordinate w can be expressed in two different forms–as a cyclic or as a non-cyclic quantity. The first form (abbreviated w_c) changes cyclically in the range from w_min to w_max with the motion of a particle between the barriers. It indicates the true position of the particle inside bounded four-dimensional space. The second additive (non-cyclic) form (abbreviated w_n) is used to express distance traveled by a particle in this dimension. It is related to the flow of particle’s proper time by the formula Δw_n = c Δτ. Coordinate difference Δw_n includes the number of cycles passed. The w-axis is identical to the τ-axis.

• The four-dimensional distance between two points in E₄-B is given by $d_{4D}=\sqrt{\Delta x^2+\Delta y^2+\Delta z^2+\Delta w_c^2}$, see Figure 1, where the values Δx, Δy, Δz and Δw_c are coordinate differences between the points. As Δw_c is always small (Δw_c ≤ $\overline{w}/2$), the four-dimensional distance d_4D is typically almost identical to the ordinary three-dimensional distance $d_{3D}=\sqrt{\Delta x^2+\Delta y^2+\Delta z^2}$. On the other hand, the length of the 4D path of a particle in space E₄-B is given by formula $c\Delta t=\sqrt{\Delta x^2+\Delta y^2+\Delta z^2+\Delta w_n^2}$.

• The EMST assumes existence of the “stationary coordinate system” which differs from all other (inertial) coordinate systems in that light moves in all directions at the same speed within it.

• In the stationary coordinate system, all particles of matter move at the same 4D speed which is equal to the speed of light (v_4D = c). The coordinate time is thus just another way to express a path, and it is not a separate or independent quantity. No extra time axis (used in SR and some Euclidean relativity theories) is needed. All of the physical world, i.e., space, time and matter, can thus be contained in four-dimensional space E₄-B.

• Since the speed of light is the only allowable speed for the matter in E₄-B, all methods of length and time interval measurements are mutually dependent. Systematic errors in the measurement of both types of quantities compensate for each other and cause all particles of matter to appear to move at the speed of light relative to any inertial reference frame. This is the origin of the apparent invariance of the speed of light in all reference systems.

• As a result of the above, it is impossible to determine which system is stationary by physical experiments, and therefore all coordinate systems appear to be equivalent.

• Another consequence of motion of particles in E₄-B space and their equal velocities is the real deformation of bodies in the direction of their motion - the so-called Lorentz-FitzGerald contraction (see [9]).

For the purposes of this article, it is necessary to recall some other relevant EMST relationships:

Figure 1

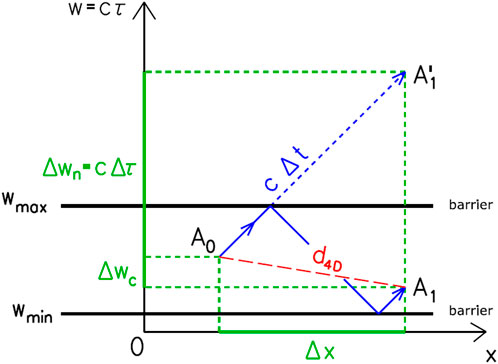
Figure 1. Motion of particle A from position A₀ to position A₁ in the x-w plane. The continuous blue line shows the actual cyclical motion in E₄-B, and the dashed blue line shows fictitious linear motion in E₄. The corresponding coordinate increments are Δx, Δw_n and Δw_c. The four-dimensional distance $d_{4D}=\sqrt{\Delta x^2+\Delta w_c^2}$ is typically much shorter than the path of the particle $c\Delta t=\sqrt{\Delta x^2+\Delta w_n^2}$. The two thick lines marked w_min and w_max are the barriers bounding space E₄-B.

The magnitude of 4D velocity v_4D is given by formula

$v_{4D}=\sqrt{v_x^2+v_y^2+v_z^2+v_w^2}=\sqrt{v_{3D}^2+v_w^2}=c(2)$

where v_x, v_y, v_z and v_w are components of the 4D velocity vector (in E₄-B) while v_3D is standard three-dimensional velocity (in ordinary E₃ space with coordinates x, y, z).

Substituting $v_{3D}=\sqrt{\delta x^2+\delta y^2+\delta z^2}/\delta t$ into Equation 1 gives $c^2\delta {\tau }^2=c^2\delta t^2-v_{3D}^2\delta t^2$. Thus,

$\delta \tau =\sqrt{1-\frac{v_{3D}^2}{c^2}}\delta t(3)$

which, is the formula for time dilation known from SR.

4D momentum p_4D is introduced by relation

$p_{4D}=\sqrt{p_x^2+p_y^2+p_z^2+p_w^2}=\sqrt{p_{3D}^2+p_w^2}$

where p_x, p_y, p_z and p_w are components of the 4D momentum vector and p_3D is standard three-dimensional momentum.

Four-dimensional Lorentz transformation is given by the following set of formulas:

$x=\frac{x^{\prime }+u{t}^{\prime }}{\sqrt{1-\frac{u^2}{c^2}}},y=y^{\prime },z=z^{\prime },w=w^{\prime },t=\frac{t^{\prime }+\frac{u}{c^2}{x}^{\prime }}{\sqrt{1-\frac{u^2}{c^2}}}$

here u is three-dimensional velocity of coordinate system S′ (x′, y′, z′, w′) with regard to system S (x, y, z, w). The velocity u is parallel to x.

The following relations are also valid

$p_{4D}=mc=\frac{E}{c}(4)$

$\left|p_w\right|=m_{0}c=\frac{E_0}{c}$

where m/m₀ is the relativistic/rest mass of the body, E/E₀ its total/rest energy and $\left|x\right|$ stands for the absolute value of x.

The reasoning behind all the above statements and derivation of the formulas is given in [9].

2 The origin of the same 4D speed of matter

The EMST is based on the assumption that all particles of matter move in E₄-B at the same 4D speed. This may seem illogical and unlikely, but only until we recall that matter has the wave form as well as the particle form. If matter is a wave and is moving in a non-dispersive medium, we can expect it to behave exactly this way.

In many physical media, waves propagate at a speed which is independent of the frequency, amplitude or shape of the waves. We call such transmission media non-dispersive. The speed of wave propagation within them depends only on the mechanical properties of the given medium, e.g., the stress and specific mass for strings, or the elastic modulus and density for solids. If these properties do not depend on position (homogeneity) and direction (isotropy) within the medium, the waves propagate through it at all points and in all directions with the same speed.

Let us start from two assumptions:

• Let us assume that space E₄-B is filled by a non-dispersive, homogeneous and isotropic medium. This medium is at rest with regard to the stationary coordinate system.

• Let us accept de Broglie’s hypothesis that all matter has a wave nature, i.e., matter is a demonstration of the wave motion of the medium filling space E₄-B.

From these assumptions, it follows that all matter must move with regard to the stationary system at the same 4D speed. Experiments with photons tell us that this speed is the “speed of light” c. We can establish the consequent conclusion:

The origin of the same 4D speed of all matter is a direct consequence of the fact that all observable matter has a wave nature and the medium through which it propagates is non-dispersive, homogeneous and isotropic.

The waves which form the matter move forwards all the time: they cannot be stopped; they cannot move faster or slower. Their speed is determined only by the properties of the “transmission medium”. At this moment, it is not important what the medium is. It suffices to assume that such a medium exists, it is non-dispersive, homogeneous and isotropic, and it totally fills space E₄-B.

3 Motion of the particle-wave in space E₄

The finding that matter has the form of waves moving through 4D space at the speed of light c is very important. This applies to all particles of matter regardless of their rest mass m₀. It applies both to photons (with m₀ = 0) as well as all particles with non-zero m₀. While the photon moves only in E₃, i.e., its v_w is zero and v_3D is equal to c, particles with non-zero m₀ also move in the fourth dimension and their v_3D velocity is less than c, see Equation 2. In other aspects, there is no significant difference between the particles of light and of other matter.

The fact that all particles move in four-dimensional space E₄-B with the speed of light c makes it possible to simplify the concept of wave-particle duality. It is possible to identify the particle directly with its wave, both propagating at the same speed, direction and frequency.

Let us reformulate the concept of a particle of matter in unbounded space E₃ into the concept of a particle-wave in E₄-B.

The particle-wave concept is based on the wave nature of all matter and the principles of the EMST. Instead of the duality of particles and their de Broglie waves, this concept works with particles represented by the real wave motion of the transmission medium in E₄-B. In order to emphasize the real wave nature of elementary particles of matter, and consequently their non-zero dimensions, they will be referred to as “particle-waves” within this text. The terms “particle” and “particle-wave” will be synonyms in the rest of this paper.

Particles of matter (particle-waves) are quanta of energy moving in space E₄-B at the speed of light. Quanta take the form of waves, and their energy is defined by the Planck-Einstein relation

$E=hf(5)$

Each particle is represented by its own wave, or, to be more precise, by a wave packet. A wave packet is a localized group of waves which is created, according to Fourier theory, by the superposition of an infinite number of harmonic (i.e., sine) waves of different but similar frequencies. The energy of the packet is spread continuously within the part of space which the packet covers.

The fact that particle-wave energy is defined by relation Equation 5 means that a packet cannot be divided into more parts without a change in the wave frequency. Otherwise, the energy conservation law would be violated. For this reason, a wave packet is indivisible, and a particle-wave enters all interactions with the whole of its energy and momentum. It therefore exhibits both wave-like and particle-like properties. Since the Planck-Einstein relation cannot be derived from the EMST postulates, it must be accepted as a further postulate of the theory.

For the purposes of this paper, the dimensions of particle-waves are not important. Their wave properties, especially their wavelength and frequency, are at the focus of attention. For simplicity of reasoning, particle-waves will not be understood as wave packets, but as infinite harmonic plane waves with a single frequency. The conclusions will not be affected by this simplification. From a physical point of view, this situation corresponds to the case of a free particle with an exactly known momentum but an unknown position.

3.1 Free particles in space E₄

In the first step, it suffices to study the motion of particle-waves in unbounded space E₄. The effect of the barriers in the fourth spatial dimension will be discussed later in Section 4.

Any wave can be understood as a phase ψ distributed in space. A certain value of phase $\mathit{\psi }\in \langle 0,1)$ is allocated to each point in space E₄ at a given moment. Points with the same ψ value create planes, or to be more exact, three-dimensional hyperplanes in E₄. For a free particle represented by a harmonic plane wave, these hyperplanes (wave fronts) are mutually parallel and perpendicular to the direction of the wave motion. The distance between neighboring hyperplanes of the same phase equals the wavelength λ_4D,

${\lambda }_{4D}=\frac{c}{f}$

The 4D momentum of a particle can be derived from the relation Equation 4 by substitution for E,

$p_{4D}=\frac{E}{c}=\frac{h\hspace{0.33em}f}{c}=\frac{h}{{\lambda }_{4D}}(6)$

A plane wave representing a particle with the wavelength λ_4D moves through space E₄ in any spatial direction s_4D, which makes an angle α to the axis w (Figure 2). We shall label s_3D the orthogonal projection of the direction s_4D into space E₃ with axes x, y, z. By ‘the orthogonal projection’ is meant the substitution of s_4D direction vector (x, y, z, w) by s_3D direction vector (x, y, z, 0). Direction s_3D will be used as an auxiliary axis in some considerations below.

Figure 2

Figure 2. A plane wave moving through space E₄ with velocity c. Hyperplanes with phase ψ = 0 are marked as well as projections of wavelength λ_4D into axes w and s_3D.

The 3D velocity of a particle is determined by the formula

$v_{3D}=c\mathit{sin}\alpha$

the velocity in the fourth dimension analogically being

$v_w=c\mathit{cos}\alpha$

It should be noted that

$\mathit{sin}\alpha =\frac{v_{3D}}{c},\hspace{0.17em}\mathit{cos}\alpha =\sqrt{1-\frac{v_{3D}^2}{c^2}}$

The wavelength of a particle λ_4D projects itself into the directions of axes s_3D and w as λ_3D and λ_w respectively,

${\lambda }_{3D}=\frac{{\lambda }_{4D}}{\mathit{sin}\alpha }={\frac{c}{v_{3D}}\lambda }_{4D}$

${\lambda }_w=\frac{{\lambda }_{4D}}{\mathit{cos}\alpha }=\frac{{\lambda }_{4D}}{\sqrt{1-\frac{v_{3D}^2}{c^2}}}$

The geometrical relation for the wavelengths

$\frac{1}{{\lambda }_{4D}^2}=\frac{1}{{\lambda }_{3D}^2}+\frac{1}{{\lambda }_w^2}$

can easily be derived from the similarities of triangles OBA and COA (Figure 2).

The wavelength λ_3D can be further projected into the directions of the coordinate axes x, y and z. The values of λ_x, λ_y, λ_z are given by the relation

$\frac{1}{{\lambda }_{4D}^2}=\frac{1}{{\lambda }_x^2}+\frac{1}{{\lambda }_y^2}+\frac{1}{{\lambda }_z^2}+\frac{1}{{\lambda }_w^2}(7)$

If we multiply relation Equation 7 by the square of Planck’s constant, we obtain

$\frac{h^2}{{\lambda }_{4D}^2}=\frac{h^2}{{\lambda }_x^2}+\frac{h^2}{{\lambda }_y^2}+\frac{h^2}{{\lambda }_z^2}+\frac{h^2}{{\lambda }_w^2}$

This relationship is very important because it expresses the decomposition of the 4D momentum of the particle $p_{4D}=h/{\lambda }_{4D}$ in the directions of the coordinate axes. It is thus equivalent to the relation

$p_{4D}^2=p_x^2+p_y^2+p_z^2+p_w^2$

It is clear that

$\left|p_x\right|=\frac{h}{{\lambda }_x},\left|p_y\right|=\frac{h}{{\lambda }_y},\left|p_z\right|=\frac{h}{{\lambda }_z},\left|p_w\right|=\frac{h}{{\lambda }_w}(8)$

and also

$p_{3D}=\frac{h}{{\lambda }_{3D}}(9)$

The last relation is very interesting as it is the famous de Broglie relation for the momentum of an arbitrary particle [11]. This fundamental relation of all quantum mechanical theories is derived here within the framework of EMST, i.e., relativistic theory!

It can be determined from the facts mentioned above that the de Broglie relation has a purely geometric origin. It is a result of the projection of a wave representing a particle in E₄ (or to be more exact in E₄-B) into E₃. In this projection the wavelength of the particle increases (${\lambda }_{3D}={\lambda }_{4D}/\mathit{sin}\alpha$), while its momentum simultaneously decreases ($p_{3D}=p_{4D}\mathit{sin}\alpha$).

In space E₄ the velocity of particle v_4D is always equal to the phase velocity of wave v_f,4D, which represents it, i.e., $v_{4D}=v_{f,4D}=c$. However, this is not true for its projection into E₃. While the 3D velocity of the particle is an orthogonal projection of the speed c into space E₃, i.e.,

$v_{3D}=c\mathit{sin}\alpha (10)$

the phase velocity $v_{f,3D}$ is result of a different projection, see Figure 3. It holds that

$v_{f,3D}=\frac{c}{\mathit{sin}\alpha }(11)$

Figure 3

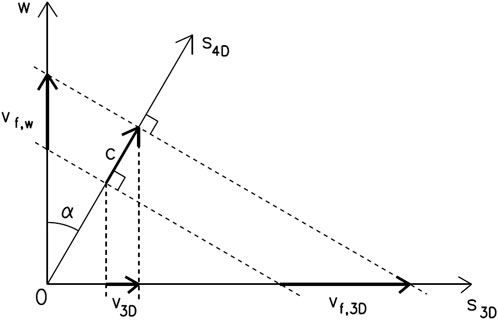
Figure 3. Projection of the velocity of a wave from space E₄ into space E₃. Two different 3D velocities, group velocity v_3D and phase velocity v_f,3D, correspond to the 4D velocity c.

We obtain a relationship between the group velocity and the phase velocity of a particle-wave in E₃ inserting Equation 10 into Equation 11,

$v_{f,3D}=\frac{c^2}{v_{3D}}(12)$

The relation Equation 12 is part of de Broglie’s theorem of phase harmony, and as such an integral part of any relativistic quantum theory. It links the speed of a de Broglie wave with the speed of the relevant particle of mass.

3.2 Lorentz transformation of plane waves in space E₄

In the EMST, just as in SR, transition between two mutually moving coordinate systems is achieved through Lorentz transformation. Transformation equations are linear with regard to spatial coordinates, and a plane wave thus transforms into a plane wave again. However, the transformed wave generally differs in its velocity, direction and wavelength from the original one.

The simplest situation occurs with the velocity. As mentioned above, the 4D speed of all objects equals c, which is applicable for any system of reference. It holds for a system S in rest as well as for system S′ in motion, $v_{4D}^{\prime }=v_{4D}=c$.

The direction of propagation of waves is always perpendicular to the hyperplanes of the constant phase ψ. The orientation of these hyperplanes with regard to the coordinate system is given by the wavelengths λ_x, λ_y, λ_z and λ_w. For a hyperplane with phase ψ which passes through the origin of the coordinate system O(0, 0, 0, 0), a neighboring hyperplane with the same phase ψ passes through four points, which can be obtained by placing the wavelengths λ_x, λ_y, λ_z and λ_w on the relevant coordinate axes.

Although it would be possible to derive the changes in wavelengths λ_x, λ_y, λ_z and λ_w using the Lorentz transformation formulas, it will be easier to use the transformation formulas for the 4D momentum components [9]:

$p_x^{\prime }=\frac{p_x-\frac{u}{c}{p}_{4D}}{\sqrt{1-\frac{u^2}{c^2}}},p_y^{\prime }=p_y,p_z^{\prime }=p_z,p_w^{\prime }=p_w,p_{4D}^{\prime }=\frac{p_{4D}-\frac{u}{c}{p}_x}{\sqrt{1-\frac{u^2}{c^2}}}(13)$

During the transition from S to S′ the momentum components in the directions perpendicular to u do not change. So it holds that ${\lambda }_y^{\prime }={\lambda }_y$, ${\lambda }_z^{\prime }={\lambda }_z$, ${\lambda }_w^{\prime }={\lambda }_w$. The value of λ_x is given by ${\lambda }_x=\frac{h}{\left|p_x\right|}$.

It can be seen that the Lorentz transformation changes only one of the wavelengths determining the direction of the hyperplanes of the constant phase. It is the one in the direction of the velocity u. The transformation has a simple form from the geometric point of view. A few examples will be shown hereinafter. These are cases for wave motion in the x-w plane, i.e., those where at least two of the four components of plane wave velocity are zero. Such cases can be easily drawn on a two-dimensional sheet of paper.

Let us start with the case v_y = v_z = 0. It holds that ${\lambda }_y^{\prime }={\lambda }_y=\infty$ and ${\lambda }_z^{\prime }={\lambda }_z=\infty$ here.

Figure 4 shows a change in the direction s_4D as well as in the wavelength λ_4D of a particle-wave as a result of the change in the reference system. During the transition from system S to system S′, the particle momentum components transform according to Formula 13. The wavelengths in the direction of the coordinate axes transform according to Equation 8, the wavelength λ_4D according to Equation 6. It is worth noticing that λ_w, i.e., the projection of the wavelength of the particle into the direction of axis w, never changes. This wavelength is an invariant of the Lorentz transformation.

Figure 4

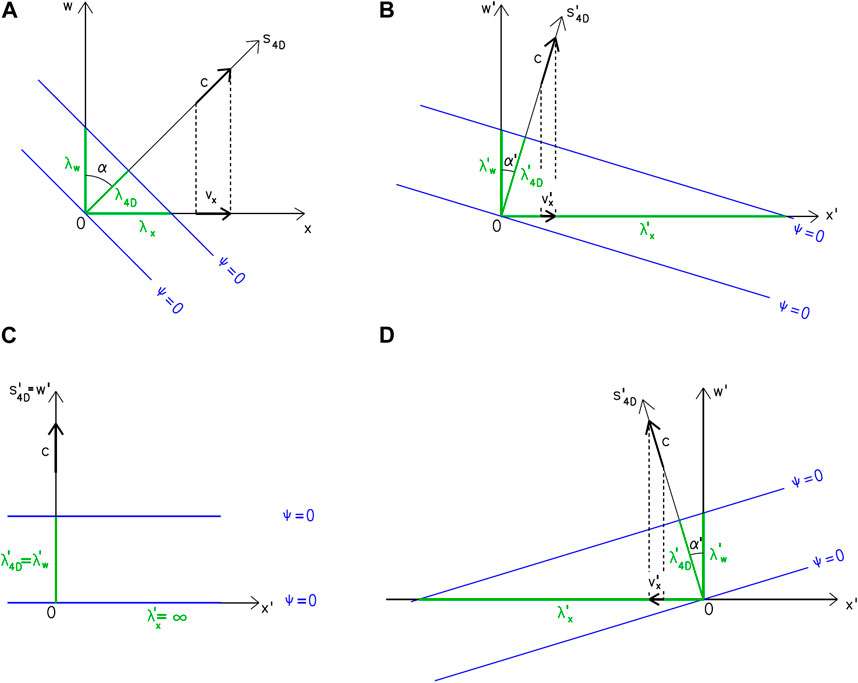
Figure 4. The Lorentz transformation of a plane wave representing a particle moving in the direction of axis x with velocity v_x. (A) Initial situation (system S). The other three figures show the situation from the viewpoint of system S′. The cases differ in terms of parameter u–i.e., the mutual velocity of the systems; (B) u < v_x; (C) u = v_x; (D) u > v_x.

For u equal to the 3D velocity of the particle ($u=v_x$) it holds that $v_x^{\prime }=0$ and ${\lambda }_x^{\prime }=\infty$ (Figure 4C). This situation describes the particle at rest in system S′. Its λ′_4D is maximal and its momentum p_4D and total energy E minimal.

For u > v_x (Figure 4D), the velocity v′_x has the opposite direction to v_x, λ′_4D is shorter than in the previous case and the energy E increases again.

Another interesting case is a particle with zero rest mass m₀. Its momentum in the fourth dimension equals zero $p_w=m_{0}c=0$, and thus ${\lambda }_w=\infty$. The front of the particle-wave is parallel to the w-axis, i.e., the angle of its motion α = π/2. The particle velocity in the fourth dimension $v_w=0$, and so $v_{3D}=v_{4D}=c$. According to the principle of the same 4D speed, such a particle must always move in E₃ at the speed of light. The Lorentz transformation changes its direction of propagation and wavelength (these phenomena are known as aberration of light and the Doppler effect), but never its speed.

The case for v_y = v_z = 0 is shown in Figure 5. In this special case, only the wavelength of the particle changes; the direction remains unchanged.

Figure 5

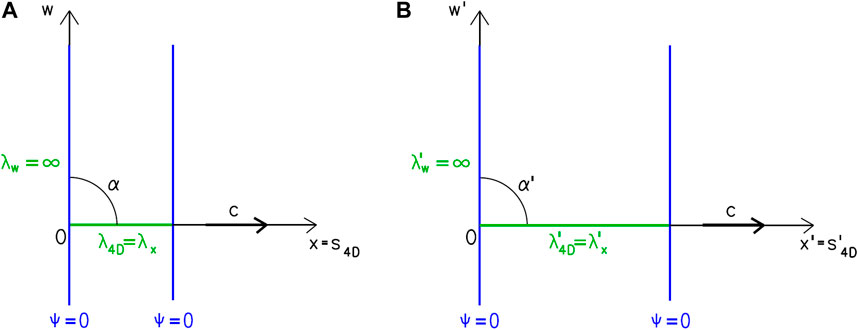
Figure 5. The Lorentz transformation of a plane wave representing a photon moving in the direction of axis x. During the transition from system S to system S′ (moving in the direction of axis x), the direction of the photon’s motion does not change but its wavelength does. (A) Situation from the viewpoint of system S; (B) Situation from the viewpoint of system S′.

Let us examine another example in which both the wavelength and the direction of propagation of a particle with m₀ = 0 changes.

Let us consider a system S with a photon with frequency f₀ in it. The photon is moving in the direction of axis y, i.e., perpendicular to the direction in which system S′ moves. In system S it holds for the photon that v_y = c, v_x = v_z = v_w = 0 (Figure 6). In system S′, this photon moves with unchanged speed c, but in a different direction. It holds that v′_z = v′_w = 0 and ${v^{\prime }}_x^2+{v^{\prime }}_y^2=c^2$ where $v_x^{\prime }=-u$. The similarity of the triangles gives $v_y^{\prime }/c={\lambda }_{4D}^{\prime }/{\lambda }_y^{\prime }$ and thus

${\lambda }_{4D}^{\prime }=\frac{v_y^{\prime }}{c}{\lambda }_y^{\prime }$

Figure 6

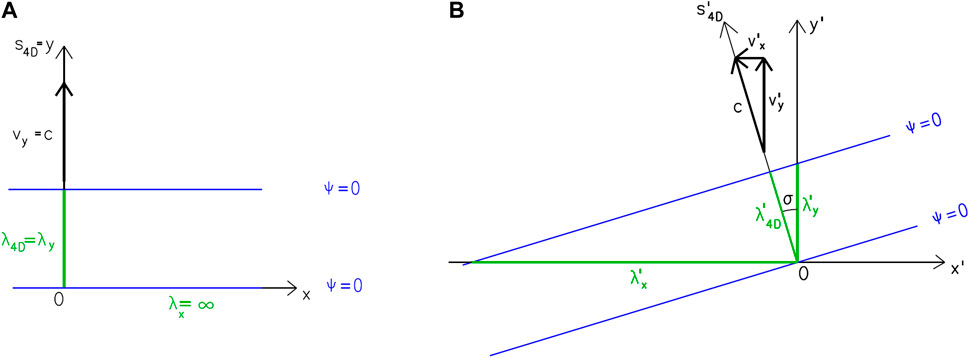
Figure 6. The Lorentz transformation of a plane wave representing a photon moving in the direction of axis y. During the transition from system S to system S′ (moving in the direction of axis x), both the direction of the particle (due to the aberration of light) and its wavelength λ_4D (due to the transverse Doppler effect) change. If in both figures the symbols y and σ were exchanged for w and α, respectively, they would depict the Lorentz transformation of a plane wave representing a particle at rest. The transition from system S to system S′ is accompanied by a decrease in the wavelength of the particle λ_4D and an increase in its total energy $E=hc/{\lambda }_{4D}$. (A) Situation from the viewpoint of system S; (B) Situation from the viewpoint of system S′.

Using ${\lambda }_y^{\prime }={\lambda }_y=c/f_0$, ${\lambda }_{4D}^{\prime }=c/f^{\prime }$ and ${v^{\prime }}_x^2/c^2+{v^{\prime }}_y^2/c^2=1$ we obtain

$\frac{c}{f^{\prime }}=\sqrt{1-\frac{{v^{\prime }}_x^2}{c^2}}\frac{c}{f_0}$

and after some editing

$f^{\prime }=\frac{f_0}{\sqrt{1-\frac{u^2}{c^2}}}(14)$

Formula 14 gives the frequency f′ of the photon as measured in system S′. We have arrived at the formula for the transverse Doppler effect.

Let us modify the task. Now the wave with frequency f₀ does not move in the direction of axis y, but in the direction of axis w. It does not represent a photon in motion but instead a massive particle at rest (v_w = c, v_x = v_y = v_z = 0). Its energy is given by the formula E₀ = hf₀.

From the viewpoint of system S′, the particle moves with velocity $v_x^{\prime }=-u$. Its energy is E′ = hf′.

The relationship between frequencies f₀ and f′ remains the same as in the case of the transverse Doppler effect; the only difference is that axis w replaces axis y in the process of its derivation. Again, we obtain Formula 14. Between the mass of the same particle at rest (m₀) and in motion (m′) the following formula applies

$m^{\prime }=\frac{m_0}{\sqrt{1-\frac{{v^{\prime }}_x^2}{c^2}}}$

It can be seen that the nature of relativistic mass increase, as well as of the transverse Doppler effect, is purely geometric. In principle, there is no difference between them.

3.3 Doppler effect in an arbitrary direction

Formula 13 describing the transformation of p_4D can be used to derive a general formula for the Doppler effect. Using the substitutions of $p_{4D}=h/{\lambda }_{4D}=hf/c$ and $p_x=p_{3D}\mathit{cos}\phi$, we obtain:

$p_{4D}^{\prime }=\frac{h{f}^{\prime }}{c}=\frac{\frac{hf}{c}-\frac{u}{c}\frac{hf}{c}\mathit{cos}\phi }{\sqrt{1-\frac{u^2}{c^2}}}$

where the quantity φ is the angle that the motion of the particle makes with the x-axis. For a photon $p_{3D}=p_{4D}$.

After some modifications we obtain

$f^{\prime }=\frac{f\left(1-\frac{u}{c}\mathit{cos}\phi \right)}{\sqrt{1-\frac{u^2}{c^2}}}(15)$

The formula gives the frequency f′ of a photon that we would measure in system S′ if it has frequency f in system S and moves at an angle φ with respect to the x-axis. The quantity u is the velocity at which system S′ moves relative to system S. The formula is identical to the formula derived by Einstein in the SR framework, see [1]. The Formula 14 derived earlier is a special case of Equation 15 for φ = π/2.

3.4 Invariant wavelength of a particle-wave

It was shown above that the value of λ_w is an invariant of the Lorentz transformation. The wavelength λ_w of a particle-wave is related to its rest mass m₀ by formula

${\lambda }_w=\frac{h}{m_{0}c}(16)$

It is obvious that λ_w can only change with a change in the rest mass of the particle. Thus, it does not change during the Lorentz transformation, nor during any of the physical interactions in which the rest mass of the particle is conserved.

It is not without interest that Formula 16 is used in particle physics to determine the so-called Compton wavelength. For that, an identical formula holds: ${\lambda }_c=h/m_{0}c$.

The quantity λ_w is thus numerically equal to λ_c, but has a clear geometric meaning. The quantity λ_w is not only an alternative way to express the inertial properties of a particle (its rest mass), it is also projection of the real wavelength of that particle into one of the spatial dimensions.

4 Motion of a particle-wave in E₄-B

In Section 3, the motion of particle-waves in E₄ space, i.e., in an unbounded four-dimensional space, was considered. However, the presence of barriers in the fourth dimension significantly affects the motion. In this section it will be shown how.

4.1 Space E₄-B as a waveguide

A particle-wave with m₀ ≠ 0 moving through space E₄-B periodically reflects from the barriers in the fourth dimension, and the incident and reflected waves compose a superposed wave. As the projections λ_w of the wavelength λ_4D of both waves are the same, the superposed wave has the character of a standing wave (normal-mode vibration) in the fourth dimension. In the remaining three dimensions nothing disrupts the free propagation of the composed wave, and so it forms a travelling wave (Figure 7). The 2D variant of this phenomenon is described in detail in [12].

Figure 7

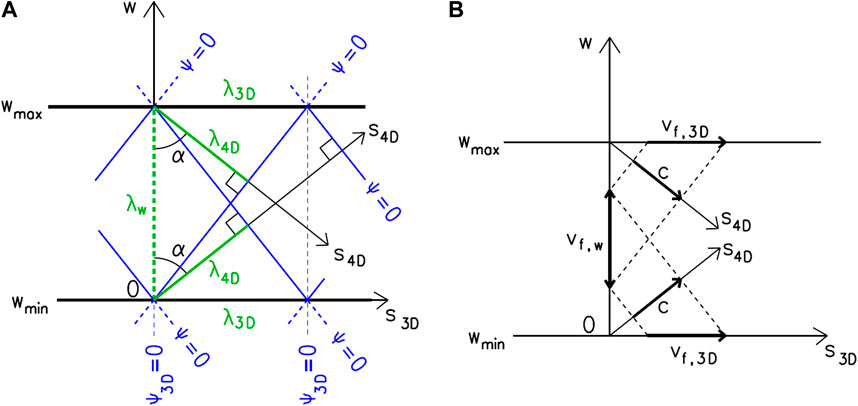
Figure 7. Propagation of a wave in the space between the barriers. A plane wave forming angle α with axis w is combined with its reflection. (A) Zero phases of the original and superposed waves; (B) Phase velocities.

In principle, space E₄-B is a specific kind of four-dimensional waveguide which only restricts the propagation of waves in one of the dimensions (flat waveguide). The side ratio x:y:z:w of this “world waveguide” is $\infty :\infty :\infty :\overline{w}/2$.

Just as we do not know the nature of the waves representing matter in E₄-B, so we do not know the nature of the barriers that confine them. In principle, there are two types of barriers enclosing a waveguide. They could be fixed boundaries with zero wave amplitude on them (nodal surfaces) or free boundaries with non-zero amplitude (with antinodes) on them. An example of the first type is an electromagnetic waveguide, an example of the second is mechanical waves in a long steel rod. It is reasonable to assume that both barriers enclosing space E₄-B are of the same type.

Regardless of the type of the barriers, the incident and reflected waves interfere inside the world waveguide. Just like other waveguides, this one also has its modes. They differ in terms of the values of the wavelength λ_w. Based on the fact that constructive interference should occur during the superposition of waves and both barriers are of the same type, the distance between the barriers $\overline{w}/2$ must be the whole multiple of half of the wavelength λ_w. Otherwise, any wave motion between the barriers would spontaneously disappear as a result of destructive wave interference.

The wave must fulfil the condition

$n\frac{{\lambda }_w}{2}=\frac{\overline{w}}{2}(17)$

where n is a nonnegative integer which defines the relevant mode of the wave motion.

This condition must be fulfilled by all particles with the lifetime longer than 1 × 10⁻²⁰ s. Particles with the shorter lifetime will not travel a distance significantly longer than $\overline{w}$ and thus will not produce standing waves between the E₄-B barriers.

Relationships between λ_w and other quantities such as p_w, E₀ and m₀ imply that condition Equation 17 limits the set of acceptable rest masses of long-lived particles. Their masses can thus only gain certain selected values. Values λ_x, λ_y and λ_z can change continuously, as can the momentum p_3D and the kinetic energy of particles.

The waves in space E₄-B have a somewhat different character than in E₄, but the main parameters that characterize them, i.e., frequency, velocity and angle α, remain unchanged. All the relationships presented in Section 3 remain valid.

4.2 Distance of the barriers in the fourth dimension

The value n = 1 from Formula 17 corresponds to the fundamental mode of the waveguide, i.e., the mode with the largest wavelength. For this the relation ${\lambda }_w=\overline{w}$ holds.

It is possible to accept the assumption that the fundamental mode of the waveguide corresponds to the wavelength of the electron, i.e., the lightest particle with non-zero rest mass (m_e = 9.11.10^–13 kg). According to Equation 16, its wavelength is equal to λ_w,e = 2.43 × 10⁻¹² m. The barrier distance $\overline{w}/2$ in this case comes out to be 1.21 × 10⁻¹² m. It would be too early to consider this value as a proven barrier distance, but it can be considered as an initial estimate.

It may be mentioned that the electron wavelength λ_w,e given above is equal to the circumference of the (fictitious) first Bohr orbit of the hydrogen atom (with radius a₀ = 5.3 × 10⁻¹¹ m) multiplied by the fine structure constant $\overline{\alpha }$.

$2\pi a_0\overline{\alpha }=2.43\times {10}^{-12}\mathrm{m}$

4.3 The second de Broglie frequency

It was mentioned in the Introduction that de Broglie assumed two different frequencies, f and f₁, for each particle of matter in motion. Their relationship to the frequency f₀ of a particle at rest is

$f_0=\frac{f_1}{\sqrt{1-\frac{v_{3D}^2}{c^2}}}=f\sqrt{1-\frac{v_{3D}^2}{c^2}}(18)$

In the submitted four-dimensional concept of particle-waves, every particle of matter in motion is represented by a wave with the frequency $f=f_0/\sqrt{1-v_{3D}^2/c^2}$, which is consistent with de Broglie’s assumption. It holds that $f=c/{\lambda }_{4D}$.

However, the particle-wave also moves in the space between the barriers. It reflects from them and the frequency of motion between the barriers (cyclic frequency) is different from the own frequency of the particle-wave. This frequency is a function of the path of the particle-wave between individual reflections. Its path Δs_4D increases with the growing 3D velocity of the particle in reference system S, and the cyclic frequency decreases reciprocally (Figure 8). For a particle at rest in S it holds that $f_0=c/\left(2\Delta s_{4D}\right)=c/\overline{w}$, while for a particle in motion $f_1=c/\left(2\Delta s_{4D}\right)=\left(c/\overline{\mathrm{w}}\right)\left(1/\mathit{cos}\alpha \right)=\left(c/\overline{w}\right)\left(v_w/c\right)=c/\overline{w}\sqrt{1-v_{3D}^2/c^2}$. So, it holds that $f_1=f_0\sqrt{1-v_{3D}^2/c^2}$. The presented example is for a particle-wave with ${\lambda }_w=\overline{w}$.

Figure 8

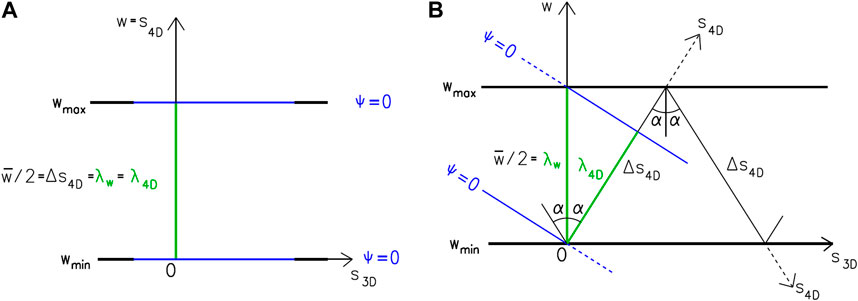
Figure 8. The change in a particle’s wavelength λ_4D and its path between the barriers Δs_4D as a result of a change in its 3D velocity. (A) Particle at rest; (B) particle in motion. The presented example is for ${\lambda }_w=\overline{w}$.

Comparison with Equation 18 shows that the second frequency f₁ predicted by de Broglie also has a physical meaning. It expresses the periodicity of particle-wave cyclic motion between the barriers, and is thus related to the flow of proper time. The resulting effect is in full accordance with description of time dilation and Formula 3 above.

It remains to show that for an observer moving with a particle, both frequencies are the same and equal to f₀. For such an observer, the cyclic frequency f₁ is apparently higher than for an observer at rest. This is caused by the use of slower reference clocks in the system in motion S′

$f_1^{\prime }=\frac{f_1}{\sqrt{1-\frac{v_{3D}^2}{c^2}}}(19)$

The frequency of waves f is also affected by the slowing down of moving clocks, but it is also affected by the Doppler effect. The observer is moving in the same direction as the waves and the frequency will thus decrease

$f^{\prime }=\frac{f}{\sqrt{1-\frac{v_{3D}^2}{c^2}}}\frac{v_{f,3D}-v_{3D}}{v_{f,3D}}$

The formula can be modified by the use of substitution for v_f,3D from Equation 12

$f^{\prime }=\frac{f}{\sqrt{1-\frac{v_{3D}^2}{c^2}}}\frac{\frac{c^2}{v_{3D}}-v_{3D}}{\frac{c^2}{v_{3D}}}=\frac{f}{\sqrt{1-\frac{v_{3D}^2}{c^2}}}\frac{\frac{c^2}{v_{3D}}\left(1-\frac{v_{3D}^2}{c^2}\right)}{\frac{c^2}{v_{3D}}}=f\sqrt{1-\frac{v_{3D}^2}{c^2}}(20)$

Comparison of Formulas 19, 20 with Formula 18 shows that $f_0=f_1^{\prime }=f^{\prime }$. Therefore, it is not possible to distinguish a system in motion from a stationary one by observing the mentioned frequencies.

5 Discussion

The particle-wave concept described above is simple, realistic and consistent with observed phenomena. The concept clarifies the origin of the well-known de Broglie formula for the momentum of a particle Equation 9 as well as the origin of de Broglie’s phase harmony theorem. The apparently strange properties of de Broglie waves are explained as a consequence of the projection of the particle-wave motion from E₄-B into E₃ space.

The particle-wave concept is fully relativistic invariant. It explains the change in momentum and energy during Lorentz boost, and explains the relativistic mass growth of a particle as well as the transverse Doppler effect. The author is not aware of any special relativistic phenomena with which the particle-wave concept is inconsistent.

The undisputed success of the particle-wave concept must be seen as a success of the EMST. This model of space and time makes it possible to identify a particle of matter with the wave and to prove the predictable fact - the wave carries all the particle’s energy.

The EMST has undeniable advantages over SR:

• The same velocity of all particles of matter, i.e., the basic postulate of the EMST, can be explained as a consequence of the fact that all matter has a wave nature.

• EMST describes relativistic phenomena such as time dilation, length contraction, and relativistic mass growth as a consequence of the same speed of all particles of matter. It is not necessary to claim that this is a property of an exotic spacetime metric as in the case of SR.

• EMST gives the particle-wave duality a much more obvious and realistic form. Each particle of matter is a wave of frequency f moving through space E₄-B at speed c. The particle and the wave occupy the same part of space, move at the same speed and in the same direction. This eliminates the need to consider the particle and the wave as two different manifestations of the same matter, differing in size and velocity.

• EMST explains the origin of the rest energy of matter. Even a body at rest is moving at the speed of light, or more precisely, all its particles are moving at that speed. What is termed “rest energy” has in fact a kinetic origin.

• EMST shows the identical geometric nature of the hitherto separately viewed phenomena of relativistic mass growth and the transverse Doppler effect.

• EMST explains the fundamental significance of the speed of light for the structure of the universe. It explains why particles with zero rest mass must move at the speed of light and why no matter can move faster. It explains why the speed of light appears as a mathematical constant in the Lorentz transformation as well as in a number of other formulas unrelated to the propagation of electromagnetic waves.

The EMST is nothing more than a logical description of a situation where waves representing matter move through a homogeneous isotropic medium. If matter does indeed have a wave nature, it has no choice but to move at the speed of light in all of the directions that a given space allows. The legitimacy of the fundamental assumption of the EMST, i.e., the same 4D speed of all particles of matter, is obvious.

If we assume the same speed of wave motion in all directions, we must also assume the existence of a reference frame to which this speed is related. Here we must seek the justification for the existence of the “stationary coordinate system,” which does not occur as a theoretical concept in SR.

The stationary coordinate system is physically represented by transmission medium filling space E₄-B. Its association with the Cosmic Microwave Background (CMB) [13] is attractive but only speculative at the moment. A cosmological model of the Universe based on the EMST that would resolve the relationship between the “stationary coordinate system” and the CMB is still missing.

The lack of experimental evidence regarding “stationary coordinate system” is not surprising. Theoretical analysis of the EMST shows that identification of the “stationary coordinate system” is difficult or even impossible [9]. The reason is the mutual dependence of distance and time measurements, where the motion of the system affects both types of quantities. Thus, the two-way speed of light always appears to be the same. The one-way speed of light cannot be determined for the same reason. The above explains the null results of all laboratory experiments designed to detect the rest frame of reference/stationary coordinate system, such as the Michelson-Morley experiment and its modern equivalents, see [14–16].

Equation 3 shows that the time of the stationary coordinate system passes faster than the time of any other coordinate system. Although the relativity of time passing can be proved in the EMST, it is only apparent (see [9]). The use of a common reference time (the time of the stationary coordinate system) leads to the conclusion that the (two-way) speed of light is slower in moving frames. The apparent constancy of the speed of light is only maintained by the corresponding slowing down of moving clocks. A variable speed of light of this type is not a violation of the Lorentz invariance [17].

The fact that EMST claims that all particles of matter move at the speed of light and at the same time assumes the existence of the stationary coordinate system may seem like a paradox. It must be remembered that any physical coordinate system must be tied to a rigid reference body of non-zero dimensions. Such a body consists of many particles of matter and as a whole is three-dimensional. The motion of its individual particles in the fourth dimension is imperceptible and, due to the cyclic nature of this motion, is zero on average. The physical body thus establish a coordinate system whose motion is limited to E₃. Nothing prevents the body from having zero 3D velocity and so being a reference for the stationary coordinate system.

Formula 5 assigns each particle a frequency f that is proportional to its total (relativistic) energy. Such frequency is commonly observed for photons, whereas it has not yet been observed for particles with m₀ ≠ 0. The main reason is the extremely high value of f. The minimum (for an electron at rest) is f = 1.2 × 10²⁰ Hz. However, an indirect observation of a higher order of this frequency is claimed [18].

The assumption that the world is bounded in the fourth dimension and takes the form of a flat waveguide is supported by the fact that the velocity dispersion relation Equation 12 valid in the “world waveguide” is identical to the velocity dispersion relation of an electromagnetic waveguide. In the second volume of his “Lectures on Physics” [12] (Section 24.4), Feynman draws attention to this surprising agreement with the explicit statement that it is interesting. However, he does not provide any explanation for it. This explanation is now provided by the EMST.

Another confirmation of the fact that space has the properties of a waveguide is hidden in the rest masses of particles. Based on Formulas 16, 17, it is certain that long-lived particle masses must satisfy the following:

1. The rest masses of particles cannot be arbitrary. Discrete spectrum of particles’ rest masses must correspond to the modes of the waveguide.

2. The rest masses of particles must be multiples of some fundamental mass, i.e., members of an arithmetic series. The corresponding formula within the EMST is m_n = hn/(c$\overline{w}$). Value m_n is the mass of the particle corresponding to the n^th mode of the waveguide.

A quick look at the rest masses of known particles shows that the first assumption is undoubtedly fulfilled - the spectrum of rest masses of particles with the lifetime longer than 1 × 10⁻²⁰ s is discrete, with significant gaps between neighboring masses.

That the second assumption is also fulfilled is suggested by previously published papers [19, 20]. These show that the masses of long-lived elementary particles (leptons, mesons as well as baryons) are, with an accuracy of about 1%, members of an arithmetic series. For example, n = 3 belongs to muons, n = 4 to pions, n = 14 to kaons, n = 27 to nucleons…. However, the rest masses of the particles (with the exception of the electron) are 1/ $2\overline{\alpha }$ times higher ($\overline{\alpha }$ is a fine structure constant) than the above formula gives, and many possible modes (values of n) do not belong to any known particle (n = 2, 5, 6…).

These partial inconsistencies show that the actual form of the waveguide and/or the nature of particle-wave motion within it is more complex than the simple model presented here assumes. Nevertheless, the fundamental fact remains clear - the rest masses of particles demonstrate that space behaves like a waveguide with respect to them.

In terms of studies of physical interactions at the subatomic level, an important contribution of the EMST is the discovery that distances are not defined in three-dimensional but in four-dimensional space. While in the domain of macroscopic distances the difference between the 3D and 4D variant of a distance is completely negligible, in the subatomic domain the situation is significantly different. Assuming $\overline{w}$/2 = 1.21 × 10⁻¹² m, the differences become more apparent at 3D distances smaller than the Bohr radius a₀ = 5.3 × 10⁻¹¹ m. The 4D distance will be longer than the 3D distance by up to 0.02% for particles with a 3D distance equal to a₀, up to 2% for a₀/10 and up to 250% for a₀/100. Such a difference is significant, and should be reflected in models of physical interactions at the subatomic level. Also, it should be detectable in physical experiments as a proof of the correctness of the EMST.

The author considers the main contribution of the EMST to be the ability to explain relativistic phenomena and the wave properties of matter within a single physical theory. The first attempt to combine these two approaches was made by de Broglie, and the “phase harmony theorem” cited above is his answer to the question of what properties matter waves must have in order to be relativistically invariant. It was difficult to find an acceptable solution because Minkowski space prevents the construction of a meaningful model of a particle as an energy-carrying wave propagating through space. Only the expansion of space by one dimension and the assumption of the same 4D speed made it possible to create a particle-wave that has no exotic properties and yet satisfies everything required. It meets the requirements of the phase harmony theorem exactly.

From the broader perspective of modern physics, the EMST has all the prerequisites to become the starting point for the mutual combination of “relativistic” and “quantum” physics into a single physical theory. It easily explains both: relativistic phenomena as well as wave properties of matter.

Data availability statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Author contributions

RM: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Project No. FAST-J-23–8386 Brno University of Technology.

Acknowledgments

The author would like to thank Brno University of Technology for supporting this research under project No. FAST-J-23–8386.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Einstein A. Zur elektrodynamik bewegter Körper. Annalen der Physik (1905) 322(issue 10):891–921. doi:10.1002/andp.19053221004

CrossRef Full Text | Google Scholar

2. Montanus H. Special relativity in an absolute euclidean space-time. Phys Essays (1991) 4(issue 3):350–6. doi:10.4006/1.3028916

CrossRef Full Text | Google Scholar

3. Montanus J. Proper time physics. Hadronic J (1999) 22(6):625–73.

Google Scholar

4. Montanus J. Proper-time formulation of relativistic dynamics. Foundations Phys (2001) 31(issue 9):1357–400.

Google Scholar

5. Almeida J. An alternative to Minkowski space-time. arXiv: Gen Relativity Quan Cosmology (2001) 18. doi:10.48550/arXiv.gr-qc/0104029

CrossRef Full Text | Google Scholar

6. Gersten A. Euclidean special relativity. Foundations Phys (2003) 33(issue 8):1237–51.

Google Scholar

7. Brannen C. The proper time geometry (2004). Available from: http://brannenworks.com/a_ptg.pdf (Accessed October 6, 2024).

Google Scholar

8. Crabbe A. Alternative conventions and geometry for special relativity. Ann de la Fondation Louis de Broglie (2004) 29(4):589–608.

Google Scholar

9. Machotka R. Euclidean model of space and time. J Mod Phys (2018) 09(issue 06):1215–49. doi:10.4236/jmp.2018.96073

CrossRef Full Text | Google Scholar

10. de Broglie L. Recherches sur la théorie des Quanta. Ann de Physique (1925) 10(issue 3):22–128. doi:10.1051/anphys/192510030022

CrossRef Full Text | Google Scholar

11. de Broglie L. The wave nature of the electron. Nobel Lectures Phys 1922-1941 (1965) 1:244–56.

Google Scholar

12. Feynman R, Leighton R, Sands M. The Feynman lectures on physics 2 6th ed. Massachusetts: Addison-Wesley (1977).

Google Scholar

13. Gawiser E, Silk J. The cosmic microwave background radiation. Phys Rep (2000) 333-4–245-67.

Google Scholar

14. Mattingly D. Modern tests of Lorentz invariance. Living Rev Relativity (2005) 8(1):5. doi:10.12942/lrr-2005-5

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Takamoto M, Ushijima I, Ohmae N, Yahagi T, Kokado K, Shinkai H, et al. Test of general relativity by a pair of transportable optical lattice clocks. Nat Photon (2020) 14(issue 7):411–5. doi:10.1038/s41566-020-0619-8

CrossRef Full Text | Google Scholar

16. Melia F. The seemingly preferred cosmic frame. Physica Scripta (2022) 97(issue 4):045001–11. doi:10.1088/1402-4896/ac5666

CrossRef Full Text | Google Scholar

17. Vavrycuk V. Cosmological consequences of the Lorentz and Doppler transformations. Mod Phys Lett A (2024) 39:2450098. doi:10.1142/S0217732324500986

CrossRef Full Text | Google Scholar

18. Catillon P, Cue N, Gaillard MJ, Genre R, Gouanère M, Kirsch RG, et al. A Search for the de Broglie Particle Internal Clock by Means of Electron Channeling. Found Phys (2008) 38:659–64. doi:10.1007/s10701-008-9225-1

CrossRef Full Text | Google Scholar

19. Nambu Y. An empirical mass spectrum of elementary particles. Prog Theor Phys (1952) 7(5-6):595–6. doi:10.1143/ptp.7.595

CrossRef Full Text | Google Scholar

20. Greulich K. Calculation of the masses of all fundamental elementary particles with an accuracy of approx. 1%. J Mod Phys (2010) 01(issue 05):300–2. doi:10.4236/jmp.2010.15042

CrossRef Full Text | Google Scholar