Design of one-dimensional phononic crystals comprising robust Fano edge modes as a highly sensitive sensor for alcohols

This work introduces various designs of phononic crystals (PnCs), referred to as topological phononic crystals (TPnCs), as novel, stable, and high-performance sensing tools. Meanwhile, we introduce the concept of the topological edge state to address the discrepancies between theoretical predictions and experimental results of PnC sensors. Consequently, the design of a PnC sensor structure that maintains high stability amidst fluctuations in layer manufacturing and deformations during construction represents the mainstay of our study. Notably, the numerical findings demonstrate the stability of the proposed sensor in the presence of various geometric changes. In addition, we assess the effectiveness of several periodic PnC designs in sensing the physical properties of fluids, specifically alcohols like butanol. Accordingly, temperature sensing of butanol is conducted over a wide range (170°C–270°C) by monitoring the displacement of Fano resonance modes. In this regard, the proposed PnC structure demonstrates an impressive sensitivity of 119.23 kHz/°C. Furthermore, our design achieves a high-quality factor and figure of merit of 378.23 and 1.085, respectively, across the temperature range of 170°C–230°C. These outcomes are promising for the development of ultrasensitive thermal sensors. Ultimately, our research provides valuable insights into the creation of highly sensitive and stable temperature sensors suitable for a range of industrial applications.

1 Introduction

Alcohols such as butanol are organic compounds characterized by one or more hydroxyl (-OH) groups attached to a carbon atom. Butanol is a volatile organic compound that could be extensively used in various industries, including the manufacture of paints, plastics, and pharmaceuticals, that introduces it as a common substance in modern life [1–5]. Despite its industrial importance, butanol poses significant health and safety risks due to its toxic and flammable nature. In this regard, prolonged exposure to butanol can cause respiratory discomfort, skin irritation, and neurological issues. Moreover, its flammability requires a careful monitoring to prevent potential disasters [3–6]. Given these hazards, it is crucial to develop sensitive and selective sensors that are capable of detecting butanol at different temperatures and infinitesimal concentrations of ppb levels [1–4], [6]. Such sensors could be of a significant interest towards high protection levels of human health and ensuring the safety of industrial processes as well. Therefore, in this research, we propose a temperature sensor for butanol using the one-dimensional phononic crystal (1D PnC) structure. In this context, temperature sensors measure temperature variations by detecting changes in some physical properties. Some of the previous research, such as the work introduced by Alaie et al., has explored an innovative method for measuring thermal conductivity via coherent phonon boundary scattering [7]. Building on these advancements, our proposed 1D PnC structure aims to enhance the development of novel temperature sensor technologies. While butanol serves as a key example in our study, the principles and applications of our sensor design are generalizable to a wide range of liquids, emphasizing the versatility and broad applicability of our approach.

Interestingly, PnCs, which provide unmatched flexibility, efficiency, and dependability, have become ground-breaking materials in the field of sensors. Periodic configurations of materials in one, two, or three dimensions with varying densities and elastic properties give rise to PnCs, which have unique qualities not found in the real environment [8–11]. PnCs can be used to control the propagating mechanical waves from the thermal energy range (THz) to the audible frequency range (1–20 kHz). Kushwaha et al. firstly proposed the concept of PnCs with the capacity to modify mechanical waves or to confine, transmit, or block their propagation at certain frequency ranges [12]. These artificial periodic structures are widely considered in many liquid sensing applications [10–13]. In this regard, these structures comprise two or more materials with different mass densities, elastic characteristics, and sound speeds in each unit cell [10–12]. Therefore, the periodic configuration of these structures could give rise to the emergence of some stop bands at some particular frequencies due to the destructive interference at the boundaries of PnCs’ layers [8, 10, 13]. These stop bands are defined as phononic band gaps (PnBGs). This response is similar to the electromagnetic Bragg condition in photonic crystals. Examining 1D PnCs can help us to understand the origin of PnBGs [8, 14, 15]. Interestingly, multiple scattering occurs at each interface between alternating layers, leading to the formation and reflection of secondary waves at each interface. PnBGs are introduced when the reflected waves constructively interfere. On the other side, acoustic waves flow easily through PnCs when destructive interference occurs [13, 16, 17]. Meanwhile, the PnBG property is exploited in numerous applications, including acoustic filters, ultrasonic imaging devices, noise reduction, sensors, acoustic metamaterial construction, and acoustic diodes [18–22]. One clear benefit of PnCs over traditional structures is their flexibility regarding several external factors, such as temperature and pressure. The properties of PnCs are determined by their filling fraction, geometry, elastic or acoustic qualities, inclusion material state, and lattice symmetry [11, 17]. Furthermore, PnCs are capable of sensing application due to the inclusion of cavities through it, which in turns breaks the periodicity and could give rise to the emergence of various resonance frequencies. Accordingly, the acoustic energy is confined by structural defects and may be extracted by using electromechanical techniques. As a result of their massive impedance mismatch, lead/epoxy materials are extensively applied in PnC designs and can offer substantial PnBGs [8–11]. As sensor technology becomes increasingly prevalent in many modern applications, PnCs have become particularly well-suited as materials for acoustic liquid sensors because they provide an attractive blend of durability, flexibility, and efficiency. PnCs are becoming progressively important in sensor technology, as seen in the creative and dependable acoustic sensing devices that have been become possible by researchers. Many studies have recently examined the use of PnCs in various sensing applications. For example, Lucklum et al. investigated the uses of new kinds of sensors based on 1D and two-dimensional (2D) PnCs in a range of technical and physical contexts [9].

However, a few basic issues could prevent PnC technology from developing further. One of these issues is the nonnegligible reduction in energy induced by mistakes in phononic device fabrication. Meanwhile, many attempts are established to develop physical principles in addition to fabrication techniques to tackle this obstacle. Topological PnCs (TPnCs) may offer a possible remedy for this type of issue [15], [23–26]. The study of geometric structures that preserves particular properties under continuous change is known as topology in mathematics. One key idea is a genus, which classifies closed surfaces by the number of holes or handles they possess [23–25], [27]. Genus resists tearing or merging and remains stable across deformations. Given their stability, geometric structures may be understood and categorized by using a strong framework that emphasizes enduring characteristics even in the face of shape changes [15, 25, 27, 28]. The emergence of topology into physics has allowed for some innovative phenomena that are robust against perturbations and may lead to transports that are impervious to flaws or issues. Recently, topology has been widely applied in several fields, including condensed matter [29–32], cold atoms [33, 34], acoustics [35–39] and mechanics [40, 41]. Devices investigated to direct elastic waves, like vibrations, through thin plates in a way that is robust to specific modifications or disturbances are known as topologically protected elastic waveguides. Devices and structures with topological protection imply that some waveguide characteristics are impervious to minute material perturbations or deformations [15, 23, 24, 27, 42, 43]. In this context, some fundamental mathematical ideas of topology, which examine qualities that do not change even under continuous deformations, are frequently linked to this protection. Topological insulators and other topologically protected states possess special characteristics that are unaffected by small changes or imperfections in materials [27]. Topologically protected edge modes play a crucial role in the Su–Schrieffer–Heeger model as well as the creation of subwavelength crystalline structures. This situation indicates that some electrical or vibrational states are localized to the edges of crystals and resistant to imperfections in structures or other local [15, 25, 27], [42–44]. As a result of topological protection, these edge modes persist even in the presence of defects. This characteristic makes them fascinating for applications that depend on information transfer or stable wave localization along a material’s edges, such as PnC structures [23–25], [27]. Applications for this idea have been explored in several domains, such as the creation of innovative electronic devices and materials with particular topological characteristics. According to recent studies, topological edge states (TESs) are stimulated at the interface of two PnCs with distinct geometrical features inside the PnBG [15, 23, 24]. Chen et al. developed a gradient PnC structure for robust acoustic sensing, achieving topological acoustic rainbow trapping by tuning structural parameters. This design enhances signal recovery and is resilient to structural disorders, advancing PnC-based sensors [23]. Z. Chen et al. investigated temperature-controlled elastic wave transport in topological PnC plates using ferroelectric ceramics. Their design enables tunable topological properties, broadband interface modes, and controllable waveguide paths, enhancing elastic wave manipulation [25]. B. Li et al. designed an acoustic energy harvesting device using topological edge states of a multi-resonant PnC. Their design lowers the operating frequency and improves robustness, demonstrating effective energy collection even with defects [45]. Phononics and topology can advance each other’s growth. The design and modification of phononic systems are less complicated than those of electronic systems. The exploration of topological states in PnC structures has emerged as a captivating realm in the field of condensed matter physics and materials science [23–27]. New physical phenomena have been discovered as a result of the complex interactions between the geometric configuration of subwavelength resonators and the special properties of wave propagation in the manufactured materials. Our work attempts to determine and demonstrate the presence of topological states in the constructed PnC framework. The concept of topological states in PnCs has become increasingly well-known because of its possible effects on edge mode stability, robust wave propagation, and resistance to local perturbations [23–25], [46]. Here, we present the concept of creating a TPnC structure on the basis of the fundamentals of crystal wave propagation and distinct signatures arising from topological aspects. As we navigate through the intricacies of our proposed PnC structure, we present compelling evidence supporting the topological nature of PnCs, emphasising key indicators, such as band inversion, edge mode stability and nontrivial band gap [23–28]. Creating a TPnC structure for a liquid sensor, including liquid butanol, involves a strategic design process to guide and manipulate acoustic waves resiliently against disturbances. A suitable crystalline lattice structure (triangular and square) must be selected, and a carefully designed unit cell with characteristics that support topologically protected qualities must be defined [15, 23, 25, 46]. A crucial part is the integration of subwavelength resonators inside the unit cell by using locally resonant devices with remarkable material contrasts [25, 27]. The selection of materials, such as epoxy and lead layers, is based on the propagation of acoustic waves and sensitivity to changes caused by butanol [11, 47]. The incorporation of elements enabling the definition of topological invariants, along with the design of topologically protected edge modes that remain stable amidst local perturbations, is crucial [48–51]. In consideration of the Zak phase, we aim for a nonzero value associated with band inversion and further ensure topological nontriviality [15, 24, 25, 46]. Numerical simulations based on techniques, such as TMM, are used to validate the design rigorously through experimentation. Optimisation for butanol sensing involves fine-tuning resonator parameters, constituent layer thickness and lattice dimensions for heightened sensitivity. Ultimately, the integration of our TPnC into a sensor device is addressed, accounting for practical considerations and potential enhancements, such as signal processing elements or interfaces with measurement systems that are tailored to meet the specific requirements of liquid sensor applications. Phononic systems are therefore good platforms for implementing new phenomena in topological physics. Therefore, our work’s objective is to create a sensor with a stable PnC structure that can withstand imperfections.

Interestingly, Fano resonance is an important aspect that improves the performance of PnC sensors. It can modify sensors by the emergence of sharp resonant or slow modes. This phenomenon, which is characterized by an asymmetric and sharp resonant mode, is caused by the interference between narrow cavities, such as apertures, and slow-varying backgrounds, such as PnC structures [16, 52–54]. Fano resonance provides a large sensitivity boost to PnC sensors; such a boost increases their flexibility and usefulness in a range of applications, including filters, waveguides, photodetectors, biosensing switches, and modulators [55–59]. For example, experimental and numerical investigations have demonstrated remarkable advancements with reported sensitivities of 8.8 MHz/ppm (part per million) and 292 MHz/(kg/m³) for 2- and 1D PnC liquid sensors, respectively [60]. In addition, destructive interference produces the characteristic line shape of Fano resonance, which has generated considerable interest in phononics and opened new avenues for sensor applications [16, 55], [57–59]. Moreover, the investigation of TPnC structures with Fano resonance in liquid sensors could offer an additional degree of design flexibility, which could result in high figure of merit (FOM), quality factors (QFs), and sensitivity (S). Thus, utilizing Fano resonance in TPnC sensor structures creates new opportunities for increasing sensitivity and efficiency in a range of applications. Such a phenomenon represents an important achievement in sensor technology.

Herein, we introduce a 1D TPnC structure for detecting butanol temperature. This structure holds great potential for various uses, including environmental monitoring, industrial processes, and medical environments. We utilize the transfer matrix technique (TMM) to investigate the sensing capabilities of periodic PnC structures and to offer a comprehensive understanding of their performance. We provide an innovative method by generating extremely sharp Fano resonance modes in the liquid structure PnC–PnBG. These Fano resonance modes are specific to periodic PnC structures and provide novel QF, S, and FOM values that are tuned for butanol detection. Furthermore, our proposed 1D TPnC liquid sensor, which uses 1D multilayered structures in sensing applications, can be easily constructed at the theoretical and experimental levels. The sensor, which is made of inexpensive materials, such as lead and epoxy, is resilient to extreme temperatures and pressures. Importantly, it removes the need for complex electric components, thus enhancing its use and streamlining its design. Given that crystal structures are susceptible to imperfections and deformations, we tackle this problem by creating 1D TPnC sensing structures, which are designed to transmit acoustic waves robustly despite disruptions or deformations.

2 Theoretical framework and model design

2.1 Model design of the PnC liquid sensor structure

In this subsection, we present our proposed periodic TPnC. Our proposed design adopts the presence of Fano resonance modes inside the PnBGs as a liquid sensor for butanol detection. The sensor structure comprises two identical PnC multilayer designs. Each PnC structure is composed of two-unit cells (N = 2). Then, a defect layer filled with butanol liquid is embedded between the two PnCs. Here, each unit cell is designed from lead and epoxy with thicknesses of d₁ = 1 µm and d₂ = 1 μm, respectively. Meanwhile, the suggested design could be configured as, [(Lead/Epoxy)² (Defect layer) (Lead/Epoxy)²]. To sum up, Figure 1 shows a three-dimensions schematic diagram of the proposed sensor in which the lattice constant, or the length of each unit cell, is expressed as a = d₁ + d₂. Here, the whole structure is sandwiched between two semi-infinite layers of nylon. Then, transducer one couples the acoustic signal to the structure, whereas transducer two detects the output signal at the opposite end. Table 1 provides an overview of the building materials’ acoustic properties (density and speed). The considerable impedance mismatch between liquids and solids used in these alternating layers makes properly adjusting the thicknesses of layers crucial to optimize the structure’s spectral response and practical feasibility. In other words, the acoustic wave is suppressed by the high thickness of the layers that constitute the proposed structure, resulting in the absence of transmission. Lead and epoxy layers must have a thickness of 1 μm, whereas defect layers must have a thickness of 0.5 µm to attain a pass band in the MHz spectral region. Additionally, the large acoustic mismatch between epoxy and lead facilitates the creation of broad PnBG, which disperses the incident acoustic waves at the interface between layers [8–11].

Figure 1

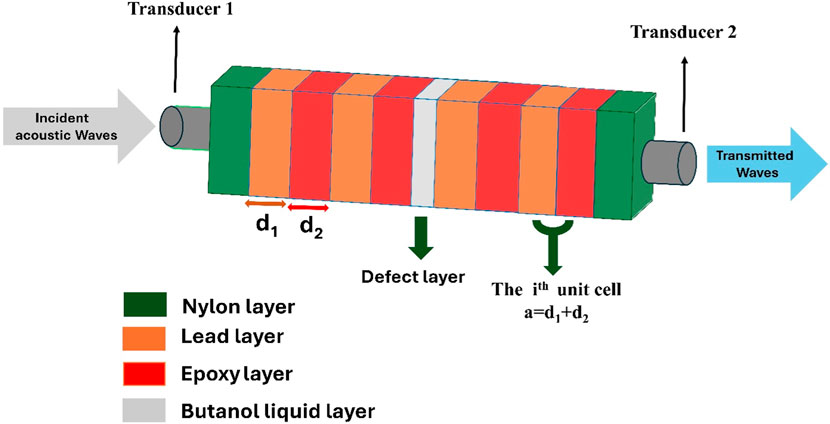
Figure 1. Schematic of a 1D periodic TPnC structure comprising lead and epoxy with a butanol liquid-filled defect layer.

Table 1

Table 1. Mass densities and sound speeds of the suggested materials for designing the periodic TPnC structure.

In addition, we can incorporate a quasi-periodic sequence in the 1D TPnC sensor designs, such as the Fibonacci, Thue-Morse, and two-period sequence, which dramatically changes the acoustic properties of the structures. Quasiperiodic arrangements introduce long-range correlations without translational symmetry [17, 61, 62]. Strong resonances arise spontaneously in a quasiperiodic structure because of the special ordering. In contrast, the emergence of resonant modes through periodic structures exhibits an intentional breach of symmetry. The structure is more resilient to small manufacturing flaws or layer defects according to its intrinsic resonance capability, which also enables increased sensitivity to environmental changes. As a result, the quasiperiodic sequence can thereby increase the TPnC structure’s adaptability and resilience for practical sensing applications [17, 47, 61, 63].

The Fibonacci sequence can be used to display the quasi-periodic PnCs structures in this suggestion. By using the recursive rule [${\mathrm{S}}_{\mathrm{n}}={\mathrm{S}}_{\mathrm{n}-1}{\mathrm{S}}_{\mathrm{n}-2}$, for $\mathrm{n}⩾2$] to arrange the two fundamental parts, A and B, side by side. It is possible to create a Fibonacci structure [47, 62–64] experimentally. S₀ = B and S₁ = A as a starting point. Consequently, the Fibonacci sequence is produced as ${\mathrm{S}}_2=\text{AB};{\mathrm{S}}_3=\text{ABA};{\mathrm{S}}_4=\text{ABAAB},\text{etc}.$

On the other hand, mirror symmetry in a periodic TPnC structure can significantly influence its acoustic behaviour, especially regarding the localization of phononic modes and the formation of band gaps [17, 61, 64]. Certain vibrational modes can exhibit symmetric or antisymmetric behavior relative to the mirror plane when a TPnC possesses mirror symmetry [17, 62, 64]. For example, antisymmetric waves may encounter destructive interference, resulting in increased band gaps, whereas symmetric modes may constructively interact throughout the mirror plane, producing areas of high transmission [64], [17, 61, 62]. Additionally, the symmetric arrangement can enhance specific acoustic features, even in the presence of minor imperfections or variations in layer thickness. As a result, mirror symmetry can improve the robustness of band gap properties. This robustness is particularly beneficial for sensor applications, where reliable performance relies on stable band gaps and consistent transmission characteristics.

2.2 Theoretical foundations of PnC liquid sensing: TMM

Herein, the periodic TPnC liquid sensor is designed as shown in Figure 1. Acoustic sound waves could be reflected or transmitted inside the multilayer PnC structures. Meanwhile, multiple methods have been established to investigate the transmission of acoustic waves, such as plane wave expansion [65–68], finite difference time domain [69–71], and transfer matrix method (TMM) as well [72–74]. However, due to its simplicity, and accuracy, TMM could be the best choice that can be applied to evaluate the propagation of incident acoustic waves through multilayer structures [11, 75].

Firstly, the mechanical characteristics of the layers, including sound speed and density varies periodically when an acoustic wave encounters our suggested 1D TPC liquid sensor effectively. Additionally, the incident acoustic wave splits into several waves inside the structure. The equation of motion in each layer for an mechanical wave incident typically from left to right on the 1D PC structure [55, 76, 77], as depicted in Figure 1, can be expressed as follows:

$\frac{\mathrm{\partial }\sigma }{\mathrm{\partial }x}+f=\rho \frac{{\mathrm{\partial }}^2\mathrm{u}}{\mathrm{\partial }{t}^2}(1)$

Where $\sigma$ = $\sigma$ ($x$, t), $\rho$ = $\rho$ ($x$, t), $f$ = $f$ ($x$, t) and u = u ($x$, t) denote the stress, material density, external body force, and displacement, respectively. The elastic material’s stress is determined by:

$\sigma =E\frac{\mathrm{\partial }u}{\mathrm{\partial }\mathrm{x}}(2)$

Such that, $E$ = $E$ ($x$) is Young’s modulus of the material. By substituting from Equation 1 into Equation 2, we have:

$E\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}=\rho \frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{t}^2}(3)$

In this regard, the response of the incident acoustic waves through the designed 1D PnC structure can be expressed in the vicinity of Equation 3 such as,

$u\left(x,t\right)=A{e}^{i\left(Kx-\omega t\right)}(4)$

where $\omega$ is the angular frequency, $K$ is the wavenumber, and (A) is the wave amplitude. Therefore, the wave equation for a gas or liquid can be simply investigated by substituting from Equation 4 into Equation 3 such as,

$\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{x}^2}=\frac{1}{C_L^2}\frac{{\mathrm{\partial }}^{2}u}{\mathrm{\partial }{t}^2}(5)$

Examine a 1D PC made up of N unit cells, each of which has two layers. The subscript $j$ = 1, two indicates that the layer j in the unit cell has the following constant material properties: $d_j,{\rho }_j,E_j,\left(\mathrm{a}=d_{1+}{d}_2\right),{\lambda }_j,{\mu }_j$ are the thickness, density, Young’s modulus, cell length, Lame constant, and shearing modulus. $d_1$ and $d_2$ are the thickness of first and second layer, respectively. Each layer’s acoustic wave velocity is $C_L=\sqrt{E/\rho }$. The following is an expression for the solution to Equation 5:

$u\left(\mathrm{x},\mathrm{t}\right)=\left[A_{+}^{\left(j\right)}{e}^{i{K}_{j}X}+A_{-}^{\left(j\right)}{e}^{-i{K}_{j}X}\right]e^{-i\omega t}(6)$

Where the wavenumber is $K_j=\frac{2\pi f}{C_L}$, the incident wave frequency is f, and the transmitted and reflected wave amplitudes are denoted by the coefficients $A_{+}$ and $A_{-}$, respectively.

Equation 7 expresses the formula for the incident wave equation through the gas layer. We are expected to introduce a defect layer within the perfect phononic structure in order to address the interaction between gases and PC. Acoustic waves are widely recognized as one type of pressure fluctuation that can occur in any compressible gas. The equation that describes the propagation of acoustic waves in gases is Equation 7, and it states that sound waves can be transmitted through the gas medium by neutral atoms and molecules [55, 78].

$\begin{array}{rr}& \frac{{\mathrm{\partial }}^{2}p}{\mathrm{\partial }{x}^2}-\frac{\rho }{\beta }\frac{{\mathrm{\partial }}^{2}p}{\mathrm{\partial }{t}^2}=0\\ & \frac{{\mathrm{\partial }}^{2}p}{\mathrm{\partial }{x}^2}-\frac{1}{C_0^2}\frac{{\mathrm{\partial }}^{2}p}{\mathrm{\partial }{t}^2}=0\end{array}(7)$

Where $p$ is the gas’s instantaneous pressure, and $C_0=\sqrt{\frac{\beta }{\rho }}$ is the speed of sound in the gas layer, $\rho$ is its mass density; $\beta$ is its bulk modulus. Equation 8 provides the solution to Equation 7:

$p\left(\mathrm{x},\mathrm{t}\right)=\left[P_{+}^{\left(0\right)}{e}^{i{K}_{j}X}+P_{-}^{\left(0\right)}{e}^{-i{K}_{j}X}\right]e^{i\omega t}(8)$

Both local pressure and density changes are produced when a sound wave passes through a gas medium. Equation 9 establishes a relationship between the acoustic impedance of gas and the speed of sound within it as follow [55].

$Z=\rho \times C_0(9)$

where $C_0$ is the speed of sound in gas and $\rho$ is the density of gas. Consequently, when the medium density and sound speed increase, so does the acoustic impedance that is working against the wave’s propagation. At the interfaces between layers, two conditions must be met: the continuation of stress and the continuity of displacement. By changing Equation 6 into Equation 2, we may provide the stress equation as follows:

$\begin{array}{rr}\sigma \left(x\right)& =Ei{K}_j\left[A_{+}^{\left(0\right)}{e}^{i{K}_{j}X}-A_{-}^{\left(j\right)}{e}^{-i{K}_{j}X}\right]\\ \sigma \left(x\right)& =i{Z}_j\left[A_{+}^{\left(0\right)}{e}^{i{K}_{j}X}-A_{-}^{\left(j\right)}{e}^{-i{K}_{j}X}\right]\end{array}$

where $Z_j=E_j{K}_j$ refers to the acoustic impedance. Consequently, the two-state vectors representing the entire propagation of acoustic waves at the left and right sides of layer j in the kth unit cell can be written as follows:

$\begin{array}{c}{V}_{jL}^{\left(k\right)}=\left\{\mathrm{u}\left({\mathrm{X}}_{\mathrm{R}}^{\mathrm{j}}\right),\mathrm{\sigma }\left({\mathrm{X}}_{\mathrm{R}}^{\mathrm{j}}\right)\right\}\\ V_{jR}^{\left(k\right)}=\left\{\mathrm{u}\left({\mathrm{X}}_{\mathrm{L}}^{\mathrm{j}}\right),\mathrm{\sigma }\left({\mathrm{X}}_{\mathrm{L}}^{\mathrm{j}}\right)\right\}\end{array}(10)$

Where the left and right sides of the layer are labeled by the subscripts R and L, respectively. As a result, in the kth unit cell, the left and right state vectors of layer j have the following relationship:

${\mathrm{V}}_{\text{jR}}^{\left(\mathrm{k}\right)}={\mathrm{D}}_j^{\prime }{\mathrm{V}}_{\text{jL}}^{\left(\mathrm{k}\right)}$

Where ${\mathrm{D}}_{\mathrm{j}}$ describes the transfer matrix for layer $j$. After that, we explain the theoretical framework for applying the transfer matrix method (TMM) to investigate stress and displacement in PnC structures begins with defining Young’s modulus for each material used in the PnC. Stress is then related through an acoustic impedance formula. A wave matrix connects the displacement and stress at the boundaries of each layer. We also present the propagation matrix, which describes how acoustic waves travel through a single layer. In the supplementary data, we detail how the transfer matrix for each layer is derived and how it can be utilized to relate stress and displacement at the interfaces of multiple layers in a multilayer PnC sensor. The transfer matrices for each layer are multiplied sequentially to obtain the overall transfer matrix for the entire structure. This approach allows us to calculate displacement and stress throughout the PnC structure based on the acoustic impedances and material properties. Thus, we can derive comprehensive insights into the system’s behavior by calculating the transfer matrix ($D_j$) for the layer j as presented in the following equation:

$D_j=\left[\begin{array}{cc}\cos \left(K_j{d}_j\right)& 1/{\mathrm{Z}}_{\mathrm{j}}\sin \left(K_j{d}_j\right)\\ -Z_{\mathrm{j}}\sin \left(K_j{\mathrm{d}}_{\mathrm{j}}\right)& \cos \left(K_j{d}_j\right)\end{array}\right](11)$

Each material’s acoustic impedances $Z_{\mathrm{j}}$ and $E_{\mathrm{j}}$ were used to build the PnC structure and ascertain the behaviour of the $D_j$ matrix. Equations 12–14 were utilized to represent the entire transfer matrix components $D_{ij}=D\left(i,j\right)$ given in Equation 11.

$D_j\left(1,1\right)=D_j\left(2,2\right)=\cos \left(K_j{d}_j\right)(12)$

$D_j\left(1,2\right)=1/Z_j\sin \left(K_j{d}_j\right)(13)$

$D_j\left(2,1\right)=-Z_j\sin \left(K_j{d}_j\right)(14)$

Given that $d_j$ denotes the layer thickness and $Z_j=E_j{K}_j$ denotes the acoustic impedance. The following formula represents the relationship between two consecutive state vectors in the kth and (k-1)th unit cells:

$V_{2R}^{\left(\mathrm{k}\right)}=D_k{V}_{2R}^{\left(\mathrm{k}-1\right)}(15)$

Consequently, $D_k$ can be expressed as a transfer matrix that links the next two-unit cells, such that:

$D_k=D_2{D}_1^{\prime }$

Then, the following formula can be used to determine the transmission coefficient of our PnC structure [77, 79]:

$\frac{U_e}{U_0}=\frac{2E_0\left(D_{11}{D}_{22}-D_{12}{D}_{21}\right)}{E_0\left(D_{11}-E_e{D}_{21}\right)-\left(D_{12}-E_e{D}_{22}\right)}$

Here, the two semi-infinite solid Young’s moduli to the left and right of the PnC structure are denoted by $E_0$ and $E_e$, respectively, then the incident and transmitted wave amplitudes are denoted by $U_0$ and $U_{\mathrm{e}}$, respectively.

2.3 Investigation of the 1D PnC’s band structure

Using Bloch-Floquet theorem, the band theory, and the energy spectrum of wave propagation can be calculated and plotted through the infinite 1D multilayered PnC structures [17, 61, 62]. In this case, the state vectors in Equation 10 at the right boundary of each unit cell satisfy the following equation:

$V_{2R}^{\left(i\right)}=V_{2R}^{\left(i-1\right)}\mathit{exp}\left(\mathrm{i}Ka\right)\left(i=2,.....,n+1\right)(16)$

Given that in every layer and unit cell, $K$ is the wave vector and its equal to kj. Equation 15 and Equation 16 can be compared to obtain the following eigenvalue problem:

$\left|T_i-e^{\mathrm{i}Ka}I\right|=0$

It can also be written in another format as follows:

$T_i{V}_{2R}^{\left(i-1\right)}=\lambda V_{2R}^{\left(i-1\right)}(17)$

Where, $V_{2R}^{\left(i-1\right)}$ describes a complex eigenvector and $\lambda =e^{\mathrm{i}Ka}$ expresses the complex eigenvalue. Then, Equation 17 can be used to compute and plot the band structure and dispersion relation of the wave propagation through the infinite 1D periodic structures in the irreducible first Brillouin zone. The wave vector $K$ is given as a complex wave number, comprising real and imaginary parts as follows:

$K=K_{\text{real}}-\mathrm{i}{K}_{\text{imaginary}}$

The following form for Equation 16 will be used if $K$ = $K_{\text{real}}$ and $K_{\text{real}}$ > 0:

${\mathrm{V}}_{2\mathrm{R}}^{\left(\mathrm{i}\right)}={\mathrm{V}}_{2\mathrm{R}}^{\left(\mathrm{i}-1\right)}{\mathrm{e}}^{\mathrm{i}\left|K_{\text{real}}\right|\mathrm{a}}$

The phase difference between the state vectors at the boundaries of each unit cell and every two successive unit cells is equal to ${\mathrm{e}}^{\mathrm{i}\left|K_{\text{real}}\right|\mathrm{a}}$, and the resulting bands are referred to as pass bands. Equation 16 will be expressed as follows if $K$ = $K_{\text{imaginary}}$ and $K_{\text{imaginary}}$ < 0.

${\mathrm{V}}_{2\mathrm{R}}^{\left(\mathrm{i}\right)}={\mathrm{V}}_{2\mathrm{R}}^{\left(\mathrm{i}-1\right)}{\mathrm{e}}^{-\left|K_{\text{imaginary}}\right|\mathrm{a}}$

The state vectors at the boundaries of each unit cell and every two successive unit cells exhibit no phase difference; rather, their spatial phase experiences an exponential attenuation with a magnitude of $\left|K_{\text{imaginary}}\right|$. Therefore, the resulting bands are referred to as stop bands.

In Figure 2A, the band structure is plotted for one unit cell (n = 1) of the two building blocks of the PnC (Pb and epoxy) with equal thickness ($d_1=d_2$ = 1 μm) as specified in Table 1. Any crystal structure can be identified by its band diagram, which only needs one unit cell to display the properties of wave propagation through the multilayer stack. The band diagram of the proposed design of TPnC structure is plotted between the non-dimensional frequency q (3.142 ≤ q ≤ 4.157) and the non-dimensional wavenumber ζ = $K$ ×a [25–27]. Here, q = $q_{LB}$ = ωa/ $c_{LB}$, where $c_{LB}$ is an arbitrary acoustic wave speed, taken as the longitudinal wave velocity in epoxy. In Figure 2B, the band diagram is shown for different thicknesses ($d_1$ = 1.05 μm and $d_2$ = 0.95 μm). Both figures illustrate the same acoustic band gap with nearly identical bandwidths, confirming that the inclusion of lead and epoxy layers in the proposed phononic crystal (PnC) design serves as a solid foundation for the suggested tapered phononic crystal (TPnC) structure. Even with variations in material thickness, the PnC structure maintains edge mode stability, promotes strong wave propagation, and shows resilience to local disturbances. The proposed TPnC structure indicates that certain waveguide properties remain unaffected by minor physical disturbances or distortions. The real part of the wavenumbers is represented by the weighted colors of the passbands, which are shown as solid lines in the band diagram. The band gaps, corresponding to the imaginary part of the wavenumber, are illustrated in gray with dotted lines. Both band diagrams reveal that the phononic band gap (PnBG) has a similar bandwidth (∆ω), as seen in Figure 2. The interaction between wide and narrow bands within the same crystal leads to Fano modes, which are enhanced by this wide bandgap. When alcohol is added, its low acoustic properties allow the wide band to interact with the confined evanescent modes in butanol, thereby improving the localization and propagation of Fano modes.

Figure 2

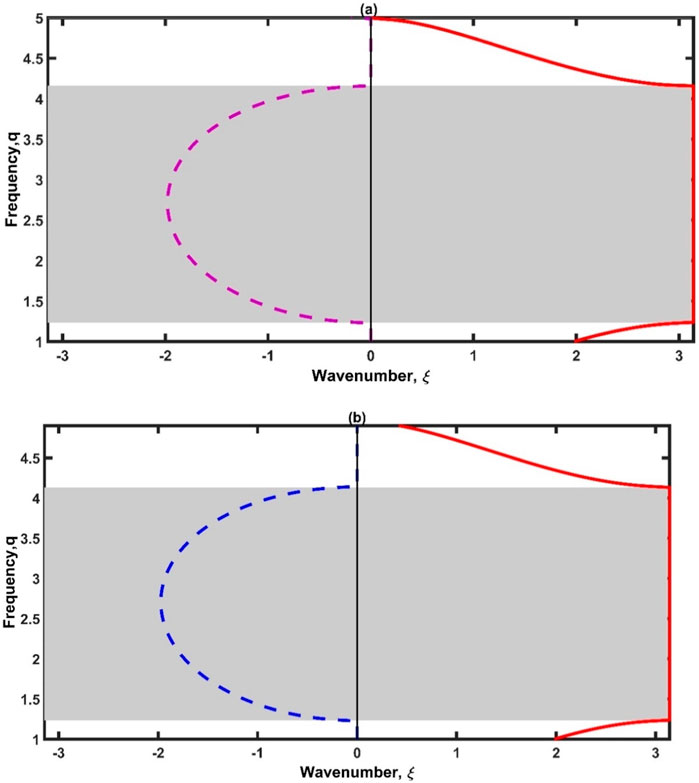
Figure 2. The band structure of the relevant stacked blocks of the PnC (Pb/epoxy)¹ in case of (A) $d_1$ = 1 μm and $d_2$ = 1 μm and (B) $d_1$ = 1.05 μm and $d_2$ = 0.95 μm as $d_1$ is the thickness of lead and $d_2$ is the thickness of epoxy.

3 Results and discussion

3.1 Acoustic properties of butanol liquid

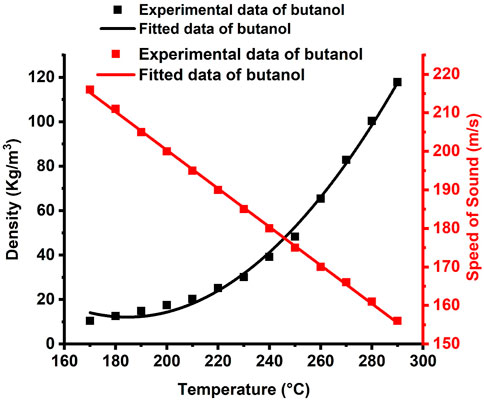
The acoustic properties of butanol liquid, particularly its response to acoustic waves, play an important role in different applications, such as ultrasonic sensing, medical imaging, and industrial processes. Density, viscosity, and compressibility are some of the variables that can be effective on the acoustic properties of butanol, a form of alcohol with four carbon atoms. We first considered the experimental data to highlight the relationship between the temperature and acoustic properties (density and sound velocity) of butanol liquid [80]. Subsequently, we numerically fitted these data to introduce such response in our study. Meanwhile, the experimental data for the mass density of butanol liquid were fitted using the following fitting equation:

$\rho \left(\frac{\text{kg}}{{\mathrm{m}}^3}\right)={\mathrm{\alpha }}_1+{\mathrm{\alpha }}_2\times T\left(°\mathrm{C}\right)+{\mathrm{\alpha }}_3\times {\left(T\left(°\mathrm{C}\right)\right)}^2$

where $\rho$ refers to the density, T refers to the temperature; $\text{and\hspace{0.17em}}{\mathrm{\alpha }}_1,{\mathrm{\alpha }}_2{\text{and}\mathrm{\alpha }}_3$ are the coefficients of the fitting relationship. The values of the fitting coefficients are ${\mathrm{\alpha }}_1=$ 335.0969$,{\mathrm{\alpha }}_2=$ −3.50009 ${\text{and}\mathrm{\alpha }}_3=$ 0.00948. Figure 3 illustrates that density increases in parallel with temperature. In this regard, Equation 26 investigates the polynomial fitting of this relationship in the form of a second-order polynomial. The compressibility and density of butanol dictate the speed of sound [80]. In general, for a liquid, its sound speed decreases as its density and compressibility increase. Therefore, the acoustic waves can also be attenuated as they travel through a liquid due to the viscosity of butanol. High viscosity tends to dampen the propagating acoustic waves, which in turns might be effective on their ability to travel over long distances [80]. Furthermore, acoustic impedance, which is the result of multiplying density by sound speed, offers some information about how well acoustic waves may enter or exit the butanol medium [80]. Comprehending these properties is essential to design and improve ultrasonic sensors that use butanol as a coupling or sensing medium. Next, the experimental results for the sound speed of the butanol liquid are fitted with the following equation:

$v\left(\frac{\mathrm{m}}{\mathrm{s}}\right)={\mathrm{\beta }}_1+{\mathrm{\beta }}_2\times T\left(°\mathrm{C}\right)$

where $v$ is the speed of sound, $T$ refers to the temperature, and $\mathrm{\alpha }\text{\hspace{0.17em}and\hspace{0.17em}}\mathrm{\beta }$ are the coefficients of the fitting relationship. The values of the fitting coefficients are ${\mathrm{\beta }}_1=$ 299.87912 and ${\mathrm{\beta }}_2=$ −0.4978. Figure 3 shows that when temperature rises, sound velocity decreases. This behaviour has a linear fit based on the previous equation. Usually, tests and experiments are conducted to describe the acoustic characteristics of certain liquids, such as butanol. In these experiments, the frequency-dependent behaviour of acoustic waves in the liquid and optical approach is analysed by using some methods, such as ultrasonic spectroscopy [80]. The data obtained could contribute to the development of some technologies, such as PnC sensors, that rely on butanol’s acoustic properties by allowing the construction of models and comprehending the interactions of acoustic waves with the material.

Figure 3

Figure 3. Changes in the acoustic properties of butanol solution with temperature variations.

3.2 TPnC structure

We adopt a novel strategy to demonstrate the topological state and stability of our proposed PnC structure: a methodical investigation of the Fano resonance peak in response to changes in the butanol layer’s thickness. Given that the thickness of the defect layer is equivalent to 0.5 μm, the Fano resonance peak appears at a normalizing frequency of 0.0497, as shown in Figure 4A. We controlled the changes in the butanol layer’s thickness and tracked the associated modifications in the Fano resonance peak to assess the robustness of the proposed structure, as illustrated in Figures 4A, C. When the thickness decreases to 0.4 μm, the peak moves slightly to a normalized frequency of 0.0509. The noteworthy aspect despite this small advancement is the stability exhibited by the PnC structure under this perturbation. Further varying butanol layer thickness to 0.45, 0.55, and 0.6 µm gives rise to the shifting in Fano resonance peak downwards lower normalized frequencies of 0.0503, 0.0492, and 0.0486, respectively, as shown in 4a. Despite this change in normalized frequency, we note that the proposed PnC structure retains its stability and exhibits a consistent response at the Fano resonance peak given the negligible shift in normalization frequency. We thus confirm the proposed PnC structure’s validity and topological integrity by showing that it is resistant to changes in the thickness of the butanol layer, as demonstrated by the steady and minute movements of the Fano resonance peak under various conditions.

Figure 4

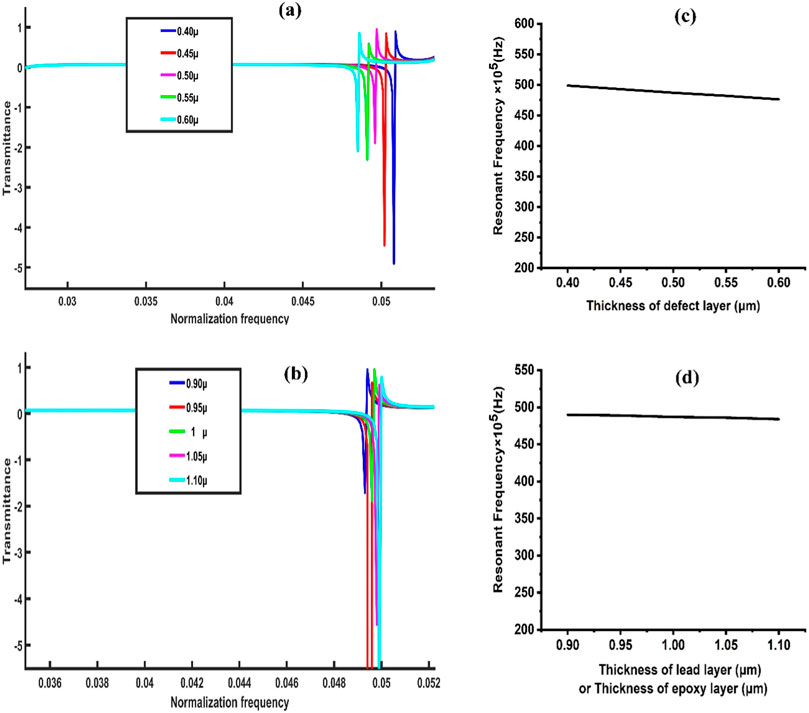
Figure 4. Effect of changing the thickness of (A) the defect layer and (B) the lead or epoxy layer on the transmission spectrum. The resonance frequency of the 1D TPnC structure at the same butanol temperature is affected by variations in the thickness of (C) the defect layer and (D) the lead or epoxy layer.

Here, we examined how the thicknesses of the defect layers affect our TPnC structure’s resonance frequency as shown in Figure 4A. Figure 4C illustrates that as the defect layer thickness changes from 0.4 to 0.6 µm, the position of the resonant peak remains almost at 50 MHz, providing strong evidence for the proposed topological structure. Therefore, we believe that this structure displays the topological edge’s condition and is robust against external distortions. Unique electrical or vibrational states that form at the limits or edges of a topologically nontrivial material or structure are referred to as topological edge states (TES). Regarding periodic structures, such as PnC, these edge states exhibit robustness and stability against certain disturbances or changes in the material. These states are topological because they are resistant to local perturbations and can persist even when defects are present.

Additionally, we have introduced the effect of lead and epoxy layers’ thicknesses on the transmission spectrum to demonstrate the topological state of our proposed PnC structure. When the lead–epoxy layer is 1 μm thick, a Fano resonance peak appears at a normalized frequency of 0.0497. The Fano resonance peak then shifts following carefully controlled variations in lead and epoxy layers’ thicknesses, as seen in Figure 4B. The peak of the lead and epoxy layers’ together shifts slightly to a normalized frequency of 0.05 when the thickness decreases to 0.9 µm. Even with this slight displacement, the stability of the PnC structure under this disturbance is remarkable. Figure 4B shows that further varying on the thicknesses of the lead and epoxy layers to 0.95, 1.05, and 1.1 µm results in the movements of the Fano resonance peaks to new normalized frequencies of 0.0499, 0.0496, and 0.0494, respectively. Despite the slight shift in normalizing frequency, the proposed PnC structure remains stable and exhibits a consistent response at the Fano resonance peak. Therefore, we established the validity of our proposed TPnC structure and its topological integrity by demonstrating its flexibility to variations in lead–epoxy layers’ thicknesses, as investigated by the consistent and small movements of the Fano resonance peak across different conditions. Accordingly, we examined how the thicknesses of the lead and epoxy layers affect the resonance frequency of the TPnC structure, as shown in Figure 4D. The proposed topological structure is strongly supported by the fact that the resonance frequency stays constant at 50 MHz when the defect layer thickness increases from 0.9 to 1.1 μm. This structure provides a TES that is robust against external deformations.

Finally, we thoroughly analysed the effect of symmetric and asymmetric structures on the transmission spectrum, as illustrated in Figure 5, to demonstrate the topological state of the proposed PnC structure. Firstly, the arrangement and regularity of the layers or unit cells that make up a crystal are classified as symmetric and asymmetric PnC structures. A symmetric PnC structure features materials and layers that are mirrored across a central point or plane, creating a configuration on one side that is essentially a reflection of the other. In such structures, the layers follow a consistent, repeating pattern, and physical properties such as density, mass, and stiffness are evenly distributed. For instance, a symmetric structure with a defect layer (D) between two-layer B units could be represented as {ABDBA}, when layers A and B are used. In contrast, an asymmetric PnC structure does not exhibit this mirroring. There is no central point or plane where the layers and materials are symmetrical. Instead, the layers in an asymmetric structure are arranged in an uneven or non-repetitive manner. As a result, the physical properties may vary, leading to differences in wave propagation characteristics. An example of an asymmetric structure, lacking a point of symmetry, could be organized as {ABDAB} using the same layers A, B, and the defect layer (D).

Figure 5

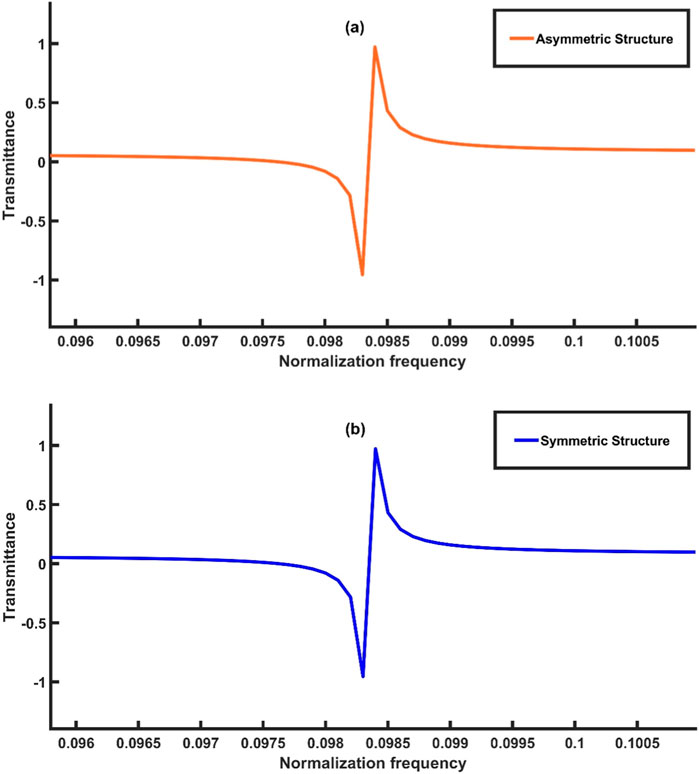
Figure 5. Transmission spectrum of 1D topological PnC structure in the case of (A) asymmetric structure and (B) symmetric structure.

Here, we investigated that the transmission spectra of symmetric and asymmetric structures provide Fano resonance peak located at the same normalized frequency of 0.0985 as shown in Figures 5A, B, respectively. This finding demonstrate that the structure is flexible and supports the topological integrity of our PnC sensor.

3.3 Analysing the transmission spectra of the proposed PnC structure

In our proposed TPnC structure, both narrow discrete resonant mode and broader, continuous background mode interfere to produce Fano resonance. We incorporate localized resonators, like narrow cavities or defects, into a periodic or quasiperiodic array while designing the PnC [11, 81, 82]. At specific frequencies, these resonators produce a limited number of resonant modes that interact with the wider transmission spectrum of the surrounding PnC layers. The distinctive asymmetric line shape of Fano resonance arises from the interference between the discrete resonant mode (originating from the narrow resonator) and the background mode (from the broader PnC structure) that a wave encounters [83–85]. Because of the constructive and destructive interference patterns that are produced in the transmission spectrum by the interaction between the discrete and continuous modes, this line shape appears. Sharp peaks and dips are thus seen in the response, which might increase sensitivity to slight changes in frequency [81, 82, 85, 86].

As described in this section, we delved into the effect of the elevated butanol temperature on the properties of Fano resonance peaks. Figure 6 provides a comprehensive overview of the correlation between different temperatures (170°C–270 °C) and corresponding variations in the sound speed and density of butanol liquid. The subsequent analysis, depicted in Figure 6, highlights the dynamic shift in the positions of Fano resonance peaks at various temperatures. The frequency of the Fano resonance peak exhibits a discernible reduction that ranges from 48.706 MHz to 36.946 MHz as butanol liquid temperatures increase. This behaviour is due to the strong dependence of the density and sound speed of butanol on temperature, as depicted in Figure 3. Concurrently, the position of the Fano resonance peaks varies. Meanwhile, a gradual increase in temperature from 190 °C to 270 °C corresponds to an observed enhancement in sensitivity from 102.9 KHz to 117.6 KHz. This insight underscores the intricate interplay between the changes in temperature and acoustic properties of butanol liquid, offering valuable implications for optimizing periodic PnC structures in temperature-sensitive applications.

Figure 6

Figure 6. Fano resonance spectra of the proposed TPnC structure at different butanol temperatures.

3.4 Analysis of the performance of the proposed TPnC structure

This section introduces the performance of our sensing tool by several related parameters, such as the FOM, QF, and S. These parameters are believed to have a potential importance for characterizing sensor’s performance. Specifically, defect mode characteristics serve as the primary basis for their values. The change in the position of the Fano resonance mode as a function of temperature variation is known as sensor sensitivity [17, 53, 87]. Its values can therefore be established by using the following relationship:

$S=\frac{∆f}{∆T}$

where $∆T$ indicates the change in butanol temperature, and $∆f$ indicates the resonance peak or transmission frequency at each temperature. Then, we computed some additional performance metrics, including QF. This metric is highly affected by the location of the Fano resonance peak [17, 87, 88] such that:

$\mathrm{Q}=\frac{f_r}{f_{HBW}}$

where $f_{HBW}$ refers to the peak’s half bandwidth frequency, and $f_r$ represents the Fano resonance peak frequency. In this case, sharp Fano resonance peaks are indicated by a high QF, increasing frequency resolution [17, 87]. Additionally, we derive a parameter called FOM, which forecasts the capability of the sensor to measure any variation in resonant frequency [17, 87, 88]. The following formula can be used to determine FOM:

$\text{FOM}=\frac{S}{f_{HBW}}$

When the half bandwidth frequency decreases, FOM increases. Lastly, we consider the damping rate, another relevant performance parameter. The sharpness of transmitted Fano resonance peaks is determined by damping, which describes how the acoustic waves in the designed PnC decay after a disturbance across the structure [53, 87, 88]. The following formula can be used to determine the damping rate:

$\mathrm{\zeta }=\frac{1}{\left(2*\mathrm{Q}\right)}(18)$

The effect of varying temperatures on the Fano resonance peaks of the topological butanol liquid sensor, which eventually influences sensitivity, is depicted in Figure 7. The Fano resonance modes shift linearly towards high frequencies when the butanol temperature drops. This response also increases the sensor’s sensitivity. Here, we can confirm that within the temperature range of 170°C–270°C, our PnC sensor offers excellent sensitivity and performance. Figure 7 shows that as the butanol temperature increases from 170 °C to 190 °C, our proposed design offers a relative high sensitivity of 102,900 Hz/°C. As butanol temperature rises, sensitivity increases till reaches 119,233.33 Hz/°C at 230 °C. Meanwhile, the investigated sensitivity of our periodic TPnC design is promising compared with those of other designs in some previous work [22, 89–93]. In particular, previously reported sensors based on 1D PnC structures provided a maximum value of 4,400 Hz/°C, whereas our proposed structure provides a maximum value of 119,233.33 Hz/°C.

Figure 7

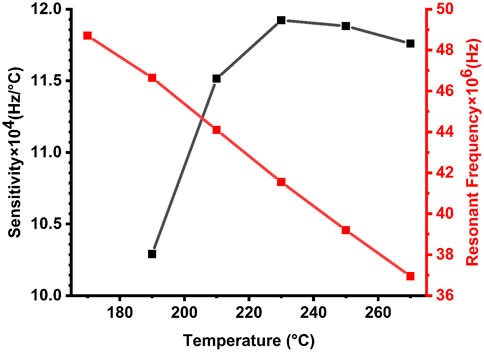
Figure 7. Effect of temperature variations on the sensitivity and Fano resonance position of the proposed TPnC structure.

Figure 8 presents the effect of the QF of our proposed sensor and the damping rate of acoustic waves. It shows that the minimum value of the damping rate is observed at the maximum value of QF. Specifically, Equation 18 establishes an inverse relationship between QF and ζ. Interestingly, high QF values are obtained when FWHM values are low [11, 17, 91, 94]. Consequently, low damping rates are obtained because FWHM values are low. Low FWHM values indicate the limited ability of the proposed structure to absorb incident acoustic waves [11, 17, 91, 94]. The Fano resonance peak sharpens as the damping rate decreases. As shown in Figure 8, the resonance peak has its highest sharpness at 250 °C, leading to a QF of 386.85. Subsequently, at this temperature, we obtain the lowest damping rate of 0.00129. However, the peak has the maximum damping rate of 0.0021 and the lowest sharpness (Q) of 240.04 when the temperature is equivalent to 190 °C. Nonetheless, the QF, which ranges from 240.04 to 386.85, is highly acceptable at all butanol temperatures. This result suggests that all Fano resonance peaks are sharp, thus increasing the frequency resolution of the proposed sensor. The numerical results provided in Figure 8 depict the unique characteristics of our sensor when compared with other sensors and their equivalents with 1D PnC designs [11, 17, 91, 94]. Comparison with those of earlier 1D PnC sensors shows that the QF of our sensor may increase to 386.85.

Figure 8

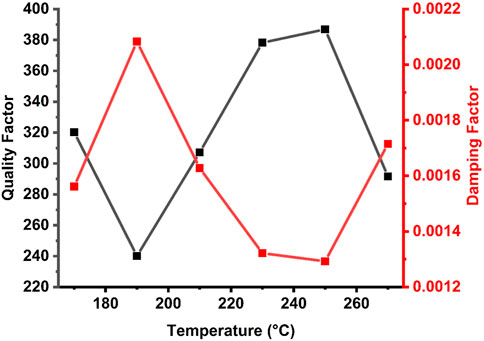
Figure 8. Analysing the role of temperature on the QF and damping rate of the proposed TPnC structure.

Figure 9 shows the response of the butanol liquid sensor’s detection limit and FOM to temperature variation. Figure 9 illustrates that FOM values decrease when butanol temperature increases. We discovered that as the temperature rises from 190 °C to 250 °C, FOM changes from 0.5295/°C to 1.173/°C. Furthermore, FOM exhibits a reaction that is comparable to that shown by sensitivity, particularly for this parameter. This reaction is also known as the reduced sensitivity. Additionally, the link between various temperatures and the detection limit of the butanol liquid sensor is depicted in Figure 9. The lowest temperature or analyte concentration in a sample that can be identified with a certain probability is known as the limit of detection [17, 22, 87, 91]. The values of the detection limit decrease from 0.0944 to 0.043 when the temperature rises from 190 °C to 250 °C. These results are acceptable, distinguishing our sensor from earlier liquid sensors of similar design [17, 22, 87, 91].

Figure 9

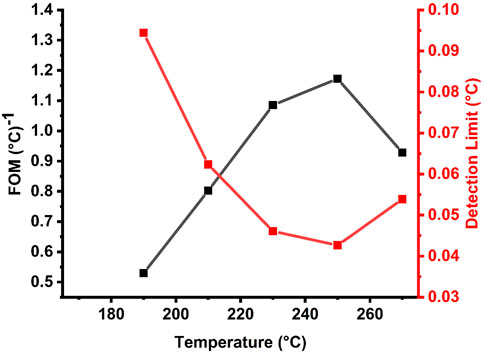
Figure 9. Exploring the influence of various temperatures on the FOM and limit of detection of the proposed TPnC structure.

4 Comparison of the proposed TPnC butanol sensor with other sensor designs

This section provides a concise comparison of the features of the proposed TPnC liquid sensor with various PnC liquid sensors that share similarities in design, dimensions, and material type, as shown in Table 2. For instance, M. Zaremanesh et al. developed a two-dimensional triangular lattice PnC biosensor designed to detect the temperature of Methyl Nonafluorobutyl Ether (MNE) within the range of 10°C–40 °C. This design achieves sharp guided modes within the bandgap, exhibiting high quality factors and a figure of merit (FOM) of 3.7 °C⁻¹ [22]. Also, H. Li et al. designed a high-sensitivite temperature sensor using surface plasmon resonance in a photonic crystal fiber filled with toluene and ethanol. The sensor achieves only FOM of 0.1169 °C⁻¹ and 7.13 nm/°C as an average sensitivity [92]. Additionally, A. H. M. Almawgani et al. developed a 1D-PnC sensor for detecting cadmium bromide in water by monitoring shifts in resonant peaks in response to changes in concentration. This sensor achieves a figure of merit (FOM) of 4.12088 × 10⁻⁵ ppm⁻¹ [95]. Interestingly, the sensitivity and figure of merit (FOM) of our proposed TPnC sensor are notably high, measuring 119,233.33 Hz/°C and 1.173°C⁻¹, respectively. This topological sensor demonstrates better sensitivity than many of the PnC liquid sensors listed in Table 2. Consequently, we leverage this advancement in liquid temperature sensors, which rely on periodic TPnC structures based on resonance phenomena. This design incorporates high transmission modes with previously unexplored sensitivity, quality parameters, and FOM, and more specifically based on a novel mechanism represented by the appearance of Fano modes in a liquid material.

Table 2

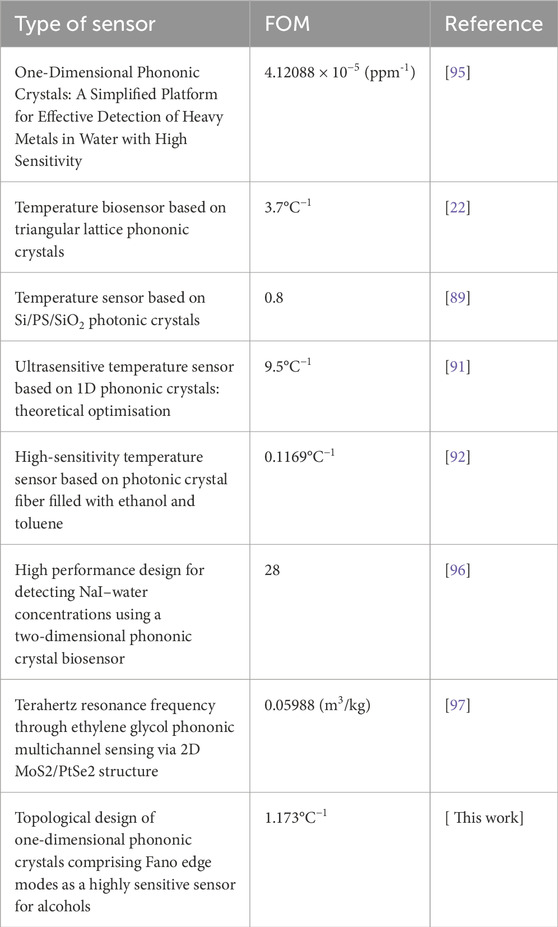
Table 2. Comparison between the FOM of our proposed TPnC temperature sensor and previously reported sensors.

Additionally, our proposed sensor can accurately distinguish temperatures within a range of 0°C–270°C, making it particularly valuable for precise detection in industrial, environmental, and medical applications. Its ability to function across a broad temperature spectrum suggests it may perform exceptionally well in measuring the temperatures of various liquids, especially alcohols. We expect our sensor to surpass traditional PnC and photonic crystal sensors, as shown in Table 2. A key advantage of our phononic sensor is its resilience to geometric changes and disruptions that frequently occur during manufacturing. The TPnC sensor preserves the stability and robustness of its edge modes, even when faced with material deformations, disorder, and imperfections. This durability is attributed to the incorporation of topological properties in the PnC design. Overall, these findings suggest that our proposed PnC structure could achieve a high degree of alignment between theoretical predictions and experimental results, particularly in the development of PnC sensors with one-dimensional multilayer designs.

5 Conclusion

Our research focused on assessing the performance of periodic phononic crystal (PnC) structures as temperature sensors for butanol. The proposed sensor utilizes Fano resonance within the phononic band gaps (PnBGs) of the designed PnCs. We also highlighted the significance of developing subwavelength crystals that remain stable despite geometric imperfections, which is vital for the practical manufacturing of PnC sensing devices. To this end, we introduced a topologically protected PnC structure specifically tailored for sensing the temperatures of various fluids and alcohols. We calculated the transmission spectra of the PnC designs using the transfer matrix method (TMM). Our findings demonstrated that the TPnC structure achieved a high sensitivity of 119,233.33 Hz/°C, with quality factor (Q) and figure of merit (FOM) values recorded at 1.17263 and 386.85, respectively. Moreover, our proposed sensor can be easily replicated for different gases and liquids and can be constructed affordably using readily available materials. Therefore, our work has the potential to provide a straightforward, precise sensor that delivers high accuracy, performance, and stability for measuring the temperature of alcohols and other substances.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions statement

HF: Software, Writing–original draft. AE-S: Writing–review and editing. WA: Funding acquisition, Writing–review and editing. AH: Writing–review and editing. HE: Writing–review and editing. RS: Supervision, Writing–review and editing. MI: Supervision, Writing–review and editing. MA: Project administration, Writing–review and editing. AM: Methodology, Project administration, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors extend their appreciation to King Saud University for funding this work through Researchers Supporting Project number (RSP2024R133), King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1497294/full#supplementary-material

References

1. Dang F, Wang Y, Gao J, Xu L, Cheng P, Lv L, et al. Hierarchical flower-like NiCo2O4 applied in n-butanol detection at low temperature. Sensors Actuators B Chem (2020) 320:128577. doi:10.1016/J.SNB.2020.128577

CrossRef Full Text | Google Scholar

2. Poloju M, Jayababu N, Rao EV, Rao RG, Reddy MVR. Development of CdO/ZnO nanocomposites for the rapid detection and discrimination of n-butanol. Surf Inter (2020) 20:100586. doi:10.1016/J.SURFIN.2020.100586

CrossRef Full Text | Google Scholar

3. Shao TC, Wang N, Zhang XF, Deng ZP, Xu YM, Huo L-H, et al. Biomass-derived porous ZnO hierarchical microtubules for conductometric detection of n-butanol vapor. Sensors Actuators B Chem (2021) 344:130293. doi:10.1016/J.SNB.2021.130293

CrossRef Full Text | Google Scholar

4. Wang T, Chen J, Chen J, Yao X, Chen G, Jiao Z, et al. UV-light enhanced gas sensor based on Ga doped ZnO for ultra-high sensitive and selective n-butanol detection. Appl Surf Sci (2023) 641:158551. doi:10.1016/J.APSUSC.2023.158551

CrossRef Full Text | Google Scholar

5. Song X, Liu T, Gu K, Luo Z, Zhang M. Highly selective and ultra-sensitive gas sensor based on Fe2O3/Ti3C2Tx MXene heterostructure for ppb-level n-butanol detection. J Alloys Compd (2024) 976:173153. doi:10.1016/J.JALLCOM.2023.173153

CrossRef Full Text | Google Scholar

6. Chen X, Liu T, Li Z, Yin XT. Recent developments in metal oxide semiconductors for n-Butanol detection. Mater Today Chem (2023) 33:101690. doi:10.1016/J.MTCHEM.2023.101690

CrossRef Full Text | Google Scholar

7. Alaie S, Goettler DF, Su M, Leseman ZC, Reinke CM, El-Kady I. Thermal transport in phononic crystals and the observation of coherent phonon scattering at room temperature. Nat Commun (2015) 6(1):7228–8. doi:10.1038/ncomms8228

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Lucklum R, Li J, Zubtsov M. 1D and 2D phononic crystal sensors. Proced Eng (2010) 5:436–9. doi:10.1016/J.PROENG.2010.09.140

CrossRef Full Text | Google Scholar

9. Lucklum R, Mukhin N. Enhanced sensitivity of resonant liquid sensors by phononic crystals. J Appl Phys (2021) 130(2). doi:10.1063/5.0046847

CrossRef Full Text | Google Scholar

10. Lu MH, Feng L, Chen YF. Phononic crystals and acoustic metamaterials. Mater Today (2009) 12(12):34–42. doi:10.1016/S1369-7021(09)70315-3

CrossRef Full Text | Google Scholar

11. Almawgani AHM, Fathy HM, Elsayed HA, Abdelrahman Ali YA, Mehaney A. A promising ultra-sensitive CO2 sensor at varying concentrations and temperatures based on Fano resonance phenomenon in different 1D phononic crystal designs. Sci Rep (2023) 13(1):15028–18. doi:10.1038/s41598-023-41999-1

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Kushwaha MS, Halevi P, Dobrzynski L, Djafari-Rouhani B. Acoustic band structure of periodic elastic composites. Phys Rev Lett (1993) 71(13):2022–5. doi:10.1103/PhysRevLett.71.2022

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Lucklum R, Li J. Phononic crystals for liquid sensor applications. Meas Sci Technol (2009) 20(12):124014. doi:10.1088/0957-0233/20/12/124014

CrossRef Full Text | Google Scholar

14. Aliev GN, Goller B. Quasi-periodic Fibonacci and periodic one-dimensional hypersonic phononic crystals of porous silicon: experiment and simulation. J Appl Phys (2014) 116(9). doi:10.1063/1.4894620

CrossRef Full Text | Google Scholar

15. Li Y, Luo Y, Zhang X. Topological design of phononic crystals for multiple wide band gaps. J Sound Vib (2022) 529:116962. doi:10.1016/J.JSV.2022.116962

CrossRef Full Text | Google Scholar

16. Miroshnichenko AE, Flach S, Kivshar YS. Fano resonances in nanoscale structures. Rev Mod Phys (2010) 82(3):2257–98. doi:10.1103/revmodphys.82.2257

CrossRef Full Text | Google Scholar

17. Almawgani AHM, Fathy HM, Elsayed HA, Ali GA, Irfan M, Mehaney A. Periodic and quasi-periodic one-dimensional phononic crystal biosensor: a comprehensive study for optimum sensor design. RSC Adv (2023) 13(18):11967–81. doi:10.1039/D3RA01155K

PubMed Abstract | CrossRef Full Text | Google Scholar

18. He C, Ni X, Ge H, Sun XC, Chen YB, Lu MH, et al. Acoustic topological insulator and robust one-way sound transport. Nat Phys (2016) 12(12):1124–9. doi:10.1038/nphys3867

CrossRef Full Text | Google Scholar

19. Xue H, Yang Y, Zhang B. Topological acoustics. Nat Rev Mater (2022) 7(12):974–90. doi:10.1038/s41578-022-00465-6

CrossRef Full Text | Google Scholar

20. Tol S, Degertekin FL, Erturk A. Gradient-index phononic crystal lens-based enhancement of elastic wave energy harvesting. Appl Phys Lett (2016) 109(6). doi:10.1063/1.4960792

CrossRef Full Text | Google Scholar

21. Pennec Y, Djafari Rouhani B, Larabi H, Akjouj A, Gillet JN, Vasseur JO, et al. Phonon transport and waveguiding in a phononic crystal made up of cylindrical dots on a thin homogeneous plate. Phys Rev B - Condens Matter Mater Phys (2009) 80(14):144302. doi:10.1103/physrevb.80.144302

CrossRef Full Text | Google Scholar

22. Zaremanesh M, Carpentier L, Gharibi H, Bahrami A, Mehaney A, Gueddida A, et al. Temperature biosensor based on triangular lattice phononic crystals. APL Mater (2021) 9(6). doi:10.1063/5.0054155

CrossRef Full Text | Google Scholar

23. Chen T, Xia B, Yu D, Bi C. Robust enhanced acoustic sensing via gradient phononic crystals. Phys Lett A (2024) 493:129242. doi:10.1016/J.PHYSLETA.2023.129242

CrossRef Full Text | Google Scholar

24. Yao L, Zhang D, Xu K, Dong L, Chen X. Topological phononic crystal plates with locally resonant elastic wave systems. Appl Acoust (2021) 177:107931. doi:10.1016/J.APACOUST.2021.107931

CrossRef Full Text | Google Scholar

25. Chen Z, Zhou W. Temperature-controlled elastic wave transport in topological ferroelectric phononic crystal plates. Int J Mech Sci (2023) 241:107964. doi:10.1016/J.IJMECSCI.2022.107964

CrossRef Full Text | Google Scholar

26. Elshahat S, Abood I, Esmail MSM, Ouyang Z, Lu C. One-dimensional topological photonic crystal mirror heterostructure for sensing. Nanomater. (2021) 11(8):1940. Page 1940. doi:10.3390/NANO11081940

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Ammari H, Davies B, Hiltunen EO, Yu S. Topologically protected edge modes in one-dimensional chains of subwavelength resonators. J Math Pures Appl (2020) 144:17–49. doi:10.1016/J.MATPUR.2020.08.007

CrossRef Full Text | Google Scholar

28. Yin J, Ruzzene M, Wen J, Yu D, Cai L, Yue L. Band transition and topological interface modes in 1D elastic phononic crystals. Sci Rep (2018) 8(1):6806–10. doi:10.1038/s41598-018-24952-5

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Kivelson S, Kohmoto M, Nightingale MP, den Nijs M. Quantized Hall conductance in a two-dimensional periodic potential. Phys Rev Lett (1982) 49(6):405–8. doi:10.1103/PhysRevLett.49.405

CrossRef Full Text | Google Scholar

30. Tsui DC, Stormer HL, Gossard AC. Two-dimensional magnetotransport in the extreme quantum limit. Phys Rev Lett (1982) 48(22):1559–62. doi:10.1103/physrevlett.48.1559

CrossRef Full Text | Google Scholar

31. Laughlin RB. Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations. Phys Rev Lett (1983) 50(18):1395–8. doi:10.1103/physrevlett.50.1395

CrossRef Full Text | Google Scholar

32. Haldane FDM. Model for a quantum Hall effect without landau levels: condensed-matter realization of the ‘parity anomaly. Phys Rev Lett (1988) 61(18):2015–8. doi:10.1103/PhysRevLett.61.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Jiang L, Kitagawa T, Alicea J, Akhmerov AR, Pekker D, Refael G, et al. Majorana fermions in equilibrium and in driven cold-atom quantum wires. Phys Rev Lett (2011) 106(22):220402. doi:10.1103/physrevlett.106.220402

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Goldman N, Budich JC, Zoller P. Topological quantum matter with ultracold gases in optical lattices. Nat Phys (2016) 12(7):639–45. doi:10.1038/nphys3803

CrossRef Full Text | Google Scholar

35. Chen C, Sun XC, Liu X, Lu MH, Feng L, Chen Y-F. Topologically protected one-way edge mode in networks of acoustic resonators with circulating air flow. New J Phys (2015) 17(5):053016. doi:10.1088/1367-2630/17/5/053016

CrossRef Full Text | Google Scholar

36. Fleury R, Sounas DL, Sieck CF, Haberman MR, Alù A. Sound isolation and giant linear nonreciprocity in a compact acoustic circulator. Science (2014) 343(6170):516–9. doi:10.1126/science.1246957

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Wang P, Lu L, Bertoldi K. Topological phononic crystals with one-way elastic edge waves. Phys Rev Lett (2015) 115(10):104302. doi:10.1103/physrevlett.115.104302

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Khanikaev AB, Fleury R, Mousavi SH, Alù A. Topologically robust sound propagation in an angular-momentum-biased graphene-like resonator lattice. Nat Commun (2015) 6(1):8260–7. doi:10.1038/ncomms9260

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Yang Z, Gao F, Shi X, Lin X, Gao Z, Chong Y, et al. Topological acoustics. Phys Rev Lett (2015) 114(11):114301. doi:10.1103/physrevlett.114.114301

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Mousavi SH, Khanikaev AB, Wang Z. Topologically protected elastic waves in phononic metamaterials. Nat Commun (2015) 6(1):8682–7. doi:10.1038/ncomms9682

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Qian K, Apigo DJ, Prodan C, Barlas Y, Prodan E. Topology of the valley-Chern effect. Phys Rev B (2018) 98(15):155138. doi:10.1103/physrevb.98.155138

CrossRef Full Text | Google Scholar

42. Ma G, Xiao M, Chan CT. Topological phases in acoustic and mechanical systems. Nat Rev Phys (2019) 1(4):281–94. doi:10.1038/s42254-019-0030-x

CrossRef Full Text | Google Scholar

43. Li X, Meng Y, Wu X, Yan S, Huang Y, Wang S, et al. Su-Schrieffer-Heeger model inspired acoustic interface states and edge states. Appl Phys Lett (2018) 113(20). doi:10.1063/1.5051523

CrossRef Full Text | Google Scholar

44. Su WP, Schrieffer JR. Soliton dynamics in polyacetylene. Proc Natl Acad Sci (1980) 77(10):5626–9. doi:10.1073/PNAS.77.10.5626

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Li B, Chen H, Xia B, Yao L. Acoustic energy harvesting based on topological states of multi-resonant phononic crystals. Appl Energ (2023) 341:121142. doi:10.1016/J.APENERGY.2023.121142

CrossRef Full Text | Google Scholar

46. Akbari-Farahani F, Ebrahimi-Nejad S. From defect mode to topological metamaterials: a state-of-the-art review of phononic crystals and acoustic metamaterials for energy harvesting. Sensors Actuators A Phys (2024) 365:114871. doi:10.1016/J.SNA.2023.114871

CrossRef Full Text | Google Scholar

47. Imanian H, Noori M, Abbasiyan A. Highly efficient gas sensor based on quasi-periodic phononic crystals. Sensors Actuators B Chem (2021) 345:130418. doi:10.1016/J.SNB.2021.130418

CrossRef Full Text | Google Scholar

48. Fan L, Yu WW, Zhang SY, Zhang H, Ding J. Zak phases and band properties in acoustic metamaterials with negative modulus or negative density. Phys Rev B (2016) 94(17):174307. doi:10.1103/physrevb.94.174307

CrossRef Full Text | Google Scholar

49. Pocock SR, Xiao X, Huidobro PA, Giannini V. Topological plasmonic chain with retardation and radiative effects. ACS Photon (2018) 5(6):2271–9. doi:10.1021/acsphotonics.8b00117

CrossRef Full Text | Google Scholar

50. Zhao D, Xiao M, Ling CW, Chan CT, Fung KH. Topological interface modes in local resonant acoustic systems. Phys Rev B (2018) 98(1):014110. doi:10.1103/physrevb.98.014110

CrossRef Full Text | Google Scholar

51. Zak J. Berry’s phase for energy bands in solids. Phys Rev Lett (1989) 62(23):2747–50. doi:10.1103/PhysRevLett.62.2747

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Pennec Y, Jin Y, Djafari-Rouhani B. Phononic and photonic crystals for sensing applications. Adv Appl Mech (2019) 52:105–45. doi:10.1016/BS.AAMS.2018.11.001

CrossRef Full Text | Google Scholar

53. Devashish D, Ojambati OS, Hasan SB, Van Der Vegt JJW, Vos WL. Three-dimensional photonic band gap cavity with finite support: enhanced energy density and optical absorption. Phys Rev B (2019) 99(7):075112. doi:10.1103/physrevb.99.075112

CrossRef Full Text | Google Scholar

54. Limonov MF, Limonov MF. Fano resonance for applications. Adv Opt Photon (2021) 13(3):703–71. doi:10.1364/AOP.420731

CrossRef Full Text | Google Scholar

55. Zaki SE, Mehaney A, Hassanein HM, Aly AH. Fano resonance based defected 1D phononic crystal for highly sensitive gas sensing applications. Sci Rep (2020) 10(1):17979–16. doi:10.1038/s41598-020-75076-8

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Ruan B, Guo J, Wu L, Zhu J, You Q, Dai X, et al. Ultrasensitive terahertz biosensors based on Fano resonance of a graphene/waveguide hybrid structure. Sensors (2017) 17(8):1924. doi:10.3390/S17081924

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Zhang T, Gao SX, Cheng Y, Liu XJ. Modulating acoustic Fano resonance of self-collimated sound beams in two dimensional sonic crystals. Ultrasonics (2019) 91:129–33. doi:10.1016/J.ULTRAS.2018.08.001

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Quotane I, El Boudouti EH, Djafari-Rouhani B. Trapped-mode-induced Fano resonance and acoustical transparency in a one-dimensional solid-fluid phononic crystal. Phys Rev B (2018) 97(2):024304. doi:10.1103/physrevb.97.024304

CrossRef Full Text | Google Scholar

59. Kronowetter F, Maeder M, Chiang YK, Huang L, Schmid JD, Oberst S, et al. Realistic prediction and engineering of high-Q modes to implement stable Fano resonances in acoustic devices. Nat Commun (2023) 14(1):6847–8. doi:10.1038/s41467-023-42621-8

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Cicek A, Trak D, Arslan Y, Korozlu N, Kaya OA, Ulug B. Ultrasonic gas sensing by two-dimensional surface phononic crystal ring resonators. ACS Sensors (2019) 4(7):1761–5. doi:10.1021/acssensors.9b00865

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Sutter-Widmer D, Deloudi S, Steurer W. Periodic average structures in phononic quasicrystals. Philos Mag (2007) 87(18–21):3095–102. doi:10.1080/14786430701370819

CrossRef Full Text | Google Scholar

62. Chen AL, Wang YS, Zhang C. Wave propagation in one-dimensional solid–fluid quasi-periodic and aperiodic phononic crystals. Phys B Condens Matter (2012) 407(3):324–9. doi:10.1016/J.PHYSB.2011.10.041

CrossRef Full Text | Google Scholar

63. MacIá E. Exploiting aperiodic designs in nanophotonic devices. Rep Prog. Phys. (2012) 75(3):036502. doi:10.1088/0034-4885/75/3/036502

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Coelho IP, Vasconcelos MS, Bezerra CG. Quasiperiodic magnonic superlattices with mirror symmetry. Solid State Commun (2010) 150(37–38):1760–5. doi:10.1016/J.SSC.2010.07.023

CrossRef Full Text | Google Scholar

65. Tanaka Y, Tamura SI. Two-dimensional phononic crystals: surface acoustic waves. Phys B Condens Matter (1999) 263–264:77–80. doi:10.1016/S0921-4526(98)01197-1

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Zhang X, Liu Y, Wu F, Liu Z. Large two-dimensional band gaps in three-component phononic crystals. Phys Lett A (2003) 317(1–2):144–9. doi:10.1016/J.PHYSLETA.2003.08.032

CrossRef Full Text | Google Scholar

67. Wu TT, Huang ZG, Lin S. Surface and bulk acoustic waves in two-dimensional phononic crystal consisting of materials with general anisotropy. Phys Rev B (2004) 69(9):094301. doi:10.1103/PhysRevB.69.094301

CrossRef Full Text | Google Scholar

68. Vasseur JO, Djafari-Rouhani B, Dobrzynski L, Deymier PA. Acoustic band gaps in fibre composite materials of boron nitride structure. J Phys Condens Matter (1997) 9(35):7327–41. doi:10.1088/0953-8984/9/35/008

CrossRef Full Text | Google Scholar

69. Vasseur JO, Deymier PA, Khelif A, Lambin P, Djafari-Rouhani B, Akjouj A, et al. Phononic crystal with low filling fraction and absolute acoustic band gap in the audible frequency range: a theoretical and experimental study. Phys Rev E (2002) 65(5):056608. doi:10.1103/PhysRevE.65.056608

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Wu F, Liu Z, Liu Y. Splitting and tuning characteristics of the point defect modes in two-dimensionalphononic crystals. Phys Rev E - Stat Physics, Plasmas Fluids Relat Interdiscip Top (2004) 69(6):066609. doi:10.1103/physreve.69.066609

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Schneider RN, Turner LE, Okoniewski MM. Application of FPGA technology to accelerate the Finite-Difference Time-Domain (FDTD) method. In: ACM/SIGDA int. Symp. F. Program. Gate arrays - fpga (2002). p. 97–105. doi:10.1145/503048.503063

CrossRef Full Text | Google Scholar

72. Kobayashi F, Biwa S, Ohno N. Wave transmission characteristics in periodic media of finite length: multilayers and fiber arrays. Int J Sol Struct. (2004) 41(26):7361–75. doi:10.1016/J.IJSOLSTR.2004.06.017

CrossRef Full Text | Google Scholar

73. Pendry JB, MacKinnon A. Calculation of photon dispersion relations. Phys Rev Lett (1992) 69(19):2772–5. doi:10.1103/PhysRevLett.69.2772

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Han L, Zhang Y, Ni ZQ, Zhang ZM, Jiang LH. A modified transfer matrix method for the study of the bending vibration band structure in phononic crystal Euler beams. Phys B Condens Matter (2012) 407(23):4579–83. doi:10.1016/J.PHYSB.2012.08.022

CrossRef Full Text | Google Scholar

75. Garus S, Sochacki W. The effect of layer thickness on the reflectance of a quasi one-dimensional composite built with zr55cu30ni5al10 amorphous alloy and epoxy resin. Arch Metall Mater (2021) 66(2):503–10. doi:10.24425/AMM.2021.135885

CrossRef Full Text | Google Scholar

76. Rams J, Sanchez M, Harmandaris V, Jacquemin F, Correa E, Micromechanics/nanomechanics, no. 2009.

Google Scholar

77. Hussein MI, Hulbert GM, Scott RA. Dispersive elastodynamics of 1D banded materials and structures: analysis. J Sound Vib (2006) 289(4–5):779–806. doi:10.1016/J.JSV.2005.02.030

CrossRef Full Text | Google Scholar

78. Khelif A, Adibi A. Phononic crystals: fundamentals and applications. In: Phononic cryst. Fundam: Appl. (2015) p. 1–245. doi:10.1007/978-1-4614-9393-8/COVER

CrossRef Full Text | Google Scholar

79. Chen AL, Wang YS. Study on band gaps of elastic waves propagating in one-dimensional disordered phononic crystals. Phys B Condens Matter (2007) 392(1–2):369–78. doi:10.1016/J.PHYSB.2006.12.004

CrossRef Full Text | Google Scholar

80. Nozdrev VF. Application of ultrasonics in molecular physics. Available from: https://cir.nii.ac.jp/crid/1130282270575466624 (Accessed January 10, 2024).

Google Scholar

81. Qiu W, Lu H, Baida FI, Ndao A, Bernal M-P. Guided resonances on lithium niobate for extremely small electric field detection investigated by accurate sensitivity analysis. Opt Express (2016) 24(18):20196–209. doi:10.1364/OE.24.020196

PubMed Abstract | CrossRef Full Text | Google Scholar

82. El Boudouti EH, Mrabti T, Al-Wahsh H, Djafari-Rouhani B, Akjouj A, Dobrzynski L. Transmission gaps and Fano resonances in an acoustic waveguide: analytical model. J Phys Condens Matter (2008) 20(25):255212. doi:10.1088/0953-8984/20/25/255212

CrossRef Full Text | Google Scholar

83. Luk’Yanchuk B, Zheludev NI, Maier SA, Halas NJ, Nordlander P, Giessen H, et al. The Fano resonance in plasmonic nanostructures and metamaterials. Nat Mater (2010) 9(9):707–15. doi:10.1038/nmat2810

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Fano U. Effects of configuration interaction on intensities and phase shifts. Phys Rev (1961) 124(6):1866–78. doi:10.1103/PhysRev.124.1866

CrossRef Full Text | Google Scholar

85. Almawgani AHM, Makhlouf Fathy H, E. Alfassam H, M. El-Sherbeeny A, Hajjiah A, A. Elsayed H, et al. Fano resonance in one-dimensional quasiperiodic topological phononic crystals towards a stable and high-performance sensing tool. Sci Rep (2024) 14(1):12067–18. doi:10.1038/s41598-024-62268-9

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Kroner M, Govorov AO, Remi S, Biedermann B, Seidl S, Badolato A, et al. The nonlinear Fano effect. Nat 2008 4517176 (2008) 451(7176):311–4. doi:10.1038/nature06506

PubMed Abstract | CrossRef Full Text | Google Scholar

87. White IM, Fan X. On the performance quantification of resonant refractive index sensors. Opt Express (2008) 16(2):1020–8. doi:10.1364/OE.16.001020

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Shaban M, Ahmed AM, Abdel-Rahman E, Hamdy H. Tunability and sensing properties of plasmonic/1D photonic crystal. Sci Rep (2017) 7(1):41983–10. doi:10.1038/srep41983

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Aly AH, Mohamed BA, Al-Dossari M, Mohamed D. A temperature sensor based on Si/PS/SiO2 photonic crystals. Sci Rep (2023) 13(1):21560–9. doi:10.1038/s41598-023-48836-5

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Sellami K, Khelif A, Christensen R, Achaoui Y, Mehaney A. Experimental and numerical evidence of using a Phononic membrane with the coupling of Fano resonant modes as a highly sensitive temperature sensor. Mech Syst Signal Process (2023) 185:109763. doi:10.1016/J.YMSSP.2022.109763

CrossRef Full Text | Google Scholar

91. Heravi FJ, Elsayed HA, Sabra W, Mehaney A. Ultra-sensitive one-dimensional phononic crystals temperature sensor: theoretical optimization. Z Naturforsch. - Sect. A J. Phys. Sci. (2023) 78(3):249–61. doi:10.1515/zna-2022-0262

CrossRef Full Text | Google Scholar

92. Li H, Ruan J, Li X, Yang Z, Xu Z, Wei G, et al. High-sensitivity temperature sensor based on photonic crystal fiber filled with ethanol and toluene. ECS J Solid State Sci Technol (2023) 12(12):127007. doi:10.1149/2162-8777/AD1208

CrossRef Full Text | Google Scholar

93. Srivastava SK, “Design of temperature sensor based on one-dimensional photonic crystal containing Si–bgo layer. Mater Open (2023) 01(17):2350003. doi:10.1142/S2811086223500036

CrossRef Full Text | Google Scholar

94. Abadla MM, Elsayed HA, Mehaney A. Novel design for the temperature sensing using annular photonic crystals. Silicon (2021) 13(12):4737–45. doi:10.1007/s12633-020-00788-5

CrossRef Full Text | Google Scholar

95. Almawgani AHM, Fathy HM, Ali GA, Elsayed HA, Mehaney A. One-dimensional phononic crystals: a simplified platform for effective detection of heavy metals in water with high sensitivity. Micromachines (2023) 14(1):204. doi:10.3390/MI14010204

PubMed Abstract | CrossRef Full Text | Google Scholar

96. Gharibi H, Mehaney A, Bahrami A. High performance design for detecting NaI–water concentrations using a two-dimensional phononic crystal biosensor. J Phys D Appl Phys (2020) 54(1):015304. doi:10.1088/1361-6463/ABB729

CrossRef Full Text | Google Scholar

97. Zaki SE, Basyooni MA, Belaid W, Tihtih M, Ibrahim JEFM, Attia GF. Terahertz resonance frequency through ethylene glycol phononic multichannel sensing via 2D MoS2/PtSe2 structure. Mater Chem Phys (2022) 292:126863. doi:10.1016/J.MATCHEMPHYS.2022.126863

CrossRef Full Text | Google Scholar