Noise suppression of infrared thermal imaging of rocket exhaust plume using SPOD

The environmental noise have a negative influence on the quality of infrared thermal imaging of the rocket exhaust plume. In this study, the noise data of the unsteady rocket exhaust plume flow field was simulated using Gaussian white noise, and the infrared thermal image of the plume was numerically calculated using the narrow band method (SNB) and the line of sight (LOS) method. The denoising of infrared thermal imaging was achieved through the spectral proper orthogonal decomposition (SPOD) inversion method. Results indicate that Gaussian white noise leads to larger infrared thermal image residuals in the intrinsic core of the plume compared to the mixed regions. The infrared thermal image in the 2.7 μm band is greatly affected by the noise with an average error of 21.1%, and the average error in the 4.3 μm band is 17.6%. After SPOD denoising, the error of the plume infrared thermal image is reduced by more than 50%.

1 Introduction

The rocket exhaust plume is a high-speed free jet of high-temperature, multi-component gas produced by the combustion of propellant in the combustion chamber, which is accelerated and sprayed into the atmospheric environment through a Laval nozzle [1]. The rocket exhaust plume often contains multiple gas-phase components such as CO₂, H₂O, CO, etc., which emit specific spectral bands of infrared radiation through vibrational-rotational energy level transitions at high temperatures [2]. In this case, the plume become a key radiation source for infrared early warning detection [3],which temporal, spatial, spectral, and intensity characteristics of the infrared signatures from the plume greatly improve the recognition ability of the early warning system.

Usually, infrared thermal imaging is inevitably affected by noise due to the presence of environmental interference and other factors during observation or experimental testing [4, 5]. For example, the hot surrounding environment, smoke particles and particulate products in the plume can all become the sources of noise. The presence of noise can blur or interfere with the actual infrared signatures, causing deviations in the infrared thermal imaging of the plume [6]. Specifically, the noise of unsteady plumes can mix with the natural frequency characteristics of the supersonic flow, which is not conducive to the feature extraction of the rocket exhaust plume. Therefore, it is necessary to denoise the infrared thermal image of the rocket exhaust plume to improve the imaging quality.

In terms of the infrared thermal image denoising, commonly used methods have the wavelet transform (WT) [7], principal component analysis (PCA) [7, 8], minimum noise fraction (MNF) [9], and deep neural network [10]. Alsberg et al. [7] applied WT to infrared spectral data and found that it had an excellent performance in infrared thermal denoising and image quality restoration. Koziol et al. [9] found that PCA and MNF have advantages in infrared thermal image denoising. Liz et al. [10] developed a deep learning denoising method to achieve image denoising. However, WT algorithm is highly sensitive to threshold parameters and requires optimal selection of threshold parameters to improve denoising performance. At the same time, its computational cost is very expensive for massive data cases. In addition, the PCA model has certain limitations in highly nonlinear cases, and the neural network models require high computational costs to deal with large samples.

In recent years, SPOD [11] has been proposed as a new denoising method, which has been successfully applied in flow field denoising. SPOD is a frequency-domain variant of Proper Orthogonal Decomposition (POD), which transforms flow field data into the frequency domain before performing POD decomposition to ensure that the mode is orthogonal to other modes at the same frequency. The SPOD method was used in the past to analyze different scale structures in flow fields [12]. In the SPOD method, modes are sorted by the magnitude of their eigenvalues. Low order modes typically represent large-scale flow structures, indicating that these modes have a higher energy proportion and reflect the main features and dominant vortex structures in the flow field. On the contrary, higher-order modes represent small-scale vortex structures with a relatively small energy contribution [13]. Sun et al. [14] used SPOD to extract the characteristic modes of the rocket plume, and it was demonstrated that SPOD had advantages in extracting noise of high Reynolds number jets. Therefore, SPOD is a potential denoise method for infrared thermal imaging of the supersonic rocket exhaust plume.

This study will evaluate the application of SPOD method in infrared thermal image denoising of rocket exhaust plumes. The exhaust plume of BEM-II (Ballistic Evaluation Engine II) [15] is taken as the research object, and the plume flow field with noise is reconstructed by applying Gaussian white noise. Based on the flow field parameters of the plume, infrared thermal images with noise are generated through the infrared radiation transfer calculation, and the SPOD frequency domain reconstruction is used for denoising processing of the infrared thermal images.

2 Methods

2.1 Computational model of unsteady plume

The rocket exhaust plume is a free turbulent flow with high Reynolds numbers, which involves multi-component non-equilibrium chemical reaction wave interference, shear, and turbulence effects, accompanied by vortex coupling effects of different scales. In order to simulate turbulent eddies and capture finer turbulence pulsation information, the Large Eddy Simulation (LES) method [16] is used. The LES method decomposes the instantaneous pulsating motion in turbulence into large-scale vortices and small-scale vortices through filtering functions. Large scale eddies that have a significant impact on the average flow field can be directly calculated using the Navier Stokes (N-S) equation, and small-scale eddies are simulated using the Sub Grid Scale (SGS) model [17]. The instantaneous pulsating is expressed in Equation 1:

$q=\overline{q}+q^{\prime }(1)$

where $\overline{q}$ represents the large-scale vortices and $q^{\prime }$ denotes the small-scale vortices. $\overline{q}$ can be obtained from the decomposition using the filtering function as Equation 2:

$\overline{q}\left(x_i,t\right)=\int G\left(x_i,x_i^{\prime }\right)q\left(x_i^{\prime },t\right)d{x}_i^{\prime }(2)$

where $x_i$ is the component in the coordinate direction, and $G\left(x_i\right)$ is the filtering function. The compressible N-S equation filtered by a filter can be expressed as Equation 3 [18]:

$\begin{array}{l}\frac{\partial \rho }{\partial t}+\frac{\partial \rho u_i}{\partial x_i}=0\\ \frac{\partial u_i}{\partial t}+\frac{\partial u_i{u}_j}{\partial x_i}=-\frac{1}{\rho }\frac{\partial P}{\partial x_i}+\frac{1}{Re}\frac{{\partial }^2{u}_j}{\partial x_i\partial x_j}+\frac{\partial {\tau }_{ij}}{\partial x_j}\end{array}(3)$

where $u$ is the filtered velocity component, $P$ is pressure, $\rho$ is the density, $Re$ is the Reynolds number, and ${\tau }_{ij}$ is a subgrid stress tensor that represents the influence of small-scale eddies on large-scale eddies.

The Smagorinsky Lilly model is adopted [18], which takes the form of Equations 4, 5:

${\tau }_{ij}-\frac{1}{3}{\tau }_{kk}{\sigma }_{ij}=2v_t{\overline{S}}_{ij}(4)$

${\overline{S}}_{ij}=\frac{1}{2}\left(\frac{\partial {\overline{u}}_i}{\partial x_j}+\frac{\partial {\overline{u}}_j}{\partial x_i}\right)(5)$

where $v_t$ is the turbulent viscosity at the grid scale, expressed as Equations 6, 7:

$v_t=C^2{\Delta }^2\left|\overline{S}\right|=C^2{\Delta }^2\sqrt{2{\overline{S}}_{ij}{\overline{S}}_{ij}}(6)$

$\Delta ={\left(\Delta x\Delta y\Delta z\right)}^{1/3}(7)$

where $\Delta$ is the grid size after grid filtering, and $\Delta x、\Delta y$ and $\Delta z$are the grid sizes.

The finite volume method (FVM) is used to discretize the governing equations. The diffusive term is processed using a second-order central difference scheme, and the convective term is discretized using a flux limited second-order upwind scheme. The chemical reaction adopts a 9-species 10-reaction finite rate kinetics with the H₂/CO system. The detailed chemical reaction kinetics are borrowed from Ref. [19].

2.2 Spectral band model

The main radiating species in the gas-phase products generated by propellant combustion have H₂O, CO₂, CO, OH, and HCl. The vibrational and rotational transition emission of high-temperature gas-phase components is the main source of plume infrared radiation. Without considering particle scattering and emission, physical parameters of infrared spectroscopy can be calculated using the Statistics Narrow Band (SNB) method [20]. The spectral transmittance is expressed as Equation 8:

$\overline{\tau }=\exp \left\{-2\overline{a}\left[{\left(1+\frac{\overline{\kappa }\dot{u}}{\overline{a}}\right)}^{1/2}-1\right]\right\}(8)$

where $\overline{\kappa }$ characterizes the ability to emit/absorb photons, $u$ is the length of the pressure path, and $\overline{a}=\pi \overline{\gamma }/\overline{d}$ denotes the fine-structure parameter related to Doppler broadening and collisional broadening. The Doppler broadening parameter ${\gamma }_{D,\mathrm{s}}$ (expressed as Equation 9) for gas component $s$ at wavenumber $\eta$ is provided based on the Single Line Group (SLG) [21] model.

${\gamma }_{\mathrm{D},s}=5.94\times {10}^{-6}\eta \sqrt{\frac{T}{273.0M_s}}(9)$

where $M$ represents the molecular weight, and $T$ represents the temperature.

The NASA-SP-3080 database [22] provided spectral band calculation parameters for six gas molecules, including H₂O, CO₂, CO, HCl, OH, and NO, in the temperature range of 300–3,000 K. Based on the given spectral parameters, the SNB method can be used to obtain the spectral parameters for the infrared radiation calculation.

2.3 Radiative transfer model

Without considering particle scattering effects, the absorption and scattering terms of the radiative transfer equation (RTE) can be simplified. By introducing the optical thickness ${\tau }_{\lambda }={\kappa }_{s\lambda }L$, the RTE is expressed as Equation 10:

$\frac{\mathrm{d}{I}_{\lambda }\left({\tau }_{\lambda }\right)}{\mathrm{d}{\tau }_{\lambda }}=-I_{\lambda }\left({\tau }_{\lambda }\right)+I_{\mathrm{b}\lambda }\left({\tau }_{\lambda }\right)(10)$

where $\lambda$ is the wavelength. $I_{\lambda }$ and $I_{b,\lambda }$ represent spectral radiation intensity and blackbody spectral radiation intensity, respectively. The line of sight (LOS) method is used to solve the RTE.

2.4 Noise suppression model

Gaussian white noise is added to the plume flow field data, and the infrared thermal imaging data is generated through infrared radiation calculation and the SPOD denoising method. The infrared radiation data after adding noise is represented as Equation 11:

$\stackrel{\sim }{\mathit{Q}}=\mathit{Q}+{\mathit{Q}}_{\text{Noise}}(11)$

where $\stackrel{\sim }{\mathit{Q}}$ represents the radiation thermal imaging data with noise, which is arranged in matrix format from thermal imaging data at different times, $\mathit{Q}$ represents the thermal imaging data without noise, and ${\mathit{Q}}_{\text{Noise}}$ represents the residual caused by noise.

The matrix $\stackrel{\sim }{\mathit{Q}}$ is partitioned into smaller matrices through block matrix processing, which is referred to as blocks. After this partitioning, the matrix $\stackrel{\sim }{\mathit{Q}}$ is divided into $N_b$ blocks, with each block containing N_f snapshots. A discrete Fourier transform is then applied to each block as Equation 12:

${\widehat{\mathit{Q}}}^{\left(n\right)}=FFT\left({\mathit{Q}}^{\left(n\right)}\right)=\left[{\widehat{q}}_1^{\left(n\right)},{\widehat{q}}_2^{\left(n\right)},\cdots ,{\widehat{q}}_{N_f}^{\left(n\right)}\right](12)$

where ${\widehat{q}}_k^{\left(n\right)}$ is the Fourier component at the k-th discrete frequency f_k in the n-th block. The data matrix ${\widehat{\mathit{Q}}}_{{\mathit{f}}_{\mathit{k}}}$ is composed of Fourier components with a frequency of f_k in each block matrix [23], expressed as Equation 13:

${\widehat{\mathit{Q}}}_{{\mathit{f}}_{\mathit{k}}}=\left[{\widehat{\mathit{q}}}_1^{\left(1\right)},{\widehat{\mathit{q}}}_2^{\left(2\right)},\cdots ,{\widehat{\mathit{q}}}_{\mathit{k}}^{\left({\mathit{N}}_{\mathit{b}}\right)}\right]\in {\mathbb{R}}^{\mathit{N}\times {\mathit{N}}_{\mathit{b}}}(13)$

where $N$ is the number of grid points. The SPOD mode and its corresponding eigenvalues can be obtained by constructing a cross spectral density matrix ${\mathit{M}}_{f_k}={\widehat{\mathit{Q}}}_{f_k}{\widehat{\mathit{Q}}}_{f_k}^{*}$ and performing eigenvalue decomposition on it. The resulting modes are then sorted according to the magnitude of their eigenvalues.

2.5 Fourier transform model

At each frequency, the Fourier transform matrix ${\widehat{\mathit{Q}}}_{m{\omega }_k}$ is reconstructed as Equation 14:

${\stackrel{\sim }{\mathit{Q}}}_{f_k}={\mathit{\Phi }}_{f_k}\sqrt{n_{blk}}{\mathit{\Lambda }}_{f_k}^{1/2}{\mathit{\Theta }}_{f_k}^{*}(14)$

The Fourier snapshot matrix of the l-th block is represented as Equation 15 [24]:

${\widehat{\mathit{Q}}}_{m\omega }^{\left(l\right)}=\left[\begin{array}{l}{\left({\displaystyle \sum _{i=1}^L}{a}_{ikl}{\varphi }_i\right)}_{k=1},{\left({\displaystyle \sum _{i=1}^L}{a}_{ikl}{\varphi }_i\right)}_{k=2}\\ ,\cdots ,{\left({\displaystyle \sum _{i=1}^L}{a}_{ikl}{\varphi }_i\right)}_{k=N_f}\end{array}\right](15)$

Data denoising can be achieved by rearranging the matrix ${\widehat{\mathit{Q}}}_{{\mathit{f}}_{\mathit{k}}}$ to form a reconstructed Fourier matrix ${\widehat{\mathit{Q}}}^{\left(n\right)}$ and then applying the inverse Fourier transform, expressed as Equation 16:

$q_k^{\left(n\right)}=\frac{1}{w\left(j\right)}{F}^{-1}\left\{{\widehat{q}}_k^{\left(n\right)}\right\}(16)$

By the inverse Fourier transform, the denoised flow field Q_Denoise can be obtained. The detailed derivation process can be found in Ref. [12]. The denoising of infrared thermal images is achieved using the SPOD inversion algorithm. Figure 1 illustrates the schematic diagram of infrared thermal image denoising using the SPOD inversion.

Figure 1

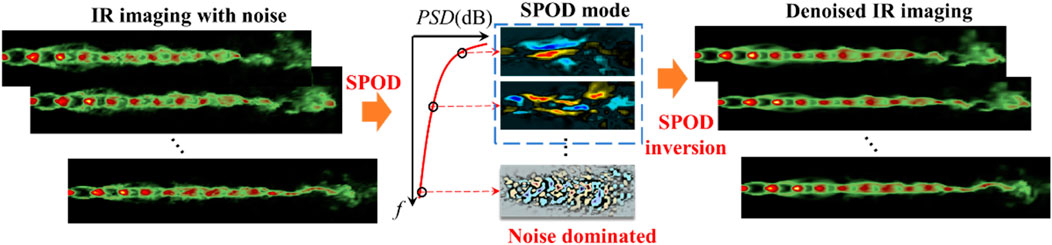
Figure 1. Schematic diagram of infrared thermal image denoising using the SPOD inversion. The denoising technique consists of five steps. (1) Separate the mode structures of different frequencies in the infrared thermal imaging field by the SPOD method, (2) Sort the mode of different frequencies by energy, (3) Truncate the mode structure dominated by noise, (4) Obtain mode truncation by assigning zero values to the corresponding eigenvalues of the truncated SPOD modes, and (5) Implement infrared thermal imaging noise filtering based on the SPOD inversion.

3 Noise model and SPOD data preparation

In practical applications, infrared thermal imaging is often affected by environmental background radiation from the atmosphere, ground, or other objects. Background noise can affect the signal of the detector, especially for highly turbulent plumes. The plume flow is unstable, and the background noise may be relatively high, which affects the quality of infrared thermal imaging. Gaussian white noise is a common type of noise characterized by a uniform distribution of signal power across all frequencies and a normal distribution of noise signals as a function of time.

Numerical results of the unsteady flow field are used as the data source, and the calculation step size of the flow field is 10^–7 s. The snapshot sampling frequency is 1 × 10⁵ Hz, and the time interval between adjacent snapshots is 1 × 10⁻⁵ s. A total of 512 snapshots are taken. The snapshots of infrared thermal images are divided into N_b = 3 segments, each segment is comprised with N_f = 256 photographs. The snapshot overlap rate across consecutive segments is 50%. Gaussian white noise is applied through the noise module of the MATLAB software. Given that the infrared radiation of plumes strongly depends on the temperature, pressure, and gas component concentration of the plume, Gaussian white noise with an amplitude of 8% of the maximum value of each parameter is introduced into the flow field data, which is sufficient to seriously pollute the original data.

4 Results

4.1 Infrared thermal imaging of unsteady plumes

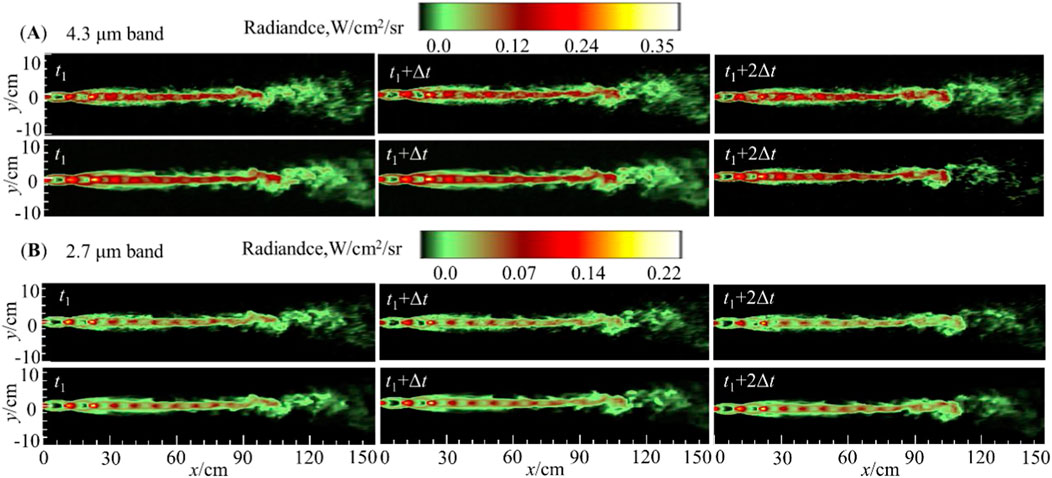
The noise applied to the unsteady flow field can be amplified after infrared radiation calculation. Figure 2 show the infrared radiation intensity map of the plume in the 2.7 and 4.3 μm wavelength bands, respectively. The illustrations from top to bottom show the snapshots of original transient infrared thermal images the thermal image with noise and the difference distribution between the two. As shown in the figure, a series of Mach cells are present in the intrinsic core of the plume, showing a trend of higher infrared radiation intensity as they approach the nozzle exit. Due to the influence of shear effects, small-scale vortex structures are rolled up in the shear layer near the third cell from the nozzle (x ≈ 20 cm). These small-scale eddies cause unstable fluctuations in infrared thermal images. The noise causes the details of the thermal image to become blurred, and the shock wave structure in the intrinsic core area also exhibits irregular changes. Figures 2C1, C2 show the residual distribution of infrared radiation intensity with and without noise influence. It can be observed that the residuals are mainly distributed in the areas where the plume passes after applying Gaussian white noise, and the residuals in the core area are relatively large, while the residuals in the turbulent mixing area are relatively small.

Figure 2

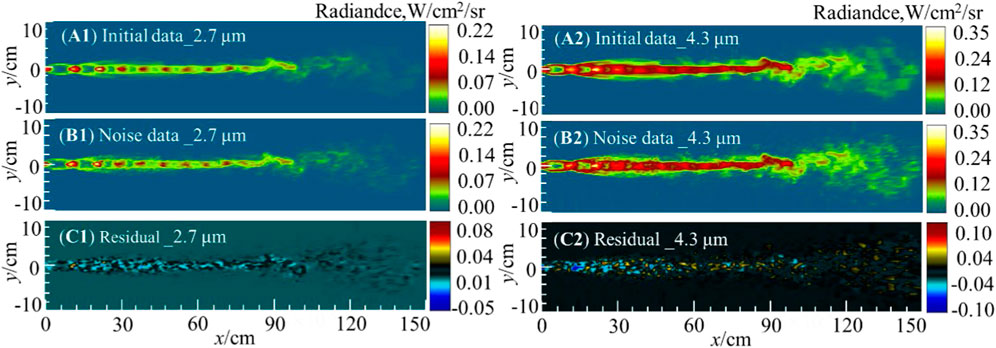
Figure 2. Infrared image snapshot of the plume in the 2.7 μm (A1–C1) and 4.3 μm (A2–C2) bands. The initial data represents the infrared thermal image before applying noise, and the noise data represents the infrared thermal image after applying noise. The residual distributions (C1, C2) of infrared radiation intensity with and without noise.

4.2 Error analyses

The relative error is used to evaluate the difference between the noisy and real data, and its formula is expressed as Equation 17:

$Error=\frac{\text{norm}\left(\stackrel{\sim }{\mathit{Q}}-\mathit{Q}\right)}{\text{norm}\left(\mathit{Q}\right)}(17)$

where norm (▪) represents the norm of a matrix or vector.

Figure 3A shows the error distribution between the thermal images with and without noise in the 2.7 and 4.3 μm bands. From Figure 3A, it can be seen that the noise increases the error level of infrared radiation intensity to varying degrees across different bands. The average errors of infrared radiation intensity in the 2.7 μm and 4.3 μm bands are 21.1% and 17.6%, respectively. It means that the infrared radiation intensity in the 2.7 μm band is more affected by noise compared with the 4.3 μm band.

Figure 3

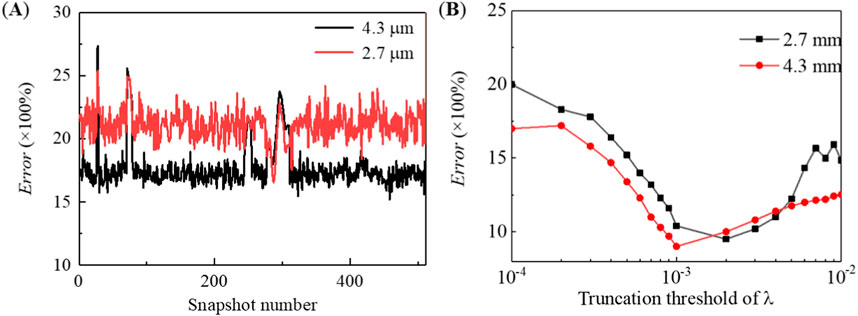
Figure 3. Error distribution of plume infrared thermal image: (A) the error distribution between the thermal images with and without noise, and (B) the error distribution of different bands before and after infrared thermal imaging denoising with threshold truncation.

The suppression of infrared noise is achieved through the SPOD frequency domain reconstruction. Gaussian white noise has different effects on the structure of the flow field at different scales. Therefore, the threshold truncation method is used to filter out the small-scale coherent structures in the plume that are greatly affected by noise, in order to preserve the large-scale flow structure. By using the SPOD inversion, it is possible to achieve radiation denoising while preserving the original data of the thermal imaging field to the greatest extent possible. Figure 3B shows the error distributions of different bands before and after infrared thermal imaging denoising. From Figure 3B, it can be seen that the error of the denoised infrared thermal image has a trend of first decreasing and then increasing with the increase of the truncation threshold. When the truncation threshold is low, the dominant noise structure in high frequency is not filtered out, resulting in poor denoising quality. An excessively large truncation threshold can result in the filtering out of low-frequency large-scale flow structures with high energy consumption in infrared thermal images, and the noise reduction quality is also poor. Numerical analysis reveals that truncation occurs around λ = 0.001, and the flow field denoising reaches its minimum value. Infrared thermal imaging errors in the 2.7 and 4.3 μm bands have been reduced from 21.1% and 17.6% to 9.4% and 9.2%, respectively.

4.3 Denoising of infrared thermal imaging

Figures 4A, B show the 4.3 μm and 2.7 μm infrared thermal images obtained by using the threshold truncation and the inversion SPOD algorithm, respectively. The upper illustration shows a thermal image snapshot with noise. It can be seen that the application of noise causes blurring of thermal image. The lower illustration shows the distribution of the thermal image contours without noise. It can be observed that the key features of the thermal image after denoising are more prominent, indicating that the proposed infrared thermal image denoising algorithm is reasonable.

Figure 4

Figure 4. Contours of plume infrared thermal image in the (A) 4.3 μm and (B) 2.7 μm bands.

5 Conclusion

This study focuses on the exhaust plume of the BEM-II rocket and reconstructs the noisy plume flow field by Gaussian white noise. Based on the flow field parameters of the plume, infrared thermal images with noise are generated through infrared radiation transfer calculations, and the SPOD frequency domain reconstruction is used to achieve denoising processing of the infrared thermal images. The main conclusions drawn are as follows:

(1) Gaussian white noise causes infrared radiation thermal images to exhibit varying degrees of influence in different regions. In the plume intrinsic core region, the residual distribution of data is relatively large, and the residual values in the turbulent mixing region are relatively small.

(2) The infrared thermal images in different bands are significantly affected by noise. The infrared radiation intensity in the 2.7 μm band is greatly affected by noise, with an average error of 21.1%. The average error of the infrared radiation intensity in the 4.3 μm band is 17.6%.

(3) The influence of noise is greatly reduced, and the details of the infrared thermal image are clearer by using the SPOD inversion. The infrared thermal imaging errors in the 2.7 and 4.3 μm bands have been reduced from 21.1% and 17.6% to 9.4% and 9.2%, respectively.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

DF: Methodology, Writing–original draft. AS: Data curation, Methodology, Writing–original draft. QN: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by the National Nature Science Foundation of China (Nos. 52006203 and U22B2045), the Fundamental Research Program of Shanxi Province (No. 202403021211078), and also supported by the Graduate Student Innovation Project of Shanxi Province (Grant No. 2023SJ191).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Sun YQ, Dong SK, Niu QL, Yang S. NIPC-based uncertainty analysis of infrared radiation from rocket exhaust plumes caused by nozzle exit conditions. Infrared Phys and Technology (2020) 108:103376. doi:10.1016/j.infrared.2020.103376

CrossRef Full Text | Google Scholar

2. Yan PP, Gao WQ, Meng XY, Wang HL, Niu QL, Dong SK. A numerical study on the influence of multiple nozzles on the infrared radiation signatures of liquid rocket exhaust plumes. Case Stud Therm Eng (2024) 61:104835. doi:10.1016/j.csite.2024.104835

CrossRef Full Text | Google Scholar

3. Paiva C, Slusher H. Space-based missile exhaust plume sensing: strategies for DTCI of liquid and solid IRBM systems. In: Space 2005; August 2005 (2005). p. 6820.

CrossRef Full Text | Google Scholar

4. Huang JW, Liu SJ, Ni Q, Mao WF, Gao X. Experimental study of extracting weak infrared signals of rock induced by cyclic loading under the strong interference background. Appl Sci (2018) 8(9):1458. doi:10.3390/app8091458

CrossRef Full Text | Google Scholar

5. Lerch P, Dumas P, Schilcher T, Nadji A, Luedeke A, Hubert N, et al. Assessing noise sources at synchrotron infrared ports. J synchrotron Radiat (2012) 19(1):1–9. doi:10.1107/s0909049511041884

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Toscano AM, Lato MR, Fontanarosa D, De Giorgi MG. Optical diagnostics for solid rocket plumes characterization: a review. Energies (2022) 15(4):1470. doi:10.3390/en15041470

CrossRef Full Text | Google Scholar

7. Alsberg BK, Woodward AM, Winson MK, Rowland J, Kell DB. Wavelet denoising of infrared spectra. Analyst (1997) 122(7):645–52. doi:10.1039/A608255F

CrossRef Full Text | Google Scholar

8. Antonelli P, Revercomb HE, Sromovsky LA, Smith WL, Knuteson RO, Tobin DC, et al. A principal component noise filter for high spectral resolution infrared measurements. J Geophys Res Atmospheres (2004) 109(D23). doi:10.1029/2004jd004862

CrossRef Full Text | Google Scholar

9. Koziol P, Raczkowska MK, Skibinska J, Urbaniak-Wasik S, Paluszkiewicz C, Kwiatek W, et al. Comparison of spectral and spatial denoising techniques in the context of high definition FT-IR imaging hyperspectral data. Scientific Rep (2018) 8(1):14351. doi:10.1038/s41598-018-32713-7

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Li Z, Luo SJ, Chen MY, Wu H, Wang T, Cheng LL. Infrared thermal imaging denoising method based on second-order channel attention mechanism. Infrared Phys and Technology (2021) 116:103789. doi:10.1016/j.infrared.2021.103789

CrossRef Full Text | Google Scholar

11. Nekkanti A, Schmidt OT. Frequency–time analysis, low-rank reconstruction and denoising of turbulent flows using SPOD. J Fluid Mech (2021) 926:A26. doi:10.1017/jfm.2021.681

CrossRef Full Text | Google Scholar

12. Sieber M, Paschereit CO, Oberleithner K. Spectral proper orthogonal decomposition. J Fluid Mech (2016) 792:798–828. doi:10.1017/jfm.2016.103

CrossRef Full Text | Google Scholar

13. Chen CW, Wang S, Ghaemi S. Spectral proper orthogonal decomposition of time-resolved three-dimensional flow measurements in the turbulent wake of the Ahmed body. J Fluid Mech (2024) 985:A19. doi:10.1017/jfm.2024.288

CrossRef Full Text | Google Scholar

14. Sun A, Niu QL, Dong SK. Spectral feature extraction of rocket exhaust plume using spectral proper orthogonal decomposition. Phys Fluids (2024) 36(3):035172. doi:10.1063/5.0200576

CrossRef Full Text | Google Scholar

15. Avital G, Cohen Y, Gamss L, Kanelbaum Y, Macales J, Trieman B, et al. Experimental and computational study of infrared emission from underexpanded rocket exhaust plumes. J Thermophys Heat transfer (2001) 15(4):377–83. doi:10.2514/2.6629

CrossRef Full Text | Google Scholar

16. Bisoi M, Das MK, Roy S, Patel DK. Large eddy simulation of three-dimensional plane turbulent free jet flow. Eur J Mechanics-B/Fluids (2017) 65:423–39. doi:10.1016/j.euromechflu.2017.02.003

CrossRef Full Text | Google Scholar

17. Wawrzak K, Boguslawski A, Tyliszczak A. LES predictions of self-sustained oscillations in homogeneous density round free jet. Flow, Turbulence and Combustion (2015) 95:437–59. doi:10.1007/s10494-015-9640-2

CrossRef Full Text | Google Scholar

18. Guan QD, Liang JH, Sun MB, Zhang L, Chen WW. Large eddy simulation of supersonic mixing layers using a compressible filtered mass density function method. Aerospace Sci Technology (2022) 24:107425. doi:10.1016/j.ast.2022.107425

CrossRef Full Text | Google Scholar

19. Niu QL, He ZH, Dong SK. IR radiation characteristics of rocket exhaust plumes under varying motor operating conditions. Chin J Aeronautics (2017) 30(3):1101–14. doi:10.1016/j.cja.2017.04.003

CrossRef Full Text | Google Scholar

20. Li JL, Bai L, Zhang LG, Bai JY, Xu YY, Guo LX. Accurate evaluation on infrared spectral radiation for booster phase rocket exhaust plumes. Int J Heat Mass Transfer (2023) 216:124606. doi:10.1016/j.ijheatmasstransfer.2023.124606

CrossRef Full Text | Google Scholar

21. Niu QL, Gao WQ, Sun YQ, Dong SK. Investigation on infrared radiation signatures of under-expanded rocket exhaust plumes due to angle of attack. IEEE Access (2021) 9:113156–68. doi:10.1109/access.2021.3103898

CrossRef Full Text | Google Scholar

22. Ludwig CB, Malkmus W, Reardon JE, Thomson JAL, Goulard R. Handbook of infrared radiation from combustion gases. Washington: NASA (1973).

Google Scholar

23. Towne A, Schmidt OT, Colonius T. Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J Fluid Mech (2018) 847:821–67. doi:10.1017/jfm.2018.283

CrossRef Full Text | Google Scholar

24. Schmidt OT, Towne A. An efficient streaming algorithm for spectral proper orthogonal decomposition. Computer Phys Commun (2019) 237:98–109. doi:10.1016/j.cpc.2018.11.009

CrossRef Full Text | Google Scholar