β-decay studies for shape coexistence

$\beta$ decay has played a key role in studies of shape coexistence throughout the nuclear chart. This has been mainly due to the sensitivity in $\gamma$-ray and conversion electron spectroscopy that can be achieved following the population of excited states by $\beta$ decay. In some regions, the spectroscopic studies using $\beta$ decay have been the first to suggest the presence of shape coexistence; in others, they have reinforced the suggestion and provided important spectroscopic data. The present work reviews some of the key regions, with a prime focus on the neutron-rich side of the valley of stability, where $\beta$-decay measurements have played an important role.

1 Introduction

Studies of shape coexistence have been at the forefront of nuclear structure research for several decades and continue to capture a great deal of attention. Once believed to be a rather exotic phenomenon, the regions of the nuclear chart in which they have been discovered, or suggested, have grown significantly over the past few decades. Identifying shape coexistence in nuclei often begins with the observation of a specific pattern of states, or the appearance of states at an excitation energy that is unexpected. For example, observing a sequence of levels that approximately follow an $I(I+1)$ energy spacing in what is regarded as a spherical or weakly deformed nucleus can provide the first clue. Important follow-up experiments can then seek the in-band transitions and ideally measure transition rates. It is not uncommon for such deformed rotational structures to be found in spherical nuclei, in part due to the lower level density observed at low excitation energies in these nuclei compared to their well-deformed counterparts. The converse example, finding spherical or weakly deformed states in a nucleus with a well-deformed ground state, can be far more challenging. Exceptions to this can occur if the shape-coexisting states lie sufficiently low in energy that their presence is completely unexpected. Examples of this are the famous cases of ⁹⁸Sr and ¹⁰⁰Zr that will be discussed below.

A particular challenge in nuclear structure studies is that as the excitation energy increases, the low-energy in-band (intra-band) $E2$ transitions become progressively weaker and more difficult to observe due to the competition with the high-energy out-of-band (inter-band) transitions. Considering competition with an inter-band $E2$ transition, we use the example of an intra-band transition of 200-keV energy vs. an inter-band transition of 1 MeV. The $E_{\gamma }^5$ phase-space factor results in the intensity ratio of 3,125 in favour of the 1-MeV $\gamma$ ray for the same value of the transition matrix element. Thus, even if the matrix element is an order of magnitude in favour of the intra-band transition, resulting in a $B(E2)$ ratio of 100, the ratio of the $\gamma$-ray intensities would still favour the 1-MeV transition by a factor of 31. Further considering that the 200-keV $\gamma$ ray would reside in a region of (generally) much higher background, the problem of observing and identifying the intra-band transitions becomes obvious. In fusion–evaporation reactions, the background continuum present in a $\gamma$-ray spectrum is generally a combination of Compton-scattered $\gamma$ rays and the statistical (or quasi-statistical) $\gamma$ rays from the compound nucleus. Although it varies from case to case, typically in $\gamma$-ray spectroscopy using such reactions, the minimum $\gamma$-ray branching ratio achieved is on the order of 1% of the most intense transition for any particular level. In contrast, $\gamma$-ray spectroscopy, following $\beta$-decay, does not have the presence of the statistical $\gamma$-ray continuum, and thus, the backgrounds are generally much lower. Furthermore, the definite $Q$-value for the decay results in a strong dependence of the backgrounds on the gating transition, and a judicious choice can effectively remove backgrounds from regions of interest in the resulting spectra. The result is that the observation of transitions with branching ratios on the order of $10^{-3}$–$10^{-4}$ can be readily achieved. These weak, low-energy transitions are vital to unravel the structure and identify shape-coexisting structures. This is a point that will be seen in many of the studies cited below.

Since the firm determination of the nuclear shape can be challenging and requires, for example, detailed Coulomb excitation studies, the initial indications often come from the pattern of excited states and the $\gamma$-ray decay properties of the levels. It is here that $\beta$-decay plays a vital role since $\gamma$-ray spectroscopy with large-scale detector arrays permit the observation of $\gamma$-ray decays from even very weakly populated levels. Although there is no guarantee of completeness, modern $\gamma$-ray spectrometers can provide the sensitivity to observe all states in a window of $\mathrm{\Delta }I=\pm 1$ of the parent spin $I_i$ up to high excitation energy, as allowed by the decay $Q$-value. Measurements using $\beta$-decay also provide the best opportunity to observe $E0$ transitions, again due to the lower background levels that can typically be achieved compared to in-beam studies. Particularly important in this regard have been measurements with low-spin parents that can have enhanced populations of $0^{+}$ states in the daughters, thus facilitating the observation of the $0^{+}\to 0^{+}$ transitions.

The discovery and understanding of shape coexistence in many nuclei have been greatly aided by data from $\beta$-decay measurements, and this is especially true for neutron-rich nuclei. The present article, therefore, has its main focus on measurements involving ${\beta }^{-}$ decay that have elucidated the presence or nature of shape coexistence in neutron-rich systems but also includes the Cd and Sn isotopes for which there has been much recent activity and with the Cd nuclei, especially, a radical shift in their interpretation. No claim for completeness of the literature is made; rather, a selection of examples is made of those the author finds as either compelling, highlighting the excellent quality of data that can be obtained, or demonstrate the progression of our understanding.

1.1 Nuclear shapes

When discussing the nuclear shape, the usual assumption is that the nucleus can be modelled as a liquid drop with the nuclear surface described as an infinite series of spherical harmonics

$R\left(\theta ,\varphi \right)=R_0\left(1+{\displaystyle \sum _{l\mu }}{\alpha }_{l\mu }^{*}{Y}_{l\mu }\left(\theta ,\varphi \right)\right),(1)$

where $R_0$ is the radius of the nuclear surface in the spherical configuration, $Y_{l\mu }$ are the spherical harmonics of degree $l$, order $\mu$, and ${\alpha }_{l\mu }$ are the (complex) time-dependent expansion parameters describing the deformation of the nuclear surface. The most important contribution to the departure from a spherical shape comes from quadrupole deformation, and the above infinite series is often reduced to the $l=2$ term

$R\left(\theta ,\varphi \right)=R_0\left(1+{\displaystyle \sum _{\mu }}{\alpha }_{2\mu }^{*}{Y}_{2\mu }\left(\theta ,\varphi \right)\right).(2)$

Equations 1, 2 describe the nuclear shape with an arbitrary orientation in space and can be transformed into the principal-axis frame using the Wigner rotation matrices, $D_{\nu \mu }^J(\alpha ,\beta ,\gamma )$, via Equation 3

$a_{2\mu }={\displaystyle \sum _{\nu }}{D}_{\nu \mu }^2\left(\alpha ,\beta ,\gamma \right){\alpha }_{2\nu },(3)$

with the Euler angles $(\alpha ,\beta ,\gamma )$ chosen such that $a_{2\pm 1}=0$. The commonly used deformation parameters ${\beta }_2$ and $\gamma$, which define the magnitude of the deformation and the deviations away from axiality, respectively, are defined in Equation 4

$a_{20}={\beta }_2\cos \gamma ,a_{22}=\frac{1}{\sqrt{2}}{\beta }_2\sin \gamma ,(4)$

with the restriction of $0\le \beta$ and $0\le \gamma \le \pi /3$ in order to not have the same quadrupole moments, and hence shapes, defined by a different set of coordinates.

1.2 Extracting shapes

In order to firmly identify shape-coexisting states, some key indicators are required. These indicators have been described in detail elsewhere (see, e.g., Ref. [1]), and those that can be extracted from $\beta$-decay studies will only be briefly outlined here.

As discussed above, locating states and determining their decays and spin-parities is a first requirement. Lifetime measurements of excited states provide an extremely important quantity since once determined, together with transition branching ratios, the reduced transition rate or $B(E2)$ value can be found from Equation 5

$B\left(E2\downarrow ;I_i\to I_f\right)=\frac{\left(9.527\times 10^6\right)BR}{E_{\gamma }^5{A}^{4/3}{t}_{1/2}\left(1+\alpha \right)}\left(\frac{{\delta }^2\left(E2/M1\right)}{1+{\delta }^2\left(E2/M1\right)}\right)\mathrm{W}.\mathrm{u}.,(5)$

where $BR$ is the total transition branching ratio (i.e., including both the $\gamma$-ray and conversion-electron fractions), $E_{\gamma }$ is given in keV, $A$ is the mass number, $t_{1/2}$ is the level half-life in $s$, and $\alpha$ is the total conversion coefficient for the transition. In the case of mixed $E2/M1$ transitions, the rate must be corrected for the transition mixing ratio $\delta (E2/M1)$. The correction for the conversion coefficient can be neglected if it is very small, and its impact is much less than the experimental uncertainties on the level lifetimes or branching ratios. In this work, the Weisskopf units (W.u.) are used throughout. Care must be used if converting from $B(E2\downarrow )$ to $B(E2\uparrow )$ as the two quantities are related by Equation 6

$B\left(E2\uparrow \right)=\frac{2I_{\mathit{upper}}+1}{2I_{\mathit{lower}}+1}B\left(E2\downarrow \right),(6)$

where the notation on the level spins is obvious.

Once a $B(E2)$ value has been determined, it can be related to an intrinsic quadrupole moment $Q_0$ via

$B\left(E2;I_{i}K\to I_{f}K\right)=\frac{5}{16\pi }{Q}_0^2{⟨I_{i}K20|I_{f}K⟩}^2{e}^2{\mathrm{b}}^2,(7)$

where the $B(E2)$ value must be in units of $e^2$b² and a $K$ quantum number (the projection of the angular momentum onto the nuclear symmetry axis) is assumed. Extracting an intrinsic quadrupole moment via Equation 7 builds in an assumption of the nuclear shape as being axially symmetric (and hence $K$ being a good quantum number). It should be noted that the value extracted in this way, often referred to as the rotational limit, gives an over-estimate of the actual quadrupole moment if the system possesses any softness or triaxiality. With $Q_0$ determined, it can be related to the deformation parameter ${\beta }_2$ via Equation 8

$\begin{array}{ll}\hfill Q_0& =\frac{3}{\sqrt{5\pi }}Z{R}_0^2{\beta }_2\left(1+\frac{2}{7}\sqrt{\frac{5}{\pi }}{\beta }_2+\cdots \right)\hfill \\ \hfill & \approx \frac{3}{\sqrt{5\pi }}Z{R}_0^2{\beta }_2\left(1+0.36{\beta }_2\right).\hfill \end{array}(8)$

Ideally, it is better to extract the rotationally invariant $⟨Q^2⟩$ and $⟨Q^3\cos 3\delta ⟩$ values that can be established using the Kumar–Cline sum rules [2–4]. In the principal-axis frame of the nucleus, the electromagnetic $E2$ operator, ${\widehat{\mathcal{M}}}^{\prime }(E2)$, which is a rank-2 SO(3) tensor, has components that can be expressed using two parameters:

$\begin{array}{ccc}\hfill {\mathcal{M}}^{\prime }\left(E2,\mu =0\right)=& Q\cos \delta \hfill & \hfill \\ \hfill {\mathcal{M}}^{\prime }\left(E2,\mu =\pm 2\right)=& \frac{1}{\sqrt{2}}Q\sin \delta .\hfill & \hfill \end{array}(9)$

The electromagnetic $E2$ matrix elements $\mathcal{M}(E2)$ measured in the laboratory frame can be related to those in the principal-axis frame by making use of the invariant property of the electric quadrupole tensor under rotational (SO(3)) transformations. The products of the $E2$ operators coupled to zero angular momentum are scalar quantities, and thus their expectation values can be expressed in terms of $Q$ by

$\begin{array}{ll}\hfill \frac{{\left(-1\right)}^{2I_i}}{\sqrt{2I_i+1}}{\displaystyle \sum _j}\langle I_i\Vert \mathcal{M}\left(E2\right)\Vert I_j\rangle & \langle I_j\Vert \mathcal{M}\left(E2\right)\Vert I_i\rangle \left\{\begin{array}{ccc}\hfill 2\hfill & \hfill 2\hfill & \hfill 0\hfill \\ \hfill I_i\hfill & \hfill I_i\hfill & \hfill I_j\hfill \end{array}\right\}\hfill \\ \hfill & =\frac{1}{\sqrt{5}\left(2I_i+1\right)}{\displaystyle \sum _j}\langle I_j\Vert \mathcal{M}\left(E2\right){\Vert I_i\rangle }^2=\frac{1}{\sqrt{5}}⟨Q^2⟩,\hfill \end{array}(10)$

where $\left\{\right\}$ is a $6j$ symbol. The sum formally extends over all states $I_j$ that can be reached from the state in question $I_i$ via a single $E2$ transition; however, typically, only a few key states contribute to it. Products of three quadrupole tensors coupled to angular momentum zero can also be formed that are used to extract $\sqrt{\frac{2}{35}}⟨Q^3\cos 3\delta ⟩$. However, this requires knowledge of not only the magnitudes but also the signs of the matrix elements which cannot be determined by $\beta$-decay.

Assuming identical charge and mass distributions, one can relate the $Q^2$ parameter to the deformation parameter ${\beta }_2$ by [5]

$\langle Q^2\rangle =q_0^2\langle {\beta }_2^2\rangle ,(11)$

with $q_0=\frac{3}{4\pi }Ze{R}_0^2$ and $R_0=1.2A^{1/3}$ fm. The extraction of the $⟨Q^2⟩$ value depends only on squares of matrix elements, and thus any experimental technique that contributes spectroscopic data required to determine the $B(E2;I_i\to I_f)$ values can be brought to bear. Once the lifetime of a level is available, the measurement of a $\gamma$-ray branching ratio provides the $B(E\lambda )$ value for that transition. Thus, a $\beta$-decay measurement can be used to determine $B(E2)$ values for previously unobserved transitions in this case. Care must be used, however, if the level lifetime is deduced from Coulomb excitation results, as is often the case in the evaluated data files. Here, depending on the details of the reaction and the analysis, the presence of a previously unobserved excitation pathway may modify the lifetime results extracted.

1.3 $E0$ transitions

The electric monopole, or $E0$, transition plays a very important role in studies of shape coexistence since the magnitude depends on the difference in the root-mean-square values of the charge radii between the initial and final states. The first application of $E0$ transition rates to shape coexistence appears in [6] in their study of shape coexistence in ¹¹⁶Sn. The operator for $E0$ transitions is given in Equation 12 [7]

$\widehat{M}\left(E0\right)={\displaystyle \sum _i}{e}_i{r}_i^2,(12)$

where the sum extends over the $A$ bodies in the nucleus with their charges $e_i$ and radial position $r_i$. $E0$ transitions are allowed only for $\mathrm{\Delta }J=0$ transitions and are sensitive to the changes in the nuclear charge-squared radii. The usual quantity quoted when referring to $E0$ transitions are the ${\rho }^2(E0)$ values, defined via Equation 13 [7]

$\mathrm{\Gamma }\left(E0\right)=\frac{1}{\tau \left(E0\right)}={\rho }^2\left(E0\right){\displaystyle \sum _j}{\mathrm{\Omega }}_j\left(Z,\mathrm{\Delta }E\right),(13)$

where $\mathrm{\Gamma }(E0)$ is the partial width for the decay, $\tau (E0)$ is the partial lifetime, and $\mathrm{\Omega }(Z,E_e)$ is the electronic factor that depends on the atomic number $Z$ and the energy of the transition $\mathrm{\Delta }E$. The quantity $\rho (E0)$ is defined by Equation 14

$\rho \left(E0\right)=\frac{1}{e{R}^2}⟨I_f\left|M\left(E0\right)\right|I_i⟩(14)$

and carries all nuclear structure information. The expression typically used for the $E0$ operator in Equation 12 takes the leading order term only of the operator that can be more generally written as in Equation 15 [8]

$\widehat{M}\left(E0\right)={\displaystyle \sum _i}{e}_i\left(r_i^2-\sigma r_i^4+\cdots \right).(15)$

The value for the parameter $\sigma$ depends on the derivatives of the electron wave functions at the origin and has a slight dependence on the electronic shell of the originating electron and the transition energy, and a stronger dependence on the nuclear charge distributions. In nearly all cases, $\sigma <0.1$ and exceeding this value only in the heaviest nuclei (above Pb) and assuming an $1/r$ charge distribution. For the case of constant charge distribution and $Z<100$, $\sigma <0.1$ always. Recently [9], extensive beyond-mean-field calculations using the Gogny forces and the five-dimensional collective Hamiltonian explored the effect of using the expanded $E0$ operator adopting $\sigma =0.1$. Figure 1 shows the results of their calculations. As expected, the addition of the $r^4$ term in the operator reduces the magnitude of the ${\rho }^2(E0)$ values, although this may be considered an over-estimate of the impact since the actual value of $\sigma$ for these particular cases is expected to be much smaller.

Figure 1

Figure 1. Comparison of calculated ${\rho }^2(E0)$ values for the $0_2^{+}\to 0_1^{+}$ transitions for the Zr isotopes (left) and the $N=82$ isotones (right). The blue curves are the results of the 5DCH calculations using collective masses in the Inglis–Belyaev approximation and the $E0$ operator using only the first term in the expansion (the so-called standard (S) approximation). The burgundy colour also uses the standard $E0$ operator but with renormalised masses in the 5DCH calculation, and the green colour, the latter calculation but with the additional term in the $E0$ operator (labelled CW). The red points are the experimental values that were taken from [10]. Figure taken from [9].

Within a two-state mixing model, ${\rho }^2(E0)$ can be expressed as

${\rho }^2\left(E0\right)=a^2{b}^2{\left(\mathrm{\Delta }⟨r^2⟩\right)}^2\frac{Z^2}{R^4},(16)$

where $a^2$ and $b^2$ are the square of the mixing amplitudes of the two states, $\mathrm{\Delta }⟨r^2⟩$ is the difference in the mean-square charge radii, and $R=1.2A^{1/3}$ fm. In the collective variables of the Bohr model, the operator is given by Equation 17 (keeping the lowest-order term in Equation 15) [11]

$\widehat{M}\left(E0\right)=\frac{3Z}{4\pi }\left(\frac{4\pi }{5}+{\beta }^2+\frac{5\sqrt{5}}{21\sqrt{\pi }}{\beta }^3\cos \gamma \right)(17)$

so that in a two-level mixing solution with deformation parameters $({\beta }_1,{\gamma }_1)$ and $({\beta }_2,{\gamma }_2),$ the $E0$ strength is given by Equation 18 [7, 11]

${\rho }^2\left(E0\right)={\left(\frac{3Z}{4\pi }\right)}^2{a}^2\left(1-a^2\right){\left[\left({\beta }_1^2-{\beta }_2^2\right)+\frac{5\sqrt{5}}{21\sqrt{\pi }}\left({\beta }_1^3\cos {\gamma }_1-{\beta }_2^3\cos {\gamma }_2\right)\right]}^2.(18)$

Although often the $E0$ transitions are interpreted as occurring between shape-coexisting shapes, they can arise in any situation where there is a difference in the ${(⟨r^2⟩)}^2$ values between two states. In the case of a spherical vibrator, for example, the nature of the $E0$ operator gives rise to a selection rule that $E0$ transitions are allowed for changes of the phonon number $\mathrm{\Delta }N=0,\pm 2$. For $0^{+}(N=2)\to 0^{+}(N=0)$, for example [7],

${\rho }^2\left(E0\right)=\frac{2}{5}{\left(\frac{3}{4\pi }Z{\beta }_{\mathit{rms}}^2\right)}^2,(19)$

where ${\beta }_{\mathit{rms}}^2$ in Equation 19 is the mean-square value of the amplitude of the surface vibration.

The vast majority of measured ${\rho }^2(E0)$ values are between $J^{\pi }=0^{+}$ states. For states with $J\ne 0$, $E0$ transitions can occur, but their extraction requires a subtraction of the $M1$ and $E2$ contributions. The intensity of the $K$-conversion electron line, for example, has three contributions from the $E0$, $M1$, and $E2$ components and is given by Equation 20

$I_K=I_K\left(E0\right)+I_K\left(M1\right)+I_K\left(E2\right)(20)$

and dividing by the $\gamma$-ray intensity, $I_{\gamma }$, yields Equation 21

${\alpha }_K\left(E0+M1+E2\right)=\frac{I_K\left(E0\right)+I_K\left(M1\right)+I_K\left(E2\right)}{I_{\gamma }}(21)$

and thus Equation 22 gives the E0 contribution to α_K

${\alpha }_K\left(E0\right)={\alpha }_K\left(E0+M1+E2\right)-\frac{{\alpha }_K\left(M1\right)+{\delta }^2\left(E2/M1\right){\alpha }_K\left(E2\right)}{1+{\delta }^2\left(E2/M1\right)}.(22)$

An often used quantity is given in Equation 23

$q_K^2\left(E0/E2\right)=\frac{I_K\left(E0\right)}{I_K\left(E2\right)}(23)$

and also using the standard $E2$ to $M1$ transition mixing ratio given in Equation 24

${\delta }^2\left(E2/M1\right)=\frac{I_{\gamma }\left(E2\right)}{I_{\gamma }\left(M1\right)}(24)$

results in Equation 25

${\alpha }_K\left(E0+M1+E2\right)=\frac{{\alpha }_K\left(M1\right)+{\delta }^2\left(E2/M1\right)\left(1+q_K^2\left(E0/E2\right)\right){\alpha }_K\left(E2\right)}{1+{\delta }^2\left(E2/M1\right)},(25)$

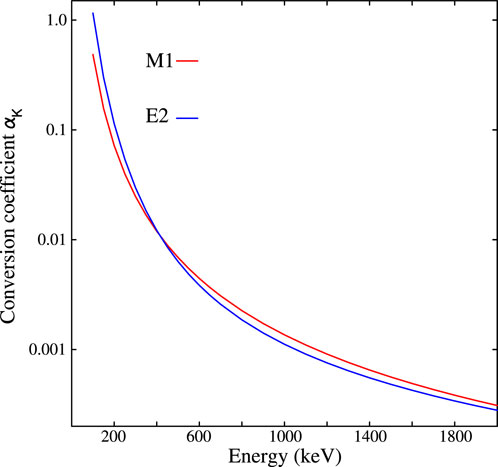
with ${\alpha }_K(M1)$ and ${\alpha }_K(E2)$ the $K$-conversion coefficients for $M1$ and $E2$ multipolarities of the transition at energy $E_{\gamma }$, respectively. Although, in principle, the multipole mixing ratio $\delta (E2/M1)$ must be known, there are situations where this is not the case. For some combinations of $Z$ and transition energy, the conversion coefficients ${\alpha }_K(E2)$ and ${\alpha }_K(M1)$ are nearly identical. Figure 2 demonstrates this for the $Z=50$ Sn isotopes; if $\delta (E2/M1)$ is known, the accuracy of the extraction of ${\alpha }_K(E0)$ can be improved, but unless very high statistics are obtained, lack of knowledge of $\delta$ may not be a limiting factor.

Figure 2

Figure 2. ${\alpha }_K$ conversion coefficient for $Z=50$ for $M1$ (red) and $E2$ (blue) multipolarity as a function of the transition energy. At approximately 400 keV, the conversion coefficients are identical, implying no error in the extraction of the $E0$ component of the $J\to J$ transition due to incomplete knowledge of the $E2/M1$ mixing ratio $\delta$. At 1 MeV, the difference in the ${\alpha }_K$ coefficients is approximately 20%. Adopting an average of the two coefficients leads to a 10% relative uncertainty on the $M1+E2$ electron intensity to be subtracted from the total $K$-electron intensity. This will become the limiting factor for $I_K(E0)$ when its magnitude is less than 10% of the total electron intensity.

2 Studies of shape coexistence

2.1 The Mg isotopes and the $N=20$ “island of inversion”

The region of nuclei surrounding the $N=20$ Mg isotope ³²Mg has been the focus of many investigations for nearly five decades. The observation from mass measurements of an increase in the two-neutron separation energies appearing between ²⁹Na and ³¹Na was interpreted with the aid of Hartree–Fock calculations [12] that the Na isotopes appeared to have deformed ground states for ^31,33Na. Later measurements of the isotope shifts by laser spectroscopy indicated deformed ground state structures already setting in at ²⁸Na [13]. The presence of a low-lying $2_1^{+}$ state in the neighbouring ³²Mg was first found in $\beta$-decay studies of ³²Na [14]. The energy of the $2_1^{+}$ state was much lower than would be expected for a closed neutron shell at $N=20,$ and given the trends observed in the masses of the Mg isotopes, it had already been speculated that the ground state of ³²Mg was deformed. This region was coined the “island of inversion” (see, e.g., Ref. [15]), i.e., a region where the deformed intruder configuration based on particle-hole excitations lies below the spherical normal configuration. The original island was suggested to be composed of the nine nuclei ^30-32Ne, ^31-33Na, and ^32-34Mg [15]. This region has since been expanded as additional data have been obtained, for example, the spin and magnetic moment of the ³¹Mg ground state are evidence of its intruder configuration [16]. As might be anticipated in a region with an inversion of configurations, shape coexistence should be manifested.

Measurements using the $\beta$-$\gamma$-$\gamma$-timing technique, following ³⁰Na decay by Mach et al. [17], found a lifetime of the 1788-keV $0_2^{+}$ state in ³⁰Mg of 3.9 (4) ns. This long lifetime was interpreted as resulting from the hindered nature of the transition from the purported intruder $0_2^{+}$ state to the $2_1^{+}$ state, where the latter is part of the normal shell model configuration [17]. From the intensity imbalance observed for the 1788-keV state, it was also hypothesized that an $E0$ branch existed. This $E0$ transition was later observed in a follow-up $\beta$-decay experiment with a value $10^3\times {\rho }^2(E0)=26.2(75)$ extracted, which is consistent with rather weak mixing between the two configurations that have a large difference in their deformations [18].

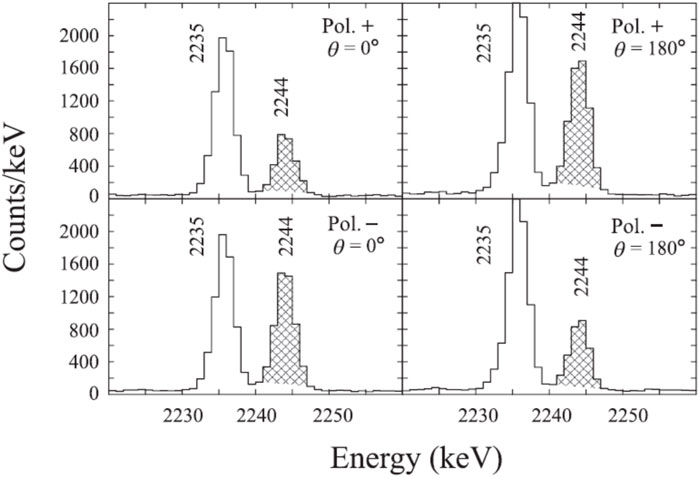
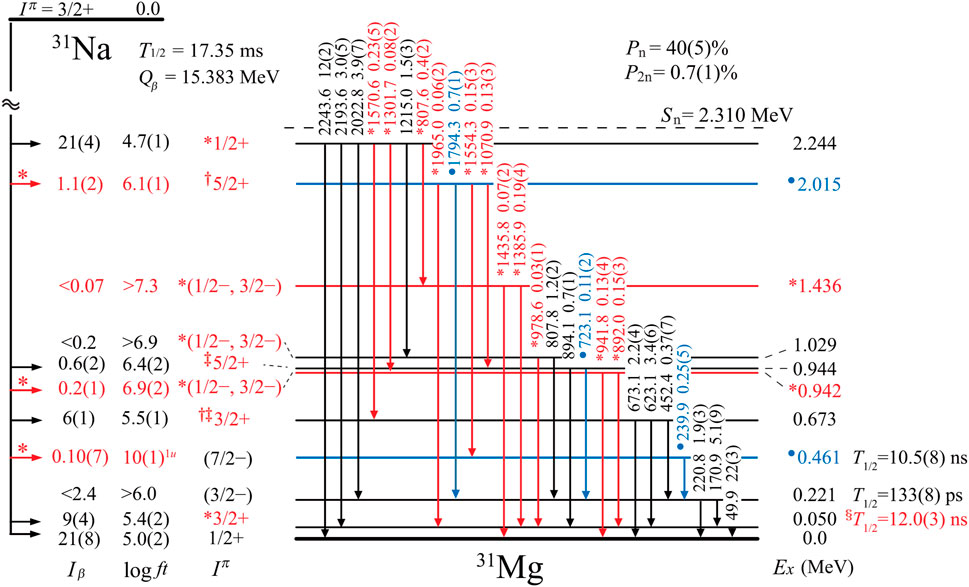
The intruder nature of the ³¹Na ground state results in the preferential population by $\beta$-decay of the intruder states in the daughter ³¹Mg. This was taken advantage of in a measurement at the TRIUMF-ISAC facility [19] to extend the level scheme of ³¹Mg and measure the $\beta$-$\gamma$ angular correlations of spin-polarized ³¹Na. Figure 3 displays the $\gamma$-ray spectra taken with HPGe detectors placed at $0°$ (left) and $180°$ (right) with respect to the polarisation axis with ³¹Na having a net positive (aligned along $0°$) or negative (aligned along $180°$) asymmetry. The degree of asymmetry can be extracted and is sensitive to the spin of the levels, and all positive-parity states below the neutron-separation energy (2.3 MeV) were firmly assigned using such data, as shown in Figure 4. A deformed band based on the $1/2^{+}$ ground state, as well as a band based on the $3/2^{-}$ 220 keV level, were assigned. The bands were interpreted [19] in terms of the Nilsson model and assigned as the $\nu 1/2^{+}[200]$ and $\nu 1/2^{-}[330]$ orbitals, respectively, which appear at the Fermi surface for $\beta \approx 0.3-0.4$. At slightly higher energy, the 673-keV $3/2^{+}$ state is assigned as the $0p-0h$ (referring to excitations of the core) spherical state. These results place ³¹Mg firmly within the island of inversion.

Figure 3

Figure 3. Portions of the $\gamma$-ray spectra observed at $0°$ (left) and $180°$ (right) with the ³¹Na aligned preferentially long the beam axis $(0°)$ (top) or anti-aligned $(180°)$ (bottom). Figure from [19].

Figure 4

Figure 4. Level scheme determined by Nishibata et al. [19] for ³¹Mg. The levels and transitions displayed in red were newly observed and in blue were observed in the $\beta$ decay for the first time. Figure taken from [19].

The above method was also applied to study ³⁰Mg [20]. A number of additional levels and transitions were proposed, and angular correlations were performed. Using $\gamma$-$\gamma$ angular correlations, they affirmed the spin $0^{+}$ of the 1788-keV level. The $\beta$-$\gamma$ angular correlations provided eight further spin-parity assignments [20]. From their data, they proposed the level scheme, as shown in Figure 5, which includes grouping of levels into various configurations. A key finding was the assignment of the $3_1^{+}$ level that would be expected for a $K=2\gamma$ band built on the deformed $0_2^{+}$ state. In a Davydov model interpretation, the location of the $K=2$ state relative to the $0_2^{+}$ level was used to extract $\gamma \approx 24°$ [20]. Very strong feeding of levels near 5 MeV permitted observation of, or stringent limits to be assigned, for their decays to the ground state and $0_2^{+}$ bands. From the decay patterns, they could be assigned as having either a collective (deformed) or spherical characteristic, with the $1^{+}$ state considered a candidate for the $M1$ “scissors” mode [20]. These results were consistent with a number of other studies (for a summary, see Ref. [1]), in which the ³⁰Mg ground state has a predominately normal configuration.

Figure 5

Figure 5. Level scheme and assignments suggested by Nishibata et al. [20] for ³⁰Mg. Newly found levels are reported in red, as are new spin assignments. Figure taken from [20].

A study [21] of ³⁴Si following the $\beta$-decay of ³⁴Al observed the $e^{-}+e^{+}$ pairs from a state at 2.719 (3) MeV that was assigned as the $0_2^{+}$ state. The half-life extracted was 19.3 (7) ns, leading to the $10^3\times {\rho }^2(E0)=13(1)$. The data leading to these results are presented in Figure 6. The $0_2^{+}$ state was interpreted as the deformed intruder state dominated by $2p-2h$ components across the $N=20$ neutron shell [21]. Weak mixing between the ground state and the $0_2^{+}$ state was deduced, with the intruder $0^{+}$ state having a deformation of ${\beta }_2=0.29(4)$. A recent study of the decay of ³⁴Mg and ³⁴Al performed at ISOLDE [22] took advantage of the preferential feeding of the two $\beta$-decaying states in ³⁴Al. The $\beta$-decay of ³⁴Mg led to the population of the $1^{+}$ state only of ³⁴Al, which then preferentially fed $0^{+}$ and $2^{+}$ states in ³⁴Si. Conversely, extracting the beam of ³⁴Al strongly favoured the ³⁴Al $4^{-}$ state, resulting in the population of higher-spin states in the ³⁴Si daughter. This work was followed by a precise new measurement of the $2_1^{+}\to 0_1^{+}$/$2_1^{+}\to 0_2^{+}$ branching ratio of 1779 (182) [22] vs. the previous result of 1380 (717) [21], resulting in $B(E2;2_1^{+}\to 0_2^{+})=7.2(31)$ W.u. strongly favouring its assignment as the $2^{+}$ band member of the $0_2^{+}$ state. Unfortunately, the $4^{+}$ band member has not yet been identified. These data place shape coexistence in ³⁴Si on a firm footing.

Figure 6

Figure 6. Data from the decay of ³⁴Al used to establish shape coexistence in ³⁴Si [21]. Panel (A) shows the energy observed in one telescope (the sum of a 1-mm-thick Si detector and a 4.5-mm-thick Si(Li) detector) vs. the energy in a second telescope for events with a total multiplicity $\ge 3$ ($\beta$-particle and an $e^{-}+e^{+}$ pair) and a time delay of 16 ns with respect to the $\beta$-particle trigger. The line corresponds to a constant energy of 1688 (2) keV for the $e^{-}+e^{+}$ pair, as shown in Panel (C), used to establish an excited state $0_2^{+}$ state at 2719 (3) keV. Panel (B) displays the time between the $\beta$-particle trigger and the $e^{-}+e^{+}$ pair showing the half-life of 19.4 (7) ns. Figure taken from [21].

2.2 The Ni isotopes and the $N=40$ “island of inversion”

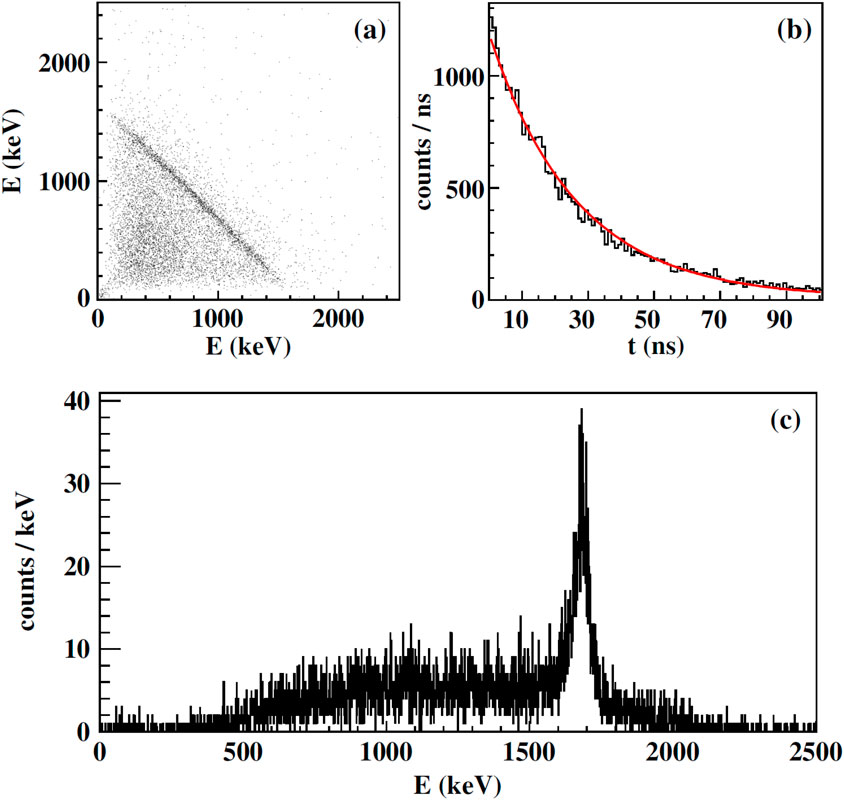
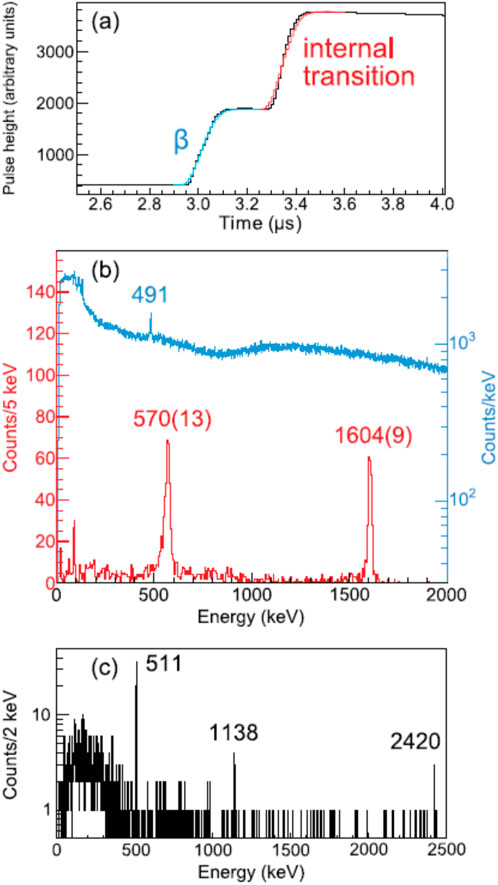
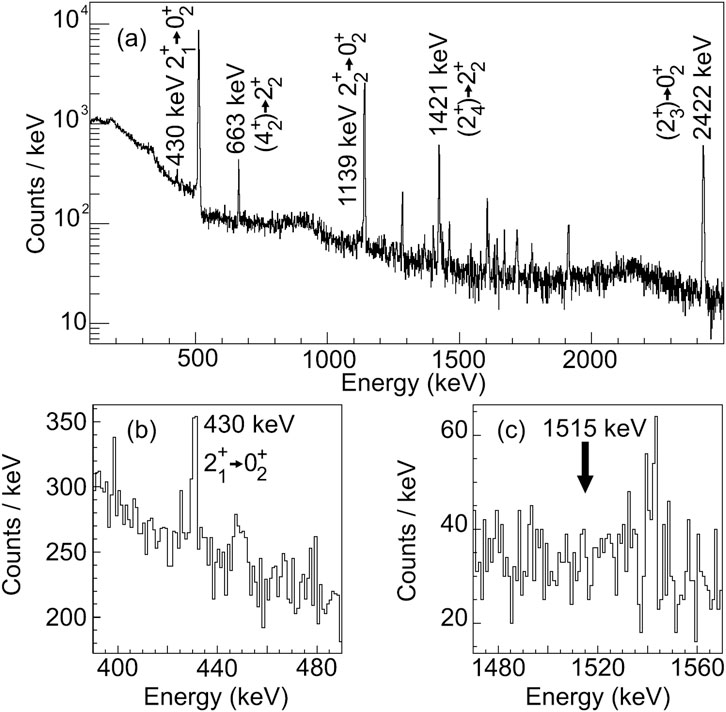
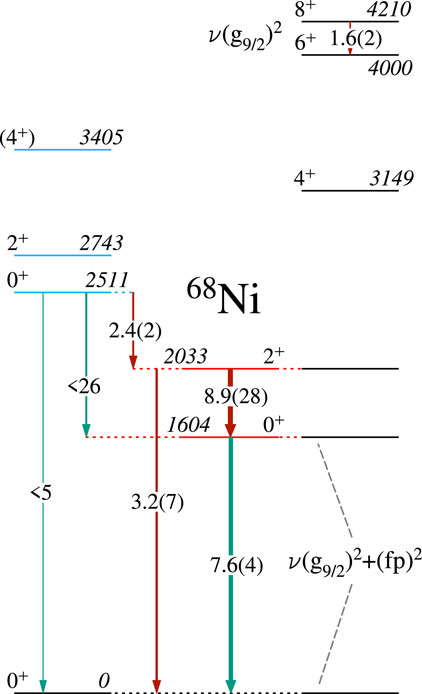
Nuclei in the vicinity of $N=40$ were first suggested to possess shape coexistence, following the observation in reaction studies [23, 24] of a $0_2^{+}$ level at the low excitation energy of 1.77(4) MeV in ⁶⁸Ni. The $\beta$-decay of ⁶⁸Co was studied [25], and with the superior energy resolution of HPGe $\gamma$-ray detectors and a Ge double-sided strip detector for conversion electrons, the $0_2^{+}$ state was determined to be located at an excitation energy of 1605 (3) keV. Figure 7 displays the data used to measure the energy of the $0_2^{+}$ state, as well as identifying the $E0$ transition to the ground state. The measured $E0$ strength of $10^3\times {\rho }^2(E0)=7.6(4)$ was deduced and interpreted as resulting from shape coexistence, with the $0_2^{+}$ state as a deformed configuration involving both proton and neutron multiparticle-multihole configurations, and the spherical ground state. The excited states in ⁶⁸Ni have also been investigated in transfer reactions (see, e.g., Ref. [26]) and were used to support an interpretation of a predominantly $\nu {(g_{9/2})}^2$ characteristic for the $0_2^{+}$ state but could not describe the magnitude of the $2_1^{+}$ cross section. An earlier suggestion of the similarity of the situation of neutron states in ⁶⁸Ni to the proton states in ⁹⁰Zr [27] – that the $0_1^{+}$ and $0_2^{+}$ states arise from the mixing of the ${(g_{9/2})}^2$ and ${(p_{1/2})}^2$ configurations—was qualitatively supported by the shell model calculations but discrepancies remained [26]. In a $\beta$-decay experiment [28] performed at the National Superconducting Cyclotron Laboratory (NSCL), the decays of ⁶⁸Fe and ⁷⁰Co were studied. The decay of ⁶⁸Fe populated selectively the low-spin $\beta$-decaying state of ⁶⁸Co, which preferentially fed the low-spin states of the ⁶⁸Ni daughter. A key observation was of the 430-keV $2_1^{+}\to 0_2^{+}$, shown in Figure 8, with a measured branching ratio of 0.12 (3)%. With the known lifetime of the $2_1^{+}$ state, a $B(E2;2_1^{+}\to 0_2^{+})=8.9(28)$ W.u. was determined [28], which was nearly a factor of 3 greater than the $B(E2;2_1^{+}\to 0_1^{+})$ value. This led the authors of [28] to conclude, through comparisons with both large-scale shell model and Monte Carlo shell model calculations, that the $0_2^{+}$ and $2_1^{+}$ states are the members of a shape-coexisting band, supporting some of the earlier interpretations [25]. The lifetime of the $0_3^{+}$ state was also measured that yielded a rather small $B(E2;0_3^{+}\to 2_1^{+})=2.4(2)$ W.u.

Figure 7

Figure 7. Panel (A) displays a portion of the GeDSSD detector signal collected with a waveform digitizer observed for ⁶⁸Co $\beta$-decay. Fast ions separated with a fragment separator were implanted into GeDSSD. Following the implantation, the $\beta$-particles were detected and the waveform analysis revealed a second event corresponding to the internal $E0$ transition from the $0_2^{+}$ state with a half-life of 268 (12) ns. Panel (B) displays the energy spectrum measured in the GeDSSD for events within 2 s of the ⁶⁸Co ion implantation (blue), showing events attributed to the detection of a single $\beta$-decay electron or the 491-keV $\gamma$ ray (attributed to time-random coincidences with an intense transition in ^67mCo decay). The spectrum in red corresponds to signals from a subsequent event within 600 ns The peaks at 570 and 1,604 keV are conversion electrons, resulting from the decay of the first excited $0^{+}$ state to the ground state in ⁶⁸Ni. Panel (C) displays the $\gamma$-ray energy spectrum detected in coincidence with “stair-step” signals in the GeDSSD. Figure taken from [25].

Figure 8

Figure 8. Portions of the $\gamma$-ray spectrum obtained in the decay of ⁶⁸Co with a coincident condition with the $0_2^{+}\to 0_1^{+}E0$ transition observed with a Ge double-sided strip detector. Panels (B) and (C) display expanded regions around the observed 430-keV $2_1^{+}\to 0_2^{+}\gamma$ ray and the region showing the lack of an observed 1515-keV $(2_3^{+})\to 0_3^{+}\gamma$ ray. Figure taken from [28].

The results from [25, 28, 29] lead to a different conclusion regarding the structure of ⁶⁸Ni than earlier interpretations [23, 24, 26, 27, 30], with the $0_2^{+}$ level as either the head of a deformed band or as a mixture of $\nu {(g_{9/2})}^2+\nu {(fp)}^2$ configurations upon which seniority-type states can be built. The arguments are outlined in [1], and the conflicting interpretations are shown in Figure 9. Clearly, additional measurements that could elucidate the structure of ⁶⁸Ni are required, including new $\beta$-decay studies to confirm the existence of the 430-keV $2_1^{+}\to 0_2^{+}$ transition.

Figure 9

Figure 9. Partial level schemes of ⁶⁸Ni reflecting two different interpretations of the level structure. The transitions are labelled with their $B(E2)$ values in W. u. (rust-coloured arrows) or $10^3\times {\rho }^2(E0)$ values (green-coloured arrows). The levels that are coloured reflect the suggested deformed configurations (blue–prolate, red–oblate), as assigned in [25, 28, 29]. The levels in black are interpreted as seniority-type levels as in [23, 24, 26, 30], where they were suggested to have significant components of the labelled configurations. Figure taken from [1].

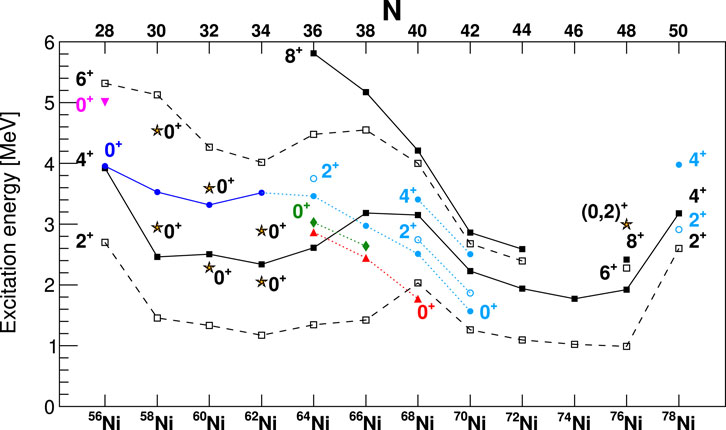
The half-life of the $0_3^{+}$ level in ⁶⁶Ni was measured following the $\beta$-decay of ⁶⁶Co by Olaizola et al. [31]. The result, shown in Figure 10, of $t_{1/2}=170(7)$ ps is considerably longer than the half-life reported in a plunger measurement by Leoni et al. [32] of 134 (9) ps. However, using either half-life leads to a small $B(E2;0_2^{+}\to 2_1^{+})$ value on the order of 0.1 W.u. Both the LSSM calculations and MCSM calculations indicate multiple shape coexistence in ⁶⁶Ni with spherical, prolate, and oblate configurations occurring for the first four $0^{+}$ states. The hindered nature of the transition was taken as evidence for substantially different shapes of the states, leading to shape isomerism. Figure 11 displays the energy level systematics for the even–even Ni isotopes, with the states coloured-coded for their presumed shapes.

Figure 10

Figure 10. Data used to determine the lifetime of the $0_3^{+}$ level in ⁶⁶Ni populated in the $\beta$-decay of ⁶⁶Co (left). A half-life of 170 (7) ps was determined. This result is considerably longer than the half-life from plunger measurements reported in [32], although the physics conclusions are unaltered. Transition rates deduced from the lifetime measurements compared with the large-scale shell model calculations using the LNPS interaction (right). The dashed lines indicate levels that were unobserved in the $\beta$-decay. The colour coding indicates the presumed spherical (black and blue), weakly deformed oblate (red), and highly deformed prolate (green). Figures taken from [31].

Figure 11

Figure 11. Excitation energy systematics for the even–even Ni isotopes showing yrast bands, three lowest $0^{+}$ excited states, and their possible bands. The normal “shell model” states are indicated with black squares. The proton $2p-2h$ states are shown with blue circles; for those observed to be populated strongly in proton-transfer reactions, dark blue is used, whereas those assigned based on calculations (which predict prolate shapes) are plotted with light-coloured circles and dotted lines. The super-deformed $4p-4h$ state in ⁵⁶Ni is denoted with a magenta triangle. The $0^{+}$ states with a presumed oblate shape are shown with red triangles, and the presumed spherical $0^{+}$ states, with green diamonds. States for which the existing information is insufficient to characterize them and with a lack of theoretical guidance are marked with yellow stars. Figure taken from [1].

The region of shape coexistence has been extended steadily in the vicinity of ⁶⁸Ni. Pauwels et al. [33] used the $\beta$-decay of ⁶⁷Fe to propose that ⁶⁷Co had a spherical $(7/2^{-})$ ground state and a deformed $(1/2^{-})$ first excited state at 492 keV interpreted as a proton 1p-2h intruder configuration with a Nilsson configuration $\pi 1/2^{-}[321]$. A similar interpretation was also suggested for the $(1/2^{-})$ state at 1,095 keV in ⁶⁵Co combining information from deep-inelastic scattering reactions and $\beta$-decay of ⁶⁵Fe [34]. The decay of ⁶⁶Fe to ⁶⁶Co was studied by Liddick et al. [35], and they identified the ⁶⁶Co ground state as a proton intruder, with positive parity based on the strong $\beta$-feeding from the ⁶⁶Fe $0^{+}$ ground state. The $\beta$-decay of the mass 66 chain, ⁶⁶Mn-⁶⁶Fe-⁶⁶Co-⁶⁶Ni, was also investigated by Stryjczyk et al. [36] who employed MCSM calculations to understand the structures of the states in the daughter nuclei. The strong $\beta$-feeding from the deformed ⁶⁶Mn ground state to the $1^{+}$ state at 2874 keV in ⁶⁶Fe was taken as evidence of the latter’s deformed characteristic. The ⁶⁶Fe ground state, on the other hand, had a rather diffuse shape in the MCSM calculations, and the $1^{+}$ ground state of ⁶⁶Co was weakly deformed, with the well-deformed configuration identified as a $1_2^{+}$ state observed at 982 keV, in contrast to the interpretation of [35].

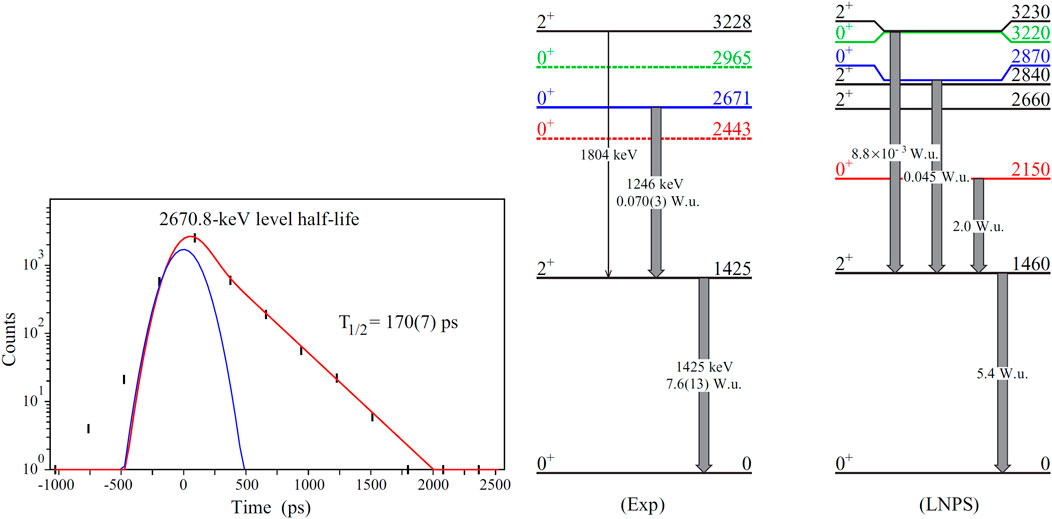
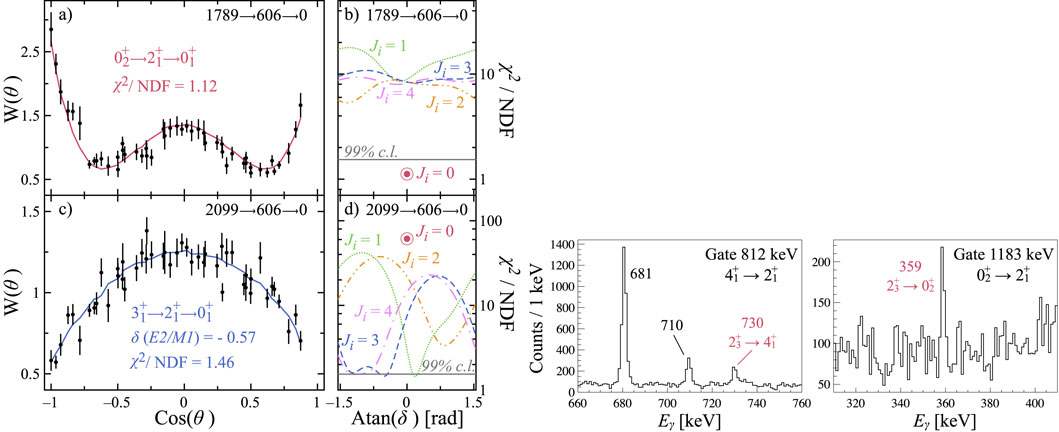
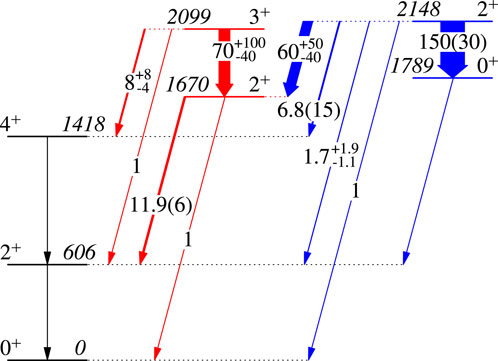
Very recently, the $N=40$ island of inversion was extended above Fe isotopes [37]. The $\beta$-decay of ⁷⁴Cu was studied with the GRIFFIN spectrometer at TRIUMF-ISAC, building on an extensive decay scheme that was developed at the Holifield radioactive beam facility using three clover HPGe detectors [38]. With the GRIFFIN array, which comprised 12 HPGe clover detectors, $\gamma$-$\gamma$ angular correlations were performed that resulted in a significant revision of the ⁷⁴Zn level scheme. As shown in Figure 12, the 2099-keV level which had been favoured to have $(4^{+})$ [38], was firmly assigned as $3^{+}$. Furthermore, additional $\gamma$-ray transitions were observed that were key to assigning band structures; the 359-keV $2_3^{+}\to 0_2^{+}$ transition and the 730-keV $2_3^{+}\to 4_1^{+}$ transition unambiguously lead to a $2^{+}$ assignment for the level at 2148 keV. With these assignments, a modified level scheme, as shown in Figure 13, was constructed, where the transitions are labelled with their relative $B(E2)$ values normalized to 1 for the highest energy transition from each level. The large relative values for the in-band transitions are consistent with the assigned structure of a “$K^{\pi }=2^{+}$” band and a $K^{\pi }=0^{+}$ band. The results were interpreted with the aid of large-scale shell model calculations, as well as beyond-mean-field calculations that indicated that the ground state band had, on average, a greater $2p-2h$ content and a slightly more deformed and triaxial nature than the $0_2^{+}$ band [37].

Figure 12

Figure 12. (Left) Examples of measured $\gamma$-$\gamma$ angular correlation functions $W(\theta )$, with $\theta$ the opening angle between the GRIFFIN detectors, and reduced ${\chi }^2$ as a function of the arctangent of the $E2/M1$ mixing ratio $\delta$ for $\gamma$-ray cascades observed, following the $\beta$-decay of ⁷⁴Cu. The top panels are data for the $0_2^{+}\to 2_1^{+}\to 0_1^{+}$ and bottom panels for the $3_1^{+}\to 2_1^{+}\to 0_1^{+}$ cascades—the latter resulting in a reassignment of the level at 2,099 keV from $(4^{+})$ [38] to $3^{+}$. (Right) Portions of $\gamma$-ray spectra observed in coincidence with the gating $\gamma$ rays indicated in ⁷⁴Zn. Figures taken from [37].

Figure 13

Figure 13. Portion of the level scheme determined using the data shown in Figure 12. The $\gamma$-ray transitions are labelled with their relative $B(E2)$ values, normalized to 1 for the highest energy branch observed. The values take into account the $E2/M1$ mixing ratios $\delta$ determined from the $\gamma$-$\gamma$ angular correlation analysis. The excited states are organized into bands, with the $K^{\pi }=2^{+}$ band built on the 1670-keV $2^{+}$ state and a $K^{\pi }=0^{+}$ band built on the 1789-keV $0^{+}$ state.

Finally, there have been two different $\beta$-decay experiments investigating the structure of ⁸⁰Ge [39, 40]. The first [39] was an experiment performed at the ALTO facility and used the decay of ⁸⁰Ga to study both the $\gamma$ rays and conversion electrons emitted. A weak peak in the conversion-electron spectrum at 628 keV was observed that was attributed to an $E0$ transition in ⁸⁰Ge and placed as feeding the ⁸⁰Ge ground state. This result implied the existence of the $0_2^{+}$ state at only 639 keV, a dramatic lowering of the $0_2^{+}$ from 1,547 keV in ⁷⁸Ge, and shape coexistence in ⁸⁰Ge [39]. However, in a $\beta$-decay experiment performed at the TRIUMF-ISAC facility with the GRIFFIN array, no such transition was observed in spite of the increase in statistics [40]. This null result ruled out shape coexistence occurring at very low excitation energies in ⁸⁰Ge.

2.3 The $N=60$ region

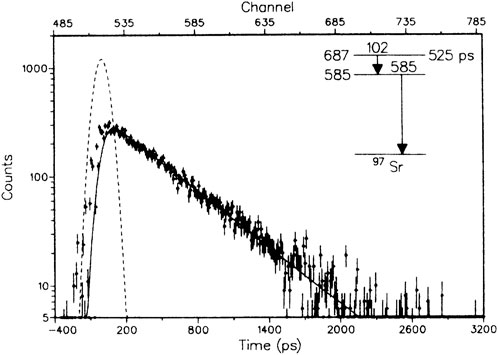
It had been suggested for some time that shape coexistence occurs in the $N=60$ mass region [41], and the observation [42] in the $\beta$-decay of ¹⁰⁰Y of the $0_2^{+}$ level in ¹⁰⁰Zr at the low excitation energy of 331 keV supported this. This discovery was quickly followed by a measurement of the $0_2^{+}$ lifetime [43] that determined $t_{1/2}=3.37(30)$ ns. A lifetime measurement [44] using the $\beta$-$\gamma$-$\gamma$ fast timing technique reported the lifetime of the $2_1^{+}$ level to be 0.55 (2) ns, yielding $B\left(E2;2_1^{+}\to 0_1^{+}=80(3)\right.$ W.u., and also found [45] a considerably longer lifetime for the $0_2^{+}$ level of 5.60(15) ns, leading to $10^3\times {\rho }^2(E0)=92(17)$ and $B(E2;0_2^{+}\to 2_1^{+})=13.3(10)$ W. u. These data were then used in a two-state-mixing calculation to determine the deformation parameters for the deformed ground-state band of ${\beta }_D=0.34(1)$, and for the spherical configuration ${\beta }_S=0.16(2)$. The ¹⁰⁰Zr lifetimes were in excellent agreement with measurements [46] performed in parallel using a $\gamma$-$\gamma$ coincidence technique involving a small-crystal Ge detector and a BaF₂ detector of 0.40 (8) ns $(2_1^{+})$ and 5.36 (23) ns $(0_2^{+})$. At around the same time, studies of the $\beta$-decay of the deformed ⁹⁷Rb [47] suggested the presence of shape coexistence in the $N=59$ ⁹⁷Sr isotope. Rotational bands based on the $\nu 3/2[422]$ and $\nu 3/2[541]$ Nilsson orbitals were suggested at excitation energies of 585 keV and 648 keV, respectively, with lower-lying levels considered to be spherical. This was confirmed shortly thereafter [48] via lifetime measurements using the $\beta$-$\gamma$-$\gamma$ technique. The lifetimes extracted within the suggested $\nu 3/2[422]$ band, an example of which is shown for the $5/2^{+}\to 3/2^{+}$ transition in Figure 14, established that the in-band transitions were indeed enhanced and corresponded to an intrinsic quadrupole moment of $|Q_0|=3.5(4)e$b.

Figure 14

Figure 14. Spectrum of the time between events registered in a plastic scintillator (start) and a BaF₂ detector (stop) with events selected with a gate taken on the 585-keV $\gamma$ ray in the BaF₂ detector and the 102-keV $\gamma$ ray selected with a Ge detector. A lifetime of the 687-keV level in ⁹⁷Sr of 525 (29) ps was determined. Figure taken from [48].

The natures of the level structures in the $N<60$ Zr isotopes were greatly speculated upon given the suggestion of shape coexistence in ⁹⁸Zr [41] and also the similarity of their structures with those of the Sr isotopes. New $0^{+}$ states were assigned [49] in ⁹⁸Zr in an experiment using mass-separated beams at the ILL to extract ⁹⁸Rb ions. The decay sequence, ⁹⁸Rb${\to }^{98}$Sr${\to }^{98}$Y, resulted in only the low-spin $\beta$-decaying state in ⁹⁸Y being populated from the ⁹⁸Sr spin $0^{+}$ parent. New $E0$ transitions of 423 keV and 564 keV were observed in the decay of ⁹⁸Y. These were placed as a cascade of $E0$ transitions from levels at 1859 keV and 1436 keV in ⁹⁸Zr, establishing them as the $0_4^{+}$ and $0_3^{+}$ states, respectively. Additionally, $\gamma$-$\gamma$ angular correlation measurements [49] performed with mass-separated beams of fission products ⁹⁸Sr and ⁹⁸Y at the Jülich research reactor proved conclusively that the states were $0^{+}$. The half-lives of these states were also measured, assuming that they are fed directly in the $\beta$-decay, with $t_{1/2}=0.69(10)$ ns $(0_3^{+})$ and 0.24(10) ns $(0_4^{+})$. The data permitted the extraction of the transition rates, and a two-state mixing model was assumed for the large $10^3\times {\rho }^2(E0)=290(80)$ value determined for the $0_3^{+}\to 0_2^{+}$ transition. With an assumption of maximal mixing and taking one configuration to be spherical, the deformed configuration must have $|\beta |>0.21$ [49]. It should be noted that while the presence of large $E0$ strengths imply significant differences in root-mean-square values of the deformation $\beta$, the structure of the $0^{+}$ states in ⁹⁸Zr remains contested. For example, [50] interpreted the $0_3^{+}$ state as the head of a well-deformed band, with the $2_2^{+}$, $4_1^{+}$, and $6_1^{+}$ states as band members. In contrast, [51] interpreted the $0_3^{+}$, $2_2^{+}$, and $4_1^{+}$ states as a two-quasiphonon triplet of weakly deformed states and $6_1^{+}$ as a three-quasiphonon state. The conversion electrons and $E0$ strengths in ⁹⁸Sr were re-investigated in [52], performing a two-state mixing analysis using the ${\rho }^2(E0)$ values, the $B(E2)$ values for the $2_1^{+}\to 0_1^{+}$, $0_2^{+}\to 2_1^{+}$, and $4_1^{+}\to 2_1^{+}$ transitions, and the energies of the states, and found a solution that minimized the total ${\chi }^2$ value that resulted in the unperturbed configurations to have ${\beta }_D=0.38(1)$ and ${\beta }_S=-0.23(2)$, i.e., that the “spherical” configuration is actually an oblate structure. The Coulomb excitation results of [53, 54] that deduced a near-zero quadrupole moment for the $2_2^{+}$ state $Q_s=+0.02_{-0.12}^{+0.13}$eb, however, is consistent with a spherical state rather than one with oblate deformation.

In ⁹⁹Zr, data from a series [55–58] of ⁹⁹Y $\beta$-decay measurements performed at Jyväskylä, ISOLDE, and at the ILL were used to suggest rotational bands based on the $\nu 3/2[541]$ and $\nu 3/2[422]$ Nilsson orbitals with band heads at 575.5 keV and 724.3 keV, respectively [55]. A short time later [55], using a superior setup at Jyväskylä, part of the evidence used for the deformed interpretation, namely an enhanced transition connecting the $5/2^{-}$ and $3/2^{-}$ band members, was found to be questionable, and the transition connecting the $7/2^{-}$ and $5/2^{-}$ band members was concluded not to exist. However, later experiments have observed the 58-keV $5/2^{-}\to 3/2^{-}$ transition and reaffirmed the existence of the $3/2[541]$ band (see, e.g., Refs. [57, 58] that includes discussions of other structures in ⁹⁹Zr).

The nature of states in the Zr isotopes with $N<58$ was probed in a ⁹⁴Y $\beta$-decay measurement [59] that discovered the $2_2^{+}\to 0_2^{+}$ transition in ⁹⁴Zr, as shown in Figure 15. The extracted branching ratio of 0.150(6)% was combined with the level lifetime from DSAM measurements, following the $(n,n^{\prime }\gamma )$ reaction resulting in $B(E2;2_2^{+}\to 0_2^{+})=19(2)$ W.u. This was the first firm determination of the shape coexistence scenario based on absolute $B(E2)$ values for the even–even Zr isotopes.

Figure 15

Figure 15. Portion of the $\gamma$-ray spectrum observed in coincidence with the 382-keV $0_2^{+}\to 2_1^{+}\gamma$ ray in ⁹⁴Zr. The branching ratio of 0.150 (6)% was determined for the 371-keV $2_2^{+}\to 0_2^{+}$ transition, leading to a $B(E2)=19(2)$ W. u. Figure taken from [59].

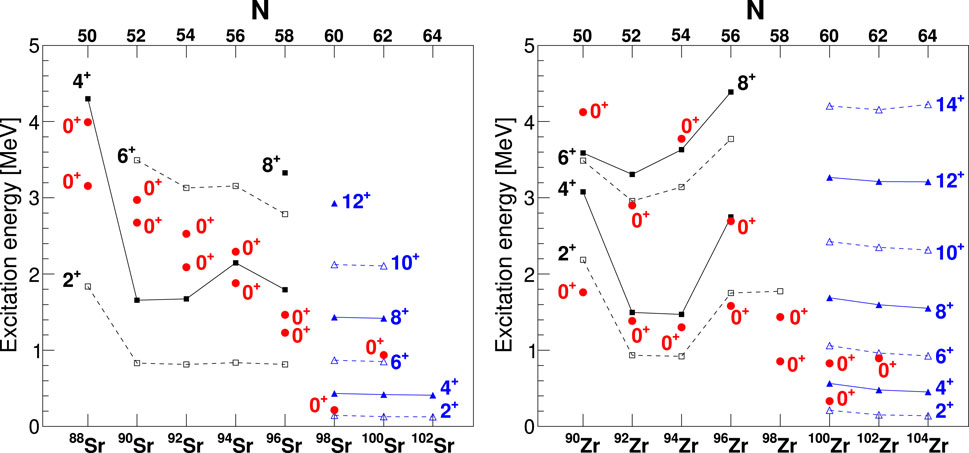
The systematics of selected states in the Zr and Sr isotopic chains are shown in Figure 16; the states assigned to the spherical ground states for $N<60$ and the deformed ground states for $N\ge 60$ and $0_2^{+}$ and $0_3^{+}$, are shown. The results of a new experiment [60] performed with Gammasphere studying the $\beta$-decay of ¹⁰⁰Y discovered the $0_4^{+}$ and $0_5^{+}$ states at 1294.5 and 1774.0 keV, respectively, in ¹⁰⁰Zr, and also observed a 366.8 keV transition placed as the $2_3^{+}\to 0_3^{+}$ transition, supporting the interpretation of a rotational band proposed in [61]. New results are also reported [62] for ⁹⁸Zr from a $\beta$-decay experiment performed at the TRIUMF-ISAC facility with the $8\pi$ spectrometer. From $\gamma$-$\gamma$ angular correlations, the $0_5^{+}$ and $0_6^{+}$ states were found at 2418 keV and 2749 keV, respectively, and many additional levels were identified as $2^{+}$ states. Further studies are required to be able to identify the existence of possible bands built on these new $0^{+}$ states.

Figure 16

Figure 16. Energy level systematics for the even–even Sr isotopes (left) and Zr isotopes (right). Only the $0_2^{+}$ and $0_3^{+}$ states are plotted together with the spherical (deformed) states based on the $0_1^{+}$ ground states in black (blue). Figure taken from Ref. [1].

2.4 The Cd isotopes

The stable Cd isotopes have been at the forefront of nuclear structure studies of shape coexistence for over 40 years. Early on [63], the even–even Cd nuclei were interpreted as having a level structure expected for spherical vibrators; however, an extra $2^{+}$ state was discovered in the vicinity of the two-phonon triplet in ¹¹⁴Cd in an $(n,\gamma )$ reaction [64]. An additional $0^{+}$ state, also close in energy to the two-phonon triplet, was soon discovered in ¹¹³Cd($d,p$) ¹¹⁴Cd reaction, as well as an extra $0^{+}$ and $2^{+}$ pair of states in the ¹¹¹Cd($d,p$)¹¹²Cd reaction [65]. Although their natures were speculated upon for some years, it was not until 1977 in an experiment studying the $\beta$-decay of the ¹¹⁰In $7^{+}$ ground state that the rotational-like band based on the 1473-keV $0_2^{+}$ level was finally elucidated [66]. This was achieved by having sufficient sensitivity for weak, low-energy transitions enabled through the use of Ge(Li) $\gamma$-ray detectors with their superior energy resolution over previous investigations using NaI detectors [67]. Using results that had nearly simultaneously been obtained from the two-proton-transfer reaction (³$\mathrm{H}\mathrm{e},n$) [68], the rotational band was interpreted as being a $2p-4h$ proton excitation, with the promotion of two $g_{9/2}$ protons into either $g_{7/2}$ or $d_{5/2}$ orbitals above the $Z=50$ closed shell. It was also postulated at that time that a similar deformed rotational band occurred in ¹¹⁴Cd. Shortly thereafter, important information was obtained from conversion electron spectroscopy of ¹¹²Cd and ¹¹⁴Cd [69]. The data for ¹¹²Cd were obtained following the $\beta$-decay of ¹¹²In, whereas that for ¹¹⁴Cd were deduced from data obtained from a neutron capture reaction. With lifetimes deduced from in-beam studies [69], $10^3\times {\rho }^2(E0)$ values were determined for the decay of the $0_2^{+}$ and $0_3^{+}$ states. The values for the $0_2^{+}\to 0_1^{+}$ transitions, 37(11) and 30(8) for ¹¹²Cd and ¹¹⁴Cd, respectively, can be contrasted with the values of 0.48(11) and 1.7(2) for the $0_3^{+}\to 0_1^{+}$ transition. For the $0_3^{+}\to 0_2^{+}$ transition, the value in ¹¹²Cd, 8.1(19), is significantly larger than that for ¹¹⁴Cd at 0.41(9). Generally, these values were in line with the expectations of the vibrational model, where for $\mathrm{\Delta }N=2E0,$ transitions are allowed [7]. Alternatively, the ${\rho }^2(E0)$ values are also consistent with a shape coexistence scenario.

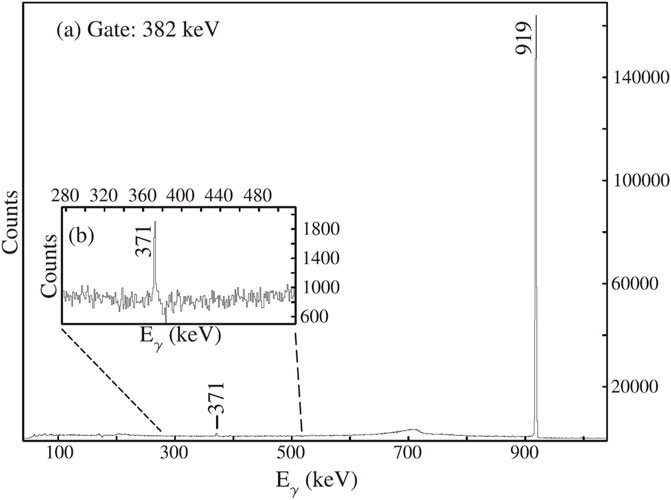
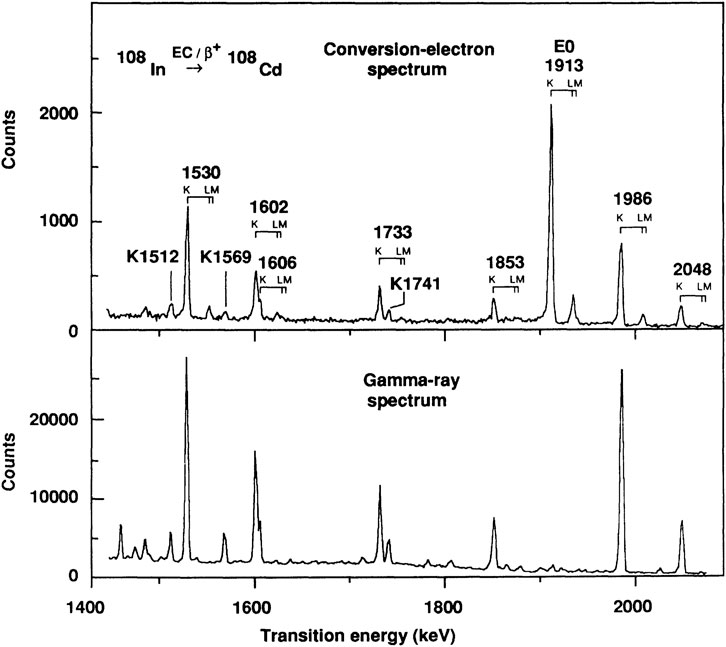
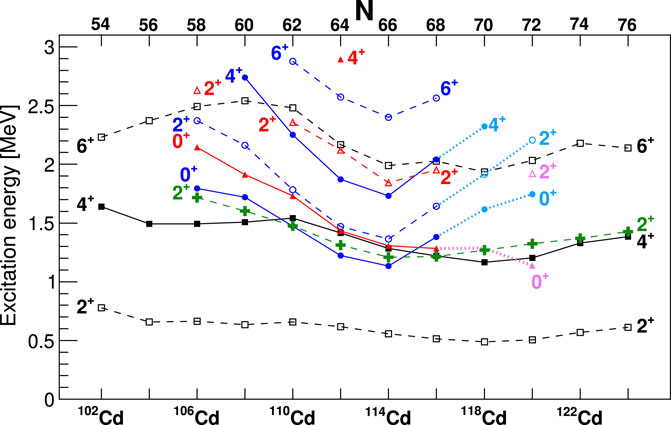
The Cd isotopes were systematically studied by the Jyväskylä group, as reported in [70], that included light-ion fusion–evaporation reactions and also the $\beta$-decay of ^106,108,110In. The In activities were produced through $(p,n)$ reactions on foils of ^106,108,110Cd with their decays studied by both $\gamma$-ray spectroscopy and conversion-electron spectroscopy. Although only singles measurements were performed, a number of conversion coefficients were extracted that included $E0$ transitions. The $e^{-}$ and $\gamma$-ray spectra for the decay of ¹⁰⁸In are shown in Figure 17, demonstrating the very high signal-to-background obtained. Specifically important were the observations of strong $E0$ transitions such as that at 1913 keV for ¹⁰⁸Cd, as shown in Figure 17. In this study, the shape-coexisting intruder bands were assigned from ¹⁰⁶Cd through ¹²⁰Cd [70]. Figure 18 shows the current state of the excitation energy systematics where the presumed nature (outlined below) of the states is reflected in the colour coding [1].

Figure 17

Figure 17. Spectra obtained from the EC/${\beta }^{+}$-decay of ¹⁰⁸In of the conversions electrons (top) and $\gamma$ rays (bottom). The electron spectrum was obtained using a cooled Si(Li) detector and a magnetic lens of the Siegbahn–Slätis type [71]. The electron spectrum includes an offset of the $K$-binding energy to align the $K$-conversion peaks with the corresponding $\gamma$-ray peaks. Figure taken from [70].

Figure 18

Figure 18. Excitation energy systematics for the even–even Cd isotopes. The prolate ground state band is shown in black, with the presumed triaxial “intruder” band in blue and the oblate band in red where the shapes have been predicted in beyond-mean-field calculations [69, 70] for ^110,112Cd. The states in neighbouring isotopes suggested to have similar shapes are shown with the same colour scheme. For states that have tentative shape assignments, dotted lines and lighter colours are used. The $2_2^{+}$ state, labelled as the “$\gamma$”-band head, is shown in green. Figure taken from Ref. [1].

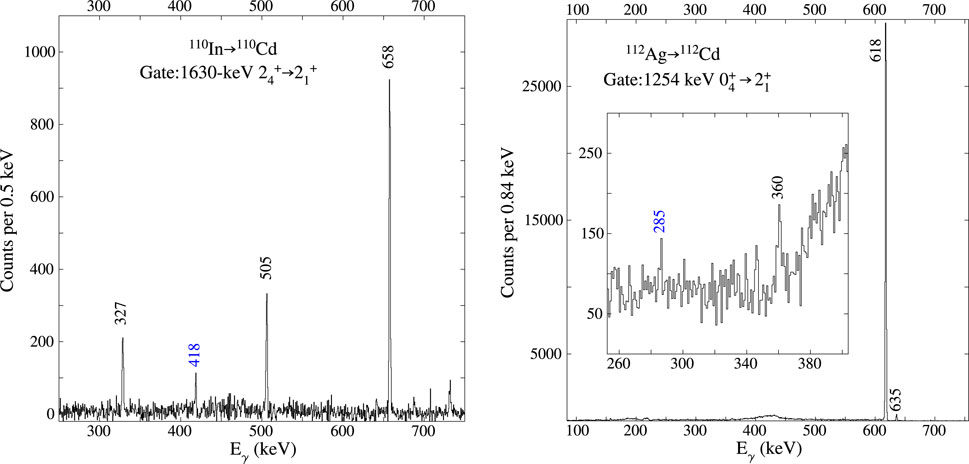
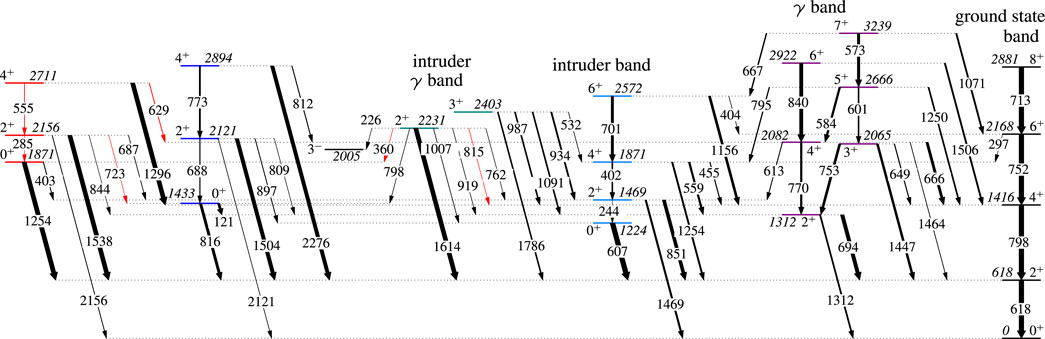
A major step forward in the understanding of the structure of the Cd isotopes occurred with the combination of lifetimes determined from analysis of Doppler-shift data from $(n,n^{\prime }\gamma )$ reaction and results from $\beta$-decay measurements performed at the TRIUMF-ISAC facility with the $8\pi$ spectrometer [72–74]. These $\beta$-decay studies reached a very high level of sensitivity for the observation of weak, low-energy $\gamma$-ray branches between states at relatively high excitation energy. It was shown conclusively that the strong-mixing scenario, proposed decades earlier to explain the decay pattern of the $0_2^{+}$ and $0_3^{+}$ states [75], led to serious discrepancies for ¹¹⁰Cd [74]. The data, with some of the key coincidence spectra shown in Figure 19, further permitted the assignment of rotational bands built on excited $0^{+}$ states and the assignment of “$K=2$” bands, as shown in Figure 20 for ¹¹²Cd. The $\gamma$-ray transitions that were newly observed in those studies are highlighted in red. It is remarkable that despite how well studied both ¹¹⁰Cd and ¹¹²Cd were, many new transitions, and even states, were found. From a comparison of the experimental results to beyond-mean-field calculations, it was suggested that ^110,112Cd possessed multiple deformed shapes ranging from prolate, triaxial, and oblate [72, 73]. This is a major shift in the interpretation of the Cd isotopes, which had long been considered excellent examples—in fact often cited in textbooks — of spherical vibrational systems. A series of Coulomb excitation experiments have been conducted with the aim of providing definitive answers to the shapes of excited states in ¹¹⁰Cd, early results of which have been published in [76].

Figure 19

Figure 19. (Left) Portion of the spectrum of $\gamma$ rays observed in coincidence with the 1630-keV $2_4^{+}\to 2_1^{+}\gamma$ ray in ¹¹⁰Cd. The inset displays the expanded region near 400 keV, highlighting the 418-keV $\gamma$ ray. This was a newly observed $\gamma$ ray assigned as the in-band $4_5^{+}\to 2_4^{+}$ transition with the extracted branching ratio 0.59 (5)%, leading to $B(E2;4_5^{+}\to 2_4^{+})=55(14)$ W. u. (Right) Portion of the spectrum of $\gamma$ rays observed in coincidence with the 1254-keV $0_4^{+}\to 2_1^{+}\gamma$ ray in ¹¹²Cd. The inset displays the expanded region near 300 keV, highlighting the 285- and 360-keV $\gamma$ rays. The 285-keV $\gamma$ ray was assigned as the $2_5^{+}\to 0_4^{+}$ in-band transition with the extracted branching ratio 0.079 (33)%, leading to $B(E2;2_5^{+}\to 0_4^{+})=34(15)$ W. u. Figures taken from [73].

Figure 20

Figure 20. ¹¹²Cd level scheme deduced from the $\beta$-decay measurements of [72, 73]. Newly observed $\gamma$-ray transitions are highlighted in red. The widths of the arrows are proportional to the branching ratio. Figure taken from [73].

A series of conversion electron measurements were performed by [77–79], following the $\beta$-decay of In parents. The measurements took advantage of Cd$(p,n)$ reactions to produce the In activities and obtained very high signal-to-background ratios that enabled the observation, or set upper limits, of many $E0$ branches including those for $2_{\mathrm{2,3}}^{+}\to 2_1^{+}$ transitions. The observations were interpreted taking into account configuration mixing within the proton–neutron interacting boson model (IBM-2) framework. A reasonable reproduction of the $E0$ strengths was obtained [78, 79], although the $2_3^{+}$ states in ^110,112,114Cd were interpreted as having a mixed-symmetry characteristic rather than of intruder origin. A conversion electron study, following the ${\beta }^{+}$/EC-decay of ¹¹⁰In, extracted a new $E0$ branch from the $4^{+}$ member of the intruder $0_2^{+}$ band [80]. The data, combined with that from [10], indicate that the shape-coexisting states continue to experience mixing with increasing spin in the bands.

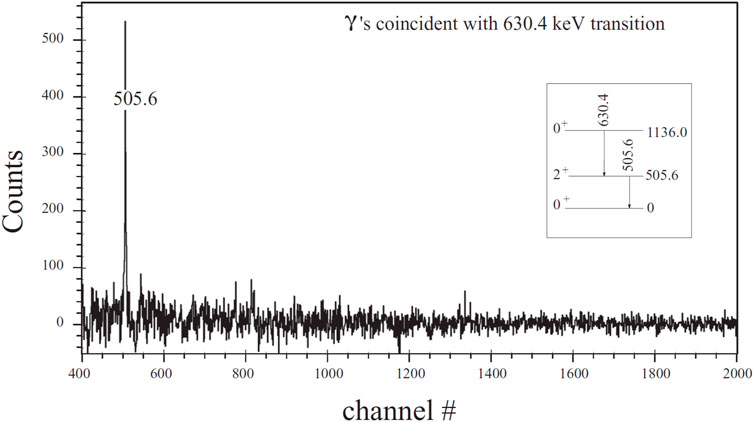
Measurements of the $\beta$-decay of Ag isotopes extending into the neutron-rich Cd region were pursued at ORNL using the CARDS array [81] that consisted of three or four clover-type HPGe detectors in close geometry and the BESCA Si(Li) detector for conversion electrons, replacing one of the clover Ge detectors. A new $\beta$-decaying isomer was discovered in the ¹¹⁶Ag parent [82]. The key for its observation was the outstanding energy resolution achieved for the BESCA detector for conversion electrons. The $\beta$-decay of three states in ¹¹⁶Ag, the $0^{-}$ ground state, the newly found 48-keV $3^{+}$ state, and the 129-keV $6^{-}$ state, populated a wide spin range of levels in the ¹¹⁶Cd daughter. Despite the sensitivity achieved, the placement of the key 262-keV $2_3^{+}\to 0_3^{+}\gamma$ ray, which has been observed in one experiment only [83] with a reported branching ratio of 0.5% and used to establish the intruder band, could not be confirmed [84]. Rather, the $\beta$-decay measurement [84] reported a $2\sigma$ upper limit of 0.6%. In ¹²⁰Cd, the data obtained [85] from the decay of the ¹²⁰Ag, which includes the $(0^{-},1^{-})$ ground state and the $4^{(+)}$ and $7^{(-)}$ isomeric states, did not observe the decay of the previously assigned $0_2^{+}$ at 1388.9 keV but did observe the decay of the higher-lying $0_3^{+}$ state at 1744.9 keV. Furthermore, a previously unobserved $\gamma$ ray was observed in coincidence with the 505.6-keV $2_1^{+}\to 0_1^{+}\gamma$ ray, as shown in Figure 21, but without any additional coincidences. These facts were used to remove the 1388.9-keV state from the level scheme and to establish a new level at 1136.0 keV that was assigned as the $0_2^{+}$ state. This new assignment is reflected in the energy systematics shown in Figure 18. If this placement is confirmed, it would imply a dramatic drop in energy for the configuration that, in the lighter Cd isotopes, is suggested to be based on an oblate shape [72, 73].

Figure 21

Figure 21. Portion of the spectrum observed in coincidence with the 505.6-keV $2_1^{+}\to 0_1^{+}\gamma$-ray transition in ¹²⁰Cd, following the $\beta$-decay of ¹²⁰Ag. The sole observed coincidence with the $2_1^{+}\to 0_1^{+}\gamma$ ray was used to argue for a $0_2^{+}$ assignment. Figure taken from [85].

Studies using the CARDS array were also performed for the decays of ^124,126Ag [86]. From their data for ¹²⁴Ag decay, they assigned a state at 1573.5 keV as the $0_2^{+}$ state, using similar arguments as for the ¹²⁰Cd $0_2^{+}$ state above. This may be the head of the “oblate” band; however, no higher-lying band members were assigned. A second excited $0^{+}$ state was suggested at 1924.8 keV. These new states would suggest that the $0_2^{+}$ state in ¹²²Cd, a nucleus which has not been thoroughly studied since the early 1990s [87], remains undetected since it is currently assigned as a level at 1705 keV, and such a dramatic rise and fall of the excitation energy of the $0_2^{+}$ state between ¹²⁰Cd and ¹²⁴Cd is unexpected.

New $\beta$-decay measurements have been initiated using the GRIFFIN spectrometer at the TRIUMF-ISAC facility that will include the study of ^104,106In decay and ^{112,116,118,120}Ag decay. The neutron-rich Ag isotopes, in particular, have multiple $\beta$-decaying states that can be separated somewhat via selective laser ionisation. The decay of ^118,120Ag will also be studied at the Jyväskylä facility that will offer the advantage of using the Penning trap mass spectrometer JYFLTRAP to achieve highly purified isomeric beams [88].

2.5 The Sn isotopes

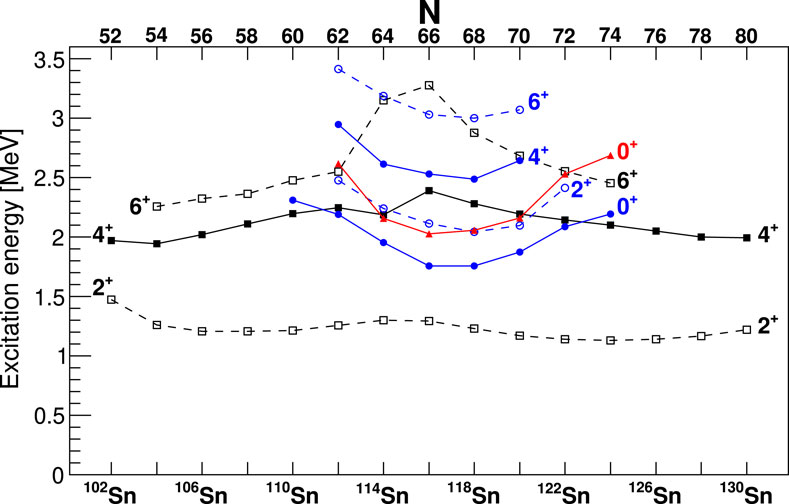
The shape-coexisting states in the mid-shell Sn isotopes were first discovered through a series of $(\alpha ,2n\gamma )$ reactions by [89] and have mostly been investigated through a variety of reaction studies. Of particular interest has been the two-proton-transfer studies [68] that observed large populations of the $0_2^{+}$ states in ^114,116,118Sn, as well as in $\alpha$-particle transfer reactions ^122,124Te(${\mathrm{d},}^6$Li)^118,120Sn [90], that reveal the microscopic natures of the $0_2^{+}$ states having important proton-pair contributions. The energy level systematics is shown in Figure 22 for the even–even Sn isotopes. Of particular interest is that both the $0_2^{+}$ and $0_3^{+}$ states display the characteristic parabolic-shaped trend expected for shape-coexisting structures with the minimum at the neutron mid-shell. The systematics plotted here use the $0_2^{+}$ level as the intruder band head based on its strong population in the proton-transfer reactions.

Figure 22

Figure 22. Excitation energy systematics for the even–even Sn isotopes. The ground state band is shown in black, with the presumed prolate “intruder” band in blue. The energies of the $0_3^{+}$ states are shown in red. The intruder states display the characteristic parabolic dependence of their energy on neutron number, a trend that is also manifest for the $0_3^{+}$ state, suggesting that it may have an intruder origin as well. Figure taken from [1].

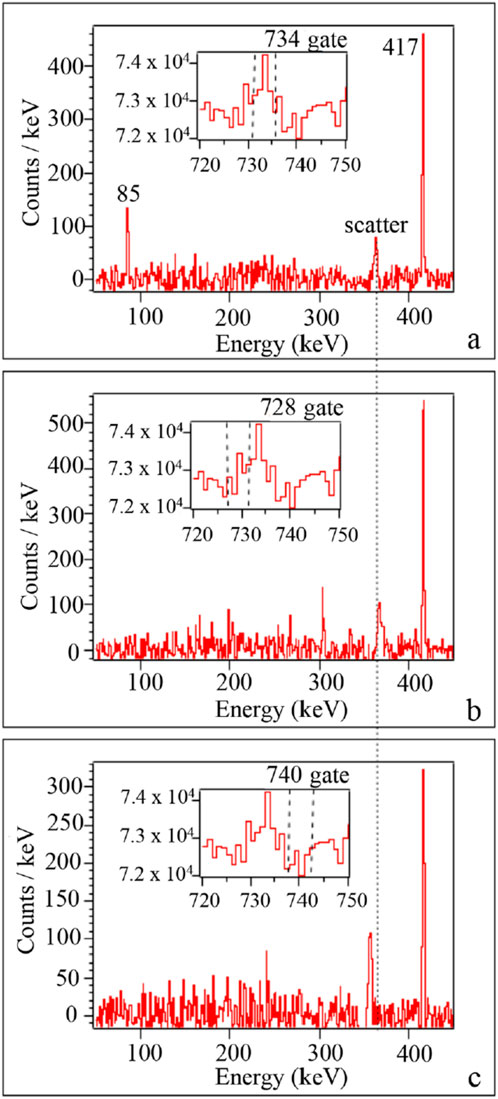
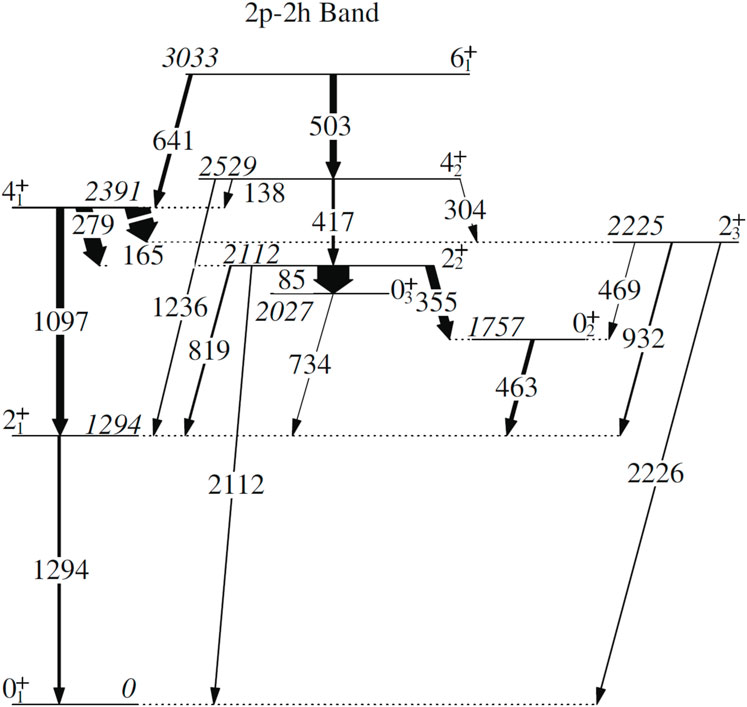
The structure of the deformed intruder bands in ^116,118Sn has recently been investigated with $\beta$-decay at the TRIUMF-ISAC facility. In ¹¹⁶Sn, the decay of ^116m1In was used to seek weak, low-energy transitions from the low-spin excited states, especially the $0^{+}$ and $2^{+}$ states. The collected data enabled the direct observation of the 85-keV $2_2^{+}\to 0_3^{+}$ transition that previously had its intensity indirectly inferred. This is shown in Figure 23. Due to the large Compton-scattering background that was present, the authors of [91] performed a careful investigation of its possible impact to contribute to the signal at 85 keV. As shown in Figure 23, the 85-keV peak is clearly due to a coincidence with the 734-keV $0_3^{+}\to 2_1^{+}\gamma$-ray transition. The measured branching ratio for the 85-keV transition results in a $B(E2)$ value of 100(8) W.u. that is a factor of 2.2(3) greater than the 355-keV $2_2^{+}\to 0_2^{+}$ transition, leading to the suggestion that the $0_3^{+}$ level should be identified as the intruder band head. This is shown in Figure 24. Interestingly, upper limits were established [92] and led to negligible $E0$ components in the $2_2^{+}\to 2_1^{+}$ and $2_3^{+}\to 2_1^{+}$ transitions, implying that the mixing of the intruder and spherical $2^{+}$ states must be very small.

Figure 23

Figure 23. Plot of the $\gamma$-ray spectra resulting from coincidence gates placed on the respective regions of the $\gamma$-$\gamma$ matrix obtained in the ${\beta }^{-}$-decay of ^116m1. Panel (A) displays the spectrum obtained from gating on the 734-keV $0_3^{+}\to 2_1^{+}\gamma$ ray. The “scatter” feature results from Compton-scatter events from the 1097-keV $\gamma$ ray. The $\gamma$-ray spectrum obtained by gating between energies 727 and 731 keV and between energies 738 and 742 keV are shown in (B) and (C), respectively. The 85-keV peak is notably absent. Figure taken from [91].

Figure 24

Figure 24. Partial level scheme of ¹¹⁶Sn with the widths of the arrows proportional to the $B(E2)$ values, with those from the 2529-keV level reflecting lower limits only, and that of the 165-keV transition as an upper limit. Figure taken from [91].

A recent study [93] of the neighbouring nucleus ¹¹⁸Sn via the ${\beta }^{-}$ decay of ¹¹⁸In was performed with the GRIFFIN spectrometer at the TRIUMF-ISAC facility. The measurement collected a very large statistical sample that resulted in significant revisions of relative intensities for decay of some levels, most notably for the 284-keV transition from the $2_2^{+}$ level that populates the $0_2^{+}$ state. This particular transition was shown to be part of a triplet of $\gamma$ rays at 285 keV, and its branching ratio for decay from the $2_2^{+}$ level was refined from 2.6(2)% down to 1.33(6)%, reducing $B(E2;2_2^{+}\to 0_2^{+})$ to 21(4) W.u. from its previously adopted 39(7) W.u [93]. However, the intruder band in ¹¹⁸Sn remained as previously assigned with the $0_2^{+}$ state as its band head.

The energy systematics presented in Figure 22 display a smooth dependence as a function of the neutron number, with the $0_2^{+}$ and $0_3^{+}$ states both displaying a parabolic dependence. If the band head in ¹¹⁶Sn is indeed the $0_3^{+}$ state, this would imply a rather abrupt shift in the systematics. The authors of [91] performed a two-state mixing calculation and suggest that the unperturbed band head energy was 1944 keV. If this is adopted, it would still imply that the intruder band head has its minimum at ¹¹⁸Sn. With the close spacing of the $0_2^{+}$ and $0_3^{+}$ states in ¹¹⁴Sn, it is likely that the mixing would be large in this isotope as well and that one may expect the existence of a $2_2^{+}\to 0_3^{+}$ transition in competition with the $2_2^{+}\to 0_2^{+}$ transition as in ¹¹⁶Sn. Indeed, this scenario was considered by Spieker et al. [94] in their study of lifetimes using the $(p,p^{\prime }\gamma )$ reaction. However, in the Cd (³He,$n$) reactions [68], from the location of the peaks in the time-of-flight spectra, it is the $0_2^{+}$ state that appears to receive the strong population, rather than the $0_3^{+}$ level (see Fig. 40 of Ref. [1]) in ^116,118Sn. In ¹¹⁴Sn, perhaps some sharing of the cross section between the $0_2^{+}$ and $0_3^{+}$ states could be postulated. These observations suggest a far more complex picture is required for the excited $0^{+}$ states in the Sn isotopes due to the contrasting conclusions from $\gamma$-ray spectroscopy and reaction spectroscopy.

2.6 Neutron-rich Rh and Ag isotopes

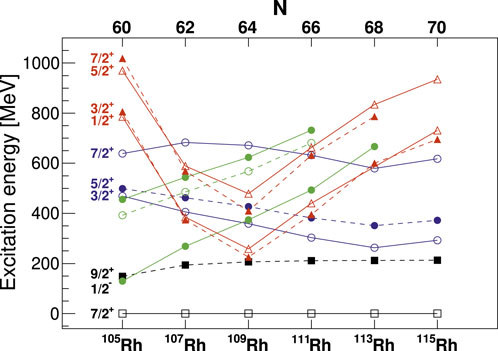
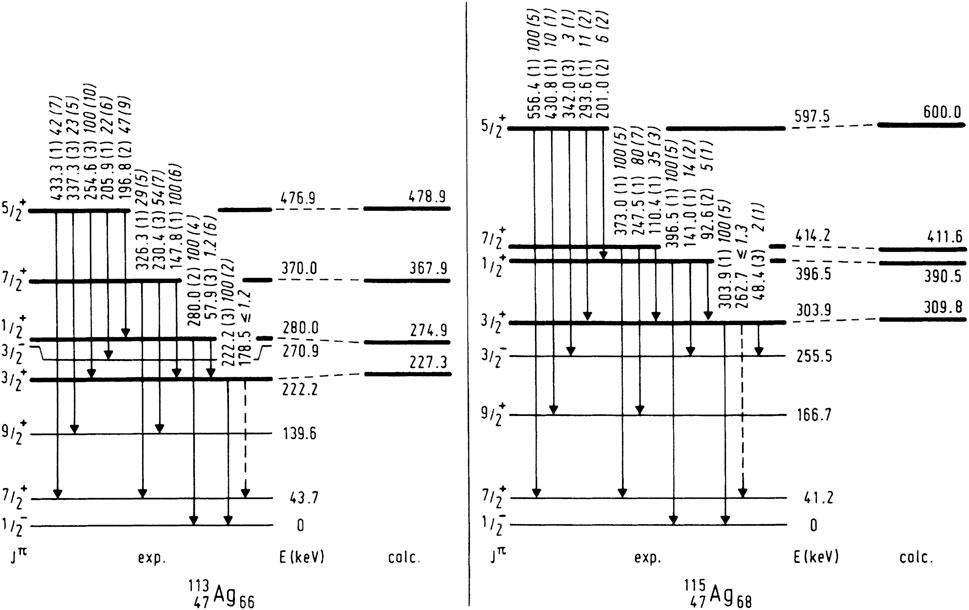
Studies of neutron-rich odd-mass Rh [95–98] via the $\beta$-decays of Pd isotopes indicated the presence of intruder states and shape coexistence. A parabolic-shaped pattern in the level energy systematics for the Rh isotopes is present (see Figure 25), and moreover, level lifetime measurements revealed enhanced $B(E2)$ values for the in-band transitions. In ¹⁰⁹Rh, for example, an enhanced $B(E2;1/2^{+}\to 3/2^{+})=173(33)$ W.u. was determined [96], leading to a deformation ${\beta }_2=0.32(3)$. At this deformation, the $\pi 1/2[431]$ Nilsson orbital is close to the Fermi surface, which is consistent with the proposed band in [96]. Shape coexistence is also proposed [99] in the Ag isotopes that have been revealed in $\beta$-decay studies. Figure 26 shows the proposed states forming the $\pi 1/2[431]$ bands in ^113,115Ag. Unfortunately, these early studies have not been followed such that little additional information has been provided.

Figure 25

Figure 25. Energy level systematics for the odd-mass Rh isotopes. A parabolic trend is observed for the deformed band (red) in contrast to the trends observed for the normal quasi-spherical states. Spin assignments are those suggested in [98].

Figure 26

Figure 26. Partial level schemes of ¹¹³Ag and ¹¹⁵Ag deduced from data from the $\beta$-decay of ^113,115Ru. The levels in bold lines were assigned to the deformed intruder configuration consistent with the $\pi 1/2[431]$ Nilsson configuration. The levels above the “calc” label are the result of a rotational band fit for the excitation energies using $K=1/2$. Figure taken from [99].

3 Summary

With the examples outlined above, it can be seen that $\beta$-decay has provided a wealth of information on shape coexistence. There are several key factors that lead to this. First, in many systems, $\beta$-decay measurements are the first experimental investigations to be applied. Second, the sensitivity provided by $\gamma$-ray and conversion-electron spectroscopy, following $\beta$-decay, is largely unmatched. This is due to both the general reduction in backgrounds present in the spectra compared to that in reaction studies and also the (typically) narrow spin range of states fed in the $\beta$-decay. Third, the aforementioned factors also greatly facilitate the use of fast-timing techniques based on $\beta$-$\gamma$-$\gamma$ or $\gamma$-$\gamma$-$\gamma$ triple coincidences. The lifetimes established are critical to firmly assign shape-coexisting structures through the use of $B(E2)$ values and ${\rho }^2(E0)$ values.

Contemporary radioactive beam facilities are generating many new, interesting results for nuclei far from stability. At the very extremes, the ability to perform $\beta$-decay measurements with beam intensities on the order of 1 ion/s while still providing sufficient detail to extract physics results is a tremendous advantage. Although there is a concentrated focus on studies at the extremes, it is also important to make detailed investigations of nuclei close to, or on, the line of stability. It is these systems that can be probed by a large variety of reactions and techniques that act as the anchor for our understanding of nuclear structure. This is aptly demonstrated in the Cd isotopes, where the $\beta$-decay studies revealed many extremely weak $\gamma$-ray transitions that, nonetheless, were highly collective in nature and resulted in an alternative interpretation being put forward in stark contrast to that proposed in many textbooks. Those results have sparked a number of new experimental programs at various laboratories worldwide to test the new interpretation. Although the outcome has yet to be determined, it underscores how “established” concepts of nuclear structure need to be continuously tested and that studies of nuclei in all locations on the nuclear chart are required to form a complete picture.

$\beta$-decay studies will continue to provide data that are vital for a deeper understanding of shape coexistence. There has been an enormous increase in resolving power of the current generation of large-scale $\gamma$-ray spectrometer arrays over those used in the previous $\beta$-decay studies performed in the 1970s and 1980s. For example, at the TRIUMF-ISAC facility, for a decade (2003–2013), the $8\pi$ spectrometer, composed of 20 coaxial HPGe detectors that provided approximately 1% total photopeak efficiency at 1332 keV, was arguably the leading spectrometer dedicated to $\beta$-decay studies and provided a huge increase in sensitivity and statistical quality compared to many of the earlier studies. The $8\pi$ spectrometer was replaced in 2014 by the GRIFFIN spectrometer, composed of 16 clover-type HPGe detectors and having approximately 10% total photopeak efficiency at 1332 keV, thus providing two orders of magnitude increase in $\gamma$-$\gamma$-coincidence efficiency. Furthermore, it has gained an enormous benefit from the use of a fully digital DAQ with a thirty-fold increase in data throughput compared to the $8\pi$ spectrometer. GRIFFIN, currently, is the world’s leading spectrometer for $\beta$-decay spectroscopy, and much of its programme is dedicated to shape coexistence studies. The use of trap-assisted $\beta$-decay spectroscopy also offers much promise of providing exceptionally clean beams, with even the separation of various isomers in the parent nuclei. The continuous development of radioactive beam facilities, moreover, with improvements in beam intensities and qualities, coupled with advanced instrumentation will enable the advancement in the understanding of shape coexistence, and undoubtedly, new regions of shape coexistence will be discovered.

Author contributions

PG: writing–original draft and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Work was supported in part by the Natural Sciences and Engineering Research Council (NSERC), Canada.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Garrett PE, Zielińska M, Clément E. An experimental view on shape coexistence in nuclei. Prog Part Nucl Phys (2022) 124:103931. doi:10.1016/j.ppnp.2021.103931

CrossRef Full Text | Google Scholar

2. Kumar K. Intrinsic quadrupole moments and shapes of nuclear ground states and excited states. Phys Rev Lett (1972) 28:249–53. doi:10.1103/PhysRevLett.28.249

CrossRef Full Text | Google Scholar

3. Cline D. Nuclear shapes studied by coulomb excitation. Ann Rev Nucl Part Sci (1986) 36:683–716. doi:10.1146/annurev.ns.36.120186.003343

CrossRef Full Text | Google Scholar

4. Zielińska M. Low-energy coulomb excitation and nuclear deformation. In: SM Lenzi, and D Cortina-Gil, editors. The euroschool on exotic beams, vol. VI. Cham: Springer (2022) p. 43–86. Lecture Notes in Physics, vol 1005. doi:10.1007/978-3-031-10751-1_2

CrossRef Full Text | Google Scholar

5. Wrzosek-Lipska K, Próchniak L, Zielińska M, Srebrny J, Hadyńska-Klȩk K, Iwanicki J, et al. Electromagnetic properties of ¹⁰⁰Mo: experimental results and theoretical description of quadrupole degrees of freedom. Phys Rev C (2012) 86:064305. doi:10.1103/PhysRevC.86.064305

CrossRef Full Text | Google Scholar

6. Kantele J, Julin R, Luontama M, Passoja A, Poikolainen T, Bäcklin A, et al. Absolute E0 and E2 transition rates and collective states in ¹¹⁶Sn. Z Phys A (1979) 289:157. doi:10.1007/BF01435933

CrossRef Full Text | Google Scholar

7. Wood JL, Zganjar EF, Coster CD, Heyde K. Electric monopole transitions from low energy excitations in nuclei. Nucl Phys A (1999) 651:323–68. doi:10.1016/S0375-9474(99)00143-8

CrossRef Full Text | Google Scholar

8. Church EL, Weneser J. Electric-monopole transitions in atomic nuclei. Phys Rev (1956) 103:1035–44. doi:10.1103/PhysRev.103.1035

CrossRef Full Text | Google Scholar

9. Delaroche J-P, Libert J, Girod M, Deloncle I, Dupuis M. Investigations of electric monopole transitions in medium-mass to heavy nuclei: beyond mean field calculations with the Gogny force. Phys Rev C (2024) 109:014320. doi:10.1103/PhysRevC.109.014320

CrossRef Full Text | Google Scholar

10. Kibédi T, Garnsworthy AB, Wood JL. Electric monopole transitions in nuclei. Prog Part Nucl Phys (2022) 123:103930. doi:10.1016/j.ppnp.2021.103930

CrossRef Full Text | Google Scholar

11. Davidson JP. Rotations and vibrations in deformed nuclei. Rev Mod Phys (1965) 37:105–58. doi:10.1103/RevModPhys.37.105

CrossRef Full Text | Google Scholar

12. Thibault C, Klapisch R, Rigaud C, Poskanzer AM, Prieels R, Lessard L, et al. Direct measurement of the masses of ¹¹Li and ²⁶⁻³²Na with an on-line mass spectrometer. Phys Rev C (1975) 12:644–57. doi:10.1103/PhysRevC.12.644

CrossRef Full Text | Google Scholar

13. Huber G, Touchard F, Büttgenbach S, Thibault C, Klapisch R, Duong HT, et al. Spins, magnetic moments, and isotope shifts of ²¹⁻³¹Na by high resolution laser spectroscopy of the atomic D1 line. Phys Rev C (1978) 18:2342–54. doi:10.1103/PhysRevC.18.2342

CrossRef Full Text | Google Scholar

14. Détraz C, Guillemaud D, Huber G, Klapisch R, Langevin M, Naulin F, et al. Beta decay of ²⁷⁻³²Na and their descendants. Phys Rev C (1979) 19:164–76. doi:10.1103/PhysRevC.19.164

CrossRef Full Text | Google Scholar

15. Warburton EK, Becker JA, Brown BA. Mass systematics for A=29–44 nuclei: the deformed A∼32 region. Phys Rev C (1990) 41:1147–66. doi:10.1103/physrevc.41.1147

CrossRef Full Text | Google Scholar

16. Neyens G, Kowalska M, Yordanov D, Blaum K, Himpe P, Lievens P, et al. Measurement of the spin and magnetic moment of ³¹Mg: evidence for a strongly deformed intruder ground state. Phys Rev Lett (2005) 94:022501. doi:10.1103/physrevlett.94.022501

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Mach H, Fraile LM, Tengblad O, Boutami R, Jollet C, Płóciennik WA, et al. New structure information on ³⁰Mg, ³¹Mg and ³²Mg. E Phys J A (2005) 25(Suppl. 1):105. doi:10.1140/epjad/i2005-06-159-0

CrossRef Full Text | Google Scholar

18. Schwerdtfeger W, Thirolf PG, Wimmer K, Habs D, Mach H, Rodriguez TR, et al. Shape coexistence near neutron Number N=20: first identification of the E0 Decay from the deformed first excited J = 0+ state in ³⁰Mg. Phys Rev Lett (2009) 103:012501. doi:10.1103/physrevlett.103.012501

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Nishibata H, Kanaya S, Shimoda T, Odahara A, Morimoto S, Yagi A, et al. Structure of ³¹Mg: shape coexistence revealed by β−γ spectroscopy with spin-polarized ³¹Na. Phys Rev C (2019) 99:024322. doi:10.1103/physrevc.99.024322

CrossRef Full Text | Google Scholar

20. Nishibata H, Tajiri K, Shimoda T, Odahara A, Morimoto S, Kanaya S, et al. Structure of the neutron-rich nucleus ³⁰Mg. Phys Rev C (2020) 102:054327. doi:10.1103/physrevc.102.054327

CrossRef Full Text | Google Scholar

21. Rotaru F, Negoita F, Grévy S, Mrazek J, Lukyanov S, Nowacki F, et al. Unveiling the intruder deformed 0₂⁺ state in ³⁴Si. Phys Rev Lett (2012) 109:092503. doi:10.1103/physrevlett.109.092503

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Lică R, Rotaru F, Borge MJG, Gréy S, Negoiţă F, Poves A, et al. Normal and intruder configurations in ³⁴Si populated in the β− decay of ³⁴Mg and ³⁴Al. Phys Rev C (2019) 100:034306. doi:10.1103/physrevc.100.034306

CrossRef Full Text | Google Scholar

23. Bernas M, Dessagne P, Langevin M, Payet J, Pougheon F, Roussel P. Magic features of ⁶⁸Ni. Phys Lett B (1982) 113:279. doi:10.1016/0370-2693(82)90039-9

CrossRef Full Text | Google Scholar

24. Girod M, Dessagne P, Bernas M, Langevin M, Pougheon F, Roussel P. Spectroscopy of neutron-rich nickel isotopes: experimental results and microscopic interpretation. Phys Rev C (1988) 37:2600–12. doi:10.1103/PhysRevC.37.2600

CrossRef Full Text | Google Scholar

25. Suchyta S, Liddick SN, Tsunoda Y, Otsuka T, Bennett MB, Chemey A, et al. Shape coexistence in ⁶⁸Ni. Phys Rev C (2014) 89:021301. (R). doi:10.1103/physrevc.89.021301

CrossRef Full Text | Google Scholar

26. Flavigny F, Elseviers J, Andreyev AN, Bauer C, Bildstein V, Blazhev A, et al. Microscopic structure of coexisting 0+ states in ⁶⁸Ni probed via two-neutron transfer. Phys Rev C (2019) 99:054332. doi:10.1103/PhysRevC.99.054332

CrossRef Full Text | Google Scholar

27. Pauwels D, Wood JL, Heyde K, Huyse M, Julin R, Van Duppen P. Pairing-excitation versus intruder states in ⁶⁸Ni and ⁹⁰Zr. Phys Rev C (2010) 82:027304. doi:10.1103/PhysRevC.82.027304

CrossRef Full Text | Google Scholar

28. Crider B, Prokop CJ, Liddick SN, Al-Shudifat M, Ayangeakaa AD, Carpenter MP, et al. Shape coexistence from lifetime and branching-ratio measurements in ^68,70Ni. Phys Lett (2016) B763:108. doi:10.1016/j.physletb.2016.10.020

CrossRef Full Text | Google Scholar

29. Recchia F, Chiara CJ, Janssens RVF, Weisshaar D, Gade A, Walters WB, et al. Configuration mixing and relative transition rates between low-spin states in ⁶⁸Ni. Phys Rev C (2013) 88:041302. doi:10.1103/physrevc.88.041302

CrossRef Full Text | Google Scholar

30. Grzywacz R, Béraud R, Borcea C, Emsallem A, Glogowski M, Grawe H, et al. New island ofμsIsomers in neutron-rich nuclei around the Z = 28 and N = 40 Shell closures. Phys Rev Lett (1998) 81:766–9. doi:10.1103/PhysRevLett.81.766

CrossRef Full Text | Google Scholar

31. Olaizola B, Fraile LM, Mach H, Poves A, Nowacki F, Aprahamian A, et al. Search for shape-coexisting 0⁺ states in ⁶⁶Ni from lifetime measurements. Phys Rev C (2017) 95:061303. doi:10.1103/PhysRevC.95.061303

CrossRef Full Text | Google Scholar

32. Leoni S, Fornal B, Mărginean N, Sferrazza M, Tsunoda Y, Otsuka T, et al. Multifaceted quadruplet of low-lying spin-zero states in ⁶⁶Ni: emergence of shape isomerism in light nuclei. Phys Rev Lett (2017) 118:162502. doi:10.1103/PhysRevLett.118.162502

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Pauwels D, Ivanov O, Bree N, Büscher J, Cocolios TE, Gentens J, et al. Shape isomerism at N = 40: discovery of a proton intruder state in ⁶⁷Co. Phys Rev C (2008) 78:041307. doi:10.1103/PhysRevC.78.041307

CrossRef Full Text | Google Scholar

34. Pauwels D, Ivanov O, Bree N, Büscher J, Cocolios TE, Huyse M, et al. Structure of ^65,67Co studied through the β decay of ^65,67Fe and a deep-inelastic reaction. Phys Rev C (2009) 79:044309. doi:10.1103/PhysRevC.79.044309

CrossRef Full Text | Google Scholar

35. Liddick SN, Abromeit B, Ayres A, Bey A, Bingham CR, Bolla M, et al. Low-energy structure of ₂₇⁶⁶Co₃₉ and ₂₇⁶⁸Co₄₁ populated through β decay. Phys Rev C f (2012) 85:014328. doi:10.1103/PhysRevC.85.014328

CrossRef Full Text | Google Scholar

36. Stryjczyk M, Tsunoda Y, Darby IG, De Witte H, Diriken J, Fedorov DV, et al. β− decay study of the Mn66−Fe66−Co66−Ni66 decay chain. Phys Rev C (2018) 98:064326. doi:10.1103/PhysRevC.98.064326

CrossRef Full Text | Google Scholar

37. Rocchini M, Garrett PE, Zielińska M, Lenzi SM, Dao DD, Nowacki F, et al. First evidence of axial shape asymmetry and configuration coexistence in ⁷⁴Zn: suggestion for a northern extension of the N = 40 island of inversion. Phys Rev Lett (2023) 130:122502. doi:10.1103/PhysRevLett.130.122502

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Tracy JL, Winger JA, Rasco BC, Silwal U, Siwakoti DP, Rykaczewski KP, et al. Updated β-decay measurement of neutron-rich ⁷⁴Cu. Phys Rev C (2018) 98:034309. doi:10.1103/PhysRevC.98.034309

CrossRef Full Text | Google Scholar

39. Gottardo A, Verney D, Delafosse C, Ibrahim F, Roussière B, Sotty C, et al. First evidence of shape coexistence in the ⁷⁸Ni region; intruder 0₂⁺ state in ⁸⁰Ge. Phys Rev Lett (2016) 116:182501. doi:10.1103/physrevlett.116.182501

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Garcia FH, Andreoiu C, Ball GC, Bell A, Garnsworthy AB, Nowacki F, et al. Absence of low-energy shape coexistence in ⁸⁰Ge: the nonobservation of a proposed excited 0₂⁺ level at 639 keV. Phys Rev Lett (2020) 125:172501. doi:10.1103/physrevlett.125.172501

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Sheline RK, Ragnarsson I, Nilsson SG. Shell structure for deformed nuclear shapes. Phys Lett B (1972) 41:115. doi:10.1016/0370-2693(72)90440-6

CrossRef Full Text | Google Scholar

42. Khan TA, Lauppe WD, Sistemich K, Lawin H, Sadler G, Selič HA. The β-decay of ¹⁰⁰Y: discovery of a very low lying 0⁺ state in ¹⁰⁰Zr. Z Phys A (1977) 283:105–20. doi:10.1007/BF01434071

CrossRef Full Text | Google Scholar

43. Khan TA, Lauppe W-D, Sistemich K, Lawin H, Selič HA. Lifetime of the 331.3 keV 0₂⁺ state in ¹⁰⁰Zr. Z Phys A (1977) 284:313–7. doi:10.1007/BF01406804

CrossRef Full Text | Google Scholar

44. Mach H, Moszyński M, Gill RL, Wohn FK, Winger JA, Hill JC, et al. Deformation and shape coexistence of 0⁺ states in ⁹⁸Sr and ¹⁰⁰Zr. Phys Lett B (1989) 230:21. doi:10.1016/0370-2693(89)91646-8

CrossRef Full Text | Google Scholar

45. Mach H, Moszyński M, Gill RL, Molnár G, Wohn FK, Winger JA, et al. Monopole strength and shape coexistence in the A. Phys Rev C (1990) 41:350–3. doi:10.1103/PhysRevC.41.350

CrossRef Full Text | Google Scholar

46. Lhersonneau G, Gabelmann H, Kaffrel N, Kratz K-L, Pfeiffer B. Lifetime measurements in ⁹⁹Sr and ¹⁰⁰Zr. Z Phys A (1989) 332:240. doi:10.1007/BF01289787

CrossRef Full Text | Google Scholar

47. Lhersonneau G, Pfeiffer B, Kratz K-L, Ohm H, Sistemich K, Brant S, et al. Structure of the N = 59 nucleus ⁹⁷Sr: coexistence of spherical and deformed states. Z Phys A (1990) 337:149. doi:10.1007/BF01294286

CrossRef Full Text | Google Scholar

48. Büscher M, Casten RF, Gill RL, Schuhmann R, Winger JA, Mach H, et al. Coexistence features in the spherical-deformed A≊100 transition region: picosecond lifetime measurements in ⁹⁷Sr, ⁹⁷Y, and ⁹⁷Zr. Phys Rev C (1990) 41:1115–25. doi:10.1103/PhysRevC.41.1115

CrossRef Full Text | Google Scholar

49. Kawade K, Battistuzzi G, Lawin H, Selič HA, Sistemich K, Schussler F, et al. Z Phys A (1982) 304:293. doi:10.1007/BF01421511

CrossRef Full Text

50. Singh P, Korten W, Hagen TW, Görgen A, Grente L, Salsac M-D, et al. Evidence for coexisting shapes through lifetime measurements in ⁹⁸Zr. Phys Rev Lett (2018) 121:192501. doi:10.1103/PhysRevLett.121.192501

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Karayonchev V, Jolie J, Blazhev A, Dewald A, Esmaylzadeh A, Fransen C, et al. Tests of collectivity in ⁹⁸Zr by absolute transition rates. Phys Rev C (2020) 102:064314. doi:10.1103/PhysRevC.102.064314

CrossRef Full Text | Google Scholar

52. Park J, Garnsworthy AB, Krücken R, Andreoiu C, Ball GC, Bender PC, et al. Shape coexistence and evolution in ⁹⁸Sr. Phys Rev C (2016) 93:014315. doi:10.1103/PhysRevC.93.014315

CrossRef Full Text | Google Scholar

53. Clément E, Zielińska M, Görgen A, Korten W, Péru S, Libert J, et al. Spectroscopic quadrupole moments in ^96,98Sr: evidence for shape coexistence in neutron-rich strontium isotopes at N=60. Phys Rev Lett (2016) 116:022701. doi:10.1103/PhysRevLett.116.022701

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Clément E, Zielińska M, Péru S, Goutte H, Hilaire S, Görgen A, et al. Low-energy Coulomb excitation of ^96,98Sr beams. Phys Rev C (2016) 94:054326. doi:10.1103/PhysRevC.94.054326

CrossRef Full Text | Google Scholar

55. Lhersonneau G, PfeifFer B, Kratz K-L, Enqvist T, Jauho PP, Jokinen A, et al. Evolution of deformation in the neutron-rich Zr region from excited intruder state to the ground state. Phys Rev C (1994) 49:1379–90. doi:10.1103/physrevc.49.1379

CrossRef Full Text | Google Scholar

56. Lhersonneau G, Dendooven P, Honkanen A, Huhta M, Jones PM, Julin R, et al. New interpretation of shape coexistence in ⁹⁹Zr. Phys Rev C (1997) 56:2445–50. doi:10.1103/PhysRevC.56.2445

CrossRef Full Text | Google Scholar

57. Urban W, Pinston J, Rzaca-Urban T, Złomaniec A, Simpson G, Durell J, et al. First observation of the ν9/2[404] orbital in the A ∼ 100 mass region. Eur Phys J (2003) A16:11. doi:10.1140/epja/i2002-10104-y

CrossRef Full Text | Google Scholar

58. Spagnoletti P, Simpson G, Kisyov S, Bucurescu D, Régis J-M, Saed-Samii N, et al. Lifetimes and shape-coexisting states of ⁹⁹Zr. Phys Rev C (2019) 100:014311. doi:10.1103/PhysRevC.100.014311

CrossRef Full Text | Google Scholar

59. Chakraborty A, Peters EE, Crider BP, Andreoiu C, Bender PC, Cross DS, et al. Collective structure in ⁹⁴Zr and subshell effects in shape coexistence. Phys Rev Lett (2013) 110:022504. doi:10.1103/PhysRevLett.110.022504

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Wu J, Carpenter MP, Kondev FG, Janssens RVF, Zhu S, McCutchan EA, et al. Determination of the spins and parities for the 0₄⁺ and 0₅⁺ states in ¹⁰⁰Zr. Phys Rev C (2024) 109:024314. doi:10.1103/PhysRevC.109.024314

CrossRef Full Text | Google Scholar

61. Heyde K, Wood JL. Shape coexistence in atomic nuclei. Rev Mod Phys (2011) 83:1467–521. doi:10.1103/RevModPhys.83.1467

CrossRef Full Text | Google Scholar

62. Mashtakov KR, Garrett PE, Olaizola B, Andreoiu C, Ball GC, Bender P, et al. J. Web of conf. in press (2024).

Google Scholar

63. Scharff-Goldhaber G, Weneser J. System of even-even nuclei. Phys Rev (1955) 98:212–4. doi:10.1103/physrev.98.212

CrossRef Full Text | Google Scholar

64. Motz HT. Slow-neutron capture gamma rays from sodium and cadmium. Phys Rev (1956) 104:1353–64. doi:10.1103/physrev.104.1353

CrossRef Full Text | Google Scholar

65. Cohen BL, Price RE. Studies of low-lying levels of even-even nuclei with (d, p) and (d, t) reactions. Phys Rev (1960) 118:1582–90. doi:10.1103/physrev.118.1582

CrossRef Full Text | Google Scholar

66. Meyer R, Peker L. Evidence for the coexistence of shapes in even-mass Cd nuclei. Z Phys A (1977) 283:379. doi:10.1007/BF01409518

CrossRef Full Text | Google Scholar

67. Katoh T, Nozawa M, Yoshizawa Y. Study of the cadmium isotopes (II). Nucl Phys (1962) 32:25–70. doi:10.1016/0029-5582(62)90317-6

CrossRef Full Text | Google Scholar

68. Fielding HW, Anderson RE, Zafiratos CD, Lind DA, Cecil FE, Wieman HH, et al. 0+ states observed in Cd and Sn nuclei with the (³He, n) reaction. Nucl Phys A (1977) 281:389. doi:10.1016/0375-9474(77)90504-8

CrossRef Full Text | Google Scholar

69. Julin R, Kantele J, Luontama M, Passoja A, Poikolainen T, Bäcklin A, et al. Decay characteristics of 0₂⁺ and 0₃⁺ states in ¹¹²Cd and ¹¹⁴Cd. Z Phys (1980) A296:315–8. doi:10.1007/BF01438525

CrossRef Full Text | Google Scholar

70. Kumpulainen J, Julin R, Kantele J, Passoja A, Trzaska WH, Verho E, et al. Systematic study of low-spin states in even Cd nuclei. Phys Rev C (1992) 45:640–61. doi:10.1103/physrevc.45.640

CrossRef Full Text | Google Scholar

71. Julin R, Kantele J, Kumpulainen J, Luontama M, Nieminen V, Passoja A, et al. A setup for spectrometry of high-energy conversion electrons. Nucl Instrum Meth A (1988) 270:74. doi:10.1016/0168-9002(88)90011-3

CrossRef Full Text | Google Scholar

72. Garrett PE, Rodriguez TR, Diaz Varela A, Green KL, Bangay J, Finlay A, et al. Multiple shape coexistence in ^110,112Cd. Phys Rev Lett (2019) 123:142502. doi:10.1103/physrevlett.123.142502

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Garrett PE, Rodriguez TR, Diaz Varela A, Green KL, Bangay J, Finlay A, et al. Shape coexistence and multiparticle-multihole structures in ^110,112Cd. Phys Rev C (2020) 101:044302. doi:10.1103/PhysRevC.101.044302

CrossRef Full Text | Google Scholar

74. Garrett PE, Bangay J, Diaz Varela A, Ball GC, Cross DS, Demand GA, et al. Detailed spectroscopy of ¹¹⁰Cd: evidence for weak mixing and the emergence of γ-soft behavior. Phys Rev C (2012) 86:044304. doi:10.1103/physrevc.86.044304

CrossRef Full Text | Google Scholar

75. Heyde K, Van Isacker P, Waroquier M, Wenes G, Sambataro M. Description of the low-lying levels in ^112,114Cd. Phys Rev C (1982) 25:3160. doi:10.1103/PhysRevC.25.3160

CrossRef Full Text | Google Scholar

76. Wrzosek-Lipska K, Próchniak L, Garrett PE, Yates SW, Wood JL, Napiorkowski PJ, et al. Quadrupole deformation of ¹¹⁰Cd studied with coulomb excitation. Acta Phys Pol B (2020) 51:789. doi:10.5506/APhysPolB.51.789

CrossRef Full Text | Google Scholar

77. Giannatiempo A, Liberati G, Sona P. The 0₁⁺→0⁺ electric monopole transition in ¹¹²Cd. Z Phys A (1979) 290:411. doi:10.1007/BF01408405

CrossRef Full Text | Google Scholar

78. Giannatiempo A, Nannini A, Perego A, Sona P. 0₂⁺ and 0₃⁺ states in ¹¹⁰Cd. Phys Rev C (1989) 41:1167–71. doi:10.1103/physrevc.41.1167

CrossRef Full Text | Google Scholar

79. Giannatiempo A, Nannini A, Perego A, Sona P. E0 components of 2i+-->2f+ transitions in even cadmium isotopes and effective monopole charges. Phys Rev C (1991) 44:1844–9. doi:10.1103/physrevc.44.1844

CrossRef Full Text | Google Scholar

80. Jigmeddorj B, Garrett PE, Diaz Varela A, Ball GC, Bangay JC, Cross DS, et al. Conversion electron study of ¹¹⁰Cd: evidence of new E0 branches. E Phys J A (2016) 52:36. doi:10.1140/epja/i2016-16036-y

CrossRef Full Text | Google Scholar

81. Batchelder JC, Bilheux J-C, Bingham CR, Carter HK, Cole JD, Fong D, et al. The CARDS array for neutron-rich decay spectroscopy at HRIBF. Nucl Instrum Methods Phys Res Sect B (2003) 204:625–8. doi:10.1016/S0168-583X(02)02141-9

CrossRef Full Text | Google Scholar

82. Batchelder JC, Bilheux J-C, Bingham CR, Carter HK, Fong D, Garrett PE, et al. New isomeric state in ¹¹⁶Ag. Phys Rev C (2005) 72:044306. doi:10.1103/PhysRevC.72.044306

CrossRef Full Text | Google Scholar

83. Juutinen S, Julin R, Jones P, Lampinen A, Lhersonneau G, Mäkelä E, et al. Band structures in ¹¹⁴Cd and ¹¹⁶Cd from heavy-ion collisions. Phys Lett B (1996) 386:80. doi:10.1016/0370-2693(96)00967-7

CrossRef Full Text | Google Scholar

84. Batchelder JC, Wood JL, Garrett PE, Green KL, Rykaczewski KP, Bilheux J-C, et al. Collective and noncollective states in ¹¹⁶Cd studied via the β decays of ^116m1,m2,gsAg. Phys Rev C (2009) 80:054318. doi:10.1103/PhysRevC.80.054318

CrossRef Full Text | Google Scholar

85. Batchelder JC, Brewer NT, Goans RE, Grzywacz R, Griffith BO, Jost C, et al. Low-lying collective states in ₁₂₀Cd populated by β decay of ₁₂₀Ag: breakdown of the anharmonic vibrator model at the three-phonon level. Phys Rev C (2012) 86:064311. doi:10.1103/PhysRevC.86.064311

CrossRef Full Text | Google Scholar

86. Batchelder JC, Brewer NT, Gross CJ, Grzywacz R, Hamilton JH, Karny M, et al. Structure of low-lying states in ^124,126Cd populated by β decay of ^124,126Ag. Phys Rev C (2014) 89:054321. doi:10.1103/PhysRevC.89.054321

CrossRef Full Text | Google Scholar

87. Zamfir NV, Gill RL, Brenner DS, Casten RF, Wolf A. Study of low-spin states in ¹²²Cd. Phys Rev C (1995) 51:98–102. doi:10.1103/PhysRevC.51.98

CrossRef Full Text | Google Scholar

88. Stryjczyk M, Kankainen A. JYFL proposal I285 (2024).

Google Scholar

89. Bron J, Hesselink WHA, Vanpoelgest A, Zalmstra JJA, Uitzinger MJ, Verheul H, et al. Nucl Phys A (1979) 318:335. doi:10.1016/0375-9474(79)90653-5

CrossRef Full Text

90. Jänecke J, Becchetti FD, Thorn CE. Alpha-cluster pickup from Te and Sn isotopes with the (d,⁶Li) reaction. Nucl Phys A (1979) 325:340. doi:10.1016/0375-9474(79)90021-6

CrossRef Full Text | Google Scholar

91. Pore JL, Cross DS, Andreoiu C, Ashley R, Ball GC, Bender PC, et al. Study of the β - decay of ^116m1In: a new interpretation of low-lying 0⁺ states in ¹¹⁶Sn. Eur Phys J A (2017) 53:27. doi:10.1140/epja/i2017-12213-x

CrossRef Full Text | Google Scholar

92. Cross DS, Pore JL, Andreoiu C, Ball GC, Bender PC, Chester AS, et al. Conversion-electron spectroscopy and gamma-gamma angular correlation measurements in ¹¹⁶Sn. Eur Phys J A (2017) 53:216. doi:10.1140/epja/i2017-12412-5

CrossRef Full Text | Google Scholar

93. Ortner K, Andreoiu C, Spieker M, Ball GC, Bernier N, Bidaman H, et al. Collective 2p-2h intruder states in ¹¹⁸Sn studied via β decay of ¹¹⁸In using the GRIFFIN spectrometer at TRIUMF. Phys Rev C (2020) 102:024323. doi:10.1103/PhysRevC.102.024323

CrossRef Full Text | Google Scholar

94. Spieker M, Petkov P, Litvinova E, Müller-Gatermann C, Pickstone SG, Prill S, et al. Shape coexistence and collective low-spin states in ^112,114Sn studied with the (p,p′γ) Doppler-shift attenuation coincidence technique. Phys Rev C (2018) 97:054319. doi:10.1103/PhysRevC.97.054319

CrossRef Full Text | Google Scholar

95. Kaffrell N, Hill P, Rogowski J, Tetziaff H, Trautmann N, Jacobs E, et al. Levels in ¹⁰⁷Rh. Nucl Phys A (1986) 460:437. doi:10.1016/0375-9474(86)90423-9

CrossRef Full Text | Google Scholar

96. Kaffrell N, Hill P, Rogowski J, Tetziaff H, Trautmann N, Jacobs E, et al. Levels in ¹⁰⁹Rh. Nucl Phys A (1987) 470:141. doi:10.1016/0375-9474(87)90125-4

CrossRef Full Text | Google Scholar

97. Rogowski J, Alstad J, Fowler MM, De Frenne D, Heyde K, Jacobs E, et al. Evidence for intruder states in ¹¹¹Rh. Z Phys A (1990) 337:233. doi:10.1007/BF01294298

CrossRef Full Text | Google Scholar

98. Lhersonneau G, Pfeiffer B, Alstad J, Dendooven P, Eberhardt K, Hankonen S, et al. Shape coexistence near the double-midshell nucleus ¹¹¹Rh. Eur Phys J A1 (1998) 285. doi:10.1007/s100500050063

CrossRef Full Text | Google Scholar

99. Rogowski J, Alstad J, Brant S, Daniels WR, De Frenne D, Heyde K, et al. Intruder states in odd-mass Ag isotopes. Phys Rev C (1990) 42:2733–6. doi:10.1103/PhysRevC.42.2733

CrossRef Full Text | Google Scholar