Precise and accurate speed measurements in rapidly flowing dense suspensions

We introduce a method for precise and accurate measurements of particle speeds in dense suspensions flowing at high rates and demonstrate the utility of the approach for revealing complex flow fluctuations during shearing in a setup that combines imaging with a confocal microscope and shearing with a rheometer. We scan the focal point in one dimension, aligned with direction of flow, producing absolute measurements of speed that are independent of suspension structure and particle shape. We compare this flow-direction line scanning approach with a complementary method we introduced previously, measuring speed using line scanning in the vorticity direction. By comparing results in various flow conditions, including shear-thinning and thickening regimes, we demonstrate the efficacy of our new approach. We find that both approaches exhibit qualitatively similar flow profiles, but a comparative analysis reveals a 15%–25% overestimation in speed measurement using vorticity line scanning, with discrepancies generated by anisotropic suspension microstructure under flow. Moreover, in the thickening regime where complex flow fields are present, both approaches capture local speed fluctuations. However, line scanning in the flow direction reveals and precisely captures stagnation and backflows, a capability not achievable with vorticity line scanning. The approach introduced here not only provides a refined technique for speed measurement in fast-flowing suspensions but also emphasizes the significance of accurate measurement techniques in advancing our understanding of flow behavior in dense suspensions, particularly in contexts where strong non-affine flows are prevalent.

1 Introduction

Characterizing and understanding the behavior of flowing suspensions is an important challenge in materials science and engineering, with significant implications across various industrial sectors [1, 2]. Suspensions exhibit diverse flow behaviors that profoundly influence their properties and applications. Understanding and controlling flow phenomena in suspensions is crucial for optimizing processes and enhancing product performance in industries ranging from pharmaceuticals to cosmetics, from food processing to petroleum extraction [2]. The flow behavior of suspensions is intricately linked to their rheological properties, including shear-thinning and thickening. Shear-thinning, characterized by a decrease in viscosity under increasing shear rates, is commonly observed in many suspensions and plays a vital role in processes such as pumping, painting, inkjet printing and mixing. Conversely, shear thickening, where viscosity increases with shear rate, is important in applications such as body armor and damping systems [3].

Shear thickening typically occurs at relatively large Péclet number, $Pe=\dot{\gamma }{t}_s$ (where $\dot{\gamma }$ is the shear rate and $t_s$ is the system intrinsic time scale), posing a challenge for accurately measuring the structure and velocities of particles. To tackle this obstacle, our prior work introduced a novel technique aimed at capturing both local structure and particle velocities [1]. In this approach, instead of scanning the focused laser in two dimensions to produce a planar image in which particles are located, the laser is scanned only along the vorticity direction, allowing for very high time resolution. The flow of particles past the scan line enables the measurement of local structure and approximate flow speed. While this method successfully captures the spatio-temporal dynamics of dense suspensions in the thickening regime, there is considerable uncertainty in the measured speed values due to the coupling between the estimated flow speed and the spatial structure of the suspension (discussed below). To address this limitation, here we introduce an alternative approach employing laser scanning in the flow direction, allowing for precise measurement of average particle speed that is independent of the degree or type of order in the suspension (or any other aspects of the suspension structure or particle shape). We compare results obtained by line scanning in each direction in various flow fields and find that both approaches capture the flow profile (below the shear-thickening regime) and speed fluctuations (seen in the shear-thickening regime). However, the line scanning in the vorticity direction, using the parameters from our previous measurements, overestimates the values of speed by approximately 15%–25%. As expected, the exact values of the discrepancy depend on the structure of the suspension under flow. Moreover, we show that line scanning in the flow direction can accurately capture backflows in highly dense suspensions of silica particles in the shear thickening regime, a phenomenon not previously reported. The two approaches in combination enable accurate and robust measurements of speed and order fluctuations in rapidly flowing dense suspensions.

2 Approach

2.1 Speed measurement by line scanning in the flow direction

Particle tracking is a widely employed method for measuring the velocity of particles in flowing suspensions. This technique involves tracing the trajectories of individual particles as they move within the fluid medium, allowing for the determination of their velocity over time [4]. For accurate particle tracking, the displacement of a particle between consecutive frames should be smaller than the interparticle spacing. Consequently, given the frame rate $(f)$ and interparticle spacing $(\delta )$, the maximum flow speed $(v_{\mathit{max}}^{\mathit{tracking}})$ must adhere to the condition $v_{\mathit{max}}^{\mathit{tracking}}\ll f\delta$. In dense suspensions, where the interparticle spacing is relatively small, successful particle tracking necessitates some combination of low velocity and high frame rate. Another technique commonly used for measuring fluid flow velocities is Particle Image Velocimetry (PIV). In this technique, instead of locating individual particles, the movement of a group of particles (in an interrogation window) is tracked using cross-correlation analysis. This allows for the measurements of larger speeds compared to particle tracking method. However, its efficacy relies on the consistent presence of a persistent unique spatial pattern among particles, which is often not maintained in the case of dense suspensions examined in this study.

Here, we introduce a different approach that facilitates measurements of speeds in fast-flowing systems. In this method, instead of employing the relatively slow 2D laser scanning technique, the laser scans back and forth exclusively along the flow direction, designated as the x-axis (see Figure 1A). In the ideal scenario where the center of the particle lies within the focal volume of the scanned line, the magnitude of the particle velocity in the flow direction can be determined as follows: $v=s\mathrm{\Delta }x$, where $s$ denotes the scan rate and $\mathrm{\Delta }x$ represents the distance over which the particle has traveled between consecutive scans. The condition that $\mathrm{\Delta }x$ must be small compared to the interparticle spacing $(\delta )$ implies that the maximum flow speed must satisfy $v_{\mathit{max}}^{\mathit{flow}}\ll s\delta$. Since the scan rate $s$ is several order of magnitude smaller than the frame rate $f$, this implies $v_{\mathit{max}}^{\mathit{flow}}\gg v_{\mathit{max}}^{\mathit{tracking}}$.

Figure 1

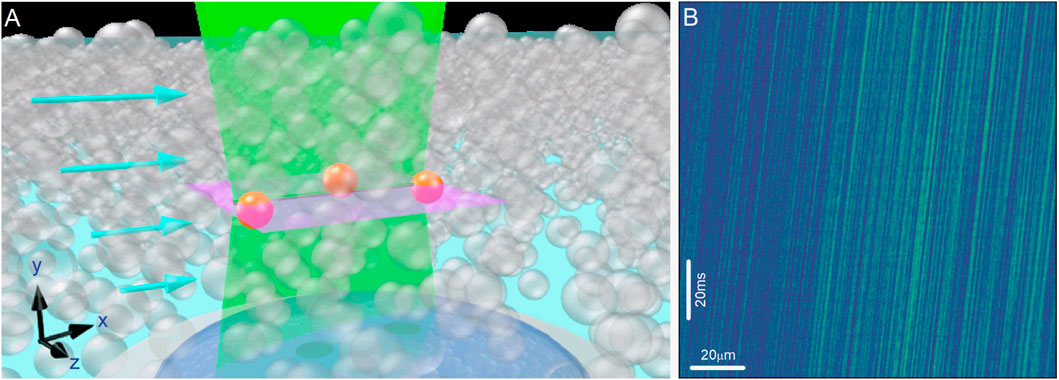
Figure 1. (A) Schematic of line scanning along the flow direction for a sheared dense suspension: The laser scans back and forth along the flow direction, $x$ (indicated by the black line). Particles transiting this line are illuminated (shown by orange color). The imaging region for the standard 2D laser scan is shown in the pink-colored area, and the arrows represent the average velocity field of the sheared suspension. (B) Representative space-time kymographs generated from line scans (horizontal) stacked vertically. Since the particles are not fluorescent, their motion along the flow direction appears as dark lines. The results are recorded at a shear rate $5s^{-1}$ and $z=20\mu$m height from the bottom plate of rheometer for a dense suspension of silica particles with diameter $1.5\mu m$ and volume fraction $\varphi =0.54$.

In the results presented below, we image non-fluorescent particles dispersed in a fluorescent background, so particles generate local intensity minima, which move along the scan line with each successive scan. Plotting the intensity along the scanned line on subsequent scans (creating a kymograph), we visualize the passage of particles along the flow direction. Figure 1B shows an example image generated from a sheared suspension of 1.5 $\mu$m diameter silica spheres, with the scan line focused 20 $\mu$m above the bottom boundary of the sheared suspension. The horizontal axis represents the position along the scanned line in the flow direction, while the vertical axis represents scans at different times. In this illustration, the motion of each particle along the flow direction is visualized as dark tilted lines. In cases of flows orthogonal to the scan direction, such as flow in the gradient or vorticity directions, particles may move away from the scanned line. When this occurs, the kymograph will not display extended dark tilted lines. Instead, it will show disconnected or oval patterns, reflecting the displacement of particles away from the scanning region. This effect is further discussed in the Results section, where we examine significant non-affine flows and their impact on the kymograph patterns.

In principle, the slope of each line could be utilized to measure the speed of individual particles. In practice, discerning individual particles poses a challenge, in part due to the variability in the particle position relative to the scan line in the directions perpendicular to the line. Therefore, we opt to derive speeds from characteristic lengths obtained through correlation analyses. This approach is similar to fiuorescence correlation spectroscopy (FCS), which has been used to measure flow speeds in situations where the volume fraction of the fiuorescent species is low [1, 5–10]. To extract the speed from the line scan intensity data, $I(x,t)$, we calculate the two-dimensional spatial autocorrelation, $g(\mathrm{\Delta }x,\mathrm{\Delta }t)={⟨\delta I(x,t)\delta I(x+\mathrm{\Delta }x,t+\mathrm{\Delta }t)⟩}_{x,t}/{⟨\delta I{(x,t)}^2⟩}_{x,t}$, where $\delta I(x,t)=I(x,t)-{⟨I(x,t)⟩}_{x,t}$. The top left inset of Figure 2 shows the color map plot of $g(\mathrm{\Delta }x,\mathrm{\Delta }t)$ for the image displayed in Figure 1B. The flow pattern is evident in $g(\mathrm{\Delta }x,\mathrm{\Delta }t)$ by distinct tilted lines, and the quantitative evolution is displayed by plotted $g(\mathrm{\Delta }x)$ at different delay times (main panel of Figure 2). A Gaussian fit is used to precisely determine the position of the central maximum of $g(\mathrm{\Delta }x,\mathrm{\Delta }t)$ at each delay time, from which the speed is calculated from the slope of the peak position with delay time (right inset of Figure 2). Note that the conversion to flow speed depends only on the laser scan rate and the microscope optics and is therefore independent of any details of the material system, including particle shape, orientation, or suspension structure.

Figure 2

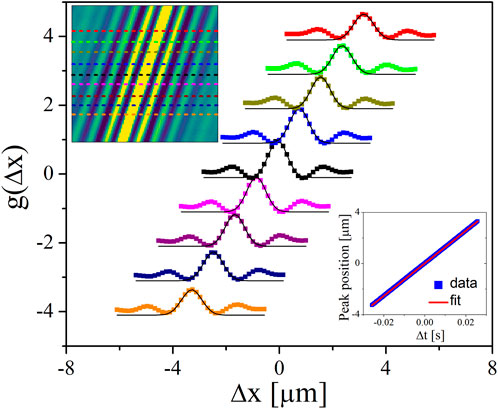
Figure 2. Top left inset: $g(\mathrm{\Delta }x,\mathrm{\Delta }t)$ for the image displayed in Figure 1B. Main panel: $g(\mathrm{\Delta }x)$ at different delay times as indicated by dashed lines in the top left inset (shifted vertically for clarity). The black solid lines in the main panel are the Gaussian fit to precisely extract the position of the central peak of $g(\mathrm{\Delta }x)$. Bottom right inset: The position of the central peak of $g(\mathrm{\Delta }x)$ versus lag time. The results are for the shear rate $5s^{-1}$ and $z=20\mu$m height from the bottom plate of rheometer. The suspension particle volume fraction is $\varphi =0.54$.

2.2 Speed measurement by line scanning in the vorticity direction

The speed of particles in the flow direction can also be determined through line scanning in the vorticity direction. One advantage of this method is that it provides information on the local structure in the flow-vorticity plane. While we briefly touch upon this method here, a more comprehensive analysis has been presented in our previous study [1]. Similar to line scanning in the flow direction, when a line is scanned in the vorticity direction, a non-fluorescent particle in a fluorescent background within the scanned line produces a local intensity minimum, facilitating the determination of its position along the vorticity direction. Plotting the intensity along the scanned line at various scanned times (kymograph) reveals the local structure in the flow-vorticity plane. Figure 3A depicts an example image produced by 1.5 $\mu$m spheres with the scan line positioned 20 $\mu$m above the bottom of the sheared suspension. The horizontal axis represents the position in the vorticity direction, while the vertical axis shows scans at successive times. Individual particles are visible as dark ovals. In theory, the vertical axis of each oval could be utilized to measure the speed of each particle. For the same reason mentioned earlier, we use correlation analyses to measure the average speed of particles. The inset in Figure 3A shows the corresponding contour plot of $g(\mathrm{\Delta }z,\mathrm{\Delta }t)$ for the kymograph displayed in Figure 3A. A hexagonal order with the expansion in the flow direction is evident. Fitting the central peak of $g(\mathrm{\Delta }z,\mathrm{\Delta }t)$ to a 2D Gaussian $g(z,t)=h\cdot exp[-({(z/\mathrm{\Delta }z)}^2+{(t/\mathrm{\Delta }t)}^2)/2]$ provides an accurate measure of the widths in the flow $\mathrm{\Delta }t$ (number of scanned lines) and vorticity $\mathrm{\Delta }z$ directions (see Gaussian fits along t and z direction in Figures 3B, C, respectively). The flow velocity, $v_{\mathit{flow}}$, can be estimated as $v_{\mathit{flow}}$ = $\mathrm{\Delta }{l}_{\mathit{flow}}/\mathrm{\Delta }t$, where $\mathrm{\Delta }{l}_{\mathit{flow}}$ represents the particle spacing in the flow direction. However, since $\mathrm{\Delta }{l}_{\mathit{flow}}$ is not directly measurable in our experiments, we approximate it using the particle spacing in the vorticity direction, $\mathrm{\Delta }z$. Consequently, the flow velocity is approximated as $v_{\mathit{flow}}\simeq \mathrm{\Delta }z/\mathrm{\Delta }t$. This approximation assumes that the structural differences between the flow and vorticity directions are small enough to not significantly affect the velocity estimation, but it does introduce a level of uncertainty, as we acknowledge in our analysis.

Figure 3

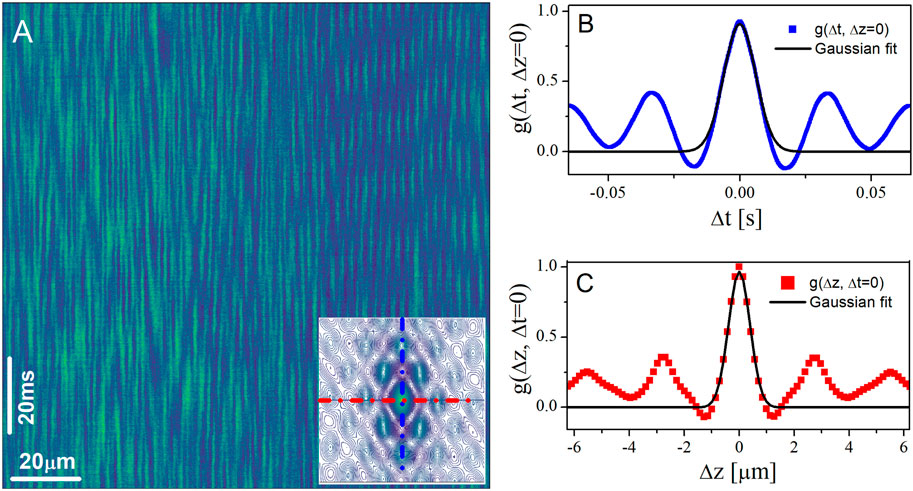
Figure 3. (A) Representative space-time kymographs generated from line scans in the vorticity direction (horizontal) stacked vertically taken in a sheared dense suspension of silica particles of diameter $1.5\mu m$, $\varphi =0.54$, at shear rate 5$s^{-1}$ and $z=5\mu m$ height from the bottom plate of the rheometer. The inset is the corresponding $g(\mathrm{\Delta }z,\mathrm{\Delta }t)$ for the image displayed in (A). (B) $g(\mathrm{\Delta }t)$ at $\mathrm{\Delta }z=0$ (along the vertical blue dashed-dotted line in the inset. (C) $g(\mathrm{\Delta }z)$ at $\mathrm{\Delta }t=0$ (along the horizontal red dashed-dotted line in the inset. The solid lines in (B) and (C) represent Gaussian fits to the central peak of $g(\mathrm{\Delta }z,\mathrm{\Delta }t)$.

3 Results and discussion

Dense suspensions at shear rates below shear-thickening: We first compare the values of speeds in the flow direction $(v_x)$ measured independently from line scanning in the flow $(v_x^{\mathit{flow}})$ and vorticity $(v_x^{\mathit{vorticity}})$ directions. Here, we report the results for a dense suspension of 1.5 $\mu$m silica spheres at a volume fraction $\varphi =0.54$% at different heights from the bottom boundary for a constant shear rate of $5s^{-1}$ (corresponding to $\sigma \approx 8Pa$). This shear rate is well below the shear-thickening regime (Supplementary Figure S1). The resulting flow profiles are presented in Figure 4, with error bars given by the standard deviation of each time series (averaged over 100 frames). Flow profiles obtained by line scanning in both directions yield qualitatively similar results, but the speed measured by scanning in the vorticity direction $v_x^{\mathit{vorticity}}$ is consistently higher than $v_x^{\mathit{flow}}$, suggesting that the structural correlations in the suspension are not isotropic. We have previously shown that the suspension is disordered at heights above $20\mu m$, so the likely explanation for the anisotropy is a larger average particle separation in the flow direction relative to the vorticity direction. Assuming that increase in separation is 1/0.85, the two speed measurements match for heights above 20 $\mu m$. The discrepancy between $v_x^{\mathit{vorticity}}$ and $v_x^{\mathit{flow}}$ is larger closer to the bottom boundary, consistent with the observation that the particles display significant hexagonal order near the wall, which produce notable asymmetries in the structure in the flow-vorticity plane [1]. Note that the ordering in the flow-vorticity plane is also associated with layering in the gradient direction, which produces a lower viscosity [11–16], as is evident in the increased shear rate (slope of the flow profile) measured near the bottom boundary.

Figure 4

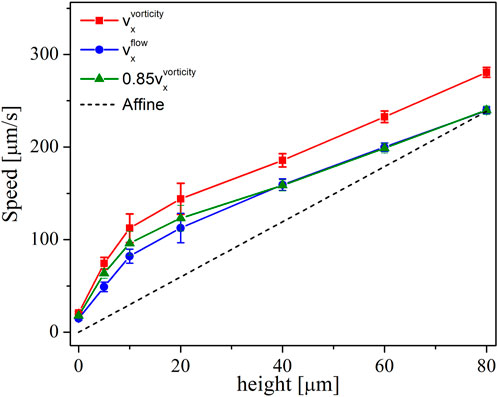
Figure 4. Profiles of average speed as a function of height from rheometer’s bottom plate for a constant shear rate of $5s^{-1}$ generated from linescan in the flow (blue circles) and vorticity (red squares) directions. Error bars are standard deviations (averaged over 100 frames). The green triangles are the velocity data obtained from line scanning in the vorticity direction scaled by a constant value of 0.85 to collapse on velocity data generated from line scanning in the flow direction for height$\ge 40\mu m$. The dashed line represents the affine flow with no wall-slip. Results are for the silica suspensions with $\varphi =0.54\%$.

Dense suspensions in the shear-thickening regime: Next, we compare the average velocity values measured by line scanning in the flow and vorticity directions in the shear-thickening regime where a more complex flow field with faster particle speeds is anticipated [1, 17]. Here, we show the results at the bottom layer for the same silica suspension ($\varphi =54$%), but with a constant applied stress of 200Pa which is well-inside shear-thickening regime (Supplementary Figure S1). Both $v_x^{\mathit{vorticity}}$ and $v_x^{\mathit{flow}}$ show intermittent spikes (see Figure 5). These velocity fluctuations have been linked to fluctuations in localized stresses at the boundary [1, 17] which leads to fluctuations in the bulk viscosity/shear rate [17–20]. Although both $v_x^{\mathit{vorticity}}$ and $v_x^{\mathit{flow}}$ show the same trend, their exact value differs; away from spikes where the structure is ordered (Figure 5D), the difference is approximately 50% which is larger than the one observed for a low shear rate of 5$s^{-1}$ (Figure 4). However, the difference reduces to about 10%–20% during the spikes where the local order is disrupted by flow (Figure 5D),

Figure 5

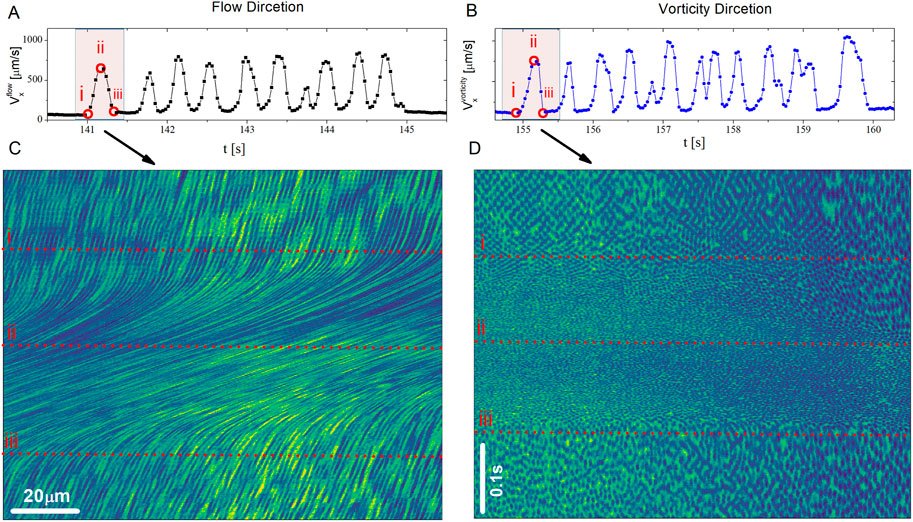
Figure 5. The averaged velocity in the flow direction measured from line scanning in the (A) flow and (B) vorticity directions for the suspension particles at the bottom boundary. (C) and (D) are the corresponding kymographs for the highlighted regions shown in (A) and (B), respectively. The horizontal dashed lines show the specific time points marked by open red squares on the plot of the average $V_x$ in (A) and (B). Results are for the suspension of silica particles ($\varphi =0.54$%) with the applied stress of $200Pa$.

In Figures 5C, D, we show the corresponding kymographs for line scanning in the flow and vorticity directions, respectively, during one spike (highlighted regions in Figures 5A, B). In the case of line scanning in the flow direction (Figure 5C), variations in speed are discernible by changes in the slope of dark lines in the kymograph, representing of particles over time along the direction of flow. In Figure 5C, for $t<i$, we observe clearly defined dark lines with relatively similar slopes, indicating uniform motion of particles along the flow direction. For $i<t<ii$, the slope of the dark lines exhibits a sharp increase, indicating that particles are moving faster. For $ii<t<iii$, the slope of the dark lines shows a gradual decrease, and finally for $t>iii$, one can observe a clear reduction in slope. We also note that the spacing of dark lines can offer insights into the relative distance between particles along the flow direction. A preliminary examination of Figure 5C suggests a noticeable alteration in interparticle spacing during velocity spikes, which may suggest a compression wave as suggested by [17, 21]. However, a detailed quantitative analysis of these variations is beyond the scope of the present study.

For line scanning in the vorticity direction, the change in speed is manifested by the change in the relative size of dark ovals (particles) in the flow direction. A longer oval corresponds to a slower flow, and vice versa. Additionally, as previously mentioned, line scanning in the vorticity direction provides information on the local structure of the suspension in the vorticity-flow plane. As shown in the kymograph of Figure 5D, for $t<i$, particles appear to have arranged in a hexagonal ordered lattice (see Figure 3B and Ref. [1]). For $i<t<ii$, the size of ovals reduces significantly, indicating an increase in particle speed. Moreover, the structure seems to be largely disordered and heterogeneous along the vorticity axis. For $ii<t<iii$, the structure remains disordered but more homogeneous with smaller oval sizes. For $t>iii$, the structure appears still amorphous, but the size of ovals shows a clear increase, indicating a slower flow. Thus by looking at lin scanning measurements along flow and vorticity directions under the same conditions, we can acquire both precise and accurate measurements of the fast, dramatic speed fluctuations (from the flow direction scans) and unambiguous observations of the order/disorder fluctuations associated with the speed fluctuations (from the vorticity direction scans).

Very dense suspensions in the shear-thickening regime: Next, we investigate the flow in a very dense silica suspension ($\varphi =0.58$%) in the shear-thickening regime. Here, we present data only for line scanning in the flow direction. Figure 6A shows the averaged particle speeds at various heights from the bottom boundary. Similar to lower volume fractions, the averaged particle speeds exhibit intermittent spikes during the application of constant stress $(200Pa)$. However, the shape of these spikes is more irregular, indicating an even more complex flow which includes the presence of velocities with negative components in the flow direction ($v_x$ values below the blue dashed lines) at all investigated heights from the bottom boundary. These backflows are manifested by dark lines with negative slopes as seen in regions $i$ and $ii$ for the kymograph during one of the speed spikes (Figure 6B). Note that line scanning in the vorticity direction cannot unambiguously identify backflow, since it operates based on the size of ovals, and there is no way to determine if particles are moving in the positive or negative direction.

Figure 6

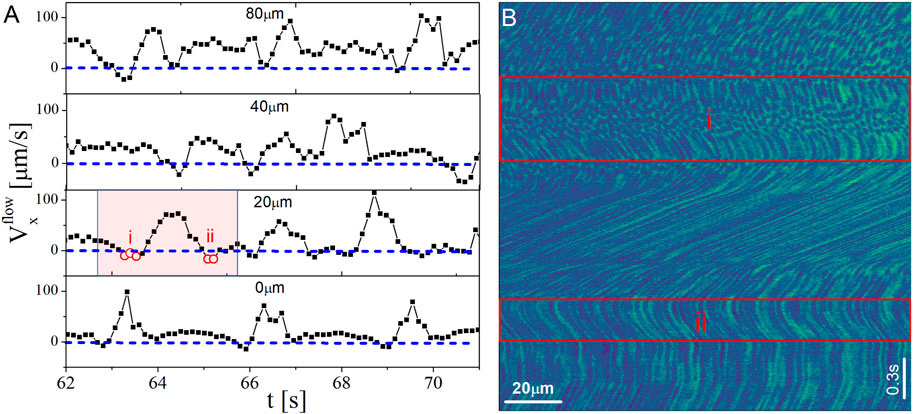
Figure 6. (A) The averaged velocity in the flow direction measured from line scanning in the flow direction at different heights from the bottom plate. (B) The kymograph for the highlighted region shown in (A). The dashed blue lines in (A) highlight zero speeds. The rectangular regions in (B) show the specific time points (negative speeds) marked by open red circles in (A). Results are for the suspension of silica particles ($\varphi =0.58$%) with the applied stress of $200Pa$.

An additional feature evident in the kymograph is that for times before the sharp increase in speed (times before and within region $i$), rather than extended dark lines indicating particles traveling along the scan line, we instead observe ovals, similar to the kymograph patterns captured by line scanning in the vorticity direction. This pattern indicates times when the particle flow field includes significant components orthogonal to the scan direction, so that particles exit the scan line relatively quickly in one of the transverse directions. This observation of non-affine flow is consistent with our previous study on dense cornstarch [17] and calcium carbonate [22] suspensions, where we identified flows in the vorticity direction during the passage of a high-stress front. Thus line scanning in the flow direction reveals a complex flow field in the shear-thickening regime for highly dense suspensions of silica particles, including the presence of backflows and orthogonal flow, highlighting the intricate nature of the flow behavior in such systems.

4 Conclusion

In conclusion, we have introduced a novel approach for precisely measuring particle speeds in fast-flowing suspensions. This approach involves scanning the laser focal point back and forth along the flow direction, effectively tracking the movement of individual particles and enabling the precise determination of their velocities over time. The rapid line scanning process facilitates the measurement of speeds far exceeding those achievable with conventional techniques such as particle tracking or PIV. We have validated our approach under various flow conditions and compared it with measurements from line scanning in the vorticity direction. Although vorticity direction scanning provides information on the local structure in the flow-vorticity plane, it approximates the values of speed since it requires assumptions about the relative interparticle spacings in the vorticity and flow directions. We first compared values of speed obtained by line scanning in the flow and vorticity directions well below the shear-thickening regime where the suspension is expected to experience a simpler flow field. Our direct comparison showed similar flow profiles obtained by both methods. However, line scanning in the vorticity direction was found to overestimate flow speeds. The exact values of the discrepancy between the two methods depends on the structure of the suspension under flow. Near the bottom boundary of the suspension, where there is layering and ordering of particles, this discrepancy was approximately 25%, whereas farther from the bottom plate where the structure becomes largely disordered the difference was smaller (about 15%). In the thickening regime, both methods showed speed fluctuations during the course of shear with quantitative differences ranging from 50% (away from fluctuations) to about 10%–20% (in the middle of the fluctuations). These fluctuations are linked to a loss of order near the bottom boundary. Linescan measurements in the flow direction detected a more complex flow field for very dense suspension of silica particles in the shear-thickening regime, which includes backflow and presence of orthogonal flows, highlighting the intricate nature of the flow behavior in such systems. Our findings underscore the importance of precise speed measurements in understanding suspension dynamics, particularly in contexts where suspensions experience strong nonaffine flows.

5 Materials and methods

Experiments were performed on the suspensions of silica particles with the size of 1.5 $\mu$m (from Angstorm, Inc.) dispersed in an index-matched mixture of water/glycerol (20/80 v/v). To visualize the particles, we added 20 mM fluorescein sodium salt into the suspension. This enabled the untagged spheres to contrast as dark spots against the fluorescent solvent background. Rheological experiments were conducted on an Anton Paar MCR 301 stress-controlled rheometer which is mounted on an inverted Leica SP5 confocal microscope [23]. A parallel plate geometry with a diameter of 5.2 mm and a gap of 170 $\mu$m was used. The linescan measurements along both flow and vorticity directions were taken at 300 $\mu$m from the edge of the plate on a length of 145 $\mu$m using 63$\times$ objective. A typical frame consists of a 2D array, with horizontal dimension being the number of pixels per scan (1,024) along either flow or vorticity directions, and the vertical dimension being the number of lines scanned per frame (1,025 lines). In the shear-thickening regime due to fast flows, the number of scans was reduced to 256.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

EM: Conceptualization, Investigation, Writing–original draft, Writing–review and editing. DB: Conceptualization, Funding acquisition, Supervision, Writing–review and editing. JU: Conceptualization, Funding acquisition, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Science Foundation (NSF) under Grants 1907705 and 2226486.

Acknowledgments

We thank Vikram Rathee and Joia Miller for their initial assistance with the experiments. We also thank Emanuela Del Gado and Peter Olmsted for their insightful discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1480376/full#supplementary-material

References

1. Miller JM, Blair DL, Urbach JS. Order and density fluctuations near the boundary in sheared dense suspensions. Front Phys (2022) 10. doi:10.3389/fphy.2022.991540

CrossRef Full Text | Google Scholar

2. Mewis J, Wagner NJ. Colloidal suspension rheology. Cambridge, United Kingdom: Cambridge University Press (2012).

Google Scholar

3. Morris JF. Shear thickening of concentrated suspensions: recent developments and relation to other phenomena. Annu Rev Fluid Mech (2020) 52:121–44. doi:10.1146/annurev-fluid-010816-060128

CrossRef Full Text | Google Scholar

4. Besseling R, Isa L, Weeks ER, Poon WC. Quantitative imaging of colloidal flows. Adv Colloid Interf Sci (2009) 146:1–17. doi:10.1016/j.cis.2008.09.008

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Koynov K, Butt HJ. Fluorescence correlation spectroscopy in colloid and interface science. Curr Opin Colloid and Interf Sci (2012) 17:377–87. doi:10.1016/j.cocis.2012.09.003

CrossRef Full Text | Google Scholar

6. Dong C, Ren J. Coupling of fluorescence correlation spectroscopy with capillary and microchannel analytical systems and its applications. Electrophoresis (2014) 35:2267–78. doi:10.1002/elps.201300648

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Kunst BH, Schots A, Visser AJ. Detection of flowing fluorescent particles in a microcapillary using fluorescence correlation spectroscopy. Anal Chem (2002) 74:5350–7. doi:10.1021/ac0256742

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Gösch M, Blom H, Holm J, Heino T, Rigler R. Hydrodynamic flow profiling in microchannel structures by single molecule fluorescence correlation spectroscopy. Anal Chem (2000) 72:3260–5. doi:10.1021/ac991448p

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Pan X, Yu H, Shi X, Korzh V, Wohland T. Characterization of flow direction in microchannels and zebrafish blood vessels by scanning fluorescence correlation spectroscopy. J Biomed Opt (2007) 12:014034. doi:10.1117/1.2435173

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Pan X, Shi X, Korzh V, Yu H, Wohland T. Line scan fluorescence correlation spectroscopy for three-dimensional microfluidic flow velocity measurements. J Biomed Opt (2009) 14:024049. doi:10.1117/1.3094947

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Lettinga MP. Colloidal dispersions in shear flow. John Wiley Sons, Inc (2016). p. 81–110.

Google Scholar

12. Chen LB, Zukoski CF, Ackerson BJ, Hanley HJM, Straty GC, Barker J, et al. Structural changes and orientaional order in a sheared colloidal suspension. Phys Rev Lett (1992) 69:688–91. doi:10.1103/physrevlett.69.688

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Holmqvist P, Lettinga MP, Buitenhuis J, Dhont JKG. Crystallization kinetics of colloidal spheres under stationary shear flow. Langmuir (2005) 21:10976–82. doi:10.1021/la051490h

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wu YL, Derks D, van Blaaderen A, Imhof A. Melting and crystallization of colloidal hard-sphere suspensions under shear. Proc Natl Acad Sci (2009) 106:10564–9. doi:10.1073/pnas.0812519106

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Derks D, Wu YL, van Blaaderen A, Imhof A. Dynamics of colloidal crystals in shear flow. Soft Matter (2009) 5:1060. doi:10.1039/b816026k

CrossRef Full Text | Google Scholar

16. Richard D, Speck T. The role of shear in crystallization kinetics: from suppression to enhancement. Scientific Rep (2015) 5:14610. doi:10.1038/srep14610

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Rathee V, Miller J, Blair DL, Urbach JS. Structure of propagating high-stress fronts in a shear-thickening suspension. Proc Natl Acad Sci (2022) 119. doi:10.1073/pnas.2203795119

CrossRef Full Text | Google Scholar

18. Boersma WH, Baets PJM, Laven J, Stein HN. Time-dependent behavior and wall slip in concentrated shear thickening dispersions. J Rheology (1991) 35:1093–120. doi:10.1122/1.550167

CrossRef Full Text | Google Scholar

19. Rathee V, Blair DL, Urbach JS. Localized transient jamming in discontinuous shear thickening. J Rheology (2020) 64:299–308. doi:10.1122/1.5145111

CrossRef Full Text | Google Scholar

20. Rathee V, Blair DL, Urbach JS. Dynamics and memory of boundary stresses in discontinuous shear thickening suspensions during oscillatory shear. Soft Matter (2021) 17:1337–45. doi:10.1039/d0sm01917h

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Rathee V, Blair DL, Urbach JS. Localized stress fluctuations drive shear thickening in dense suspensions. Proc Natl Acad Sci (2017) 114:8740–5. doi:10.1073/pnas.1703871114

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Moghimi E, Urbach JS, Blair DL. Stress and flow inhomogeneity in shear-thickening suspensions. J Colloid Interf Sci (2024) 678:218–25. doi:10.1016/j.jcis.2024.08.099

CrossRef Full Text | Google Scholar

23. Dutta S, Mbi A, Arevalo RC, Blair DL. Development of a confocal rheometer for soft and biological materials. Rev scientific Instr (2013) 84:063702. doi:10.1063/1.4810015

PubMed Abstract | CrossRef Full Text | Google Scholar