- 1Courant Institute of Mathematical Sciences, New York University, New York, NY, United States
- 2NYU-ECNU Institute of Mathematical Sciences at NYU Shanghai, Shanghai, China
- 3Department of Physics and Courant Institute of Mathematical Sciences, New York University, New York, NY, United States
- 4NYU-ECNU Institutes of Physics and Mathematical Sciences at NYU Shanghai, Shanghai, China
- 5Santa Fe Institute, Santa Fe, NM, United States
We show that the notion of critical droplets is central to an understanding of the nature of ground states in the Edwards–Anderson–Ising model of a spin glass in arbitrary dimensions. Given a specific ground state, we suppose that the coupling value for a given edge is varied with all other couplings held fixed. Beyond some specific value of the coupling, a droplet will flip, leading to a new ground state; we refer to this as the critical droplet for that edge and ground state. We show that the distribution of sizes and energies over all edges for a specific ground state can be used to determine which of the leading scenarios for the spin glass phase is correct. In particular, the existence of low-energy interfaces between incongruent ground states, as predicted by replica symmetry breaking, is equivalent to the presence of critical droplets, whose boundaries comprise a positive fraction of edges in the infinite lattice.
1 Introduction
The nature of the low-temperature phase of the Edwards–Anderson (EA) Hamiltonian [1] in finite dimensions
remains unresolved. Here,
There are, at present, four scenarios for the spin glass phase that are consistent both with numerical results and, as far as is currently known, mathematically consistent: replica symmetry breaking (RSB) [2–12], droplet-scaling [13–17], trivial–non-trivial spin overlap (TNT) [18, 19], and chaotic pairs [10, 20–22]. One of the central open questions in spin glass theory is which (if any) of these scenarios is correct and for which dimensions and temperatures.
The differences among the four scenarios at positive temperature are described elsewhere [12, 23, 24]; here, we are concerned with their different predictions at zero temperature, i.e., for the ground-state structure of the EA Hamiltonian. Of the four, two (RSB and chaotic pairs) predict the existence of many ground states, and the other two (droplet-scaling and TNT) predict the existence of only a single pair [17, 25, 26]. Although important, these differences are less fundamental than the nature of the interfaces that separate their ground states from their lowest-lying long-wavelength excitations. The presence or absence of multiplicity of ground states follows as a consequence of the nature of these excitations.
In this paper, we focus on the nature of low-energy long-wavelength excitations above the ground state and how they relate to ground state stability, with a view toward distinguishing different predictions of the four scenarios. Aside from elucidating the different (and potentially testable) predictions of these scenarios, determining the stability properties of the ground state is crucial in determining the low-temperature properties of the spin glass phase, including central questions such as multiplicity of pure states and the presence or absence of an Almeida-Thouless (AT) line [27]. We begin by defining the parameters of the study.
A finite volume
where
2 Interfaces and critical droplets
An interface between two infinite-volume spin configurations
Interfaces can be characterized by their geometry and energy. They can either be “space-filling,” meaning they comprise a positive density of all edges in
Interfaces can also differ by how their energies scale with volume. The energy might diverge (though not monotonically) as one examines interfaces contained within increasingly larger volumes, or it might remain
An excitation above the ground state is any spin configuration obtained by overturning one or more spins in the ground state (while leaving an infinite subset of spins in the original ground state intact); therefore, an interface is the boundary of an excitation. We are primarily interested in excitations consisting of overturning droplets of large, or possibly infinite, size; because an interface is the boundary of such an excitation, the energy of the excitation is simply twice the interface energy. An excitation above a ground state may itself be a new ground state (this would require the excitation to involve overturning an infinite number of spins such that Equation 2 remains satisfied). Indeed, as proven elsewhere [9], an excitation having a space-filling interface with the original ground state may generate a new ground state entirely.
With this in mind, we present the four low-temperature spin glass scenarios in Table 1, which illustrates their various relationships (and clarifies why we consider these four scenarios together).
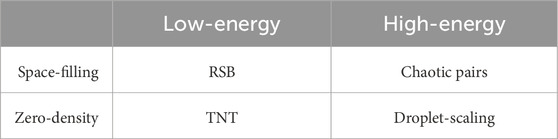
Table 1. Four scenarios described in the text for the low-temperature phase of the EA model, categorized in terms of interface geometry (rows) and energetics (columns). The column headings describe the energy scaling along the interface of the minimal long-wavelength excitations above the ground state predicted by each. Adapted from Figure 1 of [23].
As shown elsewhere [9], the existence of space-filling interfaces in the first row scenarios (RSB and chaotic pairs) implies the presence of multiple GSPs, whereas droplet-scaling and TNT both predict a single GSP [9, 25, 26, 28, 29].
Remarks on Table 1. The droplet-scaling scenario predicts a broad distribution of (free) energies for a minimal energy compact droplet of diameter
We now focus on the concepts of flexibility and critical droplets, which were introduced by Newman et al. [30, 31] and whose properties were described extensively in [24] (see also [26, 32]). Here, we only summarize their main features. We first provide some definitions (all with respect to some fixed coupling realization
Definition 2.1. (Newman et al. [24]) Consider the GSP
Remarks. Critical droplets are defined with respect to edges rather than associated couplings to avoid confusion, given that we often vary the coupling value associated with specific edges, while the edges themselves are fixed, geometric objects.
We define the energy
Definition 2.2. (Newman et al. [24]) The critical value of the coupling
We next define the flexibility
Definition 2.3. (Newman et al. [24]) Let
Remarks. The critical value
It follows from the definitions above and Equation 3 that
Therefore, couplings which share the same critical droplet have the same (strictly positive) flexibility.
A rigorous definition of critical droplets and flexibilities within infinite-volume ground states requires use of the excitation metastate, whose definition and properties are presented in [26, 30, 31, 33]. Here, we simply note that finite-volume critical droplets and their associated flexibilities converge with their properties preserved in the infinite-volume limit, for reasons presented in [24]. This result would be trivial if all critical droplets in infinite-volume ground states were finite. However, it could also be that critical droplets can be infinite in extent in one or more directions, in which case metastates can be used to define such unbounded critical droplets which enclose an infinite subset of spins: they are the infinite-volume limits of critical droplets in finite-volume ground states.
3 Classification of critical droplets
In [24], critical droplets in infinite-volume ground states were classified according to the size of their boundary
There are two kinds of critical droplets with
Finally, there is the possibility that there exist infinite number of critical droplets whose boundary has dimension
Because our ground states are chosen from the zero-temperature PBC metastate (denoted
Theorem 3.1. Let
The method of proof of this theorem is essentially identical to that used in [25, 35] and so will be omitted here. The conclusion is that there is zero probability that a ground state
4 Critical droplets and replica symmetry breaking
In [24], it was shown that there is a close connection between critical droplets and the four scenarios shown in Table 1. However, the results obtained were incomplete for the most prominent of the four scenarios, namely, replica symmetry breaking. In particular, it was proven there that the existence of SFCDs was a sufficient condition for some pairs of incongruent ground states to be separated by space-filling low-energy interfaces, hereafter referred to simply as “RSB interfaces” in accordance with Table 1. However, they were not shown to be necessary. This paper aimed to complete the correspondence between critical droplets and spin glass scenarios by demonstrating that the presence of SFCDs is not only sufficient but also a necessary condition for RSB interfaces to be present.
4.1 Sufficient condition
We first discuss the sufficient condition, which was derived in [24] as Theorem 8.2.
Theorem 4.1. (Newman et al. [24]). If a GSP
We reproduce the proof from reference [24] below.
Proof. In each finite-volume
By assumption, the procedure defined above has a positive probability of generating a positive-density critical droplet, in which case the size of the interface boundary between
Using this procedure, one such edge
4.2 Necessary condition
In [24], it was shown that a necessary condition for the existence of RSB interfaces was the presence of at least one of two kinds of edges. The first of these consists of edges having SFCDs, and the second includes edges without SFCDs, but which lie in the critical droplet boundary of a positive density (in
Using the properties of metastates, Arguin et al. [37] proved the following result for the EA Ising model:
Theorem 4.2. [37]. An edge correlation function
In [34, 35], the authors extended these ideas to a new kind of metastate called the restricted metastate. The idea behind restricted metastates is to start with a conventional metastate, which was constructed using an infinite sequence of volumes with PBCs (
where
However, this can be done (so far) only at positive temperature because of the requirement of coupling covariance. It was shown in [35] (Lemma 4.1) that at positive temperature
Now if RSB interfaces exist, then there must be ground states in the support of
Theorem 4.3. If ground states in the support of the PBC metastate
Following the discussion in Section 12 of [35], we also have the following corollary:
Corollary 4.4. If ground states in the support of the two-dimensional zero-temperature PBC metastate
5 Discussion
Replica symmetry breaking predicts that there exist space-filling, low-energy interfaces between ground states in three and higher dimensions. We have shown that this prediction is equivalent to the presence of SFCDs for a positive density of edges in
Where does this leave the other three scenarios appearing in Table 1? Like RSB, the chaotic pair scenario also predicts the appearance of multiple incongruent ground states separated by space-filling interfaces, but unlike RSB, the interface energy in chaotic pairs scales with
That is,
It follows that neither RSB nor chaotic pairs will hold if
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
CN: conceptualization, formal analysis, investigation, validation, writing–original draft, and writing–review and editing. DS: conceptualization, formal analysis, investigation, validation, writing–original draft, and writing–review and editing.
Funding
The author(s) declare no that financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
The authors thank the two reviewers for their comments on an earlier version, which helped clarify parts of this paper.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Edwards S, Anderson PW. Theory of spin glasses. J Phys F (1975) 5:965–74. doi:10.1088/0305-4608/5/5/017
2. Parisi G. Infinite number of order parameters for spin-glasses. Phys Rev Lett (1979) 43:1754–6. doi:10.1103/physrevlett.43.1754
3. Parisi G. Order parameter for spin-glasses. Phys Rev Lett (1983) 50:1946–8. doi:10.1103/physrevlett.50.1946
4. Mézard M, Parisi G, Sourlas N, Toulouse G, Virasoro M. Nature of the spin-glass phase. Phys Rev Lett (1984) 52:1156–9. doi:10.1103/physrevlett.52.1156
5. Mézard M, Parisi G, Sourlas N, Toulouse G, Virasoro M. Replica symmetry breaking and the nature of the spin glass phase. J Phys (Paris) (1984) 45:843–54. doi:10.1051/jphys:01984004505084300
6. M Mézard, G Parisi, and MA Virasoro, editors. Spin glass theory and beyond. Singapore: World Scientific (1987).
7. Marinari E, Parisi G, Ruiz-Lorenzo JJ, Ritort F. Numerical evidence for spontaneously broken replica symmetry in 3D spin glasses. Phys Rev Lett (1996) 76:843–6. doi:10.1103/physrevlett.76.843
8. Marinari E, Parisi G, Ricci-Tersenghi F, Ruiz-Lorenzo JJ, Zuliani F. J Stat Phys (2000) 98:973–1074. doi:10.1023/a:1018607809852
10. Newman CM, Stein DL. Ordering and broken symmetry in short-ranged spin glasses. Cond Mat (2003) 15:R1319–64. doi:10.1088/0953-8984/15/32/202
11. Read N. Short-range Ising spin glasses: the metastate interpretation of replica symmetry breaking. Phys Rev E (2014) 90:032142. doi:10.1103/physreve.90.032142
12. Newman CM, Read N, Stein DL In: P Charbonneau, E Marinari, M Mézard, G Parisi, F Ricci-Tersenghi, G Sicuroet al. editors Spin glass theory and far beyond: replica symmetry breaking after 40 years. Singapore: World Scientific (2023). p. 697–718.
13. McMillan WL. Scaling theory of Ising spin glasses. J Phys C (1984) 17:3179–87. doi:10.1088/0022-3719/17/18/010
14. Bray AJ, Moore MA. Critical behavior of the three-dimensional Ising spin glass. Phys Rev B (1985) 31:631–3. doi:10.1103/physrevb.31.631
15. Bray AJ, Moore MA. Chaotic nature of the spin-glass phase. Phys Rev Lett (1987) 58:57–60. doi:10.1103/physrevlett.58.57
16. Fisher DS, Huse DA. Ordered phase of short-range ising spin-glasses. Phys Rev Lett (1986) 56:1601–4. doi:10.1103/physrevlett.56.1601
17. Fisher DS, Huse DA. Equilibrium behavior of the spin-glass ordered phase. Phys Rev B (1988) 38:386–411. doi:10.1103/physrevb.38.386
18. Marinari E, Parisi G. Effects of changing the boundary conditions on the ground state of Ising spin glasses. Phys Rev B (2000) 62:11677–85. doi:10.1103/physrevb.62.11677
19. Palassini M, Young AP. Nature of the spin glass state. Phys Rev Lett (2000) 85:3017–20. doi:10.1103/physrevlett.85.3017
20. Newman CM, Stein DL. Spatial inhomogeneity and thermodynamic chaos. Phys Rev Lett (1996) 76:4821–4. doi:10.1103/physrevlett.76.4821
21. Newman CM, Stein DL. Metastate approach to thermodynamic chaos. Phys Rev E (1997) 55:5194–211. doi:10.1103/physreve.55.5194
22. Newman CM, Stein DL. Mathematics of spin glasses and neural networks. Boston: Birkhauser (1998). p. 243–87.
24. Newman CM, Stein DL. Ground-state stability and the nature of the spin glass phase. Phys Rev E (2022) 105:044132. doi:10.1103/physreve.105.044132
25. Newman CM, Stein DL. Interfaces and the question of regional congruence in spin glasses. Phys Rev Lett (2001) 87:077201. doi:10.1103/physrevlett.87.077201
26. Arguin L-P, Newman CM, Stein DL. A relation between disorder chaos and incongruent states in spin glasses on Zd. Commun Math Phys (2019) 367:1019–43. doi:10.1007/s00220-019-03418-3
27. de Almeida JRL, Thouless DJ. Stability of the Sherrington-Kirkpatrick solution of a spin glass model. J Phys A (1978) 11:983–90. doi:10.1088/0305-4470/11/5/028
28. Huse DA, Fisher DS. Pure states in spin glasses. J Phys A (1987) 20:L997–L1003. doi:10.1088/0305-4470/20/15/012
29. Fisher DS, Huse DA. Absence of many states in realistic spin glasses. J Phys A (1987) 20:L1005–10. doi:10.1088/0305-4470/20/15/013
30. Newman CM, Stein DL. Nature of ground state incongruence in two-dimensional spin glasses. Phys Rev Lett (2000) 84:3966–9. doi:10.1103/physrevlett.84.3966
32. Arguin L-P, Newman CM, Stein DL. In: In and out of equilibrium 3: celebrating vladas sidoravicius ME Vares, R Fernandez, LR Fontes, and CM Newman, editors. Cham: Birkhäuser (2021). p. 17–25.
33. Arguin L-P, Damron M, Newman CM, Stein DL. Uniqueness of ground states for short-range spin glasses in the half-plane. Commun Math Phys (2010) 300:641–57. doi:10.1007/s00220-010-1130-8
34. Newman CM, Stein DL. Overlap structure and free energy fluctuations in short-range spin glasses. J Phys A : Math Theor (2024) 57:11LT01. doi:10.1088/1751-8121/ad2b87
36. Aizenman M, Wehr J. Rounding effects of quenched randomness on first-order phase transitions. Commun Math Phys (1990) 130:489–528. doi:10.1007/bf02096933
Keywords: spin glasses, ground states, critical droplets, replica symmetry breaking, ground-state interfaces
Citation: Newman CM and Stein DL (2024) Critical droplets and replica symmetry breaking. Front. Phys. 12:1473378. doi: 10.3389/fphy.2024.1473378
Received: 30 July 2024; Accepted: 24 October 2024;
Published: 14 November 2024.
Edited by:
Stefan Boettcher, Emory University, United StatesReviewed by:
Alberto Fachechi, University of Salento, ItalyTommaso Rizzo, National Research Council (CNR), Italy
Copyright © 2024 Newman and Stein. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: D. L. Stein, ZGFuaWVsLnN0ZWluQG55dS5lZHU=
 C. M. Newman1,2
C. M. Newman1,2 D. L. Stein
D. L. Stein