- School of Biological and Chemical Engineering, Zhejiang University of Science and Technology, Hangzhou, China
In computational chemistry and molecular modeling, the interactions between biomolecules (BMs) and nanomaterials (NMs) play a crucial role in various physical and biological processes, and have significant implications in material discovery and development. While there is extensive literature on free energy calculations for drug-target interactions, reviews specifically addressing BM-NM interactions are relatively scarce. This manuscript aims to fill in this gap by presenting a comprehensive overview of the most widely used and well-established methods for free energy calculations. It provides a detailed analysis of the advantages and limitations of these methods and discusses their applicability to BM-NM systems. This work is intended to offer insights into free energy calculations and serve as a guide for future research in this field.
1 Introduction
The interactions between biomolecules (BMs) and nanomaterials (NMs) are receiving growing research interest due to their diverse applications in fields such as nanomedicine, biosensing, and biocatalysis. BMs, which include nucleic acids, proteins, and carbohydrates [1], interact with various types of NMs, such as 0D quantum dots, 1D nanotubes, 2D nanosheets, and 3D nanocomposites [2]. For example, C3N, an ultra-small nanodot, could effectively disassemble mature Aβ fibrils and hence reduce aggregation-related neuron cytotoxicity both in vitro and in vivo [3]. An ultra-thin MoS2-graphene heterostructure nanopore was shown to prolong the translocation time of λDNA and bovine serum albumin (BSA), while acquiring detailed information about these single molecules [4]. Candida rugosa lipase (CRL) adsorbed onto multi-walled carbon nanotubes has enhanced the production of geranyl propionate, doubling enzyme activity compared to free CRL [5]. Despite these successes, a deeper understanding of molecular interactions often requires the aid of an important in silico method–molecular simulation. This area has rapidly expanded over the years, driven by significant advances in computer power and revolutionized by machine learning techniques. Molecular simulations are especially adept at elucidating underlying molecular mechanisms and predicting unknown molecular properties. They have been extensively applied to study BM-NM interactions, in which free energy serves as an essential quantity to estimate the interaction strength between molecules and evaluate the spontaneity of a physical process. Unfortunately, although free energy calculations are very popular in computer-aided drug design (CADD) to accurately predict the drug-target interactions (DTIs) [6], they generally receive much less attention in BM-NM interactions, due to limited availability of experimental data, lack of standardization in interaction types, and complexity and diversity of NMs [7]. This mini-review focuses on the most widely used computational techniques for free energy calculations specifically for the BM-NM systems, providing readers with a succinct guidance on computing various kinds of free energy.
There are many classifications concerning free energy concepts. First, free energy changes help determine the direction of spontaneous processes. Whilst Helmholtz free energy difference (ΔA) is defined for systems at constant volume, Gibbs free energy difference (ΔG) applies to systems at constant pressure. In molecular simulations of condensed matter systems, the NPT ensemble is generally adopted for production runs, i.e., the number of molecules (N), the pressure (P), and the temperature (T) of the system remain constant during simulations. Consequently, this paper only takes Gibbs free energy into consideration instead of Helmholtz free energy. However, it should be noted that, in such simulations, the volume change ΔV is usually small, making the two free energy measures generally comparable. Second, the binding affinity between BMs and NMs is described using binding free energy, which comes in two forms: absolute binding free energy (ABFE) and relative binding free energy (RBFE). ABFE offers an exact value of the binding free energy between the bound state (e.g., protein-graphene complex) and the unbound states (e.g., free protein and free graphene), to be compared directly with an experimental value. By contrast, RBFE measures the difference in binding free energy between two or more ligands (e.g., proteins) binding to the same receptor (e.g., graphene), to make a comparison between different ligands. The former is typically achieved by molecular dynamics (MD) simulations with enhanced sampling techniques, while the latter is typically achieved by alchemical methods. Thirdly, to calculate free energies, some methods only consider the final bound state, some require the initial and final states, whereas others compute the free energy changes along a reaction coordinate. Accordingly, we categorize free energy calculation methods into three main types: endpoint methods, alchemical methods, and pathway methods.
This paper is organized as follows. In Section 2, we introduce two similar endpoint methods: molecular mechanics/Poisson-Boltzmann surface area (MM/PBSA) and molecular mechanics/generalized Born surface area (MM/GBSA). In Section 3, we discuss in detail three alchemical methods: Free Energy Perturbation (FEP), Thermodynamic Integration (TI), and Bennett Acceptance Ratio (BAR). In Section 4, pathway methods are elaborated including Umbrella Sampling (US), Jarzynski Equality (JE), and Metadynamics (MtD). Their relative advantages and disadvantages are compared, and some examples are illustrated especially for BM-NM systems. Finally, we outline future directions for improvement in free energy calculations.
2 Endpoint methods
MM/PBSA or MM/GBSA In these two similar methods, the binding free energy can be calculated as ΔG = ΔGBN-ΔGB-ΔGN and divided into different contributions using Equation 1:
where ΔEMM is the gas-phase molecular mechanics (MM) energy, which can be decomposed into contributions of the internal energy ΔEint (the sum of ΔEbond, ΔEangle, and ΔEdiheral), the electrostatic energy ΔEele, and the van der Waals energy ΔEvdW; ΔGsol is the solvation free energy, which can be decomposed into the polar solvation energy ΔGsol_polar calculated from either the Poisson-Boltzmann (PB) or generalized Born (GB) model, and the nonpolar contribution ΔGsol_nonpolar estimated by the solvent accessible surface area (SASA); and −TΔS denotes the change in conformational entropy of BMs, normally derived from normal mode analysis. For more detailed information about these two methods, readers are referred to the original works [8–11] and recent review articles [12–14]. Figure 1 provides a typical example of these endpoint methods, illustrating the binding of a peptide drug (ID: 7mll) to a (16,16) carbon nanotube (CNT). Several computational programs specifically designed for these methods are available, such as “g_mmpbsa” [15] and “gmx mmpbsa” [16] for Gromacs, which are popular software tools for modelling BM-NM systems [17]. These programs are user-friendly and facilitate quick access to free energy calculations. Due to their simplicity, straightforward application, and low computational cost, MM/PBSA and MM/GBSA methods have been extensively used in BM-NM systems [18–25]. These methods strike a good balance between accuracy and computational efficiency, making them among the most popular choices for calculating binding free energies. Moreover, the breakdown of energy contributions also provides useful information for further energy analysis.
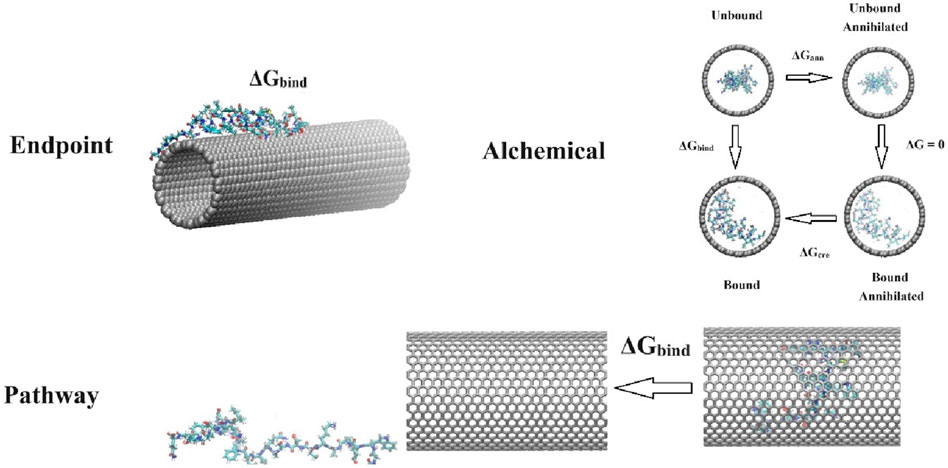
Figure 1. Schematic representations of the simulations typically performed using endpoint methods, alchemical methods, and pathway methods. For endpoint methods, a protein (ID: 7mll) binds to a (16,16) carbon nanotube (CNT). For alchemical methods, the thermodynamic cycle used to calculate the binding free energy between a protein (ID: 1fmh) and a (26,26) CNT (ΔGbind = ΔGann + ΔGcre) is depicted, where ΔGann and ΔGcre represent the free energy required to annihilate and create protein-CNT interactions in the bound and unbound states, respectively. For pathway methods, an external force is exerted on a protein (ID: 1jmq) to pull it away from a (22,22) CNT.
It is important to note that the entropic term −TΔS is not included in binding free energy calculations using “g_mmpbsa” and “gmx mmpbsa”, due to its high computational cost, trivial contributions to the total binding energy between proteins and drugs, and the substantial standard error compared to enthalpic and solvation terms [15, 16]. Consequently, strictly speaking, the binding free energies calculated by these programs are not true ABFE, and their accuracy may vary depending on the system. For instance, when a BM binds to a rigid NM, it may undergo varying degrees of conformational changes, and in some cases, its structure could be significantly altered or even disrupted [26–28]. Nevertheless, these programs are well-suited for calculating RBFE, such as comparing the binding affinities of different amino acid residues to the same material [19]. Recent developments in entropy calculation methods, such as quasi-harmonic approximation [29], interaction entropy [30], and multiscale cell correlation [31], might help address this limitation [32], though further investigation is still required [33]. Another concern over these end-point methods is the use of implicit solvent models for evaluating solvation energy, whereas MD simulations employ explicit water models that significantly influence BM structure and dynamics [34, 35].
3 Alchemical methods
Free Energy Perturbation In 1954, Zwanzig developed the equation for the FEP theory in which the binding free energy was associated with the potential energy difference of two ensemble states 1 and 0 using Equation 2 [36]:
where U1 and U0 are the potential energy of states 1 and 0, respectively; kB is the Boltzmann constant, and T is the temperature. If the initial and final states are only influenced by a small perturbation, state 1 can be considered as the final state and state 0 as the initial state. However, in most situations, state 1 and state 0 have little overlap, and therefore a series of alchemical (nonphysical) intermediate states are created via a coupling parameter λ, which varies from 0 to 1. The potential function for these intermediate states is then achieved using Uλ = λU0 + (1-λ)U1. The total free energy is finally calculated through adding all the free energy differences between successive states through constructed thermodynamic cycle. For more information about FEP, the readers can refer to more recent advances [37–41], review papers [6, 42], as well as real applications [43–47]. Of all the tools to implement FEP, perhaps the most famous is FEP+, which was developed by Schrödinger Inc. [48].
Thermodynamics Integration In 1935, Kirkwood proposed a theory of fluid mixtures, which later became the foundation for the TI method [49]. In this method, the free energy change between two states of the investigated system is connected by a coupling variable λ, being 0 for the initial state and 1 for the final state. By continuously changing λ, a series of intermediate states between the initial and final states are obtained. By sampling these intermediate states, the free energy change is finally calculated using Equation 3:
where Uλ is the potential energy function of the system as a function of λ, and the angle brackets denote an ensemble average at each λ value. The major difference between FEP and TI is that the adjacent states sampled by FEP need to be overlapped in phase space whereas those sampled by TI may not be overlapped [50]. For more information about this method, readers can further refer to many of the classical works [50–55]. To handle the complicated procedure for FEP and TI, some tools were developed based on alchemical transformations specifically for Gromacs [56] and Amber [57].
Bennett Acceptance Ratio In 1976, Bennett introduced an implicit equation obtaining free energy difference by an iterative numerical approach using Equation 4 [58]:
where U1 and U0 are the potential energy of states 1 and 0, respectively. Unlike FEP, BAR requires gathering samples of potential energies for configurations at both states 0 and 1. This method was later extended to the multistate Bennett acceptance ratio (MBAR) method in 2008, which calculates the free energy from multiple states rather than two states [59]. For more information about this method, readers can refer to method comparative studies [60, 61], relevant review papers [62–64], application-focused works [65], and recent developments [66–68].
Figure 1 also illustrates the application of alchemical methods for calculating the binding energies between an α-helical protein (ID: 1fmh) and a (26, 26) CNT. Although alchemical methods are appealing for calculating protein-ligand binding free energies and solvation free energies, they are typically limited to small ligands [35]. Many BMs, however, are macromolecules, and their interactions with NMs can involve multiple binding modes and orientations. This complexity makes it computationally expensive to adequately sample the conformational space needed for converged free energy estimates. Additionally, NMs often have complex and heterogeneous surfaces, and their properties such as hydrophobicity and charge distribution can also complicate the accurate modeling of interactions with BMs. These factors, alongside the unavailability of relevant experimental data, hinder the application of alchemical methods to BM-NM systems. Consequently, we can find a limited quantity of literature reporting the application of FEP, TI, and BAR to BM-NM systems. Shen et al. used TI to investigate the binding free energies of single nucleotides adenine (A) and thymine (T) on CNT inner walls [69]. In this scenario, A and T are relatively small ligands, which may potentially mitigate some of the major limitations associated with using alchemical methods in BM-NM systems. Additionally, alchemical methods could provide insights into how mutations in BMs or changes in NM surface chemistry influence binding and interactions. These methods could also be applied to explore the interactions between small nanoparticles (e.g., fullerene) and BMs during the formation of hybrid functional assemblies [70].
4 Pathway methods
Umbrella Sampling In statistical thermodynamics, the free energy of a system is related to the probability distribution of the system. The free energy difference from state 0 to state 1 can be obtained from the probability distribution of the system in the two states using Equation 5:
where ρ0 and ρ1 are the probability distributions of the system in states 0 and 1. However, for transitions between states that have high energy barriers, the regions near these barriers are poorly sampled. To overcome these challenges, umbrella sampling employs a series of biased simulations, where a harmonic umbrella potential is added to sample configurations within each window along the reaction coordinate ξ [71]. The unbiased free energy profile in the form of potential of mean force (PMF) [72, 73] can be constructed from data in all the windows using the weighted histogram analysis method (WHAM) [74–76]. This method was proposed by Torrie and Valleau in 1977. A typical example using US for protein-ligand interactions can be found here [77], and recent advances are also provided here [72, 78, 79]. In BM-NM systems, the US method can be widely used to compute PME versus ξ with good accuracy despite its high computational cost [26, 80–83]. It can be applied to obtain free energy differences as well as free energy profiles. For example, it was reported that a protein can spontaneously enter carbon nanotubes (CNTs) in aqueous solutions, while releasing it from the tubes is a rare event [84]. Using US, one can easily understand the spontaneity of this encapsulation process by calculating the PMF along the reaction coordinate, where a wide potential well can be clearly observed [26, 80].
Jarzynski Equality JE seeks to relate the free energy differences between two states to the work done during a non-equilibrium transformation between those states. To visit the high free energy regions between states, a possible method is steered molecular dynamics (SMD), in which the harmonic potential guides the system from low free energy regions to high free energy regions. It should be noted that US also uses SMD to build starting configurations along ξ. However, unlike in US sampling where additional harmonic potential is static, the harmonic potential in JE sampling moves at a constant speed over time. By a sufficient number of samples of irreversible work, the free energy difference of the reaction process is directly related to the irreversible work done to the system using Equation 6 [85]:
where W is the irreversible work. This Jarzynski equality, which was proposed in 1997, provides a way to calculate equilibrium free energy differences using non-equilibrium measurements. Further improvements on JE can be found in the literature [86–89]. Figure 1 depicts an example where SMD simulations are used to pull a protein (ID: 1jmq) out of a CNT. In this process, US extracts a series of configurations along the reaction pathway as sampling windows for further biased simulations, while the JE method directly calculates the work done on the protein by integrating the force over the pulling distance. Numerous studies have shown that JE can yield results comparable in accuracy to US when determining free energy for simple systems [54, 90–93]. However, there are some limitations to the JE method. First, the SMD pulling might not always align with the most physically favorable separation pathway required to accurately reproduce the binding affinity. Second, for slightly more complex systems, energy dissipation and the impact of the applied harmonic potential on the conformations of BMs can significantly affect the accuracy of free energy calculations [94–98]. Zhang et al. employed JE to calculate the adsorption free energy of biomolecules on the surface of hydroxyapatite, indicating that the structured water layer at the solid-liquid interface causes SMD simulations to produce a large amount of dissipative work [98]. They further proposed a hybrid scheme combining JE with US to address this issue.
Metadynamics MtD, similar to US and JE, uses an additional potential to sample high free energy regions of the system. However, unlike the other two methods, MtD operates by applying a time-dependent biasing potential to selected collective variables (CVs). The biasing potential is periodically introduced through the periodic addition of Gaussian-shaped repulsive potentials to the overall potential energy of the system. This prevents the system from revisiting areas of the reaction coordinate, and continually drives the system towards higher free energy regions. Ultimately, free energy can be calculated based on the series of repulsive potentials using Equation 7:
where Gi is the height of the ith Gaussian, si is the position of the ith Gaussian in CV space, and σ is the width of the Gaussian functions. This method, proposed by Laio and Parrinello in 2002 [99], offers several advantages for calculating free energy. Unlike US and JE, MtD does not require the prior determination of the reaction pathway. Instead, it accelerates the sampling of high free energy events by gradually pushing the system from low to high free energy regions through a series of added repulsive potentials. MtD is especially useful for high-dimensional free energy calculations, such as two-dimensional free energy surfaces. Consequently, it has become widely used to map the free energy landscape of protein-ligand interactions, and can be easily extended to BM-NM systems, even though the number of such studies has still been small so far. MtD can be implemented using the portable plugin PLUMED [100]. For more details, the readers are asked to see more review papers [101–104]. NM-BM systems often involve rare events, such as the dissociation of a protein from its binding NM. MtD can enhance the sampling of these events, which might be difficult to capture using conventional MD simulations. An example of using MtD to calculate the binding free energy between P-glycoprotein and two drugs, paclitaxel and doxorubicin, is presented here [105], which can also be extended to BM-NM interactions. However, the success of MtB depends on the selection of CVs, biasing potentials, and the complex interpretation of data, making it more suitable for experienced users. Also, the application of MtD to large BMs demands substantial computational resources. These drawbacks underscore the necessity for continued improvements in this method.
5 Future prospects
Free energy methods can accurately predict the interaction strength between BMs and NMs. Table 1 summarizes highlights and limitations of all the methods discussed within this paper. Future research should address several key areas to enhance these methods. First, improving and optimizing force fields are crucial for achieving accurate free energy calculations. Second, the development of more user-friendly software and programs is needed to make these methods more accessible and commercially viable. Third, while many end-to-end DTI models can precisely predict protein-ligand interactions [106–108], there is a need for extensive investigation into the application of machine learning to BM-NM interactions.
Author contributions
HF: Writing–original draft. YZ: Funding acquisition, Supervision, Writing–review and editing. QC: Conceptualization, Supervision, Writing–review and editing, Writing–original draft.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by Zhejiang Provincial Natural Science Foundation of China under Grant No. LY19B060002.
Acknowledgments
The authors acknowledge the Beijing Beilong Super Cloud Computing Co., Ltd. for providing HPC resources that have contributed to the research results reported within this paper.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Karplus M, McCammon JA. Molecular dynamics simulations of biomolecules. Nat Struct Mol Biol (2002) 9:646–52. doi:10.1038/nsb0902-646
2. Mekuye B, Abera B. Nanomaterials: an overview of synthesis, classification, characterization, and applications. Nano Select (2023) 4:486–501. doi:10.1002/nano.202300038
3. Yin X, Zhou H, Zhang M, Su J, Wang X, Li S, et al. C3N nanodots inhibits Aβ peptides aggregation pathogenic path in Alzheimer’s disease. Nat Commun (2023) 14:5718. doi:10.1038/s41467-023-41489-y
4. Gu C, Yu Z, Li X, Zhu X, Jin C, Cao Z, et al. Experimental study on single biomolecule sensing using MoS(2)-graphene heterostructure nanopores. Nanoscale (2022) 15:266–74. doi:10.1039/d2nr04485d
5. Mohamad NR, Buang NA, Mahat NA, Lok YY, Huyop F, Aboul-Enein HY, et al. A facile enzymatic synthesis of geranyl propionate by physically adsorbed Candida rugosa lipase onto multi-walled carbon nanotubes. Enzyme Microb Technol (2015) 72:49–55. doi:10.1016/j.enzmictec.2015.02.007
6. Song LF, Merz KM. Evolution of alchemical free energy methods in drug discovery. J Chem Inf Model (2020) 60:5308–18. doi:10.1021/acs.jcim.0c00547
7. Yan X, Yue T, Winkler DA, Yin Y, Zhu H, Jiang G, et al. Converting nanotoxicity data to information using artificial intelligence and simulation. Chem Rev (2023) 123:8575–637. doi:10.1021/acs.chemrev.3c00070
8. Homeyer N, Gohlke H. Free energy calculations by the molecular mechanics Poisson-Boltzmann surface area method. J Chem Inf Model (2012) 31(2):114–22. doi:10.1002/minf.201100135
9. Massova I, Kollman PA. Combined molecular mechanical and continuum solvent approach (MM-PBSA/GBSA) to predict ligand binding. Perspect Drug Discov Des (2000) 18:113–35. doi:10.1023/A:1008763014207
10. Wong S, Amaro RE, McCammon JA. MM-PBSA captures key role of intercalating water molecules at a protein-protein interface. J Chem Theor Comput (2009) 5:422–9. doi:10.1021/ct8003707
11. Srinivasan J, Cheatham TE, Cieplak P, Kollman PA, Case DA. Continuum solvent studies of the stability of DNA, RNA, and phosphoramidate-DNA helices. J Am Chem Soc (1998) 120:9401–9. doi:10.1021/ja981844+
12. Wang C, Greene D, Xiao L, Qi R, Luo R. Recent developments and applications of the MMPBSA method. Front Mol Biosci (2017) 4:87. doi:10.3389/fmolb.2017.00087
13. Wang E, Sun H, Wang J, Wang Z, Liu H, Zhang JZH, et al. End-point binding free energy calculation with MM/PBSA and MM/GBSA: strategies and applications in drug design. Chem Rev (2019) 119:9478–508. doi:10.1021/acs.chemrev.9b00055
14. Tuccinardi T. What is the current value of MM/PBSA and MM/GBSA methods in drug discovery? Expert Opin Drug Discov (2021) 16:1233–7. doi:10.1080/17460441.2021.1942836
15. Kumari R, Kumar R, Consortium OSDD, Lynn A. g_mmpbsa – a GROMACS tool for high-throughput MM-PBSA calculations. J Chem Inf Model (2014) 54:1951–62. doi:10.1021/ci500020m
16. Valdes-Tresanco MS, Valdes-Tresanco ME, Valiente PA, Moreno E. gmx_MMPBSA: a new tool to perform end-state free energy calculations with GROMACS. J Chem Theor Comput (2021) 17:6281–91. doi:10.1021/acs.jctc.1c00645
17. Pronk S, Páll S, Schulz R, Larsson P, Bjelkmar P, Apostolov R, et al. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics (2013) 29:845–54. doi:10.1093/bioinformatics/btt055
18. Guo J, Yao X, Ning L, Wang Q, Liu H. The adsorption mechanism and induced conformational changes of three typical proteins with different secondary structural features on graphene. RSC Adv (2014) 4:9953–62. doi:10.1039/c3ra45876h
19. Lan J, Peng Y, Liang L, Duan X, Kong Z, Zhang L, et al. Theoretical study of protein adsorption on graphene/h-BN heterostructures. Phys Chem Chem Phys (2023) 25:31206–21. doi:10.1039/d3cp03303a
20. Yin YW, Ma YQ, Ding HM. Effect of nanoparticle curvature on its interaction with serum proteins. Langmuir (2024) 40:15205–13. doi:10.1021/acs.langmuir.4c01642
21. Choodet C, Toomjeen P, Chuaephon A, Phanchai W, Srikulwong U, Wiwasuku T, et al. Polymeric nanoparticles engineered for optimal drug delivery using atomistic computational simulation. ACS Appl Nano Mater (2024) 7:19698–708. doi:10.1021/acsanm.4c03894
22. Rasoolzadeh R, Baptista L, Vajedi FS, Nikoofard V. Molecular insights into the binding and conformational changes of hepcidin25 blood peptide with 4-aminoantipyrine and their sorption mechanism by carboxylic-functionalized multiwalled carbon nanotubes: a comprehensive spectral analysis and molecular dynamics simulation study. ACS Omega (2024) 9:35821–36. doi:10.1021/acsomega.4c04515
23. Cao Y, Qiao Y, Cui S, Ge J. Origin of metal cluster tuning enzyme activity at the bio-nano interface. JACS Au (2022) 2:961–71. doi:10.1021/jacsau.2c00077
24. Sittiwanichai S, Archapraditkul C, Japrung D, Shigeta Y, Mori T, Pongprayoon P. Aggregation of apo/glycated human serum albumins and aptamer-saturated graphene quantum dot: a simulation study. Biochemistry (2024) 63:1697–707. doi:10.1021/acs.biochem.4c00155
25. Zhu L, Wang G, Zhu X, Zhang Q, Qian Z. Destabilization of human islet amyloid polypeptide fibrils by charged graphene quantum dots: a molecular dynamics investigation with implications for nanomedicine. ACS Appl Nano Mater (2023) 6:9649–56. doi:10.1021/acsanm.3c01332
26. Chen Q, Zhou J, Sun R. Carbon nanotube loading strategies for peptide drugs: insights from molecular dynamics simulations. Langmuir (2024) 40:13515–26. doi:10.1021/acs.langmuir.4c00973
27. Ling Y, Gu Z, Kang S, Luo J, Zhou R. Structural damage of a β-sheet protein upon adsorption onto molybdenum disulfide nanotubes. J Phys Chem C (2016) 120:6796–803. doi:10.1021/acs.jpcc.5b11236
28. Kang Y, Liu YC, Wang Q, Shen JW, Wu T, Guan WJ. On the spontaneous encapsulation of proteins in carbon nanotubes. Biomaterials (2009) 30:2807–15. doi:10.1016/j.biomaterials.2009.01.024
29. Pereira GP, Cecchini M. Multibasin quasi-harmonic approach for the calculation of the configurational entropy of small molecules in solution. J Chem Theor Comput (2021) 17:1133–42. doi:10.1021/acs.jctc.0c00978
30. Duan L, Liu X, Zhang JZH. Interaction entropy: a new paradigm for highly efficient and reliable computation of protein-ligand binding free energy. J Am Chem Soc (2016) 138:5722–8. doi:10.1021/jacs.6b02682
31. Chakravorty A, Higham J, Henchman RH. Entropy of proteins using multiscale cell correlation. J Chem Inf Model (2020) 60:5540–51. doi:10.1021/acs.jcim.0c00611
32. Menzer WM, Li C, Sun W, Xie B, Minh DDL. Simple entropy terms for end-point binding free energy calculations. J Chem Theor Comput (2018) 14:6035–49. doi:10.1021/acs.jctc.8b00418
33. Ekberg V, Ryde U. On the use of interaction entropy and related methods to estimate binding entropies. J Chem Theor Comput (2021) 17:5379–91. doi:10.1021/acs.jctc.1c00374
34. Zhang C, Li X, Wang Z, Huang X, Ge Z, Hu B. Influence of structured water layers on protein adsorption process: a case study of cytochrome c and carbon nanotube interactions and its implications. J Phys Chem B (2020) 124:684–94. doi:10.1021/acs.jpcb.9b10192
35. Blazhynska M, Goulard Coderc de Lacam E, Chen H, Roux B, Chipot C. Hazardous shortcuts in standard binding free energy calculations. J Phys Chem Lett (2022) 13:6250–8. doi:10.1021/acs.jpclett.2c01490
36. Zwanzig RW. High-temperature equation of state by a perturbation method. I. Nonpolar gases. J Chem Phys (1954) 22:1420–6. doi:10.1063/1.1740409
37. Chen H, Maia JDC, Radak BK, Hardy DJ, Cai W, Chipot C, et al. Boosting free-energy perturbation calculations with GPU-accelerated NAMD. J Chem Inf Model (2020) 60:5301–7. doi:10.1021/acs.jcim.0c00745
38. Irwin BWJ, Huggins DJ. Estimating atomic contributions to hydration and binding using free energy perturbation. J Chem Theor Comput (2018) 14:3218–27. doi:10.1021/acs.jctc.8b00027
39. Jiang W, Chipot C, Roux B. Computing relative binding affinity of ligands to receptor: an effective hybrid single-dual-topology free-energy perturbation approach in NAMD. J Chem Inf Model (2019) 59:3794–802. doi:10.1021/acs.jcim.9b00362
40. Jiang W, Roux B. Free energy perturbation Hamiltonian replica-exchange molecular dynamics (FEP/H-REMD) for absolute ligand binding free energy calculations. J Chem Theor Comput (2010) 8:2559–65. doi:10.1021/ct1001768
41. de Oliveira C, Yu HS, Chen W, Abel R, Wang L. Rigorous free energy perturbation approach to estimating relative binding affinities between ligands with multiple protonation and tautomeric states. J Chem Theor Comput (2019) 15:424–35. doi:10.1021/acs.jctc.8b00826
42. Kollman P. Free energy calculations: applications to chemical and biochemical phenomena. Chem Rev (1993) 93:2395–417. doi:10.1021/cr00023a004
43. Chen J, Wang X, Pang L, Zhang JZH, Zhu T. Effect of mutations on binding of ligands to guanine riboswitch probed by free energy perturbation and molecular dynamics simulations. Nucleic Acids Res (2019) 47:6618–31. doi:10.1093/nar/gkz499
44. Ciordia M, Perez-Benito L, Delgado F, Trabanco AA, Tresadern G. Application of free energy perturbation for the design of BACE1 inhibitors. J Chem Inf Model (2016) 56:1856–71. doi:10.1021/acs.jcim.6b00220
45. Jorgensen WL. Free energy calculations: a breakthrough for modeling organic chemistry in solution. Acc Chem Res (1989) 22:184–9. doi:10.1021/ar00161a004
46. Wade AD, Rizzi A, Wang Y, Huggins DJ. Computational fluorine scanning using free-energy perturbation. J Chem Inf Model (2019) 59:2776–84. doi:10.1021/acs.jcim.9b00228
47. Moraca F, Negri A, de Oliveira C, Abel R. Application of free energy perturbation (FEP+) to understanding ligand selectivity: a case study to assess selectivity between pairs of phosphodiesterases (PDE’s). J Chem Inf Model (2019) 59:2729–40. doi:10.1021/acs.jcim.9b00106
48. Wang L, Wu Y, Deng Y, Kim B, Pierce L, Krilov G, et al. Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field. J Am Chem Soc (2015) 137:2695–703. doi:10.1021/ja512751q
49. Kirkwood JG. Statistical mechanics of fluid mixtures. J Chem Phys (1935) 3:300–13. doi:10.1063/1.1749657
50. Wescott JT, Fisher LR, Hanna S. Use of thermodynamic integration to calculate the hydration free energies of n-alkanes. J Chem Phys (2002) 116:2361–9. doi:10.1063/1.1431588
51. Chipot C, Kollman PA, Pearlman DA. Alternative approaches to potential of mean force calculations: free energy perturbation versus thermodynamic integration. Case study of some representative nonpolar interactions. J Comput Chem (1996) 17:1112–31. doi:10.1002/(SICI)1096-987X(19960715)17:9<1112::AID-JCC4>3.0.CO;2-V
52. Mezei M. The finite difference thermodynamic integration, tested on calculating the hydration free energy difference between acetone and dimethylamine in water. J Chem Phys (1987) 86:7084–8. doi:10.1063/1.452357
53. Riniker S, Christ CD, Hansen N, Mark AE, Nair PC, van Gunsteren WF. Comparison of enveloping distribution sampling and thermodynamic integration to calculate binding free energies of phenylethanolamine n-methyltransferase inhibitors. J Chem Phys (2011) 135:024105. doi:10.1063/1.3604534
54. Rodriguez-Gomez D, Darve E, Pohorille A. Assessing the efficiency of free energy calculation methods. J Chem Phys (2004) 120:3563–78. doi:10.1063/1.1642607
55. Straatsma TP, Berendsen HJC. Free energy of ionic hydration: analysis of a thermodynamic integration technique to evaluate free energy differences by molecular dynamics simulations. J Chem Phys (1988) 89:5876–86. doi:10.1063/1.455539
56. Gapsys V, Perez-Benito L, Aldeghi M, Seeliger D, van Vlijmen H, Tresadern G, et al. Large scale relative protein ligand binding affinities using non-equilibrium alchemy. Chem Sci (2019) 11:1140–52. doi:10.1039/c9sc03754c
57. Lee TS, Allen BK, Giese TJ, Guo Z, Li P, Lin C, et al. Alchemical binding free energy calculations in AMBER20: advances and best practices for drug discovery. J Chem Inf Model (2020) 60:5595–623. doi:10.1021/acs.jcim.0c00613
58. Bennett CH. Efficient estimation of free energy differences from Monte Carlo data. J Comput Phys (1976) 22:245–68. doi:10.1016/0021-9991(76)90078-4
59. Shirts MR, Chodera JD. Statistically optimal analysis of samples from multiple equilibrium states. J Chem Phys (2008) 129:124105. doi:10.1063/1.2978177
60. Bruckner S, Boresch S. Efficiency of alchemical free energy simulations. I. A practical comparison of the exponential formula, thermodynamic integration, and Bennett’s acceptance ratio method. J Comput Chem (2011) 32:1303–19. doi:10.1002/jcc.21713
61. de Ruiter A, Boresch S, Oostenbrink C. Comparison of thermodynamic integration and Bennett acceptance ratio for calculating relative protein-ligand binding free energies. J Comput Chem (2013) 34:1024–34. doi:10.1002/jcc.23229
62. Pohorille A, Jarzynski C, Chipot C. Good practices in free-energy calculations. J Phys Chem B (2010) 114:10235–53. doi:10.1021/jp102971x
63. Matsunaga Y, Kamiya M, Oshima H, Jung J, Ito S, Sugita Y. Use of multistate Bennett acceptance ratio method for free-energy calculations from enhanced sampling and free-energy perturbation. Biophys Rev (2022) 14:1503–12. doi:10.1007/s12551-022-01030-9
64. Christ CD, Mark AE, van Gunsteren WF. Basic ingredients of free energy calculations: a review. J Comput Chem (2010) 31:1569–82. doi:10.1002/jcc.21450
65. Gutierrez M, Vallejos GA, Cortes MP, Bustos C. Bennett acceptance ratio method to calculate the binding free energy of BACE1 inhibitors: theoretical model and design of new ligands of the enzyme. Chem Biol Drug Des (2019) 93:1117–28. doi:10.1111/cbdd.13456
66. Ding X, Zhang B. DeepBAR: a fast and exact method for binding free energy computation. J Phys Chem Lett (2021) 12:2509–15. doi:10.1021/acs.jpclett.1c00189
67. Ding X. Bayesian multistate Bennett acceptance ratio methods. J Chem Theor Comput (2024) 20:1878–88. doi:10.1021/acs.jctc.3c01212
68. Giese TJ, Ekesan S, York DM. Extension of the variational free energy profile and multistate Bennett acceptance ratio methods for high-dimensional potential of mean force profile analysis. J Phys Chem A (2021) 125:4216–32. doi:10.1021/acs.jpca.1c00736
69. Shen J, Tang Y, Wei X, Zheng W, Sun T, Zhang Z, et al. On the loading mechanism of ssDNA into carbon nanotubes. RSC Adv (2015) 5:56896–903. doi:10.1039/c5ra01941a
70. Jana SK, Som NN, Jha PK. Size-dependent fullerenes for enhanced interaction of l-leucine: a combined DFT and MD simulations approach. Langmuir (2024) 40(40):13844–59. doi:10.1021/acs.langmuir.4c00806
71. Lu H, Schulten K. The key event in force-induced unfolding of titin’s immunoglobulin domains. Biophys J (2000) 79:51–65. doi:10.1016/S0006-3495(00)76273-4
72. You W, Tang Z, Chang CA. Potential mean force from umbrella sampling simulations: what can we learn and what is missed? J Chem Theor Comput (2019) 15:2433–43. doi:10.1021/acs.jctc.8b01142
73. Roux B. The calculation of the potential of mean force using computer simulations. Comput Phys Com (1995) 91:275–82. doi:10.1016/0010-4655(95)00053-I
74. Torrie GM, Valleau JP. Monte Carlo free energy estimates using non-Boltzmann sampling: application to the sub-critical Lennard-Jones fluid. Chem Phys Lett (1974) 28:578–81. doi:10.1016/0009-2614(74)80109-0
75. Torrie GM, Valleau JP. Nonphysical sampling distributions in Monte Carlo free-energy estimation: umbrella sampling. J Comput Phys (1977) 23:187–99. doi:10.1016/0021-9991(77)90121-8
76. Souaille M, Roux B. Extension to the weighted histogram analysis method: combining umbrella sampling with free energy calculations. Comput Phys Com (2001) 135:40–57. doi:10.1016/S0010-4655(00)00215-0
77. Lemkul JA, Bevan DR. Assessing the stability of alzheimer’s amyloid protofibrils using molecular dynamics. J Phys Chem B (2010) 114:1652–60. doi:10.1021/jp9110794
78. Govind Kumar V, Polasa A, Agrawal S, Kumar TKS, Moradi M. Binding affinity estimation from restrained umbrella sampling simulations. Nat Comput Sci (2023) 3:59–70. doi:10.1038/s43588-022-00389-9
80. Zhang Z, Kang Y, Liang L, Liu Y, Wu T, Wang Q. Peptide encapsulation regulated by the geometry of carbon nanotubes. Biomaterials (2014) 35:1771–8. doi:10.1016/j.biomaterials.2013.11.041
81. Sahoo AK, Kanchi S, Mandal T, Dasgupta C, Maiti PK. Translocation of bioactive molecules through carbon nanotubes embedded in the lipid membrane. ACS Appl Mater Inter (2018) 10:6168–79. doi:10.1021/acsami.7b18498
82. Chen J, Song Z, Yang J. Whether carbon nanotubes are suitable for delivering small drugs with aromatic rings through non-covalent adsorption? J Mol Liq (2023) 378:121595. doi:10.1016/j.molliq.2023.121595
83. Chen J, Mao D, Wang X, Zhou G, Zeng S, Chen L, et al. Encapsulation and release of drug molecule pregabalin based on ultrashort single-walled carbon nanotubes. J Phys Chem C (2019) 123:9567–74. doi:10.1021/acs.jpcc.9b00675
84. Chen Q, Liang L, Zhang Z, Wang Q. Release of an encapsulated peptide from carbon nanotubes driven by electric fields: a molecular dynamics study. ACS Omega (2021) 6:27485–90. doi:10.1021/acsomega.1c04436
85. Jarzynski C. Nonequilibrium equality for free energy differences. Phys Rev Lett (1997) 78:2690–3. doi:10.1103/PhysRevLett.78.2690
86. Crooks GE. Path-ensemble averages in systems driven far from equilibrium. Phys Rev E (2000) 61:2361–6. doi:10.1103/PhysRevE.61.2361
87. Hummer G, Szabo A. Free energy reconstruction from nonequilibrium single-molecule pulling experiments. Proc Natl Acad Sci U S A (2001) 98:3658–61. doi:10.1073/pnas.071034098
88. Park S, Khalili-Araghi F, Tajkhorshid E, Schulten K. Free energy calculation from steered molecular dynamics simulations using Jarzynski’s equality. J Chem Phys (2003) 119:3559–66. doi:10.1063/1.1590311
89. Park S, Schulten K. Calculating potentials of mean force from steered molecular dynamics simulations. J Chem Phys (2004) 120:5946–61. doi:10.1063/1.1651473
90. Oostenbrink C, van Gunsteren WF. Calculating zeros: non-equilibrium free energy calculations. Chem Phys (2006) 323:102–8. doi:10.1016/j.chemphys.2005.08.054
91. Oberhofer H, Dellago C, Geissler PL. Biased sampling of nonequilibrium trajectories: can fast switching simulations outperform conventional free energy calculation methods? J Phys Chem B (2005) 109:6902–15. doi:10.1021/jp044556a
92. Lua RC, Grosberg AY. Practical applicability of the Jarzynski relation in statistical mechanics: a pedagogical example. J Phys Chem B (2005) 109:6805–11. doi:10.1021/jp0455428
93. Ytreberg FM, Zuckerman DM. Efficient use of nonequilibrium measurement to estimate free energy differences for molecular systems. J Comput Chem (2004) 25:1749–59. doi:10.1002/jcc.20103
94. Kang Y, Wang Q, Liu Y, Shen J, Wu T. Diameter selectivity of protein encapsulation in carbon nanotubes. J Phys Chem B (2010) 114:2869–75. doi:10.1021/jp905995s
95. Kato M, Pisliakov AV, Warshel A. The barrier for proton transport in aquaporins as a challenge for electrostatic models: the role of protein relaxation in mutational calculations. Proteins (2006) 64:829–44. doi:10.1002/prot.21012
96. Bastug T, Chen PC, Patra SM, Kuyucak S. Potential of mean force calculations of ligand binding to ion channels from Jarzynski's equality and umbrella sampling. J Chem Phys (2008) 128:155104. doi:10.1063/1.2904461
97. Warshel A, Sharma PK, Kato M, Parson WW. Modeling electrostatic effects in proteins. Biochim Biophys Acta (2006) 1764:1647–76. doi:10.1016/j.bbapap.2006.08.007
98. Zhang Z, Wu T, Wang Q, Pan H, Tang R. Impact of interfacial high-density water layer on accurate estimation of adsorption free energy by Jarzynski’s equality. J Chem Phys (2014) 140:034706. doi:10.1063/1.4858428
99. Laio A, Parrinello M. Escaping free-energy minima. Proc Natl Acad Sci USA (2002) 99:12562–6. doi:10.1073/pnas.202427399
100. Bonomi M, Branduardi D, Bussi G, Camilloni C, Provasi D, Raiteri P, et al. PLUMED: a portable plugin for free-energy calculations with molecular dynamics. Comput Phys Comm (2009) 180:1961–72. doi:10.1016/j.cpc.2009.05.011
101. Leone V, Marinelli F, Carloni P, Parrinello M. Targeting biomolecular flexibility with metadynamics. Curr Opin Struct Biol (2010) 20:148–54. doi:10.1016/j.sbi.2010.01.011
102. Barducci A, Bonomi M, Parrinello M. Metadynamics. Wires Comput Mol Sci (2011) 1:826–43. doi:10.1002/wcms.31
103. Laio A, Gervasio FL. Metadynamics: a method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science. Rep Prog Phys (2008) 71:126601. doi:10.1088/0034-4885/71/12/126601
104. Bussi G, Laio A. Using metadynamics to explore complex free-energy landscapes. Nat Rev Phys (2020) 2:200–12. doi:10.1038/s42254-020-0153-0
105. Zhang J, Li D, Sun T, Liang L, Wang Q. Interaction of P-glycoprotein with anti-tumor drugs: the site, gate and pathway. Soft Matter (2015) 11:6633–41. doi:10.1039/c5sm01028d
106. Wang L, Zhou Y, Chen Q. AMMVF-DTI: a novel model predicting drug-target interactions based on attention mechanism and multi-view fusion. Int J Mol Sci (2023) 24:14142. doi:10.3390/ijms241814142
107. Qi X, Zhao Y, Qi Z, Hou S, Chen J. Machine learning empowering drug discovery: applications, opportunities and challenges. Molecules (2024) 29:903. doi:10.3390/molecules29040903
Keywords: MM/PBSA, free energy perturbation (FEP), thermodynamic integration, Bennett acceptance ratio (BAR), umbrella sampling (US), Jarzynski equality, Metadynamics, free energy calculations
Citation: Fu H, Zhu Y and Chen Q (2024) Free energy calculations in biomolecule-nanomaterial interactions. Front. Phys. 12:1469515. doi: 10.3389/fphy.2024.1469515
Received: 24 July 2024; Accepted: 03 September 2024;
Published: 13 September 2024.
Edited by:
Maksudbek Yusupov, Academy of Sciences Republic of Uzbekistan (UzAS), UzbekistanReviewed by:
Süleyman Selim Çınaroğlu, Faculty of Engineering, Ege University, TürkiyeCopyright © 2024 Fu, Zhu and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qu Chen, Y2hlbnF1QHp1c3QuZWR1LmNu
 Hongze Fu
Hongze Fu Qu Chen
Qu Chen