- 1Department of Physics, University of Jyväskylä, Jyväskylä, Finland
- 2International Centre for Advanced Training and Research in Physics (CIFRA), Magurele, Romania
- 3Horia Hulubei National Institute of Physics and Nuclear Engineering (IFIN HH), Magurele, Romania
Experimental and theoretical studies of
1 Introduction
Search for beyond-the-standard-model (BSM) physics involves typically rare-events experiments measuring single and double beta decays [2, 9, 14, 15]. In particular, the neutrinoless double beta
It is important to note that the
The quenching of
The enhanced SSM and the SMM exploit yet an extra degree of freedom, the so-called small relativistic NME (sNME) in order to fit simultaneously the measured (partial) half-life and the
As mentioned earlier, the reactor antineutrino spectra need to be addressed both theoretically and experimentally. This needs measurements of the total
In our present work we investigate five more interesting cases where the total
2 Outline of the theoretical aspects
The half-life of a
where
where the lowercase
Fortunately, the highly complex shape function
where
2.1 β- spectral shapes and their dependency on the small relativistic NMEs
The small relativistic NME (sNME) plays a crucial role in the combined analysis of beta spectral shapes and partial half-lives (branching ratios) [31, 33, 35, 48]. In these studies, the sNME is used as a fitting parameter alongside
Ideally, with infinite valence spaces and a perfect nuclear many-body theory, the sNME value is linked to the large vector NME (l-NME) by the Conserved Vector Current (CVC) hypothesis [8]. This relationship is expressed as:
where the left side represents the sNME, and the right side involves the l-NME, with
In our
The quadratic dependence of the computed half-lives on the sNME value results in two sNME values for each decay transition that reproduce the experimental half-life. In some cases, only complex-conjugate pairs of solutions exist, indicating that the experimental data cannot be reproduced with the adopted NSM Hamiltonian. One of these two sNMEs is closer to the CVC value, often defining the “optimal” beta spectral shape. By choosing the sNME value closest to its CVC value, we obtain the most probable spectral shape for a given
Therefore, while the “optimal” choice of sNMEs can be theoretically justified, its true validation depends on experimental data. Future experimental efforts are necessary to confirm whether this theoretical choice accurately represents the physical processes occurring during
2.2 Nuclear shell-model computations
The NSM calculations were performed using the software KSHELL [54] with the following Hamiltonians: ca48mh1, used in [53]; fpg9tb [56], obtained by modifying the two-body matrix elements in the fpg interaction [55] to fit Nickel isotopes; gxpf1a [25] and gxpf1b [26], derived from the Bonn-C potential and fitting the single-particle energies and two-body matrix elements to nuclei in the fp-region; the semi-bare G-Matrix effective interaction glekpn [38]; jj45pnb, a two-nucleon potential with a perturbative G-matrix approach, with the Coulomb single-particle energies adjusted to reproduce recent results in [37]; and SVD, a CD-Bonn nucleon-nucleon potential with the single-particle energies fitted to the region
For the
For the
Finally, the SVD model space, used for
3 Results and analyses
3.1 Nuclear observables
To assess the reliability of our adopted nuclear wave functions, we first calculate their electromagnetic properties, specifically the electric quadrupole moments
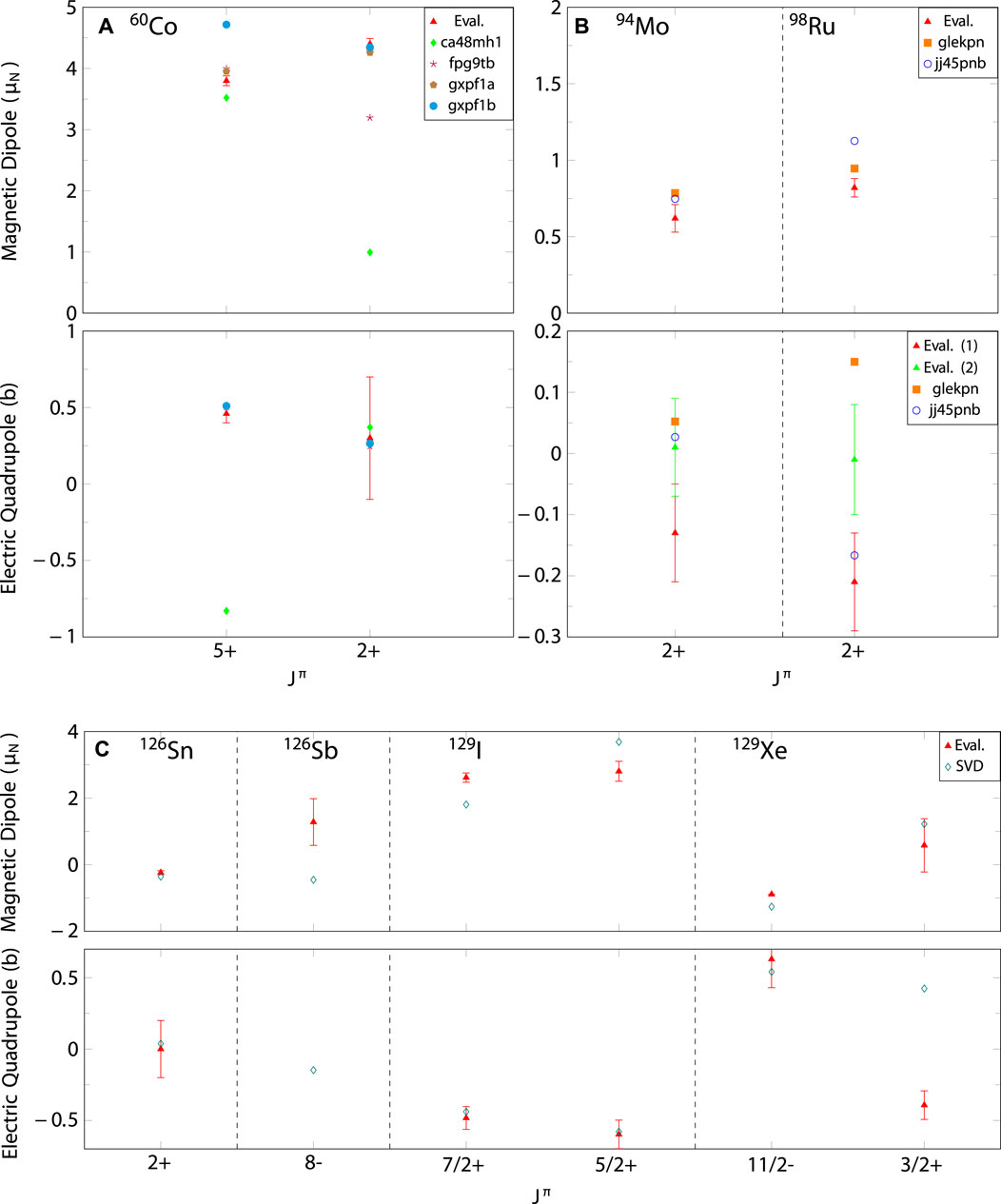
Figure 1. Comparison of the experimental and NSM-computed electric quadrupole moments
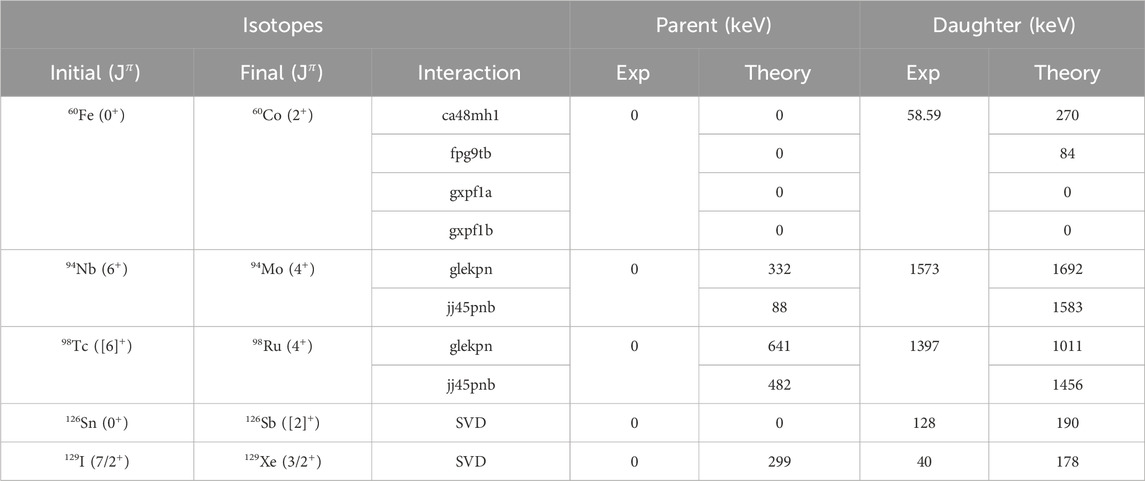
Table 1. Assessment of experimental and theoretical energy values for parent and daughter isotopes involved in non-unique second-forbidden beta decays. This table presents initial and final nuclear states with their corresponding
For the decay of 60Fe to 60Co, the interaction ca48mh1 shows significant discrepancies compared to the experimental data, failing to accurately predict both the energy levels and the nuclear moments. The fpg9tb interaction works much better, and shows good agreement with the data. In contrast, the gxpf1a and gxpf1b interactions reproduce the data less well, suggesting that these Hamiltonians should be regarded with caution, like also the ca48mh1 Hamiltonian.
For the isotopes 94Nb, 94Mo, 98Tc, and 98Ru, the interactions glekpn and jj45pnb have been applied. It is not immediately clear which of the two interactions is more reliable, as they each agree with the experimental results in different aspects. In particular, the glekpn Hamiltonian struggles to systematically predict the level schemes, despite maintaining nuclear-moment observables within acceptable limits. The jj45pnb interaction, however, consistently provides better predictions for the level schemes of the studied isotopes and shows a strong agreement with the nuclear observables of the daughter states. Overall, jj45pnb appears to be more reliable of the two, as also supported by previous studies in this mass region [48].
Lastly, the isotopes 126Sn, 126Sb, 129I, and 129Xe have been studied using the SVD Hamiltonian. This Hamiltonian shows promising results in terms of the level-scheme predictions. However, for the odd-mass nuclei 129I and 129Xe, there is a bit larger disparity in the predicted energies. This is expected, as odd-mass nuclei typically have a higher density of states, making it more challenging to accurately reproduce their experimental level schemes. The predicted electric quadrupole moments generally agree with the experimental data, except for the 129Xe
3.2 β-spectral dependency on the weak axial coupling and the small NME
As previously mentioned, we use the sNME as a fitting parameter to match, for each selected value of the axial coupling
Figures 2–4 depict the two sets of sNMEs and indicate which of the two sets is the so-called “optimal” or closest to the CVC predicted value, denoted with the * symbols. The solid lines denote sNME solution one and the dashed lines, solution 2. Only in the case of the 126Sn decay, see Figure 4A, does the closest-to-CVC-solution fall within two different solution sets. This, however, is a matter of definition of the two sets and only the experimental data on the
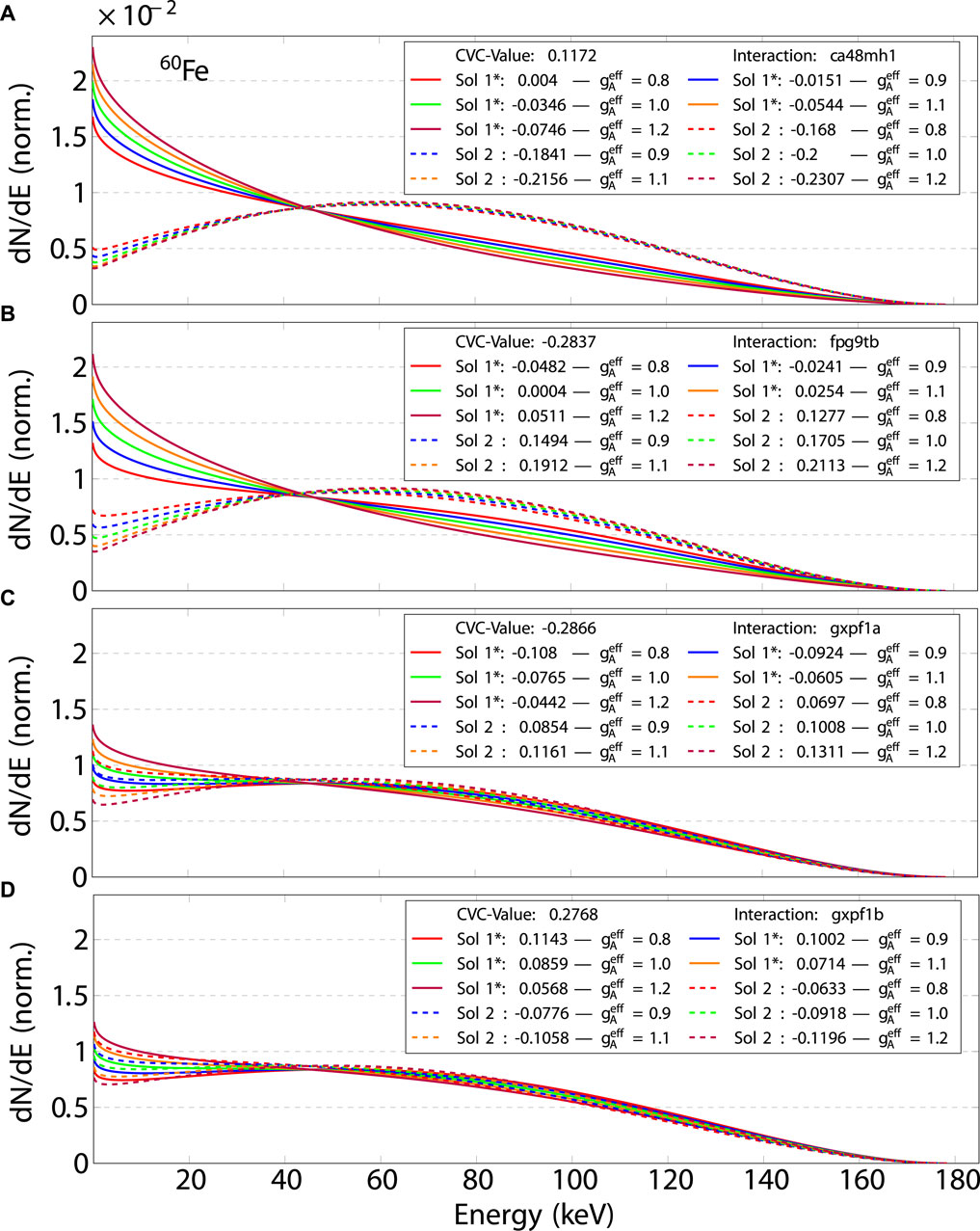
Figure 2. Computed
3.3 Spectral analysis
Analyzing Figure 2, which depicts the second-forbidden non-unique decay of 60Fe
In contrast, there is a discrepancy regarding the effect of the sNME on the spectral shape between plots (a, b) and (c, d). While plots (a) and (b) exhibit distinct differences between solution sets 1 and 2, plots (c) and (d) show nearly identical shapes for both sets, indicating very weak sNME dependence. Previous analyses, based on the predicted electric and magnetic moments, demonstrated that the Hamiltonian of plot (c) had the best agreement with the data, the Hamiltonians of plots (b) and (d) a satisfactory agreement and the Hamiltonian of plot (a) did not produce consistent results for the moments. Based on this, we could expect that this decay exhibits a rather strong dependency on
Figure 3 depicts the decays of 94Nb
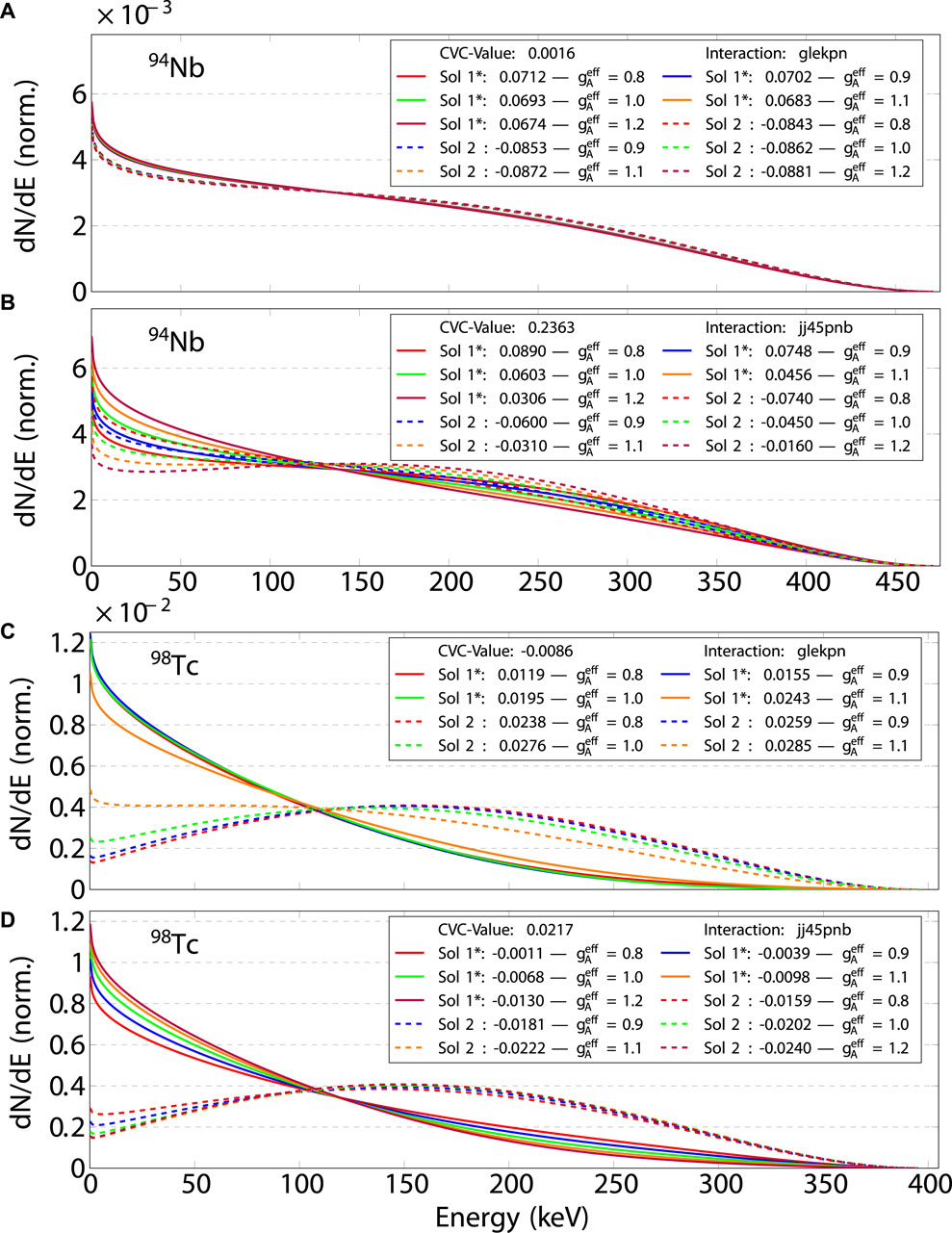
Figure 3. Similar plot as Figure 2 for the second-forbidden non-unique decays of 94Nb
For the 98Tc
Lastly, Figure 4 presents the decays of 126Sn
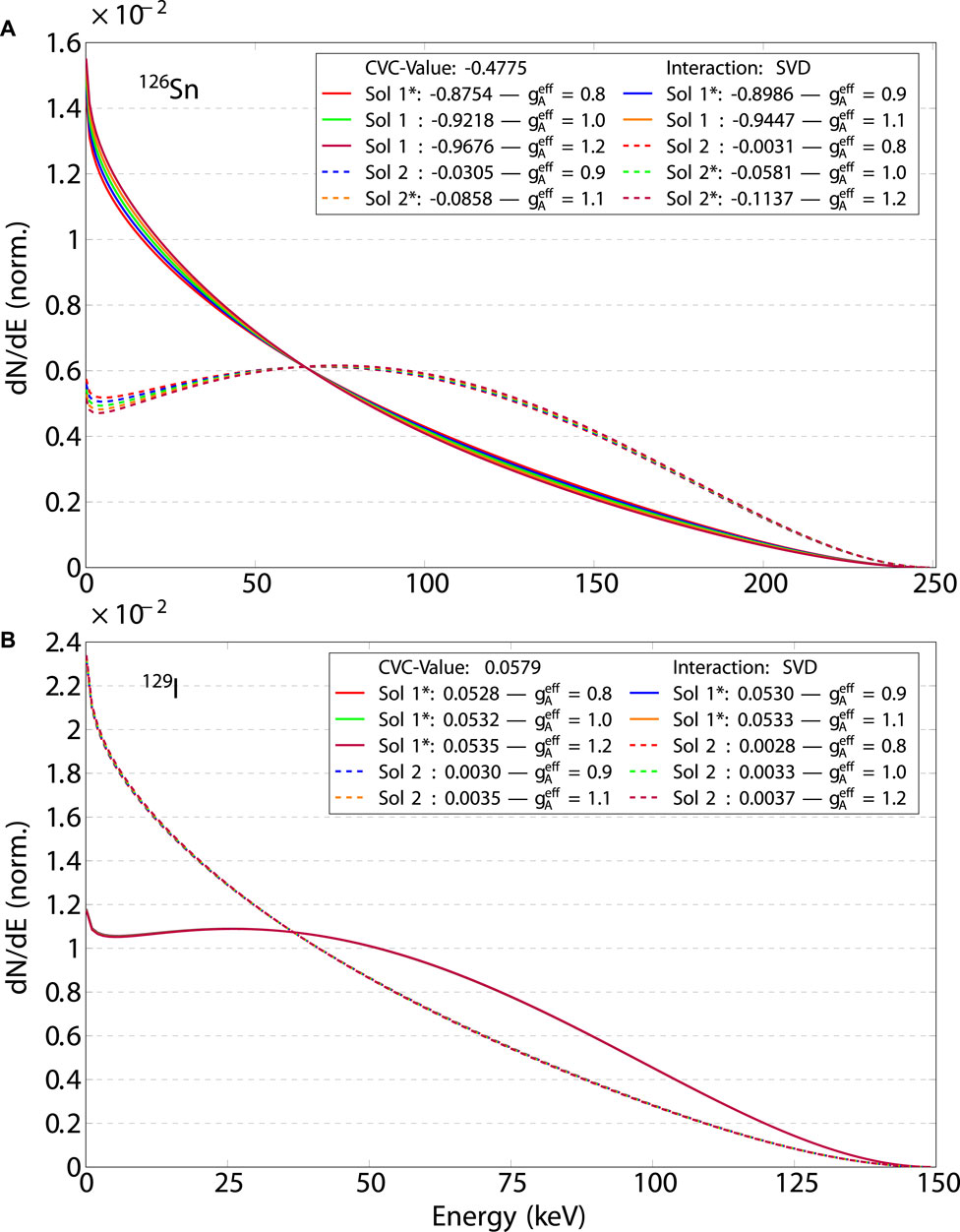
Figure 4. Similar plot as Figures 2, 3 for the second-forbidden non-unique decays of 126Sn
There is yet another way to characterize the sensitivity of the
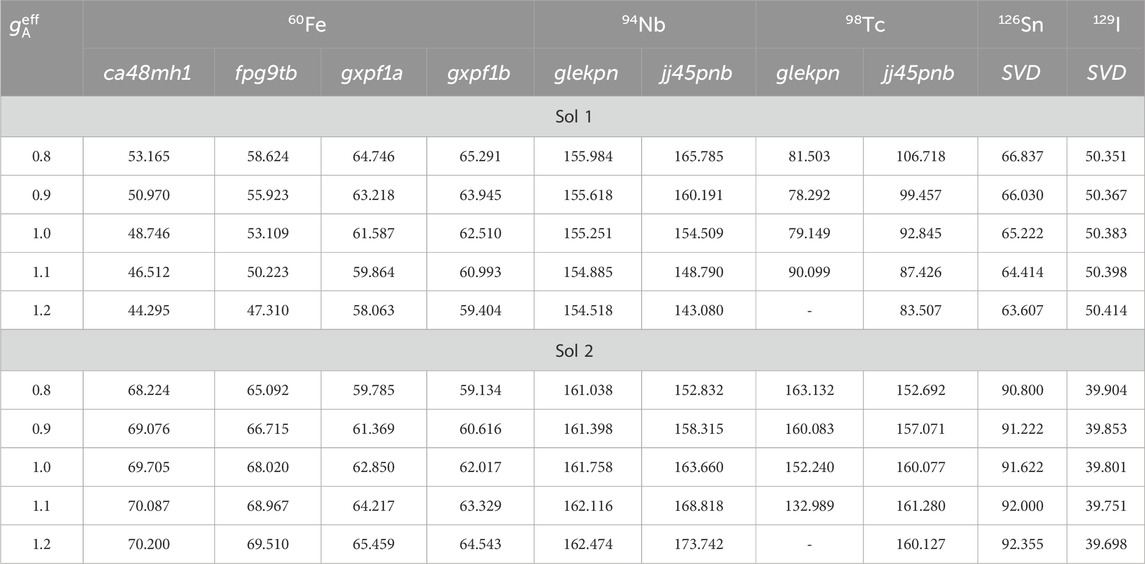
Table 2. Computed
4 Why should one measure more
A natural question arises why should one measure the presently discussed
Secondly, some theory frameworks can access the
Thirdly, the presently discussed
A further incentive for studies of the presently discussed decay transitions, and potentially others in the future, arises from needs in nuclear astrophysics [64]. First-forbidden
In the case of reactor-antineutrino spectra some of the first-forbidden
Lastly, even the more modern databases for
5 Summary and conclusion
In this article, we conduct a comprehensive survey of potential second-forbidden non-unique
We focus on the decays of 60Fe
Our investigation has identified five
Building on the shape decomposition in Equation 3, we can map the four categories to specific components within this equation: vector
Category II is characterized by the dominance of the axial component or a dominant vector-axial component with weak sNME sensitivity. Both scenarios result in shapes primarily influenced by
Lastly, Category IV describes situations where a dominant vector component, insensitive to sNME variations, leads to a decay shape unaffected by both
Based on the
Transitions from Category III play a crucial role in determining the appropriate value of the small relativistic vector nuclear matrix element (sNME). Specifically, they help establish whether the fitted value, ideally close to the Conserved Vector Current (CVC) value of sNME—termed the ‘optimal’—represents the correct physical choice. These transitions also aid in predicting which of the potential solutions is most likely to be real. This strategy is equally applicable to the
Furthermore, the transitions within Category I and Category II provide avenues to assess the effective value of the axial coupling. The transitions in Category II offer a more direct approach, enabling straightforward evaluations through direct measurements and comparisons with the predicted spectra.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
MR: Formal Analysis, Investigation, Software, Visualization, Writing–original draft. JS: Conceptualization, Funding acquisition, Methodology, Supervision, Writing–review and editing. AN: Methodology, Writing–review and editing. SS: Funding acquisition, Project administration, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. JS, AN, and SS acknowledge support from project PNRR-I8/C9-CF264, Contract No. 760100/23.05.2023 of the Romanian Ministry of Research, Innovation and Digitization (The NEPTUN project).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. [Dataset]. ENSDF database (2024). Available from: http://www.nndc.bnl.gov/ensarchivals/ (Accessed April 2024).
2. Agostini M, Benato G, Detwiler JA, Menéndez J, Vissani F. Toward the discovery of matter creation with neutrinoless ββ decay. Rev Mod Phys (2023) 95:025002. doi:10.1103/revmodphys.95.025002
3. Aker M, Beglarian A, Behrens J, Berlev A, Besserer U, Bieringer B, et al. Direct neutrino-mass measurement with sub-electronvolt sensitivity. Nat Phys (2022) 18:160–6. doi:10.1038/s41567-021-01463-1
4. Alcalá GA, Monserrat S, Mendoza L, Lozano AS, Coello EA, Benites MN, et al. Measurement of the 238U(n) cross section at the n_TOF facility of CERN. EPJ Web of Conferences (2023) 284:08001. doi:10.1051/epjconf/202328408001
5. Algora A, Tain JL, Montaner-Pizá A, Morales AI, Rubio B, Durell JL, et al. Total absorption spectroscopy study of the decay of 100Tc and the impact on reactor decay heat summation calculations. Eur Phys J A (2021) 57:85. doi:10.1140/epja/s10050-020-00316-4
6. [Dataset] Askins M, Bergevin M, Bernstein A, Dazeley S, Dye ST, Handler T, et al. The physics and nuclear nonproliferation goals of watchman: a water cherenkov monitor for antineutrinos (2015). doi:10.48550/ARXIV.1502.01132
7. Bailey G, Dronne C, Foster D, Gilbert M. Development of BNBSL: a β-ν spectra library for spectrometry applications. Appl Radiat Isot (2023) 198:110841. doi:10.1016/j.apradiso.2023.110841
8. Behrens H, Buhring W. Electron radial wave functions and nuclear beta-decay (international series of monographs on physics). Oxford: Clarendon Press (1982).
9. Blaum K, Eliseev S, Danevich FA, Tretyak VI, Kovalenko S, Krivoruchenko MI, et al. Neutrinoless double-electron capture. Rev Mod Phys (2020) 92:045007. doi:10.1103/revmodphys.92.045007
10. Bodenstein-Dresler L, Chu Y, Gehre D, Gössling C, Heimbold A, Herrmann C, et al. Quenching of gA deduced from the β-spectrum shape of 113Cd measured with the COBRA experiment. Phys Lett B (2020) 800:135092. doi:10.1016/j.physletb.2019.135092
11. Civitarese O, Suhonen J. Two-neutrino double beta decay to excited one- and two-phonon states. Nucl Phys A (1994) 575:251–68. doi:10.1016/0375-9474(94)90188-0
12. de Roubin A, Kostensalo J, Eronen T, Canete L, de Groote R, Jokinen A, et al. High-precision Q-value measurement confirms the potential of 135Cs for absolute antineutrino mass scale determination. Phys Rev Lett (2020) 124:222503. doi:10.1103/physrevlett.124.222503
13. Dombos AC, Guadilla V, Tain JL, Algora A, Agramunt J, Rubio B, et al. The β-decay of 61Fe: identification and study of a new pathway for element formation in neutron-rich environments. Phys Rev C (2021) 103:025810. doi:10.1103/PhysRevC.103.025810
14. Ejiri H, Suhonen J, Zuber K. Neutrino–nuclear responses for astro-neutrinos, single beta decays and double beta decays. Phys Rep (2019) 797:1–102. doi:10.1016/j.physrep.2018.12.001
15. Engel J, Menéndez J. Status and future of nuclear matrix elements for neutrinoless double-beta decay: a review. Rep Prog Phys (2017) 80:046301. doi:10.1088/1361-6633/aa5bc5
16. Gastaldo L, Blaum K, Chrysalidis K, Day Goodacre T, Domula A, Door M, et al. The electron capture in 163Ho experiment – ECHo. Eur Phys J Spec Top (2017) 226:1623–94. doi:10.1140/epjst/e2017-70071-y
17. Ge Z, Eronen T, de Roubin A, Tyrin K, Canete L, Geldhof S, et al. High-precision electron-capture Q value measurement of 111In for electron-neutrino mass determination. Phys Lett B (2022) 832:137226. doi:10.1016/j.physletb.2022.137226
18. Ge Z, Eronen T, Tyrin K, Kotila J, Kostensalo J, Nesterenko D, et al. 159Dy electron-capture: a new candidate for neutrino mass determination. Phys Rev Lett (2021) 127:272301. doi:10.1103/physrevlett.127.272301
19. Guadilla V, Pérez FM, Nácher E, Orrigo SEA, Algora A, Rubio B, et al. First measurements with a new β-electron detector for spectral shape studies. J Instrumentation (2024) 19:P02027. ArXiv preprint arXiv:2305.13832 [physics.ins-det]. doi:10.1088/1748-0221/19/02/P02027
20. Guadilla V, Valencia E, Tain JL, Algora A, Agramunt J, Rubio B, et al. High-precision β-decay half-lives of 66Mn, 68Co, and 70Ni: probing Gamow-Teller strengths in Ni isotopes toward the N=40 island of inversion. Phys Rev Lett (2019) 122:042502. doi:10.1103/PhysRevLett.122.042502
21. Gysbers P, Hagen G, Holt JD, Jansen GR, Morris TD, Navrátil P, et al. Discrepancy between experimental and theoretical β-decay rates resolved from first principles. Nat Phys (2019) 15:428–431. doi:10.1038/s41567-019-0450-7
22. Haaranen M, Kotila J, Suhonen J. Spectrum-shape method and the next-to-leading-order terms of the β-decay shape factor. Phys Rev C (2017) 95:024327. doi:10.1103/physrevc.95.024327
23. Haaranen M, Srivastava PC, Suhonen J. Forbidden nonunique β-decays and effective values of weak coupling constants. Phys Rev C (2016) 93:034308. doi:10.1103/physrevc.93.034308
24. Hayen L, Kostensalo J, Severijns N, Suhonen J. First-forbidden transitions in reactor antineutrino spectra. Phys Rev C (2019) 99:031301. doi:10.1103/physrevc.99.031301
25. Honma M, Otsuka T, Brown BA, Mizusaki T. Shell-model description of neutron-rich pf-shell nuclei with a new effective interaction gxpf 1. The Eur Phys J A (2005) 25:499–502. doi:10.1140/epjad/i2005-06-032-2
26. Honma M, Otsuka T, Mizusaki T, Hjorth-Jensen M, Brown BA. New effective interaction for f5pg9-shell. RIKEN Accelerator Prog Rep (2008) 41:32.
27. Huber P. Reactor antineutrino fluxes – status and challenges. Nucl Phys B (2016) 908:268–78. doi:10.1016/j.nuclphysb.2016.04.012
28. Keblbeck DK, Bhandari R, Gamage ND, Horana Gamage M, Leach KG, Mougeot X, et al. Updated evaluation of potential ultralow Q-value β-decay candidates. Phys Rev C (2023) 107:015504. doi:10.1103/physrevc.107.015504
29. Kirsebom OS, Hukkanen M, Kankainen A, Trzaska WH, Strömberg DF, Martínez-Pinedo G, et al. Measurement of the 2+→0+ground-state transition in the β decay of 20F. Phys Rev C (2019) 100:065805. doi:10.1103/PhysRevC.100.065805
30. Kirsebom OS, Jones S, Strömberg DF, Martínez-Pinedo G, Langanke K, Röpke FK, et al. Discovery of an exceptionally strong β-decay transition of 20F and implications for the fate of intermediate-mass stars. Phys Rev Lett (2019) 123:262701. doi:10.1103/PhysRevLett.123.262701
31. Kostensalo J, Lisi E, Marrone A, Suhonen J. 113Cd β-decay spectrum and gA quenching using spectral moments. Phys Rev C (2023) 107:055502. doi:10.1103/physrevc.107.055502
32. Kostensalo J, Suhonen J. Mesonic enhancement of the weak axial charge and its effect on the half-lives and spectral shapes of first-forbidden J+↔J− decays. Phys Lett B (2018) 781:480–484. doi:10.1016/j.physletb.2018.02.053
33. Kostensalo J, Suhonen J, Volkmer J, Zatschler S, Zuber K. Confirmation of gA quenching using the revised spectrum-shape method for the analysis of the 113Cd β-decay as measured with the COBRA demonstrator. Phys Lett B (2021) 822:136652. doi:10.1016/j.physletb.2021.136652
34. Kumar A, Srivastava PC, Kostensalo J, Suhonen J. Second-forbidden nonunique β-decays of 24Na and 36Cl assessed by the nuclear shell model. Phys Rev C (2020) 101:064304. doi:10.1103/physrevc.101.064304
35. Kumar A, Srivastava PC, Suhonen J. Second-forbidden nonunique β- decays of 59,60Fe: possible candidates for gA sensitive electron spectral-shape measurements. Eur Phys J A (2021) 57:225. doi:10.1140/epja/s10050-021-00540-6
36. Leder AF, Mayer D, Ouellet JL, Danevich FA, Dumoulin L, Giuliani A, et al. Determining gA/gV with high-resolution spectral measurements using a LiInSe2 bolometer. Phys Rev Lett (2022) 129:232502. doi:10.1103/PhysRevLett.129.232502
37. Lisetskiy AF, Brown BA, Horoi M, Grawe H. New T=1 effective interactions for the f5/2,p3/2, p1/2, g9/2 model space: implications for valence-mirror symmetry and seniority isomers. Phys Rev C Nucl Phys (2004) 70:044314. doi:10.1103/PhysRevC.70.044314
38. Mach H, Warburton EK, Gill RL, Casten RF, Becker JA, Brown BA, et al. Meson-exchange enhancement of the first-forbidden β decay of the low-spin isomer of 96Y(0−)→96Zr (0+) β transition. Phys Rev C (1990) 41:226–242. doi:10.1103/physrevc.41.226
39. Menéndez J, Gazit D, Schwenk A. Chiral two-body currents in nuclei: Gamow-Teller transitions and neutrinoless double-beta decay. Phys Rev Lett (2011) 107:062501. doi:10.1103/physrevlett.107.062501
40. Mougeot X. Betashape: a new code for improved analytical calculations of beta spectra. EPJ Web of Conferences (2017) 146:12015. doi:10.1051/epjconf/201714612015
41. Niţescu O, Stoica S, Šimkovic F. Exchange correction for allowed β decay. Phys Rev C (2023) 107:025501. doi:10.1103/physrevc.107.025501
42. Pagnanini L, Benato G, Carniti P, Celi E, Chiesa D, Corbett J, et al. Simultaneus measurement of half-life and spectral shape of 115In β-decay with a indium iodide cryogenic calorimeter. Phys Rev Lett (Forthcoming 2024) arXiv:2401.16059 [nucl-ex].
43. Pagnanini L, Benato G, Carniti P, Celi E, Chiesa D, Corbett J, et al. Array of cryogenic calorimeters to evaluate the spectral shape of forbidden β-decays: the ACCESS project. Eur Phys J Plus (2023) 138:445. doi:10.1140/epjp/s13360-023-03500-1
44. Paulsen M, Qian H, Liu L, Zeldes M, Zhu Y, Krane KS, et al. High precision measurement of the 99Tc β spectrum (2023). arXiv preprint arXiv:2309.14014 [nucl-ex].
45. Qi C, Xu ZX. Monopole-optimized effective interaction for tin isotopes. Phys Rev C (2012) 86:044323. doi:10.1103/physrevc.86.044323
46. Ramalho M, Ge Z, Eronen T, Nesterenko DA, Jaatinen J, Jokinen A, et al. Observation of an ultralow Q-value electron-capture channel decaying to 75As via a high-precision mass measurement. Phys Rev C (2022) 106:015501. doi:10.1103/physrevc.106.015501
47. Ramalho M, Suhonen J. Computed total β-electron spectra for decays of Pb and Bi in the 220,222Rn radioactive chains. Phys Rev C (2024) 109:014326. doi:10.1103/physrevc.109.014326
48. Ramalho M, Suhonen J. gA-sensitive β spectral shapes in the mass A=86–99 region assessed by the nuclear shell model. Phys Rev C (2024) 109:034321. doi:10.1103/physrevc.109.034321
49. Ramalho M, Suhonen J, Kostensalo J, Alcalá GA, Algora A, Fallot M, et al. Analysis of the total β-electron spectrum of 92Rb: implications for the reactor flux anomalies. Phys Rev C (2022) 106:024315. doi:10.1103/physrevc.106.024315
50. Redshaw M. Precise Q value determinations for forbidden and low energy β-decays using Penning trap mass spectrometry. Eur Phys J A (2023) 59:18. doi:10.1140/epja/s10050-023-00925-9
51. Rice S, Algora A, Tain JL, Agramunt J, Guadilla V, Rubio B, et al. Total absorption spectroscopy study of the beta decay of 86Br and 91Rb. Phys Rev C (2017) 96:014320. doi:10.1103/PhysRevC.96.014320
52. Schoppmann S. Status of anomalies and sterile neutrino searches at nuclear reactors. Universe (2021) 7:360. doi:10.3390/universe7100360
53. Schwengner R, Frauendorf S, Brown B. Low-energy magnetic dipole radiation in open-shell nuclei. Phys Rev Lett (2017) 118:092502. doi:10.1103/physrevlett.118.092502
54. Shimizu N, Mizusaki T, Utsuno Y, Tsunoda Y. Thick-restart block lanczos method for large-scale shell-model calculations. Computer Phys Commun (2019) 244:372–84. doi:10.1016/j.cpc.2019.06.011
55. Sorlin O, Leenhardt S, Donzaud C, Duprat J, Azaiez F, Nowacki F, et al. Magicity versus superfluidity. Phys Rev Lett (2002) 88:092501. doi:10.1103/physrevlett.88.092501
56. Srivastava PC. Nuclear structure study with core excitations in Ni region: for fpg9/2 space. Mod Phys Lett A (2012) 27:1250061. doi:10.1142/s0217732312500617
57. Suhonen J. Calculation of allowed and first-forbidden beta-decay transitions of odd-odd nuclei. Nucl Phys A (1993) 563:205–24. doi:10.1016/0375-9474(93)90602-t
58. Suhonen J. From nucleons to nucleus: concepts of microscopic nuclear theory. Berlin: Springer (2007).
59. Suhonen J. Impact of the quenching of gA on the sensitivity of 0νββ experiments. Phys Rev C (2017) 96:055501. doi:10.1103/physrevc.96.055501
60. Suhonen J, Civitarese O. Weak-interaction and nuclear-structure aspects of nuclear double beta decay. Phys Rep (1998) 300:123–214. doi:10.1016/s0370-1573(97)00087-2
61. Suhonen J, Kostensalo J. Double β decay and the axial strength. Front Phys (2019) 7. doi:10.3389/fphy.2019.00029
62. Suhonen JT. Value of the axial-vector coupling strength in β and ββ decays: a review. Front Phys (2017) 5. doi:10.3389/fphy.2017.00055
63. Valencia E, Tain JL, Algora A, Agramunt J, Estevez E, Jordan MD, et al. Total absorption γ-ray spectroscopy of the β-delayed neutron emitters 87Br, 88Br, and 94Rb. Phys Rev C (2017) 95:024320. doi:10.1103/physrevc.95.024320
64. Wang B.-L, Wang L.-J. First-forbidden transition of nuclear β decay by projected shell model. Phys Lett B (2024) 850:138515. doi:10.1016/j.physletb.2024.138515
65. Zhang C, Qian X, Fallot M. Reactor antineutrino flux and anomaly. Prog Part Nucl Phys (2024) 136:104106. doi:10.1016/j.ppnp.2024.104106
Keywords: beta decay, nuclear matrix elements, nuclear structure, nuclear shell model, weak axial coupling, small relativistic matrix element, electron spectral shapes
Citation: Ramalho M, Suhonen J, Neacsu A and Stoica S (2024) Spectral shapes of second-forbidden single-transition nonunique β decays assessed using the nuclear shell model. Front. Phys. 12:1455778. doi: 10.3389/fphy.2024.1455778
Received: 27 June 2024; Accepted: 23 July 2024;
Published: 15 August 2024.
Edited by:
Pedro Sarriguren, Spanish National Research Council (CSIC), SpainReviewed by:
Jonathan Engel, University of North Carolina at Chapel Hill, United StatesVladimir Zelevinsky, Michigan State University, United States
Copyright © 2024 Ramalho, Suhonen, Neacsu and Stoica. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jouni Suhonen, am91bmkudC5zdWhvbmVuQGp5dS5maQ==
 Marlom Ramalho
Marlom Ramalho Jouni Suhonen
Jouni Suhonen Andrei Neacsu
Andrei Neacsu Sabin Stoica2
Sabin Stoica2