Formation mechanism of the U-shaped spectrum based on a simple plasma–dielectric–plasma (PDP) waveguide

Manipulating electromagnetic (EM) waves by plasma–dielectric–plasma (PDP) waveguides or plasma array structures presents significant potential in microwave signal processing, such as filtering, signal delay, and EM enhancement or shielding. Owing to the simple structure and easy fabrication, the waveguide with a tooth-shaped resonator has been a strong candidate as a filtering device. Based on our previous work focusing on U-shaped filtering excited by PDP waveguides with a double-teeth structure, in this work, the formation mechanism of a U-shape filtering spectrum is systematically explored by transmission line theory (TLT) with proper field distributions. The results indicate that the U-shape spectrum consists of boundary edges and a filtering stopband. The boundary edges are attributed to Fano-type resonance, and the enhanced destructive interference from double teeth is responsible for the stopband. Such an approach shows a specific and clear mechanism for the generated U-shaped spectrum. In addition, the theoretical analysis of double teeth without Fano-type resonances is rigorously demonstrated using TLT, which significantly contributes to bandwidth modulation of stopband filtering in theory. These results contribute to the understanding of the formation mechanism of a U-shaped spectrum from a gap plasmon waveguide (such as PDP or metal–insulator–metal (MIM)) with tooth-shaped resonators, offering a feasible direction for the optimization of filtering properties, as well as offering significant parameters for subsequent experimental design.

1 Introduction

Planar waveguides (i.e., slab waveguides) can effectively confine electromagnetic (EM) waves in a planned path. To meet specific EM application scenarios, all types of resonators are suitably located around and in slab waveguides (e.g., EM waves in resonators can be coupled with ones in slab waveguides). With appropriate locations, numerous physics phenomena, such as resonance with different modes [1–3], Fano resonance [4, 5], and plasmon-induced transparency (PIT) [6, 7], can be generated and further applied in many fields, including filtering, slow light, switches, and sensors. For traditional planar waveguides, a remarkable diffraction limit affected by waveguide sizes will greatly constrain the miniaturization of EM devices. However, for modern informatization, the size of EM devices is a key to meeting the demand for highly integrated technology. Therefore, researchers have devoted to developing specific slab waveguides to overcome the diffraction limit. By exciting surface plasmon polaritons (SPPs) in specially designed slab waveguides, EM waves can propagate along the metal–insulator (or plasma–dielectric, etc.) interface to break the diffraction limit constraint. The metal, plasma, graphene, and Dirac semi-metal are several typical materials to constitute SPP waveguides. Moreover, according to the similarity principle of the Maxwell equations, the SPP theory can be regulated by the slab waveguides to be applied in different EM bands. Thus, those materials can be commonly used in near-infrared, microwave, and terahertz bands.

In slab waveguides, tooth structures are the most basic construction to control SPP propagation. As a typical application in near-infrared bands, transmission properties of tooth structures in metal–insulator–metal (MIM) waveguides have been widely investigated [8–25]. For a single tooth [8, 9], its transmission spectrum has a symmetric Lorentzian profile with resonant valleys. The generation mechanism of transmission valleys is clear, and the conventional theory can estimate their positions. For the double teeth, on the other hand, the transmission spectrum generally features a typical U-shape. Due to the property suitable for stopband filtering, many efforts have been made to understand the formation mechanism and calculate the U-shaped spectrum with different parameters. For example, for the tooth structures in MIM waveguides, analytical expressions of transmission responses have been obtained via transmission line theory (TLT), with the terms in expressions of clear physics significance [10]. However, conclusions have been drawn by comparing the expressions of single and double teeth with a not rigorously derived term for multipath interference between waves reflected by stubs. On the other hand, further studies have revealed that the bandgap of the U-shaped spectrum is attributed to the multiple superpositions of the destructive interference of each tooth [11, 12].

Because of the typical U-shaped profile suitable for stopband filtering, a certain analogy of the double teeth configuration in MIM waveguides [16–21], such as trapezoid, hexagon [21], T-shaped resonator [17], teeth with defects [19], and aperture-coupled square cavities [18], has been widely proposed and investigated, whereas simulation results tend to focus on the performance optimization of the filter and discussions of filtering change, nevertheless without a deeper analysis of the U-shaped spectrum. In other words, the formation mechanism of the U-shaped profile has been neglected previously in systematical studies, especially quantitative analysis.

As a controllable EM medium, plasma plays a significant role in developing tunable and reconfigurable microwave devices. Compared with relatively complex plasma array structures [26–29], PDP waveguides have a simple structure to control some behaviors (i.e., transmission, reflection, and absorption) of EM waves. Different from similar MIM waveguides in the optical band, the SPPs’ behaviors manipulated by PDP waveguides in the microwave regime are flexibly tunable by altering the plasma electron density. Our previous work has demonstrated that a PDP waveguide with double-teeth resonators could excite a typical U-shaped filtering spectrum [30], and its focus is to investigate filtering change rules at different structure sizes and plasma frequencies. However, its generation mechanism has not been systematically explored. In this work, TLT is introduced to verify the validity of numerical results and to quantitatively analyze the U-shaped spectrum. The U-shaped spectrum is made of two parts, boundary edges and a stopband. By our simulation results, the generation process of the two parts can be discussed in detail via field distributions and TLT. The rest of this paper is structured as follows. Section 2 illustrates the schematic diagram of the PDP waveguide with tooth resonators and the corresponding circuit model of TLT, simulation parameters, and formula derivation. Section 3 consists of two parts: first, the generation process of the U-shaped spectrum. The second part shows that the generation mechanism of the U-shaped spectrum is equally applicable to the analysis of the one with different geometrical parameters. Section 4 draws the conclusion.

2 Waveguide structures and theory analysis

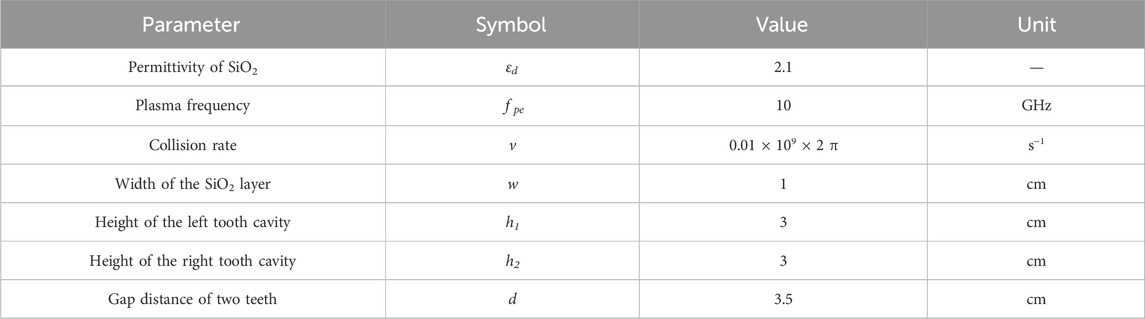
On the basis of our previous PDP waveguide models [30], considering different height combinations, the two-dimensional (2D) schematic of the PDP waveguide with a double-teeth structure is displayed in Figure 1A, where the blue region represents dielectric SiO₂ with ε_d = 2.1, enclosed by gaseous discharge plasmas marked in purple. In a convenient approximation, the plasma can be treated as a special EM medium for the wave–plasma interaction. The Drude model is thus widely applied for analyzing the propagation of EM waves in plasmas [31–34]. For simplicity, we regard the plasma as a bulk dielectric medium approximately in a uniform state. Therefore, in our study, plasma permittivity is given by

${\epsilon }_p=1-{\omega }_{pe}^2/\omega \left(\omega +iv\right),(1)$

where $\omega$ is the angular frequency of EM waves, $v$ is the collision rate in the plasma, $f_{pe}={\omega }_{pe}/2\pi$ with ${\omega }_{pe}={\left(n_e{e}^2/{\mathrm{\epsilon }}_0{m}_e\right)}^{1/2}$ is the plasma frequency, and $n_e$ and $m_e$ are the electron density and mass, respectively. The symbols in the figure, d, w, h₁, and h₂, denote the gap distance between the centerlines of two teeth, the width of the SiO₂ layer, and the height of the left and right tooth cavities, respectively.

Figure 1

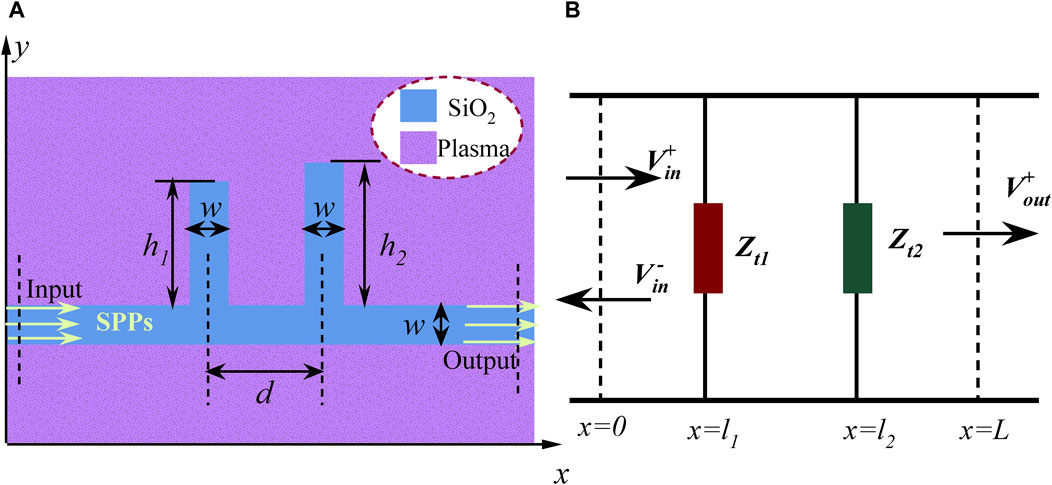
Figure 1. (A) Two-dimensional schematic of a PDP waveguide with a double-teeth cavity. (B) Simplified circuit model in TLT.

In results and discussions, the transmission, obtained via the RF module of COMSOL software, is the ratio of the collected SPPs’ power at the output port to the initial SPPs’ power at the input port. With no specific statement, the numerical simulation parameters are the same as those in Table 1. A more detailed introduction to the model can be found in our previous work [30]. In the experimental design of the interaction between gas plasmas and EM waves, an artificial gaseous plasma environment, confined in a quartz shell, usually can be generated by all types of discharge ways (i.e., ICP, CCP, or DC discharge). The designed SiO₂ structure is immersed into an artificial plasma environment to construct PDP waveguides. Moreover, antennas to excite and receive EM signals can be located in two ends of the straight waveguide to obtain S21. The transmission coefficient S21 (|S21|² is calculated in our simulations) can be obtained by the vector network analyzer. The electron density can be estimated by optical emission spectroscopy and Langmuir probe diagnostics [26].

Table 1

Table 1. Detailed simulation parameters.

In a coupled-resonator waveguide system, the resonance frequencies exhibited in the transmission spectrum usually depend on certain resonance modes in the resonator. According to the standing wave theory, the resonant wavelength of a tooth cavity can be determined as [9, 12]

${\lambda }_{tm}=4R_e\left(n_{eff}\right)h/\left[\left(2m-1\right)-\phi /\pi \right].(2)$

Different from tooth cavities, rectangular cavities with a narrow width have two reflection interfaces, and their resonant wavelength can be calculated as [4, 35]

${\lambda }_{rm}=2R_e\left(n_{eff}\right)L_{FP}/\left(m-\phi /\pi \right).(3)$

Here, $R_e\left(n_{eff}\right)$ is the real part of the effective refractive index obtained from the dispersion relation [30, 36, 37] and Equation 1, $\phi$ is the additional phase shift caused by SPP reflection at the interface between the plasma and SiO₂, and m denotes the resonance orders in the resonance cavity (m = 1, 2, 3, …). The rectangular cavity (as indicated in the inset of Figure 6) can be regarded as a Fabry–Perot (FP) cavity, and $L_{FP}$ represents the effective resonance length of the FP cavity.

TLT is a theoretical approach combining circuit and field treatments. According to TLT [8, 10, 38], the PDP waveguide with single-tooth structures can be equivalent to a circuit model (as shown in Figure 2). In this paper, we set the plane close to the input port x = 0, the one near the output port x = L, and the centerline of the tooth cavity x = l. $v_{in}^{\pm }$ and $v_{out}^{\pm }$ represent the normalized voltage values, with their square for power; + and − stand for rightward and leftward propagate voltage waves, respectively, and subscripts “in” and “out” represent voltage waves near the input port and the output port, respectively. The symbols $Z_0$ and $Z_t$ are the characteristic impedance of a straight PDP waveguide and the equivalent impedance of a tooth resonator, respectively. $Z_0=\beta w/\omega {\epsilon }_d{\epsilon }_0$, where ${\epsilon }_0$ is the vacuum permittivity and $\beta$ is the propagation constant of the PDP waveguide with $\beta ={k_{0}n}_{eff}$ ($k_0$ is the wavenumber in vacuum). To solve Z_t, load impedance Z_L, related to the phase shift and the attenuation of SPPs caused by SPP reflection at the tooth end, needs to be acquired. In the tooth cavity, the SPPs nearly encounter normal reflection at the plasma–dielectric interface of its end. According to Fresnel’s formula and TLT, the following relations are obtained by solving SPPs’ reflectance at the plasma–dielectric interface.

$\mathrm{\Gamma }=\frac{{\mathrm{Z}}_L-Z_0}{{\mathrm{Z}}_L+Z_0}\approx \frac{\sqrt{{\mathrm{\epsilon }}_p}-\sqrt{{\mathrm{\epsilon }}_d}}{\sqrt{{\mathrm{\epsilon }}_p}+\sqrt{{\mathrm{\epsilon }}_d}}.(4)$

Figure 2

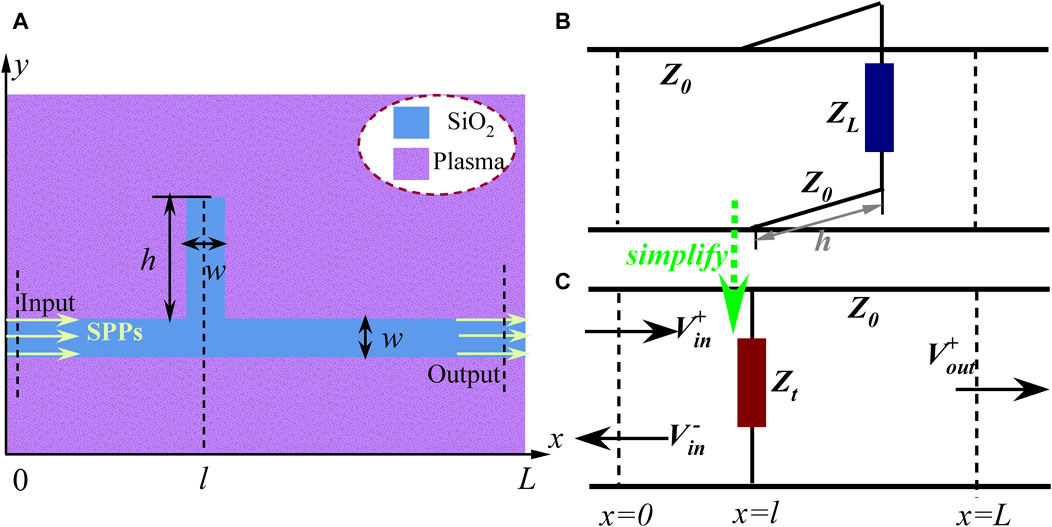
Figure 2. (A) Two-dimensional schematic of a PDP waveguide with a single-tooth cavity. (B) Equivalent circuit model related to the single-tooth structure. (C) Simplified circuit model.

Combining the corresponding circuit model in Figure 2B and TLT, the equivalent impedance of the tooth cavity with height h is written as

$Z_t=Z_0\cdot \frac{Z_L+i{Z}_0\tan \beta h}{Z_0+{iZ}_L\tan \beta h}.(5)$

The transmission of the circuit model is readily obtained by the transfer matrix method, with

$\left(\begin{array}{c}{v}_{in}^{+}\\ v_{in}^{-}\end{array}\right)=\mathit{T}\left(\begin{array}{c}{v}_{out}^{+}\\ 0\end{array}\right),(6)$

where T is obtained by $\mathit{T}=\mathit{A}\left(l\right)\mathit{B}\left(Z_t\right)\mathit{A}\left(L-l\right)$ with

$\begin{array}{c}A\left(x\right)=\left(\begin{array}{cc}\exp \left(i\beta x\right)& 0\\ 0& \exp \left(-i\beta x\right)\end{array}\right),\hfill \\ B\left(Z_t\right)=\left(\begin{array}{cc}1+Z_0/2Z_t& Z_0/2Z_t\\ {-Z}_0/2Z_t& 1-Z_0/2Z_t\end{array}\right).\hfill \end{array}(7)$

Combining Equations 5–7, the transmission of the PDP waveguide with a single-tooth structure is acquired

$T_s={\left|\frac{v_{out}^{+}}{v_{in}^{+}}\right|}^2={\left|1+\frac{Z_0}{2Z_t}\right|}^{-2}\exp \left(\frac{L}{L_{SPP}}\right),(8)$

where $L_{SPP}=\left(2\text{Im}{\left.\left(\beta \right)\right)}^{-1}\right.2\text{Im}{\left.\left(\beta \right)\right)}^{-1}$, with $\text{Im}\left(\beta \right)$ denoting the imaginary part of $\beta$. Obviously, the exponential part clearly indicates the SPP attenuation inevitable for SPP propagation in waveguides. With regards to double-teeth structures, the transfer matrix T of the equivalent circuit model is $\mathbf{A}\left(l_1\right)\mathbf{B}\left(Z_{t1}\right)\mathbf{A}\left(d\right)\mathbf{B}\left(Z_{t2}\right)\mathbf{A}\left(L-l_2\right)$. Similarly, the transmission of double-teeth structures is found

$T_d={\left|\frac{v_{out}^{+}}{v_{in}^{+}}\right|}^2={\left|\left(1+\frac{Z_0}{2Z_{t1}}\right)\left(1+\frac{Z_0}{2Z_{t2}}\right)-\frac{Z_0^2}{4Z_{t1}{Z}_{t2}}\exp \left(-2i\mathrm{\beta }d\right)\right|}^{-2}\exp \left(\frac{L}{L_{SPP}}\right).(9)$

By comparing T_S and T_d, it can be inferred that, on the right side of the equation, the first term in the modulus factor is the accumulation of the independent filtering response of each tooth cavity, while the second properly indicates interference between two tooth cavities due to factor d. To further understand the above argument, we deduct the result of the double-teeth structure when the SPP interference between double-teeth cavities is ignored. As shown in Figure 3, we split the overall circuit model in Figure 1B into two individual units connected by a gray shadow area. Corresponding to the SPP propagation process, the incident voltage wave $V_{\mathrm{i}n}^{+}$ goes through the first tooth cavity, and the next voltage wave $V_1^{+}=V_2^{+}$ enters into the second tooth cavity when ignoring the SPP propagation loss in the straight PDP channel. Assuming that the reflected wave $V_1^{-}$ is vanished by neglecting SPP interference between double-teeth structures, the one with double-teeth structures can then be approximately written

$T_d^{\prime }={\left|V_{out}^{+}/V_{in}^{+}\right|}^2={\left|V_{out}^{+}/V_2^{+}\times V_1^{+}/V_{in}^{+}\right|}^2={\left|1+\frac{Z_0}{2Z_{t1}}\right|}^{-2}{\left|1+\frac{Z_0}{2Z_{t2}}\right|}^{-2}\exp \left(\frac{L}{L_{SPP}}\right)\approx T_{s1}{T}_{s2}.(10)$

Figure 3

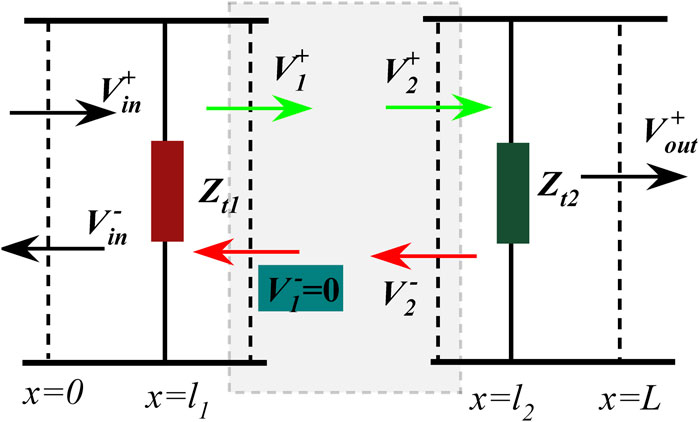
Figure 3. Simplified split circuit model of Figure 1B, to obtain the transmission by ignoring the SPP interference.

Here, T_s1 and T_s2 refer to the transmission of a single left or right tooth, respectively, as displayed in the insets of Figure 5. Apparently, ignoring the SPP interference between double-teeth constructions (i.e., $\left.V_1^{-}=0\right)$, the calculated $T_d^{\prime }$ is in good agreement with the analysis of Equation 9.

3 Results and discussions

3.1 The formation mechanism of a U-shaped spectrum

To demonstrate the validity of TLT, the comparison of transmission responses, with the calculated model indicated by two structure insets, is given in Figure 4. The red dotted lines are the results of TLT obtained by Equations 8, 9, and the black curves are numerical simulations from COMSOL. Clearly, the TLT result exhibits a strong alignment with that of numerical simulations. However, there exists some insignificnat unconformity in spectra, probably due to the approximation used in Equation 4. For the single-tooth structure, its transmission spectrum typically shows a symmetric Lorentz line shape with transmission dips. It is evident that the transmission curve in Figure 4A conforms to this characteristic. The transmission dip observed at 1.04 GHz can be elucidated by the distribution of the magnetic field component H_z. Its emergence is attributed to the destructive interference of two distinct paths of SPPs at the junction of the tooth cavity and the straight waveguide. One path involves the SPP propagation along the straight waveguide, while the other involves the SPP reflection by the end of the tooth cavity. When destructive interference occurs at the junction, there is a resonance in the tooth cavity. According to Equation 2, the theoretically obtained frequency of the dip is approximately 1.22 GHz with neglecting the phase effect of $\mathrm{\phi }$, which agrees well with the simulation result. To provide a clear explanation of the formation mechanism for the U-shaped spectrum, one can divide the spectrum into two parts. As marked by the orange oval region in Figure 4B, one part is the stopband, characterized by a flat curve with nearly zero transmission. Another is referred to boundary edges, signed by the blue oval region, with the characteristic similar to a rising (falling) edge by an impulse voltage. The boundary edge is a typical Fano-like profile with sharp and asymmetrical line shapes, in good agreement with results in MIM waveguides [22]. The U-shaped spectrum can be applied in wideband stopband filtering, where two crucial indicators, namely, bandwidth and central frequency, are of concern. Here, the bandwidth is $f_h-f_l$, the central frequency can be obtained by $\left(f_h+f_l\right)/2$, for the high and low frequencies $f_h$ and $f_l$ at 1% transmission, respectively. Next, we discuss the formation of the U-shaped spectrum from stopband and boundary edge views in detail.

Figure 4

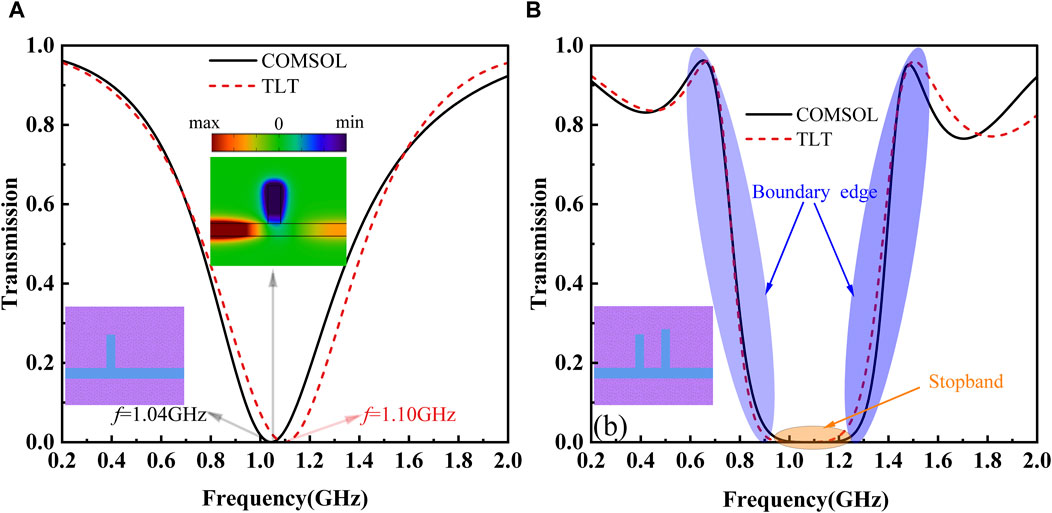
Figure 4. Comparison of transmission responses between COMSOL and TLT. (A) Transmission spectrum of a single-tooth structure, with the inset for the magnetic field distribution in the z-direction at 1.04 GHz. (B) Transmission spectrum for the double-teeth structure.

For the formation mechanism of the stopband, typically there are two types of descriptions in the literature [11, 12, 30]. One attributes to the “enhanced” destructive interference, due to the cumulative effect of the interference from each tooth when SPP waves successively propagate through it. The other, however, suggests the “superposed” destructive interference as SPP waves propagate through both teeth and thus resulting in a stopband. However, these explanations only provide mostly qualitative analysis or quantitative explanation by phase accumulation. For a quantitative explanation by the spectrum evolution process, corresponding simulation results are drawn in Figure 5, where A and B present the transmission responses from the left and right tooth structures, respectively. Based on Equation 8, we can deduce that the transmission of a single tooth is independent of the tooth position. The identical transmission spectrum observed in Figures 5A, B confirms this conclusion. Gray shadow areas in Figures 5A, B are “resonance regions” with a specific resonance width, i.e., the frequency range by 0.1 transmission. Theoretically, the filtering bandwidth of the U-shaped spectrum is equivalent to the resonance width observed in the resonance region when $h_1=h_2$ and $\frac{Z_0^2}{4Z_{t1}{Z}_{t2}}\exp \left(-2i\mathrm{\beta }d\right)=0$. According to Equation 10, without considering the SPP interference between double-teeth constructions, the transmission response is displayed by the green curve obtained by the product of T_s1 and T_s2 in Figure 5C. The orange curve is redrawn for the black curve in Figure 4B. Apparently, as anticipated, the theoretical filtering bandwidth of 0.21 GHz is a rough approximation to the filtering bandwidth of 0.26 GHz from COMSOL simulations. Note that near green or orange shadows, the green and orange spectrum curves exhibit a flat feature with nearly zero transmission. Away from the shadows, there exists a significant difference in green and orange spectra. These above phenomena can be explained as follows. For SPP interference between double-teeth cavities, there is an extremely strong interference at the (Fano-like) resonance frequency. Away from resonances, the SPP interference between double teeth is significantly weak, i.e., ${\left|\left(1+\frac{Z_0}{2Z_{t1}}\right)\left(1+\frac{Z_0}{2Z_{t2}}\right)-\frac{Z_0^2}{4Z_{t1}{Z}_{t2}}\exp \left(-2i\beta d\right)\right|}^{-2}\approx {\left|\left(1+\frac{Z_0}{2Z_{t1}}\right)\left(1+\frac{Z_0}{2Z_{t2}}\right)\right|}^{-2}$. In other words, the stopband is mainly determined by the resonance width.

Figure 5

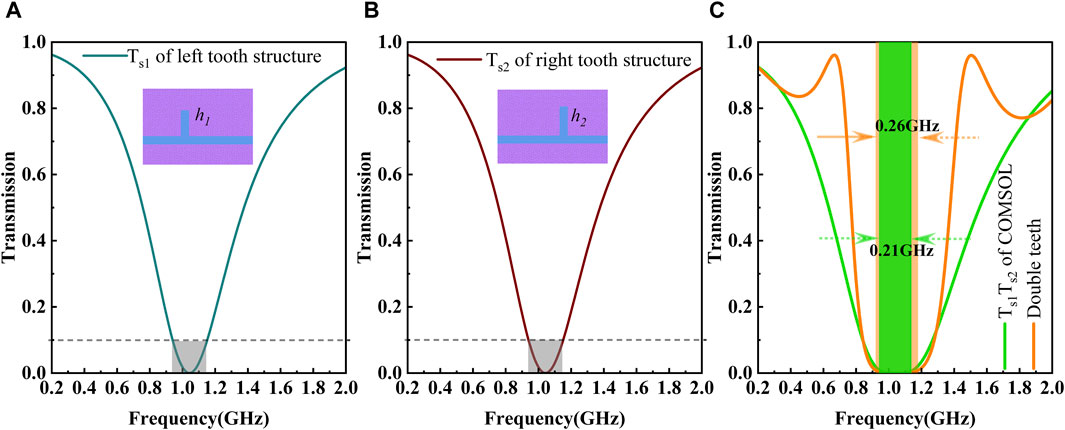
Figure 5. Transmission spectra with different waveguide structures and the product of T_s1 and T_s2. (A) Transmission spectrum of the left tooth structure. (B) Transmission spectrum of the right tooth structure. (C) Green curve for the transmission spectrum obtained by the product of T_s1 and T_s2 and orange curve for that in Figure 4B.

For the boundary edges, the spectrum response is viewed as Fano-like resonances, which exhibits a distinctively sharp and asymmetric profile. This phenomenon is commonly observed in MIM waveguides. Certain studies have illustrated that the discrete states in Fano-like resonance were constructed by the double teeth and their joint [22]. However, the formation process of Fano-like resonances lacks detailed discussion. As depicted in Figure 6, the formation elements, including specific continuous and discrete states, of the boundary edges are provided. Without considering SPPs’ interference between double teeth connected by the PDP channel with length d, the calculated result is presented in Figure 6A, which is the redrawn spectrum from the green curve in Figure 5C. It is evident from the blue curve in Figure 6A that there is a stopband along with two edges displaying monotonic change. The curve presents a wider full width at half maximum (FWHM), which is typically associated with a continuous state. For a more graphic description, the continuous state also is termed as a background spectrum. Discrete states are also an indispensable element in generating Fano-like resonances under appropriate interference conditions. Our study also assumes that the equivalent FP cavity (i.e., FP-like cavity) consists of double teeth and their connecting PDP waveguide. Additionally, the equivalent length of the FP-like cavity is approximately $L_{FP}\approx h_1+h_2+d$. As shown in the inset in Figure 6B, the end of the FP cavity is coupled to a straight PDP waveguide with a 0.2-cm gap, whose simulation result is drawn in Figure 6B. Clearly, there exist two transmission dips with extremely narrow FWHM in Figure 6B, which are considered as two discrete states. With coupling and interference between the continuous state and the two discrete states, namely, SPPs propagate and interfere in the PDP waveguide with double teeth, Fano-like profiles will appear. As the area surrounded by the gray box in Figure 6C, the Fano-like resonances with sharp and asymmetrical profiles form the boundary edges of the U-shaped spectrum. The left boundary edge is called as the LFR, and the right edge is termed as the RFR. To enhance the understanding of the formation of the Fano-like resonances, the corresponding field distributions are drawn at transmission dips and Fano-like peaks in Figure 7. Apparently, the 1st- and 2nd-order resonance modes of the FP cavity result in Dip Ⅰ and Dip ⅠⅠ, respectively. Comparing the field distribution at Dip Ⅰ (Dip ⅠⅠ) with that at LFR (RFR), we found that there exist similar features, such as the distribution situation of field antinodes or nodes. Note that the like-FP cavity exhibits a slight difference from the FP cavity, indicated by the inset in Figure 6B. For example, the FP-like cavity has vertically curved corners, which exert some impact on the SPPs’ effective resonance length. For simplification, throughout our study, the equivalent resonance length of the FP-like cavity is approximately $L_{FP}\approx h_1+h_2+d$.

Figure 6

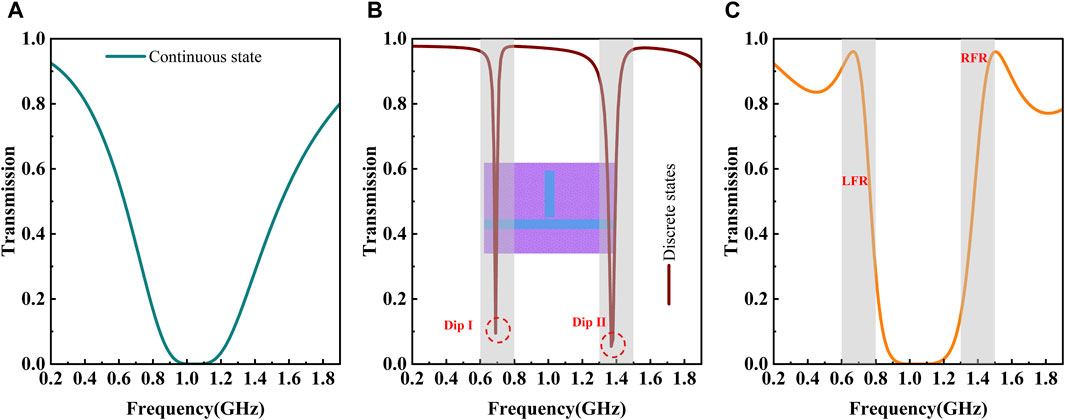
Figure 6. Transmission spectra with different waveguide structures and the product of T_s1 and T_s2. (A) Redrawn transmission spectrum for the green curve in Figure 5C. (B) Transmission spectrum of the FP cavity coupled to the straight PDP waveguide indicated by the inset. (C) Redrawn curve for that in Figure 4B.

Figure 7

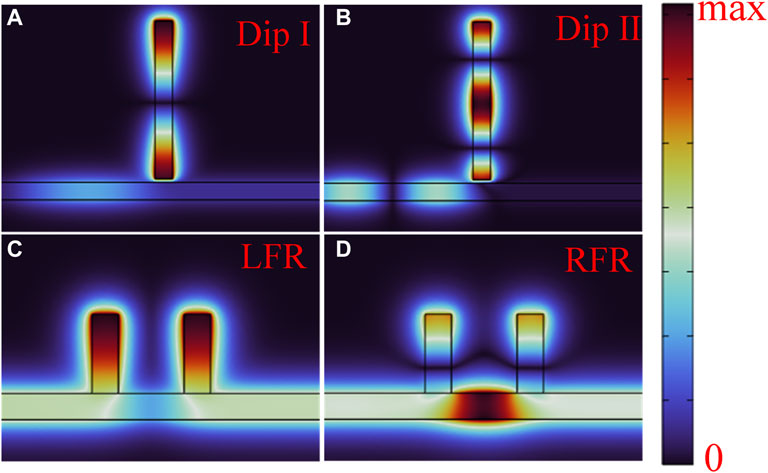
Figure 7. Magnetic field intensity in the z-direction corresponding to Figure 6. (A–D) are field distributions at Dip I, Dip II, LFR and RFR, respectively.

3.2 The modulation of the U-shaped spectrum

To fully verify the rationality of the formation mechanism of a U-shaped spectrum, we will give parameter scan calculations focusing on two aspects: boundary edges and stopband. As mentioned in Section 3.1, the positions of boundary edges primarily depend on the equivalent length of the FP-like cavity $L_{FP}\approx h_1+h_2+d$. Theoretically, the three parameters, $h_1$, $h_2$, and $d$ will exert on the locations of boundary edges. Additionally, it is easily found that the stopband is mainly influenced by $h_1$ and $h_2$.

At first, assuming that $h_2$ and $d$ are constant, we explore the influence of $h_1$ on boundary edges. As illustrated in Figures 8A–C, the U-shaped spectrum presents a complicated and varied profile, especially at boundary edges. When the height of the double-teeth cavity is inconsistent, the resonance width (discussed in Figure 11A) and resonance dip of each tooth are different, further resulting in a diverse background spectrum. Obviously, as shown in the dotted-gray curve in Figures 8A–C, the background spectrum has all types of profiles. Generally, the track of the U-shaped spectrum is similar to that of the background spectrum apart from boundary edges. Meanwhile, as displayed in the dotted-blue curve in Figures 8A–C, the position of the discrete states just locates around one of the boundary edges. Namely, the boundary edges are attributed to the interference between the background spectrum and the resonance of the FP-like cavity. Notably, as indicated in Figure 8C, there is a significant bump at the stopband, which is caused by the staggered resonance dips. The discrepancy of double teeth leads to staggered resonance dips. The bump greatly affects the stopband filtering function for the U-shaped spectrum. This is why we concern the double-teeth structure with identical height more.

Figure 8

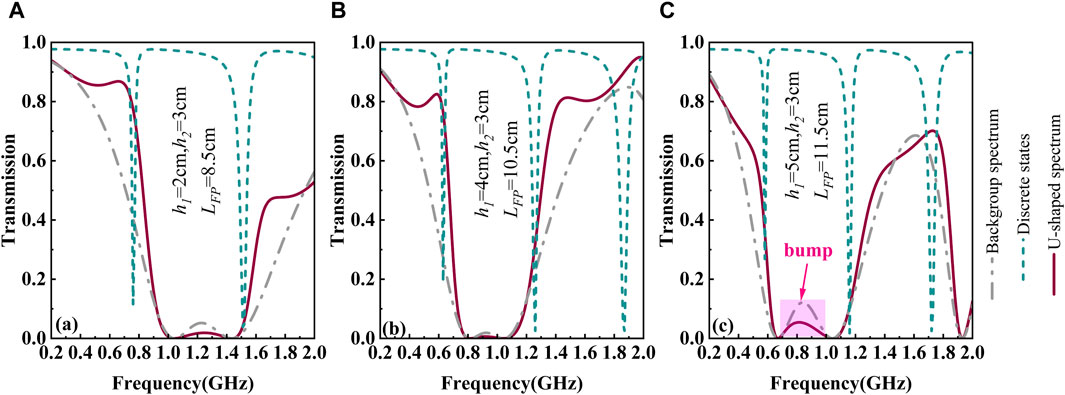
Figure 8. Transmission spectra with different $h_1$ and $L_{FP}$. The background spectrum, transmission spectrum of the FP cavity, and the transmission spectrum of double teeth are indicated by the dotted-gray curve, dotted-blue curve, and wine-red curve, respectively. (A) Parameters with h₁ = 2 cm, h₂ = 3 cm, and L_FP = 8.5 cm. (B) Parameters with h₁ = 4 cm, h₂ = 3 cm, and L_FP = 10.5 cm. (C) Parameters with h₁ = 5 cm, h₂ = 3 cm, and L_FP = 11.5 cm.

When $h_1=h_2$, and separation $d$ and height $h_1$ are set at an appropriate value, there is not a bump in the stopband as usual. It is mentioned above that the position of a stopband depends on height $h_1\left(h_2\right)$, and that of boundary edges is affected by $L_{FP}$. Evidently, height $h_1\left(h_2\right)$ affects the position of a stopband and boundary edges. In addition, their positions have simultaneous redshift (blueshift) with the increase (decrease) of parameter $h_1$, which is hard to generate bump. However, under certain conditions, there still exists a bump in the transmission spectrum. When the position of discrete states in Figures 9A–C is gradually close to the stopband area, there exists a bump in Figure 9C as prediction. However, the intensity of the bump is extremely weak because of the enhanced destructive interference at the stopband. In contrast to the phenomenon, as shown in Figure 9B, when discrete states deviate from the stopband, the Fano-like profile is evident, namely, the intensity of Fano-like resonance is stronger. In general, the wine-red U-shaped spectra in Figures 9A–C are a combination of the background spectrum and the Fano-like resonances, in accordance with the analysis of the generation mechanism of the U-shaped spectrum.

Figure 9

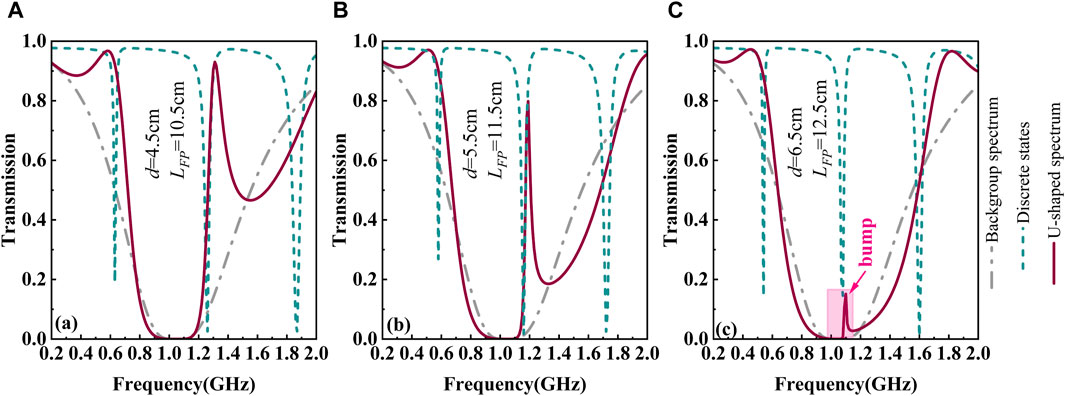
Figure 9. Transmission spectra with different $d$ and $L_{FP}$. The background spectrum, transmission spectrum of the FP cavity, and transmission spectrum of double teeth are indicated by the dotted-gray curve, dotted-blue curve, and wine-red curve, respectively. (A) Parameters with d = 4.5 cm and L_FP = 10.5 cm. (B) Parameters with d = 5.5 cm and L_FP = 11.5 cm. (C) Parameters with d = 6.5 cm and L_FP = 12.5 cm.

For the U-shaped spectrum, the bump can greatly affect the filtering function. Therefore, the parameters, $h_1,h_2$ and $d$, should be set to the appropriate values. Based on the analyses above, $h_1$ should equal to $h_2$, and $h_1$ and $d$ should meet a specific relation. In our study, the position of the stopband is evaluated by the first-order mode of a single tooth. The position of the LFR and RFR is approximately dependent on the first-order and second-order resonance of FP-like cavities, respectively. Theoretically, when the central position of the LFR and RFR just locates around the one of stopband, the U-shaped spectrum is quasi-symmetric because of the quasi-symmetric characteristic of the background spectrum (see the curve in Figure 6A). The peak frequency of the LFR and FPR is approximately predicted by Equation 3, and the central frequency of a stopband is approximately calculated by Equation 2. Herein, the additional phase $\mathrm{\phi }$ is a function of the frequency, which is a relatively small value and difficult to precisely calculate. Therefore, to demonstrate the validity of the standing theory, from both simulation and theory aspects, the dependence of resonance wavelengths on parameters $h$ and $L_{FP}$ with the neglection of $\mathrm{\phi }$ is demonstrated in Figure 10. It can be found in Figure 10 that the resonance wavelengths linearly redshift with the increase in $h\text{\hspace{0.17em}and\hspace{0.17em}}{L}_{FP}$, which agree well with Equations 2, 3. Distinctively, the resonance wavelengths of simulation are greater than the one of theory due to ignoring $\mathrm{\phi }$. To better evaluate the quasi-symmetric U-shaped spectrum, the simulation results with linear fitting are adopted to calculate the dependence of resonance wavelengths on $h\text{\hspace{0.17em}and\hspace{0.17em}}{L}_{FP}$. For single-tooth structures, the fitting result of resonance wavelength is ${\lambda }_s\approx 7.90177h+5.07655$. For double-teeth structures, the fitting wavelength of the LFR is ${\lambda }_{LF}\approx 4.04489L_{FP}+5.00635$, and the fitting wavelength of the RFR is ${\lambda }_{RF}\approx 1.98861L_{FP}+2.84727.$ When $f_s\approx \left(f_{LF}+f_{RF}\right)/2$, the U-spectrum is a quasi-symmetric profile. According to $f_s\approx \left(f_{LF}+f_{RF}\right)/2$, when $h$ is set to be 2 cm, 3 cm, 4 cm, and 5 cm, the gap distance $d$ should be 2.5 cm, 3.4 cm, 4.3 cm, and 5.4 cm, respectively. Figures 10A, B illustrate the transmission of the single tooth and double teeth, respectively. Apparently, as predicted in Figure 11B, a U-shaped spectrum is a quasi-symmetric profile. It is worth noting that the bandwidth of the U-shaped spectra is different due to different resonance widths, attributed to varied $h$. In other words, the bigger the resonance width is, the bigger the filtering bandwidth is. When h is set to be 2 cm, 3 cm, 4 cm, and 5 cm, as marked in the transparent area with colors, the resonance width is 0.26 GHz, 0.21 GHz, 0.16 GHz, and 0.13 GHz, respectively. Additionally, the corresponding filtering bandwidth is 0.38 GHz, 0.25 GHz, 0.21 GHz, and 0.17 GHz, respectively.

Figure 10

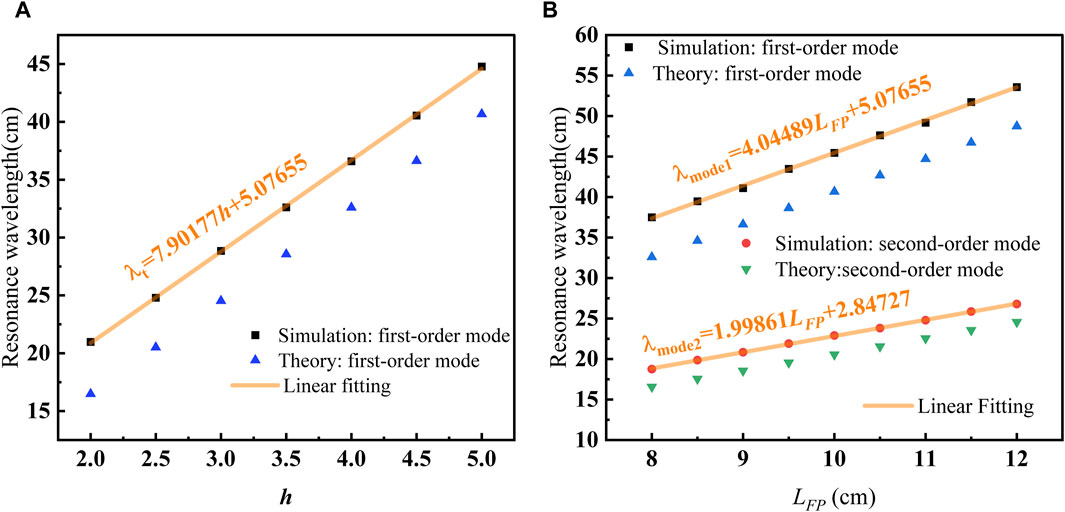
Figure 10. For different structures, a comparison of resonance wavelengths between standing theory and simulation and linear fitting of simulation results. (A) Single-tooth structure in Figure 2A. (B) Structure indicated by the inset in Figure 6B.

Figure 11

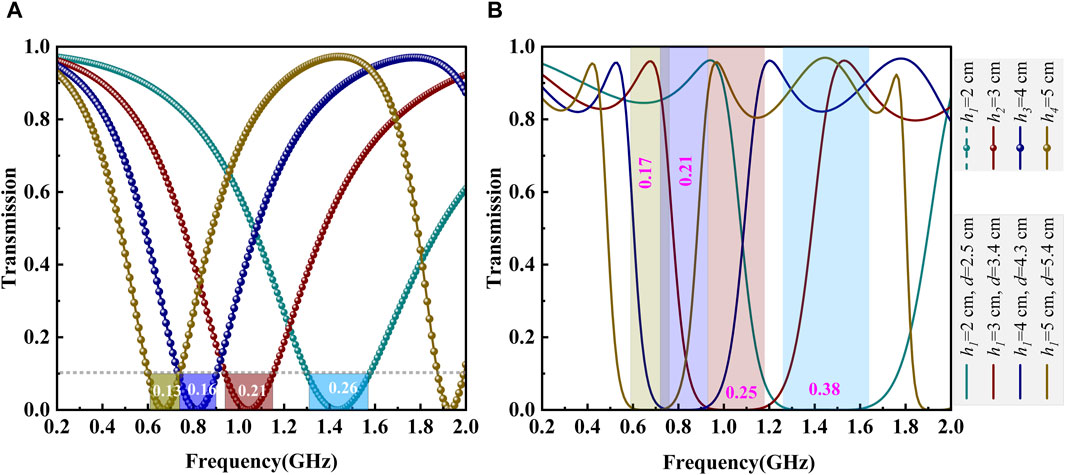
Figure 11. Transmission spectra with different structures and geometrical parameters. The parameters are shown in legend. (A) Single-tooth structure in Figure 2A, and the numbers attached to the color-transparence area represents the resonance width. (B) Double-teeth structure in Figure 1A, and the numbers attached to the color-transparence area are the filtering bandwidth.

4 Conclusion

In summary, based on our previous work focusing on filtering rules, the formation mechanism of the U-shaped spectrum excited by the PDP waveguide with a double-teeth structure is systematically investigated. The transmission responses of the waveguide with a tooth-shaped structure are investigated via numerical simulation and TLT. The simulation demonstrates that the presence of double teeth can induce a U-shaped spectrum, aligning well with the trends observed in TLT. To clarify its formation mechanism, the typical U-shaped spectrum is split into two parts: stopband and boundary edges. The stopband is attributed to the accumulation of destructive interference from each tooth, and its generated spectrum is theoretically derived via TLT and numerically demonstrated via a combination of spectra from independent tooth. Regarding the boundary edges, their formation is caused by Fano-like resonances. The coupling and interference between discrete states and a continuous state result in Fano-like resonances. The discrete states are provided by resonance modes of the equivalent FP cavity, i.e., the combination of double teeth and their connection PDP channel. The background spectrum by a combination of spectra from independent tooth can be regarded as the continuous state. In addition, the evolution process of the U-shaped spectrum is systematically explored, further demonstrating the validity of the generation mechanism. Especially in the evolution process, the bump may emerge around the stopband, which affects the filtering function greatly. At last, based on the parameter settings derived from standing theory prediction, numerical simulations have successfully observed a U-shaped spectrum with a quasi-symmetric profile. Our systematic and in-depth results contribute to understanding the evolution process of complicated spectra from double-teeth constructions, and provide feasible theory guidance in designing simple stopband filters.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

QN: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, supervision, validation, writing–review and editing, and writing–original draft. GW: conceptualization, data curation, formal analysis, investigation, methodology, validation, visualization, writing–original draft, and writing–review and editing. ZhZ: formal analysis, investigation, resources, software, and writing–review and editing. ZeZ: formal analysis, investigation, and writing–review and editing. PC: formal analysis, investigation, and writing–review and editing. XA: formal analysis, investigation, and writing–review and editing. LQ: investigation, methodology, and writing–review and editing. CY: formal analysis, investigation, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (Nos 92271202 and 92371105).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Faghani AA, Rafiee Z, Amanzadeh H, Yaghoubi E, Yaghoubi E. Tunable band-pass plasmonic filter and wavelength triple-channel demultiplexer based on square nanodisk resonator in MIM waveguide. Optik (2022) 257:168824. doi:10.1016/j.ijleo.2022.168824

CrossRef Full Text | Google Scholar

2. El Haffar R, Farkhsi A, Mahboub O. Optical properties of MIM plasmonic waveguide with an elliptical cavity resonator. Appl Phys A-mater (2020) 126:486. doi:10.1007/s00339-020-03660-w

CrossRef Full Text | Google Scholar

3. Keshizadeh H, Aghaei F, Bahador H, Heidarzadeh H. Improvement of cavity plasmon resonance in high-sensitivity MIM nanostructure with rectangular air stubs inside the hexagonal-ring resonator. Phys Scripta (2023) 98:025014. doi:10.1088/1402-4896/acb246

CrossRef Full Text | Google Scholar

4. Zhang J, Wang X, Zhu J, Chen TS, Zhang L, Yang H, et al. Metal–insulator–metal waveguide structure coupled with T-type and ring resonators for independent and tunable multiple Fano resonance and refractive index sensing. Opt Commun (2023) 528:128993. doi:10.1016/j.optcom.2022.128993

CrossRef Full Text | Google Scholar

5. Zhang RQ, Tian H, Liu Y, Cui SH. Multiple fano resonances in a metal–insulator–metal waveguide for nano-sensing of multiple biological parameters and tunable slow light. Photonics (2023) 10:703. doi:10.3390/photonics10070703

CrossRef Full Text | Google Scholar

6. Shahamat Y, Ghaffarinejad A, Vahedi M. Plasmon induced transparency and refractive index sensing in two nanocavities and double nanodisk resonators. Optik (2020) 202:163618. doi:10.1016/j.ijleo.2019.163618

CrossRef Full Text | Google Scholar

7. Khani S, Afsahi M. Optical refractive index sensors based on plasmon-induced transparency phenomenon in a plasmonic waveguide coupled to stub and nano-disk resonators. Plasmonics (2023) 18:255–70. doi:10.1007/s11468-022-01772-y

CrossRef Full Text | Google Scholar

8. Li XG, Song J, Zhang XJ. Design of terahertz metal-dielectric-metal waveguide with microfluidic sensing stub. Opt Commun (2016) 361:130–7. doi:10.1016/j.optcom.2015.10.007

CrossRef Full Text | Google Scholar

9. Lin XS, Huang XG. Tooth-shaped plasmonic waveguide filters with nanometeric sizes. Opt Lett (2008) 33:2874–6. doi:10.1364/ol.33.002874

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Pannipitiya A, Rukhlenko ID, Premaratne MT, Hattori H, Agrawal P. Improved transmission model for metal-dielectric-metal plasmonic waveguides with stub structure. Opt Express (2010) 18:6191–204. doi:10.1364/oe.18.006191

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Chen ZQ, Li HJ, Li Bo X, He ZH, Xu H, Zheng MF, et al. Tunable ultra-wide band-stop filter based on single-stub plasmonic-waveguide system. Appl Phys Express (2016) 9:102002. doi:10.7567/APEX.9.102002

CrossRef Full Text | Google Scholar

12. Wang HQ, Yang JB, Zhang JJ, Huang J, Wu WJ, Chen DB, et al. Tunable band-stop plasmonic waveguide filter with symmetrical multiple-teeth-shaped structure. Opt Lett (2016) 41:1233–6. doi:10.1364/OL.41.001233

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Zhou C, Huo YP, Guo YY, Niu QQ. Tunable multiple fano resonances and stable plasmonic band-stop filter based on a metal-insulator-metal waveguide. Plasmonics (2021) 16:1735–43. doi:10.1007/s11468-021-01437-2

CrossRef Full Text | Google Scholar

14. Najjari V, Mirzanejhad S, Ghadi A. Plasmonic refractive index sensor and plasmonic bandpass filter including graded 4-step waveguide based on Fano resonances. Plasmonics (2022) 17:1809–17. doi:10.1007/s11468-022-01667-y

CrossRef Full Text | Google Scholar

15. Zegaar I, Hocini A, Bensalah H, Harhouz A, Khedrouche D, Lahoubi M. Ultra wideband bandstop plasmonic filter in the NIR region based on stub resonators. Phys Scripta (2023) 98:055510. doi:10.1088/1402-4896/acc90a

CrossRef Full Text | Google Scholar

16. Kamari M, Hayati M, Khosravi S. Design of dual-wideband bandstop MIM plasmonic filter using multi-circular ring resonators. Opt Mater (2021) 122:111678. doi:10.1016/j.optmat.2021.111678

CrossRef Full Text | Google Scholar

17. Kamari M, Hayati M, Khosravi S. Tunable infrared wide band-stop plasmonic filter using T-shaped resonators. Mat Sci Semicon Proc (2021) 133:105983. doi:10.1016/j.mssp.2021.105983

CrossRef Full Text | Google Scholar

18. Kamari M, Hayati M, Khosravi S. Ultra-wide bandstop infrared MIM filter using aperture coupled square cavities. Phys Scripta (2023) 98:015509. doi:10.1088/1402-4896/aca43d

CrossRef Full Text | Google Scholar

19. Chou Chau YF, Chou Chao CT, Chiang HP. Ultra-broad bandgap metal-insulator-metal waveguide filter with symmetrical stubs and defects. Results Phys (2020) 17:103116. doi:10.1016/j.rinp.2020.103116

CrossRef Full Text | Google Scholar

20. Zegaar I, Hocini A, Harhouz A, Khedrouche D, Salah HB. An ultra-wideband bandstop plasmonic filter in mid-infrared band based on metal-insulator-metal waveguide coupled with an hexagonal resonator. Opt-India (2024) 53:272–81. doi:10.1007/s12596-023-01138-5

CrossRef Full Text | Google Scholar

21. Yu SL, Wang S, Zhao TG, Yu JG. Tunable ultra-width bandgap U-shaped band-stop filters of chip scale based on periodic staggered double-side trapezoidal resonators in a metallic nanowaveguide. Opt Commun (2020) 463:125439. doi:10.1016/j.optcom.2020.125439

CrossRef Full Text | Google Scholar

22. Li H, Jiao RZ. Plasmonic band-stop filters based on tooth structure. Opt Commun (2019) 439:201–5. doi:10.1016/j.optcom.2019.01.017

CrossRef Full Text | Google Scholar

23. Pae JS, Im SJ, Han YH. All-optical frequency-dependent magnetic switching in metal-insulator-metal stub structures. Appl Opt (2022) 61:2763–7. doi:10.1364/AO.452479

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Cao YH, Yan SB, Liu F, Wang J, Chang S, Liu G, et al. A refractive index sensor based on metal-insulator-metal coupling ring resonator with a stub. Front Phys (2024) 11:1342801. doi:10.3389/fphy.2023.1342801

CrossRef Full Text | Google Scholar

25. Chou Chau YF. Mid-infrared sensing properties of a plasmonic metal–insulator–metal waveguide with a single stub including defects. J Phys D Appl Phys (2020) 53:115401. doi:10.1088/1361-6463/ab5ec3

CrossRef Full Text | Google Scholar

26. Inami C, Kabe Y, Noyori Y, Iwai A, Bambina A, Miyagi S, et al. Experimental observation of multi-functional plasma-metamaterial composite for manipulation of electromagnetic-wave propagation. J Appl Phys (2021) 130:043301. doi:10.1063/5.0048004

CrossRef Full Text | Google Scholar

27. Kim H, Hopwood J. Plasma-enhanced metamaterials using microwave radiative power transfer. Plasma Sourc Sci. Technol (2018) 27:095007. doi:10.1088/1361-6595/aadb64

CrossRef Full Text | Google Scholar

28. Li JF, Wang Y, Zhou ZX, Yao JF, Liu JL, Lan ZH, et al. Experimental observations of communication in blackout, topological waveguiding and Dirac zero-index property in plasma sheath. Nanophotonics (2023) 12:10 1847–56. doi:10.1515/nanoph-2022-0800

CrossRef Full Text | Google Scholar

29. Rodríguez JA, Cappelli Mark A. Inverse design and experimental realization of plasma metamaterials. Phys Rev Appl (2023) 20:044017. doi:10.1103/PhysRevApplied.20.044017

CrossRef Full Text | Google Scholar

30. Wei GQ, Nie QY, Zhang ZL, Chen PQ, Yan CS. Plasma-based GHz tunable bandstop filter. Phys Plasmas (2022) 29:083505. doi:10.1063/5.0091487

CrossRef Full Text | Google Scholar

31. Tan HY, Zhou MJ, Zhuge LJ, Wu XM. Turning photonic band gap of one-dimensional photonic crystals on and off. J Phys D Appl Phys (2021) 54:085106. doi:10.1088/1361-6463/abc716

CrossRef Full Text | Google Scholar

32. Shi WX, Yuan B, Mao JF. Controllable enhancement of evanescent and transmitted waves by a plasma sphere. Front Phys (2022) 10:890213. doi:10.3389/fphy.2022.890213

CrossRef Full Text | Google Scholar

33. Zhang L, Ouyang JT. Experiment and simulation on one-dimensional plasma photonic crystals. Phys Plasmas (2014) 21:103514. doi:10.1063/1.4898627

CrossRef Full Text | Google Scholar

34. Wang HL, Yao JF, Fang C, Yuan CX, Li HP. The simulation of terahertz waves transmission in the arc plasma. Front Phys (2023) 11:1182972. doi:10.3389/fphy.2023.1182972

CrossRef Full Text | Google Scholar

35. Bahri H, Mouetsi S, Hocini A, Ben Salah H. A high sensitive sensor using MIM waveguide coupled with a rectangular cavity with Fano resonance. Opt Quant Electron (2021) 53:332. doi:10.1007/s11082-021-02976-y

CrossRef Full Text | Google Scholar

36. Cui PF, Huo YP, Zhang ZY, Wang YY, Song MN, Zhao C, et al. Band-stop filter and narrow band-pass filter based on metal-insulator-metal waveguide. Micro and Nanostructures (2023) 175:207503. doi:10.1016/j.micrna.2022.207503

CrossRef Full Text | Google Scholar

37. Sun YP, Qu DS, Wu QH, Li CL. MIM plasmonic sensors based on single-side ring cavity with one stub and their applications. Phys Scripta (2024) 99:025506. doi:10.1088/1402-4896/ad1862

CrossRef Full Text | Google Scholar

38. Liu JL, Fang GY, Zhao HF, Zhang Y, Liu ST. Surface plasmon reflector based on serial stub structure. Opt Express (2009) 17:20134–9. doi:10.1364/OE.17.020134

PubMed Abstract | CrossRef Full Text | Google Scholar