Abstract
The two-mass nonlinear vocal cord vibration system (VCVS) serves as a mechanical representation of the fundamental vocalization process. Traditional models of the VCVS, which are based on integer-order dynamics, often overlook the impact of memory effects. To address this limitation and enhance the accuracy of simulations, this study incorporates the memory effects of vocal cord vibrations by integrating the Grunwald–Letnikov fractional derivative into the two-mass nonlinear VCVS framework. Initially, a high-precision computational scheme is formulated for the two-mass nonlinear fractional-order VCVS. Subsequently, the model undergoes a comprehensive series of numerical simulations to investigate its dynamic characteristics. The findings reveal that the dynamics of the fractional-order VCVS exhibit a significantly higher complexity compared to the conventional integer-order models, with the emergence of novel chaotic behaviors that were previously unobserved.
1 Introduction
With the continuous development and improvement of computer technology and numerical simulation methods, the application of nonlinear vibration technology has been widely used in many fields and has become one of the hot topics in various fields.
Nonlinear dynamics can not only be used to analyze and explore certain natural phenomena and physical processes but can also be applied to other fields such as medicine, acoustics, ecology, and economics. Nonlinear vibration is very important in the study of MEMS oscillators [1, 2] and their interaction with structures. MEMS oscillators have a wide range of applications, including consumer electronics, automotive, healthcare, industries, aerospace, and many other fields. In recent years, vocal cord computer simulation technology has been used in the diagnosis of laryngeal diseases, can use the vocal cord pronunciation function [3], acoustic analysis to reflect the lesions of the vocal band. The study of the vocal cord vibration model [4] can reveal the characteristics of vocal band vibration and help understand the mechanism of vocal cord vibration. This study provides theoretical guidance for laryngeal pathology, artificial organs, voice therapy, and other medical fields and has practical application value. Researchers have also been trying to mimic human sound production by not only developing mechanical and mathematical models to describe the human organs associated with sound production but also studying the process of producing sound.
Vocal cord vibration can be simplified into various physical models, and the mass model represented by the spring mass block is a typical physical model of the vocal cord. These vocal cord vibration models represent vocal cord and polyp vibration with different numbers of spring mass blocks, such as the single-mass block model [5], the two-mass vocal cord model [6], three-mass vocal cord model, and H-C model. Latest research on the vocal cord vibration model involves the single-mass block model [5]. One of the simplest models is the single-degree-of-freedom single-mass model, which was first proposed by Dr. Flanagan and has since been studied by many researchers in related fields. Dr. Flanagan uses electricity acoustic analysis [7] which describes the dynamic knowledge of vocal cords and proposes a vocal cord model of a single-mass vibration system, in which self-excited vibration is caused by air flow that changes with pressure. [6] introduced the nonlinear properties of vocal cord organization into the two-mass model of vocal cords and proposed an improved nonlinear two-mass model of symmetrical vocal cords. In this model, the two vocal cords are assumed to be identical and move symmetrically relative to the glottic midline. When the glottis is open, the equation for vocal cord movement can be written as follows:
where is the displacement and is the quality of the Equation 1. is the damping force, and is the elastic force. In this model (1), Lucero and Koenig introduced the cubic characteristics of biological tissue elasticity [8], as shown in Equation 2:
On the other hand, for damping forces, instead of using the usual linear term , nonlinear properties are used:
represents the damping coefficient, and represent all coefficients in Equation 3.
The nonlinear term is used because when the width of the glottis increases, it is necessary to limit the amplitude of vocal cord vibration to ensure the effectiveness of the simulation.
As is known, there are many kinds of fractional derivatives, such as the Caputo fractional derivative, Caputo fractional derivative, Grnwald–Letnikov fractional derivative, and two-scale fractal derivative [9, 10] [11–13]. Fractional derivatives are widely used in many fields, such as engineering, physics, signal processing, and biomathematics. Some fractional derivatives have memory and nonlocality. In the VCVS, memory refers to the ability of the system to retain information about past events and use it to influence future behavior. Because of the memory of vocal cord vibration, the integer-order VCVS ignores the influence of memory. Therefore, in order to ensure the effectiveness of the simulation, the following fractional-order VCVS is considered in this paper:
where is the Grünwald–Letnikov differential derivative. ; the fractional-order model (4) is the integer-order model (1).
The Grnwald–Letnikov fractional calculus is named after the Czech mathematician Anton Karl Grnwald and Russian mathematician Aleksey Vasilievich. They defined Grnwald–Letnikov fractional calculus in 1867 and 1868, respectively. In the finite difference scheme of integer derivative, when calculating the derivative value of a node, the function value at the first few nodes is needed, or the function value at the next few nodes is needed. In contrast, the calculation of fractional derivatives requires the function values at all nodes before or after a certain point in time, so fractional calculus is assumed to have memory properties.
Some scholars have applied the fractional microproduct to memory modeling damping vibration systems. [14] focused on investigating the chaotic behavior of a 2-D vocal dynamical system using fractional-order Caputo difference operators, both commensurate and incommensurate. The methodology involves a dynamical analysis of the discrete fractional-order system, employing bifurcation theory, Lyapunov exponents, and coexisting attractors to understand the dynamical behavior. [15] gave a high-precision numerical approach to solving the space fractional Gray–Scott model. [16] gave some novel patterns for a class of fractional reaction–diffusion models with the Riesz fractional derivative. [17] researched on the pattern dynamics behavior of a fractional vegetation-water model in an arid flat environment. [18] researched the chaotic dynamic behavior of fractional-order financial systems with constant inelastic demand. [19] solved two-sided fractional super-diffusive partial differential equations with variable coefficients in a class of new reproducing kernel spaces. [20] studied the low frequency property of a fractal vibration model for a concrete beam. The fractal dimension formulation [21] made the fractal theory accessible to porous media and discontinuous time. [22] implemented the homotopy perturbation method for fractal duffing oscillators with arbitrary conditions. [23, 24] applied Li–He’s modified homotopy perturbation method for the doubly clamped electrically actuated microbeam-based micro-electromechanical system and the dropping shock response of a tangent nonlinear packaging system. [25] studied autonomous ordinary differential systems. [26] studied the Kaup–Newell system. [27] studied the nanobeam-based N/MEMS system, and [28] studied the fractal pull-in motion of electrostatic MEMS resonators. This paper introduces a numerical approach for the fractional-order vocal cord vibration model. [29] used the discontinuous Galerkin finite element method for the Caputo-type nonlinear conservation law. [30] used nonuniform L1/discontinuous Galerkin approximation for the time-fractional convection equation with a weak regular solution and the time fractional convection-diffusion-reaction Equation [31], and so on fractional systems [32, 33].
Fractional calculus has become a fundamental tool for modeling memory phenomena. However, due to the complexity and the nonlocality of fractional calculus, numerical methods are often used to approximate solutions to fractional differential equations, especially when analytical solutions are not feasible. The numerical computation of solving fractional differential equations is both cumbersome and time-consuming. Developing numerical and analytical methods for solving nonlinear fractional differential equations is currently a hot research topic. This paper introduces a high-precision method to study a class of fractional-order vocal cord vibration model.
2 Numerical method
Definition 2.1:[34] The Grünwald–Letnikov fractional derivative for the function with respect to of order is defined as follows:
where is the step size.
Let
Using Newton’s binomial theorem, get , and . Combining Equations 5, 6, we obtain the following Theorem 2.2.
[34] The Grünwald–Letnikov fractional derivative for the function with respect to of order can be calculated directly by the following formula:
where .
According to Equation 7, let , then Equation 4 can be converted to Equation 8 Using Theorem (2.2), we can obtain the numerical calculation scheme for Equation 8, which is Equation 9:In Ref. [35, 36] gave the construction method of generating function of any order in order to obtain high accuracy, and then gave the high-precision recursive formula of fractional derivative.
[35] The Grünwald–Letnikov fractional derivative for the function with respect to of order of the generating function for arbitrary is shown in Equation 10:where is shown in Equation 11: is shown in Equation 12:
Using Theorem (2.3), we can obtain the following the numerical calculation scheme (Equation 13) of Equation 8:
3 Numerical simulation and dynamics analysis
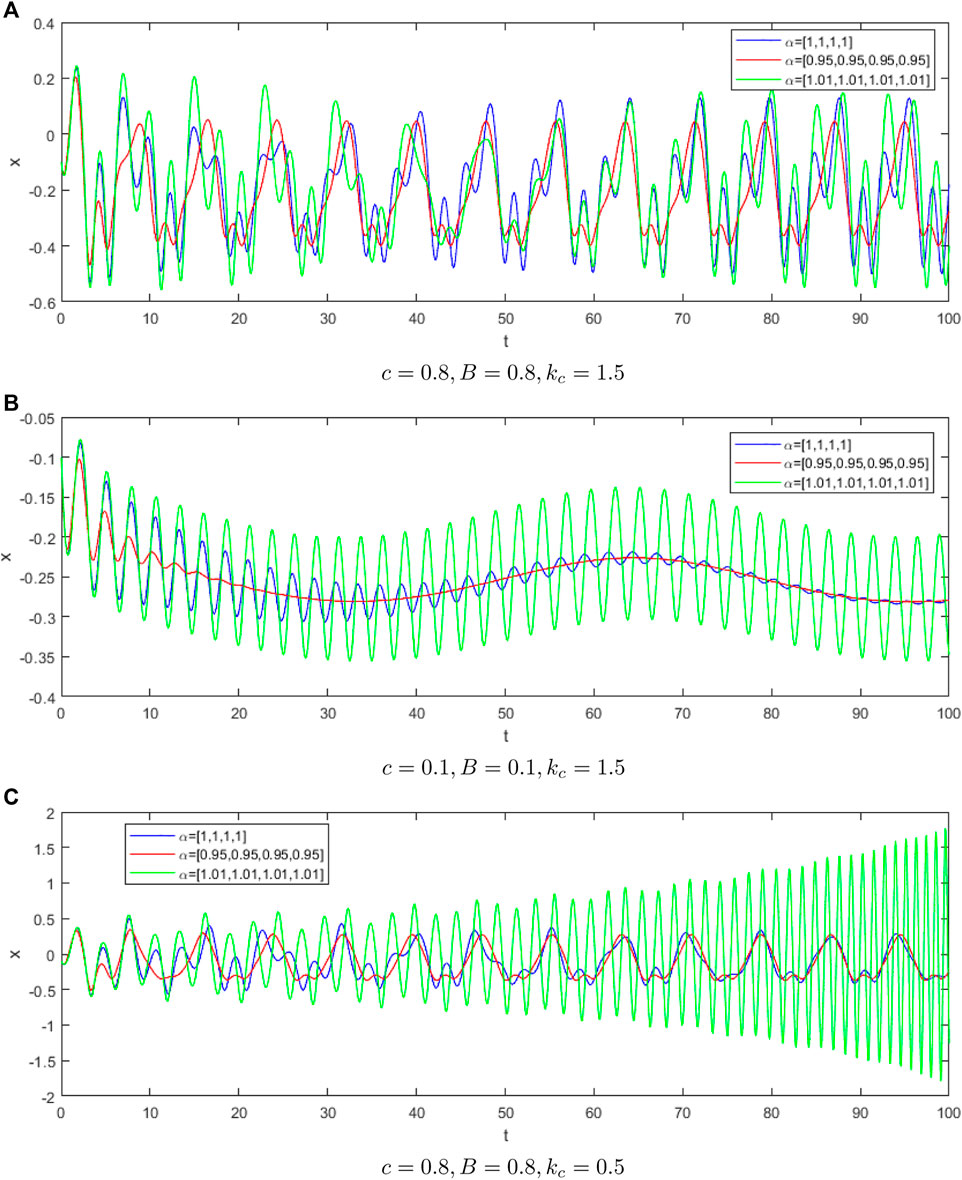
First, we consider the dynamic behavior of the VCVS with linear elasticity and resistance. Then, the dynamic behavior of the VCVS with nonlinear elasticity and resistance is considered. In numerical simulations, we set , initial values , the time step , , and .
3.1
We consider the dynamic behavior of the VCVS with linear elasticity and resistance .
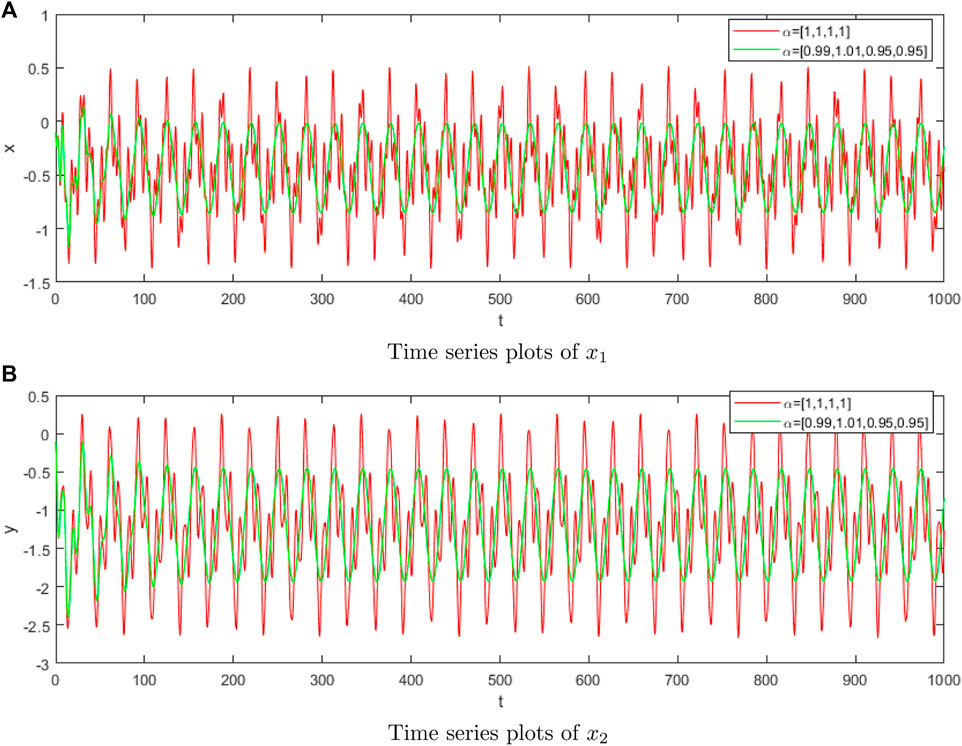
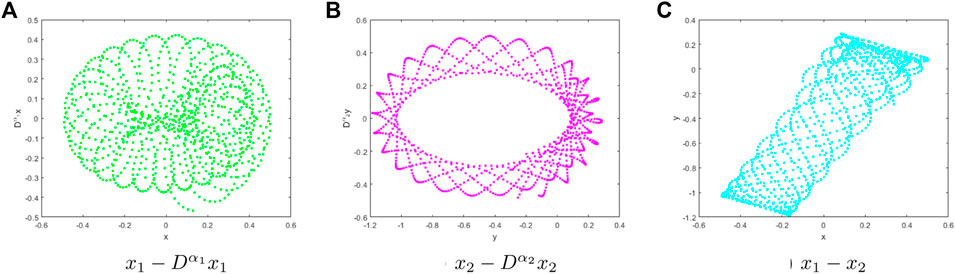
We choose different fractional derivatives and different parameters for numerical simulation. Figure 1 shows numerical simulation results of time series plots at . From Figure 1, it can be seen that the larger the derivative, the larger the amplitude of vocal cord vibration. At this time, the system is in a chaotic state. Figures 2, 3 show numerical simulation results of phase diagrams. Figure 4 shows numerical simulation results of 3D phase diagrams in different fractional derivatives.
FIGURE 1
FIGURE 2
FIGURE 3
FIGURE 4
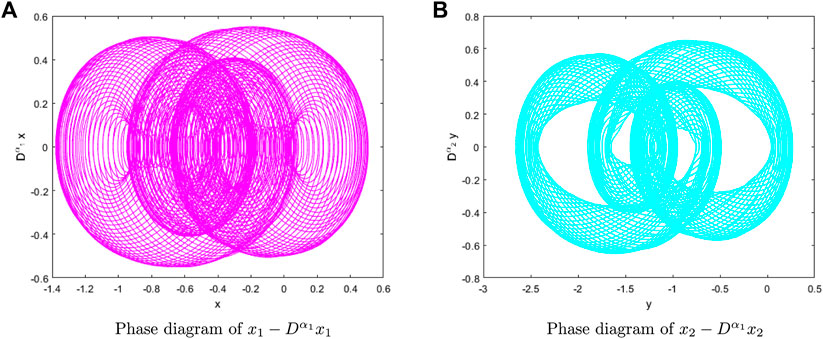
From numerical simulation results in Figure 1, we can observe the fractional derivative can control the amplitude of vocal cord vibration, which will lead to different sounds in the larynx, so as to ensure the effectiveness of the simulation. Figures 2–4 show the chaotic dynamic behavior of the fractional-order VCVS. Unstable and irregular movements of the vocal cords can indicate disease or abnormalities. The dynamic behavior of the fractional-order VCVS is much more complex than that of the integer-order model.
Figure 5 shows the Poincare surface of section at .
FIGURE 5
3.2
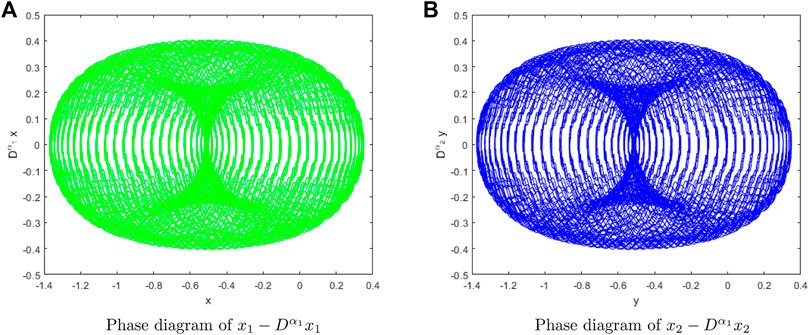
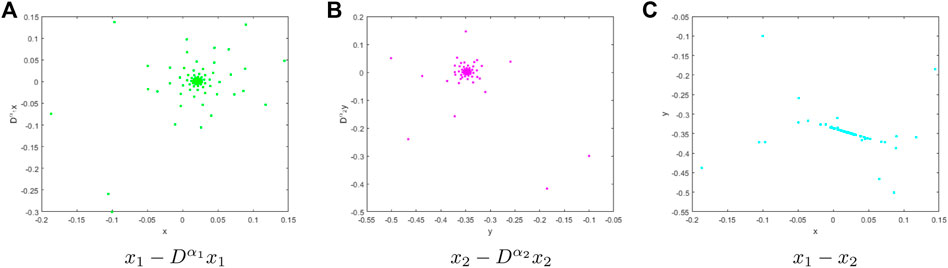
The nonlinear term is used because it is necessary to limit the amplitude and chaotic behavior of vocal cord vibration as the width of the glottis increases. are all coefficients.
Figure 6 shows the Poincare surface of section at . From Figures 5, 6, we can see that the chaotic behavior of vocal cord vibration can be controlled by adding a nonlinear term to the system.
FIGURE 6
When there is only one fixed point and a few discrete points on the Poincare section, the system can be judged to be periodically vibrating. When the Poincare section is a closed curve, it can be determined that the system is quasi-periodic vibration. When the Poincare section is a dense piece of points and there is a hierarchical structure, the system motion can be determined to be in a chaotic state.
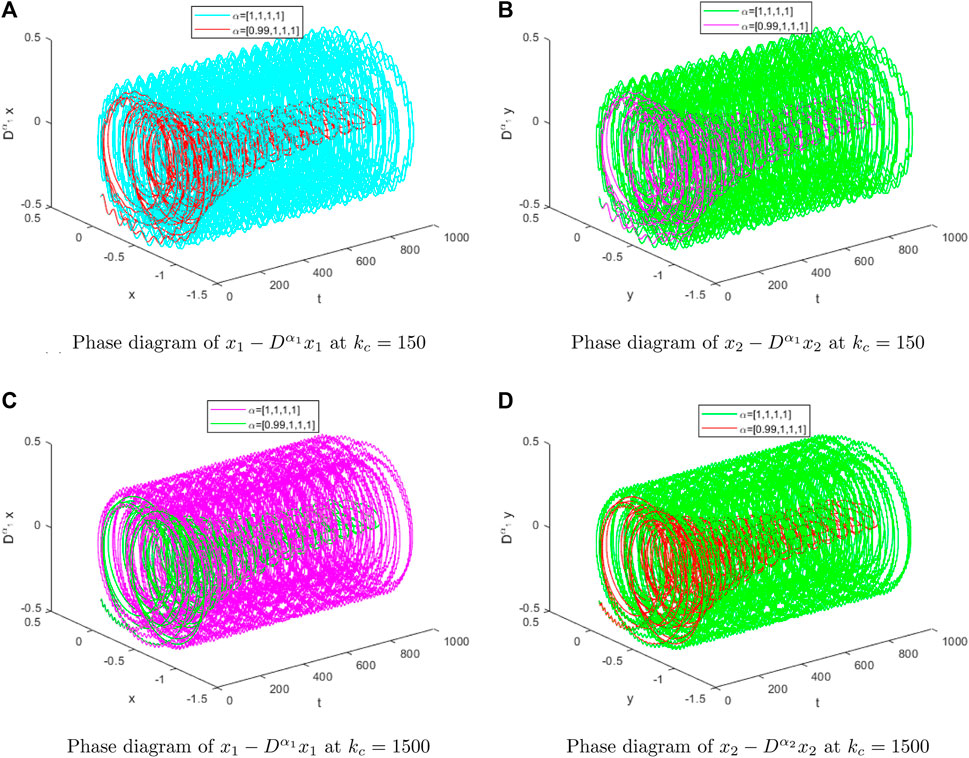
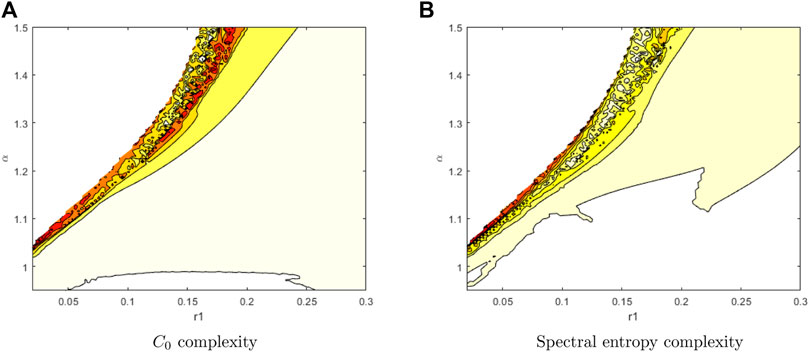
Figure 7 shows time series plots at different fractional derivatives . From Figure 8, we can see the fractional derivative can control the amplitude and chaotic behavior of vocal cord vibration.
FIGURE 7
FIGURE 8
Figure 8 shows and spectral entropy complexity at and . From Figure 8, we show the effect of parameter and fractional derivative on the complexity of the system. The chaotic behavior of vocal cord vibration cannot be completely controlled by nonlinear dynamics, where . The chaotic and periodic regions of the system can be seen more clearly by using and spectral entropy complexity.
The dynamic behavior of the system under fractional-order influence is analyzed, and the advantages of introducing fractional-order operators into the vocal cord vibration system are demonstrated. In this paper, a series of numerical simulations are carried out to explore the dynamic behavior of the model. The results show that it is very different from the traditional whole-order model, showing a richer and more complex dynamic landscape. Notably, the introduction of fractional derivatives reveals chaotic behavior in the system that was not previously observed.
4 Conclusion
This paper delves into the study of a two-mass nonlinear fractional-order VCVS, proposing a high-precision control scheme. The incorporation of nonlinear elements and fractional derivatives is motivated by their ability to regulate the amplitude and chaotic tendencies of vocal cord vibrations as the glottis widens. This regulation is essential for producing distinct vocal sounds in the throat, thereby enhancing the efficacy of the simulation. Numerical simulations reveal the system’s dynamic behavior and highlight intriguing novel chaotic dynamics. These findings offer innovative insights into the mechanical aspects of the vocal articulation process. In the future, we will study the multi-mass block model of the asymmetric vocal cord vibration system.
Statements
Data availability statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
Author contributions
Y-XH: formal analysis, software, and writing–original draft. J-XZ: software and writing–original draft. Y-LW: formal analysis, funding acquisition, methodology, and writing–original draft.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This paper is supported by the Doctoral research start-up fund of the Inner Mongolia University of Technology (DC2300001252) and the Natural Science Foundation of Inner Mongolia (2024LHMS06025).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
ShahSYNikhilBet alThe dynamics of MEMS-Colpitts oscillators. Nonlinear Dyn (2023) 111(19):17639–51. 10.1007/s11071-023-08774-3
2.
HuanRDaiHWangXYangQShiZet alAdaptive frequency-stabilization of MEMS oscillators using mode coupling. J Micromechanics Microengineering (2024) 34:065002. 10.1088/1361-6439/ad42a7
3.
AdachiSYuJ. Two-dimensional model of vocal fold vibration for sound synthesis of voice and soprano singing. J Acoust Soc America (2005) 117:3213–24. 10.1121/1.1861592
4.
WurzbacherTSchwarzRDöllingerMHoppeUEysholdtULohschellerJ. Model-based classification of nonstationary vocal fold vibrations. J Acoust Soc America (2006) 120:1012–27. 10.1121/1.2211550
5.
MehtaDDDeliyskiDDQuatieriTFHillmanRE. Automated measurement of vocal fold vibratory asymmetry from high-speed videoendoscopy recordings. J Speech, Lang Hearing Res (2011) 54:47–54. 10.1044/1092-4388(2010/10-0026)
6.
LuceroJCKoenigLL. Simulations of temporal patterns of oral airflow in men and women using a two-mass model of the vocal folds under dynamic control. J Acoust Soc America (2005) 117:1362–72. 10.1121/1.1853235
7.
CronjaegerR. Die entstehung des primaeren stimmklangs im menschlichen Kehlkopf–Ein Model. Braunschweig: University of Braunschweig (1978). Ph.D. Dissertation.
8.
OnerciTM. Diagnosis in otorhinolaryngology. London: Springer (2010).
9.
AnjumNHeCHHeJH. Two-scale fractal theory for the population dynamics. Fractals (2021) 29(7):2150182. 10.1142/s0218348x21501826
10.
HeJH. A tutorial review on fractal spacetime and fractional calculus. Int J Theor Phys (2014) 53(11):3698–718. 10.1007/s10773-014-2123-8
11.
NaveedATulAQ. Application of he’s fractional derivative and fractional complex transform for time fractional Camassa-Holm equation. Therm Sci (2020) 24(5A):3023–30. 10.2298/TSCI190930450A
12.
QuraTAHeJHAnjumNAliM. The fractional complex transform: a novel approach to the time-fractional Schrödinger equation. Fractals (2020) 28(7):2050141. 10.1142/s0218348x20501418
13.
Tul AinQAnjumNDinAZebADjilaliSKhanZA. On the analysis of Caputo fractional order dynamics of Middle East Lungs Coronavirus (MERS-CoV) model. Alexandria Eng J (2022) 61(7):5123–31. 10.1016/j.aej.2021.10.016
14.
VigneshDBanerjeeS. Dynamical analysis of a fractional discrete-time vocal system. Nonlinear Dyn (2023) 111:4501–15. 10.1007/s11071-022-08086-y
15.
HanCWangYLLiZY. A high-precision numerical approach to solving space fractional Gray-Scott model. Appl Mathematics Lett (2022) 125:107759. 10.1016/j.aml.2021.107759
16.
HanCWangYLLiZY. Novel patterns in a class of fractional reaction-diffusion models with the Riesz fractional derivative. Mathematics Comput Simulation (2022) 202:149–63. 10.1016/j.matcom.2022.05.037
17.
GaoXLZhangHLWangYLLiZY. Research on pattern dynamics behavior of a fractional vegetation-water model in arid flat environment. Fractal and Fractional (2024) 8(5):264. 10.3390/fractalfract8050264
18.
GaoXLLiZYWangYL. Chaotic dynamic behavior of a fractional-order financial system with constant inelastic demand. Int J Bifurcation Chaos (2024) 34(9):2450111. 10.1142/s0218127424501116
19.
LiZYChenQTWangYLLiXY. Solving two-sided fractional super-diffusive partial differential equations with variable coefficients in a class of new reproducing kernel spaces. Fractal and Fractional (2022) 6(9):492. 10.3390/fractalfract6090492
20.
HeCHLiuCHeJHGepreelKA. Low frequency property of a fractal vibration model for a concrete beam. Fractals (2021) 29(5):2150117. 10.1142/s0218348x21501176
21.
HeCHLiuC. Fractal dimensions of a porous concrete and its effect on the concrete’s strength. Facta Universitatis Ser Mech Engineering/(2023) 21(1):137–50. 10.22190/fume221215005h
22.
HeJHJiaoMLHeCH. Homotopy perturbation method for fractal duffing oscillators with arbitrary conditions. Fractals (2022) 30(9):2250165. 10.1142/s0218348x22501651
23.
AnjumNHeJHAinQTTianD. Li-He-s modified homotopy perturbation method for doubly-clamped electrically actuated microbeams-based microelectromechanical system. Facta Universitatis-series Mech Eng (2021) 19(4):601–12. 10.22190/fume210112025a
24.
JiQPWangJLuLXGeCF. Li-He’s modified homotopy perturbation method coupled with the energy method for the dropping shock response of a tangent nonlinear packaging system. J Low Frequency Noise, Vibration Active Control (2021) 40(2):675–82. 10.1177/1461348420914457
25.
HeJH. Variational iteration method for autonomous ordinary differential systems. Appl Mathematics Comput (2000) 114:115–23. 10.1016/s0096-3003(99)00104-6
26.
WuYHeJH. Variational principle for the Kaup-Newell system. J Comput Appl Mech (2023) 54:405–9. 10.22059/JCAMECH.2023.365116.875
27.
TangWAnjumNHeJH. Variational iteration method for the nanobeams-based N/MEMS system. MethodsX (2023) 11:102465. 10.1016/j.mex.2023.102465
28.
FengGQZhangLTangW. Fractal pull-in motion of electrostatic MEMS resonators by the variational iteration method. Fractals (2023) 9(31):1–15. 10.1142/s0218348x23501220
29.
LiCPWangZ. The discontinuous Galerkin finite element method for Caputo-type nonlinear conservation law. Mathematics Comput Simulation (2020) 169:51–73. 10.1016/j.matcom.2019.09.021
30.
LiCPWangZ. Non-uniform L1/discontinuous Galerkin approximation for the time-fractional convection equation with weak regular solution. Mathematics Comput Simulation (2021) 182:838–57. 10.1016/j.matcom.2020.12.007
31.
LiCPWangZ. Numerical methods for the time fractional convection-difusion-reaction equation. Numer Funct Anal Optimization (2021) 42(10):1115–53. 10.1080/01630563.2021.1936019
32.
GaoXLZhangHLLiXY. Research on pattern dynamics of a class of predator-prey model with interval biological coefficients for capture. AIMS Mathematics (2024) 9(7):18506–27. 10.3934/math.2024901
33.
LiCPLiZQWangZ. Mathematical analysis and the local discontinuous Galerkin method for Caputo-Hadamard fractional partial differential equation. J Scientific Comput (2020) 85(2):41. 10.1007/s10915-020-01353-3
34.
Daftardar-GejjiV, editor. Fractional calculus and fractional differential equations. Singapore: Springer (2019). 10.1007/978-981-13-9227-6
35.
XueDY. Fractional calculus and fractional-order control. Beijing, China: Science Press (2018).
36.
XueDYZhaoCNChenYQ. A modified approximation method of fractional order system. In: Proceedings of IEEE conference on mechatronics and automation. China: Luoyang (2006). p. 1043–8. 10.1109/ICMA.2006.257769
Summary
Keywords
fractional-order vibration system, novel chaotic dynamic behavior, high-precision numerical method, vibration system, vocal cord vibration system
Citation
Han Y-X, Zhang J-X and Wang Y-L (2024) Dynamic behavior of a two-mass nonlinear fractional-order vibration system. Front. Phys. 12:1452138. doi: 10.3389/fphy.2024.1452138
Received
20 June 2024
Accepted
09 August 2024
Published
04 September 2024
Volume
12 - 2024
Edited by
Jesus Manuel Munoz-Pacheco, Benemérita Universidad Autónoma de Puebla, Mexico
Reviewed by
Naveed Anjum, Government College University, Pakistan
Njitacke Tabekoueng Zeric, University of Buea, Cameroon
Guangqing Feng, Henan Polytechnic University, China
Updates
Copyright
© 2024 Han, Zhang and Wang.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yu-Lan Wang, wylnei@163.com
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.