
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 05 September 2024
Sec. Optics and Photonics
Volume 12 - 2024 | https://doi.org/10.3389/fphy.2024.1452087
The combination of high-order modulation formats and linewidth-tolerant carrier phase estimation (CPE) can effectively improve spectrum efficiency and relax the limitation of laser linewidth. This paper presents a simple two-stage CPE algorithm for polarization-multiplexed (PM) 32-quadrature amplitude modulation (32-QAM) coherent optical communication systems. The algorithm uses an enhanced QPSK partitioning algorithm combined with a simplified 4th power CPE method for coarse estimation in the initial stage and maximum likelihood (ML) detection in the subsequent fine stage. The CPE algorithm significantly increases the number of symbols used in the first stage of coarse estimation. This results in a significant increase in the stability and reliability of the phase estimation, and the CPE algorithm significantly reduces the computational complexity. The optimal parameters, phase estimation performance, and system performance of the algorithm were investigated by building a 22 Gbaud PM 32-QAM coherent system simulation platform and a 5 Gbaud PM 32-QAM coherent system experimental platform. The results show that the proposed two-stage CPE algorithm has a stronger linewidth tolerance difference than the conventional QPSK, and the two-stage CPE algorithm with an optimal block length of 105 performs comparable to blind phase search (BPS). The optical signal noise Ratio (OSNR) value is 21.2 dB and the bit error rate (BER) is 1.8 × 10−3 for the optimal block length of 105. The receiving-end DSP unit with a flexible scheme and good communication performance will have potential applications in adaptive elastic optical networks.
Coherent optical transmission systems using high-order quadrature amplitude modulation (QAM) formats joined by digital signal processing (DSP) have been paid more attention, due to their high spectral efficiency (SE) and low cost [1, 2]. Polarization-multiplexed quadrature phase-shift keying (PM-QPSK), with a data rate of 100 Gb/s, is available for commercial systems at present. Higher spectral efficiency modulation formats, such as 32-QAM, mean higher spectral resource utilization and greater per-channel transmission capacity, with reduced symbol rates and channel bandwidth [3–5].
QAM coherent optical communication can effectively improve spectral efficiency [6]. At the same time, to obtain higher data rate transmission capacity requirements, the spectral efficiency of long-distance communication can be improved by using advanced DSP schemes, which adopt higher-order data modulation formats such as 64-QAM and 128-QAM [7, 8]. For high-capacity, high-spectral efficiency optical transmission systems, the receiver-side efficient DSP algorithm is crucial in eliminating the need for expensive optical compensation devices, as it can make up for transmission impairments in the electrical digital field [9–12].
In 2024, Kumari et al. explored an optical wireless communication (OWC) system from a high-altitude platform (HAP) to a satellite, using orbital angular momentum (OAM) multiplexing orthogonal frequency division multiplexing (OFDM) technology [13]. The scheme can achieve a transmission rate of 200 Gbps per channel, maintaining a total data rate of 800 Gbps at a maximum distance of 5,000 km. It demonstrates high performance and scalability in extreme environments, especially when dealing with communications over long distances and high data rates. Reference [14] proposed a performance analysis of a symmetrical bidirectional 40 Gbps m-QAM-OFDM modulated TWDM-PON system based on multi-color LD. By combining multi-color laser diodes (LDs) for visible light communication (VLC), high-speed data transmission on a composite optical fiber/VLC network is achieved. The system can maintain a low BER under various link conditions and successfully transmit data rates up to 120 Gbps, demonstrating its effectiveness in improving transmission performance and network efficiency.
Saw et al. analyzed the FSO system based on Co-OFDM technology and analyzed the impact of atmospheric turbulence and pointing errors. An effective phase estimation algorithm can significantly reduce communication interruptions and BER caused by environmental changes, especially in higher-order QAM systems [15]. Sharma and Chaudhary proposed an OFDM-FSO integrated system to extend the FSO link at high transmission rates under clear weather conditions and evaluated the performance of the hybrid system using ODSB, OSSB, and OTSB schemes. Through accurate carrier phase control, the performance of the FSO system can be improved, especially in OFDM systems, where accurate phase estimation is crucial to signal quality [16]. In the hybrid system of wireless and wired, literature [17] studies the wired and wireless OFDM-OSSB-RoF transmission system under the high transmission rate of a 4 QAM sequence generator. It also plays a crucial role in reducing the degradation introduced by fiber dispersion under different laser spectral widths. Within a range of 10–100 km, this hybrid RoF system effectively improves the laser spectrum width by reducing it from 10 MHz to 100 kHz at a transmission rate of 10/20 Gbps.
The phase noise produced by the linewidth of the transmitter laser and the local oscillator (LO) is one of the factors conditioning the performance of the high-order QAM system, and an efficient DSP algorithm is needed for compensation and estimation. To compensate for phase noise and increase line tolerance, carrier phase estimation algorithms have attracted the attention of many scholars. They are considered key DSP algorithms for high-spectral efficiency QAM coherent optical systems [18]. Many have already researched different carrier-phase estimation methods. The extant CPE algorithms for high-order QAM systems can be divided into data-aided (DA) [19] and non-DA (NDA) methods [20, 21]. NDA CPE schemes have higher spectral efficiency because they do not cause overhead; hence, NDA CPE schemes have attracted much attention. The most popular NDA CPE schemes are the optimal-performance blind phase search (BPS) [22] or the quadrature phase-shift keying partitioning (QPSK partitioning) [23–25]. The BPS has excellent performance but high computational complexity. After constellation partition in CPE, the QPSK partitioning algorithm using a feedforward structure with low computational complexity can use conventional Viterbi–Viterbi phase estimation (VVPE) methods [26]. Moreover, multi-phase CPE algorithms exist, such as the two-stage BPS algorithms [27], the QPSK partitioning + maximum likelihood (ML) algorithm [28], and the BPS + ML algorithm [29]. However, while QPSK partitioning has relatively low computational complexity, the shortage of sufficient QPSK-like symbols and stringent linewidth requirements make it unsuitable for use as a first-stage phase estimation method for higher-order m-QAM signals, especially when the 32-QAM constellation is non-square and only a small number of QPSK symbols are available for CPE. The main innovations of this article are as follows:
(1) Innovative algorithm design: This paper uses the enhanced QPSK segmentation algorithm combined with the simplified fourth power CPE method for rough estimation, and uses ML detection for fine estimation in the subsequent stage. This two-stage design effectively increases the number of symbols available for primary estimation, thereby improving the stability and reliability of phase estimation.
(2) Excellent phase estimation: The algorithm in this article demonstrates excellent phase estimation performance and can support higher linewidth-symbol duration (
(3) Reduction of computational complexity: The method in this paper significantly reduces the computational complexity by combining the simplified fourth power method and ML detection. Compared with the BPS method in literature (15, 24), this scheme does not require a large number of test phases, thereby reducing the resource requirements and power consumption of hardware implementation. The computational complexity is significantly reduced by simplifying the calculation steps, which is extremely beneficial for hardware implementation. This method has lower complexity in practical applications, especially in achieving computational simplification while maintaining performance.
At present, coherent 100G long-distance transmission mainly uses QPSK, while that for 400G long-distance transmission is mainly 16QAM. In the pursuit of larger capacity and faster rates, high-order 32-QAM is a promising solution. Aiming at the difficulty of accurately estimating the phase of 32-QAM constellation diagrams, this paper proposes a simple two-stage CPE algorithm for 32-QAM coherent optical communication systems. This algorithm combines an improved QPSK partitioning technique with a simplified fourth-power CPE method for coarse estimation and uses ML detection for fine estimation in the subsequent stage. The results show that the two-order estimation method used by the CPE algorithm can track phase noise variations using shorter estimation block lengths with low complexity, compared to conventional algorithms based on QPSK partitioning and optimal BPS. The two-stage CPE algorithm proposed in this paper significantly increases the number of symbols available in the primary estimation stage, thereby enhancing the stability and reliability of phase estimation while reducing computational complexity. In addition, the computational complexity is significantly reduced through simplified calculation steps, allowing the scheme to maintain lower BER in noisy environments, showing stronger line width tolerance and better system performance than traditional methods.
For QPSK signals, the VVPE algorithm can achieve carrier phase recovery very well. To apply this algorithm to QAM systems, one possible way is to extract data points from the input QAM signal sequence that have the phase characteristics of the QPSK signal and use the VVPE algorithm on such data points to remove the modulation phase information, which is called the QPSK partitioning algorithm.
Figure 1 shows that the 32-QAM symbols exist on five different rings. Based on the received sample’s different amplitudes, the traditional QPSK partitioning approach raises only the symbols highlighted using red points—that is, the symbols with modulation angles of π/4 + k·π/2 (k = 0 … 3) in Figure 1A—to the 4th power to dismiss the modulation phase data. Nevertheless, only 8/32 of the 32-QAM symbols are adopted in statistics for the traditional QPSK partitioning approach, which results in poor linewidth tolerance performance and failure to detect slips in the cycle [24].

Figure 1. (A) Constellation diagram for 32-QAM. (B) The enhanced QPSK partitioning scheme for 32-QAM.
In [18], an extended QPSK partitioning scheme was detailed, in which the symbols employed in QPSK partitioning are emphasized by the red, purple, and blue points in Figure 1B. The primary purpose is to increase the available symbols in QPSK partitioning of 32-QAM. In Figure 1B, the symbols in purple are rotated by 45° to minimize the phase offsets to ±11.3° to the nearest 45° diagonal, enabling those symbols to be used for CPE. Similarly, the blue constellation point on the outermost circle can also participate in carrier-phase estimation because it has a phase offset of 14° from the nearest 45° diagonal.
To make the CPE less computationally complex, the simplified Mth-power method [30] is applied instead of the conventional Mth-power operation, where an absolute operation is approximated and the VandV algorithm is made free of a multiplier CPE. Furthermore, maximum likelihood (ML) detection is also introduced as the second fine stage to estimate the phase more accurately. The block diagram of the simple two-stage CPE algorithm for 32-QAM is shown in Figure 2, where the enhanced QPSK division combined with the simplified 4th power CPE method is used as the initial coarse phase and the ML detection is used as the subsequent fine phase, with the following steps:

Figure 2. Block diagram of the two-stage CPE algorithm for 32-QAM coherent optical communication systems.
Coarse estimation stage: the input symbol
Fine estimation stage: the input is the output signal of the coarse estimation stage, and the output signal
Figure 2 shows that, according to the enhanced QPSK partitioning algorithm, the initial stage phase estimation
The initial block of N1 symbols is selected from the input symbols
After the first-stage estimation result is obtained and the carrier-phase coarse compensation of the N1 consecutive symbols is completed, the shorter block length N2 is used as the block length of the second-stage ML algorithm to better track the phase transformation. The phase estimation in the second ML stage is expressed as follows:
Finally, as shown in Equation 4, the carrier phase estimation value
The main contribution of this article is to propose a simplified two-stage carrier phase estimation algorithm for 32-QAM coherent optical communication systems. This algorithm combines for the first time an improved QPSK segmentation and a simplified fourth power method for coarse estimation, and applies maximum likelihood (ML) detection in the subsequent fine estimation stage. With this innovative approach, the number of symbols available for phase estimation in the first stage is significantly increased, thereby enhancing the stability and reliability of phase estimation and significantly reducing computational complexity.
The flow chart of the CPE algorithm for QPSK partitioning is shown in Figure 3. The proposed quasi-QPSK segmentation is deployed in the first coarse estimation stage. The second stage is the fine estimation ML.
The proposed two-stage CPE algorithm is designed for 32-QAM coherent optical communication systems to improve the accuracy of phase estimation and reduce computational complexity. The following is a detailed step-by-step explanation of the algorithm, combined with theoretical foundations and parameter settings:
The received signal
The constellation points are classified into different rings according to their amplitude:
C1 and C3 rings usually contain points with lower amplitudes. C4 and C5 rings contain points with higher amplitudes.
The points on each ring have different phase and amplitude characteristics. For preliminary processing, the constellation points of all received signals are first transformed to the fourth power to simplify the phase complexity. Equation 5 describes the operation of raising the complex symbol
Use the simplified signal
According to the phase obtained by the rough estimation
The maximum likelihood estimation (ML) method is applied to the constellation points that have been selectively rotated to further refine the phase. This step uses a more detailed algorithm to optimize the phase estimation, as shown in Equations 2, 3.
Using the carrier phase estimation value obtained in the second stage, the carrier phase compensation is performed on the sampling point through the sliding window, which is the output signal. Use the refined phase
To explore the performance of the suggested two-stage CPE algorithm for 32-QAM coherent optical communication systems, a 22 Gbaud polarization-multiplexing (PM) 32-QAM simulation platform was constructed, with the phase noise simulated as a Wiener process, as shown in Figure 3. After the signals were sampled at 44 GSa/s (two samples per symbol), digital signal processing was performed. This consisted of chromatic dispersion compensation, channel adaptive equalization, polarization demultiplexing, frequency offset estimation, and finally, the target CPE algorithm. We assumed that the transition impairments had been fully compensated before CPE. As shown in Table 1, the simulation parameter diagram.
Figure 4 uses a coherent system, at the transmitter side, the source data is 22Gbaud PM 32-QAM, after two IQ modulation into the fiber optic link, we use VOA to adjust the signal strength. The signal is amplified by EDFA to compensate for the transmission loss. At the receiving end, the signal is decomposed into two polarized components by PBS, which go through a 90-degree Hybrid and enter into BPDs, and the I and Q components of each polarization direction each go through a pair of BPDs, thus generating four electrical signals, Ix, Qx, Iy, Qy, which are then fed into the ADC. the signals finally enter into the DSP module for data processing and parsing.
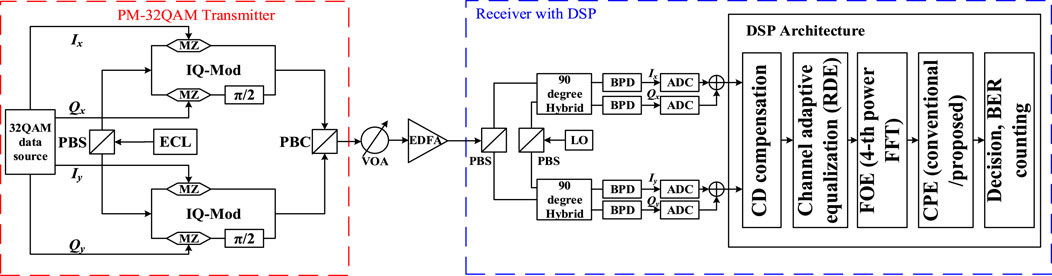
Figure 4. Block diagram of the simulation setup for 22Gbaud PM 32-QAM coherent system. IQ-Mod: in-phase-quadrature modulator. MZ: Mach-Zehnder modulator. ECL: external cavity laser. PBS: polarization beam splitter. PBC: polarization beam combiner. VOA: variable Optical Attenuator. EDFA: erbium-doped fiber amplifier. LO: local oscillator. BPD: balanced photodiode. ADC: Analog-to-digital.
As is well known, the block length has a great impact upon the BER performance for 32-QAM coherent optical systems, so the optimal length is crucial to a CPE algorithm. Usually, ASE noise coordinates with phase noise suppression are used to determine the optimal block length, because that larger block length is useful to mitigate the additive noise, while shorter block length is also expected to help maintain the phase-tracking speed. Figure 5 displays the joined linewidth–symbol duration product
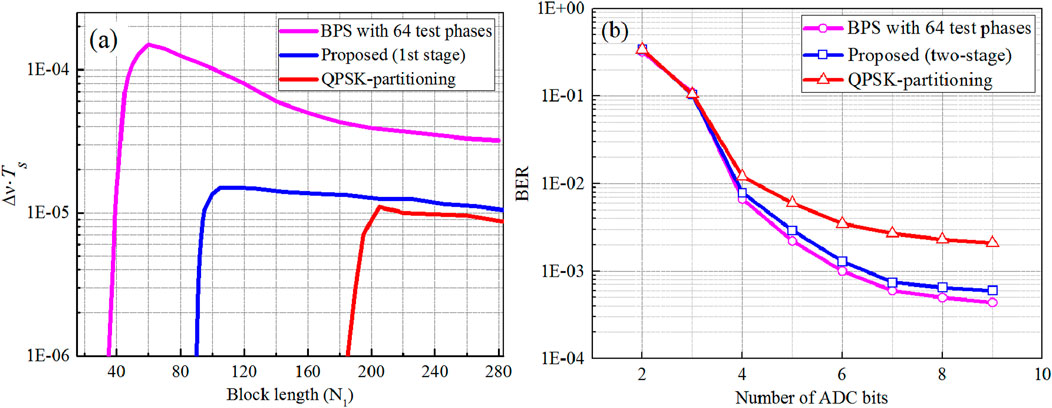
Figure 5. (A) Joined linewidth–symbol duration product
Figure 5B shows the effect of ADC resolution on BER performance for the suggested two-stage CPE and the other two algorithms at an OSNR of 24 dB with
Figure 6 demonstrates the constellation after compensation in each period at an OSNR of 24 dB with
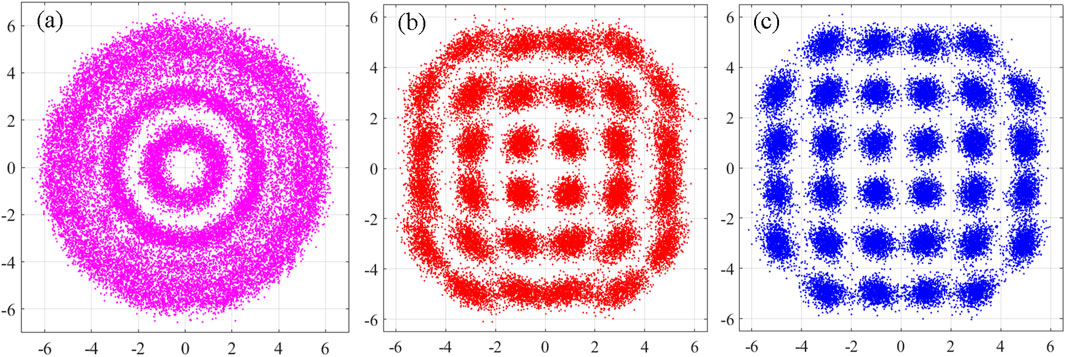
Figure 6. Constellations of 32-QAM after each stage of compensation: (A) after the frequency offset compensation; (B) after the first enhanced QPSK partitioning stage; (C) after the second ML stage. All at an OSNR of 24 dB with
As can be seen from Figure 7, under different line width-symbol duration product (
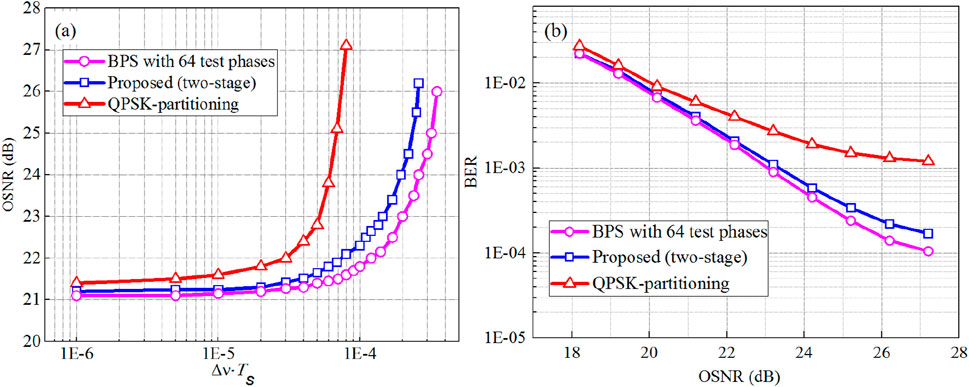
Figure 7. (A) Required OSNR versus the combined linewidth–symbol duration product
In a 32-QAM optical coherent system with
The experimental design for a 5 Gbaud PM 32-QAM back-to-back transmission system with a commercial transmitter and LO lasers is depicted in Figure 8. On the transmitter side, a pseudo-random binary sequence (PRBS) with a length of 217-1 was mapped into 32-QAM format. Then, the digital32-QAM signals were uploaded into an arbitrary waveform generator (AWG) (Keysight M8190A) operated at 5 GSa/s for digital-to-analog (D/A) conversion. A continuous-wave laser with a linewidth of <100 kHz acted as an optical carrier for the transmitter, and the carrier’s center wavelength was 1,550 nm. The two polarizations modulated using the dual-polarization IQ modulator were combined with PBC and amplified through the EDFA, which was used for the generation of certain amount of ASE noise in the process of adjusting the OSNR. Then, the back-to-back optical signal transmitted was sent into a tunable optical filter to remove the out-of-band noise. An optical spectrum analyzer (OSA) with a noise reference bandwidth of 0.1 nm was used to gauge the OSNR. The local oscillator (LO) laser was identical to the transmitter laser, with linewidth <100 kHz at 1,550 nm. With the optical signal and LO carrier transmitted to a commercial coherent receiver to achieve photoelectric conversion, the four electrical signals were digitized using an oscilloscope working at 40 GSa/s. The offline DSP was composed of the resampling signal, I/Q imbalance compensation, chromatic dispersion (CD) compensation, polarization demultiplexing, frequency offset estimation, carrier-phase estimation, and BER counting. The experimental parameters are shown in Table 4.
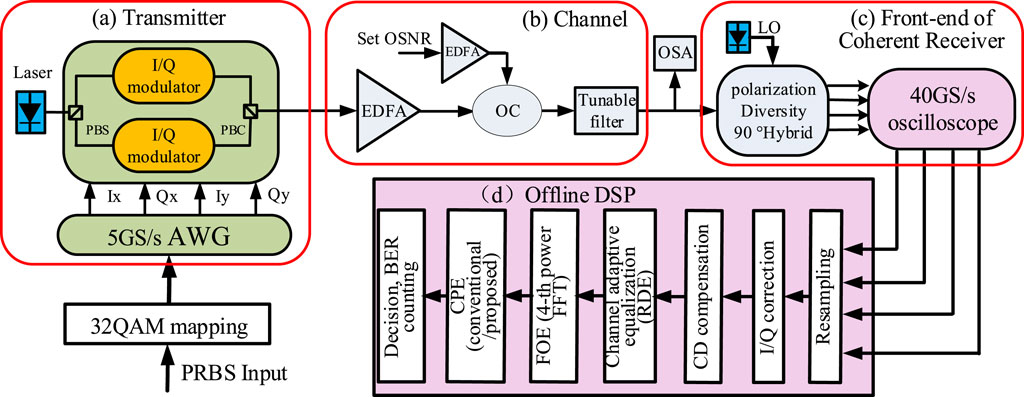
Figure 8. Block diagram of the experimental setup for the 5 Gbaud PM 32-QAM coherent system. AWG: arbitrary waveform generator. PBS: polarization beam splitter. PBC: polarization beam combiner. OC: optical coupler. EDFA: erbium-doped fiber amplifier. LO: local oscillator.
The relationship between BER and OSNR for 5 Gbaud double-polarization 32-QAM coherent optical systems using commercial lasers with a linewidth of <100 kHz is displayed in Figure 9, showing that the BER performance for the traditional QPSK partitioning was the worst in the experiment. The best BER of the conventional QPSK partitioning was still larger than 1 × 10−3, while the proposed two-stage CPE achieved a slightly worse BER performance than the BPS algorithms with 64 test phases. Similar to the simulation results, since the conventional QPSK partitioning algorithm uses only a few constellation points for carrier-phase estimation in the 32-QAM system, its phase estimation performance was significantly degraded. Figure 9 is an experimental data graph, and the BER of all algorithms gradually decreases with the increase of OSNR. The two-stage CPE and BPS perform similarly, while the QPSK splitting algorithm performs the worst. On the other hand, the proposed two-stage algorithm with remarkably reduced total computational complexity—in which enhanced QPSK partitioning combined with a simplified 4th-power method was used for the initial coarse stage, and ML detection was utilized for the subsequent fine stage—maintained a comparable performance to the BPS. This proves that the suggested low-complexity CPE algorithm is a potential candidate for the 32-QAM coherent optical system.
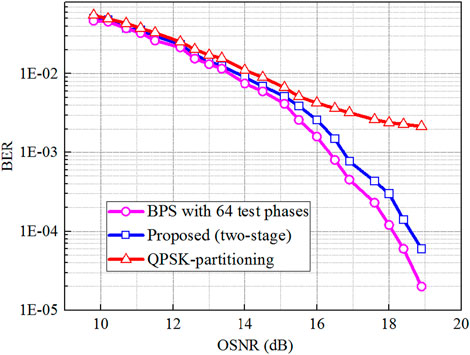
Figure 9. The relationship between BER and OSNR for the back-to-back 5 Gbaud double-polarization 32-QAM coherent optical systems.
This article builds an algorithm test platform. When the optimal block length is 105, compared with the traditional BPS, the OSNR of the proposed algorithm is 21.2 dB and the BER is 1.8 × 10−3, which shows that the proposed algorithm has good line width tolerance. Obvious advantage. At the same time, this solution demonstrates excellent phase estimation performance and can support higher linewidth-symbol duration
Although the BPS algorithm has a high computational complexity, it shows good performance in both experimental and simulation data, especially it can maintain a low bit error rate at low OSNR values, which is suitable for applications requiring high-precision phase estimation. The two-stage CPE algorithm shows comparable bit error rate performance to BPS in both experiments and simulations, especially at medium to high OSNR values. The advantage of this algorithm is that it can significantly reduce the computational complexity while maintaining performance, making it suitable for practical deployment. QPSK segmentation has the weakest performance under all conditions, especially under low OSNR conditions, where its bit error rate is significantly higher than the other two algorithms. This may be because the algorithm only uses some symbol points for phase estimation, resulting in lower flexibility and reliability in practical applications. In summary, the two-stage CPE algorithm shows excellent performance in both experiments and simulations, especially achieving a good balance between computational complexity and bit error rate performance, making it a potential application in practice. This paper significantly reduces the computational complexity by combining the simplified fourth power method and ML detection. Literature [18, 24] can also perform phase estimation well, but the algorithm complexity is high. Compared with the traditional BPS method, this method does not require a large number of test phases, thereby reducing the resource requirements and power consumption of hardware implementation, which is extremely beneficial to hardware implementation, especially achieving computational simplification while maintaining performance.
In this study, we suggested a simple two-stage CPE algorithm for 32-QAM coherent optical communication systems. In contrast to the traditional QPSK partitioning algorithms, the proposed algorithm uses QPSK-like constellation points to perform estimation, where a simplified 4th-power method is applied for removing the complex 4th-power operation in the initial stage, and ML detection is utilized for the subsequent fine stage. Optical back-to-back numerical simulations and experiments were conducted to explore the performance of the suggested algorithm. Our findings revealed that, compared with the conventional QPSK partitioning, the proposed two-stage CPE with shorter estimation blocks has a greater linewidth tolerance. The scheme reduces the computational complexity by simplifying the calculation steps and does not require a large number of test phases, thereby reducing the need for hardware resources and power consumption. Additionally, the proposed algorithm is not only less complex, but also has comparable performance to that of the standard BPS. This algorithm provides a more efficient and economical solution when dealing with high-speed, high-order modulation formats in optical communication systems. There are still some challenges in this study. The current research is mainly limited to low baud rates and short-distance SSMF transmission scenarios. Future research can be extended to higher baud rates and longer distance transmission tests to fully evaluate the practical application potential of this solution. Secondly, in actual deployment, it may be necessary to further optimize the algorithm to adapt to different transmission conditions and dynamic network environments, such as using artificial intelligence algorithms to further improve system performance and adaptability.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
MP: Conceptualization, Data curation, Formal Analysis, Methodology, Software, Writing–original draft. XW: Funding acquisition, Writing–review and editing. XY: Investigation, Validation, Visualization, Writing–review and editing. DW: Project administration, Resources, Writing–review and editing.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article. This research work was supported in part by Anhui Digital Intelligent Engineering Research Center for Agricultural Products Quality Safety (APDI202302). Anhui Education Department, and University Natural Science Research Project of Anhui Province (Grant No. 2022AH051338). This work is supported by Henan Key Laboratory of Visible Light Communications (No. HKLVLC2023-B10), Jiangxi Provincial Natural Science Foundation (20232BAB212006) and Open Fund of Advanced Cryptography and System Security Key Laboratory of Sichuan Province (Grant No. SKLACSS-202306) and (Grant No. SKLACSS-202303). This work is supported by R&D Program of Beijing Municipal Education Commission (KM202310015002), and Hubei Provincial Natural Science Foundation of China (Grant No: 2023AFB474, Grant No: 2024AFB881). This research work was supported by the Special Fund of Advantageous and Characteristic disciplines (Group) of Hubei Province.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Faruk MS, Savory SJ. Digital signal processing for coherent transceivers employing multilevel formats. J Lightw Technol (2017) 35(5):1125–41. doi:10.1109/jlt.2017.2662319
2. Winzer PJ. Beyond 100 G ethernet. IEEE Commun Mag (2010) 48(7):26–30. doi:10.1109/mcom.2010.5496875
3. Winzer P. High-spectral-efficiency optical modulation formats. J Lightwave Technol (2012) 30(8):3824–35. doi:10.1109/jlt.2012.2212180
4. Zhou X, Nelson LE, Magill P, Isaac R, Zhu B, Peckham DW, et al. PDM-Nyquist-32QAM for 450-Gb/s per-channel WDM transmission on the 50 GHz ITU-T grid. J Lightw Technol (2012) 30(4):553–9. doi:10.1109/jlt.2011.2177243
5. Otuya DO, Kasai K, Hirooka T, Yoshida M, Nakazawa M, Hara T, et al. A single-channel, 1.6 Tbit/s 32 QAM coherent pulse transmission over 150 km with RZ-CW conversion and FDE techniques. Proc Ofc/nfoec (2013) 1–3. doi:10.1364/OFC.2013.OTH4E.4
6. Nakazawa M, Yoshida M, Kasai K, Hongou J. 20 Msymbol∕s, 64 and 128 QAM coherent optical transmission over 525 km using heterodyne detection with frequency-stabilised laser. Electron Lett (2006) 42:710–2. doi:10.1049/el:20060646
7. Khanna G, Rahman T, Riccardi E, Pagano A, Piat AC, Calabro S, et al. Single-carrier 400G 64QAM and 128QAM DWDM field trial transmission over metro legacy links. IEEE Photon Technology Lett (2017) 29(2):189–92. doi:10.1109/lpt.2016.2632165
8. Qian D, Huang M, Ip E, Huang Y, Shao Y, Hu J, et al. High capacity/spectral efficiency 101.7-Tb/s WDM transmission using PDM-128qam-OFDM over 165-km SSMF within C- and L-bands. J Lightwave Technology (2012) 30(10):1540–8. doi:10.1109/jlt.2012.2189096
9. Lau APT, Gao Y, Sui Q, Wang D, Zhuge Q, Morsy-Osman MH, et al. Advanced DSP techniques enabling high spectral efficiency and flexible transmissions: toward elastic optical networks. IEEE Sig Proc Mag (2014) 31(2):82–92. doi:10.1109/msp.2013.2287021
10. Zhou X, Nelson L. Advanced DSP for 400 Gb/s and beyond optical networks. J Lightwave Technol (2014) 32(16):2716–25. doi:10.1109/jlt.2014.2321135
11. Winzer PJ, Neilson DT, Chraplyvy AR. Fiber-optic transmission and networking: the previous 20 and the next 20 years [Invited]. Opt Express (2018) 26(8):24190–239. doi:10.1364/oe.26.024190
12. Lau A, Gao Y, Sui Q, Wang D, Zhuge Q, Morsy-Osman M, et al. Advanced DSP techniques enabling high spectral efficiency and flexible transmissions: toward elastic optical networks. IEEE Signal Process Mag (2014) 31(2):82–92. doi:10.1109/msp.2013.2287021
13. Kumari M, Mishra SK. Realization of 4 × 200 Gbps 4-QAM OFDM-OWC system using higher order OAM modes for HAP-to-satellites scenario. Photonics (2024) 11(4):294. doi:10.3390/photonics11040294
14. Kumari M, Sheetal A, Sharma R. Performance analysis of symmetrical and bidirectional 40 Gbps TWDM-PON employing m-QAM-OFDM modulation with multi-color LDs based VLC system. Opt Quan Electron (2021) 53:455–29. doi:10.1007/s11082-021-03108-2
15. Saw BK, Janyani V, Singh G. Analysis of coherent-OFDM modulation for FSO communication over distribution with pointing errors. Opt Commun (2023) 545:129677. doi:10.1016/j.optcom.2023.129677
16. Sharma V, Chaudhary S. Implementation of hybrid OFDM-FSO transmission system. Int J Comput Appl (2012) 58(8):37–40. doi:10.5120/9305-3531
17. Sharma V, Kumar S. Empirical evaluation of wired-and wireless-hybrid OFDM–OSSB–RoF transmission system. Optik (2013) 124(20):4529–32. doi:10.1016/j.ijleo.2013.01.045
18. Yang T, Shi C, Chen X, Zhang M, Ji Y, Hua F, et al. Linewidth-tolerant and multi-format carrier phase estimation schemes for coherent optical m-QAM flexible transmission systems. Opt Exp (2018) 26(8):10599–10615. doi:10.1364/oe.26.010599
19. Mori Y, Zhang C, Kikuchi K. Novel configuration of finite-impulse-response filters tolerant to carrier-phase fluctuations in digital coherent optical receivers for higher-order quadrature amplitude modulation signals. Opt Express (2012) 20(24):26 236–26 251. doi:10.1364/oe.20.026236
20. Gao Y, Lau APT, Yan S, Lu C. Low-complexity and phase noise tolerant carrier phase estimation for dual-polarization 16-QAM systems. Opt Exp (2011) 19(22):21717–21729. doi:10.1364/oe.19.021717
21. Xiang M, Fu S, Deng L, Tang M, Shum P, Liu D. Low-complexity feed-forward carrier phase estimation for M-ary QAM based on phase search acceleration by quadratic approximation. Opt Express (2015) 23(15):19 142–19 153. doi:10.1364/oe.23.019142
22. Pfau T, Hoffmann S, Noe R, Lightw J. Hardware-efficient coherent digital receiver concept with feedforward carrier recovery for M-QAM constellations. Technol (2009) 27(8):989–999. doi:10.1109/JLT.2008.2010511
23. Fatadin I, Ives D, Savory SJ. Laser linewidth tolerance for 16-QAM coherent optical systems using QPSK partitioning. IEEE Photon Technol Lett (2010) 22(9):631–3. doi:10.1109/lpt.2010.2043524
24. Feng J, Li W, Xiao J, Han J, Li H, Huang L, et al. Carrier phase estimation for 32-QAM optical systems using quasi-QPSK-partitioning algorithm. IEEE Photon Technol Lett (2015) 28(1):75–8. doi:10.1109/lpt.2015.2483619
25. Chen Y, Huang X. A linewidth-tolerant two-stage CPE using a new QPSK-partitioning approach and an enhanced maximum likelihood detection for 64-QAM coherent optical systems. J Lightwave Technol (2015) 33(18):3883–9. doi:10.1109/jlt.2015.2448113
26. Viterbi AJ, Viterbi AM. Nonlinear estimation of PSK-modulated carrier phase with application to burst digital transmission. IEEE Trans Inf Theor (1983) 29(4):543–51. doi:10.1109/tit.1983.1056713
27. Yang T, Chen X, Shi S, Sun E, Shi C. Low-complexity and modulation-format-independent carrier phase estimation scheme using linear approximation for elastic optical networks. Opt Commun (2018) 410:376–84. doi:10.1016/j.optcom.2017.10.052
28. Bilal SM, Gabriella B. Dual stage carrier phase estimation for 16-QAM systems based on a modified QPSK-partitioning algorithm. In: Proceedings of the IEEE 15th international conference on transparent optical networks (ICTON); 2013 June 23–June 27; Cartagena, Spain: IEEE (2013).
29. Li J, Li L, Tao Z, Hoshida T, Rasmussen JC. Laser-linewidth-tolerant feed-forward carrier phase estimator with reduced complexity for QAM. J Lightwave Technol (2011) 29(16):2358–64. doi:10.1109/jlt.2011.2159580
Keywords: coherent optical communications, quadrature amplitude modulation, carrier phase estimation, QPSK-partitioning, blind phase search
Citation: Peng M, Wang X, Yang X and Wang D (2024) A simple two-stage carrier-phase estimation algorithm for 32-QAM coherent optical communication systems. Front. Phys. 12:1452087. doi: 10.3389/fphy.2024.1452087
Received: 20 June 2024; Accepted: 26 August 2024;
Published: 05 September 2024.
Edited by:
Sushank Chaudhary, Chulalongkorn University, ThailandReviewed by:
Abhishek Sharma, Guru Nanak Dev University, IndiaCopyright © 2024 Peng, Wang, Yang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiangqing Wang, d3hxaW5nQGZ5bnUuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.