- Institut für Physik, Technische Universität Chemnitz, Chemnitz, Germany
The description of thermodynamic phase transitions in terms of percolation transitions of suitably defined clusters has a long tradition and boasts a number of important successes, the most prominent ones being in ferromagnetic lattice models. Spin glasses and other frustrated systems are not among them as the clusters of aligned spins usually considered in this context start to percolate in the disordered phase and hence fail to indicate the onset of ordering. In this mini-review we provide an overview of the state of the art in this field, including recent advances, and outline the main open questions in the area.
1 Introduction
Percolation models were first proposed and studied by Flory and Stockmeyer in the context of polymer gelation [1, 2], and they have found applications in an astonishingly broad range of areas, from forest fires [3], over porous media in oil fields [4], to electric conductivity [5] and all the way to complex networks [6]. For lattice systems, Broadbent and Hammersley [7] first proposed the idea of what is today known as bond percolation, where the edges of a lattice are occupied at random with a probability
This behavior is reminiscent of the spatial correlations observed in other systems near criticality, for instance in the magnetic ordering transition of lattice spin models [9]. In view of the success and intuitive appeal of the percolation picture, it has been a longstanding goal in the description of phase transitions and critical phenomena to represent the ordering process in general systems as a percolation transition of suitably defined structures or droplets in the substance that form as the phase changes [10]. Fisher proposed a model [11] that postulated droplets of a certain free energy whose average size diverges at the critical point and that feature a cluster size distribution whose exponents are related to the critical indices of the thermal transition. A microscopic definition of such droplets, however, was initially not available. While it was clear that they must correspond to a spatially correlated percolation problem, it soon became clear that the clusters (connected components) of like spins do not fit Fisher’s description as they percolate away from the thermal critical point [12]. Coniglio and Klein [13] first realized that suitable clusters resulted from a merely probabilistic occupation of bonds between like spins if the occupation probability was chosen as
While these ideas are rather straightforwardly generalized from Ising to Potts variables, as well as to continuous spins [16], and even to disordered ferromagnets [17], they fail as soon as competing interactions and frustration come into play [18, 19]. Further, while FKCK clusters can be easily generalized to this case by focusing on (parallel or antiparallel) spin pairs with satisfied bonds, it is found that in three dimensions such clusters percolate far away from the spin-glass transition point as they, in fact, do not encode the relevant correlations at the spin-glass transition [20]. Instead, it has been proposed that one should consider cluster definitions based on overlap variables, as they encode the order parameter of the spin-glass transition [21]. Further, it appears that a more subtle property of clusters than the mere onset of percolation might be associated with the occurrence of the spin-glass transition. Only in two dimensions, where the situation is somewhat different as the spin-glass transition is shifted to zero temperature, does one observe for some types of overlap-based clusters the percolation points asymptotically approach the spin-glass transition [22].
Based on some of these observations, a number of cluster-update algorithms for spin glasses have been proposed, the general target being to ensure that the updated clusters undergo a percolation transition at or close to the spin-glass transition, and that the structure of clusters encodes the correlations of the underlying spin model. A general solution to this problem has not been found to date, but some approaches provide reasonably good performance for systems in two dimensions [23], for spin glasses on diluted lattices [24], or for an intermediate size range in three and higher dimensions [25]. In the remainder of this mini-review, we will provide a more detailed discussion of the connection between percolation and the spin-glass transition and the simulation algorithms based on these observations.
2 Spin clusters
While some of what is discussed below can be generalized to the cases of Potts spins as well as continuous models such as the XY and Heisenberg spin glasses, to be specific we focus on the case of the short-range (Edwards-Anderson) Ising spin glass with Hamiltonian [26]
where
There is clear numerical evidence that such clusters percolate at temperatures far above the spin-glass transition, for instance at
the situation for spin glasses is more subtle, and one can show that in this case [21, 30]
Hence, the percolation of FKCK clusters no longer implies the presence of long-range order. Since the percolation transition of FKCK clusters does not encode spin-glass criticality (but see Ref. [31] for a possible connection to damage spreading), it is expected that it is in the universality class of random percolation, and this expectation is borne out by the results of numerical simulation studies [20, 22, 32] as well as rigorous analysis [33, 34].
3 Overlap clusters
This failure is not surprising in view of the fact that the magnetization is no order parameter for the spin-glass transition and, instead, for its description one needs to turn to overlap variables [35]. Several cluster definitions have been suggested based on the site or link overlap of two spin configurations using the same disorder realization. Initially in the context of random-field models, Chayes, Machta and Redner [36] proposed a representation where doubly satisfied (“blue”) bonds in a two-replica representation are occupied with a probability
while, additionally, singly satisfied (“red”) bonds are occupied with probability
Then, it is possible to relate the percolation properties of such clusters to the occurrence of symmetry breaking of the spin system [21]: in contrast to the ferromagnet, where the appearance of a percolating cluster suffices to indicate the onset of the ordered phase, for spin glass there should be a “blue” cluster of strictly larger density than any other cluster [37]. In practise, one observes the occurrence of two percolating clusters of opposite overlap that develop a density difference at the spin-glass transition [21, 22]. A corresponding overlap configuration is shown in Figure 1 for the example of the 2D Gaussian spin glass, illustrating that there are mainly two large clusters of opposite overlap, with any further clusters being much smaller. If the weight of such smaller clusters diminishes for systems of increasing sizes, the overlap

Figure 1. Typical configuration of CMR “blue” clusters in a sample of the 2D Gaussian Edwards-Anderson spin-glass model at low temperature
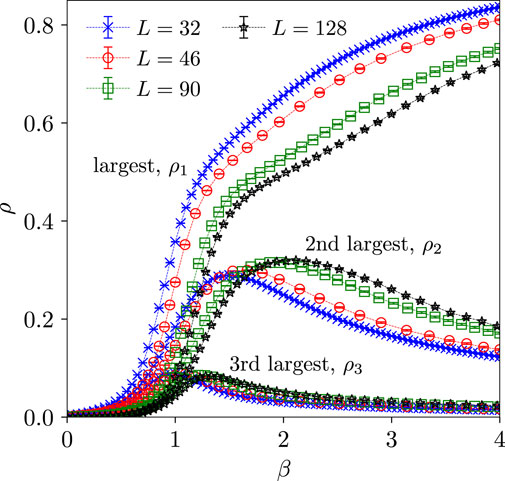
Figure 2. Average densities
Another possible cluster definition based on the overlap of two replicas results from a simple duplication of the FKCK construction on the two spin configurations, i.e., bonds are occupied independently in the two replicas according to the FKCK probability (Eq. 2), and clusters are constructed over all bonds simultaneously occupied in both replicas [38]. This is equivalent to a bond occupation probability
for doubly satisfied bonds. Such clusters might be referred to as two-replica Fortuin-Kasteleyn (TRFK) clusters. These clusters behave rather similarly to the CMR ones [21, 22], which is not surprising as they follow the same construction apart from the smaller bond occupation probability
Finally, a cluster definition based on a site percolation problem rather that a bond percolation one was first proposed in connection with a specific cluster-update algorithm for spin glasses in 2D [23]. There, clusters are grown in regions of constant overlap, and neighboring sites of the same overlap are unconditionally added to the cluster, such that the effective bond occupation probability is
One might hence think of these as some form of geometric clusters in overlap space [39]. The CMR and TRFK clusters clearly are subregions of the Houdayer clusters as for the latter one does not take into account whether a given bond is satisfied or not. In many 3D lattices such as the simple cubic one, such clusters percolate already for
4 Cluster updates
In view of the spectacular success of cluster updates in alleviating critical slowing down for ferromagnetic spin models [15, 16] it has been a natural idea to use cluster moves to counter the dramatically slow dynamics observed in spin-glass systems. In fact, the first proposal in this direction [40] even (slightly) predates the ferromagnetic algorithms. Unfortunately, the cluster component in this approach was not found to be extremely efficient, while the replica component eventually lead to the development of the replica exchange or parallel tempering method [41, 42] that is the de facto standard for spin-glass simulations.
Houdayer’s proposal [23] for a cluster update for 2D models was in this sense more successful. Geometric clusters are constructed in the way described above, by connecting neighboring sites of equal overlap, and an update consists of flipping the spins inside a cluster in both replicas. Crucially, such updates can be performed unconditionally, i.e., without adding an extra acceptance step, since they leave the total energy of the replicated system invariant. Usage of more than two replicas (per temperature) is possible, but usually not found to be efficient computationally [43]. Due to the fixed energy, it is clear that such updates are not ergodic, and hence need to be complemented, e.g., by single-spin flip moves. While this approach works well on the square lattice, where the percolation threshold
The CMR representation also suggests several cluster updates. Constructing only the blue clusters, these can flip freely as the cluster construction rules together with the bond occupation probability (Eq. 5) mean that the update satisfies detailed balance with respect to the equilibrium distribution [22]. This was used by Jörg [24] to efficiently simulate spin glasses on diluted lattices, leading to overall smaller clusters. By construction, however, the update is not ergodic since spins connected by (partially) unsatisfied bonds cannot be updated. An extension proposed in Ref. [36] (see also [21]) uses both red and blue bonds to construct blue and grey clusters, leading to a rejection-free and ergodic update which, however, is still found to be relatively inefficient due to the onset of cluster percolation above
5 Discussion
While a percolation perspective onto spin glasses and other frustrated systems has not led to the same level of revolutionary success this approach has seen for ferromagnets, significant progress has been possible. The cluster construction rules used for ferromagnets (Fortuin-Kasteleyn–Coniglio-Klein), while applicable to spin glasses, do not lead to structures that reflect spin-glass correlations. Instead, clusters must be constructed in overlap space, corresponding to the order parameter of the spin-glass transition. While there is no one-to-one correspondence between the spin-glass transition and a simple percolation transition of a cluster type that has been investigated to date, an intriguing picture has emerged: for the CMR and TRFK clusters defined on two replicas two equally large percolating clusters appear significantly above the spin-glass transition, and it is only at the spin-glass transition that their densities start to differ [21, 22]. It appears that below the percolation point smaller clusters beneath the two dominating ones are asymptotically irrelevant.
Regarding cluster updates, a fundamentally efficient algorithm only exists in two dimensions, while attempts for more general, and in particular, 3D systems have only partially been successful. While some improved results where found in cases where the average sizes of clusters constructed are reduced such as in diluted systems [24] or with algorithmic modifications [25], it is not fully clear whether such size reduction is a sufficient condition for improving performance.
In view of this state of affairs a number of interesting questions remain to be addressed in future studies. Is it possible to construct clusters that percolate at or very close to the temperature of the spin-glass transition? One promising direction in this respect is the study of multi-replica overlaps [22]. In view of Eq. 6 it is clear that, depending on their precise construction, such clusters could percolate at lower and lower temperatures as the number of replicas is increased. Regarding the algorithms, it was seen that for blue clusters there are two very dominant large clusters in the vicinity of the glass transition, such that in contrast to the ferromagnetic case close to the transition there is no multi-scale nature of spin updates for such blue clusters close to the spin-glass transition. This is likely the prime reason for the unsatisfactory performance of such algorithms. In contrast, for Houdayer’s algorithm and its extensions, what is the cluster-size distribution? How do multi-cluster variants of such algorithms perform as compared to the default single-cluster ones? Answers to (some of) these questions hold the potential for significantly advancing our understanding of the spin-glass transition while simultaneously facilitating much improved efficiency in simulating spin-glass systems with the hope of answering some more of the fundamental open questions of this field.
Author contributions
LM: Conceptualization, Investigation, Writing–original draft, Writing–review and editing. MW: Conceptualization, Investigation, Writing–original draft, Writing–review and editing.
Funding
The authors declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Flory PJ. Molecular size distribution in three dimensional polymers. I. Gelation. J Am Chem Soc (1941) 63:3083–90. doi:10.1021/ja01856a061
2. Stockmayer WH. Theory of molecular size distribution and gel formation in branched-chain polymers. J Chem Phys (1943) 11:45–55. doi:10.1063/1.1723803
3. Stauffer D, Aharony A. Introduction to percolation theory. 2nd ed. London: Taylor and Francis (1994).
4. King P, Buldyrev S, Dokholyan NV, Havlin S, Lee Y, Paul G, et al. Predicting oil recovery using percolation theory. Pet Geosci (2001) 7:S105–S107. doi:10.1144/petgeo.7.s.s105
5. Efros A, Shklovskii BI. Critical behaviour of conductivity and dielectric constant near the metal-non-metal transition threshold. Phys Status Solidi B (1976) 76:475–85. doi:10.1002/pssb.2220760205
6. Cohen R, Erez K, Ben-Avraham D, Havlin S. Resilience of the internet to random breakdowns. Phys Rev Lett (2000) 85:4626–8. doi:10.1103/physrevlett.85.4626
7. Broadbent SR, Hammersley JM. (1957). Percolation processes: I. Crystals and mazes. Math Proc Camb Phil Soc 53, 629–41. (Cambridge University Press), doi:10.1017/s0305004100032680
9. McCoy BM, Wu TT. The two-dimensional Ising model. Massachusetts: Harvard University Press (1973).
10. Stanley HE, Ostrowsky N. Correlations and connectivity: geometric aspects of physics. In: Chemistry and biology, vol. 188 of NATO Science Series E. Springer (1990).
11. Fisher ME. The theory of condensation and the critical point. Physics (1967) 3:255–83. doi:10.1103/physicsphysiquefizika.3.255
12. Müller-Krumbhaar H. Percolation in a lattice system with particle interaction. Phys Lett A (1974) 50:27–8. doi:10.1016/0375-9601(74)90337-5
13. Coniglio A, Klein W. Clusters and Ising critical droplets: a renormalisation group approach. J Phys A (1980) 13:2775–80. doi:10.1088/0305-4470/13/8/025
14. Fortuin CM, Kasteleyn PW. On the random-cluster model I. Introduction and relation to other models. Physica (1972) 57:536–64. doi:10.1016/0031-8914(72)90045-6
15. Swendsen RH, Wang JS. Nonuniversal critical dynamics in Monte Carlo simulations. Phys Rev Lett (1987) 58:86–8. doi:10.1103/PhysRevLett.58.86
16. Wolff U. Collective Monte Carlo updating for spin systems. Phys Rev Lett (1989) 62:361–4. doi:10.1103/PhysRevLett.62.361
17. Ballesteros HG, Fernández LA, Martín-Mayor V, Muñoz Sudupe A, Parisi G, Ruiz-Lorenzo JJ. Critical exponents of the three dimensional diluted Ising model. Phys Rev B (1998) 58:2740–7. doi:10.1103/physrevb.58.2740
18. Kessler DA, Bretz M. Unbridled growth of spin-glass clusters. Phys Rev B (1990) 41:4778–80. doi:10.1103/PhysRevB.41.4778
19. De Arcangelis L, Coniglio A, Peruggi F. Percolation transition in spin glasses. EPL (1991) 14:515–9. doi:10.1209/0295-5075/14/6/003
20. Fajen H, Hartmann AK, Young AP. Percolation of Fortuin-Kasteleyn clusters for the random-bond Ising model. Phys Rev E (2020) 102:012131. doi:10.1103/PhysRevE.102.012131
21. Machta J, Newman CM, Stein DL. The percolation signature of the spin glass transition. J Stat Phys (2008) 130:113–28. doi:10.1007/s10955-007-9446-2
22. Münster L, Weigel M. Cluster percolation in the two-dimensional Ising spin glass. Phys Rev E (2023) 107:054103. doi:10.1103/physreve.107.054103
23. Houdayer J. A cluster Monte Carlo algorithm for 2-dimensional spin glasses. Eur Phys J B (2001) 22:479–84. doi:10.1007/PL00011151
24. Jörg T. Cluster Monte Carlo algorithms for diluted spin glasses. Prog Theor Phys Supp (2005) 157:349–52. doi:10.1143/ptps.157.349
25. Zhu Z, Ochoa AJ, Katzgraber HG. Efficient cluster algorithm for spin glasses in any space dimension. Phys Rev Lett (2015) 115:077201. doi:10.1103/physrevlett.115.077201
26. Edwards SF, Anderson PW. Theory of spin glasses. J Phys F (1975) 5:965–74. doi:10.1088/0305-4608/5/5/017
27. Hasenbusch M, Pelissetto A, Vicari E. The critical behavior of 3D Ising spin glass models: universality and scaling corrections. J Stat Mech Theor Exp (2008) 2008:L02001. doi:10.1088/1742-5468/2008/02/l02001
28. Hartmann AK, Young AP. Lower critical dimension of Ising spin glasses. Phys Rev B (2001) 64:180404. doi:10.1103/physrevb.64.180404
29. Edwards RG, Sokal AD. Generalization of the Fortuin-Kasteleyn-Swendsen-Wang representation and Monte Carlo algorithm. Phys Rev D (1988) 38:2009–12. doi:10.1103/PhysRevD.38.2009
30. Coniglio A, di Liberto F, Monroy G, Peruggi F. Cluster approach to spin glasses and the frustrated-percolation problem. Phys Rev B (1991) 44:12605–8. doi:10.1103/physrevb.44.12605
31. Lundow PH, Campbell I. Fortuin-Kasteleyn and damage-spreading transitions in random-bond Ising lattices. Phys Rev E (2012) 86:041121. doi:10.1103/physreve.86.041121
32. Imaoka H, Ikeda H, Kasai Y. Percolation transition in two-dimensional ±J Ising spin glasses. Physica A (1997) 246:18–26. doi:10.1016/s0378-4371(97)00351-8
33. De Santis E, Gandolfi A. Bond percolation in frustrated systems. Ann Prob (1999) 27:1781–808. doi:10.1214/aop/1022677548
34. Gandolfi A. A remark on gauge symmetries in Ising spin glasses. Probab Theor Relat. Fields (1999) 114:419–30. doi:10.1007/s004400050230
35. Parisi G. Infinite number of order parameters for spin-glasses. Phys Rev Lett (1979) 43:1754–6. doi:10.1103/physrevlett.43.1754
36. Chayes L, Machta J, Redner O. Graphical representations for Ising systems in external fields. J Stat Phys (1998) 93:17–32. doi:10.1023/b:joss.0000026726.43558.80
37. Machta J, Newman CM, Stein DL. A percolation-theoretic approach to spin glass phase transitions. In: AB de Monvel, and A Bovier, editors. Spin glasses: statics and dynamics. Basel: Birkhäuser (2009). p. 205.
38. Newman CM, Stein DL. Short-range spin glasses: results and speculations. In: E Bolthausen, and A Bovier, editors. Spin glasses. Berlin, Heidelberg: Springer (2007). p. 159.
39. Akritidis M, Fytas NG, Weigel M. Geometric clusters in the overlap of the Ising model. Phys Rev E (2023) 108:044145. doi:10.1103/physreve.108.044145
40. Swendsen RH, Wang JS. Replica Monte Carlo simulation of spin glasses. Phys Rev Lett (1986) 57:2607–9. doi:10.1103/physrevlett.57.2607
41. Geyer CJ. Markov chain Monte Carlo maximum likelihood. In: Computing science and statistics: proceedings of the 23rd symposium on the interface. New York: American Statistical Association (1991). p. 156–163.
42. Hukushima K, Nemoto K. Exchange Monte Carlo method and application to spin glass simulations. J Phys Soc Jpn (1996) 65:1604–8. doi:10.1143/JPSJ.65.1604
43. Kumar R, Gross J, Janke W, Weigel M. Massively parallel simulations for disordered systems. Eur Phys J B (2020) 93:79–13. doi:10.1140/epjb/e2020-100535-0
44. Vandenbroucque A, Chiacchio EIR, Munro E. The Houdayer algorithm: overview, extensions, and applications Preprint arXiv:2211 (2022). p. 11556.
Keywords: spin glasses, percolation, lattice models, Monte Carlo simulations, phase transitions, quenched disorder
Citation: Münster L and Weigel M (2024) Spin glasses and percolation. Front. Phys. 12:1448175. doi: 10.3389/fphy.2024.1448175
Received: 12 June 2024; Accepted: 01 July 2024;
Published: 16 August 2024.
Edited by:
Gregory Kenning, Indiana University of Pennsylvania, United StatesReviewed by:
Raymond Orbach, The University of Texas at Austin, United StatesCopyright © 2024 Münster and Weigel. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Martin Weigel, bWFydGluLndlaWdlbEBwaHlzaWsudHUtY2hlbW5pdHouZGU=
 Lambert Münster
Lambert Münster Martin Weigel
Martin Weigel