- School of Computer Science and Technology, Anhui University of Technology, Ma’anshan, China
Markovian jump Hopfield NNs (MJHNNs) have received considerable attention due to their potential for application in various areas. This paper deals with the issue of state estimation concerning a category of MJHNNs with discrete and distributed delays. Both time-invariant and time-variant discrete delay cases are taken into account. The objective is to design full-order state estimators such that the filtering error systems exhibit exponential stability in the mean-square sense. Two sufficient conditions on the mean-square exponential stability of MJHNNs are established utilizing augmented Lyapunov–Krasovskii functionals, the Wirtinger–based integral inequality, the Bessel-Legendre inequality, and the convex combination inequality. Then, linear matrix inequalities-based design methods for the required estimators are developed through eliminating nonlinear coupling terms. The feasibility of these linear matrix inequalities can be readily verified via available Matlab software, thus enabling numerically tractable implementation of the proposed design methods. Finally, two numerical examples with simulations are provided to demonstrate the applicability and less conservatism of the proposed stability criteria and estimators. Lastly, two numerical examples are given to demonstrate the applicability and reduced conservatism of the proposed stability criteria and estimator design methods. Future research could explore further refinement of these analysis and design results, and exporing their extention to more complex neural network models.
1 Introduction
Neural networks (NNs) are composed of numerous interconnected neurons, providing them the ability to process large amounts of data simultaneously. Recently, NNs have been widely utilized in speech recognition [1], tracking control [2], associative memory [3], image restoration [4], and various other fields. As we all know, time delays are inevitable in the above practical applications, which may cause NNs to oscillate or become unstable [5]. This phenomenon has prompted extensive research on the stability analysis of NNs with time delays [6–9]. Notably, [10] designed an output feedback controller for NNs with time-invariant discrete delay to ensure the asymptotic stability of the closed-loop control system. The time delay considered in this study was constant. In cases where the time delay varies over time, [11] utilized a Lyapunov–Krasovskii functional (LKF) and subsequently established a stability criterion based on linear matrix inequalities (LMIs). However, these studies primarily focus on discrete delays, which may oversimplify these scenarios. In NNs, numerous interconnections between neurons form various parallel paths. Due to the varying sizes and complexities of these paths, signal transmission times are distributed within a certain period of time, resulting in distributed delays [12, 13].
On the other hand, in practical scenarios, environmental fluctuations can induce changes in the parameters of NNs. Researchers have recognized the significant advantages of Markovian jump processes in handling random changes in parameters [14–19]. Over the past few decades, many Markovian jump NN models, either in discrete-time form [20–23] or continuous-time form [24–27], have been proposed and studied. Among these models, Markovian jump Hopfield NNs (MJHNNs) have received considerable attention due to their potential for application. Notably, for an MJHNN, the neuron states are often not completely available. Thus, to achieve a given control goal, it is necessary to estimate the neuron states based on available output data, which has led to a growing focus on the topic of state estimation. [28] examined the finite-time state estimation for MJHNNs with discrete delays and presented a discontinuous estimator design method. [29] focused on the design of state estimators for continuous-time MJHNNs with both discrete and distributed delays and proposed a mean-square exponential stability (MSES) criterion and an LMI-based state estimation strategy.
It should be noted that the criterion derived in [29] was based on Jensen’s inequality, and the LKF used therein omitted some items involving time-delay-related integrals, thus leaving room for further improvement. Another discovery is that the discrete delay considered therein was assumed to be time-invariant, which restricts the application scope of the state estimation strategy since the magnitude of delays may vary over time in practice. Inspired by the observations above, we re-examine the state estimation in MJHNNs with discrete and distributed delays. Unlike the assumption of time invariance made in [29], the discrete delay under consideration here is allowed to be time-variant. The primary contributions of this study are as follows:
(1) Establishing MSES criteria for MJHNNs by integrating augmented LKFs, the Wirtinger-based integral inequality (WBII), the Bessel–Legendre inequality (BLI), and the convex combination inequality (CCI). Compared to the criteria proposed in [29], those proposed in this study are less conservative.
(2) Developing design methods for the required estimators to ensure the MSES of the filtering error systems (FESs) by eliminating nonlinear coupling terms. The estimator gain matrices can be easily determined by solving a set of LMIs.
Notation: In this paper,
2 Preliminaries
The MJHNN with time-invariant discrete and distributed delays is modeled as follows:
where
where
In the MJHNN Equation 1,
Assumption 1. For given matrices
Assumption 2. For given matrices
Remark 1. Equations 2 and 3 satisfy sector-bounded conditions [31], which have broader applicability than the standard Lipschitz conditions [32, 33] and are widely utilized in the study of NNs [9, 34].
The full-order state estimator for the MJHNN Equation 1 is designed as follows:
where
Define
where
Next, we introduce the definition of the MSES.
Definition 1. The FES Equation 5 has MSES if there exist positive scalars
holds, where
The primary objective of this paper is to establish the MSES criterion for the MJHNN and design the state estimator to ensure that the FES achieves MSES. To facilitate subsequent derivations, we have prepared four lemmas.
Lemma 1. [35, 36] (BLI) For a differentiable function
holds, where
Lemma 2. [37] (WBII) For any matrix
holds, where
Lemma 3. [38, 39] (CCI) If there exist matrices
Lemma 4. [40] Given matrices
holds, then we obtain
3 Stability analysis and state estimation of MJHNNs
In this section, we establish an MSES criterion and design a state estimator for MJHNNs with time-invariant discrete and distributed delays.
It can be deduced from Equations 2, 3, 6 that
and
where
and
Next, the MSES criterion for the MJHNN Equation 1 is established.
Theorem 1. For given positive scalars
hold, for
and the remaining symbols are defined in Equation 10. Then, the MJHNN Equation 1 achieves MSES.
Proof. Define
where
The LKF is constructed as follows:
where
The infinitesimal generator
The second components are given by
and these enable us to deduce that
where
Under Equation 11, the integral terms
Utilizing Lemma 1, the following inequality holds:
Combining Equations 16 and 17 yields
For the integral term
where
Then, it is easy to obtain
Additionally, for the system Equation 1, utilizing the free-weight matrix technique yields
From Equations 7 and 15–20, for any scalars
Applying the Schur complement to Equation 12 yields
where
Combining Equation 21 with Equation 22 results in
By utilizing Dynkin’s formula, for
where
By changing the order of integration, we can write
Substituting Equations 24–26 into Equation 23 and combining it with Equation 21, we obtain
where
One can write the following inequality:
Then, we can prove that for any
holds, where
Therefore, following a similar approach as in [29], system Equation 1 achieves MSES according to Definition 1.
Remark 2. [39] considered the BLI and proved that
Remark 3. As shown in Equation 17, the term
Next, the state estimator design method is as follows.
Theorem 2. For given positive scalars
hold, for
The remaining symbols coincide with those defined in Theorem 1. For the MJHNN Equation 1, the estimator Equation 4 with gain matrices
guarantees the MSES of the FES Equation 5.
Proof. Define
where
The LKF is constructed as follows:
where
Along similar lines to Theorem 1, by combining Equations 5 and 8, we can obtain
where
In light of Lemma 4, Equations 27 and 28 can ensure the MSES of the FES Equation 5.
4 Extension to the time-variant discrete-delay situation
Consider the MJHNN with time-variant discrete and distributed delays as follows:
where
Then, the estimator and the FES for the MJHNN Equation 31 are considered as follows:
We can provide the condition of the MSES for the MJHNN Equation 31 as follows.
Theorem 3. For given positive scalars
hold, for
and the remaining symbols coincide with those defined in theorem 1. Then, the MJHNN Equation 31 achieves MSES.
Proof. Define
where
The LKF is constructed as follows:
where
By the definition of
where
The initial
Substituting Equation 38 into Equation 37, we obtain
Therefore, we obtain
The components of
and it is easy to obtain
Then, we deduce from Equation 35 that
Hence, leveraging the matrices
One can derive from Equations 36–41 that
It follows from Equation 33 that
By applying Lemma 1 to the integral term in
and
Utilizing Lemma 2, we can deduce from Equation 45 that
leading to
According to Lemma 2,
Similar to Theorem 1, Equation 20 can be written as
From Equation 7 and Equations 42–49, for any scalars
where
Then, based on Theorem 2, we can establish the following estimator design method.
Theorem 4. For given positive scalars
hold, for
and the remaining symbols coincide with those defined in theorem 3. For the MJHNN Equation 31, the estimator Equation 32 with gain matrices
guarantees the MSES of the FES Equation 32.
5 Numerical example
Example 1. Consider MJHNNs Equation 5 and Equation 32 with
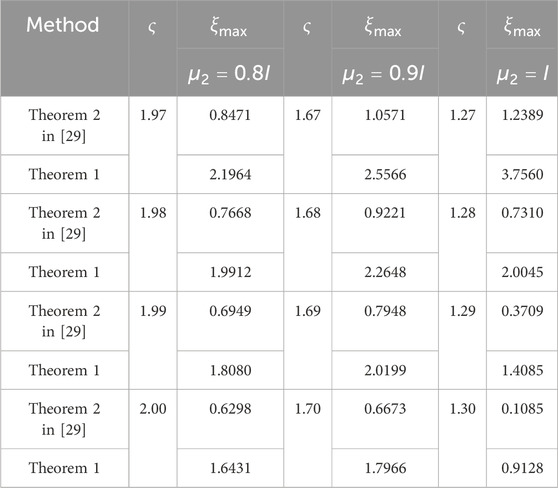
By solving LMIs in theorems 1 and 3 in this paper and Theorem 2 in [29], we can obtain the maximum admissible upper bound
The maximum admissible upper bound
In addition, for different combinations of
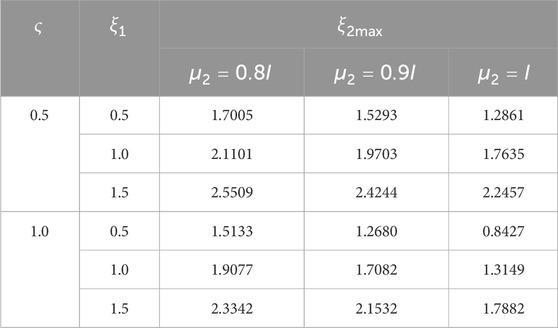
Table 3. Maximum allowable delay upper bound
Example 2. Consider MJHNNs Equation 5 and Equation 32 with
Next, we design state estimators to ensure the MSES of FESs with discrete and distributed delays, considering cases of time-invariant and time-variant discrete delays.
Case 1. Time-invariant discrete delay.
For the FES Equation 5, with
Case 2. Time-variant discrete delay.
For the FES Equation 32, with
In the simulations, we set
The simulations of the state estimators are shown in Figures 1–4. For the MJHNN with time-invariant discrete and distributed delays, Figure 1 shows the state trajectories and their corresponding estimations, while Figure 2 shows the trajectories of the FES. Figures 3, 4 show the corresponding trajectories under time-variant discrete delay scenarios. The proposed state estimator design methods are effective for MJHNNs with discrete and distributed delays in both cases of time-invariant and time-variant discrete delays.
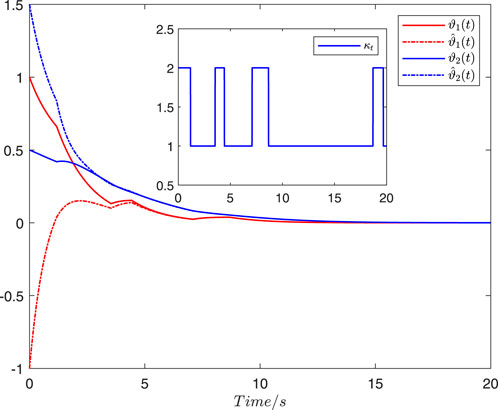
Figure 1. State trajectories
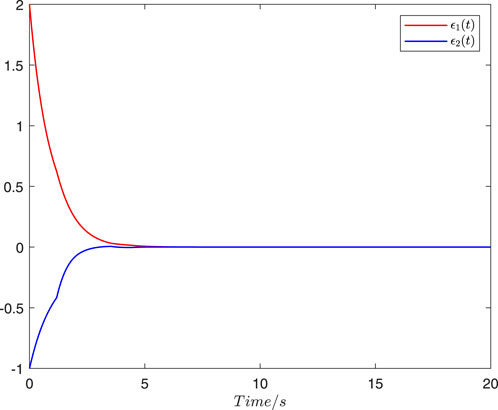
Figure 2. State trajectories of the FES
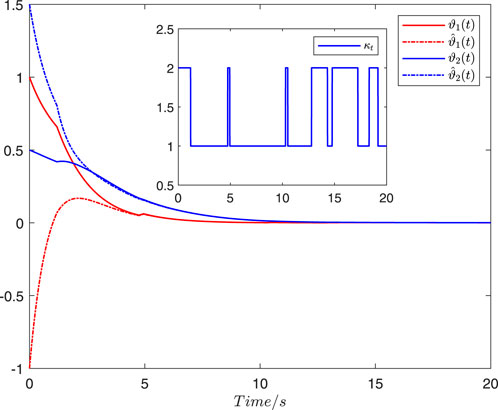
Figure 3. State trajectories
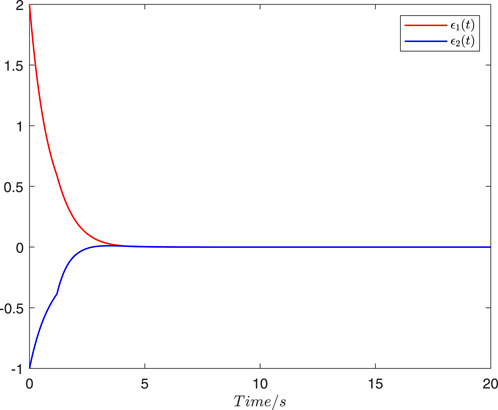
Figure 4. State trajectories of the FES
6 Conclusion
This paper has investigated the state estimation for MJHNNs with discrete and distributed delays. Specifically, both time-invariant and time-variant discrete delay cases are considered. Two conditions for the MSES of MJHNNs have been proposed utilizing augmented LKFs, the WBII, the BLI, and the CCI. The LMIs-based design methods for the required estimators have been developed by eliminating nonlinear coupling terms. Lastly, two numerical examples are given to demonstrate the applicability and reduced conservatism of the proposed stability criteria and estimator design methods. Future research could explore further refinement of these analysis and design results, and exporing their extention to more complex neural network models.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
LG: Investigation, Methodology, Writing–review and editing. WH: Writing–original draft.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Xiang S, Zhang T, Han Y, Guo X, Zhang Y, Shi Y, et al. Neuromorphic speech recognition with photonic convolutional spiking neural networks. IEEE J Sel Top Quan Electron (2023) 29:1–7. doi:10.1109/JSTQE.2023.3240248
2. Cui G, Yang W, Yu J. Neural network-based finite-time adaptive tracking control of nonstrict-feedback nonlinear systems with actuator failures. Inf Sci (2021) 545:298–311. doi:10.1016/j.ins.2020.08.024
3. Pan C, Hong Q, Wang X. A novel memristive chaotic neuron circuit and its application in chaotic neural networks for associative memory. IEEE Trans Comput Aided Des Integr Circuits Syst (2021) 40:521–32. doi:10.1109/TCAD.2020.3002568
4. Sharma P, Bisht I, Sur A. Wavelength-based attributed deep neural network for underwater image restoration. Acm T Multim Comput (2023) 19:1–23. doi:10.1145/3511021
5. Marcus C, Westervelt R. Stability of analog neural networks with delay. Phys Rev A (1989) 39:347–59. doi:10.1103/PhysRevA.39.347
6. Gunasekaran N, Thoiyab NM, Zhu Q, Cao J, Muruganantham P. New global asymptotic robust stability of dynamical delayed neural networks via intervalized interconnection matrices. IEEE Trans Cybern (2022) 52:11794–804. doi:10.1109/TCYB.2021.3079423
7. Liu M, Jiang H, Hu C, Lu B, Li Z. Novel global asymptotic stability and dissipativity criteria of BAM neural networks with delays. Front Phys (2022) 10:898589. doi:10.3389/fphy.2022.898589
8. Chang S, Wang Y, Zhang X, Wang X. A new method to study global exponential stability of inertial neural networks with multiple time-varying transmission delays. Math Comput Simul (2023) 211:329–40. doi:10.1016/j.matcom.2023.04.008
9. Tai W, Zhao A, Guo T, Zhou J. Delay-independent and dependent L2-L filter design for time-delay reaction–diffusion switched Hopfield networks. Circ Syst Signal Pr (2023) 42:173–98. doi:10.1007/s00034-022-02125-0
10. Zhou J, Ma X, Yan Z, Arik S. Non-fragile output-feedback control for time-delay neural networks with persistent dwell time switching: a system mode and time scheduler dual-dependent design. Neural Netw (2024) 169:733–43. doi:10.1016/j.neunet.2023.11.007
11. Rajchakit G, Sriraman R. Robust passivity and stability analysis of uncertain complex-valued impulsive neural networks with time-varying delays. Neural Process Lett (2021) 53:581–606. doi:10.1007/s11063-020-10401-w
12. Wang L, He H, Zeng Z. Global synchronization of fuzzy memristive neural networks with discrete and distributed delays. IEEE Trans Fuzzy Syst (2019) 28:2022–34. doi:10.1109/TFUZZ.2019.2930032
13. Wang H, Wei G, Wen S, Huang T. Generalized norm for existence, uniqueness and stability of Hopfield neural networks with discrete and distributed delays. Neural Netw (2020) 128:288–93. doi:10.1016/j.neunet.2020.05.014
14. Wang G, Ren Y, Huang C. Stabilizing control of Markovian jump systems with sampled switching and state signals and applications. Int J Robust Nonlin (2023) 33:5198–228. doi:10.1002/rnc.6637
15. Zhou J, Dong J, Xu S. Asynchronous dissipative control of discrete-time fuzzy Markov jump systems with dynamic state and input quantization. IEEE Trans Fuzzy Syst (2024) 31:3906–20. doi:10.1109/TFUZZ.2023.3271348
16. Hu B, Guan ZH, Lewis FL, Chen CP. Adaptive tracking control of cooperative robot manipulators with Markovian switched couplings. IEEE Trans Ind Electron (2020) 68:2427–36. doi:10.1109/TIE.2020.2972451
17. Chen G, Xia J, Park JH, Shen H, Zhuang G. Asynchronous sampled-data controller design for switched Markov jump systems and its applications. IEEE Trans Syst Man Cybern: Syst (2022) 53:934–46. doi:10.1109/TSMC.2022.3188612
18. Ma X, Dong J, Tai W, Zhou J, Paszke W. Asynchronous event-triggered H control for 2D Markov jump systems subject to networked random packet losses. Commun Nonlinear Sci (2023) 126:107453. doi:10.1016/j.cnsns.2023.107453
19. Ali MS, Tajudeen MM, Kwon OM, Priya B, Thakur GK. Security-guaranteed filter design for discrete-time Markovian jump delayed systems subject to deception attacks and sensor saturation. ISA Trans (2024) 144:18–27. doi:10.1016/j.isatra.2023.10.020
20. Xia W, Xu S, Lu J, Zhang Z, Chu Y. Reliable filter design for discrete-time neural networks with Markovian jumping parameters and time-varying delay. J Franklin Inst (2020) 357:2892–915. doi:10.1016/j.jfranklin.2020.02.039
21. Nagamani G, Soundararajan G, Subramaniam R, Azeem M. Robust extended dissipativity analysis for Markovian jump discrete-time delayed stochastic singular neural networks. Neural Comput Appl (2020) 32:9699–712. doi:10.1007/s00521-019-04497-y
22. Yang H, Wang Z, Shen Y, Alsaadi FE, Alsaadi FE. Event-triggered state estimation for Markovian jumping neural networks: on mode-dependent delays and uncertain transition probabilities. Neurocomputing (2021) 424:226–35. doi:10.1016/j.neucom.2020.10.050
23. Tao J, Xiao Z, Li Z, Wu J, Lu R, Shi P, et al. Dynamic event-triggered state estimation for Markov jump neural networks with partially unknown probabilities. IEEE Trans Neural Networks Learn Syst (2021) 33:7438–47. doi:10.1109/TNNLS.2021.3085001
24. Aravind RV, Balasubramaniam P. Stochastic stability of fractional-order Markovian jumping complex-valued neural networks with time-varying delays. Neurocomputing (2021) 439:122–33. doi:10.1016/j.neucom.2021.01.053
25. Yao L, Wang Z, Huang X, Li Y, Ma Q, Shen H. Stochastic sampled-data exponential synchronization of Markovian jump neural networks with time-varying delays. IEEE Trans Neural Networks Learn Syst (2023) 34:909–20. doi:10.1109/TNNLS.2021.3103958
26. Tai W, Li X, Zhou J, Arik S. Asynchronous dissipative stabilization for stochastic Markov-switching neural networks with completely-and incompletely-known transition rates. Neural Netw (2023) 161:55–64. doi:10.1016/j.neunet.2023.01.039
27. Sathishkumar V, Vadivel R, Cho J, Gunasekaran N. Exploring the finite-time dissipativity of Markovian jump delayed neural networks. Alex Eng J (2023) 79:427–37. doi:10.1016/j.aej.2023.07.073
28. Wang T, Zhao S, Zhou W, Yu W. Finite-time state estimation for delayed Hopfield neural networks with Markovian jump. Neurocomputing (2015) 156:193–8. doi:10.1016/j.neucom.2014.12.062
29. Chen Y, Zheng WX. Stochastic state estimation for neural networks with distributed delays and Markovian jump. Neural Netw (2012) 25:14–20. doi:10.1016/j.neunet.2011.08.002
30. Yao L, Huang X, Wang Z, Liu K. Secure control of Markovian jumping systems under deception attacks: an attack-probability-dependent adaptive event-trigger mechanism. IEEE Trans Control Netw Syst (2023) 10:1818–30. doi:10.1109/TCNS.2023.3269007
32. Zheng F, Li X, Du B. Periodic solution problems of neutral-type stochastic neural networks with time-varying delays. Front Phys (2024) 12:1338799. doi:10.3389/fphy.2024.1338799
33. Chen Q, Liu X, Wang F. Improved results on L2-L state estimation for neural networks with time-varying delay. Circ Syst Signal Pr (2022) 41:122–46. doi:10.1007/s00034-021-01799-2
34. Qian W, Xing W, Fei S. H state estimation for neural networks with general activation function and mixed time-varying delays. IEEE Trans Neural Networks Learn Syst (2020) 32:3909–18. doi:10.1109/TNNLS.2020.3016120
35. Seuret A, Gouaisbaut F. Hierarchy of LMI conditions for the stability analysis of time-delay systems. Syst Control Lett (2015) 81:1–7. doi:10.1016/j.sysconle.2015.03.007
36. Zeng HB, He Y, Wu M, She J. New results on stability analysis for systems with discrete distributed delay. Automatica (2015) 60:189–92. doi:10.1016/j.automatica.2015.07.017
37. Seuret A, Gouaisbaut F. Wirtinger-based integral inequality: application to time-delay systems. Automatica (2013) 49:2860–6. doi:10.1016/j.automatica.2013.05.030
38. Park P, Ko JW, Jeong C. Reciprocally convex approach to stability of systems with time-varying delays. Automatica (2011) 47:235–8. doi:10.1016/j.automatica.2010.10.014
39. Liu K, Seuret A, Xia Y. Stability analysis of systems with time-varying delays via the second-order Bessel–Legendre inequality. Automatica (2017) 76:138–42. doi:10.1016/j.automatica.2016.11.001
Keywords: Hopfield neural networks, Markovian jump, mean-square exponential stability, state estimation, time delays
Citation: Guo L and Huang W (2024) State estimation for Markovian jump Hopfield neural networks with mixed time delays. Front. Phys. 12:1447788. doi: 10.3389/fphy.2024.1447788
Received: 12 June 2024; Accepted: 26 August 2024;
Published: 12 September 2024.
Edited by:
Shiping Wen, University of Technology Sydney, AustraliaReviewed by:
Guici Chen, Wuhan University of Science and Technology, ChinaGuodong Zhang, South-Central University for Nationalities, China
Copyright © 2024 Guo and Huang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lili Guo, Z3VvbGlsaUBhaHV0LmVkdS5jbg==
 Lili Guo
Lili Guo Wanhui Huang
Wanhui Huang