High-angular resolution diffusion tensor imaging: physical foundation and geometric framework

This paper proposes a statistical physics-based data assimilation model for the mobility of water-bound hydrogen nuclear spins in the brain in the context of diffusion weighted magnetic resonance imaging (DWI or DW-MRI). Point of departure is a statistical hopping model that emulates molecular motion in the presence of static and stationary microscale obstacles, statistically reflected in the apparent inhomogeneous anisotropic DWI signal profiles. Subsequently, we propose a Riemann–Finsler geometric interpretation in terms of a metric transform that simulates this molecular process as free diffusion on a vacuous manifold with all diffusion obstacles absorbed in its geometry. The geometrization procedure supports the reconstruction of neural tracts (geodesic tractography) and their quantitative characterization (tractometry). The Riemann-DTI model for geodesic tractography based on diffusion tensor imaging (DTI) arises as a limiting case. The genuine Finslerian case is a geometric representation of high-angular resolution DTI, i.e., a generalized rank-two DTI framework without the quadratic restriction implied by a simplifying Gaussianity assumption on local diffusion or a second-order harmonic approximation of local orientation distributions.

1 Introduction

1.1 The hopping model

In an attempt to gain a deeper understanding of the physics underlying the diffusion of water in the brain [1], we propose a hopping model, in which mobile, diffusion-sensitized hydrogen spins (‘particles’ henceforth) are jumping to and from any fiducial point at a stationary, position-dependent hopping rate. Frictions and orientation preferences induced by self-diffusion and collisions with static fibrous tissue barriers and DWI-insusceptible solutes are incorporated in generic statistical constraints on the jumps. These are assumed to be spatially inhomogeneous and anisotropic, with a priori unconstrained size and orientation distributions induced by the tissue’s micro-structure (graininess $\sim$ $\mu$m) implicitly averaged over mesoscopic regimes typical of DWI (voxel size $\sim \text{mm}$). Using data assimilation, these generic distributions can be matched with the observed DWI signals (e.g., using an appropriate, complete function basis [2]; [3]) and linked to a differential geometric norm (or Riemann–Finsler metric), yielding a model-free, data-driven framework for geodesic tractography and tractometric analysis.

To appreciate the hopping model in its simplest form, the reader is referred to the one-dimensional inhomogeneous case introduced by [4] and scrutinized by [5]. Our application to water diffusion in the brain in the context of (model-free) DWI has led us to the following generalizations:

1. Generalize this to three dimensions;

2. Account for anisotropy induced by the fibrous nature of the brain (white matter) tissue; and

3. Disentangle diffusion orientations to prevent destructive interference during signal formation.

As a result, we obtain a generic model for high-angular resolution diffusion tensor imaging (DTI) not hampered by the ambiguities of its classical counterpart (by virtue of item 3). The construction, in turn, provides the necessary insight for a geometric interpretation supporting DWI-driven geodesic tractography and tractometry [6]; [7], generalizing (and including) the familiar Riemann-DTI paradigm ([8]; [9]; [10]; [11,12]; [13]; [14]; [15]). It also offers new insights in connection to established DWI representations, such as constrained spherical deconvolution, diffusion orientation distribution functions, Q-ball imaging, HARDI, and diffusion spectrum imaging (DSI) ([16]; [17]; [18]; [19, 20]; [21]; [3]; [22–24]; [25]; [24, 26]).

1.2 The master equation

The master equation governs the instantaneous rate of change in the local hydrogen spin density at a fiducial point with Cartesian coordinates $\vec{x}\in {\mathbb{R}}^3$ in terms of gain and loss terms:

$\frac{\partial u\left(\vec{x},t\right)}{\partial t}={\iiint }_{{\mathbb{R}}^3}{d}^3\vec{\xi }\left[W\left(\vec{x}|\vec{\xi }\right)u\left(\vec{\xi },t\right)-W\left(\vec{\xi }|\vec{x}\right)u\left(\vec{x},t\right)\right].(1)$

Values at a single voxel $\vec{x}$ implicitly represent mesoscopic volume aggregates of unresolvable microscopic structures at an observation scale determined by MRI resolving power. The evolution process is, thus, assumed to be completely driven by static geometry (tissue anatomy), the mesoscopic reconstruction of which is our ultimate motivation. The weighted transition density $W(\vec{x}|\vec{\xi })$ is taken as follows (this is the essence of the hopping model [4]):

$W\left(\vec{x}|\vec{\xi }\right)=W\left(\vec{\xi }\right)P\left(\vec{x}-\vec{\xi };\vec{\xi }\right)=W\left(\vec{\xi }\right){\iiint }_{{\mathbb{R}}^3}{d}^3\vec{y}P\left(\vec{y};\vec{\xi }\right){\delta }^3\left(\vec{y}-\left(\vec{x}-\vec{\xi }\right)\right).(2)$

The scalar field $W(\vec{\xi })$ is the local hopping rate at point $\vec{\xi }$, a heuristic measure for the effective (orientation-independent) local permeability or inverse local drag experienced by diffusing particles due to neighborhood interactions, including self-interactions. The product $W(\vec{\xi })u(\vec{\xi },t)$ expresses the time-dependent relative number of local hops per unit volume and per unit time. Particle conservation follows from (1) after normalization:

${\iiint }_{{\mathbb{R}}^3}{d}^3\vec{\xi }W\left(\vec{\xi }|\vec{x}\right)=W\left(\vec{x}\right).$

The left-hand side counts the number of particles per unit time jumping away from a fiducial point $\vec{x}$ and landing anywhere else in configuration space ($\vec{\xi }$-domain). By particle conservation, this must equal the local hopping rate at $\vec{x}$ on the right-hand side. The double-argument function $P(\vec{y};\vec{\xi })$ denotes the local probability density function (pdf) (aka ‘spin density’) for a jump $\vec{y}$ originating at point $\vec{\xi }$, with $\vec{\xi }$-independent normalization:

${\iiint }_{{\mathbb{R}}^3}{d}^3\vec{y}P\left(\vec{y};\vec{\xi }\right)=1.(3)$

In the quantities $W(\vec{x}|\vec{\xi })$, $W(\vec{\xi })$, and $P(\vec{y};\vec{\xi })$, $\vec{\xi }$ and $\vec{x}$ are base points in the Euclidean configuration space ${\mathbb{R}}^3$, represented by Cartesian coordinate vectors relative to an arbitrarily chosen frame. The argument $\vec{y}$ is an element of the local tangent space and represents a vectorial jump or hop away from the base point to which it is anchored. The quantities $u(\vec{\xi },t)$, $P(\vec{y};\vec{\xi })$, and $W(\vec{x}|\vec{\xi })$ are densities, i.e., amplitudes of the corresponding volume forms (on distinct domains), $u(\vec{\xi },t)d^3\vec{\xi }$, $P(\vec{y};\vec{\xi })d^3\vec{y}$, and $W(\vec{x}|\vec{\xi })d^3\vec{x}$, relative to unit 3-volume forms, $d^3\vec{\xi }\doteq d{\xi }^1\wedge d{\xi }^2\wedge d{\xi }^3$, $d^3\vec{y}\doteq d{y}^1\wedge d{y}^2\wedge d{y}^3$, and $d^3\vec{x}\doteq d{x}^1\wedge d{x}^2\wedge d{x}^3$, respectively, in Cartesian coordinates.

2 Theory

2.1 The hopping model in configuration space

Combining Equations 1, 2 yields the following integro-differential equation:

$\frac{\partial u\left(\vec{x},t\right)}{\partial t}={\iiint }_{{\mathbb{R}}^3}{d}^3\vec{y}W\left(\vec{x}-\vec{y}\right)P\left(\vec{y};\vec{x}-\vec{y}\right)u\left(\vec{x}-\vec{y},t\right)-W\left(\vec{x}\right)u\left(\vec{x},t\right).(4)$

Despite the integral, it may be interpreted as a local equation in the configuration space confined to the base point $\vec{x}$, by assuming that $\vec{y}$-integration takes place over the local tangent space attached to that point.¹ However, it will be important to appreciate the distinct natures of the base point coordinate vector $\vec{x}$ and the associated local tangent vector component $\vec{y}$ thereafter.

2.2 The Fokker–Planck equation in configuration space

Assuming the pdf $P(\vec{y};\vec{x}-\vec{y})$ in Equation 4, to be narrow in $\Vert \vec{y}\Vert$ with respect to its first argument, which amounts to predominantly small jumps, regardless of direction relative to a slowly varying second argument, we may invoke Taylor’s expansion around the base point $\vec{x}$ under the integral, truncating at the lowest nontrivial order. Using the shorthand $f(\vec{x})\doteq W(\vec{x})P(\cdot ;\vec{x})u(\vec{x},\cdot )$, the relevant approximation is (using summation convention and abbreviating ${\partial }_i\doteq \partial /\partial x^i$)

$f\left(\vec{x}-\vec{y}\right)=\exp \left(-\vec{y}\cdot \nabla \right)f\left(\vec{x}\right)\approx f\left(\vec{x}\right)-{\partial }_{i}f\left(\vec{x}\right)y^i+\frac{1}{2}{\partial }_{ij}f\left(\vec{x}\right)y^i{y}^j+\mathcal{O}\left(\Vert \vec{y}{\Vert }^3\right).(5)$

Combining Equations 4, 5 and exploiting the normalization Equation 3 for the lowest-order term and, for the first-order term, imposing the symmetry assumption

$P\left(\vec{y};\vec{x}\right)=P\left(-\vec{y};\vec{x}\right),(6)$

implying a vanishing one-point correlation function

${\iiint }_{{\mathbb{R}}^3}{d}^3\vec{y}P\left(\vec{y};\vec{x}\right)y^i=0,(7)$

one ends up with the following Fokker–Planck equation:

$\frac{\partial u\left(\vec{x},t\right)}{\partial t}={\partial }_{ij}\left(D^{ij}\left(\vec{x}\right)u\left(\vec{x},t\right)\right),(8)$

with the configuration space diffusion tensor field

$\begin{array}{ll}\hfill & D^{ij}\left(\vec{x}\right)\doteq \frac{1}{2}W\left(\vec{x}\right){\iiint }_{{\mathbb{R}}^3}{d}^3\vec{y}P\left(\vec{y};\vec{x}\right)y^i{y}^j\hfill \\ \hfill & \doteq \frac{1}{2}W\left(\vec{x}\right){\iint }_{{\mathbb{S}}^2}{d}^2\widehat{y}{\ell }^2\left(\vec{x},\widehat{y}\right){\widehat{y}}^i{\widehat{y}}^j.\hfill \end{array}(9)$

The latter integral extends over the unit sphere ${\mathbb{S}}^2\doteq \{\widehat{y}\in {\mathbb{R}}^3|\Vert \widehat{y}\Vert =1\}$, obtained after integration over the jump size $\Vert \vec{y}\Vert$, with

${\ell }^2\left(\vec{x},\widehat{y}\right)\doteq {\int }_0^{\infty }d\rho {\rho }^{4}P\left(\rho \widehat{y};\vec{x}\right).(10)$

Note the quadratic scaling with a typical jump size and the local (tissue-dependent) modulation by the hopping rate prior. These expressions are further analyzed in Section 2.5. The diffusion tensor, as defined in Equation 9, plays a pivotal role in DTI. An excellent introduction to DTI and its (potential) clinical ramifications is explained in the work by [28].

Without Equation 6, a nontrivial first-order term would emerge. Since its order of magnitude depends on the degree of symmetry violation, regardless of step size $\Vert \vec{y}\Vert$, its significance is independent of the second-order term in Equation 5, which is why one must never truncate at first order. Moreover, symmetry is irrelevant for our considerations below, cf. [29], for asymmetric distributions that may effectively arise from locally symmetric distributions due to asymmetric spatial inhomogeneities at subvoxel scales. Antipodal symmetry is imposed to explicitly discard the effect of a directional flow (in a suitably defined rest frame) so that only orientational, i.e., bidirectional, diffusion effects, on which our considerations are exclusively built, are manifest.

As remarked by [4], due to the inhomogeneity of the hopping model, the right-hand side of Equation 8 does not take the form of Fick’s law, where the diffusion tensor field would be in-between the partial-derivative operators ${\partial }_i$ and ${\partial }_j$. Fick’s law would introduce a spurious flow altering the center of mass of the particle distribution, which is clearly inconsistent with the (statistical) hop/anti-hop pair creation implied by our symmetry assumption (Equations 6, 7).

2.3 Angular resolution limitations

It is well-known that the diffusion tensor field (Equation 9), the keystone of DTI, is a relatively poor descriptor of anisotropy, among others due to destructive interference caused by the $\vec{y}$-integration process, which entails an $\infty$-to-6 mapping per base point, captured by the symmetric two-point correlation matrix on the right-hand side. The resulting ‘ground truth metamerism’ (equivalence classes of configurations inducing identical DTI measurements) is a notoriously confusing factor in tractography validation. Disregarding complicating factors due to spatial resolution limitations, the only case covered without loss of information is anisotropic Gaussian diffusion, a simplification one cannot take for granted in the complex brain tissue, where neural fiber crossings are omnipresent. Estimates range from 30% to 90% of white matter voxels, but exact figures depend nontrivially on one’s definition of a fiber in relation to spatial resolution, cf. [30,31]. To support data assimilation using more sophisticated high-angular resolution DWI signal models (at state-of-the-art spatial resolution), one would like to understand better what occurs underneath the $\vec{y}$-integral. This is the subject of the next section.

2.4 The Fokker–Planck equation in phase space

To reveal the genuine nature of anisotropy at an arbitrary angular resolution, we must refrain from $\vec{y}$-integration in Equation 10, or at least from integration over orientation encoding spherical shells. To this end, we start by introducing the phase space (or tangent bundle) as an extended six-dimensional base manifold parametrized by coordinate sextuplets $(\vec{x},\vec{y})\in {\mathbb{R}}^3\times {\mathbb{R}}^3$ of jumps $\vec{y}\in {\mathbb{R}}^3$ and their spatial anchor points $\vec{x}\in {\mathbb{R}}^3$ as a precursor of subsequent projection to the five-dimensional sphere bundle with coordinate quintuplets $(\vec{x},\widehat{y})\in {\mathbb{R}}^3\times {\mathbb{S}}^2$ via integration over the jump size distribution. [32] and [33] provide geometric interpretations of such extended manifolds in a more general geometric setting.

There is no unique way to extend the Fokker–Planck equation to phase space based on our hopping model in the configuration space. An intuitive way is obtained by considering the ‘vertically lifted’ particle density

$u^{\text{\hspace{0.17em}v}}\left(\vec{x},\vec{y},t\right)\doteq u\left(\vec{x},t\right)P\left(\vec{y};\vec{x}\right).(11)$

Consider the particles at the base point $\vec{x}$ being distributed over the local tangent space of linearized jumps $\vec{y}$, according to the local jump probability density $P(\vec{y};\vec{x})$. The geometric object represented by the sparsified density (Equation 11), is $u^{\text{\hspace{0.17em}v}}(\vec{x},\vec{y},t)d^3\vec{x}{d}^3\vec{y}$, with the 6-volume form $d^3\vec{x}{d}^3\vec{y}\doteq d{x}^1\wedge d{x}^2\wedge d{x}^3\wedge d{y}^1\wedge d{y}^2\wedge d{y}^3$ in Cartesian coordinates. By virtue of Equation 3, we may interpret the Fokker–Planck equation in the configuration space, Equations 8, 9, as arising from $\vec{y}$-integration of an extended equation in phase space, viz.,

$\frac{\partial u^{\text{\hspace{0.17em}v}}\left(\vec{x},\vec{y},t\right)}{\partial t}={\partial }_{ij}\left({\mathrm{\Delta }}^{ij}\left(\vec{x},\vec{y}\right)u^{\text{\hspace{0.17em}v}}\left(\vec{x},\vec{y},t\right)\right)+T\left(\vec{x},\vec{y},t\right).(12)$

The function $T(\vec{x},\vec{y},t)$ may be any kernel term that is, by definition, annihilated upon $\vec{y}$-integration:

${\iiint }_{{\mathbb{R}}^3}{d}^3\vec{y}T\left(\vec{x},\vec{y},t\right)\doteq 0.(13)$

Such a term could arise in various ways, e.g., as a $\vec{y}$-antisymmetric function or as the $\vec{y}$-divergence of some vector field, which vanishes upon integration by virtue of Stokes’ theorem in a physically realistic setting. The phase space diffusion tensor field is defined here as

${\mathrm{\Delta }}^{ij}\left(\vec{x},\vec{y}\right)\doteq \frac{1}{2}W\left(\vec{x}\right)y^i{y}^j.(14)$

Note its particularly simple, singular form, with only a single, isotropic local degree of freedom, the local hopping rate $W(\vec{x})$, in a trade-off with the squared jump size $\Vert \vec{y}{\Vert }^2$. Since it does not contain orientation information, which, after all, has been absorbed in the lifted particle density $u^{\text{\hspace{0.17em}v}}(\vec{x},\vec{y},t)$ via the factor $P(\vec{y};\vec{x})$, as in Equation 11, it is not a generalization of the classical diffusion tensor field (Equation 9). By construction, the Fokker-Planck equation in configuration space and the classical diffusion tensor field (Equations 8, 9) are reobtained after $\vec{y}$-integration of Equation 12.

2.5 The Fokker–Planck equation on the sphere bundle

The phase space diffusion equation (Equation 12) and its singular diffusion tensor (Equation 14) may be natural objects of study in the context of DSI, where one probes the entire phase space (again ignoring spatial resolution ambiguities), cf. [24, 26]. However, current clinical and technical constraints preclude a sufficiently dense sampling of this six-dimensional manifold. Clinical DWI typically relies on sampling of (one or a few) spherical shell(s). Moreover, anisotropy is encoded in the distribution of jump orientations, not magnitudes. We, therefore, decouple the two by considering marginal distributions for each, setting $\vec{y}\doteq \rho \widehat{y}$, with $\rho \doteq \Vert \vec{y}\Vert$ and $\widehat{y}\doteq \vec{y}/\Vert \vec{y}\Vert$ so that

${\iiint }_{{\mathbb{R}}^3}{d}^3\vec{y}\doteq {\int }_0^{\infty }d\rho {\rho }^2{\iint }_{{\mathbb{S}}^2}{d}^2\widehat{y}.(15)$

We may integrate Equation 12, over the jump size distribution using any spherical coordinate parametrization for $\widehat{y}\in {\mathbb{S}}^2$, retaining orientation information, such as spherical polar coordinates $(\theta ,\varphi )\in [0,\pi ]\times \left[0\right.,\left.2\pi \right)$, with

$\widehat{y}\doteq \left({\widehat{y}}^1=\cos \varphi \sin \theta ,{\widehat{y}}^2=\sin \varphi \sin \theta ,{\widehat{y}}^3=\cos \theta \right),$

so that

${\iint }_{{\mathbb{S}}^2}{d}^2\widehat{y}={\int }_0^{\pi }d\theta \sin \theta {\int }_0^{2\pi }d\varphi .$

Since a particular form of parametrization is irrelevant for our discussion, we focus on the notation (Equation 15), for simplicity. The five-dimensional submanifold ${\mathbb{R}}^3\times {\mathbb{S}}^2\doteq \{(\vec{x},\widehat{y})\in {\mathbb{R}}^3\times {\mathbb{R}}^3|\Vert \widehat{y}\Vert =1\}$ of phase space will, henceforth, be referred to as the (Euclidean) sphere bundle.

For the sake of definiteness, one might consider a Maxwell–Boltzmann distribution for jump sizes $\rho \ge 0$ on the sphere bundle in order to perform the jump size integration; see Supplementary Appendix 1 for details. In view of data assimilation, however, the essence is that any distribution induces a phenomenological diffusion length scale $\ell (\vec{x},\widehat{y})$ given by Equation 10 via jump size integration, which is an instance of a generalized (diffusion) orientation diffusion function (ODF), cf. [34]; [35]; [36]; [25] (without the factor ${\rho }^4$); Barnett’s adaptation [37] (with the Jacobian factor ${\rho }^2$); and the generalization by [3], including an operational scheme to compute Equation 10 from a DWI data representation, implemented in Dipy, cf. [38]. With this definition, we can evaluate the jump size integral in Equation 9, yielding

$D^{ij}\left(\vec{x}\right)\doteq \frac{1}{4\pi }{\iint }_{{\mathbb{S}}^2}{d}^2\widehat{y}{D}^{ij}\left(\vec{x},\widehat{y}\right),(16)$

in which the sphere bundle diffusion tensor field is defined in terms of the phase space diffusion tensor field (Equation 13) and jump pdf (Equation 3) as

$D^{ij}\left(\vec{x},\widehat{y}\right)\doteq 4\pi {\int }_0^{\infty }d\rho {\rho }^2{\mathrm{\Delta }}^{ij}\left(\vec{x},\rho \widehat{y}\right)P\left(\rho \widehat{y};\vec{x}\right),(17)$

or, in terms of the hopping rate and phenomenological diffusion scale with the help of Equation 11, as

$D^{ij}\left(\vec{x},\widehat{y}\right)=2\pi {\ell }^2\left(\vec{x},\widehat{y}\right)W\left(\vec{x}\right){\widehat{y}}^i{\widehat{y}}^j.(18)$

The occurrences of $4\pi$ in Equations 16, 17 are chosen such that the classical diffusion tensor $D^{ij}(\vec{x})$ in configuration space arises as an idempotent projection of its high-angular resolution counterpart $D^{ij}(\vec{x},\widehat{y})$ via spherical averaging so that the former is consistent with an orientation-independent instance of the latter. Figure 1 illustrates this high-angular resolution diffusion tensor to various orders of spherical harmonic approximation in comparison with the classical DTI case.

The sphere bundle diffusion tensor field (Equations 17, 18) supports a high-angular resolution DTI framework alluded to in the foregoing, generalizing the classical case defined in the configuration space. However, it inherits its singular nature from the phase space diffusion tensor field (Equation 14), with a single nonzero eigendirection spanned by the distinguished direction $\widehat{y}$ at $\vec{x}$, i.e., the direction indicated by the vectorial part $\widehat{y}\in {\mathbb{S}}^2$ of its five-dimensional base point $(\vec{x},\widehat{y})\in {\mathbb{R}}^3\times {\mathbb{S}}^2$.

In Section 2.6, we show how regularization is naturally realized in the DTI limit by virtue of vertical projection (19), albeit at the expense of what we determine to achieve, viz., an unrestricted angular resolution. In Supplementary Appendix 2, we elaborate on the classical DTI premise, for which projection does not incur the loss of angular resolution. In Section 2.7, we consider regularization in combination with geometrization of Equations 17, 18 on the sphere bundle, maintaining an unrestricted angular resolution, the novelty and main objective of this article.

2.6 Back to configuration space: classical diffusion tensor imaging

Recall that, in its most rudimentary form, the classical diffusion tensor in configuration space captures the second-order momenta of the stipulated transition density function Equation 2:

$D^{ij}\left(\vec{x}\right)=\frac{1}{2}{\iiint }_{{\mathbb{R}}^3}{d}^3\vec{y}W\left(\vec{x}|\vec{x}-\vec{y}\right)y^i{y}^j.$

Subsequently, based on our heuristic hopping model, we have generalized it to a diffusion tensor defined on extended domains, notably on the phase space of positions and jump vectors and, ultimately, via projection over jump size, on the sphere bundle of positions and orientations, tacitly assuming antipodal symmetry. The latter, given by Equations 17, 18 and referred to as ‘high-angular resolution DTI,’ defines our main object of interest.

By construction, spherical averaging of the singular tensor (Equations 17, 18) via Equations 16 reproduces the regular, classical diffusion tensor field (10) in configuration space. This projection expresses a correspondence principle, clarifying how classical DTI emerges as a limiting case of high-angular resolution DTI. Clearly, this procedure causes irreversible loss of orientation information due to destructive interference, unless very special conditions on the nature of the medium hold. This restrictive case is considered in more detail in Supplementary Appendix 2 as an instructive hypothetical limit.

2.7 Geometrization and geodesic tractography

In the Riemann-DTI paradigm, it is stipulated that the configuration space DTI tensor defines (up to isotropic [8]; [9] or anisotropic scaling [39]; [40]) a dual Riemannian metric, in terms of which one can express the tractography inverse problem as a (constrained) geodesic or ‘shortest path’ problem ([7]; [41]; [11]; [13]; [15, 42]). This interpretation is consistent with its symmetric positive definite nature.

It is tempting to assign a similar role in a generalized, Finsler-geometric setting, to the high-angular resolution DTI tensor (Equations 17, 18) on the sphere bundle. However, there is a fundamental obstruction, viz., its singular nature. Its eigenspace is, by construction, one-dimensional, spanned by the distinguished direction $\widehat{y}$. Instead of pursuing this case in a sub-Finslerian setting, where such degeneracies might be properly handled, it appears more convenient to search for an equivalent, regularized counterpart.

To begin with, let us stipulate a singular dual metric tensor by ‘demodulating’ the diffusion tensor on the sphere bundle, Equation 18, excluding local tissue permeability captured by the hopping rate:

$g_{\text{\hspace{0.17em}0}}^{ij}\left(\vec{x},\widehat{y}\right)\doteq k\left(\vec{x},\widehat{y}\right){\widehat{y}}^i{\widehat{y}}^j,$

with the scalar field

$k\left(\vec{x},\widehat{y}\right)\doteq 2\pi {\ell }^2\left(\vec{x},\widehat{y}\right)(19)$

as a geometric counterpart of the diffusion tensor on the sphere bundle. The reason for suppressing the hopping rate in the dual metric is threefold: (i) as a heuristic toy model parameter, the exact physical significance of the hopping rate is not well-understood; (ii) the demodulated metric reflects local anisotropic hydrogen spin mobility constraints, independent of the isotropic tissue permeability captured by the hopping rate (a manifestation of non-geometric microstructural properties in a voxel); and (iii) a demodulated metric is least committed, in the sense that it can be adapted a posteriori by a conformal scale factor, defining an effective hopping rate $W(\vec{x})$, based on application-dependent axiomatic considerations. The latter argument is a pragmatic one, which resonates with historical practice, cf. the various conformal factors proposed in the Riemann-geodesic tractography paradigm, either implicit by virtue of the (ad hoc) identification of dual metric and DTI tensor ([11]; [13]), or explicitly stipulated via certain axiomatic requirements ([8]; [9]).

Figure 1 illustrates the diffusivity glyphs arising from the scalar field $k(\vec{x},\widehat{y})$ in a truncated spherical harmonic basis. Although at second order, the glyphs of $k(\vec{x},\widehat{y})$ resemble those of the classical DTI tensor $D^{ij}(\vec{x})$—both having six local degrees of freedom—more and more directional information is obtained at higher orders.

Figure 1

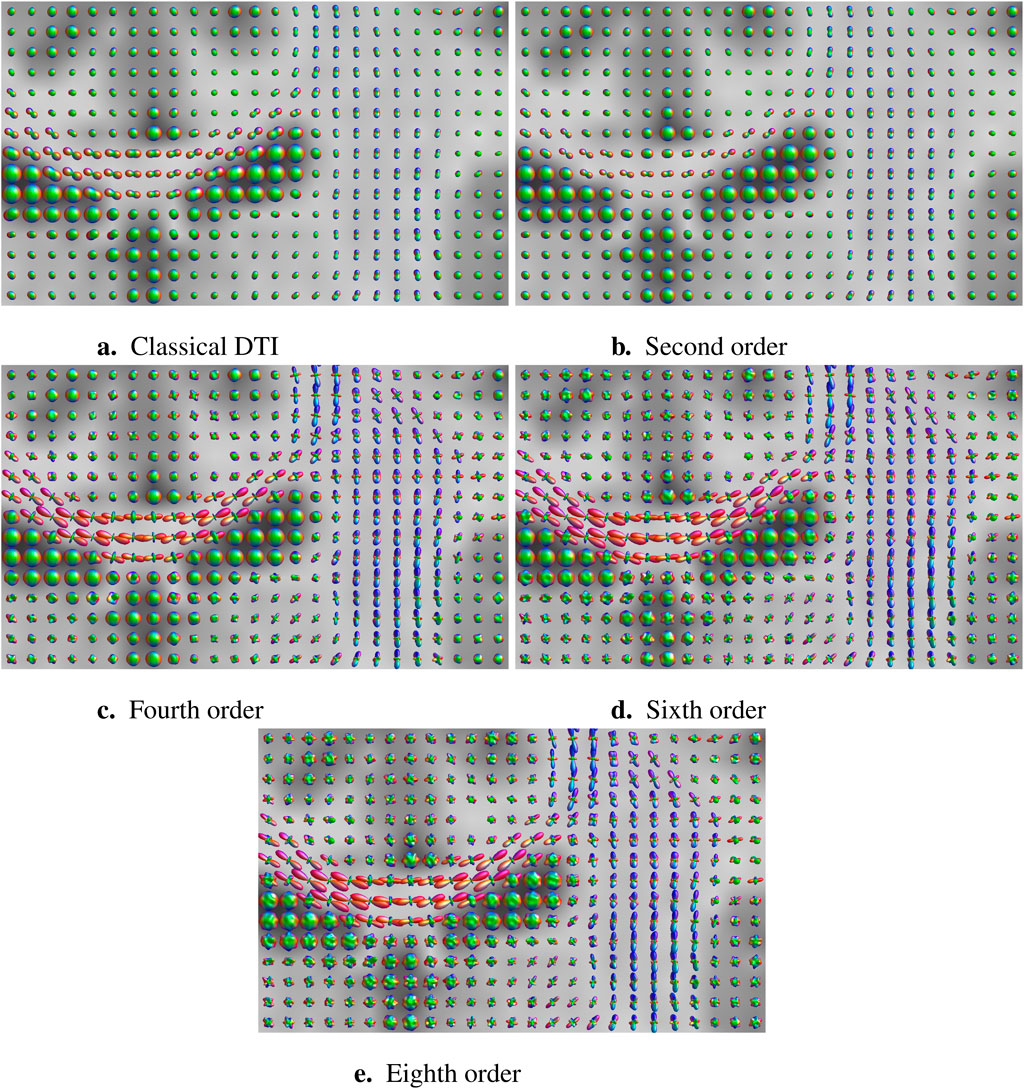
Figure 1. Classical and high-angular resolution DTI for increasing levels of spherical harmonic articulation. Glyphs represent apparent diffusivity values $D^{ij}(\vec{x},\widehat{y}){\widehat{y}}_i{\widehat{y}}_j$ at each location $x\in {\mathbb{R}}^3$ on the unit sphere $\widehat{y}\in {\mathbb{S}}^2$; recall (21). There is a trade-off between robustness of any given truncation order and the number of DWI diffusion gradients used in the acquisition. (A) Classical DTI; (B) second-order; (C) fourth-order; (D) sixth-order; (E) eighth-order.

Since $\det g_{\text{\hspace{0.17em}0}}^{ij}=0$, we cannot define a covariant metric $g_{ij}^{\text{\hspace{0.17em}0}}$ by inversion in the usual way via $g_{\text{\hspace{0.17em}0}}^{ik}{g}_{kj}^{\text{\hspace{0.17em}0}}={\delta }_j^i$. However, we may define it as a generalized inverse satisfying the modified condition

$g_{\text{\hspace{0.17em}0}}^{ik}{g}_{k\ell }^{\text{\hspace{0.17em}0}}{g}_{\text{\hspace{0.17em}0}}^{\ell j}=g_{\text{\hspace{0.17em}0}}^{ij}.$

Such a generalized inverse is easily seen to be given by

$g_{ij}^{\text{\hspace{0.17em}0}}\left(\vec{x},\widehat{y}\right)\doteq \frac{1}{k\left(\vec{x},\widehat{y}\right)}{\widehat{y}}_i{\widehat{y}}_j,$

modulo ambiguities of the form

$g_{ij}^{\text{\hspace{0.17em}0}}\to g_{ij}^{\text{\hspace{0.17em}0}}+{\lambda }_{\alpha i}{ϵ}_j^{\alpha }+{\lambda }_{\alpha j}{ϵ}_i^{\alpha },$

in which ${ϵ}^{\alpha }\doteq {ϵ}_{\ell }^{\alpha }d{x}^{\ell }$ and $\alpha =\mathrm{1,2}$ are two independent eigen-covectors satisfying $g_{\text{\hspace{0.17em}0}}^{k\ell }{ϵ}_{\ell }^{\alpha }=0$ and ${\lambda }_{\alpha i}\in \mathbb{R}$ arbitrary coefficients. This observation could be used to construct a regularized metric tensor $g_{ij}$ but does not offer a ‘canonical’ recipe for the regularizing terms. The Moore–Penrose pseudoinverse ([43]; [44]) and the Drazin inverse [45]—which are equal in this special case of a dyadic self-product—correspond to ${\lambda }_{\alpha i}=0$.

An alternative method that gracefully resolves the ambiguity proceeds via an intermediate construction of a new, generalized norm for the vector $\vec{y}$ at the base point $\vec{x}$, or positive Finsler function $F(\vec{x},\vec{y})$, defined on the slit tangent bundle $(\vec{x},\vec{y})\in {\mathbb{R}}^3\times {\mathbb{R}}^3\backslash \{\vec{0}\}$, as follows:

$F^2\left(\vec{x},\vec{y}\right)\doteq g_{ij}^{\text{\hspace{0.17em}0}}\left(\vec{x},\widehat{y}\right)y^i{y}^j.$

The Hessian of this Finsler Lagrangian defines a new metric tensor in the usual manner [32]; [33]:

$g_{ij}\left(\vec{x},\widehat{y}\right)\doteq \frac{1}{2}\frac{{\partial }^2{F}^2\left(\vec{x},\vec{y}\right)}{\partial y^i\partial y^j}.$

Since this metric exists alongside our original Euclidean metric, one must remain cautious in view of ambiguous index-raising and -lowering conventions; unless stated otherwise, index raising and lowering will henceforth pertain to the Finsler metric. Working out technicalities, setting²

$\kappa \left(\vec{x},\widehat{y}\right)\doteq \ln k\left(\vec{x},\widehat{y}\right),(20)$

and writing ${\dot{\partial }}_i\doteq \partial /\partial y^i$ for a vertical derivative, a tedious but straightforward computation yields

$\begin{array}{ll}\hfill & g_{ij}\left(\vec{x},\widehat{y}\right)=e^{-\kappa \left(\vec{x},\widehat{y}\right)}\left[{\eta }_{ij}-{\widehat{y}}_i{\dot{\partial }}_j\kappa \left(\vec{x},\widehat{y}\right)-{\widehat{y}}_j{\dot{\partial }}_i\kappa \left(\vec{x},\widehat{y}\right)\right.\hfill \\ \hfill & \left.+\frac{1}{2}\left({\dot{\partial }}_i\kappa \left(\vec{x},\widehat{y}\right)+{\dot{\partial }}_j\kappa \left(\vec{x},\widehat{y}\right)-{\dot{\partial }}_i{\dot{\partial }}_j\kappa \left(\vec{x},\widehat{y}\right)\right)\right].\hfill \end{array}(21)$

If we introduce the covariant vertical derivative

${\dot{D}}_i\doteq {\dot{\partial }}_i-A_i^{\text{\hspace{0.17em}v}},$

with a $(-1)$-homogeneous vertical diffusion gauge field $A_i^{\text{\hspace{0.17em}v}}(\vec{x},\vec{y})$ defined by the vertical gauge condition ${\nabla }^{\text{\hspace{0.17em}v}}k(\vec{x},\widehat{y})\doteq 0$, or, in terms of coordinates,

${\dot{D}}_{i}k\left(\vec{x},\widehat{y}\right)\doteq 0,(22)$

then we obtain

$A_i^{\text{\hspace{0.17em}v}}\left(\vec{x},\vec{y}\right)\doteq {\dot{\partial }}_i\kappa \left(\vec{x},\widehat{y}\right).(23)$

This allows us to rewrite Equation 21 as

$g_{ij}\left(\vec{x},\widehat{y}\right)=\frac{1}{2}{e}^{-\kappa \left(\vec{x},\widehat{y}\right)}{\dot{D}}_i{\dot{D}}_j\Vert \vec{y}{\Vert }^2.(24)$

We will refer to the regularized case (Equations 21, 24) as the Riemann–Finsler metric tensor. The vertical gauge condition (Equation 22) is the geometric ploy that allows us to sweep diffusion anisotropies under the rug. With this gauge condition, one could say that the diffusion path length $\ell (\vec{x},\widehat{y})$ is adopted as a renormalized, local, anisotropic unit of reference for length measurements, regardless of direction; recall Equation 19.

The Riemann–Finsler metric tensor is regular³ for typical media, given a physically realistic choice of Equation 20. It defines a local, orientation-dependent norm that reflects the typical diffusion path length in the local brain tissue along the corresponding orientation. This means that a vector $\vec{y}$ anchored at the base point $\vec{x}$ will have a norm $F(\vec{x},\vec{y})$ that is relatively small (large) if there are few (respectively many) diffusion obstacles at that point along the orientation $\widehat{y}$.

2.8 The Riemann–Finsler geodesic rationale

The commonly accepted tractography premise that white matter tracts follow paths of least resistance to diffusion suggests that white matter tracts are locally shortest paths, or geodesics, relative to the Riemann–Finsler metric (Equation 21). Recall that a curve between fixed end points is called locally shortest if any small perturbation of that curve increases its length. The attribute ‘local’ is necessary since two sufficiently distant points in the non-Euclidean brain space may be connected by multiple geodesics. The length of the globally shortest geodesic connection provides an unambiguous notion of distance between its endpoints.⁴ The Hopf–Rinow theorem [46] guarantees the existence of a geodesic curve between any two points (geodesic completeness), which makes geodesic tractography fundamentally different from mainstream streamline-inspired paradigms despite their shared underlying hypothesis.

In contrast to streamlines, geodesics are stipulated to optimize sensitivity, regardless of specificity. As a result, an arbitrarily chosen geodesic is almost surely a false positive since anatomical connections are sparse, whereas geodesic connections are dense. Data-driven tractometric analysis, ideally supported by external anatomical information, must, therefore, be a constitutional part of any unambiguous geodesic tractography paradigm. Recall that the Riemann–Finsler geometric representation of the brain is meant to hide local diffusivities such as to make things look homogeneous and isotropic, as a result of which there are no a priori preferred (such as ‘true’ versus ‘false positive’) members in a geodesic congruence. Tractometric invariants for pruning by false positive removal must necessarily incorporate explicit diffusion characteristics, defined only by virtue of a combined Euclidean/Finslerian perspective. Unlike Einstein’s general relativity theory, the Riemann–Finsler geodesic rationale, thus, relies on a metric transform connecting two metrics on a metrically amorphous manifold, which has been conveniently furnished with a global ‘Cartesian’ coordinate chart.

Tractometric analysis for the purpose of anatomical tract disambiguation is beyond the scope of this article and will be considered in future work, cf. also Colby et al., DeSantis et al., and St-Jean et al. for some inspiring ideas ([47]; [48]; [49]).

Geodesics are obtained by (locally) minimizing the length of a parametric curve $\gamma :\mathbb{R}\to {\mathbb{R}}^3:t\mapsto \vec{x}(t)$, keeping endpoints, $\vec{x}(0)$ and $\vec{x}(T)$, fixed. Lifted to the slit tangent bundle, we obtain a particular ‘horizontal’ curve in phase space, viz., $\gamma :\mathbb{R}\to {\mathbb{R}}^6:t\mapsto (\vec{x}(t),\vec{y}(t))$, with the ‘horizontal constraint’

$\vec{y}\left(t\right)\doteq \dot{\stackrel{⃗}{x}}\left(t\right).(25)$

Length is then expressed by the functional

$\mathcal{L}\left(\gamma \right)\doteq {\int }_{\gamma }F\left(\vec{x},d\vec{x}\right)\doteq {\int }_0^T\sqrt{g_{ij}\left(\vec{x}\left(t\right),\vec{y}\left(t\right)\right)y^i\left(t\right)y^j\left(t\right)}dt,(26)$

subject to Equation 25. Variational calculus produces the geodesic equations ([32]; [7]; [33]):

${\ddot{x}}^i+G^i\left(\vec{x},\dot{\stackrel{⃗}{x}}\right)=\frac{d\ln F\left(\vec{x},\dot{\stackrel{⃗}{x}}\right)}{dt}{\dot{x}}^i,(27)$

where the geodesic spray coefficients are given by

$G^i\left(\vec{x},\vec{y}\right)\doteq \frac{1}{2}{g}^{ik}\left(\vec{x},\widehat{y}\right)\left(y^{\ell }{\partial }_{\ell }{\dot{\partial }}_k{F}^2\left(\vec{x},\vec{y}\right)-{\partial }_k{F}^2\left(\vec{x},\vec{y}\right)\right),(28)$

cf. [32] and [33] for details. Alternatively, we have

$G^i\left(\vec{x},\vec{y}\right)={\gamma }_{jk}^i\left(\vec{x},\vec{y}\right)y^j{y}^k,(29)$

yielding

${\ddot{x}}^i+{\gamma }_{jk}^i\left(\vec{x},\dot{\stackrel{⃗}{x}}\right){\dot{x}}^j{\dot{x}}^k=\frac{d\ln F\left(\vec{x},\dot{\stackrel{⃗}{x}}\right)}{dt}{\dot{x}}^i,(30)$

with (0-homogeneous) formal Christoffel symbols of the second kind

${\gamma }_{jk}^i\left(\vec{x},\vec{y}\right)\doteq \frac{1}{2}{g}^{i\ell }\left(\vec{x},\widehat{y}\right)\left({\partial }_j{g}_{\ell k}\left(\vec{x},\widehat{y}\right)+{\partial }_k{g}_{j\ell }\left(\vec{x},\widehat{y}\right)-{\partial }_{\ell }{g}_{jk}\left(\vec{x},\widehat{y}\right)\right).(31)$

Figure 2 shows some (initialization-dependent) numerical solutions connecting seed and target regions associated with the corticospinal tract (CST) for both the classical Riemannian case and the genuine Finslerian case. In the Riemannian limit, the metric tensor becomes vertically constant. In that case, it is easy to see that the geodesic spray coefficients (Equation 29) reduce to quadratic forms, viz.,

$G^i\left(\vec{x},\vec{y}\right)=N_j^i\left(\vec{x},\vec{y}\right)y^j={\mathrm{\Gamma }}_{jk}^i\left(\vec{x}\right)y^j{y}^k,$

Figure 2

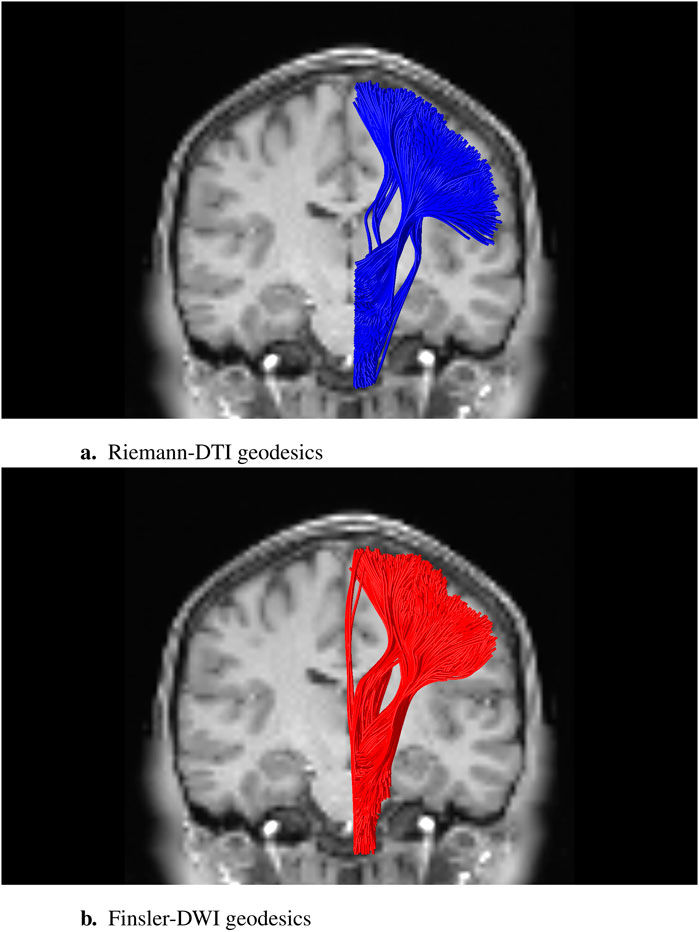
Figure 2. Sparse subset of geodesic tracts, i.e., solutions of (38), stipulated for the CST, connecting arbitrarily chosen endpoints in a seed and target region based on an anatomical atlas. These should not be mistaken for actual anatomical nerve bundles, the determination of which requires a characterization of their anatomical plausibility in terms of tractometric features and external anatomical constraints. The two-dimensional coronal background slice of the DWI image provides some qualitative anatomical context for the three-dimensional visualization of the tracts. The experiment was performed on a DWI dataset from the Human Connectome Data Project (dataset “WU-Minn HCP Data—1200 Subjects”: Subject 100,307; TE/TR/echo spacing 89.5/5520.0/0.78 ms; b = 2000 s/mm²). (A) Riemann-DTI geodesics; (B) Finsler-DWI geodesics to eighth-order spherical harmonic approximation; recall Figure 1E.

whereas the formal $\gamma$-symbols (Equation 31) reduce to the more familiar (by definition, vertically constant) Levi–Civita $\mathrm{\Gamma }$-symbols from Riemannian geometry:

${\mathrm{\Gamma }}_{jk}^i\left(\vec{x}\right)\doteq \frac{1}{2}{g}^{i\ell }\left(\vec{x}\right)\left({\partial }_j{g}_{\ell k}\left(\vec{x}\right)+{\partial }_k{g}_{j\ell }\left(\vec{x}\right)-{\partial }_{\ell }{g}_{jk}\left(\vec{x}\right)\right).$

In the Riemannian limit, we, thus, retrieve the established Riemann-DTI geodesic tractography paradigm. Reversely, a linear connection defines a Riemann–Finsler geometry of Berwaldian type, which is slightly more general than the Riemannian limit.⁵

The right-hand side of Equations 27, 30 merely contributes to a parameter-dependent ‘acceleration’ along the curve and may be set to zero (‘affine parametrization’) if one does not care about parametrization. This is automatically achieved in the variational formulation if one replaces the 1-homogeneous integrand $F$ in Equation 26 by its 2-homogeneous Lagrangian $L\doteq F^2$ (‘kinetic energy minimization’ instead of curve length minimization).

In the context of our extended slit tangent bundle furnished with a Finsler metric, Berwald’s horizontal derivatives are often encountered replacing partial derivatives for a geometrically consistent horizontal/vertical splitting:

${\delta }_i\doteq {\partial }_i-N_i^j{\dot{\partial }}_j.$

The so-called nonlinear connection coefficients in this expression satisfy

$N_j^i\left(\vec{x},\vec{y}\right)=\frac{1}{2}{\dot{\partial }}_j{G}^i\left(\vec{x},\vec{y}\right).$

Recall Equation 29, 30. Using this definition, we may define a covariant horizontal derivative:

$D_i\doteq {\delta }_i-A_i^{\text{\hspace{0.17em}h}}.$

Analogous to Equation 27, we may then set

$D_{i}k\left(\vec{x},\widehat{y}\right)\doteq 0$

to define the 0-homogeneous horizontal diffusion gauge field $A_i^{\text{\hspace{0.17em}h}}(\vec{x},\vec{y})$. With the help of the already-defined vertical diffusion gauge field (Equation 23), it follows that this is completely determined by the canonical nonlinear connection, viz., $N_i^j{A}_j^{\text{\hspace{0.17em}v}}+A_i^{\text{\hspace{0.17em}h}}=0$, or

$A_i^{\text{\hspace{0.17em}h}}\left(\vec{x},\vec{y}\right)\doteq {\delta }_i\kappa \left(\vec{x},\widehat{y}\right).$

This is the horizontal counterpart of Equation 23, rendering the scalar field $k(\vec{x},\widehat{y})$ (Equation 19), both horizontally and vertically covariantly constant. In other words, both inhomogeneous and anisotropic details of diffusion (ignoring hopping rate dependency) have been ‘geometrized away’ via the sphere bundle furnished with the Riemann–Finsler metric constructed above and the induced gauge fields under horizontal/vertical splitting.

Equations 27, 30 generalize the Riemann-DTI geodesic tractography paradigm ([7]; [40]; [15]) to genuine Finsler-DWI geodesic tractography for our new high-angular resolution DTI model. The conceptually simple but mathematically profound difference lies in the nature of the DWI-induced local anisotropic norm concept. In the Riemann-DTI case, this is an inner product-induced norm, the dual Gram matrix of which matches the DTI tensor one-to-one (at the expense of residual DWI signal loss). In the genuine Finsler-DWI case, we have a general norm, the infinitely many degrees of freedom of which admit a good match with an unconstrained DWI model based on an arbitrary number of diffusion orientations, e.g., using a suitably truncated complete function basis ([2]; [3]).

3 Summary, conclusion, and discussion

Hopping models are convenient proxies for statistical models of complex diffusion phenomena, especially when corroborated by complementary empirical evidence. The brain, considered as a porous medium for water diffusion, is an epitome of such a system, for which the convoluted interplay of molecular dynamics and the physicochemical environment would be prohibitively difficult to capture if not distilled down to its quintessential components admitting ‘model-free’ data assimilation. We have proposed such a hopping model to explain inhomogeneous anisotropic diffusion in the brain with relevant model parameters for DWI data assimilation, obviating a priori constraints on anatomical complexity.

A standard statistical procedure produces a Fokker–Planck equation that is fully determined by a classical DTI tensor defined in the three-dimensional configuration space. Its form betrays a ‘vertical projection,’ or angular average, of an underlying high-angular resolution DTI tensor. The latter is a singular, dyadic tensor, defined on the sphere bundle of base points capturing both positions and orientations, with a preferred orientation aligned with that of its underlying five-dimensional base point. This enables local scalar features, notably the diffusion path length, to be defined orientation-wise, preventing loss of information due to angular superposition inherent in classical DTI.

We have subsequently provided a geometric interpretation to support an operational scheme for geodesic tractography, generalizing the restrictive Riemann-DTI framework. The generalization entails the removal of implicit constraints on either the nature of the underlying diffusion process (Gaussianity assumption), or on the angular resolution by which it is represented in classical DTI (second-order harmonic truncation). By virtue of a metrizability trick via a so-called Finsler norm on the (slit) tangent bundle, it has turned out possible to retain a simple second-order, non-singular metric structure. The generalized, Riemann–Finsler metric, defined on the sphere bundle, adds novel structure to the metrically void ‘higher-order DTI’ model defined in the configuration space, as originally proposed by [50] and [51] to overcome classical DTI limitations. This additional metric structure enables generalized Finsler-DWI geodesic tractography, fully exploiting the generic nature of such a generalized model. Thus, the paradigm shift from low- to high-angular resolution DTI reverberates in the canonical way in which Riemann geometry is embedded into the more general Finsler setting.

The classical Riemann-DTI geodesic tractography paradigm arises as a (very) special case. This suggests a quantification of the relative global volumetric contributions of complex fiber configurations versus regions with single fiber coherence, cf. [30, 31], either in terms of the difference tensor $g_{ij}(\vec{x},\widehat{y})-{\bar{g}}_{ij}(\vec{x})$, where the latter term is the orientation average of the former, or in terms of the Cartan tensor $C_{ijk}(\vec{x},\widehat{y})\doteq \frac{1}{2}{\dot{\partial }}_k{g}_{ij}(\vec{x},\widehat{y})$ or, equivalently, its reduction to the Cartan one-form $C_k(\vec{x},\widehat{y})\doteq g^{ij}(\vec{x},\widehat{y})C_{ijk}(\vec{x},\widehat{y})$, which, by Deicke’s theorem ([32]; [33]), all vanish if and only if the brain space is Riemannian, and thus, by construction, DWI anisotropy evidence is fully captured by classical DTI.

Our heuristic approach via a hopping model defined in configuration space undergoes inherent ambiguities in the form of nontrivial kernel functions on the sphere bundle that have no manifestation in configuration space due to zero angular average. Although such ambiguities do seem harmless for our application and have been glossed over in this article, a more rigorous top–down approach, departing from a hopping model in position–velocity phase space, reflecting actual molecular motion, might be more convincing. In such a model, one would need to couple a displacement vector (or an average velocity vector over a given diffusion time interval), i.e., a jump in the ‘vertical direction’ along a tangent fiber, to a spatial displacement, i.e., a change of position in the configuration space consistent with the jump vector. In geometrical terms, phase space translations corresponding to actual molecular motions are subject to a ‘horizontality condition,’ which dictates that the displacement or instantaneous velocity vector must be consistent with the induced movement in configuration space. In such a phase space hopping model, one might stipulate a Maxwell–Boltzmann-type distribution for particle velocities with a different ‘temperature’ for each position and orientation to capture the inhomogeneous and anisotropic nature of brain tissue since this would be consistent with established physics in the limit of obstacle-free bulk water, cf. Supplementary Appendix 1.

A physically appealing but mathematically mind-boggling path integral approach may be another way to arrive at a model for high-angular resolution DTI [52]; [53]. This turns out possible, even in the mathematically closed form, for the simplified case of classical DTI. However, path integrals other than those based on quadratic forms (i.e., nearly anything beyond classical DTI) do not yield closed-form expressions and may not even be well-defined. At best, one may hope for insights via a perturbative expansion or via formal symbolic manipulation. This might nevertheless be a viable way toward theoretical underpinning.

Because it poses no a priori constraints on angular resolution, high-angular resolution DTI offers a new, generic DWI model on a par with popular existing models but, as opposed to these, is specifically geared toward a geodesic rationale. More specifically, in the operational definition of high-angular resolution DTI, a particular orientation distribution function, ‘${\text{ODF}}_4$,’ presents itself in the form of a characteristic inhomogeneous anisotropic diffusion path length, recall (11), which is the pivot of the Riemann–Finsler metric. This is a specific instance of the general class of ‘${\text{ODF}}_n$’ studied by [3].

The operational significance of the hopping rate factor $W(\vec{x})$-relating diffusion tensor and dual metric remains an open question, but it is interesting to note that several pragmatic attempts to improve classical Riemann-DTI tractography have been sought precisely in the choice of a suitably data-adapted conformal factor, cf. [8] and [9], for examples that differ from the historical case [13]; [11], which entails an implicit scaling in itself. A refinement of the hopping model might shed light on this issue from a fundamental statistical physics perspective. The analogy of hopping rate with a local ‘temperature: viscosity’ ratio—recall the Stokes–Einstein–Sutherland equation (Supplementary Equation 72)—might be useful in search for a more rigorous underpinning.

Finsler geodesic equations are well-known from the literature. From an anatomical perspective, their solutions are imbued with the same pros and cons as their Riemann-DTI counterparts and with all validation issues common to tractography methods in general. A clear advantage is their generic and (via tractometric characterization) adaptable nature, intuitive physical appeal, and mathematical rigor, with no parameters other than boundary conditions and those instantiated by DWI measurements, cf. the observations by Schilling et al., in this respect [54]. A disadvantage, in comparison to streamline methods, is their computational complexity (which may be mitigated by dimensionality reduction, cf. the geodesic tubes exploiting the linear geodesic deviation equations by [15] in the Riemann-DTI context), and their a priori lack of anatomical significance as a result of geodesic completeness. Without complementary tractometric characterization, which is beyond the scope of this article, geodesics must not be mistaken for anatomically meaningful tracts. They are optimal diffusion pathways in an operationally well-defined sense, expressing the basic tractography premise in a least committed way, with room for anatomical specification and pruning. With regard to the latter, the flexibility offered by virtue of geodesic completeness may also be clearly seen as an advantage. Note that, by virtue of a non-vanishing Cartan tensor, high-angular resolution DTI admits a richer set of tractometric invariants for tract characterization and filtering than its classical counterpart [40]; [55].

To summarize, the main result in this paper is twofold, viz. (i) freeing classical DTI from its inherent angular resolution limitation and (ii) embedding Riemann-DTI geodesic tractography into a generic Finsler-DWI framework. This puts the geodesic tractography rationale potentially (i.e., if furnished with biologically plausible tractometric criteria) on a par with state-of-the-art tractography methods. Its operationalization, including tractometric pruning, and experimental and clinical ramifications, will be considered in future work.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

LF: conceptualization, formal analysis, funding acquisition, methodology, project administration, supervision, writing–original draft, and writing–review and editing. RS: formal analysis, methodology, visualization, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This publication is part of the project Bringing Tractography into Daily Neurosurgical Practice with the project number KICH1. ST03.21.004 of the research program Key Enabling Technologies for Minimally Invasive Interventions in Healthcare, which is (partly) financed by the Dutch Research Council (NWO), Elisabeth-TweeSteden Hospital (Tilburg, Netherlands), the Erasmus Medical Center (Rotterdam, Netherlands), the Amsterdam University Medical Center (Amsterdam, Netherlands), and Medtronic are gratefully acknowledged for their support. Medtronic was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Acknowledgments

Data collection and sharing for this project was provided by the MGH-USC Human Connectome Project (HCP; Principal Investigators: Bruce Rosen, M.D., Ph.D., Arthur W. Toga, Ph.D., Van J. Weeden, MD). HCP funding was provided by the National Institute of Dental and Craniofacial Research (NIDCR), the National Institute of Mental Health (NIMH), and the National Institute of Neurological Disorders and Stroke (NINDS). HCP data are disseminated by the Laboratory of Neuro Imaging at the University of Southern California.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1447311/full#supplementary-material

Footnotes

¹Geometrically speaking, $\vec{x}-\vec{y}$ is the base point reached by traversing backward in configuration space over a vectorial jump $-\vec{y}$ via the exponential map defined at $\vec{x}$, which reduces to a trivial shift by virtue of the flat geometry of configuration space.

²The dimensionful $\ln$-argument $k$ in (30) may be normalized, without loss of generality, by a characteristic constant $k_0$ (‘Knudsen number’), e.g., in terms of the bulk water diffusion path length at some reference temperature.

³In particular, in the limiting case $\kappa \to {\kappa }_0=0$, corresponding to homogeneous isotropic diffusion in bulk water at the reference temperature, we reobtain the flat Euclidean metric $g_{ij}\to {\eta }_{ij}$ appropriate for that case.

⁴One should note that the use of absolute distance as the main criterion for anatomical brain connectivity, such as implied by some fast marching schemes based on an eikonal equation, ignores non-minimal geodesics and thus incurs loss of sensitivity, which runs counter to the geodesic tractography rationale.

⁵By Szabó’s metrizability theorem, Berwald geometries are of little interest for parameter-invariant geodesic tractography since it claims the existence of a Riemannian metric inducing the same geodesic curves, cf. [32], [33], and [56].

References

1. Le Bihan D, Iima M. Diffusion magnetic resonance imaging: what water tells us about biological tissues. PLOS Biol (2015) 13:e1002203. doi:10.1371/journal.pbio.1002203

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Fick R, Wassermann D, Pizzolato M, Deriche R (2015) A unified framework for spatial and temporal diffusion in diffusion MRI. In Proceedings of the twenty-fourth international conference on information processing in medical imaging–IPMI 2015 (sabhal mor ostaig, isle of skye, UK), eds. S Ourselin, DC Alexander, C-F Westin, and MJ Cardoso (New York: Springer-Verlag), vol. 9123 of Lecture Notes in Computer Science, 167–78. doi:10.1007/978-3-319-19992-4_13

CrossRef Full Text | Google Scholar

3. Özarslan E, Koay CG, Shepherd TM, Komlosh ME, İrfanoğlu MO, Pierpaoli C, et al. Mean apparent propagator (MAP) MRI: a novel diffusion imaging method for mapping tissue microstructure. Neuroimage (2013) 78:16–32. doi:10.1016/j.neuroimage.2013.04.016

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Kampen NGv. (1988) Diffusion in inhomogeneous media. J Phys Chem Sol,49:673–7. doi:10.1016/0022-3697(88)90199-0

CrossRef Full Text | Google Scholar

5. Bringuier E. Particle diffusion in an inhomogeneous medium. Eur J Phys (2011) 32:975–92. doi:10.1088/.0143-0807/32/4/012

CrossRef Full Text | Google Scholar

6. Dell’Acqua F, Leemans A, Descoteaux M (2024) Handbook of diffusion MR tractography: imaging methods, biophysical models, algorithms and applications. Academic Press.

Google Scholar

7. Florack L, Sengers R, Fuster A (2024) Geodesic tractography. In: Dell’Acqua et al.

Google Scholar

8. Fuster A, Dela Haije T, Tristán-Vega A, Plantinga B, Westin C-F, Florack L. Adjugate diffusion tensors for geodesic tractography in white matter. J Math Imaging Vis (2016) 54:1–14. doi:10.1007/.s10851-015-0586-8

CrossRef Full Text | Google Scholar

9. Hao X, Zygmunt K, Whitaker RT, Fletcher PT. Improved segmentation of white matter tracts with adaptive Riemannian metrics. Med Image Anal (2014) 18:161–75. doi:10.1016/j.media.2013.10.007

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Hauberg S, Schober M, Liptrot M, Hennig P, Feragen A (2015) A random Riemannian metric for probabilistic shortest-path tractography. In: N Navab, J Hornegger, WM Wells, and A Frangi, editors. Proceedings of the 18th international conference on medical image computing and computer assisted intervention—MICCAI 2015 (munich, Germany, october 5–9 2015). Berlin: Springer-Verlag. p. 597–604. doi:10.1007/.978-3-319-24553-973

CrossRef Full Text | Google Scholar

11. Lenglet C, Deriche R, Faugeras O (2004) Inferring white matter geometry from diffusion tensor MRI: application to connectivity mapping. In: T Pajdla, and J Matas, editors. Proceedings of the eighth European conference on computer vision (prague, Czech republic, may 2004). Berlin: Springer-Verlag . p. 127–40.

CrossRef Full Text | Google Scholar

12. Lenglet C, Prados E, Pons J-P, Deriche R, Faugeras O. Brain connectivity mapping using Riemannian geometry, control theory and PDEs. SIAM J Imaging Sci (2009) 2:285–322. doi:10.1137/070710986

CrossRef Full Text | Google Scholar

13. O’Donnell L, Haker S, Westin CF. New approaches to estimation of white matter connectivity in diffusion tensor MRI: elliptic PDEs and geodesics in a tensor-warped space. Proc Med Imaging Comput Computer Assisted Intervention (2002) 2488:459–66. doi:10.1007/3-540-45786-0_57

CrossRef Full Text | Google Scholar

14. Risken H (1989) The fokker-planck equation: methods of solution and applications. In: Springer series in synergetics. vol. 18. Berlin: Springer-Verlag. doi:10.1007/978-3-642-61544-3

CrossRef Full Text | Google Scholar

15. Sengers R, Florack L, Fuster A. Geodesic uncertainty in diffusion MRI. Front Computer Sci (2021) 3:718131. Invited paper. doi:10.3389/fcomp.2021.718131

CrossRef Full Text | Google Scholar

16. Dell’Acqua F, Simmons A, Williams SCR, Catani M. Can spherical deconvolution provide more information than fiber orientations? hindrance modulated orientational anisotropy, a true-tract specific index to characterize white matter diffusion. Hum Brain Mapp (2013) 34:2464–83. doi:10.1002/hbm.22080

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Dell’Acqua F, Tournier J-D. Modelling white matter with spherical deconvolution: how and why? NMR Biomed (2019) 32:e3945–18. doi:10.1002/nbm.3945

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Descoteaux M (2015). High angular resolution diffusion imaging (HARDI). In: J Webster, editor. Wiley encyclopedia of electrical and electronics engineering. John Wiley and Sons, Inc. p. 1–25. doi:10.1002/047134608X.W8258

CrossRef Full Text | Google Scholar

19. Descoteaux M, Deriche R, Knösche TR, Anwander A. Deterministic and probabilistic tractography based on complex fibre orientation distributions. IEEE Trans Med Imaging (2009) 28:269–86. doi:10.1109/tmi.2008.2004424

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Descoteaux M, Deriche R, Le Bihan D, Mangin J-F, Poupon C. Multiple q-shell diffusion propagator imaging. Med Image Anal (2010) 15:603–21. doi:10.1016/j.media.2010.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Jian B, Vemuri BC. A unified computational framework for reconvolution to reconstruct multiple fibers from diffusion weighted MRI. IEEE Trans Med Imaging (2007) 26:1464–71. doi:10.1109/TMI.2007.907552

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Tournier J-D, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution. Neuroimage (2007) 35:1459–72. doi:10.1016/j.neuroimage.2007.02.016

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Tournier J-D, Yeh C-H, Calamante F, Cho K-H, Connelly A, Lin C-P. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. Neuroimage (2004) 23:1176–85. doi:10.1016/j.neuroimage.2004.07.037

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Tournier J-D, Yeh C-H, Calamante F, Cho K-H, Connelly A, Lin C-P. Resolving crossing fibres using constrained spherical deconvolution: validation using diffusion-weighted imaging phantom data. Neuroimage (2008) 42:617–25. doi:10.1016/j.neuroimage.2008.05.002

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Tuch DS. Q-ball imaging. Magn Reson Med (2004) 52:1358–72. doi:10.1002/mrm.20279

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Wedeen VJ, Hagmann P, Tseng WYI, Reese TG, Weisskoff RM. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson Med (2005) 54:1377–86. doi:10.1002/mrm.20642

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Wedeen VJ, Wang RP, Schmahmann JD, Benner T, Tseng WYI, Dai G, et al. Diffusion spectrum magnetic resonance imaging (DSI) tractography of crossing fibers. Neuroimage (2008) 41:1267–77. doi:10.1016/j.neuroimage.2008.03.036

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Mori S, Tournier J-D. Introduction to diffusion tensor imaging and higher order models. 2nd ed. Amsterdam: Elsevier (2014).

Google Scholar

29. Poirier C, Descoteaux M. A unified filtering method for estimating asymmetric orientation distribution functions. Neuroimage (2024) 287:120516. doi:10.1016/j.neuroimage.2024.120516

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Schilling KG, Gao Y, Janve V, Stepniewska I, Landman BA, Anderson AW. Can increased spatial resolution solve the crossing fiber problem for diffusion MRI? NMR Biomed (2017) 30:1–16. doi:10.1002/nbm.3787

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Schilling KG, Tax CMW, Rheault F, Landman BA, Anderson AW, Descoteaux M, et al. Prevalence of white matter pathways coming into a single white matter voxel orientation: the bottleneck issue in tractography. Hum Brain Mapp (2021) 43:1196–213. doi:10.1002/hbm.25697

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Bao D, Chern S-S, Shen Z (2000) An introduction to riemann-finsler geometry. In: 2000 of graduate Texts in mathematics. New York: Springer-Verlag.

CrossRef Full Text | Google Scholar

33. Shen Y-B, Shen Z (2016) Introduction to modern finsler geometry. Singapore: World Scientific.

Google Scholar

34. Aganj I, Lenglet C, Sapiro G, Yacoub E, Ugurbil K, Harel N. Reconstruction of the orientation distribution function in single- and multiple-shell q-ball imaging within constant solid angle. Magn Reson Med (2010) 64:554–66. doi:10.1002/mrm.22365

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Descoteaux M, Angelino E, Fitzgibbons S, Deriche R. Regularized, fast, and robust analytical Q-ball imaging. Magn Reson Med (2007) 58:497–510. doi:10.1002/mrm.21277

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Hess CP, Mukherjee P, Tan ET, Xu D, Vigneron DB. Q-ball reconstruction of multimodal fiber orientations using the spherical harmonic basis. Magn Reson Med (2006) 56:104–17. doi:10.1002/mrm.20931

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Barnett A. Theory of Q-ball imaging redux: implications for fiber tracking. Magn Reson Med (2009) 62:910–23. doi:10.1002/mrm.22073

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Garyfallidis E, Brett M, Amirbekian B, Rokem A, van der Walt S, Descoteaux M, et al. Dipy, a library for the analysis of diffusion MRI data. Front Neuroinformatics (2014) 8:8–17. Article 8. doi:10.3389/fninf.2014.00008

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Florack L, Sengers R, Meesters S, Smolders L, Fuster A (2021) Riemann-DTI Geodesic Tractography Revisited. In: A Fuster, E Özarslan, T Schultz, and E Zhang, editors. Anisotropy Across Fields and Scales. Mathematics and Visualization. Springer, Cham. p. 155–6.

CrossRef Full Text | Google Scholar

40. Sengers HJCE (2024) Riemannian geometry in diffusion weighted imaging. Eindhoven: Eindhoven University of Technology.

Google Scholar

41. Florack LMJ, Fuster A (2014) Riemann-Finsler geometry for diffusion weighted magnetic resonance imaging. In: C-F Westin, A Vilanova, and B Burgeth, editors. Visualization and processing of tensors and higher order descriptors for multi-valued data. Springer-Verlag. p. 189–208. doi:10.1007/978-3-642-54301-2

CrossRef Full Text | Google Scholar

42. Sengers R, Fuster A, Florack L (2021) Geodesic tubes for uncertainty quantification in diffusion MRI. In: S Sommer, A Feragen, J Schnabel, and M Nielsen, editors. Proceedings of the twenty-seventh international conference on information processing in medical imaging–IPMI 2021 (bornholm, Denmark). Berlin: Springer-Verlag. p. 279–90.

CrossRef Full Text | Google Scholar

43. Axler S (2024) Linear algebra done right. Springer International Publishing. doi:10.1007/978-3-031-41026-0

CrossRef Full Text | Google Scholar

44. Penrose R. A generalized inverse for matrices. Math Proc Cambridge Philosophical Soc (1955) 51:406–13. doi:10.1017/S0305004100030401

CrossRef Full Text | Google Scholar

45. Drazin MP. Pseudo-inverses in associative rings and semigroups. The Am Math Monthly (1958) 65:506–14. doi:10.1080/00029890.1958.11991949

CrossRef Full Text | Google Scholar

46. Hopf H, Rinow W. Ueber den Begriff der vollständigen differentialgeometrischen Fläche. Commentarii Mathematici Helvetici (1931) 3:209–25. doi:10.1112/blms/7.3.261

CrossRef Full Text | Google Scholar

47. Colby JB, Soderberg L, Lebel C, Dinov ID, Thompson PM, Sowell ER. Along-tract statistics allow for enhanced tractography analysis. Neuroimage (2012) 59:3227–42. doi:10.1016/j.neuroimage.2011.11.004

PubMed Abstract | CrossRef Full Text | Google Scholar

48. De Santis S, Drakesmith M, Bells S, Assaf Y, Jones DK. Why diffusion tensor MRI does well only some of the time: variance and covariance of white matter tissue microstructure attributes in the living human brain. Neuroimage (2014) 89:35–44. doi:10.1016/j.neuroimage.2013.12.003

PubMed Abstract | CrossRef Full Text | Google Scholar

49. St-Jean S, Chamberland M, Viergever MA, Leemans A. Reducing variability in along-tract analysis with diffusion profile realignment. Neuroimage (2019) 199:663–79. doi:10.1016/j.neuroimage.2019.06.016

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Özarslan E, Mareci TH. Generalized diffusion tensor imaging and analytical relationships between diffusion tensor imaging and high angular resolution imaging. Magn Reson Med (2003) 50:955–65. doi:10.1002/mrm.10596

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Florack L, Balmashnova E, Astola L, Brunenberg E. A new tensorial framework for single-shell high angular resolution diffusion imaging. J Math Imaging Vis (2010) 3:171–81. doi:10.1007/s10851-010-0217-3

CrossRef Full Text | Google Scholar

52. Kleinert H. Path integrals in quantum mechanics, statistics, polymer physics, and financial markets. 5th ed. Singapore: World Scientific (2009).

Google Scholar

53. Özarslan E, Westin C-F, Mareci TH. Characterizing magnetic resonance signal decay due to Gaussian diffusion: the path integral approach and a convenient computational method. Concepts Magn Reson A (2015) 44A:203–13. doi:10.1002/cmr.a.21354

CrossRef Full Text | Google Scholar

54. Schilling KG, Petit L, Rheault F, Remedios S, Pierpaoli C, Anderson AW, et al. Brain connections derived from diffusion MRI tractography can be highly anatomically accurate—if we know where white matter pathways start, where they end, and where they do not go. Brain Struct Funct (2020) 225:2387–402. doi:10.1007/s00429-020-02129-z

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Sengers R, Dela Haije T, Fuster A, Florack L. Tractometric coherence of fiber bundles in DTI. In: S Cetin-Karayumak, D Christiaens, M Figini, P Guevara, T Pieciak, E Powellet al. editors 13722. Springer-Verlag (2022). p. 137–48.

CrossRef Full Text | Google Scholar

56. Vincze C. A new proof of Szabó’s theorem on the Riemann-metrizability of Berwald manifolds. Acta Mathematica Academiae Paedagogicae Nyiregyhaziensis (2005) 21:199–204.

Google Scholar

58. Balmashnova EG, Fuster A, Florack LMJ (2012) Decomposition of higher-order homogeneous tensors and applications to HARDI. In: E Panagiotaki, L O’Donnell, T Schultz, and GH Zhang, editors. MICCAI workshop on computational diffusion MRI (october 5, 2012, nice, France). p. 79–89.

Google Scholar

59. Einstein A (1956) Investigations on the theory of the brownian movement. New York: Dover Publications, Inc.

Google Scholar

60. Folland GB. How to integrate a polynomial over a sphere. The Am Math Monthly (2001) 108:446–8. doi:10.2307/2695802

CrossRef Full Text | Google Scholar