Study of the characteristics of electron firehose unstable conditions in the terrestrial magnetotail plasma sheet

Electron firehose instabilities can be excited at dipolarization fronts and in the magnetic reconnection outflow in the terrestrial magnetotail, but their occurrence rate in the plasma sheet is unclear. Here, we investigate the characteristics of electron firehose unstable conditions in the magnetotail plasma sheet based on observations of the Magnetospheric Multiscale mission. We find an Alfvénic magnetic field fluctuation accompanied by a strong field-aligned current during a flapping motion. This fluctuation occurs where the local plasma is electron firehose unstable, indicating that the electron firehose instability in the plasma sheet can occur in the region besides dipolarization fronts and magnetic reconnection outflow. We statistically find that the local plasma near the neutral sheet has a small probability with the maximum value <1.4% to be electron firehose unstable, which mainly occurs in the central plasma sheet with B_XY/B_L < 0.3. The maximum probability of T_ef > 0 (electron firehose unstable condition) is ∼1.36% (1.32%) at B_XY/B_L ≈ 0.05 (0.15) during fast (non-fast) flows. During fast flows, the plasma near the neutral sheet tends to have a higher probability of T_ef > 0 when the local V_T is larger. During non-fast flows, the plasma near the neutral sheet tends to have a higher probability of T_ef > 0 when T_e is larger. The probability of T_ef > 0 shows a dawn-dusk asymmetry during fast flows and non-fast flows. In addition, the probability of T_ef > 0 during fast flows tends to be larger when the ambient B_Z is weak, which shows opposite characteristics during non-fast flows. These findings help to assess the importance of the role of electron firehose instabilities in the magnetotail plasma sheet.

1 Introduction

Fast flows are essential to the transport of mass, magnetic flux, and energy in the terrestrial magnetotail [1, 2]. They might originate from magnetic reconnections [3, 4] or interchange instabilities [5]. Temperature anisotropies can be caused during fast flows [6, 7], which are able to provide free energy to excite various instabilities [8–11]. For example, ion firehose instabilities can be driven when T_i,|| > T_i,⊥, where T_i,|| and T_i,⊥ are the parallel and perpendicular ion temperatures with respect to the ambient magnetic field [10, 11]. Such instabilities also exist in the solar wind [12–15] and the terrestrial magnetosheath [16, 17].

Ion firehose instabilities include parallel and oblique modes [10, 11, 18–20]. In the terrestrial magnetotail, parallel firehose instabilities are more likely to occur near the neutral sheet [21], and can generate Pi2-band (40–150 s) Alfvénic fluctuations during fast flows [22, 23]. [24] further found that the parallel firehose unstable condition can affect the wave power of the Pi1-band (10–40 s) and Pi2-band fluctuations during fast flows. The probability of the plasma being parallel firehose unstable condition tends to be larger for the faster flow, and is positively correlated with the wave power of the Pi1/2-band fluctuations [24]. Oblique firehose instabilities can generate compressional fluctuations, which are linear-polarized and have a zero frequency [10]. A flapping motion of the current sheet was reported to might originate from the oblique firehose instability during a fast flow [19]. Later, [25] statistically found that both probabilities of the fast flows accompanied by large-amplitude neutral sheet oscillations and the plasma being oblique firehose unstable condition near the neutral sheet tend to be larger for faster flows. In addition, the oblique firehose unstable condition can affect the period of these oscillations. These results support that oblique firehose instabilities are a generation mechanism of some flapping motions [25].

Similar to ions, electron firehose instabilities driven by electron temperature anisotropy also have two modes based on linear theory and 2D Particle-In-Cell (PIC) simulation [26–29]. The parallel electron firehose mode is a parallel propagation with respect to the ambient magnetic field and is non-resonant with respect to electrons, while the oblique electron firehose mode is characterized by a lower instability threshold and higher growth rate, which is a non-propagated and is resonant with both electrons and ions [27, 29]; [26, 30, 31]. In the magnetotail, electron firehose instabilities can be excited at dipolarization fronts [32] and in the magnetic reconnection outflow [31]. These instabilities are believed to lead the electron to isotropization by cooling (heating) the electron in the parallel (perpendicular) direction with respect to the ambient field [31–33]. The magnetotail current sheet can become thin to the sub-ion scale [34, 35]. Energy conversion processes take place in the thin current sheet, where the anisotropic electrons can excite electron-dominated instabilities [34–36]. The occurrence rate of electron firehose instabilities helps to evaluate their impact on electrons in the plasma sheet, however, it is still unclear.

In this study, we statistically investigate the electron firehose unstable conditions in the plasma sheet using the data obtained from the Magnetospheric Multiscale (MMS) mission. We first show a magnetic field fluctuation event associated with the electron firehose instability in the plasma sheet, then statistically analyze the probability of the plasma being electron firehose unstable during fast flows and non-fast flows.

2 Observation

The MMS spacecraft, launched on March 2015, consists of four identical probes with an interspacecraft distance of 10–400 km [37]. In the present study, only the magnetic field and plasma data of the MMS1 probe from 2015 to 2022 are used without other statement since the interspacecraft distances among the probes are very small compared with the thickness of the plasma sheet. The used magnetic field data with a resolution of 16 Hz are from the fluxgate magnetometer (FGM) instrument [38], and the used plasma moment data with a resolution of 4.5 s are from the Fast Plasma Investigation (FPI) instrument [39].

2.1 An event associated with electron firehose instabilities

Figure 1 shows the magnetic field and ion moments observed by MMS1 between 15:00 and 16:00 UT on 20 July 2017. The MMS1 probe is located at [-23.3, 7.0, 3.0] R_E in the geocentric solar magnetospheric (GSM) coordinate system at 15:30 UT. The ion beta β_i, ratio of the ion thermal pressure to the magnetic pressure, is >0.5 during the whole interval, indicating that this probe is in the plasma sheet [40]. Figure 1A shows that B_X had a maximum variation from ∼9.4 nT to −21 nT in the interval of 15:21–15:33 UT, and the sign of B_X has one reversal. Such a large variation of B_X meets the expectation of a flapping motion of the current sheet [41–43]. At ∼15:24:20 UT, B_X suddenly changes from ∼4 nT to −4 nT with almost unchanged of B_T. Figure 1D, E show that V_i,X and V_i,Y are dominant and the maximum value of the total ion velocity is ∼216.9 km/s, suggesting that the sudden change of B_X occurs during a weak fast flow.

Figure 1

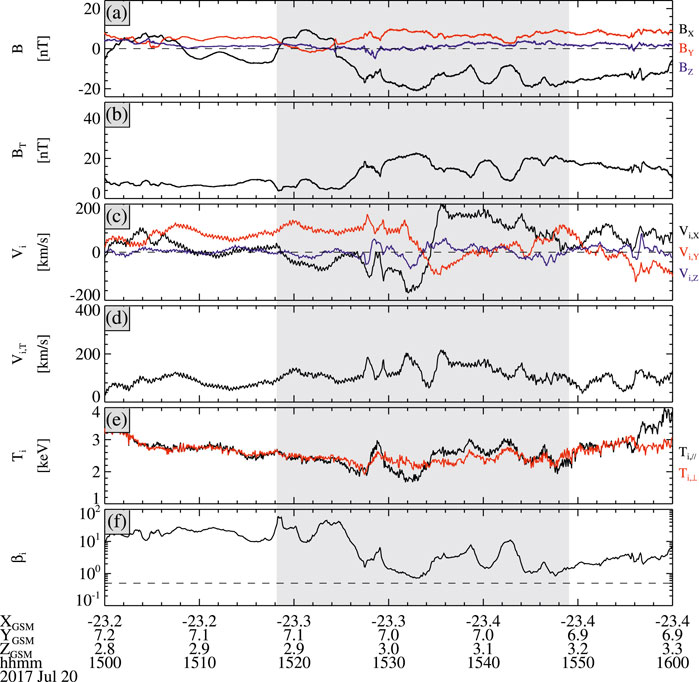
Figure 1. A fast flow event observed by MMS1 between 15:00 and 16:00 UT on 20 July 2017. From top to bottom: (A) the magnetic field in GSM, (B) the magnetic field strength, (C) ion velocities in GSM, (D) the total ion velocity, (E) the parallel (black) and perpendicular (red) ion temperatures, (F) ion beta. The gray region indicates the interval of a fast flow event.

Timing analysis can be used to determine the propagation velocity along the normal direction of a one-dimensional current sheet [44, 45]. Assuming that the magnetic field fluctuation between 15:24:10 and 15:24:30 UT is one-dimensional, its propagation velocity is ∼39.7 km/s determined by timing analysis. Thus, its length is ∼794 km along the normal direction. At this time, the local ion gyroradius ρ_i is ∼1001.9 km estimated by using the ambient ion temperature (∼2.37 keV) and B_T (∼4.96 nT). Thus, the size of the magnetic field fluctuation is ∼0.79 ρ_i along the normal direction, indicating that this fluctuation is sub-ion scale.

Figure 2 shows the electron moments in the interval of 15:23–15:26 UT. B_X changes up to ∼9.3 nT between 15:24:10 and 15:24:30 UT, while B_T is almost a constant, indicating that this fluctuation has an Alfvénic characteristic. The electron number density, velocities, and perpendicular temperature (T_e,⊥) have no significant change during the whole interval in Figure 2, while the parallel electron temperature (T_e,||) has a significant change. T_e,|| is > T_e,⊥ between 15:23 and 15:25 UT. The electron temperature anisotropy can excite electron firehose instabilities [27, 31, 33]. Based on the linear dispersion theory, the threshold of electron firehose instabilities is derived to be T_ef = $\frac{{\mathrm{T}}_{\mathrm{e},\parallel }}{{\mathrm{T}}_{\mathrm{e},\perp }}-\frac{1}{1-1.29/{\mathrm{\beta }}_{\mathrm{e},\parallel }^{0.97}}$ when the instability growth rate is larger than 0.001, which applies when the parallel electron beta β_e,|| is in the range of 2–25 [27, 31]. T_ef > 0 denotes that the local plasma is electron firehose unstable, which means that this condition is able to excite electron firehose instabilities [27, 31]. Figure 2G shows that T_ef is >0 during the magnetic field fluctuation between 15:24:06 and 15:24:38 UT, and is <0 outside this fluctuation, indicating that this fluctuation might be generated by the electron firehose instability.

Figure 2

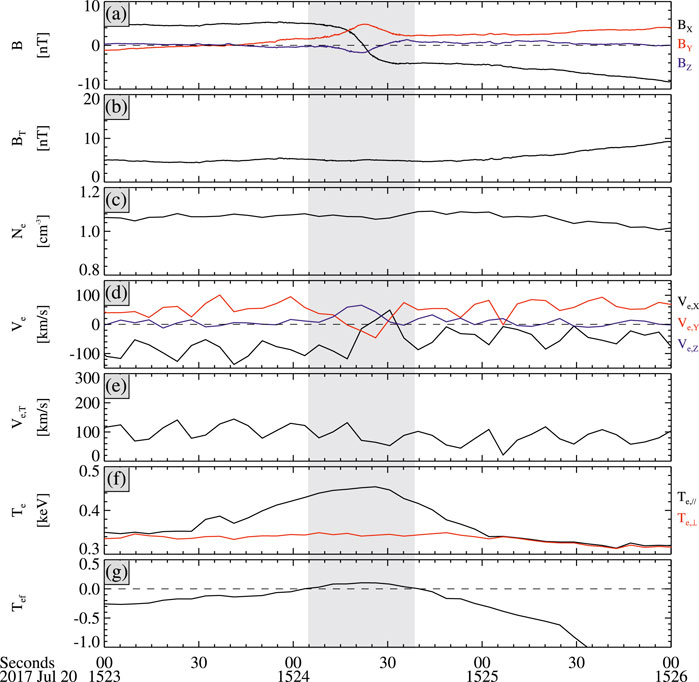
Figure 2. From top to bottom: (A) the magnetic field in GSM, (B) the magnetic field strength, (C) electron number density, (D) electron velocities in GSM, (E) the total electron velocity, (F) the parallel (blue) and perpendicular (red) electron temperatures, (G) the threshold of the electron firehose instability. The gray region indicates the interval of the magnetic field structure.

Figure 3 shows the current density between 15:23 and 15:26 UT, which is calculated by the curlometer technique [46]. It is regarded as reliable when the ratio of |∇·B| to |∇×B| is <0.2 [43, 47]. Thus, the current density is reliable in the interval 15:24:11.2–15:24:25.1 UT. The total current density tends to be larger with the maximum value of ∼26.2 nA/m² when the MMS1 probe is closer to the neutral sheet. As shown in the shaded area, the parallel current density is dominant in this interval, indicating that the magnetic field fluctuation is accompanied by a strong field-aligned current. Field-aligned currents play a significant role in the process of the ionosphere-magnetosphere coupling [48–51]. In addition, electron firehose instabilities can cause the electron to be isotropic [31, 32]. To evaluate the importance of electron firehose instabilities in the plasma sheet, a question is raised, namely, what is the probability of the plasma being electron firehose unstable in the plasma sheet.

Figure 3

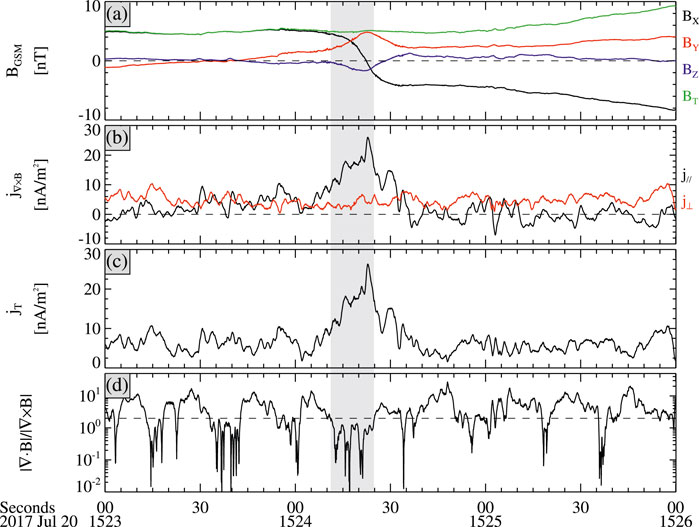
Figure 3. (A) The magnetic field in GSM, (B) the parallel and perpendicular components of the current density, (C) the total current density and (D) the ratio of |∇·B| to |∇×B| between 15:23 and 15:26 UT.

2.2 Electron firehose unstable conditions during fast flows and non-fast flows

To figure out the details of the electron firehose unstable conditions during fast flows and non-fast flows in the plasma sheet, we first select the fast flow events at X_GSM < −10 R_E and |Y_GSM| < 12 R_E using the following criteria, which are modified based on the selection criteria of bursty bulk flows proposed by Angelopoulos et al. [40]. A fast flow event is defined to be a segment of the continuous ion flow with a magnitude of |V_i| ≥ 100 km/s, during which |V_i| exceeds 150 km/s at least one sample. If two adjacent events are observed within 2 min, they are regarded to belong to the same fast flow event. In total, 5,675 fast flow events are selected.

Figure 4 shows the distribution of the data points in the space of (β_e,||, T_e,||/T_e,⊥) during the fast flows (a) and non-fast flows (b), where both the bin sizes of the logarithm of β_e,|| and T_e,||/T_e,⊥ are 0.02. About ∼79.3% (84.8%) of the data points are observed at T_e,||/T_e,⊥ > 1 during the fast flows (non-fast flows). The gray dashed line denotes the threshold of the electron firehose instability, i.e., $\frac{{\mathrm{T}}_{\mathrm{e},\parallel }}{{\mathrm{T}}_{\mathrm{e},\perp }}=\frac{1}{1-1.29/{\mathrm{\beta }}_{\mathrm{e},\parallel }^{0.97}}$. The plasma is electron firehose unstable when the data points are above the dashed line. As shown in Figure 4, electrons have a very low probability of being firehose unstable, although the electrons with parallel temperature anisotropy dominate in the plasma sheet.

Figure 4

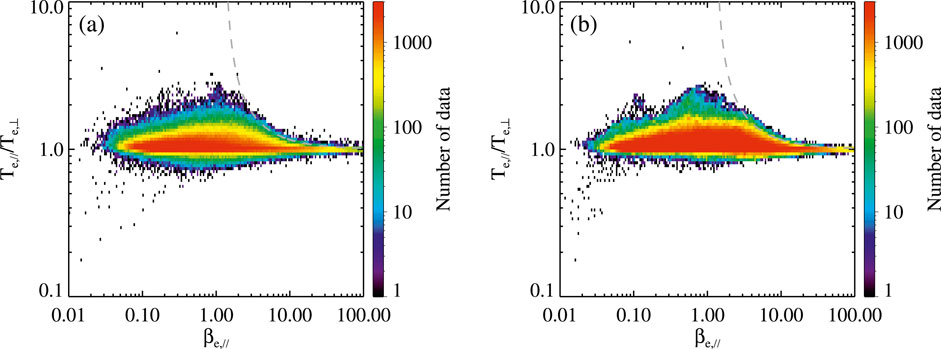
Figure 4. Number of data points in the space of (β_e,||, T_{e, ||}/T_e,⊥) during the fast flows (A) and non-fast flows (B). The color bar denotes the number of data points. The gray dashed line in each panel denotes $\frac{{\mathrm{T}}_{\mathrm{e},\parallel }}{{\mathrm{T}}_{\mathrm{e},\perp }}=\frac{1}{1-1.29/{\mathrm{\beta }}_{\mathrm{e},\parallel }^{0.97}}$.

In the magnetotail, firehose instabilities are believed to be more likely to occur near the neutral sheet [21, 24, 52]. We consider the parameter B_XY/B_L as the relative distance away from the neutral sheet [53], where B_XY = $\sqrt{{\mathrm{B}}_{\mathrm{X}}^2+{\mathrm{B}}_{\mathrm{Y}}^2}$, and B_L is the magnetic field strength in the magnetotail lobe determined by assuming that the lobe magnetic pressure is equal to the sum of the magnetic and ion thermal pressures in the plasma sheet.

Figure 5 shows the percentages of 2 ≤ β_e,|| ≤ 25 (a) and T_ef > 0 (b) at different values of (B_X/|B_X|)⋅B_XY/B_L with a step length of 0.05 during all the fast flows (black) and non-fast flows (orange). In Figure 5A, the percentage in each bin is determined by the data counts with 2 ≤ β_e,|| ≤ 25 divided by the total counts in that bin. (B_X/|B_X|)⋅B_XY/B_L < (>) 0 denotes that the satellite is located on the south (north) side of the neutral sheet. One can find that the electrons with 2 ≤ β_e,|| ≤ 25 mainly occur in the region within B_XY/B_L < 0.3. The percentages of 2 ≤ β_e,|| ≤ 25 during the fast flows are approximately symmetrically distributed relative to (B_X/|B_X|)⋅B_XY/B_L = 0, and have the maximum value at B_XY/B_L ≈ 0.15 instead of B_XY/B_L = 0. The characteristics of the percentages of 2 ≤ β_e,|| ≤ 25 during the non-fast flows are similar to those during the fast flows. Since the threshold of the electron firehose instability T_ef (=$\frac{{\mathrm{T}}_{\mathrm{e},\parallel }}{{\mathrm{T}}_{\mathrm{e},\perp }}-\frac{1}{1-1.29/{\mathrm{\beta }}_{\mathrm{e},\parallel }^{0.97}}$) is applicable under the condition of 2 ≤ β_e,|| ≤ 25 [27], we determine the probability of the plasma with T_ef > 0 by only considering the plasma under the condition of 2 ≤ β_e,|| ≤ 25 in our rest of paper.

Figure 5

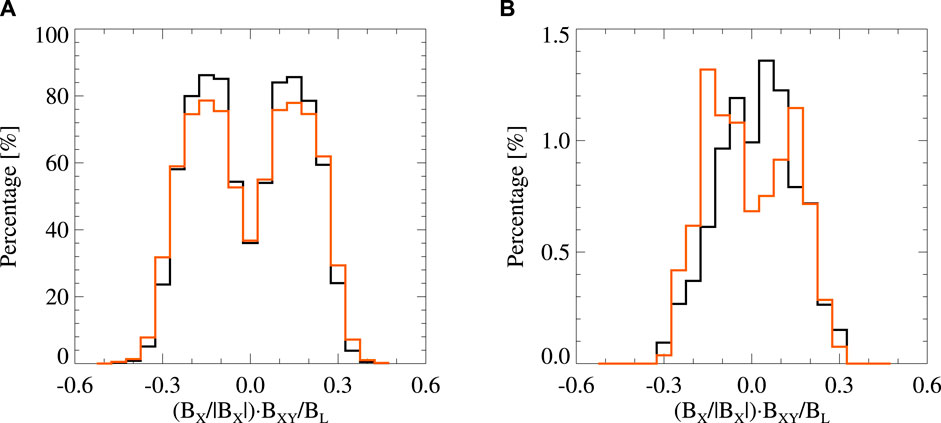
Figure 5. Percentages of 2 ≤ β_e,|| ≤ 25 (A) and T_ef > 0 (B) at different values of (B_X/|B_X|)⋅B_XY/B_L during all the fast flows (black) and non-fast flows (orange). The step length of (B_X/|B_X|)⋅B_XY/B_L is 0.05.

Figure 5B shows that the percentages of T_ef > 0 during the fast flows (non-fast flows) have the maximum value at B_XY/B_L ≈ 0.05 (0.15). In each bin, the percentage is determined by the data counts with T_ef > 0 and 2 ≤ β_e,|| ≤ 25 divided by the total counts with 2 ≤ β_e,|| ≤ 25 in that bin. The maximum percentage of T_ef > 0 during the fast flows is ∼1.36%. And the plasma during the fast flows tends to have a higher probability of T_ef > 0 when closer to the neutral sheet. By contrast, the percentage of T_ef > 0 during the non-fast flows has the maximum value of ∼1.32% at B_XY/B_L ≈ 0.15.

Figure 6 shows the percentages of T_ef > 0 during the fast flows at different values of (B_X/|B_X|)⋅B_XY/B_L under different conditions of the local ion speed V_T. At B_XY/B_L < 0.05, the maximum percentages of T_ef > 0 are ∼1.23%, 1.45%, and 1.86% when V_T is in the range of <100 km/s, 100–400 km/s, and >400 km/s, respectively, indicating that the plasma near the neutral sheet tends to have a slightly higher probability of being electron firehose unstable with the increase of the local V_T. The percentage of T_ef > 0 has the maximum value at B_XY/B_L ≈ 0.05 when V_T < 100 km/s. Under the condition of the local V_T > 400 km/s, the percentage of T_ef > 0 has the maximum value at B_XY/B_L ≈ 0.1. Obviously, the local V_T can affect the electron firehose unstable conditions during fast flows.

Figure 6

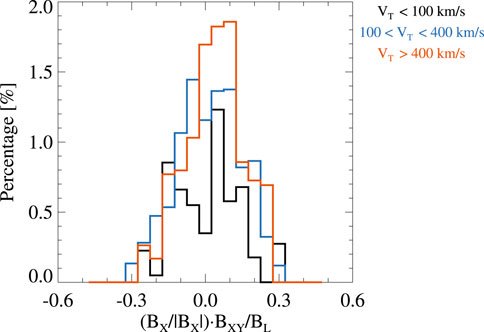
Figure 6. Percentages of T_ef > 0 at different values of (B_X/|B_X|)⋅B_XY/B_L during the fast flows when the local V_T is in the range of <100 km/s (black), 100–400 km/s (cyan), and >400 km/s (orange), respectively.

Figure 7 shows the percentages of T_ef > 0 during the fast flows (a) and non-fast flows (b) at different values of (B_X/|B_X|)⋅B_XY/B_L under different conditions of the electron number density N_e. Figure 7A shows that the percentage of T_ef > 0 has no significant change when N_e is in different range during the fast flows. As shown in Figure 7B, the maximum percentages of T_ef > 0 are ∼2.58%, 1.07%, and 1.31% at B_XY/B_L < 0.2 when N_e is in the range of <0.2 cm⁻³, 0.2–0.4 cm^-3, and >0.4 cm⁻³ during the non-fast flows, respectively. Under the condition of N_e < 0.2 cm⁻³, the percentage of T_ef > 0 has the maximum value at B_XY/B_L ≈ 0.15.

Figure 7

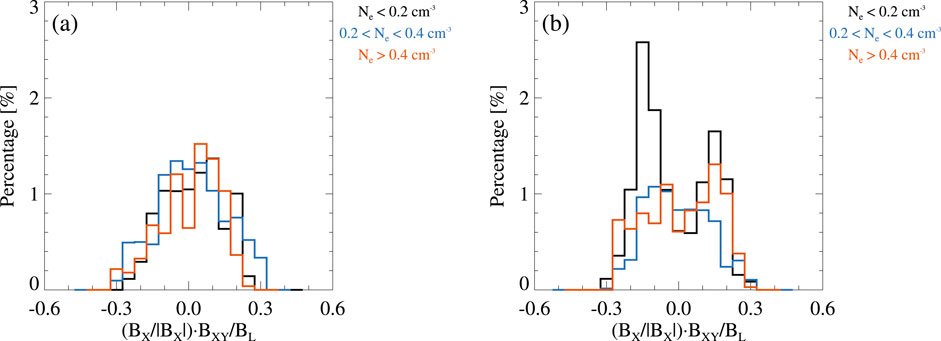
Figure 7. Percentages of T_ef > 0 at different values of (B_X/|B_X|)⋅B_XY/B_L during the fast flows (A) and non-fast flows (B) when N_e is in the range of <0.2 cm⁻³ (black), 0.2–0.4 cm⁻³ (cyan), and >0.4 cm⁻³ (orange), respectively.

Figure 8 shows the percentages of T_ef > 0 during the fast flows (a) and non-fast flows (b) under different conditions of the electron temperature T_e. During the fast flows, the percentage of T_ef > 0 has no significant change when T_e is in the range of <0.8 keV, 0.8–1.4 keV, and >1.4 keV, respectively. During the non-fast flows, the maximum percentages of T_ef > 0 are ∼0.97%, 1.51%, and 1.89% at B_XY/B_L < 0.15 when T_e is in the range of <0.8 keV, 0.8–1.4 keV, and >1.4 keV, respectively, indicating that the plasma in this region tends to have a slightly higher probability of being electron firehose unstable with the increase of T_e. Under the condition of T_e > 0.8 keV, the percentage of T_ef > 0 has the maximum value at B_XY/B_L ≈ 0.15.

Figure 8

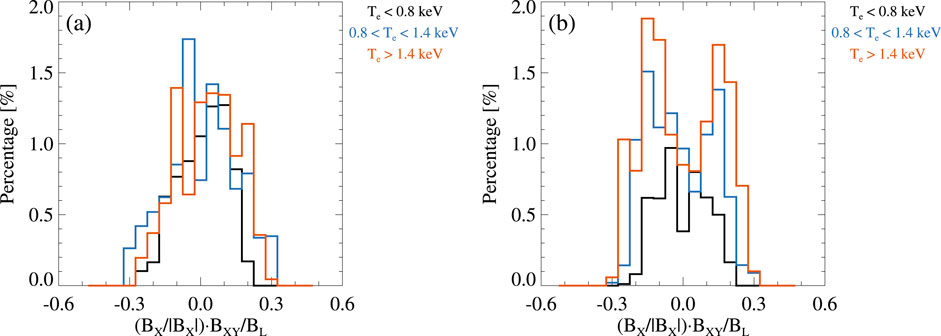
Figure 8. Percentages of T_ef > 0 at different values of (B_X/|B_X|)⋅B_XY/B_L during the fast flows (A) and non-fast flows (B) when T_e is in the range of < 0.8 keV (black), 0.8–1.4 keV (cyan), and >1.4 keV (orange), respectively.

According to the distribution of the percentages of T_ef > 0 in Figure 5, one can find that electron firehose instabilities are more likely to be excited at B_XY/B_L < 0.3 during the fast flows and non-fast flows. Next, we only analyze the characteristics of T_ef > 0 within B_XY/B_L < 0.3 in Figure 9 as well as in Figure 10. Figure 9A shows that the percentages of T_ef > 0 are ∼0.65%, 0.90% and 0.66% (0.67%, 0.86% and 0.79%) during the fast flows (non-fast flows) at −15 < X_GSM < −10 R_E, −20 < X_GSM < −15 R_E and −30 < X_GSM < −20 R_E, respectively. The percentages of T_ef > 0 at −20 < X_GSM < −15 R_E is somewhat larger than that at −15 < X_GSM < −10 R_E and −30 < X_GSM < −20 R_E. Figure 9B shows the percentages of T_ef > 0 are ∼0.80%, 0.74%, and 0.55% (0.87%, 1.38% and 0.38%) during the fast flows (non-fast flows) at 4 < Y_GSM < 12 R_E, −4 < Y_GSM < 4 R_E and −12 < Y_GSM < −4 R_E, respectively. This suggests that both electron firehose unstable conditions during the fast flows and non-fast flows have a dawn-dusk asymmetry.

Figure 9

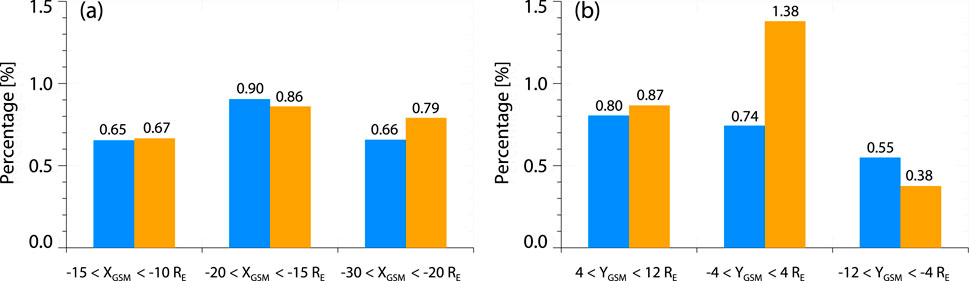
Figure 9. (A) Percentages of T_ef > 0 within B_XY/B_L < 0.3 during the fast flows (blue) and non-fast flows (orange) at −15 < X_GSM < −10 R_E, −20 < X_GSM < −15 R_E and −30 < X_GSM < −20 R_E, respectively. (B) Percentages of T_ef > 0 within B_XY/B_L < 0.3 during the fast flows (blue) and non-fast flows (orange) at 4 < Y_GSM < 12 R_E, −4 < Y_GSM < 4 R_E and −12 < Y_GSM < −4 R_E, respectively.

Figure 10

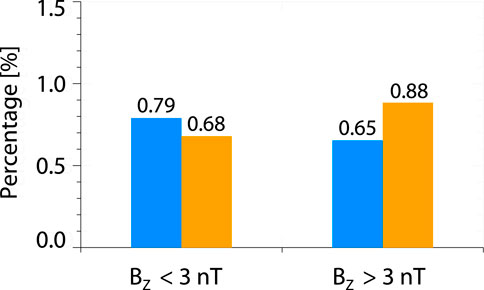
Figure 10. Percentages of T_ef > 0 under the condition of B_XY/B_L < 0.3 during the fast flows (blue) and non-fast flows (orange) when the ambient B_Z < 3 nT and B_Z > 3 nT, respectively.

We regard the smoothed B_Z with a temporal window of 20 min as the ambient B_Z. Figure 10 shows that the percentages of T_ef > 0 during the fast flows (blue) are ∼0.79% and 0.65% when the ambient B_Z is <3 nT and >3 nT, respectively. This indicates that the probability of the electron firehose unstable condition is somewhat larger when the ambient B_Z is <3 nT than that when the ambient B_Z is >3 nT. One may expect that the waves generated by electron firehose instabilities during fast flows are more likely to occur during the stretch process of the plasma sheet than that during the dipolarization process. By contrast, the percentages of T_ef > 0 during the non-fast flows (orange) are ∼0.68% and 0.88% when B_Z is <3 nT and >3 nT. This indicates that the ambient B_Z has an opposite effect on the electron firehose unstable condition during the non-fast flows.

3 Summary and discussion

Using the MMS1 data from 2015 to 2022, we investigate the electron firehose unstable condition in the magnetotail plasma sheet. Our findings are as follows:

a. A magnetic field fluctuation accompanied by a field-aligned current is found during a flapping motion. The fluctuation occurs near the neutral sheet, where the local plasma is electron firehose unstable, suggesting that this fluctuation might be generated by the electron firehose instability.

b. According to the theory of [27], the plasma being electron firehose unstable (T_ef > 0) mainly occurs within B_XY/B_L < 0.3. The probability of the plasma with T_ef > 0 tends to be larger with a maximum value of ∼1.36% when closer to the neutral sheet during the fast flows. By contrast, the maximum probability is ∼1.32% at B_XY/B_L ≈ 0.15 during the non-fast flows.

c. During the fast flows, the plasma near the neutral sheet tends to have a higher probability of T_ef > 0 when the local V_T is larger. During non-fast flows, the plasma near the neutral sheet tends to have a higher probability of T_ef > 0 when T_e is larger.

d. Within B_XY/B_L < 0.3, the probability of T_ef > 0 shows a dawn-dusk asymmetry during the fast flows as well as during the non-fast flows. During the fast flows, the probability of T_ef > 0 is larger when the ambient B_Z is <3 nT than that when the ambient B_Z is >3 nT, which shows opposite characteristics during the non-fast flows.

Flapping motions are a large movement of the current sheet in the north-south direction [41, 43]. Field-aligned currents are reported to occur near the neutral sheet during flapping motions [54, 55]. Some flapping motions can create Pi2 (period: 40–150 s) pulsations on the ground via field-aligned currents flowing into the ionosphere along the magnetic field line [42, 56]. During flapping motions, the current carriers of the current density are dominant by electrons [55], and some field-aligned currents can be explained by the chaotic motion of electrons near the neutral sheet [51]. So far, the origin of the field-aligned current during flapping motions is still not fully understood. Figure 1 shows a magnetic field fluctuation observed at the neutral sheet during a flapping motion. We find that this fluctuation is sub-ion scale, and accompanied by a strong field-aligned current. This sub-ion scale fluctuation is Alfvénic, and occurs in the region where the local plasma is electron firehose unstable. These results suggest that this Alfvénic fluctuation is possibly generated by the electron firehose instability, which might be the origin of the field-aligned current during the flapping motion in Figure 1.

In the central thin current sheet, electrons have a weak temperature anisotropy with T_e,||/T_e,⊥ ≈ 1.06, and T_e,||/T_e,⊥ is mainly in the range of 1–1.2 [57]. Here, we mainly focus on the electrons with 2 ≤ β_e,|| ≤ 25, which mainly occur at B_XY/B_L < 0.3. The average T_e,||/T_e,⊥ of these electrons during the fast (non-fast) flows is ∼1.07 (1.09), and ∼61.6% (62.6%) of these electrons have the value of T_e,||/T_e,⊥ in the range of 1–1.2. Our findings suggest that the electrons at the central current sheet have a weak parallel temperature anisotropy regardless of whether the current sheet is thin or not. Although the probability of T_e,||/T_e,⊥ > 1 for the electrons with 2 ≤ β_e,|| ≤ 25 is up to ∼73.4% (78.9%) during the fast (non-fast) flows, these electrons have a very low probability of being firehose unstable (see Figure 4).

Fast flows can cause plasma temperature anisotropies to excite various instabilities, such as mirror instabilities and ion firehose instabilities [10, 11, 20]. Similar to ions, the plasma near the neutral sheet has the maximum probability of being electron firehose unstable overall during fast flows (see Figure 5). Thus, one may expect that instabilities in the plasma sheet are more likely to occur during fast flows. However, Figure 5B shows that the probability of the plasma being electron firehose unstable during the fast flows is very close to that during the non-fast flows. This suggests that fast flows have no significant contribution to the excitation of electron firehose instabilities in the plasma sheet. The plasma tends to have a slightly higher probability of being electron firehose unstable with the increase of T_e during the non-fast flows (see Figure 8). According to the definition of T_ef, T_ef tends to be larger with the increase of T_e if we assume that the other plasma parameters are constant. This might explain why the electrons during the non-fast flows tend to have a higher probability of being firehose unstable when T_e is larger.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JW: Writing–original draft. GW: Writing–review and editing. PZ: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by Key-Area Research and Development Program of Guangdong Province (2020B0303020001), NSFC (42130204, 42241155), the Guangdong Basic and Applied Basic Research Foundation (Grant Nos 2019A1515011067, 2023B1515040021, 2022A1515011698, and 2023A1515030132), Shenzhen Natural Science Fund (the Stable Support Plan Program GXWD20201230155427003-20200822192703001), Shenzhen Science and Technology Research Program (JCYJ20210324121412034, JCYJ20210324121403009), National Key Research and Development Program of China (grant No. 2022YFF0503904), Shenzhen Key Laboratory Launching Project (ZDSYS20210702140800001), the Fundamental Research Funds for the Central Universities (HIT.OCEF.2022041), and Joint Open Fund of Mengcheng National Geophysical Observatory (No. MENGO-202315).

Acknowledgments

We acknowledge the data from the NASA MMS mission. We also acknowledge MMS project FGM and FPI teams.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Angelopoulos V, Coroniti FV, Kennel CF, Kivelson MG, Walker RJ, Russell CT, et al. (1997) Correction to Multipoint analysis of a bursty bulk flow event on April 11, 1985. J Geophys Res Space Phys 102(A1):211–2. doi:10.1029/96JA03217

CrossRef Full Text | Google Scholar

2. Cao JB, Ma YD, Parks G, Reme H, Dandouras I, Nakamura R, et al. (2006) Joint observations by Cluster satellites of bursty bulk flows in the magnetotail. J Geophys Res 111(A4):A04206. doi:10.1029/2005JA011322

CrossRef Full Text | Google Scholar

3. Machida S, Miyashita Y, Ieda A, Nishida A, Mukai T, Saito Y, et al. (1999). GEOTAIL observations of flow velocity and north-south magnetic field variations in the near and mid-distant tail associated with substorm onsets. Geophys Res Lett 26(6):635–8. doi:10.1029/1999GL900030

CrossRef Full Text | Google Scholar

4. Nagai T, Machida S. Magnetic reconnection in the near-Earth magnetotail (1998) Geophys Monograph-American Geophys Union 105:211–24. doi:10.1029/GM105p0211

CrossRef Full Text | Google Scholar

5. Chen CX, Wolf RA (1993) Interpretation of high-speed flows in the plasma sheet. J Geophys Res 98(A12):21409–19. doi:10.1029/93JA02080

CrossRef Full Text | Google Scholar

6. Kim H-S, Lee D-Y, Ohtani S-I, Lee E-S, Ahn B-H (2010) Some statistical properties of flow bursts in the magnetotail. J Geophys Res Space Phys 115(A12):A12229. doi:10.1029/2009JA015173

CrossRef Full Text | Google Scholar

7. Runov A, Angelopoulos V, Sitnov M, Sergeev VA, Nakamura R, Nishimura Y, et al. (2011) Dipolarization fronts in the magnetotail plasma sheet. Planet Space Sci 59(7):517–25. doi:10.1016/j.pss.2010.06.006

CrossRef Full Text | Google Scholar

8. Gary SP, Fuselier SA, Anderson BJ (1993) Ion anisotropy instabilities in the magnetosheath. J Geophys Res Space Phys 98(A2):1481–8. doi:10.1029/92JA01844

CrossRef Full Text | Google Scholar

9. Hasegawa A. Drift mirror instability in the magnetosphere. (1969) Phys Fluids 12(12):2642–50. doi:10.1063/1.1692407

CrossRef Full Text | Google Scholar

10. Hellinger P, Matsumoto H. New kinetic instability: oblique Alfvén fire hose (2000) J Geophys Res Space Phys 105(A5):10519–26. doi:10.1029/1999JA000297

CrossRef Full Text | Google Scholar

11. Quest KB, Shapiro VD. (1996) Evolution of the fire-hose instability: linear theory and wave-wave coupling. J Geophys Res Space Phys 101(A11):24457–69. doi:10.1029/96JA01534

CrossRef Full Text | Google Scholar

12. Hellinger P, Trávníček P, Kasper JC, Lazarus AJ. (2006) Solar wind proton temperature anisotropy: linear theory and WIND/SWE observations. Geophys Res Lett 33(9):2006GL025925. doi:10.1029/2006GL025925

CrossRef Full Text | Google Scholar

13. Hellinger P, Trávníček P. Parallel and oblique proton fire hose instabilities in the presence of alpha/proton drift: hybrid simulations (2006) J Geophys Res Space Phys 111(A1):2005JA011318. doi:10.1029/2005JA011318

CrossRef Full Text | Google Scholar

14. Markovskii SA, Vasquez BJ. The effect of solar wind turbulence on parallel and oblique firehose instabilities (2022) Astrophysical J 924(2):111. doi:10.3847/1538-4357/ac3754

CrossRef Full Text | Google Scholar

15. Opie S, Verscharen D, Chen CHK, Owen CJ, Isenberg PA (2022) Conditions for proton temperature anisotropy to drive instabilities in the solar wind. Astrophysical J 941(2):176. doi:10.3847/1538-4357/ac982f

CrossRef Full Text | Google Scholar

16. DeWeese H, Maruca BA, Qudsi RA, Chasapis A, Pultrone M, Johnson E, et al. (2022) Alpha particle temperature anisotropy in earth’s magnetosheath. Astrophysical J 941(1):12. doi:10.3847/1538-4357/ac9791

CrossRef Full Text | Google Scholar

17. Maruca BA, Chasapis A, Gary SP, Bandyopadhyay R, Chhiber R, Parashar TN, et al. (2018) MMS observations of beta-dependent constraints on ion temperature anisotropy in earth’s magnetosheath. Astrophysical J 866(1):25. doi:10.3847/1538-4357/aaddfb

CrossRef Full Text | Google Scholar

18. Astfalk P, Jenko F. Parallel and oblique firehose instability thresholds for bi-kappa distributed protons (2016) J Geophys Research-Space Phys 121(4):2842–52. doi:10.1002/2015ja022267

CrossRef Full Text | Google Scholar

19. Wang C, Liu Y, Xing X, Runov A, Artemyev A, Zhang X. An event study of simultaneous earthward and tailward reconnection exhaust flows in the earth’s midtail (2020) J Geophys Res Space Phys 125(6):e2019JA027406. doi:10.1029/2019JA027406

CrossRef Full Text | Google Scholar

20. Wu M, Volwerk M, Lu Q, Voeroes Z, Nakamura R, Zhang T. The proton temperature anisotropy associated with bursty bulk flows in the magnetotail (2013) J Geophys Research-Space Phys 118(8):4875–83. doi:10.1002/jgra.50451

CrossRef Full Text | Google Scholar

21. Treumann RA, Baumjohann W. Advanced space plasma physics. London, United Kingdom: Imperial College Press (2001). p. 51–2.

Google Scholar

22. Horton W, Xu BY, Wong HV (2004) Firehose driven magnetic fluctuations in the magnetosphere. Geophys Res Lett 31(6):L06807. doi:10.1029/2003GL018309

CrossRef Full Text | Google Scholar

23. Horton W, Xu BY, Wong HV, Van Dam JW. Nonlinear dynamics of the firehose instability in a magnetic dipole geotail (2004) J Geophys Research-Space Phys 109(A9):A09216. doi:10.1029/2003JA010288

CrossRef Full Text | Google Scholar

24. Wei J, Wang G, Zuo P. Statistical study of the relationship between pi1/2-band wave powers and firehose instability criterion during fast flows in the magnetotail plasma sheet (2022) J Geophys Res Space Phys 127(11):e2022JA030567. doi:10.1029/2022JA030567

CrossRef Full Text | Google Scholar

25. Wei J, Wang G, Zuo P. Study of the relationship between large-amplitude neutral sheet oscillations and oblique firehose instabilities during fast flows in the terrestrial magnetotail (2024). Phys Fluids 36(5):056616. doi:10.1063/5.0206101

CrossRef Full Text | Google Scholar

26. Camporeale E, Burgess D. Electron firehose instability: kinetic linear theory and two-dimensional particle-in-cell simulations (2008) J Geophys Res 113(A7):A07107. doi:10.1029/2008JA013043

CrossRef Full Text | Google Scholar

27. Gary SP, Nishimura K (2003) Resonant electron firehose instability: particle-in-cell simulations. Phys Plasmas 10(9):3571–6. doi:10.1063/1.1590982

CrossRef Full Text | Google Scholar

28. Hellinger P, Trávníček PM, Decyk VK, Schriver D (2014) Oblique electron fire hose instability: particle-in-cell simulations. J Geophys Res Space Phys 119(1):59–68. doi:10.1002/2013JA019227

CrossRef Full Text | Google Scholar

29. Li X, Habbal SR. Electron kinetic firehose instability. J Geophys Res (2000) 105(A12):27377–85. doi:10.1029/2000JA000063

CrossRef Full Text | Google Scholar

30. López RA, Micera A, Lazar M, Poedts S, Lapenta G, Zhukov AN, et al. (2022) Mixing the solar wind proton and electron scales. Theory and 2d-PIC simulations of firehose instability. Astrophysical J 930(2):158. doi:10.3847/1538-4357/ac66e4

CrossRef Full Text | Google Scholar

31. Cozzani G, Khotyaintsev YV, Graham DB, André M (2023) Direct observations of electron firehose fluctuations in the magnetic reconnection outflow. J Geophys Res Space Phys 128(5):e2022JA031128. doi:10.1029/2022JA031128

CrossRef Full Text | Google Scholar

32. Zhang X, Angelopoulos V, Artemyev AV, Liu J (2018) Whistler and electron firehose instability control of electron distributions in and around dipolarizing flux bundles. Geophys Res Lett 45(18):9380–9. doi:10.1029/2018GL079613

CrossRef Full Text | Google Scholar

33. Artemyev AV, Angelopoulos V, Vasko IY, Petrukovich AA, Runov A, Saito Y, et al. (2020) Contribution of anisotropic electron current to the magnetotail current sheet as a function of location and plasma conditions. J Geophys Res Space Phys 125(1):e2019JA027251. doi:10.1029/2019JA027251

CrossRef Full Text | Google Scholar

34. Nakamura R, Baumjohann W, Fujimoto M, Asano Y, Runov A, Owen CJ, et al. (2008) Cluster observations of an ion-scale current sheet in the magnetotail under the presence of a guide field. J Geophys Res Space Phys 113(A7):2007JA012760. doi:10.1029/2007JA012760

CrossRef Full Text | Google Scholar

35. Zelenyi LM, Malova HV, Leonenko MV, Grigorenko EE, Popov VY (2022) Equilibrium configurations of super-thin current sheets in space plasma: characteristic scaling of multilayer structures. J Geophys Res Space Phys 127(11):e2022JA030881. doi:10.1029/2022JA030881

CrossRef Full Text | Google Scholar

36. Kamaletdinov SR, Yushkov EV, Artemyev AV, Lukin AS, Vasko IY (2020) Superthin current sheets supported by anisotropic electrons. Phys Plasmas 27(8):082904. doi:10.1063/5.0018063

CrossRef Full Text | Google Scholar

37. Burch JL, Moore TE, Torbert RB, Giles BL (2016) Magnetospheric Multiscale overview and science objectives. Space Sci Rev 199(1–4):5–21. doi:10.1007/s11214-015-0164-9

CrossRef Full Text | Google Scholar

38. Russell CT, Anderson BJ, Baumjohann W, Bromund KR, Dearborn D, Fischer D, et al. (2016) The magnetospheric Multiscale magnetometers. Space Sci Rev 199(1–4):189–256. doi:10.1007/s11214-014-0057-3

CrossRef Full Text | Google Scholar

39. Pollock C, Moore T, Jacques A, Burch J, Gliese U, Saito Y, et al. (2016) Fast plasma investigation for magnetospheric Multiscale. Space Sci Rev 199(1–4):331–406. doi:10.1007/s11214-016-0245-4

CrossRef Full Text | Google Scholar

40. Angelopoulos V, Kennel CF, Coroniti FV, Pellat R, Kivelson MG, Walker RJ, et al. (1994) Statistical characteristics of bursty bulk flow events. J Geophys Res 99(A11):21257–80. doi:10.1029/94JA01263

CrossRef Full Text | Google Scholar

41. Zhang TL, Baumjohann W, Nakamura R, Balogh A, Glassmeier K -H (2002) A wavy twisted neutral sheet observed by CLUSTER. Geophys Res Lett 29(19) doi:10.1029/2002GL015544

CrossRef Full Text | Google Scholar

42. Wang GQ, Volwerk M, Nakamura R, Boakes P, Zhang TL, Yoshikawa A, et al. (2014) Flapping current sheet with superposed waves seen in space and on the ground. J Geophys Res Space Phys 119(12). doi:10.1002/2014JA020526

CrossRef Full Text | Google Scholar

43. Wang GQ, Zhang TL, Wu MY, Schmid D, Cao JB, Volwerk M (2019) Solar wind directional change triggering flapping motions of the current sheet: MMS observations. Geophys Res Lett 46(1):64–70. doi:10.1029/2018GL080023

CrossRef Full Text | Google Scholar

44. Harvey CC. Spatial gradients and the volumetric tensor (1998) ISSI Scientific Rep Ser 1:307–22.

Google Scholar

45. Sergeev V, Runov A, Baumjohann W, Nakamura R, Zhang TL, Balogh A, et al. (2004) Orientation and propagation of current sheet oscillations. Geophys Res Lett 31(5):L05807. doi:10.1029/2003GL019346

CrossRef Full Text | Google Scholar

46. Dunlop MW, Balogh A, Glassmeier K-H, Robert P (2002) Four-point cluster application of magnetic field analysis tools: the curlometer. J Geophys Res 107(A11):1384. doi:10.1029/2001JA005088

CrossRef Full Text | Google Scholar

47. Wang GQ, Volwerk M, Zhang TL, Schmid D, Yoshikawa A (2017) High-latitude Pi2 pulsations associated with kink-like neutral sheet oscillations. J Geophys Res Space Phys 122(3):2889–99. doi:10.1002/2016JA023370

CrossRef Full Text | Google Scholar

48. Kaufmann RL, Paterson WR, Frank LA. Magnetization of the plasma sheet (2004) J Geophys Res 109(A9). doi:10.1029/2003ja010148

CrossRef Full Text | Google Scholar

49. Keiling A, Takahashi K. Review of Pi2 models. Space Sci Rev (2011) 161(1–4):63–148. doi:10.1007/s11214-011-9818-4

CrossRef Full Text | Google Scholar

50. Milan SE, Clausen LBN, Coxon JC, Carter JA, Walach M-T, Laundal K, et al. (2017) Overview of solar wind-magnetosphere-ionosphere-atmosphere coupling and the generation of magnetospheric currents. Space Sci Rev 206(1–4):547–73. doi:10.1007/s11214-017-0333-0

CrossRef Full Text | Google Scholar

51. Wang GQ, Zhang TL, Wu MY, Xiao SD, Wang G, Chen YQ, et al. (2021) Field-aligned currents originating from the chaotic motion of electrons in the tilted current sheet: MMS observations. Geophys Res Lett 48(9). doi:10.1029/2020GL088841

CrossRef Full Text | Google Scholar

52. Hietala H, Drake JF, Phan TD, Eastwood JP, McFadden JP (2015) Ion temperature anisotropy across a magnetotail reconnection jet. Geophys Res Lett 42(18):7239–47. doi:10.1002/2015GL065168

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Xiao S, Zhang T, Wang G, Volwerk M, Ge Y, Schmid D, et al. (2017) Occurrence rate of dipolarization fronts in the plasma sheet: cluster observations. Ann Geophysicae 35(4):1015–22. doi:10.5194/angeo-35-1015-2017

CrossRef Full Text | Google Scholar

54. Shen C, Rong ZJ, Li X, Dunlop M, Liu ZX, Malova HV, et al. (2008) Magnetic configurations of the tilted current sheets in magnetotail. Ann Geophysicae 26(11):3525–43. doi:10.5194/angeo-26-3525-2008

CrossRef Full Text | Google Scholar

55. Vasko IY, Artemyev AV, Petrukovich AA, Nakamura R, Zelenyi LM (2014) The structure of strongly tilted current sheets in the Earth magnetotail. Ann Geophysicae 32(2):133–46. doi:10.5194/angeo-32-133-2014

CrossRef Full Text | Google Scholar

56. Sergeev V, Angelopoulos V, Carlson C, Sutcliffe P (1998) Current sheet measurements within a flapping plasma sheet. J Geophys Research-Space Phys 103(A5):9177–87. doi:10.1029/97ja02093

CrossRef Full Text | Google Scholar

57. Zhang Z, Lu S, Lu Q, Wang R, Zhan C, Li X, et al. (2024) Statistical survey of thin current sheets in earth’s magnetotail: MMS observations. J Geophys Res Space Phys 129(5):e2024JA032575. doi:10.1029/2024JA032575

CrossRef Full Text | Google Scholar