Improving the convergence of an iterative algorithm for solving arbitrary linear equation systems using classical or quantum binary optimization

Recent advancements in quantum computing and quantum-inspired algorithms have sparked renewed interest in binary optimization. These hardware and software innovations promise to revolutionize solution times for complex problems. In this work, we propose a novel method for solving linear systems. Our approach leverages binary optimization, making it particularly well-suited for problems with large condition numbers. We transform the linear system into a binary optimization problem, drawing inspiration from the geometry of the original problem and resembling the conjugate gradient method. This approach employs conjugate directions that significantly accelerate the algorithm’s convergence rate. Furthermore, we demonstrate that by leveraging partial knowledge of the problem’s intrinsic geometry, we can decompose the original problem into smaller, independent sub-problems. These sub-problems can be efficiently tackled using either quantum or classical solvers. Although determining the problem’s geometry introduces some additional computational cost, this investment is outweighed by the substantial performance gains compared to existing methods.

1 Introduction

Quadratic unconstrained binary optimization (QUBO) problems [1] are equivalent formulations of some specific type of combinatorial optimization problems, where one (or a few) particular configuration is sought among a finite huge space of possible configurations. This configuration maximizes the gain (or minimizes the cost) of a real function $f$ defined in the total space of possible configurations. In QUBO problems, each configuration is represented by a binary $N$-dimensional vector $\mathbf{q}$, and the function $f$ to be optimized is constructed using a $N\times N$ symmetric matrix $\mathbf{Q}$. For each possible configuration, we have

$f\left(\mathbf{q}\right)={\mathbf{q}}^T.\mathbf{Q}.\mathbf{q}.(1)$

The sought optimal solution ${\mathbf{q}}^{*}$ satisfies $f({\mathbf{q}}^{*})<ϵ$, where $ϵ$ is a sufficiently small positive number. It is often easier to build a system configured near the optimal solution than to build a system configured at the optimal solution.

The QUBO problem is NP-Hard and is equivalent to finding the ground state of a general Ising model with an arbitrary value and numbers of interactions, commonly used in condensed matter physics [2, 3]. The ground state of the related quantum Hamiltonian encodes the optimal configuration and can be obtained from a general initial Hamiltonian using a quantum evolution protocol. This is the essence of quantum computation by quantum annealing [4], where the optimal solution is encoded in a physical Ising quantum ground state. Hybrid quantum–classical methods, digital analog algorithms, and classical computing inspired by quantum computation are promising Ising solvers (see [5]).

Essential classes of problems, not necessarily combinatorial, can be handled using QUBO solvers. For example, the problem of solving systems of linear equations has been previously studied in the context of quantum annealing in [6–9]. The complexity and usefulness of the approach were discussed in [10, 11]. From those, we can say that quantum annealing is promising for solving linear equations even for ill-conditioned systems and when the number of rows far exceeds the number of columns.

In another context, QUBO formulation protocols were recently developed to train machine learning models with the promising expectation that quantum annealing could solve this type of hard problem more efficiently [12]. Machine learning algorithms and specific quantum-inspired formulations of these strategies in the quantum circuit approach have grown substantially in recent years; see, for example, [13–18] and references therein. At the core of the machine learning approach, linear algebra is a fundamental tool used in these formulations. Therefore, the study of QUBO formulations of linear problems and their enhancement can be of interest in the use of the quantum annealing process in machine learning approaches. Another recent example is the study of simplified binary models of inverse problems where the QUBO matrix represents a quadratic approximation of the forward non-linear problem (see [19]). It is interesting to note that in classical inverse problems, the necessity of solving linear system equations is an essential step in the whole process.

In this work, we propose a new method to enhance the convergence rate of an iterative algorithm used to solve a system of equations with an arbitrary condition number. At each stage, the algorithm maps the linear problem to a QUBO problem and finds appropriate configurations using a QUBO solver, either classical or quantum. In previous implementations, the feasibility of the method was linked to the specific binary approximation used. Generally, as the condition number increases, more bits are required, which increases the dimension of the QUBO problem. Our contribution shows that a total or partial knowledge of the intrinsic geometry of the problem helps reformulate the QUBO problem, stabilizing the convergence to the solution and, therefore, improving the performance of the algorithm. In the case of full knowledge of the geometry, we show that the associated QUBO problem is trivial. If the geometry is only partially known, we show that the QUBO problems are small in principle, solvable with low binary approximation.

The remainder of this paper is organized as follows: Section 2 briefly describes how to convert the problem of solving a system of linear equations into a QUBO problem. The conventional algorithm for this problem is presented and illustrated with examples. Subsequently, we analyze the geometrical structure of the linear problem $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$ and their relation with the function [20]; from them, a new set of QUBO configurations is proposed, taking into account the intrinsic geometry in a new lattice configuration. In Section 4.2, we implement these ideas in a new algorithm using a different orthogonality notion (that we call $\mathbf{H}$-orthogonality) related to the well-known gradient descent method. Using the $N\times N$ matrix $\mathbf{A}$, we find a new set of $N$ vectors that characterize the geometry of the problem. We compare the new algorithm with the previous version revised in Section 2. Section 4.3 uses the tools of the previous section to construct a different set of vectors grouped in many subsets mutually $\mathbf{H}$-orthogonal. This construction allows the decomposition of the original QUBO problem into independent QUBO sub-problems of smaller dimensions. Each sub-problem can be addressed using quantum or classical QUBO solvers, allowing arbitrary linear equation systems to be resolved. In Section 5, we present the final considerations.

2 System of linear equations

2.1 Writing a system of equations as a QUBO problem

Solving a system of $N$ linear equations of $N$ variables is identical to finding a $N$-dimensional vector $\mathbf{x}\in {\mathbb{R}}^N$ that satisfies

$\mathbf{A}\cdot \mathbf{x}=\mathbf{b},$

where $\mathbf{A}$ is the matrix constructed with the coefficients of the $N$ linear equations and $\mathbf{b}$ is the vector formed with the inhomogeneous coefficients. If the determinant $\mathrm{D}\mathrm{e}\mathrm{t}(A)\ne 0$, then there exists one unique vector ${\mathbf{x}}^{*}$ that solves the linear system. We can transform the linear problem of real variables into a binary optimization problem using a binary $R$-approximation of the components of one vector $\widehat{\mathbf{x}}$:

${\widehat{x}}_i={\displaystyle \sum _{r=0}^{R-1}}{q}_i^{\left(r\right)}{2}^{-r}.(2)$

Define the vector ${\mathbf{q}}^{(r)}=(q_1^{(r)},\dots ,q_N^{(r)})$. The relation between $\mathbf{x}$ and the binary numbers $q_i^{(r)}$ is

$\mathbf{x}={\mathbf{x}}_0+L{\displaystyle \sum _{r=0}^{R-1}}{2}^{-r}\left({\mathbf{q}}^{\left(r\right)}-\frac{\mathbf{I}}{2}\right),$

where $L$ is the length of the edge of the $N$-cube and $\mathbf{I}$ is the $N$-vector $(\mathrm{1,1},\dots ,1)$. Utilizing Equation 2 and recognizing the summation involving the $\mathbf{I}$ term, we can express

$\mathbf{x}={\mathbf{x}}_0+L\widehat{\mathbf{x}}-\frac{2^R-1}{2^R}L\mathbf{I},(3)$

where $\widehat{\mathbf{x}}=({\widehat{x}}_1,\dots ,{\widehat{x}}_N)$. With this notation, each binary vector

$\mathbf{q}=\left(q_1^{\left(0\right)}\cdots ,q_1^{\left(R-1\right)},q_2^{\left(0\right)},\dots ,q_2^{\left(R-1\right)},\dots ,q_N^{\left(R-1\right)}\right)$

of length $RN$ defines a unique vector $\mathbf{x}$. These choices ensure that the initial guess ${\mathbf{x}}_0$ remains at the center of the $N$-cube.

To construct the QUBO problem associated with solving the linear system, we provide a concrete example with $N=2$; the generalization to arbitrary $N$ is straightforward. Let $\mathbf{A}$ be the matrix and $\mathbf{b}$ be the vector.

$\mathbf{A}=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 2\hfill \\ \hfill 3\hfill & \hfill 4\hfill \end{array}\right),\mathbf{b}=\left(\begin{array}{c}\hfill 5\hfill \\ \hfill 6\hfill \end{array}\right).(4)$

The solution ${\mathbf{x}}^{*}=(-\mathrm{4,9}/2)$ of the system minimizes the function

$f\left(\mathbf{x}\right)=||\mathbf{A}\cdot \mathbf{x}-\mathbf{b}|{|}^2,(5)$

with $f({\mathbf{x}}^{*})=0$. We choose $R=3$, $L=10$, and ${\mathbf{x}}_0=(\mathrm{0,0})$. The binary vector $\mathbf{q}$ has six components. Figure 1A depicts the $2^6$ vectors to be analyzed. To construct the QUBO problem, we substitute Equation 2 into Equation 3 and utilize the corresponding result in Equation 5. It is not difficult to observe that the function is redefined in the binary space of the 64 $\mathbf{q}$’s, and therefore, we can construct a new $N\times RN$ matrix ${\mathbf{A}}_{\mathbf{q}}$ and an $N$-vector ${\mathbf{b}}_{\mathbf{q}}$ satisfying

$f\left(\mathbf{q}\right)=||{\mathbf{A}}_{\mathbf{q}}\cdot \mathbf{q}-{\mathbf{b}}_{\mathbf{q}}|{|}^2,(6)$

where ${\mathbf{A}}_{\mathbf{q}}=\mathbf{A}\otimes (2^0,2^{-1},2^{-2},\dots ,2^{1-R})$, with $\otimes$ denoting the matrix Kronecker product and

${\mathbf{b}}_{\mathbf{q}}=\frac{1}{L}\left(\mathbf{b}+L\frac{\left(2^R-1\right)}{2^R}\mathbf{A}\cdot \mathbf{I}-\mathbf{A}\cdot {\mathbf{x}}_0\right).$

Figure 1

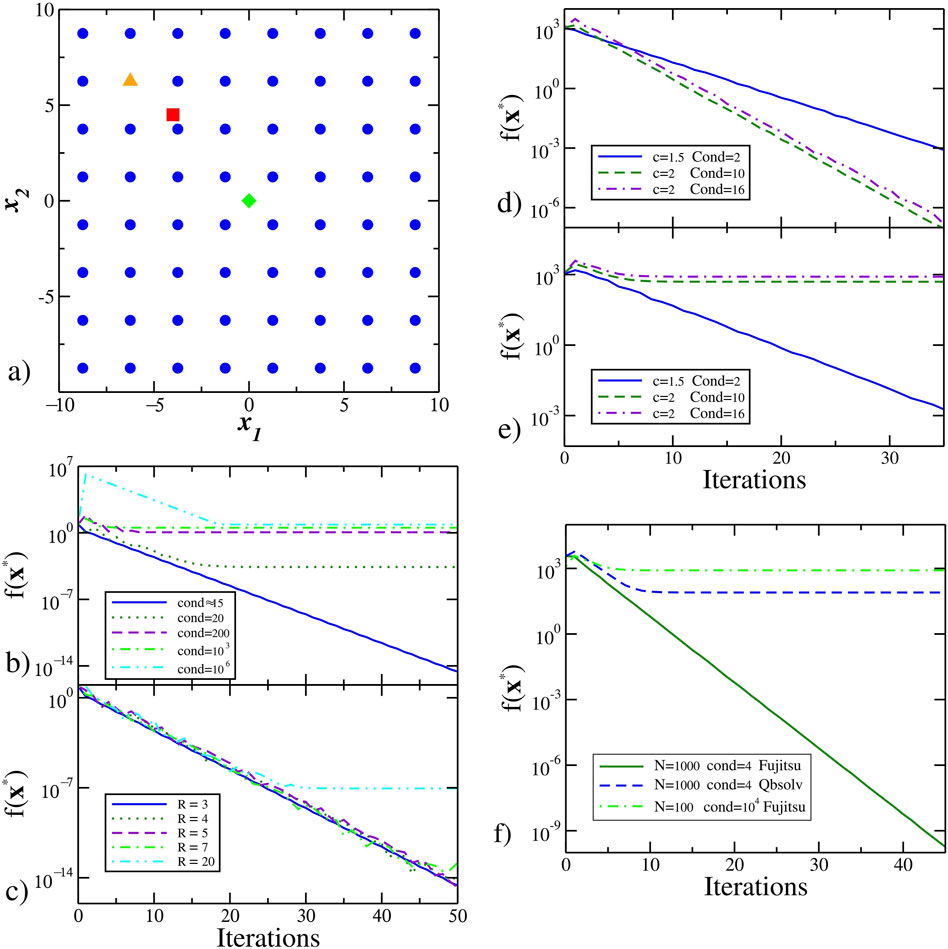
Figure 1. Performance of the original algorithm for solving linear equation systems. (A) $64=2^{3\times 2}$ vectors $\mathbf{x}(\mathbf{q})$ used to represent possible solutions, with $R=3$ and $N=2$. The green diamond corresponds with the initial guess ${\mathbf{x}}_0$, the red square is the exact solution, and the orange triangle is the vector $\mathbf{x}({\mathbf{q}}^{*})$ that minimizes the function $f(\mathbf{x})$ restricted to the possible 64 QUBO vectors, with $f\left(\mathbf{x}({\mathbf{q}}^{*})\right)=13/8$ and ${\mathbf{q}}^{*}=(\mathrm{0,0,1,1,1,0})$. (B–C) We consider the iterative QUBO resolution of the linear system $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$, for matrices with different condition numbers and $N=2$. For each iteration, a vector ${\mathbf{x}}^{*}$ is obtained, and we plot $f({\mathbf{x}}^{*})$. We use $R=3$ in (B) and different values of $R$ until convergence is reached in (C). In both cases, we use $c=2$. The blue continuous curve corresponds to the example in Equation (4). (D–E) We consider linear systems with $N=100$ and matrix condition numbers $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})=\mathrm{2,10}$, and 16 (continuous blue, green dashed, and dash-dot violet lines, respectively). (D) We use the Fujitsu system as the QUBO solver. (E) We use Qbsolv in its standard configuration. In both cases, $R=3$, and the maximum time allowed per iteration is 30 s. (F) We consider a linear system with $N=1000$ and a matrix condition number $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})=4$. We use the Fujitsu system as the QUBO solver (solid green line) and Qbsolv software in its standard configuration (blue dashed line). Additionally, we consider the case where $N=100$ and $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})=10^4$ (green dashed-dot line), demonstrating that the method does not work well for square matrices with a large condition number. In all cases, $R=3$, and the maximum time allotted per iteration is 300 s.

In our particular case, we have

${\mathbf{A}}_{\mathbf{q}}=\left(\begin{array}{cccccc}\hfill 1\hfill & \hfill 0.5\hfill & \hfill 0.25\hfill & \hfill 2\hfill & \hfill 1\hfill & \hfill 0.5\hfill \\ \hfill 3\hfill & \hfill 1.5\hfill & \hfill 0.75\hfill & \hfill 4\hfill & \hfill 2\hfill & \hfill 1\hfill \end{array}\right)\mathrm{a}\mathrm{n}\mathrm{d}{\mathbf{b}}_{\mathbf{q}}=\left(\begin{array}{c}\hfill 3.125\hfill \\ \hfill 6.75\hfill \end{array}\right).$

To construct the QUBO matrix used in Equation 1, we expand $f(\mathbf{q})=\left[({\mathbf{A}}_{\mathbf{q}}\cdot \mathbf{q}-{\mathbf{b}}_{\mathbf{q}})\cdot ({\mathbf{A}}_{\mathbf{q}}\cdot \mathbf{q}-{\mathbf{b}}_{\mathbf{q}})\right]$. Neglecting the constant positive term ${\mathbf{b}}_{\mathbf{q}}\cdot {\mathbf{b}}_{\mathbf{q}}$, we obtain the symmetric QUBO matrix

$\mathbf{Q}={\mathbf{A}}_{\mathbf{q}}^T\cdot {\mathbf{A}}_{\mathbf{q}}-2\ast \mathrm{D}\mathrm{i}\mathrm{a}\mathrm{g}\left({\mathbf{A}}_{\mathbf{q}}^T\cdot {\mathbf{b}}_{\mathbf{q}}\right),(7)$

where $\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{g}(\cdots )$ converts an $N$-vector into a diagonal $N\times N$ matrix. For our specific case, we have

$\mathbf{Q}=\left(\begin{array}{cccccc}\hfill -36.6\hfill & \hfill 5\hfill & \hfill 2.5\hfill & \hfill 14\hfill & \hfill 7\hfill & \hfill 3.5\hfill \\ \hfill 5\hfill & \hfill -20.8\hfill & \hfill 1.25\hfill & \hfill 7\hfill & \hfill 3.5\hfill & \hfill 1.75\hfill \\ \hfill 2.5\hfill & \hfill 1.25\hfill & \hfill -11.025\hfill & \hfill 3.5\hfill & \hfill 1.75\hfill & \hfill 0.875\hfill \\ \hfill 14\hfill & \hfill 7\hfill & \hfill 3.5\hfill & \hfill -46.3\hfill & \hfill 10\hfill & \hfill 5\hfill \\ \hfill 7\hfill & \hfill 3.5\hfill & \hfill 1.75\hfill & \hfill 10\hfill & \hfill -28.15\hfill & \hfill 2.5\hfill \\ \hfill 3.5\hfill & \hfill 1.75\hfill & \hfill 0.875\hfill & \hfill 5\hfill & \hfill 2.5\hfill & \hfill -15.325\hfill \end{array}\right).$

The binary vector ${\mathbf{q}}^{*}=(\mathrm{0,0,1,1,1,0})$ minimizes the function $f(\mathbf{q})$. In Figure 1A, the orange triangle represents $x({\mathbf{q}}^{*})$, which minimizes the function in Equation 6. Note that in this case, the QUBO solution is not the closest point to the exact solution of the problem (the red square). However, for the procedure to work, it is necessary only that the orange configuration lies within the same quadrant as the exact solution.

Once the vector $\mathbf{x}({\mathbf{q}}^{*})$ is found using a QUBO solver, we repeat the process to find a better solution (closest to the exact solution ${\mathbf{x}}^{*}$). This involves redefining ${\mathbf{x}}_0\to \mathbf{x}({\mathbf{q}}^{*})$ and finding a new $L^{*}$, smaller than the previous $L$, such that the new $N$-cube contains a solution closer to the exact one.

For our concrete example $(RN=6)$, verifying all the configurations and determining the best solution are easy tasks. However, when $N$ is big, this procedure becomes intractable because the space of configurations is too large. A new search algorithm, different from the brute force approach, is necessary. There are different possibilities, such as simulated annealing algorithms [20], metaheuristic algorithms [21], and particular-purpose quantum hardware such as quantum annealing machines [9, 22] and classical Ising machines [5]. Hybrid procedures using quantum and classical computation are still possible [23].

Other algorithms to tackle QUBO problems are mentioned in the review [1]. Once a QUBO solver is chosen, we can use the iterative process to find the solution of the linear equations system. We implement this procedure in Algorithm 1, as shown in Figure 2.

Figure 2

Figure 2. Preparation of the QUBO problem to solve a linear system of equations $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$, where ${\mathbf{x}}_0$ is the initial guess, $N_{\text{Iter}}$ is the number of iterations used in the algorithm, $R$ is the bit approximation used for ${\widehat{x}}_i$, and $c>1$ is a constant.

3 Methods

After developing the appropriate mathematical tools, we implemented three methods in Python to solve the associated QUBO problem.

$•$ Exhaustive search (for small problems): when the number of variables (denoted by RN) is less than 20, we directly evaluate all possible QUBO configurations and select the one that yields the optimal solution. This approach is guaranteed to find the best solution but becomes computationally expensive for larger problems.

$•$ D-Wave Qbsolv (deprecated): for larger problems, we employed Qbsolv open-source software provided by D-Wave systems (although it is currently deprecated). This Python library implements a simulated annealing algorithm, which we integrated into our code alongside Qbsolv.

$•$ Fujitsu Digital Annealer: we additionally utilized the Fujitsu Digital Annealer system. We accessed the Fujitsu system through an application programming interface (API) using Python’s requests package. This allows our code to seamlessly interact with the Fujitsu system and submit QUBO problems for optimization.

The coefficients of the linear systems that we studied were randomly generated. After transforming these coefficients into a QUBO format, we converted them into JavaScript Object Notation (JSON) for efficient data exchange. The resulting JSON data were then sent to the Fujitsu system for optimization. Inquiries regarding the implementation details or the code itself can be directed to the authors.

4 Results

Section 4.1 presents the performance of the algorithm in Figure 2 applied to problems with a small condition number. The algorithm works well in this case, but if we increase the condition number, convergence is only obtained by increasing the factor $R$ associated with the numerical binary approximation of the problem. Large condition numbers require larger $R$, and Algorithm 2 is no longer efficient.

In Section 4.2, the previous issue is addressed by determining the geometry of the hypersurfaces with ${\mathbf{x}}^T\cdot \left({\mathbf{A}}^T\mathbf{A}\right)\cdot \mathbf{x}$ constant. We reformulate the QUBO problem considering this geometry and show that solving this problem is trivial, even when using $R=1$. A linear system consisting of $N=5000$ equations with a condition number $10^6$ is solved, demonstrating the power of the method.

In Section 4.3, it is shown that partial knowledge of the geometry simplifies the QUBO approach. In particular, it is demonstrated that in a large problem with a condition number where the algorithm in Figure 2 fails, it is possible to decompose the original problem into many independent QUBO sub-problems, each with a condition number amenable to being approached by the algorithm in Figure 2. Such decomposition is obtained with only partial knowledge of the geometry.

4.1 Convergence of the conventional algorithm

The performance of Algorithm 1 strongly depends on the type of matrix $\mathbf{A}$ used in the problem, particularly on its condition number. The example described in Equation 4 has a condition number $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})\approx 15$. For this example, it is sufficient to use the parameters $R=3$ and $c=2$. As $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})$ increases, the optimal QUBO configurations deviate further from the exact solution of the problem, and it is possible that in the next iteration, the exact solution may fall outside the $N$-cube, breaking convergence. This issue can be resolved by decreasing the parameter $c$, which increases the number of iterations needed to reach convergence.

Another option is to increase the factor $R$ of the algorithm, which increases the number of QUBO configurations. This, in turn, helps the optimal QUBO solution stay closer to the exact solution of the problem. However, increasing $R$ also enlarges the dimension of the QUBO problem to $RN\times RN$, thereby escalating the difficulty of the QUBO approach, at least in principle. In Figures 1B, C, we illustrate these issues for the simpler case of $N=2$.

In Figures 1D, E, we solve three different systems of linear equations with $N=100$, $R=3$, and different $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})<20$. The vector $\mathbf{b}$ associated with the problem was generated using random numbers between −200 and 200, and the matrix $\mathbf{A}$ was generated using random unitary transformations applied to appropriate diagonal matrices. In this study, we compare the open-source heuristic algorithm Qbsolv in a classical simulation (which uses Tabu search and classical simulated annealing) and the Fujitsu system, which is a classical QUBO solver inspired by the quantum annealing approach. We observe that the Fujitsu system finds an adequate configuration in each iteration, reaching convergence when the process ends. For $N=100$, Qbsolv software reaches convergence when $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})=2$ and parameter $c=1.5$, showing that for $N=100$, it is advantageous to use the Fujitsu system.

Figure 1F shows that for $N=1000$ and $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})=4$, the method still works very well only for the Fujitsu system. However, when $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})\gg 20$, the correspondence between optimal QUBO configurations that minimize Equation 6 and the closest configuration to the solution of $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$ is lost. We can choose a larger $R$, as shown in Figure 1C, but for larger matrices with $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})\gg 20$, this procedure is not efficient.

The Fujitsu digital annealer enhances the well-known simulated annealing algorithm with other physics-inspired strategies that resemble quantum annealing procedures (see [24]). In our case, involving large matrices, small binary approximations, and small condition numbers, the Fujitsu system seems to be very efficient at solving these types of problems. Large QUBO problems can be solved using the Fujitsu system (QUBO with dimensions up to $10^5$), which includes integration with the Azure system’s blob storage to load even larger problems. However, even with an efficient QUBO solver like the Fujitsu system, in cases of large matrices with appreciable condition numbers and small binary approximations, Algorithm 1 is not adequate for solving a linear system equation with a unique solution. For matrices with larger $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})$, finding correspondence between QUBO configurations that minimize Equation 6 and configurations sufficiently close to ${\mathbf{x}}^{*}$ depends on the initial guess ${\mathbf{x}}_0$. This property resembles the gradient descent algorithm used in minimization problems, where the convergence rate can heavily depend on the initial guess. This drawback is addressed in descent methods by considering the geometry of the problem and reformulating it into a more powerful conjugate gradient descent method. Next, we demonstrate that the geometry associated with the system of linear equations can improve convergence and break down a sizable original system $\mathbf{A}$ with an arbitrary $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})$ number into smaller ones ${\mathbf{A}}_i$ with lower $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}({\mathbf{A}}_i)$ that could be solved separately using Algorithm 1.

4.2 Rhombus geometry applied to the problem $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$

4.2.1 Geometry of the problem $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$

The entire discrete set of possible configurations defines the QUBO. Generally, there is little structure in this set. However, since the problem is written in the language of vector space, there is a robust mathematical structure that we can use to improve the performance of existing algorithms. It is not difficult to observe that the subset of ${\mathbb{R}}^N$, where $f(\mathbf{x})$ (given by Equation 5 with $\mathbf{A}$ invertible) is constant, corresponds to ellipsoidal hypersurfaces of dimension $N-1$. For $N=2$, see Figure 3A.

Figure 3

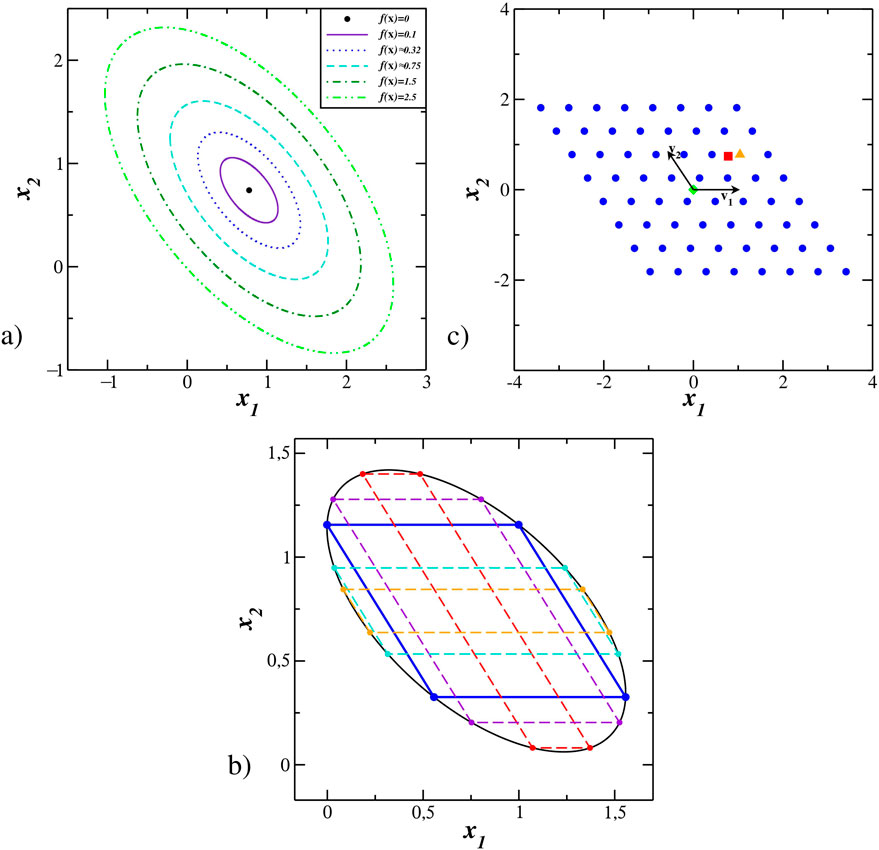
Figure 3. Geometry of the matrix problem associated with the solution of a linear system. In (A), concentric ellipsoidal geometry in the inversion problem (5) for a particular case when $N=2$. $\mathbf{A}$ is invertible and the ellipsoids corresponds to the regions in ${\mathbb{R}}^N$ where $f(\mathbf{x})$ is constant. All the ellipsoids are concentric and contractible to the point ${\mathbf{x}}^{*}$ (black point), which is the unique point that satisfies $\mathbf{A}\cdot {\mathbf{x}}^{*}=\mathbf{b}$. In (B), family of parallelograms contained in a representative ellipse of the figure (A). The parallelograms have different side lengths and congruent angles. In the figure, we highlight the parallelogram with equal-length sides (rhombus) in blue, which would be the base of our method to solve the problem $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$. In (C), space configurations of the QUBO problem in the rhombus geometry (The green diamond corresponds with the initial guess ${\mathbf{x}}_0$, the red square is the exact solution, and the orange triangle is the point $\mathbf{x}({\mathbf{q}}^{*})$ that minimizes the function $f(\mathbf{x})$ between the lattice blue points). The unitary vectors ${\mathbf{v}}_1$ and ${\mathbf{v}}_2$ are the lattice vectors that define the rhombus geometry.

All the ellipses in Figure 3A are concentric and similar. Therefore, we can take a unique representative. Each ellipse contains a family of parallelograms with different sizes but congruent angles; see Figure 3B. In Figure 1A, the problem is formulated using a square lattice geometry. However, nothing prevents us from using other geometries, especially those better suited to the problem. We can choose a lattice with the parallelogram geometry. In particular, we choose the parallelogram with equal-length sides (rhombus). Figure 3C illustrates how possible configurations are chosen using the rhombus geometry.

The choice of this geometry brings advantages in the final algorithm efficiency since we need only a few iterations with the rhombus geometry to obtain convergence to the solution. Given an initial guess ${\mathbf{x}}_0$, such a point defines a rhombus. If the solution ${\mathbf{x}}^{*}$ is also inside the same rhombus, then we can guarantee that all subsequent steps will also be inside the same rhombus as ${\mathbf{x}}^{*}$ (see proof in Supplementary Appendix S1). This property improves convergence and will be referred to here as rhombus convergence.

We emphasize that the square geometry used in previous works only coincides with the matrix inversion geometry when the matrix $\mathbf{A}$ is diagonal. For non-diagonal matrices in the square geometry, the closest point (in the conventional distance) to the exact solution ${\mathbf{x}}^{*}$ is not necessarily the point with the most negligible value of $f(\mathbf{x})$ between the finite QUBO vectors. In other words, the exact solution ${\mathbf{x}}^{*}$ would lay outside the region containing the QUBO configurations, breaking convergence. We can avoid the lack of convergence by reducing the parameter $c$ or increasing the number $R$ in the algorithm but with the consequence of increasing the number of iterations.

4.2.2 $\mathbf{H}$-orthogonality

The ellipsoid form in the matrix inversion problem is given by the symmetric matrix $\mathbf{H}={\mathbf{A}}^T\mathbf{A}$; this becomes clear when we define the new function $f_0(\mathbf{x})=\Vert \mathbf{A}\cdot \mathbf{x}\Vert$, which defines the same set of similar ellipsoids but centered at the zero vector. Particularly, the matrix $\mathbf{H}$ introduces a different notion of orthogonality referred to in the review [25] as $\mathbf{H}$-orthogonality. Two vectors ${\mathbf{v}}_1$ and ${\mathbf{v}}_2$ in ${\mathbb{R}}^N$ are $\mathbf{H}$-orthogonal if they satisfy

${⟨{\mathbf{v}}_1,{\mathbf{v}}_2⟩}_{\mathbf{H}}\equiv {\mathbf{v}}_1\cdot \left({\mathbf{A}}^T\mathbf{A}\cdot {\mathbf{v}}_2\right)=0.$

Given the $N$’s canonical vectors ${\mathbf{u}}_k$, with the $k$th coordinate equal to 1 and all others equal to 0, we can construct from them $N\mathbf{H}$-orthogonal vectors ${\mathbf{v}}_k$ associated with each ${\mathbf{u}}_k$ using a generalized Gram–Schmidt $\mathbf{H}$-orthogonalization. The method selects the first vector as ${\mathbf{v}}_1={\mathbf{u}}_1$. The vector ${\mathbf{v}}_m$ is constructed as

${\mathbf{v}}_m={\mathbf{u}}_m+{\displaystyle \sum _{k=1}^{m-1}}{\beta }_{mk}{\mathbf{v}}_k.(8)$

The coefficients ${\beta }_{mk}$ in Equation 8 are determined using the $\mathbf{H}$-orthogonality property ${⟨{\mathbf{v}}_m,{\mathbf{v}}_k⟩}_{\mathbf{H}}=0$. Explicitly,

${\beta }_{mk}=-\frac{{⟨{\mathbf{v}}_k,{\mathbf{u}}_m⟩}_{\mathbf{H}}}{{⟨{\mathbf{v}}_k,{\mathbf{v}}_k⟩}_{\mathbf{H}}}.$

This procedure is implemented in Algorithm 2, as shown in Figure 4. The calculated non-orthogonal unitary vectors (in the standard scalar product) ${\mathbf{v}}_k$ define the rhombus geometry previously described. In Supplementary Appendix S2, we improve the algorithm described above.

Figure 4

Figure 4. Gram-Schmidt procedure for the calculus of the $N$’s $\mathbf{H}$-orthogonal vectors $({\mathbf{v}}_1,\dots ,{\mathbf{v}}_N)$

4.2.3 Modified search region

Considering the intrinsic rhombus geometry, the iterative algorithm converges exponentially fast with respect to the number of iterations, making it sufficient to use $R=1$. The QUBO configurations in Equation 3 around a certain guess ${\mathbf{x}}_0$ can be rewritten as

$\mathbf{x}={\mathbf{x}}_0+L{\displaystyle \sum _{i=1}^N}\left({\widehat{x}}_i-1/2\right){\mathbf{u}}_i,$

where $\{{\mathbf{u}}_i\}$ is the canonical base. Therefore, we modified Algorithm 1 by changing ${\mathbf{u}}_i\to {\mathbf{v}}_i$ and ${\widehat{x}}_i\to q_i$, where $q_i\in \{\mathrm{0,1}\}$. The $2^N$ QUBO configurations are the vertices of a $N$-rhombus and are associated with all the possible binary vectors $\mathbf{q}=(q_1,\dots ,q_N)$. We can substitute these modifications in the function $f(\mathbf{x})$ and calculate ${\mathbf{A}}_{\mathbf{q}}$ and ${\mathbf{b}}_{\mathbf{q}}$. Considering the vectors ${\mathbf{v}}_i$ as the $i$th row of a matrix $\mathbf{V}$ (where $V_{ij}={\mathbf{v}}_i\cdot {\mathbf{u}}_j$), it is not difficult to see that

${\mathbf{A}}_{\mathbf{q}}=\mathbf{A}{\mathbf{V}}^T(9)$

and

${\mathbf{b}}_{\mathbf{q}}=\left(\mathbf{b}+\frac{L}{2}{\mathbf{A}}_{\mathbf{q}}\cdot \mathbf{I}-\mathbf{A}\cdot {\mathbf{x}}_0\right)/L.$

From Equation 7 and the $\mathbf{H}$-orthogonality of the vectors ${\mathbf{v}}_i$ (matrix rows of $\mathbf{V}$), it becomes evident that the QUBO matrix $\mathbf{Q}$ constructed from Equation 9 is always diagonal. The QUBO solution is trivial (this means that there are no necessary heuristic algorithms or quantum computers to solve the QUBO problem). The modified iterative process is shown in Algorithm 3, shown in Figure 5.

Figure 5

Figure 5. Modified iterative algorithm using the rhombus geometry. The $C_k$ numbers are calculated in Algorithm 2.

4.2.4 Implementation of the algorithm

Algorithm 3 works whenever the rhombus that contains the QUBO configurations also includes the exact solution ${\mathbf{x}}^{*}$. This is guaranteed when $L$ is sufficiently large (in particular when $L>L_0$, where $L_0$ is the “critical” value parameter to obtain convergence). In Figure 6A, we show the algorithm performance for a particular dense matrix with dimensions $5000\times 5000$. The initial guess is the $N$-dimensional zero vector $(N=5000)$. Note the dependence on the parameter value $c$; the critical value is $c=2$, and there is no convergence for $c>2$. To compare with the original algorithm, we study the case with $N=500$, corresponding to a QUBO problem with 1500 variables ($N=500$ and $R=3$). Figure 6B, C show the comparison of the two different approaches. The original Algorithm 1 in Figure 6C exhibits poorer efficiency than the modified Algorithm 3 shown in Figure 6B.

Figure 6

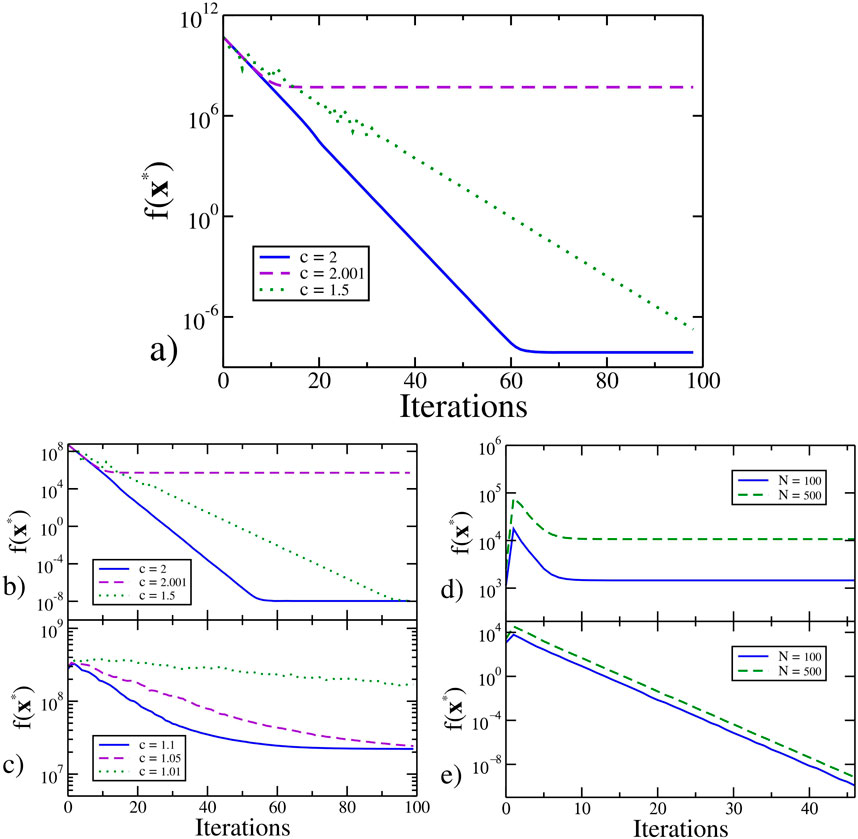
Figure 6. Performance of the new method for solving linear systems. In (A), we shown the iterative QUBO modified algorithm applied to a linear system with 5000 variables and 5000 equations and $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})\approx 10^6$. Note the fast convergence rate to the exact solution in a few iterations (cases $c=2$ and $c=1.5$). All the $2.5\times 10^7$ matrix coefficients of $\mathbf{A}$ and the 5000 vector coefficient of $\mathbf{b}$ were generated using random numbers between 0 and 200. In the modified algorithm we use $L=61000$ and initial guess ${\mathbf{x}}_0=(\mathrm{0,0},\dots ,0)$. Considering ${\mathbf{x}}_{\text{Inv}}={\mathbf{A}}^{-1}\cdot \mathbf{b}$ as the solution obtained by classical inversion algorithms, we have $f({\mathbf{x}}_{\text{Inv}})\approx 7.07\times 10^{-7}$. We obtain $f({\mathbf{x}}^{*})\approx 7.08\times 10^{-9}$ with our modified QUBO algorithm. For $c>2$, the convergence is drastically destroyed. In (B,C), we have the comparison between the iterative algorithms 3 (Panal (B)) and algorithm 1 (Panal (C)) for a matrix with $N=500$, $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})\approx 10^6$ and the same initial $L$. The modified algorithm performs substantially better than the original (see Panal (B)). The function $f({\mathbf{x}}^{*})$ for the vector ${\mathbf{x}}^{*}$ obtained in the final iteration is very close to zero). Algorithm 1 (Panal (C)) using Qbsolv as QUBO-solver in the standard configuration does not show convergence. The Fujitsu system present the same behavior (We tested only 20 iterations, and the figure is not shown). In the two cases, the initial guess ${\mathbf{x}}_0$ is the zero vector. In (D,E), we have the iterative algorithms 1 and 5 applied to two linear systems with dimensions $100\times 100$ and $500\times 500$. All the matrix coefficients of $\mathbf{A}$ and the vector coefficients of $\mathbf{b}$ were generated using random numbers between $-200$ and 200. We use $L=100$ and an initial guess ${\mathbf{x}}_0=(\mathrm{0,0},\dots ,0)$. In (d), we use the square geometry and algorithm 1. In Panal (E), we decompose the original matrix into 10 sub-problems with dimensions $10\times 10$ and 10 sub-problems with dimensions $50\times 50$. We only obtain exact convergence to the solution using the block decomposition shown in algorithm 5. In all cases, we use $R=3$ and $c=2$.

In the last section of this work, we show that having partial knowledge of the conjugated vectors ${\mathbf{v}}_i$ also simplifies the original QUBO problem considerably.

4.3 Solving large systems of equations using binary optimization

4.3.1 Decomposing QUBO matrices in smaller sub-problems

In the previous section, we show that the knowledge of the conjugated vectors that generate the rhombus geometry simplifies the QUBO resolution and improves the convergence rate to the exact solution. However, the calculus of these vectors in Algorithm 2 has approximately $O(N^3)$ steps. A faster algorithm would be desirable.

Another interesting possibility is to use the notion of $\mathbf{H}$-orthogonality to construct a different set of $N$ vectors ${\mathbf{v}}_i$ grouped in $m$ different subsets in such a way that vectors in different subsets are $\mathbf{H}$-orthogonal. In this last section, we show that such construction decomposes the original QUBO matrix in a block diagonal form, and we can use a modified version of Algorithm 3. We can tackle each block independently for some QUBO solver, and after joining the independent results, we obtain the total solution. There are $B_N$ possible decompositions, where $B_N$ is the number of possible partitions of a set with N elements (Bell numbers).

Techniques for decomposing into sub-problems are standard in the search process for some QUBO solvers. One notable example is the QUBO-solver Qbsolv, a heuristic hybrid algorithm that decomposes the original problem into many QUBO sub-problems that can be approached using classical Ising or Quantum QUBO solvers. The solution of each sub-problem is projected into the actual space to infer better initial guesses in the classical heuristic algorithm (Tabu search); see [26] for details. Our algorithm decomposes the original QUBO problem associated with $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$ into many independent QUBO sub-problems. We obtain the optimal solution directly from the particular sub-solutions of each QUBO sub-problem.

To see how the decomposition method works, we use the generalized Gram–Schmidt orthogonalization only between different groups of vectors. We choose $m$ positive numbers $a_i$, satisfying $N=a_1+a_2+\cdots +a_m$. First, call

${\mathbf{v}}_i^{\left(1\right)}={\mathbf{u}}_i,\mathrm{I}\mathrm{f}i\in \left\{1,\dots ,a_1\right\}.$

For the other vectors, we use

${\mathbf{v}}_j^{\left(1\right)}={\mathbf{u}}_j+{\displaystyle \sum _{k=1}^{a_1}}{\beta }_{jk}{\mathbf{v}}_k^{\left(1\right)},\mathrm{I}\mathrm{f}j\in \left\{a_1+1,\dots ,N\right\}.$

We also require that the first group of $a_1$ vectors be $\mathbf{H}$-orthogonal to the second group of $N-a_1$ vectors; specifically, this applies for $j\in \{a_1+1,\dots ,N\}$:

$\begin{array}{ll}\hfill {⟨{\mathbf{v}}_k^{\left(1\right)},{\mathbf{v}}_j^{\left(1\right)}⟩}_{\mathbf{H}}=0,\mathrm{i}\mathrm{f}& k\in \left\{1,\dots ,a_1\right\}\mathrm{a}\mathrm{n}\mathrm{d}\hfill \\ \hfill & j\in \left\{a_1+1,\dots ,N\right\}.\hfill \end{array}$

This last condition determines all the coefficients ${\beta }_{jk}$ for each $j$, by solving a linear system of dimension $a_1\times a_1$. For fixed $j$ and defining ${\mathit{\beta }}_j=({\beta }_{j1},{\beta }_{j2},\dots ,{\beta }_{j{a}_1})$, the linear system to solve is

${\mathit{\beta }}_j=-{\mathbf{H}}_{a_1}^{-1}\cdot {\mathbf{h}}_j,$

where ${\mathbf{H}}_{a_1}$ is the corresponding sub-matrix of $\mathbf{H}$ consisting of its first $a_1\times a_1$ block sub-matrix and ${\mathbf{h}}_j$ represents the first $a_1$’s coefficients of the $j$th column of $\mathbf{H}$. With the coefficients ${\mathit{\beta }}_j$, we can calculate ${\mathbf{v}}_j^{(1)}$ and normalize it. Grouping all these vectors as the rows of the matrix ${\mathbf{V}}_{(1)}$, it is possible to verify that

${\mathbf{V}}_{\left(1\right)}\cdot \mathbf{H}\cdot {\mathbf{V}}_{\left(1\right)}^T={\mathbf{H}}_{a_1}\oplus {\mathbf{H}}^{\left(1\right)},$

where ${\mathbf{H}}^{(1)}$ is a $(N-a_1)\times (N-a_1)$ matrix. We can put ${\mathbf{H}}^{(1)}$ in a two-block diagonal form using the same process, where one block has dimension $a_2\times a_2$ and the second block has dimension $(N-a_1-a_2)\times (N-a_1-a_2)$. In other words,

${\mathbf{v}}_i^{\left(2\right)}={\mathbf{u}}_i,\mathrm{i}\mathrm{f}i\in \left\{\mathrm{0,1},\dots ,a_1+a_2\right\}(10)$

and

${\mathbf{v}}_j^{\left(2\right)}={\mathbf{v}}_j^{\left(1\right)}+{\displaystyle \sum _{k=a_1+1}^{a_1+a_2}}{\beta }_{jk}^{\left(1\right)}{\mathbf{v}}_k^{\left(2\right)},\mathrm{i}\mathrm{f}j\in \left\{a_1+a_2+1,\dots ,N\right\}.$

To determine the new set of $\beta$ coefficients, we use

${\mathit{\beta }}_j^{\left(1\right)}=-{\mathbf{H}}_{a_2}^{-1}\cdot {\mathbf{h}}_j^{\left(1\right)},$

where ${\mathit{\beta }}_j^{(1)}=({\beta }_{j,a_1+1}^{(1)},{\beta }_{j,a_1+2}^{(1)},\dots ,{\beta }_{j,a_1+a_2}^{(1)})$, ${\mathbf{H}}_{a_2}$ is the first $a_2\times a_2$ block diagonal matrix of ${\mathbf{H}}^{(1)}$, and ${\mathbf{h}}_j^{(1)}$ represents the first $a_2$’s coefficients of the $j$th column of ${\mathbf{H}}^{(1)}$. Repeating the previous procedure, we obtain a new matrix ${\mathbf{V}}_{(2)}$, which has the property

${\mathbf{V}}_{\left(2\right)}\cdot \left({\mathbf{V}}_{\left(1\right)}\cdot \mathbf{H}\cdot {\mathbf{V}}_{\left(1\right)}^T\right)\cdot {\mathbf{V}}_{\left(2\right)}^T={\mathbf{H}}_{a_1}\oplus {\mathbf{H}}_{a_2}\oplus {\mathbf{H}}^{\left(2\right)}.$

Repeating the same process another $(m-3)$ times and defining

$\mathbf{V}\equiv {\mathbf{V}}_{m-1}\cdot {\mathbf{V}}_{m-2}\cdots {\mathbf{V}}_2\cdot {\mathbf{V}}_1$

and ${\mathbf{H}}^{(m-1)}\equiv {\mathbf{H}}_{a_m}$, we obtain

$\mathbf{V}\cdot \mathbf{H}\cdot {\mathbf{V}}^T={\mathbf{H}}_{a_1}\oplus {\mathbf{H}}_{a_2}\oplus \cdots \oplus {\mathbf{H}}_{a_m}.(11)$

We use the notation ${\mathbf{H}}_{a_k}$ to reinforce that this is a $a_k\times a_k$ matrix. We implemented this procedure in Algorithm 4, as shown in Figure 7.

Figure 7

Figure 7. Block diagonal transformation of the matrix $\mathbf{H}$ associated with the composition $(a_1,a_2,\dots ,a_m)$ from the partial $\mathbf{H}$-orthogonalization process described in the construction of equation (11). In the pseudo-code the notation is ${\mathit{\beta }}_r=({\beta }_{r1},{\beta }_{r2},\dots ,{\beta }_{r{a}_k})$ and $\mathbf{H}[a_{k-1}::a_k,r]$ correspond with the $r$ sub-column of $\mathbf{H}$ beginning in the row component $a_1+\cdots +a_{k-1}+1$ and finishing in $a_1+\cdots +a_{k-1}+a_k$.

To effectively decompose a large matrix $\mathbf{A}$ with an arbitrary condition number $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})$ into $m$ sub-problems ${\mathbf{H}}_{a_1},\dots ,{\mathbf{H}}_{a_m}$, each tractable with Algorithm 1, we need to choose adequate submatrices of $\mathbf{H}={\mathbf{A}}^T\cdot \mathbf{A}$ such that $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}({\mathbf{H}}_{a_i})<\sqrt{15}$. This is always possible for large matrices $\mathbf{H}$ using the following procedure. To construct ${\mathbf{H}}_{a_1}$, first test all the $2\times 2$ submatrices of $\mathbf{H}$ and choose the one with the minimal condition number. Next, test all the $N-2$ remaining indices to construct a $3\times 3$ matrix with the previous matrix, and choose the one with the minimal condition number; repeat this procedure until reaching the desired dimension $a_1\times a_1$ to obtain ${\mathbf{H}}_{a_1}$. Then, apply the modified orthogonalization procedure explained above to obtain a new matrix ${\mathbf{H}}^{(1)}$ with dimensions $(N-a_1)\times (N-a_1)$, and using this matrix, construct ${\mathbf{H}}_{a_2}$ in the same way. Repeat the procedure until reaching ${\mathbf{H}}_{a_m}$. Evidently, the indices of the submatrices are not ordered, but the generalization is straightforward. Each matrix ${\mathbf{H}}_{a_i}$ is associated with a set of indices ${\mathcal{A}}_i\subseteq \{1,\dots ,N\}$, where ${\mathcal{A}}_i\cap {\mathcal{A}}_j=\varnothing$ for $i\ne j$, and in Equation 10, the substitution is made where $i\in {\mathcal{A}}_1\cup {\mathcal{A}}_2$. It is not difficult to show that there exists a permutation $\sigma$ of the matrix indices such that the row–column permutation $\mathbf{P}(\sigma )\cdot \left(\mathbf{V}\cdot \mathbf{H}\cdot {\mathbf{V}}^T\right)\cdot \mathbf{P}{(\sigma )}^{-1}$ is put into an explicit block diagonal form. This remark is important because we need to manipulate each block independently, as will be shown in the next section.

4.3.2 Implementation of the algorithm

Suppose that the matrix $\mathbf{H}$ is transformed into block diagonal form with each block ${\mathbf{H}}_i$ having $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}({\mathbf{H}}_i)<\sqrt{15}$, as explained above. The procedure for decomposing and solving a QUBO problem is shown in Algorithm 5 (Figure 8). For each matrix ${\mathbf{H}}_i$ in each iterative step, the Fujitsu QUBO solver system is used. Figures 6D, E illustrate the resolution of two matrices of sizes $100\times 100$ and $500\times 500$ using block decomposition into ten $10\times 10$ sub-problems and ten $50\times 50$ sub-problems, respectively. The condition numbers of both matrices are, respectively, $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})=1.3\times 10^5$ and $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}(\mathbf{A})=8.6\times 10^5$. Note that our method, unlike the original Algorithm 1, works for arbitrary matrices and is not restricted to matrices with small condition numbers (the two matrices were generated by choosing random integers in the interval $[-\mathrm{200,200}]$).

Figure 8

Figure 8. Modified iterative algorithm using the block diagonal decomposition of $\mathbf{H}$. Here, ${\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{g}}^{(a_i)}\left({\mathbf{A}}_{\mathbf{q}}^T\cdot {\mathbf{b}}_{\mathbf{q}}\right)$ take the components of the vector $\left({\mathbf{A}}_{\mathbf{q}}^T\cdot {\mathbf{b}}_{\mathbf{q}}\right)$ from the coordinate $R\times (a_1+\cdots +a_{i-1})+1$ until the coordinate $R\times (a_1+\cdots +a_i)$ and builds a diagonal $R{a}_i\times R{a}_i$ matrix.

5 Discussion

It has recently been conjectured that the use of quantum technologies would improve the learning process in machine learning models. In the standard quantum circuit paradigm, many proposals and generalizations exist, promising better performance with the advent of quantum computers. Machine learning formulations such as QUBO problems are also another possible strategy that can be improved with the development of quantum annealing hardware. In such cases, the approach of addressing linear algebra problems through QUBO problems is of general interest because linear algebra is one of the natural languages in which machine learning is written. In this work, we proposed a new method to solve a system of linear equations using binary optimizers. Our approach guarantees that the optimal configuration is the closest to the exact solution. Additionally, we demonstrated that partial knowledge of the problem’s geometry allows decomposition into a series of independent sub-problems that can be solved using conventional QUBO solvers. The solution to each sub-problem is then aggregated, enabling rapid determination of an optimal solution. We show that the original formulation as QUBO is efficient only when the condition number of the associated matrix $\mathbf{A}$ is small (with $\mathbf{A}$ being a square matrix). Our procedure is applicable in principle to matrices with arbitrary condition numbers where the error associated with the multiplication operations is controlled. Therefore, our method is not restricted to matrices with condition numbers close to 1.

However, identifying the vectors that determine the sub-problem decomposition incurs computational costs that influence the overall performance of the algorithm. Nevertheless, two factors could lead to significant improvements: better methods for identifying the vectors associated with the geometry and faster QUBO solvers. In our study, when using a QUBO solver such as the Fujitsu digital annealer, we focus on finding elite QUBO solutions. This is because when the condition number is small, we are guaranteed that the associated configuration is very close to the solution to the problem. Finding elite solutions to QUBO problems is very costly for large problems due to their NP-hardness. However, the only criterion for obtaining convergence in Algorithm 1 is to get a configuration in the same quadrant that contains the solution to the linear system of equations. The number of configurations in each quadrant (there are $2^N$ quadrants) is $2^{RN}/2^N$. For large values of $N$, this results in a large number of configurations. Therefore, focusing on developing new methods to find configurations in the same quadrant as the solution would be an interesting strategy to overcome the NP-hardness of finding the best QUBO solution. In any case, quantum computing or quantum-inspired classical computation could be fundamental tools for developing better approaches that can be integrated with the procedures presented here. We intend to explore these interesting questions in subsequent studies, and we hope that the methods presented in this study can contribute to the discovery of better and more efficient procedures for solving extensive linear systems of equations.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

EC: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing–original draft, and writing–review and editing. EM: conceptualization, investigation, methodology, project administration, resources, software, validation, visualization, and writing–review and editing. RS: methodology, resources, supervision, validation, and writing–review and editing. AS: conceptualization, formal analysis, investigation, methodology, resources, software, supervision, validation, visualization, and writing–review and editing. IO: conceptualization, funding acquisition, methodology, project administration, resources, supervision, visualization, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Brazilian National Institute of Science and Technology for Quantum Information (INCT-IQ) (Grant No. 465 469/2 014-0), the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES)—Finance Code 001, Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), and PETROBRAS: Projects 2017/00 486-1, 2018/00 233-9, and 2019/00 062-2. AMS acknowledges support from FAPERJ (Grant No. 203.166/2 017). ISO acknowledges FAPERJ (Grant No. 202.518/2 019).

Conflict of interest

Author EM was employed by Petróleo Brasileiro S.A.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1443977/full#supplementary-material

References

1. Kochenberger G, Hao JK, Glover F, Lewis M, Lü Z, Wang H, et al. The unconstrained binary quadratic programming problem: a survey. J Comb Optim (2014) 28:58–81. doi:10.1007/s10878-014-9734-0

CrossRef Full Text | Google Scholar

2. Barahona F. On the computational complexity of ising spin glass models. J Phys A: Math Gen (1982) 15:3241–53. doi:10.1088/0305-4470/15/10/028

CrossRef Full Text | Google Scholar

3. Lucas A. Ising formulations of many np problems. Front Phys (2014) 2:1–15. doi:10.3389/fphy.2014.00005

CrossRef Full Text | Google Scholar

4. Kadowaki T, Nishimori H. Quantum annealing in the transverse ising model. Phys Rev E (1998) 58:5355–63. doi:10.1103/PhysRevE.58.5355

CrossRef Full Text | Google Scholar

5. Mohseni N, McMahon PL, Byrnes T. Ising machines as hardware solvers of combinatorial optimization problems. Nat Rev Phys (2022) 4:363–79. doi:10.1038/s42254-022-00440-8

CrossRef Full Text | Google Scholar

6. O’Malley D, Vesselinov VV. Toq.jl: a high-level programming language for d-wave machines based on julia. In: IEEE conference on high performance extreme computing. Waltham, MA, United States: D-Wave (2016). p. 1–7doi. doi:10.1109/HPEC.2016.7761616

CrossRef Full Text | Google Scholar

7. Pollachini GG, Salazar JPLC, Góes CBD, Maciel TO, Duzzioni EI. Hybrid classical-quantum approach to solve the heat equation using quantum annealers. Phys Rev A (2021) 104:032426. doi:10.1103/PhysRevA.104.032426

CrossRef Full Text | Google Scholar

8. Rogers ML, Jr RLS. Floating-point calculations on a quantum annealer: division and matrix inversion. Front Phys (2020) 8:265. doi:10.3389/fphy.2020.00265

CrossRef Full Text | Google Scholar

9. Souza AM, Martins EO, Roditi I, Sá N, Sarthour RS, Oliveira IS. An application of quantum annealing computing to seismic inversion. Front Phys (2021) 9:748285. doi:10.3389/fphy.2021.748285

CrossRef Full Text | Google Scholar

10. Borle A, Lomonaco SJ. Analyzing the quantum annealing approach for solving linear least squares problems. In: WALCOM: algorithms and computation. Springer (2019). p. 289–301doi. doi:10.1007/978-3-030-10564-8_23

CrossRef Full Text | Google Scholar

11. Borle A, Lomonaco SJ. How viable is quantum annealing for solving linear algebra problems? arXiv:2206 (2022). doi:10.48550/arXiv.2206.10576

CrossRef Full Text | Google Scholar

12. Date P, Arthur D, Pusey-Nazzaro L. Qubo formulations for training machine learning models. Sci Rep (2021) 11:10029. doi:10.1038/s41598-021-89461-4

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Gong C, Zhou N-R, Xia S, Huang S. Quantum particle swarm optimization algorithm based on diversity migration strategy. Fut Gen Comp Syst (2024) 157:445–58. doi:10.1016/j.future.2024.04.008

CrossRef Full Text | Google Scholar

14. Gong L-H, Ding W, Li Z, Wang Y-Z, Zhou N-R. Quantum k-nearest neighbor classification algorithm via a divide-and-conquer strategy. Adv Quan Technol (2024) 7:2300221. doi:10.1002/qute.202300221

CrossRef Full Text | Google Scholar

15. Gong L-H, Pei J-J, Zhang T-F, Zhou N-R. Quantum convolutional neural network based on variational quantum circuits. Opt Commun (2024) 550:129993. doi:10.1016/j.optcom.2023.129993

CrossRef Full Text | Google Scholar

16. Huang S-Y, An W-J, Zhang D-S, Zhou N-R. Image classification and adversarial robustness analysis based on hybrid quantum–classical convolutional neural network. Opt Commun (2023) 533:129287. doi:10.1016/j.optcom.2023.129287

CrossRef Full Text | Google Scholar

17. Wu C, Huang F, Dai J, Zhou N-R. Quantum susan edge detection based on double chains quantum genetic algorithm. Phys A: Statis Mech Its Appl (2022) 605:128017. doi:10.1016/j.physa.2022.128017

CrossRef Full Text | Google Scholar

18. Zhou N-R, Zhang T-F, Xie X-W, Wu J-Y. Hybrid quantum–classical generative adversarial networks for image generation via learning discrete distribution. Sign Proc Ima Commun (2023) 110:116891. doi:10.1016/j.image.2022.116891

CrossRef Full Text | Google Scholar

19. Greer S, O’Malley D. Early steps toward practical subsurface computations with quantum computing. Front Comput Sci (2023) 5:1235784. doi:10.3389/fcomp.2023.1235784

CrossRef Full Text | Google Scholar

20. Alkhamis TM, Hasan M, Ahmed MA. Simulated annealing for the unconstrained binary quadratic pseudo-boolean function. Eur J Oper Res (1998) 108:641–52. doi:10.1016/S0377-2217(97)00130-6

CrossRef Full Text | Google Scholar

21. Dunning I, Gupta S, Silberholz J. What works best when? a systematic evaluation of heuristics for max-cut and qubo. INFORMS J Comput (2018) 30:608–24. doi:10.1287/ijoc.2017.0798

CrossRef Full Text | Google Scholar

22. Hauke P, Katzgraber HG, Lechner W, Nishimori H, Oliver WD. Perspectives of quantum annealing: methods and implementations. Rep Prog Phys (2020) 83:054401. doi:10.1088/1361-6633/ab85b8

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Booth M, Berwald J, Uchenna Chukwu JD, Dridi R, Le D, Wainger M, et al. (2020). Qci qbsolv delivers strong classical performance for quantum-ready formulation. doi:10.48550/arXiv.2005.11294

CrossRef Full Text | Google Scholar

24. Aramon M, Rosenberg G, Valiante E, Miyazawa T, Tamura H, Katzgraber HG. Physics-inspired optimization for quadratic unconstrained problems using a digital annealer. Front Phys (2019) 7:48. doi:10.3389/fphy.2019.00048

CrossRef Full Text | Google Scholar

25. Shewchuk JR. An introduction to the conjugate gradient method without the agonizing pain. Pittsburgh, PA, USA: Carnegie-Mellon University, Department of Computer Science (1994).

Google Scholar

26. Booth M, Reinhardt SP, Roy A. Partitioning optimization problems for hybrid classical/quantum execution. Burnaby, BC, Canada: D-Wave The Quantum Computing Company (2017).

Google Scholar

27. Rump SM. Inversion of extremely ill-conditioned matrices in floating-point. Jpn J. Indust. Appl. Math. (2009) 26:249–77. doi:10.1007/BF03186534

CrossRef Full Text | Google Scholar