Compact freeform near-eye display system design enabled by optical-digital joint optimization

The near-eye display (NED) systems, designed to project content into the human eye, are pivotal in the realms of augmented reality (AR) and virtual reality (VR), offering users immersive experiences. A small volume is the key for a fashionable, easy-to-wear, comfortable NED system for industrial and consumer use. Freeform surfaces can significantly reduce the system volume and weight while improving the system specifications. However, great challenges still exist in further reducing the volume of near-eye display systems as there is also a limit when using only freeform optics. This paper introduces a novel method for designing compact freeform NED systems through a powerful optical–digital joint design. The method integrates a geometrical freeform optical design with deep learning of an image compensation neural network, addressing off-axis nonsymmetric structures with complex freeform surfaces. A design example is presented to demonstrate the effectiveness of the proposed method. Specifically, the volume of a freeform NED system is reduced by approximately 63% compared to the system designed by the traditional method, while still maintaining high-quality display performance. The proposed method opens a new pathway for the design of a next-generation ultra-compact NED system.

1 Introduction

The near-eye display (NED) system has undergone substantial evolution in recent 10 years. These systems, designed to project content into the human eye, play a pivotal role in the expanding sectors of augmented reality (AR) and virtual reality (VR), offering users an unparalleled immersive experience. In the design process of an NED system, volume and weight are critical factors. The volume determines the portability and wearing comfort, while the lower weight allows them to be worn for extended periods. Therefore, the volume and weight should be reduced as much as possible while maintaining the system specifications. In recent years, freeform optical surfaces have gained increasing prominence in optical system design due to their expanded design parameter space. Freeform optical surfaces have been successfully utilized in the field of imaging optics, including off-axis cameras [1–3], spectrometers [4, 5], head-mounted display [6], and scan systems [7]. In the design process of an NED system, freeform surfaces are being employed to reduce the system volume and weight. However, further reducing the volume of NED systems remains an unresolved and very challenging issue.

Image processing techniques can be used to improve the image quality of imaging systems. By fully integrating the design of a geometric imaging system and image processing algorithms, better design results can be obtained [8–10]. However, the working mode of NED systems is totally different from that of imaging systems with image sensors or detectors as the light beams are emitted from the display panel or image sources and finally travel into the eyes. In recent years, researchers have explored the design of display systems by integrating the optimization of optical systems and the use of image processing algorithms. Reference 11, through joint optimization, designed a diffractive optical element (DOE) placed in front of a projector lens and a compensation network for deblurring, realizing extended projector depth-of-field. Reference 12 used a joint optimization method to design an NED system consisting of aspherical reflectors instead of a freeform and lens-correction group. For an NED system, if a deep neural network is utilized for image compensation at the display panel, and optical–digital joint optimization of the network and freeform system is conducted, the advantages of freeform optics and the image compensation deep neural network can be fully integrated and exploited. The NED system design with an ultra-compact structure can be achieved to realize reduced system volume, while maintaining good display performance when the compensated image is displayed by the panel.

In this paper, we introduce a novel and powerful design framework for compact freeform NED systems through optical–digital joint optimization. Using the proposed framework, an NED system design with an ultra-compact structure and good display quality can be realized. The feasibility and effect of the proposed design framework are demonstrated by a design example. A freeform off-axis NED system with a significantly smaller volume (62.98% smaller than that of an original freeform system) is realized. The proposed framework opens a new pathway for developing NED systems with an ultra-small volume and can also be extended to the joint design of other kinds of NED and display systems using other surface types or phase elements, such as holographic elements and meta-surfaces.

2 Method

The design framework and process proposed in this paper, which work for NED systems, are different from the optical–digital joint design framework for traditional imaging systems as the NED systems have a totally different working mode from imaging systems, which images the outside scene on the image plane (sensors or detectors). The image with bad performance obtained directly by the imaging system can then be recovered by the recovery network in order to obtain a good final output image. The image recovery is the last step of the whole system working flow. For NED systems, a display panel is used as the “image source.” The image on the display panel is then projected by the NED optical system and, finally, images at the eye. As there is no image recovery at the exit pupil or human eye, the image projected by the freeform NED system should be good. If the freeform NED system is made to be more compact, the aberration of the system may be large. Therefore, the proposed framework uses a compensation network to generate a compensated image at the display panel (which is the first step of the system working flow in order to cooperate with the following freeform optical system with aberrations) and then projected by the NED system.

As shown in Figure 1, the framework contains forward pass and backward pass processes. In the forward pass process, by conducting ray tracing for sampled field points within the full field of view (FOV), the simulated point spread function (PSF) of the sampled field points is obtained, which serves as the basis for acquiring the simulated imaging results of the NED system. The differences between the actual display results and the target images, as well as the evaluation of aberrations, are calculated (loss function L₁); meanwhile, the constraints of the NED system can also be established using ray tracing data (loss function L₂). So the total loss function L_total can be established and calculated. Since imaging simulation of the NED system is based on images displayed on the display panel generated by the compensation network, the connection is established between the NED system and the compensation network. In the backward pass process, the partial derivative (or gradient vector) of the loss function with respect to each parameter in the freeform NED system and the network is calculated. Then, using the partial derivatives, the parameters in the freeform NED system and the neural network can be updated based on L_total. The above process is repeated, and the joint optimization of the NED system and the network is accomplished. The goal of the design framework is to generate a feasible compact freeform NED system and the corresponding well-trained image compensation neural network.

Figure 1

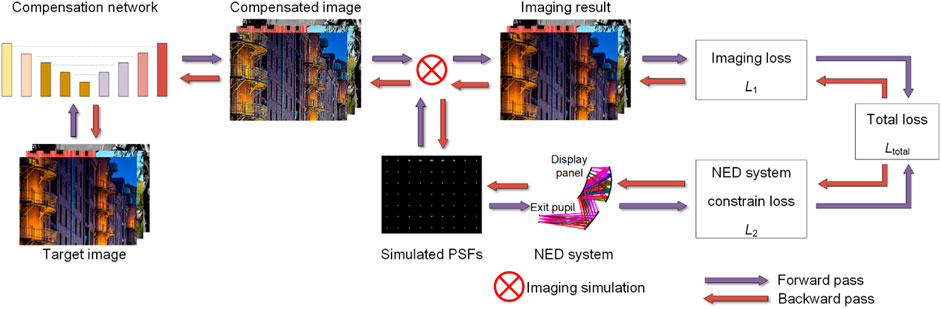
Figure 1. Design framework of the compact freeform NED system based on optical–digital joint optimization.

To realize the joint optimization of the deep learning network and freeform optical system, differentiable ray tracing has to be used so that the gradient of the optical system parameters can be calculated, which will be used to update the parameters of the system and the network. The commonly used freeform surface types include XY polynomial freeform surface, Zernike polynomial freeform surface, and Q2D polynomial freeform surface. Generally, the implicit freeform surface expression can be written as follows:

$f\left(x,y,z\right)=h\left(x,y\right)-z.(1)$

We assume that the ray can be represented with two vectors (o,d). The vector o = [o_x,o_y,o_z] represents the origin point of the ray, and the normalized vector d = [d_x,d_y,d_z] represents the propagation direction of the ray. In addition, the propagation direction can also use the exit angle along the x-axis and y-axis to represent, which can be denoted as θ = [θ_x,θ_y]. The relationship between d and θ is as follows:

$\mathit{d}=\frac{\left[\tan \left({\theta }_{\mathrm{x}}\right),\tan \left({\theta }_{\mathrm{y}}\right),1\right]}{\sqrt{{\tan }^2\left({\theta }_{\mathrm{x}}\right)+{\tan }^2\left({\theta }_{\mathrm{y}}\right)+1}}.(2)$

For one ray in the space, if the position of a point on this ray can satisfy Eq. 1, this point should be the intersection point of the ray with the surface. The ray tracing problem can be transformed into solving an equation, which can be iteratively solved using Newton’s method as Eq. 3, until the change in w is smaller than the allowed value.

$w^{\left[n\right]}=w^{\left[n-1\right]}-\frac{f\left(\mathit{o}+w^{\left[n-1\right]}\mathit{d}\right)}{f^{\prime }\left(\mathit{o}+w^{\left[n-1\right]}\mathit{d}\right)}=w^{\left[n-1\right]}-\frac{f\left(\mathit{o}+w^{\left[n-1\right]}\mathit{d}\right)}{\nabla f\cdot \mathit{d}}.(3)$

When the intersection is found, the ray will be reflected or refracted, whose propagation direction can be calculated based on the law of reflection or refraction. With the above process, the ray can be traced from the object space (display panel) to the exit pupil (human eye). As the whole process is differentiable, the partial derivative of each parameter that needs to be optimized can be calculated in the backward pass.

Rays from the full FOV and full pupil should be sampled for the evaluation and optimization process of an optical system. The ray sampling process for each field point includes three parts: searching the chief and marginal rays with an iterative method, sampling the rays in the object space with the grid-based method, and out-selecting the rays outside the aperture stop range. If the aperture stop is located at the first surface or in the object space, the sampled rays can be easily determined. However, for an NED system, the aperture stop (exit pupil) is the eye pupil, which is located in the afocal space. The size of the circular exit pupil is generally given for the NED system design, and it can be used to determine the discrete sampled rays used in the design; an iterative ray search method is proposed and used to find the chief ray and marginal ray exit angle. As the position of the field point (object point) is known, we only need to find the ray propagation angle (direction). The chief ray of each field point will intersect with the aperture stop at its center, which will be the reference for the iterative process. Assume that the initial guess of the exit angle θ^[0] = [θ^[0]_x , θ^[0]_y ] can make the ray intersect with the first freeform surface at its center, and we trace the ray to the aperture stop. According to the distance between the intersection point and the center of the aperture stop, we can update the exit angle with the following equations:

${\theta }_{\mathrm{x},j}^{\left[n\right]}={\theta }_{\mathrm{x},j}^{\left[n-1\right]}-o_{\mathrm{x},j,\text{stop}}^{\left\{\text{local}\right\}},(4)$

${\theta }_{\mathrm{y},j}^{\left[n\right]}={\theta }_{\mathrm{y},j}^{\left[n-1\right]}-o_{\mathrm{y},j,\text{stop}}^{\left\{\text{local}\right\}},(5)$

where ${\theta }_{\mathrm{x},j}^{\left[n\right]}$ and ${\theta }_{\mathrm{y},j}^{\left[n\right]}$ represent the exit angle of the field point j after the nth iteration in the x and y direction, respectively. In addition, $o_{\mathrm{x},j,\text{stop}}^{\left\{\text{local}\right\}}$ and $o_{\mathrm{y},j,\text{stop}}^{\left\{\text{local}\right\}}$ represent the x and y coordinates, respectively, of the intersection point of field point j and the aperture stop in the local coordinate system. The superscript {local} is used to represent the coordinates in the local coordinate system of the surface. The above process can be stopped until the L2-norm of the [$o_{\mathrm{x},j,\text{stop}}^{\left\{\text{local}\right\}}$, $o_{\mathrm{y},j,\text{stop}}^{\left\{\text{local}\right\}}$, $o_{\mathrm{z},j,\text{stop}}^{\left\{\text{local}\right\}}$] is smaller than the maximum allowed value. The exit angle of the chief ray for the field point is found. Due to pupil aberration, the size and shape of the entrance pupil for each field point may deviate from the ideal case. In order to sample the corrected rays of one field point used in the system, its four marginal pupil rays (top, bottom, left, and right) are found using the similar method above. After obtaining the exit angle of the marginal rays, the next step is ray sampling. The grid-based ray sampling method is used. Based on the range of the exit angle in the x and y direction, we can use the grid-based method to uniformly sample the exit angle in a rectangular range. However, a rectangle sampling range means that some rays exceeding the aperture stop range are also sampled, so the ray out-selected method based on aperture stop size is employed. After tracing all the sampled rays with the grid-based method to the aperture stop, those rays that exceed the aperture stop range will be out-selected. Using the above process, the ray sampling can be done, which will guarantee the subsequent calculation and evaluation. The whole ray sampling process for one field point is shown in Figure 2.

Figure 2

Figure 2. Illustration of the ray sampling procedure for one field point. (A) Sampling range determination based on edge ray positions in different directions for grid sampling; (B) tracing the sampled rays to the aperture stop and determining whether their inclusion within the aperture stop bounds based on their radial distance; (C) out-selecting the ray exceeding the bounds of the aperture stop; (D) ray sampling result.

The point spread function of each field point, which describes the image quality, can be calculated for a further display simulation process. As the system outputs plane waves at the exit pupil, we can add an ideal lens to simulate the eye and evaluate the PSF on the image plane. Here, we assume that the energy of a ray hit on the image plane follows Gaussian distribution [13]. For one field point, the corresponding PSF can be obtained by superimposing the energy distributions of all the sampled rays. The energy distribution of each ray can be represented with a two-dimensional matrix. For all sampled ray energy distribution matrixes, superimposing them together will yield the PSF of the field point. In practice, the center of the matrix is the image point of the chief ray, and the size of the matrix is K×K. For one ray on the image plane, the energy distribution on cell (m,n) can be calculated as follows:

$e_{m,n}^{〈\mu 〉}=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{r_{m,n}^2}{2{\sigma }^2}\right),(6)$

where r_m,n is the distance between the intersection of the ray with the image plane and the pixel (m,n) and $\sigma =\sqrt{\Delta x^2+\Delta y^2}/3$, where ∆x and ∆y represent the size of each pixel on the image in x and y directions, respectively. The PSF can be calculated as

$\mathit{P}\mathit{S}\mathit{F}={\left[{\displaystyle \sum _{\mu =1}^N}{e}_{m,n}^{〈\mu 〉}\right]}_{K\times K}\left(1\le m,n\le K\right),(7)$

where μ represents the ray number, and in total, N rays are sampled for one field point. The diffraction effect is ignored as in the visible band the diffraction effect is not significant, and the system performance is mainly determined by much larger aberrations.

In our method, one key to conducting joint optimization is compensating the ideal display image in order to generate good display performance at the exit pupil (or the new image plane). A compensation network is utilized. This network aims to generate a compensated image, which can then generate an image close enough to the target image after being displayed by the freeform NED system. The architecture of the network is ResUNet [14], which combines the advantage of both UNet [15] and a residual neural network [16]. The network comprises three components: encoding, bridge, and decoding. In each part, the residual structure was used. The network was modified to consist of three downsampling and upsampling blocks, and only in the downsampling block was the residual structure adopted. The architecture of the network is shown in Figure 3.

Figure 3

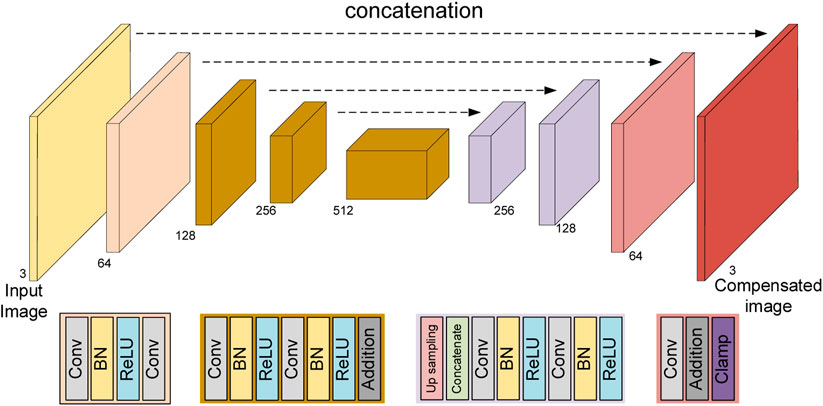
Figure 3. Architecture of the image compensation net. “Conv,” convolutional layer; “BN,” batch normalization layer; “ReLU,” rectified linear unit; “addition,” residual connection; “upsampling,” transposed convolutional layer; “concatenate,” skip connection; “clamp,” clamp layer.

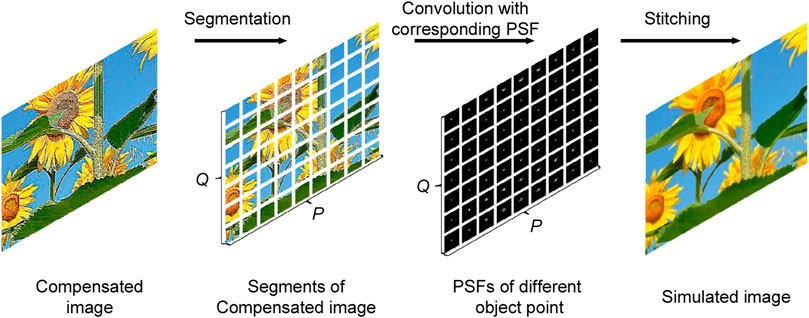
Then, we need to obtain the simulated image of the NED system, which can be obtained by the convolution of each point of the displayed image after compensation with the corresponding PSF and superimposing all convolution results. The PSF is space-variant across the object plane (FOV). However, due to the memory limitation and the computational time, here, we divide both the object plane and image plane into P×Q sub-areas, and in each sub-area, the corresponding PSF is considered to be space-invariant approximately. The imaging result IMG_u,v (1 ≤ u ≤ P, 1 ≤ v ≤ Q) of each sub-area can be obtained by the convolution of the sub-area COM_u,v (compensated image) with corresponding PSF_u,v as follows:

${\mathit{I}\mathit{M}\mathit{G}}_{u,v}={\mathit{C}\mathit{O}\mathit{M}}_{u,v}*{\mathit{P}\mathit{S}\mathit{F}}_{u,v}.(8)$

It is worth noting that information related to system aberrations is included in the PSF during the image simulation process. Therefore, for systems with significant aberrations, the P and Q values should be set as high as possible to obtain accurate simulation results. However, excessively high P and Q values will also increase the consumption of computational resources. The choice of P and Q values should strike a reasonable balance between computational resource consumption and image simulation accuracy.

Then, all image sub-areas are joined together to form the final simulated image of the compensated image. The whole image simulation process is shown in Figure 4. Since the system’s distortion can be controlled to be very small, the impact of distortion can be ignored. Furthermore, distortions do not impact image quality and can be easily corrected in practical processes.

Figure 4

Figure 4. Schematic plot of the image simulation process.

Then, the loss function should be established to optimize the freeform system and the compensation network. The goal is to obtain good display performance and a feasible freeform system with a proper structure and small volume, as well as the required system specifications. Multiple loss functions are incorporated to achieve the design goal.

The display performance of the system is decided by the NED system and compensation network. Due to the existence of the compensation network, the performance when only considering the freeform system may be worse than that of the traditional NED system. However, it should not be too bad in order to guarantee our PSF calculation method effective. In addition, the PSF should not be larger than the maximum allowable K×K grid, which is used for practical calculation in programs and further image simulation. Here, we take the maximum spot size (L_spot) among the sampled field points, which can be calculated through ray tracing as the loss function related to this imaging performance as it is related to the spread area of the PSF to some extent. Other image quality metrics (such as wavefront aberration and MTF) may also be used to construct the loss function (larger loss function corresponds to worse image quality), but their values do not correspond to the PSF size directly. For the whole framework, the simulated image at the exit pupil (image plane) obtained through the compensated network and the freeform system should be close enough to the target image. We used the structural similarity index measure (SSIM) to build the loss function to evaluate the difference between the target images and the final display results. The loss is denoted as L_img. The imaging loss L₁ can be written as follows:

$\begin{array}{l}{L}_1=w_{\text{img}}{L}_{\text{img}}+w_{\text{spot}}{L}_{\text{spot}}=w_{\text{img}}\cdot \left(1-\frac{{\displaystyle \sum _{t=1}^T}\text{SSIM}\left(\mathit{O}\mathit{B}{\mathit{J}}_t,\mathit{I}\mathit{M}{\mathit{G}}_t\right)}{T}\right)+\\ w_{\text{spot}}\cdot \max \left(\max {\left({\left(2\times {‖{\mathit{o}}_{\mu ,j}^{\left\{\text{local}\right\}}-{\mathit{o}}_{1,j}^{\left\{\text{local}\right\}}‖}_2\right)}_{1\le \mu \le N}\right)}_{1\le j\le M}\right)\end{array},(9)$

where T means T image pairs to be evaluated. o^{local} represents the local coordinates of the ray on the image plane, μ represents different pupil coordinates of N coordinates, j means different field points of M field points, and the subscript 1 represents the chief ray of the field point.

While guaranteeing good display performance, some constraints should also be added to constrain the system specifications, structure, volume, and distortion. These constraints can be added by also incorporating specific loss functions. Light obstruction must be eliminated in the off-axis reflective system. This can be done by controlling the distances from the edge of the elements to the marginal rays between different elements using real ray trace data. Violation of the minimum clearance corresponds to larger positive loss function L_obs.

$L_{\text{obs}}={\displaystyle \sum _{g=1}^D}{L}_{\text{dis},g},\text{where }{L}_{\text{dis},g}=-\min \left(0,\delta -{\delta }_{\text{target}}\right),(10)$

where D represents D locations where light obstruction may occur and δ and δ_target represent the actual distance and target distance, respectively.

Relative distortion for the field point β can be calculated through the ideal image height and actual image height obtained through real ray tracing, which are represented by h_x,ideal(β) or h_y,ideal(β) and h_x(β) or h_y(β), respectively. The loss related to distortion L_dst is the violation of the mean and maximum relative distortion in x and y directions for W sampling fields (excluding the 0° field angle) among the full FOV with respect to the given design requirements l_{mean,dst,target} and l_{max,dst,target}, respectively.

$\begin{array}{l}{L}_{\text{dst}}=\max \left(0,\text{mean}\left({\left(\left|{\gamma }_k\right|\right)}_{1\le k\le W}\right)-l_{\text{mean},\text{dst},\text{target}}\right)+w_{\max ,\text{dst}}\cdot \max \left(0,\max \left({\left(\left|{\gamma }_k\right|\right)}_{1\le k\le W}\right)-l_{\max ,\text{dst},\text{target}}\right),\\ \text{where }\gamma =\frac{h_{\mathrm{x}}\left(\beta \right)-h_{\mathrm{x},\text{ideal}}\left(\beta \right)}{h_{\mathrm{x},\text{ideal}}\left(\beta \right)}\times 100\%,\text{or\hspace{1em}}\gamma =\frac{h_{\mathrm{y}}\left(\beta \right)-h_{\mathrm{y},\text{ideal}}\left(\beta \right)}{h_{\mathrm{y},\text{ideal}}\left(\beta \right)}\times 100\%.\end{array}(11)$

For the freeform system design, it is preferable to use the central area of the freeform surface in order to reduce complexity during the optomechanical design and system assembly process, as well as to improve design convergence. Therefore, a loss L_center representing the deviation between the vertex of the freeform surface and the point where the chief ray of the central field intersects with the surface is added.

$L_{\text{center}}={\displaystyle \sum _{b=1}^B}\sqrt{{\left(o_{\mathrm{x},1}^{\left\{\text{local}\right\}}\left(b\right)\right)}^2+{\left(o_{\mathrm{y},1}^{\left\{\text{local}\right\}}\left(b\right)\right)}^2},(12)$

where B represents that the system has B surfaces in total (including the image plane), $o_{\mathrm{x},1}^{\left\{\text{local}\right\}}\left(b\right)$ means the x-coordinate of the chief ray of the central field on the surface, and $o_{\mathrm{y},1}^{\left\{\text{local}\right\}}\left(b\right)$ is by the same logic.

To control the system volume during the optimization process, a loss L_vol is added, which depicted the violation of the system size in x, y, and z directions from the target values.

$L_{\text{vol}}=\max \left(0,V_{\mathrm{x}}-V_{\mathrm{x},\mathrm{t}\arg \text{et}}\right)+\max \left(0,V_{\mathrm{y}}-V_{\mathrm{y},\mathrm{t}\arg \text{et}}\right)+\max \left(0,V_{\mathrm{z}}-V_{\mathrm{z},\mathrm{t}\arg \text{et}}\right),(13)$

where V_x, V_y, and V_z represent the actual size in x, y, and z directions, respectively. V_x,target, V_y,target, and V_z,target represent the maximum allowed size in x, y, and z directions, respectively.

In addition, the optical see-through FOV is also an essential specification for the NED system. It should be kept large by keeping the light clearance, while the system volume is reduced. As the last optical surface of the NED system is a half-transmission and half-reflection combiner, the rays of a large FOV are usually obstructed by the surfaces before the last optical surface. The see-through FOV can be calculated using the geometrical relationships between the aperture stop and the surfaces in the system or using the real ray tracing data. Here, we use a three-mirror system (same structure with the design example in Section 3) as an example. As shown in Figure 5, the see-through FOV can be calculated using the center of the aperture stop (point O), the vertex A of the last surface, and the marginal points (B and C) of mirrors. The half see-through FOV α is the smaller one of ∠AOB and ∠AOC. The loss of the see-through FOV L_OST-FOV can be written as

$L_{\text{OST}-\text{FOV}}=\max \left(0,{\alpha }_{\mathrm{t}\arg \text{et}}-\alpha \right),(14)$

where α_target represents the target of the half required see-through FOV.

Figure 5

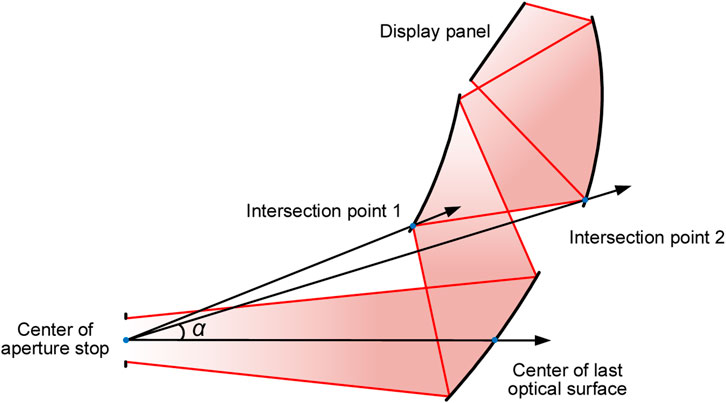
Figure 5. Schematic diagram of see-through FOV calculation. The angle α denotes the half see-through FOV, which has a unit of degree.

For a display panel, the outgoing direction perpendicular to the display panel emits the strongest intensity. To fully utilize the intensity of the display panel, a loss L_intensity is added to represent the angle deviation between the chief ray direction of the central field point and the perpendicular direction of the display panel. The center global coordinate of the display panel and first optical surface in x and y directions are denoted as o_obj = [x_obj, y_obj] and o_s1 = [x_s1,y_s1], respectively. The loss can be written as

$L_{\text{intensity}}=\sqrt{{\left({\mathit{o}}_{\text{obj}}-{\mathit{o}}_{\mathrm{s}1}\right)}^2}.(15)$

As we control the chief ray of the center field point intersecting with each surface center, Eq. 15 can be used to constrain its exit angle.

The total loss L_total of each epoch during training and optimization is the weighted sum of the above individual losses.

$L_{\text{total}}=L_1+L_2=\left(w_{\text{img}}{L}_{\text{img}}+w_{\text{spot}}{L}_{\text{spot}}\right)+\left(w_{\text{obs}}{L}_{\text{obs}}+w_{\text{dst}}{L}_{\text{dst}}+w_{\text{center}}{L}_{\text{center}}+w_{\text{vol}}{L}_{\text{vol}}+w_{\text{see}-\text{though}}{L}_{\text{see}-\text{through}}+w_{\text{intensity}}{L}_{\text{intensity}}\right).(16)$

In the forward pass, L_total can be calculated according to the compensation network and the NED system parameters. In the backward pass, the partial derivative (or gradient) of the parameters in the compensation network (weights and biases) and the parameters of the freeform NED system (surface coefficients and surface locations) can be calculated, and then the parameters can be updated in order to minimize L_total using specific optimization algorithms.

3 Design example

To show the effect of the proposed optical–digital joint optimization framework in achieving an ultra-compact NED system, a freeform three-mirror NED system design example is demonstrated. The display panel we chose is BOE VX050S0M-NH1, with a size of 10.13 mm × 7.61 mm and a resolution of 800 × 600 pixels. The pixel size of the display panel is 12.6 μm. However, this pixel size is not involved in characterizing the PSF of one field point as it is a feature of the display panel. The exit pupil FOV is 12° × 16°; meanwhile, the exit pupil diameter is 4 mm. First, we designed the freeform system using commercial optical design software, as shown in Figure 6A. The initial system structure was selected from the sample lens library of CODE V (threemrc.len). In this design, we use an XY polynomial surface, which is the simplest polynomial freeform surface type, and it matches the standard of the CNC machine. Other surface types can also be used for the joint optimization process if they are continuous and their derivatives can be calculated for the ray tracing process. During optimization, the fields were represented with the object height, and the surface type was changed to an XY polynomial freeform surface up to the fourth order, as shown in Eq. 17. The aperture stop (exit pupil) is at the end of the system, and the distance (eye relief) between the tertiary mirror and the aperture stop was controlled to be at least 34 mm. To maximize the intensity utilization of the display panel, the chief ray of the central field point of the full object plane was constrained to be perpendicular to the display panel. The relative distortion was calculated using real ray tracing data and controlled to be lower than 4%. The chief ray from the central field point was constrained to intersect at the center of each surface, including the image surface. The distances that need to be controlled to avoid light obstruction and surface interference are shown in Figure 6B with green dashed lines; each green dashed line represents a potential location for light obstruction or surface interference. In addition, to simulate the human eyes, an ideal lens with a focal length of 18 mm is added at the aperture stop (exit pupil). The PSF and the display performance are both evaluated at the image plane of the ideal lens. The error function type was set to the default transverse ray aberration type in CODE V.

$h\left(x,y\right)=\frac{c\left(x^2+y^2\right)}{1+\sqrt{1-\left(1+\kappa \right)c^2\left(x^2+y^2\right)}}+A_1{x}^2+A_2{y}^2+A_3{x}^{2}y+A_4{y}^3+A_5{x}^4+A_6{x}^2{y}^2+A_7{y}^4.(17)$

Figure 6

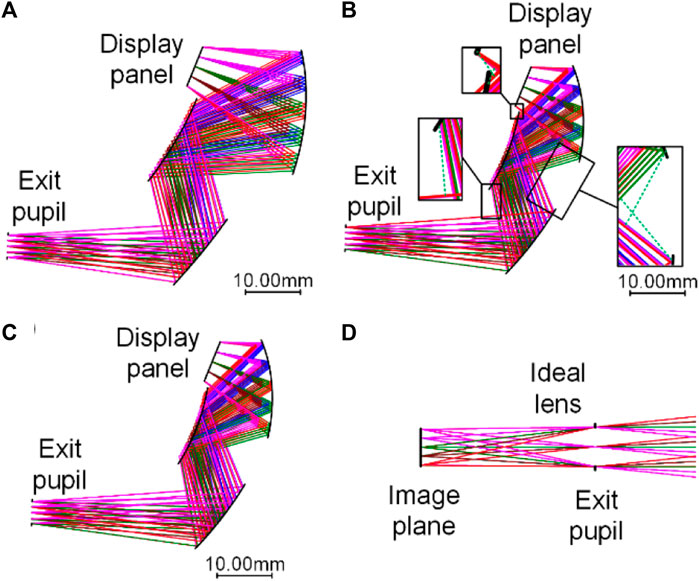
Figure 6. Layout NED freeform system. (A) System with a large volume designed using optical design software. (B) Initial system with a small volume designed using optical design software. (C) System with a small volume designed by joint optimization. For (A–C), the scale bar indicates a length of 10 mm, which can be used to evaluate the size of the systems. (D) To simulate the human eyes, an ideal lens with a focal length of 18 mm is added at the aperture stop (exit pupil). The PSF and the display performance are both evaluated at the image plane of the ideal lens.

During this stage, the goal is to minimize the aberrations. The SSIM evaluation result on the testing dataset is 0.9152. Here, in this design, the training and testing datasets are selected from DIV2K, a public dataset, and we chose 400 images and 100 images, respectively. Only the central area (800 × 600 pixels) of each image was used. Although the display performance is good, the volume of the system (16.89 mm × 47.46 mm × 24.13 mm = 19.34 mL) is large. If the volume was further reduced, aberrations will be very large. Here, we use the proposed optical–digital joint optimization framework to reduce the system volume while maintaining the high display performance. First, we reduce the system volume using optical design software directly, during which we allow for more aberrations but maintain the fundamental folding geometry of the system, control the distortion, and maintain the system specifications. The design result is shown in Figure 6B, and the volume is 7.22 mL. Because of the presence of aberrations, the system display performance is poor. The SSIM evaluation result on the testing dataset is only 0.7137 now. This system is taken as the initial system for the joint optimization process.

For the subsequent joint optimization process, all the losses were added, as shown in Eq. 16. The current value of the size in x, y, and z directions was set as the maximum allowed size, and the target see-through FOV, maximum allowed value of maximum, and mean relative distortion were also set according to the current value. The system distortion will be controlled to be small, and the impact of distortion can be ignored during image simulation. Five distances were controlled to eliminate light obstruction, as shown in Figure 6B. Thirty-five different field points across the half-object plane (zero and positive position in the x direction) were sampled and traced. In the training process, only 275 rays were uniformly sampled, while in the testing process, 2,718 rays were uniformly sampled to calculate more accurate PSF and spot sizes. The differentiable ray tracing method remains applicable for the testing. However, during the testing process, backward pass for partial derivative calculation is not required, and sampling of more rays will not cause memory issues. The ray tracing data were used to calculate the spot diameter on the image plane and the PSFs of the sampled fields. The pixel size on the image plane is 5 μm × 5 μm (close to the size of the cell on retina), and a 51 × 51-pixel grid (the center locates at the image point of the chief ray) was used to characterize the PSF of one field point. For this initial small-volume system, the simulated PSFs across the full object plane are shown in Figure 7A. The simulated images were obtained using the PSFs of these 35 field points and other 186 field points (28 fields in −x directions can be obtained using the results of the PSFs of the fields in the +x direction directly due to symmetry, and other 158 fields are calculated by interpolating). The number of the field points used to obtain the simulated images is determined based on the actual situation. Generally speaking, the more field points used, the more accurate the simulated image will be. However, there should be a balance between the sampled field point number and simulation accuracy because of limited memory and calculation speed. At least the central field point and the field points in marginal areas of different directions should be sampled. Joint optimization was performed on a computer using Intel i9-12900K CPU and NVIDIA RTX 3090Ti 24 GB Memory GPU. AdamW was chosen as the optimizer. Compared to AdamW, the inclusion of weight decay can achieve better generalization performance and improved convergence stability. It is crucial to elucidate that not all parameters share the same learning rates. This distinction arises because individual parameters exert disparate effects on the system’s loss function. Specifically, in this design, parameters such as the conic constant, surface vertex position, and surface tilt relative to the x-axis were assigned a learning rate of 1e-2, and the learning rate of the compensation network was set as 1e-4, while the learning rate for the surface curvature was 1e-5. For higher-order surface terms, their learning rates were calibrated based on the magnitude of their initial values, subsequently multiplied by 1e-2. If the learning rate is too large, the training results will not converge, while a too small learning rate will cause the convergence process to be extremely slow. The current learning rate setting is a balance between these two extremes. After completing 100 epochs, an exponential decay was applied to the learning rates. The decay factor for this learning rate was established at 0.9. After completing 160 epochs, the NED system was fixed, and we fine-tuned the image compensation network. We sampled 2,718 rays for each sampled field point during the fine-tuning and testing stages to obtain more accurate PSF. Only 40 epochs were fine-tuned using AdamW, and the learning rate was set to 1e-5 without decay.

Figure 7

Figure 7. Simulated PSFs across the full FOV of the (A) initial system and (B) system after joint optimization. Note that these PSFs are the result of the geometric optical system, and image compensation is not considered.

A total of 160 epochs were joint optimized and 40 epochs were fine-tuned, taking approximately 200 h. In addition to the time consumed by system optimization and network training, ray sampling also consumes a significant amount of time. The system aperture stop (exit pupil) is the eye pupil, which is placed at the end of the system. Therefore, during each ray sampling process, it is necessary to completely fill the aperture stop with light rays. This requires iteratively determining the chief ray and marginal rays in different directions for each sampled field and, based on these rays, defining the field sampling range. All rays within this range are then traced to the aperture stop, where rays outside the aperture are out-selected (as shown in Figure 2). This process results in a significant increase in optimization time. The final system layout is shown in Figure 6C. Table 1 presents the optimal results, delineating the volume and the average SSIM of the testing dataset across three systems, namely, the large volume system, the initial small volume system, and the system after joint optimization with image compensation considerations; the peak signal-to-noise ratio (PSNR) value of these systems is also given for reference. It is evident from Table 1 that the SSIM value of the system after joint optimization is close to the result of a large volume system, significantly surpassing the initial small volume system. The SSIM and PSNR are two main image quality metrics but have different calculation methods and features. The PSNR is a widely used metric for evaluating the consistency of two images. It measures the ratio between the maximum possible pixel value squared and the mean squared error (MSE) between the two images. Higher PSNR values indicate higher consistency. The SSIM is more consistent with the human visual system. In addition, in this work, the SSIM is used as the standard for image evaluation and used in the loss function construction during training. Therefore, only the SSIM is directly controlled during design, and the training result may not demonstrate a significant improvement in the PSNR compared with the initial small-volume system before joint optimization. The volume of the system after joint optimization is 12.74 mm × 38.80 mm × 14.48 mm = 7.16 mL, which is 62.98% smaller than the large-volume system. The simulated PSFs across the full object plane of the system after joint optimization are shown in Figure 7B; it can be seen that the PSF of different sampled field points becomes similar. The maximum relative distortion is approximately 2.00%, and the average relative distortion is approximately 0.72%. Another experiment was conducted to substantiate the efficacy of the joint optimization. An image compensation network was trained for the initial small-volume system, while parameters of the NED system are not updated. After training, the average SSIM of the testing dataset is 0.8708, demonstrating the effect of the joint optimization.

Table 1

Table 1. Quantitative evaluation of the averaged SSIM and PSNR on the testing dataset and the system volume for the NED system design.

The exit pupil size of the NED system is 4 mm, and the focal length of the ideal lens is 18 mm. For a wavelength of 587.56 nm, the Airy disk size of the system on the final image plane is approximately 7 μm. The minimum 100% spot size across the full FOV for the initial system with a small volume designed using optical design software, and the system with a small volume designed by joint optimization is 28.455 μm and 29.257 μm, respectively. In both systems, the spot size is significantly larger than the Airy disk size, indicating that the influence of diffraction effects can be neglected.

In conclusion, the above design and analyses validate that the optical–digital joint optimization framework we propose can effectively reduce the system volume while maintaining good display performance of the system. Figure 8 shows examples of the simulated images before and after the optimization process, as well as the compensated images and the target images, which demonstrates the effect of the design framework.

Figure 8

Figure 8. (A) Simulated images of the initial NED freeform system; (B) compensated images obtained through the compensation network; (C) imaging simulation results with compensated images of a small-volume NED freeform system after joint optimization; (D) simulated images of a large-volume NED freeform system; (E) target images. See detailed subsections below for full-size images. SSIM value calculated relative to the target image.

4 Conclusion

In this paper, we propose an optical–digital joint optimization framework for ultra-compact freeform NED systems. By jointly designing the image compensation network and the freeform optical system, the advantages of both freeform optics and a deep learning neural network can be deeply integrated in order to obtain good display performance with a significantly reduced system volume, which cannot be achieved using traditional design approaches. This opens a new pathway for developing next-generation AR glasses with much increased wearing comfort and portability. This powerful design framework can be directly applied to the design of systems with fewer optical components or more advanced system specifications than in traditional design. The proposed framework can also be extended to the design of systems consisting of other surface types and phase elements, such as holographic optical elements and meta-surfaces. In addition, a typical feature of the proposed design method or system framework is that image compensation is at the beginning of the whole system, and no recovery is done on the final image. Therefore, besides designing NED systems, this method can also be used in designing projector systems. In future work, we will focus on the development of the prototypes of freeform NED systems and projector systems.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

HX: writing–original draft. TY: writing–review and editing. DC: writing–review and editing. YW: writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study was supported by National Key Research and Development Program of China (2022YFB3603400); National Natural Science Foundation of China (62275019 and U21A20140); and Xiaomi Young Scholars Program.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Meng Q, Wang H, Liang W, Yan Z, Wang B. Design of off-axis three-mirror systems with ultrawide field of view based on an expansion process of surface freeform and field of view. Appl Opt (2019) 58:609–15. doi:10.1364/AO.58.000609

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Nie Y, Shafer DR, Ottevaere H, Thienpont H, Duerr F. Automated freeform imaging system design with generalized ray tracing and simultaneous multi-surface analytic calculation. Opt Express (2021) 29:17227–45. doi:10.1364/OE.426207

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Bauer A, Schiesser EM, Rolland JP. Starting geometry creation and design method for freeform optics. Nat Commun (2018) 9:1756–67. doi:10.1038/s41467-018-04186-9

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Chen L, Gao Z, Ye J, Cao X, Xu N, Yuan Q. Construction method through multiple off-axis parabolic surfaces expansion and mixing to design an easy-aligned freeform spectrometer. Opt Express (2019) 27:25994–6013. doi:10.1364/OE.27.025994

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Zhang B, Tan Y, Jin G, Zhu J. Imaging spectrometer with single component of freeform concave grating. Opt Lett (2021) 46:3412–5. doi:10.1364/OL.431975

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Cheng D, Duan J, Chen H, Wang H, Li D, Wang Q, et al. Freeform OST-HMD system with large exit pupil diameter and vision correction capability. Photon Res (2022) 10:21–32. doi:10.1364/PRJ.440018

CrossRef Full Text | Google Scholar

7. Zhong Y, Tang Z, Gross H. Correction of 2D-telecentric scan systems with freeform surfaces. Opt Express (2020) 28:3041–56. doi:10.1364/OE.381290

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Yang T, Xu H, Cheng D, Wang Y. Design of compact off-axis freeform imaging systems based on optical-digital joint optimization. Opt Express (2023) 31:19491–509. doi:10.1364/OE.492199

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Sun Q, Wang C, Fu Q, Dun X, Heidrich W. End-to-end complex lens design with differentiate ray tracing. ACM Trans Graph (2021) 40:1–13. doi:10.1145/3450626.3459674

CrossRef Full Text | Google Scholar

10. Wang C, Chen N, Heidrich W. dO: a differentiable engine for deep lens design of computational imaging systems. IEEE Trans Comput Imaging (2022) 8:905–16. doi:10.1109/TCI.2022.3212837

CrossRef Full Text | Google Scholar

11. Li Y, Fu Q, Heidrich W. Extended depth-of-field projector using learned diffractive optics. In: 2023 IEEE conference virtual reality and 3D user interfaces (VR). IEEE (2023). p. 449–59. doi:10.1109/VR55154.2023.00060

CrossRef Full Text | Google Scholar

12. Sun L, Cui Q. Optical-digital integrated design method for near-eye display imaging system. IEEE Access (2022) 10:50314–22. doi:10.1109/ACCESS.2022.3173637

CrossRef Full Text | Google Scholar

13. Li Z, Hou Q, Wang Z, Tan F, Liu J, Zhang W. End-to-end learned single lens design using fast differentiable ray tracing. Opt Lett (2021) 46:5453–6. doi:10.1364/OL.442870

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Zhang Z, Liu Q, Wang Y. Road extraction by deep residual U-net. IEEE Geosci Remote Sensing Lett (2018) 15:749–53. doi:10.1109/LGRS.2018.2802944

CrossRef Full Text | Google Scholar

15. Ronneberger O, Fischer P, Brox T. U-net: convolutional networks for biomedical image segmentation. In: N Navab, J Hornegger, WM Wells, and AF Frangi, editors. Medical image Computing and computer-assisted intervention–MICCAI 2015 lecture notes in computer science. Cham: Springer International Publishing (2015). p. 234–41. doi:10.1007/978-3-319-24574-4_28

CrossRef Full Text | Google Scholar

16. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: 2016 IEEE conference on computer vision and pattern recognition (CVPR). Las Vegas, NV, USA: IEEE (2016). p. 770–8. doi:10.1109/CVPR.2016.90

CrossRef Full Text | Google Scholar