A kinetic study of fusion burn waves in compressed deuterium–tritium and proton–boron plasmas

We present particle-in-cell simulations with Monte Carlo collisions of fusion burn waves in compressed deuterium–tritium and proton–boron plasmas. We study the energy balance in the one-dimensional expansion of a hot-spot by simulating Coulomb collisions, fusion reactions, and bremsstrahlung emission with a Monte Carlo model and inverse bremsstrahlung absorption using a new PIC model. This allows us to self-consistently capture the alpha particle heating and radiative losses in the expanding hot-spot and surrounding cold fuel. After verifying our model in a code-to-code comparison with both kinetic and fluid codes for the case of a deuterium–tritium hot-spot, we simulate the expansion of a proton–boron hot-spot initialized at 200 keV and 1,000 g/${\text{cm}}^3$. Our model predicts that energy radiated by the hot-spot is recaptured by the surrounding high-density opaque fuel reducing the expansion work done by the propagating burn wave. As a result, we find the net fusion energy produced over the course of $20$∼ps is twice the initial hot-spot energy independent of whether radiation physics is included.

1 Introduction

Recent experiments at the National Ignition Facility (NIF) demonstrated fusion ignition of an inertial confinement fusion target [1, 2]. The experiment used deuterium–tritium (D–T) fuel because it has the largest fusion cross section at the lowest center-of-mass energy, and therefore the lowest density and temperature requirements to reach ignition conditions. There are, however, various challenges that come with using DT fuel: the radioactive isotope tritium is not naturally abundant, is expensive to breed, and decays relatively quickly (half-life of $\sim$12 years). The D–T fusion reaction

$\text{D}+\text{T}\to \text{n}+\alpha +17.589\text{\hspace{0.17em}MeV}(1)$

produces a helium-4 ion (⁴He or $\alpha$) and a high-energy neutron. Unlike the charged $\alpha$ that is likely to thermalize with the surrounding plasma, the fusion-produced neutron can escape the target and damage reactor material. Potential reactors that use DT as the primary fuel will require significant radiation shielding to protect surrounding equipment and operators, as well as thermal conversion systems to extract energy from the neutrons.

Alternative fusion fuels exist; however, their reactions have smaller cross sections and need higher center-of-mass energies and so require higher densities and temperatures to reach ignition conditions. Figure 1 shows the fusion cross sections [3–5] as a function of the center-of-mass energy for D–T, deuterium–deuterium (D–D)

$\text{D}+\text{D}\to \left\{\begin{array}{c}\text{p}+\text{T}+4.03\text{\hspace{0.17em}MeV},\hfill \\ \text{n}{+}^3\mathrm{H}\mathrm{e}+3.27\text{\hspace{0.17em}MeV},\hfill \end{array}\right.(2)$

deuterium–helium-3 (D–³He)

$\text{D}{+}^3\mathrm{H}\mathrm{e}\to \text{p}+\alpha +18.35\text{\hspace{0.17em}MeV},(3)$

and proton–boron-11 (${\text{p–}}^{11}\mathrm{B}$),

$\text{p}{+}^{11}\mathrm{B}\to 3\alpha +8.68\text{\hspace{0.17em}MeV}.(4)$

Figure 1

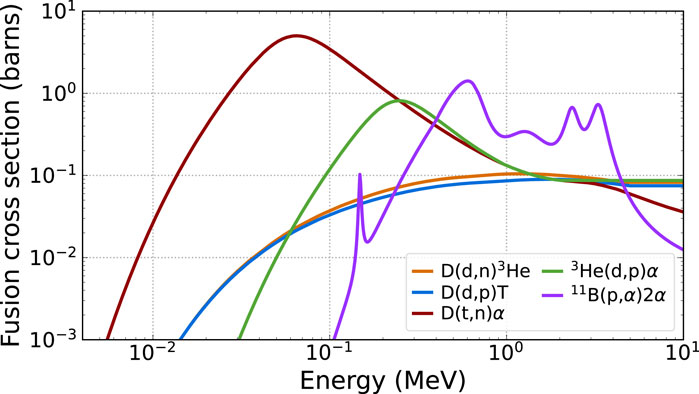
Figure 1. Fusion cross sections as a function of the center-of-mass energy from Bosch and Hale [3], the International Atomic Energy Agency Evaluated Nuclear Data File [4], and Tentori and Belloni [5].

Of these reactions, ${\text{p–}}^{11}\mathrm{B}$ is promising because the reactants are naturally abundant and the reaction products are all charged particles that can be directly captured by the surrounding plasma or directly converted to electricity, thus significantly reducing shielding requirements and improving plasma coupling. The peak cross section, however, occurs at a temperature that is an order-of-magnitude larger than the peak cross section for DT, so achieving a thermonuclear ${\text{p–}}^{11}\mathrm{B}$ burning plasma requires significantly higher temperatures (in excess of 100 keV, whereas the temperatures achieved in the recent NIF experiments were $\sim 10$ keV [2]). Additionally, the higher temperatures and effective charge of the plasma (due to boron’s higher atomic number, $Z=5$) significantly increases bremsstrahlung radiation in thermonuclear ${\text{p–}}^{11}\mathrm{B}$ plasmas. It is important to understand the balance of radiation emission and absorption to determine whether and how much net fusion energy gain is possible.

In order to improve the feasibility of ${\text{p–}}^{11}\mathrm{B}$ fusion, nonequilibrium conditions are being considered [6–10]. Mehlhorn et al. [11] discusses the need to increase the reactivity of ${\text{p–}}^{11}\mathrm{B}$ in order to achieve target gain in an inertial fusion power plant and the possibility of initiating nonequilibrium thermonuclear burn using ultrashort pulse lasers (USPL). For example, in fast ignition [12–14] a target is spherically compressed to many times solid density; then, a USPL strikes the target or a nearby foil, generating a source of high-energy particles that in turn heat the compressed fuel. This produces the high relative energies and temperatures needed to achieve ignition. Another approach proposes irradiating a solid target with high-powered lasers to produce MeV protons that are injected into a background ${\text{p–}}^{11}\mathrm{B}$ plasma confined within a magnetic bottle [8, 15]. It is theorized that sustained chain reactions and long confinement times will lead to the production of net energy gain. There are many proposed mechanisms for initiating or enhancing a fusion burn [16] that encourage further development of numerical models to help investigate.

We present numerical simulations of burning ${\text{p–}}^{11}\mathrm{B}$ plasma using the code TRIFORCE, a multiphysics code being developed to help investigate novel fusion reactor concepts [17, 18]. Part of the TRIFORCE simulation framework is a particle-in-cell code with Monte Carlo collisions (PIC-MCC) [19, 20] that models the kinetic physics present in some reactor concepts, such as the evolution of nonthermal distributions, beam–target fusion reactions, and complex particle orbits (particularly in the vicinity of magnetic nulls). In this paper, we use the PIC-MCC model to simulate the 1D planar propagation of high-density fusing plasmas into cold fuel. First, we verify our results against the extensively benchmarked PIC-MCC code LSP [21, 22] and radiation-hydrodynamics code HYDRA [23–25] for the case of a DT hot spot; then, we consider the expansion of a ${\text{p–}}^{11}\mathrm{B}$ fusion burn wave. Coulomb collisions, fusion reactions, and bremsstrahlung emission are simulated using the binary Monte Carlo collision method [20, 26–30], and a new PIC model is introduced to simulate inverse bremsstrahlung absorption (IBA). We recently verified the kinetic model in TRIFORCE for Coulomb collisions and fusion reactions [18]. Here, we discuss the implementation and verification of a bremsstrahlung model based on the work of Martinez et al. [28] and IBA model based on the expected power deposited by the radiation into the plasma [31]. Since radiation increases rapidly with density, temperature and atomic number, it is particularly important to include when considering high-density, high-temperature boron plasmas. Future improvements to the accuracy of the kinetic model include introducing Compton scattering [32] and degeneracy effects [33, 34] to the binary scattering framework.

The paper is organized as follows: in Section 2, we describe the numerical methods and present verification tests of the bremsstrahlung emission and IBA models; in Section 3, we present simulations of fusion burn waves in compressed DT and ${\text{p–}}^{11}\mathrm{B}$ plasmas; and in Section 4, we discuss our numerical results and the limitations of the current model, and share plans for future work.

2 Methods

The PIC-MCC method numerically integrates the Boltzmann equation

$\frac{\partial f_{\alpha }}{\partial t}+v\cdot \mathrm{\nabla }{f}_{\alpha }+\frac{F}{m_{\alpha }}\cdot {\mathrm{\nabla }}_v{f}_{\alpha }={\displaystyle \sum _{\beta }}{\left[f_{\alpha },f_{\beta }\right]}_{\text{coll}},(5)$

where $f_{\alpha }(x,v,t)$ is the distribution function, $t$ is time, $x$ is space, $v$ is velocity, $m_{\alpha }$ is the mass of the $\alpha$-particle species, $F$ represents the forces acting on the particles, ${\mathrm{\nabla }}_v$ is the gradient operator in velocity space, and the right-hand-side of the equation is the collision operator. The Boltzmann equation describes the evolution of the distribution function in phase space and how each particle responds to external forces (i.e., collective electromagnetic forces or gravity) and interactions with other particles (i.e., through elastic and inelastic collisions). It can be numerically integrated by first discretizing the smooth distribution function onto a discrete set of $N_{\alpha }$ simulation particles (macroparticles), each with weight $w_i$, position $x_i$ and velocity $v_i$, such that

$f_{\alpha }\left(x,v,t\right)\approx {\displaystyle \sum _{i=1}^{N_{\alpha }}}{w}_i\delta \left[x-x_i\left(t\right)\right]\delta \left[v-v_i\left(t\right)\right],(6)$

and then successively integrating particle information in time in response to the sum of the acting forces.

In this study, we consider a simplified model where the only forces that particles experience are due to binary particle interactions. This approximation is appropriate for the high-density, highly-collisional systems we consider in this report, but can lead to erroneous charge separation that will be addressed in future studies by considering electromagnetic effects. We use the binary Monte Carlo collision model [20, 26–30] to simulate Coulomb collisions, fusion reactions, and bremsstrahlung radiation. The method works by randomly pairing particles within a computational cell of the simulation domain and sampling the probability of the collision or reaction to occur. This approach allows evaluation of relativistic binary interactions between arbitrarily weighted particles. Reference [18] describes and verifies the method for several scattering channels implemented in TRIFORCE using the binary collision method, including Coulomb collisions and fusion reactions. In Sections 2.1, 2.2, we describe how the bremsstrahlung emission is implemented within the binary scattering framework and we introduce a new model for simulating radiation absorption.

2.1 Model description

2.1.1 Bremsstrahlung emission

Bremsstrahlung emission was incorporated into TRIFORCE using a method similar to the binary collision algorithm presented by Martinez et al. [28]. We implement the same kinematics and cross sections as Martinez et al., but handle arbitrary particle weighting in a different manner: Martinez et al. randomly pairs particles within a computational cell and accounts for arbitrary numerical weights when computing the reaction probability by following the methods of Nanbu and Yonemura [26] and Pérez et al. [27], while our implementation follows the corrected binary method developed by Higginson et al. [30].

The probability $P$ for bremsstrahlung emission to occur between a random pair of electron and ion macroparticles in a time step $\mathrm{\Delta }t$ is computed and sampled with a uniform random number $U\in [0;1]$. Because emission cross sections are reported in the ion rest frame, the probability that an electron–ion collision leads to the emission of a photon is computed in the ion rest frame (denoted with primed quantities):

$P=n_{\text{eff}}{\sigma }_{\text{B}}{v}_{\text{rel}}\mathrm{\Delta }t=\frac{n_{\text{eff}}{\sigma }^{\prime }{v}_{\text{e}}^{\prime }{\gamma }_{\text{e}}^{\prime }\mathrm{\Delta }t}{{\gamma }_{\text{e}}{\gamma }_{\text{i}}}(7)$

where ${\sigma }_{\text{B}}$ is the bremsstrahlung cross section and $v_{\text{rel}}=|{\mathit{v}}_{\text{e}}-{\mathit{v}}_{\text{i}}|$ is the relative electron–ion velocity. The Lorentz transformation of the electron into the ion rest frame is

${\mathit{v}}_{\text{e}}^{\prime }={\mathit{v}}_{\text{e}}+\left[\frac{{\gamma }_{\text{i}}-1}{{\beta }_{\text{i}}^2}\left({\mathit{\beta }}_{\text{e}}\cdot {\mathit{\beta }}_{\text{i}}\right)-{\gamma }_{\text{i}}\right]c{\mathit{\beta }}_{\text{e}},(8)$

${\gamma }_{\text{e}}^{\prime }={\gamma }_{\text{e}}{\gamma }_{\text{i}}\left(1-{\mathit{\beta }}_{\text{e}}\cdot {\mathit{\beta }}_{\text{i}}\right),(9)$

where ${\gamma }_{\text{i}}$ and ${\gamma }_{\text{e}}$ are the ion and electron Lorentz factors, ${\mathit{\beta }}_{\text{i}}={\mathit{v}}_{\text{i}}/c$ and ${\mathit{\beta }}_{\text{e}}={\mathit{v}}_{\text{e}}/c$ are the normalized ion and electron velocities, and $c$ is the speed of light. The pairwise effective number density is

$n_{\text{eff}}=N_{\text{ei}}{w}_{\text{max}}/V,(10)$

where the number of possible partners $N_{\text{ei}}$ is the maximum of the number of electrons $N_{\text{e}}$ and ions $N_{\text{i}}$ in the cell, $w_{\text{max}}$ is the maximum of the electron and ion weights $w_{\text{e}}$ and $w_{\text{i}}$ (accounting for particle duplications), and $V$ is the volume of the cell. Additional details on duplicating and pairing macroparticles are found in Higginson et al. [30]. To improve particle statistics, we include an additional tuning parameter $M_{\text{p}}$ that allows the user to artificially increase the probability that a photon is created, and correspondingly, reduces the weight of the emitted photon to maintain the physically-correct reaction rate.

A reaction occurs when $U<P$ and results in the reduction of the electron’s energy and the emission of a photon of normalized energy $k$ = $\hslash \omega /m_{\text{e}}{c}^2$ with weight $w_{\gamma }=\min (w_{\text{e}},w_{\text{i}})/M_{\text{P}}$. The photon macroparticle is created with the same location and direction of the electron, with energy $k^{\prime }$ sampled from the numerically inverted cumulative differential cross section $\text{d}{\sigma }_{\text{B}}^{\prime }/\text{d}{k}^{\prime }$. The electron energy is reduced by the photon energy, i.e., ${\gamma }_{\text{e}}^{\prime \prime }={\gamma }_{\text{e}}^{\prime }-k^{\prime }$, and then an inverse Lorentz transformation is computed to transfer the electron and photon into the simulation frame.

Bremsstrahlung differential cross sections as functions of the emitted photon energy are either loaded in from Seltzer and Berger [35] tables (collected from the Geant4 database [36–38]) or computed using the model introduced by Martinez et al. [28]. Seltzer–Berger differential cross sections are shown in Figure 2 for atomic numbers $Z=1$, 2, and 5. They are derived from a combination of computational and theoretical models assuming cold neutral ions. The analytic bremsstrahlung cross sections derived by Martinez et al. [28] consider screening effects in arbitrarily ionized plasmas by combining Thomas–Fermi and Debye (TFD) screening potentials and assume the plasma is charge neutral and in thermal equilibrium. Figure 3 compares differential cross sections for the two models for boron showing that the longer-range shielding at higher temperatures leads to higher cross sections at lower photon energies in the TFD model. At present, in our simulation framework we update the TFD cross sections on a cell-by-cell basis since the Debye length of the cell varies with the evolving plasma; methods to avoid frequent recalculations are under investigation.

Figure 2

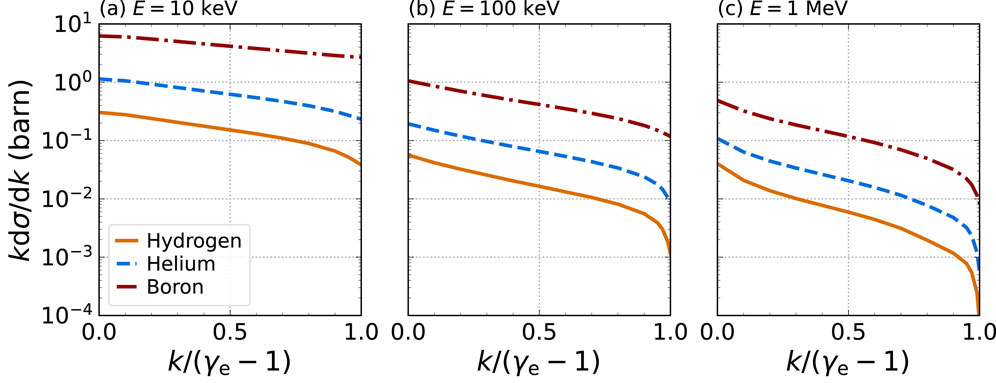
Figure 2. Bremsstrahlung differential cross sections as a function of $k/({\gamma }_{\text{e}}-1)$, the emitted photon energy normalized to the electron energy, for atomic numbers $Z=1$, 2, and 5 are shown for electron–nucleus interactions with energies equal to (A) 10 keV, (B) 100 keV, and (C) 1 MeV. Cross-section tables based on Seltzer and Berger data [35] were collected from the Geant4 database [36–38].

Figure 3

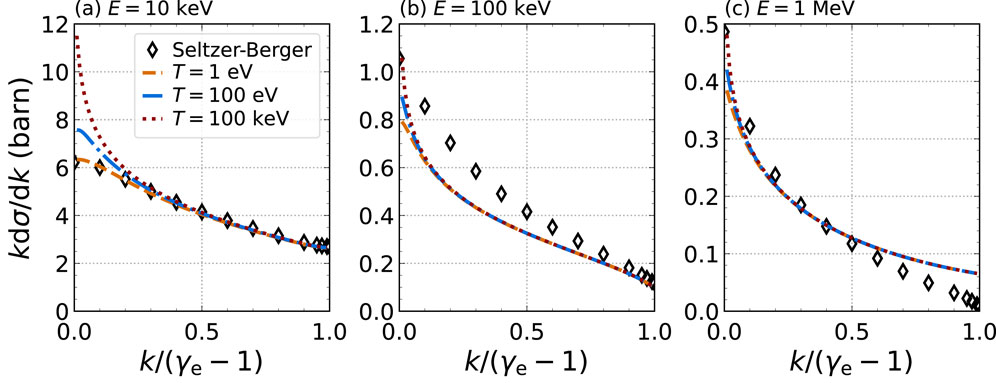
Figure 3. Bremsstrahlung differential cross sections of Seltzer and Berger [35] compared with analytic expressions from Martinez et al. including screening effects from bound electrons, free electrons, and ions (curves) for electron–ion interactions with energies (A) 10 keV, (B) 100 keV, and (C) 1 MeV. The temperature correction in Martinez’s Thomas–Fermi–Debye model results in an increase in the cross section at low photon energies, shown for plasma temperatures equal to 1 eV (orange curve), 100 eV (blue curve), and 100 keV.

2.1.2 Inverse bremsstrahlung absorption

We introduce a new PIC model for simulating IBA, the process of an electron absorbing radiation as it scatters in the Coulomb field of an ion [39, 40]. Previous PIC and Fokker-Planck studies of collisional absorption of radiation typically take wave-based approaches to study this phenomena [41–49], i.e., oscillations in the electromagnetic fields directly accelerate electrons. Since our bremsstrahlung emission model generates radiation in the form of photon macroparticles, we take a more kinetic approach for simulating radiation absorption. While our model allows us to simulate the energy deposition of photon macroparticles in the plasma, by treating photons as classical particles the model does not retain the collective behavior of the wave-based approach, and therefore, it is incapable of simulating phase-dependent phenomena [50].

Our model is based on the power deposited in a plasma by a laser, a method originally used for ray-based radiation-hydrodynamics simulations [31]. Consider a laser with wavelength $\lambda$ and intensity $I$ that produces an electric field of strength

$|E_{\text{laser}}|=\sqrt{\frac{2hc{n}_{\gamma }}{{ϵ}_0\lambda }}.(11)$

where the photon number density is related to the laser properties by $n_{\gamma }=I\lambda /h{c}^2$. The power the laser deposits in a computational cell of volume $V$ is

$P_{\text{laser}}={ϵ}_0|E_{\text{laser}}{|}^2\frac{n_{\text{e}}}{n_{\text{c}}}{\nu }_{\text{ei}}V(12)$

where $n_{\text{e}}$ is the electron density, and $n_{\text{c}}={ϵ}_0{m}_{\text{e}}{\omega }^2/q_{\text{e}}^2$ is the critical density (for laser frequency $\omega =2\pi c/\lambda$). The electron–ion collision frequency is [51]

${\nu }_{\text{ei}}=\frac{2^{1/2}{n}_{\text{i}}{q}_{\text{e}}^2{q}_{\text{i}}^2\ln \mathrm{\Lambda }}{12{\pi }^{3/2}{ϵ}_0^2{m}_{\text{e}}^{1/2}{T}_{\text{e}}^{3/2}}(13)$

where $n_{\text{i}}$ is the ion number density, $q_{\text{e}}$ and $q_{\text{i}}$ are the electron and ion charges, $\ln \mathrm{\Lambda }$ is the Coulomb logarithm, and $T_{\text{e}}$ is the electron temperature.

In the particle-based IBA method, we remove the deposited energy from each of the photon macroparticles in a cell, and then distribute it to the kinetic energy of the each of the electron macroparticles in the cell. The energy lost by a single photon in a simulation time step due to Coulomb scattering with $N_{\text{ion}}$ ion plasma species is $P_{\gamma }\mathrm{\Delta }t$ where the deposited power is

$P_{\gamma }={\displaystyle \sum _j^{N_{\text{ion}}}}\left({ϵ}_0|E_{\gamma }{|}^2\frac{n_{\text{e}}}{n_{\text{c}}}{\nu }_{\text{e}j}V\right)(14)$

and the strength of the photon’s electric field is

$|E_{\gamma }|=\sqrt{\frac{2hc}{{ϵ}_0\lambda V}}.(15)$

Finally, the total energy removed from $N_{\gamma }$ photons with numerical weights $w_{\gamma }$,

$E_{\text{IBA}}={\displaystyle \sum _k^{N_{\gamma }}}{w}_{\gamma }^k{P}_{\gamma }^k\mathrm{\Delta }t,(16)$

is evenly distributed amongst the electrons in the cell. The electron Lorentz factors ${\gamma }_{\text{e}}$ are increased by

$\delta {\gamma }_{\text{e}}=\frac{E_{\text{IBA}}}{n_{\text{e}}V{m}_{\text{e}}{c}^2}(17)$

and their momenta are increased accordingly,

$p_{\text{e}}^{\prime }=p_{\text{e}}\sqrt{\frac{{\gamma }_{\text{e}}+\delta {\gamma }_{\text{e}}-1}{{\gamma }_{\text{e}}-1}}.(18)$

2.2 Model verification

We verify the bremsstrahlung emission model within the binary collision framework and IBA PIC model by simulating three test cases: the first produces bremsstrahlung emission due to a monoenergetic electron beam incident on cold solid boron; the second is a code-to-code comparison with HYDRA of laser heating of a hydrogen plasma; and the third simulates photon emission and absorption by thermal electrons in a fully ionized thermonuclear ${\text{p–}}^{11}\mathrm{B}$ plasma.

In Figure 4, we show the photon count and spectra produced from solid boron interacting with a 1-MeV electron beam with a 10th of the solid’s ion density. The simulation consists of a single cubic cell with sides of length 1 $\mu$m, a time step of 1 fs, $N_{\text{e}}=1\times 10^3$, and $N_{\text{i}}=2\times 10^3$, $1\times 10^4$, and $2\times 10^4$ ($w_{\text{i}}=5w_{\text{e}}$, $w_{\text{i}}=w_{\text{e}}$, and $5w_{\text{i}}=w_{\text{e}}$, respectively). The simulation results are in close agreement with the expected evolution of the photon count

$N_{\gamma }=n_{\text{e}}{n}_{\text{i}}{v}_{\text{e}}l{\sigma }_{\text{B}}t,(19)$

and photon energy spectra

$\frac{\text{d}{N}_{\gamma }}{\text{d}k}=n_{\text{e}}{n}_{\text{i}}{v}_{\text{e}}l\frac{\text{d}{\sigma }_{\text{B}}}{\text{d}k}t,(20)$

(shown at 40 fs) for the three cases of particle weighting. In Figure 5, we consider the same simulation except the solid-density cold boron is replaced with fully ionized boron at 1,000 g/${\mathrm{c}\mathrm{m}}^3$ and 200 keV. Bremsstrahlung emission cross sections computed using only the Thomas–Fermi contribution to the Coulomb potential are shown in blue, and cross sections computed using the reduced potential combining Thomas–Fermi and Debye screening are shown in red. Including the temperature correction increases the total integrated radiated energy by approximately $4\%$.

Figure 4

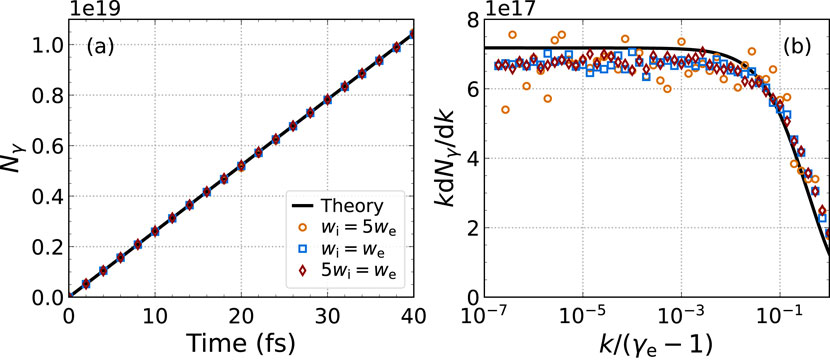
Figure 4. Bremsstrahlung emission from a 1-MeV electron beam incident on solid-density boron. The simulation results (markers) match the theoretical predictions (black curve) for the (A) total photon count and (B) normalized photon energy spectra independent of the ratio of the weights of the electron and ion macroparticles.

Figure 5

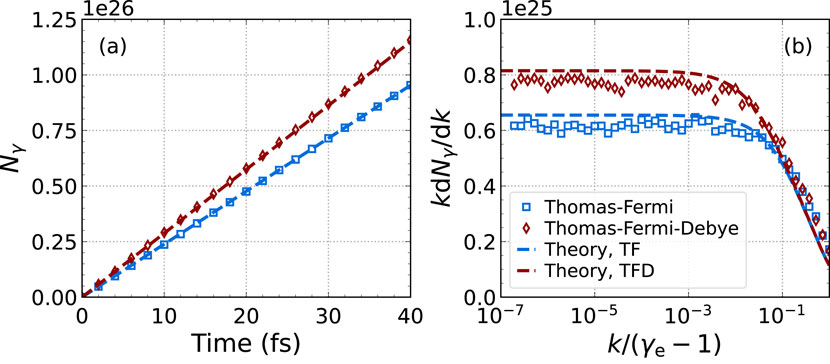
Figure 5. Bremsstrahlung emission from 1-MeV electrons in a charge-neutral fully ionized boron plasma at 200 keV and 1,000 g/${\mathrm{c}\mathrm{m}}^3$. Plotted are the simulated (markers) and expected (curves) (A) photon count and (B) normalized photon energy spectra for the combined Thomas–Fermi–Debye Coulomb potential model (red) and single Thomas–Fermi potential model (blue).

Next, we simulate laser heating of a hydrogen plasma. The charge neutral plasma starts at room temperature, has a density of $1.195\times 10^{21}$ ${\mathrm{c}\mathrm{m}}^{-3}$, and is simulated with $N_{\text{e}}=N_{\text{i}}=10^4$ particles in a single computational cell of size 1 mm $\times 1$ mm $\times 8.727$ $\mu$m; the volume was chosen to match the simulated HYDRA volume used for comparison. The laser has an intensity of $6.37\times 10^{12}$ W/${\mathrm{c}\mathrm{m}}^2$ and a wavelength of 526.5 nm. It is simulated for 1 ns by injecting photon macroparticles into the domain each time step of $\mathrm{\Delta }t=1$ fs. The $N_{\gamma }$ photons injected each step are initialized with energy $E_{\gamma }=hc/\lambda =3.27$ eV, momentum $p_{\gamma }=h/\lambda$, and numerical weight

$w_{\gamma }=\frac{n_{\gamma }V}{N_{\gamma }}\frac{c\mathrm{\Delta }t}{\mathrm{\Delta }x},(21)$

where $\mathrm{\Delta }x$ is the cell-width in the direction of the laser. Because the bremsstrahlung emission cross section is low at these conditions, we use a production multiplier of $M_{\text{p}}=100$ so photons are created by both bremsstrahlung and injection. This ensures both radiation models are tested in the simulation. Figure 6 shows the electron and hydrogen temperature simulated with TRIFORCE in blue and red, respectively. The growth in electron temperature leads the growth in the ion temperature because the radiation is absorbed directly into electrons. After the laser is turned off at 1 ns, the electrons and ions quickly reach thermal equilibrium since the relaxation time is short compared to simulation time (${\nu }_{\text{ei}}^{-1}\approx 10$ fs). A similar simulation was performed with the radiation-hydrodynamics code HYDRA for which electron temperature is shown in black and ion temperature in shown in orange. We find the two codes maintain heating rates within 5% of each other—the final equilibrium temperature is 110.5 eV for TRIFORCE and 105.5 eV for HYDRA.

Figure 6

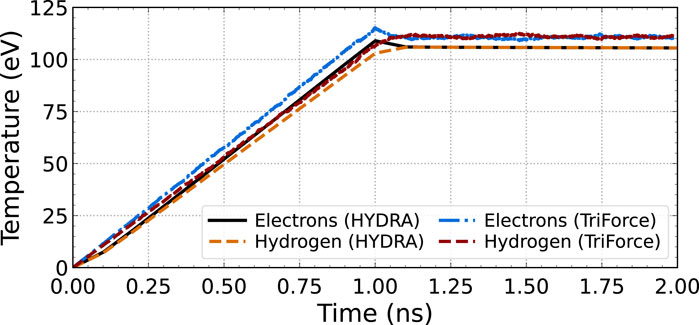
Figure 6. Simulated laser heating of a neutral electron–hydrogen plasma including bremsstrahlung emission and inverse bremsstrahlung absorption. The laser with intensity $6.37\times 10^{12}$ W/${\mathrm{c}\mathrm{m}}^2$ and wavelength of 526.5 nm is injected into the plasma with density $1.195\times 10^{21}{\mathrm{c}\mathrm{m}}^{-3}$ for 1 ns. Shown are the electron temperature (blue) and hydrogen temperature (red) simulated with TRIFORCE and the electron temperature (black) and hydrogen temperature (orange) simulated with HYDRA. The difference in heating rates between the PIC-MCC and radiation-hydrodynamics codes is less than 5%.

For the third test case, we measure the radiation and fusion power density in a fully ionized ${\text{p–}}^{11}\mathrm{B}$ at 1,000 g/${\mathrm{c}\mathrm{m}}^3$ between 50 and 700 keV. The fusion algorithm is discussed in Lavell et al. [18] and is based on the method introduced in Higginson et al. [29]; fusion cross sections are shown in Figure 1. We simulate $10^4$ electron, proton, and boron macroparticles in a single computational cell with 1-$\mu$m sides using a time step of $\mathrm{\Delta }t=0.1$ fs for ten time steps. To ensure an instantaneous power-density measurement, we take a small time step and do not compute Coulomb collisions. Figure 7 shows the simulated fusion power density in blue markers and radiation power density (including bremsstrahlung emission and IBA) in red markers for the cases $T_{\text{e}}=T_{\text{i}}$ (squares), $T_{\text{e}}=\frac{2}{3}{T}_{\text{i}}$ (circles), and $T_{\text{e}}=\frac{1}{3}{T}_{\text{i}}$ (triangles). The blue and red curves are previously predicted fusion and radiation power densities, respectively, from Putvinski et al. [52] originally performed for a lower-density system relevant to magnetic fusion systems ($n_{\text{p}}=10^{14}$ ${\mathrm{c}\mathrm{m}}^{-3}$ and $n_{\text{B}}=0.15\times 10^{14}$ ${\mathrm{c}\mathrm{m}}^{-3}$) and shown here scaled to the higher-density system. Putvinski et al. [52] (and previously Nevins [53]) computed a self-consistent electron temperature based on the energy exchange rates with thermal ions and slowing-down alpha products. As expected, our model predicts that the electron temperature must be lower than the ion temperature for fusion power to overcome radiative losses.

Figure 7

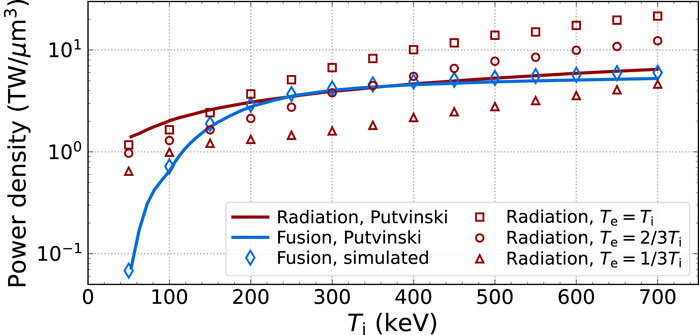
Figure 7. Simulated power density measurements (markers) for a fully ionized ${\text{p–}}^{11}\mathrm{B}$ plasma at 1,000 g/${\mathrm{c}\mathrm{m}}^3$. Calculations by Putvinski et al. [52] (curves) are linearly extrapolated from the original low-density plasma to the considered high-density system by multiplying by the ratio of the product of the electron and ion densities. Simulated fusion power density (blue) is in good agreement with the previous work. Putvinski et al.’s [52] radiation power density (red curve) considered a self-consistent electron temperature evaluated from a power balance with thermal ions and slowing-down alphas, while we consider an electron temperature in equilibrium with the ions (red squares), two-thirds the ion temperature (red circles), and one-third the ion temperature (red triangles).

3 Results

In this section, we present simulated fusion burn waves in compressed DT and ${\text{p–}}^{11}\mathrm{B}$ plasmas in planar geometry. Simulations are 1D with reflecting boundary conditions at $x_{\text{min}}=0$ $\mu$m (an approximation of the situation at the core of a spherical target) and outflow boundary conditions at $x_{\text{max}}=400$ $\mu$m. The grid resolution is $\mathrm{\Delta }x=1$ $\mu$m (the directions not simulated have sizes $\mathrm{\Delta }y=\mathrm{\Delta }z=100$ $\mu$m) and the time step is $\mathrm{\Delta }t=0.1$ fs. Particles are initialized at 1,000 particles per cell as Maxwell–Jüttner distributions [54], integrated ballistically (i.e., there are no external forces besides particle–particle collisions that only alter particle trajectories and numerical weights), and an adaptive particle manager is called every 50 simulation steps to reset the particle counts while preserving the mass and the velocity distributions [55]. For the case of a DT plasma, we compute Coulomb collisions between all charged-particle groups and fusion reactions between D–D, D–T, and D–³He (reaction cross sections are shown in Figure 1). We compare our results to the same planar simulation computed with the well-benchmarked legacy code LSP [21, 22] and a fluid simulation computed with the hydrodynamics code HYDRA [23–25]. After performing the code-to-code verification with DT plasma, we simulate an expanding ${\text{p–}}^{11}\mathrm{B}$ plasma including charged particle collisions, ${\text{p–}}^{11}\mathrm{B}$ fusion, bremsstrahlung emission from each of the electron–ion interactions, and IBA.

Figures 8–11 show plasma profiles and integrated metrics from an expanding DT hot-spot. A charge-neutral fully ionized DT plasma with uniform mass density $\rho =500$ g/${\mathrm{c}\mathrm{m}}^3$ is initialized with a temperature of $T_{\text{h}}=30$ keV in the hot region ($0<x<20$ $\mu$m) and $T_{\text{c}}=10$ eV in the cold region ($20<x<400$ $\mu$m). The total starting energy in the hot-spot region with volume 20 $\mu$m $\times 100$ $\mu$m $\times 100$ $\mu$m is 326 kJ (an equivalent spherical target with a radius of 20 $\mu$m has 55 kJ in the hot-spot). Figure 8 shows that after 4 ps the ion temperature has increased to $\sim 80$ keV and the electron temperature has increased to $\sim 60$ keV due to fusion-produced alphas coupling with the expanding hot spot. We find close agreement between our results and those computed with LSP and HYDRA. The largest discrepancy is the location of the electron front, with TRIFORCE leading the other two codes by $\sim 5$ $\mu$m. Certain other small differences, such as the location of the peak of the alpha temperature, we attribute to differences in computing the Coulomb logarithm. The presented data uses the relativistic Coulomb logarithm defined in Pérez et al. [27], and we obtain similar results using the Coulomb logarithm presented in Ref. [56]. Emitted neutrons are allowed to expand freely and show excellent agreement with LSP. The density and temperature profiles of the electrons, deuterium, tritium, and alphas are shown at 40 ps in Figure 9 (some smoothing is applied to the profiles from the PIC-MCC results). The result from TRIFORCE (orange curve) has a faster burn wave front than LSP (black curve), but we see general agreement in the expansion of the hot spot. HYDRA has the slowest electron front, lowest electron temperature, and sharpest shock, but shows general agreement with the PIC-MCC codes. Figure 10 indicates that the integrated mass and kinetic energy of each of the species are consistent between TRIFORCE (markers) and LSP (curves). Similarly, Figure 11 shows we find excellent agreement between TRIFORCE and HYDRA in the predicted fusion power and energy. To put these results into perspective, our simulated DT case is deep in the ignited regime with $\rho R=1$ g/${\mathrm{c}\mathrm{m}}^2$ and $T_{\text{h}}=30$ keV compared to the minimum energy isochoric reference case of Atzeni and Meyer-ter-Vehn [57] with $\rho R=0.5$ g/${\mathrm{c}\mathrm{m}}^2$ and $T_{\text{h}}=12$ keV.

Figure 8

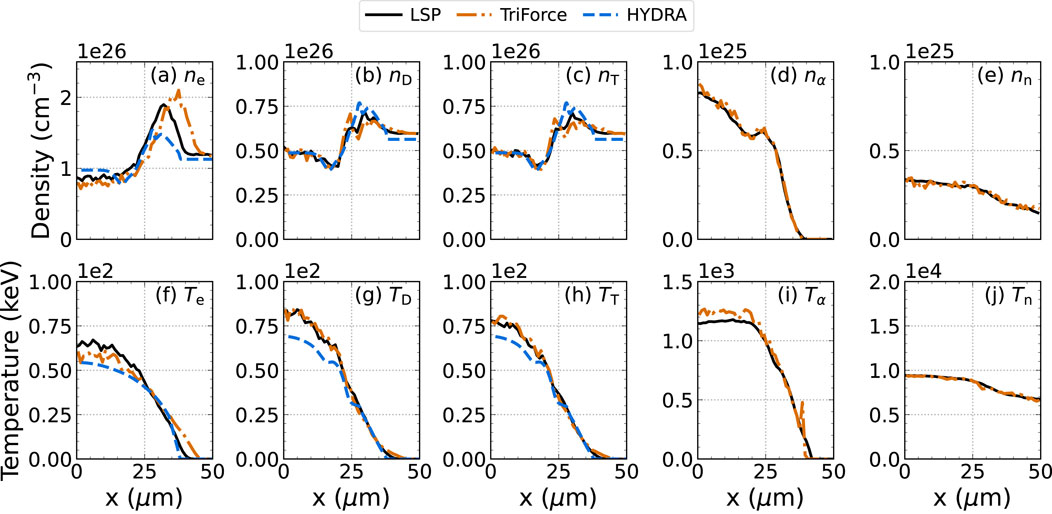
Figure 8. Simulated expansion of a 30-keV DT hot-spot into a 10-eV DT plasma considering Coulomb collisions and fusion reactions. The initial interface between the hot and cold regions with a uniform density of 500 g/${\mathrm{c}\mathrm{m}}^3$ is at 20 $\mu$m. (A, F) Electron, (B, G) deuterium, (C, H) tritium, (D, I) alpha, and (E, J) neutron density and temperature profiles are shown at 4 ps simulated with LSP (black) and with TRIFORCE (orange). Also shown are the electron and ion densities computed with HYDRA (blue).

Figure 9

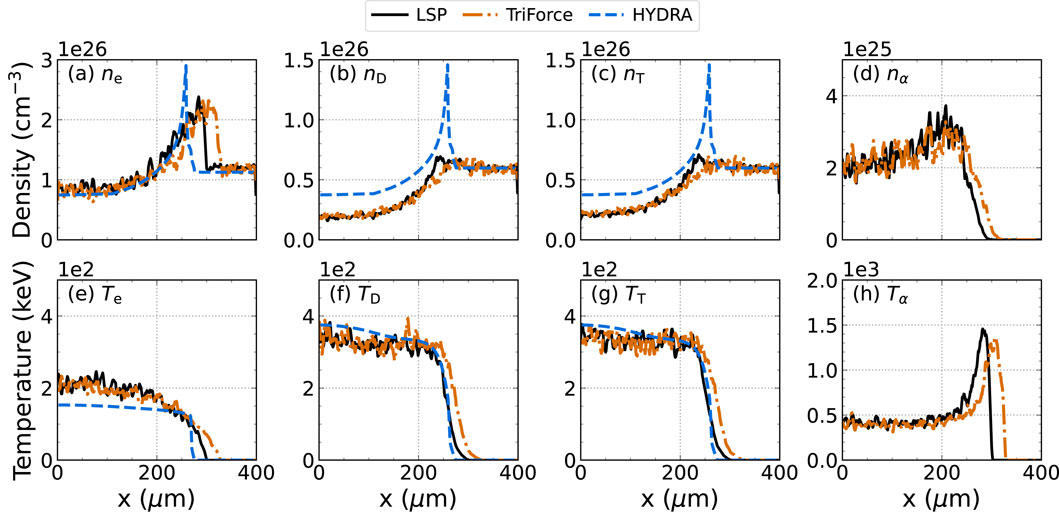
Figure 9. Simulated expansion of a 30-keV DT hot-spot into cold fuel at 40 ps simulated with LSP (black), TRIFORCE (orange), and HYDRA (blue). Plots (A-D) show density and plots (E-H) show temperature for the electron, deuterium, tritium, and alpha plasma species. Some smoothing is applied to the results from the particle codes.

Figure 10

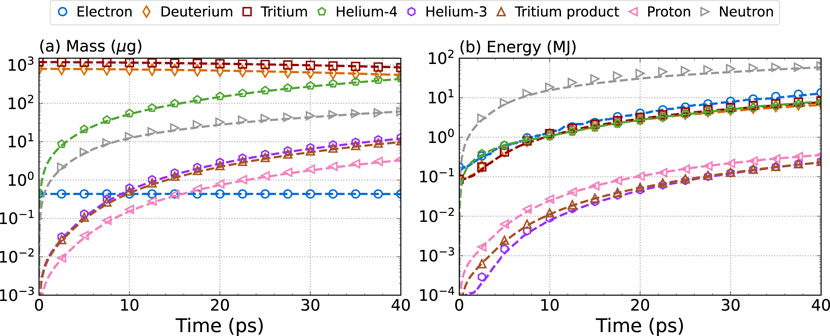
Figure 10. The total mass and energy as a function of time for the simulated release of 30-keV DT into cold DT including Coulomb collisions and fusion reactions between D–D, D–T, and D–³He. Shown are the (A) integrated mass and (B) kinetic energy for each of the plasma species simulated with TRIFORCE (markers) and LSP (curves).

Figure 11

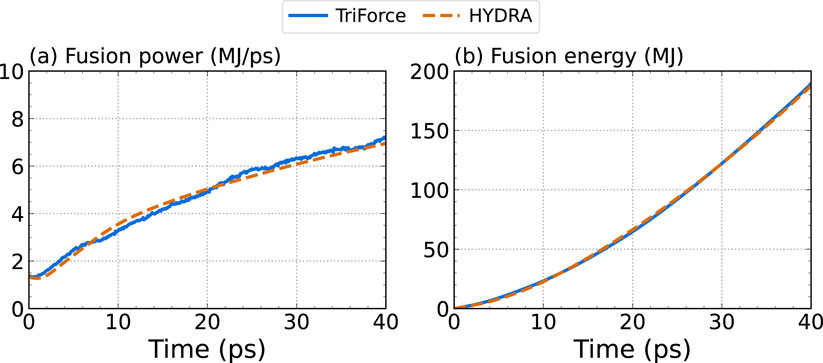
Figure 11. (A) Fusion power and (B) total fusion energy produced from the DT hot-spot simulated with TRIFORCE (blue) and HYDRA (orange).

Next, we consider the case of a ${\text{p–}}^{11}\mathrm{B}$ burn wave with increased initial density, temperature, and hot-spot radius compared to the DT configuration; the plasma is given an initial mass density of 1,000 g/${\text{cm}}^3$, ion density ratio of $n_{\text{B}}/n_{\text{p}}=0.2$, hot-spot radius of 100 $\mu$m, hot-spot temperature of 200 keV, and a temperature of 10 eV outside of the hot spot. We choose an initial hot-spot temperature of 200 keV because this temperature had the least restrictive electron–ion temperature ratio in the power balance measurement to achieve more fusion energy gain than radiative losses (see Figure 7). The initial total kinetic energy in the hot-spot region with volume 100 $\mu$m $\times 100$ $\mu$m $\times 100$ $\mu$m is 35 MJ (an equivalent spherical target with a radius of 100 $\mu$m has 147 MJ in the hot-spot). Figure 12 shows the density and temperature of the electrons, protons, boron ions, and alpha particles at 10 ps and 20 ps for three cases: radiation enabled with Seltzer–Berger bremsstrahlung cross sections (red), radiation enabled with the temperature-dependent TFD bremsstrahlung cross sections from Martinez et al. [28] (blue), and radiation disabled (orange). Including radiation removes thermal energy directly from the electrons, slows the propagation of the burn front, and reduces alpha heating of the ions. Notably, IBA quickly raises the temperature of the surrounding fuel to several keV reducing the stopping of alpha particles compared to the no-radiation case. More energy is removed from the electrons using the Seltzer–Berger cross sections because the values are larger than the TFD cross sections for boron near 100 keV, as shown in Figure 3B. The power and integrated energy from fusion and each of the three electron–ion radiation channels using the TFD model are shown in Figure 13. After 20 ps the energy produced from fusion is 70.9 MJ and the total radiated energy due to the three bremsstrahlung channels is 71.7 MJ. When the radiation model is disabled, the integrated fusion energy after 20 ps is 73.4 MJ. The model predicts only a small decrease in net fusion energy in the simulated time because most of the radiated photons are re-absorbed by the high-density opaque plasma. If radiation absorption is not included in the model, the predicted fusion power drops below 1 MJ/ps due to radiative losses.

Figure 12

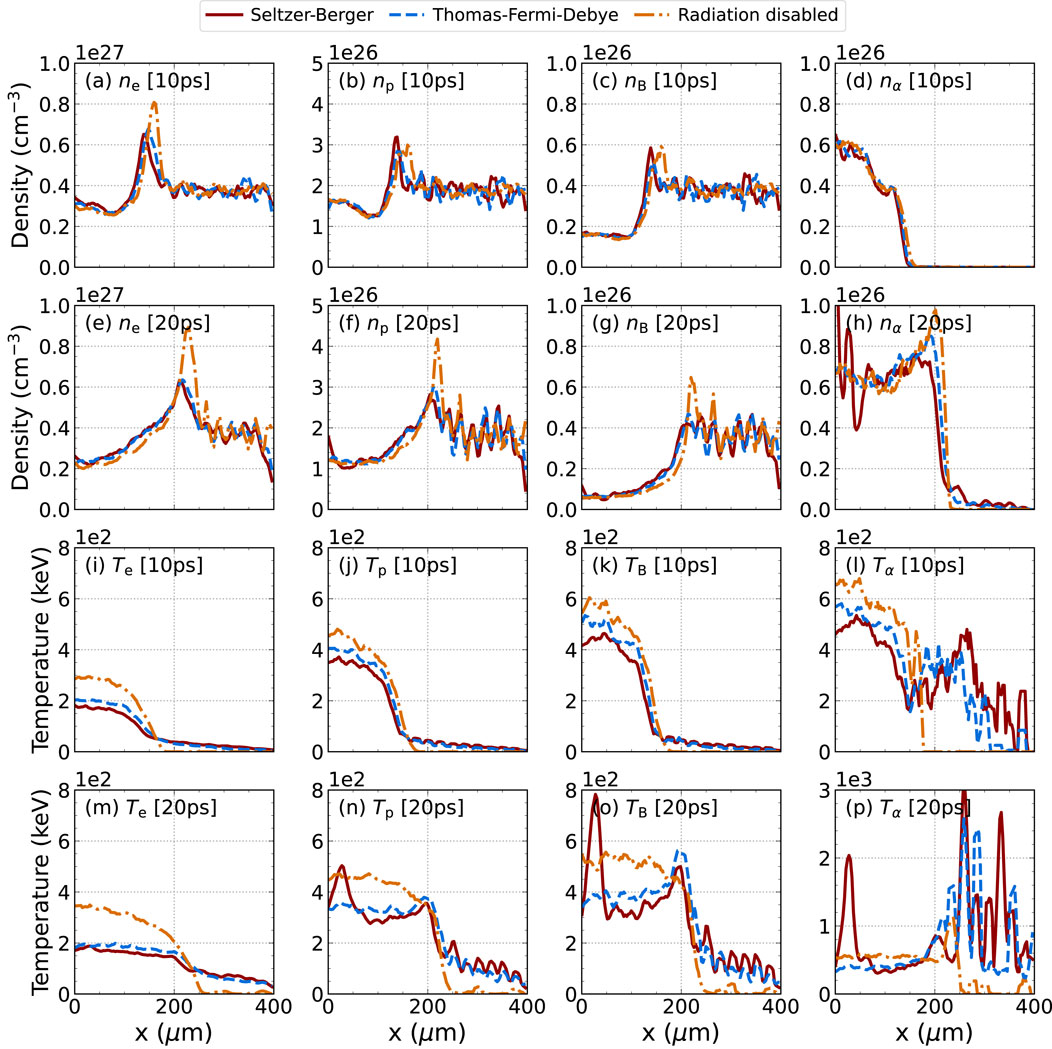
Figure 12. Simulated expansion of a 200-keV ${\text{p–}}^{11}\mathrm{B}$ hot spot into 10-eV ${\text{p–}}^{11}\mathrm{B}$ fuel at 10 ps and 20 ps. Plots (A–H) show density and plots (I–P) show temperature for each of the simulated particle groups. The initial interface between the hot and cold regions of the isochoric plasma with density 1,000 g/${\text{cm}}^3$ is at 100 $\mu$m. We compute Coulomb collisions between all particles, ${\text{p–}}^{11}\mathrm{B}$ fusion, and consider the cases where radiation emission and absorption is enabled using Seltzer–Berger tables (red) and the TFD model (blue), as well as the case where radiation is disabled (orange).

Figure 13

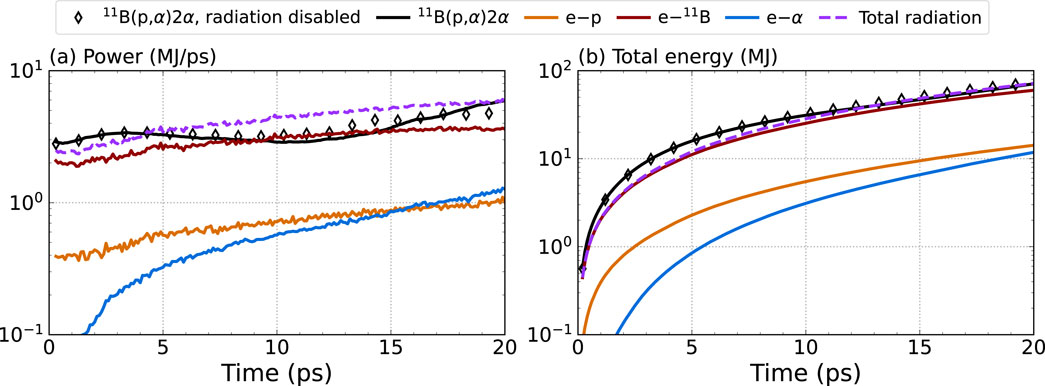
Figure 13. Fusion (black) and radiation (orange, red, blue, purple) (A) power and (B) total energy for each of the reactions using the TFD model for bremsstrahlung cross sections simulated during the expansion of a hot spot of ${\text{p–}}^{11}\mathrm{B}$ into a reservoir of colder ${\text{p–}}^{11}\mathrm{B}$ fuel.

4 Discussion

Previous studies of the energy balance in ${\text{p–}}^{11}\mathrm{B}$ burn waves solved systems of coupled differential equations dependent on analytic expressions for electron–ion energy exchange rates through collisions, bremsstrahlung power, fusion power, as well as other effects [58, 59]. In this study, we implemented and verified a bremsstrahlung emission model and introduced a new IBA model in a PIC-MCC code and used this fully kinetic model to investigate the planar propagation of fusion burn waves in compressed DT and ${\text{p–}}^{11}\mathrm{B}$ plasmas. The bremsstrahlung radiation model allows for the investigation of radiative losses in addition to simulating the exchange of energy through Coulomb collisions and fusion reactions.

Our model predicts that including radiation increases the transfer of thermal energy from the hot-spot to the surrounding fuel. While the electron temperature drops by almost a factor of two due to bremsstrahlung emission, the cold plasma temperature increases by almost four orders of magnitude (10 eV–100 keV) due to IBA over the course of 20 ps. The radiative cooling of the hot spot leads to less thermal work being done and a slower shock front, whereas, radiative heating of the cold fuel decreases the stopping of fusion alpha leading to non-local energy deposition. Currently, our model predicts the development of additional modes late in time in the density and temperature of the initially-cold region. While they appear to coincide with the spikes in the temperature of the alphas, we are still working to understand if these modes are physical or numerical artifacts.

There are certain limitations to our simulation results due to missing physics. The absence of electromagnetic fields in these simulations means that we do not currently capture the collective effects and instabilities that stem from particle coupling at long range. This is expected to have an impact on the separation of the electron and ion wave fronts and the burn wave propagation speed; more specifically, it will reduce the electron heat flow and increase the ion heat flow through a pressure gradient. The omission of field effects is evident in the discrepancy between electron and ion densities in Figure 9 where the electron pileup at the shock front exceeds the ion density. While charge separation is not seen in the charge neutral HYDRA solution, we expect long-range electron–ion coupling will play a minor role in the overall plasma dynamics. Electromagnetic LSP simulations of the DT burn wave (not shown in this report) predicted field energies that were $\sim 0.3\%$ of the total particle energy and showed little difference in the plasma motion compared to the case computed without fields.

A greater limitation to our results is that the planar description of expansion underestimates the thermal expansion work compared to spherical expansion, and therefore, our results predict a faster wave front, less ion cooling and more self-heating of the hot spot than expected in an equivalent ICF target. However, planar expansion also underestimates the available fuel mass for the wave to propagate through and burn. Simulating the strongly ignited DT case in 1D spherical geometry with HYDRA (not shown in this report) led to an increase in the fusion power from 7 MJ/ps to 45 MJ/ps and fusion energy from 190 MJ to 430 MJ at 40 ps compared to the case simulated with planar geometry.

We note that, in light of the foregoing limitations, this work is not intended to argue the case for ${\text{p–}}^{11}\mathrm{B}$ fusion or provide a design point for ICF targets. The goal of the present work is to test and verify TRIFORCE in its current state; future work with TRIFORCE (including both the physics mentioned above as well as additional effects) will address the question of what target designs might make ${\text{p–}}^{11}\mathrm{B}$ fusion feasible.

In future work, we will continue to improve the model and explore the ignition space of ${\text{p–}}^{11}\mathrm{B}$. For example, inclusion of Compton scattering [32] and elastic nuclear scattering within the binary Monte Carlo collision framework will improve the accuracy of our burn wave simulations. We anticipate these effects will improve plasma coupling and boost the fusion yield. We also plan to include quantum effects that are relevant to the warm-dense-matter regime we are considering, where it is theorized the stopping power will decrease thus increasing the likelihood of fusion chain reactions [60]. There exist methods for simulating degenerate particles with Fermi–Dirac statistics by enforcing the Pauli exclusion principle and modifying the collision frequency that we plan to include in the future [33, 61, 62]. Following the work of Liu et al. [34] that proposed proton fast ignition of warm dense ${\text{p–}}^{11}\mathrm{B}$, we expect that including degeneracy effects will improve the ion coupling and fusion gain as particle slowing on the bound and free electrons will be reduced significantly.

Additionally, we plan to improve the fidelity of future simulations by including the fast-ignition heating process of a beam heating an assembled isochoric plasma. Kinetic effects, such as nonlocal transport where density and temperature gradients are comparable to or shorter than the mean free path length, may play an increasingly important role. With TRIFORCE and the PIC-MCC approach, we can continue to investigate kinetic physics in reacting multi-species plasmas at extreme conditions.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

ML: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. AK: Software, Writing–review and editing. ATS: Software, Writing–review and editing. EE: Software, Writing–review and editing. IM: Software, Writing–review and editing. SG-R: Writing–review and editing. WS: Software, Writing–review and editing. MB: Conceptualization, Writing–review and editing. SP: Conceptualization, Writing–review and editing. TM: Conceptualization, Writing–review and editing. MT: Conceptualization, Writing–review and editing. GA: Conceptualization, Writing–review and editing. ABS: Conceptualization, Funding acquisition, Project administration, Resources, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This material is based upon work supported by the US DOE ARPA-E under Award No. DE-AR0001272, US DOE Office of Fusion Energy Science (OFES) INFUSE program under Award No. DE-SC0024460, US DOE OFES under Award No. DE-SC0017951, and US DOE NNSA University of Rochester “National Inertial Confinement Program” under Award No. DE-NA0004144. This report was prepared as an account of work sponsored by an agency of the US Government. Neither the US Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the US Government or any agency thereof.

Acknowledgments

ML and ABS thank B. Martinez and L. Gremillet for helpful discussions and the referees for their encouragement to introduce radiation absorption to the calculations.

Conflict of interest

Authors MB, SP, TM, MT, and GA were employed by HB11 Energy Holdings Pty Ltd. Author TM was employed by Mehlhorn Engineering Consulting.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Author disclaimer

The views and opinions of authors expressed herein do not necessarily state or reflect those of the US Government or any agency thereof.

References

1. Zylstra AB, Hurricane OA, Callahan DA, Kritcher AL, Ralph JE, Robey HF, et al. Burning plasma achieved in inertial fusion. Nature (2022) 601:542–8. doi:10.1038/s41586-021-04281-w

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Zylstra A, Kritcher A, Hurricane O, Callahan D, Ralph J, Casey D, et al. Experimental achievement and signatures of ignition at the national ignition facility. Phys Rev E (2022) 106:025202. doi:10.1103/physreve.106.025202

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Bosch HS, Hale GM. Improved formulas for fusion cross-sections and thermal reactivities. Nucl Fusion (1992) 32:611–31. doi:10.1088/0029-5515/32/4/i07

CrossRef Full Text | Google Scholar

4. Brown DA, Chadwick MB, Capote R, Kahler AC, Trkov A, Herman MW, et al. ENDF/B-VIII. 0: the 8th major release of the nuclear reaction data library with CIELO-project cross sections, new standards and thermal scattering data. Nucl Data Sheets (2018) 148:1–142. doi:10.1016/j.nds.2018.02.001

CrossRef Full Text | Google Scholar

5. Tentori A, Belloni F. Revisiting p–¹¹B fusion cross section and reactivity, and their analytic approximations. Nucl Fusion (2023) 63:086001. doi:10.1088/1741-4326/acda4b

CrossRef Full Text | Google Scholar

6. Hora H, Korn G, Giuffrida L, Margarone D, Picciotto A, Krasa J, et al. Fusion energy using avalanche increased boron reactions for block-ignition by ultrahigh power picosecond laser pulses. Laser Part Beams (2015) 33:607–19. doi:10.1017/s0263034615000634

CrossRef Full Text | Google Scholar

7. Liu KF, Chao AW. Accelerator based fusion reactor. Nucl Fusion (2017) 57:084002. doi:10.1088/1741-4326/aa7642

CrossRef Full Text | Google Scholar

8. Eliezer S, Martinez-Val JM. A novel fusion reactor with chain reactions for proton–boron-11. Laser Part Beams (2020) 38:39–44. doi:10.1017/s0263034619000818

CrossRef Full Text | Google Scholar

9. Kolmes EJ, Ochs IE, Fisch NJ. Wave-supported hybrid fast-thermal p–¹¹B fusion. Phys Plasmas (2022) 29:110701. doi:10.1063/5.0119434

CrossRef Full Text | Google Scholar

10. McKenzie W, Batani D, Mehlhorn TA, Margarone D, Belloni F, Campbell EM, et al. HB11—understanding hydrogen–boron fusion as a new clean energy source. J Fusion Energ (2023) 42:17. doi:10.1007/s10894-023-00349-9

CrossRef Full Text | Google Scholar

11. Mehlhorn TA, Labun L, Hegelich BM, Margarone D, Gu MF, Batani D, et al. Path to increasing p-b11 reactivity via ps and ns lasers. Laser Part Beams (2022) 2022:e1. doi:10.1155/2022/2355629

CrossRef Full Text | Google Scholar

12. Tabak M, Hammer J, Glinsky ME, Kruer WL, Wilks SC, Woodworth J, et al. Ignition and high gain with ultrapowerful lasers. Phys Plasmas (1994) 1:1626–34. doi:10.1063/1.870664

CrossRef Full Text | Google Scholar

13. Roth M, Cowan TE, Key MH, Hatchett SP, Brown C, Fountain W, et al. Fast ignition by intense laser-accelerated proton beams. Phys Rev Lett (2001) 86:436–9. doi:10.1103/physrevlett.86.436

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Fernández JC, Albright BJ, Beg FN, Foord ME, Hegelich BM, Honrubia JJ, et al. Fast ignition with laser-driven proton and ion beams. Nucl Fusion (2014) 54:054006. doi:10.1088/0029-5515/54/5/054006

CrossRef Full Text | Google Scholar

15. Eliezer S, Schweitzer Y, Nissim N, Martinez Val JM. Mitigation of the stopping power effect on proton–boron-11 nuclear fusion chain reactions. Front Phys (2020) 8:573694. doi:10.3389/fphy.2020.573694

CrossRef Full Text | Google Scholar

16. Belloni F, Batani K. Multiplication processes in high-density h-11b fusion fuel. Laser Part Beams (2022) 2022:e11. doi:10.1155/2022/3952779

CrossRef Full Text | Google Scholar

17. Sefkow AB, Shaw JG, Carroll-Nellenback J, Pai S, Blackman EG, Cao D, et al. Introduction to TriForce: a multiphysics code for hybrid fluid-kinetic simulations. Bull Am Phys Soc (2019) 64. BAPS.2019.DPP.JP10.125.

Google Scholar

18. Lavell MJ, Kish AJ, Sexton AT, Masti RL, Mohammad I, Kim MJ, et al. Verification of a Monte Carlo binary collision model for simulating elastic and inelastic collisions in particle-in-cell simulations. Phys Plasmas (2024) 31. doi:10.1063/5.0190352

CrossRef Full Text | Google Scholar

19. Birdsall CK. Particle-in-cell charged-particle simulations, plus Monte Carlo collisions with neutral atoms, PIC-MCC. IEEE Trans Plasma Sci (1991) 19:65–85. doi:10.1109/27.106800

CrossRef Full Text | Google Scholar

20. Nanbu K. Probability theory of electron–molecule, ion–molecule, molecule–molecule, and coulomb collisions for particle modeling of materials processing plasmas and cases. IEEE Trans Plasma Sci (2000) 28:971–90. doi:10.1109/27.887765

CrossRef Full Text | Google Scholar

21. Welch DR, Rose DV, Clark RE, Genoni TC, Hughes TP. Implementation of an non-iterative implicit electromagnetic field solver for dense plasma simulation. Comput Phys Commun (2004) 164:183–8. doi:10.1016/j.cpc.2004.06.028

CrossRef Full Text | Google Scholar

22. Welch DR, Rose DV, Cuneo ME, Campbell RB, Mehlhorn TA. Integrated simulation of the generation and transport of proton beams from laser-target interaction. Phys Plasmas (2006) 13:063105. doi:10.1063/1.2207587

CrossRef Full Text | Google Scholar

23. Marinak MM, Tipton RE, Landen OL, Murphy TJ, Amendt P, Haan SW, et al. Three-dimensional simulations of Nova high growth factor capsule implosion experiments. Phys Plasmas (1996) 3:2070–6. doi:10.1063/1.872004

CrossRef Full Text | Google Scholar

24. Marinak MM, Haan SW, Dittrich TR, Tipton RE, Zimmerman G. A comparison of three-dimensional multimode hydrodynamic instability growth on various National Ignition Facility capsule designs with HYDRA simulations. Phys Plasmas (1998) 5:1125–32. doi:10.1063/1.872643

CrossRef Full Text | Google Scholar

25. Marinak MM, Kerbel GD, Gentile NA, Jones O, Munro D, Pollaine S, et al. Three-dimensional HYDRA simulations of national ignition facility targets. Phys Plasmas (2001) 8:2275–80. doi:10.1063/1.1356740

CrossRef Full Text | Google Scholar

26. Nanbu K, Yonemura S. Weighted particles in coulomb collision simulations based on the theory of a cumulative scattering angle. J Comput Phys (1998) 145:639–54. doi:10.1006/jcph.1998.6049

CrossRef Full Text | Google Scholar

27. Pérez F, Gremillet L, Decoster A, Drouin M, Lefebvre E. Improved modeling of relativistic collisions and collisional ionization in particle-in-cell codes. Phys Plasmas (2012) 19:083104. doi:10.1063/1.4742167

CrossRef Full Text | Google Scholar

28. Martinez B, Lobet M, Duclous R, d’Humières E, Gremillet L. High-energy radiation and pair production by coulomb processes in particle-in-cell simulations. Phys Plasmas (2019) 26. doi:10.1063/1.5118339

CrossRef Full Text | Google Scholar

29. Higginson DP, Link A, Schmidt A. A pairwise nuclear fusion algorithm for weighted particle-in-cell plasma simulations. J Comput Phys (2019) 388:439–53. doi:10.1016/j.jcp.2019.03.020

CrossRef Full Text | Google Scholar

30. Higginson DP, Holod I, Link A. A corrected method for coulomb scattering in arbitrarily weighted particle-in-cell plasma simulations. J Comput Phys (2020) 413:109450. doi:10.1016/j.jcp.2020.109450

CrossRef Full Text | Google Scholar

31. Follett RK, Colaïtis A, Turnbull D, Froula DH, Palastro JP. Validation of ray-based cross-beam energy transfer models. Phys Plasmas (2022) 29. doi:10.1063/5.0123462

CrossRef Full Text | Google Scholar

32. Del Gaudio F, Grismayer T, Fonseca RA, Silva LO. Compton scattering in particle-in-cell codes. Plasma Phys (2020) 86:905860516. doi:10.1017/s002237782000118x

CrossRef Full Text | Google Scholar

33. Wu D, Yu W, Fritzsche S, He XT. Particle-in-cell simulation method for macroscopic degenerate plasmas. Phys Rev E (2020) 102:033312. doi:10.1103/physreve.102.033312

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Liu SJ, Wu D, Hu TX, Liang TY, Ning XC, Liang JH, et al. Proton–boron fusion scheme taking into account the effects of target degeneracy. Phys Rev Res (2024) 6:013323. doi:10.1103/physrevresearch.6.013323

CrossRef Full Text | Google Scholar

35. Seltzer SM, Berger MJ. Bremsstrahlung energy spectra from electrons with kinetic energy 1 keV–10 GeV incident on screened nuclei and orbital electrons of neutral atoms with Z= 1–100. At Data Nucl Data tables (1986) 35:345–418. doi:10.1016/0092-640x(86)90014-8

CrossRef Full Text | Google Scholar

36. Agostinelli S, Allison J, Amako K, Apostolakis J, Araujo H, Arce P, et al. Geant4—a simulation toolkit. Nucl Instrum Methods Phys Res (2003) 506:250–303. doi:10.1016/s0168-9002(03)01368-8

CrossRef Full Text | Google Scholar

37. Allison J, Amako K, Apostolakis J, Araujo H, Dubois PA, Asai M, et al. Geant4 developments and applications. IEEE Trans Nucl Sci (2006) 53:270–8. doi:10.1109/tns.2006.869826

CrossRef Full Text | Google Scholar

38. Allison J, Amako K, Apostolakis J, Arce P, Asai M, Aso T, et al. Recent developments in Geant4. Nucl Instrum Methods Phys Res (2016) 835:186–225. doi:10.1016/j.nima.2016.06.125

CrossRef Full Text | Google Scholar

39. Rand S. Inverse bremsstrahlung with high-intensity radiation fields. Phys Rev (1964) 136:B231–7. doi:10.1103/physrev.136.b231

CrossRef Full Text | Google Scholar

40. Langdon AB. Nonlinear inverse bremsstrahlung and heated-electron distributions. Phys Rev Lett (1980) 44:575–9. doi:10.1103/physrevlett.44.575

CrossRef Full Text | Google Scholar

41. Paes ACJ, Serbeto A, Alves MV, Galvão RMO, Hussein MS. A particle-in-cell simulation of nonlinear amplification of inverse bremsstrahlung electron acceleration. Journ Phys D: Appl Phys (1997) 30:1759–62. doi:10.1088/0022-3727/30/12/012

CrossRef Full Text | Google Scholar

42. Weber S, Bonnaud G, Gauthier JC. Role of collisions in particle-in-cell modeling of high-density short-pulse laser-plasma interaction. Phys Plasmas (2001) 8:387–90. doi:10.1063/1.1340619

CrossRef Full Text | Google Scholar

43. Detering F, Bychenkov VY, Rozmus W, Sydora R, Capjack CE. Langevin representation of laser heating in pic simulations. Comp Phys Commun (2002) 143:48–53. doi:10.1016/s0010-4655(01)00432-5

CrossRef Full Text | Google Scholar

44. Detering F, Rozmus W, Brantov A, Bychenkov VY, Capjack CE, Sydora R. Particle-in-cell simulations of heat flux driven ion acoustic instability. Phys Plasmas (2005) 12. doi:10.1063/1.1835344

CrossRef Full Text | Google Scholar

45. Weng SM, Sheng ZM, Zhang J. Inverse bremsstrahlung absorption with nonlinear effects of high laser intensity and non-maxwellian distribution. Phys Rev E (2009) 80:056406. doi:10.1103/physreve.80.056406

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Moritaka T, Baiotti L, Lin A, Weiwu L, Sakawa Y, Kuramitsu Y, et al. Plasma particle-in-cell simulations with qed reactions for pair production experiments using a high-z solid target. J Phys Conf Ser (2013) 454:012016. doi:10.1088/1742-6596/454/1/012016

CrossRef Full Text | Google Scholar

47. Mehdian H, Kargarian A, Hajisharifi K. Kinetic (particle-in-cell) simulation of nonlinear laser absorption in a finite-size plasma with a background inhomogeneous magnetic field. Phys Plasmas (2015) 22. doi:10.1063/1.4921934

CrossRef Full Text | Google Scholar

48. Arber TD, Bennett K, Brady CS, Lawrence-Douglas A, Ramsay MG, Sircombe NJ, et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys Controlled Fusion (2015) 57:113001. doi:10.1088/0741-3335/57/11/113001

CrossRef Full Text | Google Scholar

49. Vyskočil J, Klimo O, Weber S. Simulations of bremsstrahlung emission in ultra-intense laser interactions with foil targets. Plasma Phys Controlled Fusion (2018) 60:054013. doi:10.1088/1361-6587/aab4c3

CrossRef Full Text | Google Scholar

50. Reitsma AJW, Trines RMGM, Bingham R, Cairns RA, Mendonça JT, Jaroszynski DA. Photon kinetic modeling of laser pulse propagation in underdense plasma. Phys Plasmas (2006) 13. doi:10.1063/1.2366577

CrossRef Full Text | Google Scholar

51. Goldston RJ, Rutherford PH. Introduction to plasma physics. 1st ed. edn. Bristol, England: IOP Publishing Ltd. (1988).

Google Scholar

52. Putvinski SV, Ryutov DD, Yushmanov PN. Fusion reactivity of the pB11 plasma revisited. Nucl Fusion (2019) 59:076018. doi:10.1088/1741-4326/ab1a60

CrossRef Full Text | Google Scholar

53. Nevins WM. A review of confinement requirements for advanced fuels. J Fusion Energ (1998) 17:25–32. doi:10.1023/a:1022513215080

CrossRef Full Text | Google Scholar

54. Zenitani S, Nakano S. Loading a relativistic kappa distribution in particle simulations. Phys Plasmas (2022) 29:113904. doi:10.1063/5.0117628

CrossRef Full Text | Google Scholar

55. Welch DR, Genoni TC, Clark RE, Rose DV. Adaptive particle management in a particle-in-cell code. J Comput Phys (2007) 227:143–55. doi:10.1016/j.jcp.2007.07.015

CrossRef Full Text | Google Scholar

56. Higginson DP, Link AJ. A cartesian-diffusion Langevin method for hybrid kinetic-fluid coulomb scattering in particle-in-cell plasma simulations. J Comput Phys (2022) 457:110935. doi:10.1016/j.jcp.2021.110935

CrossRef Full Text | Google Scholar

57. Atzeni S, Meyer-ter Vehn J The physics of inertial fusion: beam plasma interaction, hydrodynamics, hot dense matter, 125. Oxford, United Kingdom: OUP Oxford (2004).

Google Scholar

58. Martínez-Val JM, Eliezer S, Piera M, Velarde G. Fusion burning waves in proton–boron-11 plasmas. Phys Lett A (1996) 216:142–52. doi:10.1016/0375-9601(96)00252-6

CrossRef Full Text | Google Scholar

59. Eliezer S, Martínez-Val JM. Proton–boron-11 fusion reactions induced by heat-detonation burning waves. Laser Part Beams (1998) 16:581–98. doi:10.1017/s0263034600011411

CrossRef Full Text | Google Scholar

60. Gryziński M. Fusion chain reaction—chain reaction with charged particles. Phys Rev (1958) 111:900–5. doi:10.1103/physrev.111.900

CrossRef Full Text | Google Scholar

61. Wu D, He XT, Yu W, Fritzsche S. Monte Carlo approach to calculate proton stopping in warm dense matter within particle-in-cell simulations. Phys Rev E (2017) 95:023207. doi:10.1103/physreve.95.023207

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Wu D, Yu W, Fritzsche S, He X. High-order implicit particle-in-cell method for plasma simulations at solid densities. Phys Rev E (2019) 100:013207. doi:10.1103/physreve.100.013207

PubMed Abstract | CrossRef Full Text | Google Scholar