- 1Aviation and Automobile School, Chongqing Youth Vocational & Technical College, Chongqing, China
- 2Department of Physics, Chongqing University, Chongqing, China
As the most prevalent element on our planet, carbon manifests a wide variety of allotropic phases, significantly contributing to its complex physical properties. Recently, several carbon allotropes have been reported to possess abundant topological phases in theory and experiment. This work focuses on a sp3 carbon allotrope, Z-ACA allotrope, which consists of 5-6-7-type Z-ACA carbon rings. This allotrope has been reported previously as a superhard material comparable to diamond. In this study, we report that it is a candidate for both an obstructed atomic insulator and a real Chern insulator. It is worth mentioning that Z-ACA exhibits an unconventional bulk-boundary correspondence due to its hinge boundary state manifestation. Our current research indicates that Z-ACA is a suitable carbon phase platform for studying the real topology and second-order bulk-boundary correspondence.
Introduction
Carbon [1–3] is widely regarded as the most active element inside the periodic table owing to its extensive capacity for sp, sp2, and sp3 hybridization. The flexibility of carbon’s bond hybridizations enables it to exhibit a wide range of allotropes, such as diamond, graphite, and amorphous carbon. There is considerable variety observed in the physicochemical features of these allotropes. Researchers are presently involved in the theoretical and experimental production of new carbon allotropes [4–10] with the aim of identifying materials that exhibit desirable electronic, magnetic, mechanical, thermal, and topological properties.
Discovering the topological properties and their physical origins for carbon materials is currently a very active area in condensed matter physics [11]. In recent years, there has been a significant surge in interest surrounding the phenomenon of magic-angle twisted bilayer graphene [12, 13]. The recently developed 2D material class, which is based on carbon, demonstrates a wide range of appealing electronic states, such as superconductivity and topological nontrivial electronic states. Several three-dimensional (3D) carbon allotropes [14–17] have been shown to display intriguing topological electronic states in addition to 2D twisted bilayer graphene. Note that 1D carbon systems, like certain graphene nanoribbons, may also host topological behaviors [18–20].
The field of topological quantum chemistry theory has made significant progress in reclassifying insulators that were previously regarded as trivial ones. These reclassifications of trivial insulators now include obstructed atomic insulators (OAIs) and atomic insulators [21–28]. This reclassification is based on the Wyckoff positions (WPs) of the orbitals that induce the band representations (BRs). Orbitals situated at atomic-occupied WPs induce the BRs of atomic insulators. On the other hand, the BRs of OAIs are generated by orbitals situated at both atom-occupied and atom-unoccupied WPs. The term “Obstructed Wannier charge centers (OWCCs)” [29, 30] pertains to atom-unoccupied WPs in OAIs.
In addition, it is crucial that the band eigenstates exhibit real topology [31–35] due to specific symmetry constraints, including spacetime inversion symmetry and the lack of spin-orbit coupling (SOC) phenomenon. The real Chern insulator (RCI) state has been discovered in numerous two-dimensional systems [36–41]. The notion is expanded to include 3D systems, which is of considerable importance. 3D RCIs are commonly linked to unconventional bulk-boundary correspondence, namely, hinge states [42–44], as they depict boundary states in two dimensions that are smaller than the 3D bulk.
In this work, using first-principle calculations, we will report that the sp3 carbon allotrope, Z-ACA allotrope, is a new candidate for OAI and RCI. We would like to point out that the stability, electronic, and mechanical properties of the Z-ACA allotrope have been investigated using a first-principles method by He et al. [45]. However, other researchers have not investigated the OAI and RCI states for Z-ACA due to materials with nontrivial real band topology having become a focus of current physics research within the last 2 years. Figure 1 shows the crystal structure of Z-ACA with Pmmn space group; the C atoms occupy an equivalent Wyckoff position of 2a (0.00000, 1.00000, 0.95706), 2b (0.00000, 0.50000, 0.93126), and 4e (0.00000, 0.76406, 0.82886). The optimized lattice constants a = 2.521 Å, b = 4.759 Å, and c = 7.930 Å in this work are comparable with others (a = 2.521 Å, b = 4.76 Å, c = 7.930 Å) [45].
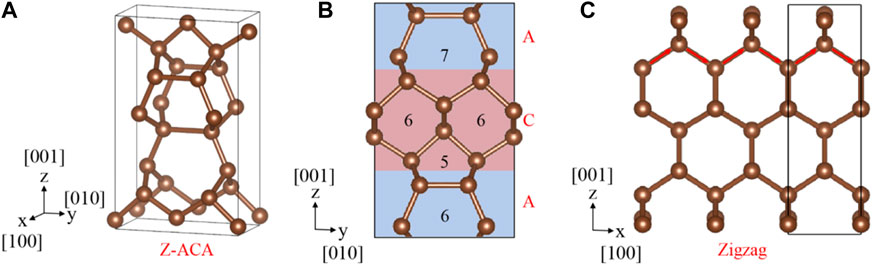
Figure 1. (A–C) The primitive cell and corresponding side and top views of Z-ACA carbon. Here, Z denotes that the framework of the system is constructed with zigzag carbon chains along the [100] direction. The numbers in the side view panels indicate the number of carbon atoms in the rings. Z-ACA contains 5-, 6- and 7-carbon rings.
Methods
The Vienna ab initio simulation package (VASP) [46] was employed to carry out the calculations within the framework of density functional theory. The Perdew-Burke-Ernzerhof [47] functional with generalized gradient approximations [48] was adopted to describe the exchange-correlation interactions. The computations were conducted using a plane-wave cutoff of 500 eV. The convergence criterion for the electronic self-consistence loop was established at 10−7 eV on the 13 × 7 × 4 Monkhorst-Pack k-point mesh. In terms of structural relaxation, the Hellmann-Feynman forces acting on each atom were assumed to be −0.01 eV/Å. The real Chern number νR can also be evaluated by using the Wilson-loop method, similar to the well-known Wilson-loop method for conventional topological insulators [49, 50]. The Wilson loop method traces the Wannier charge centre (Berry phase) evolution of valence wavefunctions between time-reversal-invariant momentum. The Wannier tight-binding method utilizes localized Wannier functions as basis orbitals to capture the compound’s physics. These basis Wannier functions are obtained from first-principles simulations. This procedure is implemented in the Wannier90 code [51].
Results and discussion
Firstly, we will assess the feasibility of identifying Z-ACA as an OAI. The OAI state of Z-ACA can be determined by applying the theory of elementary band representation (EBR). The EBRs correspond to the smallest sets of band structures that can be obtained using maximally localized atomic-like Wannier functions. The EBRs for the space group I4/mmm can be derived by combining the EBRs of the maximal WPs (2a, 2b, 4c, and 4d). Hence, we select the maximal WPs 2a, 2b, 4c, and 4d for the EBR decomposition of Z-ACA (see Figure 2).
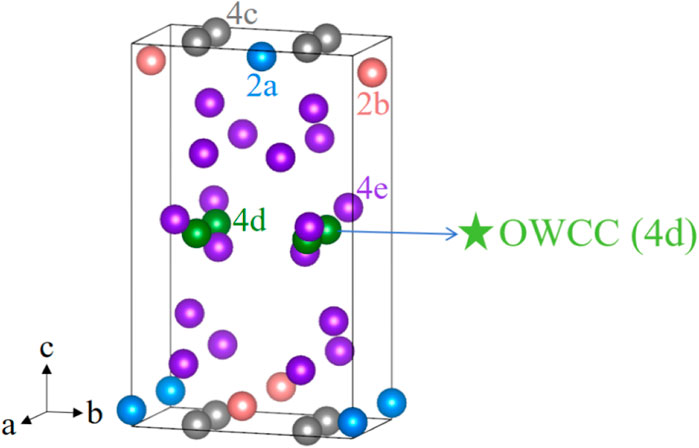
Figure 2. The 2a, 2b, 4c, and 4d WPs 2a, 2b, 4c, and 4d. Note that the green pentagram shows the OWCC located at 4d WP.
The electronic bands of trivial insulators can be represented by nonnegative integer Linear Combinations of Elementary Band Representations (LCEBRs) according to the topological quantum chemistry (TQC) theory [52]. Supplementary Table S1 presents the LCEBRs derived from the populated electronic bands of Z-ACA. Curiously, in the instance of Z-ACA, all the LCEBRs display a nonzero integer combination for EBR (Ag@4d). Hence, it may be deduced that the EBR is inseparable and must be linked to the electron-containing WPs by 4d. The carbon atom is situated at the 2a, 2b, and 4e locations, while the 4d position remains unoccupied. Z-ACA fulfills the requirements to be categorized as an OAI, and the 4d WP is the OWCC. The locations of OWCC are illustrated in Figure 2 with green pentagram. Figure 3 depicts the band structure of Z-ACA along the selected high-symmetry paths. Figure 3 clearly displays an insulating gap. Hence, Z-ACA can be viewed as a promising candidate for 3D OAI.
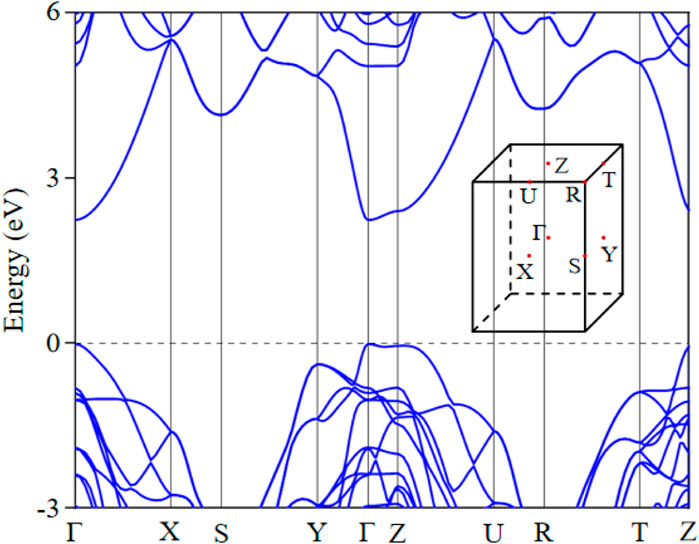
Figure 3. Band structure for Z-ACA and the 3D bulk Brillouin zone (BZ) with selected symmetry points.
In addition to its OAI nature, Z-ACA exhibits spacetime inversion symmetry and lacks the spin-orbit coupling (SOC) effect (see Supplementary Figure S1), making it a potential candidate for RCI. In order to verify the real Chern topologies of the 3D Z-ACA, it is necessary to calculate the vR values for the 2D kz-slices. In light of the system’s global band gap, it can be inferred that all 2D kz-slices are adiabatically connected, hence necessitating a shared νR.
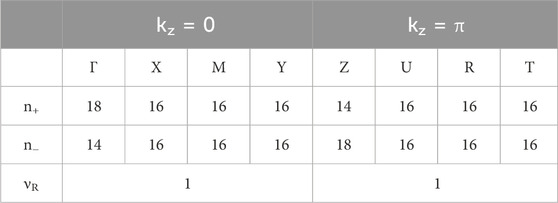
That is, one can select a particular slice, such as kz = 0 or kz = π plane, to determine the νR. To calculate the vR for the planes mentioned above, one can use the parity eigenvalues at the time-reversal invariant momentum points on each plane, as expressed by the following formula [53, 54]:
The
Table 1 presents the vR values of Z-ACA for the 2D kz = 0 and kz = π planes. A nonzero vR, which reflects the real topology, is discovered for Z-ACA. Actually, every 2D slice normal to kz has a nontrivial νR.
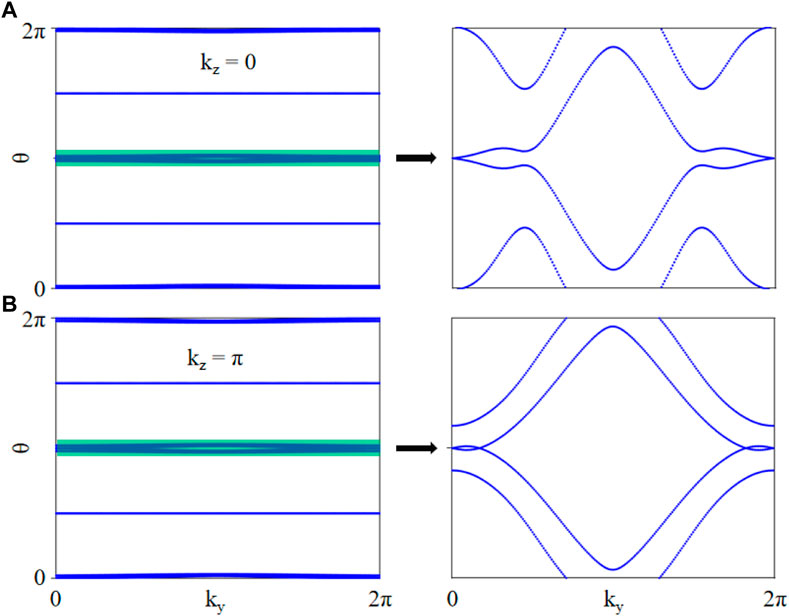
The nontrivial real topology of both planes can also be assessed using the Wilson-loop method. The computation will yield N curves in the θ-ky diagram, which represents the Wilson loop spectrum. As illustrated in Figure 4, the Wilson loop spectrum overlaps at one point and three points (an odd number of points) for θ = π in the kz = 0 and kz = π planes, showing nontrivial real topology in both planes.
Typically, 3D RCIs will demonstrate unconventional relationships between their bulk and boundary properties [44]. In other words, the 3D Z-ACA will have boundary states that exist in two dimensions less than the 3D bulk. Specifically, these boundary states will be confined to 1D hinges. In order to determine the behavior of possible hinges in Z-ACA, a tight-binding model (TB) was created for a one-dimensional tube with the geometry of Z-ACA. The sample used in the model retained its spacetime inversion symmetry. Later, the Wannier function [55–58] was used to calculate the band structure of the nanotube.
The band structure spectrum for the 1D tube geometry of Z-ACA is displayed in Figure 5. The presence of the hinge band is shown by the red line. Figure 6 depicts the spatial distributions of charges for the degenerate states (represented by red dots) at kz = 0. By examining the wave functions and seeing their localization at the two hinges of the nanotube (see Figure 6), we confirm that the degenerate states are indeed hinge states. As mentioned by Ref. [38], the hinge band for 3D RCI can be viewed as formed by stacking the corner modes of 2D RCI layers along z. Moreover, Hossain et al. [59] pointed out that the periodicity evinces quantum interference of electrons circumnavigating observed around the hinges, which can be applied to efficient topological electronic devices.
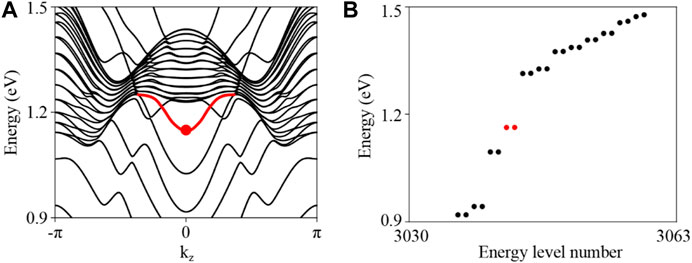
Figure 5. (A) Calculated band structure for the 1D tube geometry of Z-ACA. The hinge bands are shown in red. (B) Energy spectrum for Z-ACA sample with a 1D tube geometry.
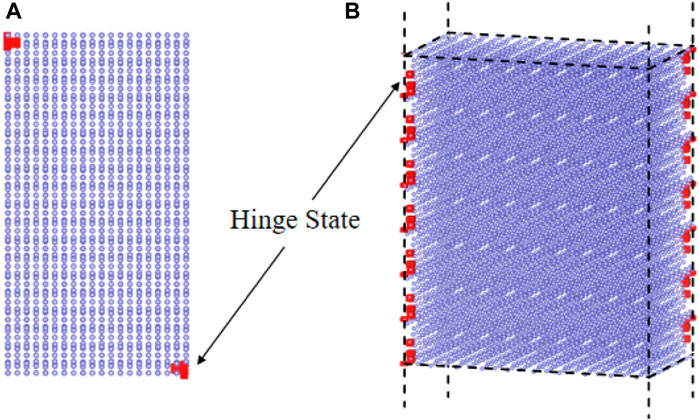
Figure 6. (A) and (B) Charge spatial distributions of the states (at kz = 0) marked by red dots in Figure 5B under different viewpoints.
Summary
Based on first-principles calculations, we suggest that the carbon allotrope Z-ACA, with the 4d site as OWCC, is a potential candidate for OAI. Further analysis reveals that Z-ACA possesses a real topology characterized by a nontrivial vR, which is safeguarded by the symmetry of spacetime inversion. The presence of hinge states, which are confined to the two hinges of the Z-ACA tube, was exhibited. The Z-ACA shows excellent potential as a subject for studying the fascinating physics related to real topological phases and hinge states.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author contributions
LW: Investigation, Software, Writing–original draft, Writing–review and editing. YL: Conceptualization, Investigation, Software, Writing–original draft, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by the Science and Technology Research Program of the Chongqing Municipal Education Commission (Grant No. KJZD-K202104101).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1437146/full#supplementary-material
References
2. Wang C, Xia K, Wang H, Liang X, Yin Z, Zhang Y. Advanced carbon for flexible and wearable electronics. Adv Mater (2019) 31(9):1801072. doi:10.1002/adma.201801072
3. Hu C, Dai L. Doping of carbon materials for metal-free electrocatalysis. Adv Mater (2019) 31(7):1804672. doi:10.1002/adma.201804672
5. Diederich F, Rubin Y. Synthetic approaches toward molecular and polymeric carbon allotropes. Angew Chem Int Edition English (1992) 31(9):1101–23. doi:10.1002/anie.199211013
6. Diederich F, Kivala M. All-carbon scaffolds by rational design. Adv Mater (2010) 22(7):803–12. doi:10.1002/adma.200902623
7. Rajkamal A, Thapa R. Carbon allotropes as anode material for lithium-ion batteries. Adv Mater Tech (2019) 4(10):1900307. doi:10.1002/admt.201900307
8. Sheng XL, Yan QB, Ye F, Zheng QR, Su G. T-carbon: a novel carbon allotrope. Phys Rev Lett (2011) 106(15):155703. doi:10.1103/physrevlett.106.155703
9. Hoffmann R, Kabanov AA, Golov AA, Proserpio DM. Homo citans and carbon allotropes: for an ethics of citation. Angew Chem Int Edition (2016) 55(37):10962–76. doi:10.1002/anie.201600655
10. Ye X, Qi M, Chen M, Zhang L, Zhang J. Zero to three dimension structure evolution from carbon allotropes to phosphorus allotropes. Adv Mater Inter (2023) 10(5):2201941. doi:10.1002/admi.202201941
11. Elcoro L, Wieder BJ, Song Z, Xu Y, Bradlyn B, Bernevig BA. Magnetic topological quantum chemistry. Nat Commun (2021) 12(1):5965. doi:10.1038/s41467-021-26241-8
12. Cao Y, Fatemi V, Fang S, Watanabe K, Taniguchi T, Kaxiras E, et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature (2018) 556(7699):43–50. doi:10.1038/nature26160
13. Cao Y, Fatemi V, Demir A, Fang S, Tomarken SL, Luo JY, et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature (2018) 556(7699):80–4. doi:10.1038/nature26154
14. Chen Y, Xie Y, Yan X, Cohen ML, Zhang S. Topological carbon materials: a new perspective. Phys Rep (2020) 868:1–32. doi:10.1016/j.physrep.2020.05.003
15. He T, Zhang X, Liu Y, Dai X, Liu G, Yu ZM, et al. Ferromagnetic hybrid nodal loop and switchable type-I and type-II Weyl fermions in two dimensions. Phys Rev B (2020) 102(7):075133. doi:10.1103/physrevb.102.075133
16. Zhong C, Chen Y, Yu ZM, Xie Y, Wang H, Yang SA, et al. Three-dimensional Pentagon Carbon with a genesis of emergent fermions. Nat Commun (2017) 8(1):15641. doi:10.1038/ncomms15641
17. Chen Y, Xie Y, Yang SA, Pan H, Zhang F, Cohen ML, et al. Nanostructured carbon allotropes with Weyl-like loops and points. Nano Lett (2015) 15(10):6974–8. doi:10.1021/acs.nanolett.5b02978
18. Rizzo DJ, Veber G, Jiang J, McCurdy R, Cao T, Bronner C, et al. Inducing metallicity in graphene nanoribbons via zero-mode superlattices. Science (2020) 369(6511):1597–603. doi:10.1126/science.aay3588
19. Jiang S, Scheurer F, Sun Q, Ruffieux P, Yao X, Narita A, et al. Length-independent quantum transport through topological band states of graphene nanoribbons (2022). arXiv preprint arXiv:2208.03145.
20. Ruffieux P, Cai J, Plumb NC, Patthey L, Prezzi D, Ferretti A, et al. Electronic structure of atomically precise graphene nanoribbons. ACS Nano (2012) 6(8):6930–5. doi:10.1021/nn3021376
21. Xu Y, Elcoro L, Song ZD, Vergniory MG, Felser C, Parkin SS, et al. Filling-enforced obstructed atomic insulators (2021). arXiv preprint arXiv:2106.10276.
22. Wang L, Jiang Y, Liu J, Zhang S, Li J, Liu P, et al. Two-dimensional obstructed atomic insulators with fractional corner charge in the M A 2 Z 4 family. Phys Rev B (2022) 106(15):155144. doi:10.1103/physrevb.106.155144
23. Ma DS, Yu K, Li XP, Zhou X, Wang R. Obstructed atomic insulators with robust corner modes. Phys Rev B (2023) 108(10):L100101. doi:10.1103/physrevb.108.l100101
24. Ding X, Jin X, Chen Z, Lv X, Ma DS, Wu X, et al. Abundant surface-semimetal phases in three-dimensional obstructed atomic insulators. Phys Rev B (2023) 108(8):085135. doi:10.1103/physrevb.108.085135
25. Marsal Q, Varjas D, Grushin AG. Obstructed insulators and flat bands in topological phase-change materials. Phys Rev B (2023) 107(4):045119. doi:10.1103/physrevb.107.045119
26. Liu XR, Deng H, Liu Y, Yin Z, Chen C, Zhu YP, et al. Spectroscopic signature of obstructed surface states in SrIn2P2. Nat Commun (2023) 14(1):2905. doi:10.1038/s41467-023-38589-0
27. Li XP, Ma DS, Liu CC, Yu ZM, Yao Y. From atomic semimetal to topological nontrivial insulator. Phys Rev B (2022) 105(16):165135. doi:10.1103/physrevb.105.165135
28. Li G, Xu Y, Song Z, Yang Q, Zhang Y, Liu J, et al. Obstructed surface states as the descriptor for predicting catalytic active sites in inorganic crystalline materials. Adv Mater (2022) 34(26):2201328. doi:10.1002/adma.202201328
29. Wang X, Li XP, Li J, Xie C, Wang J, Yuan H, et al. Magnetic second-order topological insulator: an experimentally feasible 2D CrSiTe3. Adv Funct Mater (2023) 33(49):2304499. doi:10.1002/adfm.202304499
30. Liu G, Jiang H, Guo Z, Zhang X, Jin L, Liu C, et al. Magnetic second-order topological insulators in 2H-transition metal dichalcogenides. Adv Sci (2023) 10(27):2301952. doi:10.1002/advs.202301952
31. Zhao YX, Lu Y. PT-symmetric real Dirac fermions and semimetals. Phys Rev Lett (2017) 118(5):056401. doi:10.1103/physrevlett.118.056401
32. Ahn J, Kim D, Kim Y, Yang BJ. Band topology and linking structure of nodal line semimetals with Z2 monopole charges. Phys Rev Lett (2018) 121(10):106403. doi:10.1103/physrevlett.121.106403
33. Benalcazar WA, Bernevig BA, Hughes TL. Quantized electric multipole insulators. Science (2017) 357(6346):61–6. doi:10.1126/science.aah6442
34. Sheng XL, Chen C, Liu H, Chen Z, Yu ZM, Zhao YX, et al. Two-dimensional second-order topological insulator in graphdiyne. Phys Rev Lett (2019) 123(25):256402. doi:10.1103/physrevlett.123.256402
35. Gong J, Wang Y, Han Y, Cheng Z, Wang X, Yu ZM, et al. Hidden real topology and unusual magnetoelectric responses in two-dimensional antiferromagnets. Adv Mater (2024):2402232. doi:10.1002/adma.202402232
36. Zhang X, He T, Liu Y, Dai X, Liu G, Chen C, et al. Magnetic real chern insulator in 2D metal–organic frameworks. Nano Lett (2023) 23(16):7358–63. doi:10.1021/acs.nanolett.3c01723
37. Zhu J, Wu W, Zhao J, Chen C, Wang Q, Sheng XL, et al. Phononic real Chern insulator with protected corner modes in graphynes. Phys Rev B (2022) 105(8):085123. doi:10.1103/physrevb.105.085123
38. Chen C, Wu W, Yu ZM, Chen Z, Zhao YX, Sheng XL, et al. Graphyne as a second-order and real Chern topological insulator in two dimensions. Phys Rev B (2021) 104(8):085205. doi:10.1103/physrevb.104.085205
39. Wang Y, Cui C, Zhang RW, Wang X, Yu ZM, Liu GB, et al. Mirror real Chern insulator in two and three dimensions (2024). arXiv preprint arXiv:2403.01145.
40. Li J, Liu Y, Bai J, Xie C, Yuan H, Cheng Z, et al. Phononic Weyl pair, phononic Weyl complex, phononic real Chern insulator state, and phononic corner modes in 2D Kekulé-order graphene. Appl Phys Rev (2023) 10(3). doi:10.1063/5.0159948
41. Liu BB, Zeng XT, Chen C, Chen Z, Sheng XL. Second-order and real Chern topological insulator in twisted bilayer α-graphyne. Phys Rev B (2022) 106(3):035153. doi:10.1103/physrevb.106.035153
42. Zeng XT, Liu BB, Yang F, Zhang Z, Zhao YX, Sheng XL, et al. Three-dimensional real Chern insulator in bulk γ-graphyne. Phys Rev B (2023) 108(7):075159. doi:10.1103/physrevb.108.075159
43. Chen C, Zeng XT, Chen Z, Zhao YX, Sheng XL, Yang SA. Second-order real nodal-line semimetal in three-dimensional graphdiyne. Phys Rev Lett (2022) 128(2):026405. doi:10.1103/physrevlett.128.026405
44. Wang J, Zhang TT, Zhang Q, Cheng X, Wang W, Qian S, et al. 3D carbon allotropes: topological quantum materials with obstructed atomic insulating phases, multiple bulk-boundary correspondences, and real topology. Adv Funct Mater (2024):2316079. doi:10.1002/adfm.202316079
45. He C, Sun L, Zhang C, Peng X, Zhang K, Zhong J. Four superhard carbon allotropes: a first-principles study. Phys Chem Chem Phys (2012) 14(23):8410–4. doi:10.1039/c2cp40531h
46. Sun G, Kürti J, Rajczy P, Kertesz M, Hafner J, Kresse G. Performance of the Vienna ab initio simulation package (VASP) in chemical applications. J Mol Struct THEOCHEM (2003) 624(1-3):37–45. doi:10.1016/s0166-1280(02)00733-9
47. Perdew JP, Burke K, Ernzerhof M. Perdew, burke, and ernzerhof reply. Phys Rev Lett (1998) 80(4):891. doi:10.1103/physrevlett.80.891
48. Perdew JP, Burke K, Ernzerhof M Generalized gradient approximation made simple. Phys Rev Lett (1996) 77(18):3865–8. doi:10.1103/physrevlett.77.3865
49. Yu R, Qi XL, Bernevig A, Fang Z, Dai X. Equivalent expression of Z2 topological invariant for band insulators using the non-Abelian Berry connection. Phys Rev B (2011) 84(7):075119. doi:10.1103/physrevb.84.075119
50. Soluyanov AA, Vanderbilt D. Wannier representation of Z2 topological insulators. Phys Rev B (2011) 83(3):035108. doi:10.1103/physrevb.83.035108
51. Pizzi G, Vitale V, Arita R, Blügel S, Freimuth F, Géranton G, et al. Wannier90 as a community code: new features and applications. J Phys Condensed Matter (2020) 32(16):165902. doi:10.1088/1361-648x/ab51ff
52. Bradlyn B, Elcoro L, Cano J, Vergniory MG, Wang Z, Felser C, et al. Topological quantum chemistry. Nature (2017) 547(7663):298–305. doi:10.1038/nature23268
53. Pan M, Li D, Fan J, Huang H Two-dimensional stiefel-whitney insulators in liganded xenes. npj Comput Mater (2022) 8(1):1. doi:10.1038/s41524-021-00695-2
54. Zhao YX. Equivariant PT-symmetric real Chern insulators. Front Phys (2020) 15(1):13603. doi:10.1007/s11467-019-0943-y
55. Marzari N, Mostofi AA, Yates JR, Souza I, Vanderbilt D. Maximally localized Wannier functions: theory and applications. Rev Mod Phys (2012) 84(4):1419–75. doi:10.1103/revmodphys.84.1419
56. Mostofi AA, Yates JR, Lee YS, Souza I, Vanderbilt D, Marzari N. wannier90: a tool for obtaining maximally-localised Wannier functions. Comput Phys Commun (2008) 178(9):685–99. doi:10.1016/j.cpc.2007.11.016
57. Wu Q, Zhang S, Song HF, Troyer M, Soluyanov AA. WannierTools: an open-source software package for novel topological materials. Comput Phys Commun (2018) 224:405–16. doi:10.1016/j.cpc.2017.09.033
58. Guo Z, Jiang H, Jin L, Zhang X, Liu G, Liu Y, et al. Second-order topological insulator in ferromagnetic monolayer and antiferromagnetic bilayer CrSBr. Small Sci (2024) 4:2300356. doi:10.1002/smsc.202300356
Keywords: topological carbon material, obstructed Wannier charge center, real topology, hinge states, Z-ACA allotrope
Citation: Wu L and Li Y (2024) Z-ACA allotrope: a topological carbon material with obstructed Wannier charge center, real topology, and hinge states. Front. Phys. 12:1437146. doi: 10.3389/fphy.2024.1437146
Received: 23 May 2024; Accepted: 24 June 2024;
Published: 19 July 2024.
Edited by:
Dipanjan Mazumdar, Southern Illinois University Carbondale, United StatesReviewed by:
Saurabh Basu, Indian Institute of Technology Guwahati, IndiaDongfei Wang, Beijing Institute of Technology, China
Copyright © 2024 Wu and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lunsheng Wu, bHN3dUBjcXl1LmVkdS5jbg==; Yang Li, bGl5YW5nQGNxd3UuZWR1LmNu
 Lunsheng Wu1*
Lunsheng Wu1* Yang Li
Yang Li