1 Introduction
Weak transition rates in stellar environments relevant to astrophysical processes in stars were evaluated with new shell-model Hamiltonians in the shell [1] and shell [2–4], which can describe spin responses in nuclei quite well. Electron-capture and -decay rates thus obtained were applied to study nuclear Urca processes in ONeMg cores of stars with 8–10 [5–7] and nucleosynthesis of iron-group elements in type Ia supernova (SN) explosions [8, 9]. New shell-model calculations lead to remarkable improvements in the weak rates induced by GT transitions. The quenching of the axial–vector coupling constant is introduced to take into account the effects of the truncation of the shell-model space as well as the coupling to non-nucleonic degrees of freedom such as resonance.
Neutron-rich nuclei in the island of inversion (– shell) [10] have been studied by shell-model [11] calculations with phenomenological interactions whose cross-shell part is constructed based on monopole-based universal interactions [12]. One of such interactions, SDPF-M [13], which induces a large admixture of -shell components, was successful in reproducing reduced excitation energies of states and enhanced B (E2) values. However, it failed to explain low-lying levels of 31Mg. The new effective interaction, EEdf1 [14, 15], obtained by the extended Kuo–Krenciglowa (EKK) method [16], is shown to be successful in explaining the structure of 31Mg. The weak rates for nuclei in the island of inversion are investigated in the – shell with the use of the effective interaction, EEdf1, especially for the pair of nuclei with A = 31, 31Al-31Mg, which are important for the nuclear Urca processes in neutron star crusts [17]. The -decay rates for -shell nuclei induced by GT transitions are evaluated by shell-model calculations in the – shell using an effective interaction obtained by the EKK method. The effects of the extension of the configuration space on the quenching factor of are investigated.
-decay and e-capture rates induced by second-forbidden transitions in 20F-20Ne were evaluated with the Behrens–Bühring (BB) [18, 19] and Walecka [20, 21] methods. The difference between the two methods was found to be insignificant as far as the conserved vector-current (CVC) condition was taken into account [22]. A possible important role of double e-capture reactions in 20Ne on the heating of the ONeMg cores in the late stages of star evolution was discussed [22–25]. The e-capture rates induced by first-forbidden transitions in 78Ni were studied with both the BB and the Walecka methods. The effect of electron distortion was found to be rather minor for the nucleus [22]. -decay rates induced by first-forbidden transitions were studied with the BB method for the isotones with = 126 and applied to r-process nucleosynthesis [26–28].
Here, the -decay rates induced by first-forbidden (FF) transitions in 206Hg and 207Tl are investigated with both the BB and the Walecka methods, and the two methods are compared. The effects of the electron distortion are examined.
2 -decay and e-capture rates induced by GT transitions
2.1 Weak rates in stellar environments
The -decay rate at finite density and temperature is given as follows in the multipole expansion method by Walecka [20, 21]:
where is the up–down element in the Cabibbo–Kobayashi–Maskawa quark mixing matrix with the Cabibbo angle; the weak vector coupling constant; and are electron energy and momentum, respectively; and is the Fermi–Dirac distribution for the electron. is the Fermi coupling constant, is the Fermi function, and = with and are the neutrino and electron momenta, respectively, and are the corresponding unit vectors, and = . and are the excitation energies (spins) of initial and final nuclear states, respectively. The value is determined from , where and are the masses of parent and daughter nuclei, respectively. The Coulomb, longitudinal, transverse magnetic, and electric multipole operators with multipolarity are denoted as , , , and , respectively, and the factor denotes the blocking of the decay by electrons in high-density matter.
In the case of an allowed GT transition, the sum of the axial electric dipole and axial longitudinal dipole terms contribute to the rate, and the shape factor becomes independent of the electron energy.
where is the total spin of the initial state and . This formula for the allowed transition given by Eq. 2 is equivalent to that in [3, 4, 29], which is based on the Behrens–Bühring method [18].
The e-capture rate at finite density and temperature is given by changing the integral in the first line of Eq. 1 as [20, 21], , where is the threshold energy for the electron capture and is the neutrino energy. is replaced by in the second line of Eq. 1. The shape factor is expressed in the same way as shown in Eq. 1, except that an integral is replaced by 1. is the momentum transfer, and the phase of the lepton matrix elements in the interference term of magnetic and electric form factors is reversed. In the nuclear transition matrix, is replaced by and .
Electron-capture and -decay rates in the shell were evaluated with the USDB Hamiltonian [1], with the quenching of the axial–vector coupling ( = = 0.764 [30]) at high temperatures ( = - K) and high densities ( = - g with the electron fraction) and applied to nuclear Urca processes in ONeMg cores. The e-capture rates increase, while the -decay rates decrease, as the density increases due to the increase in electron chemical potential at high densities. Both the weak rates coincide at a certain density, called an Urca density, almost independent of temperatures. Both and are emitted at the Urca density, thus taking away the energy from the star, which results in a drastic cooling of the core of the star. This mechanism, called the nuclear Urca process, occurs quite efficiently for the nuclear pairs with = 23 and 25, where the transitions between the ground states (g.s.s) are GT ones [5, 6]. The weak rates for the nuclear pairs, 23Na–23Mg and 25Mg–25Na, and the cooling of the ONeMg core of a star with 8.8 were studied in Refs [5, 7].
2.2 Weak rates of nuclei in the island of inversion
Urca processes for nuclear pairs in the island of inversion [10] such as 31Mg–31Al and 33Mg–33Al pairs have been pointed out to be important for the cooling of neutron star crusts [17]. We discuss the weak rates of the 31Mg–31Al pair. The SDPF-M interaction fails to reproduce the energy levels of 31Mg, that is, state becomes the g.s., while the experimental g.s. is . The Urca density cannot be clearly assigned for the weak rates for SDPF-M, as the transitions between the g.s.’s are forbidden. This shortcoming can be improved for the effective interaction obtained by the EKK (extended Kuo–Krenciglowa) method [14], starting from the chiral EFT LO [31] and Fujita–Miyazawa 3N interaction [32]. The EKK method can treat Q-box calculations in two major shells without divergence problems [16]. For this interaction, referred to as EEdf1 [15], neutron effective single-particle energies between -shell and -shell orbits become much closer in the neutron-rich region, = 10–12, compared with the conventional – shell Hamiltonian, SDPF-M [13]. This results in larger admixtures of -shell components for the EEdf1. Including up to 6p–6h excitations, energy levels of 31Mg can be well-explained by the EEdf1 [14, 15]. The g.s. of 31Mg is calculated to be , which is consistent with the experimental observation [33]. The first excited state is predicted to be , which is very close to the g.s. . As the g.s. of 31Al is , the GT transition between the state in 31Mg and in 31Al gives the main contribution to the e-capture and -decay rates for the = 31 pair. The weak rates in stellar environments obtained with the EEdf1 are shown in Figure 1. The GT transitions between 31Mg (, ) and 31Al (, , ) are taken into account. The free value for is used as the shell-model space is large. There exists an Urca density at () = 10.14, as shown in Figure 1 (left panel) for the EEdf1, since the excitation energy of the state in 31Mg is as small as 0.05 MeV. If the g.s. of 31Mg is taken to be , there does not exist an Urca density, as shown in Figure 1 (right panel), because of the non-existence of GT transitions between low-lying states. The transitions between the g.s.’s of 31Mg () and 31Al () are second-forbidden transitions. Their rates can be evaluated with the method explained in Refs [22, 23], and their contributions to the weak rates prove to be quite tiny and negligible in contrast to the case for the 20Ne ()-20F () pair.
2.3 -decay strengths of -shell nuclei in – shell configurations
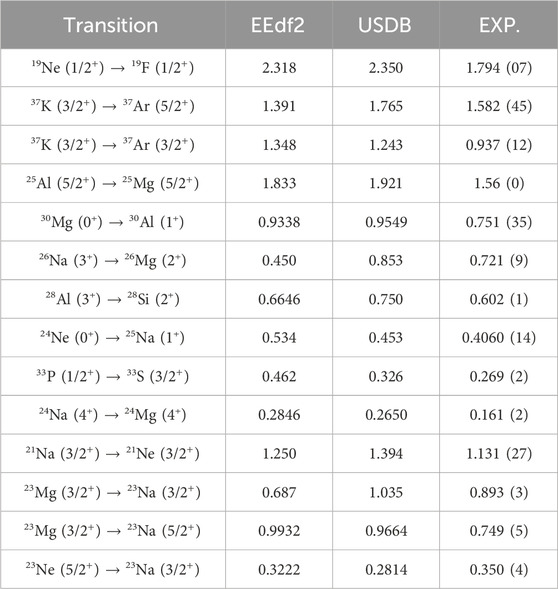
Although -decay rates in -shell nuclei are usually evaluated within the shell with a quenching for the axial–vector coupling, = 0.764 for USDB [30]; for example, we study here -decay strengths of -shell nuclei in an extended shell-model space, that is, in - shell. An effective interaction obtained with the EKK method is used. A modified version of EEdf1, which will be referred to as EEdf2 [34], is used. In EEdf2, the chiral LO three-nucleon interaction [35] is adopted instead of the Fujita–Miyazawa force. The following -decay transitions treated in Ref. [36] except for 34P 34S and four additional ones with A = 21 and 23, 21Na () 21Ne (), 23Mg () 23Na (), 23Mg () 23Na (), and 23Ne () 23Na () are examined. The quenching factor for is obtained by chi-squared fittings to the experimental data of the GT matrix element, which is defined as
where is the spin of the initial state. The quenching factor for is obtained to be = 0.86 0.06 for the EEdf2 for the configurations including up to 2p–2h excitations outside the shell. The quenching factor is obtained to be = 0.81 0.02 for the USDB in the shell. Calculated for the EEdf2 and USDB as well as the experimental data [37, 38] are shown in Figure 2 and Table 1. The quenching factor for in the – shell is found to become closer to = 1, compared with the case within the shell. The inclusion of more transitions is in progress. When about 90 more transitions in nuclei with = 19–34 are included, for EEdf2 remains higher than that for USDB by 0.05, while the latter comes close to = 0.77, which is consistent with the value reported in Ref. [30] for USDB [39].
An ab initio calculation with the valence-space in-medium renormalization group (VS-IMSRG) approach gives = 0.89 0.04 and = 0.96 0.06 for the case without and with the two-body current contributions, respectively [36]. The quenching factor would come closer to = 1 with the two-body current contributions.
3 -decay rates induced by first-forbidden transitions
The shape factors in the low momentum transfer limit obtained by the Walecka method are given as follows [22]:
where
with as the electron energy (=). Here, , where is the -value for the reaction and is the angular momentum of the initial state. The matrix elements, , , and , are contributions from spin-dipole transitions. , , and are Coulomb, transverse electric, and terms, respectively. The relation, = with , is satisfied from the CVC.
In the Behrens–Bühring (BB) method, distorted electron wave functions are used, which results in extra interference terms between the operators and the electron wave functions: , where = with the fine structure constant, for = , and for = (see Refs [18, 22] for the details). When these distortion effects are added to Walecka’s formulas, Eqs 4, 5, the method will be referred to as “Walecka with distortion.” Moreover, the following higher-order terms are usually added in the BB method. They can become important when dominant terms cancel to each other.
where = and and are distortion parameters, which are usually taken to be 1.0. The values of and are close to 1, but can become as small as 0.7 in the low electron momentum region for Z 80 [40]. , , and are modified from x, u, and w, respectively, by taking account of the finite-size effect of the nucleus. The -decay rate is obtained from the shape factors, and the half-life is given by .
The shape factors and log values are evaluated by (A) the BB method, (B) BB method with = = 1.0, and (C) the BB method with = = 1.0, but without the subdominant term (Eq. 6), which is equivalent to the Walecka method with distortion effects added ( 0): “Walecka with distortion” and (D) Walecka method (without the distortion ( = 0); Eqs 4, 5), and they are compared to each other. Calculated results of the averaged shape factors [26] and log values for -decays in 206Hg and 207Tl are shown in Table 2. Shell-model calculations are performed with the same modified G-matrix and model space, as used in Refs [26, 28]. A closed = 126 core is assumed for the parent nucleus. For proton holes, full configurations with the 0, 0, 1, 1, and 2 orbits are taken into account. The quenching factors for the axial-vector and vector coupling constants are taken to be = 0.34 and = 0.68, respectively [26, 41], and the enhancement factor for the term in transition is taken to be = 1.75 [26, 42]. Similar large quenching of and in and transitions was also reported in Ref. [27].
As we can see from Table 2, the approximation to use = = 1 is good enough, and the Walecka method with the electron distortion, , is satisfactory, while the deviation from the results of the BB method becomes large when the distortion is switched off in the Walecka method.
4 Summary and discussion
The new effective interaction in the – shell obtained by the EKK method [14, 16] from fundamental interactions [31, 32, 35] proves to be successful in the description of the structure in the island of inversion [10] and is used to evaluate the -decay and e-capture rates for the nuclear pair, 31Mg–31Al, in stellar environments. The Urca density for the pair can be assigned because dominant transitions between low-lying states are induced by GT transition. This leads to nuclear Urca processes in neutron star crusts [43]. The quenching of the axial–vector coupling constant in selected -shell nuclei is examined with the use of the effective interaction in the - shell. The extension of the model space to the – shell is found to enhance the quenching factor by 0.05 compared to the conventional Hamiltonians within the shell. More systematic studies including more -shell nuclei with contributions from two-body currents [36] are an interesting future issue.
-decays in 206Hg and 207Tl induced by first-forbidden transitions are studied with both the Behrens–Bühring (BB) [18] and the Walecka [20, 21] methods. The Walecka method with electron distortion corrections is shown to give results close to those of the BB method for the averaged shape factors and log values. Unless accidental cancellations among the dominant terms take place, the Walecka method with the distortion corrections, simpler and more accessible than the BB method, can be a useful approximation with enough accuracy even in the Z 80 region. It would be interesting to find out to what extent this statement is valid.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
TS: writing–original draft and writing–review and editing. NS: methodology, software, and writing–review and editing.
Funding
The authors declare that financial support was received for the research, authorship, and/or publication of this article. NAT Research Center; evaluation of the weak rates, shell-model calculations, publication charge, MEXT, Japan (JPMXP1020230411) “Program for promoting research on supercomputer FUGAKU,” and KAKENHI 24H00239; shell-model calculations, publication charge.
Acknowledgments
The authors would like to acknowledge the support from the “Program for promoting research on the supercomputer Fugaku,” MEXT, Japan (JPMXP1020230411), and KAKENHI budget 24H00239. TS would also like to acknowledge support from the NAT Research Center.
Conflict of interest
Author TS was employed by NAT Corporation.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
2. Honma M, Otsuka T, Mizusaki T, Hjorth-Jensen M, Brown BA. Effective interaction for nuclei of A = 50–100 and Gamow–Teller properties. J Phys Conf Ser (2005) 20:7–12. doi:10.1088/1742-6596/20/1/002
CrossRef Full Text | Google Scholar
3. Suzuki T, Honma M, Mao H, Otsuka T, Kajino T. Evaluation of electron capture reaction rates in Ni isotopes in stellar environments. Phys Rev C (2011) 83:044619. doi:10.1103/PhysRevC.83.044619
CrossRef Full Text | Google Scholar
4. Langanke K, Martínez-Pinedo G (2001). Rate tables for the weak processes of pf-shell nuclei in stellar environments. At. Data Nucl Data Tables 79:1. doi:10.1006/adnd.2001
CrossRef Full Text | Google Scholar
5. Toki H, Suzuki T, Nomoto K, Jones S, Hirschi R. Detailedβ-transition rates for URCA nuclear pairs in 8–10 solar-mass stars. Phys Rev C (2013) 88:015806. doi:10.1103/PhysRevC.88.015806
CrossRef Full Text | Google Scholar
6. Suzuki T, Toki H, Nomoto K. Electron-capture and β-decay rates for sd-shell nuclei in stellar environments relevant to high-density o–ne–mg cores. Astrophysical J (2016) 817:163. doi:10.3847/0004-637X/817/2/163
CrossRef Full Text | Google Scholar
7. Jones S, Hirschi R, Nomoto K, Fischer T, Timmes FX, Herwig F, et al. Advanced burning stages and fate of 8-10m☉stars. Astrophysical J (2013) 772:150. doi:10.1088/0004-637X/772/2/150
CrossRef Full Text | Google Scholar
8. Mori K, Famiano MA, Kajino T, Suzuki T, Garnavich PM, Mathews GJ, et al. Nucleosynthesis Constraints on the explosion mechanism for Type Ia Supernovae. J (2018) 863:176. doi:10.3847/1538-4357/aad233
CrossRef Full Text | Google Scholar
9. Mori K, Suzuki T, Honma M, Famiano MA, Kajino T, Kusakabe M, et al. Screening effects on electron capture rates and Type Ia supernova nucleosynthesis. J (2020) 904:29. doi:10.3847/1538-4357/abbb32
CrossRef Full Text | Google Scholar
11. Schatz H, Gupta S, Möller P, Beard M, Brown EF, Deibel AT, et al. Strong neutrino cooling by cycles of electron capture and β− decay in neutron star crusts. Nature (2014) 505:62–5. doi:10.1038/nature12757
PubMed Abstract | CrossRef Full Text | Google Scholar
12. Otsuka T, Suzuki T, Honma M, Utsuno Y, Tsunoda N, Tsukiyama K, et al. Novel Features of nuclear forces and shell evolution in exotic nuclei. Phys Rev Lett (2010) 104:012501. doi:10.1103/PhysRevLett.104.012501
PubMed Abstract | CrossRef Full Text | Google Scholar
13. Utsuno Y, Otsuka T, Mizusaki T, Honma M. Varying shell gap and deformation in 𝑁∼20 unstable nuclei studied by the Monte Carlo shell model. Phys Rev C (1999) 60:054315.
CrossRef Full Text | Google Scholar
14. Tsunoda N, Otsuka T, Shimizu N, Hjorth-Jensen M, Takayanagi K, Suzuki T. Exotic neutron-rich medium-mass nuclei with realistic nuclear forces. Phys Rev C (2017) 95:021304. doi:10.1103/PhysRevC.95.021304
CrossRef Full Text | Google Scholar
15. Otsuka T, Gade A, Sorlin O, Suzuki T, Utsuno Y. Evolution of shell structure in exotic nuclei. Rev Mod Phys (2020) 92:015002. doi:10.1103/RevModPhys.92.015002
CrossRef Full Text | Google Scholar
16. Takayanagi K (2011) Effective interaction in non-degenerate model space, Nucl Phys A 852, 61–81. doi:10.1016/j.nuclphysa.2011.01.003
CrossRef Full Text | Google Scholar
17. Schatz H, Gupta S, Möller P, Beard M, Brown EF, Deibel AT, et al. Strong neutrino cooling by cycles of electron capture and β− decay in neutron star crusts. Nature (2014) 505:62–5. doi:10.1038/nature12757
PubMed Abstract | CrossRef Full Text | Google Scholar
19. Schopper H. Weak interactions and nuclear beta decays. North-Holland, Amsterdam (1966).
Google Scholar
20. Walecka JD. In: VW Hughes, and CS Wu, editors. Muon Physics, II. New York: Academic (1975).
Google Scholar
21. O’Connell JS, Donnelly TW, Walecka JD. Semileptonic weak interactions withC12. Phys Rev C (1972) 6:719–33. doi:10.1103/physrevc.6.719
CrossRef Full Text | Google Scholar
23. Kirsebom OS, Jones S, Strömberg D, Martínez-Pinedo G, Langanke K, Röpke F, et al. Discovery of an Exceptionally Strong β-decay transition of F20 and Implications for the fate of intermediate-mass stars. Phys Rev Lett (2019) 123:262701. doi:10.1103/PhysRevLett.123.262701
PubMed Abstract | CrossRef Full Text | Google Scholar
24. Kirsebom OS, Hukkanen M, Kankainen A, Trzaska WH, Strömberg DF, Martínez-Pinedo G, et al. (2019). Measurement of the 2+→0+ ground-state transition in the 𝛽 decay of 20F. Phys Rev C 100, 065805. doi:10.1103/PhysRevC.100.065805
CrossRef Full Text | Google Scholar
25. Zha S, Leung S-C, Suzuki T, Nomoto K. Evolution of ONeMg core in Super-AGB stars toward electron-capture Supernovae: effects of Updated electron-capture rate. Astrophysical J (2019) 886:22. doi:10.3847/1538-4357/ab4b4b
CrossRef Full Text | Google Scholar
26. Suzuki T, Yoshida T, Kajino T, Otsuka T. βdecays of isotones with neutron magic number ofN=126andr-process nucleosynthesis. Phys Rev C (2012) 85:015802. doi:10.1103/PhysRevC.85.015802
CrossRef Full Text | Google Scholar
27. Zhi Q, Caurier E, Cuenca-García JJ, Langanke K, Martínez-Pinedo G, Sieja K. Shell-model half-lives including first-forbidden contributions forr-process waiting-point nuclei. Phys Rev C (2013) 87:025803. doi:10.1103/PhysRevC.87.025803
CrossRef Full Text | Google Scholar
28. Suzuki T, Shibagaki S, Yoshida T, Kajino T, Otsuka T. β-Decay rates for exotic nuclei and r-process nucleosynthesis up to thorium and Uranium. The Astrophys J (2018) 859:133. doi:10.3847/1538-4357/aabfde
CrossRef Full Text | Google Scholar
29. Fuller GM, Fowler WA, Newman MJ, Astrophysical J (1980) Stellar weak-interaction rates for sd-shell nuclei. I - nuclear matrix element systematics with application to Al-26 and selected nuclei of importance to the supernova problem, Astrophys J Suppl Ser, 42, Suppl. 42, 447, doi:10.1086/190657
CrossRef Full Text | Google Scholar
30. Richter WA, Mkhize, S S, Brown BA. sd-shell observables for the USDA and USDB Hamiltonians. Phys Rev C (2008) 78:064302. doi:10.1103/PhysRevC.78.064302
CrossRef Full Text | Google Scholar
31. Entem DR, Machleidt R. Accurate charge-dependent nucleon-nucleon potential at fourth order of chiral perturbation theory. Phys Rev C (2003) 68:041001(R). doi:10.1103/PhysRevC.68.041001
CrossRef Full Text | Google Scholar
33. Terry JR, Brown BA, Campbell CM, Cook JM, Davies AD, Dinca DC, et al. Single-neutron knockout from intermediate energy beams ofMg30,32: Mapping the transition into the “island of inversion”. Phys Rev C (2008) 77:014316. doi:10.1103/PhysRevC.77.014316
CrossRef Full Text | Google Scholar
34. Suzuki T, Shimizu N, Phys.Rev C 108, 014611 (2023). Neutrino-induced neutral- and charged-current reactions on Ar40, doi:10.1103/PhysRevC.108.014611
CrossRef Full Text | Google Scholar
35. Gazit D, Quaglioni S, Navratil P, Erratum: three-nucleon low-energy constants from the consistency of interactions and currents in chiral effective field theory Phys Rev Lett 103, 102502 (2009). Phys. Rev. Lett. 122, 029901 (2019), doi:10.1103/PhysRevLett.122.029901
PubMed Abstract | CrossRef Full Text | Google Scholar
36. Gysbers P, Hagen G, Holt JD, Jansen GR, Morris TD, Navratil P, et al. Discrepancy between experimental and theoretical β-decay rates resolved from first principles. Nat Phys (2019) 15:428–31. doi:10.1038/s41567-019-0450-7
CrossRef Full Text | Google Scholar
38. Brown BA, Wildenthal BH (1985) Experimental and theoretical Gamow-Teller beta-decay observables for the sd-shell nuclei. Data Nucl Data Tables 33, 347–404. doi:10.1016/0092-640x(85)90009-9
CrossRef Full Text | Google Scholar
39. Suzuki T, Kumar A, Shimizu N. To be reported.
40. Behrens H, Janecke J. Numerical Tables for beta-decay and electron capture. In: Landolt-bornstein, new Series, group I, 4. Berlin: Springer-Verlag (1969).
Google Scholar
41. Rydstrom L, Blomqvist J, Liotta RJ, Pomar C. Structure of proton-deficient nuclei near Pb. Nucl Phys A (1990) 512:217–40. doi:10.1016/s0375-9474(05)80002-8
CrossRef Full Text | Google Scholar
43. Ong W-J, Brown E, Browne J, Ahn S, Childers K, Crider B, et al. β decay of V61 and its role in cooling Accreted neutron star crusts. Phys Rev Lett (2020) 125:262701. doi:10.1103/PhysRevLett.125.262701
PubMed Abstract | CrossRef Full Text | Google Scholar