
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
MINI REVIEW article
Front. Phys. , 18 October 2024
Sec. Condensed Matter Physics
Volume 12 - 2024 | https://doi.org/10.3389/fphy.2024.1431805
This article is part of the Research Topic Current Research On Spin Glasses View all 12 articles
Over the past decade, spin-glass simulations have improved to the point that they now access time- and length-scales comparable to experiments at the mesoscale. A recent series of thin-film field-cooled/zero-field-cooled magnetization (FC/ZFC) experiments demonstrated activated spin dynamics, with a temperature-independent activation energy proportional to the logarithm of the film thickness and with coefficients in remarkable agreement with the simulation. These measurements require the application of small magnetic fields, which has been shown to affect the spin-glass energy landscape. Measurements of the
Spin-glasses are an archetypal complex system. The same rugged energy landscape characteristic to these frustrated magnets can describe polymers, structural glasses, the stock market, and even neural networks. Yet, despite the passage of more than 5 decades since their discovery, accompanied by intensive experimental and theoretical efforts, the underlying physics of the spin-glass state remains a mystery, with even the existence of a single ground state (in three dimensions) being an open question [1].
Experimentally, spin-glass systems are notoriously difficult to study. Spin-glasses are a magnetic system; however, absent the application of a magnetic field (either before or during a measurement), the magnetization will be 0. In order to directly probe the dynamics, an experimenter must apply a small magnetic field, which has been shown to alter the dynamics of the system, reducing the free-energy barriers due to the Zeeman interaction. Indeed, even small fields may fundamentally alter the nature of the system, with the “droplet” model [2, 3] predicting that the spin-glass state is destroyed by any field, no matter how small, although this has proven difficult to distinguish experimentally from the mean-field prediction of a (de Almeida–Thouless) phase transition in a field [4].
Moreover, spin-glass systems rapidly fall out of equilibrium. Their dynamics are slow and exhibit memory: in general, the result of a measurement on a spin-glass will depend on the parameters (e.g., applied field and temperature) at the time of the measurement and on the values of those parameters at all previous time points since cooling into the spin-glass state, although this description is complicated by effects such as temperature chaos. For this reason, for an unambiguous comparison between simulation and experiment, a well-defined cooling protocol should be used.
In this mini-review, we discuss recent spin-glass magnetometry measurements, which have been interpreted through the spin-glass coherence length. The coherence length is defined using a four-spin correlation function, and it is physically the characteristic length-scale of the thermally equilibrated domains within a spin-glass sample. Well below the spin-glass transition temperature, the domains grow very slowly and the system is out-of-equilibrium. In experiments, one way to probe the coherence length is to fabricate devices where the coherence length can increase to the sample thickness. Then, the dynamics should change from three- to two-dimensional, and the apparent freezing temperature is reduced. In simulations, the ground state is never known and may not be unique, so to measure the coherence length, researchers look at the overlap between many replicas of the system [5]. Because the computing power has increased (and costs have decreased) dramatically over the past decades, the JANUS collaboration has been able to design and build an FPGA-based, ultra-parallelized processor optimized specifically for Monte Carlo simulations of spin-glasses [6]. These simulations provide access to the spin-glass coherence length, and for the first time, experiments and simulations on mesoscale systems are able to probe comparable time- and length-scales, allowing direct comparison between the two.
After the discussion of the state-of-the-art conventional measurements and simulation, we will move to the main topic of this review: electronic noise measurements. These measurements are an ideal complement to the more conventional measurements for measurements on mesoscale systems, where dimensional effects play a role. The techniques discussed here are not new, but they are of renewed importance due to the advances in simulation and recent measurements of the spin-glass coherence length.
When a spin-glass is quenched from above its glass temperature
where
according to the Arrhenius law.
Recently, variations on this approach have been employed on Ge:Mn [8, 9], single-crystal Cu:Mn [10–13], polycrystalline Cu:Mn [14], and Cu:Mn thin-films [15, 16]. Moreover, in the decades since the work by Kisker et al., it has become possible to simulate spin-glasses on the same time- and length-scales probed experimentally [10, 11, 17–19]; the agreement between the dynamics of the coherence length extracted experimentally and from simulation has been remarkable [20].
In the Cu:Mn thin-film experiments (e.g., Refs. [15, 16]), the coherence length
In the vicinity of
Using this approach, Zhai et al. was able to fit data for multiple film thicknesses (ranging from 4 nm to 20 nm), taken at multiple temperatures, to Equation 3 with
Applying a magnetic field will reduce the maximum barrier height, due to the Zeeman interaction. Here,
where the Zeeman energy is given by
Thin-film spin-glasses are of intrinsic interest, however from both an academic and practical perspective. For instance, the performance of SQUID-based superconducting circuits—including frequency-tunable qubits enabling fast quantum gates—is limited by anomalous
While measurements of the field-cooled, zero-field-cooled, and thermoremanent magnetization, as well as measurements of the AC susceptibility, of mesoscale spin-glass devices have been tremendously successful, they are intrinsically limited due to magnetization being an extrinsic quantity: measurement signal-to-noise (SNR) always decreases with decreasing volume. These measurements require carefully designed systems and multi-layer samples, with many thin spin-glass layers separated by non-magnetic spacing layers [15, 16, 26–28]. Moreover, interesting spin-glass dynamics are the result of a rich energy landscape, consisting of many metastable states, and the application of even weak magnetic fields can alter this landscape [9, 16]. Finally, while this scheme works well for devices “small” in one dimension (thickness), it is difficult to imagine efficiently scaling the process to devices small in two or even three dimensions.
In the 1980s and 1990s, M.B. Weissman et al., demonstrated that transport measurements—specifically, measurements of either the fluctuations of the resistance of a mesoscale spin-glass device or measurements of the fluctuations in the fluctuations of the resistance—can provide similar and complementary information to the more conventional magnetometric probes [29–33]. Despite their non-ergodic nature, the fluctuation-dissipation theorem has been shown to apply to spin-glass dynamics, meaning that these noise measurements provide the same information as direct measurements of the AC susceptibility [34]. However, because resistance fluctuations are not an extrinsic property, going to smaller volumes does not degrade and can even improve the SNR. Additionally, noise measurements allow the spin-glass energy landscape to be probed without any perturbing magnetic field, eliminating any concern over whether the system is in the linear-response regime.
Transport measurements are a proven method of probing spin-glass dynamics. While the resistivity of a spin-glass shows no sharp signature near
The observed noise is due to universal conductance fluctuations (UCFs). Here, elastic scattering off of the magnetic dopants dominates over inelastic scattering, and the noise is due to changes in the interference in the Feynman paths of the electrons due to the reorienting of the magnetic moments of the dopants (spins). The UCF theory does result in a temperature-dependent
Measurements of the
If the barrier distribution is not uniform, but weighted more heavily at higher (lower) energies, the spectral exponent will not be exactly
This is illustrated in Figure 1. The key assumption here is that the barrier heights are independent of temperature, i.e., that the dynamics are activated. If they are not, one can repeat this analysis, but allow
where we have converted from
but it is defined at all temperatures, including well away from
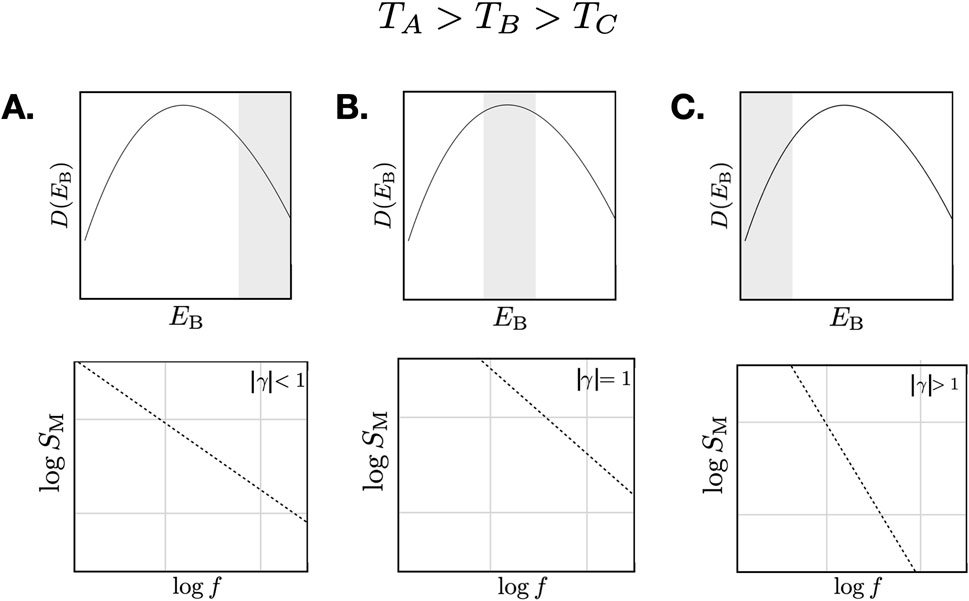
Figure 1. Dutta–Horn picture for a simple barrier distribution. (A) At high temperatures, a measurement will probe larger barriers. If the barrier distribution is weighted to lower energy, as shown, the spectral exponent will be smaller than unity. (B) At a lower temperature, the measurement will probe smaller barriers. Here, the experimental bandwidth is near the peak of the barrier distribution, which is approximately flat. The result is a spectral density with a spectral exponent near unity. The magnitude of the spectral density has also increased due to the larger density of barriers. (C) At a lower temperature still, the measurement will probe barriers below the peak. As the barrier distribution is now weighted to higher energy, the spectral exponent will be larger than unity, and because the barrier distribution is now smaller than at the peak, the magnitude of the noise has also decreased. Temperature-dependent barriers result in deviations from this picture.
We again note that
First, we compare recent transport measurements in spin-glasses. The effect of the cooling protocol on spin-glass thin-film measurements is still an open question; it is possible that temperature chaos renders the details of the experimental temperature quench moot, while Ref. [37] suggests that it is critical to rapidly quench from well above the bulk
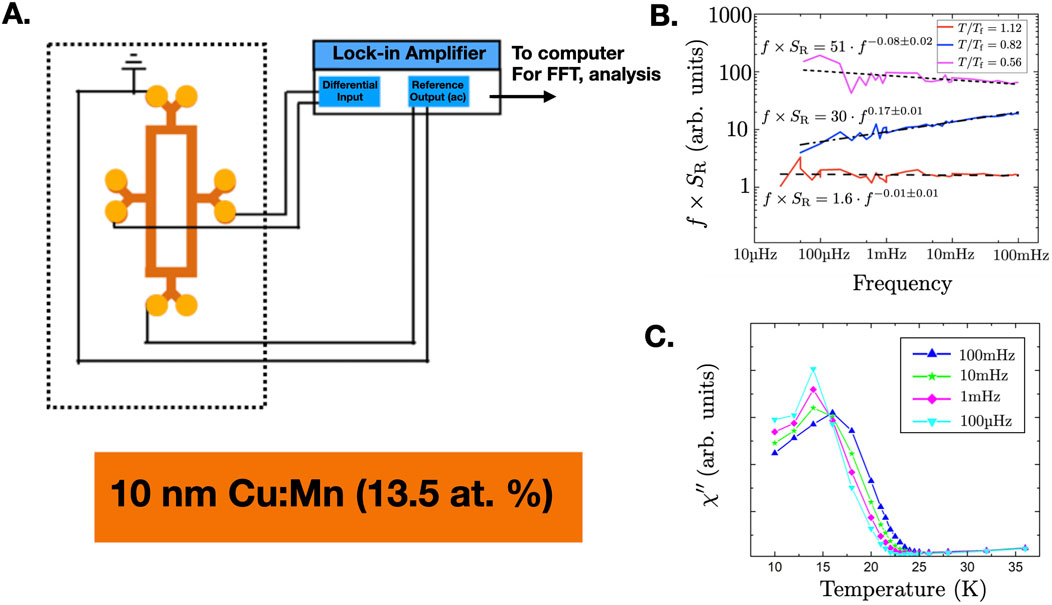
Figure 2. (A) Experimental setup for noise measurements; the dashed box denotes the inside of the cryostat. The spin-glass samples are patterned in a bridge configuration and measured with a lock-in technique. (B)
The analysis by Zhai et al. in Refs. [15, 16] takes the maximum barrier height, which governs the dynamics of a spin-glass, to be fixed once the spin-glass coherence length reaches the film thickness. In other words, the continued increase (if any) in the coherence length in the plane of the sample is taken to have no effect on the maximum barrier height. At this point, the dynamics are activated over fixed (temperature-independent) barriers. As discussed earlier, this implies
Fortunately, transport measurements offer a clear path in testing this physics. One possibility would be to fabricate samples small in two dimensions (e.g., 20-nm-wide wires) or in all three dimensions (e.g., 40-nm cubes). In order to get an acceptable SNR for the one-dimensional cubic devices, it would certainly be necessary to fabricate long chains with non-magnetic spacers, and it would be difficult to align and make good contact. However, while daunting, this is well within the limits of modern electron-beam lithography tools. With such devices, there would be only one length scale set by the film geometry, making it possible to rule out in-plane coherence length growth as the cause of temperature-dependent barriers. These measurements would leverage both advantages of transport techniques, which would enable the measurement of devices with such small volume while, and—because they do not rely on a Zeeman energy—would provide an independent confirmation of the previous measurements of in-plane correlation growth.
In addition, measurements of the second spectral density, i.e., the noise in the
DH: writing–original draft and writing–review and editing.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Newman CM, Stein DL. Ground-state stability and the nature of the spin glass phase. Phys Rev E (2022) 105:044132. doi:10.1103/physreve.105.044132
2. Fisher DS, Huse DA. Nonequilibrium dynamics of spin glasses. Phys Rev B (1988) 38:373–85. doi:10.1103/physrevb.38.373
3. Fisher DS, Huse DA. Equilibrium behavior of the spin-glass ordered phase. Phys Rev B (1988) 38:386–411. doi:10.1103/physrevb.38.386
4. de Almeida JR, Thouless DJ. Stability of the Sherrington-Kirkpatrick solution of a spin glass model. J Phys A: Math Gen (1978) 11 (5):983. doi:10.1088/0305-4470/11/5/028
5. Kisker J, Santen L, Schreckenberg M, Rieger H. Off-equilibrium dynamics in finite-dimensional spin-glass models. Phys Rev B (1996) 53:6418–28. doi:10.1103/physrevb.53.6418
6. Baity-Jesi M, Baños RA, Cruz A, Fernandez LA, Gil-Narvión J, Gordillo-Guerrero A, et al. Comp Phys Comm (2014) 185:550. doi:10.1016/j.cpc.2013.10.019
7. Joh YG, Orbach R, Wood GG, Hammann J, Vincent E. Extraction of the spin glass correlation length. Phys Rev Lett (1999) 82:438–41. doi:10.1103/physrevlett.82.438
8. Guchhait S, Orbach R. Direct dynamical evidence for the spin glass lower critical Dimension2<dℓ<3. Phys Rev Lett (2014) 112:126401. doi:10.1103/physrevlett.112.126401
9. Guchhait S, Orbach R. Magnetic field dependence of spin glass free energy barriers. Phys Rev Lett (2017) 118:157203. doi:10.1103/physrevlett.118.157203
10. Zhai Q, Paga I, Baity-Jesi M, Calore E, Cruz A, Fernandez LA, et al. Phys Rev Lett (2020) 125:237202. doi:10.1103/PhysRevLett.125.237202
11. Paga I, Zhai Q, Baity-Jesi M, Calore E, Cruz A, Cummings C, et al. Phys Rev B (2023) 107:214436. doi:10.1103/PhysRevB.107.214436
12. Zhai Q, Orbach RL, Schlagel DL. Evidence for temperature chaos in spin glasses. Phys Rev B (2022) 105:014434. doi:10.1103/physrevb.105.014434
13. Kenning GG, Schlagel DL, Thompson V. Experimental determination of the critical spin-glass correlation length in single-crystal CuMn. Phys Rev B (2020) 102:064427. doi:10.1103/physrevb.102.064427
14. Tennant DM, Orbach RL. Collapse of the waiting time effect in a spin glass. Phys Rev B (2020) 101:174409. doi:10.1103/physrevb.101.174409
15. Zhai Q, Harrison DC, Tennant D, Dahlberg ED, Kenning GG, Orbach RL, et al. Phys Rev B (2017) 95:054304. doi:10.1103/PhysRevB.95.054304
16. Zhai Q, Harrison DC, Orbach RL. Effect of magnetic fields on spin glass dynamics. Phys Rev B (2017) 96:054408. doi:10.1103/physrevb.96.054408
17. Baity-Jesi M, Calore E, Cruz A, Fernandez LA, Gil-Narvion JM, Gordillo-Guerrero A, et al. Phys Rev Lett (2018) 120:267203. doi:10.1103/PhysRevLett.120.267203
18. Fernandez LA, Marinari E, Martin-Mayor V, Parisi G, Ruiz-Lorenzo JJ. An experiment-oriented analysis of 2D spin-glass dynamics: a twelve time-decades scaling study. J Phys A: Math Theor (2019) 52:224002. doi:10.1088/1751-8121/ab1364
19. Fernandez LA, Marinari E, Martin-Mayor V, Paga I, Ruiz-Lorenzo JJ Phys Rev B (2019) 100:184412. doi:10.1103/PhysRevB.100.184412
20. He J, Orbach RL. Spin glass dynamics through the lens of the coherence length. Front Phys (2024) 12. doi:10.3389/fphy.2024.1370278
21. Zhai Q, Martin-Mayor V, Schlagel DL, Kenning GG, Orbach RL Phys Rev B (2019) 100:094202. doi:10.1103/PhysRevB.100.094202
22. Sendelbach S, Hover D, Kittel A, Mück M, Martinis JM, McDermott R. Magnetism in SQUIDs at millikelvin temperatures. Phys Rev Lett (2008) 100:227006. doi:10.1103/physrevlett.100.227006
23. Kumar P, Sendelbach S, Beck MA, Freeland JW, Wang Z, Wang H, et al. Phys Rev App (2016) 6:041001. doi:10.1103/PhysRevApplied.6.041001
24. Faoro L, Ioffe LB. Microscopic origin of low-frequency flux noise in josephson circuits. Phys Rev Lett (2008) 100:227005. doi:10.1103/physrevlett.100.227005
25. Sendelbach S, Hover D, Mück M, McDermott R. Complex inductance, excess noise, and surface magnetism in dc SQUIDs. Phys Rev Lett (2009) 103:117001. doi:10.1103/physrevlett.103.117001
26. Kenning G, Slaughter JM, Cowen JA. Finite-Size effects in a CuMn spin-glass. Phys Rev Lett (1987) 59:2596–9. doi:10.1103/physrevlett.59.2596
27. Granberg P, Nordblad P, Svedlindh P, Lundgren L, Stubi R, Kenning GG, et al. Dimensionality crossover in CuMn spin-glass films. J Appl Phys (1990) 67:5252–4. doi:10.1063/1.344627
28. Sandlund L, Granberg P, Lundgren L, Nordblad P, Svedlindh P, Cowen JA, et al. Dynamics of Cu-Mn spin-glass films. Phys Rev B (1989) 40:869–72. doi:10.1103/physrevb.40.869
29. Weissman MB, Israeloff NE, Alers GB J Magn Magn Mater (1992) 87:114. doi:10.1016/0304-8853(92)90336-M
31. Israeloff NE, Weissman MB, Nieuwenhuys GJ, Kosiorowska J. Electrical noise from spin fluctuations in CuMn. Phys Rev Lett (1989) 63:794–7. doi:10.1103/physrevlett.63.794
32. Israeloff NE, Alers GB, Weissman MB. Spin-fluctuation statistics inCuMn. Phys Rev B (1991) 44:12613–6. doi:10.1103/physrevb.44.12613
33. Fenimore PW, Weissman MB. Resistance noise as a technique for measuring finite-size effects in single-layer Cu_Mn spin-glass films. J Appl Phys (1999) 85:8317–21. doi:10.1063/1.370676
34. Reim W, Koch RH, Malozemoff AP, Ketchen MP, Maletta H. Magnetic equilibrium noise in spin-glasses: Eu0.4Sr0.6S. Phys Rev Lett (1986) 57:905–8. doi:10.1103/PhysRevLett.57.905
35. Van der Ziel A. On the noise spectra of semi-conductor noise and of flicker effect. Physica (1950) 16:359–72. doi:10.1016/0031-8914(50)90078-4
36. Dutta P, Horn P. Low-frequency fluctuations in solids:1fnoise. Rev Mod Phys (1981) 53:497–516. doi:10.1103/revmodphys.53.497
37. Guchhait S, Kenning GG, Orbach RL, Rodriguez GF. Spin glass dynamics at the mesoscale. Phys Rev B (2015) 91:014434. doi:10.1103/physrevb.91.014434
Keywords: spin-glass, noise, dimensional crossover, 1/f, resistance fluctuations
Citation: Harrison DC (2024) Electronic
Received: 12 May 2024; Accepted: 30 August 2024;
Published: 18 October 2024.
Edited by:
Ralph Chamberlin, Arizona State University, United StatesReviewed by:
Sebastiano Pilati, University of Camerino, ItalyCopyright © 2024 Harrison. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David C. Harrison, ZGNoYXJyaXNvbkB3aXNjLmVkdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.