- 1Applied Physics Department, Soreq Nuclear Research Center, Yavne, Israel
- 2Lab of Matter Structure and Laser Physics, Technical University of Crete, Chania, Greece
In this paper we explore the possibility of boosting the reactivity of non-thermal proton-boron fusion triggered by an external proton beam in a plasma at densities near and lower than solid density and temperature characteristic to laser plasma interaction. Suprathermal protons generated by collisions with alpha particles, as well as energetic protons created by the beam protons that do not undergo fusion during the stopping down in the bulk plasma, are accounted for. In addition, we conduct calculations for non-neutral plasma, motivated by recent suggestion that the number of fusion events in such system may be increased.
1 Introduction
During the last decades there has been renewed interest in proton - boron fusion, triggered by increasing yields of alpha particles in experiments with laser generated proton beams. Proton–boron fusion in the thermonuclear regime is prohibitive due to the low reactivity of pB11 fuel at temperatures lower than 100 keV and large bremsstrahlung radiation losses at higher temperatures. High intense laser pulses create non-thermal conditions and enable acceleration of ions to many MeV energies, opening the possibility to obtain nuclear fusion at temperatures of several and up to a few tens of keV. Non-thermal fusion was demonstrated experimentally in several configurations, based on high intensity short pulse lasers. “In-target” configuration, is realized by direct irradiation of solid targets containing hydrogen and boron [1–4]. In the “pitcher-catcher” scheme, protons are accelerated at the rear side of a thin foil target, the “pitcher”, through the mechanism of TNSA (target normal sheath acceleration [5]) and irradiate a solid boron-nitride target, the “catcher” [3, 6–8]. The “pitcher-catcher” scheme resembles traditional beam fusion, triggered by energetic protons generated in particle accelerators. However, the energy spectrum of protons accelerated through the TNSA mechanism is wider than the energy spectrum of accelerator-based protons. Recently, a high yield of alpha particles was measured in experiments with cellulite triacetate foam targets preheated by radiation from a laser generated hohlraum and irradiated by an intense short pulse laser generated proton beam [9].
Alongside experiments reporting alpha particle yields from non-thermal p-B fusion, additional configurations were proposed, based on analytic, molecular dynamics, particle in cell and kinetic calculations. A design for table-top p-B fusion based on Coulomb explosion of hydrogen nanodroplets, irradiated by intense femtosecond laser pulse, contained in a solid boron cylinder was reported in [10]. A non-thermal laser-driven mixed fusion reactor concept based on nano-structures confined by electric and magnetic fields generated in-situ was suggested in [11]. A path to proton-boron fusion based on simulation of the interaction of a high energy attosecond pulse with a solid proton-boron target was proposed in [12]. A recent review of the challenges of non-thermal proton-boron fusion configurations was reported by [13].
Almost a decade ago, the possibility of increasing non-thermal p-B fusion reactivity in laser generated plasmas by energy transfer from the alpha particles to plasma protons was suggested [14]. It was claimed that this phenomenon, called also avalanche or chain reaction, could explain the high yield of alpha particles in an experiment at the PALS facility [2]. In the experiment in presented in [2], a yield of 108 alpha particles per pulse was obtained by irradiating a hydrogen-enriched boron-doped silicon target with a 500 J, 0.3 ns laser pulse. The avalanche mechanism has been a subject of debate. After criticism from [15, 16], the possibility of enhancement of p-B fusion reactivity by energetic protons generated via alpha-proton elastic collision was further elaborated by [17–19] and [20, 21]. It was shown that this process is inhibited by thermalization of the energetic protons, and that, during the alpha particles slowing down, most of the alpha energy is transferred to the plasma electrons. Using a model based on binary collisions, [17] calculated an avalanche time longer than the time scale of the PALS experiment. Moreover, [8] generalized the model to densities several order of magnitudes higher than solid density and temperatures up to 100 keV. While [22] considered reducing the stopping power by injecting a MeV proton beam into a highly compressed quantum degenerated boron target.
Recently, alpha heating leading to self-sustained fusion at temperatures higher than tens of keV, however, lower than the characteristic temperature for thermal fusion, at low density proton-boron plasma, was shown in simulations by [23].
In this paper we explore the possibility of boosting the reactivity of non-thermal proton-boron fusion triggered by an external proton beam in a plasma at density of the order of solid density, and the critical density, characteristic to laser plasma interaction.
2 The model
In the framework of the pitcher-catcher scheme, we consider a proton beam generated by an intense laser pulse, typically through the TNSA mechanism, interacting with a proton-boron plasma. In the simulations, we assume that the protons’ energy spectrum is a delta function. Calculations were also made for a broad energy spectrum, characteristic to TNSA, however, it was found that the main findings of the present model do not change. The fusion probability Pf for the reaction
where nB is the boron plasma number density, v0 is the initial proton velocity, the cross section for fusion is σf, and the stopping power of the protons in the boron plasma is S.P. The term in the brackets inside the product denotes the probability that the proton does not participate in a fusion event within a velocity decrease of Δvp. The stopping power of a projectile particle in a plasma is calculated by [24]:
Where
The cross section for p-B fusion as function of the proton energy in the center of mass of the p-B system is given in Figure 1. The resonance of interest for the model considered here is the resonance at 675 keV with a width of 300 keV. In the calculations the cross section (CS) based on recent evaluation reported by Sikora [26] was used (the green line).
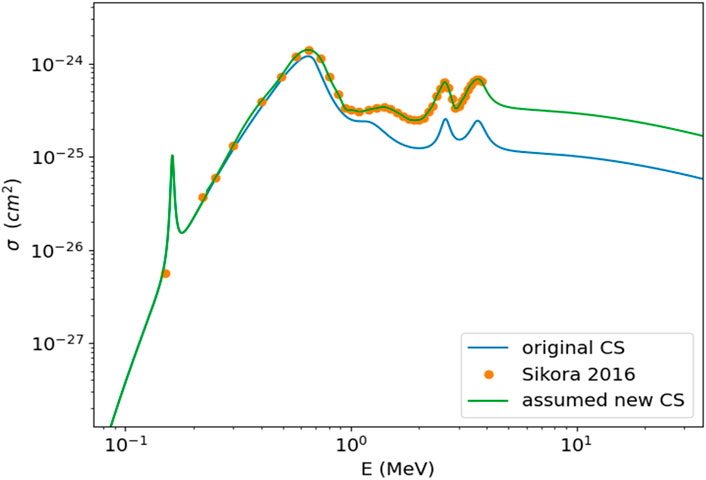
Figure 1. The cross section (CS) fusion probability as a function of the proton energy in the center of mass system based on analytical approximations of [27] original CS - blue, new evaluation from [26] - orange, the cross section used in the calculation presented here - green.
Figure 2A shows the primary fusion probability calculated from Equations 1, 2, as a function of the proton energy at plasma temperature and density for the cases considered in the following (see also Tables 1, 2), for
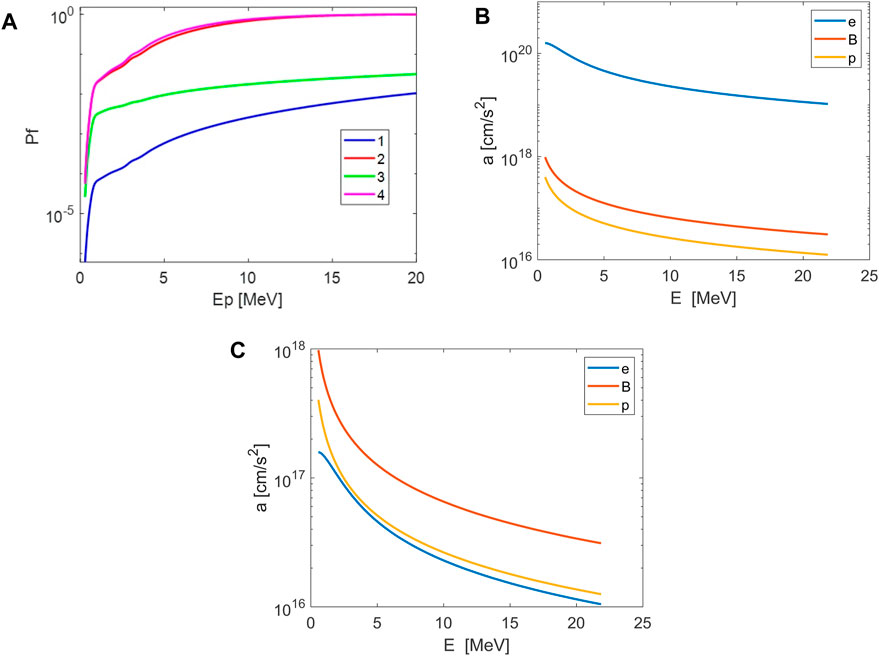
Figure 2. (A) The primary fusion probability as a function of the proton energy for neutral and non-neutral plasma with
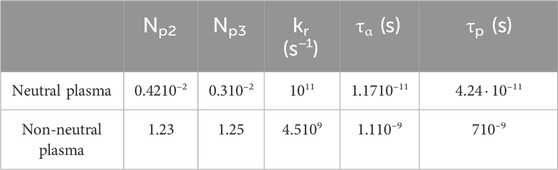
Table 1. Plasma parameters used for solving Equations 3 at density np = 1023 cm−3 and temperature Te = 340 eV, Ti = 100 eV.
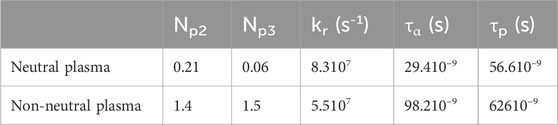
Table 2. Plasma parameters used for solving Equations 3 at density np = 1021 cm−3 and temperature Te = 10 keV, Ti = 1 keV.
Extending the model reported by Eliezer et al. [14] and Belloni et al. [17], the bulk protons number density is
The time dependent equations for the alpha particles and the energetic bulk protons number densities,
In the calculations presented here
The bulk proton-boron plasma is characterized by the electron and ion temperatures
where
Where
In our calculations, the cross section for the coulomb scattering,
The energy range of the scattered bulk protons is taken in the range (0.280 MeV - Epmax), determined by a minimum energy for the “useful protons” considered by Shmatov [15] and Belloni et al. [17], and the maximum energy.
The number of protons
In addition to Coulomb binary collisions, the nuclear contribution may increase the alpha particle–proton scattering cross section
The rate of relaxation
In the calculations, a monochromatic proton beam was used with energy of 6.4 MeV and effective beam proton density npb = 1021 cm−3. This value corresponds to an effective volume given by,
3 Results
In the following, the solution of the time dependent Equations 3 is shown for neutral and non-neutral plasma for two cases of proton-boron plasma. In all the calculations it is assumed that
First, we assume near solid proton density of 1023 cm−3, Te = 340 eV (the ionization energy of B4+ for an isolated atom [29]), Ti = 100 eV. These plasma parameters were chosen to extend the high density and degenerate plasma range considered by [18], to proton-boron fusion triggered by an external proton beam. The number of secondary protons generated by the alpha particles and the beam protons are calculated from Equations 5–7. At these plasma conditions for neutral plasma, the probability for a proton beam with energy of several MeV to produce one fusion event in neutral proton-boron plasma is less than 1%. The graphs in Figures 3–11 are calculated for beam proton energy of 6.4 MeV and alpha particle energy of 4 MeV, at the peak of the fusion generated alpha-particles energy spectrum. At this proton beam energy, plasma temperature and density, the probability for a proton to produce a fusion event is 0.001 in neutral plasma and 0.36 in non-neutral plasma with

Figure 3. The kinetic energy of a proton beam with initial energy of 6.4 MeV and alpha particle with energy of 4 MeV, as a function of time during their slowing down in a proton-boron plasma with np = 1023 cm−3,
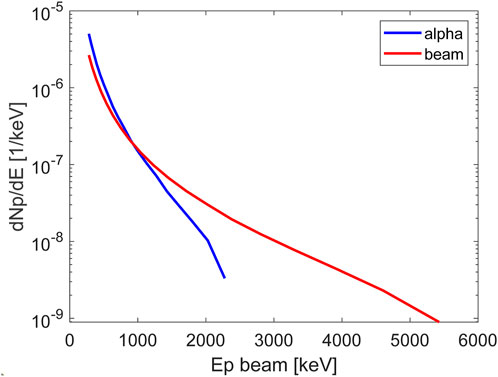
Figure 4. The energy spectrum of the secondary protons generated by an alpha particle with energy 4 MeV and a proton with energy 6.4 MeV during their slowing down to the ambient temperature in a proton-boron plasma with np = 1023 cm−3,
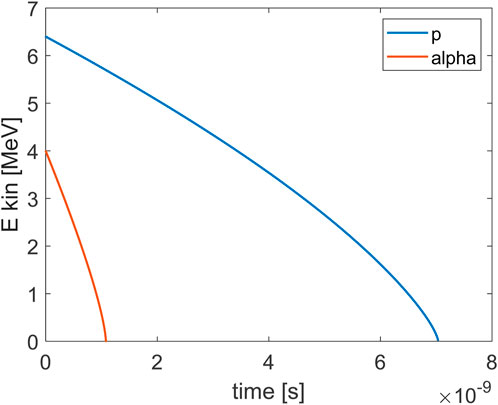
Figure 5. The kinetic energy of a proton beam with initial energy of 6.4 MeV and alpha particle with energy of 4 MeV, as a function of time during their slowing down in a proton-boron plasma with np = 1023 cm−3,
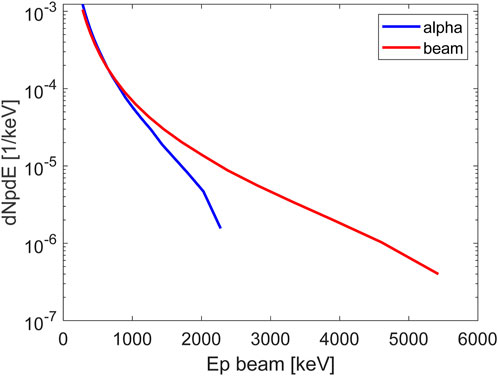
Figure 6. The energy spectrum of the secondary protons generated by an alpha particle with energy 4 MeV and a proton beam with energy 6.4 MeV during their slowing down to the ambient temperature in a proton-boron plasma with np = 1023 cm−3,
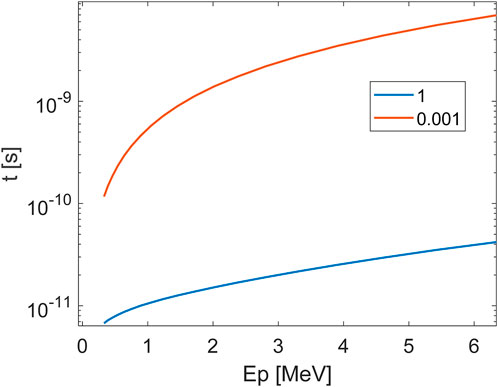
Figure 7. The relaxation time of the secondary protons as a function of energy in a proton-boron plasma with np = 1023 cm−3,
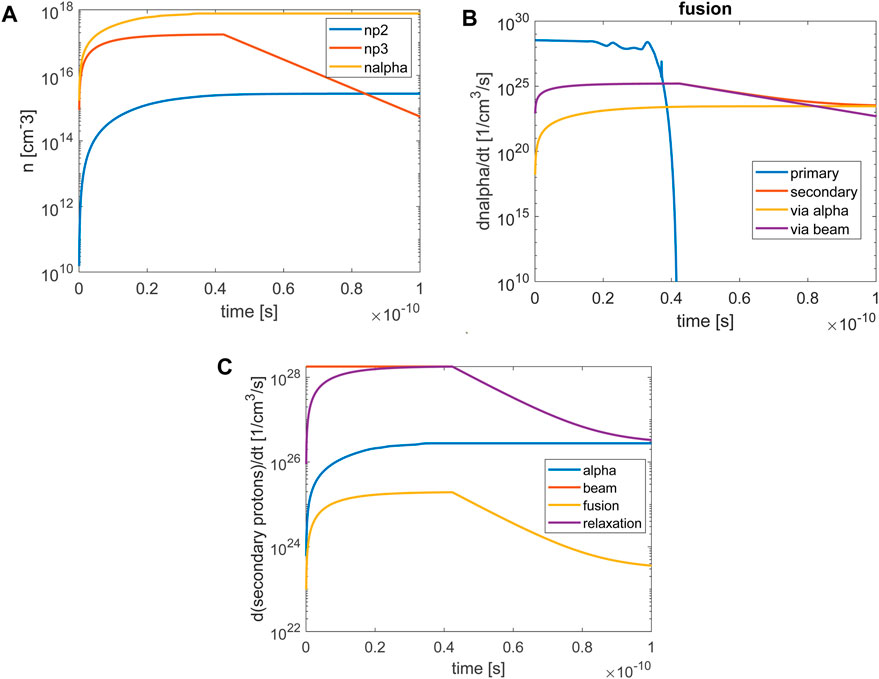
Figure 8. (A) The number density of alpha particles and secondary protons as a function of time, (B) the fusion reaction rate, (C) the source and sink terms for the secondary protons, as a function of time for neutral plasma and parameters in Table 1.
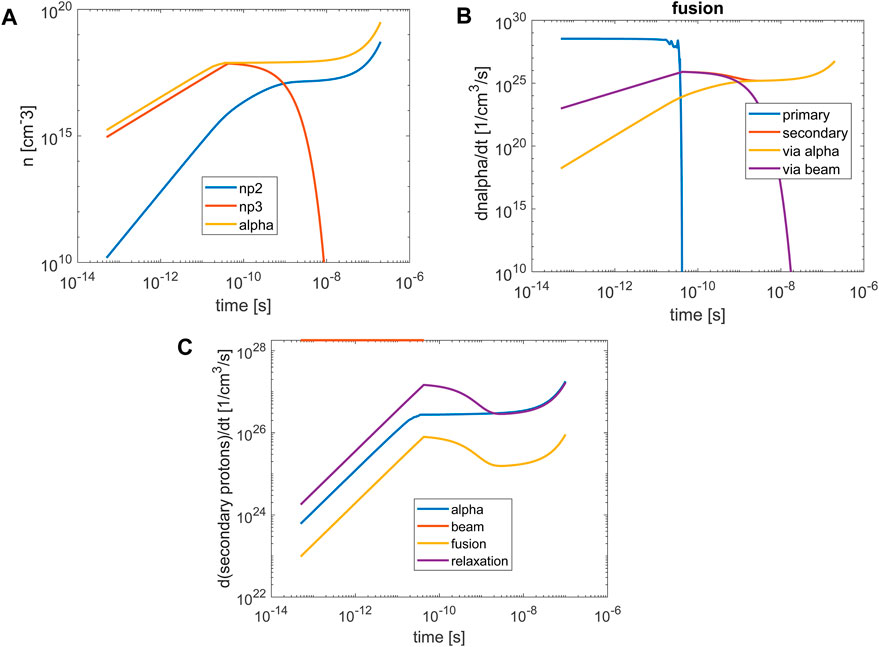
Figure 9. (A) The number density of alpha particles and secondary protons as a function of time, (B) The fusion reaction rate, (C) the source and sink terms for the secondary protons, as a function of time for neutral plasma and parameters in Table 1, with relaxation term for the secondary protons smaller by a factor of 50.
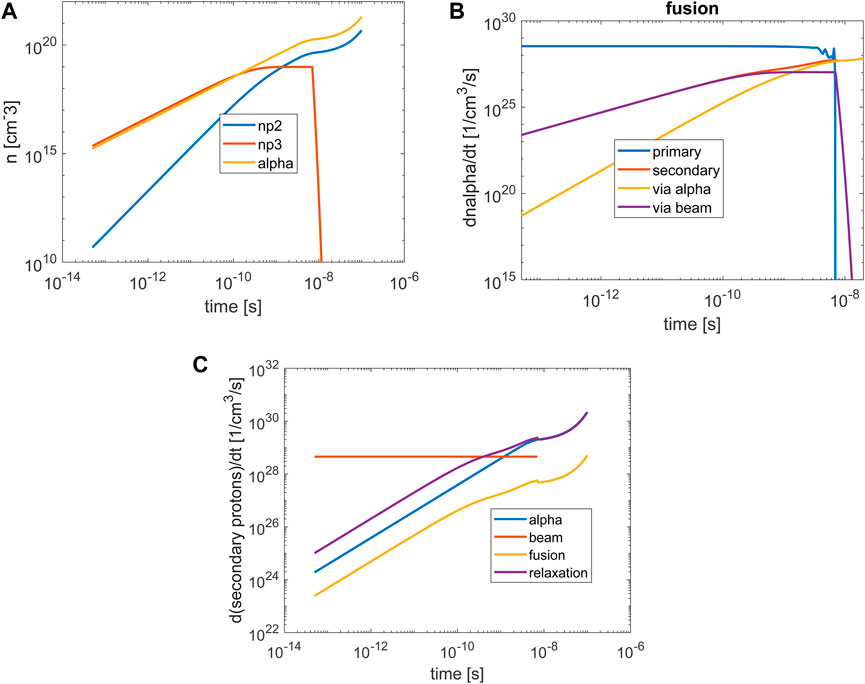
Figure 10. (A) The number density of alpha particles and secondary protons, (B) the rate of fusion events, as a function of time, for non-neutral plasma, (C) the number of secondary protons calculated with
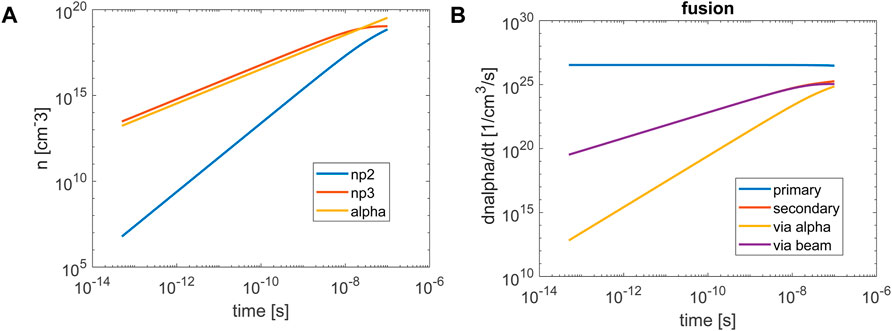
Figure 11. (A) The number density of the alpha particles and the secondary protons as a function of time for non-neutral plasma, density np = 1021 cm−3 and temperature Te = 10 keV, Ti = 1 keV, (B) the reaction rate of the fusion events. (C) the time dependence of the secondary protons.
In Table 1 the plasma parameters used for solving the equations are given. Np2 is the number of secondary protons generated by one alpha particle with energy 4 MeV, calculated using the scattering cross section
In the following, a figure of merit describing boosting of reactivity by alpha generated secondary protons is defined by
The effective density of the proton beam in the calculations is
Figures 8 displays the solution of Equations 3 for a neutral plasma. Figure 8A shows the number density of the alpha particles and secondary protons generated by the alpha and the external beam as a function of time, Figure 8B shows the fusion reactivity, while Figure 8C shows the terms relevant for the secondary fusion reaction rate. At early times the secondary protons are mainly generated by the external beam. As the beam slows down, these secondary protons decay. With onset of primary fusion secondary protons are generated by the alpha particles (Figure 8A). However, the fusion reaction rate generated by the secondary protons is about five orders of magnitude lower than the primary fusion (Figure 8B). An avalanche process does not occur, as it is mitigated by the secondary protons’ relaxation term. The terms relevant for secondary fusion (Figure 8C) are:
The terms in Equations 8–10 are calculated and presented in Figures 8–10 for different plasma parameters. After the external beam slows down, the generation of secondary protons is balanced by their relaxation and secondary fusion is not boosted.
To illustrate the inhibition effect of the secondary fusion by the thermalization of the secondary protons, Equations 3 were solved for a lower relaxation term. Figures 9 shows the number density and the fusion reactivity, for a lower relaxation term by a factor of 50. After about 30 ns, the number density of the secondary protons increases, and secondary fusion is set. The confinement of the plasma to tens of nanoseconds might be achieved by magnetic fields, however, the possibility of decreasing the relaxation term is challenging.
Figure 10 displays the solution of Equations 3 for non-neutral plasma, with
In this case, the number of secondary protons created by the alpha particles increases after the external beam slows down and the primary fusion stops (Figure 10A). The number of fusion events rises due to the secondary protons generated by the alpha particles. (Figure 10B). Figure 10C shows the terms that determine the time dependence of the secondary protons. The generation of the secondary protons due to the beam (red line) is constant and stops after the beam stops. The number of secondary protons generated by the alpha particles increases as the primary fusion develops and continues to increase after the beam stops, i.e., avalanche or boosting of fusion occurs (Figure 10C).
Secondly, we assume plasma parameters characteristic to laser plasma interaction, density np = 1021 cm−3 and temperature Te = 10 keV, Ti = 1 keV. The number of secondary protons and their relaxation time for neutral and non-neutral plasma are given in Table 2. Similarly to the high plasma density case, due to the large relaxation rate, the secondary protons do not induce secondary fusion in neutral plasma. Decreasing the relaxation rate by one order of magnitude, the secondary protons density reaches
Figure 11 shows the number density of the alpha particles and the secondary protons for non-neutral plasma as a function of time for the plasma parameters shown in Table 2. The number densities of the alpha particles, secondary protons produced by the beam and by the alpha particles are shown in Figure 11A. It is seen that in this case the number of secondary protons reach
4 Conclusion
The possibility of boosting non-thermal proton-boron fusion by energetic secondary protons generated by the alpha-particles through elastic scattering was investigated. Such a boosting may possibly lead to a self-sustained chain reaction. We consider proton-boron fusion induced by an external proton beam in a homogenous plasma of density and temperature of interest for laser driven experiments. The secondary protons energy spectrum and their thermalization was calculated, leading to three parameters, the effective number of secondary protons generated by an alpha particle and a beam proton during their slowing down and the relaxation rate of the secondary protons. With these three parameters, the possibility of secondary fusion was calculated, based on a simple three-population model. The results show that secondary fusion is inhibited by the fast thermalization of the secondary protons. The slowing down of the beam protons and the alpha particles in the bulk plasma were calculated using a stopping power based on Maxwellian distribution function for the particles in the plasma. In the framework of this model the charged particles transfer most of their energy to the electrons, inhibiting generation of suprathermal ions.
To decrease the effect of the thermalization of the secondary protons, non-neutral plasma was also considered in the calculation. In this case the relaxation rate of the secondary protons is much lower and secondary fusion occurs, leading to the desired avalanche effect.
Indeed, achieving such non-neutral plasma for fusion purposes is not trivial, however, such low electron density plasmas do occur, for example, in a double layer created at the interface of a laser-target interaction [30], or in a Debye sheath at a tokamak boundary [31].
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
NN: Writing–original draft, Writing–review and editing, Conceptualization. ZH: Formal Analysis, Methodology, Software, Writing–original draft, Writing–review and editing. SE: Conceptualization, Writing–original draft, Writing–review and editing. YS: Methodology, Software, Writing–review and editing. CD: Writing–review and editing. SM: Formal Analysis, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Israeli Ministry of Energy and the Israeli Institute for Fusion Research.
Acknowledgments
We gratefully acknowledge the fruitful discussions with Fabio Belloni during the writing of this manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2024.1428608/full#supplementary-material
References
1. Belyaev VS, Krainov VP, Matafonov AP, Zagreev BV. The new Possibility of the Fusion p + 11 B chain reaction being Induced by intense laser pulses. Laser Phys Lett (2015) 12:096001. doi:10.1088/1612-2011/12/9/096001
2. Picciotto A, Margarone D, Velyhan A, Bellutti P, Krasa J, Szydlowsky A, et al. Boron-proton nuclear-fusion enhancement induced in boron-doped silicon targets by low-contrast pulsed laser. Phys Rev X (2014) 4:031030. doi:10.1103/physrevx.4.031030
3. Margarone D, Picciotto A, Velyhan A, Krasa J, Kucharik M, Mangione A, et al. Advanced scheme for high-yield laser driven nuclear reactions. Plasma Phys Control Fusion (2015) 57:014030. doi:10.1088/0741-3335/57/1/014030
4. Giuffrida L, Belloni F, Margarone D, Petringa G, Milluzzo G, Scuderi V, et al. High-current stream of energetic α particles from laser-driven proton-boron fusion. Phys Rev E (2020) 101:013204. doi:10.1103/physreve.101.013204
5. Passoni M, Bertagna L, Zani A. Target normal sheath acceleration: theory, comparison with experiments and future perspectives. New J Phys (2010) 12:045012. doi:10.1088/1367-2630/12/4/045012
6. Labaune C, Baccou C, Depierreux S, Goyon C, Loisel G, Yahia V, et al. Fusion reactions initiated by laser-accelerated particle beams in a laser-produced plasma. Nat Commun (2013) 4:2506. doi:10.1038/ncomms3506
7. Baccou C, Depierreux S, Yahia V, Neuville C, Goyon C, De Angelis R, et al. New scheme to produce aneutronic fusion reactions by laser-accelerated ions. Beams (2015) 33:117–22. doi:10.1017/s0263034615000178
8. Bonvalet J, Nicolaï P, Raffestin D, D'humieres E, Batani D, Tikhonchuk V, et al. Energetic α -particle sources produced through proton-boron reactions by high-energy high-intensity laser beams. Phys Rev E (2021) 103:053202. doi:10.1103/physreve.103.053202
9. Zhao Y, et al. Proton-boron fusion: a dark horse in the fusion race shows yield much beyond expectation.
10. Last I, Ron S, Jortner J, Aneutronic H+ B11 nuclear fusion driven by coulomb explosion of hydrogen nanodroplets. Phys Rev A (2011) 83:043202. doi:10.1103/physreva.83.043202
12. Ribeyre X, Capdessus R, Wheeler J, d’Humières E, Mourou G. Multiscale study of high energy attosecond pulse interaction with matter and application to proton–boron fusion. Sci Rep (2022) 12:4665. doi:10.1038/s41598-022-08433-4
13. McKenzie W, Batani D, Mehlhorn TA, Margarone D, Belloni F, Campbell EM, et al. HB11—understanding hydrogen-boron fusion as a new clean energy source. J Fusion Energ (2023) 42:17. doi:10.1007/s10894-023-00349-9
14. Eliezer S, Hora H, Korn G, Nissim N, Martinez Val JM. Avalanche proton-boron fusion based on elastic nuclear collisions. Phys Plasmas (2016) 23:050704. doi:10.1063/1.4950824
15. Shmatov ML. Comment on “avalanche proton-boron fusion based on elastic nuclear collisions” phys. Plasmas. Phys Plasmas (2016) 23:094703. doi:10.1063/1.4963006
16. Shmatov ML, Batani D. Analysis of the P- 11 B fusion Scenario with Compensation of the Transfer of kinetic Energy of Protons and alpha Particles to the gas Medium by the electric field, laser part. Beams (2022) 2022:e13. doi:10.1155/2022/7473118
17. Belloni F, Margarone D, Picciotto A, Schillaci F, Giuffrida L. On the enhancement of P-11B fusion reaction rate in laser-driven plasma by α → p collisional energy transfer. Phys Plasmas (2018) 25:020701. doi:10.1063/1.5007923
18. Belloni F. On a fusion chain Reaction via suprathermal Ions in high-density H– 11 B plasma. Plasma Phys Control Fusion (2021) 63:055020. doi:10.1088/1361-6587/abf255
19. Belloni F, Batani K. Multiplication Processes in high-density H- 11 B fusion fuel, laser part. Beams (2022) 2022:e11. doi:10.1155/2022/3952779
20. Ochs IE, Kolmes EJ, Mlodik ME, Rubin T, Fisch NJ. Improving the feasibility of economical proton-boron-11 fusion via alpha channeling with a hybrid fast and thermal proton scheme. Phys Rev E (2022) 106:055215. doi:10.1103/physreve.106.055215
21. Ochs IE, Fisch NJ. Lowering the reactor breakeven requirements for proton–boron 11 fusion. Phys Plasmas (2024) 31:012503. doi:10.1063/5.0184945
22. Liu SJ, Wu D, Hu TX, Liang TY, Ning XC, Liang JH, et al. Proton-boron fusion scheme taking into account the effects of target degeneracy. Phys Rev Res (2024) 6:013323. doi:10.1103/physrevresearch.6.013323
23. Moustaizis S, Daponta C, Eliezer S, Henis Z, Lalousis P, Nissim N, et al. Alpha heating and avalanche effect simulations for low density proton-boron fusion plasma. J Inst (2024) 19:C01015. doi:10.1088/1748-0221/19/01/c01015
24. Huba JD. Beam Physics Branch, Plasma Physics Division. Washington, DC: Naval Research Laboratory (2007): 20375.
25. Nissim N. Parametric scan of plasma parameters for optimization of the avalanche process in p_11B fusion. In: The 2nd international workshop on proton-boron fusion. Catania, Italy (2022).
26. Sikora MH, Weller HR. A New Evaluation of the 11B (p,α) α α Reaction Rates. J Fusion Energ (2016) 35:538–43. doi:10.1007/s10894-016-0069-y
27. Nevins WM, Swain R. The thermonuclear fusion rate Coefficient for P- 11 B reactions. Nucl Fusion (2000) 40:865–72. doi:10.1088/0029-5515/40/4/310
28. Gurbich AF. SigmaCalc recent development and present status of the evaluated cross-sections for IBA. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2016) 371:27–32. doi:10.1016/j.nimb.2015.09.035
29. Lide DR. CRC handbook of chemistry and physics: 2000-2001 a ready-reference book of chemical and physical data. 81st ed. Boca Raton New York Washington: CRC Press (2000).
30. Eliezer S, Nissim N, Martínez Val JM, Mima K, Hora H. Double layer acceleration by laser radiation. Laser Part Beams (2014) 32:211–6. doi:10.1017/s0263034613001018
Keywords: proton boron fusion, stopping power, plasma, avalanche, beam
Citation: Nissim N, Henis Z, Eliezer S, Schweitzer Y, Daponta C and Moustaizis S (2024) Boosting of fusion reactions initiated by laser accelerated proton beam in a non-thermal neutral and non-neutral proton-boron plasma. Front. Phys. 12:1428608. doi: 10.3389/fphy.2024.1428608
Received: 06 May 2024; Accepted: 15 October 2024;
Published: 11 November 2024.
Edited by:
Krishnamurthy Manchikanti, Tata Institute of Fundamental Research, IndiaReviewed by:
Prashant Kumar Singh, Tata Institute of Fundamental Research (Hyderabad), IndiaDong Wu, Shanghai Jiao Tong University, China
Copyright © 2024 Nissim, Henis, Eliezer, Schweitzer, Daponta and Moustaizis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: N. Nissim, bm9hem5pc3NpbUBnbWFpbC5jb20=
 N. Nissim
N. Nissim Z. Henis
Z. Henis S. Eliezer
S. Eliezer Y. Schweitzer
Y. Schweitzer C. Daponta
C. Daponta S. Moustaizis
S. Moustaizis