Abstract
Accurately predicting landslide displacement is essential for reducing and managing associated risks. To address the challenges of both under-decomposition and over-decomposition in landslide displacement analysis, as well as the low predictive accuracy of individual models, this paper proposes a novel prediction model based on time series theory. This model integrates a Convolutional Neural Network (CNN) with a Bidirectional Long-Short Term Memory network (BiLSTM) and an attention mechanism to form a comprehensive CNN-BiLSTM-Attention model. It harnesses the feature extraction capabilities of CNN, the bidirectional data mining strength of BiLSTM, and the focus-enhancing properties of the attention mechanism to enhance landslide displacement predictions. Furthermore, this paper proposes utilizing the Variational Mode Decomposition (VMD) method to decompose both landslide displacement and its influencing factors. The VMD algorithm’s parameters are optimized through the Sparrow Search Algorithm (SSA), which effectively minimizes the influence of subjective bias while maintaining the integrity of the decomposition. A fusion of the Maximal Information Coefficient (MIC) and Grey Relational Analysis (GRA) is then employed to identify the critical influencing factors. The selected sequence of factors that conforms to the criteria is used as the input variable for displacement prediction via the CNN-BiLSTM-Attention model. The cumulative displacement prediction is derived by aggregating the results from each sequence. The study reveals that the SSA-VMD-CNN-BiLSTM-Attention model introduced herein achieves superior predictive accuracy for both periodic and random term displacements than individual models. This advancement provides a dependable benchmark for forecasting displacement in similar landslide scenarios.
1 Introduction
Landslides are frequent and destructive geological disasters in China, posing constant threats to the safety of nearby villagers. The deformation evolution of landslides is a complex nonlinear system influenced by both intrinsic geological conditions and external environmental factors. [1]. Displacement serves as a direct indicator of the progression trends and kinematic patterns of landslides. A thorough analysis of landslide displacement is crucial for accurately identifying the evolutionary stages of landslides, effectively mitigating disaster risks, and minimizing losses. [2, 3].
Currently, scholars typically decompose landslide displacement sequences using time series theory and construct prediction models to forecast displacement component [4]. Commonly used displacement decomposition methods include the moving average method [5, 6], empirical mode decomposition (EMD) [7–9], ensemble empirical mode decomposition (EEMD) [10–12], wavelet transform (WT) [13–15] and Variational Mode Decomposition (VMD) [16–20]. Although the methods mentioned above have yielded positive outcomes in decomposing displacement sequences, they also have their limitations. For instance, while the moving average method is clear physical interpretation, it cannot decompose the random term displacement. Although EMD, EEMD, and WT have addressed the limitations of the moving average method, the number of decomposed sequences is uncontrollable, and the physical meaning of each component is unclear. Furthermore, it should be noted that WT and Discrete Wavelet Transform (DWT) differ in their approach to determining basis functions and wavelet orders. VMD, on the other hand, addresses the issue of modal aliasing and allows for the specification of the number of components after decomposition, with each component having a clear physical interpretation. However, the effectiveness of the decomposition and the fidelity of the results depend heavily on the selection of parameters. To fully utilize the benefits of the VMD algorithm, which has high adaptability and clear physical meaning for each component, this paper optimizes the penalty factor and the rise time step in the VMD model using the Sparrow Search Algorithm (SSA). The VMD decomposition effect and fidelity are measured using the sample entropy of the periodic term displacement or the low frequency of the influencing factor as the root mean square error of the original displacement and the reconstructed displacement.
The construction of a prediction model plays a pivotal role in determining the precision of landslide displacement forecasts. Models for predicting landslide displacement can be categorized into three types: historical experience models, statistical models, and machine learning models. The empirical model based on historical experience requires a significant amount of data and experimentation to verify its accuracy and has strict application conditions. Although the statistical model is effective in monitoring landslides influenced by a single factor, its ability to consider and predict the impact of multiple factors is often limited. As computer technology advances rapidly, machine learning models have become increasingly prevalent for predicting landslide displacement. These models, with their straightforward calculation procedures, accurate prediction outcomes, and low computational requirements, are adept at managing nonlinear relationships. Machine learning models are increasingly popular for predicting landslide displacement. Due to their simple calculation processes, accurate prediction results, low computational costs, and ability to handle nonlinear relationships [21], machine learning models are widely employed for landslide displacement prediction. For instance, Yang et al. [22] employed support vector machines (SVM) to predict landslide displacement. However, the prediction error for individual points was significant. Du et al. [23] established a neural network model for predicting landslide displacement based on the analysis of inducing factors. Wang et al. [24] developed a prediction model for landslide displacement by combining the Extreme Learning Machine (ELM) with Random Search Support Vector Regression (RS-SVR) sub-models. Li et al. [25] proposed an ensemble-based extreme learning approach to study landslide displacement prediction. The results demonstrated that the integrated model achieved higher prediction accuracy compared to a single model. Wang et al. [26] studied and compared the predictive capabilities of reservoir landslide displacement using various machine learning approaches. Relying solely on individual prediction accuracy to assess the superiority of machine learning methods may not be reliable, whereas the combined model offers improved average prediction accuracy and predictive stability. However, the model does not fully consider the dynamic characteristics of landslide evolution. This is because the evolution process of a landslide is inherently a dynamic system, and treating it as a static regression problem reduces the accuracy of displacement predictions [27, 28]. Accurate prediction of landslide displacement necessitates a dynamic prediction model capable of simulating the changes in landslide displacement. Li et al. [28] proposed a modeling and prediction framework for landslide displacement based on a deep belief network and the exponentially weighted moving average (EWMA) control chart, obtaining excellent prediction results. The Long Short-Term Memory (LSTM) model is a type of dynamic neural network that integrates delay units and feedback into the static network, enhancing its sensitivity to historical factors and output. This trait renders it more suitable for predicting landslide displacement influenced by multiple factors.
The LSTM model is a dynamic modelling method commonly used to predict landslide displacement [29, 30]. Previous studies have demonstrated that the prediction accuracy of LSTM is superior to that of backpropagation neural network, ELM or SVM [31]. However, the LSTM model relies exclusively on past state information, which qualifies it as a unidirectional network. The bidirectional LSTM (BiLSTM) network is an enhancement and expansion of the traditional LSTM. It can increase its predictive accuracy by learning input time series data from both forward and backward directions, as noted in references [32–34]. More recently, the progression of deep neural networks has given rise to stable and highly accurate models for data processing and industrial predictions, such as the convolutional neural network (CNN) and BiLSTM. The combined CNN-BiLSTM model merges CNN’s feature learning capabilities with BiLSTM’s time series memory function, resulting in further improvements in prediction accuracy and operational efficiency [35,36].. Nava et al. [37] used seven different machine learning models to predict four types of landslide displacement, taking into account various geographic locations, geological settings, time intervals, and measurement instruments. The results indicated that deep learning ensemble models surpassed others in performance, especially for the seasonal Baishuihe landslide. Lin et al. [38] proposed a combined model based on the CNN-BiLSTM framework. This model demonstrated higher prediction accuracy when compared to both the traditional LSTM model and the CNN-LSTM combined model. Wang et al. [39] applied the CNN-LSTM model to dynamically predict landslide displacement, finding that the CNN-BiLSTM model’s prediction accuracy exceeded that of BP, LSTM, and GRU models. However, the deep learning methods mentioned previously fall short when handling multi-dimensional feature data, such as in predicting landslide displacement, due to the absence of an effective weighted input feature mechanism. Not all input features equally influence landslide deformation; certain factors may contribute minimally to the prediction of landslide displacement. An excessively large proportion of feature weights could compromise the prediction model’s accuracy.
In recent years, attention mechanisms have become increasingly prominent in image recognition and machine translation. These mechanisms function as an effective resource allocation system by assigning differential weights to input features in order to emphasize the most significant information [40]. Tang et al. [41] applied a BiLSTM model with an attention mechanism to predict landslide displacement, and it was found that this combination yielded better results than using the traditional LSTM model alone. Furthermore, it’s common for researchers to rely on correlation evaluation methods to select input variables for prediction models. However, this method may result in one-sided evaluations and the inclusion of irrelevant data, which can increase computational complexity and reduce prediction accuracy.
To summarize, this article uses the BaiShuihe landslide in the Three Gorges Reservoir area as an example. It first applies the SSA-VMD model to deconstruct the landslide displacement sequence into trend term displacement, periodic term displacement, and random term displacement, while simultaneously decomposing the triggering factors into high-frequency and low-frequency parts. Next, it employs a fusion technique that combines the Maximal Information Coefficient and Grey Relation Analysis (MIC-GRA) to filter the influencing factors of landslide displacement from different angles. Finally, the CNN-BiLSTM-Attention composite model is utilized to predict the various displacement components. The predicted trend, periodic term, and random term displacements are then aggregated and reconstructed, with an evaluation and analysis of the results following. The forecasting performance has been confirmed, and the insights from this study establish a robust foundation for the future development of landslide displacement prediction and early warning systems.
2 Methodology
2.1 Displacement time series additive model
Predicting time series data presents a significant challenge in the field of statistical analysis, especially when employing time series analysis methods. Previous studies [5, 10, 17, 19, 30] have documented that the cumulative displacement of landslides is a complex, nonlinear sequence. Time series analysis facilitates the decomposition of cumulative displacement into three distinct segments. Predominantly, landslide deformation is influenced by trend term displacement, which arises from internal geological conditions such as the topography, geological structure, and strata lithology. The trend term displacement, which is influenced by internal factors, can be represented as an approximately monotonic increasing function over time [5, 11, 16]. This paper explores the impact of time on the trend term, along with the periodic and random term displacements. The periodic term displacement arises through the collective effects of external factors such as rainfall and reservoir water levels, resulting in displacement that typically exhibits an approximate periodic pattern, as identified in earlier studies [17, 19, 21]. Meanwhile, the random term displacement is attributed to stochastic factors including wind load, vehicular load, and seismic activity, as documented in the literature [22, 29]. The cumulative displacement of landslides, according to the findings from time series additive model research, can be expressed as Eq. 1:where is the displacement value of the time series, is a trend term function, is a periodic term function, and is an random term function with uncertainty.
2.2 Specific steps of variational mode decomposition
In 2014, K. Dragomiretskiy and D. Zosso proposed the variational mode decomposition (VMD) as an adaptive, non-recursive method for signal processing based on the EMD model [42]. The VMD decomposes a real input signal into multiple Intrinsic Mode Function (IMF) components with specific sparse characteristics. This approach determines the number of modal components in advance, overcoming the endpoint effects and modal component aliasing problems of EMD methods. Furthermore, it can decrease the non-stationary nature of time series data with high complexity and strong nonlinearity, leading to subsequences with distinct sparse features. The equation for the IMF in VMD is a form of amplitude modulation frequency modulation signal uk(t), which is expressed as Eq. 2:where is the phase, is the instantaneous amplitude, is the non decreasing function, and is consistent with the mean positive number.
The sum of the input signal sequence and modes is used as the constrained variational expression. The constrained variational expression is written as Eqs 3 and 4:where is the required number of modal components, which is an integer between one and . is the modal component obtained from the final decomposition. is the actual center frequency of each modal component. is a partial derivative symbol. is the Dirac function. is a convolution operator.
To solve the equation above, we introduce the Lagrange operator to transform the constrained variational problem into an unconstrained one. The extended Lagrange expression is obtained as Eq. 5:where is used to decompose and reduce the interference of Gaussian noise. The optimal solution of the constrained model can be obtained by using the alternating direction multiplier iterative algorithm to optimize the modal components and center frequencies, and searching for the saddle points of the unconstrained model, thereby obtaining K modal components. The aim of this study was to decompose landslide displacement and influencing factors using VMD. The time series additive model of landslide displacement was used to set the number of modal components K = 3. The influence factor time series K = 2 modal components. The low frequency component of the influence factor mainly affected the periodic displacement of the landslide, while the high-frequency component contributed to the random displacement [19]. Utilizing the VMD algorithm to dissect landslide displacement into three components, it is pivotal to recognize that the outcomes might not carry practical or tangible physical relevance. The parameters and K have been determined, and they will affect the decomposition effect and fidelity. Efficient and accurate selection of parameters in the VMD algorithm will be crucial for the decomposition of displacement time series. The SSA was chosen to optimize the penalty function and rise time step in the VMD model. This approach effectively avoids the influence of subjective factors.
2.3 Variational modal decomposition for the sparrow optimization algorithm
2.3.1 Sample entropy
Sample entropy is a complexity metric for time series analysis, proposed by Richman [43] in response to the limitations encountered with approximate entropy. This measure effectively mitigates deviations arising from template matching issues, by considering the probability and complexity of emergent patterns within a time series. Contrary to approximate entropy, Sample entropy maintains independence from the length of the sequence, yielding higher consistency across analyses. This attribute renders it an essential tool for researchers and practitioners seeking to accurately gauge the intricacies of time series data.
For a given time series with length N, the sample entropy calculation steps of the time series are as follows:
(1) The m-dimensional vector is constructed at time t, where m is the embedding dimension of the vector. The distance between the time series is defined as the absolute value of the maximum difference between the elements of the two sub-sequences is , and the calculation formula is as Eq. 6:
(2) Setting the similarity tolerance , and calculating the number ratio of the distance between and less than , denoted as , and the calculation formula is as Eq. 7:where is the counting function. By calculating the number of vectors whose distance between and is less than , the formula for calculating the average template match probability is as Eq. 8:
(3) The dimensional sequence is constructed, and the average template match probability with a distance less than between and is calculated by repeating the Eqs 7 and 8, where and are the probabilities of and points respectively under the condition of similar tolerance , respectively. The sampling entropy of is defined as Eq. 9:
When the length of the time series is finite, the sample entropy can be calculated as Eq. 10:where m is the embedding dimension, generally taken as one or 2. r is the similarity tolerance, generally taken as , and is the standard deviation of the sequence. The sample entropy value increases with the complexity of the time series and decreases with its simplicity. This paper uses the sample entropy of the decomposed periodic term displacement sequence as an indicator to evaluate the decomposition effect of the VMD algorithm. A smaller entropy value of periodic term displacement indicates a better decomposition effect.
2.3.2 Basic principles of sparrow optimization algorithm
The Sparrow Search Algorithm (SSA) is a population-based intelligent optimization algorithm introduced by Xue et al. [44]. The algorithm derives its optimization strategy from the foraging and anti-predation behavior observed in sparrows. As a swarm intelligence algorithm, it outperforms many others in terms of search precision, convergence speed, stability, and resilience. Its successful applications span a range of problems in diverse domains, including workshop scheduling, parameter optimization, image classification, and graphical optimization tasks. Building on this success, the present article employs SSA to autonomously determine the optimal parameters for the penalty factor and the rise time step within the VMD algorithm.
The SSA categorizes sparrows into three roles during the search process: the discoverer, the follower, and the sentinel. Their positional updates are as Eqs 11-13:where is the current number of iterations, is the maximum number of iterations, is a uniform random number of , is a standard normal distribution random number, is the position information of i sparrow in j dimension, is a matrix with all elements one, is the warning value, is the warning threshold. is the worst position in the global, is the optimal position occupied by the discoverer, is a multidimensional matrix of one or -1, n is the number of sparrows. is the current global best position, is the control parameter for the step size, is a uniform random number between , K represents the direction of movement of the sparrow, is the fitness of the current sparrow, is the best fitness value of the global, is the worst fitness value, is a small constant.
To optimize SSA, determining the fitness function is a crucial step. The fidelity of the decomposed VMD algorithm is evaluated by accumulating and reconstructing the decomposed subsequences into m. To measure the integrity of the decomposed sequence, the root mean square error (RMSE) between the reconstructed sequence and the original sequence M is calculated using the following formula:where is the value of the original sequence at time t, is the value of the reconstructed sequence at time t, and n is the length of the sequence.
Eq
14demonstrates that a smaller RMSE value implies a smaller error between the reconstructed sequence
mand the original sequence
M, indicating a reduced loss of the original sequence. This paper combines sample entropy and root mean square error to effectively reflect the completeness of the decomposed sequence and the success of the decomposition. The function expression is as Eq.
15:
where
is the root mean square error between the reconstructed sequence and the original sequence.
is the sample entropy value of the low-frequency part of the periodic term displacement sequence or influencing factor after decomposition. The fitness value of the SSA algorithm is determined using the calculated value of Equation
15. To find the optimal fitness, the penalty factor α and rise time step τ are optimized. The process is outlined in the following steps:
(1) Input displacement time series signal.
(2) Initialize the parameter input of the sparrow optimization algorithm, and randomly generate a series of α and τ as the initial position of the sparrow population.
(3) Perform VMD decomposition on the displacement sequence of the current sparrow position. Calculate the sample entropy of the decomposed periodic term sequence or low-frequency part of the influencing factors with confidence.
(4) The acclimatization value for each sparrow was calculated according to Eq 10, identify the optimal and worst fitness individuals, and update the positions of discoverers, followers, and early warning individuals according to Eqs 11–13.
(5) Repeat (3) and (4) until the maximum number of iterations is reached, and output the sparrow position and fitness values at this time as the optimal solution.
2.4 Maximal information coefficient
Mutual information (MI) [45] developed from Shannon entropy theory, is a method for analyzing the statistical correlation between two random variables. It is adept at detecting both linear and non-linear relationships among variables. Despite its utility, mutual information is not a normalized metric, which limits its capacity to provide a quantitative assessment of correlation strength. To address this limitation, this article introduces the Maximal Information Coefficient (MIC). Proposed by Reshef et al. in 2011 in the journal Science [46], MIC builds upon MI to evaluate the degree of dependency between variables comprehensively. It is competent in quantifying not only linear but also non-linear and non-functional correlations among variables.
The principle of the MIC is for a given two random variables and a finite ordered data set , the and regions in are divided respectively into grids of . Then, the probability distribution of the data set on the grid is , and the mutual information value under this segmentation mode is calculated. Finally, the maximum mutual information value under all possible grid segmentations is obtained as Eq. 16:
By normalizing function, the characteristic matrix element of the variable can be obtained by Eq. 17:
Different values divide the grid to get different values, and the maximum is called the MIC of variable , and the maximum is expressed as Eq. 18:where is the maximum number of meshes, is the capacity of the data sample and usually set to [47, 48], This paper also adopts this value.
2.5 Construction of CNN-BiLSTM-attention combination model
2.5.1 CNN principle structure
A Convolutional Neural Network (CNN) is the neural network model most frequently employed in deep learning [49]. Its potent feature-learning capability substantially diminishes the model’s parameter count, which has led to its extensive application in image recognition and computer vision domains. Over recent years, a growing number of researchers have effectively utilized CNN for time series analysis. The model’s distinct features, such as weight-sharing and localized connections, can significantly diminish the parameter quantity needed for training. These attributes facilitate faster model training velocities and allow for the more proficient extraction of features from the input data [50].
The CNN consists of a convolution layer, pooling layer, fully connected layer, and output layer. The convolution layer applies the activation function to perform non-linear operations on the input time series data and extract local feature information. The pooling layer uses a pooling function to decrease the dimensionality of the convolution output, and improve the model’s robustness and generalization ability. The fully connected layer then maps the data output from the pooling layer to a fixed-length column vector. This paper uses a two-layer one-dimensional CNN convolution structure to extract feature information, as shown in Figure 1.
FIGURE 1
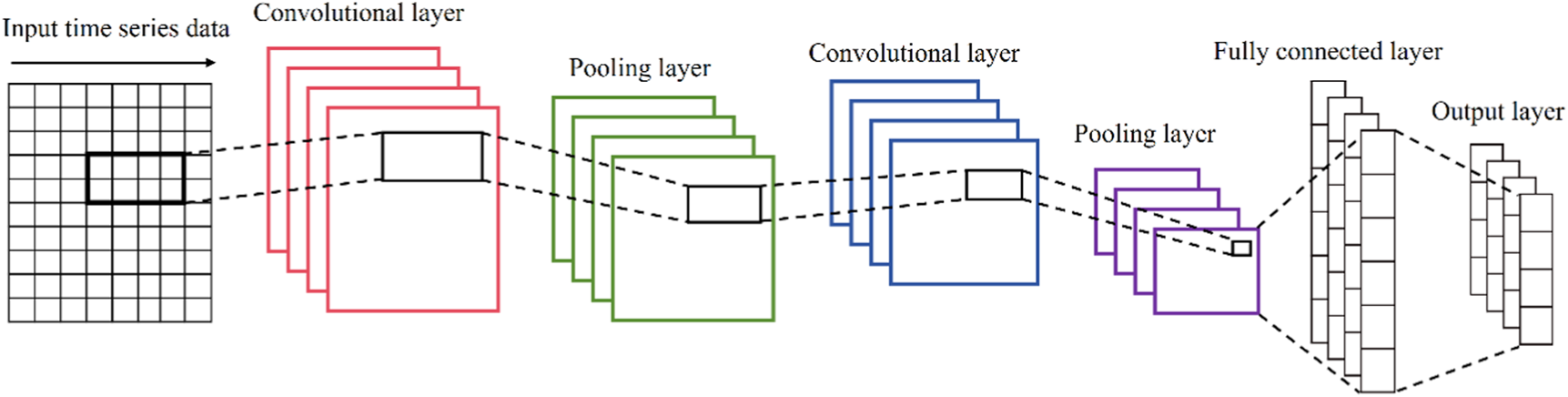
Two-layer one-dimensional CNN convolution structure.
2.5.2 BiLSTM model
In 1997, Sepp Hochreiter et al. proposed long short-term memory networks (LSTM). The gate structure and internal memory unit effectively solve the problem of gradient disappearance and explosion in long sequence training of the RNN model [51]. The model’s control unit consists of a forget gate, an input gate, and an output gate. The respective calculation formulas for these components are as Eqs 19-24:where denote the forgetting gate, the input gate and the output gate, respectively, denote the weights of the corresponding gates, denote the corresponding bias, denote the input time series data, t denote the sigmoid activation function, and is the hyperbolic tangent activation function, and denote the cell state and temporary state of the cell, respectively.
The Bidirectional Long Short-Term Memory (BiLSTM) model significantly enhances the traditional LSTM model. By leveraging both forward and reverse LSTM processes, it effectively integrates information from both past and future contexts, enabling it to make more accurate predictions. Consequently, it outperforms the LSTM model in prediction accuracy [33,34,52]. The structure of the BiLSTM model is depicted in Figure 2.
FIGURE 2
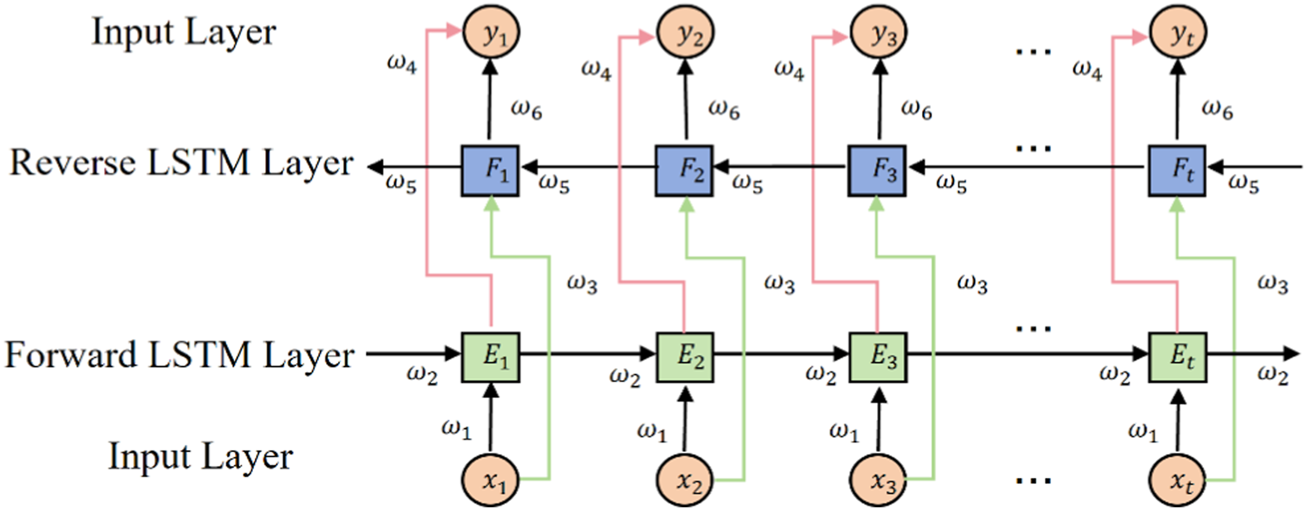
BiLSTM network structure diagram [53].
2.5.3 Attention mechanism
The Attention mechanism allocates weights to different features, assigning greater weights to key content and smaller weights to other content. This allocation improves the efficiency of information processing and the prediction accuracy of the model [54]. The Attention unit structure is displayed in the Figure 3. The formula of attention mechanism can be referred to [53].
FIGURE 3
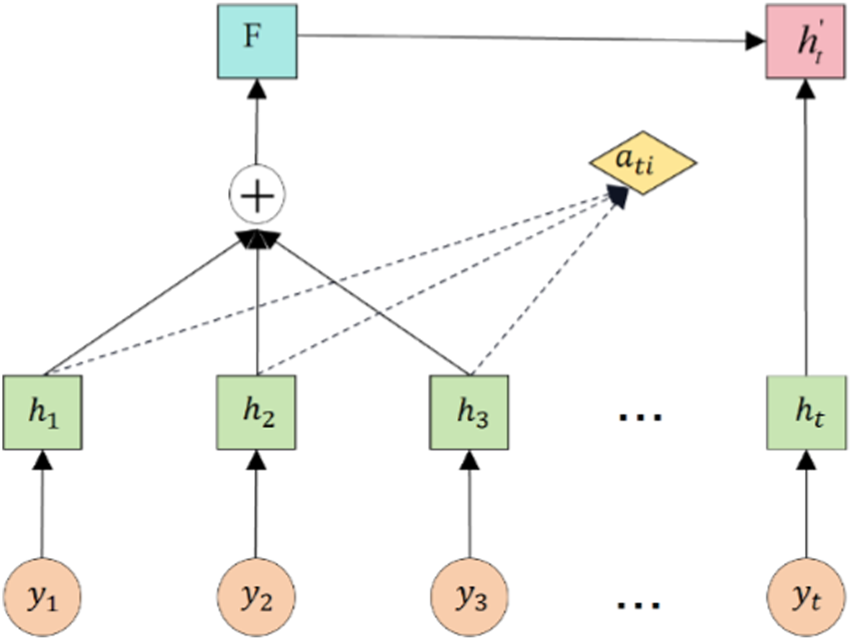
Attention mechanism structure diagram [53].
2.5.4 Prediction process of CNN-BiLSTM-attention combined model
This paper presents a dynamic displacement prediction method based on the CNN-BiLSTM-Attention model. The model utilizes a CNN framework comprising of a two-layer one-dimensional convolutional layer and a pooling layer to automatically extract the internal features of the displacement sequence. The convolutional layer efficiently performs nonlinear local feature extraction of the time series, while the pooling layer condenses the extracted features using the maximum pooling method to generate crucial feature information.
The BiLSTM hidden layer model effectively learns the internal dynamic changes of the local features extracted by CNN and iteratively extracts intricate global features from the local features. The BiLSTM hidden layer generates features that are adeptly harnessed by the Attention mechanism, which discerns the significance of temporal information. This facilitates the extraction of profound temporal dependencies and enhances the utilization of the displacement time series’ temporal characteristics. By preserving historical information and emphasizing critical historical time points, the Attention mechanism mitigates the impact of superfluous information on the displacement prediction outcomes. The outputs from the Attention layer serve as the input for the fully connected layer, which then precisely yields the final prediction of displacement. In optimizing the network parameters for this study, the Adam optimization algorithm is adopted to meticulously adjust the parameters across the layers, with the mean square error (MSE) serving as the loss function. The architecture of the combined CNN-BiLSTM-Attention model is depicted in Figure 4.
FIGURE 4
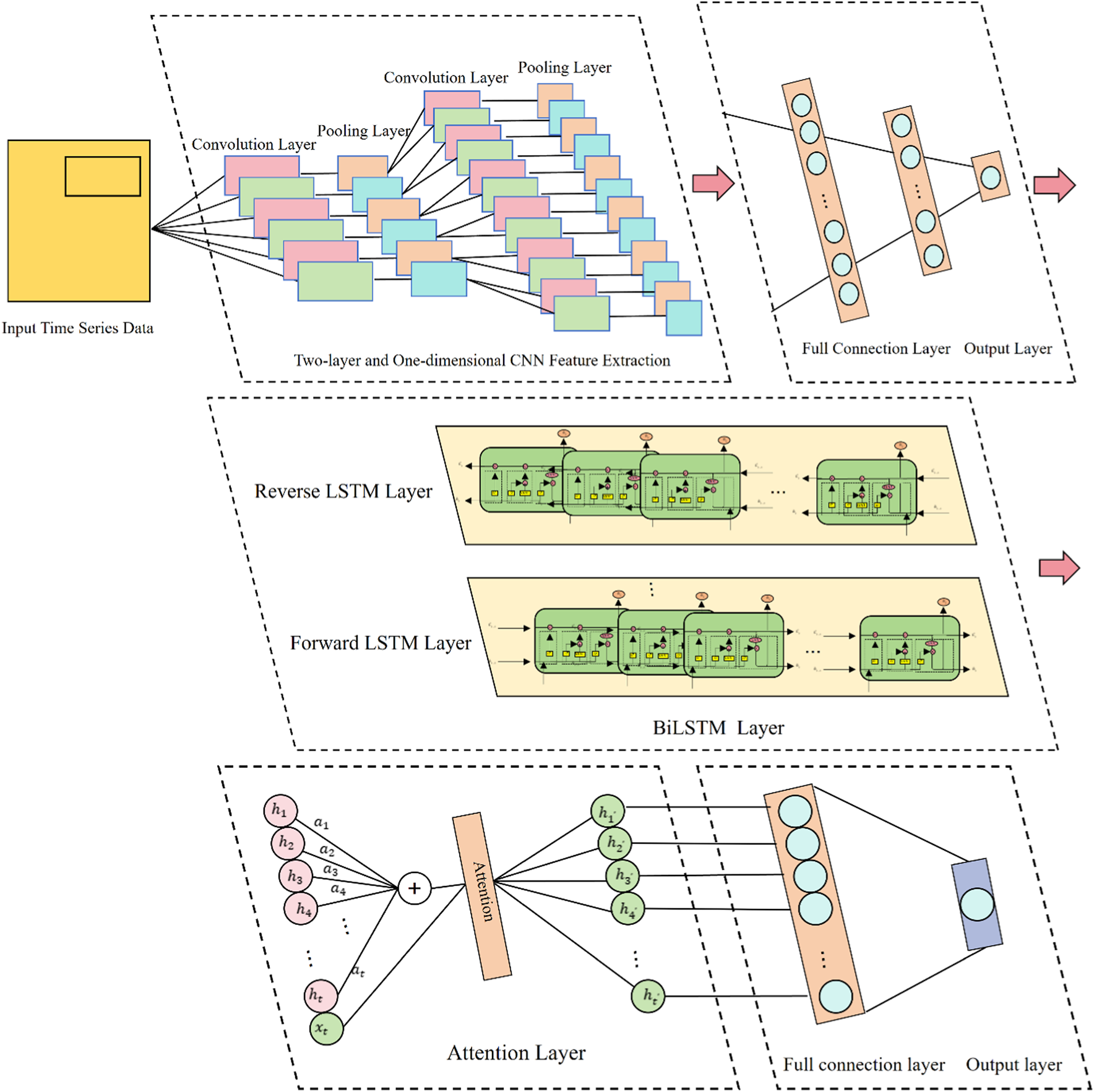
Diagram of CNN-BiLSTM-Attention network structure.
2.5.5 Displacement prediction processTo predict landslide displacement using the model, follow these steps with confidence
(1) The original landslide displacement time series is divided into three sub-sequences by using the SSA-VMD model. The landslide’s cumulative displacement can be broken down into three sub-sequences: trend term displacement T(t), periodic term displacement P(t), and random term displacement R(t), determined by the optimal fitness function value.
(2) The influence factor sequence is decomposed into two sub-sequences using SSA-VMD. The low-frequency and high-frequency parts of the influence factor sequence are represented by these sub-sequences. Using the optimal fitness function, we derived the optimal decomposition subsequence. We then calculated the maximum MIC and GRA values for the decomposition subsequence of each factor and displacement subsequence. Our comprehensive analysis allowed us to confidently assess the correlation between the influencing factor subsequence and the displacement subsequence.
(3) The input data is divided into a training dataset and a verification dataset based on the predetermined sequence of each displacement term and influencing factor. A single-factor CNN-BiLSTM-Attention model was constructed and trained for predicting trend term displacement, while a multi-factor CNN-BiLSTM-Attention model was established and trained for predicting periodic term displacement and random term displacement.
(4) Ultimately, the predicted values of trend displacement, periodic displacement, and random displacement are accumulated to form the cumulative landslide displacement prediction results, which are then compared with the cumulative landslide displacement monitoring results, and the predictive performance of the new model is evaluated. The process of the combined landslide displacement prediction model, involving SSA-VMD and CNN-BiLSTM-Attention, is confidently illustrated in Figure 5.
FIGURE 5
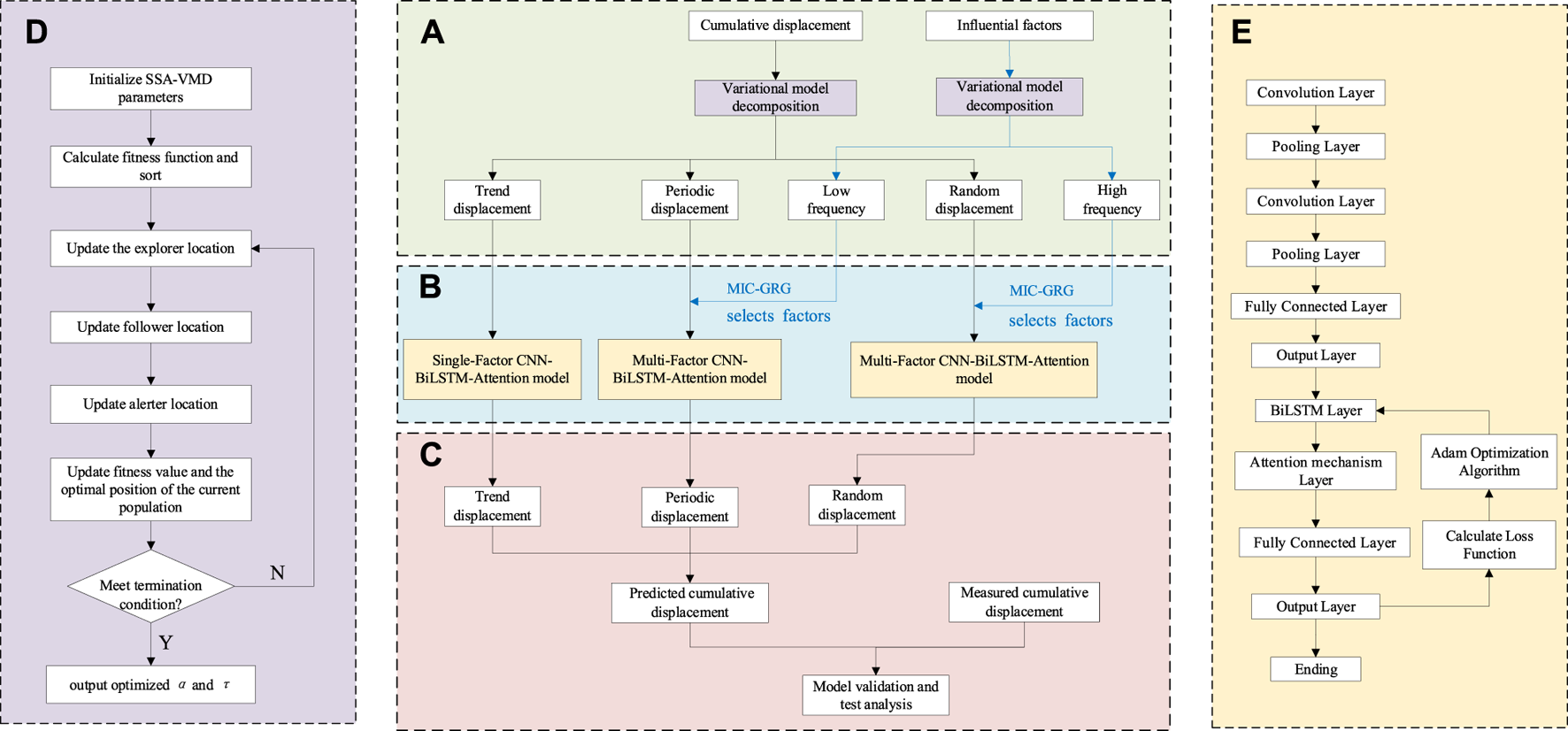
Flowchart of the displacement prediction. (A). Landslide displacement decomposition and data set establishment; (B). Training of CNN-BiLSTM-Attention model; (C). Verification of CNN-BiLSTM-Attention model; (D). SSA optimize the parameters of VMD; (E). CNN-BiLSTM-Attention model establishment.
3 Case study
3.1 Engineering geological survey and displacement analysis of Baishuihe landslide
The Baishuihe landslide, located in Zigui County within the Three Gorges Reservoir region, as illustrated in Figure 6 exhibits a monoclinic bedding slope structure, This structure is characterized by a gradient that is elevated in the south and decreases towards the north, aligning in a stepwise fashion towards the Yangtze River. The elevation measures approximately 410 m at the landslide’s trailing edge and descends below the 135 m water level at its leading edge. The overall inclination of the Baishuihe landslide is estimated at 30°, with its topographical layout depicted in Figure 7. Since the commencement of monitoring activities in 2003, the landslide has experienced numerous significant deformation events. Geological surveys of the Baishuihe region elucidate the landslide’s irregular ‘U-shaped’ configuration, extending 500 m in length from north to south, and 430 m across from east to west, covering an area of approximately 21.5 × 104 m2. The sliding mass maintains an average thickness of about 30 m, culminating in a volume of roughly 645 × 104 m3, with the principal direction of slide oriented at 20°.
FIGURE 6
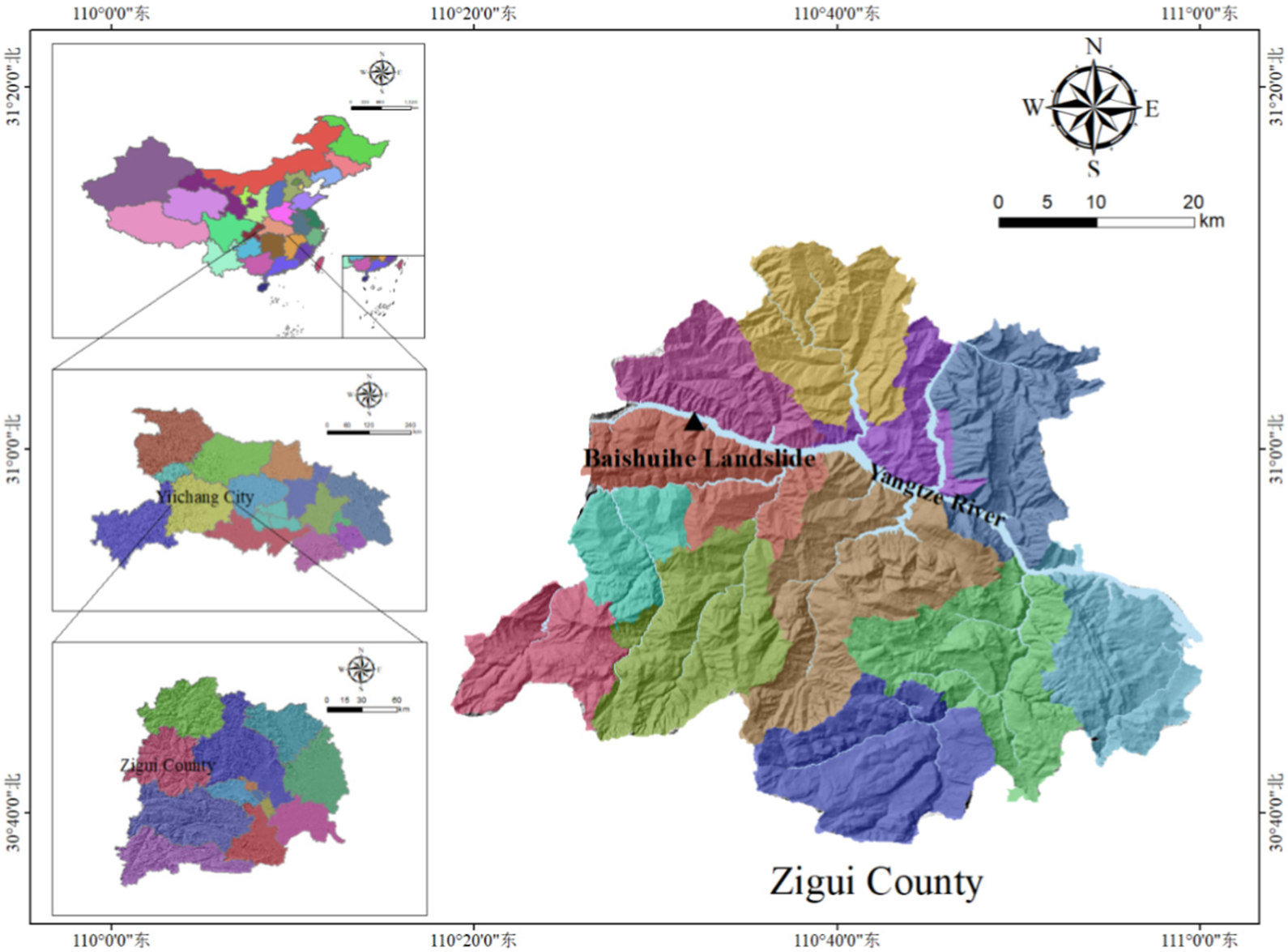
The geographical location of Baishuihe landslide.
FIGURE 7
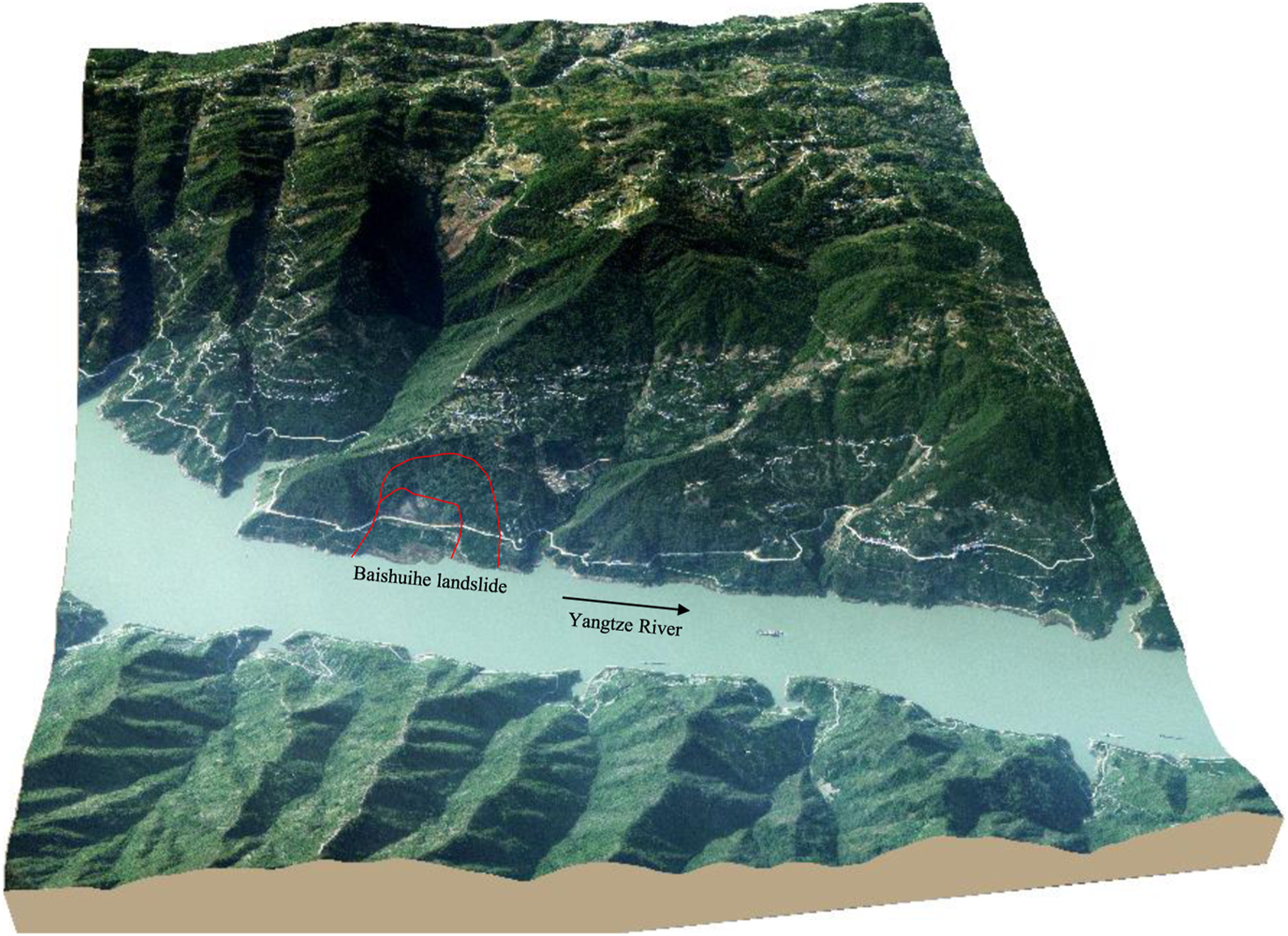
The topography of Baishuihe landslide.
Figure 8 demonstrates that every displacement change is linked to a rise in rainfall and a substantial shift in reservoir water level. Rainfall has an impact on the stability of the landslide by influencing the strength of rock and soil, physical and mechanical parameters, and pore water pressure [55–57]. The landslide motion state is influenced by the reservoir water level through hydrostatic pressure, hydrodynamic pressure, pore water pressure, and other factors [58,59]. The reservoir area experiences a flood season from May to September each year, resulting in increased rainfall and a wider fluctuation and influence range of the reservoir water level. Conversely, the non-flood season occurs from October to April of the following year, during which rainfall is scarce and the deformation of the landslide tends to be less severe. The periodic influence of reservoir water levels and rainfall causes the displacement of the landslide to exhibit a step-type characteristic.
FIGURE 8
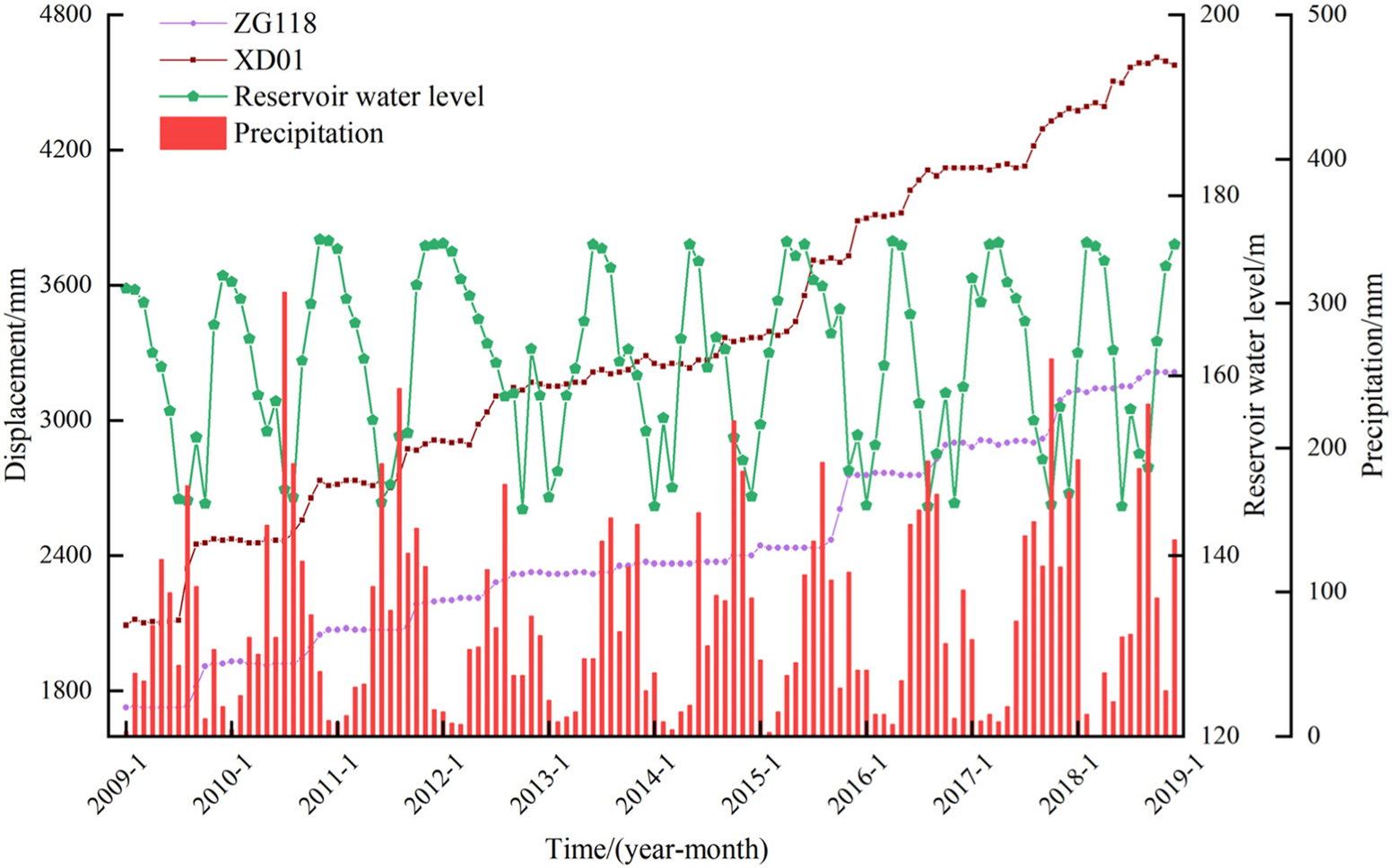
Displacement and environmental data variation in the Baishuihe landslide.
3.2 Landslide displacement decomposition of VMD
The SSA utilizes a population size of 50 and a maximum of 100 iterations. , The optimization ranges for the penalty factor and rise time step are [0.1,1000] and [0,1], respectively. Table 1 displays the optimization results, while Figures 9, 10 shows the corresponding decomposition results.
TABLE 1
| Monitoring point | ||
|---|---|---|
| ZG118 | 74.19 | 0.56 |
| XD01 | 90.13 | 0.17 |
SSA-VMD optimization results.
FIGURE 9
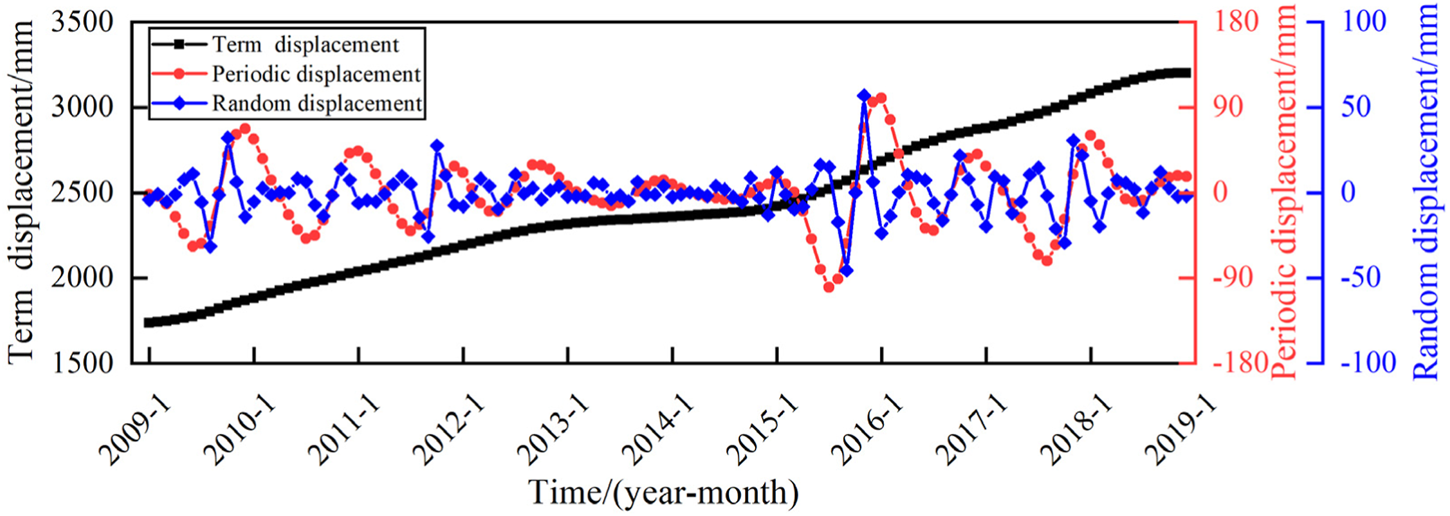
Decomposition results of ZG118 cumulative displacement.
FIGURE 10
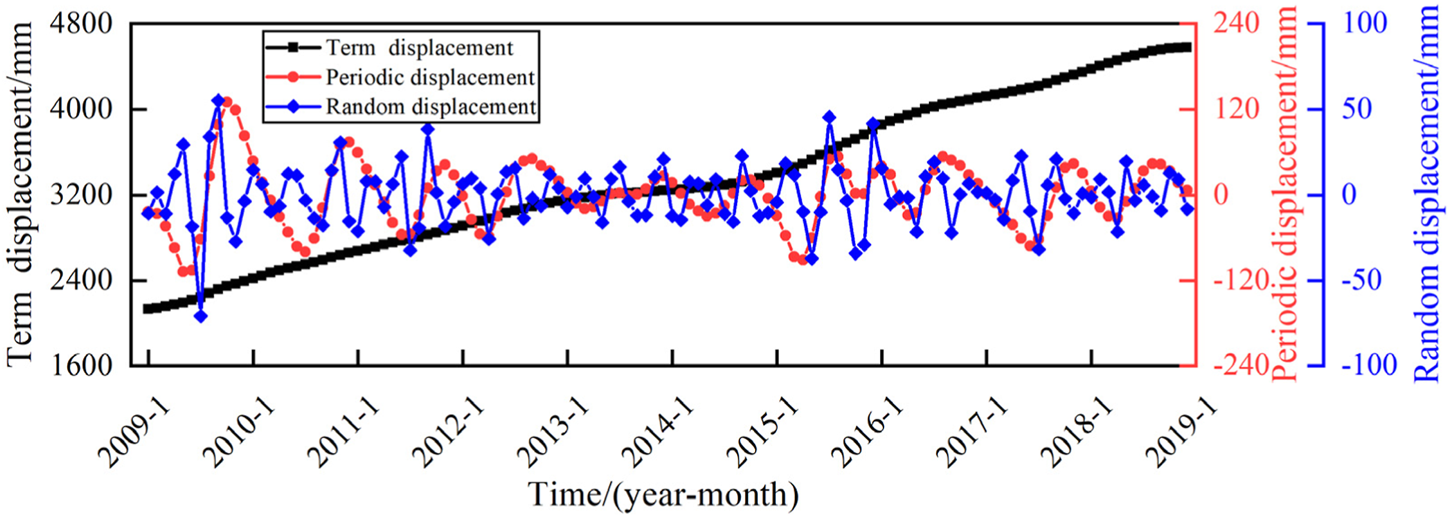
Decomposition results of XD01 cumulative displacement.
3.3 Selection of landslide displacement influencing factors
3.3.1 Analysis of landslide displacement influence factors
Examining the progression traits of the Baishuihe landslide, and building upon existing domestic and international research, many scholars have traditionally narrowed down the influencing factors of landslide displacement to rainfall and reservoir water level changes. However, Figure 8 illustrates a discrepancy where the peak increase in landslide displacement occurred in 2015, despite there being neither the highest rainfall nor the most significant variation in reservoir water levels that year. This suggests that rainfall and reservoir water level changes do not singularly dictate landslide displacement. Such a dynamic may be attributed to the deformation evolution state of the landslide at the time, with different states responding variably to external influences. For instance, in phases where the landslide maintains relative stability, it is less likely to experience significant displacements, even when subjected to intense external forces. Conversely, in a state of instability, even moderate external influences can induce substantial movements [60,61]. Thus, it becomes evident that a landslide’s deformation response hinges not only on the magnitude of the external triggers but also intimately connects with its current evolutionary stage. Accordingly, this study advances beyond conventional considerations by incorporating the displacement evolution state of the landslide as an additional input characteristic for the prediction model.
The analysis above identifies the indicators that have the most influence on landslide displacement. These are 1-month cumulative rainfall () and 2-month cumulative rainfall (). Additionally, the monthly average reservoir water level elevation (), the amplitude of reservoir water level in the previous month (), and the amplitude of reservoir water level in the previous 2 months () are the influential factors for reservoir water level on landslide displacement. This information is presented with confidence and clarity to ensure a thorough understanding of the topic. To characterize the evolution state of landslide displacement, we choose the displacement () from the previous month and the displacement () from the previous 2 months.
The VMD algorithm decomposes the influencing factor sequence into high-frequency and low-frequency sequences. The high-frequency factors, such as , and , are used as the influencing factors of the random term displacement. The low-frequency factors, such as , and , are used as the influencing factors of the periodic term displacement. The correlation between the decomposition sequence of the impact factor and the periodic displacement and random term displacement sequence is comprehensively measured using the MIC and GRA.
3.3.2 Sequence decomposition of optimal VMD displacement influencing factors
The SSA utilizes a population size of 50 and a maximum number of iterations set to 100, with optimization ranges for the penalty factor α and rise time step τ being [0.01,1000] and [0,1], respectively. The optimization results are presented in Table 2, while the corresponding decomposition results are illustrated in Figures 11–14.
TABLE 2
| Influencing factors | Precipitation | Reservoir water level | The landslide state of ZG118 | The landslide state of XD01 | |||||
|---|---|---|---|---|---|---|---|---|---|
| 0.65 | 0.15 | 0.19 | 30.16 | 20.20 | 12.18 | 1.15 | 1.19 | 12.17 | |
| 0.57 | 0.57 | 0.27 | 0.46 | 0.24 | 0.19 | 0.21 | 0.11 | 0.26 | |
SSA-VMD optimization results.
FIGURE 11
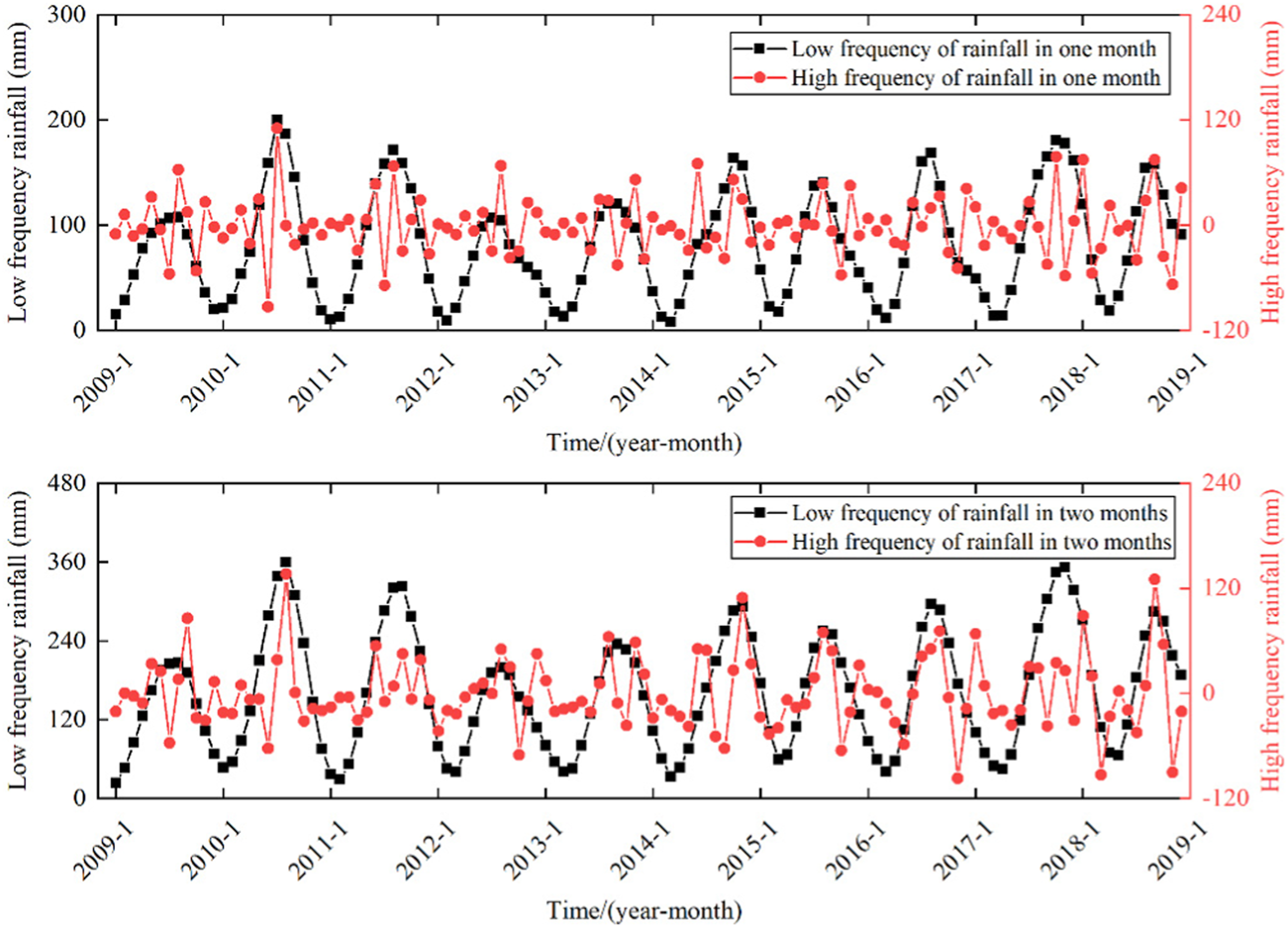
Decomposition results of cumulative rainfall.
FIGURE 12
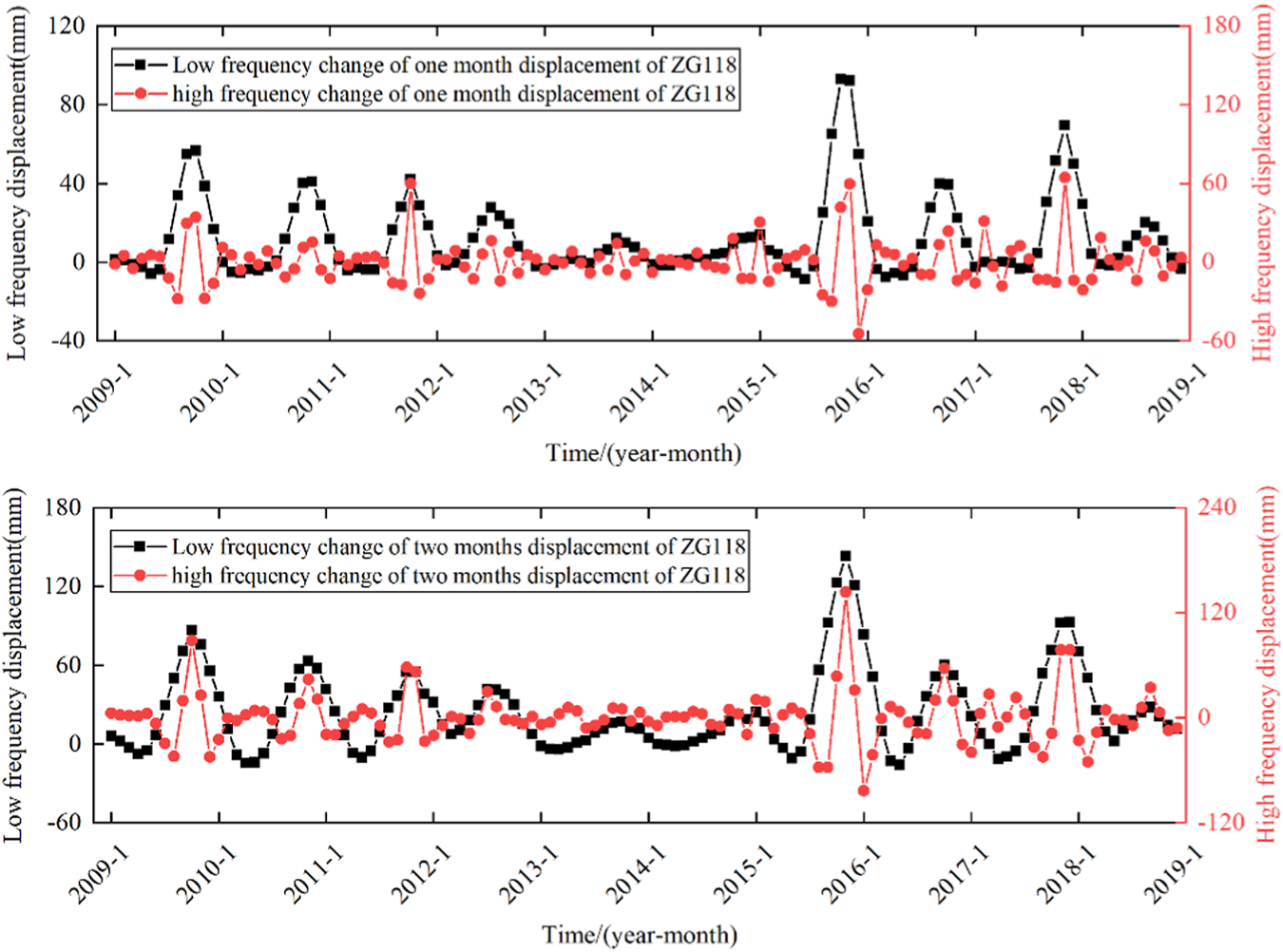
Decomposition results of displacement variation of ZG118.
FIGURE 13
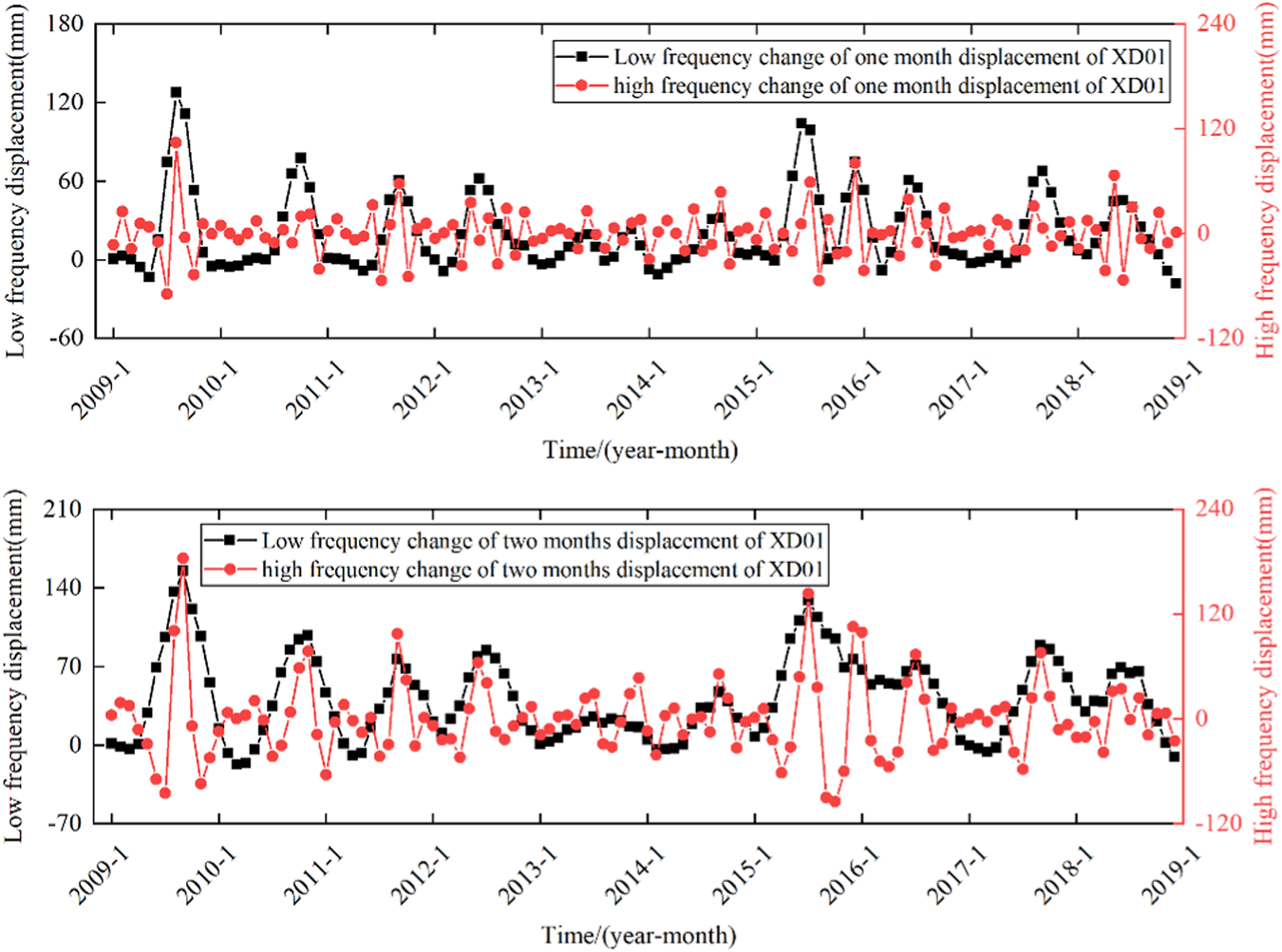
Decomposition results of displacement variation of XD01.
FIGURE 14
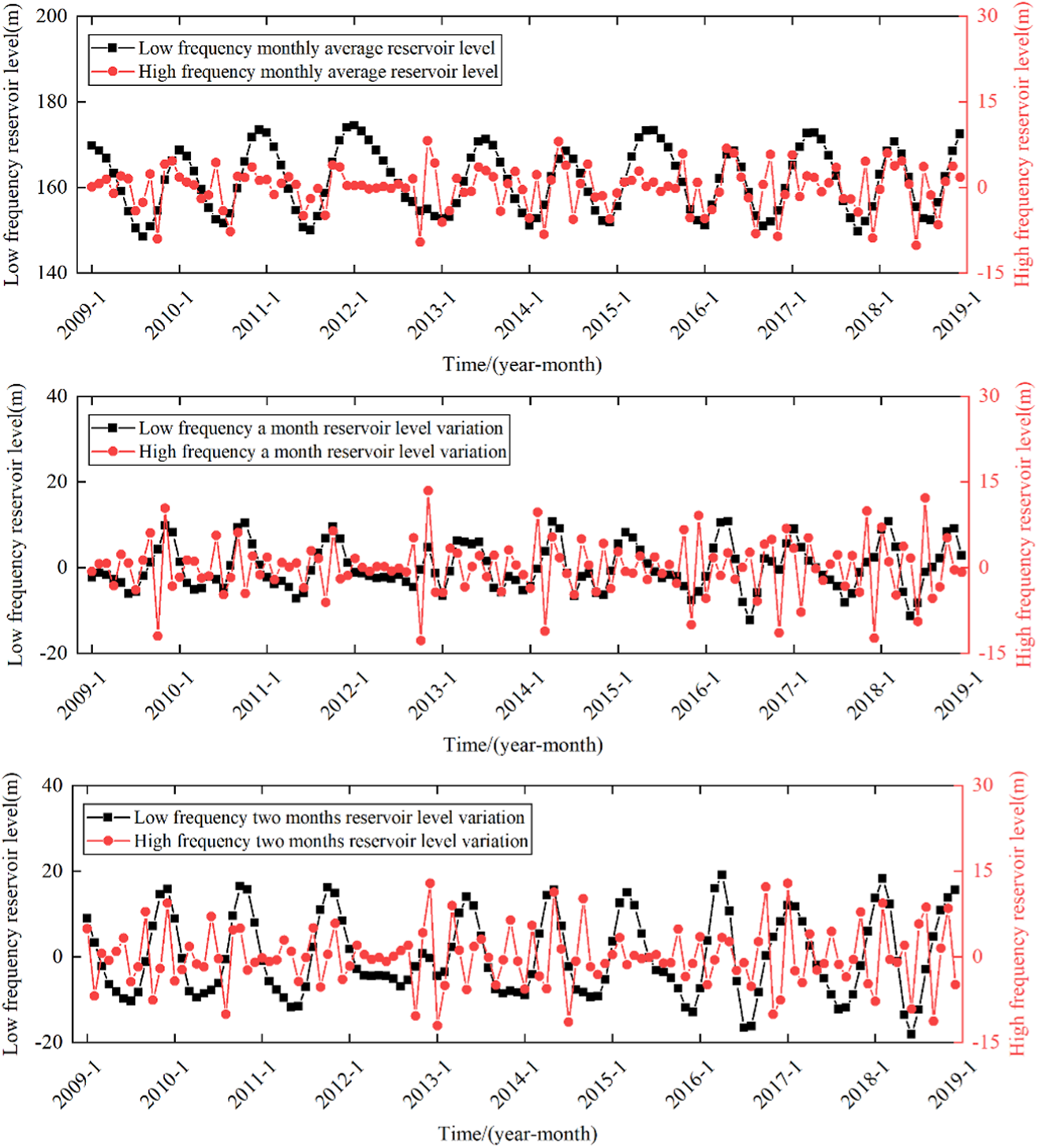
Decomposition results of reservoir level.
3.3.3 Correlation analysis between displacement and influence factors
In the quest to elucidate the correlation between landslide displacement and its influencing factors, it is imperative to conduct a detailed analysis and decomposition of these factors. Selecting highly correlated factors is crucial for enhancing the predictive accuracy and efficacy of the model. Nonetheless, the availability of sufficiently high-quality data for model training is paramount. The inclusion of factors with minimal correlation risks incorporating extraneous data, potentially diminishing the precision and effectiveness of the landslide displacement prediction model. Optimally selected influencing factors can markedly elevate both the performance and accuracy of the model. In existing research, most scholars predominantly utilize a single method to assess the correlation between displacement components and influencing factors. However, a sole evaluation method can only provide perspective from a singular angle, resulting in a one-sided assessment and the loss of significant data portions. To address this, This study incorporates the MIC-GRA fusion method for a more comprehensive selection. Table 3 present the computation outcomes of both methods and, through comparative analysis in the subsequent prediction, the supremacy of this method is affirmed.
TABLE 3
| Influencing factors | Periodic displacement | Random displacement | |||||||
|---|---|---|---|---|---|---|---|---|---|
| XD01 | ZG118 | XD01 | ZG118 | ||||||
| MIC | GRA | MIC | GRA | MIC | GRA | MIC | GRA | ||
| rainfall | 0.255 | 0.67 | 0.403 | 0.63 | 0.252 | 0.66 | 0.175 | 0.78 | |
| 0.308 | 0.68 | 0.347 | 0.65 | 0.316 | 0.64 | 0.322 | 0.75 | ||
| Reservoir water level | 0.234 | 0.63 | 0.307 | 0.66 | 0.260 | 0.69 | 0.290 | 0.71 | |
| 0.287 | 0.69 | 0.220 | 0.73 | 0.253 | 0.67 | 0.204 | 0.77 | ||
| 0.373 | 0.67 | 0.303 | 0.72 | 0.192 | 0.66 | 0.253 | 0.75 | ||
| State of landslide | 0.289 | 0.66 | 0.299 | 0.65 | 0.563 | 0.65 | 0.421 | 0.87 | |
| 0.393 | 0.70 | 0.369 | 0.68 | 0.386 | 0.60 | 0.574 | 0.85 | ||
Correlation coefficient between periodic term displacement and influencing factors.
3.4 Displacement prediction results and analysis
3.4.1 Trend displacement prediction
The displacement of a landslide is influenced by topography, geological structure, and rock and soil properties. The displacement trend exhibits a monotonically increasing curve over time. While polynomial functions are frequently used in existing research to fit the trend displacement sequence, it may be necessary to perform piecewise fitting due to differences in deformation characteristics across different stages. This is because a single function often fails to fit the entire trend displacement curve. This paper presents a single-factor CNN-BiLSTM-Attention model for predicting trend item displacement. The model takes the displacement values of the previous month, the first 2 months, the first 3 months, the displacement change value of the previous month and the change value of the previous 2 months as input. The prediction results are presented in Figure 15 which show that monitoring points ZG118 and XD01 have R2 values of 0.995 and 0.999, respectively, with corresponding RMSE values of 3.195 and 6.573.
FIGURE 15
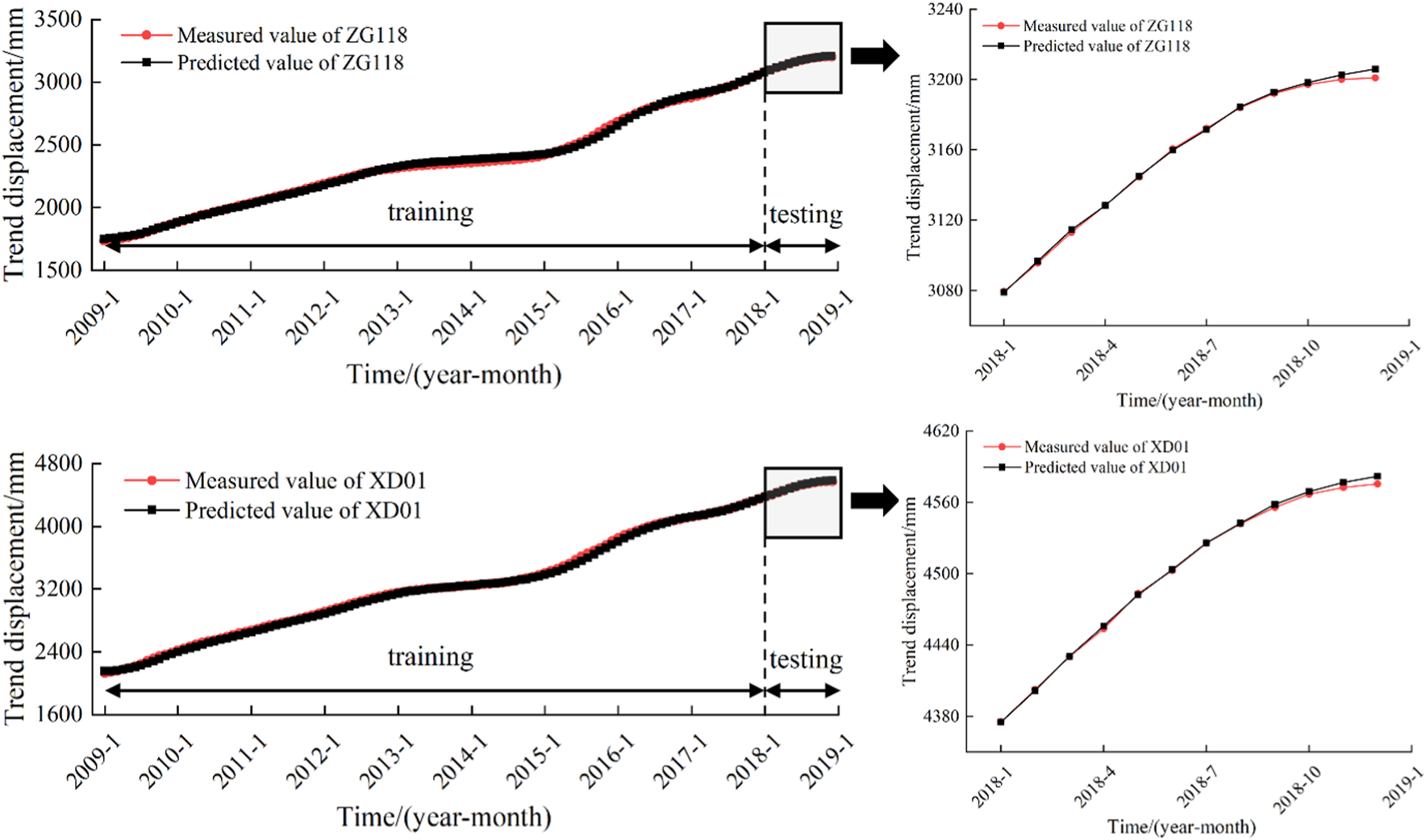
Displacement prediction results of trend items.
3.4.2 Period displacement prediction
In this paper, the factor sequence was selected based on a MIC value greater than 0.25 and a GRA value greater than 0.60. We conducted multiple selections and trial calculations to ensure complete in our final selection. The periodic term displacement sequence and the low-frequency influencing factor sequence were chosen and will be used as input for the prediction model. A multi-factor CNN-BiLSTM-Attention model was constructed for training and prediction. The predictive outputs for this model are showcased in Figure 16, which show that monitoring points ZG118 and XD01 have R2 values of 0.994 and 0.995, respectively, with corresponding RMSE values of 1.670 and 1.798.
FIGURE 16
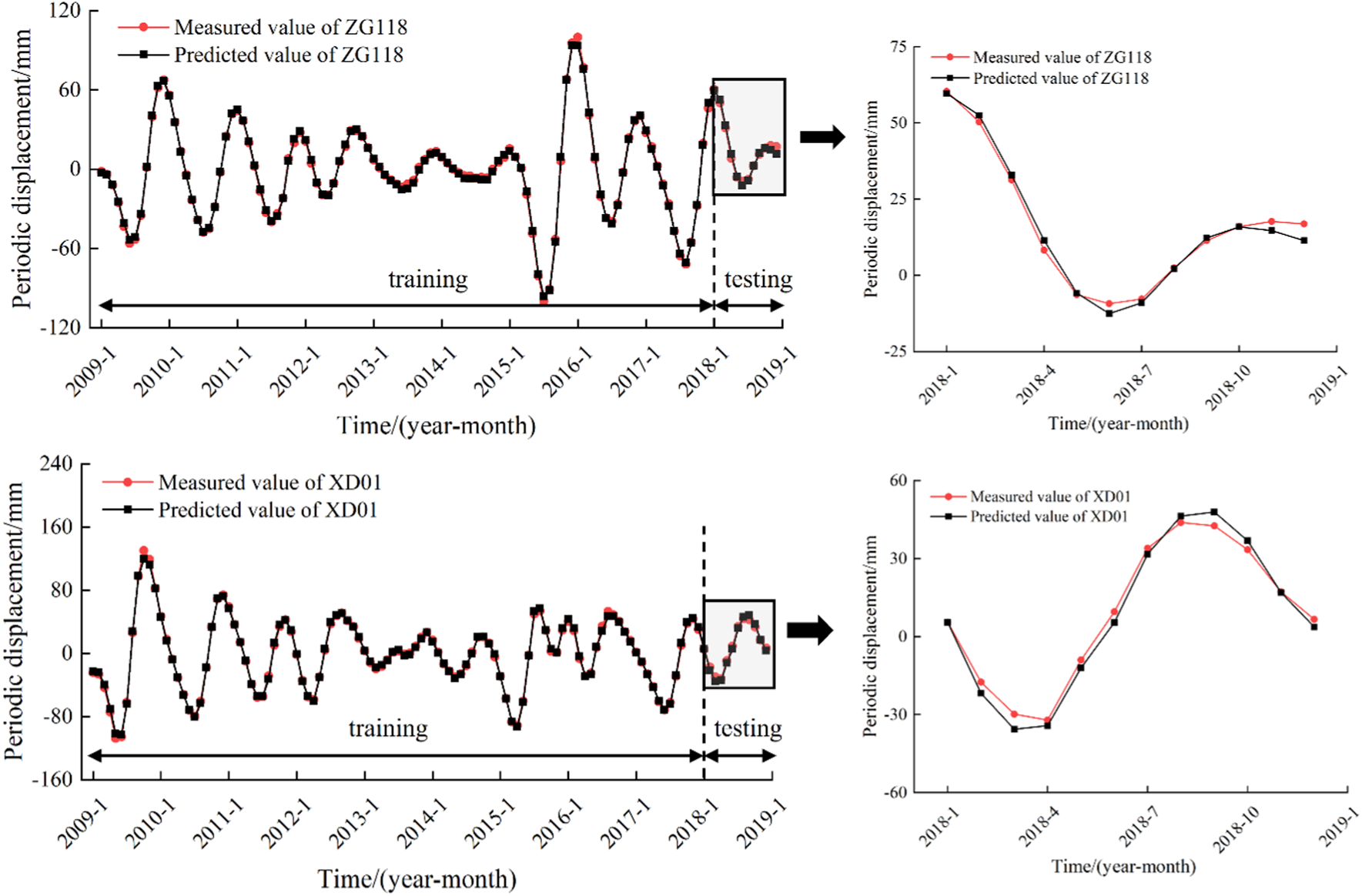
Prediction results of periodic term displacement.
3.4.3 Random term displacement prediction
In this study, factors with a MIC value exceeding 0.25 and a GRA value above 0.60 were chosen from the random term displacement sequence and the high-frequency influencing factor sequence. These factors served as inputs for the multi-factor CNN-BiLSTM-Attention model, which was utilized for training and forecasting. The predictive outputs for this model are showcased in Figure 17; they demonstrate an R2 value of 0.723 and an RMSE value of 4.296 at monitoring point ZG118, alongside an R2 value of 0.612 and an RMSE value of 5.472 at monitoring point XD01.
FIGURE 17
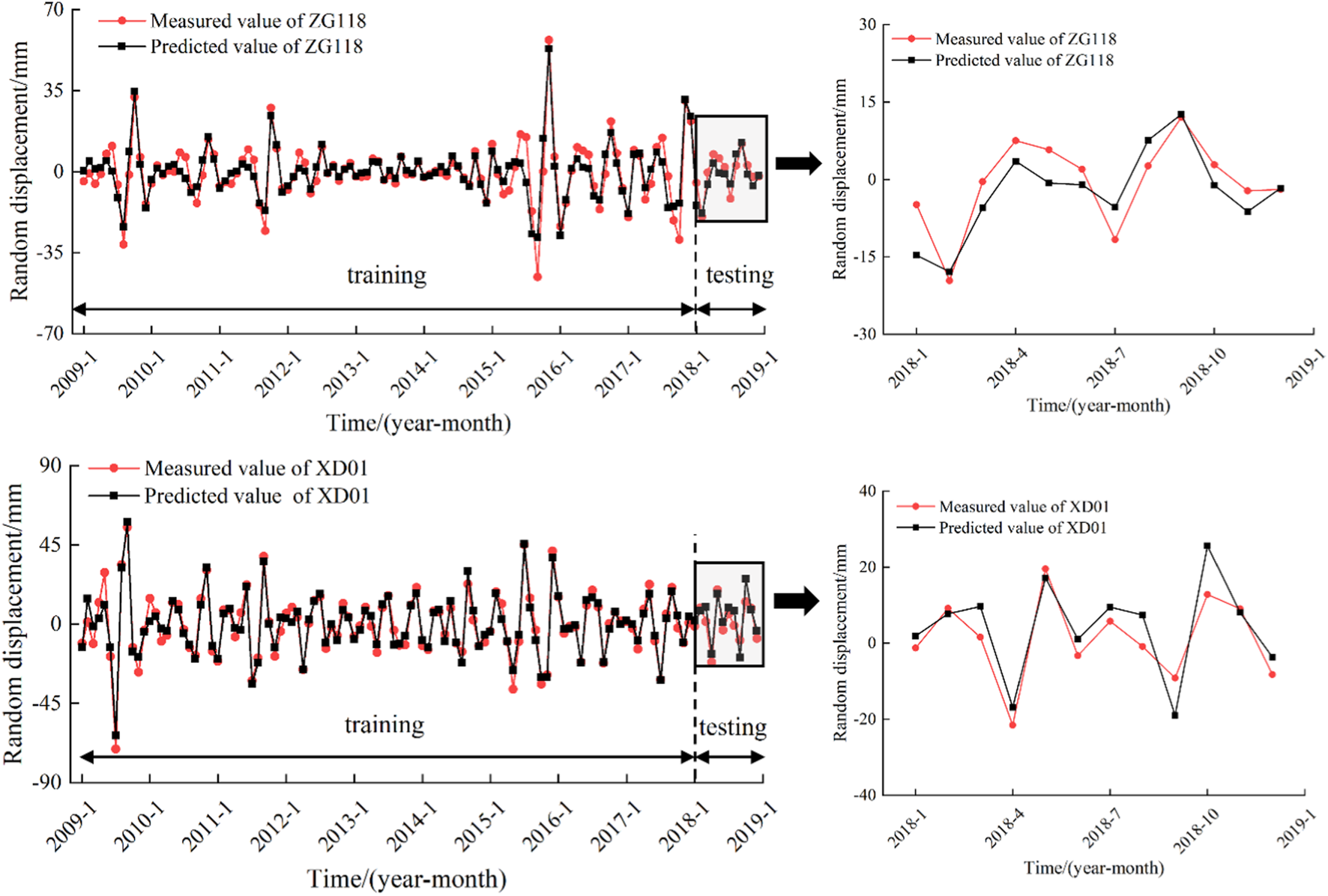
Displacement prediction results of random terms.
3.4.4 Cumulative displacement prediction
By summing the prediction outcomes of trend term displacement, periodic term displacement, and random term displacement in accordance with time series summation principles, cumulative predictions for landslide displacement are derived. These results are illustrated in Figure 18, exhibiting R2 values of 0.975 for monitoring point ZG118 and 0.988 for XD01. Correspondingly, the RMSE values are reported as 12.458 mm for ZG118 and 9.579 mm for XD01. Such high R2 values alongside low RMSE values attest to the model’s robust prediction accuracy, thereby reaffirming its efficacy in forecasting landslide events.
FIGURE 18
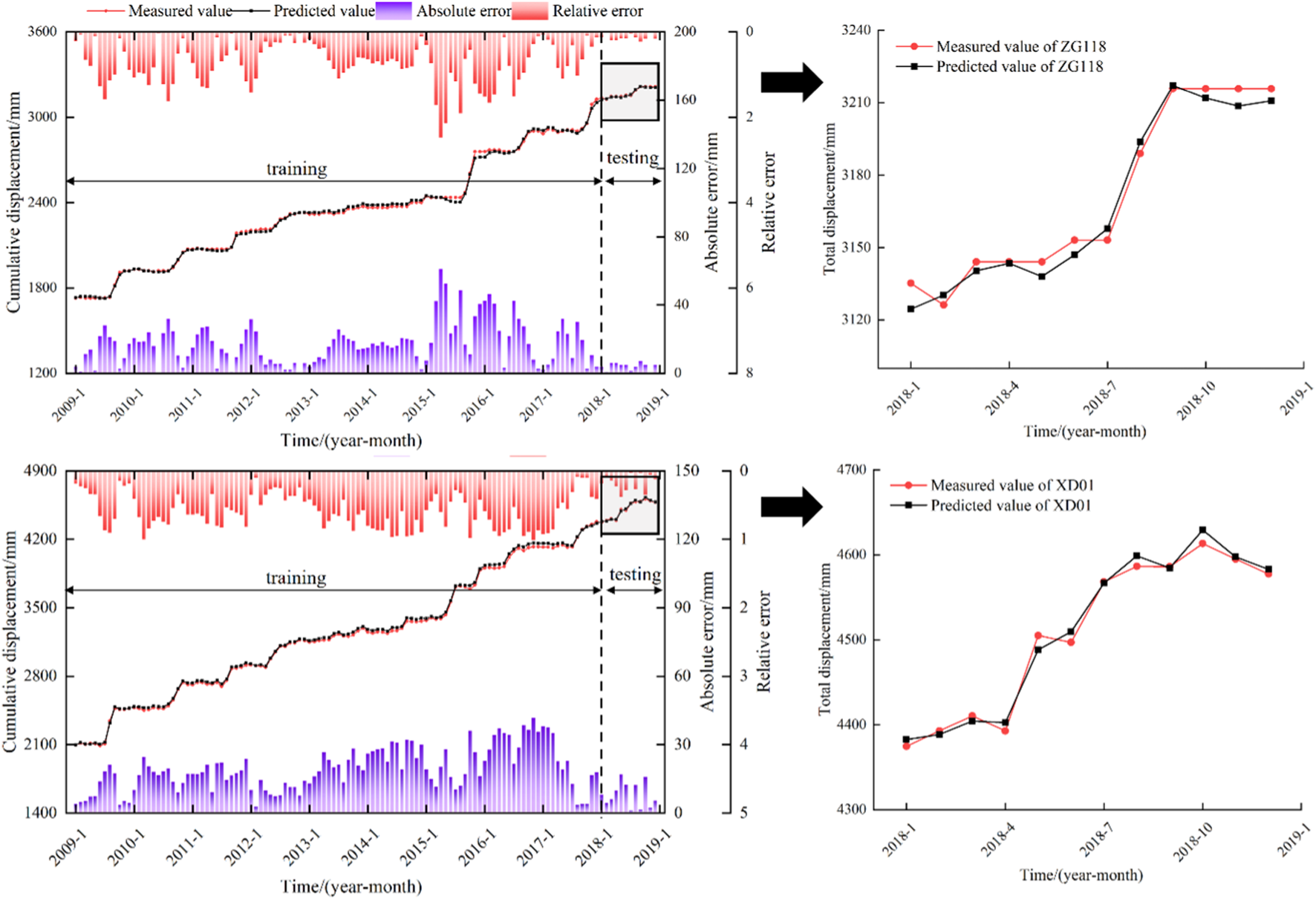
Cumulative displacement prediction results.
3.5 Comparative analysis
3.5.1 Selection of impact factors
To enhance the predictive performance, this research adopts several models CNN-BiLSTM-Attention, GRA-CNN-BiLSTM-Attention, MIC-CNN-BiLSTM-Attention, and (MIC- GRA)-CNN-BiLSTM-Attention for the prediction and comparative analysis of the two components of landslide displacement under uniform conditions. The prediction results of various influencing factor selection methods are shown in Table 4.
TABLE 4
| Models | Periodic term displacement | Random term displacement | ||||||
|---|---|---|---|---|---|---|---|---|
| ZG118 | XD01 | ZG118 | XD01 | |||||
| RMSE/mm | R2 | RMSE/mm | R2 | RMSE/mm | R2 | RMSE/mm | R2 | |
| CNN-BiLSTM-Attention | 6.517 | 0.901 | 7.024 | 0.911 | 7.015 | 0.483 | 9.561 | 0.323 |
| GRA-CNN-BiLSTM-Attention | 5.646 | 0.928 | 6.854 | 0.930 | 5.258 | 0.585 | 8.404 | 0.332 |
| MIC-CNN-BiLSTM-Attention | 5.036 | 0.943 | 6.854 | 0.930 | 4.478 | 0.699 | 8.063 | 0.385 |
| (MIC-GRA)-CNN-BiLSTM-Attention | 1.670 | 0.994 | 1.798 | 0.995 | 4.296 | 0.723 | 5.472 | 0.612 |
Comparison of prediction performances of the CNN-BiLSTM-Attention model under different inputs.
From Table 4, it can be deduced that using the GRA algorithm or MIC algorithm effectively selects influencing factors. The predictive results indicate that the models combined with these two algorithms exhibit higher precision, which reflects the role of both algorithms in selecting influencing factors. Moreover, the model that utilizes the MIC- GRA evaluation method to select related influencing factors achieves the highest precision in prediction results, indirectly showcasing the superiority of the MIC- GRA algorithm. This is because when the MIC- GRA algorithm is integrated with the model, it can select influencing factors from two different perspectives, eliminating data with low relevance and retaining high-relevance influencing factors. Due to the input of effective influencing factors, the predictive accuracy of the model combined with the MIC- GRA algorithm is enhanced.
3.5.2 Comparative analysis of periodic displacement prediction
The predictive results of the CNN-BiLSTM-Attention model were compared with the static machine learning models such as the BP Neural Network and SVM models, and the deep learning models’ predictions such as LSTM, BiLSTM, CNN-BiLSTM, all of which are widely used in landslide displacement prediction. The predictive results of each model are presented in Table 5.
TABLE 5
| Models | ZG118 | XD01 | ||
|---|---|---|---|---|
| RMSE/mm | R2 | RMSE/mm | R2 | |
| (MIC-GRA)-BP | 11.476 | 0.796 | 10.932 | 0.848 |
| (MIC-GRA)-SVM | 12.170 | 0.695 | 11.910 | 0.786 |
| (MIC-GRA)-LSTM | 5.341 | 0.931 | 6.862 | 0.915 |
| (MIC-GRA)-BiLSTM | 3.913 | 0.961 | 3.717 | 0.967 |
| (MIC-GRA)-CNN-BiLSTM | 3.003 | 0.972 | 2.912 | 0.975 |
| (MIC-GRA)-CNN-BiLSTM-Attention | 1.670 | 0.994 | 1.798 | 0.995 |
Comparison of periodic term displacement prediction models.
Table 5 details the predictive outcomes, illustrating that the CNN-BiLSTM-Attention model achieves superior accuracy in forecasting periodic displacement when contrasted with the standalone BP and SVM models, which are inherently static. This improvement is attributed to the dynamic features of the BiLSTM model, which is adept at processing the dynamic nature of landslide displacement sequences via its bidirectional training capability. Concurrently, the convolutional neural networks and attention mechanisms facilitate the distillation of pertinent information, simplifying data complexity and thus enhancing accuracy for periodic terms. This conclusion is further reinforced through the comparative analysis with the LSTM, BiLSTM, and CNN-BiLSTM models. Collectively, the evidence indicates that the prediction accuracy of deep learning models eclipses that of traditional machine learning models, and that combined models deliver improved results over singular models.
3.5.3 Random term displacement prediction model comparative analysis
The predictive efficacy of the CNN-BiLSTM-Attention model in forecasting landslide displacement is assessed by comparing it with the LSTM, BiLSTM, and CNN-BiLSTM models. Results of this comparative analysis are delineated in Table 6.
TABLE 6
| Models | ZG118 | XD01 | ||
|---|---|---|---|---|
| RMSE/mm | R2 | RMSE/mm | R2 | |
| (MIC-GRA)-LSTM | 8.506 | 0.309 | 13.587 | 0.252 |
| (MIC-GRA)-BiLSTM | 8.331 | 0.357 | 12.835 | 0.267 |
| (MIC-GRA)-CNN-BiLSTM | 8.054 | 0.448 | 10.212 | 0.312 |
| (MIC-GRA)-CNN-BiLSTM-Attention | 4.296 | 0.723 | 5.472 | 0.612 |
Comparison of random item displacement prediction models.
Table 6 illustrates the superior prediction accuracy of the CNN-BiLSTM-Attention model compared to its LSTM, BiLSTM, and CNN-BiLSTM counterparts for random item displacement. This heightened accuracy is ascribed to the model’s robust handling of the random item displacement sequence, characterized by its high frequency and considerable volatility. The CNN-BiLSTM-Attention model excels beyond traditional LSTM and BiLSTM models, particularly in capturing nonlinear information embedded within time series data. This model adeptly retains vital information by employing the bidirectional training capabilities of BiLSTM. In addition, the attention mechanism’s capacity to assign differentiated weights to disparate data points streamlines the process, culminating in the effective and precise training of random item displacement sequences.
4 Discussion
Accurately assessing reservoir landslide deformation is vital for averting landslide calamities, given the considerable nonlinearity and intricacy inherent in landslide displacement and its causative factors. This study introduces a data-driven framework comprising a deep learning ensemble model twinned with an optimal variational mode decomposition, designed to forecast future landslide movements. This framework’s benefits are twofold. First, it applies the SSA-VMD algorithm to decompose the landslide displacement sequence and its influencing factors, thereby improving the time series displacement prediction model’s efficacy. Second, this trailblazing research harnesses a CNN-BiLSTM-attention ensemble model to anticipate reservoir landslide shifts. This deep learning ensemble model synergizes the strengths of individual models, providing enhanced capability in feature extraction from datasets marked by nonlinearity and complexity.
While various displacement decomposition methods offer substantial decomposition effects, it is essential to highlight that the SSA-VMD model introduced in this study distinguishes itself by its ability to accurately capture random term displacement. Nevertheless, the current limitation in making more precise predictions stems from the inadequate availability of monitoring data on relevant influencing factors.
Moreover, existing landslide displacement monitoring data are exclusively sourced from slopes already exhibiting deformation. The inherent nonlinearity of slope characteristics complicates the task of forecasting landslide deformation accurately using historical, static data. Future research endeavors must focus on incorporating real-time monitoring data into predictive models. Such integration would not only enhance the precision and promptness of the models’ predictions but also render them more effective for early warning systems.
Prediction methods based on single-point displacement remain central within the domain of landslide deformation research. However, the inherent uncertainty in landslide systems makes some degree of error in traditional point prediction methods inevitable. To address this, our study applies prediction intervals to improve the accuracy of landslide displacement forecasts [62]. Although the current focus is primarily on reservoir landslides influenced by hydrological factors, the scope of the predictive model should be expanded. Future developments could include additional influencing factors such as soil mechanics and seismic activity, paving the way for a more generalized displacement prediction model.
5 Conclusion
In this study, we introduce the (SSA-VMD)-(CNN-BiLSTM-Attention) model for predicting landslide displacement, which synergizes the SSA-VMD technique with the CNN-BiLSTM-Attention model applied to landslide displacement sequences and their influencing factors. Employed in the study of Baishuihe landslide’s displacement prediction, the research leads to the following conclusion:
(1) In the VMD model, the SSA algorithm is utilized to dynamically optimize parameters, reducing the influence of subjective assumptions and avoiding the laborious process of manual parameter tuning. When designing the innovative fitness functions, the reliability and decomposition efficiency of the VMD model are enhanced by adopting sample entropy and root mean square error.
(2) The SSA-VMD algorithm allows for the extraction of subsequences of landslide displacement and subsequences of influencing factors, enabling an in-depth analysis of the relationships between landslide displacement, rainfall, reservoir water levels, and the state of landslide displacement. The correlations between the displacement subsequences and influencing factors are calculated using the MIC and GRA methods. Furthermore, the integration of MIC-GRA as a fusion technique is utilized for selecting significant influencing factors for landslide displacement. The results indicate that using influencing factors selected by the MIC-GRA method as input data can significantly enhance prediction accuracy, demonstrating that this method can improve the effectiveness and efficiency of the input data. By eliminating less relevant data, the predictive accuracy of the model is increased.
(3) The study introduces a novel integrated model, CNN-BiLSTM-Attention, designed for training and predicting landslide displacement. This composite model combines the strengths of CNN, BiLSTM, and the Attention mechanism to adeptly extract essential information from landslide displacement data. The CNN component handles feature extraction, while BiLSTM processes both past and future data, and the Attention mechanism assigns variable weights to the data, thereby optimizing the prediction process for landslide displacement. Empirical results suggest that the proposed model surpasses both single and dual combined models in prediction accuracy. The pronounced accuracy of this model better captures the step process of landslides and serves as a foundational study for the prediction and early warning of similar landslide events.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
RW: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Writing–original draft, Writing–review and editing. YL: Data curation, Formal Analysis, Investigation, Methodology, Supervision, Writing–review and editing. YY: Data curation, Formal Analysis, Methodology, Writing–review and editing. WX: Conceptualization, Funding acquisition, Methodology, Writing–review and editing. YW: Data curation, Methodology, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the National Natural Science Foundation of China (No. 51939004).
Acknowledgments
We thank the National Field Observation and Research Station of Landslides in the TGRA of Yangtze River for their help in providing monitoring data for this study.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
PengLNiuRQWuT. Time series analysis and support vector machine for landslide displacement prediction. J Zhejiang University(Engineering Science) (2013) 47(09):1672–9. 10.3785/j.issn.1008-973X.2013.09.024
2.
XuQHuangRQLiXZ. Research progress in time forecast and prediction on of landslides. Adv Earth Sci (2004) 19(03):478–83. 10.11867/j.issn.1001-8166.2004.03.0478
3.
LiHj.HeYSXuQDengJHLiWLWeiYet alSematic segmentation of loess landslides with STAPLE mask and fully connected conditional random field. Landslides (2023) 20(2):367–80. 10.1007/s10346-022-01983-8
4.
XuFWangYDuJYeJ. Study of displacement prediction model of landslide based on time series analysis. Chin J Rock Mech Eng (2011) 30(04):746–51.
5.
ZhangJYinKLWangJJHuangMF. Displacement prediction of Baishuihe landslide based on time series and PSO-SVR model. Chin J Rock Mech Eng (2015) 34(02):382–91. 10.13722/j.cnki.jrme.2015.02.017
6.
ZhouCYinKLCaoYAhmedB. Application of time series analysis and PSO-SVM model in predicting the Bazimen landslide in the Three Gorges Reservoir. Eng Geology (2016) 204:108–20. 10.1016/j.enggeo.2016.02.009
7.
LiuYLYinKLWangYWangW. Study of landslide deformation prediction based on EMD and neural network. Saf Environ Eng (2013) 20(04):14–7.
8.
XuSLNiuRQ. Displacement prediction of Baijiabao landslide based on empirical mode decomposition and long short term memory neural network in Three Gorges area, China. Comput Geosci (2018) 111:87–96. 10.1016/j.cageo.2017.10.013
9.
ZhangKZhangKBaoRLiuXHQiFF. Intelligent prediction of landslide displacements based on optimized empirical mode decomposition and K-Mean clustering. Rock Soil Mech (2021) 42(01):211–23. 10.16285/j.rsm.2020.1300
10.
DengDMLiangY. Displacement prediction method based on ensemble empirical mode decomposition and support vector machine regression— a case of landslides in Three Gorges Reservoir area. Rock Soil Mech (2017) 38(12):3660–9. 10.16285/j.rsm.2017.12.034
11.
WangZHNieWXuHHJianWB. Prediction of landslide displacement based on EEMD-Prophet-LSTM. J Univ Chin Acad Sci (2023) 40(04):514–22. 10.7523/j.ucas.2022.002
12.
DuHSongDQChenZShuHPGuoZZ. Prediction model oriented for landslide displacement with step-like curve by applying ensemble empirical mode decomposition and the PSO-ELM method. J Clean Prod (2020) 270:122248. 10.1016/j.jclepro.2020.122248
13.
ZhangKXNiuRQHuYJWuXL. Landslide displacement prediction based on wavelet transform and external cause. J China Univ Mining& Tech (2017) 46(04):924–31. 10.13247/j.cnki.jcumt.000716
14.
ZhouCYinKCaoYIntrieriEAhmedBCataniF. Displacement prediction of step-like landslide by applying a novel kernel extreme learning machine method. Landslides (2018) 15:2211–25. 10.1007/s10346-018-1022-0
15.
ZhouCYinKLHuangFM. Application of the chaotic sequence WA-ELM coupling model in landslide displacement prediction. Rock Soil Mech (2015) 36(09):2674–80. 10.16285/j.rsm.2015.09.030
16.
LuoHYJangYNXuQTangB. Displacement prediction of reservoir bank landslide based on optimal decomposition mode and GRU model. Geomatics Inf Sci Wuhan Univ (2023) 48(05):702–9. 10.13203/j.whugis20200610
17.
JiangYHWangWZhouLFWangRBLiuSP. Research on dynamic prediction model of landslide displacement based on particle swarm optimization-variational mode decomposition, nonlinear autoregressive neural network with exogenous inputs and gated recurrent unit. Rock Soil Mech (2022) 43(S1):601–12. 10.16285/j.rsm.2021.0247
18.
XingYYueJPChenCQinYLHuJ. A hybrid prediction model of landslide displacement with risk-averse adaptation. Comput Geosci (2020) 141:104527. 10.1016/j.cageo.2020.104527
19.
LiLWWuYPMiaoFSLiaoKZhangLF. Displacement prediction of landslides based on variational mode decomposition and GWO-MIC-SVR model. Chin J Rock Mech Eng (2018) 37(06):1395–406. 10.13722/j.cnki.jrme.2017.1508
20.
XuFFanCJXuXJLiLNiJJ. Displacement prediction of landslide based on variational mode decomposition and AMPSO-SVM coupling model. J Shanghai Jiaotong Univ (2018) 52(10):1388–95+1416. 10.16183/j.cnki.jsjtu.2018.10.030
21.
ZhouCYinKLCaoYHuangFM. Displacement Prediction of step-like Landslide Based on the response of inducing factors and support vector machine. Chin J Rock Mech Eng (2015) 34(S2):4132–9. 10.13722/j.cnki.jrme.2014.0290
22.
YangFXuQFanXMYeW. Prediction of landslide displacement time series based on support vector regression machine with artificial bee colony algorithm. J Eng Geology (2019) 27(04):880–9. 10.13544/j.cnki.jeg.2017-256
23.
DuJYinKLChaiB. Study of displacement prediction model of landslide based on response analysis of inducing factors. Chin J Rock Mech Eng (2009) 28(09):1783–9.
24.
WangRBZhangKWangWMengYDYangLLHuanHF, Hydrodynamic landslide displacement prediction using combined extreme learning machine and random search support vector regression model. Eur J Environ Civ Eng, 27, 2020, 2345–57. 10.1080/19648189.2020.1754298
25.
LiHj.XuQHeYSDengJH. Prediction of landslide displacement with an ensemble-based extreme learning machine and copula models. Landslides (2018) 15:2047–59. 10.1007/s10346-018-1020-2
26.
WangYk.TangHMHuangJSWenTMaJWZhangJR. A comparative study of different machine learning methods for reservoir landslide displacement prediction. Eng Geology (2022) 298:106544. 10.1016/j.enggeo.2022.106544
27.
YaoWLianCChengL. A dynamic probabilistic model for landslide displacement prediction. Hydrogeology Eng Geology (2015) 42(05):134–9+148. 10.16030/j.cnki.issn.1000-3665.2015.05.22
28.
YaoWLianC. Prediction of landslide displacement based on reservoir computing and fractal interpolation. J Yangtze River Scientific Res Inst (2014) 31(12):43–8. 10.3969/j.issn.1001-5485.2014.12.009
29.
YangBBYinKLDuJ. A model for predicting landslide displacement based on time series and long and short term memory neural network. Chin J Rock Mech Eng (2018) 37(10):2334–43. 10.13722/j.cnki.jrme.2018.0468
30.
XingYYueJPChenC. Interval estimation of landslide displacement prediction based on time series decomposition and long short-term memory network. IEEE Access (2020) 8:3187–96. 10.1109/access.2019.2961295
31.
YangBBYinKLLacasseSLiuZQ. Time series analysis and long short-term memory neural network to predict landslide displacement. Landslides (2019) 16:677–94. 10.1007/s10346-018-01127-x
32.
GravesAJaitlyN. Towards end-to-end speech recognition with recurrent neural networks. In: 31st international conference on machine learning. Beijing, China: W&CP (2014). p. 1764–72.
33.
LinZJiYLiangWSunX. Landslide displacement prediction based on time-frequency analysis and LMD-BiLSTM model. Mathematics (2022) 10(13):2203. 10.3390/math10132203
34.
ZhangKZhangKCaiCLiuWXieJ. Displacement prediction of step-like landslides based on feature optimization and VMD-Bi-LSTM: a case study of the Bazimen and Baishuihe landslides in the Three Gorges, China. Bull Eng Geology Environ (2021) 80:8481–502. 10.1007/s10064-021-02454-5
35.
NiuQCaoAMChenXYZhouD. Short-term load forecasting based on flower pollination algorithm and BP neural network. Power Syst Clean Energ (2020) 36(10):28–32.
36.
LiuDWeiXWangWQYeJHRengJ. Short-term wind power prediction based on SSA-ELM. Smart Power (2021) 49(06):53–9+123.
37.
NavaLCarraroEReyes-CarmonaCPulieroSBhuyanKRosiAet alLandslide displacement forecasting using deep learning and monitoring data across selected sites. Landslides (2023) 20(10):2111–29. 10.1007/s10346-023-02104-9
38.
LinZJiYSunX. Landslide displacement prediction based on CEEMDAN method and CNN–BiLSTM model. Sustainability (2023) 15(13):10071. 10.3390/su151310071
39.
WangCYLiLMWenZZZhangMYWeiXW. Dynamic prediction of landslide displacement based on time series and CNN-LSTM. Foreign Electron Meas Tech (2022) 41(03):1–8. 10.19652/j.cnki.femt.2103321
40.
ZhuZLRaoYWuYQiJNZhangY. Research progress of attention mechanism in deep learning. J Chin Inf Process (2019) 33(06):1–11.
41.
TangFFTangTJZhuHZHuCMaYLiX. Rainfall landslide deformation prediction based on attention mechanism and Bi-LSTM. Bull Surv Mapp (2022)(09) 74–9+104. 10.13474/j.cnki.11-2246.2022.0267
42.
DragomiretskiyKZossoD. Variational mode decomposition. IEEE Transactions Signal Processing (2013) 62(3):531–44. 10.1109/tsp.2013.2288675
43.
RichmanJSMoormanJR. Physiological time-series analysis using approximate entropy and sample entropy. Am J Physiology-Heart Circulatory Physiol (2000) 278(6):H2039–49. 10.1152/ajpheart.2000.278.6.h2039
44.
XueJXResearch and application of A novel swarm intelligence optimization technique: sparrow search algorithm. China: Donghua University (2021).
45.
KraskovAStögbauerHGrassbergerP. Estimating mutual information. Phys Rev E (2004) 69(6):066138. 10.1103/physreve.69.066138
46.
ReshefDNReshefYAFinucaneHKGrossmanSRMcveanGTurnbaughPJet alDetecting novel associations in large data sets. Science (2011) 334(6062):1518–24. 10.1126/science.1205438
47.
GuoZYuBHaoMWangWJiangYZongF. A novel hybrid method for flight departure delay prediction using Random Forest Regression and Maximal Information Coefficient. Aerospace Sci Tech (2021) 116:106822. 10.1016/j.ast.2021.106822
48.
HuangXLuoYPXiaL. An efficient wavelength selection method based on the maximal information coefficient for multivariate spectral calibration. Chemom Intell Lab Syst (2019) 194:103872. 10.1016/j.chemolab.2019.103872
49.
ZhouFYJinLPDongJ. Review of convolutional neural network. Chin J Comput (2017) 40(06):1229–51.
50.
KhanSRahmaniHShahSAABennamounMA guide to convolutional neural networks for computer vision. San Rafael. USA: Morgan and Claypool Publishers (2018).
51.
GravesAMohamedAHintonG. Speech recognition with deep recurrent neural networks. In: Proceedings of International Conference on Acoustics, Speech and Signal Processing Acoustics; 4-10, June 2023; Vancouver, Canada, 6. IEEE (2013). p. 645–6 649.
52.
KhanSFazilMSejwalVKAlsharaMAAlotaibiRMKamalAet alBiCHAT: BiLSTM with deep CNN and hierarchical attention for hate speech detection. J King Saud University-Computer Inf Sci (2022) 34(7):4335–44. 10.1016/j.jksuci.2022.05.006
53.
RenJJWeiHHZouZLHouTTYuanYLShenJQet alUltra-short-term power load forecasting based on CNN-BiLSTM-Attention. Power Syst Prot Control (2022) 50(08):108–16. 10.19783/j.cnki.pspc.211187
54.
KnudsenEI. Fundamental components of attention. Annu Rev Neurosci (2007) 30:57–78. 10.1146/annurev.neuro.30.051606.094256
55.
ZhuYJHeNZhongWKongJM. Physical simulation study of deformation and failure accumulation layer slope caused by intermittent rainfall. Rock Soil Mech (2020) 41(12):4035–44. 10.16285/j.rsm.2020.0318
56.
HeKQGuoLChenWG. Research on displacement dynamic evaluation and forecast model of colluvial landslide induced by rainfall. Chin J Rock Mech Eng (2015) 34(S2):4204–15. 10.13722/j.cnki.jrme.2014.1010
57.
WangRBXiaRXuWYWangHLQiJ. Study on physical simulation of rainfall infiltration process of landslide accumulation body. Adv Eng Sci (2019) 51(04):47–54. 10.15961/j.jsuese.201900295
58.
LiuXXXiaYYZhangXSGuoRQ. Effects of drawdown of reservoir water level on landslide stability. Chin J Rock Mech Eng (2005) 24(8):1439–44.
59.
TanLYHuangRQPeiXJ. Deformation characteristics and inducing mechanisms of a super-large bedding rock landslide triggered by reservoir water level decline in Three Gorges Reservoir area. Chin J Rock Mech Eng (2021) 40(02):302–14. 10.13722/j.cnki.jrme.2020.0728
60.
LiuZGuoDLacasseSLiJYangBChoiJ. Algorithms for intelligent prediction of landslide displacements. J Zhejiang University-SCIENCE A (2020) 21(6):412–29. 10.1631/jzus.a2000005
61.
LiuYXuCHuangBRenXLiuCChenBHandZet alLandslide displacement prediction based on multi-source data fusion and sensitivity states. Eng Geology (2020) 271:105608. 10.1016/j.enggeo.2020.105608
62.
WangYKTangHMWenTMaJW. A hybrid intelligent approach for constructing landslide displacement prediction intervals. Appl Soft Comput (2019) 81:105506. 10.1016/j.asoc.2019.105506
Summary
Keywords
landslide displacement prediction model, variational mode decomposition, maximal information coefficient, bidirectional long short term memory network, attention mechanism
Citation
Wang R, Lei Y, Yang Y, Xu W and Wang Y (2024) Dynamic prediction model of landslide displacement based on (SSA-VMD)-(CNN-BiLSTM-attention): a case study. Front. Phys. 12:1417536. doi: 10.3389/fphy.2024.1417536
Received
15 April 2024
Accepted
14 May 2024
Published
11 June 2024
Volume
12 - 2024
Edited by
Zhenqiu Shu, Kunming University of Science and Technology, China
Reviewed by
Huajin Li, Chengdu University, China
Kang Liao, Southwest Jiaotong University, China
Updates
Copyright
© 2024 Wang, Lei, Yang, Xu and Wang.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rubin Wang, rbwang_hhu@foxmail.com; Yipeng Lei, yipenglei@163.com; Yue Yang, youngy0528@163.com
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.